A Joint Linear Reconstruction for Multi-Shot Diffusion Weighted non-CPMG Fast Spin Echo With Full Signal

Abstract

Purpose:

Diffusion weighted Fast Spin Echo (DW-FSE) is a promising approach for distortionless DW imaging that is robust to system imperfections such as eddy currents and off-resonance. Due to non-Carr-Purcell-Meiboom-Gill (CPMG) magnetization, most DW-FSE sequences discard a large fraction of the signal ($\sqrt{2}-2\times$), reducing SNR efficiency compared to DW-EPI. The full FSE signal can be preserved by quadratically incrementing the transmit phase of the refocusing pulses, but this method of resolving non-CPMG magnetization has only been applied to single-shot DW-FSE due to challenges associated with image reconstruction.

We present a joint linear reconstruction for multi-shot quadratic phase increment data that addresses these challenges and corrects ghosting from both shot-to-shot phase and intra-shot signal oscillations. Multi-shot imaging reduces T2 blur and joint reconstruction of shots improves g-factor performance. A thorough analysis on the condition number of the proposed linear system is described.

Methods:

A joint multi-shot reconstruction is derived from the non-CPMG signal model. Multi-shot quadratic phase increment DW-FSE was tested in a standardized diffusion phantom and compared to single-shot DW-FSE and DW-EPI in vivo in the brain, cervical spine, and prostate. The pseudo multiple replica technique was applied to generate g-factor and SNR maps.

Results:

The proposed joint shot reconstruction eliminates ghosting from shot-to-shot phase and intra-shot oscillations. g-factor performance is improved compared to previously proposed reconstructions, permitting efficient multi-shot imaging. ADC estimates in phantom experiments and in vivo are comparable to those obtained with conventional methods.

Conclusion:

Multi-shot non-CPMG DW-FSE data with full signal can be jointly reconstructed using a linear model.

1 |. INTRODUCTION

Diffusion weighted (DW) imaging is a highly desired contrast for neuroimaging, cancer imaging and treatment evaluation. EPI is the most commonly used readout trajectory for DW imaging, but it suffers from geometric distortions caused by off-resonance. Although multi-shot EPI performs extremely well in areas such as the brain or knee, it fails in regions with air-tissue interfaces or high susceptibility. These applications include: head and neck imaging[1], lung imaging [2], prostate imaging in subjects with hip prostheses or bowel gas[3, 4], subjects with external off-resonance sources such as metal screws [5] or breast biopsy clips and implants, and whole body DWI [6]. Cartesian Fast Spin Echo (FSE) is robust to off-resonance induced distortion and other system imperfections such as gradient delays and eddy currents. The primary challenges with DW-FSE are T2 blurring from long echo trains and maintenance of the Carr-Purcell-Meiboom-Gill (CPMG) condition [7]. The CPMG condition requires that the RF phase of the refocusing pulse be offset 90°from the excitation. If the CPMG condition is violated, magnetization will oscillate in the echo train causing signal loss and ghosting [8]. In DW-FSE, random phase arising from motion-sensitizing diffusion gradients and eddy currents causes the CPMG condition to be broken.

Multiple methods have been developed to resolve non-CPMG artifacts in DW-FSE, each with different tradeoffs. The Alsop method [8] returns non-CPMG magnetization to the longitudinal axis before the refocusing train but reduces the measured signal by a factor of 2×. Diffusion weighted magnetization can be measured through a stimulated echo pathway [9, 10, 11], but this also reduces the signal by a factor of 2×. Both CPMG and non-CPMG components can be preserved in the echo train using the split-echo method [12, 13, 14], but echo spacing is marginally increased and SNR is reduced by a factor of $\sqrt{2}\times$ since the in-phase and out-of-phase components are measured in separate readouts.

Le Roux [15] demonstrated that the full signal can be measured by applying a quadratic phase increment to the transmit phase of the refocusing pulses, which creates an echo train with stable magnitude regardless of the initial magnetization. This method produces an echo train with a stable steady state for refocusing flip angles as low as 120°, but a constant refocusing flip angle of 150°or greater is required to maintain stability during the seven-echo stabilization period used to enter the steady state. Notably, the high flip angle requirement prevents Variable Flip Angle readouts from being applied, which results in significant T2 blurring.

To date, Le Roux’s technique has only been applied to single-shot DW-FSE with long echo trains, further compounding the effects of T2 decay. This is because of the challenges associated with reconstructing data following the Le Roux signal model (henceforth referred to as the non-CPMG model), where the out-of-phase component changes sign after every refocusing pulse. A naive reconstruction of single-shot data obtained by simply applying the Fourier transform will produce an image containing the superposition of the in-phase component and a ghost from the out-of-phase component shifted by FOV/2 in the phase encode direction. These ghosts can be removed by repeating the k_y phase encode for even and odd lines, and adding or subtracting the even/odd echo images [15]. This approach doubles the effective echo spacing and the effect of T2 blur.

Gibbons et al. [16] demonstrated that the FOV/2 ghost can be eliminated by applying SENSE separately to even and odd lines from a single shot as an R_y = 2 problem (referred to as Split-Echo SENSE). The sequence was applied to single-shot diffusion weighted imaging of the abdomen for acquisition of a full volume in a single breath hold. The T2 blur of this method is equivalent to a standard single-shot acquisition. Applying this reconstruction to multi-shot data imposes a large g-factor penalty since the acceleration factor of each subproblem is twice the number of shots (R_y = 4 for 2-shot data after separating even/odd lines).

In this paper, we show that multi-shot DW data following the non-CPMG signal model can be combined with low g-factor penalty [17] using an entirely linear reconstruction if a phase navigator for each shot is available. Low-resolution phase navigators are widely used for correcting multi-shot ghosts from varying shot-to-shot phase [18], and can be obtained by applying parallel imaging to each individual shot as in multiplexed sensitivity encoding (MUSE) [19]. Surprisingly, this phase navigator can be used to correct image artifacts caused by intra-shot oscillations of the out-of-phase component, as well as ghosts from varying shot-to-shot phase. This formulation has improved g-factor performance compared to Split-Echo SENSE since data from all shots are jointly used to reconstruct the image. We also show how phase navigators can be estimated from the entirety of the data acquired in a single shot, which improves efficiency since no external phase navigator need be acquired. We present a comprehensive analysis on how the condition number of the proposed linear system differs from conventional phase-navigator based diffusion reconstructions. We validate our method in the ISMRM-NIST breast diffusion phantom [26]. Application in vivo in the brain shows that g-factor can be improved by a factor of 3× compared to Split-Echo SENSE, and T2 blur can be reduced by a factor of 2 – 3× compared to single-shot non-CPMG DW-FSE. We also apply the multi-shot non-CPMG technique to obtain distortionless DW images of the prostate and cervical spine.

2 |. THEORY

2.1|. Multiplexed Sensitivity Encoding

Bulk motion during diffusion gradients impart a random, spatially dependent phase on each voxel. It is assumed that between excitations, magnitude images are registered, and image phase from sources such as off-resonance, and transmit and receiver phase are constant. For multi-shot diffusion acquisitions, each shot draws k-space samples from an image where the image phase is the sum of constant phase sources, eddy currents, and random bulk motion. Naive complex summation of multi-shot data where k-space is undersampled will have aliasing and dropout. Multiplexed Sensitivity Encoding (MUSE) [19] corrects shot-to-shot non-linear phase [18] by estimating low resolution phase navigators from shot images reconstructed with parallel imaging. Although individual shots are highly undersampled, the phase navigator resolution is low enough to compensate for noise amplification from increased g-factor. The phase navigator need not be a diagnostic image: it is only an intermediate value used for image reconstruction. The phase navigators are combined with coil sensitivities in the following block linear system [20]:

$$\left[\begin{array}{c}{S}_1\\ ⋮\\ S_{Ns}\end{array}\right]=A_{\text{MUSE}}M=\left[\begin{array}{ccc}{D}_{1}FC& & \\ & \ddots & \\ & & D_{Ns}FC\end{array}\right]\left[\begin{array}{c}{P}_1\\ ⋮\\ P_{Ns}\end{array}\right]M,$$ (1)

where $M\in {ℂ}^{N\times 1}$ is a vectorized N × 1 image to estimate, P_i is an N × N diagonal matrix representing the phase navigator of the ith shot, C is a block diagonal (N_c · N) × N matrix representing the coil sensitivities applied to each shot, F is a block N × N Fourier transform applied to each coil image, D_i is the sampling pattern of the ith shot, and S_i is the k-space of the ith shot.

2.2 |. Effects of non-CPMG magnetization and the Le Roux Quadratic Phase Increment Signal Model

The DW monopolar pulsed-gradient spin-echo with FSE readout is shown in Figure 1. The Carr-Purcell-Meiboom-Gill (CPMG) condition requires that the axis of rotation of the refocusing pulse be 90°out of phase from the magnetization when two or more refocusing pulses are applied.

FIGURE 1.

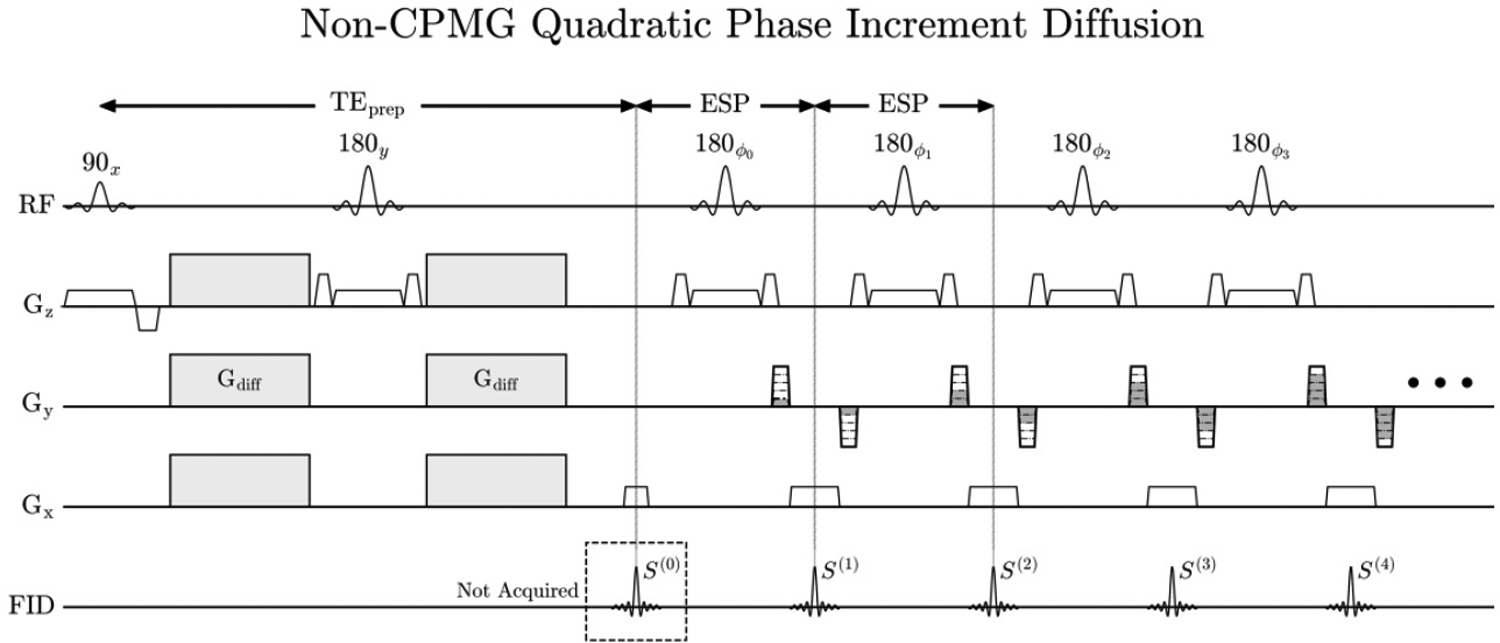
Stejskal-Tanner monopolar pulsed gradient spin echo with an FSE readout. The transmit phase of the first seven refocusing pulses are preset (referred to as the stabilization period), and were designed via optimization by Le Roux to enter the steady state. After the seven echo stabilization period, the transmit and receiver phase both increment quadratically.

Consider a single voxel with signal $S^{(0)}=M_x+j{M}_y=M_0{e}^{j\theta }$ at time TE_prep, where M_x is the in-phase CPMG component, M_y is the out-of-phase non-CPMG component, $M_0=\sqrt{M_x^2+M_y^2}$, and θ = arctan(M_y/M_x), where $M_x,M_y\in ℝ$. In the absence of diffusion gradients, M_y = 0. With diffusion gradients enabled, eddy currents and random bulk motion will create a random, non-zero phase θ that changes between shots. The CPMG and non-CPMG components will vary between shots according to M_x = M₀ cos(θ) and M_y = M₀ sin(θ).

In Figure 1, all magnetization can be made non-CPMG in the absence of diffusion gradients if the rotation axis of the refocusing pulses is ŷ(ϕ_n = 90°for all n). In this scenario, the signal will rapidly decay and oscillate over the echo train if the flip angle deviates from 180°, shown by simulation in Figure 2 A–B. The resulting image is shown in Figure 2 C–D via single-shot images of a grid phantom acquired with a CPMG train applied to globally in-phase magnetization (90_y · 180_x · 180_x…) and globally out-of-phase magnetization (90_y · 180_y · 180_y…). Rapid decay of the echo train in Figure 2D results in only low-resolution k_y lines having signal, which creates severe blurring in the phase encode direction.

FIGURE 2.

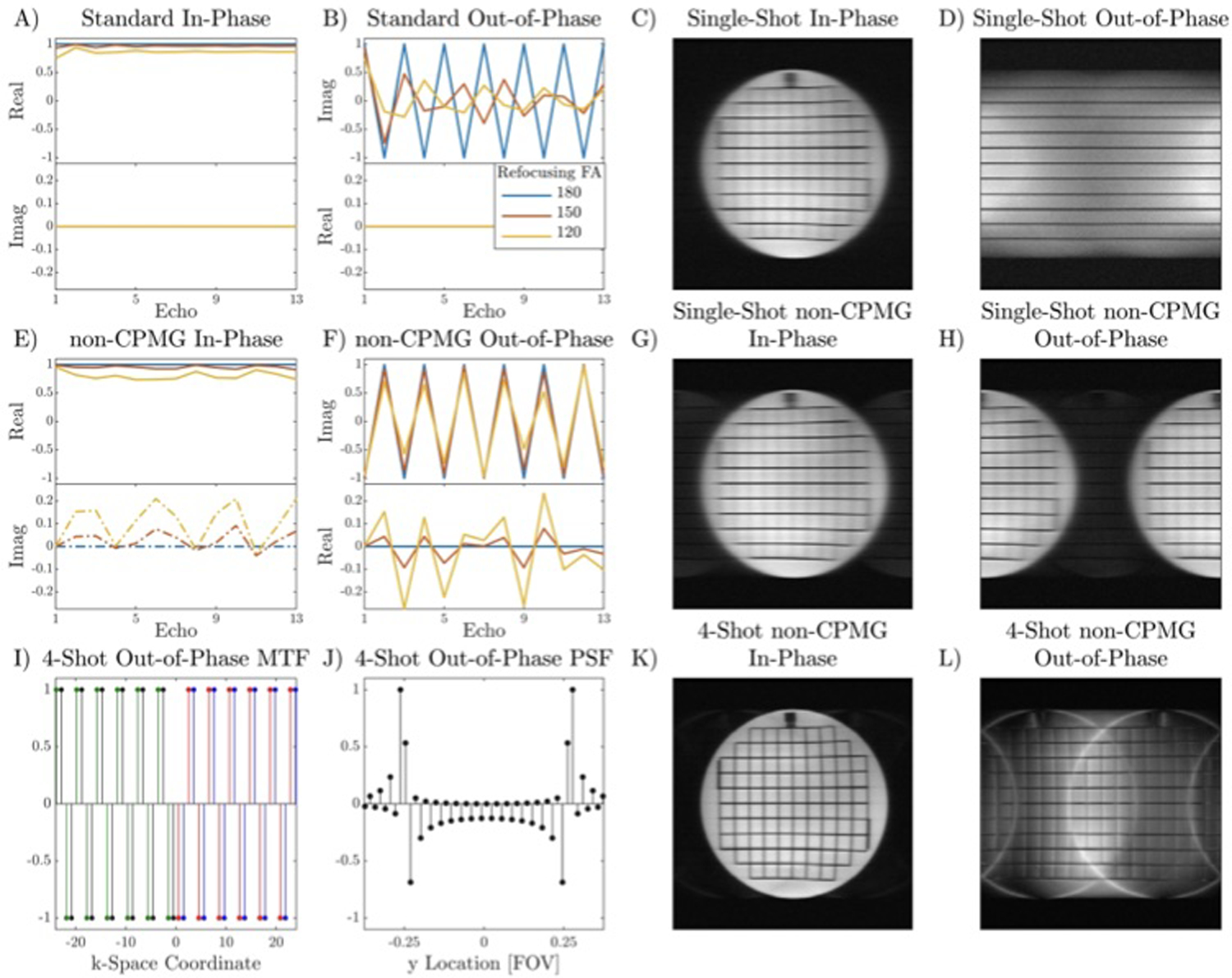
Simulated signal evolution of the first thirteen echoes of CPMG and non-CPMG magnetization and its effects on image formation for two-sided center-out trajectories in a grid phantom with T2 ~ 300 ms, ETL 32. A-B) Signal modulation of in-phase and out-of-phase components without T2 decay for conventional CPMG. Out-of-phase magnetization has stable magnitude if the refocusing flip angle is 180°but will rapidly approach 0 if the flip angle deviates from 180°. C-D) In-phase and out-of-phase images obtained by offsetting the phase of the excitation pulse. Since the refocusing flip angle is not exactly 180°, out-of-phase magnetization rapidly decays, drastically reducing resolution. E-F) Quadratic phase increments maintain a stable echo train amplitude for out-of-phase magnetization if the refocusing flip angle is greater than 150°. G-H) For single-shot non-CPMG, the out-of-phase image is shifted by FOV/2 compared to the in-phase image (minor ghosts are visible due to slight flip angle or phase error). I-J) Center region of k-space modulation transfer function (MTF) and point spread function (PSF) for 4-shot out-of-phase condition. Different colors in the MTF represent different shots. The out-of-phase magnetization has FOV/2 replicas shifted by FOV/4 with multiple harmonics due to the rectangular k-space modulation. A discontinuity of the periodicity at the center of k-space creates an edge filter effect. K-L) Multi-shot in-phase and out-of-phase non-CPMG images.

The non-CPMG sequence achieves a stable echo train regardless of initial phase by quadratically incrementing the transmit phase ϕ_i of the refocusing pulses after a seven echo stabilization period [15]. The magnitude of the signal is stable for refocusing flip angles larger than 150°, but the out-of-phase component changes sign between consecutive echoes. The received signal S^(t) at each echo t for a quadratic-phase-incremented refocusing train of length T, ignoring T2 decay is:

$$\left[\begin{array}{c}{S}^{(1)}\\ S^{(2)}\\ S^{(3)}\\ ⋮\\ S^{(T)}\end{array}\right]=e^{j{\theta }_C}\left[\begin{array}{cc}1& -1\\ 1& 1\\ 1& -1\\ ⋮& ⋮\\ 1& {(-1)}^T\end{array}\right]\left[\begin{array}{c}{M}_x\\ j{M}_y\end{array}\right]$$ (2)

where θ_C is the global receiver phase from the coil sensitivity profile and other system phase sources. This signal evolution is shown for different refocusing flip angles in Figure 2 E–F. For single-shot acquisitions with sequential phase encoding, the out-of-phase magnetization produces an image offset by FOV/2 in the phase encode direction, Figure 2 G–H.

For multi-shot non-CPMG acquisitions, the k-space modulation transfer function (MTF) of out-of-phase magnetization depends on the sampling pattern. For a center-out trajectory where each shot sweeps one side of k-space, the MTF is a square wave. The MTF and PSF are shown for 4 shots in Figure 2 I–J. The 4-shot images for the in-phase and out-of-phase condition are shown in Figure 2 K–L. As expected, T2 blurring is reduced by 4× compared to the single-shot acquisition. Out-of-phase components appear as FOV/2 ghosts with multiple harmonics, offset by FOV/4 in the phase encode direction. Harmonics of the square wave MTF create smearing in the phase encode direction. The sharp transition from positive to negative in the PSF at ±FOV/4 is caused by the discontinuity of periodicity at the center of k-space.

2.3 |. Joint Reconstruction of Multi-Shot Quadratic Phase Increment Data

We now describe a linear reconstruction for multi-shot data following the signal model in Equation 2. Let $M\in {ℂ}^{N\times 1}$ represent the magnetization of a 1D object, and assume that an estimate of the magnetization phase at TE_prep is available for all voxels and shots, given by θ₁ … θ_Ns which are N × N diagonal matrices. The data for the ith shot is:

$$\left[\begin{array}{c}{S}_{ie}\\ S_{io}\end{array}\right]=\left[\begin{array}{cc}{D}_{ie}FC& 0\\ 0& D_{io}FC\end{array}\right]\left[\begin{array}{cc}{I}_N& I_N\\ I_N& -I_N\end{array}\right]\left[\begin{array}{c}\text{cos}\left({\theta }_i\right)\\ j\text{\hspace{0.17em}sin}\left({\theta }_i\right)\end{array}\right]M,$$ (3)

where D_ie and D_io are wide (N · N_c/2N_s) × (N · N_c) matrices representing the sampling patterns for the even and odd lines of the ith shot, F is a block N × N Discrete Fourier transform matrix applied to each coil image, $C\in {ℂ}^{\left(N\cdot N_c\right)\times N}$ represents the coil sensitivities, and I_N is the N × N identity matrix. The coil sensitivities are assumed to include receive phase and other constant image phase sources such as transmit phase and off-resonance. In this model, magnetization is first split into in-phase and out-of-phase components that are weighted by cos(θ_i) and j sin(θ_i) respectively. In-phase and out-of-phase components are then combined and measured through the SENSE model. Equation 3 resembles the combined phase correction and parallel imaging formulation in Equation 1 where additional spatial weights are cos(θ_i) + j sin(θ_i) and cos(θ_i) − j sin(θ_i). Note that the variable M is complex-valued instead of a magnitude since noise and small errors in the estimation of the coil sensitivities or magnetization phase add a small imaginary component (described in Supporting Information Section 1). Keeping M complex-valued also distinguishes this reconstruction from explicit joint phase and magnitude formulations [21, 22, 23, 24, 25].

Assuming that the phase navigator completely captures all shot-to-shot phase variations and M is constant between shots, the full model incorporating all shots can be obtained by applying Euler’s identity e^jx = cos(x) + j sin(x) to Equation 3 and substituting $P_i=e^{j{\theta }_i}$:

$$\left[\begin{array}{c}{S}_1{}_e\\ S_{1o}\\ ⋮\\ S_{Nse}\\ S_{Ns}{}_o\end{array}\right]=A_{\text{non}–\text{CPMG }}M=\left[\begin{array}{cccc}{D}_{1e}FC& & & \\ & D_{1o}FC& & \\ & & \ddots & \\ & & D_{Nse}FC& \\ & & & D_{Nso}FC\end{array}\right]\left[\begin{array}{c}{P}_1\\ P_1^{*}\\ ⋮\\ P_{Ns}\\ P_{Ns}^{*}\end{array}\right]M,$$ (4)

where * denotes complex conjugation. This linear system is similar to Equation 1 except odd lines are weighted by the complex conjugate of the phase navigator in the forward model. The phase navigator allows for correction of both the random phase between shots and the oscillating out-of-phase component in the echo train. Since this is a linear system, a least squares solution can be used to estimate M.

2.4 |. Estimation of Phase Navigators with Combined-Echo SENSE

We now consider only data acquired in a single shot and describe how parallel imaging can be applied to estimate the absolute phase of the magnetization at time TE_prep. Since the out-of-phase component oscillates between refocusing pulses, even and odd lines could be reconstructed separately using Split-Echo SENSE. However, this doubles the effective undersampling factor of each shot and increases g-factor, which may prevent accurate phase estimation at higher shot counts. Instead, we would like to employ all of the data acquired in a single shot to estimate the phase navigator.

Let Q = M_x + jM_y be a vectorized N × N image where M_x and M_y are the in-phase and out-of-phase components respectively. The linear model incorporating coil sensitivities and oscillating out-of-phase components for a single shot is:

$$\left[\begin{array}{l}{S}_e\hfill \\ S_o\hfill \end{array}\right]=\left[\begin{array}{cc}{D}_{e}FC& 0\\ 0& D_{o}FC\end{array}\right]\left[\begin{array}{c}Q\\ Q^{*}\end{array}\right].$$ (5)

Split-Echo SENSE inverts diagonal elements in this block matrix to estimate Q and Q* independently. By applying the Fourier identity ℱ{C(x, y)Q(x, y)} = S(k_x, k_y) ⇒ ℱ{C*(x, y)Q*(x, y)} = S*(−k_x, −k_y), Equation 5 becomes:

$$\left[\begin{array}{c}{S}_e\\ S_{\mathit{\text{o virtual }}}\end{array}\right]=\left[\begin{array}{c}{D}_{e}FC\\ D_{\mathit{\text{o virtual }}}F{C}^{*}\end{array}\right]Q,$$ (6)

where S_{o virtual} are odd lines that have been flipped about k_x = 0 and k_y = 0, and the sampling mask D_{o virtual} has been adjusted accordingly. The creation of virtual odd echo k-space samples is shown in Figure 3. Note that virtual odd lines are obtained after multiplying the object by C* instead of C. This substitution allows even and odd lines to be used jointly to reconstruct Q and notably differs from the virtual conjugate coils (VCC) concept [27]. Equation 6 does not assume that Q is real, which would prevent estimation of ∠Q, and the number of equations is unchanged. We refer to a reconstruction using Equation 6 as Combined-Echo SENSE.

FIGURE 3.

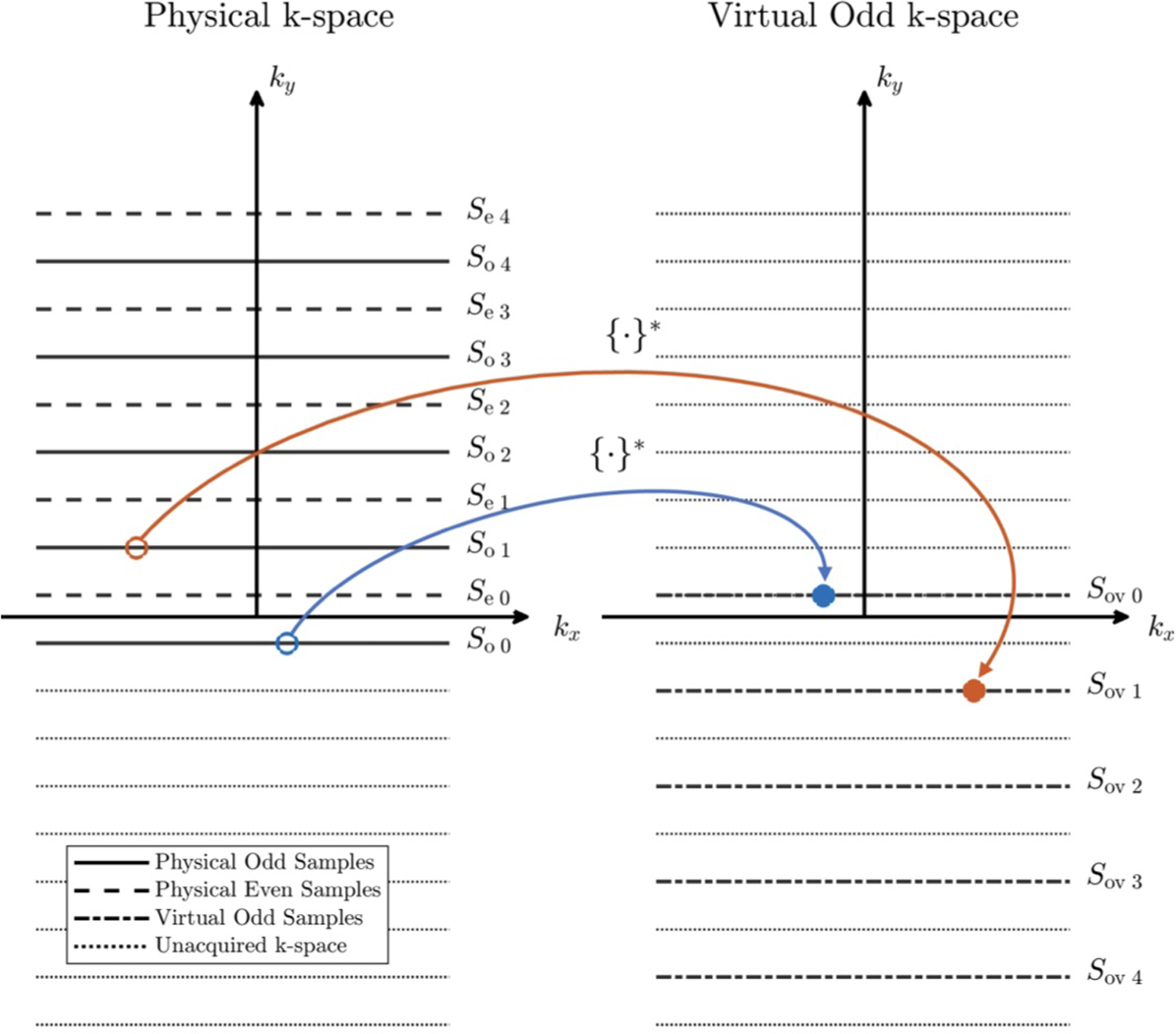
Creation of virtual odd echo k-space from physical odd k-space samples by flipping about k_x = 0 and k_y = 0. {·}* denotes complex conjugation of the value.

2.5 |. Conditioning of Joint Multi-Shot non-CPMG Reconstruction

The condition number of A_non–CPMG with multiple coils is derived in this section. A simplified single coil analysis is presented in Supporting Information Section 2.

Because the multi-shot non-CPMG reconstruction in Equation 4 is a linear system, its noise performance is dependent on its condition number: κ(A_non–CPMG) = σ_max(A_non–CPMG)/σ_min(A_non–CPMG), where σ(A) is the set of singular values of A. A natural question is whether weighting even lines with P, and odd lines with P* affects the conditioning of A_non–CPMG, and how the condition number of A_non–CPMG compares to A_MUSE from Equation 1.

Unfortunately, A_non–CPMG has equal or worse conditioning than A_MUSE for single-shot acquisitions, and this relationship likely extends to multi-shot acquisitions:

$$\kappa \left(A_{\text{non}–\text{CPMG }}\right)\ge \kappa \left(A_{\text{MUSE }}\right)$$ (7)

We show that Equation 7 is true for single-shot non-CPMG acquisitions by comparing the system matrix of an even-odd line combination when both even and odd lines are weighted by P as in standard MUSE, and when even lines are weighted by P and odd lines are weighted by P* as in the non-CPMG model. Analysis of this system matrix also reveals that the worst case conditioning of a single-shot non-CPMG reconstruction is equal to a parallel imaging problem with 2× acceleration:

$$\kappa \left(A_{\text{non}–\text{CPMG }-\text{ CPMG ss }}\right)\le \kappa \left(A_{\text{SENSE }2\times }\right).$$ (8)

Consider a fully sampled single-shot acquisition with uniform Cartesian k-space sampling. Separating even and odd k-space lines creates a FOV/2 replica in image domain. With uniform sampling, the unaliasing problem can be written in image domain as in SENSE [17]. Because odd lines are shifted one k-space sample relative to even lines, the replica of the odd image is weighted by −1. A proof is provided in Supporting Information Section 3. The system of equations to unalias voxels at locations r₁ and r₂, given by $M_{{\text{r}}_1}$ and $M_{{\text{r}}_2}$ with coil sensitivities $C_{{\text{r}}_1},C_{{\text{r}}_2}\in {ℂ}^{N_c\times 1}$ is:

$$\left[\begin{array}{c}{Y}_{{e\text{r }}_1}\\ Y_{{o\text{r }}_1}\end{array}\right]=A_{\text{non}–\text{CPMG ss }}\left[\begin{array}{l}{M}_{{\text{r}}_1}\hfill \\ M_{{\text{r}}_2}\hfill \end{array}\right]=\left[\begin{array}{cc}{C}_{{\text{r}}_1}{P}_{{\text{r}}_1}& C_{{\text{r}}_2}{P}_{{\text{r}}_2}\\ C_{{\text{r}}_1}{P}_{{\text{r}}_1}^{*}& -C_{{\text{r}}_2}{P}_{{\text{r}}_2}^{*}\end{array}\right]\left[\begin{array}{l}{M}_{{\text{r}}_1}\hfill \\ M_{{\text{r}}_2}\hfill \end{array}\right],$$ (9)

where $Y_{e{\text{r}}_1}$ and $Y_{o{\text{r}}_1}\in {𝒞}^{N_c\times 1}$ are the voxels at location r₁ of the coil images from even and odd lines respectively. The linear system A_{non–CPMG ss} in Equation 9 has size (2·N_c) × 2. To determine its condition number, we must calculate the eigenvalues of the information matrix (A_{non–CPMG ss})^HA_{non–CPMG ss}, where H is the complex conjugate transpose. Using Euler’s identity, trigonometric identities, and $P_k^{*}{P}_k=1$, we obtain:

$${\left(A_{\text{non}–\text{CPMG ss }}\right)}^H{A}_{\text{non}–\text{CPMG ss }}=2\left[\begin{array}{cc}{C}_{{\text{r}}_1}^H{C}_{{\text{r}}_1}& -j{C}_{{\text{r}}_1}^H{C}_{{\text{r}}_2}\text{sin}\left(\angle P_{{\text{r}}_1}-\angle P_{{\text{r}}_2}\right)\\ j{C}_{{\text{r}}_2}^H{C}_{{\text{r}}_1}\text{sin}\left(\angle P_{{\text{r}}_1}-\angle P_{{\text{r}}_2}\right)& C_{{\text{r}}_2}^H{C}_{{\text{r}}_2}\end{array}\right]$$ (10)

Intermediate steps are shown in Appendix Equations A4 and A5. Equation 10 indicates that the condition number of A_{non–CPMG ss} is dependent on the phase difference between aliased voxels, which scales the off-diagonal element by a factor between −1 and 1.

The best case conditioning in Equation 10 is achieved if $\angle P_{{\text{r}}_1}-\angle P_{{\text{r}}_2}=n\pi$, in which case the matrix is diagonal, the eigenvalues are equal to the diagonal elements, and:

$$\kappa {\left(A_{\text{non}–\text{CPMG ss }}\right)}_{\text{best case }}=\kappa \left(A_{\text{MUSE ss }}\right)=\sqrt{\frac{\text{max}\left(C_{{\text{r}}_1}^H{C}_{{\text{r}}_1},C_{{\text{r}}_2}^H{C}_{{\text{r}}_2}\right)}{\text{min}\left(C_{{\text{r}}_1}^H{C}_{{\text{r}}_1},C_{{\text{r}}_2}^H{C}_{{\text{r}}_2}\right)}}$$ (11)

The information matrix for a standard MUSE combination is shown in Appendix Equation A3. This proves the equality condition of Equation 7.

The worst case conditioning is when $\angle P_{{\text{r}}_1}-\angle P_{{\text{r}}_2}=(2n+1)\pi /2$. Equation 10 becomes:

$${\left({\left(A_{\text{non}–\text{CPMG ss }}\right)}^H{A}_{\text{non}–\text{CPMG ss }}\right)}_{\text{worst case }\kappa }=2\left[\begin{array}{cc}{C}_{{\text{r}}_1}^H{C}_{{\text{r}}_1}& -j{C}_{{\text{r}}_1}^H{C}_{{\text{r}}_2}\\ j{C}_{{\text{r}}_2}^H{C}_{{\text{r}}_1}& C_{{\text{r}}_2}^H{C}_{{\text{r}}_2}\end{array}\right]$$ (12)

The matrix in Equation 12 is similar to the A^H A matrix for R = 2 SENSE in Appendix Equation A7, except off-diagonal elements are weighted by j and −j. However, the characteristic polynomials of these two matrices are equal, as shown in Appendix Equation A8. Therefore, they have equal eigenvalues, equal condition numbers, and the worst case conditioning of a single-shot non-CPMG reconstruction is equal to an R = 2 parallel imaging reconstruction. The upper bound on κ(A_{non–CPMG ss}) is essentially the Split-Echo SENSE solution. Extending this proof to multi-shot non-CPMG acquisitions requires consideration of shots jointly as in Equation 4, and increasing the undersampling factor of each shot which will change the number of voxels to unalias.

2.6 |. Modified Joint Multi-Shot non-CPMG Reconstruction

In Section 2.5, we showed that the conditioning of A_non–CPMG is dependent on the phase difference between aliased voxels. This may not be desirable because the random phase from diffusion gradients is difficult to control, and poor conditioning may cause unpredictable noise amplification. By assuming that the image is real, and by applying the relationship ℱ{C(x, y)P(x, y)M(x, y)} = S(k_x, k_y) ⇒ ℱ{C*(x, y)P*(x, y)M*(x, y)} = S*(−k_x, −k_y) to odd lines, the dependence of κ on the phase difference can be eliminated. Since we assume that the image is real, we have M(x, y) = M*(x, y). The modified linear reconstruction is:

$$\left[\begin{array}{c}{S}_{1e}\\ S_{1\mathit{\text{ ov }}}\\ ⋮\\ S_{Nse}\\ S_{Ns\mathit{\text{ ov }}}\end{array}\right]=A_{\text{non}-\text{CPMG }2}M=\left[\begin{array}{ccccc}{D}_{1e}FC& & & & \\ & D_{1ov}F{C}^{*}& & & \\ & & \ddots & & \\ & & & D_{Nse}FC& \\ & & & & D_{Nsov}F{C}^{*}\end{array}\right]\left[\begin{array}{c}{P}_1\\ P_1\\ ⋮\\ P_{Ns}\\ P_{Ns}\end{array}\right]M.$$ (13)

This system’s condition number is invariant with P. An analysis of the condition number is presented in Supporting Information Section 4. The phase invariance of this system is shown numerically in Supporting Information Figure S1. Although the modified system has different conditioning properties, in preliminary experiments we have observed little difference between g-factor maps obtained with the initial and modified multi-shot reconstructions.

3 |. METHODS

3.1 |. Acquisitions

Acquisitions were performed at 3T on a GE Signa Premier MRI scanner (GE Healthcare). The slice thickness of the refocusing pulse with time bandwidth product 2 was widened to 2× the excited slice thickness to create a uniform 180°slice profile and reduce ghosting from slice profile effects [28]. Fat suppression was achieved with standard fat-saturation, a non-selective 90°pulse centered on fat. For the prostate, B1-insensitive fat suppression was achieved with a spectrally selective adiabatic 180°inversion pulse centered on fat. The seven echo stabilization period described in [15] was used. All three gradient axes were enabled for diffusion encoding with 50 mT/m per axis amplitude and 200 T/m/s slew rate.

The center four lines of k-space were sampled in each shot to improve phase navigator estimation by reducing the likelihood of missing the center of k-space. These center lines were included in the reconstruction. For correct phase navigator estimation, k-space must be symmetrically sampled after generating virtual odd lines using Equation 6. For fully sampled multi-shot non-CPMG, this is achieved by traversing one side of k-space after the initial four center lines. For partial Fourier sampling, odd phase encodes in the symmetric part of k-space must be flipped about the k-space center in the physical sampling pattern. Sampling patterns are described in Supporting Information Figures S2 and S3.

3.2 |. Reconstruction

Coil sensitivities were estimated from a separate single-shot acquisition using VCC-ESPIRIT [29], which enforces that the b = 0 s/mm² image is real. The real b = 0 s/mm² image serves as a phase reference where all magnetization satisfies the CPMG condition. VCC-ESPIRIT ensures that the phase navigator estimates the absolute angle (relative to perfect CPMG) of the magnetization at time TE_prep, and is not offset by an arbitrary phase which would occur if coil sensitivities were estimated with standard ESPIRIT [30]. Conventional DW navigator reconstructions do not require the absolute phase, but it is needed here because the linear model depends on P and P* to separate the oscillating out-of-phase component from in-phase magnetization.

The joint multi-shot linear reconstruction was compared to Split-Echo SENSE [16] and Combined-Echo SENSE applied to center oversampled data. Equations 4, 6, and 13 were solved with the conjugate gradients method using 10 iterations. Data was pre-whitened and coil compressed to 12 virtual coils using software coil compression [31]. Phase navigators for joint shot reconstruction were estimated with Combined-Echo SENSE. Phase navigators obtained with Combined-Echo SENSE were compared to phase navigators estimated using Split-Echo SENSE with and without center oversampling. Split-Echo SENSE echo images were combined by summing the even-echo image with the complex conjugate of the odd-echo image.

The pseudo multiple replica (PMR) method with 30 repetitions [32] was used to generate g-factor and SNR maps for the brain acquisition. To avoid magnitude operations in the PMR reconstruction, shots in multi-shot split-echo SENSE were combined using the phase navigator. Partial Fourier reconstruction was performed by applying POCS-homodyne to the shot and coil-combined conjugate gradients solution.

3.3 |. Phantom Experiment

The ISMRM-NIST breast diffusion phantom [26] was imaged using a 16-channel breast coil (NeoCoil). Scan parameters for multi-shot non-CPMG were: FOV 25 × 25 cm, matrix size 256 × 128, voxel size 1 × 2 mm, 5 mm slice thickness, 4 shots, ETL 32 + 4 center oversampled lines, readout BW ±125 kHz, TE_prep = 35 ms, b = 0, 800 s/mm². Vendor-provided DW-FSE PROPELLER [35] was used to compare ADC estimates: matrix size 180 × 180, voxel size 1.4 × 1.4 mm, ETL 32. Mean ADCs in each vial were compared using linear regression analysis.

3.4 |. in vivo Acquisitions

DW-FSE with non-CPMG quadratic phase increment FSE was applied to two healthy male volunteers (one brain, one prostate), and one healthy female volunteer (cervical spine), following IRB approval and informed consent.

Scan parameters for 4-shot brain acquisition: FOV 25 × 25 cm, matrix size 256 × 128, 3 mm slice thickness, ESP 5 ms, readout BW ±125 kHz, TE_prep = 39 ms, b = 0, 1 000 s/mm², TR 3000 ms, 12 slices, 48-channel head coil. ETLs were: 32 + 4 center oversampled for fully sampled multi-shot non-CPMG, ETL 20 + 4 center oversampled lines, for partial Fourier multi-shot non-CPMG, and ETL 78 for partial Fourier single-shot non-CPMG. Scan time for 12 slices: 30 seconds for 4-shot non-CPMG, and 12 seconds for single-shot. The single-shot acquisition was not 4× shorter than the 4-shot acquisition due to SAR.

4-shot DW-FSE axial prostate scan parameters were identical to the brain scan except: FOV 38 × 38 cm, b = 0, 800 s/mm², 3 mm slices, anterior AIR coil (GE Healthcare), TR 7500 ms, 10 slices, scan time 30 seconds. Scan parameters for sagittal cervical spine were identical to the brain except: FOV 25 × 25 cm, b = 0, 600 s/mm², 5 mm slices, 21-channel head and neck coil + spine coil, TR 7500 ms, 10 slices, scan time 30 seconds. Vendor-provided 4-shot DW-EPI MUSE with matrix size 256 × 128, TR 3000 ms and TEs ranging from 55–65 ms were acquired for comparison in all anatomies.

4 |. RESULTS

4.1 |. Phantom Experiment

Multi-shot non-CPMG images and ADC maps of the diffusion phantom are shown in Figure 4. Diffusion acquisitions of static phantoms generally exhibit no ghosting since little shot-to-shot phase variation is present. Ghosting in the naive shot combination (Figure 4B), obtained by summing all shots and combining coils with root-sum-of-squares, is from the out-of-phase component created by eddy currents. Separate reconstruction of odd and even lines from each shot using Split-Echo SENSE has residual aliasing, shown in Figure 4D. This aliasing is eliminated by jointly reconstructing shots with the low-resolution phase estimate, shown in Figure 4E. The low-resolution phase estimate allows the oscillating non-CPMG component to be separated from the CPMG component. Regression analysis between mean ADCs in each vial for DW-FSE PROPELLER (Figure 4C) and multi-shot non-CPMG (Figure 4F) gave the following linear fit: ADC_non-CPMG = 1.04 · ADC_{FSE PROP} − 0.14 × 10⁻³ mm²/s, R² = 0.968, p < 0.001.

FIGURE 4.

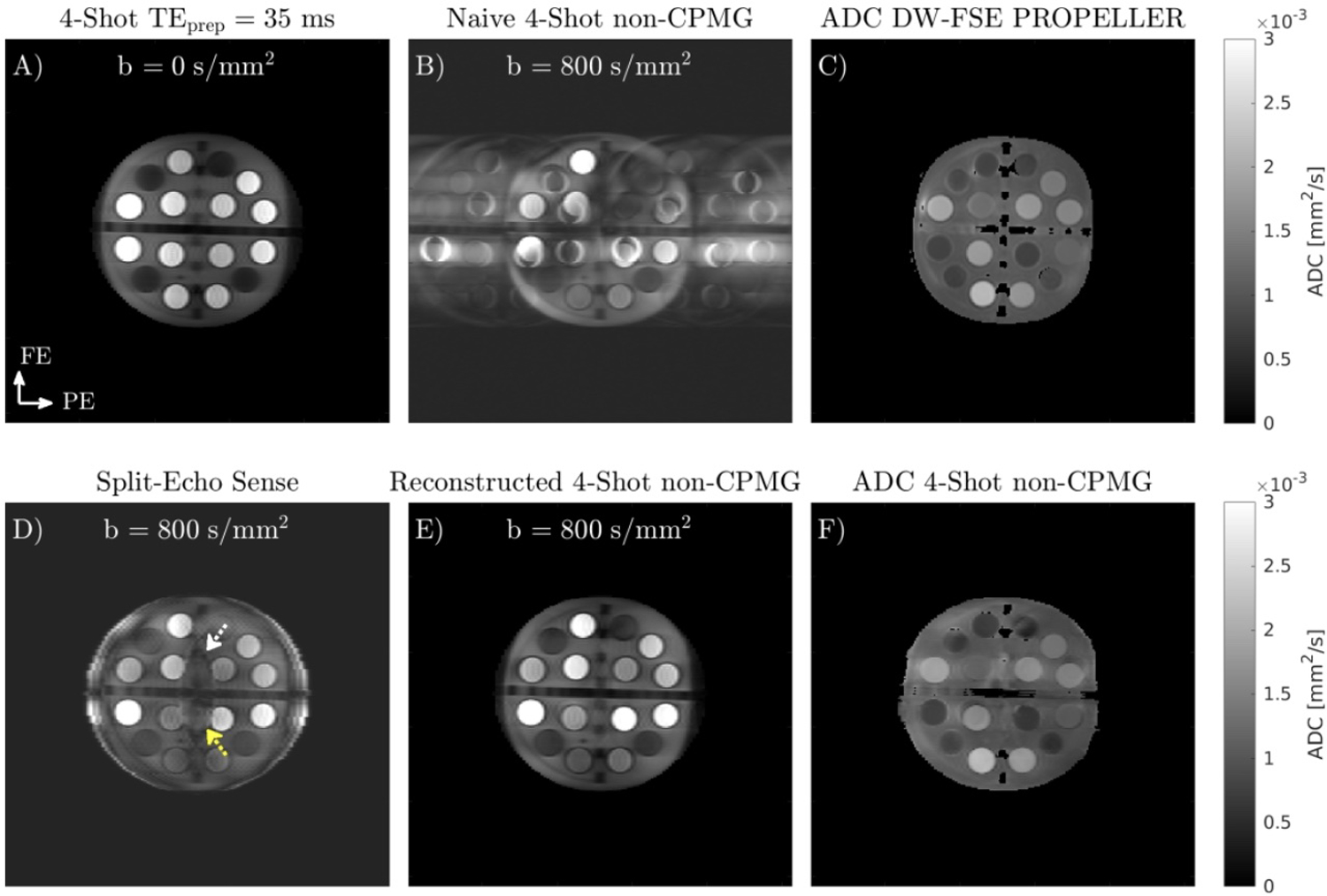
A) 4-shot b = 0 s/mm² image of ISMRM-NIST breast diffusion phantom. B) Naive combination of b = 800 s/mm² data obtained using quadratic phase increment FSE readout has ghosts in the phase encode direction from the oscillating out-of-phase component. C) ADC map obtained with DW-FSE PROPELLER. D) Split-Echo SENSE, obtained by separately reconstructing odd and even lines from each shot. Yellow and white arrows indicate residual aliasing due to the high undersampling factor of each split shot. E) Joint reconstruction of all b = 800 s/mm² shots using linear model and phase navigators estimated from data. F) Multi-shot non-CPMG ADC map.

4.2 |. in vivo Experiments

A comparison of different phase navigator reconstructions obtained in the DW brain acquisition is shown in Figure 5. Applying Split-Echo SENSE to uniformly sampled data can result in signal dropout and poor phase estimation (yellow arrow) due to the center of k-space being missed. The addition of four center lines improves phase navigator estimation in these regions. Between Split-Echo SENSE and Combined-Echo SENSE, their phase images are similar but the magnitude images differ. The magnitude images of Combined-Echo SENSE have improved SNR compared to Split-Echo SENSE, which may benefit reconstructions with greater b-values or acquisitions with inferior coil geometries.

FIGURE 5.

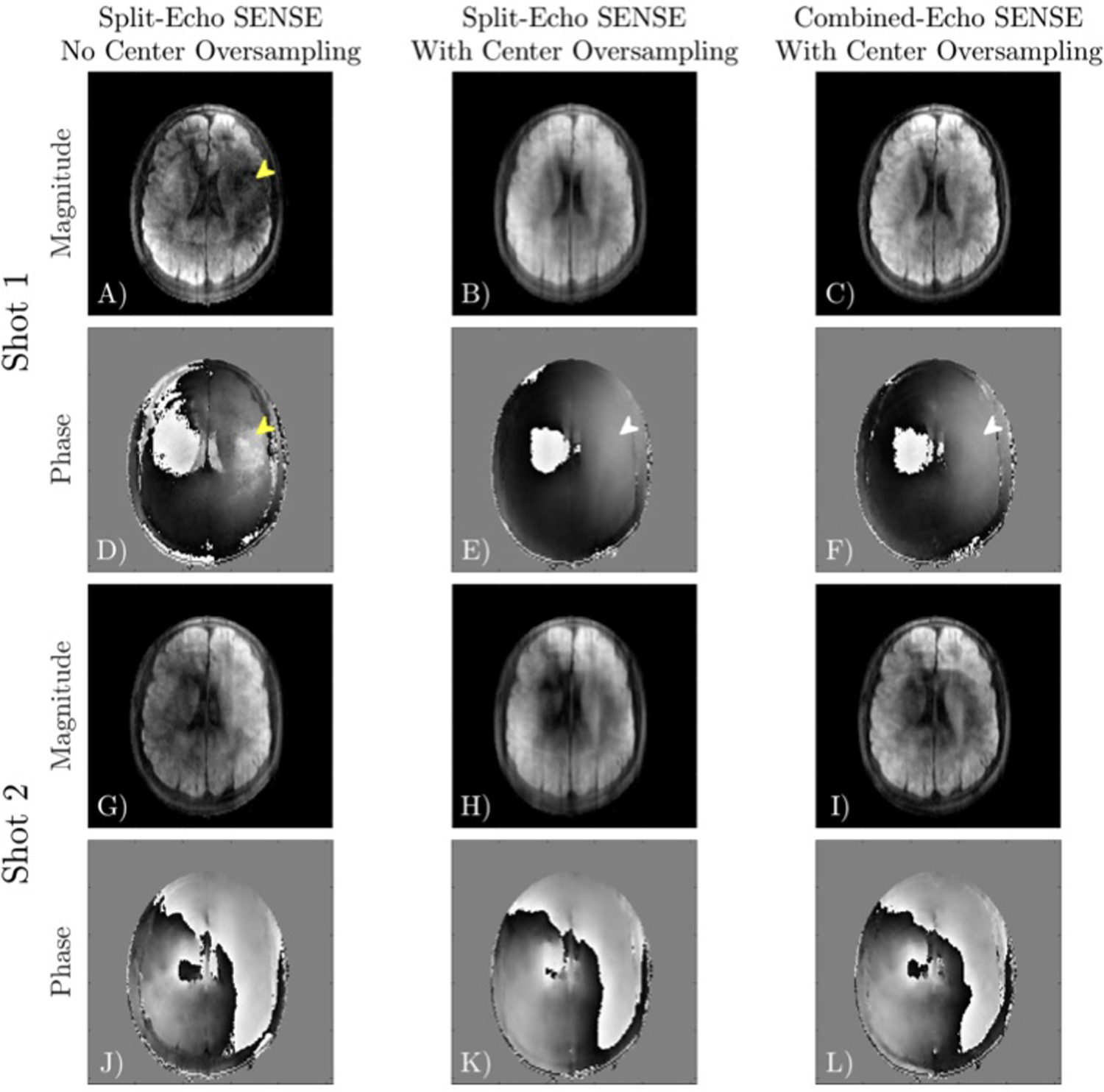
Different phase navigator reconstructions for shot 1 (A-F) and shot 2 (G-L) of a 4-shot acquisition. Without center oversampling, a shot may miss the center of k-space, resulting in dropout and poor estimation of the phase (yellow arrow). Center oversampling improves phase estimation in this region (white arrow). Split-Echo SENSE and Combined-Echo SENSE with center oversampling obtain similar phase estimates.

A comparison of different linear reconstructions for multi-shot non-CPMG data is shown in Figure 6. Dividing even and odd echoes using Split-Echo SENSE has extremely poor g-factor performance for 4-shot data. Shading in the center of the Split-Echo SENSE reconstruction is due to the high undersampling factor (8×) and the slight center oversampling. Combined-Echo SENSE reduces the average g-factor by a factor of 2× from 2.80 to 1.38, but elevated g-factors are still present in the center region with coil overlap. Jointly reconstructing shots has the best mean g-factor performance and the most uniform g-factor maps.

FIGURE 6.

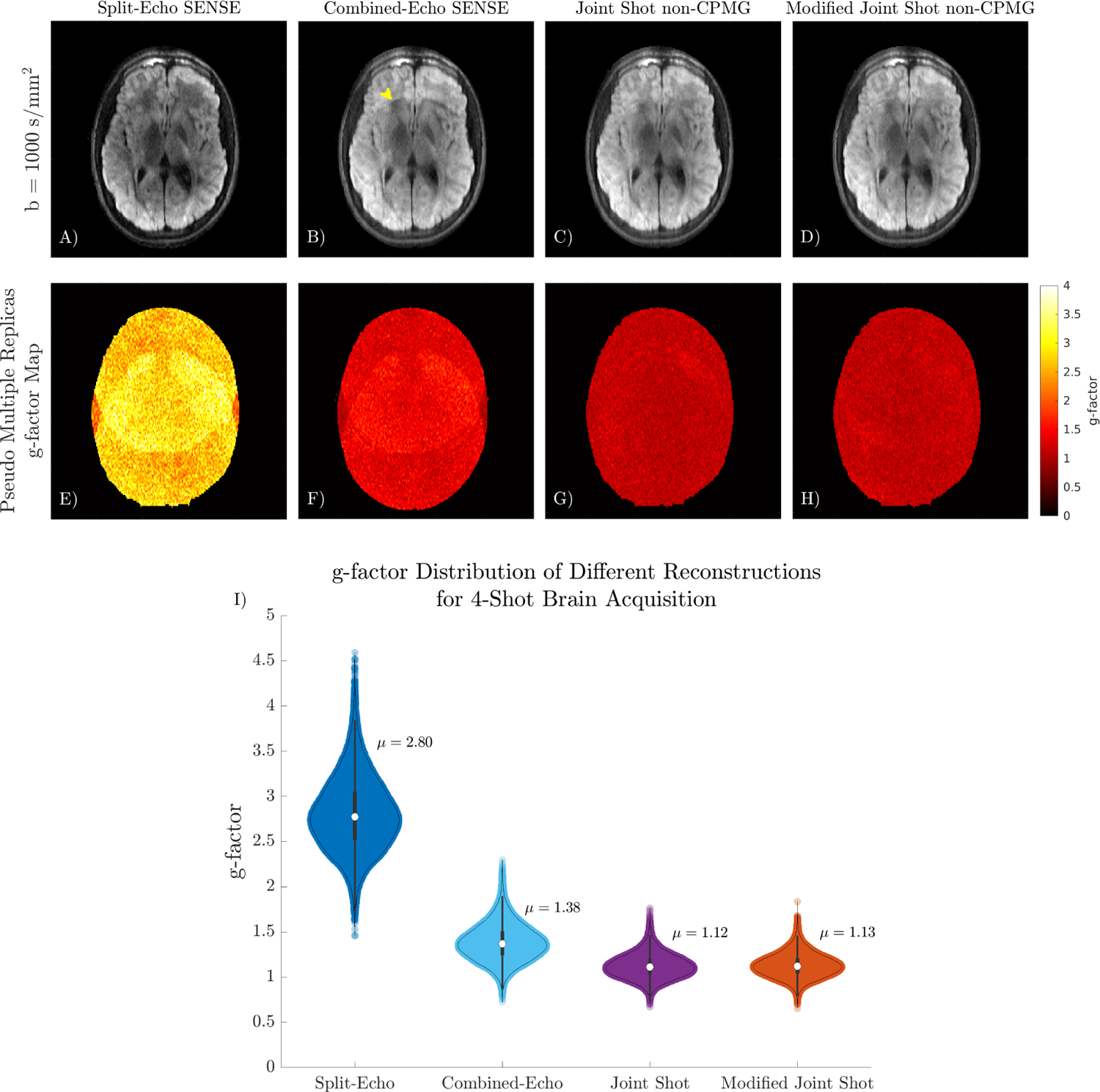
A-D) Comparison of different linear reconstructions on 4-shot DW non-CPMG data. Split-Echo SENSE has low SNR in the region with large coil overlap due to the high acceleration factor. Some aliasing is present in the Combined-Echo reconstruction (yellow arrow). E-H) g-factor maps obtained using pseudo multiple replicas quantify the improved conditioning from jointly reconstructing all shots. I) Violin plot summarizing the distribution of g-factor in the slice.

An in vivo comparison of DW-EPI, single-shot non-CPMG, and multi-shot non-CPMG in the brain is shown in Figure 7. Images have different magnetization transfer contrast and T2-weighting due to differing ETLs and echo times. Multi-shot non-CPMG has improved delineation of white and gray matter compared to single-shot due to reduced T2 blur (yellow arrow). Multi-shot non-CPMG has lower apparent resolution than DW-EPI due to T2 blur.

FIGURE 7.

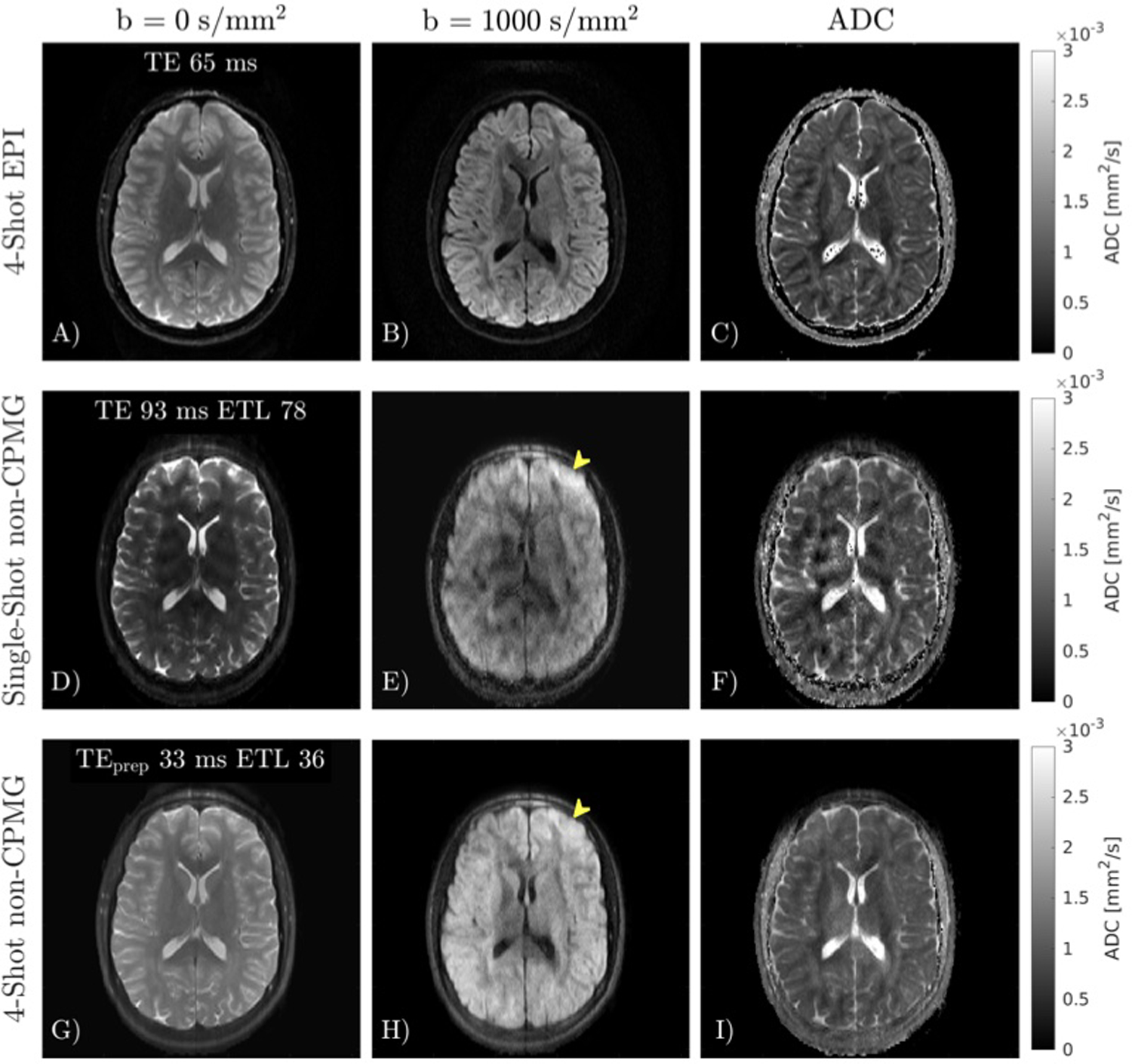
In vivo comparison of 4-shot EPI MUSE, and single-shot and multi-shot quadratic phase increment FSE. A-C) 4-shot EPI reconstructed with MUSE. D-F) Single-shot FSE has considerable T2 blurring compared to EPI. G-H) Multi-shot FSE reduces T2 blur compared to single-shot FSE (yellow arrow). Despite reduced T2 blur, the apparent resolution of multi-shot FSE is still lower than EPI.

A comparison of Split-Echo SENSE and the initial joint multi-shot reconstruction (Equation 4) in the brain is shown in Figure 8. SNR maps obtained using pseudo multiple replicas show that SNR in regions with high aliasing overlap is improved from 10 to 30 by jointly reconstructing shots. The SNR map of Split-Echo SENSE is dependent on coil geometry and g-factor, whereas the fully sampled joint shot reconstruction has more uniform SNR across the image. Prospective partial Fourier reconstruction of multi-shot non-CPMG data has comparable resolution to the fully sampled acquisition with some residual ringing form Fourier truncation, visible in the SNR map.

FIGURE 8.

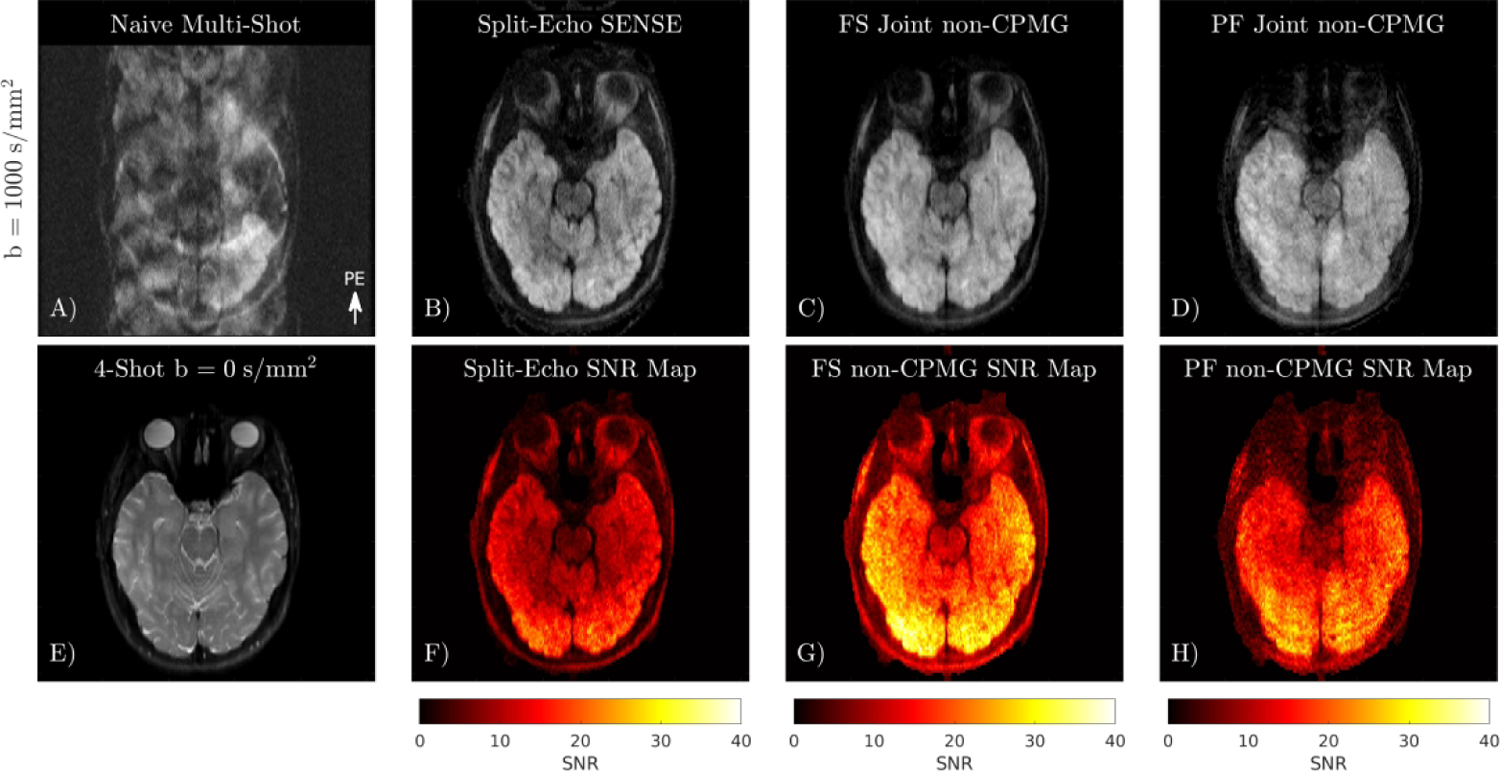
Comparison of different linear reconstructions on multi-shot non-CPMG diffusion data. A) Naive combination of 4-shot data exhibits severe ghosting from shot-to-shot phase, and aliasing of the out-of-phase component. B) Reconstruction of each shot split into even and odd lines. C) Joint reconstruction of shots using phase navigator. D) Joint reconstruction of partial Fourier data. E) 4-shot b = 0 s/mm² image. F-H) SNR maps obtained using pseudo multiple replicas.

Application of multi-shot non-CPMG in the prostate and a comparison to DW-EPI is shown in Figure 9. There is no apparent ghosting in the multi-shot non-CPMG images which indicates that the proposed linear reconstruction succeeds at correcting ghosting from both out-of-phase magnetization and shot-to-shot phase. Partial Fourier sampling has lower SNR compared to the fully sampled non-CPMG image but produces similar ADC maps. Mean and standard deviations of ADCs in the prostate, excluding the urethra in the ROI were: 1.3 ± 0.4 × 10⁻³ mm²/s for DW-EPI, 1.5 ± 0.4 × 10⁻³ mm²/s for both fully sampled and partial Fourier multi-shot non-CPMG.

FIGURE 9.

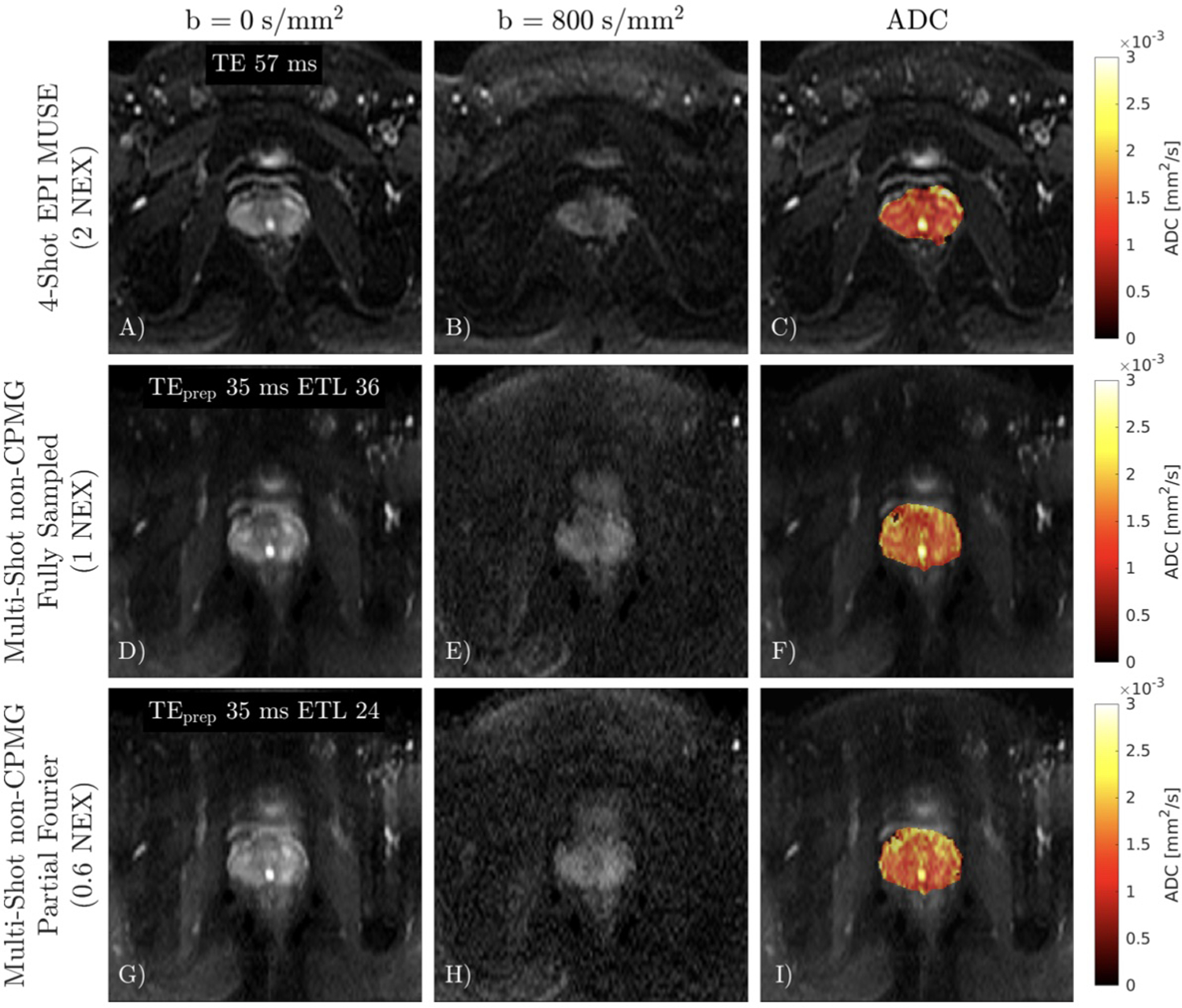
A-C) 4-shot DW-EPI with 2 NEX reconstructed with MUSE. D-F) Fully sampled non-CPMG image. There is no apparent ghosting in the multi-shot non-CPMG images. G-I) Partial Fourier non-CPMG reconstruction has lower SNR compared to the fully sampled acquisition.

Application of multi-shot non-CPMG in the cervical spine is shown in Figure 10. DW-FSE exhibits no distortion compared to DW-EPI, which allows the tongue, nose, and lips to be clearly seen. Joint reconstruction of shots improves SNR compared to Split-Echo SENSE, which exhibits low SNR in gray matter in the spine. Prospective partial Fourier reconstruction of multi-shot non-CPMG data has comparable image features to the fully sampled acquisition but with reduced SNR. Keeping the matrix size and shot count constant, partial Fourier sampling shortens echo trains which reduces SAR. The shorter echo train also reduces T2 blur, although the apparent resolution of the final image relies on a successful homodyne reconstruction.

FIGURE 10.

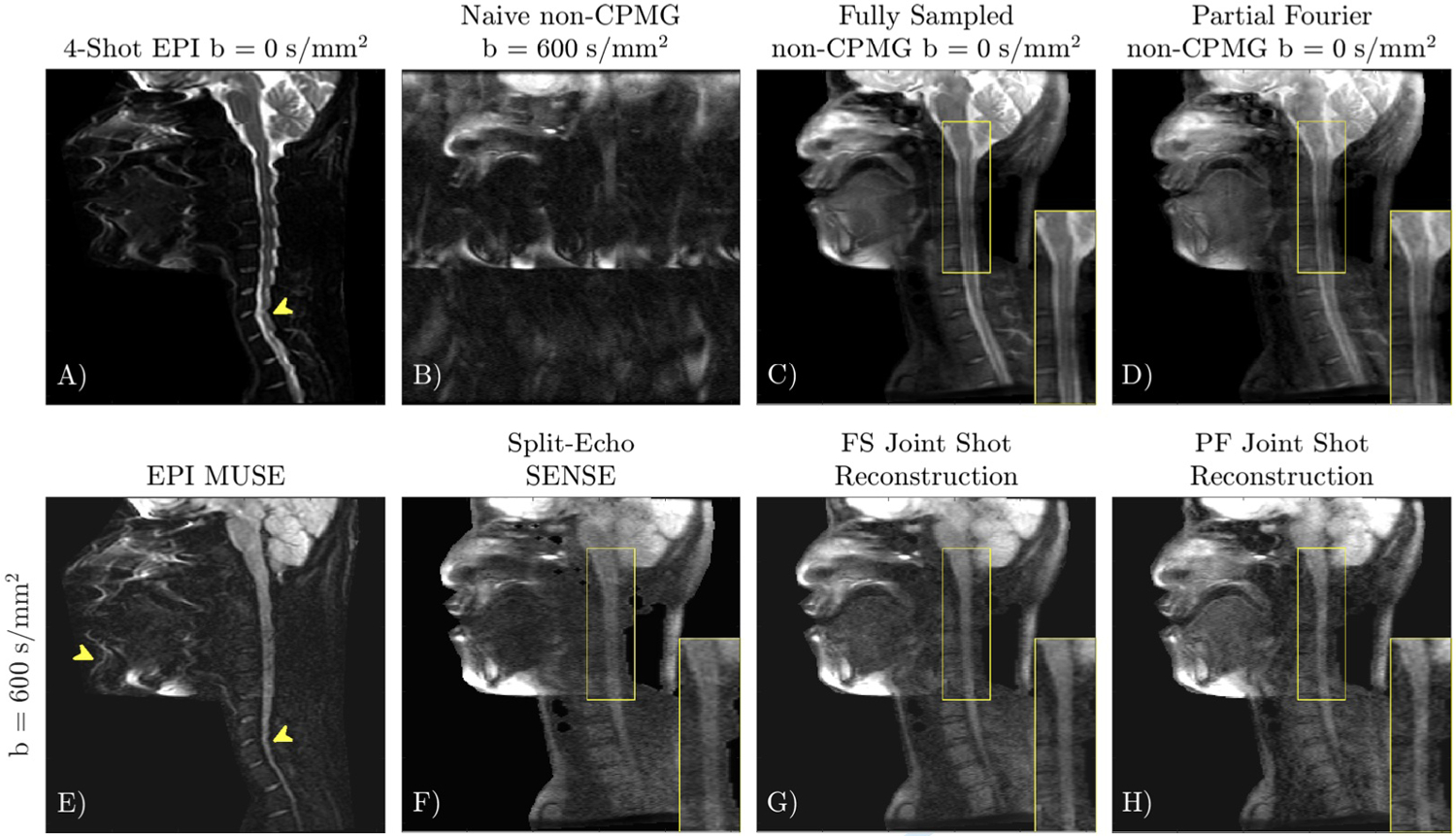
Application of multi-shot quadratic phase increment FSE in the cervical spine. 4-shot DW-EPI (A, E) has distortion due to off-resonance (yellow arrows). Quadratic phase increment DW-FSE (F-H) exhibits no distortion. Split-Echo SENSE (F) can correct ghosts from shot-to-shot phase and intra-echo train oscillations, but has low SNR (inset) and magnitude bias. Joint reconstruction of shots (G) improves SNR. The non-CPMG reconstruction applied to prospectively acquired partial Fourier data (H), has similar resolution to the fully sampled acquisition (G).

5 |. DISCUSSION

DW-FSE considerably reduces geometric distortion compared to the commonly used EPI trajectory. We have presented a linear model that can reconstruct multi-shot DW-FSE data with full signal acquired with a non-CPMG quadratic phase increment refocusing scheme. This linear model accounts for shot-to-shot phase variations from motion, as well as intra-shot oscillations of the non-CPMG component. Multi-shot FSE shortens echo trains, reducing T2 blur, and joint reconstruction of shots improves SNR.

The primary benefit of Cartesian DW-FSE over alternate DWI trajectories is that it is insensitive to off-resonance induced distortions. Severe distortion in DWI can obscure anatomy, and may impact tumor characterization, delineation, and response assessment. Other techniques that reduce distortion include: multi-shot EPI, PSF-EPI [33] accelerated with ky-t interpolation [34], and DW EPI/FSE PROPELLER (Periodically Rotated Overlapping ParallEL Lines with Enhanced Reconstruction). [35, 36] While multi-shot EPI reduces distortion compared to single-shot EPI, moderate off-resonance from sources such as unsuppressed fat still poses issues, as shown in the sinuses and mouth in Figure 10. Multi-shot EPI and PSF-EPI are both sensitive to T2* decay. Accelerated PSF-EPI [34] depends on interpolation using a ky-t kernel estimated using a fully sampled low resolution ky-t calibration scan, which can fail to capture spatially rapidly off-resonance variations such as those near metal implants, or transitions from fat to water. PROPELLER uses hybrid radial-Cartesian sampling to acquire a low-resolution navigator for motion and phase correction each excitation [37]. Compared to Cartesian sampling, PROPELLER trajectories are limited to circular FOVs, require 1.5× more samples (and hence shots) to fully sample k-space due to center oversampling, and exhibit streaking artifacts which reduces apparent resolution if not oversampled. The presented reconstruction of quadratic phase modulation data can be integrated with DW-FSE PROPELLER.

The main advantage of the non-CPMG method for handling non-CPMG magnetization is the 2× increased SNR compared to the Alsop [8] and stimulated echo methods [9], and $\sqrt{2}\times$ increased SNR compared to split-echo readouts [14]. Although the full signal is measured, the realized SNR efficiency improvement is smaller.

The primary penalty to SNR efficiency with the non-CPMG method is the increased TR due to SAR constraints. A high refocusing flip angle is required because echoes during the stabilization period do not follow the signal model described in Equation 2 if the flip angle is smaller than 150°. These early echoes can therefore not be reliably used for image formation or phase navigator estimation. Echoes in the stabilization period may be skipped, permitting a lower refocusing flip angle, but the increased TE would offset the benefits of Le Roux’s technique for handling non-CPMG magnetization while preserving full signal.

We compared the SNR efficiency of the half and full signal DW-FSE sequences in a 3T SAR limited scenario, ignoring T2 decay, in Supporting Information Table S1 using minimum TRs obtained from the scanner. The methodology for this comparison is described in the Supporting Information Section 5. In the SAR limited scenario, the SNR efficiency of the full signal non-CPMG sequence using 180°refocusing flip angles exceeds the non SAR-restricted, half signal SNR efficiency by 30%. This is because the minimum TR of the non SAR-restricted sequence is bounded by the time required to play the diffusion preparation and all refocusing pulses. At lower field strengths where SAR is reduced, the full signal non-CPMG sequence will have 2× the SNR efficiency of the half signal method (ignoring conditioning of the reconstruction). The DW-FSE quadratic phase increment method is especially applicable to low-cost portable systems that may lack shimming or active gradient shielding hardware that enables DW-EPI in high-field scanners [38].

A second penalty is the conditioning of the linear reconstruction. We showed in Section 2.5 that a linear reconstruction of the non-CPMG signal model has worse conditioning than a linear reconstruction of conventional diffusion signal models. The worst case conditioning of the non-CPMG reconstruction is equal to Split-Echo SENSE. The increase in the condition number is dependent on the phase difference between aliased voxels (Equation 12). In a brain acquisition with a 48-channel head coil, g-factors obtained using the phase-difference insensitive multi-shot non-CPMG reconstruction were similar to the initial model. This may be because the sampling pattern includes center lines, and the spatial phase variation (shown in Figure 5) is not great enough to force the worst case condition. Applying the phase insensitive reconstruction in a 6-shot acquisition with a greater b-value of 2000 s/mm² provided a negligible g-factor improvement, as shown in Supporting Information Figure S4. Techniques such as moment-nulled or eddy current-nulled diffusion gradients [39, 40, 41] to reduce in-plane phase differences may also be advantageous. Randomly sampled Cartesian k-space, which can easily be achieved with DW-FSE [42], may also improve the conditioning of the linear non-CPMG reconstruction [43].

A third penalty is slice-dependent magnetization transfer (MT) effects, which are prominent due to the high refocusing flip angles. Signal attenuation from MT can be predicted by simulation [44].

Although the echo train is stable for 150◦, a nominal refocusing flip angle of 180°was prescribed to prevent B1 inhomogeneity from reducing the refocusing flip angle below 150°. We also used a widened refocusing slice thickness to reduce ghosting of the non-CPMG component from low flip-angles in the transition band [28]. Delay Insensitive Variable Rate Selective Excitation (DI-VERSE) pulses [45] employed by Gibbons et al. [16] can reduce slice cross-talk and SAR.

Compared to single-shot non-CPMG partial Fourier sampling, 4-shot FSE shortened echo trains by ~2× for fully sampled data, and ~3× using partial Fourier sampling. T2 blur could be further reduced with even shorter echo trains, but aliasing in the phase navigator increases with shot count due to the increased undersampling factor of each shot. Additional echoes may be added at the beginning or end of the echo train to improve phase navigator estimation. Because the linear model is similar to MUSE, extensions such as POCS-MUSE [46] and POCS-ICE [22] are likely applicable. Navigator-less shot combination techniques such as multi-shot sensitivity-encoded recovery using structured low-rank matrix completion (MUSSELS) [47] or shot-locally low rank (Shot-LLR) [48] could be used to reconstruct data with higher shot counts. We demonstrated that phase navigators can be estimated from all of the data acquired in a single shot by generating virtual conjugate k-space lines from the odd echoes. For MUSSELS and Shot-LLR, Combined-Echo SENSE can be applied to combine coils for each shot without having to treat even and odd lines as separate shots.

6 |. CONCLUSION

Multi-shot non-CPMG DW-FSE data with full signal can be jointly reconstructed with low g-factor penalty using a phase navigator and a linear model.

Supplementary Material

Fig. S1

FIGURE S1: Numerical demonstration of the dependence of condition number on the phase difference between aliasing voxels for a jointly reconstructed single-shot non-CPMG acquisition. Coil sensitivities for each voxel were a random complex vector of size 8 × 1. The g-factor of the phase difference insensitive reconstruction is not equal to 1 due to the coupling of the coils. The MATLAB script used to generate this figure is provided in the Supporting Information.

Fig. S2

FIGURE S2: Sampling patterns for partial Fourier sampling with PF factor 0.6. Each shot includes the middle 4 center lines at the beginning of the echo train. The physical sampling pattern (used to calculate phase encoding amplitudes) of each shot does not always include both halves of k-space. In shots 2 and 4, the physical k-space sampling repeats the same k_y line for echoes 6–12. This is done so that after generating virtual conjugate odd lines, the symmetric part of k-space has samples on both sides of low-resolution k-space. This is critical for accurate phase estimation for self-navigation.

Fig. S3

FIGURE S3: Sampling patterns for fully sampled multi-shot non-CPMG. Like partial Fourier sampling, there are samples on both sides of k-space after generating virtual odd lines.

Fig. S4

FIGURE S4: A-D) Comparison of reconstructions in a high b-value (2000 s/mm2) and 6-shot acquisition. Other parameters: 256 × 128, FOV 24 cm, slice thickness 5 mm, 4-line center oversampled, 48-channel head coil, diffusion encoding all gradient axes used. A greater b-value increases the motion-induced phase, and increased shot counts increases the number of aliasing voxels. Visually, there is little difference in the reconstructions and g-factor maps. E) A histogram of the g-factors shows a slight improvement in g-factor using the phase difference insensitive reconstruction.