Abstract
Thermalization is a ubiquitous process of statistical physics, in which details of few-body observables are washed out in favor of a featureless steady state. Even in isolated quantum many-body systems, limited to reversible dynamics, thermalization typically prevails [1]. However, in these systems, there is another possibility: many-body localization (MBL) can result in preservation of a non-thermal state [2, 3]. While disorder has long been considered an essential ingredient for this phenomenon, recent theoretical work has suggested that a quantum many-body system with a uniformly increasing field—but no disorder—can also exhibit MBL [4], resulting in ‘Stark MBL’ [5]. Here we realize Stark MBL in a trapped-ion quantum simulator and demonstrate its key properties: halting of thermalization and slow propagation of correlations. Tailoring the interactions between ionic spins in an effective field gradient, we directly observe their microscopic equilibration for a variety of initial states, and we apply single-site control to measure correlations between separate regions of the spin chain. Further, by engineering a varying gradient, we create a disorder-free system with coexisting long-lived thermalized and nonthermal regions. The results demonstrate the unexpected generality of MBL, with implications about the fundamental requirements for thermalization and with potential uses in engineering long-lived non-equilibrium quantum matter.
Many-body localization was first formulated as a generalization of the non-interacting Anderson transition [6–9]. With disorder, quantum particles can experience destructive interference through multiple scattering, causing a transition to exponentially localized wavepackets. Over time, a cohesive picture of MBL in interacting systems has also developed [10, 11]. In this description, the MBL regime has extensive local conserved quantities that generalize the particle occupancies in Anderson localization. However, interactions result in additional slow spreading of correlations via entanglement. Strikingly, MBL creates a phase of matter that is non-ergodic: for a range of parameters, local features of the initial state are preserved for all times, preventing thermalization [2].
In considering MBL, it is natural to ask whether random disorder is a requirement. A partial answer has long been known: MBL is possible with incommensurate periodic potentials [12]. However, the question of whether an MBL phase might exist which preserves translational symmetry, for instance in a system with gauge invariance [13] or multiple particle species [14, 15], has continued to generate extensive discussion [16]. Recently, this problem has been approached from a different starting point: the Bloch oscillations and Wannier-Stark localization of non-interacting particles in a uniformly tilted lattice [17]. From this, it has been predicted that interacting systems with a strong linear tilt can also display MBL-like behavior [4, 5]. This effect, sometimes called Stark MBL, has attracted considerable theoretical and experimental interest [18–27]. However, clear experimental realization of Stark MBL has been complicated by exact degeneracies between states with the same center of mass that occur in the limit of short-range interactions [4, 5, 26]. The setting of a trapped-ion quantum simulator with long-range interactions naturally overcomes this complication.
EXPERIMENTAL SETUP
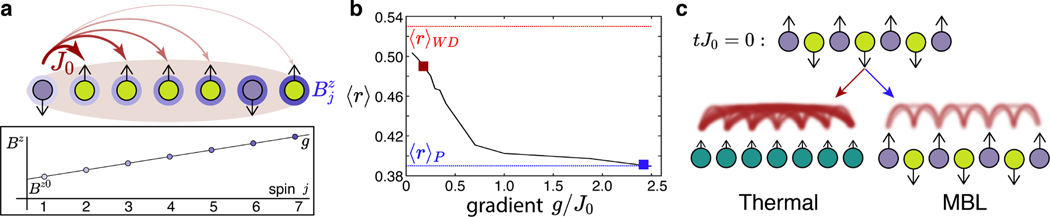
Investigation of many-body localization has been driven in part by the development of isolated quantum simulator platforms with site-resolved control and detection [28–31]. Our experimental apparatus (Fig. 1a) exemplifies these capabilities. It consists of a chain (N = 15–25) of 171Yb+ ions, with pseudospin states and encoded in hyperfine ground-state levels. The Hamiltonian has two ingredients. The first is an overall spin-spin interaction, mediated by global laser beams coupling spin and motion using the Mølmer-Sørensen scheme [32]. The second, a tightly-focused beam creating a programmable effective Bz magnetic field at each ion using the AC Stark effect [33]. A key feature of this platform is its high degree of controllability. In addition to turning on or off either Hamiltonian term, we use the tightly-focused beam to initialize spins in any desired product state, and we measure arbitrary local observables with state-dependent fluorescence collected onto a CCD camera.
FIG. 1.
Experimental setup. a, Each trapped ion in a chain of length N encodes a pseudospin. Global lasers controllably mediate a long-range spin-spin interaction (red), which is parameterized by the nearest-neighbor rate J0. A tightly-focused beam provides a site-resolved effective Bz magnetic field (blue) that is used to engineer a field gradient with slope g. For clarity, we show N = 7. b, The parameter , a measure of the level statistics of the experimental Hamiltonian (N = 15), shows a progression from statistics near the Wigner-Dyson limit (, red dotted line) at low g/J0, characteristic of a generic ergodic system, to Poisson statistics (, blue dotted line) at high g/J0, characteristic of a localized system. c, We probe the system using a quench from a non-equilibrium initial state, such as the Néel state shown here. At low g/J0, an initial spin pattern will quickly relax to a uniform average magnetization, while at high g/J0 the initial pattern persists. The former is consistent with a thermal state, in which uniformity is combined with entanglement reaching across the entire chain, while the latter is consistent with many-body localization, in which the magnetization remains non-uniform and entanglement spreads slowly.
Combining the global spin-spin interactions with a programmable local field set to a linear gradient results in the tilted long-range Ising Hamiltonian ():
| (1) |
Here we have the long-range spin-spin interactions , approximately following a power-law: , with J0 the nearest-neighbor coupling and α = 1.3. Bz0 is an overall bias field, and g the gradient strength, with . In practice, we apply the terms in this Hamiltonian sequentially in time, using a Trotterization scheme that reduces decoherence while still resulting in evolution closely following the Hamiltonian in Eq. 1 (see Methods). The bias field Bz0 is set to be large , so that the total magnetization is approximately conserved. With this constraint, and neglecting edge effects, and this Hamiltonian is translationally invariant: the operation for integer n is equivalent to a shift in Bz0, which has no effect in the bulk. For an initial state of definite total magnetization, this model can then be mapped to a chain of hard-core bosons with long-range hopping in a tilted lattice (see Methods), indicating that it has similar ingredients to models previously shown to realize Stark MBL [4, 5]. This system has also been used previously to study MBL in a disordered field [28].
A useful numeric diagnostic of whether a model exhibits an MBL regime can be found in the level statistics, which feature similar behavior in regular MBL [34] and Stark MBL [4, 5]. A generic thermalizing ergodic system has energy levels following the Wigner-Dyson distribution that characterizes random matrices, while a generic many-body localized system has a Poissonian level distribution [34]. This difference can be quantified by the average ratio of adjacent energy level gaps, defined as
| (2) |
The quantity varies from 0.53 for the Wigner-Dyson case to 0.39 for the Poissonian case [4, 5, 34]. Diagonalizing the Hamiltonian (Eq. 1) for N = 15, we find that moves from 0.50 to 0.39 as the gradient g/J0 is increased, suggesting localization (Fig. 1b). While Fig. 1b shows the exact experimental Hamiltonian, including deviations from uniform interactions near the edges of the chain, this behavior persists for the ideal power-law Hamiltonian (see Methods). Unlike the first studies of Stark MBL, where a small amount of disorder or curvature was required to create a state with generic Poissonian level statistics [4, 5], Eq. 1 exhibits these properties without any terms perturbing the translational symmetry.
We probe the degree of localization using a quench procedure, shown schematically in Fig. 1c. The initial state, such as a Neel state of staggered up and down spins, is highly excited and far-from-equilibrium. If it thermalizes, it will result in a high-temperature equilibrium in which each spin has nearly equal probabilities of being up or down. Many-body localization will instead result in persisting memory of the initial configuration, breaking ergodicity.
ERGODICITY BREAKING IN STARK MBL
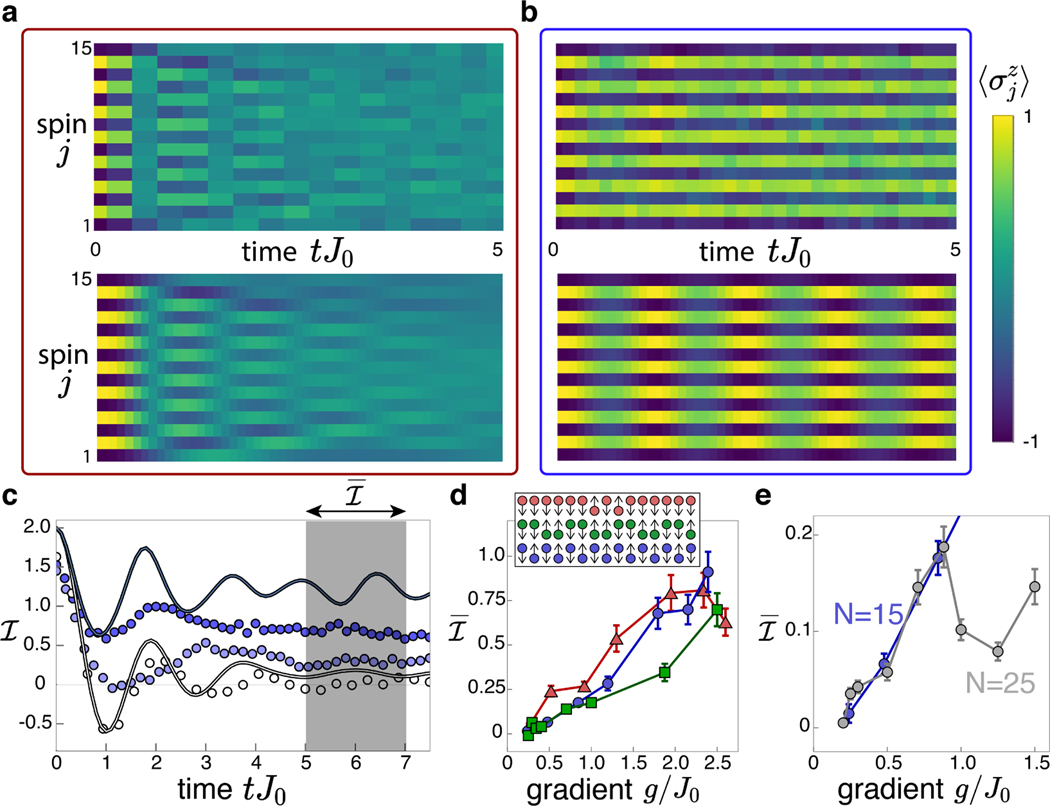
Performing the quench experiment, we see the expected signature of localization: a low gradient results in quick equilibration of the spins (Fig. 2a), while in a strong gradient they are nearly unchanged from their initial values (Fig. 2b). The experimental data correspond closely to exact numerics for the system evolution.
FIG. 2.
Ergodicity breaking in Stark MBL. a, Ion-resolved dynamics for an initial Neel state (N = 15) at g/J0 = 0.24, and b, at g/J0 = 2.4, corresponding to the red and blue points on Fig. 1b. While the state quickly relaxes to a uniform magnetization in the low gradient, the large gradient results in a persisting memory of the initial state. The top row are experimental data, and the bottom row are exact numerics. c, Memory of the initial state, here a Néel state (N = 15), can be quantified by the generalized imbalance. For a state of frozen up and down spins, = 2, and for complete relaxation to a uniform state, = 0. As the gradient is increased (light to dark), the imbalance crosses from quick relaxation towards zero to a persistent finite value. Points are experimental data at g/J0 = {0.24, 1.2, 1.8}, with statistical error bars smaller than the symbol size, and lines are exact numerics for the lowest and highest gradient. d, For various initial states, shown at top, we see a similar value of the late-time imbalance at large gradient, suggesting complete localization. From top to bottom, the three initial states correspond to the {triangle, square, round} points. e, Dependence of the late-time imbalance on system size is shown, using an initial Neel state with N = 15 (a subset of the data in panel b) and N = 25. The overall increase of late-time imbalance with gradient is robust to the system size increase. The pronounced dip in near g/J0 = 1.0 may be partly due to a resonant feature that appears near this value (see Methods and Extended Data Fig. 5). Error bars throughout represent statistical uncertainty of the mean value (s.e.m.).
To quantify the amount of initial state memory as the gradient is increased, it is useful to define a measure that can serve as an effective order parameter. We choose a generalized imbalance, , which reflects the preservation of the local magnetizations of the initial state. This observable is similar to other previously used measures of initial state memory, such as the imbalance [35] or the Hamming distance [28], but is advantageous for comparing different initial states (see Methods). For an initial state with M spins that are up, and N – M down, is equal to the subsequent difference between the average magnetizations of the two groups:
| (3) |
where the sums are respectively over the spins initially up and initially down. In general, reaches a maximum value of 2 for perfect memory of an initial state with up and down spins, and is zero for a uniform state as at thermal equilibrium.
The imbalance shows a clear trend as we increase the gradient (Fig. 2c). At lower gradients, it quickly relaxes to a decaying oscillation about zero, indicating quick thermalization. However, as the gradient is increased, the imbalance instead settles to a progressively higher value. Compared to exact numerics, we observe a damping of the imbalance oscillations, resulting in a lower steady-state imbalance. Furthermore, at the highest gradient values, decoherence causes a slow decay of over time. These are both attributed primarily to intensity fluctuations in the tightly-focused beam, as well as to residual coupling to ion-chain motion from the Mølmer-Sørensen beams. However, the separation between this decoherence time and the fast relaxation dynamics allows us to characterize the late-time imbalance.
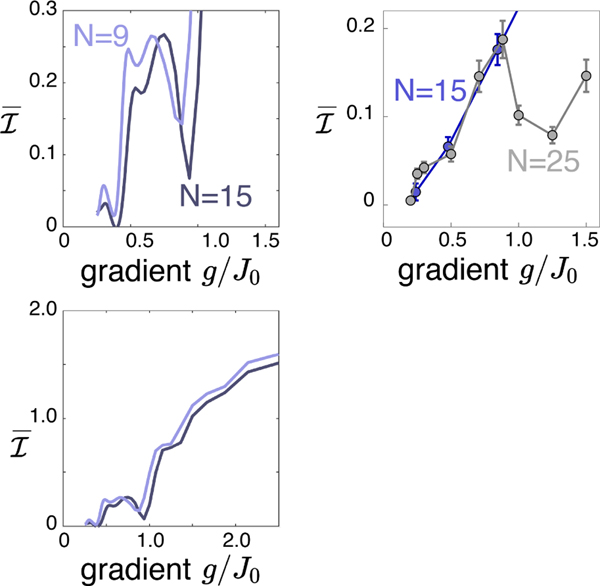
To study initial-state memory for different gradients, we average over a time window tJ0 from 5 to 7. This window is chosen to be late enough that transient oscillations have largely decayed, while early enough that decoherence is limited. This late-time imbalance, , captures the amount of initial-state memory after fast relaxation has subsided, and thus the approximate degree of localization (Fig. 2d). is consistent with zero at the lowest gradient: averaging over the initial states shown in Fig. 2d we have = 0.017 ± 0.027, with the standard deviation as the uncertainty. With a larger gradient, becomes clearly distinct from zero and progressively increases, reflecting an increasing memory of the initial state. Crucially, this memory does not show strong dependence on the specific initial state chosen: for states with different numbers of initial spin flips and different symmetry properties, similar behavior is observed. The initial state insensitivity observed here is consistent with many-body localization, which can have some energy dependence [20] but is a robust mechanism for breaking ergodicity that can span the entire spectrum. This insensitivity distinguishes our observations from other effects that cause thermalization to have a strong dependence on the initial state, such as quantum many-body scars [36] and domain wall confinement [37].
A key further test of the stability of Stark MBL is to characterize the dependence of the observed behavior on increasing system size. This is especially relevant to localization in systems with long-range interactions, where finite-size effects may be particularly important [28, 38]. Increasing the spin chain length to N = 25, we see a rise in the imbalance at low g/J0 that is similar to the N = 15 case (Fig. 2e). This length reaches a regime that is challenging for numerical simulation, and beyond our ability to compute exact dynamics. While we are unable to reach the deeply localized regime for N = 25, due to the scaling of the experimentally achievable maximum gradient with N (see Methods), the small nonzero value of that we observe indicates the persistence of a Stark MBL regime.
REVEALING THE CORRELATED STARK MBL STATE
Probes of the local magnetization, as in Fig. 2, can establish non-ergodicity, but they do not reveal the correlations that characterize a localized phase. The structure of the regular MBL phase is understood as being defined by emergent local conserved quantities [10, 11]. These conservation laws result in localization, but the localized regions still have interactions with one another, resulting in slow spreading of correlations via entanglement after a quench from a product state (typically logarithmic spreading in time, but potentially faster for long-range interactions [39]). While the existence of similar conserved quantities in Stark MBL is debated [23, 24], there are indications that it can display similar entanglement dynamics [5, 18].
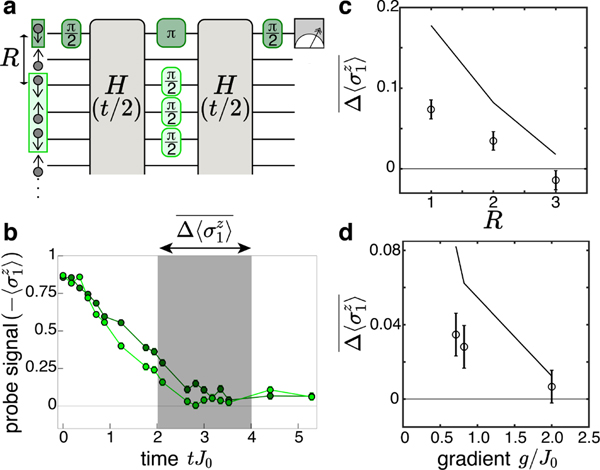
Some observables have been established to directly probe this correlation spreading, such as quantum Fisher information [27, 28] (see Methods and Extended Data Fig. 6) or techniques to measure subsystem entanglement entropy [30, 31]. Here we instead adopt a local interferometric scheme, the double electron-electron resonance (DEER) protocol, to reveal the spread of correlations controlled by the structure of the localized state [18, 29, 40]. This protocol, shown in Fig. 3a, compares two experimental sequences: one that is a standard spin-echo sequence on a probe spin within a system of interest, and one that combines this with a set of π/2-pulse perturbations on a separate subregion, the ‘DEER region’. The spin-echo sequence cancels out static influences on the probe spin, either from global external fields or from fixed configurations of the surrounding spins. If this cancellation is perfect, the probe spin will return to its initial magnetization. The DEER sequence, by contrast, removes this cancellation for the DEER spins acting on the probe spin. As a result, a difference in the return to the initial probe magnetization between the two sequences reflects correlations between the probe and DEER region generated by the dynamics. At sufficiently long times, a difference between these signals will develop in an MBL phase, but not in a non-interacting localized phase. In addition, this differential measurement setup naturally makes the signal robust against common-mode non-idealities, including experimental noise.
FIG. 3.
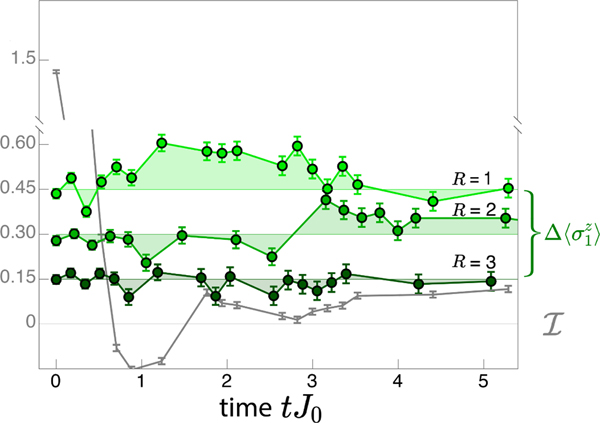
DEER Protocol. a, In the spin-echo procedure (dark green), a single probe spin undergoes a spin-echo sequence, while the rest of the spins experience normal evolution under H for total time t. In the DEER procedure (dark and light green), there are additional perturbing π/2 pulses on a region, here fixed at a size of three spins, that is R spins away. The difference in the probe magnetization following these procedures reflects the ability of the DEER region to influence the dynamics at the probe spin. We study this protocol using an initial Neel state (N = 15). b, At intermediate times, before the spin-echo signal approaches zero due to decoherence, a difference develops between the spin-echo (dark green) and DEER (light green) signals. We quantify this by taking the average difference (DEER-spin echo) between tJ0 = 2 and 4 (shaded region) after imbalance dynamics have stabilized. These data are for R = 1 and g/J0 = 0.71. c, As R is increased (at g/J0 = 0.71), the difference signal drops to zero, reflecting the incomplete spread of correlations through the system at finite time. d, As g is increased (at R = 2), the difference signal also decreases with increasing gradient, consistent with the expectation that within the Stark MBL phase, increasing localization leads to progressively slower development of correlations. Points in c. and d. are the experimental data, and solid lines are exact numerics.
In Fig. 3b-d, we demonstrate the DEER protocol and show its use in characterizing the Stark MBL regime. As time evolves, a difference accumulates between the probe magnetization in the two procedures, reflecting the spread of correlations (Fig. 3b). These correlations continue to move through the system after imbalance dynamics have stabilized (see Methods and Extended Data Fig. 7), indicating that they are not solely due to the transient imbalance evolution. Picking a time range after these transient dynamics, tJ0 = 2–4, we characterize the structure of these spreading correlations by taking the average difference between the signals over this time, . This time window is slightly earlier than the window used for the steady-state imbalance, as the DEER signal is more sensitive to experimental decoherence. Varying the DEER spin distance, R, we see that this difference signal drops as the DEER spins move progressively farther from the probe, reflecting the local nature of correlation propagation (Fig. 3c). Similarly, by sitting at a fixed separation and increasing the gradient, we observe the reduction of the difference signal at a given time, confirming that the correlation spread is controlled by the degree of localization (Fig. 3d). The dependences of the difference signal on both R and g/J0 track exact numerics, with an overall scaling difference due to decoherence reducing the experimental signal. Taken together, these probes identify the Stark MBL regime as one in which correlations spread slowly through the system despite persisting memory of the initial state. These correlations capture the role that interactions play in Stark many-body localization, distinguishing it from non-interacting localization.
DISORDER-FREE MBL BEYOND A LINEAR FIELD
If many-body localized effects are possible in the simple setting of a linearly increasing field, might they also appear in a more general class of smoothly varying fields? Utilizing the high degree of tunability of this simulator, we investigate a natural generalization: a quadratic, rather than linear, potential. We parameterize the Hamiltonian as:
| (4) |
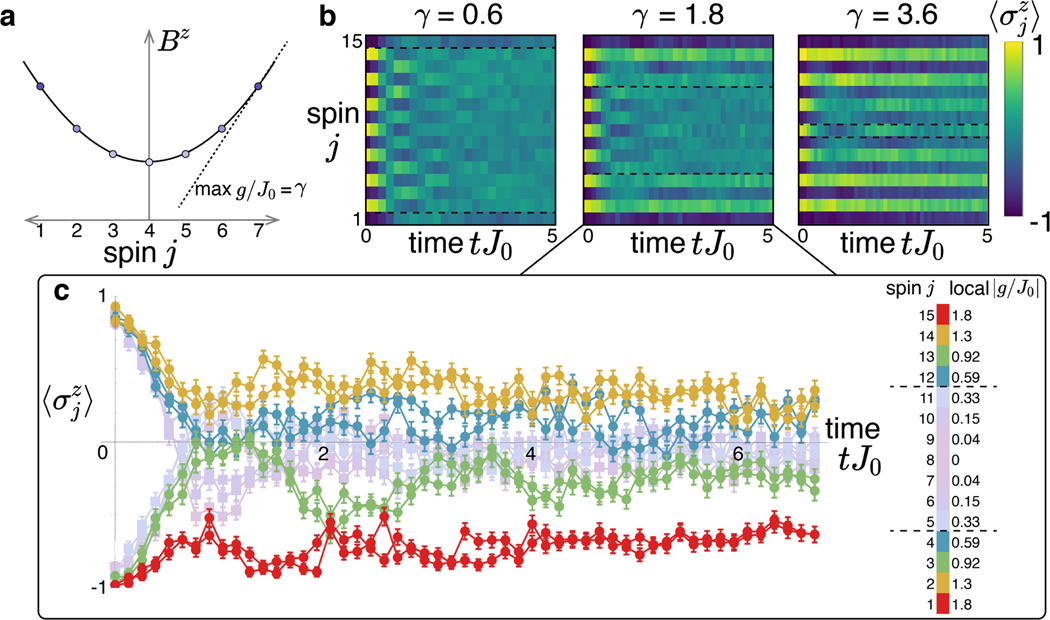
Eq. 4 describes a quadratic effective Bz field with a minimum in the center of the system and a maximum slope of at the ends of the chain. Similar models have been predicted to feature a persistent spatial separation into an ergodic core near the center and many-body localized edges [21].
We summarize the results in Fig. 4. Taking an initial Néel state (N = 15), we observe a separation of the spins into thermalizing and localized regions, which appear to evolve largely independently. We determine an approximate dividing line between these regions by the innermost spins that are clearly distinct from the thermalizing region. For a range of slowly-varying gradients γ< 3.6, this occurs at a local slope of approximately g/J0 ~ 0.5 (see Methods and Extended Data Fig. 8), comparable to observations in Fig. 2. The strongest curvature of γ = 3.6 deviates from this trend, possibly indicating a breakdown of the local-gradient approximation.
FIG. 4.
Relaxation in a quadratic field. a, We reconfigure the site-resolved field from a linear gradient to a quadratic, characterized by the maximum slope γ. For clarity, we show N = 7. b, Dynamics are split into a thermalizing region near the center of the system and localized regions near the edges, with the approximate boundaries indicated by the dashed lines. As the maximum gradient is increased, the fraction of the system in the thermalizing regime shrinks. c, Ion-resolved traces of the dynamics for max g/J0 = 1.8, showing separation of the spins into localizing regions (bright hues with round points) and thermalizing regions (faded hues with square points). Colors reflect the local field strength at each ion.
The quadratic field is an intriguing venue to explore the stability of disorder-free many-body localization in proximity to an ergodic region. In regular MBL, it is believed that such a coupling can induce many-body avalanches that destabilize the MBL region over long times [41, 42]. The extension of this effect to disorder-free MBL, which does not feature any resonances between sites, is unclear, although there are some indications that it may be more resilient than regular MBL in general [22]. The observation of a localized region in a quadratic field is also directly relevant to longstanding questions about the state of correlated ultracold atoms in an optical lattice with harmonic confinement [43].
DISCUSSION
We have seen the signatures of many-body localization in a system without disorder, suggesting that the concept of MBL may be relevant in settings well beyond the original considerations [8, 9]. Further work could analyze these observations in terms of Hilbert space fragmentation (or shattering) [23, 24, 26, 44], clarifying the connection between Stark and disordered MBL. Our realization of Stark MBL would not appear to naturally extend to the thermodynamic limit, as this results in infinite energy differences between different parts of the system. However, the Stark MBL Hamiltonian (Eq. 1) is equivalent via a gauge transformation to a Hamiltonian without a linear potential that is periodically varying in time, which has a well-defined thermodynamic limit [4].
Beyond these conceptual questions, from the perspective of near-term quantum devices, our results suggest that Stark MBL retains key aspects of the disordered MBL phase while offering certain advantages, such as not requiring a fine-grained field and being free of rare-region effects or the need for disorder averaging of observables. We summarize some aspects of the comparison in Table I. Stark MBL may be a useful resource for such devices, serving as a tool to stabilize driven non-equilibrium phases [19, 45], or as a means of making a quantum memory [3] with each site spectroscopically resolved.
TABLE I.
Comparison of disordered MBL and Stark MBL requirements, focusing on applications with near-term quantum devices. Quasi-periodic MBL occupies an intermediate position from this perspective, with some of the advantages of both disordered and disorder-free localization. For all types of MBL, questions about the conditions for asymptotic stability of localization remain, particularly in long-range interactions or more than one dimension [4, 41, 46].
METHODS
EXPERIMENTAL APPARATUS
State preparation and readout
Our apparatus has been previously described in [47–50]. We employ a three-layer Paul trap to confine 171Yb+ ions in a harmonic pseudopotential with trapping frequencies MHz and either fz = 0.51 MHz (N = 15) or 0.35 MHz (N = 25). There is a 1–2% day-to-day variation in these frequencies. Pseudospins are encoded in the two clock ground hyperfine states, with and . We drive coherent global rotations between these spin states using stimulated Raman transitions. Long-range spin-spin interactions are generated via a bichromatic beatnote that couples these states via motional modes along the direction. This is generated by three Raman beams from a pulsed 355 nm laser driving a symmetric pair of transitions, with average detunings of μ/2π = 200 kHz from the red and blue sideband transitions of the highest frequency (center-of-mass) transverse motional mode along . The resulting distribution of couplings has a best-fit power law of α = 1.28 for N = 15 and a = 1.31 for N = 25, and a best-fit J0/2π between 0.25 and 0.33 kHz, depending on day-to-day variations in laser power. This value of J0, calibrated for a given day, is used to scale energies and times in the main text.
Each experimental cycle begins with state initialization via optical pumping and Doppler and resolved-sideband cooling, which prepares the spin state with fidelity > 0.99 and the ground motional state with fidelity > 0.9. Arbitrary product states are initialized using the site-dependent AC Stark shift from the individual addressing beam (from the same 355 nm light generating the Ising interactions), combined with overall rotations, with typical preparation fidelities of > 0.9 per spin. Readout is performed via state-dependent fluorescence using the 369.5 nm transition collected on a CCD camera, with typical detection errors of 3%. All measurements presented in the main text, except for the DEER measurements, are repeated at each setting 200 times for statistics. For the DEER measurements, we instead average over 2000 repetitions, which are taken alternating between DEER and spin-echo sequences every 100 measurements so that to a very good approximation both sample any noise profile equally. The data presented have not been corrected for state preparation and measurement (SPAM) errors.
Calibration of Hamiltonian parameters
The experimental matrix is determined by measurements of motional sideband Rabi frequencies and trap parameters. Past work has validated this model against direct measurements of the matrix elements [28].
We directly measure and calibrate the linear field for each spin individually. As this calibration process is imperfect, each spin has a finite amount of deviation from the ideal linear gradient and thus there is a finite amount of effective site-by-site disorder in the experimental realization, with . While a small amount of disorder can be crucial in simulations of Stark MBL with short-ranged interactions, because it breaks the exact degeneracies of that problem [4], in the context of long-range interactions the level statistics are already generic, and this disorder does not have a substantial effect on the system in numerics. As such, we call our system ‘disorder-free’ in the sense that we only have small, technical and well-understood imperfections limiting our realization of the ideal disorder-free Hamiltonian. Any real quantum simulator can only hope to asymptotically approach a perfectly uniform environment, just as any quantum simulator can only hope to approximately realize MBL because there will always be some residual coupling to the environment that restores ergodicity at sufficiently long times.
NUMERICS
Studies of Hamiltonian level statistics with use exact diagonalization of the Hamiltonian. For simulations of dynamics we solve the Schroedinger equation using the Krylov space technique [51, 52].
For all numerics, except those shown in the subsequent Methods sections ‘Numerical studies of the ideal power-law Hamiltonian’ and ‘Scaling of with system size,’ we use the experimentally determined matrix. These couplings show some inhomogeneity across the chain, with the nearest-neighbor hopping varying 7% for N = 15. At large ion-ion separation they also show deviations from power-law behavior, with the couplings falling off faster than the best-fit power law [50]. The comparison to power-law numerics shows that each of these effects does not strongly alter the dynamics.
TROTTERIZED M-S HAMILTONIAN
We generate two types of Hamiltonian terms in this work. The first is the Mølmer-Sørensen Hamiltonian in the resolved sideband and Lamb-Dicke limits [50], created with a pair of detuned bichromatic beatnotes:
| (5) |
Here j is the ion index and v is the normal mode index, av is the destruction operator of a phonon of motion for a given normal mode of the ion chain, Ω is the carrier Rabi rate, is the Lamb-Dicke parameter, is the mode amplitude for ion j, ων is the mode frequency, and δB(R) is the red(blue) detuning. This term generates spin-motion entanglement, and in the limit the motion can be adiabatically eliminated for an effective spin-spin interaction.
The second Hamiltonian term is the local field generated by the individual addressing beam. This beam only addresses one ion at a time, and is rastered across the chain to create an overall field landscape. A single cycle of this term can be written as:
| (6) |
with as the Heaviside theta and tpulse the time for a pulse of the beam on one ion, which we experimentally fix at tpulse = 0.5 μs.
When these terms are applied simultaneously, in the limit , the transverse Ising Hamiltonian is approximately realized:
| (7) |
However, the validity of this Hamiltonian is limited to small . Therefore, when realizing a linear field gradient, , this results in the constraint , which prevents the simultaneous attainment of long chains and large linear field gradients. For example, for typical experimental parameters of N = 15, ηΩ = 2π · 30 kHz, and J0 = 2π· 250 Hz, this would require that . When this is not satisfied, additional phonon terms are present in the Hamiltonian that result in undesired spin-motion entanglement, or effective decoherence of the dynamics when measuring only spin.
We can reduce these constraints by applying a Trotterized Hamiltonian [53]. The evolution under this time-varying Hamiltonian can be analyzed using the Magnus expansion, to find the dominant contributions to time-averaged dynamics [50]. Within this framework, the undesired effects arise from the commutator [H1(t), H2(t)]. Intuitively, when these terms are no longer applied simultaneously the effect of this commutator is reduced.
Consider unitary evolution of a single Trotter cycle, using the lowest-order symmetrized sequence:
| (8) |
The Hamiltonians governing each part of the unitary evolution may be approximately replaced by their time-averaged values, simplifying both. For H2 we have
| (9) |
an exact identity since each of the terms in H2(t) commute with one another. For H1(t) we have
| (10) |
However, this is just the usual M − S Hamiltonian, and in the limit that the only significant contributing terms are the stationary ones. When this results in the pure interaction. When instead a small rotating frame transformation is applied we generate the Ising Hamiltonian with a small overall transverse field [50]:
| (11) |
The combined evolution of the full Trotter cycle is then, to lowest order, described by the Hamiltonian
| (12) |
We program to the desired functional form and absorb the factors with Δt1 and Δt2 into re-definitions of J0 and , leading to Eqs. 1 and 4 of the main text. The constant term does not depend on these times, because it is created by moving into a rotating frame that is applied to the entire time evolution. This approximation requires that (for Eq. 11), which is satisfied in the experiment: kHz and Δt1 ≥ 18 μs, whose product is 22.6. Additionally, Δt1 and Δt2 must not be so long that the Trotter approximation (Eq. 12) breaks down. However, the low energy scale of J0 and the use of the symmetrized Trotter form make this limit less constraining than the limit for continuous evolution, allowing us to reach g/J0 = 2.5 (1.5) for 15 (25) spins. Because the Trotter error consists of undesired spin terms, rather than spin-phonon terms, it can also be easily simulated numerically. Extended Data Fig. 1 shows comparisons of the Trotterized and ideal evolution in the case of the strongest gradient, showing that the Trotter error is negligible over the experimental timescale and that the Trotterization results in a significant improvement in the simulation fidelity.
In addition to reducing phonon errors, this scheme has the advantage of allowing us to tune the average Hamiltonian (Eq. 12) simply by varying Δt1 and Δt2, because . This capability allows us to scan over a range of gradient values with a single calibration, and it makes any errors on the gradient calibration common to all these scans. In the data presented here, we fix the instantaneous values of g and J0 and vary Δt1 (see Trotterized Hamiltonian parameters). In addition, we ramp the interactions up and down over 9 μs with a shaped Tukey profile to reduce adiabatic creation of phonons [48].
This implementation of Trotterized Stark MBL dynamics would be difficult to extend to more than tens of spins, as the maximum instantaneous shift required on the edge ion scales as N2, leading to the requirement of an increasingly fast drive. However, given the unbounded nature of a linear gradient, any large-scale simulation of Stark MBL is likely to be challenged by the required field difference between the two ends.
Throughout this discussion, we have taken the perspective of a Trotterized quantum simulation of a desired Hamiltonian. We could also understand this experiment in terms of Floquet theory. From this perspective, this driven system is described stroboscopically by a Floquet Hamiltonian, which to lowest order is the Hamiltonian (12), and the steady-state equilibration that we see represents prethermal evolution under this effective Hamiltonian that is expected be altered at long times by Floquet heating arising from the higher-order terms. While this picture offers a complementary way to understand these results, and interesting connections to studies of driven localization [54], for simplicity we focus on the Trotterized perspective.
Trotterized Hamiltonian parameters
For imbalance measurements at N = 15, we calibrate to g/J0 of 2.5 for Δt1 = Δt2. To scan the gradient strength, Δt2 is fixed at 18 μs and Δt1 is varied from 18–180 μs. In addition, there is an extra 9 μs of effective dead time per Trotter step associated with the Tukey pulse shaping. We fix Bz0 at 2π 1.25 kHz. For data in a quadratic field, we set = 2.0 for Δt1 = Δt2, and vary Δt2 from 10–180 μs, with all other settings kept the same as in the linear gradient.
For N = 25, we instead set g/J0 to 1.25 for Δt1 = Δt2. Δt1 is fixed at 30 μs, and Δt2 is varied between 25 and 190 μs, again with an extra 9 μs of effective dead time per cycle due to pulse shaping. Bz0 is again fixed at 2π 1.25 kHz.
For DEER measurements, we calibrate to g/J0 of 2.0. Δt2 is fixed at 18 μs and Δt1 is varied from 18–180 μs, plus an extra 9 μs of dead time associated with Tukey pulse shaping. We fix Bz0 at values varying for different datasets between 2π 0.9 and 1.25 kHz.
MAPPING TO BOSON MODEL
Our experimental Hamiltonian, from Eq. 1 of the main text, is:
| (13) |
In the limit of , and assuming that and g have the same sign, the total magnetization is conserved. For an initial state of definite total magnetization, the system then reduces to the long-range tilted XY Hamiltonian [55]:
| (14) |
This can be mapped to a system of hard-core bosons taking and , resulting in the Hamiltonian:
| (15) |
with , taking the limit U → ∞, and dropping a constant energy contribution.
This model clarifies the connection between our system and work studying Stark MBL in the context of hopping particles with interactions [4, 5]. It also illustrates the translational symmetry in our system. If j is shifted by an integer, this is equivalent to changing the chemical potential term , which has no effect in a closed system with particle conservation.
FULL LEVEL STATISTICS OF EXPERIMENTAL HAMILTONIAN
A typical ergodic system has a single-particle density matrix with support throughout the bulk, and thus has a high degree of overlap between particles. This results in level repulsion in the many-body spectrum, leading to a Wigner-Dyson energy level distribution characteristic of random matrices [34]. A typical localized system, on the other hand, has single particles that are spatially confined, and thus have little overlap, resulting in a Poissonian distribution of the many-body spectrum. In Extended Data Fig. 2 we show the full distribution of r, the ratio of adjacent energy level spacings, for the experimental Hamiltonian at selected values of g/J0. We compare it to the probability density distributions resulting from Poisson and Wigner-Dyson statistics [5]:
| (16) |
| (17) |
where Eq. 17 is an analytic approximation to the Gaussian Orthogonal Ensemble based on the Wigner Surmise [57].
While a small field gradient is needed to break the approximate integrability of the Hamiltonian [56] in the limits of g = 0 and , over the range of tilts studied experimentally the level statistics cross from being close to the Wigner-Dyson limit, with an evident dip at low r due to the proliferation of avoided crossings, to very close to the Poisson limit at high gradients. This should be contrasted with the case of short-range hopping, in which the level statistics may be highly non-generic due to exact degeneracies associated with center-of-mass conservation, making concepts of Hilbert space shattering especially relevant [4, 5, 24, 26, 44]. However, we cannot exclude the possibility of a ‘quasi-ergodic’ regime at low gradient [23]. Although the level statistics shown here are for an experimentally measured Hamiltonian, featuring small deviations from a perfectly linear gradient, these deviations do not substantially affect the level statistics, as the long-range interactions already lift the degeneracies. In the next section we show this explicitly, using the ideal power-law Hamiltonian to study more general features of Stark MBL with long-range interactions such as the scaling behavior.
NUMERICAL STUDIES OF THE IDEAL POWER-LAW HAMILTONIAN
The experimental system is approximately described by a Hamiltonian with a power-law hopping. However, as the exact experimental couplings feature inhomogeneity across the chain and deviations from power-law scaling for large ion separations, all numerics shown in the main text (as well as the previous section) use the exact Hamiltonian as determined by experimental measurements of mode structure and detuning. Nonetheless, to study the general behavior of the system it is useful to also look at the power-law Hamiltonian, which captures the dominant behavior while being translation-invariant and therefore having a more natural scaling with size. We study this numerically to characterize the behavior of with respect to α and g/J0, and to study the finite-size dependence.
Dependence of on α and g/J0
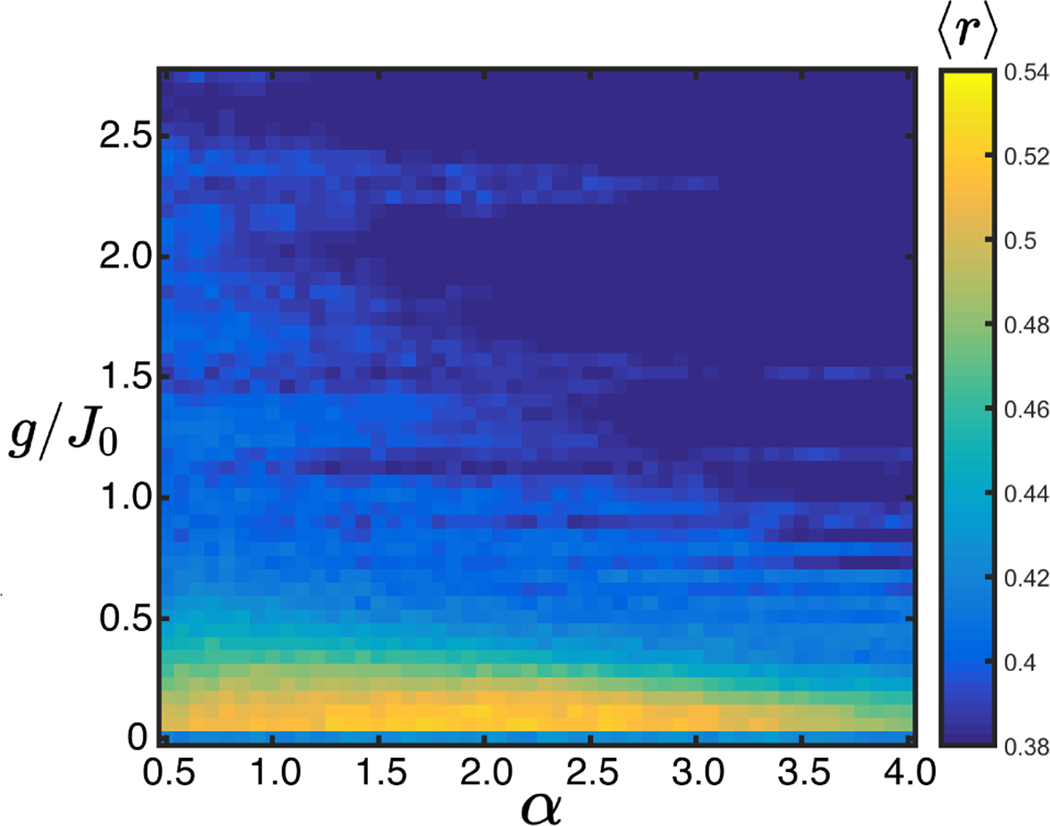
Extended Data Fig. 3 shows the dependence of the level statistics on the Hamiltonian parameters α and g/J0. The primary features of the experimental Hamiltonian statistics are retained, such as non-generic statistics for very low gradient values and a crossover from ≈ 0.5 to 0.39 for g/J0 between 0.1 and 2.0. For α < 1, the ergodic regime progressively increases, as the interaction energy is superextensive in this regime and thus delocalization is always expected for a sufficiently large system. For large α, generally decreases, which may reflect an approach to the exact degeneracies that are present in the short-range limit. The general features observed are consistent with a recent study of long-range hopping in a tilt [22] that also found persistence of a crossover in up to N = 18 and for α ≥ 1.
Dependence of on system size
Using the power-law Hamiltonian, we can study the dependence of the level statistics on system size. Extended Data Fig. 4 shows this for N ranging from 9 to 15. In general, the curves do not exhibit a simple finite-size scaling. This may be due to the long-range interactions, which also cause a system size-dependent shift in the transition in numerics for the disordered MBL case [38]. We see that the gradient-driven localization persists up to the largest systems we can diagonalize, coinciding with the size used for most of the data presented in the main text, with a full study of the scaling left as an interesting subject for future work.
GENERALIZED IMBALANCE
The generalized imbalance used in the main text is defined as:
| (18) |
For an initial state that is a product of up and down spins along z, this reduces to a simple form: the average magnetization of the spins initialized up minus the average magnetization of the spins initialized down. For an initial state that is fully polarized this imbalance is undefined, which may be considered as a drawback to this measure, but such a state is already near equilibrium and thus is not useful for quantifying equilibration.
This definition is similar to many other variations of the imbalance. For an initial Néel state with an even number of spins it is identical up to scaling factors to both the imbalance and the Hamming distance. However, in general this definition offers a few advantages:
Unlike the imbalance, it is exactly zero for a thermalized system with an odd number of spins.
It does not require any knowledge of the initial state to be added in by hand, unlike alternative observables in which the initially flipped spins are tracked.
Unlike the Hamming distance, this generalized imbalance is zero for a thermalized system, and has units of magnetization difference (therefore ranging from −2 to 2).
Finally, this generalized imbalance is less sensitive to noise than the Hamming distance. An example is useful: consider an initial state of one flipped spin ( = 1), with N = 10, and a background of spin-down ( = −1). Then, suppose that after some time this system has either evolved to a completely uniform system with an average magnetization of −1, or a state where the initially flipped spin relaxes to a magnetization of +0.8 and the remaining spins relax to −0.8. Both of these final spins have the same Hamming distance from the initial state, because they both represent a system that is an average of one spin flip from the initial state. However, the first final state is completely equilibrated, while the second has a strong memory of the initial state. The Hamming distance, therefore, is not an optimal measure of initial state memory in a situation where a few flipped spins give you more information about the initial state than the background spins.
While the Hamming distance is always 1 at time zero, this generalized imbalance only starts at 2 for an initial state in which each spin is in a definite state of σz. In Fig. 2c the experimental imbalances do not start exactly at 2, reflecting SPAM errors.
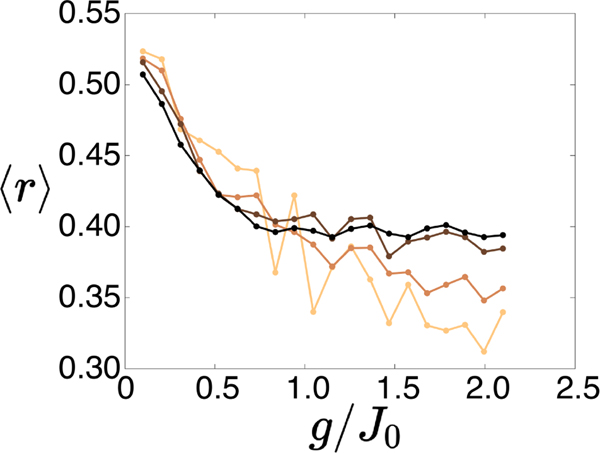
SCALING OF WITH SYSTEM SIZE
Extended Data Fig. 5 shows a comparison of our data for varying system size (Fig. 2e) with numerics. We cannot present an exact comparison, due to the computational resources needed to solve the Schroedinger equation for a 25-spin system. However, we instead present data for N = 9 and N = 15, corresponding to the same scaling factor and the lower of the two experimental system sizes. To facilitate system size comparison, we use the ideal power-law Hamiltonian for these numerics.
For the most part, only shows a slight shift with increasing N. However, there is a sharp feature near g/J0 = 1.0 that grows more prominent with increasing size, and appears similar to the experimental dip observed for N = 25. Interpretation of this feature in experimental data is complicated by decoherence that increases both with g/J0 and with N.
The dip feature seen here is initial-state dependent, and may reflect a few-body delocalization process that is especially favorable for the Néel state. This illustrates the challenge of determining the onset of localization in finite size systems, and in quenches from a particular initial state [23]. However, any such few-body process would only occur for g/J0 < 1, the regime where such resonances are possible, and we expect (consistent with the bottom panel of Extended Data Fig. 5) that for g/J0 > 1 the localization that we observe is not strongly affected by this consideration.
QUANTUM FISHER INFORMATION
Quantum Fisher information (QFI) has gained attention as a scalable entanglement witness [28, 58]. For a pure state, it is nothing more than the variance of the witness operator . For fQ > 1, entanglement is guaranteed to be present within the system [58]. As a two-point correlator that carries some information about entanglement, QFI is also similar in spirit to measures such as the Quantum Mutual Information [18] and the configurational correlator [30].
In the context of the Néel state we measure the QFI for a staggered magnetization operator, which reduces to:
| (19) |
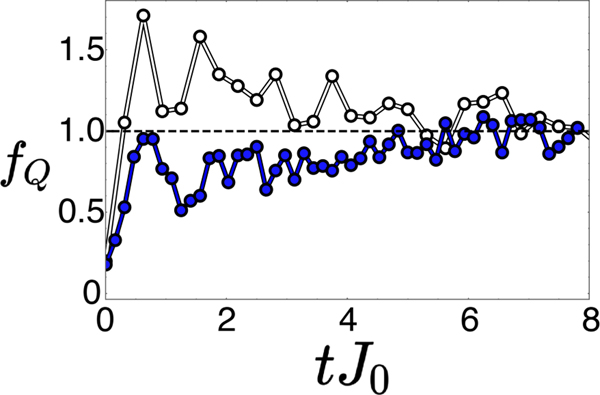
The results are shown in Extended Data Fig. 6. We see a significant difference between with weak and strong field gradients. In a weak gradient, entanglement builds up rapidly before slowly tapering off. In a strong gradient instead grows slowly, exhibiting similar behavior as expected for entanglement in an MBL phase and in Stark MBL [5].
A few shortcomings limit the value of the QFI. First, it is only easily calculated when assuming a pure state. Second, it can only be interpreted as an entanglement witness when it exceeds one, challenging in a strongly localized phase. Finally, unlike the DEER protocol it does not give spatially resolved information. Still, within its limits the QFI behavior is consistent with the expectations for an MBL phase. The QFI dynamics also closely resemble previous observations for disordered MBL [28], consistent with expectations that disorder or strong gradients result in similar entanglement spreading.
ADDITIONAL DEER DATA
Additional data for the DEER protocol difference signal is shown in Extended Data Fig. 7. Looking at the DEER difference signal, we see that correlations develop more slowly as the DEER region R is moved progressively away from the source. For R = 2, these correlations are only visible after the imbalance dynamics have reached a steady state. This rules out attribution of the correlations to the transient population dynamics, and instead resembles the slow correlation dynamics that occur in a disordered MBL system after populations have reached a steady state [10, 11, 30].
CRITICAL SLOPE IN QUADRATIC FIELD
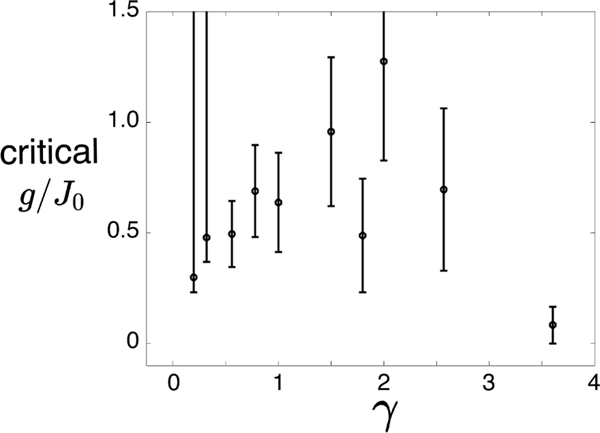
Extended Data Fig. 8 presents the dependence of the critical value of g/J0 for a quadratic field with different values of the curvature . The critical value is determined by the innermost pair of spins that are both separated from the center spin by more than their mutual error bars, judged by taking the mean and standard deviation of the average magnetizations for the last five time points.
The data are largely consistent in suggesting a critical gradient value on the order of g/J0 = 0.5. However, the strongest curvature is notably different, possibly reflecting a breakdown of the local gradient approximation for this case. For curvatures less than this, we conclude that the system seems roughly consistent with a picture of localization that is determined by the local Stark MBL field slope at any given spin.
Extended Data
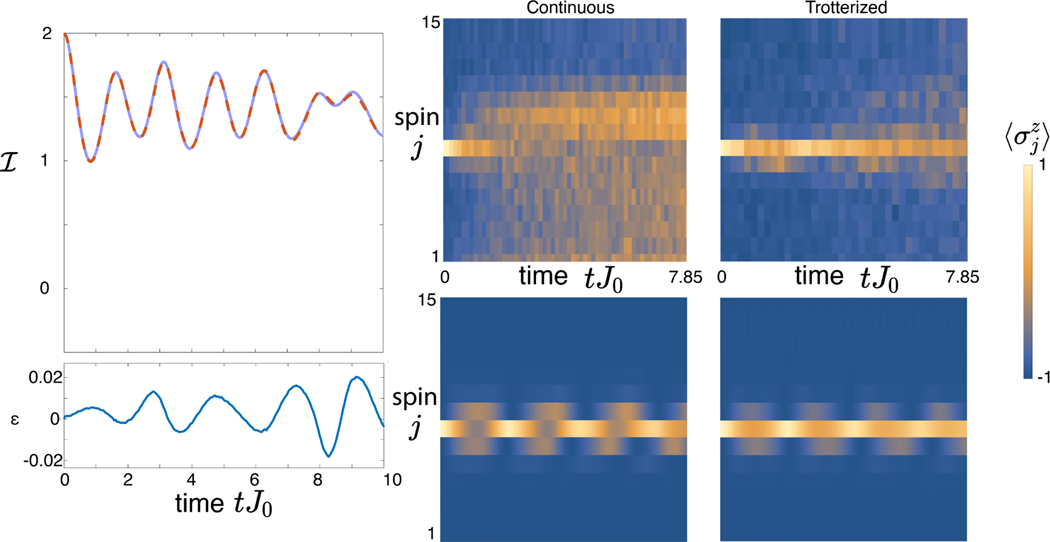
Extended Data Figure 1.
Trotterization scheme. Left top: Comparison of the imbalance dynamics for the averaged Hamiltonian of Eq. 12 (solid blue line) with the full Trotter evolution (dashed orange), for the case of an initial Neel state (N = 15) and parameters corresponding to the strongest experimental field gradient. Left bottom: difference (averaged - Trotter), showing the the error over experimental timescales is on the order of one percent. Right: experimental examples (top row) of continuous and Trotterized evolution, both at g/J0 = 1.5, compared to simulations (bottom row) using the (slightly different) parameters of the individual experimental realizations. Although the Trotterized evolution lasts nearly twice as much time in absolute units, since the averaged J0 is roughly half as large, it nonetheless shows a substantial reduction in decoherence and improvement in fidelity to the desired Hamiltonian. An initial state with one spin flip is chosen for this comparison, as it makes the effect of decoherence due to phonons more pronounced compared with a state near zero net magnetization.
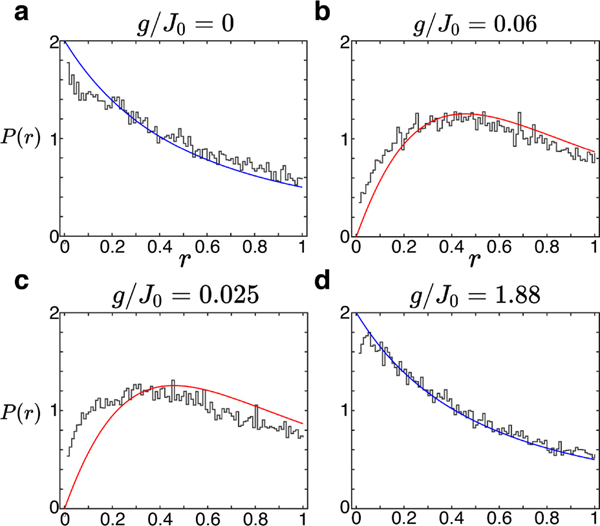
Extended Data Figure 2.
Probability density distributions of r, the ratio of adjacent energy level spacings, for the experimental Hamiltonian (Eq. 1 of the main text) at various values of g/J0 and N = 15. Numerics are compared with the distribution expected for either a Poisson level distribution (blue lines in a. and d.) or a Wigner-Dyson distribution (red lines in b. and c.). The level statistics in the absence of a field gradient are near the Poissonian limit, which may reflect the proximity to an integrable limit for the low-energy sector [56]. A small gradient results in statistics near the Wigner-Dyson limit, followed by an approach to Poisson statistics as the gradient is increased.
Extended Data Figure 3.
Dependence of 〈r〉 on power-law range α and g/J0 (N=13, Bz0/J0 = 5). In the experiments presented in the main text α ≈ 1.3.
Extended Data Figure 4.
Dependence of level statistics on system size. Level statistics for N = {9,11,13,15} (light to dark), for α = 1.3 and Bz0/J0 = 5.
Extended Data Figure 5.
Scaling of with system size. Top left: As the system increases from N = 9 to N = 15, the largest change is in a sharpening feature near g/J0 = 1 that shifts downward and towards higher gradient. Top right: while we cannot solve for for N = 25, experimentally we see a similar dip (reproduced from Fig. 2e of the main text). Bottom left: expanded view of for N = 9 and N = 15, showing similar localization beyond g/J0 = 1.
Extended Data Figure 6.
Quantum Fisher information. Normalized quantum Fisher information for a Neel state (N = 15) with g/J0 = 0.24 (white) and g/J0 = 2.4 (blue), corresponding to the lowest and highest-gradient data in Fig. 2d. Points are experimental observations, with lines as guides to the eye. A value greater than one (dashed line) is an entanglement witness. After the initial fast dynamics up to tJ0 ≈ 1, the QFI is consistent with saturation for the low gradient, and with slow entanglement growth for the high gradient, with behavior very similar to that previously observed in disordered MBL [28].
Extended Data Figure 7.
DEER Difference signal for R = {1,2,3} (light to dark), compared with the imbalance for the same parameters. Data are offset for clarity but otherwise share the same axes. is taken from the same dataset as the R = 1 spin-echo data, with the probe spin excluded from the imbalance calculation. After tJ0 ≈ 2, the imbalance is essentially constant at the low but finite steady-state value corresponding to this gradient strength. However, correlation dynamics are still progressing- in particular, correlations as measured by the difference signal only begin to develop for R = 2 after this point. This is similar to the disordered MBL state, in which slow entanglement dynamics continue after the locally conserved populations have reached a steady state [10, 11, 30].
Extended Data Figure 8.
Dependence of the critical slope separating thermalizing and non-thermalized regions on the curvature . As the quadratic curvature is varied, the division between thermalizing and nonthermal regions is largely consistent with a critical slope near g/J0 = 0.5. However, the strongest curvature of = 3.6 deviates from this rule. For the lowest two values of the system was completely delocalized, and thus only the lower bound is meaningful. Error bars (aside from the first two points) denote a variation of ±1 spin location.
ACKNOWLEDGEMENTS
This work is supported by the DARPA Driven and Non-equilibrium Quantum Systems (DRINQS) Program (D18AC00033), NSF Practical Fully-Connected Quantum Computer Program (PHY-1818914), the DOE Basic Energy Sciences: Materials and Chemical Sciences for Quantum Information Science program (DE-SC0019449), the DOE High Energy Physics: Quantum Information Science Enabled Discovery Program (DE-0001893), the DoE Quantum System Accelerator, the DOE ASCR Quantum Testbed Pathfinder program (DE-SC0019040), DOE Award DE-SC0019449, the DoE ASCR Accelerated Research in Quantum Computing program (DE-SC0020312), and the AFOSR MURI on Dissipation Engineering in Open Quantum Systems (FA9550-19-1-0399).
Footnotes
CODE AVAILABILITY
The code used for analyses is available from the corresponding author upon request.
COMPETING INTERESTS
The authors declare competing financial interests: C.M. is Co-Founder and Chief Scientist at IonQ, Inc.
DATA AVAILABILITY
The data that support the findings of this study are available from the corresponding author upon request.
References
- [1].Rigol M, Dunjko V, and Olshanii M, Thermalization and its mechanism for generic isolated quantum systems, Nature 452, 854 (2008). [DOI] [PubMed] [Google Scholar]
- [2].Abanin DA, Altman E, Bloch I, and Serbyn M, Colloquium: Many-body localization, thermalization, and entanglement, Reviews of Modern Physics 91, 021001 (2019). [Google Scholar]
- [3].Nandkishore R. and Huse DA, Many-Body Localization and Thermalization in Quantum Statistical Mechanics, Annual Review of Condensed Matter Physics 6, 15 (2015). [Google Scholar]
- [4].Van Nieuwenburg E, Baum Y, and Refael G, From Bloch oscillations to many-body localization in clean interacting systems, Proceedings of the National Academy of Sciences of the United States of America 116, 9269 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Schulz M, Hooley CA, Moessner R, and Pollmann F, Stark Many-Body Localization, Physical Review Letters 122, 040606 (2019). [DOI] [PubMed] [Google Scholar]
- [6].Anderson PW, Absence of Diffusion in Certain Random Lattices, Physical Review 109, 1492 (1958). [Google Scholar]
- [7].Lee PA, Disordered electronic systems, Reviews of Modern Physics 57, 287 (1985). [Google Scholar]
- [8].Gornyi IV, Mirlin AD, and Polyakov DG, Interacting Electrons in Disordered Wires: Anderson Localization and Low-T Transport, Physical Review Letters 95, 206603 (2005). [DOI] [PubMed] [Google Scholar]
- [9].Basko D, Aleiner I, and Altshuler B, Metal–insulator transition in a weakly interacting many-electron system with localized single-particle states, Annals of Physics 321, 1126 (2006). [Google Scholar]
- [10].Serbyn M, Papić Z, and Abanin DA, Local Conservation Laws and the Structure of the Many-Body Localized States, Physical Review Letters 111, 127201 (2013). [DOI] [PubMed] [Google Scholar]
- [11].Huse DA, Nandkishore R, and Oganesyan V, Phenomenology of fully many-body-localized systems, Physical Review B 90, 174202 (2014). [Google Scholar]
- [12].Iyer S, Oganesyan V, Refael G, and Huse DA, Many-body localization in a quasiperiodic system, Physical Review B 87, 134202 (2013). [Google Scholar]
- [13].Brenes M, Dalmonte M, Heyl M, and Scardicchio A, Many-Body Localization Dynamics from Gauge Invariance, Physical Review Letters 120, 030601 (2018). [DOI] [PubMed] [Google Scholar]
- [14].Grover T. and Fisher MPA, Quantum disentangled liquids, Journal of Statistical Mechanics: Theory and Experiment 2014, P10010 (2014). [Google Scholar]
- [15].Yao NY, Laumann CR, Cirac JI, Lukin MD, and Moore JE, Quasi-Many-Body Localization in Translation-Invariant Systems, Physical Review Letters 117, 240601 (2016). [DOI] [PubMed] [Google Scholar]
- [16].Alet F. and Laflorencie N, Many-body localization: An introduction and selected topics, Comptes Rendus Physique 19, 498 (2018). [Google Scholar]
- [17].Wannier GH, Dynamics of Band Electrons in Electric and Magnetic Fields, Reviews of Modern Physics 34, 645 (1962). [Google Scholar]
- [18].Taylor SR, Schulz M, Pollmann F, and Moessner R, Experimental probes of Stark many-body localization, Physical Review B 102, 054206 (2020). [DOI] [PubMed] [Google Scholar]
- [19].Kshetrimayum A, Eisert J, and Kennes DM, Stark time crystals: Symmetry breaking in space and time, Physical Review B 102, 195116 (2020). [Google Scholar]
- [20].Zhang L, Ke Y, Liu W, and Lee C, Mobility edge of Stark many-body localization, (2020), arXiv:2009.08357.
- [21].Chanda T, Yao R, and Zakrzewski J, Coexistence of localized and extended phases: Many-body localization in a harmonic trap, Physical Review Research 2, 032039 (2020). [Google Scholar]
- [22].Bhakuni DS and Sharma A, Stability of electric field driven many-body localization in an interacting long-range hopping model, Physical Review B 102, 085133 (2020). [Google Scholar]
- [23].Doggen EVH, Gornyi IV, and Polyakov DG, Stark many-body localization: Evidence for Hilbert-space shattering, (2020), arXiv:2012.13722.
- [24].Khemani V, Hermele M, and Nandkishore R, Localization from Hilbert space shattering: From theory to physical realizations, Physical Review B 101, 174204 (2020). [Google Scholar]
- [25].Guardado-Sanchez E, Morningstar A, Spar BM, Brown PT, Huse DA, and Bakr WS, Subdiffusion and Heat Transport in a Tilted Two-Dimensional Fermi-Hubbard System, Physical Review X 10, 011042 (2020). [Google Scholar]
- [26].Scherg S, Kohlert T, Sala P, Pollmann F, Bloch BHM,I, and Aidelsburger M, Observing non-ergodicity due to kinetic constraints in tilted Fermi-Hubbard chains, (2020), arXiv:2010.12965. [DOI] [PMC free article] [PubMed]
- [27].Guo Q, Cheng C, Li H, Xu S, Zhang P, Wang Z, Song C, Liu W, Ren W, Dong H, Mondaini R, and Wang H, Stark many-body localization on a superconducting quantum processor, (2020), arXiv:2011.13895. [DOI] [PubMed]
- [28].Smith J, Lee A, Richerme P, Neyenhuis B, Hess PW, Hauke P, Heyl M, Huse DA, and Monroe C, Many-body localization in a quantum simulator with programmable random disorder, Nature Physics 12, 907 (2016). [Google Scholar]
- [29].Chiaro B, Neill C, Bohrdt A, Filippone M, Arute F, Arya K, Babbush R, Bacon D, Bardin J, Barends R, Boixo S, Buell D, Burkett B, Chen Y, Chen Z, Collins R, Dunsworth A, Farhi E, Fowler A, Foxen B, Gidney C, Giustina M, Harrigan M, Huang T, Isakov S, Jeffrey E, Jiang Z, Kafri D, Kechedzhi K, Kelly J, Klimov P, Korotkov A, Kostritsa F, Landhuis D, Lucero E, McClean J, Mi X, Megrant A, Mohseni M, Mutus J, McEwen M, Naaman O, Neeley M, Niu M, Petukhov A, Quintana C, Rubin N, Sank D, Satzinger K, Vainsencher A, White T, Yao Z, Yeh P, Zalcman A, Smelyanskiy V, Neven H, Gopalakrishnan S, Abanin D, Knap M, Martinis J, and Roushan P, Direct measurement of non-local interactions in the many-body localized phase, (2019), arXiv:1910.06024.
- [30].Lukin A, Rispoli M, Schittko R, Tai ME, Kaufman AM, Choi S, Khemani V, Léonard J, and Greiner M, Probing entanglement in a many-body-localized system, Science 364, 256 (2019). [DOI] [PubMed] [Google Scholar]
- [31].Brydges T, Elben A, Jurcevic P, Vermersch B, Maier C, Lanyon BP, Zoller P, Blatt R, and Roos CF, Probing Rényi entanglement entropy via randomized measurements, Science 364, 260 (2019). [DOI] [PubMed] [Google Scholar]
- [32].Mølmer K. and Sørensen A, Multiparticle Entanglement of Hot Trapped Ions, Physical Review Letters 82, 1835 (1999). [Google Scholar]
- [33].Lee AC, Smith J, Richerme P, Neyenhuis B, Hess PW, Zhang J, and Monroe C, Engineering large Stark shifts for control of individual clock state qubits, Physical Review A 94, 042308 (2016). [Google Scholar]
- [34].Oganesyan V. and Huse DA, Localization of interacting fermions at high temperature, Physical Review B 75, 155111 (2007). [Google Scholar]
- [35].Schreiber M, Hodgman SS, Bordia P, Luschen HP, Fischer MH, Vosk R, Altman E, Schneider U, and Bloch H, Observation of many-body localization of interacting fermions in a quasi-random optical lattice, Science 349, 842 (2015). [DOI] [PubMed] [Google Scholar]
- [36].Bernien H, Schwartz S, Keesling A, Levine H, Omran A, Pichler H, Choi S, Zibrov AS, Endres M, Greiner M, Vuletić V, and Lukin MD, Probing many-body dynamics on a 51-atom quantum simulator, Nature 551, 579 (2017). [DOI] [PubMed] [Google Scholar]
- [37].Tan WL, Becker P, Liu F, Pagano G, Collins KS, De A, Feng L, Kaplan HB, Kyprianidis A, Lundgren R, Morong W, Whitsitt S, Gorshkov AV, and Monroe C, Observation of Domain Wall Confinement and Dynamics in a Quantum Simulator, (2019), arXiv:1912.11117.
- [38].Wu Y-L and Das Sarma S, Understanding analog quantum simulation dynamics in coupled ion-trap qubits, Physical Review A 93, 022332 (2016). [Google Scholar]
- [39].Pino M, Entanglement growth in many-body localized systems with long-range interactions, Physical Review B 90, 174204 (2014). [Google Scholar]
- [40].Serbyn M, Knap M, Gopalakrishnan S, Papić Z, Yao NY, Laumann CR, Abanin DA, Lukin MD, and Demler DA, Interferometric Probes of Many-Body Localization, Physical Review Letters 113, 147204 (2014). [DOI] [PubMed] [Google Scholar]
- [41].De Roeck W. and Huveneers F, Stability and instability towards delocalization in many-body localization systems, Physical Review B 95, 155129 (2017). [Google Scholar]
- [42].Léonard J, Rispoli M, Lukin A, Schittko R, Kim S, Kwan J, Sels D, Demler E, and Greiner M, Signatures of bath-induced quantum avalanches in a many-body–localized system, (2020), arXiv:2012.15270.
- [43].Kondov SS, McGehee WR, Xu W, and DeMarco B, Disorder-Induced Localization in a Strongly Correlated Atomic Hubbard Gas, Physical Review Letters 114, 083002 (2015). [DOI] [PubMed] [Google Scholar]
- [44].Sala P, Rakovszky T, Verresen R, Knap M, and Pollmann D, Ergodicity Breaking Arising from Hilbert Space Fragmentation in Dipole-Conserving Hamiltonians, Physical Review X 10, 011047 (2020). [Google Scholar]
- [45].Else DV, Monroe C, Nayak C, and Yao NY, Discrete Time Crystals, Annual Review of Condensed Matter Physics 11, 467 (2020). [Google Scholar]
- [46].Agarwal K, Altman E, Demler E, Gopalakrishnan S, Huse DA, and Knap M, Rare-region effects and dynamics near the many-body localization transition, Annalen der Physik 529, 1600326 (2017). [Google Scholar]
- [47].Islam R, Edwards EE, Kim K, Korenblit S, Noh C, Carmichael H, Lin GD, Duan LM, Joseph Wang CC, Freericks JK, and Monroe C, Onset of a quantum phase transition with a trapped ion quantum simulator, Nature Communications 2, 1 (2011). [DOI] [PubMed] [Google Scholar]
- [48].Zhang J, Hess PW, Kyprianidis A, Becker P, Lee A, Smith J, Pagano G, Potirniche I-D, Potter AC, Vishwanath A, Yao NY, and Monroe C, Observation of a discrete time crystal, Nature 543, 217 (2017). [DOI] [PubMed] [Google Scholar]
- [49].Zhang J, Pagano G, Hess PW, Kyprianidis A, Becker P, Kaplan H, Gorshkov AV, Gong ZX, and Monroe C, Observation of a many-body dynamical phase transition with a 53-qubit quantum simulator, Nature 551, 601 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Monroe C, Campbell WC, Duan LMM, Gong ZXX, Gorshkov AV, Hess P, Islam R, Kim K, Pagano G, Richerme P, Senko C, and Yao NY, Programmable quantum simulations of spin systems with trapped ions, (2019), arXiv:1912.07845.
- [51].Luitz DJ and Lev YB, The ergodic side of the many-body localization transition, Annalen der Physik 529, 1600350 (2017). [Google Scholar]
- [52].Nauts A. and Wyatt RE, New approach to many-state quantum dynamics: The recursive-residue-generation method, Physical Review Letters 51, 2238 (1983). [Google Scholar]
- [53].Lanyon BP, Hempel C, Nigg D, Muller M, Gerritsma R, Zahringer F, Schindler P, Barreiro JT, Rambach M, Kirchmair G, Hennrich M, Zoller P, Blatt R, and Roos CF, Universal Digital Quantum Simulation with Trapped Ions, Science 334, 57 (2011). [DOI] [PubMed] [Google Scholar]
- [54].Ponte P, Papić Z, Huveneers F, and Abanin DA, Many-Body Localization in Periodically Driven Systems, Physical Review Letters 114, 140401 (2015). [DOI] [PubMed] [Google Scholar]
- [55].Richerme P, Gong ZX, Lee A, Senko C, Smith J, Foss-Feig M, Michalakis S, Gorshkov AV, and Monroe C, Non-local propagation of correlations in quantum systems with long-range interactions, Nature 511, 198 (2014). [DOI] [PubMed] [Google Scholar]
- [56].Neyenhuis B, Zhang J, Hess PW, Smith J, Lee AC, Richerme P, Gong Z-XX, Gorshkov AV, and Monroe C, Observation of prethermalization in long-range interacting spin chains, Science Advances 3, e1700672 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Atas YY, Bogomolny E, Giraud O, and Roux G, Distribution of the Ratio of Consecutive Level Spacings in Random Matrix Ensembles, Physical Review Letters 110, 084101 (2013). [DOI] [PubMed] [Google Scholar]
- [58].Hyllus P, Laskowski W, Krischek R, Schwemmer C, Wieczorek W, Weinfurter H, Pezzé L, and Smerzi A, Fisher information and multiparticle entanglement, Physical Review A 85, 022321 (2012). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon request.