A new alternative quantile regression model for the bounded response with educational measurements applications of OECD countries

Abstract

This article introduces a new distribution with two tuning parameters specified on the unit interval. It follows from a ‘hyperbolic secant transformation’ of a random variable following the Weibull distribution. The lack of research on the prospect of hyperbolic transformations providing flexible distributions over the unit interval is a motivation for the study. The main distributional structural properties of the new distribution are established. The different estimation methods and two simulation works have been derived for model parameters. Subsequently, we develop a related quantile regression model for further statistical perspectives. We consider two real data applications based on the educational measurements of both OECD and some non-members of OECD countries. Our regression model aims to relate the desire to get top grades on certain young students in the OECD countries with some of their Education and School Life Index such as reading performance, work environment at home, and paid work experience. It is shown that the elaborated quantile regression model has a better fitting power than famous regression models when the unit response variable possesses skewed distribution as well as two independent variables are significant in the statistical sense at any standard significance level for the median response.

1. Introduction

Education is the most important phenomenon that develops a country. In order to adapt to the ever-changing and developing world, countries use education as a tool and, in parallel, work to improve the quality of education. For this last aspect, all the important outcomes are examined. While the evaluation of education provided in formal education institutions at the national level and success rates in national exams are the most important factors, the results obtained in international exams are considered among the significant outputs. Countries that read both national and international outputs correctly make an important investment for their education systems and the development of their countries. In this context, suitable analysis and correct interpretation of the educational data sets have a very important place in terms of inferences. For these inferences, educational data sets can be related to various statistical models such as regression models (ordinary least squares), probabilistic models and advanced statistical models. These models make important contributions to the education data of countries. They can also provide important information to those concerned about how to achieve more success in various situations and what aspects of countries should pay attention to their educational development. For instance, the educational measurements can be explained by quantile regression models to relate a dependent (response) variable with independent (covariates, regressors) variables. The quantile regression has been introduced by Koenker and Bassett [25] to obtain more robust inferences than classic regression models. In the literature, there are many studies related to educational data, which have been modeled with quantile regression. For example, Reference [13] has used the quantile regressions to decide whether the relationship between school quality and performance on standardized tests differs at some point in the conditional distribution of test score gains. Reference [33] has analyzed the dispersion of returns to education in various Western countries in the mid-1990s, aiming to address the link between schooling and intra-level inequalities. Reference [42] has studied school composition effects in Denmark from the Program for International Student Assessment (PISA) 2000 data using quantile regression. Reference [43] has studied gender gaps in math, science, and reading in several countries among 15-year-old students using a quantile regression approach. Reference [19] has assessed the socio-demographic characteristics that affect student mathematics performance in the context of equal educational opportunity for a sample of PISA 2012 Turkey conducted with quantile regression analysis. Reference [30] has related the measure of the educational attainment of OECD countries with some of their Better Life Index such as life satisfaction, homicide rate, and voter turnout based on the quantile regression with the new unit probability model. In addition, Reference [2] has associated the educational attainment values of OECD countries with homicide rate and labor market insecurity variables via regression of the mean response.

Recently, the work on the unit distribution has increased with great interest in many different fields. This is mainly motivated by the practitioner's dissatisfaction with the classic unit distributions. For instance, the beta distribution can be inadequate in order to both model and predict based on the real data phenomena. The beta distribution does not take into account the events of the end zone or more flexibility in specifying the variance. For this aspect, we may refer to [6]. In light of this, the existing unit distributions have generally been elaborated by transforming well-known probability distributions. The main interest of using the transformation based on these distributions is that they do not add new parameters to them on the unit interval. To transform a positive random variable (rv) into new unit rvs, the most used transformation is centered on the negative exponential function. For instance, the Kumaraswamy [31], log-Lindley [17], unit-Weibull [37], unit Gompertz [35], log-xgamma [4], unit inverse Gaussian [16], unit generalized half normal [27], log-weighted exponential [2] and log-extended exponential geometric [22] distributions have been obtained via this method. One may see [3,18,20,26,34] for other unit models that were obtained with other transformation methods. These proposed unit distributions can present more flexible density shapes on the $(0,1)$ interval than those of their baseline distribution.

In another aspect, classical regression models are related to the mean response as a function of certain values of the covariates. If the response variable is set to the standard unit interval, the beta-by-regression model invented by Ferrari and Cribari-Neto [14] comes to mind in the first place for this purpose. Further, some alternative unit regression models can be found in [2,3,6,17,24,34]. In the case where the response variable has a skewed distribution or outliers, the classical regression model is useless since the mean is precisely affected by these situations. Quantile regression modeling can be used to solve the above problem [25]. Therefore, the regression parameters are interpretable in terms of quantile response. In particular, modeling the median response is a more robust estimate for this situation. For more details on the regression modeling of the unit median response, see [5,22,29,36]; articles on unit response quantile regression are rather rare.

In view of the foregoing, the purpose of this paper is to suggest a new unit distribution as well as quantile regression modeling for it. For scenarios when the response variable is described as rates or proportions, i.e. on the support $(0,1)$, we will give a very flexible unit distribution and its quantile regression mode. In this case, we employ a new and simple transformation of the Weibull distribution. In terms of data modeling, our suggested unit Weibull distribution will have more variable probability density and hazard rate shapes than the usual Weibull distribution. This transformation is based on the hyperbolic secant function or its inverse, the inverse hyperbolic secant function, also called the ‘arcsech’ function. To our knowledge, this direction of research remains almost unexplored in the area of unit distributions, despite the interest of hyperbolic functions in various branches of probability and statistical modeling (see [15]). ‘Almost’ because, to our knowledge, in this framework, only the arsech normal distribution by Korkmaz et al. [29] and the logitSHASHo distribution by Nakamura et al. [40] use such a hyperbolic transformation approach. Here, we motivate the fact that the considered hyperbolic transformation is able to carry the applicability of the Weibull distribution to the unit interval. Hence, we confer into the different probability density function (pdf) and hazard rate function (hrf) characteristics that the Weibull distribution does not possess over the unit interval. The motivations of the study also includes a new quantile regression modeling since the quantile function (qf) of the proposed distribution can be obtained with a closed form. Thus, its pdf and cumulative distribution function (cdf) can be easily re-parameterized in terms of any of its quantiles. This re-parameterization is applied like those of Refs. [6,36,39]. It is also to show its modeling ability with its applications based on the proportion of the educational measurements.

The paper has been set as follows. Section 2 contains the definition of the new model. Its basic distributional structural properties were obtained by Section 3. Diverse parametric estimation methods are derived by Section 4. The simulation studies and the univariate real data modeling are given in Section 5. Section 6 is devoted to the new quantile regression model. Finally, the article ends with the conclusion in Section 7.

2. Definition of the new unit Weibull type distribution

The proposed unit distribution has a special random structure which is described below. First, let us introduce a rv T having the Weibull distribution with parameters $\alpha >0$ and $\beta >0$, that is $T\sim W(\alpha ,\beta )$ with cdf given as $H(t,\alpha ,\beta )=1-e^{-\alpha t^{\beta }}$ for t>0, and $H(t,\alpha ,\beta )=0$ for $t\le 0$. Now, we introduce the rv

$$X=\mathrm{sech}T,$$

where $\mathrm{sech}y=2/(e^y+e^{-y})=2e^y/(e^{2y}+1)\in (0,1)$ for $y\in \mathbb{R}$. The taking into account of this hyperbolic transformation to define an unit distribution is an originality of the study, even if its use is not so rare in other domains of probability, as discussed in [15], for instance.

The main distributional functions of X are given in the following result.

Proposition 2.1

For $x\in (0,1)$, the cdf and pdf of the proposed distribution are given as

$$F(x,\alpha ,\beta )=e^{-\alpha (\mathrm{arcsech}x{)}^{\beta }}$$ (1)

and

$$f(x,\alpha ,\beta )=\frac{\alpha \beta }{x\sqrt{1-x^2}}(\mathrm{arcsech}x{)}^{\beta -1}{e}^{-\alpha (\mathrm{arcsech}x{)}^{\beta }},$$ (2)

respectively, where $\mathrm{arcsech}x=\log [(1+\sqrt{1-x^2})/x]\in (0,+\mathrm{\infty })$ for $x\in (0,1)$.

In the Supplemental file, the verification of this proposition, as well as those of all the subsequent results, is postponed.

In the special case where $\beta =1$, note that the cdf and pdf are reduced to

$$F(x,\alpha ,\beta )=\frac{x^{\alpha }}{(1+\sqrt{1-x^2}{)}^{\alpha }},f(x,\alpha ,\beta )=\frac{\alpha }{\sqrt{1-x^2}}\frac{x^{\alpha -1}}{(1+\sqrt{1-x^2}{)}^{\alpha }},$$

for $x\in (0,1)$, which are new in the literature.

In full generality, we call the new distribution as arc-secant hyperbolic Weibull distribution and denote the distribution of X with $\mathrm{ASHW}$ or $\mathrm{ASHW}(\alpha ,\beta )$ when the showing of α and β is needed. Identifiability is an important property of the statistical distributions to satisfy the precise inference for the model parameters. The following proposition is given to prove the identifiability property of the ASHW distribution.

Proposition 2.2

The ASHW distribution is identifiable.

Based on Equations (1) and (2), the hrf of the $\mathrm{ASHW}$ distribution is indicated as

$$h(x,\alpha ,\beta )=\frac{\alpha \beta }{x\sqrt{1-x^2}}(\mathrm{arcsech}x{)}^{\beta -1}[e^{\alpha (\mathrm{arcsech}x{)}^{\beta }}-1{]}^{-1}.$$ (3)

From Equation (2), the possible mode(s) of the $\mathrm{ASHW}$ distribution is obtained as the solution(s) of the following nonlinear equation:

$$-\frac{1}{x}+\frac{x}{1-x^2}-(\beta -1)\frac{(x\sqrt{1-x^2}{)}^{-1}}{\mathrm{arcsech}x}+\alpha \beta (x\sqrt{1-x^2}{)}^{-1}(\mathrm{arcsech}x{)}^{\beta -1}=0.$$

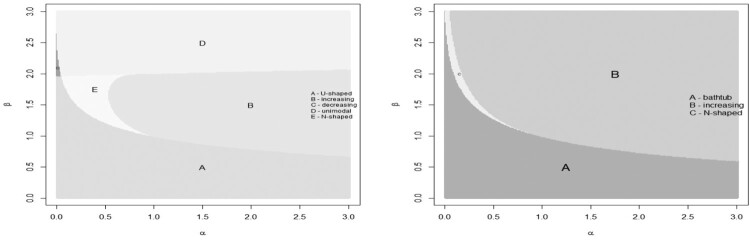
The set of solution(s) of this equation is complicated to determine via an analytical approach. This high level of complexity still holds for the analysis of the possible shapes of $f(x,\alpha ,\beta )$ and $h(x,\alpha ,\beta )$, motivating a graphical work in this regard. Figure 1 presents the reachable shape regions of the pdf and hrf of the ASHW distribution. Figure 2 also supports shapes of these regions.

Figure 1.

Possible shape regions of the pdf (left panel) and hrf (right panel).

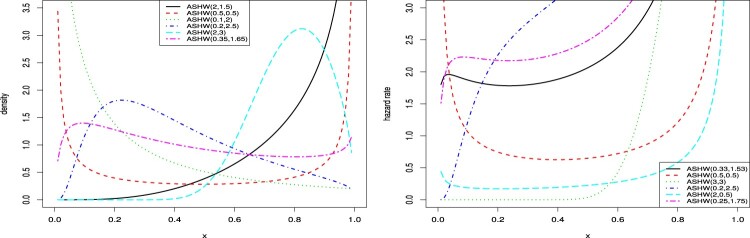
Figure 2.

Curves of the pdf (left panel) and hrf (right panel).

According to these figures, both parameters of the new model are the shape parameters since they play a role for the model shapes. In addition, the shapes of the pdf can be seen as various shapes such as U-shaped, increasing, decreasing, unimodal and N-shaped as well as its hrf shapes can be bathtub, increasing and N-shaped.

Moreover, the linear transformation $Z=(\kappa -\theta )X+\theta$ transports the domain of X to other bounded interval $(\theta ,\kappa )$, with $\theta <\kappa$ for $\theta ,\kappa \in \mathbb{R}$. Thus, its pdf and hrf flexibility can be extended to the different domains. Consequently, the new unit model has distinguished density and hrf shapes such as N-shaped, its modeling ability is very flexible beyond the unit interval.

3. Properties

This section examines some characteristics and properties of interest satisfied by the $\mathrm{ASHW}$ distribution. Discussions on some aspects of the new distribution and well-established distributions take place.

3.1. Some stochastic ordering results

The behavior comportment of the cdf with respect to the parameters is studied below.

Proposition 3.1

The following properties hold for $x\in (0,1)$.

• The cdf $F(x,\alpha ,\beta )$ is decreasing and convex with respect to the parameter α.

• The cdf $F(x,\alpha ,\beta )$ is decreasing with respect to β if $x\in (0,2e/(e^2+1))$, and increasing with respect to β if $x\in (2e/(e^2+1),1)$.

In particular, the first item in Proposition 3.1 shows that the following first-order stochastic dominance of the $\mathrm{ASHW}$ distribution is satisfied: for any ${\alpha }_1\le {\alpha }_2$, we have $F(x,{\alpha }_2,\beta )\le F(x,{\alpha }_1,\beta )$.

The proposition below refined this result through the concept of likelihood order (see [44] for further details).

Proposition 3.2

For ${\alpha }_1\le {\alpha }_2$, the $\mathrm{ASHW}({\alpha }_2,\beta )$ distribution dominates the $\mathrm{ASHW}({\alpha }_1,\beta )$ distribution in the likelihood ratio order, that is the following ratio function:

$$q(x,{\alpha }_1,{\alpha }_2,\beta )=\frac{f(x,{\alpha }_1,\beta )}{f(x,{\alpha }_2,\beta )}$$

is decreasing with respect to x.

The consequences of Proposition 3.2 are numerous, implying diverse important stochastic orders, including the first-one involving the cdf. We again refer to [44] in this regard.

The following result compares the stochastic behavior of the $\mathrm{ASHW}$ distribution and one of the most famous unit distributions of the literature: the unit-Weibull distribution by Mazucheli et al. [37].

Proposition 3.3

The $\mathrm{ASHW}$ distribution first-order stochastically dominates the unit-Weibull, that is, for any $x\in \mathbb{R}$, we have

$$F(x,\alpha ,\beta )\le F_{\ast }(x,\alpha ,\beta ),$$

where $F^{\ast }(x,\alpha ,\beta )=e^{-\alpha (-\log x{)}^{\beta }}$ for $x\in (0,1)$, $F^{\ast }(x,\alpha ,\beta )=0$ for $x\le 0$ and $F^{\ast }(x,\alpha ,\beta )=1$ for $x\ge 1$.

In the sense described in Proposition 3.3, the $\mathrm{ASHW}$ distribution can be viewed as an alternative to the unit-Weibull distribution.

3.2. Percentiles and random number generation

The percentiles of the $\mathrm{ASHW}$ distribution are defined by the inverse function of $F(x,\alpha ,\beta )$. It is specified in the result above. By inverting Equation (1), we obtain

$$x_u(\alpha ,\beta )=\mathrm{sech}[(-{\alpha }^{-1}\log u{)}^{1/\beta }]$$ (4)

for $u\in (0,1)$. In the special case $\beta =1$, we have $x_u(\alpha ,\beta )=2/(u^{-1/\alpha }+u^{1/\alpha })$. In full generality, the qf is quite manageable, which is a real plus for the practical use of the $\mathrm{ASHW}$ distribution in various applications, including statistical analyses. As an immediate measure, one can derive the median of the $\mathrm{ASHW}$ distribution given as $M=x_{1/2}(\alpha ,\beta )=\mathrm{sech}[({\alpha }^{-1}\log 2{)}^{1/\beta }]$. Furthermore, for a rv U following the unit uniform distribution, the rv $V=x_U(\alpha ,\beta )\sim \mathrm{ASHW}(\alpha ,\beta )$. Consequently, one can easily generate values from V based on generated values of U; if $u_1,u_2,\dots ,u_n$ are observed values from U, then $v_1,v_2,\dots ,v_n$ with $v_i=x_{u_i}(\alpha ,\beta )$ are observed values for V. This result will be used later in the study for simulation purposes.

3.3. Moments and extensions

Since the domain of the $\mathrm{ASHW}$ distribution is $(0,1)$, for any continuous function $\psi (x)$ with $x\in (0,1)$ and $X\sim \mathrm{ASHW}(\alpha ,\beta )$, $E(\psi (X))$ exists. In particular, for any integer r, the rth ordinary and central moment of X exist and are given as

$$m_r=E(X^r),m_r^{\circ }=E[(X-m_1{)}^r].$$

The variance of X corresponds to $V=m_2^{\circ }$, and the skewness and kurtosis coefficients of X to

$$C_s=\frac{m_3^{\circ }}{(m_2^{\circ }{)}^{3/2}},C_k=\frac{m_4^{\circ }}{(m_2^{\circ }{)}^2},$$

respectively.

Mathematically, there are several ways to express these measures. The most direct way remains the integral forms. For instance, by applying the transfer theorem, we have

$$m_r={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{x}^{r}f(x,\alpha ,\theta )\mathrm{d}x=\alpha \beta {\int }_0^1\frac{x^{r-1}}{\sqrt{1-x^2}}(\mathrm{arcsech}x{)}^{\beta -1}{e}^{-\alpha (\mathrm{arcsech}x{)}^{\beta }}\mathrm{d}x,$$

which can be evaluated by using integral numerical procedures.

The following result proposes an alternative analytic expression through infinite sums involving the famous gamma function.

Proposition 3.4

Let $X\sim \mathrm{ASHW}(\alpha ,\beta )$ distribution. Then, the rth ordinary moment of X can be expressed as

$$m_r=\sum _{k,\ell =0}^{+\mathrm{\infty }}{u}_{k,\ell }^{[r]}\mathrm{\Gamma }(\frac{\ell }{\beta }+1),$$

where

$$u_{k,\ell }^{[r]}=2^r(\genfrac{}{}{0ex}{}{-r}{k})\frac{(-1{)}^{\ell }}{\ell !}(r+2k{)}^{\ell }{\alpha }^{-\ell /\beta },$$ (5)

and $\mathrm{\Gamma }(x)$ denotes the useful gamma function.

Via Proposition 3.4, $m_r$ can be investigated numerically through the following series approximation:

$$m_r\approx \sum _{k,\ell =0}^K{u}_{k,\ell }^{[r]}\mathrm{\Gamma }(\frac{\ell }{\beta }+1),$$

where K designates any arbitrary large integer.

As a numerical illustration, various moment measures of the $\mathrm{ASHW}$ distribution are determined in Table 1.

Table 1.

Some means, variance, skewness and kurtosis coefficient values of the $\mathrm{ASHW}$ distribution for selected parameter values.

$(\alpha ,\beta )$	$m_1$	V	$C_s$	$C_k$
(0.5,0.5)	0.4351	0.1825	0.2454	1.2723
(1,1)	0.6931	0.0903	−0.7692	2.2923
(1,2)	0.7049	0.0392	−0.4902	2.3828
(1,0.5)	0.6684	0.1498	−0.7287	1.8443
(0.5,1)	0.4875	0.1293	0.0607	1.4730
(2,0.5)	0.8736	0.0599	−2.2485	7.0555
(0.5,2)	0.5639	0.0597	−0.0332	1.9522
(2,5)	0.7460	0.0076	0.1023	2.5731
(2,10)	0.7038	0.0027	0.5894	3.3482
(2,2)	0.8174	0.0199	−0.9050	3.3163
(0.05,5)	0.3812	0.0184	0.9135	3.7404
(0.05,0.5)	0.0573	0.0431	3.7727	15.9425
(0.05,0.05)	0.0492	0.0458	4.1595	18.7880
(10,10)	0.7689	0.0019	0.5097	3.2001

Table 1 attests that the $\mathrm{ASHW}$ distribution can be skewed in all the directions since $C_s$ can be negative or positive, with a varying kurtosis coefficient. These features are desirable for modeling aims.

As an useful extension of the ordinary moment, one can discuss the incomplete moment. For $t\in (0,1)$, let us consider the rv $Y_t$ as X if $\{X\le t\}$ holds and 0 otherwise. Based on this truncated rv, the rth incomplete moment of X is defined by

$$m_r(t)=E(Y_t^r)={\int }_{-\mathrm{\infty }}^t{x}^{r}f(x,\alpha ,\theta )\mathrm{d}x=\alpha \beta {\int }_0^t\frac{x^{r-1}}{\sqrt{1-x^2}}(\mathrm{arcsech}x{)}^{\beta -1}{e}^{-\alpha (\mathrm{arcsech}x{)}^{\beta }}\mathrm{d}x.$$

The incomplete moments are involved in the determination of various mean deviations, conditional moments, various curves and reliability functions. In this regard, see [7].

The next proposition offers a manageable series expansion for these incomplete moments.

Proposition 3.5

Let $X\sim \mathrm{ASHW}(\alpha ,\beta )$ distribution. Then, the rth incomplete moment of X evaluated at t can be expressed as

$$m_r(t)=\sum _{k,\ell =0}^{+\mathrm{\infty }}{u}_{k,\ell }^{[r]}\mathrm{\Gamma }(\frac{\ell }{\beta }+1,\alpha (\mathrm{arcsech}t{)}^{\beta }),$$

where $u_{k,\ell }^{[r]}$ is defined as in (5) and $\mathrm{\Gamma }(x,v)$ denotes the standard upper incomplete gamma function.

An approximation of $m_r(t)$ follows from Proposition 3.5 by substituting $+\mathrm{\infty }$ by any large number. Also, Proposition 3.5 generalizes Proposition 3.4; Proposition 3.4 follows by taking t = 1.

3.4. Order statistics

The notion of order statistics is one of most useful in probability and statistics, from both the theoretical and practical sides. This motivates the discussion of crucial features of the order statistics of the $\mathrm{ASHW}$ distribution. Some fundamental formulas in [11] are used. Let us consider n rvs denoted by $X_1,X_2,\dots ,X_n$ following the $\mathrm{ASHW}(\alpha ,\beta )$ distribution, and $X_{(1)},X_{(2)},\dots ,X_{(n)}$ be their ordered statistics. Then, for any $j=1,\dots ,n$, based on Equations (1) and (2), $X_{(j)}$ has the following pdf:

$$f_{X_{(j)}}(x,\alpha ,\beta )=c_{i,n}\frac{\alpha \beta }{x\sqrt{1-x^2}}(\mathrm{arcsech}x{)}^{\beta -1}{e}^{-\alpha j(\mathrm{arcsech}x{)}^{\beta }}[1-e^{-\alpha (\mathrm{arcsech}x{)}^{\beta }}{]}^{n-j},$$

for $x\in (0,1)$, where $c_{i,n}=n!/[(j-1)!(n-j)!]$ and $f_{X_{(j)}}(x,\alpha ,\beta )=0$ for $x\notin (0,1)$.

For $x\in (0,1)$, in the special case where j = 1, we get

$$f_{X_{(j)}}(x,\alpha ,\beta )=n\frac{\alpha \beta }{x\sqrt{1-x^2}}(\mathrm{arcsech}x{)}^{\beta -1}{e}^{-\alpha (\mathrm{arcsech}x{)}^{\beta }}[1-e^{-\alpha (\mathrm{arcsech}x{)}^{\beta }}{]}^{n-1},$$

and in the special case where j = n, it comes

$$f_{X_{(j)}}(x,\alpha ,\beta )=n\frac{\alpha \beta }{x\sqrt{1-x^2}}(\mathrm{arcsech}x{)}^{\beta -1}{e}^{-\alpha n(\mathrm{arcsech}x{)}^{\beta }}.$$

One can notice that this last pdf corresponds to the one of the $\mathrm{ASHW}(\alpha n,\beta )$ distribution.

Thanks to the simplicity of the $\mathrm{ASHW}$ distribution, the moments of the order statistics are quite manageable, as developed in the next result.

Proposition 3.6

For any integer s, the sth ordinary moment of $X_{(j)}$ is obtained as

$$m_{s,(j)}^{\ast }=E(X_{(j)}^s)=\sum _{k=0}^{n-j}{v}_{j,k}{m}_{j,k,s}^{†}$$

where

$$v_{j,k}=c_{i,n}(\genfrac{}{}{0ex}{}{n-j}{k})\frac{(-1{)}^k}{k+j}$$

and $m_{j,k,s}^{†}=E(W_{j,k}^s)$ denoting the sth ordinary moment of $W_{j,k}$ is a rv following the $\mathrm{ASHW}(\alpha (j+k),\beta )$ distribution, as described in Proposition 3.4.

Proposition 3.6 is useful for studying various characteristics of $X_{(j)}$, including its central and dispersion parameters. Some simple parameters of them will be used in our coming estimation procedures.

3.5. Reliability

Here, we derive a reliability parameter related to the $\mathrm{ASHW}$ distribution that can appear in many applications based on the engineering concepts. It is defined by

$$\tau =P(X_2\le X_1),$$ (6)

when $X_1$ and $X_2$ are two independent rvs following two $\mathrm{ASHW}$ distributions, possibly the same. It appears in a random system when we need to measure the chance that a certain characteristic with unit value modeled by $X_1$ is greater than another comparable characteristic modeled by $X_2$. Details on the notion of reliability parameter can be found in [32,38].

The proposition below gives a closed-form expression of τ under a precise configuration on the parameter.

Proposition 3.7

Suppose that $X_1\sim \mathrm{ASHW}({\alpha }_1,\beta )$ and $X_2\sim \mathrm{ASHW}({\alpha }_2,\beta )$. Then, the reliability parameter given in Equation (6) is expressed as

$$\tau =\frac{{\alpha }_1}{{\alpha }_1+{\alpha }_2}.$$

The simple expression of τ allows further investigations on it, like its estimation via the maximum likelihood procedure, as performed in [32] for the Weibull distribution, among others.

4. Model parameters estimation

Here, we describe six well-reputed parametric estimation methods employed in the context of the $\mathrm{ASHW}$ model. The maximum likelihood estimations (MLEs) of the model parameters have been pointed out firstly. We start by a random sample denoted by $X_1,X_2,\dots ,X_n$ from an rv following the $\mathrm{ASHW}$ distribution and with observed values denoted by $x_1,x_2,\dots ,x_n$. Then, the log-likelihood function related to $\mathbf{\Lambda }=(\alpha ,\beta {)}^{\mathrm{T}}$ is given by

$$\begin{array}{rl}\ell (\mathbf{\Lambda })& =n\log \alpha +n\log \beta -\sum _{i=1}^n\log \left[x_i\sqrt{1-x_i^2}\right]\\ & +(\beta -1)\sum _{i=1}^n\mathrm{arcsech}{x}_i-\alpha \sum _{i=1}^n(\mathrm{arcsech}{x}_i{)}^{\beta }.\end{array}$$ (7)

Based on this function, the maximum likelihood estimations (MLEs) of α and β, say $\hat{\alpha }$ and $\hat{\beta }$, respectively, are specified by

$${\hat{\mathbf{\Lambda }}}_1=(\hat{\alpha },\hat{\beta }{)}^{\mathrm{T}}=\underset{\mathbf{\Lambda }}{\mathrm{argmax}}\{\ell (\mathbf{\Lambda })\}.$$

In theory, their solving equations and profile log-likelihood (PLL) function of the β have been given in the Supplemental file.

Since theoretic equations for the MLEs contain a non-linear function according to the parameters they have to be obtained via numerical methods. After it is obtained, the MLE $\hat{\alpha }$ follows by using $\hat{\beta }$. We point out the existence of the MLEs in the Supplemental file.

Under conditions of moderate regularity, the bivariate normal distribution is useful for establishing certain statistical tools or procedures. It is well known that the MLEs have bivariate normal distribution $N_2(\mathbf{\Lambda },I^{-1})$, where I denotes the $2\times 2$ observed information matrix whose components are given in the Supplemental file. Therefore, asymptotic $100(1-\vartheta )\mathrm{\%}$ confidence intervals (CIs) for α and β are $[\hat{\alpha }\pm z_{\vartheta /2}{s}_{\hat{\alpha }}]$ and $[\hat{\beta }\pm z_{\vartheta /2}{s}_{\hat{\beta }}]$, respectively, where $z_{\vartheta /2}$ refers to the $(\vartheta /2)$th upper percentile of the standard normal distribution, and $s_{\hat{\alpha }}$ and $s_{\hat{\beta }}$ are the standard errors (SEs) of $\hat{\alpha }$ and $\hat{\beta }$, respectively, defined by the square root of first and second diagonal elements of $I^{-1}$, respectively.

Now, for the unknown model parameters, we focus on the different type estimation methods such as the maximum product spacing estimation (MPSE) [8], least squares estimation, (LSE), weighted least squares estimation (WLSE), Anderson–Darling estimation (ADE) and Cramér–von Mises estimation (CVME). Let us define the following functions which are used to define the these different type of estimators:

$$\begin{array}{rl}{Q}_{\mathrm{MPSE}}(\mathbf{\Lambda })& =\frac{1}{n+1}\sum _{i=1}^{n+1}\log [F(x_{(i)},\alpha ,\beta )-F(x_{(i-1)},\alpha ,\beta )],\\ Q_{\mathrm{LSE}}(\mathbf{\Lambda })& =\sum _{i=1}^n{(F(x_{(i)},\alpha ,\beta )-\frac{i}{n+1})}^2,\\ Q_{\mathrm{WLSE}}(\mathbf{\Lambda })& =\sum _{i=1}^n\frac{(n+2)(n+1{)}^2}{(n-i+1)i}{(F(x_{(i)},\alpha ,\beta )-\frac{i}{n+1})}^2,\\ Q_{\mathrm{ADE}}(\mathbf{\Lambda })& =-n-\sum _{i=1}^n\frac{2i-1}{n}\{\log [1-F(x_{(n+1-i)},\alpha ,\beta )]+\log [F(x_{(i)},\alpha ,\beta )]\},\end{array}$$

and

$$Q_{\mathrm{CVME}}(\mathbf{\Lambda })=\frac{1}{12n}+\sum _{i=1}^n{\left[F(x_{(i)},\alpha ,\beta )-\frac{2i-1}{2n}\right]}^2,$$

where $x_{(1)},x_{(2)},\dots ,x_{(n)}$ are the ordered values of $x_1,x_2,\dots ,x_n$. Then MPSE, LSE, WLSE, ADE, and CVME of $\mathbf{\Lambda }$ are given by

$$\begin{array}{rl}{\hat{\mathbf{\Lambda }}}_2& =\underset{\mathbf{\Lambda }}{\mathrm{argmax}}\{Q_{\mathrm{MPSE}}(\mathbf{\Lambda })\},\end{array}$$ (8)

$$\begin{array}{rl}{\hat{\mathbf{\Lambda }}}_3& =\underset{\mathbf{\Lambda }}{\mathrm{argmin}}\{Q_{\mathrm{LSE}}(\mathbf{\Lambda })\},\end{array}$$ (9)

$$\begin{array}{rl}{\hat{\mathbf{\Lambda }}}_4& =\underset{\mathbf{\Lambda }}{\mathrm{argmin}}\{Q_{\mathrm{WLSE}}(\mathbf{\Lambda })\},\end{array}$$ (10)

$$\begin{array}{rl}{\hat{\mathbf{\Lambda }}}_5& =\underset{\mathbf{\Lambda }}{\mathrm{argmin}}\{Q_{\mathrm{ADE}}(\mathbf{\Lambda })\},\end{array}$$ (11)

$$\begin{array}{rl}{\hat{\mathbf{\Lambda }}}_6& =\underset{\mathbf{\Lambda }}{\mathrm{argmin}}\{Q_{\mathrm{CVME}}(\mathbf{\Lambda })\}.\end{array}$$ (12)

respectively. It is noted that one may see these estimation procedures in [18,26–29]. Most of the above equation systems have no explicit solutions. Therefore, they need to be solved via standard numerical methods. In addition, Equations (7), (8), (9), (10), (11) and (8) may be optimized in a direct way by employing mathematical software such as R, Python, and Matlab; the numerical optimization of the functions $\ell (\mathbf{\Lambda })$, $Q_{\mathrm{MPSE}}(\mathbf{\Lambda })$, $Q_{\mathrm{LSE}}(\mathbf{\Lambda })$, $Q_{\mathrm{WLSE}}(\mathbf{\Lambda })$, $Q_{\mathrm{ADE}}(\mathbf{\Lambda })$ and $Q_{\mathrm{CVME}}(\mathbf{\Lambda })$ is always possible.

5. Empirical results for the comparing estimation methods

This section offers simulation studies and univariate data modeling for the proposed distribution. The details are provided below.

5.1. Simulation studies

We now perform two complementary graphic simulation studies to evaluate the efficiency of the above estimates compared to variable sample size n. Our methodology is as follows. First, we get $N=1000$ samples of size $n=20,25,\dots ,1000$ from an rv following the $\mathrm{ASHW}$ distribution with parameter values $\alpha =1,\beta =2$ and $\alpha =0.5,\beta =5$ for the first and second simulation studies, respectively. The needed random numbers are obtained by using the classical qf technique. All the estimates are obtained by using the R software and, more precisely, the constrOptim function. Further, we determine the average estimates (or empirical mean), bias, and mean square error (MSE) of the estimates. By setting $\hslash =\alpha$ or β, the formulas are

$${\mathrm{AE}}_{\hslash }(n)=\frac{1}{N}\sum _{i=1}^N{\hat{\hslash }}_i,{\mathrm{Bias}}_{\hslash }(n)=\frac{1}{N}\sum _{i=1}^N(\hslash -{\hat{\hslash }}_i),{\mathrm{MSE}}_{\hslash }(n)=\frac{1}{N}\sum _{i=1}^N(\hslash -{\hat{\hslash }}_i{)}^2,$$

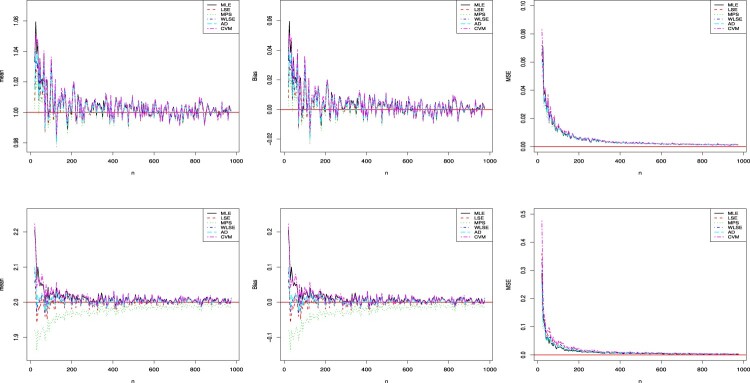
respectively, where the sums are taken over all the samples, the ith sample being symbolized by the index i. The obtained results are collected in Figure 3.

Figure 3.

Results regarding $\alpha$ (top level) and $\beta$ (bottom level) for the first simulation.

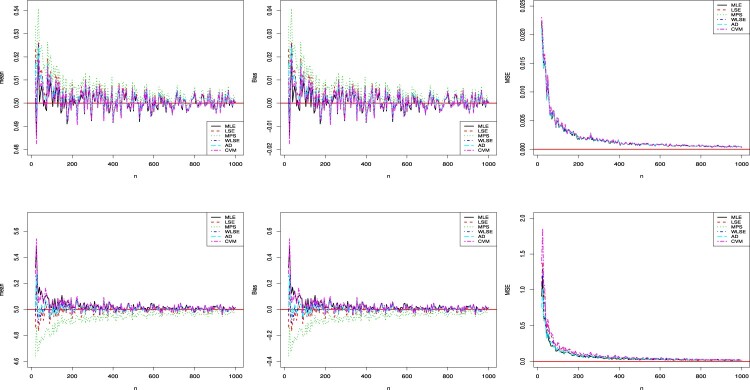
Figures 3 and 4 indicate that all the underlying estimators are consistent since the MSE and the bias decrease to zero with increasing n. The estimators are also asymptotic without bias. The quantity of the biases and MSEs of the MPS, CVM and MLE methods are initially larger than the other methods, but they are very close as n increases. parameter settings.

Figure 4.

Results regarding $\alpha$ (top level) and $\beta$ (bottom level) for the second simulation.

5.2. Real data application with univariate data

In this subsection, we analyze a real data set to see modeling ability of the $\mathrm{ASHW}$ distribution model. We obtain the data set from OECD.Stat with the following electronic link: https://stats.oecd.org/. It contains data for OECD countries and selected non-member economies. The OECD.Stat consists of themes such as Agriculture, Demography, Education and Training, Health, Finance, Labour, and Social Protection and Well-being. Each theme is divided into topics. Used data set consists of the percentage of the teachers aged 50 and below for the 48 countries which are the OECD countries and selected non-member of OECD economies. Data set can be found in an indicator of the TALIS (Teaching and Learning International Survey) in the Education and Training theme of the OECD.Stat. The reference year is 2018 for the data set.

Table 2 presents a statistical summary of the data.

Table 2.

Some summary statistics of the data set.

Minimum	Mean	Median	Maximum	Variance	Skewness	Kurtosis	n
0.4330	0.6881	0.6770	0.9450	0.0160	−0.0332	2.5009	48

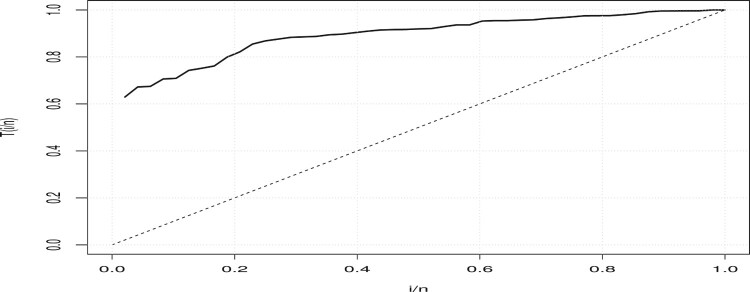
Based on Table 2, the data are clearly skewed to the left and have a lower kurtosis than the normal kurtosis. The total time test (TTT) plot [1] is an important graphical approach to verify whether the data can be applied to a specific distribution or not. According to Aarset [1], the empirical version of the TTT plot is given by plotting $T(r/n)=[\sum _{i=1}^r{y}_{(i)}+(n-r)y_{(r)}]/\sum _{i=1}^n{y}_{(i)}$ against r/n, where $r=1,\dots ,n$ and $y_{(i)}$ are the order statistics of the sample for $i=1,\dots ,n$. Aarset [1] showed that the hrf is constant if the TTT plot is graphically presented as a straight diagonal, the hrf is increasing (or decreasing) if the TTT plot is concave (or convex). The hrf is U-shaped if the TTT plot is convex and then concave. If not, the hrf is unimodal. The TTT plot for the data set is displayed in Figure 5. It can be said that the empirical hrf of the data set is increasingly shaped.

Figure 5.

TTT plot for data set.

Now, we aim to compare the adjustment power of the $\mathrm{ASHW}$ distribution according to the maximum likelihood method with those of referenced unit distributions. These competing distributions are described in the Supplemental file with their respective pdfs. They are the beta, Kumaraswamy (Kw), Johnson $S_B$ distribution by [23], and unit Gompertz (UG) distribution by Mazucheli et al. [35].

Classically, the $\hat{\ell }$ values, the following classical criteria: Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC), as well as Cramér–von-Mises, ( $W^{\ast }$), Anderson–Darling ( $A^{\ast }$) and Kolmogorov–Smirnov (KS) goodness of-fit statistics are calculated based on all distribution models to define the optimum model. It can be chosen as the optimal model which has the smallest values of AIC, BIC, $W^{\ast }$, $A^{\ast }$ and KS with the largest values of $\hat{\ell }$. The calculations are obtained by the maxLik (see [21]) and goftest functions of the R software.

Results of the data analysis based on all competitor models in Table 3. Table 3 indicates that the $\mathrm{ASHW}$ model is the best; it has the lowest values of AIC, BIC, $A^{\ast }$ and $W^{\ast }$ statistics with a higher $\hat{\ell }$ value.

Table 3.

MLEs, SEs put in parentheses, $\hat{\ell }$ and goodness-of-fits statistics for the considered data set.

Model	$\hat{\alpha }$	$\hat{\beta }$	$\hat{\ell }$	AIC	BIC	$A^{\ast }$	$W^{\ast }$	KS
ASHW	0.9363	3.8416	32.2902	−60.5805	−56.8381	0.3527	0.0562	0.0899
	(0.1448)	(0.4309)
Beta	8.0508	3.6189	31.1669	−58.3337	−54.5913	0.4740	0.0736	0.0869
	(1.4352)	(0.6412)
Johnson $S_B$	−1.2827	1.4566	29.7690	−55.5380	−51.7956	0.7137	0.1134	0.0999
	(0.1949)	0.1487
Kw	5.2872	4.0389	30.3267	−56.6534	−52.9110	0.6132	0.1003	0.0955
	(0.7289)	(0.9837)
UG	0.2025	3.8275	30.4142	−56.8284	−53.0860	0.7640	0.1274	0.1228
	(0.0949)	(0.6830)

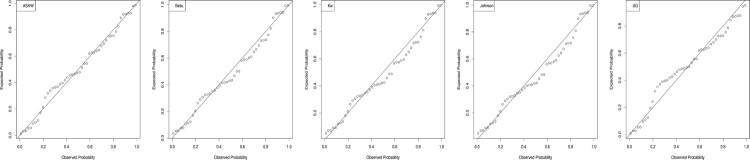
Figure 6 displays the estimated pdfs, cdfs of all distributions, and Quantile–Quantile (QQ) plots of the $\mathrm{ASHW}$ distribution to see the suitability of the fittings graphically. The proposed distribution has captured the skewness and kurtosis quite successfully. Also, the estimated cdf is near to empirical cdf. The QQ plot indicates the acceptable fitting of the $\mathrm{ASHW}$ distribution for the data set. The fitted hrf also deals with results of the TTT plot.

Figure 6.

Estimated pdfs, cdfs, QQ plot, and hrf of the $\mathrm{ASHW}$ distribution for the used data.

Figure 7 indicates that the plotted lines of the probability–probability (PP) plot of the $\mathrm{ASHW}$ distribution is closer to the diagonal reference line than those of the other models. Hence, its fitting performance is remarkable.

Figure 7.

PP plots for the fitted models based on the data set.

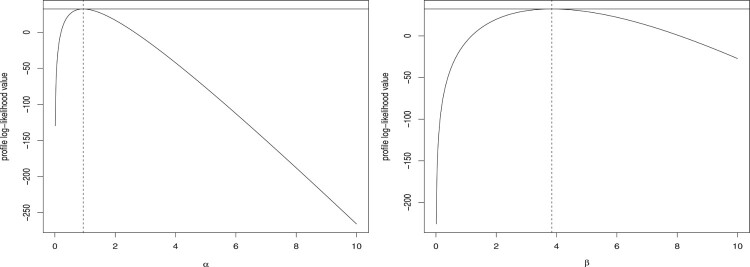
The fact that the likelihood equations have unique solutions can be shown wit the PLL functions of the parameters. This is illustrated in Figure 8.

Figure 8.

The plots of the PLL functions for the data set.

From Figure 8, the uniqueness of MLEs is demonstrated.

6. Related quantile regression model

6.1. Quantile ASHW distribution

The principle of regression modeling is to connect a response variable to a set of the regressor (independent variables or covariates). It is a statistical procedure that is generally aimed to explain the mean of the response variable via independent variables. However, the mean of the $\mathrm{ASHW}$ distribution is not a closed form (see Section 3.3). Despite this drawback, its qf given as (4) is very tractable. For this reason, we emphasize with the quantile regression modeling, also thanks to its nice features recalled below. First, the quantile regression model explains the conditional median or other quantiles of the response variable via set of the regressors. It is a strong and robust alternative model to the regular LSE model, which estimates the conditional mean of the response variable, when the response variable has outliers in the measures.

Also, regression models can be introduced based on unit distributions for unit response variables. For instance, Ferrari and Cribari-Neto [14] has proposed the beta regression model using the beta distribution, which has a simple mean based on its parameters, to model the mean of the unit response variable. In addition, as examples of the modeling quantiles of the unit response variable, there are the Kumaraswamy (see [5,39]), unit Weibull (see [36]), and log-extended exponential-geometric (LEEG) (see [22]) quantile regression models. It is noticed that the baseline models of these quantile regression models have no moments with a closed form.

Now, we focus on introducing an alternative quantile regression based on the $\mathrm{ASHW}$ distribution. First, we recall that the qf of the $\mathrm{ASHW}$ distribution is given by Equation (4). Now, the pdf of the quantile $\mathrm{ASHW}$ ( $\mathrm{QASHW}$) distribution can be given with re-parameterized based on the qf of the $\mathrm{ASHW}$ distribution. Let $\mu =x_u(\alpha ,\beta )$ and $\alpha =-\log u/(\mathrm{arcsech}\mu {)}^{\beta }$. Then, under this configuration, the pdf and cdf of the $\mathrm{QASHW}$ distribution are given by

$$g(y,\alpha ,\mu )=\frac{\beta (-\log u)}{(\mathrm{arcsech}\mu {)}^{\beta }y\sqrt{1-y^2}}(\mathrm{arcsech}y{)}^{\beta -1}{u}^{{\left(\frac{\mathrm{arcsech}y}{\mathrm{arcsech}\mu }\right)}^{\beta }}$$ (13)

and

$$G(y,\alpha ,\mu )=u^{{\left(\frac{\mathrm{arcsech}y}{\mathrm{arcsech}\mu }\right)}^{\beta }},$$ (14)

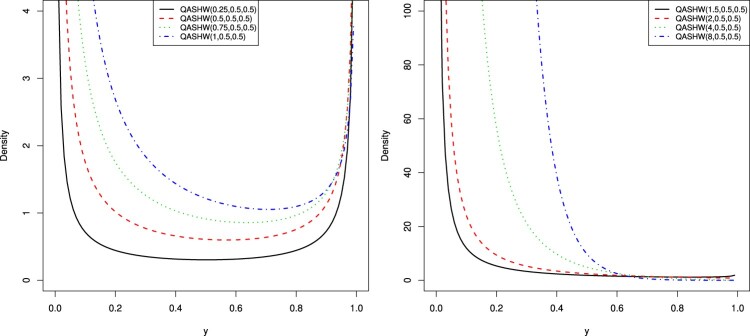
respectively, where $\beta >0$, $\mu \in (0,1)$, and $u\in (0,1)$ are known. We call it as quantile $\mathrm{ASHW}$ distribution and denote it as $\mathrm{QASHW}(\beta ,\mu ,u)$. A sample of the possible shapes of the $\mathrm{QASHW}$ distribution is presented in Figure 9. We see that it can be bathtub shaped and decreasing.

Figure 9.

The possible pdf shapes of the $\mathrm{QASHW}$ distribution.

Let, $Y_1,Y_2,\dots ,Y_n$ be n rvs from the $\mathrm{QASHW}$ distribution such that, for $i=1,2,\dots ,n$, $Y_i\sim \mathrm{QASHW}(\beta ,{\mu }_i,u)$, where ${\mu }_i$ and α are unknown parameters, and u is known. Now, let $y_1,y_2,\dots ,y_n$ be observed values of $Y_1,Y_2,\dots ,Y_n$. Then, for $i=1,2\dots n$, the $\mathrm{QASHW}$ quantile regression model is obtained as

$$g({\mu }_i)={\mathbf{x}}_i{\mathit{\delta }}^{\mathrm{T}},$$

where $\mathit{\delta }=({\delta }_0,{\delta }_1,{\delta }_2,\dots ,{\delta }_p{)}^{\mathrm{T}}$ and ${\mathbf{x}}_i=(1,x_{i1},x_{i2},x_{i3},\dots ,x_{ip})$ are the unknown regression parameter vector and the known ith vector of the covariates, respectively. The function $g(x)$ corresponds to the link function. For example, when u = 0.5, the covariates are connected to the conditional median of the response variable. A wide variety of link functions can be employed to link covariates to the response variable. In the next, we use the logit-link function specified by

$$g(x)=\mathrm{logit}(x)=\log \left(\frac{x}{1-x}\right).$$

6.2. MLE method for the model parameters

Therefore, we consider

$$g({\mu }_i)=\log \left(\frac{{\mu }_i}{1-{\mu }_i}\right)={\mathbf{x}}_i{\mathit{\delta }}^{\mathrm{T}}.$$ (15)

From Equation (15), we get

$${\mu }_i=\frac{e^{{\mathbf{x}}_i{\mathit{\delta }}^{\mathrm{T}}}}{1+e^{{\mathbf{x}}_i{\mathit{\delta }}^{\mathrm{T}}}}.$$ (16)

Inserting Equation (16) in Equation (13), the log-likelihood function of the QASHN quantile regression model is given by

$$\begin{array}{rl}\ell (\mathbf{\Delta })& =n\log \beta +n\log (-\log u)-\beta \sum _{i=1}^n\log (\mathrm{arcsech}{\mu }_i)-\sum _{i=1}^n\log \left(y_i\sqrt{1-y_i^2}\right)\\ & +(\beta -1)\sum _{i=1}^n\log (\mathrm{arcsech}{y}_i)+\log u\sum _{i=1}^n{\left(\frac{\mathrm{arcsech}{y}_i}{\mathrm{arcsech}{\mu }_i}\right)}^{\beta },\end{array}$$ (17)

where $\mathbf{\Delta }=(\beta ,\mathit{\delta })$ is the unknown parameter vector. The derivatives of the Equation (17) with respect to model parameters β and $\mathit{\delta }$ are given in the Supplemental file.

If we take u = 0.5, this quantile regression modeling is equivalent to the conditional median modeling. Under conditions of mild regularity, the asymptotic distribution of $\hat{\mathbf{\Delta }}$ is multivariate normal $N_{p+1}(\mathbf{\Delta },I^{-1})$, where $I^{-1}$ is the expected information matrix, which can be replaced by the observed information matrix. The elements of this matrix can be calculated numerically by any software. In this study, we use the avalaible maxLik function [21] of the software R, which allows us to maximize without effort Equation (17). The asymptotic SEs are also deduced.

6.3. Residual analysis

Residual analysis may be necessary to verify if the regression model is suitable. There exist several kinds of residuals. Here, we emphasize with the randomized quantile residuals developed by Dunn and Smythe [12] and the Cox–Snell residuals proposed by Cox and Snell [9].

For $i=1,\dots ,n$, we define the ith randomized quantile residual by

$${\hat{r}}_i={\mathrm{\Phi }}^{-1}[G(y_i,\hat{\beta },{\hat{\mu }}_i)],$$

where $G(y,\beta ,\mu )$ is given by Equation (14), ${\mathrm{\Phi }}^{-1}(x)$ refers to the qf of the standard normal distribution, and ${\hat{\mu }}_i$ is obtained as Equation (16) with $\hat{\mathit{\delta }}$ instead of $\mathit{\delta }$. The rule is the following: If the underlying distribution of the randomized quantile residuals are in adequateness with the standard normal distribution, then the fitted model successfully processes the data.

Alternatively, for $i=1,\dots ,n$, we list the ith Cox and Snell residual as

$${\hat{e}}_i=-\log [1-G(y_i,\hat{\beta },{\hat{\mu }}_i)].$$

In the case where the model fits to data accordingly, the distribution of the ${\hat{e}}_i$'s will distribute the unit scale parameter exponential distribution.

6.4. Data set analysis

In this subsection, a real data application is performed to show the applicability and efficiency of the proposed quantile regression model. Three competitor regression models also have been considered for comparing the fitting result. They are beta regression by the Ferrari and Cribari-Neto [14] model as well as Kw and LEEG quantile regression models, [22,39], respectively. Their pdfs are recalled in the Supplemental file.

The OECD.Stat, which is pointed out in Section 5.2, is used for the data sets again. We consider as variables the proportion of the adolescents (15-year-olds) who want top grades at school, reading performance at age 15 (PISA), proportion of the adolescents with a desk and a quiet place to study at home, and proportion adolescents who do paid work in the extra school time, of the education and school life sub-indicator of the Child Well-Being indicator in the Social Protection and Well-being theme of the OECD.Stat as data set. The reference year is 2015 for all variables. Thus, the variables represent values of the OECD countries. For the first time, PISA 2015 asked students to indicate whether they worked for pay and/or worked from home in the extra school time on the most recent day they attended school. On average in the OECD country, 23% of students reported working for pay and 73% reported working at home before or after school. Note that 15-year-olds and/or 15-year-olds are used as a shortcut for the PISA target population. PISA covers students aged 15 years at the time of assessment who are enrolled in school and have completed at least 6 years of formal education, regardless of the type of institution they belong to, whether they study full-time or part-time, whether they follow university or professional programs and whether they attend public or private schools or foreign schools in the country.

In this application, we use the proportion of the adolescents who want top grades at school percentage of the 37 OECD countries as the response variable. More precisely, the response variable is the percent of 15-year-old students who report that they agree or strongly agree with the statement I want top grades in most or all of my courses. The reference year is 2015 for the data set.

The goal is to relate the response values y with covariates $x_1$, $x_2$, and $x_3$, where

• y: adolescents who want top grades at school (%);

• $x_1$: reading performance at age 15 (PISA);

• $x_2$: adolescents with a desk and a quiet place to study at home (%);

• $x_3$: adolescents who do paid work, before or after school (%).

The regression model based on ${\mu }_i$ is given by

$$\mathrm{logit}({\mu }_i)={\delta }_0+{\delta }_1{x}_{i1}+{\delta }_2{x}_{i2},+{\delta }_3{x}_{i3}i=1,2,\dots ,37,$$

where ${\mu }_i$ is the mean for the beta model, whereas it denotes the median for the LEEG, Kw, and $\mathrm{QASHW}$ quantile regression models.

A statistical summary of the data set is given in Table 4. Based on this table, the unit response variable is left skewed and has a lower kurtosis than normal kurtosis. Hence, the use of the quantile regression is conceptually better for its inferences. For this reason, we use the unit median response modeling based on $\mathrm{QASHW}$ quantile regression modeling to obtain more informative and robust estimates.

Table 4.

Summary statistics of the used data sets.

Variable	Minimum	Mean	Median	Maximum	Variance	Skewness	Kurtosis	n
y	0.6060	0.8375	0.8520	0.9660	0.0101	−0.5054	2.2943	37
$x_1$	423.3000	490.2000	498.0000	526.7000	695.3056	−1.0763	3.7353	37
$x_2$	0.4930	0.8546	0.9020	0.9320	0.0095	−2.0060	7.1513	37
$x_3$	0.0590	0.2394	0.2310	0.4530	0.0079	0.1641	2.5454	37

Table 5 displays the results of our regression analysis. From this table, we see that the $\mathrm{QASHW}$ regression model presents lower values of the AIC and BIC with upper log-likelihood values than those of other regression models. Therefore, in this context, it can be decided that the proposed regression model is the best. Further, all parameters except ${\delta }_1$ are significant in the statistical sense at standard level for the $\mathrm{QASHW}$ regression model. The reading performance variable is not statistically significant for the median response variable. The parameter ${\delta }_2$ has affected negatively the median response, whereas the parameter ${\delta }_3$ has affected positively the median response. It is noticed that the statistically significant parameters are obtained only for the $\mathrm{QASHW}$ regression model at any significant usual level. Thus, the desire for success of adolescents, who do paid work in the extra school time, is high. However, the desire for success among adolescents, who have quiet places to study at home, remains low.

Table 5.

The results of fitted regression models with the considered criteria.

	Beta			Kw			LEEG			QASHW
Parameters	Estimate	SE	p-Value	Estimate	SE	p-Value	Estimate	SE	p-Value	Estimate	SE	p-Value
${\delta }_0$	3.4354	2.4048	0.1531	6.9321	4.2948	0.1065	1.0516	3.5265	0.7656	3.8843	1.9562	0.0471
${\delta }_1$	−0.0003	0.0049	0.9482	−0.0054	0.0072	0.4504	0.0088	0.0072	0.2219	0.0006	0.0043	0.8858
${\delta }_2$	−2.5946	1.4085	0.0655	−3.2836	1.9815	0.0975	−5.1747	1.9184	0.0070	−3.7594	1.3076	0.0040
${\delta }_3$	2.6277	1.2799	0.0401	1.5631	1.3811	0.25787	3.5001	1.8891	0.0639	3.2190	1.1611	0.0055
β	18.2200	4.2340	<0.0001	9.6263	1.6283	<0.0001	11.8175	2.5005	<0.0001	3.7775	0.4919	<0.0001
$\hat{\ell }$	43.3294			40.4710			41.3005			46.2727
AIC	−76.6588			−70.9420			−72.6010			−82.5455
BIC	−68.6042			−62.8874			−64.5464			−74.4909

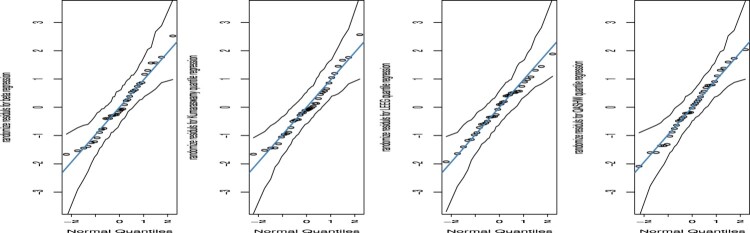
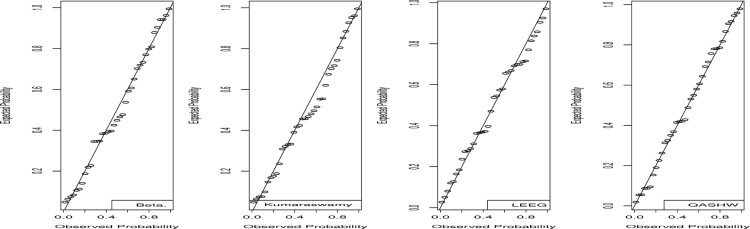
Further, Figures 10 and 11 show the QQ and PP plots of some residuals for all regression models, respectively. It can be said that the fitted points of the $\mathrm{QASHW}$ quantile regression model are close to the diagonal line for both the PP and QQ plots. Hence, these figures show a good fit of the $\mathrm{QASHW}$ regression model to the data set.

Figure 10.

The QQ plots of the randomized quantile residuals.

Figure 11.

The PP plots of the Cox–Snell residuals.

The results of the KS, $A^{\ast }$ and $W^{\ast }$ goodness-of-fits statistics are given in Table 6.

Table 6.

The goodness-of-fit results of the randomized quantile residuals for the regression models.

Models	KS	p-Value	$A^{\ast }$	p-Value	$W^{\ast }$	p-Value
QASHW	0.0678	0.9913	0.1461	0.9989	0.0184	0.9985
Beta	0.0914	0.8890	0.2624	0.9633	0.0383	0.9437
LEEG	0.0952	0.8597	0.2788	0.9529	0.0407	0.9317
Kw	0.1214	0.6037	0.3936	0.8542	0.0712	0.7472

From Table 6, we observe that the $\mathrm{QASHW}$ quantile regression model possesses the more convincing randomized quantile residuals.

7. Conclusions

We define a new alternative unit distribution model designed for the analysis of proportions and percentages of the educational measurements for OECD countries. The new quantile regression model is also developed. We have compared the results of the proposed quantile regression with those of the well-known regression models in the literature based on a data set which is related to the educational measurements for OECD countries.

The findings obtained in this study provide important suggestions for all stakeholders of education, especially those who determine educational policies, school administrators, and teachers. At the same time, the new quantile regression model constitutes a model example for future researchers.

It has been also aimed to relate the desire to get the top grades of the students with 15 year olds in the OECD countries with their reading performance, their quiet working environment at home and their situation paid work before or after school via median quantile regression modeling. The results introduce important results about how these covariates affect the response variable entitled the desire to get top grades of the students. The most surprising of these is the result that, according to the estimated regression coefficients, there is no significant relationship between reading performance and students' desire for top marks, statistically in any usual significance level. That is reading performance is not affected by the reading performances. In addition, in any usual significance level, when the percentages of the students who have a quiet working environment at home increase, the desire to get the top grades of the students decreases surprisingly.

As the rates of those who do paid work before or after school, which is another variable of the study, their desire to get the top grades also increases. Hence, it can be said that their desire to get top grades is higher than students who do not work with paid work before or after school. When the PISA 2015 result report is analyzed, it is seen that data have been collected for the first time in 2015 on this response variable. On average across OECD countries, 23% of students reported working for pay and 73% reported working at home before or after school [41]. This situation can be interpreted as the fact that students living in difficult conditions want to be more successful. The results of a study examining the differences between the career attitude and career knowledge of working and non-working students for a wage support our finding. Students with work experience showed a higher career attitude than those without [10].

In summary, the following findings have been obtained by this paper.

1. A new alternative unit distribution and its quantile regression model for the analysis of measures of proportions and percentages have been proposed.

2. The desire to get the top grades with 15 year old students in the OECD countries has been related to covariates, which are their reading performance, their quiet working environment at home, and their situation paid work before or after school. Two covariates were considered statistically significant at any level of usual significance for the median response.

3. For describing the median of the data, the quantile regression analysis application has indicated that the proposed model has provided better fits than the famous beta and Kumaraswamy regression models based on a skewed unit response variable.

4. It has been seen that the proposed modeling strategy is suitable for illustrating its potential usages.

The results based on real measurements reveal that the $\mathrm{ASHW}$ model produces better fits than popular unit probability distributions, mainly for their quantile regression models. The $\mathrm{ASHW}$ distribution is expected to attract attention both in education and in many other disciplines in demand for unit models.

Disclosure statement

No potential conflict of interest was reported by the author(s).