Don’t lose samples to estimation

Summary

In a typical predictive modeling task, we are asked to produce a final predictive model to employ operationally for predictions, as well as an estimate of its out-of-sample predictive performance. Typically, analysts hold out a portion of the available data, called a Test set, to estimate the model predictive performance on unseen (out-of-sample) records, thus “losing these samples to estimation.” However, this practice is unacceptable when the total sample size is low. To avoid losing data to estimation, we need a shift in our perspective: we do not estimate the performance of a specific model instance; we estimate the performance of the pipeline that produces the model. This pipeline is applied on all available samples to produce the final model; no samples are lost to estimation. An estimate of its performance is provided by training the same pipeline on subsets of the samples. When multiple pipelines are tried, additional considerations that correct for the “winner’s curse” need to be in place.

The bigger picture

Every predictive model needs to be accompanied by an estimate of its predictive performance on unseen data. Typically, some samples are held out to estimate performance and thus, are “lost to estimation.” This is impractical in low-sample datasets, precluding the development of advanced machine learning models. However, it can be avoided: (1) train your final model on all the data, (2) estimate its performance by training proxy models using the same machine learning pipeline on subsets of the data and testing on the rest, and (3) when trying numerous pipelines correct the estimate for multiple tries. Two protocols that abide to the above principles are presented: the Nested Cross Validation and the Bootstrap Bias Corrected Cross Validation, along with practical advice for small sample datasets. Computational experiments show that the performance of complex (e.g., non-linear and containing multiple steps) machine learning pipelines can be reliably estimated, even in small sample size scenarios.

Every predictive model needs to be accompanied by an estimate of its out-of-sample generalization) predictive performance. The typical Train-Test or Train-Validation-Test estimation protocols hold out portions of the available data for estimation purposes, thus “losing samples to estimation”. When sample size is low this practice is inappropriate. Is there a way to accurately estimate the predictive performance of our model without losing any samples to estimation?.

Introduction

We just produced a predictive machine learning model for our client or as part of scientific research of high accuracy. Unfortunately, our job as a data scientist is not done, yet! Almost invariably we don’t just deliver the model to put into production; we also need to provide an estimate of its predictive performance on new, unseen data called out-of-sample performance. Predictive performance may be measured by the area under the curve (AUC), accuracy, F1, mean squared error, or whatever metric is sensible for the problem at hand. Is performance better than random guessing, is it better than existing models, or is it as perfect as the Delphi Oracle?

Ideal performance estimation protocol

Ideally, we would like to estimate performance prospectively in the exact operational environment where the model is to be used:

• Ideal direct estimation protocol: Train a model given the available data, install it in its operating environment, wait until you prospectively gather a sizable future test dataset where the outcome also becomes known, estimate the performance of the model on the prospective data. This protocol considers anything that may go wrong when we deploy the model, from batch effects to software bugs in retrieving the data to feed into the model. Of course, it is completely impractical to perform a prospective evaluation on each model we consider. We need to know how predictive a model is before we deploy it and without having to wait to gather more data. Hence, several estimation protocols appeared that simulate this ideal estimation protocol, one or multiple times, called out-of-sample estimation protocols.

Traditional model production and estimation

The Train-Test protocol

The samples on which to measure performance should never be seen by the model generating algorithm. The standard way to provide an estimate of the model’s out-of-sample predictive performance (i.e., on unseen data), hereafter simply referred to as model performance, is to hold out a portion of the data, typically called a Test set, for estimation purposes. The rest of the data are called the Training set, used to train (fit, learn) the model to return. The Train-Test protocol directly simulates a single time the ideal estimation method, pretending the Test set comes from the “future.” Unfortunately, the samples in the Test set are lost to estimation of performance instead of being used for training and model improvement. When sample size is plenty, losing a small percentage to estimation is acceptable. The Train-Test (a.k.a., hold-out) estimation protocol is simple, has no additional computational overhead, and is highly recommended. But when sample size is small, the Train-Test protocol is unacceptable. Is there any solution out of this conundrum? The answer is yes, but we’ll have to change our perspective of what is the performance we estimate based on a key observation described below.

Key observation

The monotonicity of the learning curve of a learner

Let us plot the average performance or loss of the predictive models learned by a specific learning algorithm (say Decision Tree algorithm) on a given problem as a function of the available training sample size, shown in Figure 1. The training size is shown as a percentage of an initial available total dataset sample size. The remaining data are used as the Test set. The y axis is the loss of the model, so lower is better. What shape do we expect the curve to have? Most likely, on average, the error will monotonically be decreasing as the sample size increases (see Remarks for a discussion on this assumption). Let’s say we are given 1,000 samples in our training data. When we decide on a training set of 900 samples and apply the Decision Tree learning algorithm, we will get a specific Decision Tree model. At this point, it is useful to distinguish between the Decision Tree learning algorithm and a specific Decision Tree model providing predictions. Let’s call them the Tree Learner and Tree Model. In general, the Learner may be an analysis pipeline consisting of several steps, including preprocessing, imputation, feature selection, and not just a single modeling algorithm. The Tree Learner accepts data (predictor values + outcomes) and spits out a Tree Model. The Tree Model accepts data (only predictor values) and outputs predictions. The true performance of the Tree Model will be varying around the point on the curve on the 90% x axis point. There is variance due to the exact training set feeding the Tree Learner: different training sets will spit out different Tree Models with better or worse true average performance around the mean value on the curve. In addition, our performance estimate will have additional variance because our test set is not infinite. In fact, the smaller the test set, the larger the variance of our performance estimate, but the better performance our model will exhibit due to a larger train set and vice versa, as shown in Figure 1.

Figure 1.

The learning curve of a learning method and the Train-Test tradeoffs

A larger test set implies a smaller variance of estimation but worse model performance on average.

Which tree model to return to avoid losing samples to estimation?

Obviously, the better performing one will be—on average, not always—the one learned from 100% of the available data. But then, we have no samples left for estimation! Here is the main idea: why don’t we use a Tree Model learned from a portion of the data, e.g., 90%, and estimate its performance as a proxy of the performance to the Tree Model learned from 100% of the data! The latter will have better performance than the one we report (again, on average). Our estimate will be conservative (on average). But that is acceptable for most applications; it is optimistic estimations that are problematic. Let’s summarize:

• Principle 1: Always return the Model learned by the Learner (machine learning pipeline that includes all steps of analysis) on 100% of the available data.

• Principle 2: Estimate its performance, by Models trained by the Learner on a portion of the available data (proxies) and applied on the held-out data.

Applying these principles to the Train-Test protocol leads to the following procedure: train the Learner on the Train data, apply it on the Test data to get an estimate, and retrain using all the data to get the final model. Let us call it Train-Test-Retrain to distinguish it from the Train-Test procedure above.

Improving estimation and reducing its variance

When sample size is low (e.g., 50 samples), estimating performance using 10% or 20% (e.g., 10 samples) of the data in the Test set will still have a large variance. Our exact estimate value depends on how well we do on these specific 10 samples, i.e., it depends on how we partitioned the data to train and test sets. We can reduce this uncertainty by repeating the estimating procedure several times and averaging out. Specifically, we can partition several times to train and test sets, simulating the ideal protocol multiple times. Each time we learn a Tree Model using Tree Learner on 90% of the data, test and estimate performance on the remaining 10%, and return the average of these performances. The averaging reduces the component of the variance due to the specific split to train and test sets. This is called the Repeated Hold-Out protocol.¹ In the Repeated Hold-Out, the test sets may have some overlap. Hence, some samples may be used multiple times for performance estimation (providing predictions that are not independent given the model) and some not at all. We can enforce the test sets to be mutually exclusive and cover all available samples. We can partition samples to K (e.g., 5) equally sized folds and each time train on all but one, and estimate using the held-out fold. This is the famous K-fold Cross Validation protocol (CV).² It guarantees each sample will be used once and only once in a test set. The maximum value of K can equal the number of samples leading to the Leave-One-(sample)-Out CV or LOO-CV. We can further reduce the variance of estimation of the K-fold Cross Validation by repeating it with a different partitioning to folds and averaging out. This is the Repeated K-fold Cross Validation protocol,³ highly recommended for tiny sample sizes. It guarantees each sample will be used the same number of times for testing predictions. Stratification of folds is a technique that further reduces variance of estimation.^4,5 It partitions data to folds with the extra constraint that the distribution of the outcome in each fold is close to the distribution of the outcome in all samples. Overall, we have replaced the Train-Test-Retrain protocol with a CV-Retrain or Stratified, Repeated CV-Retrain protocol to reduce the variance. Notice that, according to Principle 1, the final model is always produced by training on all data. It is only the estimation process that is changing. Finally, focusing on the value K of the number of folds, we warn against blindly applying the maximum K and LOO-CV that can catastrophically fail in some situations.⁶ We propose that at least one sample per class should be in each fold, leading to a maximum K equal to the size of the minority class.

• Practical advice: For small sample sizes (<100 per class) use a Stratified, Repeated K-fold Cross Validation, of 4 to 5 repeats, with retraining on all data to produce the final model with a maximum K the number of samples in the rarest class.

A shift of perspective in estimating performance

In 5-fold Cross Validation we’ll build five Tree Models from 80% of the data, estimate their performance on a 20% test, and return the average. But the actual Tree Model to use in operational environment is the Tree Model learned on 100% of the data. We never directly apply the final Tree Model on a test set to get the estimate; we have no samples left. So, what performance are we estimating? We are estimating, the average performance of the Tree Models produced by the Tree Learner when trained on 80% of the samples in the given data distribution; let us define this quantity as the Learner performance, in contrast to the Model performance defined above. A subtle, but quite important, shift of perspective just occurred:

• Perspective shift: We do not directly estimate the predictive performance of a specific predictive model instance. We estimate the performance of the learning function (machine learning pipeline) that produces the final predictive model.

This approach is what saves us from losing samples to estimation. It is depicted in Figure 2. In fact, it is our only current alternative for tiny sample sizes, e.g., fewer than 20 per class in a classification problem. Notice I write “per class” because one may have 1,000,000 samples available, but if one of the classes is rare (say 1 in 100,000) that still makes estimation challenging. For time-to-event (survival analysis) problems, what matters is not the total sample size but the non-censored cases, meaning the samples for which the event has occurred (e.g., patients who have died). There is a psychological downfall, however: we never directly apply and test the specific Tree Model we’ll be using. Some practitioners feel uneasy about this. Nevertheless, this is a sound statistical methodology and there is plenty of empirical evidence that it works correctly, even in the most challenging of data analysis scenarios with quite low sample size and hundreds of thousands of predictors (features).^5,7 To ease one’s mind, it is better to not only return a point estimate of performance, but also a confidence or credible interval (see Tsamardinos et al.⁴ for methods to produce such intervals).

Figure 2.

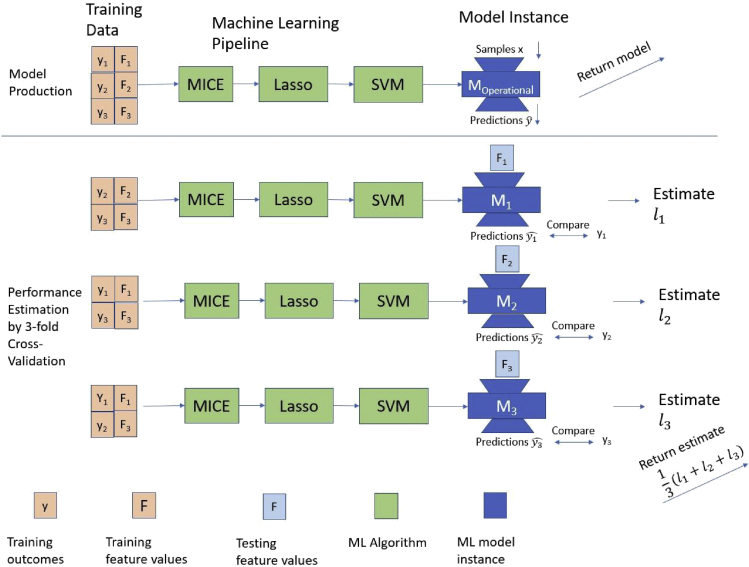
An example of the proposed estimation principles

The model to return M_operational is trained on all available data so there is no loss of samples to estimation. It is produced by a machine learning pipeline (Learner) consisting of an imputation of missing values algorithm (MICE), a feature selection algorithm (Lasso), and a modeling algorithm (SVM) with default hyper-parameters. The pipeline is 3-fold cross validated. Each time two-thirds of the data are used for training, and one-third for testing: the feature values F_i are input to the corresponding model instance M_i, predictions $\widehat{y_i}$ are obtained, they are compared with the true outcomes y_i, and the performance (loss) l_i is computed. The average loss is returned as an estimate of the loss of M_operational. We do not directly estimate the loss of M_{operationally} by applying it on a hold-out test set; we are estimating the loss of the pipeline that produced M_operational. The pipeline is cross validated as an atom (see Remarks) thus simulating the ideal estimation protocol in each iteration; we do not cross-validate just the final modeling step which uses the SVM algorithm.

Disclaimer: statistical validation versus external validation

The methodology presented estimates the performance of the Learner, and the respective predictive model. Does this mean that we do not need an external validation set then? Well, the presented methodology is correct assuming the data distribution in the operational environment of the final model is the same as in the training data. It is a statistical validation of our analysis. However, the procedure cannot account for differences in the data distribution in the operational environment, due to systematic sampling biases, batch effects, systematic measurement errors, software bugs, or distributional shifts. For example, we may estimate the accuracy of a Tree Model to classify spam e-mail trained on data with 50% spam and 50% non-spam e-mail distribution. But a user who receives only 5% spam e-mail will experience a much different accuracy by the model, since accuracy depends on the class distribution (AUC on the other hand, is invariant to the class distribution and should remain the same). In a clinical setting, a model’s performance estimated from data on Americans may not transfer to Europeans, as the data distribution of their clinical, demographics, and lifestyle values may be systematically different. External validation sets are required to operationally validate the model and ensure results transfer to other laboratories, settings, measuring equipment, or operational environments; but they are not required to statistically validate a learning pipeline.

Model production and estimation in the age of hyper-parameter optimization, tuning, and model selection

What we presented holds true only for a single learning function! In a typical analysis, we do not apply just a single pipeline or Learner but numerous ones, depending on the choice of algorithms as well as their hyper-parameter values. The problem of optimizing these choices leads to the Hyper-Parameter Optimization (HPO) or Combined Algorithm Selection and HPO (CASH)⁸ problems (we’ll use the terms interchangeably), or simply Tuning. It is not uncommon for modern HPO libraries⁹ to try thousands of pipelines. How should we produce the final model and its performance estimate when tuning takes place?

The challenge of performance estimation when tuning

First, let’s examine the estimation problem and challenge arising from trying multiple Learners. Let’s assume we cross-validate 100 pipelines and the winning pipeline had 90% CV-ed accuracy. Should we just report that the final model’s accuracy is expected to be 90% on new data? Unfortunately, no! The 90% estimate is expected to be optimistic (biased). When we try several pipelines and choose the one with the highest estimated performance, statistical phenomena like the “winner’s curse” a.k.a. the “multiple comparisons (in induction algorithms) problem” in machine learning appear.¹⁰ Our performance estimates become optimistic because we choose the best among many. The winner’s curse is conceptually equivalent to the problem of multiple hypothesis testing. Simple simulation examples are in Document S1. A simple mathematical proof is in Tsamardinos et al.⁴ but it is easy to intuitively see why this phenomenon occurs: we are incorrectly simulating the ideal estimation protocol. We pretend the test set(s) comes from the “future,” but we use the test set(s) to pick the winning model! It sounds innocuous enough, but in low sample sizes, the optimism could be as much as 20 AUC points.⁵ Another interpretation of this phenomenon is that we are more likely to choose a pipeline that is particularly “lucky” on the specific test set or sets (i.e., it overfits the test data). The conclusion is that we need estimation protocols that correct for the “winner’s curse.”

Model production and estimation when tuning

The traditional approach of Train-Tune-Estimate, a.k.a., Train-Validate-Test

Since trying multiple pipelines on the same held-out set (or sets if we CV) leads to optimistic estimation, let’s reserve a second, untainted held-out set for applying only the winning pipeline. To differentiate between the two different held-out sets, one is called the Validation, and the other the Test set. This leads to the Train-Validate-Test protocol. The Validation set is used several times, but it is used only to select the winning model, not to report the final performance estimate. The Test set is used only once. Train-Validate-Test correctly simulates the ideal protocol: we simulate the fact that we put into operational use the winning model after validation, and then prospectively measure performance on the Test set. This protocol is the simplest generalization of the Train-Test protocol when Tuning is taking place. Again, when sample size is ample, it is the simplest to implement and highly recommended. The terminology “validation” set comes from early artificial neural network jargon. The terms “validation” and “test” are quite overloaded; hence, we propose the terms “Tune” and “Estimate” sets to clearly indicate their purpose is to tune our choices of hyper-parameters and algorithms to use (the learning pipeline) and estimate final performance, respectively. The obvious problem with the traditional approach is that both the Tune and Estimate sets are lost to estimation purposes. Can we do better?

Model production when tuning

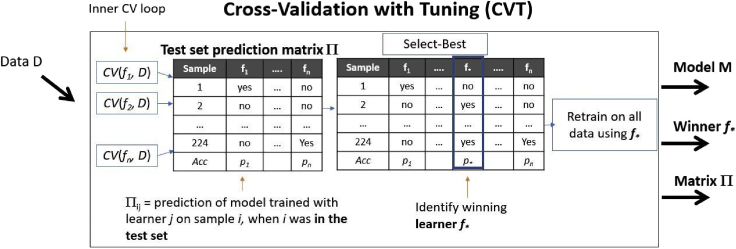
When tuning, the procedure that takes us from data to model, i.e., our Learner, includes a tuning step where multiple pipelines (sub-Learners) are tried and evaluated to find the winning one. In that sense, it is a meta-learning procedure that internally tries other Learners. One such methodology is presented in Figure 3. This is the arguably the simplest methodology; see Remarks for a discussion on more advanced techniques. In Figure 3, a number of pipelines f₁, …, f_n are cross validated, denoted by function CV (any other estimation protocol can be used like the Train-Tune), and the winner is found. Let us call it Cross Validation with Tuning or CVT. Just like Train-Tune, we use held-out sets (the folds of CV) to select the winning pipeline. The main difference is that according to Principle 1, we retrain on all input data using the winner. Hence, CVT trains K×C+1 models, where C is the number of pipelines and K the number of folds. Notice that in the figure, we assume that the predictions made by each pipeline f_i on each sample, when the latter is serving in a held-out fold, are stored in a matrix Π. These are the out-of-sample predictions of all models by all pipelines on all samples. Any performance metric can be computed on this matrix to select the winning pipeline. Π will prove itself useful in the estimation protocols discussed below.

Figure 3.

CV with Tuning (CVT) procedure

CVT is a Learner that includes an internal tuning step: it cross-validates several pipelines and identifies the winning Learner f_∗. It then produces a model using f_∗ on all input data. It is a generalization of the Train-Test-Retrain procedure. We assume that function CV also returns the predictions from the models produced by each f_i on each test fold, which are stored in matrix Π. Thus, matrix Π contains the predictions of each pipeline on each sample, when the latter was not used for training (out-of-sample predictions). The final model is produced by training on all data and does not lose samples to estimation.

Estimation protocols when tuning: Nested cross validation

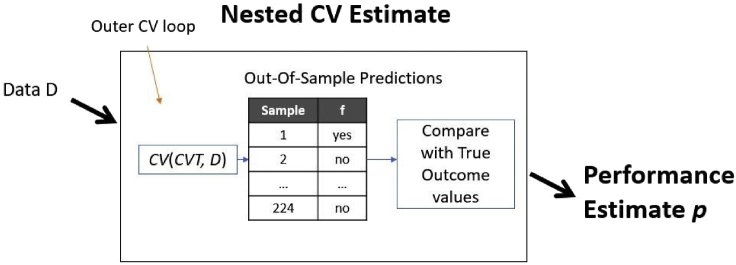
Figure 3 leaves no data for estimation. Returning the CV estimate of the winner computed during CVT as a proxy is optimistic, as mentioned. So, how are we supposed to estimate the performance of the final model? Several ideas appeared in the literature (see Tsamardinos et al.^4,5 and Ding et al.¹¹ for a review). Tibshirani and Tibshirani¹² try to estimate and remove the error bias due to the winner’s curse. Ding et al.¹¹ learn models from increasing-size subsets of samples and extrapolate the performance (error rate) on 100% of the available data, while Bernau et al.¹ weights the error rate of learners on all test sets. However, the first technique for estimation that appeared is the Nested Cross Validation (NCV)¹³ (Figure 4) and has shown excellent results in massive evaluation in small sample datasets.^4,5,14 The first hints and pointers to nested cross validation appeared as early as 1997, see Salzberg,¹⁵ and it was probably independently invented several times.^16,17 Conceptually, it is very simple: we just CV our CVT Learner in Figure 3 (Principle 2). The only difference is that the latter now contains an internal tunning step, again using CV, hence the name nested CV. NCV is similar to the “Train-Tune-Estimate” where each fold of data serves once as the “Estimate” set (outer CV loop) and serves multiple times (one for each Estimate fold) as a Tune set. But there is a difference: after the winning configuration is selected in each outer iteration, there is retraining step taking place (Figure 3). A detailed pseudocode of the procedure is in Tsamardinos et al.,⁴ and a fictional execution trace is in Supplementary 2. While estimations of NCV are quite accurate and unbiased even for tiny sample sizes,⁵ it is undeniably a computationally intensive procedure. Specifically, running CVT to produce a model and then NCV to estimate its performance trains a total of K² × C + K + 1 models, where K is the number of folds of data partitioning, and C the number of pipelines to choose from.

Figure 4.

The Nested Cross-Validation procedure

Nested cross validation (NCV) returns an estimate of the predictive performance of model M produced by the (meta)Learner in Figure 3. It just cross-validates a procedure that internally cross-validates other learners, namely the CVT procedure in Figure 3. It is an accurate protocol that does not lose samples to estimation as well as including tuning of algorithms and hyper-parameters (model selection); however, it is computationally intensive.

Estimation protocols when tuning: Bootstrap bias corrected CV

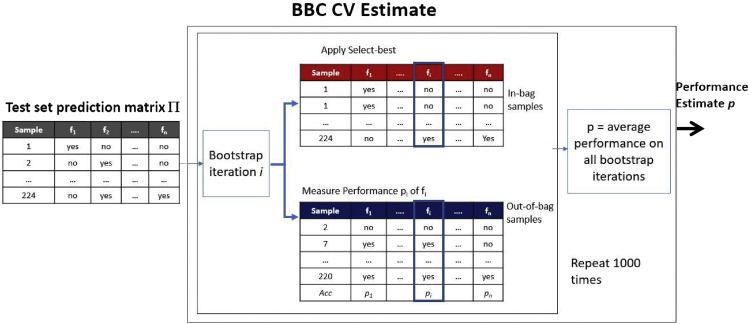
A more computationally efficient procedure has appeared recently called Bootstrap Bias Corrected CV⁴ or BBC-CV. It was inspired by the Tibshirani and Tibshirani algorithm.¹² Its main idea is to estimate the performance of the “Select-Best” step of CVT, since this is the step that creates the estimation bias. In other words, estimate how predictive is on average the pipeline selected as the winning one, among all the ones tried. BBC-CV is shown in Figure 5. In each iteration, the input matrix Π produces a bootstrap version of itself using random selection of rows with replacement. The “Select-Best” step is applied to this matrix to find the winning configuration (f_∗ in the figure). The performance of the winning configuration is estimated on the out-of-bag samples, i.e., the ones not selected by bootstrapping and not seen by the “Select-Best” step. The process is repeated 1,000 times and the average performance estimate is returned. There are no new models trained, hence the total number of models trained are the ones trained by CVT to create matrix Π. Usually, the computational overhead of bootstrapping matrix Π is negligible compared with the model training. BBC has been extended for versions of CVT where the Repeated CV is used producing multiple matrices Π_i in each repetition of the CV with different fold partitionings (see Tsamardinos et al.⁴). A major problem of the BBC is that it does not work with dynamic search strategies for the optimal pipeline, such as the Sequential Bayesian Optimization.

• Practical advice: When tuning is taking place, one should always be aware of the “winner’s curse” estimation problem.

Figure 5.

The Bootstrap Bias Corrected Cross-Validation (BBC-CV) procedure

BBC-CV returns an estimate of the predictive performance of model M produced by the (meta)Learner CVT in Figure 3. The estimate is an out-of-bag bootstrap estimation of the Select-Best step performance in Figure 3: in each iteration, the input matrix Π produces a bootstrap version of itself using random selection of rows with replacement. The “Select-Best” step is applied to this matrix to find the winning configuration (f_∗). The performance of the winning configuration is estimated on the out-of-bag samples, i.e., the ones not selected by bootstrapping and not seen by the “Select-Best” step. The process is repeated 1,000 times and the average performance estimate is returned. BBC-CV estimates the performance of the model produced by CVT on all data without training any further models.

When a static search strategy is used on small sample data, i.e., the set of pipelines to try is fixed a priori, BBC-CV is the current method of choice to estimate the prediction performance of the model produced on all data by the winning pipeline.

These ideas presented above have been incorporated into the JADBio AutoML platform. A recent comparative evaluation of the system on more than 360 low-sample, high-dimensional omics datasets, spanning hundreds of different diseases and disease subtypes has been recently published.⁷ The results show that the BBC estimation is accurate, saving us from losing samples to estimation.

Conclusion

In several analysis scenarios, we cannot afford to lose samples to estimation and hold out a separate test set. This is the case for example, when the total sample size, the sample size of at least one class (highly imbalanced data), the number of non-censored samples in time-to-event (survival analysis), or the number of most fresh and reliable data, in a data-streaming, data-distribution changing setting, is small. In such scenarios, we need to shift our perspective of estimation: the final model is always produced by training on all available data; instead of directly estimating its predictive performance, we estimate the performance of the learner (machine learning pipeline) that produced it. This is possible by applying the learner on subsets of the data and getting estimates on the held-out test sets to use as proxies. These principles can be generalized when numerous pipelines are applied, and hyper-parameter optimization is taking place. They provide a statistical validation of our analysis pipeline; an external validation is still required to ensure the models transfer to more general operational settings. Estimating the performance of a model without ever directly applying it on a held-out test set is feasible statistically and computationally; it is up to us to also accept it psychologically.

Remarks

Word of caution: Validating pipelines as an atom. All estimation protocols that partition data to train and test sets, try to simulate the ideal estimation protocol. To correctly simulate this situation, one needs to make all decisions to produce the model from the available (training) data and only. If one performs standardization, feature selection, imputation, or whatever other data preprocessing and then partitions data to train and test, they are not correctly simulating the ideal protocol: information from the supposedly future test sets leak into the training. Hence, all steps of the analysis need to be cross validated as an atom, as one function.

Remark: What is a Learner? By the term “Learner,” we mean the function that takes us from the input dataset to a specific predictive model. Hence, the Learner incorporates not only the final modeling step, but all steps of the analysis. The equivalent statistical terminology for Learner is “statistical model” (e.g., linear model). The term “model” emphasizes the last final step of the analysis and may lead to confusion: a pipeline that applies first PCA, then performs feature selection with Lasso, then applies an SVM algorithm does not sound like a “model” of the data generating process anymore. We propose to drop the term “model” from the machine learning literature when referring to the modeling process (the learning pipeline).

Word of caution: The assumption of increasing performance with increasing sample size. The fundamental assumption of this new perspective is that loss decreases (equivalently, performance increases), on average, with increased sample size for our Learner. This is true for the most part, but caution needs to be exercised. For example, if you are training an artificial neural network with a fixed number of epochs as a hyper-parameter, they may suffice to converge on 80% of sample size as training, but when you apply it to 100% of sample size, more epochs may be required for convergence. The error of the network when trained with more samples could conceivably be higher. Such problems often stem from hyper-parameters (in this example, the number of epochs) whose interpretation depends on the sample size. Adjusting these hyper-parameter values for sample size typically solves this problem: one could use as hyper-parameters the “epochs per sample” for a neural network instead of number of epochs, or the “cost C per sample” in SVMs instead of just cost C.

Remark: Model production when tuning. The procedure in Figure 3 is the simplest methodology for selecting among numerous pipelines. The set of pipelines to try is pre-specified (static strategy) and they are all exhaustively executed. This optimization strategy effectively corresponds to what is called “grid-search” in the Hyper-Parameter Optimization literature.⁸ More sophisticated search procedures like Sequential Bayesian Optimization (ibid) dynamically decide the next pipeline to execute based on the performance of the previous pipelines tried. Another type of algorithms and heuristics decides to early stop computations on configurations that are deemed non-promising.⁴ Another class of algorithms does not select a single best pipeline to produce the final model but construct an ensemble of model produced by possibly different pipelines.¹⁸ Research on effectively searching for the optimal pipeline is a hot research area in the Automated Machine Learning community.

Remark: Can data augmentation save the day? The ideas presented above are applicable when at least one class numbers few samples. Can’t we just generate new, synthetic data to our heart’s desire and complement our sample size? For certain data types, such as image, speech, and biological signals, there are techniques that create images similar to the input ones from the existing samples. For example, including rotations of our images in the data will make our classifier rotational invariant. However, such techniques are data specific. While they can make our image classifier robust to translations, rotations, lighting conditions, etc. they cannot make our classifier extrapolate to unseen situations. For example, including rotated images in our data cannot improve a classifier trained on European Cats, to correctly classifying Elf Cats. General data type techniques, such as SMOTE¹⁹ and ADASYN²⁰ generate new samples by taking linear combinations of existing ones. They are not without problems.²¹ When one is using data augmentation techniques, it is important to remember that the synthetic data are not identically and independently distributed (i.i.d.), i.e., they are still correlated given the true data distribution. Blindly cross-validating our classifiers on non i.i.d. data leads to severe overestimation problems. It violates the Ideal Estimation Protocol: the test set should not contain synthetic data stemming from training set samples. When the data are very imbalanced, the classifier may be biased toward the majority class. The techniques presented in this paper are still valid and will accurately estimate the predictive performance. However, in order to fix the classification bias, techniques that specifically deal with imbalancing could also be tried in a synergistic fashion, including undersampling of the prevalent classes, oversampling (e.g., SMOTE), giving different weights to the loss of each class, and others.