Abstract
Over the last decade, spatial capture–recapture (SCR) models have become widespread for estimating demographic parameters in ecological studies. However, the underlying assumptions about animal movement and space use are often not realistic. This is a missed opportunity because interesting ecological questions related to animal space use, habitat selection, and behavior cannot be addressed with most SCR models, despite the fact that the data collected in SCR studies — individual animals observed at specific locations and times — can provide a rich source of information about these processes and how they relate to demographic rates. We developed SCR models that integrated more complex movement processes that are typically inferred from telemetry data, including a simple random walk, correlated random walk (i.e., short‐term directional persistence), and habitat‐driven Langevin diffusion. We demonstrated how to formulate, simulate from, and fit these models with standard SCR data using data‐augmented Bayesian analysis methods. We evaluated their performance through a simulation study, in which we varied the detection, movement, and resource selection parameters. We also examined different numbers of sampling occasions and assessed performance gains when including auxiliary location data collected from telemetered individuals. Across all scenarios, the integrated SCR movement models performed well in terms of abundance, detection, and movement parameter estimation. We found little difference in bias for the simple random walk model when reducing the number of sampling occasions from T = 25 to T = 15. We found some bias in movement parameter estimates under several of the correlated random walk scenarios, but incorporating auxiliary location data improved parameter estimates and significantly improved mixing during model fitting. The Langevin movement model was able to recover resource selection parameters from standard SCR data, which is particularly appealing because it explicitly links the individual‐level movement process with habitat selection and population density. We focused on closed population models, but the movement models developed here can be extended to open SCR models. The movement process models could also be easily extended to accommodate additional “building blocks” of random walks, such as central tendency (e.g., territoriality) or multiple movement behavior states, thereby providing a flexible and coherent framework for linking animal movement behavior to population dynamics, density, and distribution.
Keywords: abundance, capture–recapture, Langevin diffusion, movement ecology, NIMBLE, population ecology
INTRODUCTION
Understanding the ecological processes that drive population dynamics requires knowledge not only of demographic processes (e.g., abundance, survival, reproduction) but also animal movement and space use. Animal movement patterns reflect habitat selection, landscape connectivity, and behavior, all of which influence the distribution of individuals in space. In addition to their spatial distributions, how animals move in response to habitat and resources affects their individual fitness, which ultimately influences population dynamics (Gaillard et al., 2010). Conversely, the distribution of animals in space can also be regulated by population‐level processes; e.g., the spatial patterns of animal locations may reveal how survival and reproductive rates are influenced by habitat quality and individual movements (Boyce & McDonald, 1999). Therefore, integrating movement ecology and population ecology into a comprehensive analytical framework will provide ecologists with the opportunity to better understand the interplay of movement, landscape ecology, and population dynamics (McClintock et al., 2021; Morales et al., 2010).
However, it is often difficult to integrate population abundance, demographic rates (e.g., survival, movement), and space use because studies of these phenomena have tended to be conducted through different lenses with an eye toward a particular type of data or model. For example, in studies of abundance or related demographic rates, population‐level inferences have traditionally been drawn using models for count or capture–recapture data (e.g., Buckland et al., 2001; Schaub & Abadi, 2011; Williams et al., 2002). Conversely, in studies of movement, resource selection, or space use, individual‐level inferences are typically drawn using models for location data collected from animal‐borne telemetry devices (e.g., Hooten et al., 2017; Thurfjell et al., 2014). Integrating these two perspectives requires a flexible and adaptable framework that can link individual processes, such as movement and habitat selection, to population‐level processes. One way to do this is to incorporate more realistic movement models (e.g., Hooten et al., 2017) into spatial capture–recapture models (SCR; e.g., Royle, Chandler, Sollmann, & Gardner, 2013). In the introductory article to this Special Feature, McClintock et al. (2021) identified many of the potential advantages of integrating these approaches, including novel and improved inferences at the interface of population, movement, and landscape ecology.
Spatial capture–recapture models provide a flexible framework for estimating density and other demographic rates, while accounting for individual detection heterogeneity attributable to the location of each animal's “activity center.” The spatial distribution of individual activity centers is directly modeled using an underlying point process, therefore providing a mechanism to incorporate movement of individuals into the estimation framework. For example, in open population SCR models, which allow for survival and recruitment processes, the location of activity centers can change (e.g., individuals can disperse) between sampling periods according to a movement model (Bischof et al., 2020; Efford & Schofield, 2020; Ergon & Gardner, 2014; Gardner et al., 2010, 2018; Glennie et al., 2019). These types of movements operate at a different temporal scale (e.g., months or years) compared with most traditional movement models, with the focus on capturing changes in the expected location of an individual between sampling periods rather than the (instantaneous) location of individuals at a particular point in time. However, the same structure can be used at a finer temporal scale, allowing these expected locations to move within the (typically shorter) sampling periods for closed population models (Royle et al., 2016). Whereas this type of movement may cause violations of the assumptions of no immigration or emigration in typical non‐spatial closed capture–recapture models, in SCR models, the detection process is a function of the expected location and therefore animals that are within the population can move into or out of the sampling area without causing bias.
Spatial capture–recapture models have also been extended to incorporate resource selection functions (RSFs) and landscape connectivity (Linden et al., 2018; Royle et al., 2018; Royle, Chandler, Sun, & Fuller, 2013; Sutherland et al., 2015), in which the focus is on incorporating habitat covariates into the detection function or the underlying point process. However, despite the potential advantages, models that integrate both movement and resource selection have not been well developed in the SCR literature (but please refer to Bischof et al., 2020 for an open population example). McClintock et al. (2021) highlighted many of the challenges and uncertainties that remain in the development and implementation of integrated SCR movement models, including determination of an appropriate spatio‐temporal formulation, additional data requirements, and computational hurdles associated with model fitting. Given these challenges, it is likely to be no coincidence that the few integrated SCR movement models that have been successfully implemented are almost entirely limited to simple (Gaussian) random walk movement processes in open population SCR models.
As a first step in tackling these challenges, we extend integrated SCR movement models for closed populations to accommodate movement processes more typically associated with animals responding to their internal and external environments, including the correlated random walk and habitat‐driven Langevin diffusion. We demonstrate how these models can be formulated, simulated from, and fitted to conventional SCR data in a Bayesian framework. SCR data alone may be inadequate to estimate the parameters of more complex movement models, and we therefore evaluate performance gains when auxiliary location data are available for inclusion in our integrated models. While we focus on closed population models, our methods can be easily extended to open population models. The movement process models could also be extended to accommodate additional “building blocks” of random walks, such as central tendency (e.g., territoriality) or multiple movement behavior states, thereby providing a flexible and coherent framework for linking animal movement behavior (e.g., dispersal, migration, habitat selection) to population dynamics, density, and distribution (sensu McClintock et al., 2021).
METHODS
Standard closed population SCR models assume that the i = 1, …, N individuals in the population have “activity centers,” , that are uniformly distributed over a region (i.e., the “state space”), where s x,i and s y,i are the easting and northing coordinates, respectively. These activity centers correspond to the expected location of each individual over the course of the sampling period and are the basis for modeling individual variation in detection probability that is attributable to space use. Standard SCR models are commonly formulated in discrete time, in which the detection process pertains to intervals of time (e.g., daily or weekly sampling) and individuals can move and/or be detected at any time within these intervals. To incorporate an explicit movement process, our discrete‐time formulation therefore models the movement of the expected location for each individual during the sampling interval between times t − 1 and t (s i,t , t ∈ {2, 3, …, T}), given an initial expected location s i,1, instead of the movement of the instantaneous locations at time t (denoted as μ i,t in McClintock et al., 2021). This is consistent with other discrete‐time formulations for open SCR models (Efford & Schofield, 2020; Gardner et al., 2010, 2018; Glennie et al., 2019), but here we focus on more complex movement processes and shorter time periods than is typical in open SCR models. The goal is to differentiate between the underlying movement process model and the detection process model (which is conditionally dependent on the movement process), using standard SCR data (and auxiliary location data, if available). After describing the detection and movement processes in more detail, we will use Bayesian parameter‐expanded data augmentation and Markov chain Monte Carlo (MCMC) to estimate N while integrating over the latent s i,t . We define where z i ∼ Bernoulli(ψ) such that ψ is the probability that any given individual in the “superpopulation” of M individuals is a member of the N individuals in the population, and M ≫ N (e.g., Royle et al., 2007; Royle & Dorazio, 2012).
SCR detection process model
For demonstrative purposes, we will use a Poisson observation model commonly applied to camera trapping data, y ijt ∼ Poisson(λ ijt ), where y ijt is the number of captures for individual i at trap j during sampling occasion t. The encounter rate under this model is:
| (1) |
where is the Euclidean distance between the location of trap j (x j ) and s i,t , λ0 is the baseline encounter rate at distance zero, and is the scale parameter that can be related to the use of space around s i,t . As the time interval of the sampling occasions becomes smaller (Δt → 0), will become smaller as animals have less time to move about s i,t , which results in reducing the likelihood of being detected farther from s i,t . Also, as Δt → 0, we expect that λ0 will become smaller as animals will have less time to be detected.
Movement process models
Simple and correlated random walks
Many movement models are based on the random walk, and complex movements can be modeled using a combination of random walks (Hooten et al., 2017; McClintock et al., 2021; Morales et al., 2004). We start by allowing individuals to move between occasions according to a simple (Gaussian) random walk (Royle et al., 2016):
| (2) |
where σ2 is the variance of the random walk and directly related to the movement of the individual between sampling occasions. This is different from in Equation (1), which is the scale parameter of the detection function in standard SCR models and only implicitly related to movement around s i,t within sampling occasion t. Another common animal movement model is the correlated random walk with short‐term directional persistence:
| (3) |
where γ controls the degree of correlation in the movement path and is bounded between 0 and 1 (Hooten et al., 2017) When γ approaches 0, this model reduces to a simple random walk. Neither the simple nor correlated random walk has a limiting distribution describing the long‐term (Eulerian) spatial distribution of the population, in which case can simply be used as the point process model for the initial expected location (e.g., McClintock et al., 2021; Royle et al., 2016). In section “ Simulation design and implementation ,” we demonstrate how to integrate these basic movement processes into SCR models, which are the building blocks for more complex variants as described in McClintock et al. (2021).
Langevin movement model
We have so far only described movement models that assume individuals are moving in a homogeneous environment without regard to any underlying conditions. However, habitat and resources can drive animal movement and space use within a study area. Habitat data are often collected in discrete space (e.g., remotely sensed elevation models), which is likely to be part of the reason most SCR–RSF models have been formulated in discrete space (Linden et al., 2018; Royle, Chandler, Sun, & Fuller, 2013). The formulation we describe below (and implement in section “Simulation design and implementation”) relies on a continuous‐space, discrete‐time movement process in which both movement and the spatial distribution of individuals are driven by habitat covariates in a coherent framework.
The habitat‐driven Langevin diffusion of Michelot et al. (2019) provides a mathematical framework to model animal movement as a function of habitat (please refer to Figure 2). It has some very useful properties because the limiting distribution of the movement model is the standard form of a RSF (e.g., Manly et al., 2007). For regular sampling intervals with reasonably small Δ t = Δ t−1 ∀ t ∈ {2, 3, …, T}, a discrete‐time approximation of this continuous‐time model is:
| (4) |
where δ k is the selection coefficient for habitat covariate c k and is the gradient of the kth covariate evaluated at s i,t−1. The gradient is the partial derivative of the covariate in both the easting and northing directions. As such, it is a vector field where the sign (positive or negative) points in the direction of the greatest rate of increase and the magnitude corresponds to the rate of increase in that direction (e.g., Dawber, 1987, Chapter 4).
FIGURE 2.
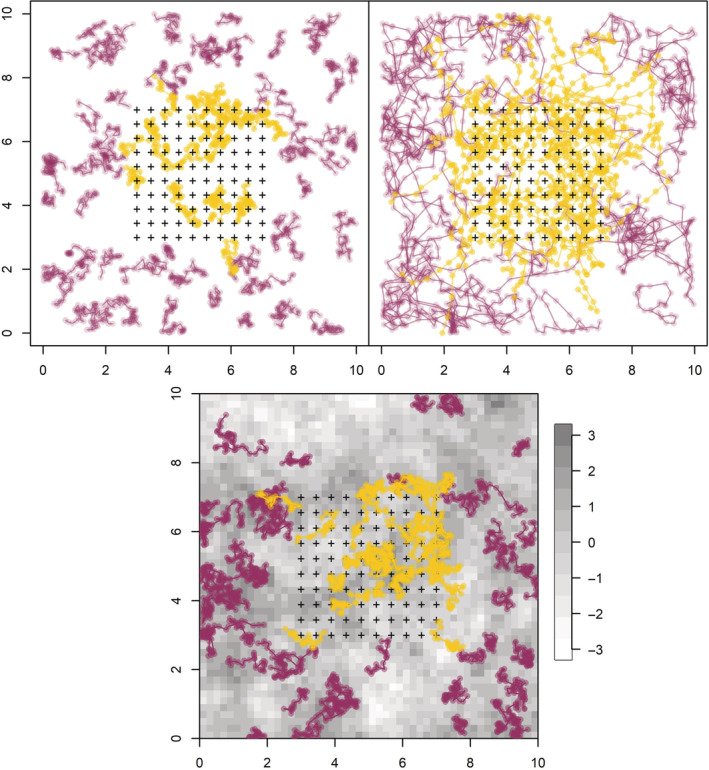
Examples of two different underlying movement processes with the same number of individuals (N = 100), in which yellow indicates tracks of individuals detected in the trap array, purple indicates tracks of individuals not detected in the trap array, and “+” indicates the locations of 100 traps. The top left panel shows a simple random walk trajectory with σ = 0.1 and σdet = 0.15 (Scenario 3). The top right panel shows a realization of a correlated random walk (i.e., short‐term directional persistence) movement model with σ = 0.2, σdet = 0.05, and γ = 0.5 (Scenario 10). The bottom panel shows a realization under the Langevin model with σ = 0.2, σdet = 0.05, and δ = 0.7 (Scenario 17), along the underlying habitat covariate used in the simulations.
Bilinear interpolation (please refer to Kirkland, 2010, pp. 261–263) is one way of approximating gradients along a discretized grid of covariates:
| (5) |
where the (x, y) are the centroids of the four neighboring cells of s i,t (please refer to Figure 1). The cells containing these centroids form a two‐by‐two square. The value (x 1, y 1) is the centroid of the bottom‐left cell, (x 1, y 2) the upper‐left cell, (x 2, y 1) the lower‐right cell, and (x 2, y 2) the top right cell (please refer to Figure 1), and is the value of the kth covariate at (x, y).
FIGURE 1.
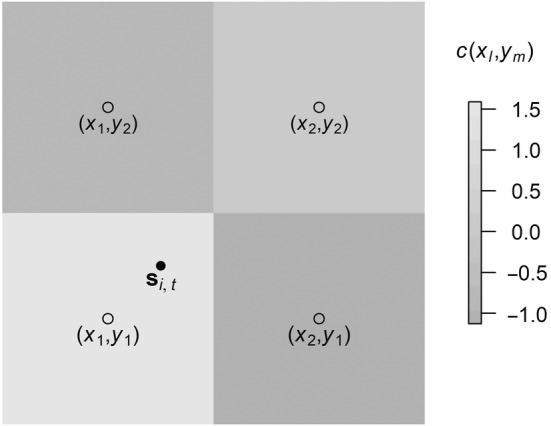
Ingredients for approximating the gradient of a covariate along a discretized grid using bilinear interpolation, where is the expected location of individual i between times t − 1 and t, are the neighboring grid cell coordinates surrounding s i,t , and is the value of the covariate at .
The resulting limiting distribution of the approximate Langevin diffusion model is:
| (6) |
which we use as the point process model for the initial expected locations (s i,1). Therefore the Langevin diffusion can be used to coherently link the individual‐level movement process to the population‐level utilization distribution, and the population density surface will be distributed accordingly. In practice, π(s) must also be approximated when covariates lie on a discretized grid. We accomplish this by first assuming that each s i,1 resides in a grid cell (g i ) following a categorical distribution:
| (7) |
where , G is the number of grid cells in ,
| (8) |
and c k (x g , y g ) is the value of the kth covariate at the coordinates (x g , y g ) of grid cell g. It is common for each s i,1 to be assigned the centroid of cell g i (Royle, Chandler, Sun, & Fuller, 2013); however, we used a more realistic assumption where each s i,1 is uniformly distributed within cell g i , that is, , where is the area of the state space occupied by cell g i .
Auxiliary animal location data
Standard SCR data can be used to estimate the parameters of the SCR movement models above. However, SCR data alone may not be sufficient, and this will probably depend on the study design, detection process, and movement process (Hostetter et al., 2022; McClintock et al., 2021). One way to improve the parameter estimates of SCR models is to use data from animal‐borne devices, for example radiotelemetry or GPS collars (Linden et al., 2018; Sollmann et al., 2013). There are several things to consider when working with auxiliary location data in the context of SCR models, including whether the locations arise from individuals in the target population, the temporal scale of the data, and the accuracy of the locations (e.g., McClintock et al., 2021). We describe here the methods we used to incorporate auxiliary location data (please refer to the “Discussion” section for further considerations).
In developing SCR models that integrate auxiliary location data from individuals fitted with animal‐borne devices (from this point forward “telemetered individuals”) there are important considerations in regard to spatially and temporally aligning the telemetry data with SCR data. We assumed that telemetered individuals were within the state space, and location data were collected simultaneously with the SCR sampling. We also assumed that all telemetry devices were deployed prior to the start of the SCR sampling, but telemetered individuals were not necessarily captured as part of the SCR sampling. The temporal scale of location information can vary from coarse‐scale to fine‐scale resolution (e.g., one study may observe radiotelemetry locations once a week, whereas another study has GPS collars set to record locations every 5 min). One way to accommodate these conditions is by assuming , where μ i,τ is an observed location (without measurement error) for individual i at time τ ∈ (t − 1, t].
As noted above, we use parameter‐expanded data augmentation to estimate N and integrate over the latent s i,t in “Simulation design and implementation” section. To separate telemetered individuals such that they do not directly influence the estimation of the data augmentation parameter (ψ), we used a binary covariate (q = 0 if an animal is not telemetered, q = 1 if an animal is telemetered):
| (9) |
where .
This approach is akin to spatial mark‐resight models (e.g., Sollmann et al., 2013), in which we are using data augmentation to estimate the number of untelemetered individuals, N − n A ∈ {0, 1, …, M − n A }, but still allowing the telemetered individuals to inform the movement and detection processes. Therefore, the interpretation of ψ is different than in our other formulations as it now pertains only to untelemetered individuals in the population. We note that Equation (9) allows the inclusion of telemetered individuals that were marked prior to the SCR sampling. In cases in which animals are first captured in the SCR sampling and then telemetered (e.g., search–encounter, live trapping), standard data augmentation can be used to estimate N ∈ {0, 1, …, M}.
Simulation design and implementation
For each of the three movement models, we simulated data to explore the effects of different study designs, detection parameters, and movement parameters (please refer to Table 1 for a description of the parameter values used in each scenario). In all scenarios, we set N = 100, M = 250, T = 25, and assumed 100 traps placed in a square grid (please refer to Figure 2). We considered six scenarios for both the simple random walk (Scenarios 1–6) and the correlated random walk (Scenarios 7–12) with different parameter values for σ (0.1 and 0.2) and σdet (0.05, 0.1, and 0.15). We note that when σ is large relative to σdet, this leads to individuals being able to move their expected locations farther than they move about the expected locations within a time step/occasion. Although this may not be feasible biologically, it could arise under certain conditions in which sampling occurs only over a portion of the time step (e.g., in a mist‐netting study, nets may be open for only a few hours whereas the time step for the model is 1 day). We included a range of values of σdet relative to σ to assess the model performance under a suite of movement conditions. We varied the value of λ0 in the six scenarios to maintain a similar number of captured individuals. In addition, for the random walk scenarios, we also considered T = 15 to evaluate the effect of the number of capture occasions on parameter estimates. All scenarios of the correlated random walk model were evaluated with SCR data only and then again with the addition of 10 telemetered individuals with two observed locations per sample occasion, in which we assumed that location data were obtained without measurement error. Please refer to Figure 2 for an example of how different parameter settings influence the tracks and captures in the simple versus correlated random walk models.
TABLE 1.
Parameter settings for each of the simulation scenarios.
| Scenario | Model type | σ | σdet | λ0 | γ | δ | T |
|---|---|---|---|---|---|---|---|
| 1 | Simple random walk | 0.1 | 0.05 | 3 | 15,25 | ||
| 2 | Simple random walk | 0.1 | 0.10 | 2 | 15,25 | ||
| 3 | Simple random walk | 0.1 | 0.15 | 0.5 | 15,25 | ||
| 4 | Simple random walk | 0.2 | 0.05 | 3 | 15,25 | ||
| 5 | Simple random walk | 0.2 | 2 | 15,25 | |||
| 6 | Simple random walk | 0.2 | 0.5 | 15,25 | |||
| 7 | Correlated random walk | 0.1 | 0.05 | 5 | 0.5 | 25 | |
| 8 | Correlated random walk | 0.1 | 0.10 | 3 | 0.5 | 25 | |
| 9 | Correlated random walk | 0.1 | 0.15 | 1 | 0.5 | 25 | |
| 10 | Correlated random walk | 0.2 | 0.05 | 5 | 0.5 | 25 | |
| 11 | Correlated random walk | 0.2 | 0.10 | 3 | 0.5 | 25 | |
| 12 | Correlated random walk | 0.2 | 0.15 | 0.5 | 0.5 | 25 | |
| 13 | Langevin | 0.1 | 0.1 | 2 | 0.7 | 25 | |
| 14 | Langevin | 0.1 | 0.1 | 2 | 0.3 | 25 | |
| 15 | Langevin | 0.2 | 0.1 | 1 | 0.7 | 25 | |
| 16 | Langevin | 0.2 | 0.1 | 1 | 0.3 | 25 | |
| 17 | Langevin | 0.2 | 0.05 | 3 | 0.7 | 25 | |
| 18 | Langevin | 0.2 | 0.05 | 3 | 0.3 | 25 |
Note: For the correlated random walk model (Scenarios 7–12), we also ran a separate set of simulations with 10 telemetered individuals in which auxiliary location data are included (labeled as Scenarios 7A–12A in the text). In all scenarios, the population size was set as N = 100.
For the Langevin movement model, we simulated data under six scenarios (Scenarios 13–18) using K = 1 simulated habitat covariate. We set N = 100, M = 250, T = 25 and used the same trapping array as in the simple and correlated random walk simulations. We generated a single realization of a spatially correlated habitat covariate that was standardized and used in all simulations (Figure 2). We allowed resource selection to vary between weak to strong selection (δ = 0.3 and 0.7). We also varied σ (0.1 and 0.2) and σdet (0.05 and 0.1). We used bilinear interpolation (Equation 5) to approximate the gradient of the simulated covariate. For the initial expected locations, we used Equations 7 and 8 and assumed as described in the “Langevin movement model” section. To fit this model using Bayesian MCMC, we wrote a custom sampler to jointly update g i (the grid cell location) and s i,t (please refer to Appendix S2).
For all scenarios, we assumed a 10 × 10 trapping array with 0.444 spacing between traps. We buffered the trap array by 3 units on all sides to create the state space for analysis (please refer to Figure 2). The buffer size is large relative to the values of σ and σdet compared with a traditional SCR model, but this is due to the increased movement of individuals about the state space. We note that this buffer should be considered in relation to both the timing of the study (number and length of time steps), the type of movement model, and the associated parameters such as σ, σdet, or γ. It is important when deciding on a state space for each analysis to consider the potential effects on the estimated parameters, in which case a simulation may be useful (Gardner et al., 2018). In addition, as the state space increases, so will the computational requirements and the time needed to run the models.
We fitted all models using the R package NIMBLE (de Valpine et al., 2017, 2020) in R 3.6.3 (R Core Team, 2020) using a set of custom samplers to increase the speed of the computations. We used the relatively vague priors σ ∼ Uniform(0,5), σdet ∼ Uniform(0,5), λ0 ∼ Uniform(0,10), and the approximate scale prior ψ ∼ Beta(1e−6,1), as recommended by Link (2013). For the correlated random walk model, we used γ ∼ Beta(1,1). For the Langevin model, we used δ ∼ Normal(0, 10). For the simple random walk model, we used a burn‐in of 10,000 and then ran an additional 40,000 iterations for three chains and did not thin. For the correlated random walk with telemetry and Langevin models, unless otherwise noted, we used a burn‐in of 15,000 and then ran an additional 55,000 iterations for three chains and thinned by two. With 40,000–55,000 iterations, the simple random walk and Langevin scenarios required 2–3 h to fit the model to one data set with one chain on a standard desktop computer using a single core. For the correlated random walk models with no telemetered individuals, some parameters took longer to converge and effective sample sizes were smaller; therefore, we used a burn‐in of 20,000 and then ran an additional 100,000 iterations for three chains and thinned by two (note that with these settings, it took 6–8 h per chain to fit the model to one data set). To improve mixing of σ, we updated it six times per MCMC iteration within NIMBLE for Scenarios 1–12. Under the Langevin scenarios, σ mixed reasonably well without the extra updating. In all scenarios, individuals were prevented from leaving the state space using a truncated Normal distribution; therefore Equations ((2), (3), (4)) describing the movement of the expected locations (s i,t ) were truncated at the boundary of the state space . The value was checked for all parameters, where any simulation with an of more than 1.05 was removed and a new data set generated until there were 100 simulations for each scenario with s <1.05 (please refer to Appendix S1: Table S6 for more details). We note that many of these simulations would have converged if we had set the number of iterations higher, but doing so would have made a relatively large simulation study such as this much less feasible.
RESULTS
For all scenarios of the simple random walk movement model with T = 25, we found that N was well estimated with bias ranging from −1.4% to 2.2% and credible interval coverage from 94% to 98% (please refer to Appendix S1: Table S1). Results were similar for estimates of N in the scenarios with T = 15, although the coverage was lower (93% to 97%) and the bias slightly higher, particularly for Scenario 1 (close to 5%, Appendix S1: Table S2). Parameter estimates of σ and σdet had minimal bias across all of the random walk scenarios, with precision decreasing from T = 25 to T = 15 (Figure 3).
FIGURE 3.
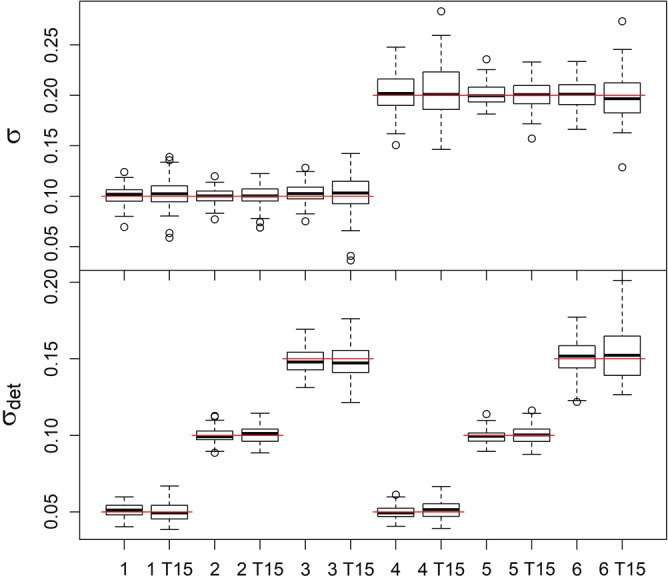
Boxplots of parameter estimates under the random walk model. Scenarios 1–6, those labeled T15 had T = 15 sampling occasions, all others had T = 25 sampling occasions. The top panel shows σ and the bottom panel shows σdet. Scenario 1: σ = 0.1 and σdet = 0.05, Scenario 2: σ = 0.1 and σdet = 0.1, Scenario 3: σ = 0.1 and σdet = 0.15, Scenario 4: σ = 0.2 and σdet = 0.05, Scenario 5: σ = 0.2 and σdet = 0.1, Scenario 6: σ = 0.2 and σdet = 0.15. Red lines indicate the true value for each scenario.
The correlated random walk model, without telemetry data, also resulted in estimates of abundance with minimal bias of −1.16% to 1.56% and coverage ranging from 95% to 97% (Appendix S1: Table S3). The estimates of σ and σdet had minimal bias; however, estimates of γ showed negative bias in some scenarios, up to 18% in Scenario 7 (Figure 4). The average number of individuals captured ranged across the six scenarios from 24.65 to 38.00, with an average number of recaptures per individual ranging from 5.03 to 16.42. Including the telemetry data markedly improved the movement parameter estimates, specifically γ, but also σ and σdet (Figure 4). Estimates of N were slightly improved when telemetered individuals were included, with bias between −1.10% to 0.50% and similar coverage of 95% to 98% (Appendix S1: Table S4).
FIGURE 4.
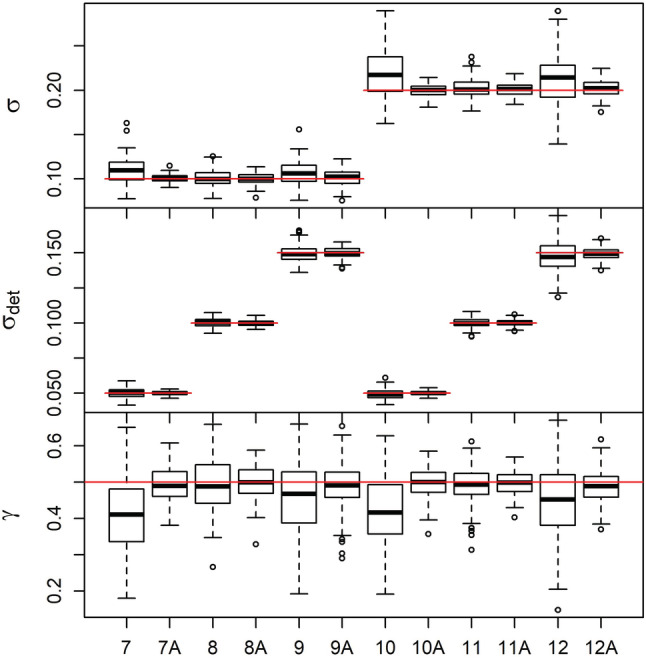
Boxplots of parameter estimates under the correlated random walk model without telemetry data (Scenarios 7–12) and with telemetry data (Scenarios 7A–12A). The top panel shows σ, the middle panel shows σdet, and the bottom panel shows γ. Scenario 7: σ = 0.1 and σdet = 0.05, Scenario 8: σ = 0.1 and σdet = 0.1, Scenario 9: σ = 0.1 and σdet = 0.15, Scenario 10: σ = 0.2 and σdet = 0.05, Scenario 11: σ = 0.2 and σdet = 0.1, Scenario 12: σ = 0.2 and σdet = 0.15. For all scenarios, γ = 0.5. Red lines indicate the true value for each scenario.
The estimate of N under the Langevin movement model had good coverage 94% to 97%, but showed a little more consistent positive bias (0.6%–5.0%) compared with the other two movement models (Appendix S1: Table S5). The Langevin movement model returned unbiased results for σ, σdet, and δ (Figure 5). In Scenarios 17 and 18, which had σdet = 0.05 (the smallest detection values of the Langevin scenarios), the estimates of σ were more imprecise than in the other Langevin scenarios; these two scenarios also had the lowest number of average recaptures. The same was true for the strength of habitat selection (δ), in which the estimates were somewhat imprecise for both the weak and strong selection values in the simulation (and most imprecise in Scenarios 17 and 18).
FIGURE 5.
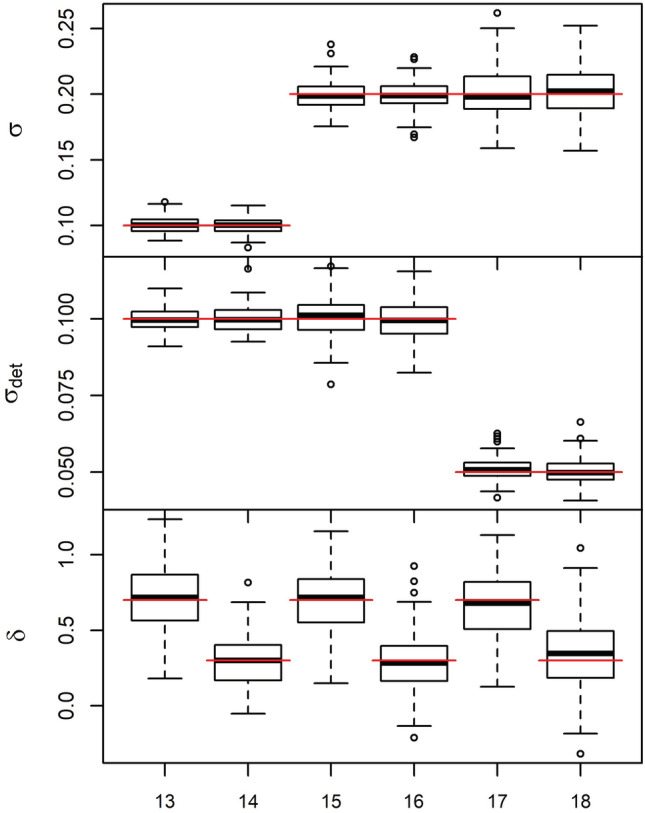
Boxplots of parameter estimates under the integrated Langevin model (Scenarios 13–18). The top panel shows σ, the middle panel shows σdet, and the bottom panel shows δ. Scenario 13: σ = 0.1, σdet = 0.1, and δ = 0.7, Scenario 14: σ = 0.1, σdet = 0.1, and δ = 0.3, Scenario 15: σ = 0.2, σdet = 0.1, and δ = 0.7, Scenario 16: σ = 0.2, σdet = 0.1, and δ = 0.3, Scenario 17: σ = 0.2,σdet = 0.05, and δ = 0.7, Scenario 18: σ = 0.2, σdet = 0.05, and δ = 0.3. Red lines indicate the true value for each scenario.
DISCUSSION
Spatial capture–recapture models are now widely applied in ecological studies and easily allow for incorporation of individual heterogeneity due to differences in traits (e.g., sex, age class, weight) which affect demography (Plard et al., 2019). Despite this, SCR models have lagged in incorporating other individual traits such as movement. Movement reflects how individuals use resources, avoid risks, and select habitats, which not only drive the spatial distribution of populations, but also demographic rates including survival, reproduction, and dispersal (Boyce & McDonald, 1999). Here, we highlighted how to incorporate more complex animal movement explicitly into SCR models to address questions regarding animal ecology and habitat selection. We also demonstrated that more realistic movement models typically applied to telemetry data can be informed by SCR data alone. In all three models that we developed (simple random walk, correlated random walk, and habitat‐driven Langevin), new insights can be gained about how animals are moving and where they are using resources while simultaneously estimating density. Inferences about movement parameters therefore apply to a well defined population in both space and time. These movement processes can be extended to include additional “building blocks” of random walks (e.g., McClintock et al., 2021; Theng et al., 2022) and can also be incorporated into open SCR models to investigate relationships between movement and demographic rates (e.g., survival, recruitment).
All of the models we examined performed well and further demonstrated that SCR data alone can be sufficient for distinguishing the detection process parameters (e.g., λ0, σdet) from the movement process parameters (e.g., σ, γ, δ) in integrated SCR movement models. However, we simulated fairly large data sets and note that demands for capture and recapture data will increase as movement models become more complex. In the simple random walk, for Scenarios 5 and 6, we found the precision of σ and σdet declined when going from T = 25 to T = 15 sampling occasions. Based on this, we expect that SCR data sets with fewer than 20 individuals recaptured three or four times on average may not produce precise estimates of the movement parameters. This was also clear with the correlated random walk model where γ was estimated with bias. Scenarios 7 and 10, which had σdet = 0.05, had the lowest number of recaptures of all the scenarios (e.g., individuals were recaptured on average 6.47 times in Scenario 10) and the most bias and imprecise estimates of γ. Despite values that indicate convergence, the MCMC chains for γ in these cases often showed autocorrelation. The small number of recaptures over T = 25 time steps implies that there was little information on animal locations between any two or three time steps on average, which likely contributed to the bias in estimates of γ.
We found that incorporating auxiliary location data in the correlated random walk models improved performance (generally faster convergence with improved accuracy and precision for most parameters). This is consistent with other work integrating telemetry data to inform σdet in standard SCR‐type models (Linden et al., 2018; Sollmann et al., 2012; Tenan et al., 2017). Fortunately, it is becoming more common to collect auxiliary location data on species of all sizes, in both terrestrial and aquatic environments, and with higher resolution (Kays et al., 2015). Indeed, some are calling this the “bio‐logging decade” (Lowerre‐Barbieri et al., 2019). Taking advantage of advancements in bio‐logging data, we can fully capitalize on integrated SCR movement models and provide a means for a better understanding of the ecological processes driving movement and demography. However, this integration presents some challenges, including spatial or temporal mismatch between the SCR data and the location data (Mitchell et al., 2021). In cases of spatial mismatch, auxiliary location data could be used as the basis for an informative prior on the movement model parameters (e.g., σ2, γ) or included in the movement model likelihood, but they should not be used to inform the detection parameters (e.g., , λ0) or population size (N). In this bio‐logging decade, the temporal resolution of animal‐borne telemetry location data is often occurring at rates ≫1 location per SCR sampling occasion, whereas SCR sampling commonly occurs at daily or weekly intervals (e.g., data collected from hair snares). When the temporal resolution of auxiliary locations is finer than the (discrete‐time) SCR sampling data, there are at least two options: (1) model the auxiliary locations as a function of s i,t and σdet as done here; or (2) use a continuous‐time movement model that can be integrated over the time scale of the SCR sampling occasions (McClintock et al., 2021). The latter would also open the door to integrating continuous‐time movement models with continuous‐time SCR models (e.g., Borchers et al., 2014).
The Langevin movement model is a very useful tool because it links animal movement as a function of habitat directly to the spatial distribution of individuals on the landscape. SCR explicitly models the spatial distribution of individuals, and therefore is fundamentally compatible with the concept underlying Langevin movement. We found that standard SCR data alone can inform the habitat selection parameter (δ), as these data also inform the underlying distribution of individuals. Although we included only one habitat covariate and did not need auxiliary location data to estimate the parameters well, there was some lack of precision in δ estimates that was likely to be due to relatively small sample sizes. In our simulations, there were approximately n = 28 individuals captured on average 12 times (which is equivalent to having 12 relocations per individual) in the scenarios with σdet = 0.1 and approximately n = 25 individuals captured on average five times when σdet = 0.05. Street et al. (2021) showed that the required sample size in resource selection analyses is dependent on the strength of the selection and the landscape variation. Therefore, with additional habitat covariates or more complex movement models, auxiliary location data may become necessary to tease out the habitat selection coefficients. Landscape heterogeneity may play another important role in the parameter estimates of N. Similar to SCR–RSF simulations performed by Royle, Chandler, Sun, and Fuller (2013), we found a slight positive bias in N of up to 5% in some of our Langevin simulation scenarios. However, we used the same underlying habitat layer in every scenario; this could at least partially explain the consistent bias. We also note that the median of the posterior distribution was less biased (−0.41% to 3.67%) and was likely to be attributable to the right skew in the posterior of N that is common in Bayesian implementations of SCR models (Chandler et al., 2013). This is an area that requires further study to understand the effects of spatial variation in habitat covariates on parameter estimates.
The Langevin model holds particular promise as it extends previous work integrating RSFs with SCR (Royle, Chandler, Sun, & Fuller, 2013) into a new framework in which habitat directly affects animal movement patterns, not just the detection function. Additionally, the Langevin–SCR model offers a single‐stage approach for density surface modeling that explicitly links habitat‐driven movement and population abundance. This initial simulation study shows that the integrated Langevin–SCR model performs well under a specific set of conditions. Moving forward, there are some other questions that should be investigated such as the effect of landscape variation on required sample sizes (Street et al., 2021) and on the optimal grid layout (Dupont et al., 2020). It would also be valuable to directly compare the Langevin–SCR model to previous SCR–RSF models to evaluate potential strengths and weaknesses.
Our study focuses on simulations and technical issues, but our findings are widely applicable in directing ecological studies. For example, 22 individual leopards were photocaptured in a study of leopard density and space use at a mean rate of 7.3 recaptures per individual (Balme et al., 2019). These capture and recapture rates are very similar to our simulations and, based on our findings, their data would support the random walk model, but would probably be insufficient to estimate parameters from the correlated random walk without auxiliary data. More common in SCR studies is that the recapture rate is lower, for example, López‐Bao et al. (2018) detected 65 individual wolves from scat surveys, but the recapture rate was only 1.46. Similarly, Mitchell et al. (2021) found 143 individual tortoises in their study but had very few recaptures. However, both studies collected concurrent telemetry data that were used to improve the fit of standard SCR models and, with the models presented here, these types of studies could be expanded to examine resource use and the potential effects on the demographic rates. For practical purposes, increasing the number of sampling occasions in these studies may not be helpful as the capture rate was so low and for the correlated random walk model we found that having few to no recaptures between time steps led to bias in estimates of γ. Conversely, for studies with higher recapture rates, we found in general that changing from T = 25 to T = 15 occasions did not noticeably affect the results for the random walk model. Therefore, practitioners will need to balance the complexity of the movement model with the probable recapture rate of their study species and may need to include auxiliary data to achieve reliable results, especially for complex movement models.
Incorporating more explicit movement processes into SCR models provides a means for asking more mechanistic questions of how animals are using space, but movement is also an individual trait that may impact the parameter estimates in SCR. SCR models can be biased when important individual traits, such as sex, are ignored (Tobler & Powell, 2013). Therefore, although standard SCR models generally perform well in simulations in terms of point estimates of abundance (or density) despite violations of the assumptions that activity centers are static and home ranges are symmetric (Efford, 2019), it is important to recognize that oversimplifying movement processes can bias SCR parameter estimates. For example, the estimate of σdet in a standard SCR model would include both movement associated with the detection process and extra variation due to more realistic animal movement patterns (Royle et al., 2016), and overestimating σdet can lead to bias in density (Sollmann et al., 2012). Movement processes such as resource selection can induce individual heterogeneity in detection, which can also lead to significant bias in standard SCR density estimators (Royle, Chandler, Sun, & Fuller, 2013). For some species in which movement behavior changes, say, seasonally, this could lead to extra variation in estimates of σdet and, therefore, variation in density estimates that are in fact caused by changes in individual behavioral (Harmsen et al., 2020) or habitat use. Being able to separate out the movement process as we have demonstrated here, and to be informed by habitat as in the Langevin model, provides a mechanism to improve estimates of σdet, λ0, and density, as well as a clear link between movement, detection, and demography, which were previously conflated.
The simulation study here lays the groundwork for integrating SCR and movement models as well as assessing their performance. But this study also opens the doors for future research that warrants investigation such as trap placement relative to movement parameters and in heterogeneous habitat, variation in the strength of the directional persistence (γ) or habitat selection (δ) parameters, integration with continuous‐time models, maximum likelihood analysis using “semicomplete” data likelihoods, and extensions to open population models (e.g., McClintock et al., 2021). Understanding the limitations of using SCR data alone to estimate more complex movement model parameters will also be important for designing future studies. The integration of SCR with movement models holds much promise for addressing questions at the intersection of population, movement, and landscape ecology, but some technical and data challenges remain to be explored.
CONFLICT OF INTEREST
The authors declare no conflict of interest.
Supporting information
Appendix S1
Appendix S2
Data S1
ACKNOWLEDGMENTS
This work arose from a workshop supported in part by the Washington Cooperative Fish and Wildlife Research Unit (WACFWRU) with participants B. Abrahms, R. Chandler, P. Conn, R. Emmet, D. Johnson. We thank Matthew Schofield, Ben Stevenson, David Chan, and Krishna Pacifici for comments on an earlier draft. We thank the North Pacific Research Board and WACFWRU for supporting NJH. The scientific results and conclusions, as well as any views or opinions expressed herein, are those of the author(s) and do not necessarily reflect those of NOAA or the Department of Commerce. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the United States Government.
Gardner, Beth , McClintock Brett T., Converse Sarah J., and Hostetter Nathan J.. 2022. “Integrated Animal Movement and Spatial Capture–Recapture Models: Simulation, Implementation, and Inference.” Ecology 103(10): e3771. 10.1002/ecy.3771
Handling Editor: Viviana Ruiz‐Gutierrez
Funding information Department of Commerce; North Pacific Research Board, Grant/Award Number: Project1809
DATA AVAILABILITY STATEMENT
All R scripts (Gardner et al., 2022a) to simulate the data are available on Zenodo at https://doi.org/10.5281/zenodo.6471397. Example detection history data produced from the scripts (Gardner et al., 2022b) are provided on Dryad at https://doi.org/10.5061/dryad.pc866t1r9.
REFERENCES
- Balme, G. , Rogan M., Thomas L., Pitman R., Mann G., Whittington‐Jones G., Midlane N., et al. 2019. “Big Cats at Large: Density, Structure, and Spatio‐Temporal Patterns of a Leopard Population Free of Anthropogenic Mortality.” Population Ecology 61: 256–67. [Google Scholar]
- Bischof, R. , Milleret C., Dupont P., Chipperfield J., Tourani M., Ordiz A., de Valpine P., et al. 2020. “Estimating and Forecasting Spatial Population Dynamics of Apex Predators Using Transnational Genetic Monitoring.” Proceedings of the National Academy of Sciences 117: 30531–8 https://www.pnas.org/content/117/48/30531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borchers, D. , Distiller G., Foster R., Harmsen B., and Milazzo L.. 2014. “Continuous‐Time Spatially Explicit Capture–Recapture Models, with an Application to a Jaguar Camera‐Trap Survey.” Methods in Ecology and Evolution 5: 656–65. [Google Scholar]
- Boyce, M. S. , and McDonald L. L.. 1999. “Relating Populations to Habitats Using Resource Selection Functions.” Trends in Ecology & Evolution 14: 268–72 https://www.sciencedirect.com/science/article/pii/S0169534799%. [DOI] [PubMed] [Google Scholar]
- Buckland, S. T. , Anderson D. R., Burnham K. P., Laake J. L., Borchers D. L., Thomas L., et al. 2001. Introduction to Distance Sampling: Estimating Abundance of Biological Populations. Oxford: Oxford University Press. [Google Scholar]
- Chandler, R. B. , Royle J. A., et al. 2013. “Spatially Explicit Models for Inference about Density in Unmarked or Partially Marked Populations.” The Annals of Applied Statistics 7: 936–54. [Google Scholar]
- Dawber, P. G. 1987. Vectors and Vector Operators. Boca Raton, FL: CRC Press. [Google Scholar]
- de Valpine, P. , Paciorek C., Turek D., Michaud N., Anderson‐Bergman C., Obermeyer F., Wehrhahn Cortes C., Rodríguez A., Temple Lang D., and Paganin S.. 2020. “NIMBLE: MCMC, Particle Filtering, and Programmable Hierarchical Modeling.” https://cran.r-project.org/package=nimble.
- de Valpine, P. , Turek D., Paciorek C., Anderson‐Bergman C., Temple Lang D., and Bodik R.. 2017. “Programming with Models: Writing Statistical Algorithms for General Model Structures with NIMBLE.” Journal of Computational and Graphical Statistics 26: 403–17. [Google Scholar]
- Dupont, G. , Royle J., Nawaz M. A., and Sutherland C.. 2020. “Towards Optimal Sampling Design for Spatial Capture‐Recapture.” BioRxiv. 10.1101/2020.04.16.045740. [DOI] [PubMed]
- Efford, M. G. 2019. “Non‐circular Home Ranges and the Estimation of Population Density.” Ecology 100: e02580. [DOI] [PubMed] [Google Scholar]
- Efford, M. G. , and Schofield M. R.. 2020. “A spatial open‐population capture‐recapture model.” Biometrics 76: 392–402. [DOI] [PubMed] [Google Scholar]
- Ergon, T. , and Gardner B.. 2014. “Separating Mortality and Emigration: Modelling Space Use, Dispersal and Survival with Robust‐Design Spatial Capture–Recapture Data.” Methods in Ecology and Evolution 5: 1327–36. [Google Scholar]
- Gaillard, J.‐M. , Hebblewhite M., Loison A., Fuller M., Powell R., Basille M., and Van Moorter B.. 2010. “Habitat–Performance Relationships: Finding the Right Metric at a Given Spatial Scale.” Philosophical Transactions of the Royal Society B: Biological Sciences 365: 2255–65. 10.1098/rstb.2010.0085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner, B. , McClintock B. T., Converse S. J., and Hostetter N. J.. 2022a. “Integrated Animal Movement and Spatial Capture‐Recapture Models: Simulation, Implementation, and Inference.” Zenodo, Software. 10.5281/zenodo.6471397. [DOI] [PMC free article] [PubMed]
- Gardner, B. , McClintock B. T., Converse S. J., and Hostetter N. J.. 2022b. “Integrated Animal Movement and Spatial Capture‐Recapture Models: Simulation, Implementation, and Inference.” Dryad, Dataset. 10.5061/dryad.pc866t1r9. [DOI] [PMC free article] [PubMed]
- Gardner, B. , Reppucci J., Lucherini M., and Royle J. A.. 2010. “Spatially Explicit Inference for Open Populations: Estimating Demographic Parameters from Camera‐Trap Studies.” Ecology 91: 3376–83. [DOI] [PubMed] [Google Scholar]
- Gardner, B. , Sollmann R., Kumar N. S., Jathanna D., and Karanth K. U.. 2018. “State Space and Movement Specification in Open Population Spatial Capture–Recapture Models.” Ecology and Evolution 8: 10336–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glennie, R. , Borchers D. L., Murchie M., Harmsen B. J., and Foster R. J.. 2019. “Open population maximum likelihood spatial capture‐recapture.” Biometrics 75: 1345–55. [DOI] [PubMed] [Google Scholar]
- Harmsen, B. J. , Foster R. J., and Quigley H.. 2020. “Spatially Explicit Capture Recapture Density Estimates: Robustness, Accuracy and Precision in a Long‐Term Study of Jaguars (Panthera onca).” PLoS One 15: e0227468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hooten, M. B. , Johnson D. S., McClintock B. T., and Morales J. M.. 2017. Animal Movement: Statistical Models for Telemetry Data. Boca Raton, FL: CRC Press. [Google Scholar]
- Hostetter, N. J. , Regehr E. V., Wilson R. R., Royle J. A., and Converse S. J.. 2022. “Modeling Spatiotemporal Abundance and Movement Dynamics Using an Integrated Spatial Capture‐Recapture Movement Model.” Ecology. 10.1002/ecy.3772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kays, R. , Crofoot M. C., Jetz W., and Wikelski M.. 2015. “Terrestrial Animal Tracking as an Eye on Life and Planet.” Science 348: aaa2478. [DOI] [PubMed] [Google Scholar]
- Kirkland, E. J. 2010. Advanced Computing in Electron Microscopy. Boston, MA: Springer. [Google Scholar]
- Linden, D. W. , Sirén A. P., and Pekins P. J.. 2018. “Integrating Telemetry Data into Spatial Capture–Recapture Modifies Inferences on Multi‐Scale Resource Selection.” Ecosphere 9: e02203. [Google Scholar]
- Link, W. A. 2013. “A Cautionary Note on the Discrete Uniform Prior for the Binomial N.” Ecology 94: 2173–9. [DOI] [PubMed] [Google Scholar]
- López‐Bao, J. , Godinho R., Pacheco C., Lema F., García E., Llaneza L., Palacios V., and Jiménez J.. 2018. “Toward Reliable Population Estimates of Wolves by Combining Spatial Capture‐Recapture Models and Non‐invasive Dna Monitoring.” Scientific Reports 8: 2177. 10.1038/s41598-018-20675-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowerre‐Barbieri, S. K. , Kays R., Thorson J. T., and Wikelski M.. 2019. “The ocean's Movescape: Fisheries Management in the Bio‐Logging Decade (2018–2028).” ICES Journal of Marine Science 76: 477–88. 10.1093/icesjms/fsy211. [DOI] [Google Scholar]
- Manly, B. , McDonald L., Thomas D. L., McDonald T. L., and Erickson W. P.. 2007. Resource Selection by Animals: Statistical Design and Analysis for Field Studies. Berlin: Springer Science & Business Media. [Google Scholar]
- McClintock, B. T. , Abrahms B., Chandler R. B., Conn P. B., Converse S. J., Emmet R. L., Gardner B., Hostetter N. J., and Johnson D. S.. 2021. “An Integrated Path for Spatial Capture–Recapture and Animal Movement Modeling.” Ecology: e3473. 10.1002/ecy.3473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michelot, T. , Gloaguen P., Blackwell P. G., and Étienne M.‐P.. 2019. “The Langevin Diffusion as a Continuous‐Time Model of Animal Movement and Habitat Selection.” Methods in Ecology and Evolution 10: 1894–907. [Google Scholar]
- Mitchell, C. I. , Shoemaker K. T., Esque T. C., Vandergast A. G., Hromada S. J., Dutcher K. E., Heaton J. S., and Nussear K. E.. 2021. “Integrating Telemetry Data at Several Scales with Spatial Capture–Recapture to Improve Density Estimates.” Ecosphere 12: e03689. [Google Scholar]
- Morales, J. M. , Haydon D. T., Frair J., Holsinger K. E., and Fryxell J. M.. 2004. “Extracting More out of Relocation Data: Building Movement Models as Mixtures of Random Walks.” Ecology 85: 2436–45. [Google Scholar]
- Morales, J. M. , Moorcroft P. R., Matthiopoulos J., Frair J. L., Kie J. G., Powell R. A., Merrill E. H., and Haydon D. T.. 2010. “Building the Bridge between Animal Movement and Population Dynamics.” Philosophical Transactions of the Royal Society B: Biological Sciences 365: 2289–301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plard, F. , Fay R., Kéry M., Cohas A., and Schaub M.. 2019. “Integrated Population Models: Powerful Methods to Embed Individual Processes in Population Dynamics Models.” Ecology 100: e02715. 10.1002/ecy.2715. [DOI] [PubMed] [Google Scholar]
- R Core Team . 2020. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing; https://www.R-project.org. [Google Scholar]
- Royle, J. A. , Chandler R. B., Sollmann R., and Gardner B.. 2013. Spatial Capture–Recapture. Cambridge, MA: Academic Press. [Google Scholar]
- Royle, J. A. , Chandler R. B., Sun C. C., and Fuller A. K.. 2013. “Integrating Resource Selection Information with Spatial Capture–Recapture.” Methods in Ecology and Evolution 4: 520–30. [Google Scholar]
- Royle, J. A. , and Dorazio R. M.. 2012. “Parameter‐Expanded Data Augmentation for Bayesian Analysis of Capture–Recapture Models.” Journal of Ornithology 152: 521–37. [Google Scholar]
- Royle, J. A. , Dorazio R. M., and Link W. A.. 2007. “Analysis of Multinomial Models with Unknown Index Using Data Augmentation.” Journal of Computational and Graphical Statistics 16: 67–85. [Google Scholar]
- Royle, J. A. , Fuller A. K., and Sutherland C.. 2016. “Spatial Capture–Recapture Models Allowing Markovian Transience or Dispersal.” Population Ecology 58: 53–62. [Google Scholar]
- Royle, J. A. , Fuller A. K., and Sutherland C.. 2018. “Unifying Population and Landscape Ecology with Spatial Capture–Recapture.” Ecography 41: 444–56. [Google Scholar]
- Schaub, M. , and Abadi F.. 2011. “Integrated Population Models: A Novel Analysis Framework for Deeper Insights into Population Dynamics.” Journal of Ornithology 152: 227–37. [Google Scholar]
- Sollmann, R. , Gardner B., and Belant J. L.. 2012. “How Does Spatial Study Design Influence Density Estimates from Spatial Capture‐Recapture Models?” PLoS One 7: e34575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sollmann, R. , Gardner B., Parsons A. W., Stocking J. J., McClintock B. T., Simons T. R., Pollock K. H., and O'Connell A. F.. 2013. “A Spatial Mark–Resight Model Augmented with Telemetry Data.” Ecology 94: 553–9. [DOI] [PubMed] [Google Scholar]
- Street, G. M. , Potts J. R., Börger L., Beasley J. C., Demarais S., Fryxell J. M., McLoughlin P. D., et al. 2021. “Solving the sample size problem for resource selection analysis.” bioRxiv https://www.biorxiv.org/content/early/2021/02/23/2021.02.22.432319.
- Sutherland, C. , Fuller A. K., and Royle J. A.. 2015. “Modelling Non‐euclidean Movement and Landscape Connectivity in Highly Structured Ecological Networks.” Methods in Ecology and Evolution 6: 169–77. 10.1111/2041-210X.12316. [DOI] [Google Scholar]
- Tenan, S. , Pedrini P., Bragalanti N., Groff C., and Sutherland C.. 2017. “Data Integration for Inference about Spatial Processes: A Model‐Based Approach to Test and Account for Data Inconsistency.” PLoS One 12: e0185588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theng, M. , Milleret C., Bracis C., Cassey P., and Delean S.. 2022. “Confronting Spatial Capture–Recapture Models with Realistic Animal Movement Simulations.” Ecology n/a: e3676. 10.1002/ecy.3676. [DOI] [PubMed] [Google Scholar]
- Thurfjell, H. , Ciuti S., and Boyce M. S.. 2014. “Applications of Step‐Selection Functions in Ecology and Conservation.” Movement Ecology 2: 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tobler, M. W. , and Powell G. V.. 2013. “Estimating Jaguar Densities with Camera Traps: Problems with Current Designs and Recommendations for Future Studies.” Biological Conservation 159: 109–18 https://www.sciencedirect.com/science/article/pii/S0006320712005071. [Google Scholar]
- Williams, B. K. , Nichols J. D., and Conroy M. J.. 2002. Analysis and Management of Animal Populations. San Diego, CA: Academic Press. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1
Appendix S2
Data S1
Data Availability Statement
All R scripts (Gardner et al., 2022a) to simulate the data are available on Zenodo at https://doi.org/10.5281/zenodo.6471397. Example detection history data produced from the scripts (Gardner et al., 2022b) are provided on Dryad at https://doi.org/10.5061/dryad.pc866t1r9.


