The Scale Transformed Power Prior for Use with Historical Data from a Different Outcome Model

Summary

We develop the scale transformed power prior for settings where historical and current data involve different data types, such as binary and continuous data. This situation arises often in clinical trials, for example, when historical data involve binary responses and the current data involve some other type of continuous or discrete outcome. The power prior, proposed by Ibrahim and Chen (2000), does not address the issue of different data types. Herein, we develop a new type of power prior, which we call the scale transformed power prior (straPP). The straPP is constructed by transforming the power prior for the historical data by rescaling the parameter using a function of the Fisher information matrices for the historical and current data models, thereby shifting the scale of the parameter vector from that of the historical to that of the current data. Examples are presented to motivate the need for such a transformation, and simulation studies are presented to illustrate the performance advantages of the straPP over the power prior and other informative and non-informative priors. A real data set from a clinical trial undertaken to study a novel transitional care model for stroke survivors is used to illustrate the methodology.

1 |. INTRODUCTION

The availability and use of historical data has become increasingly common in the design and analysis of clinical trials and observational studies covering a wide array of research applications. The incorporation of historical data has been a widely discussed topic over the past 25 years with a vast literature including the use of hierarchical models and various informative priors. One such tool for incorporating historical data into a Bayesian design or analysis is the power prior¹. The power prior has been used by many researchers in applications for the design and analysis of clinical trials and observational studies^2,3,4. The use of the power prior has also been explored in epidemiological studies and clinical trials^5,6. A thorough review of the power prior and its variants, with a detailed discussion on the theory, and numerous applications of the power prior has been conducted⁷. Notably, the power prior has been modified and adapted in numerous ways to, for example, enable the use of historical data in biosimilars trials⁸, allow for multiple historical data sets^1,9,10, and facilitate adaptive clinical trial design^11,12,13. Additional popular priors that incorporate historical data include the robust meta-analytic-predictive (MAP) prior¹⁴ and the commensurate prior³. A challenging issue that arises in a variety of study designs or analyses is when the historical and current data have different data types. For example, scenarios arise often in clinical trials in which the historical data may be binary, such as response data from a Phase 2 trial, but the current data may be continuous such as with a normally distributed outcome in a Phase 3 trial.

The power prior¹ and its adaptations are not well equipped to handle this setting since the scales of the response variables in the historical and current data may be quite different and, as a result, the regression coefficients for the corresponding models may have non-comparable magnitudes. To solve this dilemma, the regression coefficients from the power prior based on the historical data need to be scaled in such a way so as to result in a reasonable prior for the regression coefficients in the current data likelihood. To achieve such a transformation, we propose to scale the regression coefficient by the matrix square root of the Fisher information matrix via the spectral decomposition (i.e., the eigendecomposition). We call this newly scaled power prior the scale transformed power prior (straPP). We use the term “historical data” in a general sense. The historical data that are incorporated could be for a single arm (e.g., only a control arm) or for multiple arms of a study (e.g., treated and control arms). We focus on the latter in this paper. The straPP and its generalization, which we refer to as the generalized straPP, are a broad class of priors closely related to the power prior and commensurate prior. A key aspect of the power prior is that the historical and current data share a common parameter, whereas the commensurate prior³ assumes the parameter for the current data is normally distributed about the historical data parameter.

The rest of this paper is organized as follows. In Section 2, we give a detailed motivating example motivating the straPP for a Bayesian analysis. Section 3 gives a brief review of existing priors that utilize historical data. Section 4 presents the proposed methodology for the straPP in detail, develops the generalized straPP, and discusses connections with the commensurate prior, while focusing on the straPP for generalized linear models (GLMs). Section 5 presents detailed simulation studies using the straPP and its generalizations under various settings and data types within the class of GLMs. Section 6 presents a real data analysis using the straPP and its generalizations to demonstrate the advantages of the straPP over other priors. We close the article with some discussion in Section 7.

2 |. MOTIVATING EXAMPLE

The Comprehensive Post-Acute Stroke Services (COMPASS) study¹⁵ was a two-arm, cluster-randomized pragmatic trial designed to evaluate the effectiveness of a novel transitional care model (COMPASS care model) compared to usual care in mild-to-moderate stroke and transient ischemic attack (TIA) patients across a diverse set of hospitals within North Carolina, USA. The study consisted of two phases. In Phase 1 of the COMPASS study, 40 hospital units were randomized in a 1:1 allocation scheme to either implement the COMPASS care model (i.e., the intervention) or to maintain their usual care practices. The primary comparative effectiveness analyses for the COMPASS study were based on data from Phase I and can be found in Duncan et al¹⁶. During Phase I, the study team provided hospitals randomized to the intervention arm with significant support to help with implementation of the COMPASS care model. In a second phase (Phase 2; an optional extension phase), intervention hospitals attempted to sustain real-world delivery of the intervention with minimal support. Moreover, interested usual care hospitals that continued into Phase 2 were transitioned to provide the intervention as their standard of care. Thus, Phase 2 comparative effectiveness data were considered exploratory and were not published with the primary results. One of the exploratory objectives of the COMPASS study was to assess whether intervention arm patients who received a specialized electronic care plan (eCare plan) had better health outcomes than patients who did not after adjustment for key covariates to account for potential selection bias regarding which patients choose to attend the clinic visit at which they received a customized eCare plan.

We consider that exploratory objective and, in part motivated by the fact that receipt of the eCare plan is a participant-specific (not cluster-specific) variable, we do not address the clustered nature of the COMPASS study in this paper. Of note, Phase 2 of the COMPASS study added a continuous measure of physical health (the PROMIS Global Health Scale) that was not collected in Phase 1. We consider the analysis of Phase 2 patient outcomes based on the PROMIS measure from one large hospital that provided the COMPASS care model during both phases of the study. This relatively large hospital was selected due to having provided the intervention with consistency and high fidelity in both phases of the study. We use data from Phase 1 as historical data to inform analysis of the Phase 2 PROMIS data.

Since the PROMIS outcome was not collected for Phase 1 patients, we consider the incidence of one or more falls as the Phase 1 outcome. This variable is an indicator of whether the participant had at least one fall between hospital discharge and 90 days post-stroke (no falls versus at least one fall). As the historical and current outcomes measure related concepts (global disability versus global health) but are different scales (e.g., one binary, one continuous), these data sets make an ideal case study for comparing performance of the straPP to other commonly used informative prior distributions. In fact, we were able to investigate this relationship empirically as the incidence of falls outcome was collected during Phase 2 of the COMPASS study. Using a simple logistic regression model with incidence of falls as the outcome and the continuous PROMIS measure as the covariate, we estimated the area under the Receiver Operating Characteristic (ROC) curve to be 0.64 indicating fair predictive ability of the incidence of falls for the PROMIS measure. Accordingly, the Phase 1 dataset based on incidence of falls may be useful for inference on covariate effects for the PROMIS Global Health as measured in Phase 2.

The covariates of interest for our analyses were an indicator for receipt of the eCare plan within 30 days of hospital discharge, an indicator for having a history of stroke or TIA, an indicator for having non-white race, and categorized NIH stroke scale score (NIHSS; 0 = no stroke symptoms, 1–4 = minor symptoms, and ≥ 5 = moderate-to-severe symptoms).

The analyses presented in this paper are for illustration purposes only as they make use of data only from complete cases from the aforementioned hospital that participated in the COMPASS study. A more sophisticated analysis that incorporates information from patients with partially missing covariates and/or missing outcomes is beyond the scope of this paper.

3 |. EXISTING PRIORS FOR INCORPORATION OF HISTORICAL DATA

3.1 |. The Power Prior

The power prior¹ is an informative prior derived from historical data that contain information on the same response and covariates as measured in a current study. The power prior, denoted π_p(·), is a meaningful semi-automatic informative prior for the p × 1 parameter of interest θ and is given by

$${\pi }_p\left(\mathit{\theta }|D_0\right)\propto ℒ{\left(\mathit{\theta }|D_0\right)}^{a_0}{\pi }_0(\mathit{\theta }),$$ (1)

where ℒ(θ | D₀) denotes the historical data likelihood, D₀ = (n₀, Y₀, X₀) denotes the historical data, n₀ denotes the sample size, Y₀ denotes the n₀ × 1 response vector, and X₀ denotes the n₀× p covariate matrix. The distribution π₀(θ) is called the initial prior and is often taken to be non-informative. The scalar 0 ≤ a₀ ≤ 1 is called the discounting parameter and its value controls the weight given to the historical data. For example, a value of a₀ = 0 discards the historical data altogether resulting in a prior equal to the initial prior (complete discounting) and a value of a₀ = 1 weights the historical and current data equally. The power prior is robust under many settings¹ but does not account for scale differences in the response variable for the historical and current data.

3.1.1 |. Extensions of the Power Prior

Several extensions and generalizations of the power prior have been developed including several that treat a₀ as a random variable. Additional articles provide information on how to choose a₀^17,18. The normalized power prior¹⁹ models a₀ as a random variable, resulting in a joint distribution for a₀ and θ, written as

$${\pi }_{np}\left(\mathit{\theta },a_0|D_0\right)=\frac{1}{C\left(a_0\right)}ℒ{\left(\mathit{\theta }|D_0\right)}^{a_0}{\pi }_0(\mathit{\theta })\pi \left(a_0\right),$$ (2)

where $C\left(a_0\right)=\int ℒ{\left(\mathit{\theta }|D_0\right)}^{a_0}{\pi }_0\left(\mathit{\theta }\right)d\mathit{\theta }$ is the normalizing constant for the conditional distribution for θ given a₀ and π(a₀) is a marginal prior for a₀.

The partial-borrowing power prior²⁰, provides a useful generalization of the power prior described above. This power prior borrows information on a subset of parameters common to both the historical and current models. Let θ = (θ₁,θ₂,θ₃), where θ₁ is a set of parameters common to both models, θ₂ is a set of parameters that pertain only to the current data model, and θ₃ is a set of parameters that pertain only to the historical data model. The partial-borrowing power prior is given as

$${\pi }_{pb}\left(\mathit{\theta }|D_0\right)\propto ℒ{\left({\mathit{\theta }}_1,{\mathit{\theta }}_3|D_0\right)}^{a_0}{\pi }_0(\mathit{\theta }),$$ (3)

where π₀(θ) is an initial prior for all components of θ. This is a flexible extension of the power prior since there are many cases where historical information may only be available for certain parameters (e.g., parameters associated with a control group).

Additionally, the power prior or normalized power prior can accomodate multiple historical data sets²¹. Forcusing on the power prior, suppose there are K historical data sets, denoted D_0k for k = 1, … ,K. Let D₀ = (D₀₁,…, D_0K) and a₀ = (a₀₁,…, a_0K), then the power prior is defined as

$${\pi }_{mp}\left(\mathit{\theta }|{\mathbf{\text{D}}}_0\right)\propto \left[\prod _{k=1}^Kℒ{\left(\mathit{\theta }|D_{0k}\right)}^{a_{0k}}\right]{\pi }_0(\mathit{\theta }).$$ (4)

The development for a normalized power prior for multiple historical data sets is analogous. When a_0k = a₀ for all k, the power prior for multiple data sets effectively pools the historical data.

3.2 |. Commensurate Prior

Unlike the power prior, the commensurate prior³ allows the model parameters in the historical and current data models, denoted ƞ and θ, respectively, to be different. The influence of the historical data is then controlled by the commensurability parameter, τ, which characterizes the degree to which the historical and current data are comparable. The commensurate prior³ can be written as

$${\pi }_c\left(\mathit{\theta }|D_0,\mathit{\eta },\tau \right)\propto ℒ\left(\mathit{\eta }|D_0\right)N_p\left(\mathit{\theta }|\mathit{\eta },{\tau }^{-1}{\mathit{I}}_p\right){\pi }_0(\mathit{\theta }),$$ (5)

where π₀(·) and ℒ(θ | D₀) are as defined in (1) and I_p is the p × p identity matrix.

4 |. THE SCALE TRANSFORMED POWER PRIOR

In this section, we develop the scale transformed power prior (straPP) which can be derived through a transformation of the regression coefficients in a power prior. Thus, the straPP is explicitly connected to the power prior. It can be viewed as a transformation of the power prior that is designed to modify the scale of the historical data model parameter ƞ to better align with the current data model. The derivation for the straPP is based on the assumption that the standardized parameter values are approximately equal for the historical and current data models and it makes sense to consider such a prior when historical and current data have different outcomes, but nonetheless outcomes that measure related characteristics (e.g., aspects of physical disability).

Let ƞ and θ denote the parameters for the historical and current data models, respectively. Denote the Fisher information matrix for the current data model by I(θ) and consider its square root I^1/2(θ) obtained via a spectral decomposition, i.e., I^1/2(θ) = P(θ)Ʌ^1/2(θ)P(θ)′, where Ʌ^l/2(θ) is a diagonal matrix consisting of square roots of the eigenvalues of I(θ) and P(θ) is a orthogonal matrix of corresponding eigenvectors. Note that I^−1/2(θ) is the square root of the asymptotic covariance matrix for the maximum likelihood estimator for θ. The quantity I^1/2(θ)θ can thus be viewed as a standardized or scaled version of θ. The resulting quantity is unitless and the scaling action can be interpreted as converting the parameter from the original scale into standard deviation units based on the asymptotic covariance matrix. One can of course define the analogous quantities for ƞ. Formally, the assumption of equal standardized parameter values can be expressed as

$${\mathit{I}}_0^{1/2}(\mathit{\eta })\mathit{\eta }={\mathit{I}}_1^{1/2}(\mathit{\theta })\mathit{\theta },$$ (6)

where I₀(·) and I₁(·) denote the Fisher information matrix based on the historical data model and the current data model, respectively. The solution to (6) is denoted by ƞ = g(θ) for some function g(θ). In order to rescale the power prior in (1) by applying the transformation in (6), one would have to solve for the historical data model parameter vector. One can take the power prior, indexed by parameter ƞ ≡ g(θ), and apply the transformation to obtain a prior for θ that is rescaled to match the current data model. The straPP, denoted π_s(·), is then

$${\pi }_s\left(\mathit{\theta }|D_0\right)\propto ℒ{\left(g(\mathit{\theta })|D_0\right)}^{a_0}{\pi }_0(g(\mathit{\theta }))\left|\frac{dg(\mathit{\theta })}{d\mathit{\theta }}\right|,$$

where ƞ = g(θ), a₀ and π₀(·) are as described in Section 3.1, and |dg(θ)/dθ| is the determinant of the Jacobian matrix for the transformation. The expression for the Jacobian matrix can be found in Appendix A of the Supporting Information. The fact that the transformation in (6) is locally one-to-one follows directly from the implicit function theorem²². As a result, propriety of the power prior implies propriety of the straPP. Establishing propriety of the power prior for GLMs and survival models has received significant treatment in the literature^23,24,21, among others. By locally one-to-one, we mean that the mapping $\mathit{\eta }\to {\mathit{I}}_0^{1/2}(\mathit{\eta })\mathit{\eta }$ will not generally be one-to-one for the full domain of ƞ for all models. We discuss the implications of the transformation being only locally one-to-one in Appendix B of the Supporting Information.

When the expression in (6) can be solved for ƞ, analysis using Markov Chain Monte Carlo methods implemented in standard software can be used to perform analysis with the straPP (e.g., Hamiltonian Monte Carlo in rstan²⁵). This is still the case when cannot be solved for ƞ but the procedure is slightly more involved. Full details on model fitting using the straPP are given in Appendix C of the Supporting Information. This includes an efficient procedure that can be applied when the expression in (6) can be solved for θ but not ƞ, termed complementary sampling, and a procedure that can be applied when the expression cannot be solved for either parameter.

When a₀ = 0 and π₀(·) is a uniform improper prior, the straPP will be an improper prior and its use may result in an improper posterior since the kernel of the straPP is simply the determinant of the Jacobian matrix. To avoid this complexity, we simply define the straPP to be equal to the initial prior when a₀ = 0. The intended purpose of the straPP is for cases where one would want to incorporate historical data to some degree in the analysis of the current data. Thus, the case where a₀ = 0 is of no practical relevance.

Lastly, it is straightforward to develop the straPP for multiple historical data sets. However, since the straPP transformation is a function of the historical data covariates, the covariate matrices for the data sets must be stacked in order to have a single, well-defined transformation. We discuss how to develop the straPP for multiple historical data sets in Appendix D of the Supporting Information.

4.1 |. The Normalized straPP

As an alternative to choosing a fixed value of a₀, one can develop a normalized straPP. The normalized straPP can be derived by applying the transformation in (6) to a normalized power prior. The normalized straPP, denoted π_ns(θ, a₀ | D₀), is given by

$${\pi }_{ns}\left(\mathit{\theta },a_0|D_0\right)=\frac{1}{C\left(a_0\right)}ℒ{\left(g(\mathit{\theta })|D_0\right)}^{a_0}{\pi }_0(g(\mathit{\theta }))\pi \left(a_0\right)\left|\frac{dg(\mathit{\theta })}{d\mathit{\theta }}\right|,$$ (7)

where, in this scenario, the normalizing constant is calculated before the scale transformation, such that

$$C\left(a_0\right)=\int ℒ{\left(\mathit{\eta }|D_0\right)}^{a_0}{\pi }_0(\mathit{\eta })d\mathit{\eta }.$$

For computational simplicity, the power prior can be formulated using a normal approximation to the historical data likelihood⁷. Such a power prior is referred to as an asymptotic power prior. Under the normal approximation, the normalizing constant for a normalized asymptotic power prior has a closed form, greatly simplifying computations. For our implementation of the normalized straPP, we develop the prior based on a normalized asymptotic power prior.

4.2 |. Partial-Borrowing with the straPP

One may wish to utilize the straPP to borrow information for a subset of components in the parameter vector. Let the p × 1 vector θ be partitioned into two vectors such that θ = (θ_l, θ₂), where θ₁ is r × 1 and θ₂ is (p - r)×1. Suppose we would like to specify a straPP that borrows information on θ₁ but does not borrow information on θ₂. To arrive at a partial borrowing straPP, we integrate over the parameters for which information will not be borrowed and further include an initial prior for the parameters only in the new data model. Specifically, the partial-borrowing straPP is given by

$${\pi }_{pbs}\left(\mathit{\theta }|D_0\right)=\left[\int {\pi }_s\left({\mathit{\theta }}_1,{\tilde{\mathit{\theta }}}_2\right)d{\tilde{\mathit{\theta }}}_2\right]{\pi }_0\left({\mathit{\theta }}_2\right),$$ (8)

where ${\tilde{\mathit{\theta }}}_2$ represents the parameters induced the straPP transformation but on which information will not be borrowed. The initial prior π₀(θ₂) therefore pertains to the parameters θ₂ only informed by the current data model. In practice, the integration in (8) is conducted implicitly in the MCMC scheme, not analytically.

The partial-borrowing straPP enables use of the straPP in a variety of settings. Perhaps the most intuitive example is for situations where it is not appropriate to borrow information on the intercept parameter for the current data model. For example, the partial-borrowing straPP may be desirable when the historical response data is binary and the current response data is normal. In this case, the intercept terms will often have no logical connection even though covariate effects are related. Another instance where the partial-borrowing straPP may be preferred is the case where it is of paramount interest to borrow information on a treatment effect parameter, but borrowing information on nuisance parameters in the regression model is avoided simply to add a degree of robustness provided the current data alone are sufficient to estimate the other covariate effects.

4.3 |. The Generalized Scale Transformed Power Prior (Gen-straPP)

The straPP is derived under the assumption that the standardized parameter values for the historical and current data models are equal. Such an assumption leads to a reasonable transformation to scale the parameter in a power prior when the historical data model is not the same as that of the current data. Nonetheless it is important to be able to conduct sensitivity analyses of the core assumption of the straPP. Thus, it is useful to develop a generalization of the straPP that provides a degree of robustness when the assumption of equal standardized parameter values does not hold. Towards this goal, we develop a generalized scale transformed power prior (Gen-straPP), in which we specify

$${\mathit{I}}_0^{1/2}(\mathit{\eta })\mathit{\eta }={\mathit{I}}_1^{1/2}(\mathit{\theta })\mathit{\theta }+{\mathit{c}}_0,$$ (9)

where c₀ is a p × 1 vector that allows component-specific deviations from the assumption of equal standardized parameter values for ƞ and θ. We denote the transformation as $\mathit{\eta }=g_{{\mathit{c}}_0}(\mathit{\theta })$. We note that c₀ = 0 corresponds to the straPP. In practice, the most natural choice would be to take c₀ to be a random vector and assign it a prior distribution. Therefore, we suggest taking c₀ to be a random vector and assign it a normal prior, i.e., c₀ ~ N_p(0, ω₀I_p), where the variance parameter ω₀ is given a standard half-normal hyperprior. The Gen-straPP can be derived from the power prior in (1) using the transformation in (9) as

$${\pi }_{gs}\left(\mathit{\theta },{\mathit{c}}_0,{\omega }_0|D_0\right)\propto ℒ{\left(g_{{\mathit{c}}_0}(\mathit{\theta })|D_0\right)}^{a_0}{\pi }_0\left(g_{{\mathit{c}}_0}(\mathit{\theta })\right)\left|\frac{d{g}_{{\mathit{c}}_0}(\mathit{\theta })}{d\mathit{\theta }}\right|{\pi }_0\left({\mathit{c}}_0,{\omega }_0\right),$$ (10)

where π₀(c₀, ω₀) denotes the joint prior for c₀ and ω₀. The transformation to obtain the Gen-straPP is a combination of (9) and an identity transformation for c₀. It is straightforward to show the determinant of that full-rank transformation is equal to the determinant shown in (10). Extending the Gen-straPP for partial-borrowing is equally straightforward.

The Gen-straPP is closely related to a commensurate prior formulated on the standardized parameter values. To see this, note that the Gen-straPP transformation in (9) can be re-written as

$${\mathit{I}}_1^{1/2}(\mathit{\theta })\mathit{\theta }={\mathit{I}}_0^{1/2}(\mathit{\eta })\mathit{\eta }-c_0.$$

Let ${\mathit{\theta }}^{*}={\mathit{I}}_1^{1/2}(\mathit{\theta })\mathit{\theta }$ denote the standardized current data model parameter and ${\mathit{\eta }}^{*}={\mathit{I}}_0^{1/2}(\mathit{\eta })\mathit{\eta }$ denote the standardized historical data model parameter. For c₀ ~ N_p(0,ω₀I_p) and given ƞ*, the standardized current data model parameter satisfies θ* | ƞ* ~ N_p(ƞ*, ω₀I_p). This is precisely the form of a commensurate prior and thus the hyperparameter ω₀ is closely related to the commensurability parameter in a commensurate prior. In the context of the Gen-straPP, commensurability pertains to the standardized parameter values.

4.4 |. The straPP for Generalized Linear Models

For the remainder of the paper, we assume that outcomes for the historical and current data arise from the class of generalized linear models (GLMs). Without loss of generality, we focus on development of the straPP (conditional on dispersion parameters) and note that with minor modifications one can similarly develop the partial-borrowing straPP, Gen-straPP, or partial-borrowing Gen-straPP. When discussing GLMs, in a departure from previous notation, we represent the parameters for the historical data model as ξ₀ = (β₀, ϕ₀) and current data model as ξ₁ = (β₁, ϕ₁), where β₀ and β₁ are the regression parameter vectors and ϕ₀ and ϕ₁ are the scalar dispersion parameters.

Let k index the historical (k = 0) and current (k = 1) data models, ${\mathit{Y}}_k^T=\left(y_{k1},\dots ,y_{k{n}_k}\right)$ be the n_k × 1 response vector, X_k be the n_k × p covariate matrix (with intercept) with ${\mathit{x}}_{k\mathit{I}}^T$ denoting the covariate vector for the ith observation, and ξ_k = (β_k, ϕ_k) be the GLM parameters. The likelihood contribution for the ith case for dataset k can be written as

$$f\left(y_{k\mathit{I}}|{\mathit{\xi }}_k\right)=\text{exp}\left[{\varphi }_k\left\{y_{k\mathit{I}}{h}_k\left({\mathit{x}}_{k\mathit{I}}^T{\mathit{\beta }}_k\right)-b_k\left(h_k\left({\mathit{x}}_{k\mathit{I}}^T{\mathit{\beta }}_k\right)\right)-c_k\left(y_{k\mathit{I}}\right)\right\}-\frac{1}{2}{s}_k\left(y_{k\mathit{I}},{\varphi }_k\right)\right],$$ (11)

where h_k(·) is the link function, and b_k(·), c_k(·), and s_k(·) are known functions based on the particular GLM family member. For the canonical link function, the p × p Fisher information matrix for the regression parameters based on the likelihood associated with (11) is given as

$${\mathit{I}}_k\left({\mathit{\xi }}_k|{\mathit{X}}_0\right)={\varphi }_k{\mathit{X}}_0^T{V}_k\left({\mathit{\beta }}_k\right){\mathit{X}}_0,$$ (12)

where V_k(β_k) = diag {ν_ki(β_k)}, with ${\upsilon }_{k\mathit{I}}\left({\mathit{\beta }}_k\right)={\ddot{b}}_k\left(h_k\left({\mathit{x}}_{0\mathit{I}}^T{\mathit{\beta }}_k\right)\right)$ for i = 1, …,n_k. Here diag {v_ki(β_k)} denotes a diagonal matrix with the (i, i) element as (v_ki(β_k)) and ${\ddot{b}}_k$ represents the second derivative of the function b_k(·) taken with respect to its scalar argument.

Consider a situation in which we only wish to borrow information on the regression parameters. Based on the general form of (12), the transformation leading to the straPP for GLMs is given by

$${\mathit{I}}_0^{1/2}\left({\mathit{\xi }}_0|{\mathit{X}}_0\right){\mathit{\beta }}_0={\mathit{I}}_1^{1/2}\left({\mathit{\xi }}_1|{\mathit{X}}_0\right){\mathit{\beta }}_1.$$ (13)

Solving for β₁, we denote the transformation implied by (13) as g_reg (ξ₁, ϕ₀|x₀). Note that in (13), we develop the straPP by computing the Fisher information matrices for the current and historical data models using the covariate matrix X₀ associated with the historical data. This is done to ensure the effective sample size for the straPP is equal to that of the power prior from which it is derived and to allow the straPP to be constructed using information entirely derived from the historical data (e.g., outcome and covariates) which is appealing. The straPP for GLMs can be written as

$${\pi }_s\left({\mathit{\beta }}_1,{\varphi }_0|{\varphi }_1,D_0\right)\propto ℒ{\left(g_{\text{reg}}\left({\mathit{\xi }}_1,{\varphi }_0|{\mathit{X}}_0\right),{\varphi }_0|D_0\right)}^{a_0}{\pi }_0\left(g_{\text{reg}}\left({\mathit{\xi }}_1,{\varphi }_0|{\mathit{X}}_0\right),{\varphi }_0\right)\left|\frac{d{g}_{\text{reg}}\left({\mathit{\xi }}_1,{\varphi }_0|{\mathit{X}}_0\right)}{d{\mathit{\beta }}_1}\right|,$$ (14)

where π₀ (g_reg (ξ₁, ϕ₀|X₀), ϕ₀) is the inital prior for ξ₀ and ϕ₀. Similar to above developments, the transformation to obtain the partial-borrowing straPP for GLMs is a combination of (13) and identity transformations for ϕ₀ and ϕ₁. It is straightforward to show the determinant of that full-rank transformation is equal to the determinant in (14). The expression for the Jacobian matrix where both the historical and current data models have the canonical link can be found in Appendix E of the Supplemental Materials.

4.5 |. The Linear Model Special Case

For illustrative purposes, we consider a special case in which both the historical and current data arise from linear regression models with known variances (i.e., ${\sigma }_0^2$ and ${\sigma }_1^2$ are known), henceforth referred to as the normal-normal case. When variances are known, ξ_k = β_k and so, for ease of exposition, we simply write β₀ and β₁ to represent the complete parameter vector for the historical and current data models, respectively. This simple example is helpful for pedagogical reasons as an elegant closed-form can be derived for the straPP which provides insight into its rescaling properties. For the linear model, the Fisher information matrix in (12) reduces to ${\mathit{I}}_k\left({\mathit{\beta }}_k|{\mathit{X}}_0\right)={\sigma }_k^{-2}{\mathit{X}}_0^T{\mathit{X}}_0$.where ${\varphi }_k={\sigma }_k^{-2}$ is the inverse variance. Based on this, the transformation leading to the straPP in (6) reduces to β₀/σ₀ = β₁/σ₁, which nicely illustrates the equality of parameter values once scaled by the standard deviations for the associated outcomes. In this simple setting, both the power prior and the straPP can be shown to be normal distributions, with power prior as

$${\mathit{\beta }}_1\stackrel{\mathit{PP}}{~}N\left({\left({\mathit{X}}_0^T{\mathit{X}}_0\right)}^{-1}{\mathit{X}}_0^T{\mathit{Y}}_0,\left(\frac{{\sigma }_0^2}{a_0}\right){\left({\mathit{X}}_0^T{\mathit{X}}_0\right)}^{-1}\right).$$ (15)

For deriving the straPP, one can understand the scale transformation as a variable transformation on the regression parameter of the power prior for the historical data. We can write the power prior for the historical parameter as ${\mathit{\beta }}_0~N\left({\left({\mathit{X}}_0^T{\mathit{X}}_0\right)}^{-1}{\mathit{X}}_0^T{\mathit{Y}}_0,\left({\sigma }_0^2/a_0\right){\left({\mathit{X}}_0^T{\mathit{X}}_0\right)}^{-1}\right)$. The straPP transformation β₁ = (σ₁/σ₀)β₀ is a function of the historical parameter, thus the current regression parameter is also distributed normally with mean (σ₁/σ₀)E(β₀) and variance $\left({\sigma }_1^2/{\sigma }_0^2\right)\text{Var}\left({\mathit{\beta }}_0\right)$. We have

$${\mathit{\beta }}_1\stackrel{\mathit{\text{straPP}}}{~}N\left(\frac{{\sigma }_1}{{\sigma }_0}{\left({\mathit{X}}_0^T{\mathit{X}}_0\right)}^{-1}{\mathit{X}}_0^T{\mathit{Y}}_0,\left(\frac{{\sigma }_1^2}{a_0}\right){\left({\mathit{X}}_0^T{\mathit{X}}_0\right)}^{-1}\right).$$ (16)

One can see that the mean for the power prior in (15) is equal to the maximum likelihood estimate of β based on the historical data, which we denote as ${\widehat{\mathit{\beta }}}_0$. Therefore, the mean for the straPP is equal to $\left({\sigma }_1/{\sigma }_0\right){\widehat{\mathit{\beta }}}_0$. Of equal importance, the variance of the straPP is equal to the variance of the power prior apart from the former being a function of ${\sigma }_1^2$ and the latter ${\sigma }_0^2$. Thus, the information contained in the straPP is essentially recalibrated to be a function of the variance associated with the current data model instead of the historical data model.

4.5.1 |. Properties of the straPP for the Linear Model

For the normal-normal case when the assumption of the straPP transformation holds, the posterior mean based on an analysis with the straPP can be shown to be unbiased as a point estimator in the frequentist sense (see Appendix F of the Supporting Information). It follows that the posterior mean based on an analysis with the (unscaled) power prior is biased. However, the rescaling property of the straPP can result in a prior with less precise information about the parameter (e.g., when σ₁ > σ₀) and thus the variance of the posterior mean from an analysis with the straPP can exceed that of the power prior. This implies a trade-off between the bias and variance of the posterior mean point estimators, which becomes apparent when comparing their mean-squared error (MSE). Theorem 1 gives conditions under which the posterior mean based on the straPP has a smaller MSE than the posterior mean based on the power prior.

Theorem 1. Let β_1j denote the (j + 1)th element of β₁(j =0,… ,p - 1). Further ${\widehat{\beta }}_{s,1j}$ and ${\widehat{\beta }}_{p,1j}$ denote the posterior mean point estimators for the straPP and power prior, respectively. For the normal-normal case, when β₀ = g(β₁) (i.e., the relationship of the straPP transformation holds), the straPP estimator ${\widehat{\beta }}_{s,1j}$ has a lower MSE than the power prior estimator ${\widehat{\beta }}_{p,1j}$ under the following condition:

$$\frac{\text{Var}\left({\widehat{\beta }}_{s,1j}\right)-\text{Var}\left({\widehat{\beta }}_{p,1j}\right)}{{\left[\text{Percent\hspace{0.17em}Bias}\left({\widehat{\beta }}_{p,1j}\right)\right]}^2}\le {\beta }_{1j}^2.$$ (17)

In general, the percent bias of ${\widehat{\beta }}_{p,1j}$ depends on β_1j. The proof of Theorem 1 can be found in Appendix F of the Supporting Information.

5 |. SIMULATION STUDIES

In this section, we present and discuss results from a collection of simulation studies designed to evaluate the performance of the straPP compared to the normalized straPP and Gen-straPP, as well as to the power prior, normalized power prior, commensurate prior, and use of a reference non-informative improper prior. The purpose of these simulations is to illustrate that the straPP and its variations have improved performance compared to other priors. Our comparison against the power prior, normalized power prior, and commensurate prior is to demonstrate empirically that these priors are not appropriate unless the data types (i.e., models) for the current and historical data are the same. Though this point is perhaps obvious to the reader, it is nonetheless helpful to see how poorly such priors perform in terms of bias-variance tradeoff.

In Section 5.1, we present simulation studies for the normal-normal case described in Section 4.5, where both the historical and current data models are linear regression models with known variances. In Section 5.2, we present simulation studies for a case where the historical data follow a logistic regression model and the current data follow a linear regression model with known variance, which we denote the binary-normal case. We generated 5,000 historical and current data sets for each unique parameter combination. For each simulated data set for Section 5.2, we used Hamiltonian Monte Carlo methods in rstan²⁵ to obtain 25,000 posterior samples after 5,000 burn in.

5.1 |. Simulation Studies for the Normal-Normal Case

For the normal-normal case, we performed simulation studies using parameter values that obey the assumption of the straPP transformation (e.g., β₀ = g(β₁)). We then simulated the historical data and current data based on the corresponding linear regression models. Thus, for this simulation, we are effectively evaluating the performance of the straPP compared to the alternative priors for the case where the straPP transformation assumption holds.

For the normal-normal case, the percent bias of the posterior mean estimator for the treatment effect based on the power prior (i.e.,${\widehat{\beta }}_{p,11}$) does not depend on the true treatment effect (i.e., β₁₁). As a result, one can calculate the exact threshold, denoted as ${\beta }_{11}^{*}$, where the MSE for the posterior mean estimators based on the straPP and power prior are equal, as

$${\beta }_{11}^{*}=\pm \frac{\sqrt{\text{Var}\left({\widehat{\beta }}_{s,11}\right)-\text{Var}\left({\widehat{\beta }}_{p,11}\right)}}{\text{ Percent Bias}\left({\widehat{\beta }}_{p,11}\right)}=\pm \frac{2\left(n_1{\sigma }_0^2+a_0{n}_0{\sigma }_1^2\right)}{a_0{n}_0\left({\sigma }_0-{\sigma }_1\right)}\sqrt{\frac{n_1+a_0^2{n}_0}{{\left(n_1+a_0{n}_0\right)}^2}-{\sigma }_0^2\frac{n_1{\sigma }_0^2+a_0^2{n}_0{\sigma }_1^2}{{\left(n_1{\sigma }_0^2+a_0{n}_0{\sigma }_1^2\right)}^2}}.$$

We performed two sets of simulation studies for the normal-normal case. In both sets of simulations, the following were considered: n₀ = 50, n₁ = 100, a₀ = 0.5, β₁₀ = 1, and β₁₁ ∊ {0.0,0.09,…, 1.71, 1.8}. For the first set of simulation studies, we considered a case where the historical data variance exceeded that of the current data (i.e., σ₀ = 3 > σ₁ = 1). For the second set of simulation studies, we reversed the relationship between the variances. The values of the historical data model parameters were then identified by solving β₀ = (σ₀/σ₁)β₁.

Figure 1 panels (a)-(d) present the results of the first set of the simulation studies and panels (e)-(h) present the results from the second set. For the first set of simulation studies, since the rescaling action of the straPP leads to more precise information about the parameter in the current data model, the theoretical threshold for MSE equivalence between the power prior and straPP is never crossed and it can be seen that the straPP has uniformly better performance than the power prior and the uniform improper prior. For the second set, where the variance of the historical data is less than that of the current data, the rescaling action of the straPP results in a prior that provides more accurate inference (e.g., less bias in the posterior mean) but also less precision on average (i.e., larger variability in the posterior mean). For this case, there is a tradeoff in terms of MSE with the straPP having superior MSE only for values of β₁₁ that exceed ${\beta }_{11}^{*}=0.9364$. Nonetheless, the straPP still provides more accurate information even if the MSE of the posterior mean is not always superior to that of the power prior. Furthermore, the coverage probability of the straPP remains approximately 0.95, while that of the power prior decreases greatly as the true value of β₁₁ increases. Additional simulation studies were performed using other inputs. Importantly, the results presented here are indicative of the general behavior of the straPP with the only material difference between simulations being that the threshold for MSE equality between the straPP and the power prior varies depending on the particular inputs used for simulation.

FIGURE 1.

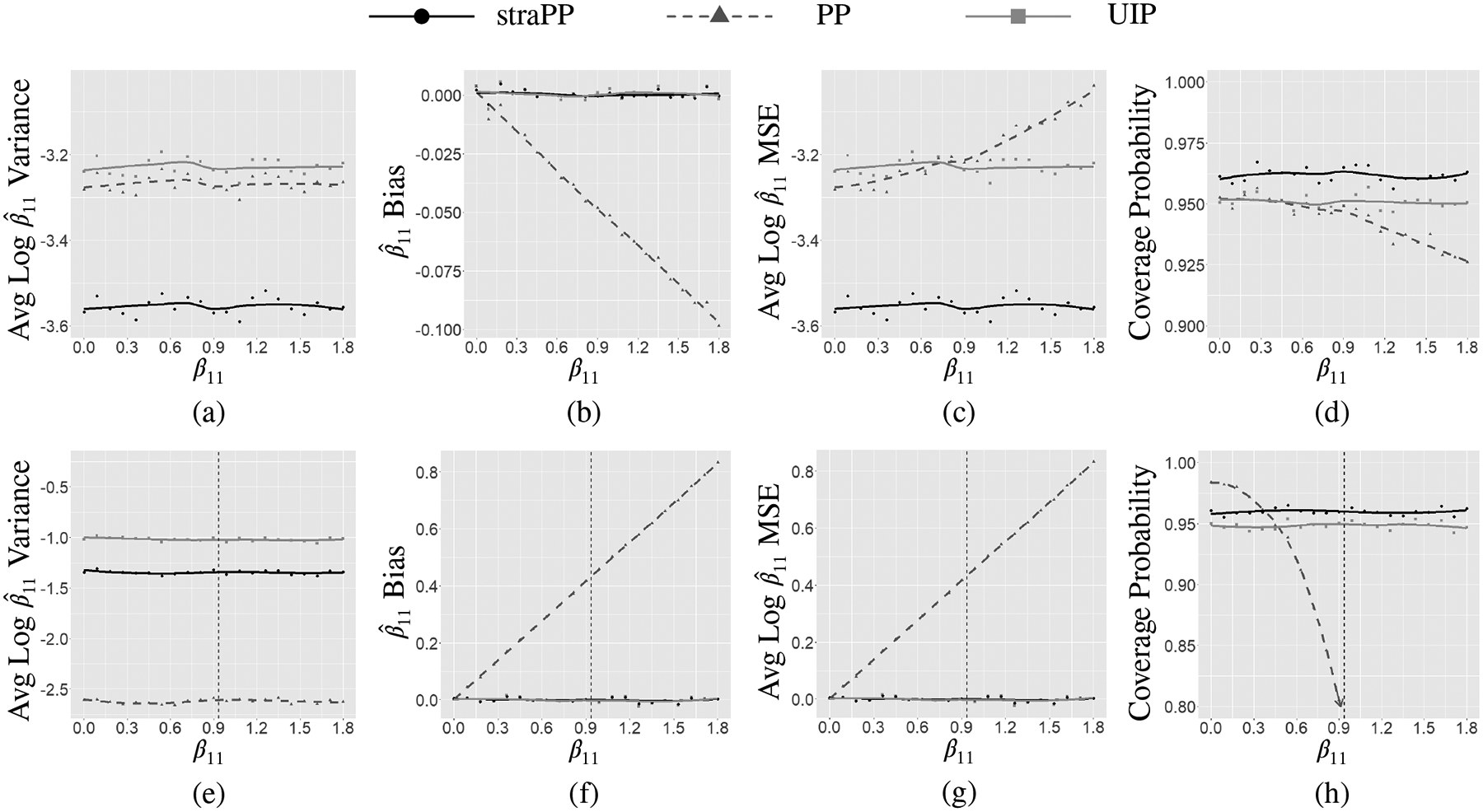
Panels (a)-(d) present the average log variance, bias, log MSE, and coverage probability for the posterior mean of β₁₁, respectively, as a function of the true value of β₁₁ plotted on the x-axis for the case where σ₀ = 3,σ ₁ = 1 for the scale transformed power prior, power prior, and uniform improper prior. Panels (e)-(h) present the same information for the case where σ₀ = 1, σ₁ = 3. straPP, scale transformed power prior; PP, power prior; UIP, uniform improper prior.

5.2 |. Binary-Normal Case Simulation

For the binary-normal case, we consider the case where the parameters in the historical and current data models satisfy the assumption of the straPP transformation. The primary purpose of this simulation is to compare the straPP to the normalized (asymptotic) straPP. Additionally, the power prior, normalized power prior, and a non-informative reference prior were included for further comparison.

Unlike the normal-normal case, the form of ${\mathit{I}}_1^{-1/2}{\mathit{I}}_0^{1/2}\left({\mathit{\beta }}_0\right)$ does not simplify and thus no elegant relationship between the parameters can be seen. We considered the following inputs: n₀ = 100, n₁ = 100, a₀ = 0.5, β₀₀ = −0.5, σ₁ = 2, and β₀₁ ∊ {0.0,0.1,…, 1.9,2.0}. The values of the current data model parameters were then identified by solving β₁ = g⁻¹(β₀). Note that the value of the parameters for the historical data model were chosen so that 0.38 ≤ p₀, p₁ ≤ 0.82 and are thus consistent with our recommendations in Appendix B of the Supporting Information for when a straPP may be appropriate. This constraint was implemented for the added purpose of ensuring the simulated data sets from the logistic model had sufficient variability in the outcome across treatment groups to avoid instability issues in model fitting. More complete details on prior specifications can be found in Appendix H of the Supporting Information.

Figure 2 panels (a)-(d) present results comparing performance characteristics of the straPP, normalized straPP, power prior, normalized power prior, and reference prior. Focusing first on MSE, one can see that the MSE (panel c) for the straPP and normalized straPP is smaller than for the other priors over the full range of β₁₁. This is largely attributable to the reduction in the sampling variability of the posterior mean estimator (panel a). The normalized straPP admits the least biased point estimator among the set of priors that borrow information from the historical data. The straPP appears to have non-negligible bias for all values of β₁₁, but less bias than the power prior and normalized power prior when β₁₁ > 1.25. It is important to note that there is no theoretical guarantee that the posterior mean estimator will be unbiased (as there was in the normal-normal case). The fact that bias increases with β₁₁ is related to the straPP transformation being less appropriate for extreme success probabilities as described in Appendix B of the Supporting Information.

FIGURE 2.

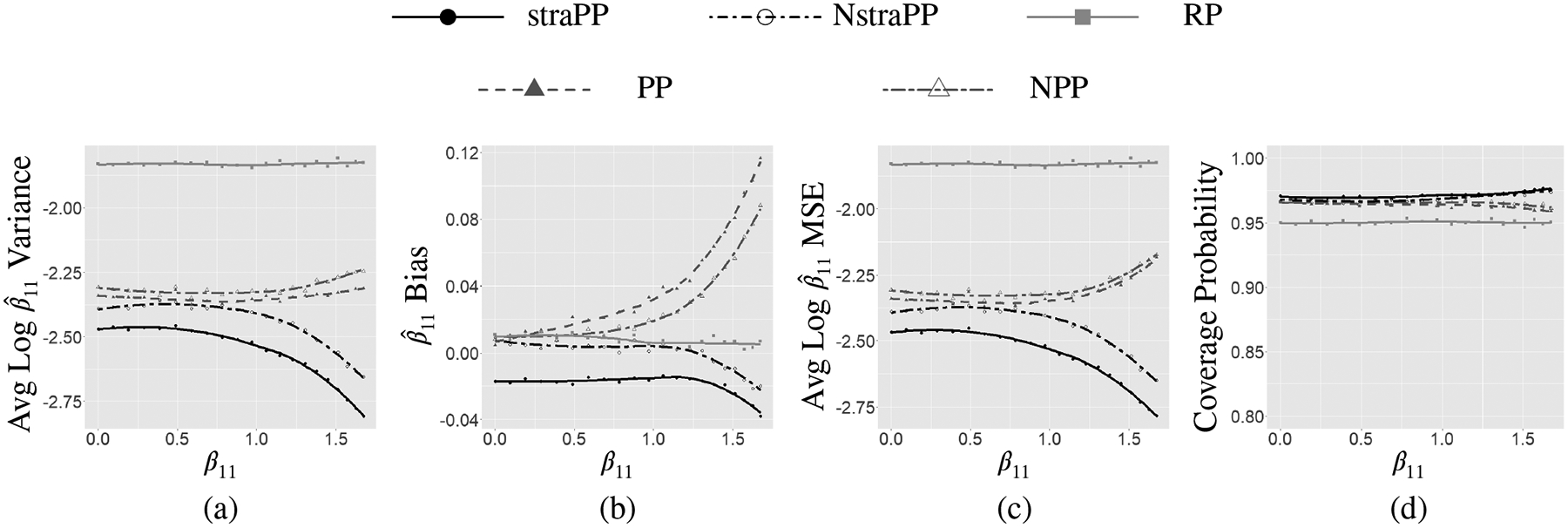
Panels (a)-(d) present the average log variance, bias, log MSE, and coverage probability for the posterior mean of β₁₁, respectively, as a function of the true value of β₁₁ plotted on the x-axis for the straPP, normalized straPP, power prior, normalized power prior, and reference prior. straPP, scale transformed power prior; NstraPP, normalized straPP; PP, power prior; NPP, normalized power prior; RP, reference prior.

6 |. ANALYSIS OF THE COMPASS STUDY DATA

For analysis of the COMPASS data, we use incidence of falls as the Phase 1 outcome data (i.e., historical data) and the continuous PROMIS outcome as the Phase 2 outcome data (i.e., current data). The analysis assumes that the historical patient outcomes are independently distributed according to a logistic regression model and the current patient outcomes are independently distributed according to a linear regression model. As with any real data analysis, the true value of the variance parameter for the linear regression model is not known and thus we appropriately treat that parameter as random. The focus of this analysis is restricted to borrowing information on covariate effects as there is no rationale for borrowing information on the intercept parameters. Thus, information borrowing priors are based on partial-borrowing. For the purposes of comparison, we analyzed the COMPASS data using the straPP, Gen-straPP, power prior, commensurate prior, and a non-informative reference prior. As in the simulations, we consider use the partial-borrowing power prior and the partial-borrowing commensurate prior to highlight that these priors are not appropriate in this context. The initial priors for the power and commensurate priors were taken as in Section 5.2. All analyses were performed using Hamiltonian Monte Carlo with rstan²⁵. For each prior, a total of 25,000 MCMC posterior samples were obtained after a burn in of 5,000 samples. To compare the overall quality of models fit based on the set of selected priors, we used the deviance information criterion²⁶ (DIC), where $\text{DIC}\left(a_0\right)=2E\left\{\text{Dev}\left({\mathit{\xi }}_1\right)|D_1,D_0,a_0\right\}-\text{Dev}\left({\overline{\mathit{\xi }}}_1\right)$, where $\overline{{\mathit{\xi }}_1}=E\left\{{\mathit{\xi }}_1|D_1,D_0,a_0\right\}$ and $\text{Dev}\left({\mathit{\xi }}_1\right)=-2{\sum }_{\mathit{I}=1}^n\text{log}f\left(y_{1\mathit{I}}|{\mathit{x}}_{1\mathit{I}},{\mathit{\xi }}_1\right)$. Lower values of DIC indicate better fit.

For this illustration, we focus on the covariate effect associated with receipt of the COMPASS eCare plan, a key component of the intervention. The regression model included an indicator for receipt of the COMPASS eCare plan, an indicator for having a history of stroke or TIA, NIHSS score, and an indicator for having non-white race. After removing observations with missing values for the covariates of interest, the historical data sample size was 244 and the current data sample size was 385.

Table 1 presents the DIC value for different choices of a₀ for the straPP, Gen-straPP, and power prior. For each prior, the DIC value roughly increases in a₀ though the magnitude of increase is most substantial for the power prior. For the values of a₀ considered by the authors, a₀ = 0.1 was the optimal choice for the Gen-straPP and power prior and a₀ = 0.25 for the straPP. Though beyond the scope of this paper, in sample size determination contexts, the value of a₀ may also be chosen a priori to ensure high Bayesian power and a well controlled Bayesian type I error rate²⁷. Here, we simply take the optimal value from Table 1 to use for analysis of the COMPASS data.

TABLE 1.

DIC for the Gen-straPP, straPP and PP with Various Values of a₀

	a 0
Model	0.10	0.25	0.50	0.75	1.00
Gen-straPP	2815.38	2815.65	2816.38	2816.82	2816.93
straPP	2815.38	2815.37	2817.25	2819.23	2821.30
PP	2816.44	2819.01	2822.20	2823.83	2824.92

Gen-straPP, generalized scale transformed power prior; straPP, scale transformed power prior; PP, power prior.

Table 2 presents the DIC, posterior estimates, ratio of posterior variances (used as a measure of relative effective sample size), and 95% highest posterior density (HPD) intervals based on an analysis with each of the selected priors. We define the ratio of posterior variances as the posterior variance of the covariate effect for a given prior, divided by the corresponding posterior variance from an analysis based on the straPP. Posterior summaries for the intercepts and variance parameter for the linear regression model can be found in Appendix I of the Supporting Information.

TABLE 2.

Posterior Estimates for the COMPASS Data

			eCare Plan			History of Stroke			Minor NIHSS			Moderate-Severe NIHSS			Non-white
Model	a 0	DIC	Mean (SD)	RPV	95% HPD	Mean (SD)	RPV	95% HPD	Mean (SD)	RPV	95% HPD	Mean (SD)	RPV	95% HPD	Mean (SD)	RPV	95% HPD
Gen-straPP	0.10	2815.38	0.80 (0.92)	1.17	(−1.01, 2.60)	−0.97 (1.13)	1.17	(−3.13, 1.30)	−1.29 (1.05)	1.08	(−3.34, 0.78)	−3.54 (1.16)	1.48	(−5.85, −1.35)	−1.61 (1.55)	1.98	(−4.65, 1.51)
straPP	0.25	2815.37	0.47 (0.85)	1.00	(−1.21, 2.14)	−0.54 (1.05)	1.00	(−2.52, 1.56)	−1.05 (1.01)	1.00	(−3.04, 0.92)	−2.79 (0.95)	1.00	(−4.63, −0.89)	−1.64 (1.10)	1.00	(−3.35, 1.03)
RP	–	2816.65	1.14 (0.97)	1.29	(−0.78, 3.02)	−1.05 (1.22)	1.36	(−3.43, 1.36)	−1.29 (1.10)	1.18	(−3.46, 0.87)	−4.27 (1.31)	1.89	(−6.83, −1.70)	−2.10 (2.08)	3.56	(−6.20, 1.97)
PP	0.10	2816.44	0.46 (0.76)	0.80	(−1.04, 1.96)	−0.25 (0.96)	0.83	(−2.17, 1.57)	−0.53 (0.80)	0.63	(−2.12, 1.02)	−2.80 (1.17)	1.51	(−5.14, −0.58)	−2.02 (1.84)	2.77	(−5.75, 1.41)
COM	–	2818.47	0.53 (0.84)	0.97	(−1.01, 2.28)	−0.31 (0.96)	0.83	(−2.32, 1.41)	−0.25 (0.86)	0.73	(−2.04, 1.36)	−2.01 (1.25)	1.72	(−4.55, 0.23)	−1.45 (1.34)	1.47	(−4.23, 1.08)

RPV, ratio of posterior variances; Gen-straPP, generalized scale transformed power prior; straPP, scale transformed power prior; RP, reference prior; PP, power prior; COM, commensurate prior.

In Table 2, analysis with the Gen-straPP and straPP resulted in the smallest DIC when compared to analyses with other priors. This suggests that the rescaling action of the straPP family is useful for translating the information on covariate effects from the incidence of falls outcome to the continuous PROMIS outcome. Aside from the general performance of the priors as measured by DIC, we also investigated the posterior estimates for the eCare Plan effect of interest. Compared to the straPP, power and commensurate priors, the posterior mean effect based on the Gen-straPP is much closer to the value based on the reference prior. While the posterior variance is reduced for analysis based on the straPP family of priors compared to the reference prior, the degree of variance reduction is substantially less than that based on the power and commensurate priors. These properties coupled with the higher DIC for the power and commensurate priors illustrate why the Gen-straPP may be more appropriate for this context than the other priors.

7 |. DISCUSSION

In this paper, we developed the straPP to provide a mechanism for informative prior elicitation using historical data when the historical and current data types are different. The straPP is developed based on an assumption that parameter values between the models for the historical and current data are equivalent after appropriate rescaling. The Gen-straPP was developed to provide robustness to violations of the underlying assumption of the straPP. Additional research is needed to evaluate the extent to which the Gen-straPP can provide sufficient robustness across different GLMs (e.g., poisson, negative binomial, and gamma GLMs). Though we have developed the straPP and Gen-straPP as transformations of a power prior, the transformation could be applied to any prior (e.g., a robust mixture prior).

As is discussed in Appendix B of the Supporting Information, use of the straPP can only be advised when the historical data model regression parameters are consistent with the subspace of the overall parameter space where the straPP transformation is one-to-one. For example, applying the straPP to binary historical data with extreme success probabilities is not advised in general. Additional research will be needed to facilitate use of the straPP family of priors more broadly in these extreme contexts.

The straPP family of priors were developed specifically for univariate GLMs. In future work, the authors plan to extend development to allow for historical and/or current data models with time-to-event outcomes (e.g., proportional hazards models). Developing the straPP for time-to-event data poses several new challenges not addressed in this paper, including dealing with right-censoring and modeling higher dimensional nuisance parameters (e.g., baseline hazard). Additionally, the authors plan to develop Bayesian sample size determination methodology for use with the straPP and its generalizations in the design of clinical trials.

Abbreviations:

Gen-straPP

generalized scale transformed power prior

straPP

scale transformed power prior

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available on request from the authors. The data are not publicly available due to their containing information that could compromise the privacy of research participants.