Optimal high-throughput virtual screening pipeline for efficient selection of redox-active organic materials

Summary

As global interest in renewable energy continues to increase, there has been a pressing need for developing novel energy storage devices based on organic electrode materials that can overcome the shortcomings of the current lithium-ion batteries. One critical challenge for this quest is to find materials whose redox potential (RP) meets specific design targets. In this study, we propose a computational framework for addressing this challenge through the effective design and optimal operation of a high-throughput virtual screening (HTVS) pipeline that enables rapid screening of organic materials that satisfy the desired criteria. Starting from a high-fidelity model for estimating the RP of a given material, we show how a set of surrogate models with different accuracy and complexity may be designed to construct a highly accurate and efficient HTVS pipeline. We demonstrate that the proposed HTVS pipeline construction and operation strategies substantially enhance the overall screening throughput.

Graphical abstract

Highlights

• •Optimal computational campaigns were designed for screening redox-active materials
• •ML models were trained to construct an effective virtual screening pipeline
• •The proposed framework can maximize the return-on-computational-investment (ROCI)
• •The proposed framework generally applies to any high-fidelity virtual screening tasks

Organic chemistry; Materials science

Introduction

With the increasing interest in renewable energy sources, there has been a pressing need to develop novel energy storage devices that can overcome the practical shortcomings of conventional Li-ion batteries.^1,2,3,4 Especially, organic electrode material-based energy storage devices have gained increasing attention as they possess a number of favorable characteristics. First of all, organic materials can be synthesized from earth-abundant precursors such as C, H, O, or N. Moreover, they do not utilize toxic heavy metals that cause serious environmental issues. Additionally, organic redox-active material-based batteries have significant potential to substantially increase energy storage capabilities as opposed to traditional inorganic material-based batteries.¹

One fundamental challenge in developing novel energy storage devices based on organic electrode materials is to rapidly identify a subset of promising materials candidates that possess target redox potential (RP)—computed at the desired fidelity—from a large set of candidate materials. Since there may be a huge number of candidate organic materials to be screened and as the estimation of RP at the desired fidelity level may require a substantial amount of computational resources per molecule, an exhaustive computational screening campaign is practically infeasible. Recently, several studies have demonstrated the utility of machine learning (ML) models for predicting the structure-electrochemical property relationships efficiently.^5,6,7,8 For example, a fully connected neural network (fcNN) with two hidden layers accurately approximated the RP of molecules based on ten predictive features—the number of B/C/Li/O/H, the number of aromatic rings, highest occupied molecular orbital (HOMO), lowest unoccupied molecular orbital (LUMO), HOMO-LUMO gap, and electron affinity (EA).⁵ However, despite the predictive efficiency, such ML approaches have not been systematically exploited in the context of an objective-driven computational screening campaign. Instead, their application has mainly remained in prioritizing desirable materials for further evaluation based on the properties predicted by ML surrogates.

One practical goal-driven approach for the effective selection of promising candidates is to build a high-throughput virtual screening (HTVS) pipeline that consists of various mathematical or surrogate models with different fidelity and computational cost. In general, such HTVS pipelines use computationally efficient models in earlier stages to efficiently filter out samples that are unlikely to possess the desired property. The remaining samples are passed to the next stage for further investigation based on higher fidelity models that are also computationally more costly. The molecules that survive until the penultimate stage are assessed based on the highest fidelity model at the final stage for final validation. The crux of an HTVS pipeline is to efficiently assign computational resources across different stages to maximize the return-on-computational-investment (ROCI). Thanks to the capability to efficiently screen a large set of candidates, HTVS pipelines have been widely used in various fields including biology,^{9,10,11,12,13,14} chemistry,^{15,16,17,18,19,20,21} and materials science.^22,23

Conventionally, operational strategies for such HTVS pipelines in the past have relied on expert intuition, often resulting in reasonable but suboptimal screening performance. Recently, a mathematical optimization framework has been proposed to address this limitation, where the screening policy is optimized for throughput and computational efficiency.²⁴ The central idea is to exploit the relationship between the predictive scores computed at different stages by estimating the joint score distribution, based on which the screening threshold values are jointly optimized to maximize throughput and accuracy while minimizing the computational resource requirement. It was shown that the optimized screening policy improves the computational efficiency of the HTVS pipeline by a significant margin while effectively achieving the objective of the screening campaign. While the optimization framework provides a systematic way of designing effective operational strategies for general HTVS pipelines, which obviates the need for and reliance on heuristic and suboptimal screening policies, this study assumed that the HTVS pipeline is already given and only the screening policy needs to be determined. However, when such an HTVS pipeline does not yet exist and only a computationally costly high-fidelity property prediction model is available, how should one construct the HTVS pipeline? In other words, assuming that the given high-fidelity model will be placed at the end of the HTVS pipeline, how should one design lower fidelity surrogate models to be placed at earlier stages in the pipeline such that the overall efficiency can be enhanced without deteriorating the screening accuracy? This HTVS pipeline construction problem remains an open problem to date.

The objective of this study is 2-fold. First, we aim to fill a critical gap in the current HTVS literature by proposing a principled way of constructing an efficient HTVS pipeline from the ground up to meet the screening objective based on a high-fidelity property prediction model. Second, we apply our proposed optimal HTVS design and operational strategies to the problem of efficient and accurate screening of redox-active organic materials, an important materials screening problem for designing next-generation energy storage devices. To accomplish this, we propose an effective strategy for the construction of an HTVS pipeline, where the highest fidelity RP predictor is based on a computational model via density functional theory (DFT), and ML surrogates for the DFT computational model are constructed to enable the trade-off between efficiency and fidelity. To be specific, we decompose the high-fidelity DFT model into four sequential ML surrogate models, each of which computes intermediate properties, such as HOMO, LUMO, HOMO-LUMO gap, and EA, that are needed to compute RP using the high-fidelity DFT model. The constructed sub-models form the building blocks of the HTVS pipeline. Next, we learn five surrogate models that serve as different screening stages in the pipeline, where each model predicts the RP using a combination of different (intermediate) properties, at various complexity and fidelity. Furthermore, we also explore the use of “sub-surrogate” models that predict the next available intermediate properties based on the features available at a given stage. The predicted properties are used as “virtual” features for the surrogate models to improve the predictive accuracy. Finally, we generalize the HTVS pipeline optimization framework²⁴ such that the framework can be used to optimize the screening policy for identifying materials whose RP is within a target range, instead of based on a minimum (or maximum) required RP. We rigorously evaluate the performance of our optimized HTVS pipelines under various scenarios and demonstrate that they lead to significant improvement over the baseline in terms of efficiency, accuracy, as well as consistency.

In the following section, we provide an overview of the proposed HTVS construction and optimization scheme for detecting promising redox-active materials, followed by a comprehensive performance assessment and analysis results. Further technical details of our proposed HTVS pipeline design and operational strategies can be found in the STAR Methods section.

Results

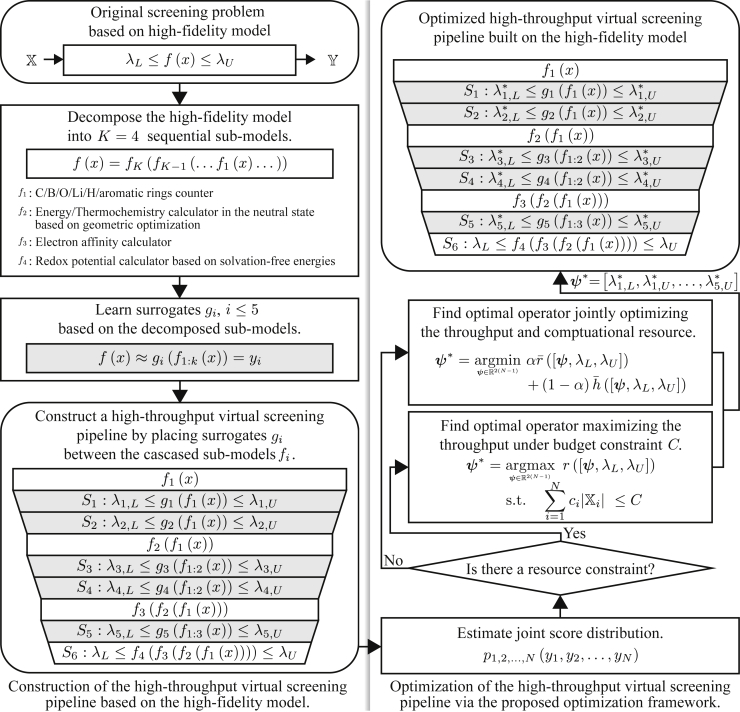
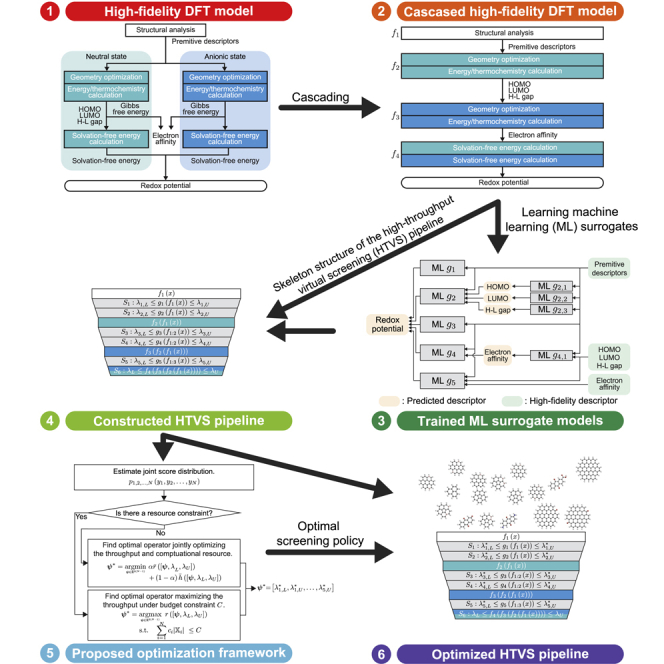
Figure 1 provides an overview of the proposed scheme for the design and operation of efficient computational screening campaigns to detect promising organic electrode materials. Formally, the operational objective of the campaign is to find subset $\mathbb{Y}=\left\{x\mid {\lambda }_L\le f\left(x\in \mathbb{X}\right)\le {\lambda }_U\right\}$ that consists of promising redox-active materials whose RP $f\left(x\right)$ computed via the given high-fidelity DFT model $f$ is within target screening range $\mathit{\lambda }=\left[{\lambda }_L,{\lambda }_U\right]$, where the set $\mathbb{X}$ of all candidate materials may be huge. We assume that the target screening range $\mathbf{\lambda }$ is pre-specified by domain experts. Due to the excessive computational complexity of the high-fidelity model $f$ for RP, it is practically impossible to screen all the materials based solely on the high-fidelity model $f$⁵. In order to overcome this critical limitation, we propose a two-phase computational campaign design scheme: First, we construct an HTVS pipeline structure by decomposing the high-fidelity model $f$ into four sub-models $f_1,f_2,\dots ,f_4$ and learning five machine learning-based surrogate models $g_1,g_2,\dots ,g_5$ that serve as screening stages in the pipeline. Second, we identify the optimal screening policy $optimalscreeningpolic{y}^{\ast }=\left[{\lambda }_{1,L}^{\ast },{\lambda }_{1,U}^{\ast },\dots ,{\lambda }_{N-1,U}^{\ast }\right]$ for the constructed HTVS pipeline. For this purpose, we generalize the optimization framework proposed in the previous study²⁴ such that the framework can identify the optimal screening policy based on the target screening range, not a screening threshold as in the previous study.²⁴

Figure 1.

An overview of the proposed strategy for the design and operation of a high-throughput virtual screening (HTVS) pipeline, whose primary objective is to efficiently detect promising organic electrode materials whose redox potential (RP) computed via the high-fidelity DFT-based model $f$ is within pre-specified target range $\left[{\lambda }_L,{\lambda }_U\right]$

In the first phase (left panel), we decompose the high-fidelity model $f$ into four sequential sub-models $f_1,f_2,\dots ,f_4$, computing intermediate properties that are needed to compute RP at high fidelity, to form a skeleton structure of the HTVS pipeline. Then, we learn the surrogate models $g_i$, $i=\mathrm{1,2},\dots ,5$ based on a different set of intermediate properties to build screening stages with different fidelity (left panel). In the second phase (right panel), we find the optimal screening policy ${\mathit{\psi }}^{\ast }=\left[{\lambda }_{1,L}^{\ast },{\lambda }_{1,U}^{\ast },\dots ,{\lambda }_{N-1,U}^{\ast }\right]$ for the constructed HTVS pipeline via the generalized optimization framework.

The first phase is illustrated in the left panel of Figure 1. Given a high-fidelity computational model $f$ with target screening range $\mathit{\lambda }=\left[{\lambda }_L,{\lambda }_U\right]$, the goal is to construct an HTVS pipeline that can efficiently screen all candidate materials without degrading the accuracy. First, we decompose the high-fidelity DFT model $f$ into four sequential sub-models $f_i$, $i=\mathrm{1,2},\dots ,4$, each of which computes intermediate properties (e.g., HOMO, LUMO, HOMO-LUMO gap, and EA) of a candidate material. Then, we cascade the sub-models to construct the skeleton structure of the HTVS pipeline. Between sub-models $f_i$ and $f_{i+1}$, we learn up to two surrogate models $g_j$ that predict the redox potential based on available intermediate properties as features. For the second surrogate model between the sub-models $f_i$ and $f_{i+1}$, we learn sub-surrogate models $g_{j,l}$ that predict intermediate properties which will be computed via the following sub-model and use the predicted intermediate properties as features to improve the predictive accuracy of the surrogate model $g_j$. As shown in Figure 1 (left bottom), the resulting HTVS pipeline consists of five surrogate models, where surrogate model $g_i$ is associated with screening stage $S_i$ with screening policy ${\mathit{\lambda }}_i=\left[{\lambda }_{i,L},{\lambda }_{i,U}\right]$. Each stage $S_i$ associated with surrogate model $g_i$ or sub-model $f_j$ predicts the RP of all the samples (i.e., candidate materials) passed from the previous stage $S_{i-1}$. Then, $S_i$ discards the materials whose predicted potential is outside the screening range ${\mathit{\lambda }}_i=\left[{\lambda }_{i,L},{\lambda }_{i,U}\right]$ and passes the remaining samples to the next stage for further evaluation. It should be noted that the use of a more complex (and more complete) sub-model $f_{i+1}$ requires additional DFT computation to use features that were not available to $f_i$ in the previous stages. In this manner, we can gradually narrow down the search space while continuing to compute the intermediate features that are essential to computing RP at a higher fidelity for the candidate redox-active materials that passed the previous screening stages.

In the second phase, we identify the optimal screening policy which is used for making decisions in the respective screening stages as to whether to pass a given sample to the next stage for further evaluation or discard it to save computations. To accomplish this, we generalize the original optimization framework proposed in the previous study.²⁴ The original framework²⁴ was designed to pass candidate samples whose predicted property score exceeds a given threshold value. In this work, we generalize the framework to identify the optimal screening policy for computational screening campaigns, where each stage has a target screening range rather than a minimum threshold (see STAR Methods section for further details). The proposed optimization framework takes a two-step approach as shown in the right panel of Figure 1. First, we estimate joint distribution $p_{\mathrm{1,2},\dots ,N}\left(y_1,y_2,\dots ,y_N\right)$ of the RP values predicted via machine learning surrogate models or computed through the high-fidelity model. The joint score distribution provides information on how the screening stages are interrelated. Then, based on the joint score distribution $p_{\mathrm{1,2},\dots ,N}\left(y_1,y_2,\dots ,y_N\right)$, we formulate the objective function and find the optimal screening policy ${\mathit{\psi }}^{\ast }=\left[{\lambda }_{1,L}^{\ast },{\lambda }_{1,U}^{\ast },\dots ,{\lambda }_{N-1,U}^{\ast }\right]$. In that regard, we considered two practical scenarios in the current study. The first case considered is when we want to maximize the throughput of the HTVS pipeline for a fixed computational budget constraint $C$. In the second case, the objective is to jointly optimize the throughput of the HTVS pipeline and computational efficiency. For the second scenario, we introduce weight $\alpha \in \left[\mathrm{0,1}\right]$ that determines the relative importance between the relative reward $\overline{r}\left(\mathit{\psi },{\lambda }_L,{\lambda }_U\right)$ and normalized cost function $\overline{h}\left(\mathit{\psi },{\lambda }_L,{\lambda }_U\right)$.

In what follows, we provide comprehensive simulation results demonstrating the efficacy of the proposed HTVS pipeline construction strategy and the performance of the optimized HTVS pipelines under various setups. Technical details of the optimization framework are presented in the STAR Methods section.

Correlation analysis between RP values predicted by the surrogate models and the high-fidelity model

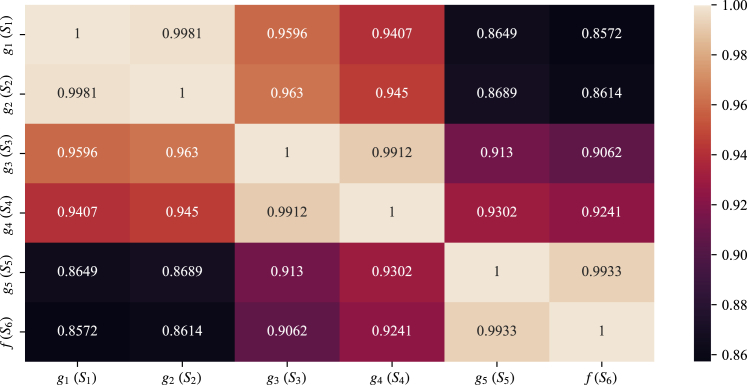
For preliminary evaluation of the surrogate models and the proposed HTVS pipeline construction strategy, we computed the Pearson’s correlation between the RP value computed via the high-fidelity model $f$ and those predicted using the surrogate models $g_i$, $i=\mathrm{1,2},\dots ,5$. We used the kernel ridge regression (KRR) model that effectively regresses the response in general (see Section S1 in the supplemental information for the performance comparison of several different machine learning models). We optimized the hyperparameters of each surrogate via a grid search based on 5-fold cross-validation (see Section S2 in the supplemental information for further details on the optimized hyperparameters). Note that we used all the materials to learn the surrogate models as our main focus is demonstrating the efficacy of the proposed HTVS pipeline construction and operation strategy rather than designing the best surrogate models. Nevertheless, for completeness, we also provide the performance evaluation results based on a strict 5-fold cross-validation where only part of the dataset (i.e., 4 out of the 5-folds) is used for learning the surrogates (see Section S5 in the supplemental information). As shown in Figure 2, the correlation between the RP values computed by the surrogate model $g_i$ and the high-fidelity model $f$ gradually increased as the number of predictive features (hence also the total amount of computation required to acquire the features) increased. For example, the correlation between the RP values predicted via the first surrogate model $g_1$ that uses only the primitive features to the RP values computed via the high-fidelity model $f$ was 0.8572. The predicted HOMO, LUMO, and HOMO-LUMO gap via the sub-surrogate models $g_{\mathrm{2,1}}$, $g_{\mathrm{2,2}}$, and $g_{\mathrm{2,3}}$ helped improve the correlation of the second surrogate model $g_2$ to 0.8614. Similarly, the predicted EA via the sub-surrogate model $g_{\mathrm{4,1}}$ helped improve the correlation of the surrogate model by 0.0179–0.9241. Finally, the last surrogate model that utilizes all the chemical descriptors showed the highest correlation with respect to the high-fidelity model $f$, which was 0.9933. These simulation results indicate that the proposed HTVS construction strategy can effectively design surrogate models that correlate well with the given high-fidelity model, where each model strikes a different balance between computational cost and fidelity. Given an ensemble of surrogate models, where models with higher complexity may be used to attain higher fidelity predictions, we can maximize the screening performance by building an HTVS pipeline comprised of the surrogates and designing an optimal screening policy.²⁴

Figure 2.

Pearson’s correlation between the RP values computed by different models (i.e., the high-fidelity DFT model $f$ and the surrogate models $g_i$, $i=\mathrm{1,2},\dots ,5$)

As shown, more computationally expensive surrogate models with a larger number of descriptors result in estimates that better correlate with the RP computed by the high-fidelity DFT model. Also, note that the predicted descriptors via the sub-surrogate model helped improve the regression performance.

Optimal computational campaign for selecting potential organic electrode materials with minimum target RP

To evaluate the performance of the optimized HTVS pipeline, we first considered a realistic computational screening scenario where the operational objective is to effectively select the organic redox-active materials whose RP computed at high fidelity is above target threshold 2.5 V vs. Li/Li⁺ (i.e., $\lambda =\left[2.5\mathrm{V},\infty \mathrm{V}\right]$) which is exhibited by many organic cathode materials under a typical voltage window of $1\sim 4$ V vs. Li/Li⁺.²⁵ The target threshold of 2.5 V was selected as a boundary to eliminate candidates whose RP is too low for practical application as a cathode. While the target potential may differ in different applications, the best corresponding screening policy can be automatically identified through optimization as we demonstrate in what follows.

Optimized HTVS pipeline maximizing the throughput under computational budget constraint

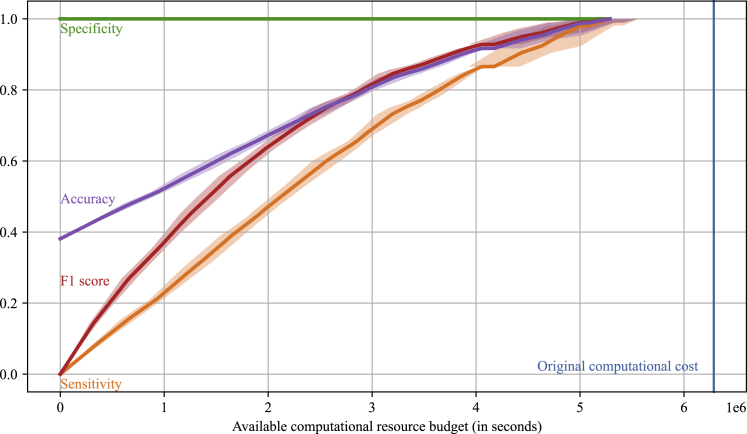
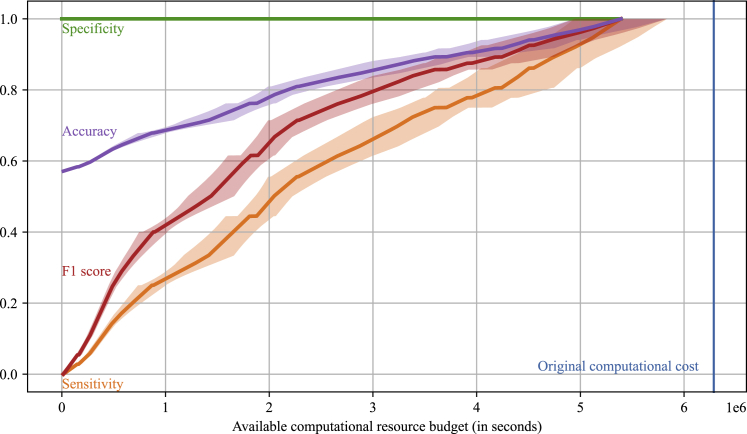
Figure 3 shows the performance evaluation results of the optimized HTVS pipeline under a computational resource constraint in seconds ($x$ axis) in terms of sensitivity, specificity, F1 score, and accuracy based on 5-fold cross-validation. Sensitivity (recall) is a ratio of the detected potential candidates whose RP exceeds or is equal to the minimum target threshold of 2.5 V to all the materials in the test dataset that satisfy the criteria. Specificity is defined as a ratio of the true negative samples discarded by the HTVS pipeline to all negative samples. F1 score is a harmonic mean between the positive predictive value (precision) and sensitivity. Lastly, accuracy (ACC) is the ratio of materials that are correctly selected or discarded based on the target criteria. The shaded area along each performance curve (showing the mean of the corresponding performance metric) depicts the SD$\left(\pm \sigma \right)$ of the metric based on 5-fold cross-validation. As shown, the optimized HTVS pipeline effectively distributed a given computational budget over the different stages to maximize the overall screening throughput (i.e., the number of promising redox-active materials that meet the target criteria detected by the screening pipeline). On average, the optimized HTVS pipeline selected all potential materials with only $84.11$% of the original computational cost (6,286,056, blue vertical line) that would be required for screening all the materials via the high-fidelity model $f$ alone. Besides, $80$% of potential materials was detected with $58.62$% of the original budget. Note that specificity was always 1 throughout all simulations as the final stage (i.e., $S_6$) of the HTVS pipeline involved screening all potential redox-active materials reaching this stage based on the high-fidelity model for final validation. In other words, the HTVS pipeline is configured such that no negative sample would be included in the final screening result, as such samples would be discarded at the final stage if they have not yet been discarded by the lower fidelity surrogate models. We could observe a similar trend in accuracy. Specifically, the accuracy reached $80.17$% when only $46.73$% of computational resources were given. The pipeline achieved perfect accuracy at the cost of 5,287,453 s ($84.11$% of the original cost) on average.

Figure 3.

Performance evaluation of the optimized high-throughput virtual screening (HTVS) pipeline based on 5-fold cross-validation

The shaded area along each curve represents the SD of the performance on the five cross-validation datasets. The optimal screening policy maximized the throughput (i.e., the number of potential candidates whose RP exceeds or is equal to the target threshold of 2.5 V) under the given computational budget constraint ($x$ axis). The optimized HTVS pipeline effectively allocated the computational resource across the multiple screening stages, thereby detecting all the potential candidates at only $84.11$% of the original computational cost of 6,286,056 (blue vertical line) which would be required if solely the high-fidelity model $f$ were used for screening.

We also evaluated the performance at each stage in the optimized HTVS pipeline in terms of sensitivity, specificity, F1 score, and accuracy based on 5-fold cross-validation (see Figure S2 in the supplemental information). The sensitivity of the screening stages tended to increase as the computational resource budget increased. For a given computational budget, the sensitivity of $S_i$ was always greater than or equal to that of later stages $S_j$ for $j>i$. This was due to the structure of the HTVS pipeline, where the later stages processed only the materials delivered from the previous screening stages. On the other hand, except for the final stage, the specificity tended to decrease as the available budget increased. In other words, as the computational resource grew, the earlier screening stages allowed the later stages with higher accuracy to get involved more actively in the screening campaign. As a result, the F1 score tended to increase sharply at the beginning but the tendency to rise slowed down later on. The accuracy showed similar trends as the F1 score due to the same reason. The accuracy of the earlier stages eventually fell since they passed too many materials to later stages for further evaluation, resulting in higher false-positive rates. Note that while the performance metrics of the individual stages (esp., the earlier stages) showed relatively high fluctuations as the available computational budget grew, the overall performance of the HTVS pipeline (i.e., $S_6$) changed gradually without abrupt changes. This implies that the optimal screening policy may not be unique and there may be multiple different policies that lead to similar screening performance.

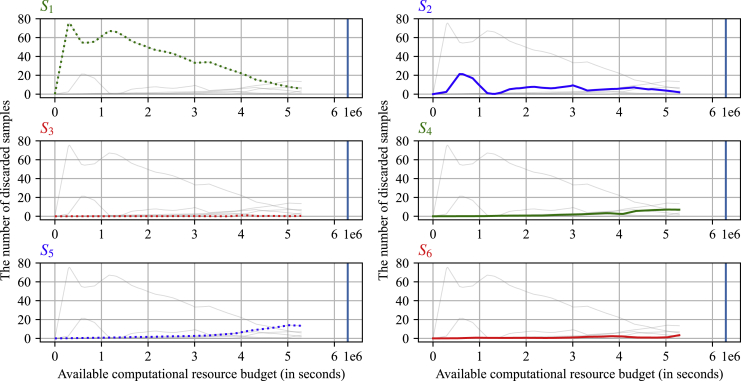
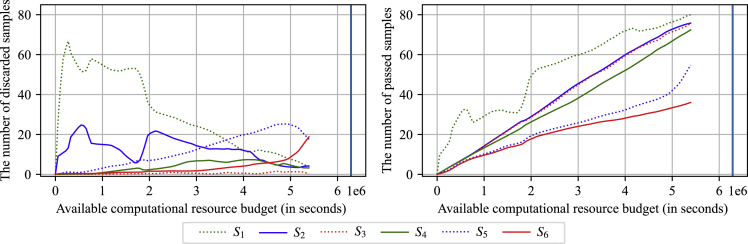
Figure 4 shows the number of discarded materials at each stage in the optimized HTVS pipeline with respect to an available computational budget ($x$ axis). Average results are shown based on 5-fold cross-validation. For easy comparison, every subplot shows the trends at all six different stages, while only the curve that corresponds to a specific stage is shown in a colored bold line. On average, the first stage $S_1$ (left top, green dotted line), which predicts the RP using only primitive features (such as the numbers of various atoms and aromatic rings), actively screened and discarded a large number of materials when the available computational budget was limited. As the computational budget increased, the number of materials discarded in the first stage decreased gradually, allowing subsequent stages with higher accuracy to get involved in screening more actively. For example, the surrogate models discarded $75.09\%$, $4.62\%$, $0\%$, $0\%$, $0.21\%$, and $0.01\%$ materials, respectively, when the available computational budget was 320,452 s (only $5.1\%$ of the original computational cost). With a computational budget of 5,287,453 s, the screening stages eliminated $5.8\%$, $5.8\%$, $0.4\%$, $7.0\%$, $13.4\%$, and $3.4\%$ materials, respectively. During the simulation, stages $S_1$ to $S_6$ rejected $37.72\%$, $6.42\%$, $0.13\%$, $2.23\%$, $4.13\%$, and $0.95\%$ of the screened materials on average, respectively.

Figure 4.

The number of discarded molecules at each screening stage for different amounts of available computational budget ($x$ axis)

The first stage $S_1$ (left top, green dotted line) that predicts the RP based only on primitive features filtered out a significant proportion of candidates when the computational budget was tightly constrained. As the computational budget increased, the number of molecules discarded at the first stage gradually decreased, allowing subsequent higher accuracy stages to get more actively involved in screening.

Joint optimization of HTVS pipeline for maximizing throughput while minimizing computational cost

Table 1 shows the performance evaluation results of the HTVS pipeline jointly optimized to maximize throughput while minimizing the computational cost based on a 5-fold cross-validation. Three different values of $\alpha$ were considered, and the average number of detected materials, total cost (in seconds), effective cost, sensitivity, specificity, F1 score, and accuracy is shown. $\alpha \in \left[\mathrm{0,1}\right]$ is a weight parameter that determines the balance between the throughput and computational efficiency of the pipeline (see STAR Methods). The column “detected materials” shows the number of materials in the final set $\mathbb{Y}$ obtained from screening. Total cost is the amount of time needed to screen the entire input set $\mathbb{X}$, and the effective cost is defined as the cost per detected material. As $\alpha$ increased from 0.25 to 0.75, the number of selected materials whose RP value at high fidelity is greater than or equal to 2.5 V rose from 40.4 to 49.8 out of 52 promising organic electrode materials. To be specific, on average, the pipeline picked 49.8 out of 52 promising materials when $\alpha =0.75$ at an effective cost of 93,291. When $\alpha =0.25$, the optimized HTVS pipeline detected 40.4 samples at an effective cost of 85,407. In terms of computational savings, although the total computational cost and the effective cost grew when $\alpha$ increased from 0.25 to 0.75, the overall computational cost was nevertheless significantly less than that of the original computational cost of 6,286,056 and the original effective cost of 120,886, respectively. Besides, other evaluation metrics, including accuracy, sensitivity, and F1 score, noticeably improved when $\alpha$ increased. Overall, for various values of $\alpha$, the optimized HTVS pipeline results in good screening performance that sensibly balances the screening throughput (i.e., in terms of the number of materials detected by the HTVS pipeline that satisfy the target criteria) and the total computational cost.

Table 1.

Performance evaluation of the jointly optimized HTVS pipeline based on 5-fold cross-validation (target RP threshold at the last stage set to 2.5 V)

$\alpha$	Detected materials	Total cost (seconds)	Effective cost (seconds)	Sensitivity	Specificity	F1 score	Accuracy
0.25	40.4	3,450,440	85,407	0.7769	1	0.8714	0.8619
0.5	47.8	4,365,990	91,339	0.9192	1	0.9574	0.95
0.75	49.8	4,645,890	93,291	0.9577	1	0.9782	0.9738

As the weight parameter $\alpha$, which determines the balance between the throughput and computational efficiency, increased from 0.25 to 0.75, all the throughput-related performance metrics tended to improve at the cost of higher computational cost (i.e., increased total cost and effective cost). Overall, the optimized HTVS pipeline struck a good balance between throughput and computational efficiency.

Optimal computational campaign for selecting potential organic electrode materials whose RP at the desired fidelity is within a target range

We next considered another practical scenario for a computational screening campaign, where the objective is to efficiently detect promising redox-active materials whose RP computed at the desired fidelity is within a target range. Theoretically, higher RP of organic cathode materials leads to a higher output voltage of a Li-ion cell. However, from a practical perspective, the peak voltage could be constrained as it is closely related to the thermodynamic stability of the organic electrolyte material. Based on our previous studies,^{5,7,26,27,28,29,30,31,32} we selected 3.2 V vs. Li/Li⁺ as the target upper bound for the computational screening campaign. As a result, we aimed to optimize the HTVS screening pipeline for screening materials whose RP values belong to a target range of $\left[2.5\mathrm{V},3.2\mathrm{V}\right]$.

Optimized HTVS pipeline that maximizes the throughput under computational budget constraint

Figure 5 shows the performance evaluation results of the optimized HTVS pipeline for screening materials whose RP belongs to a target range, where the optimal screening policy aims to maximize the screening throughput under a given computational budget constraint. As before, the average sensitivity, specificity, F1 score, and accuracy were obtained from a 5-fold cross-validation and are shown in the figure as a function of the budget constraint ($x$ axis). The shaded area around each performance curve indicates the SD of the corresponding performance metric evaluated on the five cross-validation datasets. As shown in Figure 5, the screening policy optimized by the proposed optimization framework that generalizes the original approach²⁴ effectively allocated the available computational budget across different stages of the HTVS pipeline. As a result, significant computational savings were achieved while maximizing the throughput that is attainable at a given computational budget. On average, the optimized HTVS screening reduced the computational cost by $14.22$% compared to the original computational cost of 6,286,056 (in seconds) without using a screening pipeline. When the computational budget is further reduced, the detection performance starts to degrade but the optimized screening policy re-balances the budget across different screening stages to maximize the ROCI nevertheless. For example, the optimized pipeline selected $80$% of the promising organic electrode materials at only $65.85\%$ of the original cost. Note that the constructed HTVS pipeline always guarantees perfect specificity (i.e., 1) by design. This is because the same high-fidelity model $f$, based on which the target RP is specified, is placed at the end of the HTVS pipeline for the final validation of any material candidate that reaches the last stage. As a result, the F1 score displayed a similar trend with respect to the computational resource constraint as the sensitivity. In terms of accuracy, the HTVS pipeline trivially assured the accuracy of 0.5714, which is nothing but the proportion of negative samples in dataset $\mathcal{X}$ containing all material candidates. The accuracy of the optimized HTVS pipeline gradually increased as the available computational budget increased, attaining perfect accuracy at the computational budget of 5,391,914 (i.e., $85.78\%$ of the original cost).

Figure 5.

Performance evaluation of the optimized HTVS pipeline based on 5-fold cross-validation

The goal is to detect promising redox-active materials whose RP is within the target range $\left[2.5\mathrm{V},3.2\mathrm{V}\right]$. The average performance metrics are shown as a function of the total available computational budget ($x$ axis). The shaded area along each performance curve represents the SD of the performance on the five cross-validation datasets. The optimized HTVS pipeline detected all promising materials that meet the target screening condition at only $85.78\%$ of the original computational cost (blue vertical line) that would be required for screening all materials solely based on the high-fidelity model $f$. By design, the HTVS pipeline achieved perfect specificity regardless of the available computational budget by utilizing the high-fidelity model at the end of the pipeline for the final validation of the candidates.

Next, we evaluated the performance of the individual stages in the optimized HTVS pipeline designed to detect organic electrode materials whose RP belongs to the range of $\left[2.5\mathrm{V},3.2\mathrm{V}\right]$ based on 5-fold cross-validation. Results are shown in Figure S3 in the supplemental information. We could observe a similar trend to the previous computational campaign scenario (shown in Figure S2). The sensitivity of the screening stages tended to increase as the computational resource budget increased. Furthermore, for a given computational budget, the sensitivity of $S_i$ was always greater than or equal to those of later stages $S_j$ (for $j>i$). For example, stages $S_1,S_2,\dots ,S_6$ achieved sensitivities of 0.9874, 0.8716, 0.8698, 0.8130, 0.6882, and 0.6882, respectively, when the available computational complexity was 3,158,898 ($50.25\%$ of the original computational cost). Again, we could observe that the specificity generally decreased (except for the final stage) as the available budget increased. As a result, both the F1 score and the accuracy tended to sharply increase at the beginning but eventually decreased later on.

Figure 6 shows the number of materials discarded at each stage when all candidate materials are screened by the HTVS pipeline based on the optimized screening policy. Results shown in the figure have been obtained based on 5-fold cross-validation. As can be seen in Figure 6, as the available computational budget increased, the number of materials discarded in the first stage $S_1$ decreased gradually. For example, the screening stages $S_1,S_2,\dots ,S_6$ discarded 66.72, 13.23, 0, 0.08, 1.17, and 0.4 candidate materials, respectively, when the available budget was only 272,294 ($4.33\%$ of the original computational cost). With a computational budget of 5,391,914 ($85.783$% of the original cost), the average number of discarded candidate materials at stages $S_1,S_2,\dots ,S_6$ changed to 4.0, 4.2, 0.2, 3.2, 17.6, and 18.8, respectively.

Figure 6.

The number of molecules that were discarded at each stage (left) and passed to the next stage (right) for the case when the target RP range was set to $\left[2.5\mathrm{V},3.2\mathrm{V}\right]$

The results were obtained based on 5-fold cross-validation for different amounts of available computational budget ($x$ axis). As before, when the computational budget was tightly constrained, the most efficient first stage $S_1$ (top left, green dotted curve) filtered out a significant number of materials and passed only a relatively few candidate materials that are expected to satisfy the target criteria. In general, the number of molecules discarded in the first stage decreased gradually as the computational budget increased, allowing subsequent screening stages with higher accuracy to get more actively involved in screening.

Joint optimization of HTVS pipeline for maximizing throughput while minimizing computational cost

Table 2 shows the performance evaluation results of the HTVS pipeline jointly optimized to maximize throughput and minimize the computational cost. The optimal screening policy was predicted by our generalized optimization framework and the results are obtained via 5-fold cross-validation. Performance trends were similar to the previous scenario where the computational campaign aimed at detecting the potential materials whose RP values exceed the minimum required threshold (i.e., $\left[2.5\mathrm{V},\infty \mathrm{V}\right]$) (see Table 1). As $\alpha$ increased, the quality metrics related to the throughput of the HTVS pipeline improved at the cost of higher computational costs (i.e., total cost and effective cost). When $\alpha$ was set to 0.25, the jointly optimized pipeline operated conservatively from the perspective of resource utilization. To be specific, the optimized pipeline with $\alpha =0.25$ consumed 2,923,471 s to detect 23.4 promising candidate materials among the 36 organic electrode materials in the test datasets whose RP belongs to the target range of 2.5–3.2 V. On the other hand, the optimized HTVS pipeline with $\alpha =0.75$ detected, on average, 29.8 promising candidates at a computational cost of 4,257,906. Overall, the HTVS pipeline operated using the jointly optimized screening policy resulted in good screening performance that automatically balances throughput and screening cost for a given value of $\alpha$.

Table 2.

Performance evaluation of the jointly optimized HTVS pipeline based on 5-fold cross-validation, where the target RP range was set to $\left[2.5\mathrm{V},3.2\mathrm{V}\right]$

$\alpha$	Detected materials	Total cost (seconds)	Effective cost (seconds)	Sensitivity	Specificity	F1	Accuracy
0.25	23.4	2,923,471	124,935	0.65	1	0.7689	0.85
0.5	29.2	3,921,249	134,289	0.8111	1	0.8892	0.9190
0.75	29.8	4,257,906	142,883	0.8278	1	0.9003	0.9262

As $\alpha$ increased, the overall throughput of the HTVS pipeline increased with the higher consumption of the computational resources (i.e., increased total cost and effective cost). As before, the optimized HTVS pipeline struck a good balance between throughput and computational efficiency.

Discussion

In this study, we designed optimal computational screening campaigns, where the operational objective is to efficiently screen a given set of candidate materials to accurately detect promising cathodic organic electrode materials whose RP—computed by a high-fidelity model—meets the desired condition. As the high-fidelity model of estimating RP, we adopted the first-principles method, where we computed DFT using Schrödinger Jaguar,³³ with PBE0³⁴ functional and $6-31+G\left(d,p\right)$ basis set.³⁵ Based on this, we computed RP via the thermodynamic cycle suggested by Truhlar.^36,37 Two screening scenarios were considered: (i) detection of candidate materials whose RP exceeds a minimum threshold; and (ii) detection of materials whose RP belongs to a target range. At the core of the proposed scheme lies the strategy for constructing an HTVS pipeline from a single high-fidelity model $f$ by designing ML surrogate models, each of which provides a unique trade-off between complexity and accuracy. Once the HTVS pipeline is constructed, the optimal screening policy can be designed based on the optimization framework, originally proposed in the previous study²⁴ and generalized in the current study. As shown in Figure 1, during the first phase of our proposed scheme, we first decomposed the high-fidelity model $f$ into four sub-components $f_i$, $i=\mathrm{1,2},\dots ,4$, each of which computes an intermediate property of a given material (i.e., HOMO, LUMO, HOMO-LUMO gap, or EA). Then, we cascaded them to construct a skeleton structure of the HTVS pipeline. Based on the structure, we learned five ML surrogate models that predict the RP with the intermediate descriptors available to them at the corresponding screening stage, where they are placed. Surrogate model $g_i$ was associated with screening stage $S_i$ with screening policy $\left[{\lambda }_{i,L},{\lambda }_{i,U}\right]$ in order to pass only those materials to the next stage $S_{i+1}$ that are likely to meet the desired condition at the last stage by the high-fidelity model $f$. Since passing candidate materials to the next stage requires further computation, discarding unpromising materials that likely will not meet the target condition can lead to significant computational savings. Besides, we introduced the concept of “sub-surrogate” models that predict the next available descriptors and used the predicted descriptors as virtual features to improve the predictive accuracy of the surrogate models. During the second phase, we optimized the screening policy for the HTVS pipeline, where each stage is associated with a different ML surrogate model. Specifically, we identified the optimal screening range $\left[{\lambda }_{i,L}^{\ast },{\lambda }_{i,U}^{\ast }\right]$ for stage $S_i\left(i=\mathrm{1,2},\dots ,5\right)$, which is expected to lead to the optimal performance of the entire HTVS pipeline. To this aim, we generalized the screening policy optimization framework in the previous study²⁴ to enable optimizing HTVS pipelines that screen candidate materials based on whether the property of interest belongs to a target range and not just based on a required minimum value.

For validation, we first optimized the constructed HTVS pipeline for a screening campaign whose operational goal was to detect promising redox-active materials according to the target RP threshold set to 2.5 V. As shown in Figure 3, the optimized pipeline consumed $84.11$% of the original computational resources to detect all promising redox-active materials whose RP (evaluated at the desired fidelity using the high-fidelity model $f$) exceeds or is equal to the threshold 2.5 V. The HTVS pipeline consumed only $58.62$% of the original computational cost to find $80$% of the potential materials. Next, we also optimized the screening policy for both throughput and computational efficiency. For different values of $\alpha$ that were considered in this study, the pipeline detected $77.69$% to $95.77$% of the promising redox-active materials that meet the target criterion, with an accuracy ranging between $86.19$% and $97.38$% and at an effective computational cost between 85,407 and 93,291.

The proposed approach was further validated for carrying out screening campaigns that aim to efficiently detect organic redox-active materials whose RP (computed by the high-fidelity model $f$) is within the target range $\left(\left[2.5\mathrm{V},3.2\mathrm{V}\right]\right)$. We utilized the same HTVS pipeline structure that was used for the first computational screening campaign, but the screening policy was optimized by the generalized optimization framework presented in this work. As shown in Figure 5, the optimized HTVS pipeline detected all promising organic electrode materials that meet the target criterion by consuming only $85.78$% of the original computational cost. We also assessed the performance by optimizing the screening policy jointly for throughput and efficiency. When $\alpha$ was set to 0.75, the optimized HTVS pipeline detected 29.8 potential candidates (i.e., $82.78$% of all candidate materials in the test dataset whose RP is within the target range) at a computational cost of 4,257,906. When $\alpha$ was set to 0.25, the optimized HTVS pipeline detected $65\%$ of the targeted candidate materials at a cost of 2,923,471.

Based on the correlation analysis results shown in Figure 2, we further simplified the structure of the HTVS pipeline by removing some of the surrogate models that are highly correlated with other surrogates in the original pipeline structure. By assessing the optimal performance of the simplified HTVS pipeline, our goal was to investigate the impact of reducing potential redundancies across screening stages on the overall throughput and efficiency. Specifically, we discarded the first state $S_1$ and the third stage $S_3$ from the original HTVS pipeline structure and found the optimal screening policy for the simplified pipeline $\left[S_2,S_4,S_5,S_6\right]$. Comprehensive evaluation results of this pipeline can be found in the supplemental information (see Section S4). These results showed that discarding stages $S_1$ and $S_3$, which are computationally very efficient and moderately correlated with the last stage $S_6$, which uses the high-fidelity model $f$, did not significantly impact the performance of the optimized HTVS pipeline. Figure 2 shows that the scores computed at stage $S_1$ are highly correlated with the scores computed at $S_2$ and so are the scores at $S_3$ with those at $S_4$, which may be why removing these redundant stages from the HTVS pipeline did not affect the overall screening performance. However, simplifying the HTVS pipeline structure reduces the dimensionality of the joint score distribution, which may potentially improve the quality of the probability density estimation. Additionally, there may be other benefits such as saving computations at “idle” stages, which do not actively sift out unpromising candidates but delegate the job to other surrogate models by letting most materials pass through, and reducing the burden of training a larger number of ML surrogates.

It is important to note that the computational screening campaign considered in this study has a fundamental performance bound due to its setting. In the screening scenarios that we considered, it was assumed that the high-fidelity model $f$ will be used for final validation at the last stage of the HTVS pipeline in order to assess all candidate materials that survive the penultimate stage. For example, suppose $80\%$ of the candidate materials in the initial set $\mathcal{X}$ meets the target criterion. If the HTVS pipeline perfectly sifts out the undesirable $20\%$ and passes only the $80\%$ with the desired RP to the last stage that uses the high-fidelity model $f$ for final validation, the total computational cost would be at least $80\%$ of the original computational cost that would be needed for screening the entire set $\mathcal{X}$ without a screening pipeline and solely by $f$. In fact, the positive sample ratio in this study was relatively high for both the first and second computational campaigns (i.e., 0.619 and 0.4286, respectively), which affects the maximum computational savings that can be attained by taking the proposed HTVS pipeline construction and operation strategies. However, in real-world screening campaigns (e.g., drug screening campaigns²¹), the positive sample ratio tends to be very small. In such cases, our proposed HTVS pipeline construction scheme and the optimal operation of the resulting pipeline can lead to substantial computational savings virtually without any degradation of the screening accuracy. Screening scenarios considered in a previous study²⁴ demonstrate this potential. For example, we performed a strict 5-fold cross-validation to evaluate the performance of our optimized HTVS pipeline when the target RP threshold was increased to 4.3 V. In this case, only one out of 21 samples in the test dataset met the target criterion. The optimized HTVS pipeline accurately detected the desired redox-active material at only $18.78\%$ of the original computational cost (see Section S6 in the supplemental information).

While, in this study, we focused on the design and operation of an HTVS pipeline to efficiently screen an entire set of candidate materials to identify a subset of promising organic electrode materials that possess the desired properties, it is worth mentioning that there also exist a number of alternative methods proposed for the design or discovery of novel materials.^38,39 For example, Bayesian optimization (BO) was used to efficiently search an immense compositional materials space for hybrid organic-inorganic perovskites.³⁸ This study demonstrated the potential advantages of BO for discovering enhanced materials with optimized target properties in a data-scarce setting. The problem of designing novel materials was tackled based on multiple design objectives in the presence of substantial model uncertainty and limited data availability.³⁹ To efficiently explore the huge material design space, they adopted the widely popular efficient global optimization scheme⁴⁰ based on a multi-dimensional expected improvement (EI) criterion. By taking a multi-task ANN-based EI approach, this study showed that the resulting scheme can significantly accelerate the search for novel materials with enhanced properties.

In this study, we utilized the KRR model for building the surrogate models for predicting the RP. Theoretically, one may be able to further enhance the screening performance of the HTVS pipeline by exploring alternative ML models for the regression task and selecting the best model, although it is beyond the scope of the current study. Potential future search directions include improving the predictive power of the surrogate models by employing more powerful deep learning models and incorporating additional highly structured descriptors or features, such as Simplified molecular-input line-entry system,⁴¹ self-referencing embedded strings,⁴² and various molecular fingerprints^{43,44,45,46,47,48,49,50,51} that have been shown to be effective for various property prediction tasks.

Limitations of the study

Similar to the HTVS pipeline optimization framework originally proposed in the previous study,²⁴ the generalized optimization framework presented in this study takes a two-step approach. First, we estimate the joint distribution of all scores computed at different screening stages, which is crucial in evaluating the objective function. Then, based on the joint score distribution, we formally define the objective function and find the optimal screening policy that optimizes the given objective function using a differential evolution (DE) algorithm.⁵² However, accurate estimation of the joint score distribution can be practically challenging when the available training data are limited and the HTVS screening pipeline consists of a relatively large number of stages, which makes the distribution high-dimensional. Any discrepancy between the true underlying distribution and the estimated distribution may affect the overall screening performance, since the best screening policy that optimizes the objective function may not necessarily optimize the performance for candidate materials whose scores may follow a different distribution. Furthermore, the discrepancy between the true and estimated joint score distributions may lead to inaccurate estimations of the expected screening cost. Consequently, the optimized screening policy predicted based on an inaccurate joint score distribution may lead to the violation of the computational budget constraint or lead to a suboptimal distribution and utilization of the available resources across screening stages. In the current study, we tried to alleviate the problem of potentially violating the budget constraints by having each screening stage operate as follows. By default, each stage operates based on the predicted optimal screening policy operators. However, each screening stage can discard molecules before predicting their RP if the computational resource allocated to the stage is less than the total computational cost for screening all molecules passed from the previous stage. The stage drops samples based on the RP predicted in the previous stage until the expected computational cost for screening the remaining samples is within the allocated computational resources. That is, the molecule with the lowest RP is discarded first.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
Simulation source code	This paper	https://github.com/bjyoontamu/occ-rp
Differential evolution (DE)	Storn and Price, 199752	https://doi.org/10.1023/A:1008202821328
Expectation Maximization (EM)	Dempster et al., 197753	https://doi.org/10.1111/j.2517-6161.1977.tb01600.x
Python (3.9.7)	Python Software Foundation	https://www.python.org
Scikit-learn (0.24.2)	Pedregosa et al., 201154	https://scikit-learn.org
Other
Organic electrode materials	Allam et al., 20185	https://doi.org/10.1039/C8RA07112H
	Allam et al., 20207	https://doi.org/10.1016/j.mtener.2020.100482
	Park et al., 201726	https://doi.org/10.1002/cssc.201601730
	Kim et al., 201627	https://doi.org/10.1021/jacs.5b13279
	Liu et al., 201528	https://doi.org/10.1021/acs.chemmater.5b00314
	Kim et al., 201629	https://doi.org/10.1039/C6CP02692C
	Kang et al., 201830	https://doi.org/10.1021/acs.jpcc.8b00827
	Zhu et al., 201831	https://doi.org/10.1039/C8TA01671B
	Liu et al., 201732	https://doi.org/10.1039/C6EE02641A

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Byung-Jun Yoon (bjyoon@ece.tamu.edu).

Materials availability

This study did not generate any physical materials.

Method details

Simulation environment

We evaluated the average time complexity of each surrogate model for RP computation of a candidate material on a workstation equipped with Intel Xeon E5-2650 v3 and 64 GB memory. We utilized the differential evolution (DE) algorithm⁵² to optimize the screening policy for the HTVS pipelines considered in the work.

Data collection

In order to validate the proposed approach, we collected 109 organic electrode materials designed in previous studies^{5,7,26,27,28,29,30,31,32} (see Data S1). Figure S19 depicts representative organic electrode materials–such as ketones,²⁶ quinones,²⁷ functionalized graphene flakes,^28,29 boron-doped corannulenes,³⁰ and boron-doped coronenes³¹–considered in this study.

High-fidelity model for computing the redox potential of organic electrode materials

First-principles method

We computed DFT using Schrödinger Jaguar,³³ with PBE0³⁴ functional and $6-31+G\left(d,p\right)$ basis set.³⁵ After geometry optimization using DFT, we compute the electronic features, such as HOMO, LUMO, HOMO-LUMO gap, and EA.

Then, we used the thermodynamic cycle suggested by Truhlar^36,37 as described in Figure S20 to calculate the RP. To evaluate the reduction free energies at 298 K in the gas phase $\Delta G_{\text{gas}}^{\text{red}}$, the vibrational frequencies were analyzed for both the anionic and neutral states for all the organic species. To evaluate the solvation-free energies of the anionic and neutral states ($\Delta G_{\text{sol}}\left(R^{-}\right)$ and $\Delta G_{\text{sol}}\left(R\right)$, respectively) in the mixture of ethylene carbonate and dimethyl carbonate, the Poisson–Boltzmann implicit solvation model was used with a dielectric constant of 16.14. Using the thermodynamic cycle in Figure S20, the reduction free energy in solution phase $\left(\Delta G_{\text{sol}}^{\text{red}}\left(R\right)\right)$ was calculated by:

$$\Delta G_{\text{sol}}^{\text{red}}\left(R\right)=\Delta G_{\text{gas}}^{\text{red}}\left(R\right)+\Delta G_{\text{sol}}\left(R^{-}\right)-\Delta G_{\text{sol}}\left(R\right)\text{.}$$ (Equation 1)

Finally, the RP in the solution phase with respect to Li/Li⁺ electrode was calculated based on the free energy change for the reduction in the solution phase using,

$$E_{\mathrm{w}.\mathrm{r}.\mathrm{t}.\text{Li}}^0=\left(-\frac{\Delta G_{\text{sol}}^{\text{red}}\left(R\right)}{nF}+E_H\right)-E_{\text{Li}}\text{,}$$ (Equation 2)

where $n$ and $F$ denote the number of electrons transferred and the Faraday constant $\left(\mathrm{96,485}{\mathrm{C}\text{mol}}^{-1}\right)$, respectively. E_H and E_Li correspond to the absolute potential of the hydrogen electrode $\left(4.44\mathrm{V}\right)$, and the potential of the Li electrode with respect to the standard hydrogen electrode $\left(-3.05\mathrm{V}\right)$⁵⁵, respectively. In the previous studies, we showed that this computational strategy produced RPs with staggering accuracy, within $0.3\mathrm{V}$ vs. Li/Li⁺ relative to experimental results.^{26,27,28,29,30,31,32,56,57} In addition to the RP, the adiabatic electron affinity was calculated from the difference in energy between the organic molecules in their neutral state and in their anionic state. Additional details of the DFT calculations used to predict the RP are found in the past studies.^{26,27,28,29,30,31,32,56,57}

Estimating the time complexity of the high-fidelity model

Since our DFT dataset has been developed over multiple studies and under several different computational machines, we needed a method to estimate the computational complexity (to calculate RP, as well as the input DFT features) for all the molecules in our dataset in a fair and consistent manner. Therefore, for consistency, we performed the necessary calculations on a single representative case, anthraquinone, and recorded the computational time. Using the computational time for this case and the well-known scaling factor for standard DFT computational complexity $O\left(N^3\right)$^58,59, we estimated the computational complexity for the remaining cases accordingly. We included detailed information on the time complexity for computing the properties of each molecule in Data S1.

Constructing the HTVS pipeline based on a high-fidelity DFT computational model

Cascading the high-fidelity computational model

As shown in Figure S21 (right panel), the high-fidelity DFT computational model computes several features of a given molecule in neutral and anionic states to compute the redox potential. In order to construct the skeleton structure of the HTVS pipeline, we first decompose the high-fidelity model $f$ into four computational modules $f_1,f_2,\dots ,f_4$ and cascade them sequentially, as shown in the right panel of Figure S21. For a given redox-active material, we first compute the primitive features such as the number of C, B, O, Li, H, and aromatic rings via $f_1$. Then, we perform geometric optimization and thermochemistry calculations to compute the HOMO, LUMO, and HOMO-LUMO gap for the material in a neutral state $\left(f_2\right)$. Next, we compute the EA of the material based on the available intermediate features and geometrically optimized material in the neutral and anionic states via $f_3$. Finally, we calculate the solvation-free energies of the materials in both states to obtain the RP through $f_4$.

Learning machine learning (ML) surrogate models that comprise the HTVS pipeline

Based on the skeleton structure of the HTVS pipeline as shown in the right panel of Figure S21, we learned five surrogate models to build screening stages, which will be placed between the sequential computational modules $f_1,f_2,\dots ,f_4$. The five surrogate models predict the RP using a different set of descriptors available to each surrogate model based on its location in the HTVS pipeline. For example, surrogate model $g_1$ located right after $f_1$ predicts the RP based on only the primitive descriptors. We introduce the concept of a “sub-surrogate” model that predicts the next descriptors not yet available at the given stage (as they need additional computational modules) and use the predicted descriptors as virtual features to improve the prediction accuracy of the surrogate models. For example, the second surrogate model $g_2$ located between $g_1$ and $f_2$ uses additional predicted features such as HOMO, LUMO, and HOMO-LUMO gap predicted via sub-surrogate models $g_{\mathrm{2,1}}$, $g_{\mathrm{2,2}}$, and $g_{\mathrm{2,3}}$ in order to improve the prediction accuracy. Acquiring these virtual features through ML-based sub-surrogate models is very cheap as it does not require any DFT calculations. Table S1 in the supplemental information shows the specification of all the (sub-)surrogate models trained in this study. We use a KRR model that effectively regresses the response in general (see Sections S1 and S2 in the supplemental information).

Generalized optimization framework for finding the optimal screening policy for materials whose RP belongs to a target range

Estimating the joint distribution of the predictive scores from all screening stages constituting the HTVS pipeline

Similar to the screening policy optimization framework originally proposed in the previous study,²⁴ the first step of the generalized optimization framework for identifying the screening policy that can maximize the performance of a given HTVS pipeline is to estimate the joint distribution $p$ of the scores computed at different screening stages, each of which is associated with a different model (i.e., machine learning-based surrogates $g_i$ and the high-fidelity model $f$). In this study, we use parametric spectral estimation based on a multivariate Gaussian mixture model. Specifically, we estimate the parameters of a bimodal multivariate Gaussian distribution via the expectation maximization (EM) algorithm.⁵³

Generalized framework for HTVS policy optimization under computational budget constraint

In this computational screening campaign scenario, we assume that the operational objective of screening is to maximize the number of detected organic electrode materials whose RP, computed via a given high-fidelity model $f$, is within a pre-specified target range $\left[{\lambda }_L,{\lambda }_U\right]$ under computational budget constraint $C$. To this aim, we identify the optimal screening policy ${\mathit{\psi }}^{\ast }=\left[{\lambda }_{1,L}^{\ast },{\lambda }_{1,U}^{\ast },\dots ,{\lambda }_{N-1,U}^{\ast }\right]$ of the screening stages $S_i$, $i=\mathrm{1,2},\dots ,N-1$, where each stage is associated with a machine learning (ML) surrogate model $f_i$. Under the available computational budget $C$, the optimal screening policy should maximize the size of the output set $\mathbb{Y}$, which contains candidate materials whose RP belongs to the target range $\left[{\lambda }_L,{\lambda }_U\right]$ when evaluated by the high-fidelity model $f$ in the last stage $S_N$ of the HTVS pipeline.

Let $p\left(y_1,y_2,\dots ,y_N\right)$ be a joint distribution of the RP values, where $y_N$ is computed via the high-fidelity DFT model $f$ and $y_1,\dots ,y_{N-1}$ are computed by ML surrogate models $g_i$,. In this study, we considered a $N=6$ stage HTVS pipeline with 5 ML surrogate models. Let us denote the reward function $r\left(\mathit{\lambda }\right)$ according to screening ranges ${\mathbf{\lambda }}_{1:N}=\left[{\lambda }_{1,L},{\lambda }_{1,U},{\lambda }_{2,L},\dots ,{\lambda }_U\right]$ of the screening stages $S_i$, $i=\mathrm{1,2},\dots ,N$, as follows:

$$r\left({\mathbf{\lambda }}_{1:N}\right)=\stackrel{\left[{\lambda }_N,{\lambda }_{N-1,U},\dots ,{\lambda }_{1,U}\right]}{\underset{[{\lambda }_L,{\lambda }_{N-1,L},\dots ,{\lambda }_{1,L}]}{\int \dots \int }}p\left(y_1,y_2,\dots ,y_N\right)d{y}_{1}d{y}_2\cdots d{y}_N\text{.}$$ (Equation 3)

Note that $r\left({\mathit{\lambda }}_{1:N}\right)$ is proportional to the number of the potential candidate materials that are detected by the HTVS pipeline by passing all screening stages.

We can find the optimal screening policy ${\mathbf{\psi }}^{\ast }=\left[{\lambda }_{1,L}^{\ast },{\lambda }_{1,U}^{\ast },\dots ,{\lambda }_{N-1,U}^{\ast }\right]$ of the surrogate-based screening stages $S_i$, $i=\mathrm{1,2},\dots ,N-1$, maximizing $\left|\mathbb{Y}\right|$, by solving the constrained optimization problem as follows:

$${\mathbf{\psi }}^{\ast }=\underset{\mathbf{\psi }\in {\mathbb{R}}^{2\left(N-1\right)}}{\arg \max }r\left(\left[\mathbf{\psi },\mathbf{\lambda }\right]\right)$$ (Equation 4)

$$\mathrm{s}.\mathrm{t}.\sum _{i=1}^N{c}_i\left|{\mathbb{X}}_i\right|\le C\text{.}$$ (Equation 5)

$\left|{\mathbb{X}}_i\right|$ is the number of candidate materials that passed the previous stages from $S_1$ to $S_{i-1}$, defined as follows:

$$\left|{\mathbb{X}}_i\right|=\left|\mathbb{X}\right|\stackrel{\left[{\lambda }_{i-1,U},{\lambda }_{i-2,U},\dots ,{\lambda }_{1,U}\right]}{\underset{\left[{\lambda }_{i-1,L},{\lambda }_{i-2,L},\dots ,{\lambda }_{1,L}\right]}{\int \dots \int }}{p}_{1:i-1}\left(y_1,y_2,\dots ,y_{i-1}\right)d{y}_{1}d{y}_2\cdots d{y}_{i-1}\text{,}$$ (Equation 6)

where $p_{1:i-1}$ is a marginal score distribution of $\left(y_1,y_2,\dots ,y_{i-1}\right)$ obtained by marginalizing $p$ over $y_i,\dots ,y_N$.

Generalized framework for HTVS policy optimization for throughput and computational efficiency

In this scenario, we jointly optimize the HTVS pipeline to maximize the throughput and minimize the computational resource consumption. The optimal screening policy is obtained by solving the optimization problem as follows:

$${\mathit{\psi }}^{\ast }=\underset{\mathbf{\psi }\in {\mathbb{R}}^{2\left(N-1\right)}}{\arg \min }\alpha \overline{r}\left(\left[\mathit{\psi },\mathit{\lambda }\right]\right)+\left(1-\alpha \right)\overline{h}\left(\left[\mathit{\psi },\mathit{\lambda }\right]\right)\text{.}$$ (Equation 7)

The weight parameter $\alpha \in \left[\mathrm{0,1}\right]$ determines the relative importance between the relative reward function $\overline{r}\left(\left[\mathit{\psi },\mathit{\lambda }\right]\right)$ and the normalized total cost function $\overline{h}\left(\left[\mathit{\psi },\mathit{\lambda }\right]\right)$, which are defined as follows:

$$\overline{r}\left(\left[\mathit{\psi },\mathit{\lambda }\right]\right)=\frac{r\left(\left[-\infty ,\infty ,\dots ,\infty ,\mathit{\lambda }\right]\right)-r\left(\left[\mathit{\psi },\mathit{\lambda }\right]\right)}{r\left(\left[-\infty ,\infty ,\dots ,\infty ,\mathit{\lambda }\right]\right)}$$ (Equation 8)

$$=\frac{{\int }_{{\lambda }_L}^{{\lambda }_U}{p}_N\left(y_N\right)d{y}_N-r\left(\left[\mathit{\psi },\mathit{\lambda }\right]\right)}{{\int }_{{\lambda }_{N,L}}^{{\lambda }_{N,U}}{p}_N\left(y_N\right)d{y}_N}\text{,}$$ (Equation 9)

$$\overline{h}\left(\left[\mathit{\psi },\mathit{\lambda }\right]\right)=\frac{1}{N\left|\mathbb{X}\right|{\max }_i{c}_i}\sum _{i=1}^N{c}_i\left|{\mathbb{X}}_i\right|\text{.}$$ (Equation 10)

Here, $p_N$ is the marginal score distribution obtained by marginalizing $p$ over $y_1$ to $y_{N-1}$.

Published: January 20, 2023

Data and code availability

• •All original code has been deposited at GitHub and is publicly available as of the date of publication. DOIs are listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.