The discriminative potential of palatal geometric analysis for sex discrimination and human identification

Abstract

Previous 3D superimposition studies of digital scans of the human palate, using geometric and surface morphology comparisons, have shown its usefulness in assisting in the identification process, including its ability to distinguish identical twins. This study aimed to evaluate the discriminative potential when only simple geometric analysis is used. Its aim is not only to determine if geometric comparison alone is sufficient not only to assist in identification but if it supports the hypothesis of assisting in sex discrimination when no other comparative data is available. The palates of 64 monozygotic (M.Z.T.) and 39 dizygotic (D.Z.T.) twins were digitized three times using a scanner. Digital smoothing was used to remove the rugae, and palatal height, depth, and width were measured. The study confirmed that the smoothing function had little effect on the discriminatory function since the Mean Absolute Distance (MAD) between M.Z.T. (0.430 ± 0.018 mm versus 0.425 ± 0.022 mm p = 0.061) or D.Z.T. (0.621 ± 0.058 mm versus 0.586 ± 0.053 mm, p = 0.284) scans show little change. By combining the height, depth, and width into a discriminative function, the sex correctly correlated 83.9% of the time, identity by 91.2% sensitivity, and twining by 68.5%. The difference in the 3D palatal model between twin siblings is primarily due to palate geometrics. Since geometric comparison requires far less computation time, geometric comparison alone can be used as an adjunct metric for limiting the possible matches in a dental 3D database in determining both sex and identity, especially if no other evidence is available.

Highlights.

• Geometric analysis of the palate without surface morphology have the potential to assist in human identification.

• Geometric analysis of the palate vault is a valuable adjunct to sex determination where no other data is available.

• 3D data consisting only the palate's height, depth, and width can be an adjunct in ranking possible dental matches.

1. INTRODUCTION

DNA analysis is a sensitive and specific method in human identification [1, 2]. However, it requires a laboratory or specialized field equipment, is expensive to perform, requires antemortem reference data, and, as a general rule, cannot give answers as rapidly as identification by other means. The fingerprint database is also limited in most countries, and fingers are the first body parts damaged during accidents [3]. Therefore, dental identification is essential in many disasters [4]. However, identification based on dental charting (decayed, missing teeth, restoration, etc.) is mainly a manual analog method, time‐consuming [5], and requires antemortem radiographs. In addition, the quantitative assignment of a probability value of possible matches is limited to restoration distribution [6].

The anterior part of the palate is well protected by the teeth and maxillary bone, the buccal pad of fat, the lips, and the neurocranium [7]. Moreover, it is considered resistant to external factors such as burning [8]. In addition, dentists' use of intraoral scanners (IOS) has grown exponentially, building vast 3D dental databases. IOS can accurately capture the entire dental arch without hazardous effects such as radiation [9, 10]. Although most intraoral scanning is to restore dentition via computer‐aided manufacturing (C.A.M.) [11], palatal scans are often incidentally included. In addition, palatal scans are mandatory for the fabrication of immediate transitional dentures [12], complete dentures [13, 14], and as a reference point to evaluate orthodontic outcomes [15, 16]. Finally, due to legal [17], diagnostic [18], and rehabilitation [19] reasons, it is far easier for the dentist to store scans than dental gypsum models, which are discarded after treatment [20]. This makes them an ideal source of antemortem data. Recently, a biometric database has been introduced for forensic purposes [21].

Previous studies have lent support to the hypothesis that palatal features can be used to distinguish individuals [22, 23]. In fact, it has been used in a previous study [23] to show a 10‐fold high correlation between the repeated palatal scans of the same individuals compared to monozygotic (M.Z.T.) twins siblings (31 μm vs. 411 μm). As a result, the twin siblings could be distinguished with 99% confidence [23]. The distinctness of palatal features was also superior to the tooth morphology in a case study [24], making the palatal features a valuable adjunct for humans. The result of the studies [22, 23, 24, 25] strengthens the theory of palatal uniqueness, suggesting the possibility that 3D palatal scans might be a helpful adjunct in identifying individuals based on the complex morphology of the palate.

In addition, the concept of sex classification based on palatal and dento‐alveolar metrics has been established. Previous studies [26, 27, 28] have also suggested that the number of the rugae and pattern distribution can be used to determine the sex of an individual. However, manual marking, measuring, and classifying each ruga is time‐consuming and subjective. It is also challenging to automatize. The geometric measurement of the palate on the skeleton could also be used for sex discrimination [29, 30, 31], but only one study was done on soft tissues using gypsum casts [32].

The primary purpose of this paper is to determine if the use of digital palatal scans is a good candidate for prescreening for human identification and as an adjunct in forensic dental identification, and as contextual evidence for sex determination investigation.

1.1. Comparison methodology and algorithm simplification

The Mean Absolute Distance (MAD) is one method for calculating the similarity between two surfaces. Each surface is assigned landmarks, and points on the surface, based on the resolution of the scan data in the S.T.L. file. Open‐source software such as GOM Inspect® (Suite 2020, GOM GmbH, Braunschweig, Germany) attempts to superimpose the image by comparing the points on the comparative surface. The software attempt to align the two surfaces, via a method called best‐fit alignment, by comparing all the distance calculations and selecting the alignment that shows the least difference. The software then takes the absolute value of the remaining differences and creates a mean value. The lower the MAD, the more likely the two images are “identical.”

However, because a desktop P.C. takes approximately 30 seconds per alignment, the searching process in an extensive database during identification would be prolonged using MAD for calculations. This is also true for conventional visual observation and classification for identification purposes [33, 34, 35]. Pattern recognition for palatal rugae can also be developed but requires intensive computational algorithms. Therefore, finding more specific metric parameters (areas, surface morphology, dimensions) on the palate which still reflect individuality is essential to decrease file size and accelerate searching and matching algorithms. 3D palate features can be classified into geometric features (i.e., anthropology) such as curvature, width, depth, height, and morphologic (surface) features such as the palatal rugae. However, it is unclear from current studies [22, 23] how each contributes to the difference obtained after 3D superimpositions. Furthermore, suppose the metrics from a geometric analysis 3D digital palatal scan can show the same sexual dichotomy. In that case, it could prove to be a beneficial adjunct to other anthropological contextual evidence for sex determination in cases where only the maxilla is present.

The study aimed to determine how much the geometrics of the palate contribute to the difference between individuals (twin siblings versus strangers) and between sexes (females versus males).

2. MATERIALS AND METHODS

61 M.Z.T. and 27 same‐sex D.Z.T. twin pairs were selected from the National Twin Register database [36]. Written informed consent was obtained from the participants, and the study was carried out according to the Declaration of Helsinki. Ethical approval was granted (36699–2/2018/E.K.U.), zygosity was determined by a questionnaire [37, 38], and the digital impression was taken with Emerald® intraoral scanner with ROMEXIS® PlanCAD Easy software (version 5.2.1, Planmeca Oy, Helsinki, Finland). The palatal area was scanned three times with a standard scanning pattern to create replicates within each subject. A single D.Z.T. pair was excluded due to a flawed scan.

2.1. The effect of the surface morphology (rugae) on MAD

Three replicates of all the remaining subjects (522 scans) were included in the measurement. The scans were imported into the GOM Inspect® 3D mesh processing software and then duplicated to retain an unmodified copy of the imported scans. The teeth and the marginal gingiva were digitally removed, generating a palate‐only model. The images were further processed by an additional 3D processing software (Meshmixer, version 3.5, Autodesk Inc., San Rafael, CA, U.S.A.) which removed the palatal rugae surface morphology using the “Sculpt” function in the software and generated smoothed scans (Figure 1B). The superimposition was performed between the three replicates of the twin siblings on the original and smoothed scans by the GOM Inspect® software local best‐fit function using an iterative closest point algorithm [39]. Finally, a MAD analysis was done, and the software calculated the intra‐twin MAD for the original and the smoothed superimposition.

FIGURE 1.

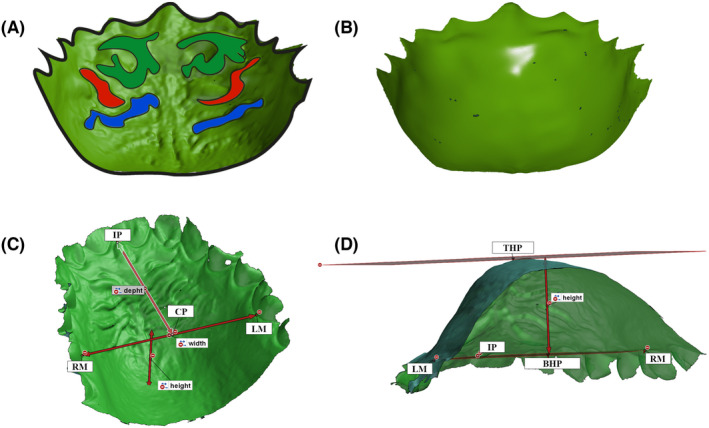
(A) Methods for analyzing the palate‐only model. Palatal rugae are depicted in three colors (green, red, and blue) on the original model. (B) the same model after smoothing the rugae. (C) the following points and distances were determined for width and depth measurements, R.M.: A point at the gingiva of the right molar, L.M.: A point at the gingiva of the left molar, I.P.: The most anterior point of the incisive papilla, CP: Central point, width: Distance between R.M. and L.M., depth: Distance between I.P. and C.P. (D) the method of the height measurement. The horizontal plane (B.H.P.) was defined by the points I.P., R.M., and L.M. the top plane (T.H.P.) was defined as parallel to the horizontal plane at the highest point of the palatal vault. Height: The distance between the two planes.

2.2. Geometric measurement of the palate

For the geometric measurement of the palate, an additional 28 twin pairs scans were excluded due to inadequate imaging of the first molar in at least one of the sibling's scans. Therefore, only 42 M.Z.T. and 17 D.Z.T. for a total of 59 scans could be analyzed.

The scans were imported into GOM Inspect software, and height, depth, and width were measured according to Ferrario et al. [40]. Briefly, the Intermolar Line (I.M.L.), drawn between the right (R.M.) and left molar's (L.M.) palatal groove at the level of the gingival margin (Figure 1C), determined the palatal width. Next, the I.M.L. was projected perpendicular to the most anterior point of the incisive papilla (I.P.), and the intersection point was named Central Point (C.P.). The line connecting the C.P. with the I.P. defined the palatal depth, while the three points (R.M., L.M., I.P.) defined the Bottom Horizontal Plane (B.H.P.). Then, a second horizontal plane, the Top Horizontal Plane (T.H.P.), parallel to B.H.P. and tangential to the highest point of the palate, was constructed using Chebyshev's best‐fit algorithm (Figure 1D). Finally, the palatal height, the distance between the two planes (T.H.P. and B.H.P.) was calculated.

2.3. Statistical analysis

The MAD showed a right‐skewed distribution in the previous twin study [23], indicating the greater frequency of scan pairs with lower MAD. The data also shows heteroscedasticity (standard deviation is unequal across the range of values), meaning higher MAD has a greater data range (higher standard deviation). Therefore, the MAD was evaluated by the generalized linear mixed model using the log‐link function and gamma distribution. From the variables being analyzed, zygosity (M.Z.T., D.Z.T.), smoothing (original, smoothed), age (covariant), and their interactions were the fixed effects.

In geometric measurement (height, depth, and width), one scan from the three replicates of each subject was evaluated by two observers to assess the inter‐observer variability. The single (I.C.C. [2,1]) and the average rater (I.C.C. [2,2]) absolute agreement and the mean difference between the observers were calculated by the two‐way random‐effects model [41]. The technical error of measurement (T.E.M.) and its relative forms (% T.E.M.) were calculated according to Ulijaszek and Kerr [42].

The male and female palatal width, depth, and height were compared using a linear mixed model. The Pearson correlation coefficients between geometric parameters were calculated for M.Z.T. and D.Z.T. pairs.

Linear discriminant analysis (LDA) created discriminant functions, where the discriminant loadings of the height, the depth, and the width provide information on the relative importance of each variable in determining the sex class. 0.30 is seen as the cut‐off between important and less important variables [43]. Additionally, two classification equations (i.e., Fisher's linear discriminant functions) were calculated for the female and the male classes, then used for predictive discriminant analysis. Two classification scores were calculated from the two classification equations for each test case. The likelihood of the sex of a scan was calculated from the classification score for each case using the Bayesian theorem [44].

A second analysis was performed using a combination algorithm implemented using M.S. Excel Visual Basic to create all permutations (n = 62,481) between scans (n = 354), excluding the same scan pairs. Each pair was classified as identical (repeated scans of the same subject), M.Z.T. sibling, D.Z.T. sibling, or stranger. The absolute value of the differences between geometric parameters was calculated and square rooted to normalize the distribution (sqrd_height, sqrd_depth, and sqrd_width). Finally, LDA was applied to assess the probability of the classification. All analyses were carried out using IBM SPSS Statistics, Version 27 (Armonk, NY: I.B.M. Corp.). A p‐value of less than 0.05 was considered statistically significant.

3. RESULTS

3.1. The effect of the surface morphology (rugae) on MAD

The intra‐twin MAD of the original scan was not significantly different from the smoothed scan in either M.Z.T. (0.430 ± 0.018 mm versus 0.425 ± 0.022 mm, p = 0.061) or D.Z.T. (0.621 ± 0.058 mm versus 0.586 ± 0.053 mm, p = 0.284) (Figure 2A).

FIGURE 2.

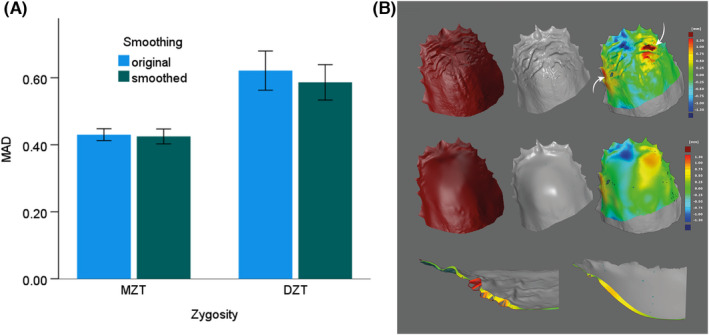
(A) Comparison of the mean absolute distance (MAD) between original and smoothed scans in monozygotic twin pairs (M.Z.T.) and dizygotic twin pairs (D.Z.T.). (B) Representative scans of an M.Z.T. pair. The first row shows the original scan of sibling A (red) and sibling B (gray). The primary rugae pattern is quite similar, but some differences can be seen. The white arrow in the original superimposed image (third image) indicates an area with a high distance (white arrows). The second row shows the smoothed scans of the identical twin pair. In their superimposition (third image in the second row), a high deviation area (redish spots) can be seen in the same area as in the original superimposition. It indicates that the distance between scans is primarily caused by geometrics. The cross‐section of the models (third row) shows that the distance between the two surfaces did not change significantly after smoothing (second image).

When geometric smoothing occurs, MAD is expected to decrease due to the elimination of the “hills and valleys” of the rugae. However, the representative case (Figure 2B) shows that the overall MAD does not change significantly because of the shallowness of the rugae.

3.2. Accuracy of the geometric measurement of palate

The coefficient of variation shows the variability of repeated scans in relation to the mean and is calculated by dividing the standard deviation by the mean. The coefficient of variation was 3.7% for the height, 3.5% for depth, and 1.0% for width, indicating excellent scanning repeatability (high precision).

The I.C.C. was used to quantify the degree of agreement of the measurement between the two observers. For height, depth, and width, the single and average measurements between observers show a high level of agreement (Table 1). However, the statistical analysis revealed that the first observer had a statistically significantly (p < 0.05) higher measurement for height than the second observer, the average difference between the two observers was less than 0.1 mm for all measurements. The T.E.M., measured in mm, expresses the error in anthropometry (the science of measuring the human body) and represents the inter‐observer variability of the measurements. % T.E.M. is the relative error calculated by dividing the T.E.M. by the measurement mean. The T.E.M. and % T.E.M. were the lowest for the height and highest for the depth.

TABLE 1.

The inter‐observer agreement for height, depth, and width

	Absolute agreement (I.C.C.)		Difference between observers			Technical error of measurement
	Single observer (type I.C.C. 2,1)	Average observer (type I.C.C. 2,2)	Mean	SE	p	TEM	%TEM
height (mm)	0.996	0.998	0.07	0.01	0.000	0.10	0.7%
depth (mm)	0.955	0.977	−0.06	0.07	0.380	0.53	1.8%
width (mm)	0.986	0.993	0.04	0.04	0.324	0.31	0.9%

Abbreviations: I.C.C., intraclass correlation coefficient; T.E.M., technical error of measurement; % T.E.M., relative T.E.M.

3.3. Effect of sex on the geometrics

The metric data for height, depth, and width are shown in Table 2. As expected, palatal height and width were significantly higher in males than in females by 2.4 mm and 1.6 mm, respectively. However, the difference in depth proved statistically insignificant.

TABLE 2.

Geometric comparison of palate between sexes

		Valid N	Mean	SE	SD	Minimum	Maximum	Range	p<
height	female	90	15.1	0.16	1.54	11.7	18.5	6.8	0.001
	male	28	17.5	0.42	2.24	14.4	24.1	9.7
depth	female	90	28.1	0.26	2.48	22.2	34.1	11.9	=0.149
	male	28	29.1	0.37	1.97	25.7	32.8	7.0
width	female	90	34.0	0.27	2.56	27.0	41.0	14.0	0.05
	male	28	35.6	0.52	2.73	30.3	41.8	11.5

Abbreviations: SE, Standard Error of Mean; SD, Standard Deviation.

3.4. Geometric parameters correlation between palate

No correlation (r = 0.13, p = 0.164) was seen between palatal height and palatal depth nor between palatal width and either palatal height (r = −0.04, p = 0.689) or palatal depth (r = 0.13, p = 0.163). Therefore, based on this study, it is clear data that palatal height, palatal width and palatal depth are independent variables, and are suitable for LDA.

3.5. Linear discriminant analysis for sex prediction

The LDA used to predict the sex classification of an individual produced a function with significant Wilks' Lambda, a measurement of how well a function separates cases into groups (0.66, p < 0.001). The data suggest that height has the highest degree of discrimination for sex classification (r = 0.83), width (r = 0.37) and depth (r = 0.24) have lower degrees of discrimination.

Linear discriminant analysis of the data produced the following two classification formulas, which were then used to test how well these measurements could differentiate between sexes (i.e., predictive classification),

Y_female = 6.45 × height + 5.56 × width + 4.23 × depth – 204.

Y_male = 7.35 × height + 5.91 × width + 4.33 × depth – 233.

The three geometric parameters were inputted into both the female and male equation, and the predicted class was assigned based on whichever equation gave the higher score. Based on the Bayesian theorem, the greater the difference between the two scores, the higher the probability of correct classification [44].

For example, one test subject with a palatal height of 13.9 mm, a palatal depth of 25.1 mm, and a palatal width of 34.1 mm would yield a female classification score of 182 and a male classification score of 179. Therefore, these calculations would predict females, and the classification was correct in that particular case. In addition, because of the considerable difference between the two scores, the Bayesian probabilities were 0.94 for the female and only 0.06 for the male. The second example (height = 13.8, depth 28.0, width 41.0) produced a female score of 232 and a male score of 231. Consequently, the probabilities (female, 0.54; male, 0.46) are close to 50%. Although the predicted memberships were still correct (i.e., female), the prediction probability was significantly lower than in the first example.

When the equations were run on the entire data set using a simple majority (p > 0.50) as the predictor, the function correctly classified 74 of the 90 females (sensitivity, 82.2%, specificity, 89.3%) and 25 of the 28 males (sensitivity, 89.3%; specificity, 82.2.%).

3.6. The discriminant function of geometric parameters for identification

A similar LDA was used to classify repeated scans of the same subject (Y_identity), M.Z.T. sibling (Y_MZT), D.Z.T. sibling (Y_DZT), and stranger (Y_stranger), and it produced significant functions (Wilks' Lambda, 0.955; p < 0.001). In all these cases, the data showed that the height had the highest discrimination potential (0.63), followed by width (0.62) and depth (0.47). The absolute difference in the geometric parameter between all combinations of scans needed to be calculated. These square root of the differences needed to be inputted into the following equations.

Y_identity = 1.01 × sqrd_height + 1.00 × sqrd_width + 1.73 × sqrd_depth – 2.46.

Y_MZT = 2.25 × sqrd_height + 2.15 × sqrd_width + 2.75 × sqrd_depth – 5.07.

Y_DZT = 2.87 × sqrd_height + 2.81 × sqrd_width + 3.20 × sqrd_depth – 7.02.

Y_stranger = 3.59 × sqrd_height + 3.27 × sqrd_width + 3.65 × sqrd_depth – 9.23.

Again, the classification was based on whichever equation gave the highest score. The function correctly classified scans of the same individuals by (91.2% sensitivity and 97.8% specificity) (Table 3). Due to the similarity of the Y_MZT and Y_DZT formulas, the groups were combined. The “twin classification” was determined with 68.5% sensitivity and 61.9% specificity.

TABLE 3.

Identification based on palate geometrics

	Original class	Predicted group membership				Total
		identical	M.Z.T. pair	D.Z.T. pair	stranger
True	identity	323	21	3	7	354
	M.Z.T. sibling	76	217	58	27	378
	D.Z.T. sibling	19	44	45	45	153
	stranger	1291	12,653	10,922	36,730	61,596
%	Identity	91.2	5.9	0.8	2.0	100
	M.Z.T. siblingz	20.1	57.4	15.3	7.1	100
	D.Z.T. sibling	12.4	28.8	29.4	29.4	100
	stranger	2.1	20.5	17.7	59.6	100
True	M.Z.T. + D.Z.T.	95	364		72	531
%	M.Z.T + D.Z.T	17.9	68.5		13.6	100

Abbreviations: M.Z.T., monozygotic twins; D.Z.T., dizygotic twins.

4. DISCUSSION

The study found no significant difference between original and smoothed scans in intra‐twin MAD. It is important to note that the iterative closest point algorithm is designed to find the “best match comparison” by minimizing the distance between as many points as possible. Therefore, the software is not looking at comparing identical structures [39, 45, 46]. Although we expected the actual MAD to be smaller in the smoothed scans, this did not prove correct. This can be explained by the fact that the distance added by the variation in surface morphology is considerably less than the total palatal distance. Therefore, surface morphology (i.e., rugae) only adds a little to the MAD due to the inherent property of the alignment method. Although rugae have little effect on the geometric comparison, they still can be a significant factor for morphological comparison. Visual inspection of M.Z.T. twins rugae confirms that they are not the same, although similar. Therefore, since geometrics primarily drive surface alignment, rugae only play a role in distinguishing twin pairs when the morphological comparison is utilized. However, these results still suggest that the geometrics of the palate may have some potential to reduce the number of presumptive candidates. This study did not show a correlation between the three palatal parameters supporting their suitability for multivariate discriminate analysis.

Knowing the presumptive sex of an unidentified individual based on palatal morphology has the potential to reduce 3D database searches by almost 50%. In this investigation, the linear discriminant analysis for the Caucasian population (Central European) correctly predicted sex 84% of the time, which could be helpful when no other anthropological data was available. In cases of greater difference between the calculation, the probability of correct classification would be even higher. Although previous sex classification criteria using rugae pattern, teeth size, teeth morphology [26, 28, 47], and complex craniometry [48] have been proposed, the method used here is far simpler, using three palatal landmarks. It also has the potential for an A.I. algorithm to perform the entire analysis. Although previous studies have lent support to the hypothesis that palatal features can be used to distinguish individuals, all had lower prediction levels. This study suggests that this may be due to the fact that none of these studies measured height which has shown to have the most distinguishing potential for sex and identity. Another advantage of using the proposed linear parameters is that they can also be measured from a skull specimen extended the method to the skeletal remains.

4.1. Ethnicity and palatal metrics

One of the limitations of the current study was that linear discriminant analysis was performed on a homogenous Caucasian Central European population (C.C.E.) and has not been adjusted for ethnic differences. A study of a mixed male/female Chinese population [49] showed a similar average height to C.C.E. (16.6 mm versus 16.3 mm), but the width was higher (38.0 mm versus 34.8 mm) than the mixed male/female C.C.E. average. A Lebanese study showed that the width difference between males and females was 1.5 mm [28] which compared well to our study (1.6 mm). Previous anthropological studies concerning the ethnic difference between palatal measurements are rare and have yielded mixed results. For example, a study of human skeletal palatal geometric measurement successfully discriminated against three American races (Indian, Afro‐ and Euro‐Americans) 66% of the time [50]. At the same time, the width and depth of the palate were a successful discriminator between American blacks and whites 83% [51]. These studies suggest that width gives the greatest level of ethnic discrimination. However, additional soft tissue scans of various ethnic populations will be needed to confirm the use of automated geometric measurement as a discriminator of ethnicities.

4.2. Use of geometric measurement for human identification

In the previous study [23], 64 MZ twin siblings were distinguished by 100% sensitivity from the identity class. Based on our assumption that the morphometric between siblings might be higher than between strangers, the closest point alignment had much higher accuracy than the linear metrics. However, it was impractical to make 73,536 combinations for 128 subjects with 384 scans by manual method. Therefore, we could not test that our hypothesis was correct. This geometrics‐based study revealed that twins resemble each other more than a stranger since the mean discriminant scores for classes were −2.54 for identity, −1.25 for MZ twins, and −0.02 for the stranger. Oral scans can be utilized to assist in verifying identity and excluding false‐positive cases by superimposing two palatal scans and comparing morphology [23]. However, since this is compute‐intensive in an extensive database, prescreening using geometric parameters comparisons can significantly reduce the dataset and narrow the presumptive candidate pairs. Geometric comparisons of oral scans from identical subjects were classified correctly with high sensitivity (91.2%) and specificity (97.8%). The study also confirmed that the geometric analysis of twin pairs produces intermediary result between inclusion and exclusion. The D.Z.T. pairs' variance was only slightly higher than the M.Z.T. pairs.

The study also revealed some shortcomings with the technique, such as the difficulty in cases of missing the first upper molars. In addition, 16% of the subject had missing molars, which correlates well with the population data of Odontosearch (http://www.odontosearch.com/en/3.2/index.html) [6]. The mean age was 32 years, but it ranged from 17 to 74 years. 90% of the discarded scans come from the elderly. In the future, a horizontal plane can be “digital overlaid” onto the edentulous ridge to simulate a height measurement, the geometric parameter with the highest discrimination rate. Another area of concern is changes to the landmark R.M., L.M. due to the gingival recession. In those cases where the recession is significant, the cementoenamel boundary should be used. However, this too may be of limited value when prosthetic restorations prevent visualization of the location of these landmarks. Finally, scans made for small restorations might not include the entire arch. However, because of IOS's improved accuracy and speed [9, 10, 18, 52], many more complete scans are being performed to improve bite registration data [53].

5. CONCLUSION

The study confirms that data obtained from an IOS can produce individualizing characteristics of the human palate and has potential usefulness as a screening tool to assist in the identification process. In addition, as the use of IOSs increases, the availability of 3D data will increase, and this technique could be a valuable triage tool by reducing the possible limiting matches. Finally, this study supports the belief that palate geometrics could serve as additional contextual evidence to corroborate other supporting data in sex determination.

FUNDING INFORMATION

Supported by the ÚNKP‐21‐3‐II‐SE‐4 New National Excellence Program of the Ministry for Innovation and Technology from the source of the National Research, Development and Innovation Fund. Supported by the EFOP‐3.6.3‐VEKOP‐16‐2017‐00009 Semmelweis 250 + Excellence PhD Scholarship from the source of the National Research, Development and Innovation Fund through Semmelweis University. Supported by MEC_R 140705 "Scientific Patronage Call for proposals" MEC_21 from the source of the National Research, Development and Innovation Fund. Supported by the American Society of Forensic Odontology (ASFO) Research Grant 2020. Financed from the National Research, Development and Innovation Fund by the 2019‐2.1.11‐TÉT‐2019‐00048 grant.

Simon B, Aschheim K, Vág J. The discriminative potential of palatal geometric analysis for sex discrimination and human identification. J Forensic Sci. 2022;67:2334–2342. 10.1111/1556-4029.15110