Recent Developments in Plasmonic Alloy Nanoparticles: Synthesis, Modelling, Properties and Applications

Abstract

Despite the traditional plasmonic materials are counted on one hand, there are a lot of possible combinations leading to alloys with other elements of the periodic table, in particular those renowned for magnetic or catalytic properties. It is not a surprise, therefore, that nanoalloys are considered for their ability to open new perspectives in the panorama of plasmonics, representing a leading research sector nowadays. This is demonstrated by a long list of studies describing multiple applications of nanoalloys in photonics, photocatalysis, sensing and magneto‐optics, where plasmons are combined with other physical and chemical phenomena. In some remarkable cases, the amplification of the conventional properties and even new effects emerged. However, this field is still in its infancy and several challenges must be overcome, starting with the synthesis (control of composition, crystalline order, size, processability, achievement of metastable phases and disordered compounds) as well as the modelling of the structure and properties (accuracy of results, reliability of structural predictions, description of disordered phases, evolution over time) of nanoalloys. To foster the research on plasmonic nanoalloys, here we provide an overview of the most recent results and developments in the field, organized according to synthetic strategies, modelling approaches, dominant properties and reported applications. Considering the several plasmonic nanoalloys under development as well as the large number of those still awaiting synthesis, modelling, properties assessment and technological exploitation, we expect a great impact on the forthcoming solutions for sustainability, ultrasensitive and accurate detection, information processing and many other fields.

Developing plasmonic nanoalloys: In this review, we give a general overview of the most recent advances in synthesis, modelling, properties assessment, and technological application of plasmonic nanoalloys.

1. Introduction

Plasmons are collective oscillations of free electrons, which can be promoted by electromagnetic light in nanoscale metals, where they have not‐propagating nature and are usually defined as localized surface plasmons (LSPs).[ ¹ , ² ] Over the last decades, plasmon excitations were exploited for an impressive range of technological applications and research studies, principally in sensing, ^[3] biotechnology, ^[4] light‐enhanced catalysis, ^[5] thermoplasmonic effects, ^[6] fundamental studies connected to local electric field enhancement of optical processes ^[2] and modelling of the interaction with nearby molecules down to the atomic level. ^[7]

Although all materials with conduction electrons can potentially originate plasmons, only a few of them are chemically stable as nanostructures and provide plasmon resonances with appreciable intensity at optical frequencies.[ ⁸ , ⁹ , ¹⁰ ] Most metals undergo oxidation or degradation in ordinary conditions, such as Na, K or Al. Almost all the other elements have a poor plasmonic response, quantifiable by the plasmonic quality factor at optical frequencies.[ ⁸ , ⁹ , ¹¹ ] This has restricted most of the studies about plasmonics to the nanostructures made of gold and silver, missing all the range of chemical, physical and other properties (low cost, earth abundance, sustainability, magnetism, chemical selectivity…) available from the periodic table. This problem is frequently raised due to the necessity of cheaper and alternative nanomaterials with, for instance, plasmonic and catalytic or plasmonic and magnetic properties. The simultaneous presence of these features in a single nanoparticle (NP) makes these nanosystems highly promising for several frontier research endeavours.

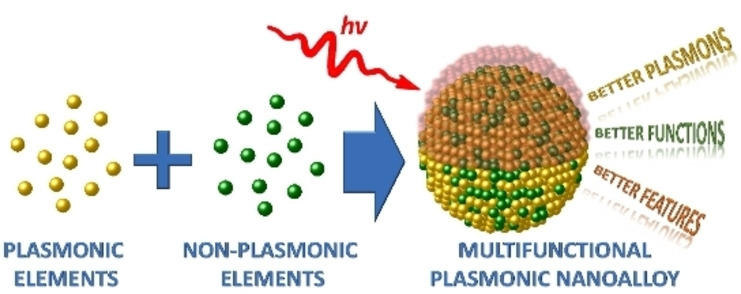
Alloying is a strategy to re‐introduce the range of properties of the periodic table into nanostructures with an appreciable plasmonic response (Figure 1).[ ¹² , ¹³ ] It is well known that alloying two or more metals leads to new materials with properties that are not simply the average of their monometallic counterparts. In effect, this approach can open the way to multifunctional plasmonic objects of great appeal for several applications and can offer the opportunity of moulding the electronic structure of the metal to improve and maximize the efficacy for a specific plasmonic effect. In special cases, alloying can be associated with novel and still unexplored physical or chemical phenomena mutually influenced by the collective excitation of conduction electrons with light. Alloying allows the change of some undesired features connected to a plasmonic material such as cost, chemical instability, and sustainability of the final device. This scenario should not be limited to “volume” properties of a nanomaterial but also concerns the surface properties and, in particular, the surface chemistry of nanoalloys, which is markedly modified compared to single element nanoparticles (NPs).

Figure 1.

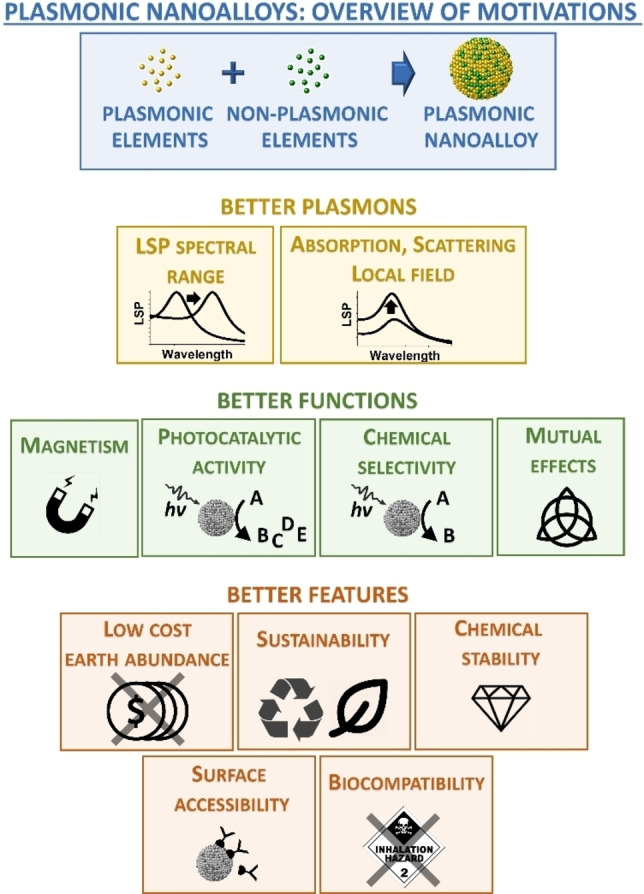
Overview of the main motivations for the realization of plasmonic nanoalloys: achieving better plasmonic properties, better non‐plasmonic or hybrid plasmonic functions and better overall features compared to single element NPs.

To have an idea of the possibilities opened by alloying a plasmonic metal with one or more plasmonic or non‐plasmonic elements, one should think also about the range of atomic ratios in which each alloy can be achieved. Moreover, one also needs to consider the size, shape and environment (substrate, surface coating, etc.) as additional parameters.

On the other hand, several challenges can be identified in the field of plasmonic nanoalloys, especially concerning the synthesis with advanced control of composition, crystalline order, size, product implementation in the desired matrix. The achievement of metastable phases and disordered compounds is another crucial point because most of the possible element combinations are not thermodynamically favoured.

For these reasons, the modelling of the electronic, structural and optical properties is necessary to the development of new plasmonic nanoalloys in a more efficient and fast way than allowed by random experiments or the intuition of materials scientists. Indeed, also the modelling of nanoalloys structure and properties still suffers from a gap concerning the accuracy of results, the reliability of structural predictions, the development of suitable models for describing disordered phases on the nanoscale and their evolution over time, especially in operating conditions such as during a catalytic reaction or under photothermal heating.

Whilst there have been a few previous reviews on specific aspects of the topic,[ ² , ⁸ , ¹³ , ¹⁴ , ¹⁵ ] here we provide a general overview of the latest achievements in the field of plasmonic nanoalloys, organized according to synthetic progresses, modelling strategies, prominent plasmon‐related properties and recently reported applications, with a special focus on plasmon‐enhanced catalysis, sensing and biotechnology.

The general aim of this review is that of fostering the research on plasmonic nanoalloys, either those already under development or the large number of those still waiting for synthesis, modelling, properties assessment and technological exploitation, which we expect will greatly impact the fields of sustainability, ultrasensitive and accurate detection, information processing and many others in the next future.

2. Synthesis of Plasmonic Nanoalloys

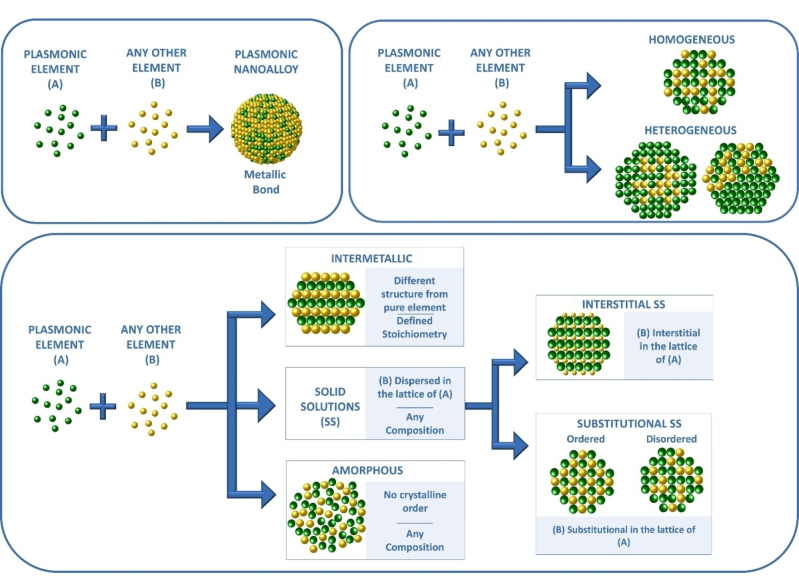
A (metallic) nanoalloy is a nanostructure composed of a mixture of elements of which at least one is a metal, all held together by metallic bonding (Figure 2). ^[16] Homogeneous (i. e. single phase) alloys can be classified according to the atomic arrangement of their constituents as solid solutions (SS) or amorphous. ^[17] A SS has a well‐defined crystal structure in which the lattice of a host element contains the guest elements as substitutional or interstitial dopants. Substitutional SSs can be disordered (the guests occupy random positions in the unit cell) or ordered (the guests are at fixed positions in the unit cell). SSs are distinguished from alloys with a well‐defined stoichiometry and a crystalline structure differing from that of single constituents, which are called intermetallics. On the opposite side, amorphous alloys do not have crystalline order (i. e. glassy metals). ^[18] When multiple homogeneous alloy phases coexist in heterostructures with various arrangements (Janus, dumbbells, core‐shells, matrix with embedded domains, etc.), the alloy is defined as heterogeneous. Heterogeneous alloys are frequent and, indeed, the homogeneity of products represents one major challenge in the synthesis of several nanoalloys.

Figure 2.

Classification of plasmonic alloys: the metallic bond between atomic constituents is a prerequisite. Their structure can be homogeneous or heterogeneous. The homogeneous domains can be amorphous, intermetallic or solid solutions (interstitial or substitutional).

It is worth stressing that, according to the definition of alloy provided above, the plasmonic materials based on multinary semiconductor nanocrystals are beyond the scope of this review, because of the non‐metallic nature of the chemical bond and, consequently, a density of conduction electrons which is orders of magnitude lower than in metals. Indeed, this also implies a much lower plasmonic response such as an extinction cross‐section for unit volume several orders of magnitude lower in plasmonic semiconductors than in metallic NPs, with a consequent lower capability of generating local electromagnetic field enhancement and light‐harvesting effects. Besides, non‐metallic plasmonic nanostructures were already reviewed recently.[ ¹⁹ , ²⁰ ]

The Hume‐Rothery rules identify some key parameters for the formation of alloys, ^[17] such as the difference of atomic radii (<15 % for substitutional SSs and >40 % for interstitial ones), electronegativity and valency (as close as possible) and, for substitutional SSs, the crystal structure of the pure constituents, which should be similar (Figure 3). Nonetheless, metastable alloys are possible and frequent whenever the synthetic procedure allows freezing the system in a nanophase which is a relative thermodynamic minimum. Besides, the Hume‐Rothery rules do not consider the technical problems connected to the synthesis or the stability at ambient conditions when some of the alloy elements undergo oxidation very easily. This is the main issue for most of the elements in the periodic table, which are base metals with low oxidation potentials (i. e., easy loss of electrons).

Figure 3.

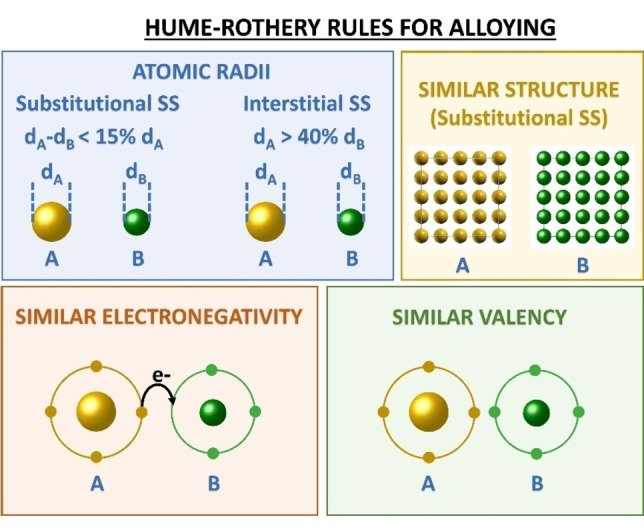
Hume‐Rothery rules prescribe that alloying depends on atomic radii, crystalline structure, electronegativity and valency of the pure elements.

In plasmonic nanostructures, the control of size, shape and surface accessibility is also crucial, because these features are relevant for most of the relevant properties in a nanoalloy (optical, photocatalytic, magnetic, hot‐carriers generation, etc.).

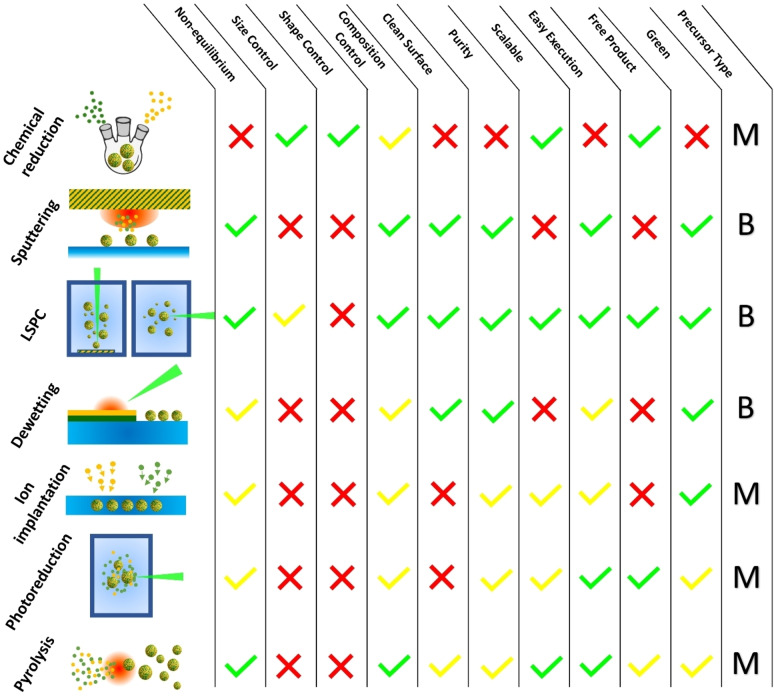
In the last decades, the advances in the synthetic routes for nanomaterials allowed tackling the challenge of obtaining new plasmonic alloys. Wet‐chemistry approaches traditionally guarantee the highest control on products in terms of composition and morphology but are limited to those metal precursors soluble in liquids and to phases at the thermodynamic equilibria. Indeed, one of the frontier topics in nanoscience is the synthesis of metastable phase alloys, requiring more drastic synthetic conditions running out‐of‐equilibrium, which may also prevent the problems of precursor solubility and different reactivity of the elements in the alloy.[ ²¹ , ²² ] This explains the prevalence of physical or hybrid physical‐chemical approaches to the top‐down and bottom‐up synthesis of plasmonic nanoalloys reported in the recent literature (Figure 4). In general, for nanoalloys the synthetic approaches can be differentiated also on several other parameters such as the reaction environment (gaseous, liquid or solid), the precursor type (bulk metal or chemical compounds such as metal salts and coordination compounds), the dispersion of final nanoalloys (powder, colloid, substrate, embedded in a solid matrix).

Figure 4.

Overview of the most frequently reported synthetic approaches for plasmonic nanoalloys and list of their advantages and limitations. “B”: bulk, “M”: molecular. For details see text.

2.1. Laser Synthesis and Processing of Colloids

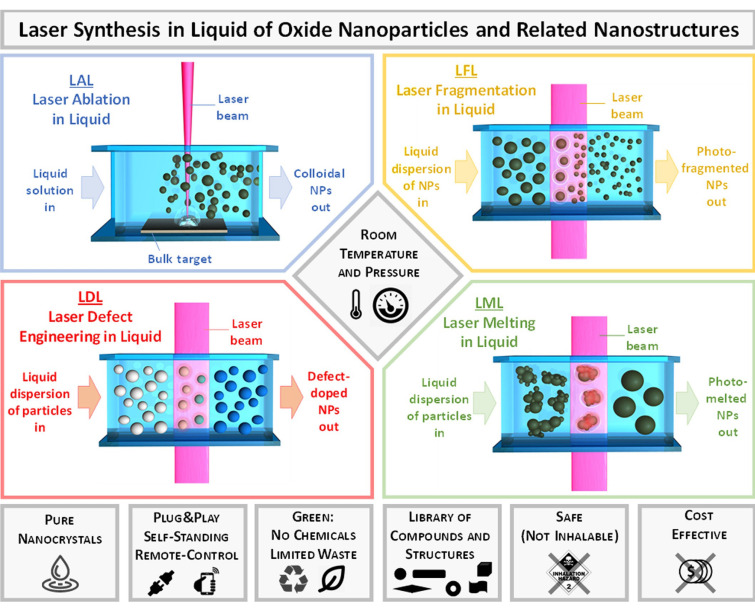
Laser‐assisted synthesis of nanomaterials in liquid phase includes a family of four different approaches described in the literature as laser ablation in liquid (LAL), laser fragmentation in liquid (LFL), laser melting in liquid (LML) and laser‐defect engineering in liquid (LDL), which are sketched in Figure 5.[ ²³ , ²⁴ , ²⁵ , ²⁶ ] These approaches are of general applicability for any phase or structure, not only alloys, such as pure metals, semiconductors, oxides, metal‐oxides core‐shells and doped oxides, all harvested as colloids, hence the definition of laser synthesis and processing of colloids (LSPC).[ ²³ , ²⁷ ]

Figure 5.

Sketch of the different methodologies in the family of LSPC and overview of their main advantages. Adapted with permission from Ref. [23] under a Creative Commons (CC‐BY 4.0) license. Copyright (2020) The Authors. Published by Wiley‐VCH Verlag GmbH & Co. KGaA.

LAL consists in the use of focused laser pulses for the ablation of a solid target immersed in a liquid solution and is a “green” technique. Currently, the variety of nanomaterials produced by this technique is high, thanks to the progress made to optimize the process. Among the advantages of LAL there are the low‐cost of the synthesis, the ease to obtain different types of NPs with the same set‐up, the speed and the simplicity of the method.[ ²³ , ²⁴ , ²⁵ ] Besides, it is possible to control the synthesis remotely, even with a PC or a smartphone. ^[28]

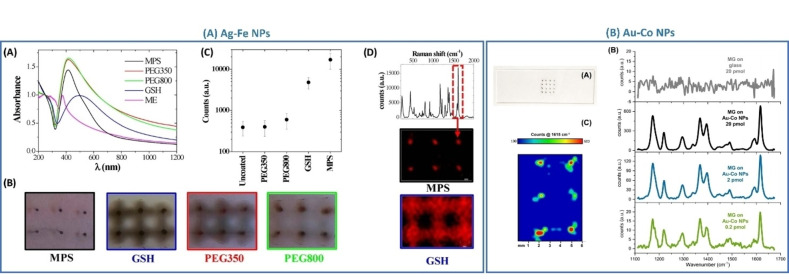
LAL proved to be useful to obtain equilibrium alloys as well as metastable phases, that have been frequently exploited for plasmonics. For instance, Au−Fe NPs were obtained by LAL and studied for the coexistence of magnetic and plasmonic properties, but also in electrocatalysis.[ ²⁹ , ³⁰ , ³¹ , ³² ] Alloying can be an advantage for the productivity of colloids by LAL. For instance, the production rate of NPs increased from 4 g/h with a pure Au target to 8 g/h with an Au/Pt 90/10 alloy target with an ultrashort‐pulsed laser and fast lateral target scanning. ^[33] It was also demonstrated with single‐pulse ns LAL experiments with Au/Fe multilayers that element mixing into homogeneous Au−Fe nanoalloys is possible during the synthesis.[ ³⁴ , ³⁵ ] On the other hand, in bulk targets the ablated volume is much larger than in the thin film experiments described in Ref. [34,35]. Recently, Waag et al. performed ps and ns laser ablation experiments on mixed metal powder targets to assess that, in bulk powder targets, the mixing of different metals prevalently takes place in the heat‐affected but initially not ablated parts of the target, instead of during material ejection. ^[36] Longer laser pulses (ns) have more extended thermal effects on the target than ps and fs pulses, favouring the formation of homogeneous nanoalloys starting from heterogeneous targets.

Recently Guadagnini et al. synthesized the Au−Co metastable random substitutional SSs in a single step using a nanosecond laser, resulting in Au₈₄Co₁₆ composition that is above the thermodynamic limit. ^[31] The obtained particles showed useful properties as substrates for surface‐enhanced Raman scattering (SERS). With the same method, Ag−Co NPs with an Ag₈₃Co₁₇ at % composition were also synthesized as a heterogeneous alloy made of an Ag matrix embedding metastable disordered Ag−Co domains. ^[37]

A similar approach was exploited by Johny et al. to obtain either Au−Co SS or core@shell (CS) Co@Au NPs. ^[38] Their work shows how the Co content in the ablation targets affects the final structure and composition of the NPs. LAL synthesis has been exploited also for the formation of Au−Fe CS NPs.[ ³⁴ , ³⁹ , ⁴⁰ ] Even in this case, a systematic study of the synthetic conditions pointed out how the liquid environment, the target composition and its structure affect the final products. By varying the laser pulse duration from ps to ns and using pre‐alloyed targets instead of multilayers of the pure metals, CS can be obtained instead of SS NPs in acetone, which is a less oxidising environment than water.[ ³⁴ , ³⁹ , ⁴⁰ ] These studies evidenced also that smaller NPs are SS, differing from the larger ones that are CS NPs. The reason is due to the dependence of the surface free energy on size, which is lower in SS with a size smaller than ca. 10 nm and in CS with a size larger than ca. 10 nm.

Johny et al. recently studied how micro‐inhomogeneities evolve in Au−Fe NPs obtained by LAL. ^[41] Structure evolution was studied by applying sufficient temperature to Au₈₀Fe₂₀ NPs to reach the thermodynamic equilibrium to facilitate the atomic mobility, while the evolution of crystallite sizes and lattice parameters were monitored in situ by x‐ray diffraction (XRD) and scanning transmission electron microscopy (STEM). At temperatures lower than 700 °C, the experiments evidenced the presence of two face‐centred cubic (fcc) phases with lower and larger lattice constant and, respectively, with larger and smaller size, suggesting the presence of a complex heterogeneous SS inside the NPs. By increasing the temperature above 700 °C, a single fcc phase and a larger crystallite size appeared with the decrease of microstrain, which is the lattice deformation resulting from local stress heterogeneity and dislocation density. The same analyses on Au₅₀Fe₅₀ NPs indicated three different fcc phases with the composition of Au₇₄Fe₂₆, Au₈₂Fe₁₈, and Au₉₆Fe₀₄ in addition to a Fe body‐centred cubic (bcc) phase. Also in this case, a single fcc phase appeared only above 700 °C, when the initial heterogeneous alloy relaxed to a more stable conformation driven by the thermodynamic driving force and temperature enhanced atomic diffusion.

Frequently, LAL is coupled with LFL for obtaining alloy NPs from the mixing of single element educt NPs. For instance, Fazio et al. produced Au−Ag NPs by synthesizing the Au and Ag colloidal NPs by LAL and, later, irradiating their mixture with different Au : Ag ratios to obtain Au₇₇Ag₂₃, Au₅₃Ag₄₇ and Au₃₄Ag₆₆ nanoalloys. ^[42] An aqueous dispersion of Ag NPs and Fe powder was irradiated with focused 1064 nm, ns laser pulses to obtain spherical Ag−Fe NPs. ^[43]

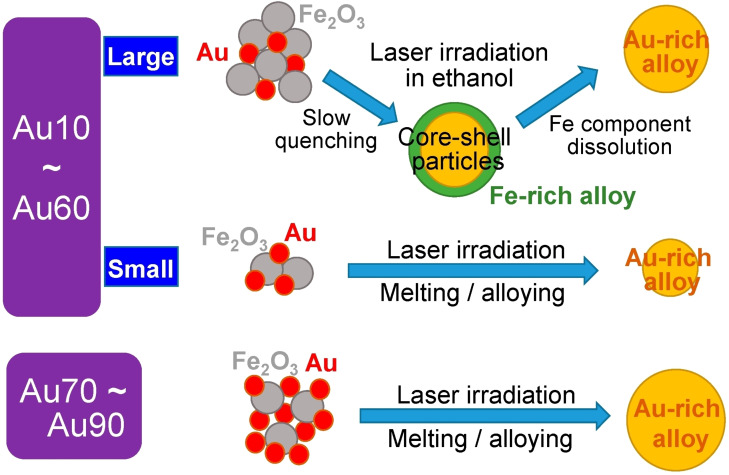
LML was exploited by Swiatkowska et al. to obtain Au−Ni metastable nanoalloys with the 56 wt% of nickel. In the LML procedure, Au−Ni NPs have been obtained by irradiating a mixture of Au and NiO NPs dispersed in a liquid, despite the Au−Ni system is difficult to obtain due to the almost complete immiscibility of the two metals. ^[44] In the same way, also Au−Fe submicrometric particles and other alloys were obtained. ^[45] The Au−Fe NPs were synthesized starting from a mixture of Au and Fe₂O₃ NPs (Figure 6). Interestingly, by changing the ratio between educt Au and Fe₂O₃ NPs, the structure of products changed. Starting with 10–60 % of Au, the largest NPs prevalently had a phase‐separated CS morphology. In the 70–90 % of Au range, all the analysed particles were compositionally homogeneous. The composition of the alloys was obtained by XRD using Vegard's law and showed a discontinuity of gold content between 20 and 70 wt% of Au in the educt, which is explained by the immiscibility gap of the Au−Fe system. For instance, in the NPs obtained from the educt with 30 wt% of Au, the gold content in the final NPs resulted in ∼75 wt%. Essentially, the NPs resulted to be gold‐rich, and a higher irradiation time corresponded to a larger content of gold.

Figure 6.

Sketch of Au−Fe NPs formation mechanism by LML for different initial gold content in the Au‐Fe₂O₃ educt nanoaggregates. For highest Au content, only alloy NPs are obtained. For low Au content, core‐shell morphologies are observed with a Fe‐rich shell. Reprinted with permission from Ref. [45] under a Creative Commons (CC‐BY 4.0) license. Copyright (2019) the Authors.

2.2. Laser‐Induced Dewetting and Inter‐Melting

As an alternative to LSPC, laser irradiation can be performed in a gas environment for the preparation of ultrapure alloy nanocrystals supported on substrates or collected as powders. The advantage of an inert gaseous environment is, however, balanced by the complex, expensive and not scalable set‐up (typically vacuum chambers) and by the collection of products as agglomerated powders or intrinsically embedded on a surface.

Dewetting requires the melting of thin metallic films to form nanodroplets on an inert substrate, which then will solidify in NPs. In specific cases, dewetting also allows the tuning of nanocrystal morphology and size.[ ⁴⁶ , ⁴⁷ , ⁴⁸ , ⁴⁹ ] Because of the high melting temperature of most metals, a laser source can be used, known as pulsed laser‐induced dewetting (PLiD). The driving force for the NPs formation is the minimization of the total free energy at the interface with gas and substrate.

Laser dewetting and laser welding have been recently exploited to generate Au−Ag,[ ⁵⁰ , ⁵¹ ] Au−Fe, ^[45] Ag‐Ni ^[52] Ag−Co/Fe ^[53] and Au‐Ni ^[44] nanoalloys. Au−Ag nanoalloys with different compositions were obtained by laser dewetting of Au/Ag thin films with various relative thicknesses of the two layers. ^[50] TEM elemental analysis confirmed that the NPs are Ag−Au alloys, with two elements well mixed over the whole volume of the particle. The fact that bimetallic alloys were produced with a single 6 ns laser pulse suggested that Ag and Au atoms are intermixed in the liquid phase on a nanosecond time scale.

Production of Ag−Ni magnetic‐plasmonic NPs by laser dewetting was studied starting from Ag and Ni thin films. ^[52] The system is interesting because the two metals have limited miscibility in the liquid and solid phases, lower than Au−Ni. Immiscibility across a large temperature and compositional range is expected to facilitate the emergence of complex particle morphologies during the liquid phase dewetting process. In fact, by acting on the initial film geometry, substrate, and laser heating conditions, various particle architectures were achieved, including Janus, core‐shell and homogeneous SS NPs. Ag and Ni were co‐sputtered at a 1 : 1 ratio and the thin films were exposed to 20 ns laser pulses to induce liquid‐state dewetting, observing a correlation of the final NPs size distribution to the as‐deposited film thickness. Starting from an initial thickness of 20, 10, 5, 3, and 2 nm, predominantly Janus NPs with an average size of, respectively, 300, 180, 45, 20 and 8 nm were obtained. Again by laser‐dewetting, Sachan and co. obtained ferromagnetic plasmonic NPs made of Ag and Co or Co−Fe (8 % of Fe) heterostructures. ^[53]

In a similar approach, a laser source can be exploited to weld single element metallic NPs already present on a substrate, to form an alloy, in a process called “laser welding”. In the case of adjacent plasmonic NPs, the “hot spot” effect is possible by using a laser beam resonant and polarized according to the plasmon mode oscillating along the dimer axis. Hence, the plasmonic NPs can be preferentially heated at the interparticle gap, resulting in a higher welding efficiency compared with the uniform thermal welding. Xu et al. made a thorough study for a better understanding of the laser welding process in the case of Au−Ag NPs. ^[51] They applied ultrafast TEM measurement in situ during the laser welding experiment on a dimer of Au and Ag NPs, to visualize the alloy formation. This evidenced that the Ag NPs shrink while Au NPs became larger, due to the inter‐diffusion between the two NPs. From the direct visualization of the process at different pulse number and time, the formation of Au−Ag NPs was divided into different stages: (i) neck formation, (ii) Ag shell formation, (iii) Au‐rich shell formation, (iv) alloy dimer formation and (v) homogeneous alloy NP formation. The neck formation is favoured by the localized heating at the inter‐particle gap, while the neck size increases with surface diffusion due to the minimization of the surface energy in heated NPs.

2.3. Sputtering, Dewetting and Arc‐Discharge

Sputtering is one of the most popular and versatile approaches for achieving nanoalloys on a substrate by a physical top‐down route and produces highly pure nanocrystals. As shown, for instance, by Nguyen and co. with Au−Ag alloys, ^[54] the composition can be controlled by co‐sputtering two (or more) targets to obtain NPs with different stoichiometry. By acting on the sputtering current of each target, they obtained Au−Ag NPs with five different compositions in gold from 25 to 33, 60, 66 and 75 % as well as Au−Cu NPs with different compositions in a range from Au₆₆Cu₃₄ to Au₂₉Cu₇₁. ^[55]

Suzuki et al. instead, used the sputter deposition from a unique bimetallic target to obtain Au−Cu NPs. ^[56] The purpose was the control over the order‐disorder transition between the fcc phase and the L1₀ structure of the Au−Cu system, which have different mechanical, catalytic and plasmonic properties. The same synthetic approach was successfully tested on Au−Pt NPs. ^[57]

Pd−Au is another system frequently investigated for catalytic purposes, also by sequential sputter deposition.[ ⁵⁸ , ⁵⁹ ] Cai's group exploited the sputtering deposition to control the Pd−Au ratio in ternary alloys of Au, Pd and Pt to obtain electrocatalytic systems with different performances. ^[60]

Vahl et al. suggested a novel approach for the fabrication of alloy NPs with variable composition and better size control by introducing a custom‐made multicomponent target for magnetron sputtering in a Haberland type gas aggregation cluster source. This type of source combines magnetron sputtering with gas cluster aggregation. ^[61] From their results for Au−Ag NPs, they show that the composition and size depend on the pressure of the gas agglomerate source and demonstrate for gold‐rich NPs that the composition can be adjusted in‐operando.

In some cases, high temperature is exploited to promote dewetting of the sputtered thin film and the formation of NPs. Heat‐induced dewetting of a co‐sputtered Ag−Au‐Cu film was devised for the identification of crystalline and grain border defectivity when the three elements are homogeneously distributed in the NPs (Au₅₃Ag₃₃Cu₁₄) or when the high Cu content promotes element segregation (Au₂₂Ag₂₆Cu₅₂). ^[62]

Sputtering can be performed also on liquid substrates and, indeed, lots of progresses have been made to obtain high‐quality NPs with this method. The advantages are the combination of a physical top‐down technique to produce highly pure nanocrystals NCs with the chemical methods to capture, stabilize, control the size and surface functionalize NPs in the liquid medium, similar to the synthesis of a colloid. Moreover, because there is no necessity of using toxic reducing agents and organic solvents, the method can be considered as a green approach to generate NPs in liquids. ^[63] Nguyen et al. exploited this technique for alloy and core‐shell NPs such as Ag−Au,[ ⁵⁴ , ⁶¹ ] Au−Cu,[ ⁵⁵ , ⁵⁶ ] Pd−Au/Pt, ^[60] Pt−Au, ^[57] Pd−Au.[ ⁵⁸ , ⁵⁹ ]

Another method compatible with the production of nanoalloys as a colloid or a powder is the arc discharge. In this technique, the metal composing the electrode is etched by the plasma formed in the surrounding environment (gaseous or liquid) upon application of high electric potential and consequent electric discharge.[ ⁶⁴ , ⁶⁵ ] The NPs will have the composition of the electrode and is thus variable in a wide range, as demonstrated recently in a vacuum chamber for the synthesis of Au−Ag nanoalloys. ^[65]

2.4. Wet Chemistry and Other Methods from Chemical Precursors in Liquid or Gas Environment

Most synthetic methods for plasmonic nanoalloys start from chemical precursors of the metal elements which are converted into alloys in a liquid or gaseous environment. The transformation into the solid‐state is triggered by other chemical compounds, such as a reducing agent, or by a physical process such as heat or laser irradiation.

The most widely used method to produce metal (alloy) NPs consists of the chemical reduction of metal salts in liquid environment. When metal elements are prone to oxidation, organic liquids under an inert atmosphere are required. These wet‐chemistry methods have unmatched control on size, stoichiometry and shape of nanocrystals, but run under thermodynamic equilibrium, meaning that the largest part of plasmonic nanoalloys is inaccessible. Besides, surface stabilizers are required, which in most cases remain on the surface of nanocrystals affecting their properties, primarily the (photo)catalytic ones. There are several examples of alloy NPs obtained by this approach. For instance, with the co‐reduction method, Cu/Au/Pt trimetallic NPs (TMNPs) were synthesized from HAuCl₄, CuSO₄ and K₂PtCl₄ with the addition of NaBH₄ at room temperature. ^[66] The Cu/Au/Pt TMNPs had an irregular shape and an average size of ∼10 nm, although the three elements were uniformly distributed. Co‐reduction is well suited for the deposition of alloy nanocrystals on substrates such as fibers, as demonstrated with Cu−Ag NPs obtained by immersion of electrospun hydrogels in a solution containing both CuSO₄ and AgNO₃ and addition of NaBH₄. ^[67]

Often, the seeded growth technique is exploited, in which the alloy is formed on pre‐existing metal seeds which facilitate the control over shape and size. Au−Pd nanostructures have been synthesized starting from Au nanorods (NRs) made by the seed‐mediated method and, subsequently, the Pd was added in different concentrations to change the resulting NRs morphology. ^[68] Almost the same approach has been exploited by Rioux and Meunier to produce Au@Au−Ag NPs. ^[69]

With the seed‐mediated process, Ma et al. succeeded in obtaining NPs with an external crystalline Au layer which stabilized the internal Au−Cu alloy and Cu core against oxidation in water. ^[70] Cu NPs were first prepared as seeds by the thermal decomposition of copper acetylacetonate in oleylamine and then mixed with the Au³⁺ precursor, to replace the Cu atoms on the surface with Au through a galvanic replacement process. This led to a thin shell composed of an intermediate Au−Cu layer and an outer Au layer around the Cu core.

The inverse process, starting from Au seeds and proceeding with the co‐reduction of Au and Cu precursors, was exploited for the synthesis of Au−Cu alloy nanotetrapods unstable towards corrosion in an aqueous environment. ^[71] The 3 nm Au seeds were added into an aqueous solution containing HAuCl₄ and CuCl₂ with glucose and hexadecylamine as, respectively, reducing and stabilizing agents, with subsequent heating to 100 °C under a nitrogen atmosphere.

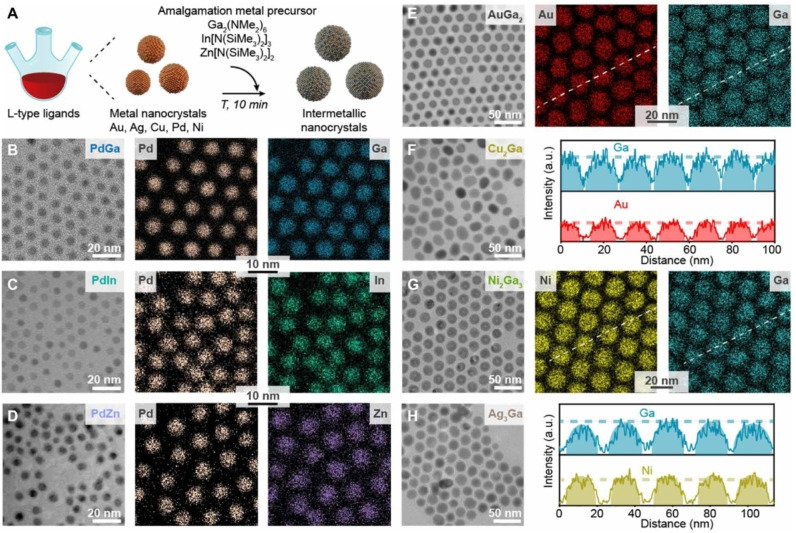
Recently, Clarysse et al. developed the amalgamation seeded growth synthesis to achieve intermetallic NPs. ^[72] They coupled the seed‐assisted synthesis with a controlled amalgamation of low melting point metals to produce nanocrystal with controlled size and composition. Amalgamation is referred to the process in which a low melting‐point metal inter‐dissolves inside the lattice of a solid host metal. With this method, Ga was amalgamated with Au, Ag, Cu, Pd, and Ni seeds. Besides, In and Zn were used to form Pd−In and Pd−Zn NCs. A remarkable advantage of this approach is that all the obtained intermetallic nanocrystals resulted in uniform size and composition, although structural homogeneity was not optimal for all the combinations tested (Figure 7). The control in the average composition is directly related to the concentration of the metallic precursors. For instance, by varying the concentration of Ga precursors, various intermetallic NPs like AuGa₂, AuGa, Au₇Ga₂ or Ga‐doped Au were obtained as prevalent products.

Figure 7.

(A) Illustration of the amalgamation reaction, converting monometallic seeds into intermetallic NCs. As‐synthesized PdGa, PdIn, PdZn, AuGa₂, Cu₂Ga, Ni₂Ga₃, and Ag₃Ga intermetallic NPs are shown in TEM images (B to H) and STEM EDX maps (B to E and G). Line profile scans for AuGa₂ and Ni₂Ga₃ NPs (E and G) highlight the compositional uniformity of the intermetallic NPs. Reprinted with permission from Ref. [72] under a Creative Commons (BY‐NC 4.0) license. Copyright (2021) the Authors, some rights reserved; exclusive licensee American Association for the Advancement of Science.

An alternative wet method for the formation of plasmonic nanoalloys has been demonstrated for a liquid Ga metal alloy by ultrasonication. ^[73] A bulk Ga−In liquid metal has been prepared mixing pure Ga and In at 75/25 wt% and a droplet of this is then transferred in a vial, diluted in ethanol and sonicated obtaining Ga−In NPs stabilized by a Ga₂O₃ shell.

Another recent synthetic approach exploits the supercritical carbon dioxide as dispersing medium for the so‐called supercritical reactive metallization, or supercritical fluid reactive deposition. This is a bottom‐up method that offers scalability in environmentally friendly conditions. ^[74] With this technique, it is possible to obtain monometallic NPs, thin films or alloys such as Au−Ag, ^[75] Cu−Ag, ^[76] Pd−Pt, ^[77] Fe−Ni, ^[77] Au−Pt, ^[78] and Au‐Pd ^[78] NPs.

Hydrothermal routes are being studied for the realization of plasmonic nanoalloys, such as Au−Ag NPs, through the reduction of metal salts at high temperature and pressure in the presence of green reducing agents. ^[79]

More violent methods starting from chemical precursors can produce also non‐equilibrium and disordered alloys. For instance, Yao and co. developed a two‐step synthesis for high entropy alloy (HEA) NPs with carbothermal shock. ^[80] The carbothermal shock employs flash heating and cooling of metal precursors supported on oxygenated carbon fibers to produce binary (Pt−Ni, Au−Cu, and Fe−Ni), and ternary (Pt−Pd−Ni, Au−Cu‐Sn, and Fe−Co−Ni) NPs with compositional uniformity typical of a SS. Furthermore, by adding other metal salt precursors they synthesized quinary (Pt−Co−Ni−Fe−Cu and Pt−Pd−Co−Ni−Fe), senary (Pt−Co−Ni−Fe−Cu−Au), septenary (Pt−Pd−Co−Ni−Fe−Cu−Au) and octonary (Pt−Pd−Co−Ni−Fe−Cu−Au−Sn) SSs of HEA NPs. Compared to other techniques for the synthesis of HEA NPs, such as LAL, ^[81] carbothermal shock does not require a bulk HEA target but just a mixture of metal precursors.

Photoreduction of metal salts has been intensely investigated in recent years with a multitude of variants. The most traditional technique is the laser spray pyrolysis and its variants such as thermal spray pyrolysis and flame spray pyrolysis, which allows massive production of agglomerated NPs, also with non‐equilibrium composition, collected on a substrate or in a liquid. In the spray pyrolysis, the liquid mixture of metal precursors is reduced by irradiation with an intense laser beam, heat or by contact of the solution with a flame, eventually with the addition of reducing chemicals or hydrogen, as demonstrated with Au−Ag and Ag−Cu NPs.[ ⁸² , ⁸³ ]

Photoreduction of metal salt precursors can take place in standard laboratory set‐up by irradiation with a xenon lamp, as demonstrated with Au−Pt nanoalloys supported on Bi₂O₃ NPs, ^[84] or by irradiation with pulsed lasers to collect a colloid, such as Au−Ag NPs, ^[85] or a film of NPs on a substrate, such as Au−Ag−Pt NPs on glass. ^[86] This is possible by the formation of hydrated electrons produced in the laser plasma and the simultaneous addition of scavengers of hydroxyl ions such as isopropyl alcohol.

A special method to produce nanoalloys from metal ions is ion implantation, in which the ionized atoms are accelerated by an electric field up to the kinetic energy required for the penetration in a solid matrix. In the matrix, the NPs can nucleate already during the implantation process or successively, by thermal activation which also serves for annealing and particles growth. Although the final NPs are embedded in a solid matrix, historically this method proved to be useful for the realization and the study of alloys not easily achievable by other synthetic approaches, such as the Au−Fe NPs, ^[87] or in matrices which are otherwise difficult to be loaded with NPs, such as Au−Ag NPs in TiN films. ^[88]

3. Modelling

A comprehensive understanding of the electronic and structural properties, as well as the optical behaviour of nanoalloys, is fundamental to enlarge the number of possible applications and direct the synthesis to optimized systems among all the possibilities available. ^[13] On the other hand, the variety and structural complexity of nanoalloys pose great challenges also for modelling, in particular when dealing with the most heterogeneous and disordered systems.

The large range of structures and properties of nanoalloys is usually managed exploiting different approaches, where the most suited one must be chosen considering the complexity of the system and the property to be computed. In fact, the choice of a suitable computational approach is a short blanket dilemma. Predictive, high‐quality approaches, able to provide accurate properties (optical, magnetic, catalytic, etc.), are limited to simple models of the real systems, thus neglecting defects, segregation, grain boundaries, etc. Only approximate methods, conversely, can be applied to accurate models of complex systems. This picture becomes even more challenging when the complexity of the nanoalloy is coupled with its structural evolution during operation, especially at the interface with the environment, where phenomena such as surface segregation of some elements, changes of the oxidation state, dealloying, corrosion, etc. are crucial to explain the behaviour of the nanoalloy during its function.

The computational methods employed in this field can be grouped into two families: quantum‐mechanics approaches, where electrons are treated explicitly, and parametric methods, where the interaction between atoms are described through a series of parameters.

Quantum methods exploited in the modelling of NPs are mostly implemented within the density functional theory (DFT). In this context, the energy of the system is computed over electron states and the electron‐electron interaction is approximated as a local functional of the electron density (and derived quantities). A key parameter of DFT is the type of functional adopted to describe the electron density.

Ab‐Initio molecular dynamics (AIMD) is rarely exploited in this context, but molecular dynamics, its parametric counterpart where interatomic interactions are modelled through classical potentials, is routinely used. Parameterized energy contributions are used also in statistical approaches such as Monte Carlo (MC), which allows the exploration of equilibrium properties, and kinetic MC (kMC), which is used to model dynamic processes. For an introduction to the methodologies mentioned above, we refer the reader to Ref. [89].

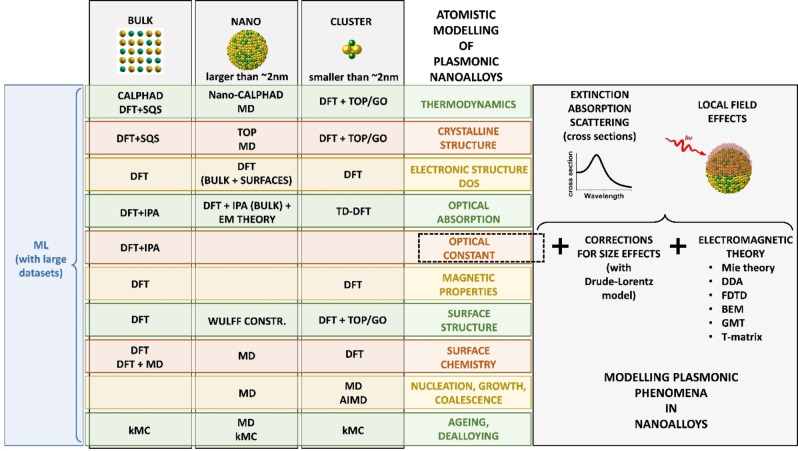
From the nanoparticle size perspective, very small systems can be modelled as clusters using DFT (Figure 8). Large nanoparticles can be treated explicitly only with MD or MC because the application of DFT to systems with many electrons is computationally unfeasible. On the other hand, DFT can be exploited also in the modelling of large NPs, provided that the property of interest can be derived from separate calculations on the bulk and the surfaces. As an example, nanocrystals equilibrium shapes can be devised using the Wulff construction, namely a method for the determination of the equilibrium shape of a crystal from surface energies (which can be conveniently obtained from DFT calculations). Of course, not all the properties are accessible by both families of methods. DFT is best suited to investigate electronic properties such as reactivity, magnetism and optical response, the latter requiring the evaluation of electronic excitations, usually performed within the independent particle approximation (IPA) or the time‐dependent DFT (TD‐DFT).

Figure 8.

Map of mainstream atomistic modelling approaches for specific aspects of plasmonic nanoalloys. Modelling of the plasmonic properties is possible starting from the optical constant. For details see text.

MD is the method of choice to inquire dynamic properties happening at the time‐scale of μs, such as coalescence and NPs formation. Phenomena happening at a longer time scale and involving activated processes, such as its structural evolution during operation, can be faced using kMC methods. MD and MC are used also to obtain equilibrium structures at finite temperatures and to predict the evolution path of alloy NPs towards their thermodynamically stable form.

In the last few years, applications of machine learning (ML) to the study of alloy NPs are also becoming popular. Within this approach, the output of a very complex function is modelled using a ML algorithm, that must be trained over a large dataset of known outputs obtained from either experiments or calculations. ML promises to be very flexible, as it can be trained to provide the desired output, which can be a fundamental property such as the interatomic interaction to be used in MD ^[90] or a complex observable of the systems. ^[91]

3.1. Modelling of Structure and Electronic Properties of Plasmonic Nanoalloys

The stability of an alloy is typically extracted from experimental phase diagrams, which are tabled for most binary and ternary systems. Even if accessible, however, phase diagrams do not usually contain information on all the metastable phases and do not take into account nanoscale effects related to the increased surface‐area‐atoms‐to‐volume‐atoms, sometimes leading to deviations from the bulk behaviour.

A thermodynamic method called CALculation of PHAse Diagrams (CALPHAD) has been developed and intensely investigated to infer the phase diagrams of multicomponent bulk systems. ^[92] CALPHAD is based on the bulk Gibbs energies as a function of state variables which are obtained with accurate thermodynamic models and appropriate interpolations and extrapolation of experimentally available quantities. Especially for ternary and multicomponent systems, the measured phase diagrams are needed for validation of the method. CALPHAD neglects any surface or interfaces interaction between the phases, which are relevant at the nanoscale below 100 nm and are considered in the nano‐CALPHAD (Calculation of Phase Diagrams for nano‐systems) model by including an additional surface term to the Gibbs free energy of the system. This method is formally valid above the size threshold where surface topology and quantum effects become important, that is below 3–5 nm.[ ⁹² , ⁹³ ]

Concerning atomistic approaches, Gong et al. used DFT calculations of Au−Ag alloys to explain the experimental LSP energy shift with composition. ^[94] The valence band evidenced a clear shift of the d‐band position by varying the chemical composition of the Au−Ag alloy. By increasing the Au fraction, the d‐band moves closer to the Fermi level at the Γ‐point, with a consequent decrease of the energy difference with the first empty state in the conduction band. This finding agrees with the red‐shift of the interband transition of Ag−Au alloys when the Au content increases.

Koley and Jana performed DFT calculations to explore the phase stability of Au₃Cd₅ and Au₃Mg₅. ^[95] They discuss the alloys stability based on their density of states (DOS) and their crystal orbital Hamiltonian populations (COHP), a quantity providing the bonding, nonbonding and antibonding character of each band. The negative integrated COHP up to the Fermi level deliver information on the energy stabilization of the material, due to orbital interactions. The analysis of computational outcomes pointed out that the major contribution to the stabilization is given from the M−M (M=Mg and Cd) and Au−M interactions rather than the Au−Au ones. Moreover, they deduced that the structures are stabilized through the interaction between the Fermi surface and the Brillouin zone through a Hume‐Rothery mechanism. The observed behaviour is thus consistent with that of Hume‐Rothery phases (also called “electron phases”), which are alloys of noble metals with sp‐valent elements such as Al, Zn, Si, Ge and Sn and are renowned for the adoption of a different crystal structure depending on the average number of valence electrons per atom (the valence electron concentration or VEC). ^[96]

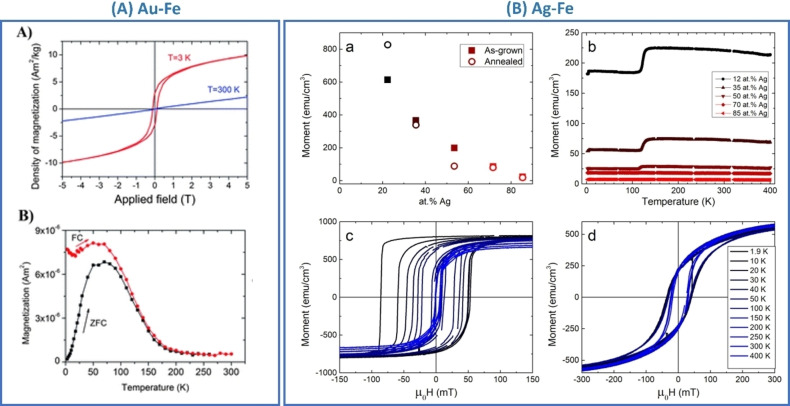
Alsalmi et al. ^[97] explored the phase stability in the formation of high‐temperature bcc phases of Zn alloys of the coinage metal group elements Au−Zn, Ag−Zn, and Cu−Zn. They exploited DFT calculations implemented in the VASP package. To evaluate the phase stability, the chemical and elastic formation energies have been calculated, as well the charge density distribution and the DOS. Results show that the trends are not always monotonic down the 11^th group of the periodic table. The strength of the X−Zn bond decreases on passing from Cu to Ag, but then increases to its largest value for Au. The reason for this behaviour was identified in the trends of atomic‐core sizes and spatial extents of valence d‐orbitals, both increasing down the group. The effect of the first is that of increasing the repulsion between neighbouring atoms, thus pulling them apart and reducing their orbital interaction, while that of the latter is the opposite. The competing effects of these factors lead to the mentioned overall trend of the bond strength (Figure 9). Interestingly, this same mechanism could explain also the larger mixing enthalpy calculated for Ag−Fe and Ag−Co alloys compared to Au−Fe, in agreement with the experimental phase diagrams. ^[37]

Figure 9.

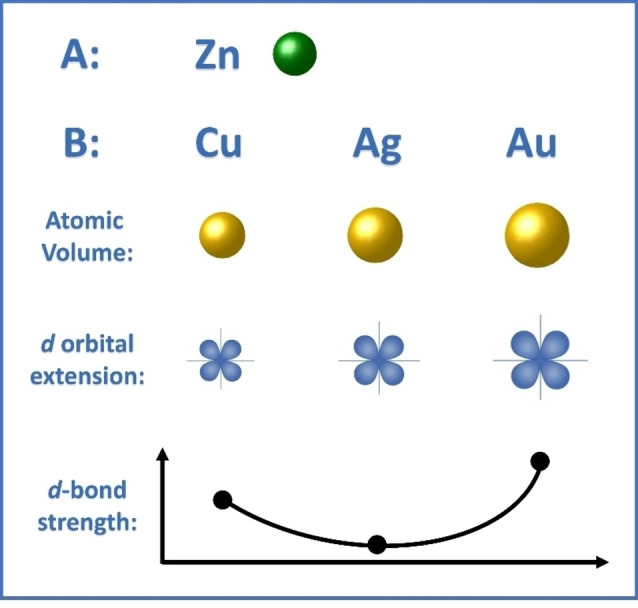
Sketch of atomic volume and d‐orbital extension for the coinage metals Cu, Ag and Au and the effect on d‐bond strength in alloys with Zn, according to Ref. [97]. The minimum is predicted for Ag−Zn alloys because of the worst compromise between atomic volume (which destabilize d‐bond formation) and d‐orbital extension (which favours d orbital hybridization).

Structure optimization and the knowledge of the electronic structure helped Alexander et al. to describe the plasmonic properties of Au−Fe nanoalloys. ^[40] DFT calculations were performed within a plane‐wave/pseudopotential approach as implemented in the Quantum‐ESPRESSO suite. The contraction of the lattice parameter with the iron content, observed experimentally in multiple cases, ^[29] was well predicted from calculations and, with the shift of the Fermi level, allowed the estimation of the increase of conduction electron density in the alloy compared to pure gold. It was estimated that the Fe atoms contribute with 1.3 electrons in the fcc cell of the alloy, and this affected the LSP peak position causing a blue shift.

Au−Fe chemical stability in an aqueous environment was investigated by DFT calculations in Ref. [98]. The estimation of Gibbs free energies of the iron oxidation at the surface, as a function of the Fe concentration, confirmed that Fe readily reacts with adsorbed water molecules or dissolved atmospheric oxygen. This leads to oxidized iron species that can be easily dissolved in solution, similar to what is found in pure metallic iron. It was also showed that the energy barriers for the diffusion of Au, Fe, and O atomic species towards the alloy bulk, computed using the climbing‐image nudged elastic band (CINEB) method, are too high to allow atomic mobility at room temperature. These results explained the stability of Au−Fe alloys as a function of composition: Au‐rich nanoalloys are stable because they are passivated by an Au skin, while in alloys with a Fe concentration above a certain threshold, oxidation can proceed by pitting due to the appearance of percolation paths. In thermodynamically stable alloys, such as Au−Ag, such percolation paths are observed around 50 at % of the less noble element. ^[99] Conversely, in the Au−Fe system, whose mixing enthalpy is positive, the estimated threshold for the appearance of percolation paths can be much lower. Hence, a MC algorithm was exploited to simulate the distribution of Fe atoms in an Au−Fe slab where segregation was allowed, indicating that percolation appeared in 100 % of the considered structures already at Fe contents of 30–40 at %. This is due to the thermodynamic tendency to element segregation and phase separation into pure Au and Fe domains, which is inhibited at room temperature only because of the high diffusion barriers inside the metal lattice.

Atomistic models require a precise structure as input, which is usually unavailable. This problem must be faced in the modelling of bulk phases, surfaces, as well as whole nanoparticles, and affects in particular DFT but also MD methods. Different schemes were proposed to overcome this limitation. The simplest one consists in building a limited series of alloy models using chemical intuition and possibly available experimental evidence. ^[100] A more efficient approach, that can be exploited in DFT calculations of bulk phases, is the special quasirandom structure (SQS). This approach was introduced in the 90’s by Zunger et al. to describe the properties of wholly random crystalline systems. ^[101] SQSs are small models of an alloy, where elements occupy precise crystal sites, but the periodic structure mimics the long‐range correlation function of a real random alloy. SQSs were successfully employed in the calculation of structural and elastic properties, ^[102] as well as electronic structures. ^[103]

When modelling the whole NP instead of a single unit cell, optimal structures can be obtained with the topological approach (TOP) developed by Kozlov et al. in 2015. ^[104] The TOP allows the exploration of the chemical ordering of surface sites (facets, edges and corners) for each type of element. The method shows an accuracy comparable to DFT also for relatively large NPs. In fact, the TOP was developed to overcome the limitations of the DFT alone, which is computationally cumbersome for particles composed of hundreds of atoms and thousands of electrons. Given a certain composition and shape, the number of not‐equivalent arrangements of atoms (homotops) is of the order of 10⁵⁰ for ∼200 atoms. The TOP deals with such a large number of homotops by categorizing them into classes where elements have the same local topology, and then computing the topological energy for each class. For example, the reactivity of NPs depends on their surface, therefore homotops can be grouped in terms of their exposed surface, which means the site occupancy (facets, edges and corners) of each element and the number of homoatomic or heteroatomic bonds. The topological energy could be resumed as the sum of energy contributions of the site occupancy and the interatomic bonds.

Vega et al. studied the reactivity of Pt−Au, Pt−Ag and Pt−Cu NPs using a topological approach based on preliminary DFT calculations. ^[105] The topological energy was estimated from DFT calculations on a limited set of homotops and MC simulations were then used to extract the most stable structures, which were finally further optimized by DFT. Their analysis revealed that gold tends to reach the surface and create a shell in small Au−Pt NPs (201 atoms) when the Au : Pt ratio is 3 : 1. When the percentage of gold is decreased to 1 : 1 and 1 : 3, an incomplete shell is formed, due to the insufficient amount of gold. Similar behaviour was found for Pt−Ag, while Pt−Cu behaves differently. Despite Cu surface energy being lower than that of Pt, in Pt−Cu 3 : 1 NPs the outer layer is composed mostly of Pt because the smaller size of Cu atoms destabilizes the surface in small NPs. The analysis was extended also to larger alloy particles of ∼4.4 nm (1463 atoms) and the effect of temperature on the chemical ordering. In Pt−Au and Pt−Ag the core‐shell geometry is preferred, with the shell composed by Au and Ag respectively. Instead, Pt−Cu NPs expose only a small amount of Cu at the surface, preferably located at edges and corners. Increasing the temperature, only a few atoms of Pt reach the surface in the case of Pt−Au and Pt−Ag. Conversely, in Pt−Cu NPs, the rearrangement is more evident: the outer layer exposes more Cu atoms scattered over Pt atoms in the facets, and the bulk is composed of randomly distributed atoms of both metals.

The TOP has been applied to several other alloys and sizes as Ag−Pt clusters with 116 and 201 atoms, ^[106] Pd−Au, ^[107] Pd−Au (201 and 405 atoms), Pd−Ag (201 and 405 atoms) and Pt−Au (201 and 405 atoms). ^[108]

Rapetti and Ferrando investigated the chemical ordering in Au−Ag clusters with fixed geometry using a global optimization (GO) algorithm based on DFT energies. ^[109] Despite the lower cohesion and surface energy of Ag, computational outcomes show that Au tends to occupy surface sites. To explain this counterintuitive behaviour, electrostatics must be considered. Au atoms acquire a negative charge, become bigger, and therefore are preferentially placed at the surface. Authors point out that charge transfers are often neglected in MD, and in some cases, this can lead to qualitative errors in MD predictions.

An example of the MD approach combined with MC simulations is found in the report of Andreazza et al. The study started from the experimental growth of Co−Ag NPs by depositing Co atoms on Ag seeds, which was followed in real‐time by grazing incidence x‐ray scattering at small and wide angles (GISAXS and GIWAXS). Then, MC was exploited to obtain equilibrium structures of the NPs, while MD was used to study the growth process. ^[110] Combining GISAXS, GIWAXS, MD and MC outcomes, it was shown that Co@Ag structures finally form, but the growth process is quite complex. The sequence starts with the incorporation of single Co atoms in the subsurface of the Ag seed. As the deposition proceeds, Co atoms in the subsurface act as traps for newly deposited Co units, due to the strong Co−Co interaction. Aggregates then grow and eventually merge, giving rise to a quasi‐Janus asymmetric structure. The NPs then reaches their equilibrium Ag@Co morphology when their atomic composition is 70 % Co. Proceeding further with the deposition, the structure becomes Co@Ag in the Co‐rich limit.

Nelli and Ferrando exploited MD and GO to shed light on the Au−Co, Ag−Ni, and Ag−Cu NPs evolution towards equilibrium. ^[111] All systems were made of metals with low bulk miscibility and high lattice mismatch. Particles of general formula X₂₉₃Y₂₉₃ having a truncated octahedral (TO) geometry and an Icosahedral (Ih) Ag₂₈₀Cu₂₈₁ structure were studied. The composition was such to allow the formation of a complete monolayer thick shell. In all cases, the global minimum was a CS particle with the noblest element as a shell, while some differences in the final shape were found. Overall, the authors confirm a complex evolution path of random alloy NPs towards their equilibrium structure, in some cases involving the formation of core@shell@shell forms, that can be possibly synthesized as metastable, kinetically trapped species.

3.2. Modelling the Optical Constants of Plasmonic Nanoalloys

In the last years, many DFT calculations have been carried out to obtain the optical constants (OC) of nanoalloys. This is particularly relevant in plasmonics due to the lack of experimentally measured optical constants for a variety of alloys, especially in certain compositions that are difficult to obtain in conventional laboratory conditions. The measurement of the OCs is done by ellipsometry on thin films, which is critically influenced by surface roughness, chemical homogeneity and chemical composition. These are relevant issues in the case of metastable phases and elements prone to oxidation but also for pure element films, even in ultra‐high vacuum conditions.[ ¹¹² , ¹¹³ ]

Recently, Bubas and Parramon proposed an approach based on the GLLB‐SC functionals to calculate the OCs of Au−Ag, Au−Cu, Ag−Cu and Pd−Au systems, which represent a satisfactory compromise between computational cost, efficiency and accuracy. ^[114] They used the GPAW package, based on the projector augmented wave (PAW) method, and chose the GBLL‐SC functional because of its computational efficiency and the better treatment of d‐band electrons compared to other GGA functionals. They computed the OCs of bulk alloy (Au−Ag, Au−Cu, Ag−Cu, Pd−Au) systems and monometallic equivalents within the independent‐particle approximation (IPA) and compared the results obtained with LDA, PBE (and its revisions), vdW‐DF and GLLB‐SC to the experimental reference. The GLLB‐SC functional showed overall the best performance among the others considered there, most notably it provided the best results concerning the interband transitions (IB) onset, which is particularly relevant for the LSP spectral position.

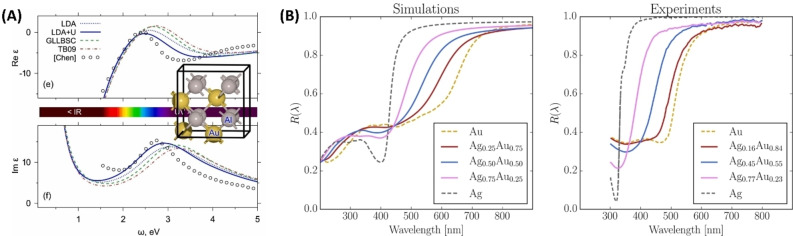
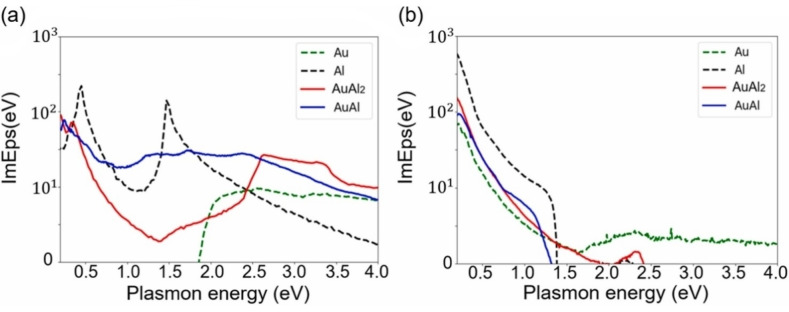
Avakyan et al. used LDA, LDA+U, GLLB‐SC and TB09 functionals to calculate the OCs of Au, Ag, Al and Mg and their alloys Au−Ag, Au‐Al₂ and Mg−Au, also within the IPA as implemented in GPAW. ^[115] They found out that LDA+U outperforms GLLB‐SC (Figure 10A), provided that it is fed with the proper values of the U parameter. The weakness and strength of LDA+U is indeed the presence of the U parameter that, on one side requires a considerable effort to pick the correct value, but on the other side allows to fine‐tune the results to match the experiment. The TB09 functional turned out to be very precise for reproducing OCs in Ag systems, however, compared to LDA+U it failed in reproducing the crystal structure and in general the ground state properties of the system.

Figure 10.

(A) Comparison of the dielectric functions calculated for AuAl₂ with different functionals and experimental data (open circles). Reprinted from Ref. [115], Copyright (2020), with permission from Elsevier. (B) Comparison between calculated (PBE functional) and experimental reflectivity spectra for various Ag−Au alloys. Reprinted with permission from Ref. [116] under a Creative Commons (CC‐BY 4.0) license. Copyright (2020), The Author(s).

Prandini et al. used the PBE functional to obtain the electronic structures for Au, Cu, Ag and the mixed alloys (Au−Ag, Au−Cu, Ag−Cu, Au−Cu−Ag). They exploited the IPA to calculate the OCs of these systems and other intermetallic compounds as AuAl₂, AuIn₂ and AuGa₂ (Figure 10B) to simulate the colour of these metals. ^[116] The comparison between the calculated and experimental reflectivity of Au−Ag alloys showed that the IPA simulation reproduced well the shift of the reflectivity to a longer wavelength with the increase in the gold content. Calculations successfully reproduced the trends in reflectivity, but the reflectivity edge was found to be systematically shifted to larger wavelengths compared to experiments. This bias is due to the underlying PBE functional, indeed semi‐local functionals are well‐known to overestimate the energy of d‐bands, thus shrinking the gap between valence d‐bands and conduction sp‐bands. ^[117] Nevertheless, this approach is useful for a systematic study for the photorealistic simulation of metal alloy surfaces and was tested also for AgCu, AuAl₂, AuGa₂, and AuIn₂.

Shahcheraghi et al. combined both experimental and DFT results to study the Cu−Al system (Al 15 at %). ^[118] They used the linearized augmented plane wave plus local orbital (LPAW+lo) method, as implemented in wien2k, alongside the PBE functional. To calculate the dielectric function, they exploit the random phase approximation (RPA) considering the polarizability of the system as a sum over independent transitions not considering the local field effects (LFE). Hence, they checked the quality of the calculated OCs against the ones measured via ellipsometry. Despite the general trend resulting similar, the calculated OC had an absorption edge shifted of 0.53 eV (180 nm) and the optical losses defined from the imaginary part of the OC were 2 units larger than in the experiment. The calculated OCs were used to simulate the reflectance measurement with results in qualitative agreement.

It is worth noting that the addition of Al to the Cu crystal leads to a random substitutional SS, while the DFT is based on models with inherent periodicity. To better mimic the alloy‘s randomness, they built different structures with various atomic arrangements by substituting the Cu atoms with Al atoms in random positions. The same strategy was used to explore the structural order‐disorder effect on the OCs of the Au−Cu system. However, the results indicated that the effect of the random site occupancy in these alloys is not crucial for the resulting OCs. ^[119]

Cortie et al. previously reported a seminal study about the plasmon properties of a series of Au alloys modelled with the DFT using the LAPW+lo. ^[120] They started from the consideration that Au is chemically inert but relatively lossy compared to other metals like Ag and Al, which however are prone to oxidation in most real operating conditions. Hence, they investigated the effect of alloying Au with other elements on the electronic structure, DOS and plasmonic quality factor. These parameters were calculated for substitutional alloys of Au with Al, Cd, Mg, Pd, Pt, Sn, Ti, Zn and Zr. As a result, only alloys with Al, Cd, Mg and Zn slightly improved the plasmonic response in a limited spectral region.

3.3. Analytical Models for the OC

An alternative to DFT for the description of OCs in plasmonic nanoalloys resort to the integration of analytical models with band structure calculations. For instance, the dielectric functions in metals can be modelled with the Drude–Lorentz (or Drude–Lorentz–Sommerfeld) formula.[ ² , ⁴⁰ , ¹²¹ , ¹²² ] This is an improvement of the Drude–Sommerfeld model for conduction electrons in a metal with the addition of a Lorentzian contribution to take into account the IB transitions [Eq. 1]:

$${\displaystyle ϵ\left(\omega \right)={ϵ}_{\infty }-\frac{{\omega }_p^2}{{\omega }^2-i\gamma \omega }-\sum _j^N\frac{a_j}{{{\omega }_{0j}}^2-{\omega }^2-i{\gamma }_j\omega }}$$ (1)

where ϵ _∞ is the contribution from cores polarization and can be approximated as a constant, ω is the plasma frequency of the free electron gas, γ is the damping constant, j denotes the index of a Lorentz oscillator (a maximum index of j=N is assumed), a_j, ω _0j and γ_j are the amplitude, the resonant frequency and the damping constant of the given oscillator j, and ω is the frequency of light. ^[123] The first two terms are the same as the Drude model describing the free electron gas in the metal, while the summation spans over the N Lorentzian contributions chosen to represent the IB transitions. This model is very useful for fitting the experimental OC of metals but cannot be used to predict it. For instance, Hashimoto et al. easily fitted the OCs of Au−Ag−Cu nanoalloys with the Drude–Lorentz model in a wide range of compositions. ^[124] Ma et al. implemented the Drude–Lorentz model to calculate the OCs of Au−Ag, Au−Cu, Ag−Cu, Au−Pt, and Ag−Pt alloys. ^[125] They assumed that the mass, the energy of bound and free electrons and in general the quantities that describe an alloy between noble metals obey the bowing rule, and thus can be described by a quadratic polynomial. The results were generally satisfactory for the alloys between noble metals at the level of a first approximation in the absence of other data.

Rioux et al. instead, modified the model by including the electronic structure of Au−Ag alloys in the IB transitions contribution, as calculated with DFT. ^[126] They developed a parametric analytical model that considers that the main features of the OC are in critical points (the Van Hove singularities) of the joint Density of States (jDOS). Thus, the interband contribution was modelled with the convolution of the jDOS with a single Lorentzian oscillator [Eq. 2]:

$${\displaystyle {ϵ}_{ib}=A\underset{0}{\overset{\infty }{\int }}\frac{jDOS\left({\omega }_{lk}\right)}{{{\omega }_{lk}({\omega }_{lk}}^2-{(\omega -i\gamma )}^2}}$$ (2)

where k and l define the occupied and empty states, γ is the broadening factor, and A is an amplitude factor. This model implemented on the Au−Ag system well reproduced the dielectric functions obtained from ellipsometry measurement and the plasmonic peak position in the extinction spectra simulated with Mie theory for different compositions (Figure 11).

Figure 11.

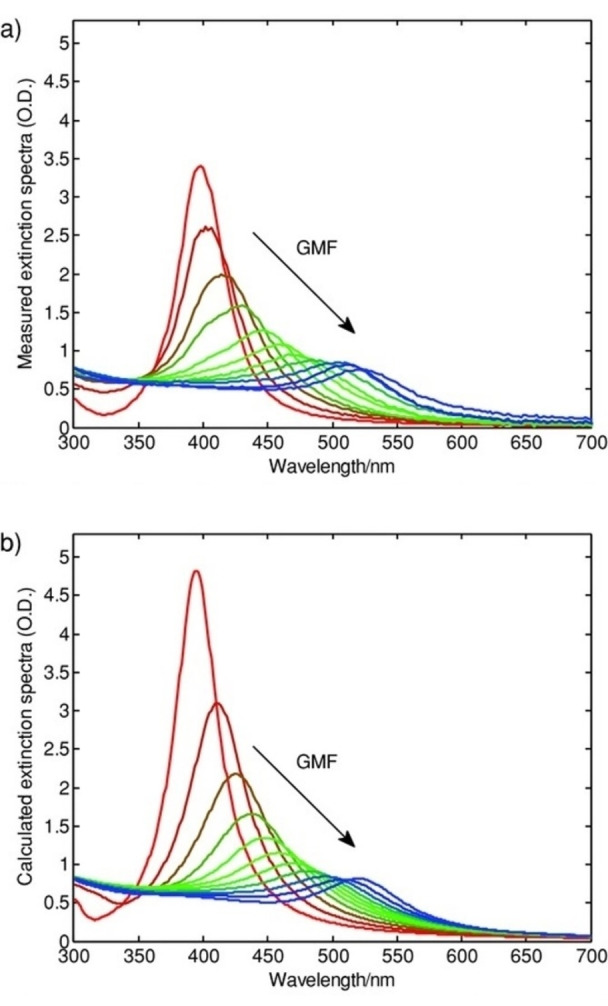
Measured (a) and calculated (b) extinction spectra of Au−Ag alloy NPs with different gold metal fractions. The interband contribution was modelled with the convolution of the jDOS with a single Lorentzian oscillator. Reprinted with permission from Ref. [126]. Copyright (2013) WILEY‐VCH Verlag GmbH & Co. KGaA, Weinheim.

3.4. Modelling the Optical Extinction Properties of Plasmonic Nanoalloys

OCs are the required input for the calculation of the extinction (i. e. absorption plus scattering) cross‐sections of alloy NPs, as well as of the local electromagnetic field effects. There is a variety of numerical models for the calculation of optical properties at various degrees of accuracy depending on the size, shape, composition and assembly of NPs, as reviewed for instance in Ref. [2,127].

The simplest case is that of isolated spherical particles, also core‐shell, which are excellently described with the analytical Mie theory. The Mie model is based on the solution of the Maxwell equations by considering multipolar expansion of the incident, internal and scattered electromagnetic field. ^[128] By applying the boundary conditions, it is possible to obtain the expansion coefficients that are related to the extinction cross‐sections (absorption and scattering). With the Gans theory, the model can be extended to elliptical particles under the dipolar approximation, i. e. field homogeneity along the whole NP volume, which happens only for photon wavelength much larger than particle size.

For any shape and assembly, the most common numerical models are the discrete dipole approximation (DDA), the finite‐difference time‐domain (FDTD) and the boundary elements method (BEM).[ ² , ¹²⁷ ] All of them use the OCs directly or mediated by a Drude–Lorentz fit. In DDA the particles are modelled as a simple cubic array of polarizable volumes (dipoles) interacting with the electromagnetic wave and mutually with the surrounding dipoles. The FDTD model is based on the solution of the Maxwell's equations in the time domain within a finite space volume (the Yee cell). The space and the time discretization allow to determine the value of the electric field at that timeframe by solving the derivatives of the electric and magnetic fields. ^[127] The BEM model is based on the boundary conditions for the continuity of the tangential components of the electric and magnetic fields at the surface and interfaces of the system. In this way, a system of surface‐integral equations is obtained, which is solved by discretization of the integrals using a set of N representative points distributed at the boundaries of the system. In the specific case of ensembles of spherical particles, the generalized Mie theory (GMT) approach and the T‐matrix methods can provide exact electromagnetic solutions with the best computational efficiency.[ ² , ¹²⁹ ]

Literature provides several examples of the use of Maxwell‐Garnett effective medium theory (EMT) as a simple model for the description of mixed phases or when particles are distributed with high density in a small region of space. For interacting spherical particles, the interaction is considered in the model with a parameter K measuring the extent of local electromagnetic field contribution from nearby NPs. The model can be adapted also to elongated particles with the approach proposed by Garcia et al. ^[130] However, the accuracy of this theory is limited and not comparable to the numerical models listed above.

3.5. First‐Principles Modelling of the Optical Absorption of Small Alloy NPs

In spatially confined materials, where the surface and interface break the periodicity of the bulk phases and quantum effects make the bulk OC no more representative, first‐principles approaches like TD‐DFT can be used to obtain directly the optical absorption. This is the case of NPs composed of at most a few hundred atoms, while for thousands of atoms it is usually more accurate and computationally affordable to extract the OCs from the bulk phase and correct it with size effects as described in detail in Ref. [2,122]. The first‐principles approaches are the only one capable of predicting and understanding the appearance of plasmon resonances in ultrasmall alloy NPs. Besides, the predominance of core‐shell ordering over other chemical configurations emerges in this size range at the boundary between molecular and solid‐state behaviour, which is evidenced by the models and must be considered for the interpretation of the resulting optical properties. ^[131]

Recently, TD‐DFT and TD‐DFT+TB (tight binding) were used to compute the absorption spectra of Au−Ag clusters in the 10–10² atoms range.[ ¹³² , ¹³³ ] They evaluated how the scalar‐relativistic (SR) and the spin‐orbit (SO) contribution affect the optical properties and the transition from molecular‐like to metal‐like (plasmonic) optical excitations. ^[133] This evidenced how the screening of s‐electrons by the d‐electrons as well the s‐d hybridization leads to the quenching of plasmonic excitation in Au‐rich clusters compared to Ag‐rich ones. In fact, the Ag/Au ratio correlates with a decrease of the s‐d hybridization and an increase of the s‐s transitions that enhance the intensity of collective excitations, shifting the LSP energy and intensity toward higher values with larger Ag contents. This shows that the doping of Au clusters with Ag atoms is a good method to modulate the optical response between molecular and metallic behaviours by acting on the SR and SO effects. In a subsequent study, they exploited a TD‐DFT integrated with a tight binding model as an alternative method that starts with the full DFT ground state calculation and apply approximations only for the excited state part to reduce the computational cost without significantly affecting the precision of the calculations. ^[132] The results for Au−Ag icosahedral and tetrahedral clusters were in good agreement with the ones obtained with the more accurate standard TD‐DFT calculations, despite the lower computational effort. ^[133]

Danielis et al. also used a TD‐DFT method to calculate the absorption spectra for Ag−Pd, Au−Pd, and Au−Pt clusters. They exploit the complex polarizability TD‐DFT algorithm on the ADF program to extract the spectra from the imaginary part of the polarizability. ^[108] The same method has been used by Olobardi et al. to study in depth the optical properties of Ag−Pt and the role of the Pt→Ag or Ag→Ag transitions in the low and high energy parts of the spectrum. ^[106] Medves et al. used the same complex polarizability TD‐DFT approach to simulate the photo‐absorption spectra of Au−Ag alloys, in particular Ag₂₄Au(DMBT)₁₈ ⁻ in which DMBT is a thiolate ligand (dimethylbenzenethiolate). ^[134] The good agreement of the spectra with the experimental data depended on the choice of the exchange‐correlation functional and of the geometry of the cluster.

It is worth mentioning that in TD‐DFT all excitations are treated on the same footing, and thus it is not obvious how to distinguish plasmonic peaks from pure electron‐hole excitations in the computed spectra. To overcome this limitation, plasmonicity indexes were proposed, that allow inquiring the nature of electronic excitations obtained from TD‐DFT. ^[135] Less obvious to read, but just as useful, Transition Contributions Maps (TCM) decompose each electronic excitation in electron‐hole transitions, giving a direct visualization of TD‐DFT outcome and facilitating the discussion on the nature of the excitation. ^[136]

3.6. ML Approaches to the Modelling of Plasmonic Nanoalloys

ML approaches are exploited for the identification of trends and patterns in big sets of data. Thus, the ML computational technologies are highly versatile and are being exploited to solve problems at different levels in the field of plasmonic nanoalloys.

Saidi et al. reported on the training, use and validation of a ML potential (deep neural‐network potential, DNP) for modelling Ag−Au alloys with accuracy comparable to the standard DFT method, but with lower computational cost. ^[90] The DNP was trained with the DFT and applied for the prediction of various alloy properties such as equilibrium crystalline structures, mechanical properties, defect energies and diffusion energy barriers for Au or Ag adatoms on the principal surfaces of the Au−Ag alloy. Besides, the DNP allowed the simulation of the nucleation and growth of a shell of Ag (or Au) on the core of Au (or Ag), as in the real case of seeded growth, confirming the preferential growth of {111} facets at the expense of the {100} ones.

Kitchin et al. trained a neural network with >5000 DFT calculations to predict the potential energy of ternary Cu−Pd−Au alloys in the whole compositional range and then used Monte Carlo simulations to obtain the segregation profile at 600 K. ^[137] Results showed a limited agreement with experimental data and this was explained with the inapplicability of ideal ordered crystalline models to the more complex and defective real alloys.

Mirkin et al. extended the ML approach to the synthesis of a library of multi‐element and multi‐interface nanocrystals by the scanning probe block copolymer lithography (SPBCL). ^[91] In SPBCL, a scanning probe is used for the deposition of microscopic volumes of liquids containing a block copolymer and metal salts, to synthesize metal NPs. This method allows the rapid screening of synthetic parameters such as metal precursor concentration. Indeed, for an eight‐dimensional chemical space (Au−Ag−Cu−Co‐Ni−Pd−Sn−Pt), the number of variables is so high that a ML approach was required to limit the number of tests and identify the conditions to harvest the desired nanomaterials. Starting from the experimental data for a smaller set of 5 metals, the ML method was trained and extended to the larger dataset in a feedback loop approach, allowing the discovery of NPs with unprecedented composition and number of interfaces.

4. Properties of Plasmonic Nanoalloys

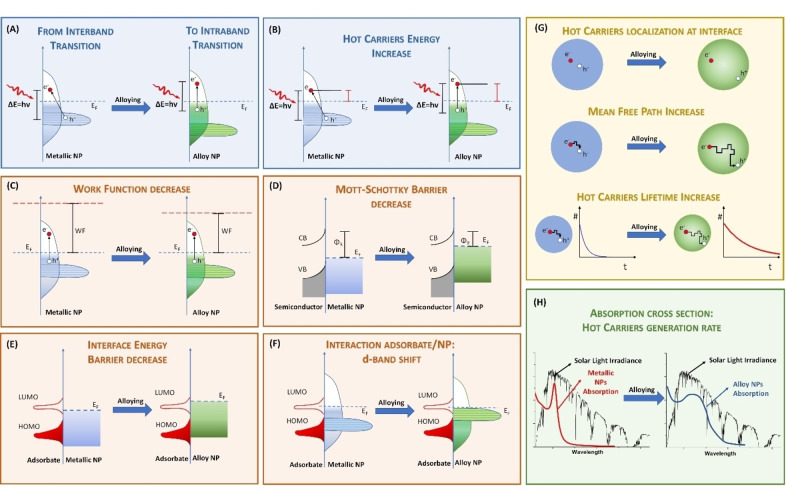
Among the long list of properties of plasmonic nanoalloys, some general trends can be identified in the recent literature which specifically takes advantage of alloying compared to single element NPs. These trends can be tentatively grouped in the plasmonic response, the hot carriers generation and the coupling of magnetic with plasmonic features.

4.1. Plasmonic Response

Alloying usually has a deep influence on the plasmonic response of single element constituents. In terms of plasmonic efficiency versus losses, these can be quantified with the dimensionless plasmonic quality factor Q_P . A reliable expression of Q_P has been proposed as a function of the real (ϵ ₁) and imaginary (ϵ ₂) components of the OC at a specific frequency of light ω [Eq. 3]:[ ⁸ , ¹⁹ ]

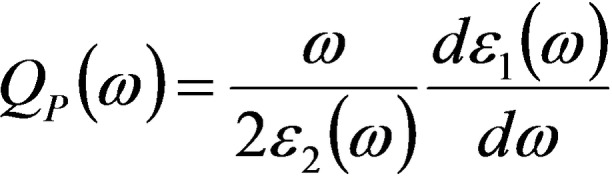
which can be further approximated in the limit of low loss and the quasistatic regime for the LSP in a nanostructure as [Eq. 4]:[ ² , ⁸ ]

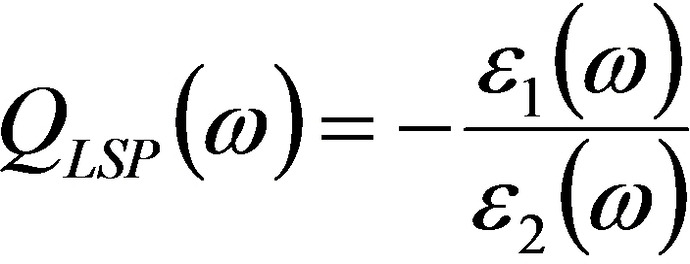
However, the expression for Q_LSP is better suited to indicate the extinction cross‐section and local field enhancement features, both connected to ϵ ₁. Instead, all those effects related to the efficiency of light‐to‐heat conversion (thermoplasmonics), that are connected to ϵ ₂, are not directly considered by Q_LSP . For this reason, Baffou et al. introduced two dimensionless parameters, named Faraday and Joule numbers, to simply quantify the ability of a NP to, respectively, enhance the optical near field and produce heat just starting from the material OC, geometry and surrounding environment. ^[138]

Since alloying modifies the OC of a material, also the plasmonic figure of merits will be altered. For instance, gold and silver are the most prominent plasmonic materials[ ² , ¹³⁹ ] and retain their superior plasmon capabilities also in the Au−Ag alloys.

For what concerns the LSP position, taking as a reference the common case of spherical NPs in the dipolar regime, it is defined as a first approximation by the frequency of electromagnetic light at which the following relation ^[122] is satisfied:

Equation (5) means that the LSP spectral position and extinction cross‐section can be easily tuned by changing the real and imaginary components of the OC. For instance, in Au−Ag alloys the LSP is tuned in the 400–520 nm spectral range (for spherical NPs) simply by acting on the Au/Ag ratio and taking advantage of the full miscibility of the two elements. Indeed, the Au−Ag alloy is by far the most studied and well‐known bimetallic plasmonic system, which is often used as a benchmark for testing computational and analytical models.

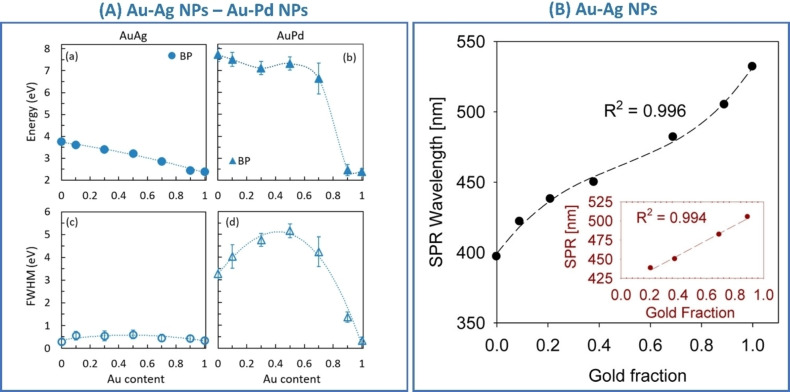
Kadkhodazadeh et al. systematically studied the plasmon resonance of single Au−Ag and Au−Pd nanodisks with different compositions using electron energy loss spectroscopy (EELS). ^[140] From EELS, they also obtained the complex dielectric function applying the Kramers‐Kronig analysis. The advantage of this approach was that of demonstrating at the single‐NP level the correlation of LSP energy and full width at half maximum (FWHM) with the composition. In this way, the highest FWHM in Au−Ag nanodisks was found for alloys with nearly equimolar composition, while in Au−Pd nanodisks the FWHM continuously increased with Au fraction (Figure 12A). Indeed, Au, Ag and their alloys have an identical fcc crystal structure and lattice parameter, making the precise identification of alloying very difficult in ensemble samples. Even scanning TEM elemental analysis based on energy dispersive spectroscopy (EDS) with a resolution of few nm is insensitive to surface segregation or inhomogeneities at the level of 1 nm in most cases. This helps explaining why literature reports conflicting experimental evidence about linear or non‐linear LSP position shift with composition.[ ¹⁴¹ , ¹⁴² , ¹⁴³ , ¹⁴⁴ ] However, the nearly linear dependence of the plasmon resonance position in spherical Au−Ag NPs is most frequently observed for Ag fraction <80 at % (Figure 12B).[ ¹⁴² , ¹⁴³ ]

Figure 12.

(A) Energy and FWHM of the bulk plasmon in Au−Ag (a, c) and Au−Pd alloys (b, d) as a function of the Au content, measured by EELS in alloy nanodisks. Reprinted with permission from Ref. [140]. Copyright (2019) American Chemical Society. (B) Composition dependence of the surface plasmon resonance (SPR) wavelength for 20 nm spherical Au−Ag alloy nanoparticles with different compositions in water. The R² value corresponds to a third‐order polynomial fit. Inset corresponds to a linear regression of the composition dependence of the SPR wavelength at intermediate gold fractions. Reprinted with permission from Ref. [142]. Copyright (2013) American Chemical Society.

The LSP tuneability in Au−Ag alloys was at the basis of broadband plasmonic substrates synthesized via radiofrequency sputtering of Ag/Au bilayer on glass followed by annealing in Ar for dewetting and alloying into Au−Ag NPs. ^[145] The LSP was tuned towards blue or red by increasing respectively the Ag and Au film thickness. The experimental results were checked with FDTD calculations and the observed LSP peak shifts were well matched.

Similarly, the optical properties of Au₇₇Ag₂₃, Au₅₃Ag₄₇, and Au₃₄Ag₆₆ NPs in a colloidal solution were studied experimentally and compared with good agreement with those calculated with a T‐matrix model, exploiting dielectric functions measured by ellipsometry. ^[42] From the plot of the real component of the refractive index (n) versus the wavelength, it was possible to see that the onset of IB transitions shifts from ∼500 nm to 315 nm going from Au to Ag. Besides, n values in the NIR region are higher for the alloys than in pure Ag and Au, which may be due to the increase of alloy defectivity introduced by the adopted LFL synthetic approach. Also, Nishijima et al. have seen from experimental data and FDTD simulations of LSP extinction and local electric field enhancement that all the alloys have lower performances than the arithmetic average between gold and silver, and attributed this to the defectivity introduced by alloying. ^[141]

Borah et al. also studied the absorption and scattering properties, the near field enhancement and the photothermal effect of Au−Ag alloy and CS NPs with spherical and non‐spherical shapes. ^[146] From their simulation with the model developed from Rioux et al. ^[126] they observed that the addition of Au to Ag induces the red‐shift of LSP peak, the decrease of scattering cross‐section and the increase of absorption due to interband transitions for both alloy and CS NPs. Interestingly, the decrease of plasmonic response upon alloying Ag with Au is not seen in anisotropic NPs such as nanorods or nanotriangles with the main LSP peaks located in the red or NIR, where no IB transitions occur. Further analysis on how composition affects the spectra shows that in CS systems the plasmonic shift is not proportional to the Au (or Ag) content as in the alloy and that the LSP position in Au@Ag and Ag@Au CS NPs are located at a longer wavelength than in alloy NPs with the same elemental composition.

Interestingly, by exploiting the dependence of LSP peak position on composition, Barcikowski and co‐workers used hyperspectral dark‐field imaging to monitor dealloying due to silver ion leaching from individual Au−Ag spherical NPs deposed on a transparent substrate and immersed in an acidic aqueous solution. ^[147]

According to literature, also the plasmon response in the Au−Cu alloy changes with the Au/Cu ratio with a shift of the LSP peak in the range of the monometallic counterparts, similarly to the Au−Ag system.[ ¹⁴⁸ , ¹⁴⁹ ] In cases like these, the composition‐weighted average of the OCs of single element constituents is found in literature as a first approximation to infer the plasmonic properties of the real alloys, although only the experimentally measured OCs can provide reliable results. Majhi et al. studied Au−Cu spherical NPs in a silica medium, showing the presence of a single LSP shifted with the composition between ∼535 nm (Au) and 590 nm (Cu).[ ¹⁴⁴ , ¹⁵⁰ ] The FWHM of the plasmon band becomes broader due to the contribution of IB transitions in Cu. The same approach was exploited for the Ag−Cu system, which however is not miscible and very difficult to obtain as a homogeneous sample, despite still showing intermediate plasmon absorption between the pure Ag and Cu equivalent nanostructures.[ ¹⁴⁴ , ¹⁵¹ , ¹⁵² ]

The Au−Ni and Ag−Ni alloys have also been studied for their properties and possible applications. The optical properties of Au−Ni within the whole range of composition have been studied by Collette et al., ^[153] who synthesized Au−Ni thin films via RF magnetron co‐sputtering of Au and Ni targets in the whole alloy compositional range. Despite both Au and Ni having fcc crystals in their elemental composition, a large miscibility gap is present in the phase diagram due to the high difference in the lattice parameters. Collette's group studied the optical properties by measuring the dielectric functions of the SS and calculating the plasmonic quality factor Q_LSP . While the real part of the OC in pure Au has a large negative value below 2.5 eV, which enables LSP modes in NPs, its absolute value decreases with nickel content whereas the imaginary part increases, with a consequent exponential decrease of Q_LSP . Besides, the spectral position of the maximum of Q_LSP blue‐shifts linearly with the Ni content. By annealing the as deposited thin films at 300 and 600 °C, phase segregation into gold‐rich and nickel‐rich phases was observed, with consequent effects on the OCs which resulted as the weighted average of the various phases in the samples (Figure 13).

Figure 13.

The real and imaginary parts of dielectric constant and plasmonic quality factor in Au−Ni thin films with different compositions (indicated in the legend) as deposited (left panels) and after annealing at 300 and 600 °C (middle and right panels). Insets in OCs components show the magnification for specific energy intervals. Insets in the quality factor show the dependence of quality factor maximum value and energy location versus Ni content. Reprinted from Ref. [153], Copyright (2019), with permission from Elsevier.

The effect of phase segregation on plasmonic properties of immiscible alloys as Au−Ni and Ag−Ni have been studied by Mueller et al. considering the thermodynamically stable geometries of NPs extracted according to the nano‐CALPHAD model. ^[93] The calculations evidenced three possible morphologies resulting from the phase segregation, which are the Janus, core‐shell and separated NPs. Both silver and gold have surface energy (1.28 vs 1.92 J/m²) lower than nickel (2.01 J/m²), meaning that the plasmonic metals are both preferentially on the surface of NPs. Moreover, Ni−Ag has lower miscibility than Ni−Au, causing the preferential phase‐separated morphology for a nickel composition of 30–50 at % in Ag. Conversely, Au−Ni does not form separated NPs but the CS morphology is favoured at the extreme compositional values (Au <16 at % and >80 at %), where the shell is formed by the metal with higher concentration. Note that the threshold for Ni‐shell formation is larger than for the Au shell because of the difference in the surface energy of the two metals. FDTD calculations of the electric field enhancement evidenced the superiority of noble metal‐rich surfaces compared to the Ni‐rich ones, although in all cases an enhancement effect was predicted which is expected to be compatible with SERS applications.

A key point in this type of calculation is the identification of the OCs for a given alloy because reliable quantitative predictions are not possible when the OCs are obtained from the composition‐weighted average of the OCs of pure elements. Nonetheless, by the comparison of OCs measured in thin Au−Ni films from Collette et al., ^[153] with the optical properties predicted with averaged OCs for the same alloy by Bhatia et al., ^[154] a qualitative agreement was found. They simulated with the DDSCAT package Au−Ni and Ag−Ni spherical and non‐spherical NPs with various sizes and Ni content varying from 0 to 25, 50, 75 and 100 at %. Both systems indicated a LSP blue shift and intensity decrease with the Ni content.

The most reliable evaluation of the optical properties is possible using the experimentally measured OCs and single NP measurements. Alexander et al. studied the relation between size and composition in Au−Fe spherical nanoalloys obtained by LAL, using combined single NPs EDS‐EELS experiments. ^[40] The EELS spectra were modelled with the Mie theory with Fe content in the range 0–25 at % (Figure 14). The simulations exploited the OCs of Au−Fe alloys experimentally measured by ellipsometry, when available, or resorting to a composition‐weighted average of data from alloys with the nearest composition, when necessary. Single NPs results and simulations indicated that, at parity of size, the increase in iron content causes the damping and blue‐shift of the LSP maximum respect to the pure gold NPs. At parity of alloy composition, the intensity of the LSP increases with size and its position slightly red‐shifts.

Figure 14.

(A) Simulated EELS spectra of a 40 nm Au−Fe alloy NP with various compositions. The quenching of the LSP is clearly appreciable while increasing Fe content. (B) The plot of calculated LSP resonance (LSPR) maximum versus composition for the same alloy and different sizes and compositions, showing the blue‐shift. (C) DOS calculated with DFT for pure Au, Au₉₄Fe₆ and Au₇₅Fe₂₅ showing the appearance of VBS close to Fermi energy (E_F) in the alloys. (D) Calculated free electron density versus alloys composition. (E) Calculated and experimental cell volume versus alloy composition. Reprinted with permission from Ref. [40]. Copyright (2019) American Chemical Society.

To explain these trends, DFT was used for the calculation of the DOS, equilibrium crystal structure and electron density of Au−Fe alloys. The results indicated that the LSP damping is due to the appearance of new electronic states with a dominant Fe d‐level character in the proximity of the Fermi energy (Figure 14 C). These new levels, called “virtual bound states” (VBS), enable low frequencies interband (LFIB) transitions to the conduction band.[ ⁸ , ¹²⁰ ] LFIB transitions are common for alloys of plasmonic metals (Au, Ag) with other non‐plasmonic transition metals with empty d levels (i. e., Fe, Co and so on) as well as with non‐plasmonic noble metals as Pd and Pt and also sp‐group elements.[ ⁸ , ³¹ , ¹²⁰ , ¹⁵⁵ ] This is because plasmonic metals as Au and Ag have d‐band levels far from the Fermi energy, which is key for achieving high quality factor LSP at energies lower than the onset of IB transitions, while magnetic and catalytic metals have d‐band centers close to the Fermi level and their optical properties are dominated by IB transitions. ^[15] In the case of Au−Fe alloys, the LFIB effect is not compensated by the fact that the iron‐doping induces the shift of the Au d‐band edge downwards from the Fermi level, which taken alone would have been beneficial for the Q_LSP . The downward shift of the d‐band is a frequent result for Au alloys with d‐group and sp‐group elements, which is expected due to the presence of additional s‐p valence electrons from the substitutional metals.

Concerning the LSP blue shift measured in Au−Fe nanoalloys, it agrees with the increase of the electron density of the alloy, due to both the number of conduction electrons brought from Fe (1.3 vs 1 for Au) and the contraction of the cell parameter. Indeed, d‐group and sp‐group metals usually have higher plasma frequencies than plasmonic noble metals, resulting in LSP in the blue‐UV range where Au IB transitions are located (Figure 15). Nonetheless, a recent study indicated that alloying induces the single elements in an alloy to lose their characteristic DOS features, opening the possibility of creating a predetermined desired DOS. This study considered HEA NPs composed of all eight noble‐metal‐group elements (Ru, Rh, Pd, Ag, Os, Ir, Pt, Au) and investigated the electronic structure with the hard X‐ray photoelectron spectroscopy of a synchrotron radiation source, supporting the results with DFT calculations. ^[156]

Figure 15.

Overview of problems observed in literature when plasmonic elements have been alloyed with non‐plasmonic elements, resulting in a decrease of the plasmonic quality factor.

Another study focused on the fact that, in Au−Fe alloys, the LFIB transitions enabled by the new d‐states around the Fermi level are associated with the sensible increase of the imaginary part of the OCs, especially in the red and NIR. Although the plasmonic quality factor is depressed by the increase of ϵ ₂, as shown by the damping of the LSP, the absorption cross‐section is proportional to the ϵ ₂. ^[155] Consequently, all those plasmonic effects relying on the conversion of light into heat benefit of the increase in ϵ ₂ due to alloying. It has been calculated, for instance, that Au−Fe CS NPs with silica core and size of the order of 100 nm have 100 % better efficiency in light‐to‐heat conversion than pure Au analogues (Figure 16). This beneficial effect is observed especially for large (>100 nm) Au−Fe nanostructures with LSP position in the red and NIR, because they are in the size range most affected by the competition of absorption versus light scattering and exhibit a LSP in the spectral region with the largest increase of ϵ ₂. This is the only case reported to date in which a purely plasmonic effect is improved by alloying a plasmonic metal like Au with a non‐plasmonic one like Fe.

Figure 16.

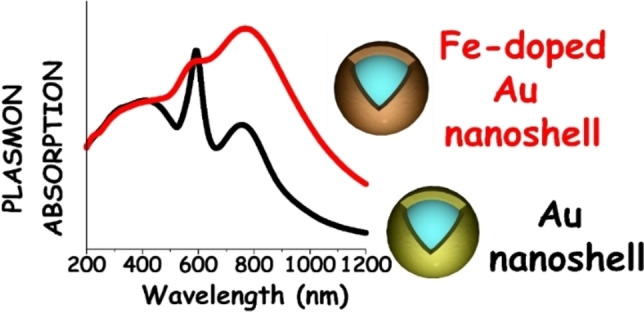
Sketch of absorption in silica‐metal core‐shell NPs with size >100 nm, showing that at parity of geometrical shape, the Au−Fe alloy shell (with Fe content close to 20 at %) have much larger absorption in the red and NIR compared to a pure Au shell. Reprinted with permission from Ref. [155]. Copyright (2015) The Royal Society of Chemistry.

Conversely, all those plasmonic effects relying on light‐scattering, including the local electric field enhancement, suffer from the decrease of Q_LSP . It has been shown experimentally and with DDA calculations that the SERS enhancement factor decreases of 20‐folds going from pure Au to Au₈₇Fe₁₃ spherical NPs with a size of ca. 20 nm. ^[30] However, the calculations also evidenced that the 20 nm Au₈₇Fe₁₃ nanospheres generated a SERS enhancement factor of 10⁶ at 633 nm, which allowed the detection of intense Raman signals from organic analytes. The exploitability of Au alloys for SERS was recently demonstrated also with Au−Co alloy NPs, whose plasmonic properties resulted similar to those of Au−Fe nanoalloys. ^[37] Interestingly for applications, both Au−Fe and Au−Co alloys with Au at % >80 % showed the formation of an Au rich skin, eventually associated with oxidised Fe or Co species, which passivated and stabilized the nanoalloy in an aqueous environment, even at acidic or basic pH and in a physiological environment.[ ³⁰ , ³¹ , ⁹⁸ ]

Blue shift, intensity decrease and broadening of the LSP has been observed also with single‐particle dark field spectroscopy in Au nanorods upon amalgamation with Hg (Figure 17A). ^[157] Exposure to air produced a small red shift of the LSP and a reduction of the FWHM due to Hg oxidation and partial de‐alloying.

Figure 17.

(A) LSP blue shift, intensity decrease and broadening in a single Au NR upon amalgamation with Hg. Reprinted with permission from Ref. [157]. Copyright (2022) American Chemical Society. (B) GIXRD recorded before and after annealing of Au−Al thin films with different Al content (x). The samples are shown as black lines before annealing and as red lines after annealing. (C) Measured OCs (real and imaginary components) for the thin films as‐deposited and after annealing at 500 °C. (B) and (C) reprinted with permission from Ref. [167]. Copyright (2018) American Chemical Society.

Ag−Fe and Ag−Co alloys were also studied experimentally for plasmonic applications, by resorting to the LAL synthesis.[ ¹⁵⁸ , ¹⁵⁹ , ¹⁶⁰ , ¹⁶¹ ] However, the large positive mixing enthalpy of these systems brought to segregated bimetallic NPs with crystalline Ag matrix embedding Fe−Ag or Co−Ag domains. These domains are supposed to be amorphous based on EXAFS and Mossbauer investigations because they are not detectable from XRD analysis. Indeed, compared to Au−Fe and Au−Co alloys, the Ag analogues evidenced a high yield of nonspherical particles (defined as “nanotruffles”), interpreted as the tendency to phase segregation of the two elements. Therefore, the resulting optical properties nearly corresponded to the sum of Ag NPs and metallic Fe or Co NPs. The experimental spectra were successfully modelled with the DDA method considering this type of homogeneous phase‐segregated structure. The DDA simulations evidenced the good local electric field enhancement capabilities of these nanoalloys, which were confirmed by SERS experiments.

Recently, Bhatia et al. succeeded in reproducing the general trend of the optical properties of Au−Fe and Ag−Fe alloys with OCs averaged from pure elements and using the DDA method for NPs with various sizes, shapes and compositions.[ ¹⁶² , ¹⁶³ ] Boldman et al. even succeeded in the synthesis of the Ag−Fe random substitutional SS by RF magnetron co‐sputtering at various compositions from 12 to 82 at %. ^[164] The XRD Ag [111] peak of the as‐deposited samples continuously shifted towards higher 2θ values, indicating a decrease in lattice cell parameter as the Fe concentration increased but, after annealing at >800 °C in an inert atmosphere, the diffraction peak returned in all cases to the position of pure Ag, indicating the phase segregation of the supersaturated Fe component. The OCs of the films were measured by ellipsometry and used to extract the Q_LSP , which indicated an exponential increase and blue shift of its maximum with the Ag fraction.

Ag−Al alloys were recently studied for the realization of chiral plasmonic substrates with high thermal resistance. ^[165] Plasmonic chiral NPs are promising as asymmetric catalysts and plasmon enhanced catalysts but often suffer of loss of optical activity due to the limited thermal stability and reshaping. Ag−Al 1 : 1 alloy NPs were fabricated by glancing angle deposition in a chiral lattice which resisted up to 700 °C thanks to the formation of a Al₂O₃ layer. The combination of alloying and Al oxide shell maintained the LSP and the consequent peak of the optical activity in the 400 nm spectral region of pure Ag NPs.

The Au−Al alloys are noteworthy systems for plasmonic applications, considering that both gold and aluminium possess high Q_LSP .[ ⁸ , ¹²⁰ ] Keast et al. suggested that the intermetallic AuAl₂ perform better than Au in the blue‐green part of the visible light. ^[120] On the other hand, De Silva et al. described the effect of small fractions of Al as random substitutional impurities in the Au lattice. ^[166] In the range 0 to 12.5 at %, Al atoms cause the bleach of gold surface plasmon peak due to the decrease of the real part and the increase of the imaginary part of the OC. Collette et al., with the same approach before described for the Au−Ni system, studied Au−Al alloys with nominal compositions covering almost the whole phase diagram (Au₁₆Al₈₄, Au₂₆Al₇₄, Au₄₁Al₅₉ Au₅₆Al₄₄, and Au₇₂Al₂₈). ^[167] The system is studied before and after annealing with grazing incidence XRD (GIXRD) and the dielectric functions were obtained by ellipsometry. The results for Au−Al films remarkably differ from Au−Ag or Au−Cu ones, where OCs are close to the composition‐weighted average (Figure 17B–C). In fact, the formation of intermetallic Au−Al phases introduces remarkable discontinuities in the evolution of the OCs. Despite this, a general trend is observed because below 2.6 eV the real part of the OC increases and the imaginary part decreases with Au content. The imaginary part increases instead above 2.6 eV. After the annealing procedure at 500 °C, the XRD peak position in Au‐rich samples shifted toward pure gold, whereas in Al‐rich films the pure Al and AuAl₂ components prevailed. SERS performances were also tested experimentally in Au−Al nanoislands, indicating an enhancement effect comparable to pure Au analogues with up to 30 at % of Al in Au, from which it was extrapolated a SERS enhancement factor of 10⁵–10⁷ versus the 10⁶–10⁸ of gold.

Several reports addressed the intense purple colour of AuAl₂ surfaces suggesting the origin was due to interband absorption. ^[118] Samaimongkol and Robinson recently verified the existence of a low energy surface plasmon after that some OCs’ calculations alluded to it. ^[168] They launched surface plasmon in AuAl₂ thin film with Kretschmann configuration and the surface plasmon resulted quite lossy and lying at lower energy (2.1 eV). This is unusual for gold but may be interesting in spherical NPs due to the high absorption cross‐section in the red spectral range.

Beyond the plasmonic noble metals, which have high Q_LSP and are active from the visible to the NIR with appropriate morphologies, other elements of the periodic table have been considered as possible alternatives for their different characteristics. ^[19] The transition metals (d‐metals), for example, can be considered for light‐to‐heat conversion in the UV region, because of the high energy of their LSP but also for the relevance of IB transitions which imply a high imaginary part of the OC. Instead, because of the very large Q_LSP , the s and sp metals such as Mg, Al, In and Ga are appealing candidates for UV plasmonic applications, including those requiring local electric field enhancement like SERS. However, the ease with which these metals undergo oxidation hamper their use. Hence, alloying is a possible strategy to avoid the intrinsic limitations of not‐noble plasmonic metals. For instance, Wu et al. studied the plasmonic properties of Ga−Mg alloy and CS NPs. ^[169] Gallium and Al, have the best Q_LSP in the UV range but, while Al oxidises very easily, Ga is relatively more stable in air. Mg also oxidises very easily but has useful properties for hydrogen sensing and storage. Therefore, molecular beam epitaxy has been exploited for the synthesis of Ga−Mg NPs, achieving CS, segregated or alloy structures by acting on the temperature and the order of deposition. The real‐time spectral evolution taken during the NPs deposition showed a redshift in the Ga−Mg NPs compared to the initial pure Ga NPs. The NPs were exposed to air for 10 months and a small shell of gallium oxide was detected, explaining the LSP redshift of 0.5 eV. Besides, the LSP showed a remarkable tunability with composition, with a red shift from 3.4 to ∼1.8 eV for Mg varied between 0 and 55 at %. This range is larger than that achieved with Au−Ag (from 2.35 to 3.20 eV).

UV plasmonic properties have been observed also in eutectic Ga−In liquid‐metal NPs suspended in ethanol. ^[170] In particular, the two main resonances were located at 213 nm and 275 nm for 100 nm nanospheres. The eutectic has useful properties for reconfigurable and tuneable liquid‐metal plasmonics by deforming the shape of the NP but has an even lower melting point (15.5 °C) compared to pure Ga (30 °C).

Transition metal nitrides such as Ti−N, Zr−N and Hf−N are another class of materials intensely investigated for their plasmonic and refractory properties. ^[171] These binary semiconductors are very stable even at temperatures of thousands of K, at which all the traditional plasmonic materials melt. However, they suffer from limited chemical stability in air and humid or aqueous environments at high temperatures and have larger losses not ideal for local field enhancement applications.[ ¹⁹ , ²⁰ , ¹³⁸ , ¹⁷² ] In search of better refractory plasmonic materials, Huang et al. fabricated Au−Zr and Au−Hf thin films by DC magnetron sputtering.[ ¹⁷³ , ¹⁷⁴ ] Also in these cases, crystalline orientation resulted critical for thermal stability and appreciable plasmonic quality factors, and oxidization emerged as a critical issue for high‐temperature applications in an ambient environment without protective coatings.

4.2. Hot‐Carriers Generation in Plasmonic Nanoalloys

Hot‐carriers are charged particles (electrons) or quasiparticles (holes) in excited states. They are of great interest because can have sufficient kinetic energy to pass the potential barrier at the interface between two materials. Hence, hot‐carriers are crucial for plasmon‐enhanced catalysis (PEC) of redox reactions, also defined as “photoredox” reactions, and represent one main field in which plasmonic nanoalloys are largely exploited and investigated.

In plasmonic materials, hot carriers result from the non‐radiative decay of plasmon modes. ^[2] The non‐radiative LSP decay is the sum of different anelastic scattering contributions such as electron‐electron, electron‐phonon, electron‐defects and electron scattering at the surface (Landau damping ^[175] ), the latter being also significantly influenced by chemically bound molecules.[ ² , ¹²¹ , ¹⁷⁶ , ¹⁷⁷ , ¹⁷⁸ ] All these phenomena contribute to the overall plasmon decay mechanism, which ultimately causes the transformation of the LSP energy into the excitation of electron‐hole pairs.

The hot‐carriers generation rate scales with the absorption cross‐section of the NP meaning that this is the first obvious parameter for evaluating the hot‐carriers generation ability in nanoalloys and NPs (Figure 18).[ ¹⁷⁹ , ¹⁸⁰ ] The absorption cross section linearly depends on the imaginary part ϵ ₂ of the OC. ^[179] However, the absorption cross‐section also depends on the electric field intensity inside the NP, which scales with the plasmonic quality factor and is strongly dependent on NP shape and size, in addition to the composition which determines the OC.[ ² , ¹⁵⁵ ] For a generic NP at the photon frequency ω, the absorption cross‐section σ_Abs (ω) can be expressed as [Eq. 6]:[ ² , ¹⁵⁵ ]

Figure 18.

Overview of the main motivations for the realization of nanoalloys for plasmon‐enhanced catalysis. (A) Plasmon decay preferentially with intraband transitions. (B) The energy of hot carriers increases. (C) The metal work function decreases. (D) The Mott–Schottky barrier decreases. (D) The interface energy barrier with molecular adsorbates decreases. (F) The metal d‐band is shifted to facilitate the interaction with molecular adsorbates. (G) Hot‐carriers localization, mean free path and lifetime are improved. (H) Hot‐carriers generation rate increases.

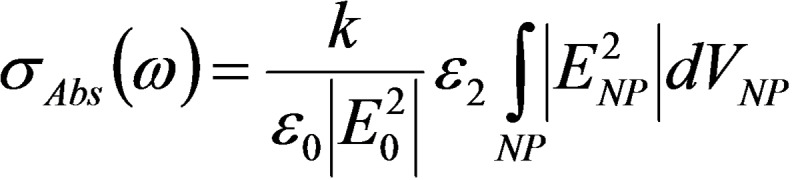
where E₀ is the electric field of the incident light, measured in the medium surrounding the NP of volume V_NP, ϵ ₀ is the vacuum dielectric permittivity and E_NP is the electric field of the electromagnetic radiation inside the NP. On the one hand, σ_Abs (ω) is proportional to the lossy part of the optical constant ϵ ₂. On the other hand, σ_Abs (ω) is proportional to the square of the electric field E_NP inside the NP, which is maximized when the Q_LSP is maximum.

The plasmon‐enhanced catalysis mechanism always implies that charge transfer (CT) occurs from the metal to the coupled material (semiconductor or molecular adsorbate). Hence, the transfer ability of hot carriers primarily depends on their energy, which must be higher than the energy barrier with the coupled material or molecule. In the case of nanoalloys coupled with semiconductors, the metal/semiconductor energy difference is called the Schottky barrier and generally is of the order of 1 eV or less.[ ¹⁷⁹ , ¹⁸¹ ] In the case of molecules adsorbed on the metal surface, this barrier can be much higher, up to >3 eV.[ ¹⁷⁹ , ¹⁸² ] The energy barrier also depends on the work function of the nanoalloy, with lower values meaning a lower tendency of the metal to keep the electrons.

Clearly, the hot carriers should be generated close to the interface between the nanoalloy and the acceptor or should be able to reach the interface. This implies that the transfer ability of hot carriers is critically connected to their relaxation time and mean free path, which should be the largest possible. In noble metals and their alloys, both parameters are determined by the electron‐electron and electron‐phonon scattering rate, which are usually lower in low energy states in the proximity of the Fermi level, where they reach typical maximum values of, respectively, tens of fs and tens of nm.

Electroneutrality must be respected throughout the process to avoid charging the nanoalloy and the growth of the potential barrier with the acceptor. Therefore, sacrificial electron donors or acceptors must be present in the PEC system to close the redox circle. ^[183]

The distribution of hot carriers in the band structure is another key parameter for plasmon‐enhanced catalysis and hot‐carriers transfer ability.

A crucial aspect for hot‐carriers application is whether the plasmon decays in interband or intraband electron‐hole pairs.[ ¹⁸⁰ , ¹⁸⁴ ] Transitions from states in the conduction band (intraband excitations) can produce high‐energy hot electrons and holes, while IB transitions (e. g. from the d band to unoccupied states in the conduction band) can produce high‐energy holes (i. e. well below the Fermi level) but the electrons have low‐energy because occupy states close to the Fermi level. ^[185] Conversely, intraband transitions are more likely to produce low energy hot holes but high energy hot electrons in the conduction band.

Thus, modelling the electronic structure of bulk alloys is a crucial step to obtain information about the features of the hot carriers (Figure 18), which mainly concern their generation rate and transfer ability (energy, interface energy barrier, coupling with the environment to maintain electroneutrality and so on).

For instance, in Au the IB transitions after plasmon decay form hot holes in transfer‐disadvantageous d bands, which are more localized than transfer‐favourable sp bands, where the hot electrons form. This is not the case in pure Al and in the AuAl₂ and AuAl intermetallic compounds, where hot‐electrons are almost uniformly generated in the d and sp bands, according to Jian et al. ^[179] Starting from the calculation of the electronic structure, the work aimed to analyse the possible direct or indirect electronic transitions between the various bands. The electron binding ability of alloys vs pure metals was inferred from the calculated work functions of the (111) surface, resulting in 5.13 eV (Au), 4.12 eV (Al), 4.45 eV (AuAl₂), and 4.65 eV (AuAl). This is a remarkable indication that alloying of the two metals decreases the electron binding ability. Besides, the band structure and DOS showed a shift of the d‐bands to lower energy in AuAl₂ (−5 eV) compared to AuAl (−3.7 eV), meaning that only AuAl is compatible with d‐sp IB transitions in the range 0–4 eV as in pure Al. However, both alloys resulted compatible with sp‐sp IB transitions at an energy below 2 eV. To predict the hot carriers generation rate, ϵ ₂ was calculated at the first order of the perturbation theory considering direct transitions, and at the second‐order perturbation for the three‐body phonon‐assisted transitions. The Au−Al intermetallics have appreciable good values of first‐order ϵ ₂ contribution, also higher than pure Al and Au at specific wavelengths (Figure 19). The second‐order ϵ ₂ contribution due to the phonon‐assisted transitions resulted higher than Au at energy lower than 1.3 eV and are appreciable at 2.5 eV for AuAl₂. Furthermore, the maps of hot carriers energy distribution versus plasmon excitation energy indicated that Au−Al intermetallics can generate high energy hot holes and hot electrons.

Figure 19.

The plot of the imaginary components of the OC in Au, Al, AuAl₂, and AuAl. (a) Contribution due to first‐order perturbation accounting for direct inter‐band and intraband electronic transitions. (b) The contribution due to second‐order perturbation theory due to phonon‐assisted indirect electronic transitions. Reprinted from Ref. [179], Copyright (2021), with permission from Elsevier.

Another interesting system suitable for hot‐carriers generation is the Cu−Ag alloy. Although this alloy has a high positive mixing enthalpy and a high tendency to segregation, ^[186] Jian et al. studied from a theoretical and computational point of view the effect of alloying Ag and Cu on the non‐radiative LSP decay processes. ^[187] Starting from electronic structure and DOS calculations, they simulated the absorption spectra of Cu−Ag in alloys with 12.5, 25, and 50 atomic % of Cu. The absorption coefficient due to interband transitions resulted higher for the Cu_0.5Ag_0.5 alloy compared to pure Ag and Cu in the 1.5–3.2 eV range, which includes most of the solar spectrum. Consequently, the contribution of intraband transitions is reduced in the alloy. The increase of IB transitions is due to the hybridization of the Cu and Ag d‐bands that shift their energy closer to the Fermi level.

Chavez et al. affirmed that the structure of the plasmonic particles will also influence the subsequent energy flow by determining the location of the generated hot‐carriers (i. e. at NP surface or in its core). ^[180] They used core‐shell NPs with Au or Ag cores coated with Pt shell to show that absorption and hot‐carriers generation is mostly located in the Pt shell (lower plasmonic quality factor because of higher lossy component of the OC) for Ag cores (high Q_LSP ). Conversely, with Au core and Pt shell (smaller difference of Q_LSP ), hot‐carriers generation is not limited to the shell. Therefore, an important factor is a ratio between the imaginary part of the OCs of shell and core metals, although the local field enhancement has been also indicated as a relevant parameter in agreement with eq. 6.

According to Valenti et al., alloying is a way to optimize the coupling between plasmonic and semiconductor crystals (SC) for the injection of hot electrons (HEI) into the SC. ^[185] In HEI, the hot electrons are transferred from the conduction band of the metal to the conduction band of the SC.

Only the electrons with energy higher than the Schottky barrier, can be transferred to the SC. This is the main cut‐off for HEI, although another relevant criterion to be satisfied is electroneutrality. Electroneutrality requires a hot hole‐extraction counterpart acting simultaneously to hot‐electron transfer to the SC.

Regarding the hot‐carriers energy, silver is known to produce highly energetic hot electrons via intraband excitations, unlike gold in which less energetic hot electrons are generated due to the IB transitions available at lower energy. On the other hand, the criterion of hot‐carriers generation requires a high absorption cross‐section in the visible range, but spherical Ag NPs absorb in the blue as most of the SC for HEI applications. Alloying Au and Ag can tune the LSP position and increase the generation rate of high energy hot electrons, allowing a higher HEI efficiency in Au₅₀Ag₅₀ alloy supported on TiO₂ than in pure Au NPs. However, the alloy still performed lower than pure Ag NPs. This is due to intraband and IB transitions in the alloy with intermediate energy between the Au and Ag ranges, generating few hot electrons with enough energy to overcome the Schottky barrier.

These results agree with those of Haider et al., which studied a richer Au−Ag alloy (Ag_0.6Au_0.4) performing more efficiently for HEI than the monometallic systems in the photoelectrochemical oxygen evolution reaction (OER). ^[181] They asserted that the improved photocatalytic activity of the alloy results from the increased absorption cross‐section in the visible range. However, also the d bands structure and metal work function change, increasing the height of the Schottky barrier with the Au content of the alloy. Nonetheless, the generation of hot holes on the NPs surfaces allowed better carriers dynamics and improved the OER photocatalytic capabilities for the Au−Ag NPs supported on TiO₂.

Sahoo et al. also exploited alloying for tuning the Schottky barrier and hot carriers generation ability. ^[188] With Au−Ag alloy NPs coupled with Zn−Cr layered double hydroxide/graphene oxide (LHD/GO) nanocomposite, they improved the charge separation and boosted the photoredox reactions of oxidation of benzyl alcohol and the reduction of nitrobenzene.

Sahoo et al. also studied the effect of Au−Pd NPs supported on LHD/GO for the Suzuki coupling reaction. ^[189] In this case, the alloy contributed to the catalytic process with the Pd sites, while Au is used to increase the absorption cross‐section for visible light. The hot electrons generated by plasmon absorption increased the chemisorption capabilities of Pd sites at the NPs surface. For charge neutrality, when the electron‐rich Pd transfer one electron for the coupling reaction, the nanoalloy also receives one electron from the LHD through the GO substrate. This improved the photocatalytic efficiency compared to the mechanical mixture of pure Au and Pd NPs.

The Ag−Pt nanoalloy has been also studied when coupled with TiO₂ for the generation of singlet oxygen under UV‐visible light. ^[190] Singlet oxygen had the function of promoting the selective oxidation of benzylamine into its imine. The higher charge mobility and hot electron density compared to pure Ag or Pt NPs was identified as the reason for the better photocatalytic effect with the alloy. The Ag−Pt nanoalloy also acts as an electron receiver from the TiO₂ with a better charge transfer than the monometallic counterparts because of the higher work function compared to Pt NPs and the lower back‐injection of hot carriers of Ag NPs, which have higher plasmon absorption than the alloy. The experiments also evidenced the formation of hybrid levels under the conduction band of the semiconductor in the alloy‐TiO₂ system, which increase the electron transfer efficiency. The electrons donated to the alloy are subsequently used to produce the singlet oxygen that is needed for the selective oxidation of benzylamine.

Martirez and Carter explored with DFT calculations the thermodynamic limits to the use of Au−M alloy (M=Fe, Co, Ni or Mo) for the N₂ dissociation reactions.[ ⁵ , ¹⁹¹ ] Although relatively less studied in the field of plasmon‐enhanced catalysis, N₂ dissociation and subsequent hydrogenation are crucial steps for the Haber–Bosch process for NH₃ synthesis, which has a massive footprint in agriculture and is one of the crucial chemical processes required for a sustainable future. ^[192] DFT calculations were carried out using the VASP package with PBE‐GGA XC functional and a PAW method, considering the substitution of Au atoms on the (111) surface with the transition metals. First, the segregation of the substituents was modelled, evidencing that Mo and Co have the lower tendency to alloy compared to Fe and Ni. Furthermore, the formation of oxides on the surface needs to be considered. Oxidation can stabilize the structure but also reduce the interaction with the nitrogen. Besides, the hydrogenation of the transition metal should also reduce the surface oxide. Calculations of the oxidation free energy showed that Mo is more easily oxidized than the other metals. Concerning N₂ adsorption, it is predicted that one N atom vertically points to one M atom and that the N−M interaction is more favoured than the Au−N bond. Due to the entropic contribution to N₂ adsorption, an increase in temperature leads to a less efficient catalytic effect. Dissociation energies on the doped Au surface are lower than pure gold, with the smallest values expected in Au−Fe and Au−Mo. The results were supported by further density functional embedding theory (DFET) studies focused on the alloy electronic excited states and their effect on the reaction kinetics, as well as with the aim of avoiding the limits of DFT in describing charge‐transfer reactions.[ ⁵ , ¹⁸² ] The DFET effort evidenced that the Au plasmonic component may harvest the light and acquire the energy required on the Mo active site to generate excited states which lower the energy barriers for nitrogen dissociation.[ ⁵ , ¹⁸² ] The conclusion was that Au−Mo and Au−Fe alloys are the best candidates for the plasmon‐enhanced catalysis of N₂ dissociation and hydrogenation of the Haber–Bosch process. However, the oxidation of Mo and the fact that the Au−Fe nanoalloys were already produced[ ³² , ¹⁹³ ] indicate this last one as the best candidate. A crucial point of these calculations was that, when the LSP is in the visible or NIR (<3 eV), hot carrier injection in N₂ is unlikely in metals with a large work function as the Au alloys. Thus, another mechanism based on Förster resonance energy transfer (FRET mechanism) was hypothesized, also defined as plasmon‐induced resonance energy transfer (PI‐RET). FRET is considered more probable for the excitation of the lowest unoccupied molecular orbitals too high in energy for the generation of transient negative ions (TNI) by HEI.[ ⁵ , ¹⁸² ]

4.3. Magneto‐Optical Properties of Plasmonic Nanoalloys

Frequently, alloying noble metals with transition metals has been sought for introducing magnetic properties in the plasmonic NPs. This enabled a series of studies in which the plasmonic nanoalloys can be manipulated with external magnetic fields for irreversible or reversible assembly, which is important for applications like catalysis or magneto‐optics. In a few cases, new mutual magnetic‐plasmonic effects have been observed, illuminating an area still poorly investigated in nanoalloys.

Plasmonic metals (e. g., Au, Ag, Cu, Al) alloyed with magnetic ones (e. g., Fe, Co, Ni) typically suffer the presence of d‐band levels close to the Fermi level, leading to the effects described for Au−Fe on the Q_LSP . Indeed, Ag alloys may appear as exceptions in the sense that the transition metals may segregate homogeneously in the silver fcc lattice, leading to the sum of the properties of the two metals, roughly weighted by their molar fractions.[ ³⁷ , ¹⁵⁸ ]

The Au−Fe system was thoroughly studied from the magnetic point of view both in homogeneous SSs and CS nanostructures.[ ²⁹ , ³⁴ ] Room‐temperature magnetization experiments on SS NPs with Au₈₉Fe₁₁ composition evidenced a paramagnetic behaviour typical of a diamagnetic system (gold) doped with paramagnetic impurities (iron). At 3 K, a magnetic correlation among Fe atoms appeared as a hysteresis curve and this, together with the other magnetic characterizations, indicated the overall behaviour of a spin glass at low temperature, which evolved into a paramagnetic system at room temperature (Figure 20A). This agrees with the percolation limit for the ferromagnetic behaviour in bulk Au−Fe alloys, which is above 15.5 at % of Fe. Nonetheless, high magnetic polarization of Au atoms was inferred from the magnetic moment per Fe atom, which resulted larger than in bulk Fe. ^[29]

Figure 20.

(A) NPs: hysteresis loops (top, A) and zero‐field cooled (ZFC) and field‐cooled (FC) magnetization dependence on temperature (bottom, B) showing paramagnetic response at room temperature with a hysteresis loop at 3 K and ZFC‐FC behaviour typical of spin glass arrangement. Reprinted with permission from Ref. [29], Copyright (2013) The Royal Society of Chemistry 2013. (B) Magnetic properties of Ag−Fe thin films: (a) Saturation magnetization versus Ag composition. (b) M−T curves from the annealed samples. (c–d) Hysteresis loops for the 78 at % Fe sample (c) as deposited and (d) after annealing at various temperatures. Reprinted from Ref. [164], Copyright (2021), with permission from Elsevier.

Bogani et al. observed that the magnetic properties in Au−Fe nanoalloys can influence the plasmonic response, resulting in a new magneto‐plasmonic phenomenon. ^[194] In these experiments, the Au−Fe nanoalloys were embedded in a silica matrix by ion implantation. The nanocomposite exhibited a reversible variation of the magnetic moment by laser irradiation in resonance with the LSP. This opened interesting perspectives for the use of plasmonic nanoalloys instead of heterostructures and multilayers for the realization of photoswitchable nanomagnets that can be controlled and monitored by light.

Boldman et al. explored the Ag−Fe system by synthesizing thin films with different Ag at % (12, 35, 50, 75, and 82) and by measuring the magnetization before and after annealing. ^[164] In all cases, the magnetization increased with iron content with a non‐linear trend (Figure 20B). Together with the measure of magnetization versus temperature, this confirmed an incomplete ferromagnetic ordering. For the iron‐rich samples (Fe >50 at %), the magnetization curves indicated an exchange bias behaviour possible only by the interaction between ferromagnetic and antiferromagnetic phases, which form in the Ag−Fe films. In annealed samples, there is a clear increase of coercivity at all temperatures, which indicates the segregation of the two metals and the pinning of magnetic atoms at defects and interfaces.

The magnetic properties of Ag−Fe nanotruffles with 15 at % Fe were also reported. ^[158] The nanotruffles were obtained by LAL of a bimetallic Ag/Fe target with a molar ratio of 66/34, in which the two elements were homogeneously mixed but not alloyed. The magnetic nanotruffles were separated from the non‐magnetic NPs in the colloidal solution with the help of an external magnetic field. Superconducting quantum interference device (SQUID) magnetometry analysis was conducted to measure the hysteresis loops at 2.5 and 300 K, also with zero field cooled (ZFC) – field cooled (FC) analysis, suggesting the presence of single‐domain magnetic NPs with magnetic moments blocked at 2.5 K but in the superparamagnetic state at room temperature.

Fe−Ag NPs were obtained also by LFL of pure Ag and Fe powders at various molar ratios (20/80, 50–50 and 80/20) in aqueous solutions of polyvinyl alcohol. These NPs were analysed by vibrating sample magnetometer (VSM), which indicated a superparamagnetic behaviour and optimum magnetic properties for equal Fe−Ag content. ^[43]

Guadagnini et al. extended the LAL approach to the synthesis of Ag−Co and Au−Co alloy NPs and studied their plasmonic and magnetic properties.[ ³¹ , ³⁷ ] The resulting Ag₈₃Co₁₇ NPs were analysed with a VSM at room temperature to show a superparamagnetic hysteresis loop as in the Ag−Fe nanotruffles. ^[37] The saturation magnetization per Co mass resulted in half of the pure Co, due to the presence of some Co(II) oxide that is paramagnetic at RT. The Au₈₆Co₁₄ NPs analysed with VSM at 300 K also showed a superparamagnetic behaviour and the hysteresis loop were fitted with the Langevin model. In all these samples, the physical separation of NPs from the colloidal solution using an external magnet confirmed the superparamagnetic properties and the coexistence with the plasmonic properties. This marked a difference with the paramagnetic Au₈₉Fe₁₁ NPs described above, suggesting that magnetic percolation of Co atoms in the Au alloys NPs was possible. Similarly, a sharp superparamagnetic response in Au−Fe alloys was observed in CS Fe@Au−Fe NPs obtained in one‐step by LAL of thin films in organic solvents.[ ³⁴ , ³⁸ ] These CS NPs readily formed stripes by application of an external magnetic field, and responded to the external field by migrating and accumulating in predetermined points, such as glass slides or silicon substrates.

Luong et al. also studied the magnetic properties of Ag−Co thin films and nanotriangle arrays, confirming the linear increase of the saturation magnetization with Co content. ^[195] Instead, Garfinkel et al. focused on the magnetic behaviour of Ag_0.5Ni_0.5 thin film as deposited with different thicknesses and of NPs generated with PLID. ^[52] The hysteresis loops obtained by VSM at 300 K for the as‐deposited thin films revealed a superparamagnetic behaviour evolving in a ferromagnetic response at 1.9 K. The transition from a blocked ferromagnetic to an unblocked superparamagnetic material resulted size dependent. For instance, the blocking temperature was lower than 50 K for 8 nm particles, between 150 and 200 K for 20 nm NPs, and higher than 300 K for 45 nm NPs.

Appealing magneto‐plasmonic properties were reported in a system of Au−Cu alloys integrated into a core‐shell Co_0.25Ni_0.25@Au_0.25Cu_0.25 hybrid nanopillar with ferromagnetic alloy core (CoNi) and plasmonic shell (Au−Cu), all embedded in a BaTiO₃ matrix. ^[196] The array of core‐shell alloy nanopillars exhibited multi‐functionality as high magnetic anisotropy, magneto‐optical coupling response, tailorable plasmonic resonance wavelength, tuneable hyperbolic properties, strong optical anisotropy, and a response indicative of a strong magneto‐plasmonic coupling enabled by the core‐shell interface.

5. Applications

The applications of plasmonic nanoalloys are typically related to the improved, innovative or unique properties that are achieved through the alloying. Of the large variety of uses reported in the literature for plasmonic nanoalloys, the most recent ones are principally oriented to plasmon assisted catalysis and various photoredox reactions, photothermal effects for chemical and biomedical purposes, optical sensing and as SERS substrates (Figure 21). However, this is not a comprehensive list of the many studies which, to date, involved plasmonic nanoalloys, sometimes also including photodetection, photovoltaics, chemical transformations, linear spectroscopy and circular dichroism. The possibility of tailoring the LSP, offered by alloying, is crucial also for applications in anticounterfeiting and electrochromic color switching. ^[197]

Figure 21.

Overview of the most frequent applications of plasmonic nanoalloys in recent literature: optical sensing based on LSP spectral position or evolution; photothermal effects for nanomedicine applications, towards hyperthermia effects or nanocavitation phenomena; plasmon‐enhanced catalysis and SERS for analytical or biolabeling purposes.

5.1. Photocatalysis and Plasmon Enhanced Catalysis

As anticipated in the previous paragraph about hot‐carriers generation, plasmonic nanoalloys have been extensively applied in experiments of photocatalysis based on electron or hole transfer (Figure 22). The studies about plasmon‐enhanced catalysis can be divided into pure photocatalysis, hybrid photo‐electrocatalysis and photothermal activation of chemical processes (thermal catalysis). ^[15] The catalytic activity can rely on direct hot‐electron or hot‐hole transfer to a molecular compound or indirectly to a mediator for the chemical reaction such as a semiconductor nanocrystal, in a configuration defined as an antenna (metal NP) – reactor (SC NP). Of crucial importance is the modification of the surface chemistry possible in alloys by the introduction of d‐group catalytic metals, whose d‐band levels couple well with the key adsorbates of the chemical reactions to be photocatalysed, according to the d‐band model of chemisorption. ^[15]

Figure 22.

Overview of chemical processes reported in the recent literature about plasmon‐enhanced catalysis with nanoalloys.

Several relevant examples of PEC are based on the Ag−Pt alloy, which was exploited for selective oxidation of benzylamine in the imine. ^[190] Besides, Au@Ag@Pt CS and Au@Ag−Pt nanorattles (i. e. Au nanosphere in a hollow Ag−Pt shell) were used for the photocatalytic hydrogenation of phenylacetylene. ^[198] In this particular case, the nanorattles led to a higher photocatalytic effect, with the conversion of phenylacetylene being increased from 48 % in dark to 98 % under light irradiation. The difference between CS and nanorattles is in the hybridization of shell and core plasmons that, in the nanorattles, is associated with higher local field enhancement and absorption in the red and NIR. This allowed an improved availability of hot electrons in the Pt atoms responsible of the hydrogenation of phenylacetylene.

Au−Ag nanoalloys are also interesting for reduction reactions. The reduction of 4‐nitrophenol (4‐NTP) to 4‐aminophenol (4‐AP) is frequently used as a model reaction to test the catalytic behaviour of NPs because the reaction can be monitored by UV‐Vis spectroscopy due to the appearance of the absorption band related to the 4‐AP and the lowering of the absorption of the 4‐NTP band. Dwivedi et al. tested Au−Ag alloys with different Au/Ag ratios for the photoreduction of 4‐NTP ^[199] observing that, only for the specific Ag/Au ratio 0.2/1, the alloy performed better than Au and Ag (the latter was always the worst). The reaction implies the binding of the 4‐nitrophenolate ion via the two oxygen atoms of the nitro group to the metal surface. Hence, the authors suggested that the results may be due to a better match of the Ag/Au 0.2/1 alloy d‐band with the energy of the adsorbate.

Due to the global rise of carbon dioxide emission, the catalysis of CO₂ reduction is currently under intense investigation, also resorting to plasmon enhancement of the chemical process. Stanley et al. exploited Au−Ni nanoalloys supported on Si to speed up this reaction. ^[200] They proved the plasmonic contribution to the catalytic performances with experiments in dark and under illumination, observing improved performances in the latter case. However, the study pointed out also the simultaneously lowering of the selectivity for conversion of CO₂ into CH₄ in favour of CO when using the alloy. This was attributed to the LSP effects and the promotion of the reverse water‐gas shift reaction by the Au atoms.

Another example of an interesting reaction is the photoelectrochemical OER in alkaline media that lead to the O₂ and water production from HO⁻ ions. Here, the Ag_0.6Au_0.4 nanoalloys have been suggested as an efficient photocatalyst with superior performances than pure Au and Ag NPs. ^[181]

Pd nanoalloys are among the most used for PEC because of the activity of Pd for Suzuki coupling reactions. Han et al. ^[201] and Sahoo et al. ^[189] both showed the advantages of Au−Pd nanoalloys for this type of reaction. Han et al. demonstrated that the catalytic pathway in Suzuki coupling of iodobenzene and phenylboronic acid includes the contribution from the LSP of Au−Pd NPs supported on TiO₂. ^[201] The yield under illumination was 98 % versus 17 % in the dark at RT and 88 % in the dark at 80 °C. Electron rich Pd atoms become available at NP surface after LSP excitation, becoming optimal sites for iodobenzene adsorption and the subsequent oxidative addition. The charge of the hot holes is re‐equilibrated by the electrons generated on the titania substrate. The same mechanism is reported from Sahoo et al. with Au−Pd alloy coupled with the GO/LDH substrate which speeds up the reaction by equilibrating the hot‐holes via a more efficient absorber as LDH. ^[189]

Recently, Zhang et al. developed an Au−Pd Mott–Schottky catalyst for plasmon enhanced hydrogen evolution from formic acid. ^[202] Here Au₂Pd, AuPd, and AuPd₂ alloy NPs were distributed on carbon nitride nanospheres (CNS). Carbon nitride is a semiconductor, hence the CNS/Au−Pd NPs is a semiconductor/metal or Mott–Schottky junction. Because of electron equilibration at the Mott–Schottky junction, an electric field is present at the semiconductor/metal interface which efficiently injects (Schottky effect) into the metal the electrons generated in the CNS by photon absorption, as substantiated with DFT calculations. Besides, from photocatalytic tests emerged that Au−Pd alloys surprisingly speeded up the reaction more than pure Pd, which is the catalytic active center. This means that LSP contribution was not negligible. CNS photoluminescence analysis was carried out to verify that Au−Pd/CNS led to the best charge separation, corresponding to the lowest emission because of the effective electron transfer from the nitride to the alloy. On the other hand, the transient photocurrent response evidenced the superior generation of photoinduced carriers in the Au−Pd/CNS compared to Pd/CNS, Au/CNS and CNS samples. The proposed PEC mechanism is slightly different than in the previous examples about Au−Pd NPs because the HEI from the CNS should be considered.

The production of hot holes helped Huang et al. to activate the methanol oxidation by using Pd_xAg_1‐x with different Pd content (x=0.62, 0.52, 0.41, 0.33). ^[203] The alloys, with a nanotube morphology, were supported on a network of carbon nanotubes (CNTs). Pd is an active electrocatalyst for methanol oxidation but only the Pd−Ag alloy exhibited electrocatalytic performance improvement under light illumination. The hypothesized mechanism relies on hot electrons injection in the carbon nanotubes network, to reach electron‐acceptor adsorbates under the externally applied electromotive force, while hot‐holes are “transferred” to methanol molecules coordinated to Pd atoms at NPs surface, producing a photooxidation in direct relationship with light intensity. As in all plasmon‐enhanced phenomena, ^[6] both thermal effects and hot‐carriers generation can participate in the catalytic process. In this case, the reaction was temperature insensitive, excluding thermal effects from the mechanism.

In all plasmon‐enhanced catalysis experiments, the discrimination between charge transfer by hot‐carriers generation and thermal catalysis is an open point. A general rule is that the transfer of hot carriers is associated with a linear dependence of the reaction rate on the light intensity, whereas thermal effects have an Arrhenius‐type dependence.[ ⁵ , ¹⁸³ , ²⁰⁴ ] However, it is more frequent that heat and light work synergistically, such that the efficiency of the purely charge‐transfer PEC increases with the temperature for most reactions. ^[205] The Halas and the Carter groups have investigated experimentally and with state of the art modelling efforts the two contributions in a series of relevant PEC processes. The decomposition of NH₃ and N₂ generation by Ru‐doped Cu NPs has been reported to follow first‐order kinetics in ammonia concentration under light illumination, which turns to zeroth order in the dark despite thermal catalysis.[ ⁵ , ²⁰⁵ ] The limiting steps of the reaction, according to the DFT calculations for a Ru‐doped Cu(111) surface, are the N−H bond scission and the associative desorption of N₂. The latter is sensitive to thermal catalysis, while the N−H bond scission is favoured by LSP excitation.[ ⁵ , ²⁰⁵ ]

In another study, syngas (a mixture of CO and H₂) generation by methane dry reforming with CO₂ was obtained on the same Ru‐doped Cu NPs. ^[206] Similarly to the Haber–Bosch process, syngas formation is energy consuming because performed at high temperature, representing an ideal case study for the development of PEC alternative routes. The Ru−Cu NPs demonstrated long‐term stability and high selectivity (>99 %) as photocatalysts. Based on modelling results, the substantial reduction of the kinetic barrier for CH₄ activation was ascribed to the excited‐state activation of adsorbates upon hot carriers generation after LSP excitation and to the Ru electronic.

Finally, the plasmon‐enhanced activation of C(sp3)−F bonds towards hydrodefluorination has been demonstrated with Al−Pd nanostructures. ^[207] The C−F bond energy is relatively large and requires extreme conditions, but the plasmonic alloy NPs were able to promote the process under illumination thanks to the adsorption of hydrogen on the surface Pd atoms and the light‐harvesting ability of Al.

5.2. Nanomedicine Applications Based on Photothermal Effects

Photothermal effects in plasmonic nanoalloys attracted the interest for biomedical applications such as photothermal therapy or light‐induced bubble generation (Figure 21). In photothermal therapy, cancer cell death is induced by temperature increase above the threshold for apoptosis (spontaneous cell death), while in bubble generation high intensity laser pulses are exploited for the generation of localized mechanical damage which will also bring to cell death or permeation of anticancer drugs. Details on this topic can be found in various reviews in literature.[ ²⁰⁸ , ²⁰⁹ , ²¹⁰ ] For what concerns recent examples about nanoalloys, Cu−Au−Pt trimetallic NPs were synthesized by Ye et al. for biosensing and cancer theranostics. ^[66] The efficiency of light‐to‐heat conversion was tested with a 780 nm laser source resulting in improved heating compared to the bimetallic and monometallic NPs. The theranostic activity was tested by conjugation of the NPs to an aptamer targeting a specific type of cancer cells, resulting in >90 % of cancer cell death during photothermal therapy experiments.

Au−Cu tetrapods were synthesized by a seed‐mediated growth and used for photothermal therapy in the second near‐infrared (NIR‐II) region (1000–1350 nm), which is difficult to reach with plasmonic nanomaterials. ^[71] In addition to the significant therapeutic effects upon photothermal treatment, the Au−Cu alloy showed the ability to dissolve in smaller NPs which are better removed from the organism. Indeed, biodegradability is a recently emerging and extremely appealing feature that is not found in most single element NPs but can be enabled by alloying. This was demonstrated recently for various nanosystems such as Au−Fe, Ag−Fe, Ga−In and Fe−B NPs, setting a milestone for the new generation of nanomedicines.[ ⁹⁸ , ¹⁶¹ , ²¹¹ , ²¹² ]

The use of multimetallic NPs as antimicrobial agents was also deepened from Basavegowda and Baek in a recent review, pointing out the possibility of photothermal effects for this purpose. ^[213]

The problem of nanoscale bubble formation, also defined nanocavitation, was afforded by Meunier et al. ^[214] They highlighted the nonlinear dependence of nanocavitation on the wavelength and absorption cross‐section of the LSP, namely to the careful choice of NP composition and morphology. Therefore, it is foreseen a great room for improvement of the field by resorting to plasmonic nanoalloys for localized generation of mechanical damage in malignant tissues or for antimicrobial applications.

5.3. LSP‐Based Sensing with Alloy NPs

Sensing is one of the main applications sought for plasmonic nanoalloys because alloying offers the possibility of tuning the LSP but also the surface chemistry of the metal NPs, introducing the selectivity for specific chemical compounds or chemical processes. The literature about this topic is wide and includes several reviews. For instance, Loiseau et al. ^[215] focused their attention on the Ag NPs and Ag‐alloys for biosensing application, while Srinoi et al. described the use of Au, Cu, Ag and other alloy NPs for biosensing, bioimaging, drug delivery application, and thermal treatment. ^[216]

A recent study by Darmadi et al. focus on the design of a Pd−Au−Cu ternary alloy for fast plasmonic hydrogen sensing. ^[217] Hydrogen is considered a possible energy carrier for a sustainable future because its reaction with oxygen only produces water. However, among the disadvantages of hydrogen there is its high flammability range and low ignition energy threshold. Hence, there is a need for reliable and fast hydrogen sensors. In this regard, the LSP sensors are considered helpful because the optical detection has a low risk of spark generation and can be fast, highly sensitive (up to the single NP level) and selective. Selectivity exploits the absorption of hydrogen on interstitial metal sites by the formation of metal‐hydrides and the consequent change of the LSP absorption. Palladium is by far the most appropriate metal for this application due to its ability to dissociate hydrogen gas and reversibly change its phase from metal to metal‐hydride. Despite this, problems occur due to the hysteresis of the phase‐transformation and to the poisoning of hydrogen dissociation by adsorption of CO, hydrocarbons and sulfuric compounds. The ternary alloy synthesized by Darmadi et al. resulted able to overcome these problems. They initially studied the Au−Pd and Cu−Pd alloy NPs, from which it resulted that Au helps in increasing the sensitivity for hydrogen detection while Cu helps against CO poisoning and sensor hysteresis. Thus, the combination of Au and Cu in the trimetallic NPs led to a sensor with a detection limit in the ppm range, a CO poisoning resistance, and a sub‐second response.

Previous studies on Au−Pd NPs, made by the same group, unveiled how the LSP shift and FWHM are related to the Pd/H ratio. ^[218] The spectral shift, given by the dehydrogenation process, was monitored simultaneously to the weight change using a quartz crystal microbalance. The optical response per hydrogen atom adsorbed on the surface resulted linearly correlated with the fraction of hydrogenated Pd atoms for alloy composition up to 25 at % of Au. Moreover, the amplitude of the optical response is set by the spectral position of the nanoalloy in the non‐hydrogenated condition, meaning that it can be increased by red shifting the LSP. This is achieved by acting on NPs size or shape. Starting from these results, in a more recent work, they chose the Pd₇₀Au₃₀ alloy to create a plasmonic metal‐polymer sensor. ^[219] The composition was chosen because of the ideal amount of gold to increase the accuracy and avoid hysteresis. They coated the NPs with polytetrafluoroethylene (PTFE) to red‐shift the LSP by increasing the refractive index around the NPs. The metal‐polymer structure resulted in more sensitivity for H₂ detection compared to the uncoated NPs. They verified that the same quantity of hydrogen was absorbed on coated and uncoated NPs, hence excluding the interaction between hydrogen and the PTFE as the source of the better sensitivity. DFT calculations further confirmed that the interaction between hydrogen and PTFE is just a matter of dispersion forces. The detection limit was in the ppm range and the time response was below the 1 second threshold, both resulting in better performances than with pure Pd. However, the PTFE coating was inefficient for the protection against the poisoning of the alloy, hence a combination of PTFE and poly(methyl methacrylate) resulted in higher selectivity for H₂ gases retaining the benefits of PTFE alone.

Plasmonic nanoalloys are also sought for improving the sensitivity of biosensors. The application for biosensing depends on the LSP performance but also on the possibility to functionalize the NPs to confer selectivity. Ag NPs have the best plasmon quality factor for these purposes, but they fail in terms of chemical stability and corrosion resistance, especially in a physiological environment. Conversely, Au NPs are known for biocompatibility, high physicochemical stability, and corrosion resistance. Hence, alloying of Au with Ag is a widely investigated strategy in the field of LSP sensing. For instance, Qiu et al. recently tested Au−Ag alloy nanoislands for biosensing of human immunoglobulin G (IgG). ^[220] They produced the NPs by thermal dewetting of sputtered thin metal films on a BK7 glass substrate and studied the response after covalent functionalization with thiols or a coating with aminosilanes to block the human antibody IgG. Among different alloy compositions, the Au_0.6Ag_0.4 was the ideal one due to the best LSP response in the visible range. The alloy NPs allowed the detection of human IgG until the lower limit of 0.9 pM, with the aminosilane‐coated NPs resulting in the most stable in a physiological environment.

Mattei et al. exploited nanosphere lithography coupled with reactive ion etching and magnetron sputtering co‐deposition to obtain an ordered array of Au−Ag semi‐nanoshells and tested them as LSP biosensors. ^[221] The sensing performance was verified with the biotin‐streptavidin receptor‐ligand approach or with a homogeneous change in the refractive index of the buffer over the sensor (bulk sensitivity). When compared to a benchmark as the Au−Ag nanoprisms array, both the local and bulk sensitivities resulted higher, in agreement with finite‐element methods simulations for the two morphologies.

The combination of plasmonic alloys with hybrid perovskite thin films in a multilayer surface plasmon resonance (SPR) sensor was studied by Dhibi et al. ^[222] They calculated the effect of Au_(1‐x)Ag_x and Au_(1‐x)Al_x layers with various compositions and thickness on the figure of merit (FOM) of the surface plasmon resonance sensors. Although the OC of the alloys was approximated with the average of pure metals, the general trend showed the increase of sensitivity in all the sensors as the Au content increased. However, this was associated with an increase in the plasmon bandwidth, resulting in an overall decrease in the FOM. The thickness of the various layers was also found to affect the FOM. For instance, the presence of a high number of graphene layers on the alloy film leads to the decrease of the detection accuracy due to the plasmon damping for the non‐negligible graphene absorption ^[223] but it resulted that few layers of graphene may increase the sensitivity due to the better adsorption of biomolecules on the surface.

5.4. Alloy NPs as SERS Substrates

SERS has been investigated deeply for the theoretical possibility to detect up to a single molecule thanks to the amplification of the local electric field and, in turn, the effective Raman scattering cross‐section of the analytes adsorbed on the surface of plasmonic NPs. Plasmonic nanoalloys have also been frequently considered as SERS substrates for the possibility of improving the local electric field enhancement in the proximity of the NPs surface or for the introduction of new beneficial properties. Because of the relationship between Q_LSP and SERS capability, it is straightforward that Ag is the best noble metal immediately before Au, with other metals (e. g. Al) being excluded for their instability towards chemical transformations such as surface oxidation. Hence, the alloying of Ag and Au are systematically exploited to achieve large local field enhancement and superior stability in various environments.

Au−Ag alloy porous NPs were synthesized by dealloying through galvanic replacement reaction to improve the SERS enhancement. ^[224] The porous hollow nanoshells have a rough surface and porosity around 30–60 %, desirable for adsorption of Raman active molecules, with a LSP that can be shifted up to the NIR. This resulted in 68‐fold more intense Raman signals than with 100 nm AuNP and was successfully used for quantitative monitoring of the release of the anticancer drug doxorubicin.

Park et al. produced Au−Ag NPs on a cellulose‐based substrate for biosensing by SERS. The paper substrates were selected for compatibility with chromatography and lateral flow assays. ^[225] The substrates were produced with NPs at different Au/Ag fractions from 0/1 to 0.12/0.88, 0.52/0.48, 0.81/0.19, and 1/0. Selective detection of dyes in a liquid mixture was successfully obtained with a chromatographic separation on cellulose (Figure 23). The best conditions were reached with paper substrates whose alloy composition led to a match with the used laser wavelength for Raman excitation, thus exploiting the advantages brought by alloying on the LSP of Au−Ag NPs. Adenine is a fundamental DNA constituent and vitamin B9 (folic acid) as a typical cancer biomarker was selected for the SERS detection. Adenine peaks were well distinguishable with the Au_0.12Ag_0.88 substrate and picomolar SERS detection of folic acid was demonstrated down to 1 pM concentration, which is one of the lowest values reached for this molecule on SERS.

Figure 23.

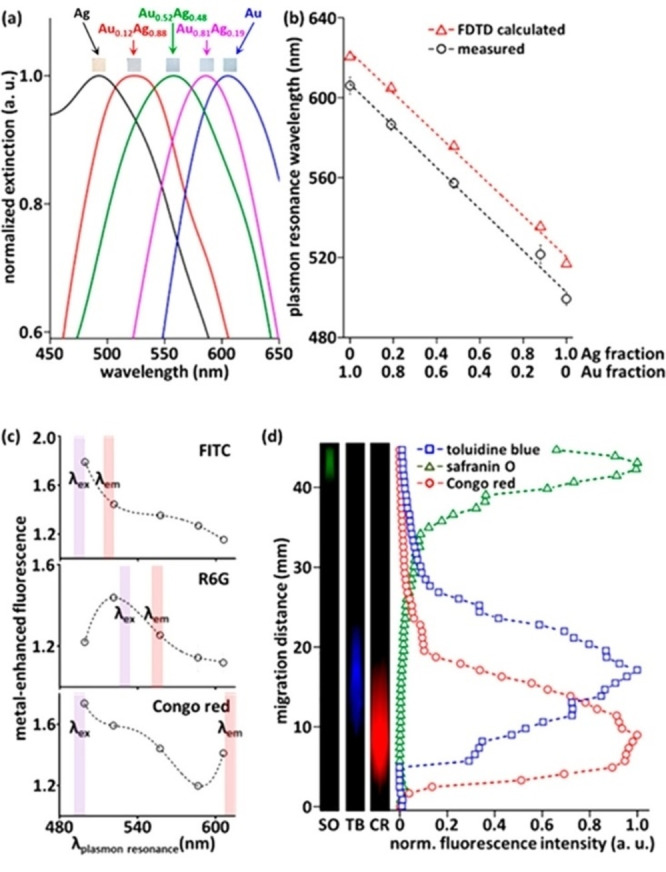
MEF with Au−Ag nanoalloys in the paper substrate. (A) Optical extinction spectra showing a magnification of the LSP range for five Au−Ag NPs on cellulose substrates. (B) LSP wavelength calculated with FDTD simulations for the Au−Ag alloy NPs. (C) Fluorescence signal enhancement from three dyes (FITC, R6G and CR) showed twofold MEF from the substrates compared to the Whatman chromatography paper. The enhancement occurs when the LSP of Au−Ag alloy NPs matches the emission band of each specific dye. (D) Chromatographic MEF analysis. A three‐dye mixture was separated using paper chromatography, and then each component was selectively detected. Reprinted with permission from Ref. [225]. Copyright (2017), American Chemical Society.

Also, the plasmon‐enhanced fluorescence was studied on the same substrates. The MEF of fluorescein isothiocyanate (FITC), Rhodamine 6G (R6G), and Congo red (CR) was measured on this NPs‐on‐paper substrate and normal Whatman chromatography paper, showing a twofold enhancement value. The response was larger in the substrate whose LSP position matched with the excitation and emission wavelength of the dye.

Recently, Kluender et al. displayed one of the first examples of Au_0.5Ag_0.5 NP on a SiO₂/Cr/Au/SiO₂ mirror for SERS application. ^[226] The thickness of the topmost SiO₂ layer sets the gap between the gold film and the Au−Ag NP and was of 5 or 10 nm. By placing the NP onto the mirror, the LSP was split into two peaks: the original peak at 460 nm is slightly red‐shifted and a second more intense peak appears at 600 nm, or 575 nm in case of a 10 nm SiO₂ layer. FDTD calculations of the intensity of the backscattered light and near‐field spatial distributions around the NP on the mirror indicate that the 5 nm gap has the highest local field amplification. The experimental Raman measurements of 1,4‐benzene dithiol with 633 nm excitation confirmed an estimated SERS enhancement factor of 10⁷. The choice of Au−Ag alloy NPs was motivated by the purpose of better matching the 633 nm laser excitation compared to pure Au or Ag NPs, pointing to the importance of composition for optimal SERS performance.

Ag−Al NPs for SERS have been obtained from Sun et al. by ablating an Ag/Al bilayer film. ^[227] By increasing the laser power, they obtained six samples with Ag content from 54 to 92 at %. Then, the intensity of the Raman signal at 633 nm from Rhodamine B samples was correlated to the laser power used to ablate the thin film. The spectra indicate that the higher the power of the laser, the higher the Raman signal. Indeed, higher laser power also led to higher Ag content, larger NPs and superior roughness. However, the advantage of using Al−Ag NPs was not clearly outlined compared to pure Ag NPs in this case.

Instead, alloying brought advantages in the case of Fe or Co‐doped plasmonic Ag or Au NPs. Scaramuzza et al. in 2017 included the magnetic properties of Fe in Ag by LAL synthesis of Fe−Ag NPs for SERS. ^[160] This allowed the control of the NPs with an external magnetic field, enabling different possibilities. The Fe−Ag NPs were used for the magnetic assembly of plasmonic arrays exploitable as SERS substrates. The magnetic assembly of NPs allowed a 28‐fold increase in the SERS signal of analytes compared to not‐assembled NPs. The advantages in SERS sensitivity brought by the magnetic accumulation of plasmonic NPs on a substrate was confirmed later also with Au−Fe core‐shell NPs. ^[34] Besides, the magnetic assembly is linearly scalable with the number of magnets, allowing the realization of plasmonic dot arrays on small as well as large areas.

The versatility of substrate preparation and the SERS performances were investigated as a function of Fe−Ag NPs surface coating, which is helpful to prevent the sedimentation of NPs in complex environments (Figure 24).

Figure 24.

Application of magnetic‐plasmonic nanoalloys as SERS substrates. (A) Ag−Fe NPs: (A) UV‐Vis spectra of the NPs coated with various ligands. (B) Photo of the magnetically assembled NPs on a glass substrate (distance between spots is 4 mm). (C) The intensity of the Raman band of malachite green (MG) at 1617 cm⁻¹ measured on Ag−Fe NPs with different surface coatings. (D) 2D Raman map of the major band of MG collected on NPs coated with MPS and GSH. Reprinted with permission from Ref. [160]. Copyright (2017) Wiley‐VCH Verlag GmbH & Co. KGaA, Weinheim. (B) Au−Co NPs: (A) A 4×4 Array of magnetic‐plasmonic dots obtained on glass by drop‐casting and evaporation at room temperature of an Au−Co NPs solution. During the evaporation of the solution, a squared array of 16 permanent cylindrical magnets (2 mm in diameter ×8 mm length) was placed below the glass slide. (B) Raman spectra were collected with 647 nm excitation by deposing 20, 2 or 0.2 pmol of MG on the magnetic‐plasmonic dots (and reference with 20 pmol MG on the bare glass). (C) 2‐D map of the Raman intensity at 1615 cm⁻¹ collected on 6 dots after deposition of 20 pmol of MG. Laser excitation at 532 nm. Reprinted with permission from Ref. [31]. Copyright 2021 Wiley‐VCH GmbH.

Among the coatings with 2‐mercaptoethanol (ME), sodium‐3‐mercapto‐1‐propane sulfonate (MPS), glutathione (GSH), O‐(2‐mercaptoethyl)‐O’‐methylhexa(ethylene glycol) (PEG350), and poly(ethylene glycol) methyl ether thiol (PEG800), MPS and PEG800 allowed the sharpest plasmonic dot. Malachite Green (MG) was used at 10 pmol to evaluate the SERS efficiency and MPS‐coated NPs resulted in the best substrate leading to the highest signal. Also, the concentration of Fe−Ag NPs was studied to see how this affected the Raman signal, finding a small dependence in the range 1–16 mg/mL with an optimum at 4 mg/mL.

Guadagnini et al. also exploited the combination of plasmonic and magnetic properties in Au−Co and Ag−Co NPs for SERS detection of MG in magnetically assembled plasmonic dot arrays.[ ³¹ , ³⁷ ] For Au−Co nanoalloys, the Raman spectra were recorded with different concentrations of MG (20, 2, and 0.2 pmol) and the pattern were detected for all the samples. This was the first demonstration of SERS in Au−Co nanoalloys. In the case of Co−Ag NPs, a SERS enhancement factor higher than 10⁶ was predicted with DDA calculations and the NPs coated with glutathione and without coating provided the highest Raman signal compared to those coated with MPS.

The advantages brought by magnetic properties of plasmonic NPs for SERS have been demonstrated also in colloidal solutions with PEG‐coated and MPS‐coated Fe−Ag NPs. Using MG as an analyte and an external magnet for the reversible accumulation of the NPs in a small volume of the liquid solution, the SERS signal increment was demonstrated as well as the substrate reusability after the analysis by dialysis to remove the analyte.[ ¹⁵⁸ , ¹⁵⁹ , ¹⁶⁰ ] This is a general demonstration of the possibility of using the magnetic separation of SERS analytes in complicated mixtures. Besides, the use of external magnetic fields and PEG coatings with variable lengths permitted the reversible tuning of electromagnetic hot‐spots between Fe−Ag NPs. ^[159]

The first demonstration that SERS was possible in alloys of plasmonic NPs with magnetic elements was reported with Au−Fe NPs synthesized by LAL. ^[30] Even in that case, the MG was successfully detected thanks to a SERS enhancement factor resulting only 20 times lower going from pure Au to an Au₈₇Fe₁₃ alloy. Due to the paramagnetism of Au−Fe alloys in such a composition range, as discussed in the previous paragraphs, no response to external magnetic fields was possible.

SERS can be also exploited for Raman labelling, when a Raman active molecule (Raman reporter) is stably attached to suitable plasmonic NPs, to generate stable, ultra‐intense and reporter‐specific Raman signals. Ma et al. described an efficient way to exploit the hybridization of plasmonic modes of Au core and Au−Ag shell in Au/Au−Ag CS NPs while also avoiding possible desorption of the Raman reporter. ^[228] The Raman active molecule is embedded in the gap between Au and Au−Ag shell during NPs synthesis to achieve a superior electric field enhancement and avoid the desorption of molecules over time. The gap size allows tuning the LSP position and optimal excitation wavelength for Raman spectroscopy, but the experiments evidenced that the thinner is the gap the higher is the Raman signal. This was explained with calculations of electric field distribution in the NPs. The number of layers was also investigated, pointing to the CS with three gaps as those with the highest Raman signal.

The combination of magnetic and plasmonic properties in Au−Fe alloy NPs was also exploited for the realization of multimodal contrast agents for Raman imaging, magnetic resonance imaging (MRI) and x‐ray computed tomography (CT). ^[229] While MRI and CT are total‐body pre‐operative techniques, Raman imaging is an intraoperative tool exploitable in situ during surgeon intervention. Hence, the Au−Fe alloy NPs demonstrated for the first time the advantages of plasmonic nanoalloys for the simultaneous generation of contrast for the three different techniques.

Compared to fluorescence imaging, SERS labelling has the advantage of lower background interference and unique signal identification associated with the vibrational fingerprint of the Raman reporter. However, the analysis time is typically longer than for fluorescence or optical microscopy, which is not optimal for other types of investigations as histopathological analysis. To this end, Au−Ag alloys with 10 and 50 % of gold were used by Valiquette et al. for dark‐field multispectral imaging of cytological stained samples. ^[230] The exploitation of plasmonic alloys in standard cytopathological bioimaging procedures showed the possibility to use these NPs in cancer diagnostic with high sensitivity and specificity.

6. Conclusions

In this review, an overview of the most recent advances in the field of nanoalloys for plasmonic‐related applications was provided. Alloying traditional plasmonic materials has attracted considerable interest because of the several advantages (Figure 25):

Figure 25.

Summary of key advantages and open challenges in the field of plasmonic nanoalloys.

• the optimization of plasmonic properties (extinction, absorption, local field enhancement),

• the introduction of additional functionalities (magnetism, catalytic efficiency, chemical selectivity),

• the improvement of intrinsic features (cost reduction, biocompatibility, chemical stability or surface coupling with other materials),

• or just to benchmark current knowledge of synthetic and modelling skills and promote their further refinement.

All this is expected to expand the range of applications and, ultimately, the market of nanomaterials, which is already in continuous growth since more than two decades.

The synthesis of most plasmonic nanoalloys is still a challenge due to the low miscibility of plasmonic metals with magnetic or catalytic ones, as well as to the different tendency to oxidation. Several synthetic strategies to overcome these difficulties have been mentioned, in particular those acting under a controlled environment (high vacuum, gas atmosphere) or running out of equilibrium by fast heating and fast cooling.

Moreover, at the nanoscale, the phase diagrams may deviate from the bulk state. Therefore, it is still difficult to foresee the thermodynamic stability of a new unexplored nanoalloy and choose the right synthetic method to produce it. A map of modelling approaches for plasmonic nanoalloys was provided, showing the many computational techniques available and the possibility of their integration to address the multifaceted problem of nanoalloys structure, properties and stability under operating conditions.

The knowledge of the OC of plasmonic nanoalloys is crucial because it allows the prediction of the optical properties of real systems. It cannot be obtained by the average of single‐element materials, except for a few limited exceptions that are generally not challenging from the synthetic point of view. Consequently, the reliable modelling of the OC and its relationship with the electronic structure of the metal has been deeply investigated in the literature.

The optical, hot‐carriers generation and magnetic features of plasmonic nanoalloys have stimulated a wide list of investigations and opened a series of possible applications, mostly in the fields of plasmon‐enhanced catalysis, nanomedicine, optical sensing and detection of analytes by local electric field enhancement (SERS, MEF).

The above panorama evidenced some open issues:

• An obvious list of synthetic challenges exists, given a large number of possible alloys of interest, mostly related to the control of composition shape, size homogeneity, surface coating, purity, surrounding matrix, dispersion, processing of products, sustainability of the method and its scalability in case of large‐scale exploitation. A special chapter is for metastable phases and immiscible compounds, especially those not yet synthesized, requiring an improved control on out‐of‐equilibrium synthetic routes.

• Characterization of alloys is more complex than what is generally believed in literature. The understanding of nanoalloys structure at the atomic scale is missing because the resolution of most techniques is unable to observe subnanometric segregation and disordered domains, which instead are highly likely in several immiscible systems (Au−Fe, Ag−Fe, Au−Co, Ag−Co etc.). Surface and core compositions may be different and immiscible phases tend to have relevant amorphous domains, often imperceptible with standard characterization techniques. This lack of information poses a serious problem for the real understanding of the property‐structure relationship and the reliability of modelling approaches.

• Concerning properties and applications, while nanoalloys are relatively close to real‐world applications in nanomedicine (biodegradable alloys) and sensing (Au−Ag alloys), mutual phenomena like magneto‐optics, optical activity and nonlinear optics are still poorly investigated and understood.

• A better comprehension of hot carriers generation and the distinction of the various processes involved are currently at the forefront of research endeavours in plasmonics and nanoalloys. Indeed the typical efficiency of plasmon‐enhanced catalytic processes is of few %, then much more effort is required in the future to bring plasmonic nanoalloys inside chemical processes of relevance for a sustainable future.

Nonetheless, by addressing the above challenges in the field of plasmonic nanoalloys, relevant improvements about profound concepts of materials science, photonic technologies, magneto‐optics, healthcare and sustainability are expected.

Conflict of interest

The authors declare no conflict of interest.

Biographical Information

Vito Coviello received the B.Sc. in Chemistry in 2018 from the University of Basilicata and the M.Sc. in Chemistry in 2020 from the University of Padova. He is currently a PhD student in Science and Engineering of Materials and Nanostructures at the University of Padova, working in the Laser Assisted Synthesis and Plasmonics, and he has been a visiting PhD Student at the Universitè Claude Bernard Lyon 1. His research focuses on the study of the relationship between electronic and plasmonic properties in alloys nanoparticles for plasmon‐enhanced photocatalysis.

Biographical Information

Daniel Forrer received his Ph.D. in Chemical Sciences at the University of Padova in 2010. Since 2012 he has been a researcher at the National Research Council of Italy. During his career he was visiting fellow at the University of Naples “Federico II” and at the University of Princeton, New Jersey. His current research is focused on the computational modeling of metal alloys with specific interest in their optical response, and on the modeling of electrocatalytic processes at surfaces.

Biographical Information

Vincenzo Amendola is Professor of Physical Chemistry at Padova University, where he established and directs the Laser Assisted Synthesis and Plasmonics lab. His research activity is focused on the mechanisms behind laser processing of colloids and its application to the synthesis of unconventional and metastable nanomaterials, that are exploited for experimental and theoretical investigations in the fields of plasmonics, sensing, nanomedicine and heterogeneous catalysis. He obtained the PhD in Materials Science and Engineering in 2008 and the Italian qualification as Full Professor in 2017, after research experience at Massachusetts Institute of Technology and Cambridge University. He is part of the Program Committee of the ANGEL conference series and he is a currently a member of the ChemPhysChem and Nanomaterials Editorial Advisory Boards. He was honoured with the Levi prize, the Semerano prize, the Young Innovators Award, the Alceste Mion Award and the Belloni prize. He is in the top 100 k scientists of the last “science‐wide author databases of standardized citation indicators” (year 2020).

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

V. Coviello, D. Forrer, V. Amendola, ChemPhysChem 2022, 23, e202200136.