Abstract
This study investigated the systematic rise in cognitive ability scores over generations, known as the Flynn Effect, across middle childhood and early adolescence (7–15 years; 291 monozygotic pairs, 298 dizygotic pairs; 89% White). Leveraging the unique structure of the Louisville Twin Study (longitudinal data collected continuously from 1957 to 1999 using the Wechsler Intelligence Scale for Children [WISC], WISC–R, and WISC–III ed.), multilevel analyses revealed between-subjects Flynn Effects—as both decrease in mean scores upon test re-standardization and increase in mean scores across cohorts—as well as within-child Flynn Effects on cognitive growth across age. Overall gains equaled approximately three IQ points per decade. Novel genetically informed analyses suggested that individual sensitivity to the Flynn Effect was moderated by an interplay of genetic and environmental factors.
In 1984, James Flynn found that American standardization samples, including children, scored systematically higher on older versions of IQ tests than they did on newer versions, reflecting a 13.8-point rise in mean IQ scores between 1932 and 1978 (approximately three points per decade; Flynn, 1984). The secular rise in standardized intelligence scores, now known as the Flynn Effect (FE), has since been replicated widely in children and adults (Pietschnig & Voracek, 2015). The FE is typically documented by giving the same sample two versions of a cognitive ability test and noting lower mean scores on newer versions than on older versions, as in Flynn’s original study (we refer to these as test version effects). Other evidence comes from studies of European military conscripts, in which cohorts from more recent generations scored systematically higher than previous cohorts on the same test version (cohort effects; e.g., Sundet et al., 2004; Teasdale & Owen, 2008).
Meta-analytic estimates have been roughly consistent with Flynn’s original observation of an increase in three IQ points per decade, with measures of fluid intelligence (problem solving and abstract reasoning that do not rely on previous knowledge; measures include performance IQ [PIQ]) frequently showing greater gains over time than measures of crystallized intelligence (application of knowledge previously acquired through experience and education; measures include verbal IQ [VIQ] and vocabulary; Pietschnig & Voracek, 2015). Studies from developing regions tend to yield even larger effects (e.g., children in rural Kenya; Daley et al., 2003), whereas IQ gains in developed regions appear to have decelerated over the past century (Pietschnig & Voracek, 2015), and evidence suggests that scores have even started to decline slightly (Sundet et al., 2004; Teasdale & Owen, 2005, 2008). These results suggest that the FE is positively linked to societal modernization and development; scores appear to rise as regions develop until possibly reaching an asymptote.
The FE has had a profound impact on developmental researchers’ conceptualizations of cognitive ability. It provides evidence that broad changes to environments in which children are raised can influence cognitive development, which is driven by a dynamic interplay of genetic and environmental factors (Dickens & Flynn, 2001; Flynn, 2007; Pietschnig & Voracek, 2015). Findings regarding the relative strength of the FE at different stages of development have been inconsistent, with one meta-analysis observing larger effects in adults than in children (Pietschnig & Voracek, 2015) and another finding no differences across ages (Trahan et al., 2014).
Practical implications
In addition to informing theoretical perspectives on cognitive development, the FE has altered the day-to-day lives of individual children. Howard (2001) provided correlational evidence of real-world changes that may reflect rising cognitive ability. More disconcertingly, the FE influences outcomes that depend on falling above or below a set IQ score cutoff, especially for children. In the United States, intellectual disability is commonly identified in part as having an IQ score below 70 (e.g., American Psychiatric Association, 2013). Work by Kanaya, Ceci, and Scullin has demonstrated that rates of intellectual disability diagnosis drop steadily in the years prior to the introduction of a new IQ test version; due to the FE, the number of children scoring below the 70-point cutoff gradually decreases (Scullin, 2006). Upon the introduction of a new test version, intellectual disability diagnoses increase significantly because children who would have scored just above the cutoff on the older version score below it on the new one (Kanaya, Ceci, et al., 2003; Kanaya, Scullin, et al., 2003; Scullin, 2006). Since children with intellectual disability typically qualify for special education programs, this results in a large, rather sudden increase in the number of children in special education, creating a host of challenges for school districts (e.g., allocation of financial and teacher resources).
Kanaya and Ceci (2012) found that the FE also changes the prevalence of learning disability diagnosis among children. Diagnosis of a learning disability often requires a child’s IQ score to be markedly higher than their achievement score. By causing IQ scores to drop, test re-standardization can shrink the gap between IQ and achievement scores, significantly reducing the probability that a child previously diagnosed with learning disability using an old test version will be re-diagnosed. This creates an opposite problem to that seen in intellectual disability: children who were once enrolled in special education programs become ineligible. Abruptly losing special education resources can be extremely difficult for children, forcing them to grapple with academic and social challenges without the supports on which they formerly relied.
Research implications
The FE poses a serious problem in cross-sectional studies of cognitive ability that include multiple generational cohorts or multiple test versions. In one striking example, the FE accounted for about 85% of supposedly age-related IQ disparities between 20- and 70-year olds (Dickinson & Hiscock, 2010). Even when comparing groups at a single age, failing to adjust for between-group differences in cohort or test version could make groups appear more dissimilar than they really are.
The FE may also confound longitudinal studies in which individuals take multiple IQ test versions, such as studies of cognitive growth in children. Consider a longitudinal analysis in which two different versions of the Wechsler Intelligence Scale for Children (WISC; commonly used to measure cognitive ability in children) were administered at ages 8 and 16. If intra-individual changes in cognitive ability are observed over that span, how can one be sure that they reflect actual cognitive changes and not test version artifacts introduced by the FE? If changes are not observed, could test re-standardization have flattened effects that otherwise would have been observed? The FE could be particularly problematic in analyses of unstandardized raw scores, which change substantially as children grow intellectually.
What causes the FE?
Potential causes of the FE have been debated extensively (see Neisser, 1998). Although a comprehensive summary of that debate falls outside the current study’s scope, it is worth emphasizing that the FE is almost certainly driven by environmental, as opposed to genetic, influences. Indeed, as mentioned above, one of the FE’s most important implications is that environmental factors can substantially affect cognitive development at a population level (Dickens & Flynn, 2001; Flynn, 2007; Pietschnig & Voracek, 2015).
Various potential environmental mechanisms have been proposed, including improvements in education (Williams, 1998) and nutrition (Lynn, 2009), increasing environmental complexity (Schooler, 1998), technological advancement (Neisser, 1997), decreasing family sizes (Sundet et al., 2008), and reductions in exposure to harmful pathogens (Kaufman et al., 2014) and disease (Eppig et al., 2010). No single environmental factor appears to be solely responsible for increasing mean IQ scores. Rather, the FE likely emerges from a complex combination of multiple factors, which may vary by cohort and environmental context (see Dickens & Flynn, 2001).
Some have argued that the FE is caused by neither genetic nor environmental influences on intelligence, but instead by measurement artifacts that alter the nature of IQ tests. Kaufman (2010), for example, asserted that the content, administration, and scoring of the Similarities subtest changed so substantially during the update from the original version of the WISC (Wechsler, 1949) to the WISC–Revised (WISC–R; Wechsler, 1974) that any cross-test analysis amounts to comparing apples to oranges. Because the subtest itself changed, he argued, it is impossible to be sure that children’s gains on Similarities reflect actual improvement in abstract reasoning; the subtest could have just gotten harder, causing mean scores on Similarities (and therefore also IQ) to drop. The same logic could be applied to any other subtest for which test re-standardization resulted in a drop in scores. However, others have argued that test sophistication-related gains would not be large enough to explain a meaningful proportion of the FE (Ceci & Kanaya, 2010), and test sophistication cannot explain effects observed in cohort studies that used a single test version.
Changes in test-taking behavior have also been cited as a measurement artifact that could cause the FE, particularly in cohort studies. Brand (1987) speculated that test-takers have engaged in increasingly more guessing behavior over time, resulting in higher scores, particularly on fluid intelligence measures (which are often multiple-choice and therefore more amenable to guessing). The validity of Brand’s hypothesis has been debated, with some suggesting that guessing-related effects would be too small to explain the FE (Flynn, 1990; Pietschnig & Voracek, 2015).
Within- and between-level FEs
The FE has usually been documented as a between-subjects phenomenon, either as mean increases in cognitive ability scores over generations or mean decreases between test versions. There is reason to suspect that environmental influences associated with between-subjects FEs also influence cognitive ability at the individual level, boosting intellectual growth across development above and beyond typical age-related gains. Dickens and Flynn (2001), for example, proposed that environmental enrichment makes it easier for children to select into environments that match their cognitive ability. Cognitively beneficial environments, in turn, boost cognitive growth, which facilitates further self-selection into more positive environments, in turn boosting cognitive ability, and so on, creating a reciprocal cycle that makes individual children exhibit greater intellectual growth across development. The individual gains brought about by individual multipliers, as Dickens and Flynn (2001) called them, can be thought of as within-person FEs. If enough children in a given population show such within-person FEs, the group mean will also rise, eventually resulting in a between-subjects FE across cohorts. A reciprocal process of social multipliers, which is the between-subjects analog of the individual multipliers process, can compound mean cognitive ability gains over time.
Although the possible connection between within- and between-level FEs has been discussed for two decades, few studies have examined this empirically. Effective investigation of within-person FEs requires longitudinal data to model individual cognitive growth across age and isolate within-person FEs from age-related gains, as well as multilevel data across cohorts to distinguish within-level FEs from between-level FEs. Datasets meeting those criteria are rare and, perhaps because of this rarity, nearly all previous FE studies have performed solely cross-sectional, between-subjects analyses. Only two previous reports have investigated within-person FEs using a multilevel approach. In two distinct multilevel analyses of math scores collected longitudinally across childhood between 1986 and 2012, O’Keefe and Rodgers (2017) observed significant within-person FEs, along with between-subjects gains. Later, O’Keefe and Rodgers (2020) performed a follow-up analysis of the same data. Results highlighted the utility of examining within-person FEs using longitudinal, multilevel approaches, to arrive at a more nuanced understanding of the FE.
Gaps in the existing literature
Hundreds of studies on the FE have been conducted to date. Nevertheless, several substantial gaps in the literature remain. First, no study of which we are aware has examined both test version and cohort effects simultaneously within a single sample. Test version studies and cohort studies each face limitations: the former could be affected by measurement artifacts (Kaufman, 2010), whereas the latter (historically conducted in adult, European, almost entirely male military conscript samples) may not generalize to other populations, including children. Analyzing test version and cohort effects together in the same sample could improve researchers’ ability to address these limitations. Observing both types of effects simultaneously would increase confidence that a genuine FE exists above observing one or the other alone. Furthermore, the magnitude of FE estimates may vary depending on whether the test version or cohort approach is used (Weiss et al., 2016). Estimating test version effects while controlling for cohort effects, and vice versa, would clarify the relative magnitude of each type of FE.
Second, given concerns about the representativeness of military conscript samples, the extent to which previously observed cohort FEs generalize to other populations remains unclear. Few previous studies have examined cohort effects in children or adolescence (see Bocéréan et al., 2003; Graves et al., 2019; Must et al., 2009; Rodgers & Wänström, 2007; Weiss et al., 2016). Similarly, although test version effects have been well documented in U.S. samples, studies of cohort FEs in U.S. samples of any age are relatively rare. The closest American analog to large, European military conscript IQ datasets is the Armed Services Vocational Aptitude Battery, but it is arguably more of a literacy test than an IQ test (Marks, 2010) and has been updated periodically.
Third, as mentioned above, only two previous studies, the second of which was an extension of the first (O’Keefe & Rodgers, 2017, 2020) have examined FEs on within-person growth in cognitive ability across development. That study analyzed math performance, a measure of fluid intelligence, but the presence of within-person FEs on other cognitive domains is unknown. Furthermore, O’Keefe and Rodgers (2017) used the cohort design; within-person FEs have never been examined in studies that included multiple test versions. Along with enabling within-person FE analyses, longitudinal models yield more stable estimates of differences between cohorts (Schaie et al., 2005) and offer more statistical power than cross-sectional models (Giangrande et al., 2019).
Finally, although the FE is at the crux of debates over the relative influence of genetic and environmental factors on cognitive development, genetically informed studies of cognitive ability gains across generations have never been conducted. This, again, may be due to a lack of studies with the necessary data structure (i.e., family data on cognitive ability collected longitudinally across cohorts). O’Keefe and Rodgers (2017) included siblings in their multilevel FE analyses, but did not conduct genetically informed analyses. The FE is likely caused by environmental factors, but the extent to which a given individual receives an environmental boost may be moderated by genetic factors, as is true of any trait (Turkheimer, 2000). Returning to the theory of individual and social multipliers, Dickens and Flynn (2001) hypothesized that complex gene–environment interplay results in a positive association between children and beneficial environments, boosting individual cognitive ability across development (within-person gains) and ultimately group means (between-subject FEs) as well. Genetically informed FE studies may help clarify this sort of gene–environment interplay, both in the context of the FE and cognitive development more generally.
Current study
In this study, we examined the FE in data from the Louisville Twin Study (LTS), an intensive longitudinal study of cognitive development (Rhea, 2015; Wilson, 1983). Analyses focused on middle childhood and early adolescence (ages 7–15 years). Several features of the LTS data make them particularly well-suited for FE analyses and for addressing the gaps in the literature described above. First, initial data were collected continuously from 1957 to 1999, making it possible to test for rising IQ scores across generational cohorts of U.S. boys and girls over a long time span. Second, three versions of the WISC were administered over the course of the study (WISC, WISC–R, and WISC, 3rd ed. [WISC–III]). This allowed us to examine whether test re-standardization resulted in systematic drops in mean IQ scores. Third, children were followed longitudinally, with some taking multiple versions of the WISC over the course of their participation. This enabled us to test for FEs not only between subjects (i.e., rises in mean scores), but also within children (i.e., rate of within-person cognitive growth), all while taking advantage of the statistical benefits offered by longitudinal models (e.g., distinguishing age effects from cohort effects, increased power). Finally, because the LTS is a twin study, we were able to partition the variance of the within-person FE into genetic and environmental components (also referred to as biometric components) and examine the relative influence of genetic and environmental factors on individual sensitivity to the FE. In doing so, we performed the first-ever genetically informed analyses of the FE.
Thus, the unique structure of the LTS data enabled us to examine the FE as both cohort effects and test version effects simultaneously in a single sample. This data structure also made it possible to analyze FEs both within children and between children, and to examine the relative influence of genetic and environmental factors on within-person FEs. By modeling all of these elements, we were able to isolate specific aspects of the FE while controlling for alternate effects (i.e., cohort vs. test version effects, within- vs. between-level effects, genetic vs. environmental components). At the between-subjects level, we hypothesized that we would observe evidence of the FE in two ways: (1) for a given age and test version, children who participated more recently in the LTS testing period would have higher cognitive ability scores on average than previous cohorts; (2) for a given age and cohort, children who took newer WISC versions would score lower on average than children who took older versions. Within individual children, we expected that within-person FEs would boost the rate at which children grew intellectually between ages 7 and 15 beyond expected age-related growth. Because this was the first genetically formed study of the FE, we treated our biometric analyses as exploratory.
METHOD
Participants
All participants were from in and around Louisville, Kentucky in the United States. The sample was predominately White (89%) and of average IQ (Table 1). The entire distribution of socioeconomic status (SES) was represented, with comparable numbers of low, average, and high SES children included: lower quartile, median, and upper quartile for scores on the Hollingshead Index (a continuous 0- to 100-point scale collected at initial registration, with higher scores indicating higher SES) were 24, 49, and 70, respectively (Hollingshead, 1975). We analyzed data from 589 twin pairs (291 monozygotic [MZ], 298 dizygotic [DZ]; 241 same sex female, 219 same sex male, 129 opposite sex). Zygosity was determined by blood serum analysis. Twins were enrolled in the LTS shortly after birth, and then followed prospectively until age 15. Data were collected continuously, with new participants registered on a rolling basis. The present study analyzed longitudinal cognitive data collected at ages 7, 8, 9, 12, and 15 years (3838 individual cognitive measurements). Typically, twins were tested within 1 week of their birthdays. Table 2 summarizes longitudinal data coverage. In the earlier years of the LTS, age 12 data were not collected systematically, resulting in fewer observations than other ages. Average number of observations per twin was 3.25 (SD = 1.23). 12.87%, 10.41%, 32.35%, 27.60%, and 16.77% of the sample were tested at one, two, three, four, and five ages, respectively.
TABLE 1.
Demographic and descriptive information
| Age (years) | MZ/DZ pairs | SS female/SS male/OS | % White/Black/“Other”/Multiracial | SES | FSIQ | % WISC/WISC–R/WISC–III |
|---|---|---|---|---|---|---|
| 7 | 239/242 | 207/173/101 | 89/10/1/1 | 47.89 (25.89) | 98.18 (14.12) | 23/56/21 |
| 8 | 254/257 | 216/190/105 | 90/8/1/0 | 47.53 (26.40) | 101.85 (14.02) | 31/51/17 |
| 9 | 194/200 | 161/139/94 | 88/9/1/1 | 46.68 (27.15) | 102.80 (14.45) | 12/67/22 |
| 12 | 71/84 | 55/59/41 | 81/17/1/1 | 44.32 (28.91) | 100.79 (14.43) | 1/59/40 |
| 15 | 192/186 | 164/141/73 | 93/6/1 | 46.48 (26.30) | 99.88 (14.06) | 0/81/19 |
| All ages | 291/298 | 241/219/129 | 89/9/1/1 | 47.74 (26.61) | 100.65 (14.27) | 17/62/21 |
Note: Race data were missing for four twin pairs. “Other” is the designation used in the archival Louisville Twin Study data; more detailed race information was unavailable. Some total percentages are not exactly 100 due to rounding. SES and FSIQ presented as mean (SD).
Abbreviations: DZ, dizygotic; FSIQ, full-scale IQ; MZ, monozygotic; OS, opposite sex; SES, socioeconomic status; SS, same sex; WISC, Wechsler Intelligence Scale for Children; WISC–R, WISC–Revised; WISC–III, WISC, 3rd ed.
TABLE 2.
Longitudinal data coverage
| Age (years) | 7 | 8 | 9 | 12 | 15 |
|---|---|---|---|---|---|
| 7 | 0.82 | — | — | — | — |
| 8 | 0.71 | 0.86 | — | — | — |
| 9 | 0.53 | 0.63 | 0.67 | — | — |
| 12 | 0.25 | 0.24 | 0.24 | 0.26 | — |
| 15 | 0.52 | 0.62 | 0.49 | 0.19 | 0.64 |
Note: Diagonal values indicate the proportion of the total sample that had cognitive data at each age. Off-diagonal values represent the proportion of the total sample available to calculate a covariance between cognitive measures at two ages.
Measures
We analyzed WISC, WISC–R, and WISC–III IQ scores (Wechsler, 1949, 1974, 1991). WISC IQ scores are age-standardized to a mean of 100 and standard deviation of 15. We divided IQ scores by 10 to facilitate model fitting. Full-scale IQ (FSIQ) is a measure of general cognitive ability, while VIQ and PIQ measure crystallized and fluid intelligence, respectively. For age, we used the earliest participants’ date of birth (DOB; in May, 1956) as an anchor. All other children’s dates of birth were then defined as the number of days between their actual birthdays and the anchor DOB. To simplify interpretation, we rescaled DOB in decades. Neither test version nor DOB varied within twin pairs; twins in a pair always took the same test version at a given age and, obviously, had the same DOB.
Procedure
We used R (R Core Team, 2020) to prepare the data, calculate descriptive statistics, create plots, and compare the fit of nested models, and fit all models in Mplus Version 8 (Muthén & Muthén, 2017). Missing data were handled using full information maximum likelihood.
To estimate the FE as both between-subjects gains in cognitive ability across generations (indexed by test version and cohort effects) and within-person cognitive growth relative to age-based norms, we developed a three-level multilevel model of cognitive growth. We describe the model below; a path diagram is presented in Figure 1. Repeated measures of cognitive ability between ages 7 and 15 (Level 1) were nested within individual children (Level 2). Individual children, in turn, were nested within twin pairs (Level 3). For person i in pair j at age t, administered test Vjt (i.e., WISC, WISC–R, or WISC–III; test version was coded as −1, 0, 1, assuming linearity across versions for simplicity; members of a twin pair were always administered the same version at a particular age), we first estimated the test version effect b1.
FIGURE 1.
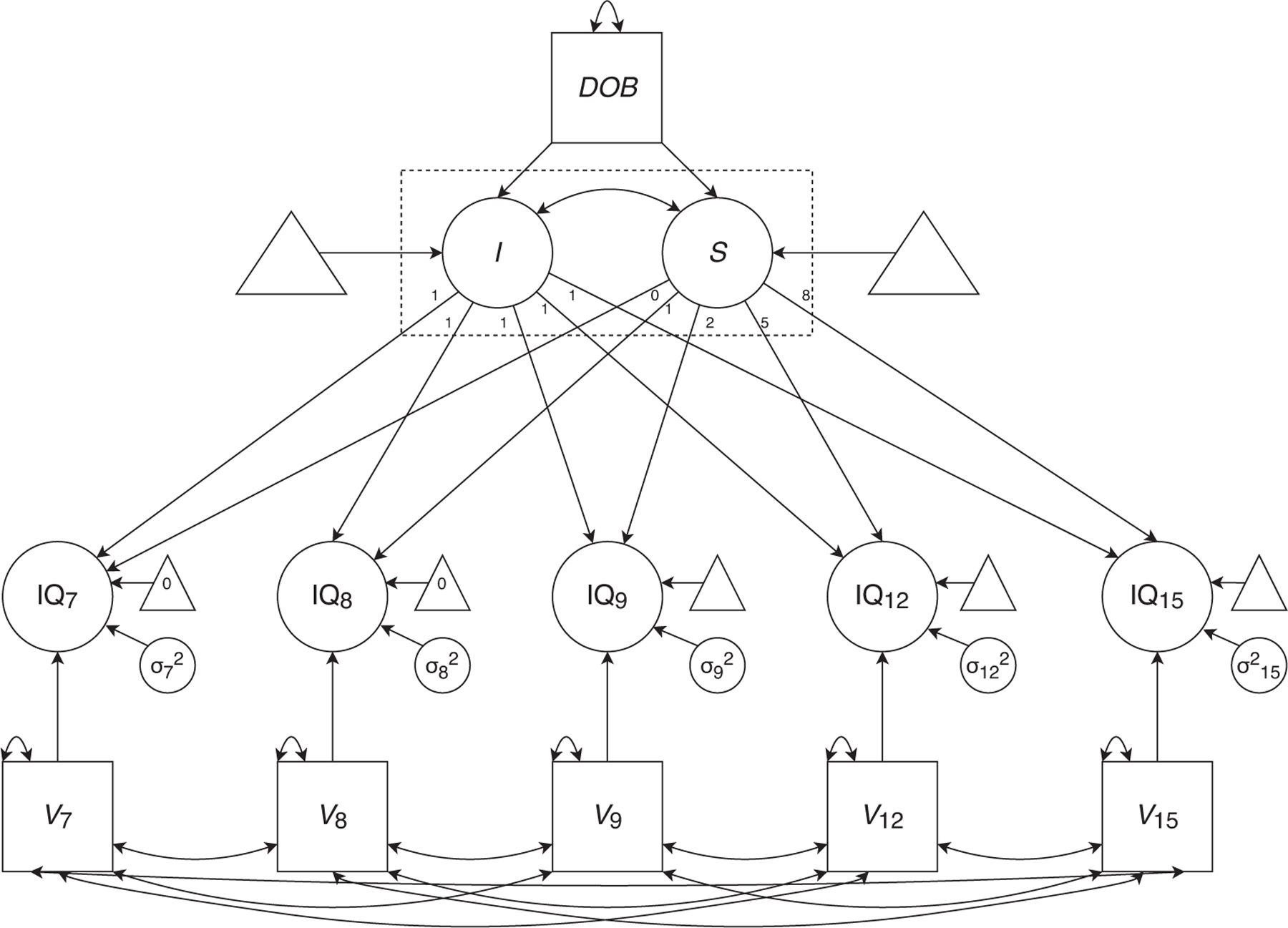
Path diagram of multilevel latent growth curve model. Note. DOB: date of birth. I: latent intercept factor. S: latent slope factor. IQ: placeholder for the specific WISC IQ score we analyzed (FSIQ, VIQ, or PIQ). V: test version (WISC, WISC-R, WISC-III). Parameters in the dotted box were estimated both within- and between-pairs, separately for MZ and DZ twin pairs. The unstandardized regression of I on DOB (b1IB) was constrained to be equal to the mean of the individual-level slopes . Covariances among DOB and V7–15, as well as covariances among between-pair I, between-pair S, and V7–15, were modeled, but are not depicted for the sake of clarity.
We modeled test version effects on observed scores at each age (rather than on latent intercept and slope) because some children took more than one WISC version over the course of their participation in the LTS. Test version effect magnitude was held constant across ages, and all test version parameters covaried with each other and with DOB. We predicted that test version effect estimates would be negative, as this would indicate that mean scores decreased upon the introduction of a new WISC version.
Next, we fit a latent growth model to the cognitive ability scores residualized on test version. Intercepts of the observed cognitive ability scores were fixed to 0 at ages 7 and 8, and estimated freely at other ages.
Two latent growth factors were estimated for each twin. The first, intercept (I), pooled information from all available time points to estimate a twin’s performance at the initial measurement occasion. The second, slope (S), estimated the rate of change from that initial performance over time. We fixed I at age 7. Loadings on S were weighted to account for different time gaps between measurement occasions (e.g., 1 year between ages 7 and 8; 8 years between 7 and 15). Between-pair I and S covaried with each other. Because test version varied across time, between-pair I and S covaried with test version at each age, and these covariances were constrained to be equal across ages.
Within pairs, I and S had means of 0 and variances ( and , respectively), estimated separately for MZ and DZ pairs. Between pairs, I and S had means and . , the average slope of individual IQ scores as a function of age, is the within-person estimate of the FE. We will refer to this within-person estimate as sensitivity to the FE, as it measures the extent to which a given individual shows FE-related gains. The between-pair variances of I and S were modeled as linear functions of date of birth (DOB).
b1IB, the unstandardized regression of the between-pair intercept on DOB, is the between-pair estimate of the FE (specifically, cohort FEs). We hypothesized that the gain per year in mean IQ across cohort (b1IB) would be roughly equivalent to the average gain per year across age in individual twins (; Figure 2). Therefore, we set b1IB equal to . We predicted the resultant estimate would be positive, as this would provide evidence that the FE not only increases mean cognitive ability scores across generations, but also boosts cognitive ability growth within individual children across middle childhood and early adolescence. Covariances were modeled among DOB and test version at each age.
FIGURE 2.
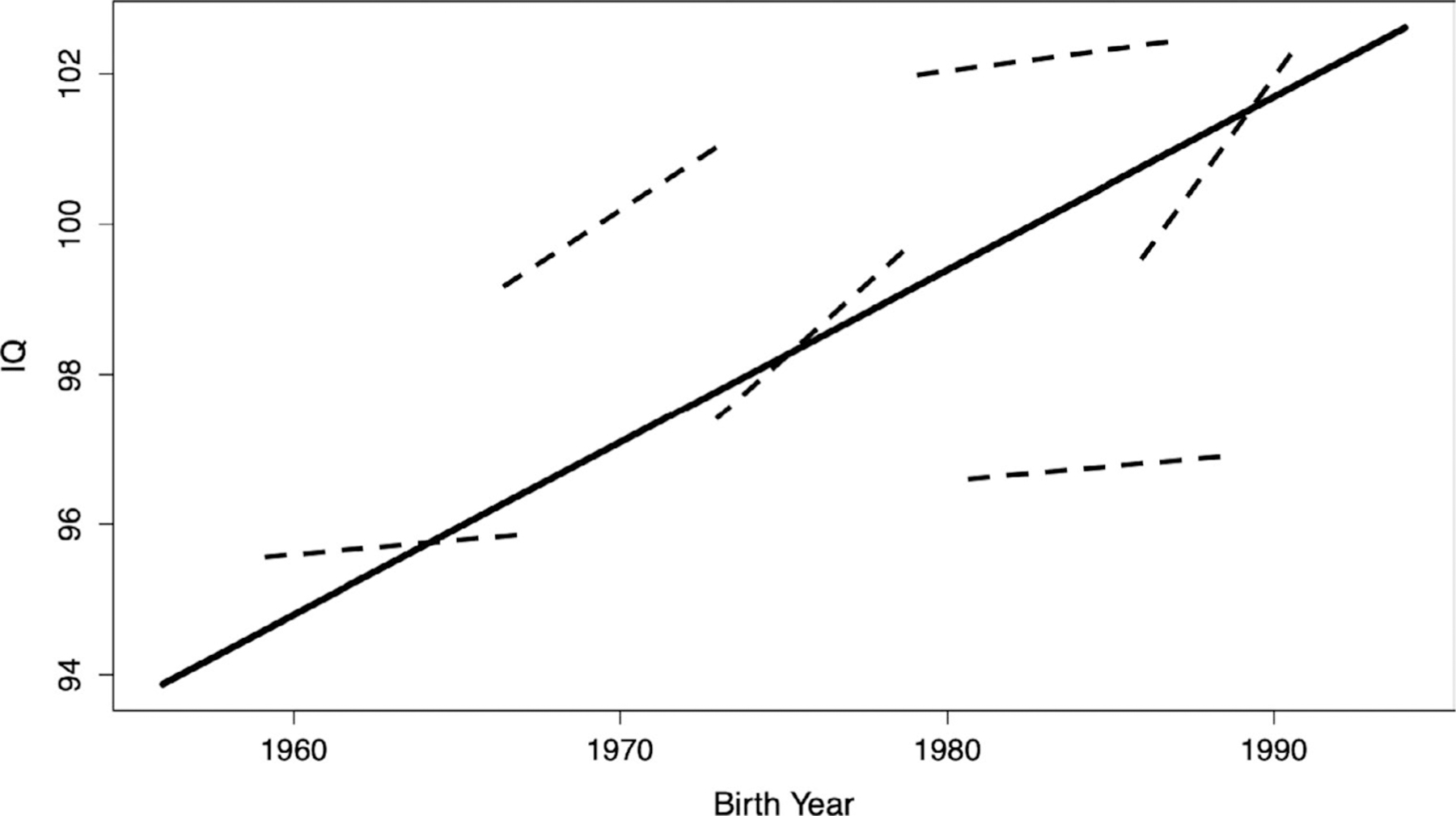
Schematic diagram of the hypothesized association between cohort effects and within-person Flynn Effects. Note. Solid line: unstandardized regression of the between-pair intercept on date of birth (b1IB), which is an estimate of the between-pair cohort effect. Dashed lines: individual-level slopes (Sij) indexing within-person cognitive growth related to the FE between ages 7 and 15. We hypothesized that the FE resulted in both between-pair IQ gains across cohort and within-person gains across age such that average individual-level slope is roughly equivalent to b1IB.
Because the individual-level slopes (Sij) were modeled as a random effect within and between twin pairs, we were able to compute intraclass correlations for MZ and DZ twin pairs (who share roughly 100% and 50% of their genetic material, respectively) and use them to estimate biometric components of the within-person FE. Following the classical twin study design, we computed unstandardized estimates of the proportions of variance in individual-level sensitivity to the FE associated with additive genetic (A; “heritability”), shared environmental (C), and non-shared environmental (E) variance, and then algebraically transformed those into standardized ACE estimates.
To examine the validity of constraining the between-pair cohort effect to be equal to the within-person FE, we used the Satorra–Bentler scaled chi-square difference test (Satorra & Bentler, 2010) to compare the fit of two nested models: one in which b1IB and were held equivalent, as described above, and a second in which those parameters were estimated freely. Individual tests were performed for FSIQ, VIQ, and PIQ.
RESULTS
Descriptive results
Before reviewing the results of our analyses, we will summarize descriptive FSIQ results to give the sense of the LTS data structure as it relates to the FE. Sizeable samples were available for all three WISC versions at ages 7, 8, and 9 (Figure 3; Table S1). Age 12 data were not collected systematically in the early years of the LTS, resulting in a smaller sample size than other ages, and a lack of early cohort and original WISC data at that age. By the time even the earliest LTS participants reached age 15, the WISC was no longer in use.
FIGURE 3.
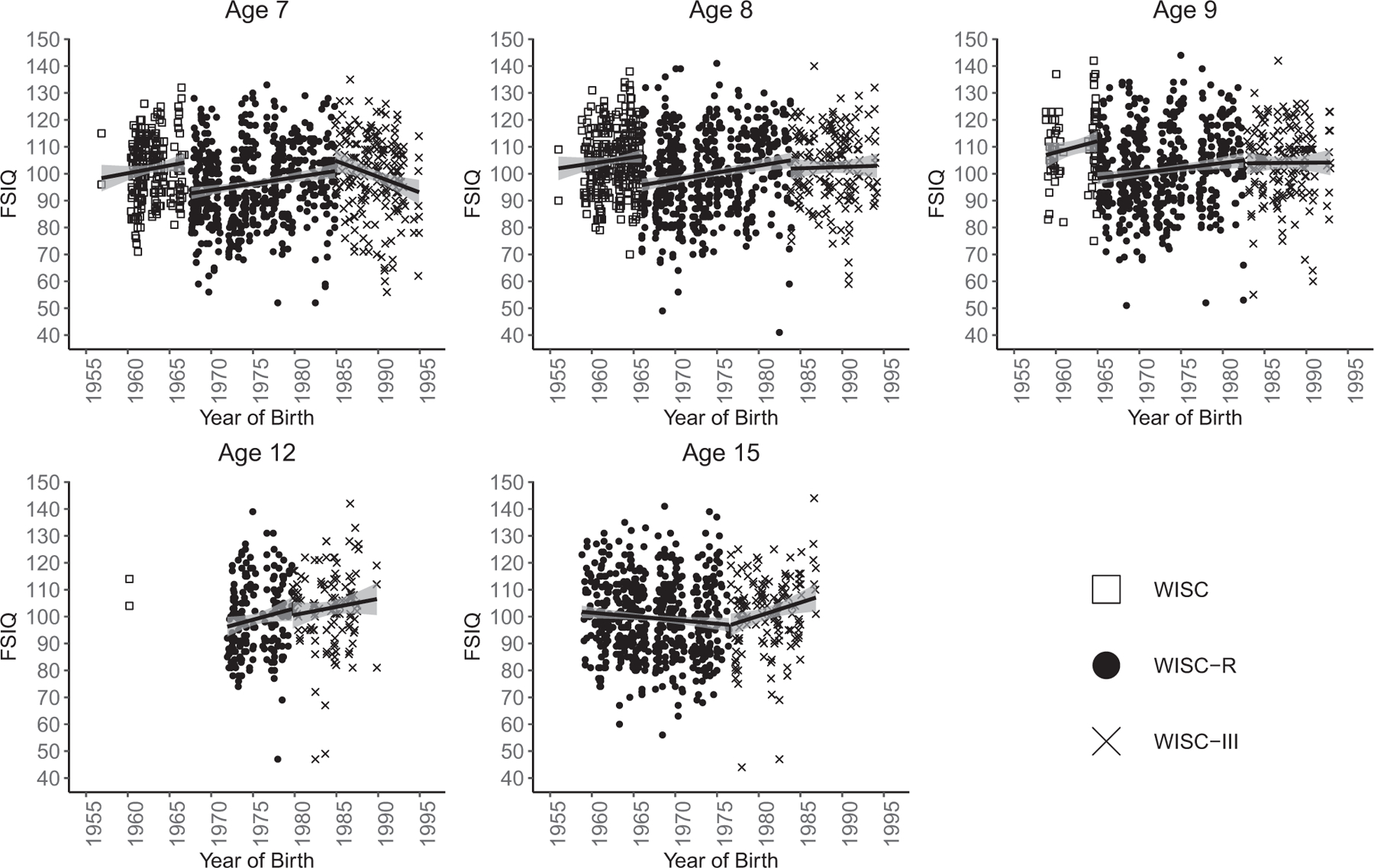
Descriptive scatterplots. Note. FSIQ: full scale IQ.
Descriptive results provided preliminary evidence of the hypothesized between-level FEs. Although mean FSIQ scores were roughly 100 at each age (Table 1), plots of the raw FSIQ data suggested that this stability was a product of mean scores increasing over time (a possible cohort effect) until the introduction of a new WISC version, at which point mean scores decreased suddenly (possible test version effects; Figure 3). Age 8, for which we had the largest sample, showed the clearest preliminary evidence of this pattern of FEs. The consistency of the pattern fluctuated somewhat across the other ages. Scores appeared to increase across cohorts for the WISC at ages 7, 8, and 9, and for the WISC–R at ages 7, 8, 9, and 12. Although WISC–III scores appeared to rise with cohort at ages 12 and 15, WISC–III scores did not appear to change substantially across cohort at ages 8 and 9 and possibly decreased across cohort at age 7. We observed clear decreases in mean cognitive ability scores between the WISC and WISC–R. While mean FSIQ scores decreased modestly between the WISC–R and WISC–III at ages 8 and 12, possible test version effects due to the switch from the WISC–R to the WISC–III were not clearly observable at other ages.
Multilevel latent growth curve model results
Results of multilevel twin analyses are presented in Table 3. The model fit the data well (Table S2). Overall, results supported our hypotheses, and we observed clear evidence of FEs across ages 7–15. Test version effects on the IQ scores were all significantly negative (ps < .001).
TABLE 3.
Multilevel latent growth curve model results
| Measure | b1IB / | S on DOB | IQ on V |
|---|---|---|---|
| FSIQ | 0.32 (0.03)*** | −0.01 (0.01) | −0.49 (0.04)*** |
| VIQ | 0.28 (0.03)*** | −0.01 (0.01) | −0.33 (0.05)*** |
| PIQ | 0.27 (0.04)*** | −0.01 (0.01) | −0.56 (0.05)*** |
Note: Presented as estimate (SE).
Abbreviations: , mean of the individual-level slopes; b1IB and were constrained to be equal; b1IB, unstandardized regression of between-pair intercept (I) on date of birth; DOB, date of birth; FSIQ, full scale IQ; PIQ, performance IQ; S, between-pair slope; V, test version; VIQ, verbal IQ.
p < .001.
Constraining the unstandardized regression of the between-pair intercept on DOB (b1IB) to be equal to the average individual slope across age yielded a significant, positive parameter for FSIQ, VIQ, and PIQ (ps < .001). This constraint did not affect model fit— scaled chi-square difference tests comparing the fit of constrained and unconstrained models were not significant (ps > .25 for all cognitive measures)—and did not alter other parameter estimates substantially (Tables S3 and S4). Furthermore, in models where b1IB and were allowed to differ, the within-person FE estimate was significantly positive (ps < .001), indicating that the within-person FE was present independent of between-level FEs (Table S3). Thus, consistent with our hypotheses and the theory of individual and social multipliers (Dickens & Flynn, 2001), both between-pair cohort effects and within-person FEs were present in our sample, and were roughly equivalent. FSIQ, VIQ, and PIQ all showed gains of approximately three points per decade.
Biometric results are presented in Table 4. Individual-level sensitivity to the FE on FSIQ, VIQ, and PIQ were all associated with substantial proportions of additive genetic, shared environmental, and non-shared environmental variance. Given that not all biometric estimates reached statistical significance and some standard errors were large, some restraint should be exercised when interpreting the magnitudes of the observed ACE components, or how they might differ across cognitive domains. That being said, sensitivity to the FE on FSIQ scores showed the highest heritability, with 64% of the variance associated with additive genetic factors (A; SE = 0.22). The remaining variance was associated with smaller, but sizeable shared (C = 0.26, SE = 0.20) and non-shared environmental and error (E = 0.10, SE = 0.06) components. For sensitivity to the FE on VIQ and PIQ, just under half of the variance was associated with additive genetic factors (VIQ: A = 0.48, SE = 0.18; PIQ: A = 0.45, SE = 0.42). The remaining variance associated with shared environmental (VIQ: C = 0.35, SE = 0.17; PIQ: C = 0.48, SE = 0.38) and non-shared environmental and error variance (VIQ: E = 0.17, SE = 0.05; PIQ: E = 0.08, SE = 0.13).
TABLE 4.
Biometric results: within-person sensitivity to the Flynn Effect
| Measure | ICC MZ | ICC DZ | A | C | E |
|---|---|---|---|---|---|
| FSIQ | .90 (.06)*** | .58 (.10)*** | 0.64 (0.22)** | 0.26 (0.20) | 0.10 (0.06) |
| VIQ | .83 (.05)*** | .59 (.08)*** | 0.48 (0.18)** | 0.35 (0.17)* | 0.17 (0.05)** |
| PIQ | .93 (.13)*** | .70 (.19)*** | 0.45 (0.42) | 0.48 (0.38) | 0.08 (0.13) |
Note: As presented, standardized ACE estimates do not all sum exactly to 1 due to rounding. Presented as estimate (SE).
Abbreviations: A, standardized additive genetic variance; C, shared environmental variance; DZ, dizygotic; E, nonshared environmental variance; FSIQ, full scale IQ; ICC, intraclass correlation; MZ, monozygotic; PIQ, performance IQ; VIQ, verbal IQ.
p < .05.
p < .01.
p < .001.
DISCUSSION
In this study, we conducted a multifaceted investigation of the FE across middle childhood and early adolescence (ages 7–15). Compared to previous studies, which have documented the FE between-subjects either as increases in mean cognitive ability scores across generations (cohort effects) or as sudden decreases in mean scores upon the introduction of a newer WISC version (test version effects), we performed a relatively comprehensive analysis of the FE by leveraging the unique data structure of the LTS (longitudinal twin data collected prospectively over four decades, using three WISC versions) and a multilevel approach. Results indicated that the FE was present in the LTS data in a variety of forms. Consistent with our hypotheses, we observed between-subjects FEs as both cohort effects and test version effects, suggesting that LTS participants from more recent cohorts scored systematically higher on measures of cognitive ability than those born earlier. We also observed evidence of significant within-individual FEs, which were roughly equivalent in magnitude to between-pair cohort effects. Effect sizes were consistent with Flynn’s original finding of three IQ points per decade in gains (Flynn, 1984). Results from novel biometric analyses suggested that individual-level sensitivity to the FE emerged from both genetic and environmental factors.
Developmental changes in cognitive ability can be difficult to observe when cohort, test version, and age are all varying simultaneously. To our knowledge, this was the first study to document cohort and test version FEs together in a single sample. Studies that use either the cohort or test version approach face major limitations inherent in each method (limited representativeness of military conscripts in the former, vulnerability to changes in content between test versions in the latter). The fact that we documented both types of effects substantially increases our confidence that the FE is robust in the LTS sample. Furthermore, modeling both cohort and test version effects enabled us to document the full manifestation of the FE in the LTS, which otherwise might not have been apparent. Although mean IQ scores were approximately 100 at each age (Table 1), this apparent stability was the result of a complex process in which gains across cohorts and within individuals across age were balanced out by decreases in scores due to test re-standardization. Analyzing one type of FE without controlling for the other would have revealed only half of the story.
Using longitudinal data to model the individual-level slope of cognitive ability enabled us to control for age effects when measuring cohort effects, thereby yielding more stable FE estimates (Schaie et al., 2005). We did not observe any significant cohort effects on between-pair slope, suggesting that within-individual gains in cognitive ability across age remained relatively stable over the 40-year span of the sample. It is possible that our use of age-scaled scores (rather than raw scores) impeded our ability to detect between-pair slope effects, should they exist; by definition, scaling scores results in means and standard deviations that remain constant across ages, which flattens intra-individual change in unstandardized cognitive ability across childhood. LTS raw scores are unavailable at this time (originally, only scaled scores were entered into electronic databases), but the LTS team is currently working to enter item-level WISC data, which will enable deeper investigation of possible slope effects. Alternatively, our null between-pair slope findings may indicate that the rate at which children develop cognitive ability has not changed across cohorts. Additional longitudinal studies are needed to resolve these possibilities.
The longitudinal, multilevel data structure of the LTS also enabled us to examine the extent to which the FE manifests not only as between-subjects gains across generations, but also within-person, consistent with Dickens and Flynn’s (2001) theory of individual and social multipliers. The average of each child’s rate of cognitive change (slope) was significant in unconstrained models, and we were able to equate this estimate of the within-person FE with the between-level cohort effect. These results suggest that the FE boosted both individual cognitive growth between ages 7 and 15 relative to age-based norms and mean cognitive ability scores across generations. Our results provide novel evidence of within-person FEs not only on fluid intelligence, as documented previously (O’Keefe & Rodgers, 2017), but also crystallized and general cognitive ability (as measured by VIQ and FSIQ, respectively). Moreover, our within-person FE findings speak to the importance of modeling the FE at multiple levels of analysis, where possible. By capturing both within- and between-level FEs, multilevel models offer a more nuanced understanding of how the FE operates across development. At least in our sample, the FE was not only a population-level phenomenon that drives broad gains in mean cognitive ability across generations. The FE also appeared to influence the cognitive development of individual children, boosting their intellectual growth beyond what would have occurred without positive environmental inputs. Had we only measured between-level FEs, as is traditionally done in FE research, we would have missed this important aspect of cognitive development.
Unique to the LTS, a multilevel approach also set the stage for twin analyses. Theories about the relative role of genetic and environmental factors in the FE have been debated for decades, but no previous study has examined this empirically. By partitioning the variance in within-pair sensitivity to the FE, we were able to perform the first-ever genetically informed investigation of the FE. As Dickens and Flynn (2001) hypothesized, individual differences in sensitivity to the FE were associated with variance in both genetic and environmental background, suggesting that the FE reflects a complex interplay of genetic sensitivity and environmental change that unfolds across cognitive development. Our finding that sensitivity to the FE on FSIQ, VIQ, and PIQ all showed substantial heritability (A) serves as a fascinating example of gene–environment interplay—the extent to which a child’s growth in cognitive ability received a boost from the environment was influenced by genetic factors. The environment also plays an important role, as variance in shared (C) and non-shared (E) environmental factors were both associated with individual-level sensitivity to the FE. Given the magnitudes of the observed standard errors, interpretations about possible biometric differences across cognitive domains should be made with some caution. That being said, results suggested that sensitivity to the FE on FSIQ may be more heritable than sensitivity to the FE on more specific cognitive domains (i.e., crystallized intelligence and fluid intelligence as estimated by VIQ and PIQ, respectively). If robust, this variability speaks to the utility of analyzing the FE in multiple cognitive domains, as biometric results from FE analyses of general intelligence (e.g., IQ) may not apply directly to more specific measures of cognitive ability.
Our findings have important methodological implications for cognitive development researchers. Although the FE is often ignored in developmental studies of cognitive ability, our results show that the FE can confound studies of cognitive development in a variety of ways. Cohort effects can muddy analyses that include participants from multiple generations. Test version effects create difficulties in studies that administered multiple cognitive assessments. Perhaps most challengingly, within-person FEs can alter estimates of individual cognitive growth, making it difficult to parse gains in childhood due to age from environmental boosts. We observed evidence of within-person FEs on scaled scores beyond age-related gains, suggesting that age-standardization may not sufficiently correct for the FE. Of course, few datasets besides the LTS include multiple cohorts, multiple test versions, and longitudinal data, so it will rarely be necessary for a researcher to correct for all of these types of FEs. Nevertheless, even in studies where only type of FE is present, researchers must correct for it in order to obtain accurate estimates of cognitive growth. Because the FE itself may vary considerably depending on context, the exact analytic steps needed to correct for it may vary across studies.
Strengths of the present study include simultaneous analysis of cohort and test version effects in a single sample; the ability to test for the FE across a long time span (four decades) and three test versions; data from across middle childhood and early adolescence, an important developmental period for which cohort effects have been rarely documented; a high proportion of participants with longitudinal data, facilitating within-person analyses; twin data, which made it possible to conduct genetically informed analyses; and a socioeconomically diverse sample, which is useful when studying a putatively environmental effect such as the FE. This study also faces several limitations. First, our results do not rule out the possibility that artifacts of test sophistication could have contributed to observed test version effects (Kaufman, 2010). However, the cohort effects we observed provide independent evidence that cognitive ability scores did indeed rise, and suggest that test version effects at least partially reflected FE gains. Second, we assumed linear FEs. This is common practice in the FE literature, but some evidence suggests that IQ gains across generations may have been nonlinear (Pietschnig & Voracek, 2015). Third, as mentioned above, our use of scaled scores may have limited our ability to detect FEs on between-level rate of change in cognitive ability over time (between-pair slope). Finally, given that the most recent data were collected over 20 years ago using WISC versions that are outdated today, results do not speak to the FE’s current status, and they do not necessarily generalize beyond children from the generational cohorts we examined. Relatedly, although the LTS sample is diverse socioeconomically, almost 90% of twins were White, and all twins were reared in the United States. The extent to which our results would replicate in more diverse sociodemographic samples is unclear. FE research using more diverse samples is needed, particularly given previous evidence that the magnitude of the FE varies considerably depending on environmental context.
Now that we have documented evidence of the FE in the LTS, our group is pursuing several avenues of future research. As mentioned above, the LTS team is in the process of entering previously unanalyzed item-level WISC data, which will enable more sophisticated modeling of within-person change. Soon, it will be possible to extend LTS analyses of the FE across much of the life span; cognitive ability data are available starting at 3 months of age, and a current project is collecting adult cognitive ability data on the twins at midlife (Beam et al., 2020). These efforts will further the field’s understanding of the FE and how to measure and control for it, both in the LTS and other studies of cognitive development.
Supplementary Material
Funding information
This work was supported by the National Institute on Aging (R01AG063949-01 and R03AG048850-01).
Abbreviations:
- DOB
date of birth
- DZ
dizygotic
- FE
Flynn Effect
- FSIQ
full-scale IQ
- LTS
Louisville Twin Study
- MZ
monozygotic
- PIQ
performance IQ
- SES
socioeconomic status
- VIQ
verbal IQ
- WISC
Wechsler Intelligence Scale for Children
- WISC–III
Wechsler Intelligence Scale for Children, 3rd ed.
- WISC–R
Wechsler Intelligence Scale for Children–Revised
Footnotes
SUPPORTING INFORMATION
Additional supporting information may be found in the online version of the article at the publisher’s website.
REFERENCES
- American Psychiatric Association. (2013). Diagnostic and statistical manual of mental disorders (5th ed.). American Psychiatric Association. 10.1176/appi.books.9780890425596.744053 [DOI] [Google Scholar]
- Beam CR, Turkheimer E, Finkel D, Levine ME, Zandi E, Guterbock TM, Giangrande EJ, Ryan L, Pasquenza N, & Davis DW (2020). Midlife study of the Louisville twins: Connecting cognitive development to biological and cognitive aging. Behavior Genetics, 50, 73–83. 10.1007/s10519-019-09983-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bocéréan C, Fischer JP, & Flieller A (2003). Long-term comparison (1921–2001) of numerical knowledge in three to five-and-a-half year-old children. European Journal of Psychology of Education, 18, 405–424. 10.1007/BF03173244 [DOI] [Google Scholar]
- Brand C (1987). Bryter still and bryter? Nature, 328, 110. 10.1038/328110a0 [DOI] [PubMed] [Google Scholar]
- Ceci SJ, & Kanaya T (2010). “Apples and oranges are both round”: Furthering the discussion on the Flynn Effect. Journal of Psychoeducational Assessment, 28, 441–447. 10.1177/0734282910373339 [DOI] [Google Scholar]
- Daley TC, Whaley SE, Sigman MD, Espinosa MP, & Neumann C (2003). IQ on the rise. Psychological Science, 14, 215–219. 10.1111/1467-9280.02434 [DOI] [PubMed] [Google Scholar]
- Dickens WT, & Flynn JR (2001). Heritability estimates versus large environmental effects: The IQ paradox resolved. Psychological Review, 108(2), 346–369. 10.1037//0033-295X.108.2.346 [DOI] [PubMed] [Google Scholar]
- Dickinson MD, & Hiscock M (2010). Age-related IQ decline is reduced markedly after adjustment for the Flynn Effect. Journal of Clinical and Experimental Neuropsychology, 32, 865–870. 10.1080/13803391003596413 [DOI] [PubMed] [Google Scholar]
- Eppig C, Fincher CL, & Thornhill R (2010). Parasite prevalence and the worldwide distribution of cognitive ability. Proceedings of the Royal Society B: Biological Sciences, 277, 3801–3808. 10.1098/rspb.2010.0973 [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Flynn JR (1984). The mean IQ of Americans: Massive gains 1932 to 1978. Psychological Bulletin, 95, 29–51. 10.1037/0033-2909.95.1.29 [DOI] [Google Scholar]
- Flynn JR (1990). Massive IQ gains on the Scottish WISC: Evidence against Brand et al’.s hypothesis. The Irish Journal of Psychology, 11, 41–51. 10.1080/03033910.1990.10557787 [DOI] [Google Scholar]
- Flynn JR (2007). What is Intelligence? Cambridge University Press. [Google Scholar]
- Giangrande EJ, Beam CR, Carroll S, Matthews LJ, Davis DW, Finkel D, & Turkheimer E (2019). Multivariate analysis of the Scarr-Rowe interaction across middle childhood and early adolescence. Intelligence, 77, 101400. 10.1016/j.intell.2019.101400 [DOI] [Google Scholar]
- Graves LV, Drozdick L, Courville T, Farrer TJ, Gilbert PE, & Delis DC (2019). Cohort differences on the CVLT-II and CVLT3: Evidence of a negative Flynn Effect on the attention/working memory and learning trials. The Clinical Neuropsychologist, 35(3), 615–632. 10.1080/13854046.2019.1699605 [DOI] [PubMed] [Google Scholar]
- Hollingshead AB (1975). Four factor index of social status [Unpublished manuscript] Department of Sociology, Yale University. [Google Scholar]
- Howard RW (2001). Searching the real world for signs of rising population intelligence. Personality and Individual Differences, 30, 1039–1058. 10.1016/S0191-8869(00)00095-7 [DOI] [Google Scholar]
- Kanaya T, & Ceci S (2012). The impact of the Flynn Effect on LD diagnoses in special education. Journal of Learning Disabilities, 45, 319–326. 10.1177/0022219410392044 [DOI] [PubMed] [Google Scholar]
- Kanaya T, Ceci SJ, & Scullin MH (2003). The rise and fall of IQ in special ed: Historical trends and their implications. Journal of School Psychology, 41, 453–465. 10.1016/j.jsp.2003.08.003 [DOI] [Google Scholar]
- Kanaya T, Scullin MH, & Ceci SJ (2003). The Flynn Effect and U.S. policies: The impact of rising IQ scores on American society via mental retardation diagnoses. American Psychologist, 58, 778–790. 10.1037/0003-066X.58.10.778 [DOI] [PubMed] [Google Scholar]
- Kaufman AS (2010). “In what way are apples and oranges alike?” A critique of Flynn’s interpretation of the Flynn Effect. Journal of Psychoeducational Assessment, 28, 382–398. 10.1177/0734282910373346 [DOI] [Google Scholar]
- Kaufman AS, Zhou X, Reynolds MR, Kaufman NL, Green GP, & Weiss LG (2014). The possible societal impact of the decrease in U.S. blood lead levels on adult IQ. Environmental Research, 132, 413–420. 10.1016/j.envres.2014.04.015 [DOI] [PubMed] [Google Scholar]
- Lynn R (2009). What has caused the Flynn Effect? Secular increases in the Development Quotients of infants. Intelligence, 37, 16–24. 10.1016/j.intell.2008.07.008 [DOI] [Google Scholar]
- Marks DF (2010). IQ variations across time, race, and nationality: An artifact of differences in literacy skills. Psychological Reports, 106, 643–664. 10.2466/pr0.106.3.643-664 [DOI] [PubMed] [Google Scholar]
- Must O, te Nijenhuis J, Must A, & van Vianen AEM (2009). Comparability of IQ scores over time. Intelligence, 37, 25–33. 10.1016/j.intell.2008.05.002 [DOI] [Google Scholar]
- Muthén LK, & Muthén BO (2017). Mplus user’s guide (8th ed.). Muthen & Muthen. 10.13155/29825 [DOI] [Google Scholar]
- Neisser U (1997). Rising scores on intelligence tests. American Scientist, 85, 440–447. [Google Scholar]
- Neisser U (Ed.). (1998). The rising curve: Long-term gains in IQ and related measures American Psychological Association. [Google Scholar]
- O’Keefe P, & Rodgers JL (2017). Double decomposition of level-1 variables in multilevel models: An analysis of the Flynn Effect in the NSLY data. Multivariate Behavioral Research, 52, 630–647. 10.1080/00273171.2017.1354758 [DOI] [PubMed] [Google Scholar]
- O’Keefe P, & Rodgers JL (2020). The Flynn Effect can become embedded in tests: How cross-sectional age norms can corrupt longitudinal research. Intelligence, 82, 101481. 10.1016/j.intell.2020.101481 [DOI] [Google Scholar]
- Pietschnig J, & Voracek M (2015). One century of global IQ gains: A formal meta-analysis of the Flynn Effect (1909–2013). Perspectives on Psychological Science, 10, 282–306. 10.1177/1745691615577701 [DOI] [PubMed] [Google Scholar]
- R Core Team. (2020). R: A language and environment for statistical computing R Foundation for Statistical Computing. https://www.r-project.org
- Rhea SA (2015). Reviving the Louisville Twin Study: An introduction. Behavior Genetics, 45, 597–599. 10.1007/s10519-015-9763-1 [DOI] [PubMed] [Google Scholar]
- Rodgers JL, & Wänström L (2007). Identification of a Flynn Effect in the NLSY: Moving from the center to the boundaries. Intelligence, 35, 187–196. 10.1016/j.intell.2006.06.002 [DOI] [Google Scholar]
- Satorra A, & Bentler PM (2010). Ensuring positiveness of the scaled difference chi-square test statistic. Psychometrika, 75, 243–248. 10.1007/s11336-009-9135-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaie KW, Willis SL, & Pennak S (2005). An historical framework for cohort differences in intelligence. Research in Human Development, 2, 43–67. 10.1080/15427609.2005.9683344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schooler C (1998). Environmental complexity and the Flynn Effect. In Neisser U (Ed.), The rising curve: Long-term gains in IQ and related measures (pp. 67–79). American Psychological Association. 10.1037/10270-002 [DOI] [Google Scholar]
- Scullin MH (2006). Large state-level fluctuations in mental retardation classifications related to introduction of renormed intelligence test. American Journal on Mental Retardation, 111. 10.1352/0895-8017(2006)111[322:LSFIMR]2.0.CO;2 [DOI] [PubMed] [Google Scholar]
- Sundet JM, Barlaug DG, & Torjussen TM (2004). The end of the Flynn Effect? A study of secular trends in mean intelligence test scores of Norwegian conscripts during half a century. Intelligence, 32, 349–362. 10.1016/j.intell.2004.06.004 [DOI] [Google Scholar]
- Sundet JM, Borren I, & Tambs K (2008). The Flynn Effect is partly caused by changing fertility patterns. Intelligence, 36, 183–191. 10.1016/j.intell.2007.04.002 [DOI] [Google Scholar]
- Teasdale TW, & Owen DR (2005). A long-term rise and recent decline in intelligence test performance: The Flynn Effect in reverse. Personality and Individual Differences, 39, 837–843. 10.1016/j.paid.2005.01.029 [DOI] [Google Scholar]
- Teasdale TW, & Owen DR (2008). Secular declines in cognitive test scores: A reversal of the Flynn Effect. Intelligence, 36, 121–126. 10.1016/j.intell.2007.01.007 [DOI] [Google Scholar]
- Trahan LH, Stuebing KK, Fletcher JM, & Hiscock M (2014). The Flynn Effect: A meta-analysis. Psychological Bulletin, 140, 1332–1360. 10.1037/a0037173 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turkheimer E (2000). Three laws of behavior genetics and what they mean. Current Directions in Psychological Science, 9, 160–164. 10.1111/1467-8721.00084 [DOI] [Google Scholar]
- Wechsler D (1949). Wechsler Intelligence Scale for Children The Psychological Corporation. [Google Scholar]
- Wechsler D (1974). Wechsler Intelligence Scale for Children-Revised The Psychological Corporation. [Google Scholar]
- Wechsler D (1991). Wechsler Intelligence Scale for Children (3rd ed.). The Psychological Corporation. [Google Scholar]
- Weiss LG, Gregoire J, & Zhu J (2016). Flaws in Flynn Effect research with the Wechsler scales. Journal of Psychoeducational Assessment, 34, 411–420. 10.1177/0734282915621222 [DOI] [Google Scholar]
- Williams WM (1998). Are we raising smarter children today? School- and home-related influences on IQ. In Neisser U(Ed.), The rising curve: Long-term gains in IQ and related measures (pp. 125–154). American Psychological Association. [Google Scholar]
- Wilson RS (1983). The Louisville Twin Study: Developmental synchronies in behavior. Child Development, 54, 298–316. 10.2307/1129693 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


