Abstract
Angular measurements are often modeled as circular random variables, where there are natural circular analogues of moments, including correlation. Because a product of circles is a torus, a d-dimensional vector of circular random variables lies on a d-dimensional torus. For such vectors we present here a class of graphical models, which we call torus graphs, based on the full exponential family with pairwise interactions. The topological distinction between a torus and Euclidean space has several important consequences.
Our development was motivated by the problem of identifying phase coupling among oscillatory signals recorded from multiple electrodes in the brain: oscillatory phases across electrodes might tend to advance or recede together, indicating coordination across brain areas. The data analyzed here consisted of 24 phase angles measured repeatedly across 840 experimental trials (replications) during a memory task, where the electrodes were in 4 distinct brain regions, all known to be active while memories are being stored or retrieved. In realistic numerical simulations, we found that a standard pairwise assessment, known as phase locking value, is unable to describe multivariate phase interactions, but that torus graphs can accurately identify conditional associations. Torus graphs generalize several more restrictive approaches that have appeared in various scientific literatures, and produced intuitive results in the data we analyzed. Torus graphs thus unify multivariate analysis of circular data and present fertile territory for future research.
Key words and phrases. Graphical models, circular statistics, network analysis
1. Introduction.
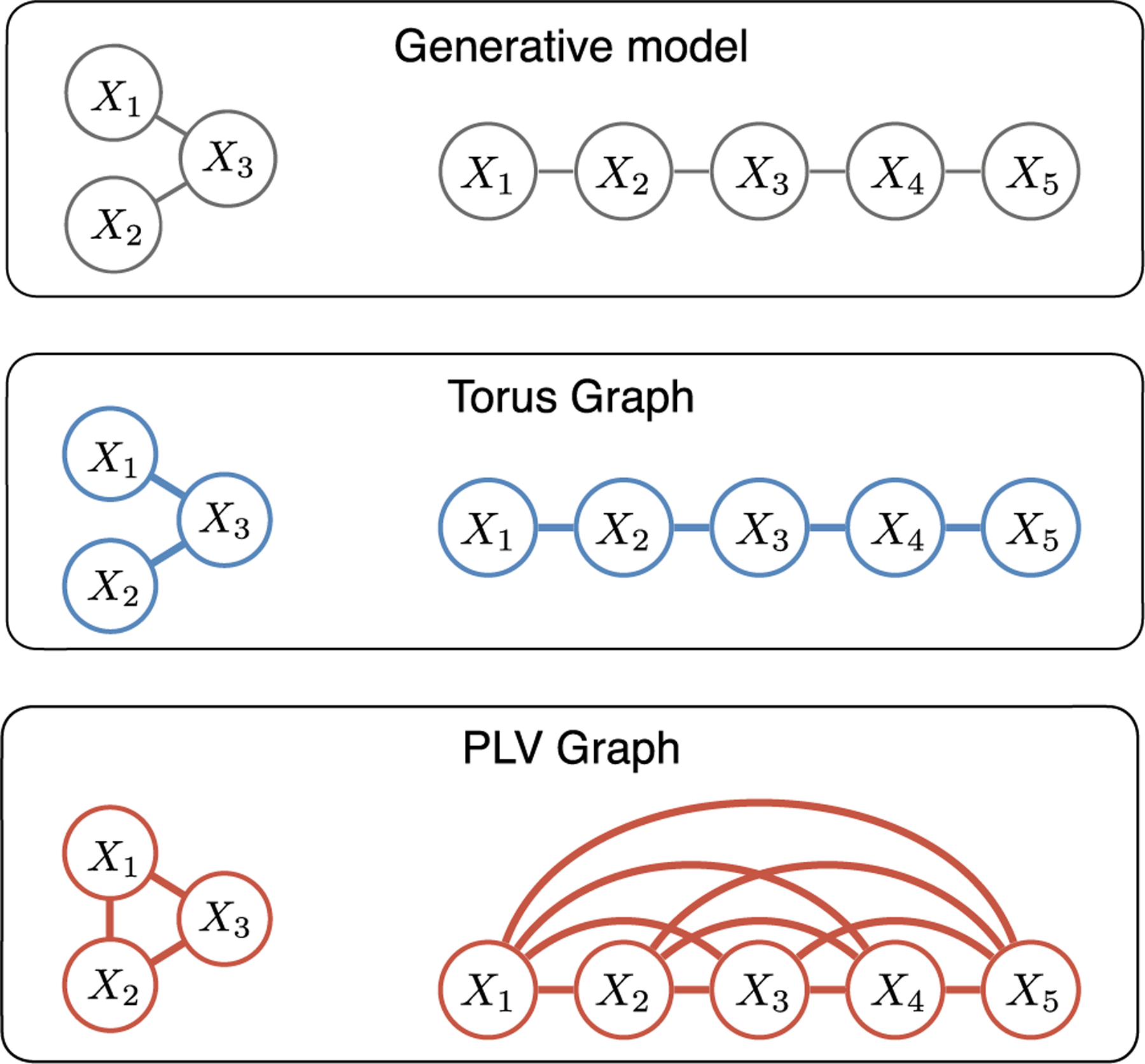
New technologies for recording electrical activity among large networks of neurons have created great opportunities to advance neurophysiology, and great challenges in data analysis (e.g., Steinmetz et al. (2018)). One appealing idea, which has garnered substantial attention, is that under certain circumstances, long-range communication across brain areas may be facilitated through coordinated network oscillations (Buzsáki and Draguhn (2004), Ching et al. (2010), Fell and Axmacher (2011), Sherman et al. (2016)). To demonstrate coordination among oscillatory networks, computational neuroscientists have examined phase coupling across replications (trials) of the experiment. That is, when the phase of an oscillatory potential at a particular location, and a particular latency from the beginning of the trial, is measured repeatedly it will vary; phase coupling refers to the tendency of two phases, measured simultaneously at two locations, to vary together, i.e., to be associated, across trials. The data we analyze here consist of 24 phase angles recorded simultaneously, on each of many trials, from several brain regions known to play a role in memory formation and recall (Brincat and Miller (2015, 2016)), prefrontal cortex (PFC) and three sub-areas of the hippocampus, the dentate gyrus (DG), subiculum (Sub) and CA3. Being angles, phases may be considered circular random variables. A commonly-applied measure of phase coupling, known as Phase Locking Value (PLV), is an estimator of the natural circular analogue of Pearson correlation under certain assumptions (which we review). PLV, however, like correlation, cannot distinguish between direct association and indirect association via alternative pathways. Thus, a large PLV between PFC and DG does not distinguish between direct coupling and indirect coupling via a third area, such as via CA3 (neural activity in PFC could be coupled directly with that in CA3, and that in CA3 with that in DG). To draw such a distinction we need, instead, a circular measure that is analogous to partial correlation. More generally, we wish to construct circular analogues of Gaussian graphical models. Because key properties of Gaussian graphical models are inherited by exponential families, and the product of circles is a torus, we consider exponential families on a multidimensional torus and call the resulting models torus graphs. We used torus graphs to provide a thorough description of associations among the 24 repeatedly-measured phases in the Brincat and Miller data and, in particular, we found strong evidence that the association between activity in PFC and DG is indirect, via both CA3 and Sub, rather than direct.
When circular random variables are highly concentrated around a central value, there is little harm in ignoring their circular nature, and multivariate Gaussian methods could be applied. However, in most of the neurophysiological data we have seen, including those analyzed here, the marginal distributions of phases are very diffuse, close to uniform, so the topological distinction between the circle and the real line is important. The torus topology is consequential not only for computation of probabilities but also for the interpretation of association. Figure 1 displays the inability of rectangular coordinates to preserve the clustering of points around a diagonal line under strong positive association. Furthermore, unlike the Gaussian case where a single scalar, correlation, describes both positive and negative association, on the torus, positive and negative association each have both an amplitude and a phase, so each pairwise association is, in general, described by 2 complex numbers. Also, in the Gaussian case, it is possible to interpret the association of two variables without knowing their marginal concentrations. This is no longer true for torus graphs.
Fig. 1.
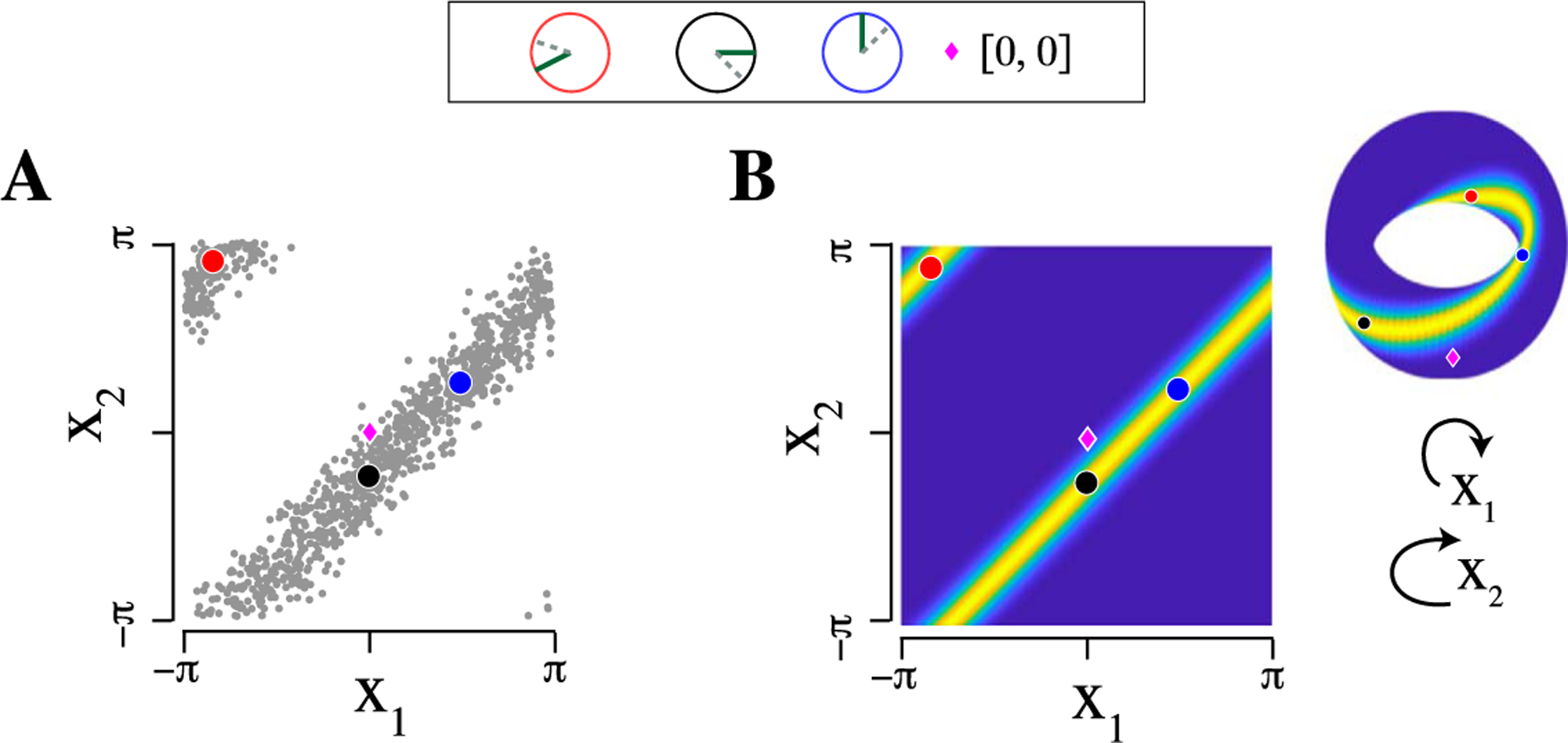
Rectangular coordinates are unable to accurately represent strong positive association between two circular random variables. (A) Scatter plot of simulated observations from a pair of dependent circular variables in rectangular coordinates, with three observations highlighted in red, black, and blue (simulated plot is similar to real data plots, but somewhat more concentrated for visual clarity; see Klein et al. (2020a), Figure S5). The highlighted observations are shown on circles at the top of the figure (one angle as a dashed line, one as a solid line; positive dependence implies a consistent offset between the angles). While the black and blue points follow the diagonal line, the red point falls near the upper left corner due to conversion to rectangular coordinates. (B) Probability density representing the two variables, plotted both in rectangular coordinates and on the torus, with the same three points marked. On the torus, there is a single band with high probability, which wraps around and connects to itself as a Möbius strip, and all three points fall on this strip.
After defining torus graphs and providing a few basic properties in Section 2, in Section 3 we consider several important alternative families of distributions for multivariate circular data that have appeared in the literature, and show that they are all special cases of torus graphs. In Section 4, we step through the interpretation of phase coupling in torus graphs by considering in detail the bivariate and trivariate cases. In Section 5, we provide estimation and inference procedures and, in Section 6, document via simulation studies the very good performance of these procedures in realistic settings. Our analysis of the data appears in Section 7 and we make a few closing remarks in Section 8.
2. Torus graph model.
Suppose X is a d-dimensional random vector with jth element Xj being a circular random variable, which may be expressed as an angle in [0, 2π), though other choices of angular intervals, such as [−π, π), are equivalent. When d = 2, X lies on the product of two circles (a torus), and in general it lies on a multidimensional torus. When considering phase coupling in neural data, X represents a vector of phase angle values extracted from oscillatory signals for a single time point from each of d signals, with repeated trials providing multiple observations.
The torus graph model may be developed by analogy to the multivariate Gaussian distribution, a member of the exponential family that models dependence between d real-valued variables. In general, for a random vector Y, an exponential family distribution is specified through a vector of natural parameters η that multiply a vector of sufficient statistics S(y) summarizing information from the data that is sufficient for the parameters (Wainwright et al. (2008)) and has a density of the form:
In the bivariate Gaussian distribution, and the sufficient statistics corresponding to the natural parameters are y and yyT, which describe the first- and second-order behavior of the variates. For a vector of angular variables X ∈ [0, 2π)2, we follow Mardia and Patrangenaru (2005) by representing the angles using rectangular coordinates on the unit circle as Y1 = [cosX1, sinX1] and Y2 = [cosX2, sinX2]. The first-order sufficient statistics are y1 and y2. The second-order behavior is described by:
This choice of sufficient statistics leads to the following natural exponential family density parameterized by η = [η1, η2, η12]:
| (2.1) |
The first two terms correspond to marginal circular means and concentrations of each variable, while the third term is a pairwise coupling term describing dependence between the variables. In the absence of pairwise coupling, the marginal distributions are all von Mises (Fisher (1993), p. 48), and if d = 1, the torus graph model is itself von Mises. Extending Equation (2.1) to d > 2 yields
| (2.2) |
The normalization constant is intractable, though numerical approximations may be used in the bivariate case (Kurz and Hanebeck (2015)).
Applying trigonometric product-to-sum formulas to the pairwise coupling terms of Equation (2.2) yields an equivalent, alternative parameterization in terms of natural parameters ϕ:
| (2.3) |
We define a d-dimensional torus graph to be any member of the family of distributions specified by Equations (2.2) or (2.3). In the form of Equation (2.3), the sufficient statistics involving only a single angle are
and the sufficient statistics involving pairs of angles are
We will use ϕ and S ≡ [S1,S2] to refer to the full vectors of parameters and sufficient statistics for all angles. The natural parameter space is given by
which implies that (because each angle has two marginal parameters, and each unique pair of angles has four coupling parameters, leading to 2d + 4[d(d − 1)/2] = 2d2 parameters).
We prefer the parameterization of Equation (2.3) because it offers a simple interpretation: the sufficient statistics containing phase differences correspond to positive rotational dependence between the angles, while the sufficient statistics containing phase sums correspond to negative rotational (or reflectional) dependence. Positive rotational dependence occurs when phase differences are consistent across observations, that is, Xj − Xk ≈ ξ or Xj ≈ Xk + ξ, for some angle ξ. Then conditionally on Xj = xj, Xk is obtained by rotating from xj by approximately ξ. Reflectional dependence instead refers to consistency in the phase sums so that Xk ≈ −Xj + ξ, meaning that conditionally on Xj = xj, Xk is obtained by rotating from −xj by approximately ξ. To demonstrate how each type of dependence might arise in repeated observations of neural oscillations, we show pairs of phase angles under each type of dependence in Klein et al. (2020a), Figure S2; in addition, bivariate torus graph densities dominated by each type of dependence are displayed in Klein et al. (2020a), Figure S1. While we have observed both kinds of dependence in neural phase angle data, rotational dependence appears to dominate in the data we analyze in this paper (see Section 7).
Because the natural parameter space is and the d-dimensional torus is compact, the full 2d2-dimensional exponential family is regular (see Brown (1986), p. 2). We call the full family a torus graph model and we summarize its properties, given above, in the following theorem.
Theorem 2.1 (Torus graph model). The d-dimensional torus graph model is a regular full exponential family. Equation (2.3) provides a reparameterization of the family in Equation (2.2) in which the expectations of the sufficient statistics are the first circular moments and, for d ≥ 2, the second circular moments represent rotational and reflectional dependence between pairs of variables. In Equation (2.3), the natural parameter has components corresponding to the first circular moment of Xj and corresponding to the second circular moments representing dependence between Xj and Xk.
We prove Theorem 2.1 in Klein et al. (2020a), Section S1 by writing the angles as complex numbers and considering the complex first moments and complex-valued covariances between the variables.
Because the torus graph is an exponential family distribution with sufficient statistics corresponding to first circular moments and to pairwise interactions between variables, it is similar to the multivariate Gaussian distribution, and, as in a Gaussian graphical model, the parameters correspond to a conditional independence graph structure. Specifically, as we state in Corollary 2.1 and prove in Klein et al. (2020a), Section S3, the pairwise coupling parameters ϕjk correspond to the structure of an undirected graphical model, where an edge is missing if, and only if, the corresponding pair of variables are conditionally independent given all the other random variables. This suggests that an undirected graphical model structure may be learned through inference on the pairwise interaction parameters, or by applying regularization in high dimensions to shrink the pairwise interaction parameters.
Corollary 2.1 (Torus graph properties). The d-dimensional torus graph model has the following properties:
It is the maximum entropy model subject to constraints on the expected values of the sufficient statistics.
In the torus graph model, the random variables Xj and Xk are conditionally independent given all other variables if and only if the pairwise interaction terms involving Xj and Xk vanish (that is, if the entire vector ϕjk = 0 in the density of Equation (2.3)).
Another interesting property of the torus graph model, given in Theorem 2.2 and proven in Klein et al. (2020a), Section S6, is that the univariate conditional distributions of one variable given the rest are von Mises, enabling Gibbs sampling to be used to generate samples from the distribution. In addition, Theorem 2.2 shows torus graphs are similar to other recent work in graphical modeling in which the joint distribution is specified through univariate exponential family conditional distributions (Chen, Witten and Shojaie (2015), Yang et al. (2015)).
Theorem 2.2 (Torus graph conditional distributions). Let X−k be all variables except Xk. Under a torus graph model, the conditional density of Xk given X−k is von Mises; specifically,
where Im denotes the modified Bessel function of the first kind of mth order and Aand Δ are defined as
where
and ϕ·k denoting all coupling parameters involving index k, hj = −1 if j < k and hj = 1 otherwise.
3. Important subfamilies of the torus graph model.
In this section, we discuss some important subfamilies of the torus graph model that are particularly relevant to the application to neural data. In particular, for neural phase angle data, the marginal distributions are often nearly uniform, prompting consideration of a uniform marginal model in which the parameters ϕj corresponding to the first moments of each variable are set to zero, resulting in a model with uniform marginal terms. In addition, while in our experience neural phase angle data exhibit both rotational and reflectional covariance, in many data sets, the primary form of dependence is rotational, prompting us to consider a submodel with parameters corresponding to reflectional dependence set to zero, which we will call the phase difference submodel since all pairwise relationships are described by the sufficient statistics involving xj − xk. A subfamily that combines these two (that is, restricts the torus graph to have marginal uniform distributions and no reflectional dependence) coincides with the models of Zemel, Williams and Mozer (1993) and Cadieu and Koepsell (2010), which were developed from Boltzmann machines and coupled oscillators, respectively.
The uniform marginal model, phase difference model, and a phase difference model with uniform margins all correspond to affine restrictions on the parameter space. This implies (see Klein et al. (2020a), Section S2) that each is itself a regular exponential family, so that each inherits many nice properties, such as concavity of the loglikelihood function, as a function of the natural parameter. Most previous work in multivariate circular distributions has focused on the so-called sine model (e.g., Mardia, Taylor and Subramaniam (2007)), which is again a subfamily, but it is not itself a full regular exponential family and does not, in general, have a concave loglikelihood function. As a result, estimation and inference are less straightforward than for either the torus graph model or the full regular exponential family submodels (Mardia, Kent and Laha (2016)). We summarize properties of these subfamilies in Theorem 3.1, which is proven in Klein et al. (2020a), Section S2.
Theorem 3.1 (Torus graph subfamilies). The uniform marginal model, the phase difference model, and a model combining both parameter space restrictions, form full regular exponential families but the sine model does not.
We note that the sine model may provide parsimonious fits to data for which the marginal distributions appear unimodal. Even though the torus graph is a full regular exponential family, and is therefore identifiable, when the data are highly concentrated it may be hard to estimate all four coupling parameters, a phenomena we explore with simulations in Klein et al. (2020a), Figure S3. Neural phase angle data, however, often tend to have low concentrations while still exhibiting strong pairwise dependence (Figure 9). As shown in Mardia, Taylor and Subramaniam (2007), when the concentration is low relative to the pairwise interaction strength, the sine model fitted density enters a regime of multimodality. In Section 7 we demonstrate lack of fit of the sine model to our neural data.
Fig. 9.
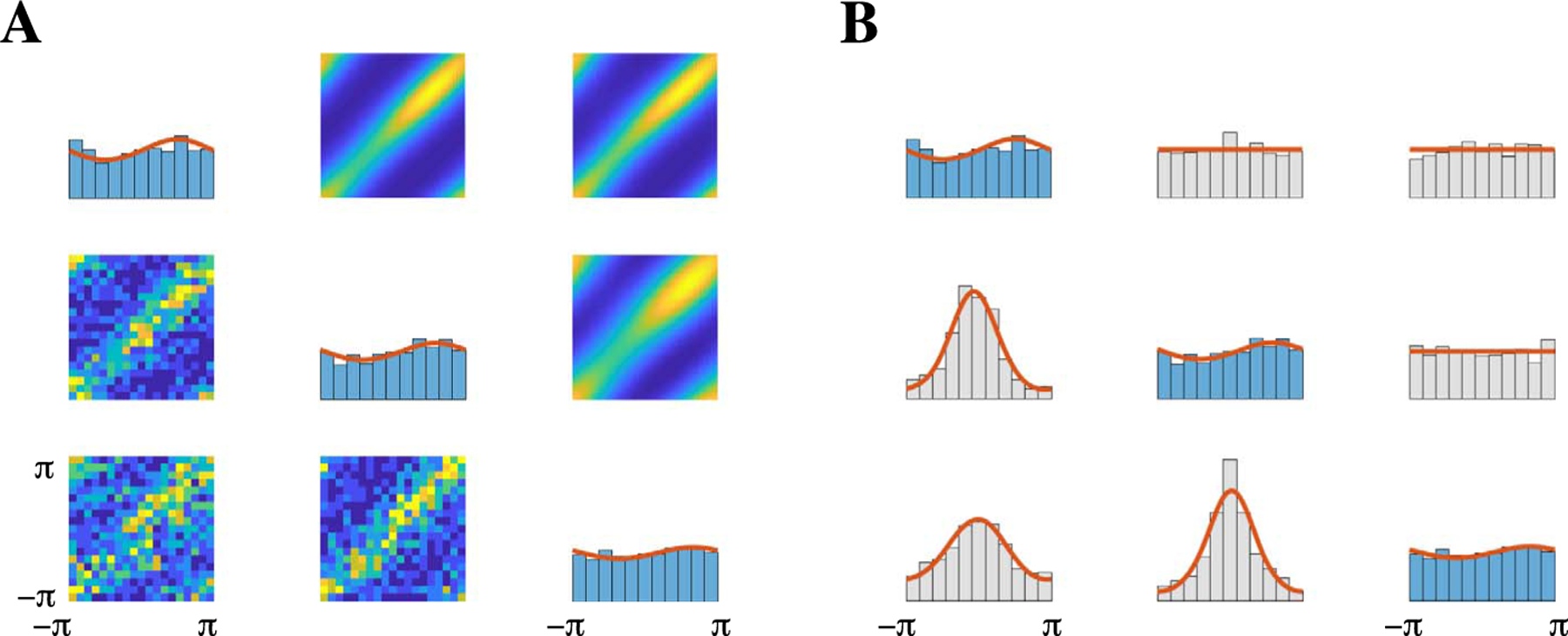
Comparison between phase angles from three LFPs located in PFC and the theoretical torus graph distribution demonstrates that torus graphs capture the salient first- and second-order behavior present in the LFP phase angles. In contrast, the sine model fails to fit the data accurately (Klein et al. (2020a), Figure S6). (A) Along the diagonal are the marginal distributions of the phase angles. The real data are represented by blue histograms and the theoretical marginal densities from the torus graph model are overlaid as solid red traces. Two-dimensional distributions (off-diagonal) show bivariate relationships, with theoretical densities above the diagonal and real data represented using two-dimensional histograms below the diagonal. (B) Plots along the diagonal same as panel A. Below the diagonal are distributions of pairwise phase differences and above the diagonal are distributions of pairwise phase sums, represented by histograms for the real data and by solid red density plots for the theoretical torus graph model. Both the real data and theoretical distributions exhibit concentration of phase differences but not phase sums, suggesting prevalence of rotational covariance, and the sufficient statistics are very similar for the theoretical and real data.
4. Phase coupling in torus graphs.
In this section, we discusss the distinction between bivariate measures of phase coupling, such as PLV, and multivariate measures. In Section 4.1, we briefly review bivariate phase coupling measures based on the marginal distributions of pairwise phase differences. In Sections 4.2 and 4.3 we investigate bivariate and trivariate examples analytically. We show that when a trivariate distribution of angles follows a torus graph, the marginal distributions of pairwise phase differences may be influenced by the marginal distributions of each variable and by indirect coupling through other nodes. This fundamental limitation of bivariate phase coupling measures can produce inaccurate phase coupling descriptions in multivariate systems. For the special case of phase difference models with uniform margins, in Section 4.4 we propose a transformation of the torus graph parameters that produces a generalization of PLV to multivariate data (where coupling between two variables is measured conditionally on all other variables), having the nice feature that, like PLV, it falls between 0 and 1.
4.1. Bivariate phase coupling measures.
The most common bivariate phase coupling measure between angles Xj and Xk is the Phase Locking Value (PLV) (Lachaux et al. (1999)), defined by
| (4.1) |
where is the nth observation of Xj.
We have used the notation to indicate it may be viewed as an estimator of its theoretical counterpart Pjk. In Klein et al. (2020a), Section S7, we show that Pjk corresponds to a measure of positive circular correlation under the assumption of uniform marginal distributions. The value of Pjk falls between 0 and 1, with 0 indicating no consistency in phase differences across trials and 1 indicating identical phase differences across trials.
One way to assess significance of is Rayleigh’s test for uniformity of the phase differences (Kass, Eden and Brown (2014), p. 268); other assessments of significance typically involve permutation tests or comparison to non-task recording periods (Rana, Vaina and Hämäläinen (2013)).
A similar approach to characterizing bivariate phase coupling follows from considering the univariate random variable Yjk = Xj − Xk. If Yjk is distributed as von Mises with concentration parameter κ, then
| (4.2) |
where is the maximum likelihood estimator for κ (Forbes et al. (2011), p. 191). More generally, any measure of the concentration of the marginal distribution of phase differences around a mean direction may be used as a measure of bivariate phase coupling (Aydore, Pantazis and Leahy (2013)). We will refer to measures based on the marginal distribution of phase differences as bivariate phase coupling measures.
4.2. Marginal distribution of phase differences in a bivariate torus graph.
Because bivariate phase coupling measures are based on the marginal distributions of phase differences, we investigate here the form of the marginal phase difference distributions in a bivariate torus graph model to determine how the torus graph parameters influence the phase differences. For the most straightforward and analytically tractable exposition, we consider the bivariate phase difference model. We will use the notation
to refer to elements of the pairwise coupling parameter vector, and use trigonometric identities to write the marginal terms as a function of κ and μ (see Klein et al. (2020a), Section S2, for details). Then the bivariate phase difference model density is
Let W = X1 − X2(mod 2π) be the phase differences wrapped around the circle so that W ∈ [0, 2π). As shown in Klein et al. (2020a), Section S4, the unnormalized theoretical distribution of W is a product of two functions:
| (4.3) |
where
and
| (4.4) |
The first factor, f, is proportional to the density of the difference of two independent von Mises random variables with concentrations κ1, κ2 and means μ1, μ2 (Mardia and Jupp (2000), p. 44) and reflects the influence of the marginal distributions of X1 and X2 on the phase differences. Such convolved densities are unimodal on [0, 2π) with mode μ1 − μ2(mod 2π) and concentration increasing with the argument of I0(·). The second factor, g, is proportional to a von Mises density that depends only on the phase difference and the coupling parameters.
The functional forms of f and g show that the distribution of phase differences is influenced both by the coupling parameters and by the marginal concentration parameters, which implies that bivariate phase coupling measures reflect both coupling and marginal concentration. In Figure 2, we illustrate effects on of pairwise dependence and marginal concentration. Even when the variables are independent, if the marginal distributions are not uniform, the distribution of phase differences will have nonzero concentration due to the influence of f. Thus, PLV is only appropriate when the marginal distributions are uniform. In contrast, torus graph parameters can separate the influence of marginal concentration and phase coupling to provide a measure of the dependence between angles.
Fig. 2.
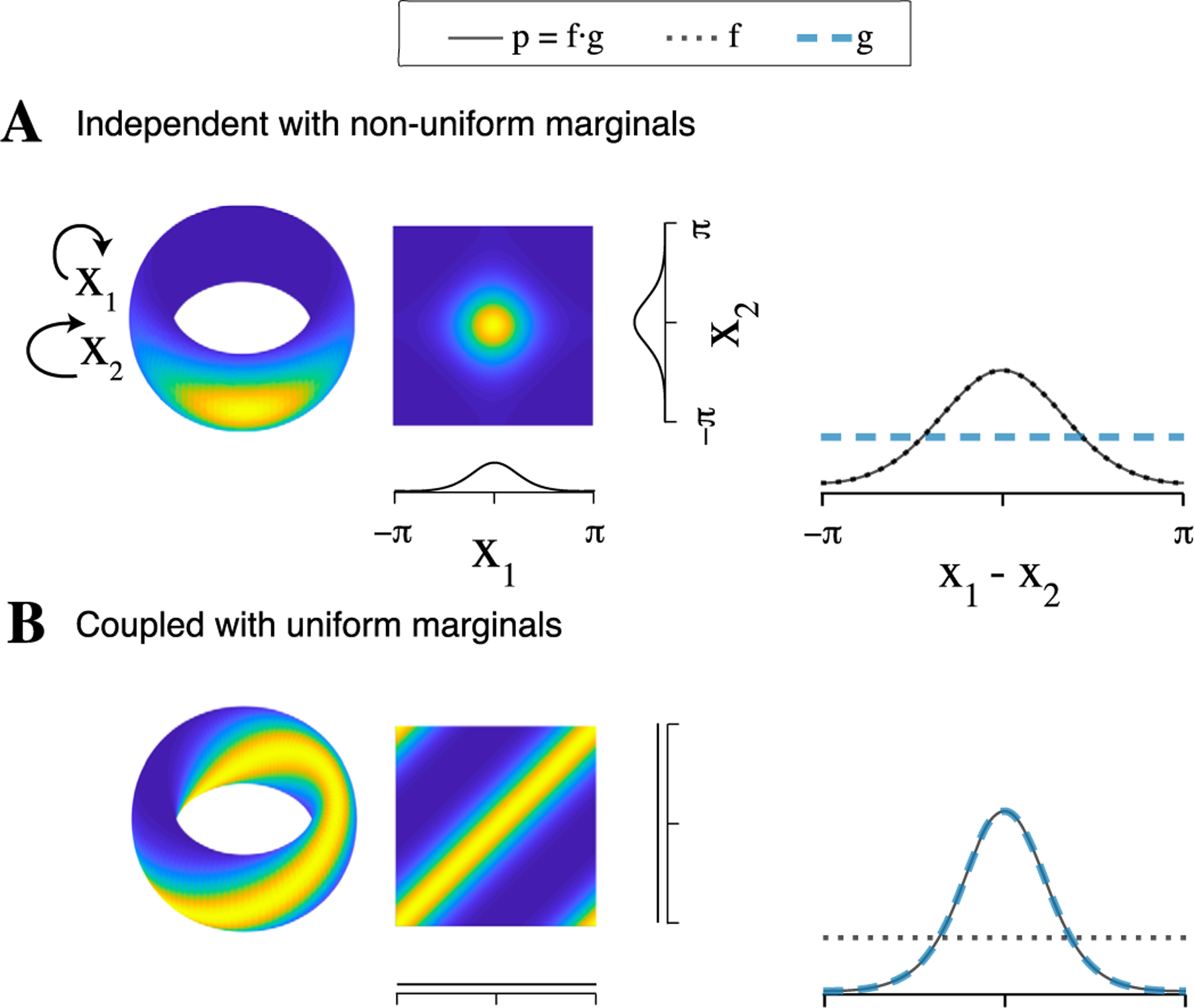
Examples of bivariate torus graph densities and the resulting marginal distributions of phase differences upon which bivariate phase coupling measures would be based. As shown in Equation (4.3), the density of phase differences, p, is affected not only by coupling (through g) but also by marginal concentration (through f). As a result, bivariate phase coupling measures like PLV could give misleading results. (A) Left: bivariate torus graph density with independent angles and non-uniform marginal distributions; density is shown on the torus and flattened on [−π, π] with marginal densities on each axis. Right: analytical phase difference density (p, solid) which is a product of a direct coupling factor (g, dashed) and a marginal concentration factor (f, dotted). Here, p is concentrated solely through the marginal concentration factor f, implying bivariate phase coupling measures would indicate coupling despite the independence of X1 and X2. (B) Similar to A, but with coupling between angles and uniform marginal distributions; only in this case does p correctly reflect the coupling.
4.3. Marginal distribution of phase differences in a trivariate torus graph model.
While we have shown that torus graph models are preferable to bivariate phase coupling measures in the bivariate case, the biggest advantage of using torus graphs comes from the ability to work with multivariate data and determine unique associations between each pair of variables after conditioning on the other variables. For instance, in a trivariate torus graph model with direct coupling only from nodes 1 to 3 and nodes 2 to 3 (Figure 3(A)), if we were to apply bivariate phase coupling measures to all pairwise connections, we would likely infer a connection between 1 and 2 because we would be measuring the bivariate association between phase angles without taking into account node 3.
Fig. 3.

Examples of trivariate torus graph densities and the resulting densities of phase differences for each pair of variables. As shown in Equation (4.6), in general, the density of phase differences, p, is affected not only by direct coupling (through g) but also by indirect connections (through h). As a result, bivariate phase coupling measures like PLV will generally reflect both direct and indirect coupling. (A) Left: ground truth graphical model, with no direct connection between X1 and X2 but an indirect connection through X3. Right: analytical phase difference densities for each pair of angles (p, solid) which are each a product of a direct coupling factor (g, dashed) and an indirect coupling factor (h, dotted). The concentration in the phase difference X1 − X2 arises solely due to indirect connections. (B) Similar to A, but with direct connection only between X1 and X2; in this case, p reflects the direct coupling. (C) Similar to A, but with direct connections between all nodes. Notice that indirect connections (h) still influence the distribution of phase differences X1 − X2 by multiplying with the direct connection term (g), which increases the concentration of p and shifts the mean (compared to g).
To demonstrate analytically how this happens, we consider a trivariate phase difference model with marginal concentrations equal to zero for simplicity, which has density
| (4.5) |
where the edge set E = {(1, 2), (1, 3), (2, 3)}. Letting W = X1 − X2(mod 2π) be the phase difference between nodes 1 and 2, we show in Klein et al. (2020a), Section S4, that the unnormalized density of W is given by the product of two factors:
| (4.6) |
The first factor is the same as g in Equation (4.4) and reflects direct connectivity between X1 and X2 as it depends only on the coupling parameters for the pair, ϕ12. The second factor reflects indirect connectivity through the other nodes, as it depends on the coupling parameters for the other pairs:
where
Therefore, h is proportional to the density of the difference of two independent von Mises random variables with concentrations and and mean directions arctan(β13/α13) and − arctan(β23/α23), respectively.
Equation (4.6) implies that the density of the phase differences for one pair of variables depends on all of the coupling parameters, so a bivariate phase coupling measure such as PLV will be unable to distinguish between the effects of direct coupling and indirect coupling through other nodes. Consequently, bivariate phase coupling measures will accurately represent the direct coupling between 1 and 2 only when there is no indirect path between 1 and 2 through the other nodes. In the most extreme case, bivariate phase coupling measures could indicate coupling even when there are only indirect connections between two nodes through the rest of the network. In Figure 3, we show examples to demonstrate how the phase difference distribution is affected by both direct and indirect connections, which may result not only in contributions to the observed phase difference concentration but also in shifts in the mean phase difference. This demonstrates that bivariate phase coupling measures generally reflect both direct and indirect coupling; in contrast, torus graph parameters identify direct coupling.
4.4. Interpreting phase difference model parameters.
An appealing feature of PLV is that it always falls between 0 and 1, so it is easy to interpret its magnitude and to compare PLV values for different pairs of variables. Unfortunately, the torus graph parameters lack these qualities. However, for the special case of the phase difference model with uniform margins, we propose a generalization of PLV based on a transformation of the torus graph model parameters that offers increased interpretability, and that, unlike PLV, measures pairwise relationships conditional on the other nodes.
As shown in Equation (4.2), if the marginal phase difference is distributed according to a von Mises distribution, then PLV corresponds to a function of the maximum likelihood estimator of the marginal concentration parameter. Under the phase difference model with uniform margins, we showed the marginal density of the phase difference X1 − X2 factors into terms corresponding to direct and indirect connections; the direct connectivity term g(w; ϕ12) of Equation (4.4) has the form of a von Mises density depending only on the parameters ϕ12. Therefore, in analogy to the definition of PLV for von Mises-distributed phase differences, we propose the following transformation of the parameters:
Like PLV, the measure always falls between 0 and 1 and therefore may be used to compare relative edge strengths in the phase difference model with uniform margins.
5. Torus graph estimation and inference.
Because the normalization constant is intractable for the torus graph density and it cannot easily be approximated even for moderate dimension, estimation and inference are not straightforward. In particular, maximum likelihood estimation is not feasible. Instead, we turn to an an alternative procedure for estimation and inference called score matching. In Section 5.1, we establish the applicability of the score matching estimator, originally defined for densities on , to multivariate circular densities like torus graphs, then give the explicit form of the objective function and derive closed-form estimators that maximize the objective function. Section 5.2 discusses two main approaches for determining a graph structure, one based on the asymptotic distributions of score matching estimators and the second based on regularization, which is particularly relevant for high-dimensional problems.
5.1. Estimation.
Score matching is an asymptotically consistent estimation method that does not require computation of the normalization constant and is based on minimizing the expected squared difference between the model and data score functions (gradients of the log-density functions), which leads to a tractable objective function for estimating the parameters (Hyvärinen (2005)). It can be seen as analogous to maximum likelihood estimation, which uses the negative log likelihood as a scoring rule; score matching instead uses the gradient and Laplacian of the log density (with respect to the data) as a scoring rule (Dawid and Musio (2014)). In addition, for real-valued exponential family distributions, the estimator comes from an unbiased linear estimating equation, so asymptotic inference is straightforward (Forbes and Lauritzen (2015), Yu, Drton and Shojaie (2019)). However, the original score matching estimator requires the density to be supported on and the proof of consistency relies on tail properties of such densities. We show that score matching estimators applied to circular densities such as the torus graph model retain the same form and therefore remain consistent. Score matching estimators have been considered previously for the phase difference model with uniform margins (Cadieu and Koepsell (2010)) and the sine model (Mardia, Kent and Laha (2016)), where the procedure requires modification because the sine model is a curved exponential family distribution (Theorem 3.1).
The score matching objective function is the expected squared difference between the log gradients:
| (5.1) |
The objective function depends on the unknown data density pX(x) in a nontrivial way, but we show in Theorem 5.1, using techniques similar to Hyvärinen (2005, 2007), that the objective function may be simplified to depend on the data density only through an expectation, allowing it to be estimated as an average over the sample (proof in Klein et al. (2020a), Section S5).
Theorem 5.1 (Score matching estimators for torus graphs). Under some mild regularity assumptions (given in Klein et al. (2020a), Section S5), the score matching objective function for the torus graph model takes the form
where
is a vector with dimension 2d2 that is a simple function of the sufficient statistics and
where
is the 2d2 × d Jacobian of the sufficient statistic vector. Specific expressions for the Jacobian elements are given in Klein et al. (2020a), Section S5.
Theorem 5.1 shows that the score matching objective may be estimated empirically by averaging over N observed samples. The empirical objective function is
| (5.2) |
where
with x(n) denoting sample n. Taking the derivative of Equation (5.2) with respect to the parameter vector yields an unbiased estimating equation (Dawid and Musio (2014)), which has a unique solution when is invertible:
The number of parameters for a d-dimensional torus graph is 2d2 so sample sizes may not be sufficient for to be invertible. In particular, is a sum with Nd terms, so N must be greater than 2d for to be invertible. In practice, the variance of estimated parameters will be high if N is not much larger than 2d, leading to less accurate point estimates and inference. We investigate the effect of sample size on the resulting inferences, using simulated data, in Section 6.
For higher-dimensional problems, Equation (5.2) is a convex objective function that may be minimized numerically with regularization. In torus graphs, a group ℓ1 penalty may be placed on the groups of pairwise coupling parameters ϕjk to enforce sparsity in the estimated edges, yielding the following objective function:
Here, λ is a tuning parameter that may be selected by criteria such as cross-validation or extended BIC (Lin, Drton and Shojaie (2016)). Other structured penalties may be used to encourage the model toward specific submodels (such as the phase difference model or the uniform marginal model). For instance, separate group ℓ1 penalties could be applied to the pairs of coupling parameters corresponding to positive and negative dependence, or an ℓ2 penalty on the marginal parameters ϕj could encourage low concentration. This type of penalization may improve behavior of the objective function, and could be especially useful when certain subfamilies appear reasonable based on exploratory data analysis. The computational burden of calculating may be reduced using the conditional independence structure of the graph, as we may estimate each four-dimensional group of parameters ϕjk using score matching on the conditional distribution p(xj, xk|x−jk), which involves only 8(d − 1)-dimensional sufficient statistics and thus uses only a subset of the rows of D(x), lessening the computational burden of matrix inversion (Yu, Kolar and Gupta (2016)).
5.2. Inference.
In our setting, the goal of inference is to determine a graph structure by determining which pairs of variables {j, k} have nonzero ϕjk, indicating an edge between nodes j and k. As shown in previous work, score matching estimators are asymptotically normal (Dawid and Musio (2014), Forbes and Lauritzen (2015), Yu, Drton and Shojaie (2019)), that is,
| (5.3) |
where the asymptotic variance is given by
with
Sample averages may be substituted for the expectations to obtain an estimate of the asymptotic variance, and because the true value of ϕ is unknown, we may substitute either our estimate or a null hypothetical value.
By considering the marginal Gaussian distribution of each element of ϕ, confidence intervals may be constructed in a standard way. However, in the torus graph model, there are four parameters per edge, so individual parameters are not of primary interest. In addition, we may be interested in testing hypotheses about groups of edges (for example, the null hypothesis might be that there are no edges between regions A and B). Fortunately, inference on groups of edges is also straightforward, as specified in the following lemma.
Lemma 5.1 (Asymptotic distribution for groups of torus graph parameters.). A vector of parameters indexed by an index set E of size |E|, denoted ϕE, satisfies
where ΣE is the corresponding submatrix of the asymptotic variance Σ of Equation (5.3). We also have
Lemma 5.1 enables computation of p-values for single edges (if E indexes the four parameters for a single edge) or for groups of edges. In particular, if E indexes the four parameters corresponding to a single edge, then under the null hypothesis that ϕE = 0,
so for an observed value of the test statistic , the probability statement , which gives a p-value for the edge, may be evaluated using the χ2 distribution with 4 degrees of freedom. Similarly, a χ2 distribution with two degrees of freedom may be used to test for only rotational or only reflectional covariance, or to test for nonzero marginal parameters.
Inference after regularization is less straightforward. Recent work has addressed inference for score matching estimators when using an ℓ1 penalty on each parameter (Yu, Kolar and Gupta (2016)), which could potentially be extended to torus graphs with a group ℓ1 penalty. Other approaches for inference in high dimensions include the bootstrap or stability selection (Meinshausen and Bühlmann (2010)). One parametric bootstrap approach is as follows. Assume we are interested in testing the null hypothesis that some particular subset of edges is missing from the graph. We may first fit a null torus graph model in which the coupling parameters corresponding to the edge set of interest are set to zero, selecting the regularization parameter by cross-validation of the score matching objective function. Next, B times, we would draw samples of the same size as the data from the null torus graph model, re-select the regularization parameter by cross-validation, and fit the unrestricted torus graph model to the samples using this regularization parameter. By computing the distribution of a suitable statistic (such as the number of nonzero edges or the maximal edgewise parameter vector norm) from these fitted null models, we obtain an empirical estimate of the null distribution of the statistic, which can then be used to judge the size of the same statistic computed on the original data.
6. Simulation study.
As our analytical results of Section 4 show, torus graphs can separate the effects of pairwise coupling and marginal concentration and have pairwise coupling parameters that represent direct connections between nodes. In contrast, bivariate phase coupling measures like PLV are sensitive to the marginal distribution of the variables and can reflect not only direct connections but also indirect paths through the other nodes. We conducted simulations to demonstrate these results. In addition, we explored the performance of torus graphs in recovering graph structures in simulated data similar to real data to determine how well we expect torus graphs to perform in the real data. Section 6.1 gives the simulation details and Section 6.2 provides the results.
6.1. Simulation methods.
When comparing PLV to torus graphs, we chose to generate data using the notion of positive rotational dependence discussed in Section 2. This was done to demonstrate that torus graphs recover interactions of this type even when data were not directly generated from a torus graph model. To generate bivariate data with rotational dependence and nearly uniform marginal distributions, we first drew N trials of phase angles x1 from a von Mises distribution with low circular concentration κ1. Then, for each trial, we let x2 = x1+ ξ +ϵ where ξ is a fixed phase offset and ϵ is noise drawn from a concentrated mean-zero von Mises distribution with concentration κϵ (where, on a small number of trials, we used less concentrated noise to emulate the noisiness present in real data). Extending to more than two nodes follows a similar process, where data for an additional node is generated based on data from a neighbor in the graph.
We generated synthetic data with two ground truth phase coupling structures that are intended to reflect realistic scenarios (and with parameters chosen to produce samples that emulate real neural phase angle data; Klein et al. (2020a), Figure S10 compares the simulated data to real data, showing similar first- and second-order behavior and similar observed pairwise PLV values). First, we constructed five-dimensional data meant to emulate the effects of spatial dependence, such as dependence between electrodes on a linear probe situated within a single functional region, which, under a nearest-neighbor Markov assumption, would induce sparse conditional independence graph structures (because each node would be directly dependent only on its nearest neighbors on the probe). We coupled nodes in a linear chain and chose ξ = π/100 and κϵ = 40 (with 15 of 840 trials contaminated with extra noise with concentration 0.1). Second, we constructed three-dimensional data meant to emulate the effects of indirect connections, which may occur when electrodes are in different regions, but not all of the regions are communicating directly. In particular, x2 was concentrated at κ2 = 0.01, x1 and x3 had phase offsets of ξ = π/6 and ξ = π/100, respectively, from x2, and the coupling noise had concentration κϵ = 2 (with 75 of 840 trials contaminated with extra noise with concentration 0.1). For each scenario, we simulated data of sample size 840 (to match the sample size of the real data). Then, for each data set, we fitted a torus graph and selected edges based on Lemma 5.1; we also used the Rayleigh test of uniformity to construct a graph based on PLV (Kass, Eden and Brown (2014), p. 268). For both tests, we used an alpha level of α = 0.001 with Bonferroni correction for multiple tests.
To gain intuition on how well torus graphs could be expected to perform in the real LFP data we analyze in Section 7, we investigated how well torus graphs recover the edges for varying dimensions, sample sizes, and underlying levels of sparsity in the edges. For this simulation, we generated data from a torus graph model of varying dimension with zero marginal concentration and with either 25% or 50% of edges present in the generating distribution. By varying the threshold on the edgewise X2 statistics (Lemma 5.1), we computed an ROC curve for each simulated data set. The ROC curves were averaged across 30 data sets, then the area under the curve (AUC) was calculated as a measure of performance.
6.2. Simulation results.
For the first set of simulations, Figure 4 shows that in both the three-dimensional and five-dimensional cases, the torus graph recovered the correct structure while the PLV graph recovered a fully connected graph. Although the performance of PLV may be better for other graph structures, our analytical results in Section 4 suggest that graph structures with indirect paths between nodes are likely to induce excess edges in the PLV graph. To follow up on this result, we further explored the False Positive Rate (FPR) and False Negative Rate (FNR) for PLV and torus graphs by repeating the simulations. We found that PLV graphs have low FNR (near 0), but also have a very high FPR (near 1), so PLV likely will not miss a true edge but will also add many additional edges (Klein et al. (2020a), Figure S11). This result agrees with the notion that hypothesis testing based on PLV, even when corrected for multiple comparisons, cannot be reliably used to control FPR for multivariate graphs because PLV measures both direct as well as indirect connectivity and thus tends to overestimate connectivity. In contrast, torus graphs are more conservative in assigning edges and control the FPR at the nominal level (though they tend to have higher FNR, especially for low sample sizes).
Fig. 4.
The torus graph recovers the ground truth graph structures (top panel) from realistic simulated data sets while a bivariate phase coupling measure, phase locking value (PLV), does not (edges shown for corrected p < 0.001). Left: a 3-dimensional simulated example of cross-area phase coupling where regions X1 and X2 are not directly coupled, but are both coupled to region X3. Right: a 5-dimensional simulated example of a graph structure that could be observed for channels on a linear probe with nearest-neighbor spatial dependence. In both cases, PLV infers a fully-connected graph due to indirect connections.
Figure 5 displays the results of the second set of simulations, which investigated the ability of torus graphs to recover the true structure as a function of true edge density, sample size, and data dimension. Importantly, for simulated data of dimension 24 and sample size of 840 (matching the real LFP data), the torus graph model is able to achieve 0.9 AUC as long as the graph is sufficiently sparse (around 25% of all possible edges present). In the real data results of Figure 8(B), we in fact observe approximately 25% of edges present, suggesting that this graph density may be reasonable for the real data. A more detailed investigation of the ROC curves and precision curves by dimension with fixed sample size 840 is given in Klein et al. (2020a), Figure S4, which again demonstrates that for a sufficiently sparse underlying graph structure, the torus graph method is expected to perform well for the sample size and dimension in the real LFP data. However, prior beliefs about the sparsity of the underlying graph will play a role in judging the likely accuracy of results.
Fig. 5.
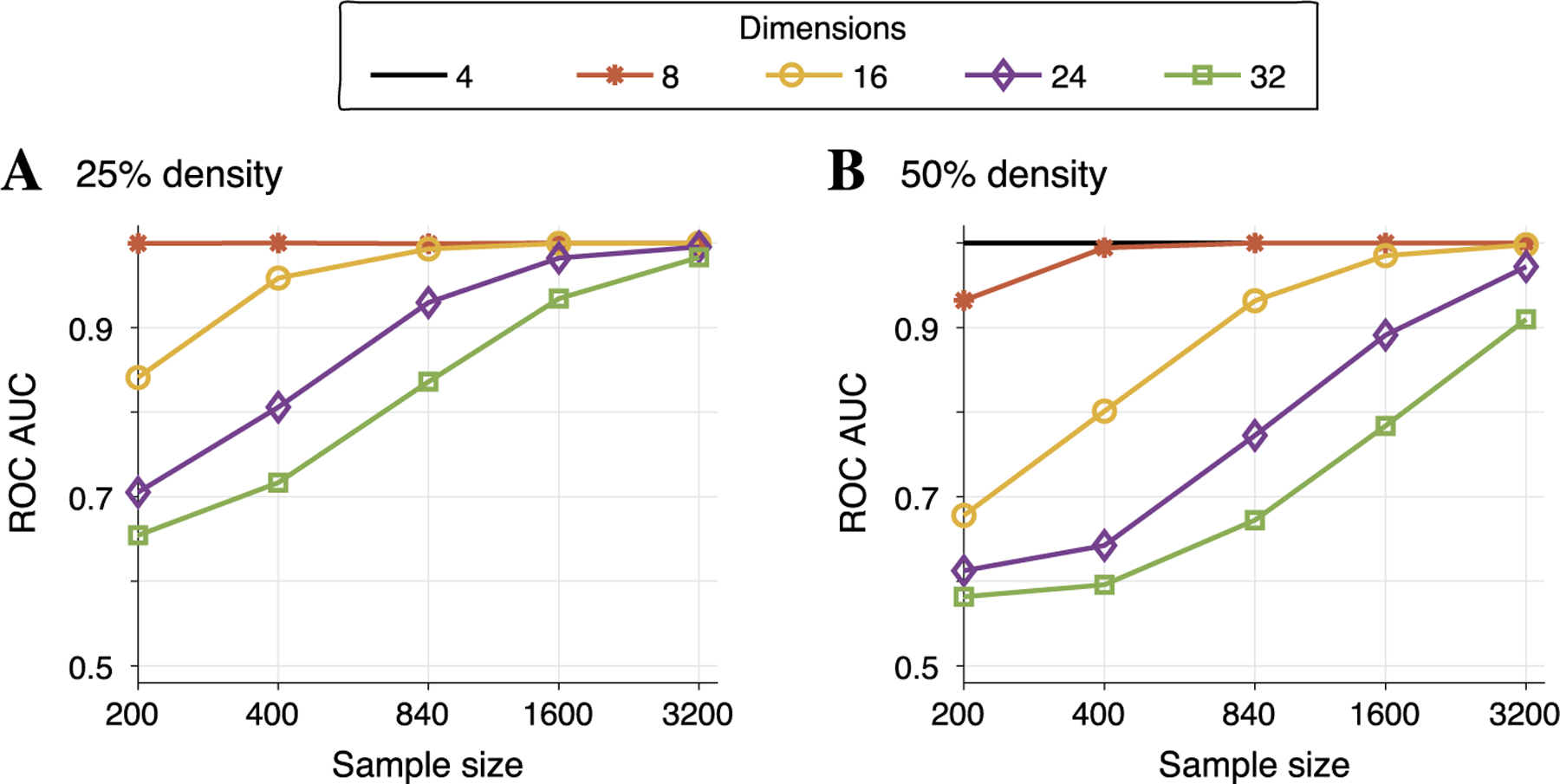
In simulated data with two different underlying edge densities, the average ROC curve area under the curve (AUC) was computed across 30 simulated data sets as a function of sample size (shown along the horizontal axis). The dimension of the data is indicated by line color and different markers. Panel A demonstrates that if the true underlying graph has only 25% of all possible edges present, then even for 24 dimensional data (diamond markers), a sample size of 840 (the size of our real LFP data set) is sufficient to reach AUC above 0.9. While performance degrades when the underlying graph is more dense, panel B shows that performance is still reasonable (AUC near 0.8) for 24 dimensional data with 840 samples.
Fig. 8.
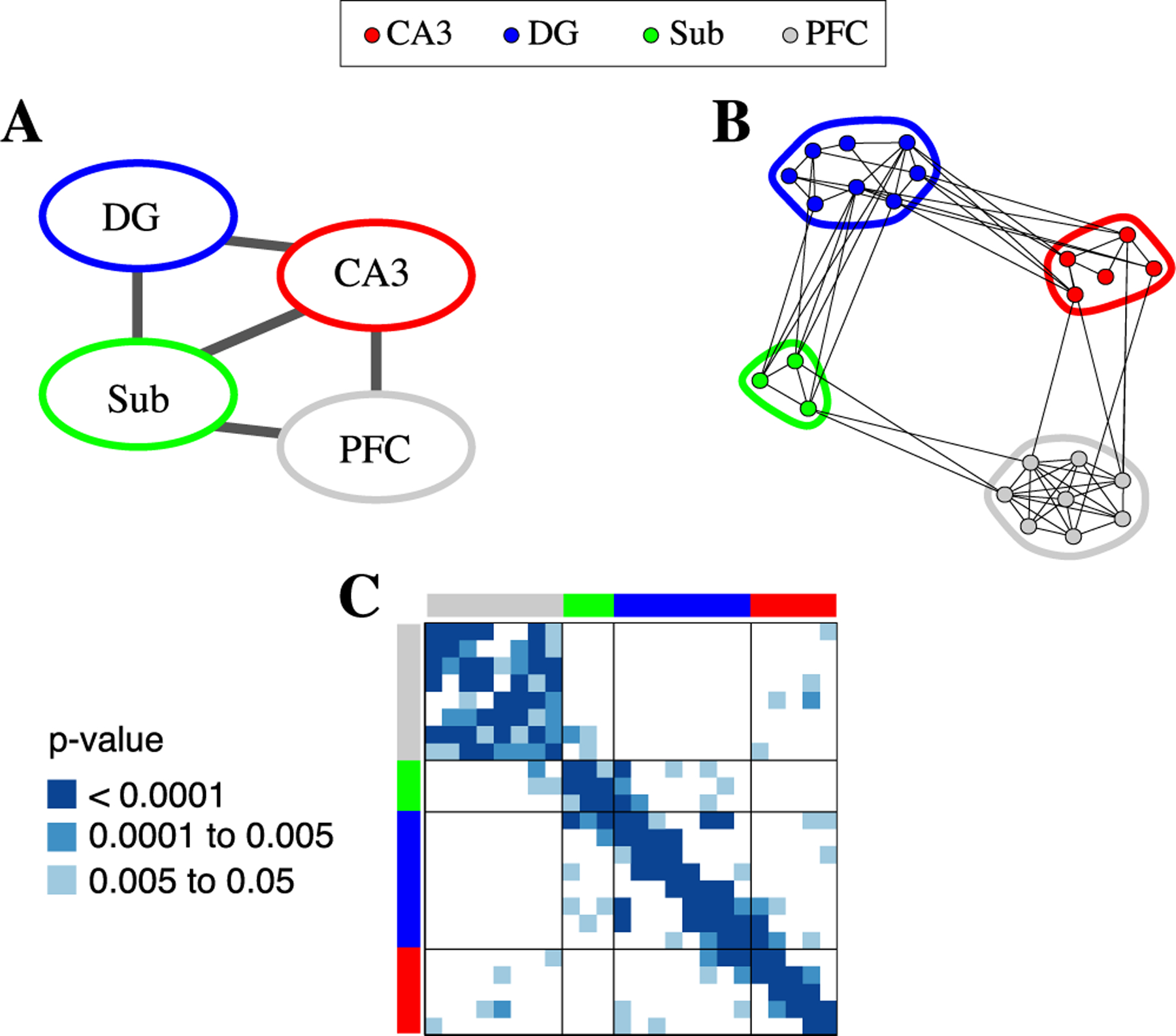
Torus graph analysis of coupling in 24-dimensional LFP data with four distinct regions: CA3 (red), dentate gyrus (DG; blue), subiculum (Sub; green), and prefrontal cortex (PFC; grey). (A) Cross-region tests indicated evidence for edges between DG and CA3, DG and Sub, CA3 and Sub, PFC and CA3, and PFC and Sub (determined by testing the null hypothesis that there were no edges between a given pair of regions, corrected p < 0.001). (B) For the significant cross-region connections, a post-hoc edgewise significance test examined the specific connections between regions, with the 24-dimensional graph containing edges for p < 0.05. Compared to the cross-region graph in A, notice that no edges from Sub to CA3 were individually significant at p < 0.05. (C) The 24-dimensional adjacency matrix (with hippocampal electrodes ordered by position on linear probe) with non-significant cross-region connections in white and other entries colored by edgewise p-value (with p > 0.05 in white). Despite having no built-in knowledge of spatial information, the torus graph recovered the linear probe structure within hippocampus.
7. Analysis of neural phase angles.
We demonstrate torus graphs in a set of local field potentials (LFPs) collected from 24 electrodes in the prefrontal cortex (PFC) and hippocampus (HPC) of a macaque monkey during a paired-associate learning task. Previous analysis of these data in Brincat and Miller (2016) found that beta-band (16 Hz) phase coupling between PFC and HPC peaked during the cue presentation and also increased with learning after the subject received feedback on each trial. Here, we sought a more fine-grained description of the phase coupling between PFC and HPC during the cue presentation period, and focused on describing relationships between PFC and three distinct subregions of HPC: subiculum (Sub), dentate gyrus (DG), and CA3.
First, we applied torus graphs to two different low-dimensional subnetworks: (i) a subnetwork consisting of five electrodes arranged linearly along a probe within CA3 and (ii) a collection of all trivariate subnetworks consisting of an electrode in each of the regions Sub, DG, and PFC. The five-dimensional subnetwork was chosen as a proof of concept, because electrodes in the same region and with a linear spatial arrangement ought to exhibit a nearest-neighbor conditional independence structure. We chose to examine connectivity between Sub, DG, and PFC because the patterns of connectivity between these three regions could be informative about whether hippocampal activity is leading prefrontal activity and because torus graphs should be able to disentangle the effect of direct and indirect connections to give a more informative connectivity structure than could bivariate phase coupling measures. Second, we applied torus graphs to the full 24-dimensional data set by first testing for the presence of any cross-region edges between PFC, Sub, DG, and CA3, and then following up with post-hoc tests of individual cross-region and within-region edges to construct a full 24-dimensional graph. Finally, we used a subset of the PFC electrodes to examine the goodness-of-fit of the torus graph model to the data and to investigate whether any torus graph subfamilies appeared to be appropriate for this data set.
We describe the data and preprocessing in Section 7.1 and give an outline of our data analysis methods in Section 7.2. Section 7.3 presents the results and we discuss implications of the results in Section 7.4.
7.1. Experiment and data details.
The experimental design and data collection procedures are described thoroughly in Brincat and Miller (2015, 2016). We use data from a single animal in a single session comprising 840 trials in which a correct response was given. (The sample size here is 840; a very small number of animals, usually 1 or 2, is standard practice in nonhuman primate neurophysiology because, even though there is large subject-to-subject variability in the fine details of brain structure and function, the overall structure and function of major brain regions is conserved, as are, typically, the primary scientific conclusions, though it is common to replicate in a second animal results found in a single animal; we also note that while part of the purpose of the original experiment involved learning, we are here ignoring any transient learning effects, which take place rapidly.) Briefly, four images of objects were randomly paired; the subject learned the associations between pairs through repeated exposure to the pairs followed by a reward for correctly identifying a matching pair. In each trial, the pairs of images were presented sequentially with a 750 ms delay period between the images, during which a fixation mark was shown. All procedures followed the guidelines of the MIT Animal Care and Use Committee and the US National Institutes of Health. (The experimental procedures were painless to the animals, as all forms of sensation originate outside the brain.) The data used in this paper contain 8 single-channel electrodes in PFC and a linear probe with 16 channels in HPC, with HPC channels categorized based on neural spiking characteristics into three subregions: dentate gyrus (DG), CA3, and subiculum (Sub). Recording regions and data processing steps are depicted in Figure 6. We focus on a time point at 300 ms after initial cue presentation, as PLV pooled across all sessions identified phase coupling peaking near 16 Hz at this time point (Brincat and Miller (2016), Supplementary Figure 5); we verified that the session we used showed the same overall phase coupling relationship. After downsampling the data to 200 Hz and subtracting the average (evoked) response, we used complex Morlet wavelets with 6 cycles to extract the instantaneous phase of each channel at 16 Hz in each trial.
Fig. 6.
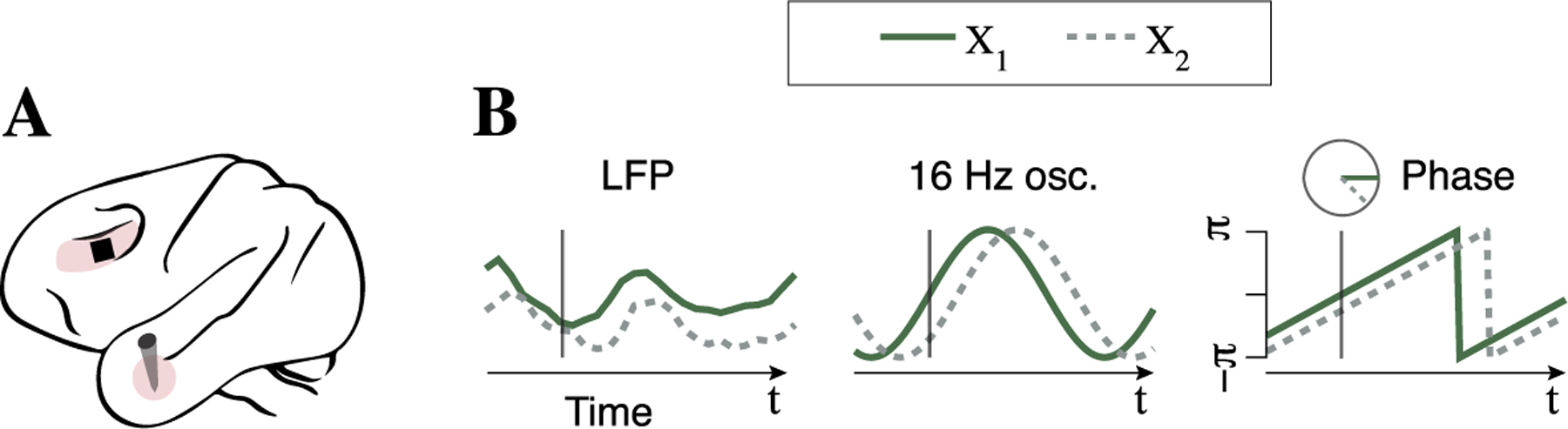
(A) Depiction of recording sites in ventrolateral prefrontal cortex (PFC) and hippocampus. (B) Preprocessing to obtain phase angles: local field potential (LFP) signals are filtered using Morlet wavelets to extract phase angles from 16 Hz oscillations at a time point of interest (two signals are shown for a single trial; repeated observations of phase angles are collected across repeated trials).
7.2. Data analysis methods.
To examine whether torus graphs could recover the spatial features we would expect along the linear probe, we first applied torus graphs to the 5-dimensional network containing channels on a linear probe that are all within CA3, likely to exhibit strong spatial dependence between neighboring channels, and used a hypothesis test for each edge with α = 0.0001. We chose a stringent threshold because, based on the first simulation study of Section 6, we expected PLV to add extraneous edges, yet we wanted to demonstrate that torus graphs and PLV give very different results even when a small threshold is used. Then, to examine whether torus graphs appeared to disentangle the effects of direct and indirect edges, we focused first on a trivariate network containing Sub, DG, and PFC where there is a simple interpretation of direct edges because CA3 and Sub send output signals from hippocampus while DG receives input signals to the hippocampus. Therefore, prominent connections between CA3 and PFC and/or Sub and PFC would suggest hippocampal activity may be leading PFC activity during this period of the task, while dominance of connections between DG and PFC would suggest the opposite. Because there are multiple channels in each of the three regions, we aggregated results across all possible triplets of channels from the three regions by inferring edges by majority vote across all possible trivariate graphs (using an alpha level of p < 0.0001 for each edgewise test).
We also investigated the graphical structure between the four regions (PFC, DG, CA3, and Sub) using a 24-dimensional torus graph on all electrodes; based on model selection techniques described in the next paragraph, we used a phase difference model. First, we assessed between-region connectivity between each pair of regions using the results of Lemma 5.1 to test the set of null hypotheses that there were no edges between each pair of regions. For example, there are 40 total possible edges between CA3 and PFC with two parameters for each edge, so the hypothesis test for the existence of any edges between CA3 and PFC was based on a χ2(80) distribution. For each pair of regions, we obtained a p-value for the entire group of edges between the two regions under the null hypothesis that there are no edges between the two regions. Because we were interested only in further investigating cross-region interactions with strong evidence, for this set of hypothesis tests, we chose a stringent alpha level of α = 0.001 with a Bonferroni correction across all 6 between-region tests to control for multiple tests. To better understand the individual connections driving this cross-region connectivity, and to investigate within-region connectivity patterns, we then applied post-hoc tests on the individual edges. That is, for each possible edge between pairs of regions that were identified as having some connection by the first step, we obtained a p-value using a χ2(2) distribution. Similarly, we calculated a p-value for each possible edge connecting electrodes within the same region. In this case, we assigned edges using a less stringent alpha level of α = 0.05 without correcting for multiple tests, as we expected the evidence for any specific edge would be weaker than the evidence for cross-region connections and because multiple comparisons were already taken into account in the first set of between-region tests.
To assess the appropriateness of torus graphs for this data set and to assess whether any submodels were appropriate, we explored the first- and second-order behavior of the LFP phase angles. To determine whether the uniform marginal model should be fitted, we tested for uniform marginal distributions using a Rayleigh test on each electrode, marginally, then obtained an overall decision regarding the null hypothesis that all distributions were uniform using Fisher’s method to combine p-values (Kass, Eden and Brown (2014), p. 301). Equation (4.6) showed that the marginal distribution of phase differences in a torus graph model depends on the coupling parameters for all possible direct and indirect paths between two nodes, so that any observed concentration of phase differences, marginally, could indicate the presence of some nonzero coupling parameters (possibly corresponding to indirect paths). Therefore, we applied the Rayleigh test to the observed phase differences for each pair of variables, then combined p-values using Fisher’s method to test the null hypothesis that all marginal phase difference distributions were uniform; we also performed a similar procedure on the observed pairwise phase sums. For these exploratory tests, we used a p-value threshold of p < 0.05 so that we would be sensitive to departures from uniformity in either the marginal distributions or the distributions of phase differences/sums. Finally, after fitting the chosen model, we used Kolmogorov–Smirnov (KS) goodness-of-fit tests to determine whether there was any evidence that LFP angles were drawn from a different distribution than the fitted theoretical model. In particular, we tested for differences in the marginal distributions of the angles, then tested for differences in the marginal distributions of pairwise phase differences and pairwise phase sums, and used Fisher’s method to combine p-values within each of the three groups of tests. We used an alpha level of 0.05 for each test.
7.3. Data results.
In the low-dimensional subnetworks, we found that the torus graph recovered a structure consistent with nearest-neighbor coupling along the linear probe (Figure 7, top panel), while PLV suggested a fully-connected graph; Klein et al. (2020a), Figure S7.B, shows p-values for the five-dimensional graph for both torus graphs and PLV. In addition, the top panel of Figure 7 shows that torus graphs appear to capture an interesting trivariate network with no coupling between PFC and DG, but with each of PFC and DG coupled with Sub. Klein et al. (2020a), Figure S7.C, shows p-values for all of the individual trivariate graphs, indicating that in the majority of individual trivariate graphs, there was no evidence for an edge between PFC and DG, while again, PLV suggested a fully connected graph.
Fig. 7.
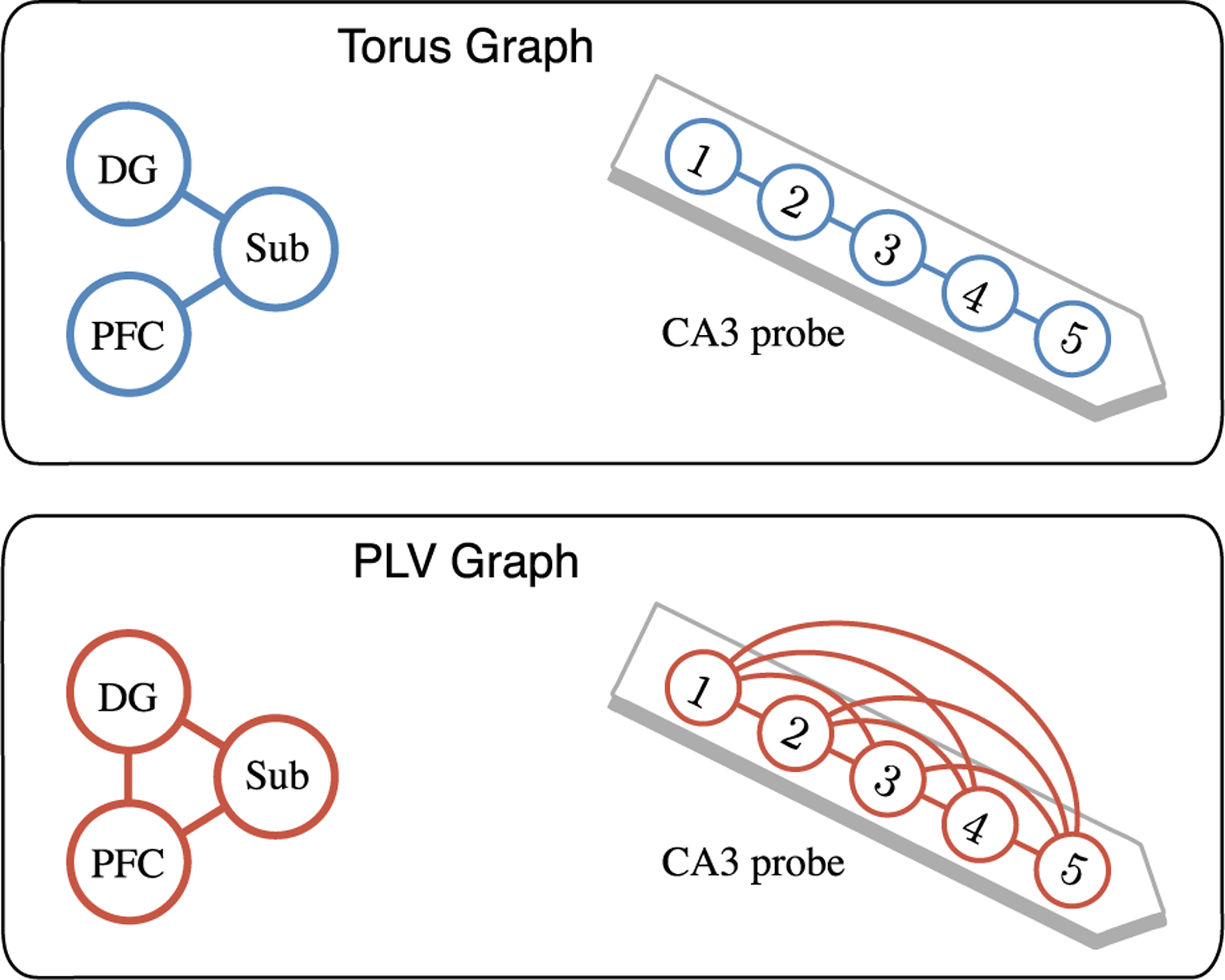
Torus graphs and PLV graphs from low-dimensional networks of interest in LFP data. Left: cross-region connectivity between dentate gyrus (DG), subiculum (Sub), and PFC, where the torus graph (top panel) indicated that DG and PFC are each coupled to Sub; in contrast, PLV (bottom panel) inferred a fully-connected graph. Right: within-region connectivity in CA3, where the torus graph indicated a spatial dependence structure which reflects the placement of channels along a linear probe, while PLV inferred a fully-connected graph.
For the 24-dimensional torus graph applied to all electrodes, we found, first, using the overall tests for the presence of any edges between each pair of regions, that there was apparent connectivity between all hippocampal subregions (CA3, DG, and Sub) and connectivity from CA3 to PFC and Sub to PFC (Figure 8(A)). In the follow-up post-hoc tests of individual edges, we observed dense connectivity within regions and somewhat sparser connectivity between regions (as judged by the number of edges out of the possible number that could be present; graph and adjacency matrix shown in Figure 8 panels B and C). Interestingly, none of the individual CA3 to Sub connections were significant (the smallest p-values were around 0.1), suggesting that the aggregate effect of several weak edges led to the edge between CA3 and Sub in Figure 8(A). In the adjacency matrix corresponding to the 24-dimensional graph, which is ordered to respect the position of channels on the hippocampal linear probe, entries are colored by p-value (with white indicating non-significant entries at level α = 0.05); notably, torus graphs recovered the linear probe structure across the entire hippocampus without prior knowledge of this structure being used in the model or estimation procedure.
In our investigation of the appropriateness of submodels and goodness-of-fit, we show results for three electrodes from PFC (results on the full data set were similar). Based on a visual analysis of the marginal and pairwise behavior of the data, the phase difference model appeared to be a reasonable candidate for these data. We found evidence that neither the marginal distributions nor the phase differences were uniform (Rayleigh/Fisher’s method, p < 0.001); however, there was no evidence for concentration in the phase sums (Rayleigh/Fisher’s method, p > 0.05). As a result, we selected the phase difference model to investigate goodness-of-fit. In Figure 9(A), we show data from three PFC electrodes along with their theoretical (fitted) phase difference model; along the diagonal, histograms for the real data (blue bins) are shown with theoretical model densities (solid red traces), indicating similar marginal distributions. Below the diagonal are two-dimensional histograms from the real data and above the diagonal are two-dimensional theoretical model densities, demonstrating that the torus graph appears capable of accurately representing the first- and second-order behavior present in the real data. Figure 9(B) shows histograms of sufficient statistics from the real data (phase angles along the diagonal, phase sums for each pair above the diagonal, and phase differences for each pair below the diagonal), along with kernel density estimates (solid red traces) for the statistics from the theoretical model. There is visual similarity between the distributions of sufficient statistics, and, in both cases, we observed the concentration of the pairwise phase differences indicating a prevalence of rotational dependence; this pattern held in the observed sufficient statistics for all 24 LFP channels shown in Klein et al. (2020a), Figure S9. The KS tests comparing the sufficient statistics of the fitted torus graph model to the data failed to reject the null hypothesis (KS/Fisher’s method, p > 0.05, for each group of statistics), indicating no evidence that the data were drawn from a different distribution than the fitted model.
7.4. Summary and discussion of results.
In the 24-dimensional analysis, PFC to hippocampal connections appeared to be driven by a relatively small number of significant connections from Sub to PFC and CA3 to PFC. However, the results did not show evidence for connections between PFC and DG, which coincides with the analysis of the trivariate subnetwork. In contrast, the PLV edgewise adjacency matrix (shown in Klein et al. (2020a), Figure S8) was very densely connected and shows little resemblance to the structure recovered by torus graphs; for any reasonable p-value threshold, the PLV graph would be nearly fully connected, suggesting that PLV was unable to distinguish between direct and indirect connections.
Because the patterns of connectivity between hippocampal subregions and PFC recovered by these analyses suggested that hippocampal activity was leading prefrontal activity during this time period in the task, as a follow-up analysis, we considered whether lead-lag relationships could be detected in the distribution of phase differences between PFC and hippocampus (specifically, CA3 and Sub). Since most of the edgewise dependence in this data set appears to correspond to positive rotational dependence (as judged by the relative magnitude of the torus graph coupling parameters and the concentration of phase differences but not phase sums in the observed sufficient statistics shown in Klein et al. (2020a), Figure S9), the distributions of phase differences between PFC and Sub and between PFC and CA3 can summarize the overall PFC-hippocampus coupling. Figure 10(A) displays a circular histogram of the PFC to hippocampus phase differences with the mean phase difference and a 95% confidence interval, pooling across all significant (p < 0.05) pairwise phase differences to compute an overall circular mean phase offset. These phase differences were centered at −8.5° (95% CI: [−10.4°, −6.6°]), indicating that on average, hippocampal phase angles led PFC phase angles, providing more evidence that hippocampal activity was leading PFC activity. The phase differences agree with those displayed in Brincat and Miller (2015), Figure 5.a (though we examined a different time period of the trial and pooled only across significant PFC to hippocampus connections). In contrast, Figure 10(B) displays within-region phase differences tightly clustered around 0° (mean: −0.04, 95% CI: [−0.2°, 0.2°]), indicating that within-region phase coupling may be driven mostly by spatial correlations in the recordings. These results suggest that due to the CA3 to PFC and Sub to PFC connections identified in both the trivariate and 24-dimensional analyses and the overall negative phase difference (PFC-hippocampus), hippocampal activity leads PFC activity during this period of the task. Importantly, while aggregated pairwise phase differences may have given some evidence of directionality, torus graphs provided detailed information about direct connections between hippocampal output subregions and PFC.
Fig. 10.
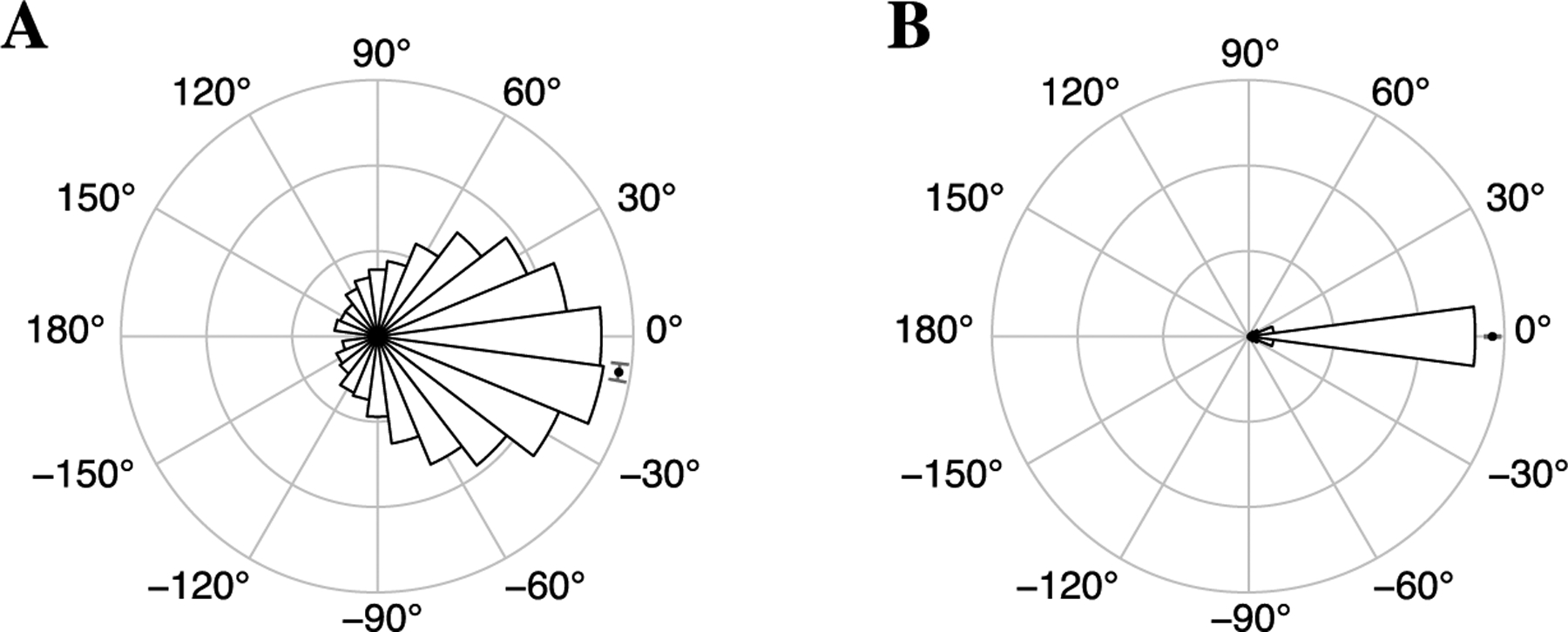
Circular histograms of phase differences, in degrees, from 24-dimensional LFP data for (A) significant connections between PFC and hippocampus (specifically, CA3 and Sub) and (B) significant PFC, CA3, and Sub within-region connections, The mean phase offset with 95% confidence interval is shown as a black dot with a narrow gray interval. Observations were pooled across all significant edges within or between the regions. The within-region phase differences were tightly concentrated around zero while the PFC-hippocampus phase differences were centered below zero, indicating a possible lead-lag relationship with hippocampus leading PFC.
In the low-dimensional subnetworks, we found that torus graphs yielded intuitive results while PLV did not. In particular, for the five-dimensional subnetwork consisting of electrodes along a linear probe, torus graphs inferred a nearest-neighbor conditional independence structure which we would expect for electrodes arranged linearly in space, while PLV inferred a fully connected graph. In the trivariate subnetworks, torus graphs suggested connectivity between PFC and Sub and DG and Sub, but not between PFC and DG, while again, PLV inferred a fully connected graph. Based on our analytic derivations in Section 4 and simulation study in Section 6, PLV is likely not reflecting the correct dependence structures in either low-dimensional network, and is instead reflecting both direct and indirect connections between the nodes.
When we investigated possible use of submodels, we found that a phase difference model appeared reasonable due to the lack of concentration in the phase sums, but that a uniform marginal model was not warranted. While we used the phase difference model on the full 24-dimensional data set, we found that we would have obtained nearly the same results using the full torus graph model, with discrepancies for only a few edges in the post-hoc edgewise test results shown in Figure 8(B) (which do not change the overall conclusions). We found that torus graphs appeared to fit the data reasonably well, with both visual summaries and KS tests suggesting that the marginal distributions of each angle and of the pairwise sum and difference sufficient statistics were similar in the data and the fitted model. In contrast, when we followed up by fitting a sine model to the same data (using code from Rodriguez-Lujan, Larrañaga and Bielza (2017)), we observed multimodality in the bivariate densities of the fitted model and a poor correspondence between the fitted and observed sufficient statistics, leading us to conclude that, as discussed in Section 3, the sine model fails to match the second-order dependence structure in the neural data due to low marginal concentration (Klein et al. (2020a), Figure S6). KS tests comparing the fitted sine model phase sums and differences to the data also suggested the data distribution does not match the sine model distribution (KS/Fisher’s method, p < 0.0001, for both phase sums and phase differences).
Torus graphs provided a good description of the neural phase angle data and provided substantive conclusions that could not have been obtained using bivariate phase coupling measures like PLV.
8. Discussion.
We have argued that torus graphs provide a natural analogue to Gaussian graphical models: Theorem 2.1 and Corollary 2.1 show that starting with a full torus graph, which is an exponential family with two-way interactions, setting a specific set of interaction coefficients ϕjk to zero results in conditional independence of the jth and kth circular random variables. We provided methods for fitting a torus graph to data, including identification of the graphical structure, i.e., finding the non-zero interaction coefficients, corresponding to edges in the graph (code, tutorial, and data provided in the supplements (Klein et al. (2020b)) and at https://github.com/natalieklein/torus-graphs). We also demonstrated that previous models in the literature amount to special cases, and therefore make additional assumptions that may or may not be appropriate for neural data. In particular, while the uniform marginal model or the phase difference model may be reasonable for neural phase angle data, the most widely studied model in multivariate circular statistics, the sine model, is less well-behaved and does not appear to be capable of matching the characteristics of neural phase angle data. In addition, we showed that PLV is a measure of positive circular correlation under the assumption of uniform marginal distributions of the angles, but that PLV is unable to recover functional connectivity structure that takes account of multi-way dependence among the angles. In our analysis of LFP phases 300 ms after cue presentation in an associative memory task, the fitted torus graph correctly identified the apparent dependence structure of the linear probe within CA3; it suggested Sub may be responsible for apparent phase coupling between PFC and DG; and it led to the conclusion that, at this point in the task, hippocampus phases lead those from PFC (by 8.5° with SE = 0.95°).
Here, our torus graphs were based on phases of oscillating signals, with no regard to their amplitudes. This is different than phase amplitude coupling in which the phase of one oscillation may be related to the amplitude of an oscillation in a different frequency band (Tort et al. (2010)). Also, like other graph estimation methods, interpretations based on torus graphs assume that all relevant signals have been recorded, while in reality, they could be affected by unmeasured confounding variables (e.g., activity from other brain regions). In addition, in applications such as phase angles in LFP, several preprocessing steps (referencing, localization, and filtering) are needed to extract angles from the signals. The torus graph implementation we have described here ignores these steps, and takes well-defined angles as the starting point for analysis. Furthermore, local field potentials tend to be highly spatially correlated, suggesting that inclusion of spatial information might be helpful for identifying structure.
Future work could include further investigation and theoretical analysis of how well torus graphs perform when the sample size is smaller relative to the dimension of the data. In some data sets, the full torus graph with 2d2 parameters may be overparameterized, and estimation and inference may be more accurate using one of the subfamilies; we demonstrated a model selection approach that indicated that the phase difference submodel would be reasonable for this data set. Furthermore, even when a full torus graph model is used, interpretability of the results could be enhanced by assessing evidence for reflectional and rotational dependence separately; that is, instead of putting a single edge based on the test of all four coupling parameters, we could construct a graph based only on the two parameters corresponding to rotational (or reflectional) dependence. Finally, in the uniform marginal phase difference model, the strength of coupling for each type of dependence could be quantified using the measure we introduced in Section 4.4, which falls between 0 and 1, facilitating comparison of relative strengths of the connections.
By extending existing models, torus graphs are able to represent a wide variety of multivariate circular data, including neural phase angle data. Extensions to this work could study changes in graph structure across time or across experimental conditions, and could investigate latent variable models involving hidden states, or a spatial hierarchy of effects. We anticipate a new line of research based on torus graphs.
Supplementary Material
Acknowledgments.
The authors thank the reviewers for their valuable feedback. Robert E. Kass, N. Klein and J. Orellana are supported by National Institute of Mental Health (NIMH, http://www.nimh.nih.gov, R01MH064537). J. Orellana is also partially supported by the Commonwealth of Pennsylvania Department of Health SAP4100072542, and Presidential Ph.D. Fellowships from The Richard King Mellon Foundation and William S. Dietrich II. E. K. Miller and S. Brincat are supported by National Institute of Mental Health (NIMH, http://www.nimh.nih.gov, R37MH087027) and The M.I.T. Picower Institute Innovation Fund. The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript.
Footnotes
SUPPLEMENTARY MATERIAL
Supplement A. Supplement to “Torus graphs for multivariate phase coupling analysis” (DOI: 10.1214/19-AOAS1300SUPPA; .pdf). PDF file containing several sections of supplemental text with derivations, proofs, and further detailed discussion of points in the main text, in addition to extra supporting figures (referenced in the main text) with descriptive captions to assist in interpretation.
Supplement B. Code and tutorial (DOI: 10.1214/19-AOAS1300SUPPB; .zip). Code and tutorial (latest version will be available at https://github.com/natalieklein/torus-graphs).
REFERENCES
- Aydore S, Pantazis D and Leahy RM (2013). A note on the phase locking value and its properties. NeuroImage 74 231–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brincat SL and Miller EK (2015). Frequency-specific hippocampal-prefrontal interactions during associative learning. Nat. Neurosci 18 576–581. 10.1038/nn.3954 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brincat SL and Miller EK (2016). Prefrontal cortex networks shift from external to internal modes during learning. J. Neurosci 36 9739–9754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown LD (1986). Fundamentals of Statistical Exponential Families with Applications in Statistical Decision Theory. Institute of Mathematical Statistics Lecture Notes—Monograph Series 9. IMS, Hayward, CA. [Google Scholar]
- Buzsáki G and Draguhn A (2004). Neuronal oscillations in cortical networks. Science 304 1926–1929. [DOI] [PubMed] [Google Scholar]
- Cadieu CF and Koepsell K (2010). Phase coupling estimation from multivariate phase statistics. Neural Comput. 22 3107–3126. 10.1162/NECO_a_00048 [DOI] [Google Scholar]
- Chen S, Witten DM and Shojaie A (2015). Selection and estimation for mixed graphical models. Biometrika 102 47–64. 10.1093/biomet/asu051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ching S, Cimenser A, Purdon PL, Brown EN and Kopell NJ (2010). Thalamocortical model for a propofol-induced α-rhythm associated with loss of consciousness. Proc. Natl. Acad. Sci. USA 107 22665–22670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawid AP and Musio M (2014). Theory and applications of proper scoring rules. Metron 72 169–183. 10.1007/s40300-014-0039-y [DOI] [Google Scholar]
- Fell J and Axmacher N (2011). The role of phase synchronization in memory processes. Nat. Rev. Neurosci 12 105–118. 10.1038/nrn2979 [DOI] [PubMed] [Google Scholar]
- Fisher NI (1993). Statistical Analysis of Circular Data. Cambridge Univ. Press, Cambridge. 10.1017/CBO9780511564345 [DOI] [Google Scholar]
- Forbes PGM and Lauritzen S (2015). Linear estimating equations for exponential families with application to Gaussian linear concentration models. Linear Algebra Appl 473 261–283. 10.1016/j.laa.2014.08.015 [DOI] [Google Scholar]
- Forbes C, Evans M, Hastings N and Peacock B (2011). Statistical Distributions. Wiley, Hoboken, NJ. [Google Scholar]
- Hyvärinen A (2005). Estimation of non-normalized statistical models by score matching. J. Mach. Learn. Res 6 695–709. [Google Scholar]
- Hyvärinen A (2007). Some extensions of score matching. Comput. Statist. Data Anal 51 2499–2512. 10.1016/j.csda.2006.09.003 [DOI] [Google Scholar]
- Kass RE, Eden UT and Brown EN (2014). Analysis of Neural Data. Springer Series in Statistics. Springer, New York. 10.1007/978-1-4614-9602-1 [DOI] [Google Scholar]
- Klein N, Orellana J, Brincat S, Miller EK and Kass RE (2020a). Supplement A. Supplement to “Torus graphs for multivariate phase coupling analysis.” 10.1214/19-AOAS1300SUPPA. [DOI] [PMC free article] [PubMed]
- Klein N, Orellana J, Brincat S, Miller EK and Kass RE (2020b). Supplement B. Supplement code and data to “Torus graphs for multivariate phase coupling analysis.” 10.1214/19-AOAS1300SUPPB. [DOI] [PMC free article] [PubMed]
- Kurz G and Hanebeck UD (2015). Toroidal information fusion based on the bivariate von Mises distribution. In IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems MFI. IEEE. [Google Scholar]
- Lachaux JP, Rodriguez E, Martinerie J and Varela FJ (1999). Measuring phase synchrony in brain signals. Hum. Brain Mapp 8 194–208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin L, Drton M and Shojaie A (2016). Estimation of high-dimensional graphical models using regularized score matching. Electron. J. Stat 10 806–854. 10.1214/16-EJS1126 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mardia KV and Jupp PE (2000). Directional Statistics. Wiley Series in Probability and Statistics. Wiley, Chichester. [Google Scholar]
- Mardia KV, Kent JT and Laha AK (2016). Score matching estimators for directional distributions. Preprint. Available at arXiv:1604.08470.
- Mardia KV and Patrangenaru V (2005). Directions and projective shapes. Ann. Statist 33 1666–1699. 10.1214/009053605000000273 [DOI] [Google Scholar]
- Mardia KV, Taylor CC and Subramaniam GK (2007). Protein bioinformatics and mixtures of bivariate von Mises distributions for angular data. Biometrics 63 505–512. 10.1111/j.1541-0420.2006.00682.x [DOI] [PubMed] [Google Scholar]
- Meinshausen N and Bühlmann P (2010). Stability selection. J. R. Stat. Soc. Ser. B. Stat. Methodol 72 417–473. 10.1111/j.1467-9868.2010.00740.x [DOI] [Google Scholar]
- Rana KD, Vaina LM and Hämäläinen MS (2013). A fast statistical significance test for baseline correction and comparative analysis in phase locking. Front Neuroinform 7 3. 10.3389/fninf.2013.00003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez-Lujan L, Larrañaga P and Bielza C (2017). Frobenius norm regularization for the multivariate von Mises distribution. Int. J. Intell. Syst 32 153–176. [Google Scholar]
- Sherman MA, Lee S, Law R, Haegens S, Thorn CA, Hämäläinen MS, Moore CI and Jones SR (2016). Neural mechanisms of transient neocortical beta rhythms: Converging evidence from humans, computational modeling, monkeys, and mice. Proc. Natl. Acad. Sci. USA 113 E4885–E4894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinmetz NA, Koch C, Harris KD and Carandini M (2018). Challenges and opportunities for large-scale electrophysiology with neuropixels probes. Curr. Opin. Neurobiol 50 92–100. 10.1016/j.conb.2018.01.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tort AB, Komorowski R, Eichenbaum H and Kopell N (2010). Measuring phase-amplitude coupling between neuronal oscillations of different frequencies. J. Neurophysiol 104 1195–1210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wainwright MJ, Jordan MI et al. (2008). Graphical models, exponential families, and variational inference. Found. Trends Mach. Learn 1 1–305. [Google Scholar]
- Yang E, Ravikumar P, Allen GI and Liu Z (2015). Graphical models via univariate exponential family distributions. J. Mach. Learn. Res 16 3813–3847. [PMC free article] [PubMed] [Google Scholar]
- Yu S, Drton M and Shojaie A (2019). Graphical models for non-negative data using generalized score matching. Preprint. Available at arXiv:1802.06340. [PMC free article] [PubMed]
- Yu M, Kolar M and Gupta V (2016). Statistical inference for pairwise graphical models using score matching. In Advances in Neural Information Processing Systems 2829–2837. [Google Scholar]
- Zemel RS, Williams CKI and Mozer MC (1993). Directional-unit Boltzmann machines. Adv. Neural Inf. Process. Syst [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


