Four-Compartment Diffusion Model of Cortisol Disposition: Comparison With 3 Alternative Models in Current Clinical Use

Abstract

Context

Estimated rates of cortisol elimination and appearance vary according to the model used to obtain them. Generalizability of current models of cortisol disposition in healthy humans is limited.

Objective

Development and validation of a realistic, mechanistic model of cortisol disposition that accounts for the major factors influencing plasma cortisol concentrations invivo (Model 4), and comparison to previously described models of cortisol disposition in current clinical use (Models 1-3).

Methods

The 4 models were independently applied to cortisol concentration data obtained for the hydrocortisone bolus experiment (20 mg) in 2 clinical groups: healthy volunteers (HVs, n = 6) and corticosteroid binding globulin (CBG)–deficient (n = 2). Model 4 used Fick's first law of diffusion to model free cortisol flux between vascular and extravascular compartments. Pharmacokinetic parameter solutions for Models 1-4 were optimized by numerical methods, and model-specific parameter solutions were compared by repeated measures analysis of variance. Models and respective parameter solutions were compared by mathematical and simulation analyses, and an assessment tool was used to compare performance characteristics of the four models evaluated herein.

Results

Cortisol half-lives differed significantly between models (all P < .001) with significant model–group interaction (P = .02). In comparative analysis, Model 4 solutions yielded significantly reduced free cortisol half-life, improved fit to experimental data (both P < .01), and superior model performance.

Conclusion

The proposed 4-compartment diffusion model (Model 4) is consistent with relevant experimental observations and met the greatest number of empiric validation criteria. Cortisol half-life solutions obtained using Model 4 were generalizable between HV and CBG-deficient groups and bolus and continuous modes of hydrocortisone infusion.

Cortisol circulates in the blood (vascular or plasma) volume as free, corticosteroid binding globulin (CBG)-bound, and albumin-bound cortisol [1, 2], the sum of which constitutes the concentration of plasma total cortisol (X_TotF). According to the free hormone hypothesis, the free but not protein-bound fraction of X_TotF is able to diffuse across the capillary endothelial membrane [1, 3]. Therefore, plasma concentrations of free cortisol (X_F) are considered to be the more reliable indicator of cellular cortisol concentrations, which in turn bear a functional relationship to intracellular concentrations of ligand-bound glucocorticoid receptor (GR) and biological activities of cortisol in vivo. This view is consistent with observations that X_F has superior diagnostic performance relative to X_TotF in the clinical laboratory assessment of several disorders of adrenocortical function [4–6]. However, methods for direct measurement of X_F by equilibrium dialysis or ultrafiltration are not well suited to the clinical laboratory and their use is generally restricted to the research setting [7–9].

Several factors influence the time-varying concentrations of X_F and X_TotF in vivo. These include (1) rate of cortisol appearance (R_a), (2) rate of cortisol elimination (α), and (3) concentrations (and cortisol-binding affinities) of CBG and albumin [6, 7, 10, 11]. Of these factors, dynamic variation in the cortisol secretion rate (CSR) by the adrenal cortex appears to be the principal mechanism by which X_F is dynamically regulated through the integrated functions of the hypothalamic–pituitary–adrenal and immunoregulatory axes in vivo [12, 13]. Terms including treatment effect, euadrenal, and critical illness–related corticosteroid insufficiency are defined in the context of randomized, placebo-controlled trials of corticosteroid replacement therapy (CRT) (Section A [14]). Pharmacokinetic parameter terms, including CSR, cortisol appearance rate (R_a), cortisol elimination rate (α), and cortisol half-life (τ) are specified elsewhere (Sections B and C [14]).

The clinical condition of adrenal insufficiency (AI) is associated with subnormal rates of cortisol secretion leading to relative reductions in X_F [4, 7]. Among patients with AI during episodes of concurrent critical illness, so-called adrenal crisis, X_F is subnormal to a variable but often marked degree and, consequently, treatment effects of CRT are large [15, 16]. This point is highlighted by the clinical importance of CRT in the treatment of adrenal crisis [15] and also by the historical perspective of high mortality rates in adrenal crisis patients prior to availability of CRT or, in some cases, recognition of AI [17].

In contrast to patients with AI, among euadrenal, critically ill patients (ECI), X_F and, to a lesser extent, X_TotF, are remarkably but variably supranormal (compared with euadrenal persons during usual health) [6, 18, 19], and the treatment effects of CRT are modest and conditional [20–22]. There is controversy concerning the mechanisms underlying the observed elevations of X_F in the setting of critical illness [23]. For example, some studies show significantly increased while others show significantly decreased rates of cortisol appearance in ECI relative to controls [24–27]. In addition, several but not all studies have reported a significantly longer cortisol half-life (τ) in ECI, suggesting a potential role for reduced cortisol metabolism in ECI [18, 25–27]. Relative to controls, the magnitude of increased cortisol half-life reported in ECI is quite variable (2.3- to 7-fold) [18, 25, 26].

These inconsistent results for CSR and cortisol half-life may be related in part to differences in methods used to measure and compare rates of cortisol appearance and elimination in ECI and control groups. One such method involves primed infusion of ²H-labeled cortisol (D4-cortisol). By comparing plasma concentrations of labeled and unlabeled cortisol and knowing the rate of D4-cortisol infusion, inferences may be made concerning the rate of endogenous cortisol secretion/appearance [25] (see Section B [14]). Alternatively, numerical methods define pharmacokinetic parameters of cortisol appearance and elimination in the context of models and, depending on the complexity of the model, use either simple (log-transformation) or more complex (computer-assisted) methods to select parameter solutions that minimize the difference between experimentally measured and model-predicted cortisol concentrations [18, 24, 26, 27] (see Section C [14]).

Three different models of cortisol disposition have been applied in the determination of cortisol half-life (τ) and CSR in humans [18, 19, 24–27]. We designate them as Models 1 to 3; their equations are given elsewhere (Section D [14]). Models 1 and 2 are descriptive, 1-compartment models for X_TotF and X_F, respectively [9, 28, 29], and both are expressed by single, linear differential equations. Model 3 represents a more mechanistic approach and is formulated as 3, nonlinear differential equations; its 3 compartments include X_F as well as CBG-bound (X_C) and albumin-bound (X_A) cortisol in the plasma volume [2, 26, 30, 31]. Stable isotope methods typically model cortisol appearance and elimination in the context of X_TotF as a single compartment (Model 1) [25].

None of the above Models 1 to 3 consider the distribution of cortisol outside the vascular (plasma) volume (V) [19, 24, 25, 32–35], which may be substantial in view of its lipophilic nature. Therefore, the objective of the present study was development and implementation of a novel, realistic, mechanistic model of cortisol disposition that includes the major factors affecting plasma concentrations of X_F and X_TotF. The model was developed in the context of the bolus experiment using cortisol and CBG concentration data measured before and after intravenous (IV) bolus administration of hydrocortisone (20 mg) in healthy volunteers (HVs) and CBG-deficient subjects [9]. The proposed 4-compartment, diffusion model (Model 4) includes an extravascular distribution volume (V_e) [36–39] and accounts for both concentration and mass of cortisol in the vascular and extravascular distribution volumes. The flux of free cortisol between V and V_e was modeled using Fick's first law of diffusion [40] (see “Materials and Methods” Eqs. 1-4) (see Section E [14]). Compared with Models 1 to 3, Model 4 demonstrated superior performance characteristics and better consistency with relevant experimental observations reported in the literature [19, 28, 41]. The physiologic and clinical implications of Model 4 equations and cognate parameter solutions are also discussed.

Materials and Methods

Study Subjects and Experimental Protocol

Subject characteristics, experimental procedures, and cortisol and CBG concentration data have been previously reported [9]. Briefly, hydrocortisone (20 mg) was administered as a 20-second bolus infusion at 09:00 hours in healthy subjects in whom endogenous cortisol secretion was suppressed by administration of dexamethasone (DEX) (4 mg) at 22:00 hours on the prior evening [9]. Baseline CBG and cortisol concentrations were obtained, then serum concentrations of total (X_TotF) and free (X_F) cortisol were measured at specified time points (10-480 minutes) after IV hydrocortisone bolus. Subjects included HVs (n = 6) and CBG-deficient subjects (n = 2) homozygous for the Gly237Val substitution in the CBG (SERPINA6) gene [42]. Comparison of HV and CBG-deficient group characteristics is included elsewhere (Section F [14]). The clinical study that generated data for this secondary analysis was conducted in accordance with guidelines of the 1975 Declaration of Helsinki with institutional review committee approval. Written informed consent was obtained in all subjects participating in the original study [9].

Selection and Description of Models 1 to 3

We evaluated models that have been used to obtain pharmacokinetic parameter solutions in human subjects and were published in several endocrine journals in the past decade [18, 19, 24, 26–28].

Application of Fick's First Law of Diffusion to Free Cortisol Flux Between Vascular and Extravascular Volumes (Model 4)

Several previous cortisol disposition models have included an extravascular distribution volume [36–39]. Model 4 differs in 2 respects: (1) the time-varying change in cortisol concentrations in vascular and extravascular compartments are modeled by Fick's first law of diffusion [40] rather than first-order reaction rate constants [36–39], and (2) diffusion applies to free but not protein-bound cortisol, which is consistent with the free hormone hypothesis [1, 3, 43, 44]. Fick's first law equation [40] for the bidirectional flux of free cortisol across the capillary endothelial membrane barrier gives dQ_F/dt = k*[X_F − X_Fe] [45], where Q_F is the mass of free cortisol (nmol or mg), k (L/min) is defined as a permeability constant (proportional to D ∗ A/δ, where D is the diffusion constant, A is barrier area, and δ is barrier thickness), and [X_F – X_Fe] is the difference in free cortisol concentrations in the vascular (X_F) and extravascular (X_Fe) volumes. This equation indicates that the rate of free cortisol flux (dQ_F/dt, mass/time) between the vascular (V) and extravascular (V_e) distribution volumes is proportional to the free cortisol concentration gradient [X_F – X_Fe], the sign of which determines the direction of net cortisol flux (Section E [14]).

Model 4 Equations

The proposed 4-compartment diffusion model (Model 4) is formulated by 4 non-linear differential equations (Eqs. 1-4 below). Model 4 is distinguished from Model 3 by (1) the circled term in Eq. 1 beginning with –k/V, which is Fick's law rewritten in terms of cortisol concentration via Q_Fe = V_e * X_Fe and (2) Eq. 4. Note that with the exception of the circled term in Eq. 1, the remaining terms of Eq. 1 to 3 constitute the mathematical formulation of previously described 3-compartment model (Model 3) [2, 26, 31, 46].

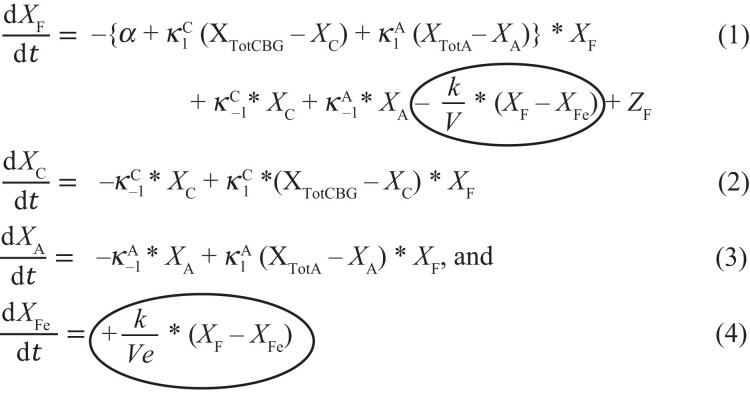where $\frac{dX}{dt}$ = the derivative of a concentration X with respect to time t, change in concentration per unit time, or rate of change of X, here in units of nmol/L/min = nM/min;

• X _F = the time-varying concentration of plasma free cortisol in the vascular volume (V);

• X _C = the time-varying concentration of CBG-bound cortisol in the vascular volume (V);

• X _A = the time-varying concentration of albumin-bound cortisol in the vascular volume (V);

• X _Fe = the time-varying concentration of free cortisol in the extravascular volume (V_e);

• X _TotCBG = the total CBG concentration equal to the sum of free CBG and cortisol-bound CBG, such that X_TotCBG = X_freeCBG + X_C, here measured;

• X _TotA = the total albumin concentration equal to the sum of free and cortisol-bound albumin, such that X_TotA = X_freeA + X_A, typically measured;

• Z _F = the time-varying free cortisol appearance rate (nmol/L/min);

• α = the free cortisol elimination rate constant (min⁻¹);

• k = the permeability constant in Fick's first law: $\frac{d{Q}_{Fe}}{dt}=k(X_F-X_{Fe});$

• where Q_Fe is the quantity (nmol) of free cortisol in the extravascular compartment, and the permeability constant (k, L/min) is proportional to D∗A/δ, where D is the diffusion constant (area/time, cm²/min), A is the area (cm²), and δ is the barrier (membrane) thickness (cm).

• ${\kappa }_1^C$ = the forward (association) rate constant (on-rate in units of 1/(nM-sec)), and

• ${\kappa }_{-1}^C$ = the backward (dissociation) rate constant (off-rate in units of 1/sec). Both for the reversible binding reaction X_freeCBG + X_F ⇌ X_FC;

• ${\kappa }_1^A$ = the forward (association) rate-constant (on-rate in units of 1/(nM-sec)) and

• ${\kappa }_{-1}^A$ = the backward (dissociation) rate constant (off-rate in units of 1/sec). Both for the reversible binding reaction X_freeA + X_F ⇌ X_FA.

• X _TotF = the time-varying concentration of total cortisol in the vascular volume (V) equal to the sum of free, CBG-bound, and albumin-bound cortisol concentrations in the vascular volume (X_TotF =X_F + X_C + X_A).

Note that X_TotF is not in any of Eqs. 1 to 4. However, it is the plasma cortisol concentration to which models are typically fit, and may be calculated as the sum of its components, X_F, X_C, and X_A, which are represented in the above equations.

Equations 1 to 4 above are expressed in units of cortisol concentrations (X_F, X_Fe, X_C, and X_A, respectively). However, these equations may be alternatively expressed in units of cortisol mass (Q) by multiplying cortisol concentrations in vascular and extravascular compartments by their respective distribution volumes, V and V_e (see Section G [14]). Numerical methods, calculation of plasma volume [47], and steady-state solutions for Models 1 to 4 are described elsewhere (Section H [14]).

Additional Statistical Analysis

Descriptive data are reported as mean and SD. Cortisol half-life (τ) was calculated as an inverse function of α (see Section I [14]). Comparisons of parameter solutions by model and clinical group (HV vs CBG-deficient) was by repeated measures (RM) analysis of variance (ANOVA) with post hoc pairwise comparisons. The different forms of the equations in Models 1 to 4 predict a monoexponential pattern of cortisol elimination for 1-compartment Models 1 and 2, but more complex patterns of cortisol concentration elimination in multicompartment Models 3 and 4 (see Section C [14]). Goodness of fit was summarized as bias, SD, and the root mean squared error (RMS) using RMS = sqrt[bias² + SD²] reported as percent error. The fit between model-predicted and measured cortisol concentrations used total cortisol concentrations (X_TotF) for Models 1, 3, and 4, as measurements of X_TotF had better precision in our data set (intra-assay coefficient of variation < 2.8%) compared to X_F (coefficient of variation < 9.5%) [9]. X_F was used directly for Model 2 solutions. For solutions obtained using Models 3 and 4, measured concentrations of plasma free cortisol (X_F) were used to calculate group-specific equilibrium disassociation constants for CBG-cortisol binding (see Section J [14]). Comparison of goodness of fit summary measures used RM ANOVA with models and groups as repeated and grouping factors, respectively. SDs of correlated residuals were compared using the Wilks test. The error structure for measured vs computed cortisol concentrations (residual plots) was assessed visually. Model 4 simulations were used to illustrate behavior of the model and differences with Models 1 to 3 (Section K [14]).

Assessment Tool for Model Comparisons

Categories for model comparisons included (1) general model requirements, (2) inclusion of mechanistic modeling elements validated in prior experimental work, (3) goodness of fit, and (4) performance measures. Goodness of fit between model-predicted and experimental data was considered to be a necessary but not sufficient measure of model validity. Performance measures included consistency of parameter solutions between bolus and continuous infusion experiments. This measure was based on model-predicted time to steady state and steady-state cortisol concentrations in comparison with experimental results for continuous infusion reported by Prete et al [19], as previously described [33] (see Section L [14]). The premise for considering significant group differences in τ as a performance criterion was based on evidence that the observed model–group interaction was due to bias in model errors (see “Results” and “Discussion”).

Results

Specification of Model-Specific Parameters (Models 1 to 4)

Table 1 gives various specifications of Models 1 to 4, including (1) number of compartments and distribution volumes, (2) input data used to obtain pharmacokinetic parameter solutions, (3) fixed parameters, (4) adjustable parameters, and (5) degrees of freedom.

Table 1.

Parameter specifications for Models 1 to 4

Model	Description	Input data (concentrations by time)	Fixed parameters	Adjustable pharmacokinetic parametersa	Adjustable initial condition	Degrees of freedom
1	1-compartment for total cortisol (XTotF) Single distribution volume	Total cortisol		α1	y-intercept	2
2	1-compartment for free cortisol (XF) Single distribution volume	Free cortisol		α2	y-intercept	2
3	3-compartment for free, CBG-bound, albumin-bound cortisol Single distribution volume	Total cortisol XTotF CBG albumind	On and off rates for cortisol binding to CBG and albumin	α3	y-intercept	2
4	4-compartment for free, CBG-bound, albumin-bound, and extravascular cortisol 2 distribution volumesb	Total cortisol CBG Albumind Hematocritd	On and off rates for cortisol binding to CBG and albumin, Plasma volume (V)	α4k (permeability parameter), Ve (extravascular volume)	Calculatedc	3

Table 1 compares parameterization scheme for Models 1 to 4, including general description, input data, fixed parameters, adjustable parameter, initial condition, and degrees of freedom.

^a In Models 1 to 3, the adjustable pharmacokinetic parameter (α) and the adjustable initial condition (y-intercept) are estimated simultaneously by numerical methods.

^b Model 4 has 2 distribution volumes for cortisol: (1) plasma volume, which contains 3 compartments, namely free (X_F), CBG-bound (X_C), and albumin-bound (X_A) cortisol, and (2) extravascular volume, which contains 1 compartment, namely (free) extravascular cortisol (X_Fe).

^c For Model 4, the bolus can be represented by initial conditions (20 mg into calculated plasma volume) or by a brief (20 seconds) continuous infusion of hydrocortisone (eg, 20 mg given IV push over 20 seconds) into the calculated plasma volume (see “Materials and Methods”).

^d Generally albumin concentration and hematocrit are measured at baseline. However, as they were not measured in the data used in the present analysis, values were assigned based on age and gender (see Methods).

Model-Specific Parameter Solutions for Cortisol Elimination Rate (α₁-α₄) and Half-Life (τ₁-τ₄) in HVs

Among HV subjects, solutions for elimination rate (α₁- α₄) as well as half-life (τ₁-τ₄) were all significantly different (RM ANOVA, overall P < .001). The rank order for model-specific solutions was α₄ > α₃ > α₂ > α₁ (all P ≤ .001) and τ_{1 >} τ₂ > τ₃ > τ₄ (all P < .001), as shown in Table 2. These ordered relationships between model-specific solutions were consistently observed in simulation and, in ancillary analysis, were shown to be inherent to the model equations (Section M [14]). Parameter solutions for α₁ to α₃ in our subjects were significantly correlated with one another, whereas α₄ was not correlated with other model-dependent alphas (see Section N [14]).

Table 2.

Parameter solutions for Models 1 to 4 (HV vs CBG-deficient groups)

Model	Elimination rate constant (α, min−1)	Half-life (τ, min)	y-intercept (nmol/L)	Permeability parameter (k, L/min)	Extravascular volume (Ve, L)	Vascular volume (V, L)
Healthy volunteers
1	α1 = 0.006 ± 0.0007	τ1 = 117 ± 13.2	1308 ± 225a
2	α2 = 0.01 ± 0.001	τ2 = 71.2 ± 8.6	167.5 ± 17.6
3	α3 = 0.13 ± 0.04	τ3 = 6.0 ± 1.6	1817 ± 415
4	α4 = 0.89 ± 0.13b	τ4 = 0.8 ± 0.14c		1.87 ± 0.35	94.9 ± 16.7	2.6 ± 0.4
CBG-deficient subjects
1	α1 = 0.01 ± 0.0007	τ1 = 63.9 ± 3.9d	1037 ± 301
2	α2 = 0.01 ± 0.0002	τ2 = 65.8 ± 1.5	225 ± 63.6
3	α3 = 0.07 ± 0.01	τ3 = 10.5 ± 1.5d	1312 ± 371
4	α4 = 0.8 ± 0.22	τ4 = 0.9 ± 0.25		1.62 ± 0.03	62.8 ± 6.5d	2.0 ± 0.01d

Mean and SD values for model-specific pharmacokinetic parameters and initial conditions (y-intercept) and their comparisons among the 4 models for HV and model–group interactions between CBG-deficient and HV subjects

^a y-intercept for Models 1 to 3 are significantly different from one another, P < .001 for all comparisons (HVs). Note that the y-intercept for Model 2 is for free cortisol (X_F), whereas y-intercepts for Models 1 and 3 are for total cortisol (X_TotF).

^b α₄>α₃>α₂>α₁, all P ≤ .001by paired t-test (HVs).

^c τ₁>τ₂>τ₃>τ₄, all P < .001 by paired t-test (HVs).

^d Pharmacokinetic parameter estimates in CBG-deficient group different compared with HVs (both P ≤ 0.01).

Comparison of Model-Specific Parameter Solutions by Clinical Group (HV vs CBG-Deficient Subjects)

There was a statistically significant interaction between model and group (HV vs CBG-deficient) for cortisol half-life estimates (RM ANOVA, overall P < .001). In post hoc testing and compared with HVs, τ₁ was shorter and τ₃ was longer in the CBG-deficient subjects (both P ≤ 0.01, see Table 2), whereas Model 4 solutions for α₄ and permeability constant (k) were similar between groups. Vascular (V) and extravascular (V_e) volumes were significantly smaller in CBG-deficient subjects than in HVs (Table 2), which was likely related, at least in part, to decreased weight, height, and body surface area (BSA) in the CBG-deficient subjects (see Section F [14]).

Model-Specific Goodness of Fit Summary Measures (bias, SD, RMS)

Significant model-dependent differences in bias, SD, and RMS of residuals were observed (RM ANOVA, overall P < .001). In post hoc testing, the rank order was RMS₁ < RMS₄ < (RMS₂, RMS₃) (all P < .001 except for those shown in parentheses were not significantly different, see Table 3). Optimized solutions for Models 1 to 4 and corresponding summary measures of goodness of fit for a representative HV subject are shown elsewhere (Section O and Fig. S1 [14]).

Table 3.

Goodness of fit measures for model-dependent cortisol solutions (summary of residuals)

Model	Bias (%)	SD (%)	RMS (%)
1	−0.3a	7.5b	7.5b
2	−6.7	23.3	24.2
3	−1.2	19.7	19.7
4	−0.9	13.7c	13.7c

Bias, standard deviation (SD), and root mean squared error (RMS) for residuals (measured minus model-predicted cortisol, percent error) for pooled HV and CBG-deficient subjects. Bias and RMS were compared by RM ANOVA, SDs were compared using Wilks test. Lower residuals correspond to better agreement between model-predicted and measured cortisol concentrations

^a Bias Model 1 < Model 2 (P < .001).

^b Model 1 < Models 2 to 4 (all P < .001).

^c Model 4 < Models 2 and 3 (both P < .001).

Assessment Tool for Model Comparisons

In the assessment tool for model comparisons, Model 4 satisfied the most and Model 1 the fewest number of model validation criteria, with overall rank order Model 4 > Model 3 > Model 2 > Model 1. Models 1 to 3 were judged to be too simple in the category of model requirements in the assessment tool, as discussed in more detail below. Briefly, the basis for that determination may be summarized by our observations that cortisol flux to and from the extravascular volume had a significant impact on plasma cortisol concentrations and, when unaccounted for (as in Models 1 to 3), was a significant and predictable source of bias in model-specific solutions for α and τ (Table 4) (also see Sections M and S [14]).

Table 4.

Assessment tool (rubric) for comparisons of Models 1 to 4

Model	1	2	3	4	Comments
Section 1. General model requirements
Model supports use of individual (measured) concentrations of CBG and albumin (rather than assumed population values)	No	No	Yes	Yes	Variation in CBG and albumin concentrations significantly affect parameter solutions [7, 9] Models 3 and 4 support use of individualized [CBG], [albumin], etc.
Parameter solutions are generalizable between bolus and continuous modes of hydrocortisone administration	No	No	No	Yes	Predictive accuracy of cortisol concentrations when α1-α4 values from the bolus are applied to continuous cortisol Reference data: Prete et al [19] (see Section 4)
“as simple as possible but not too simple” The model accounts for the major factors that influence cortisol concentrations measured in plasma	No	No	No	Yes	Cortisol flux contributes significantly to plasma cortisol concentrations. See discussion of model-group interactions (Table 2) elsewhere (Section M [14])
Section 2. Mathematical formulation of the model accounts for relevant elements of experimentally validated physiology
Model equations include a term for concentration-dependent elimination of free cortisol (XF)	No	Yes	Yes	Yes	Cortisol elimination is restricted to free rather than protein-bound cortisol [3, 48]
Applies law of mass action to reversible binding of cortisol binding to serum binding proteins	No	No	Yes	Yes	Cortisol binding to CBG (Eq. 2) and albumin (Eq. 3) in human serum at 37 °C has been well characterized
Includes vascular and extravascular distribution volumes for cortisol	No	No	No	Yes	Cortisol is not restricted to the vascular volume in vivo [41]
Free cortisol exchange between V and Ve modeled by diffusion	N/A	N/A	N/A	Yes	Diffusion is simple and realistic [43, 44]
Section 3. Summary of residuals (observed minus predicted)
Goodness of fita (RMS as %)	7.5a	24.2	19.7	13.7	See Table 3
Residuals demonstrate random pattern	No	No	No	No	Modeling objective is white noise pattern of residuals
Section 4. Empiric performance measures
Dynamic: Model-predicted time to steady state (h) applying α1-α4 derived from bolus experiment (HVs, Table 2) to continuous cortisol infusion approximate experimental data	No (10.2 hours)	No (6.2 hours)	Yes (2.9 hours)	Yes (2.6 hours)	Prete et al reported time to steady state of ≈2 hours following initiation of continuous hydrocortisone infusion (8 mg/h) [19]
Steady state: steady-state cortisol concentrations (nmol/L) predicted from the bolus experimentb match experimental data	No XTotFS = 23 560	No XFS = 14 154	No XFS = 1089	Yes XFS = 159	At constant infusion of cortisol (368 nmol/min) Prete et al reported median steady-state plasma concentrations of total (XTotF) and free (XF) cortisol of 836 and ≈144 nmol/L, respectively [19]
Cortisol half-life (τ) independent of unrelated measures, represented by significant differences in τ between CBG-deficient and HV groups	No	Yes	No	Yes	See model-group interactions (Table 2) and elsewhere (Section M [14])

Models 1 to 4 were compared by several criteria, including general model requirements, inclusion of relevant physiology in the mathematical formulation of the model, residuals between model-predicted and experimentally measured cortisol concentrations, and empiric performance measures.

^a RMS values are based on cortisol concentration data of Perogamvros et al [9]. However, in other data sets used for Model 1 solutions, different values for τ₁ were required to fit cortisol concentration during early (10-40 minutes) and terminal (60-360 minutes) periods after bolus [28, 49].

^b Model-predicted steady-state cortisol concentrations calculated from steady-state equations (Section E [14]) used vascular volume (V) = 2.6 L (Table 2, HVs).

Among the models evaluated, only Model 4 solutions, developed from the bolus experiment, transitioned realistically to steady state in the continuous infusion experiment without changing the parameter values. For example, model-predicted time to steady state for Models 1 and 2 exceeded experimental observations (≈2 hours in Prete et al [19]) by more than 2-fold (Table 4). Similarly, steady-state cortisol concentrations predicted from the bolus experiment approximated experimental data of Prete et al [19] only for Model 4 solutions (see Table 4; Section L [14]). None of Models 1 to 4 met the performance criterion of white noise pattern of residuals. For example, Model 4 solutions were associated with negative residuals (measured cortisol lower than computed) at the first postbolus cortisol time point (10 minutes) and positive residuals (measured cortisol greater than computed) at the last (480 minutes) (eg, see Section N [14]).

Model 4 Simulation of Hydrocortisone Bolus (20 mg) in HVs

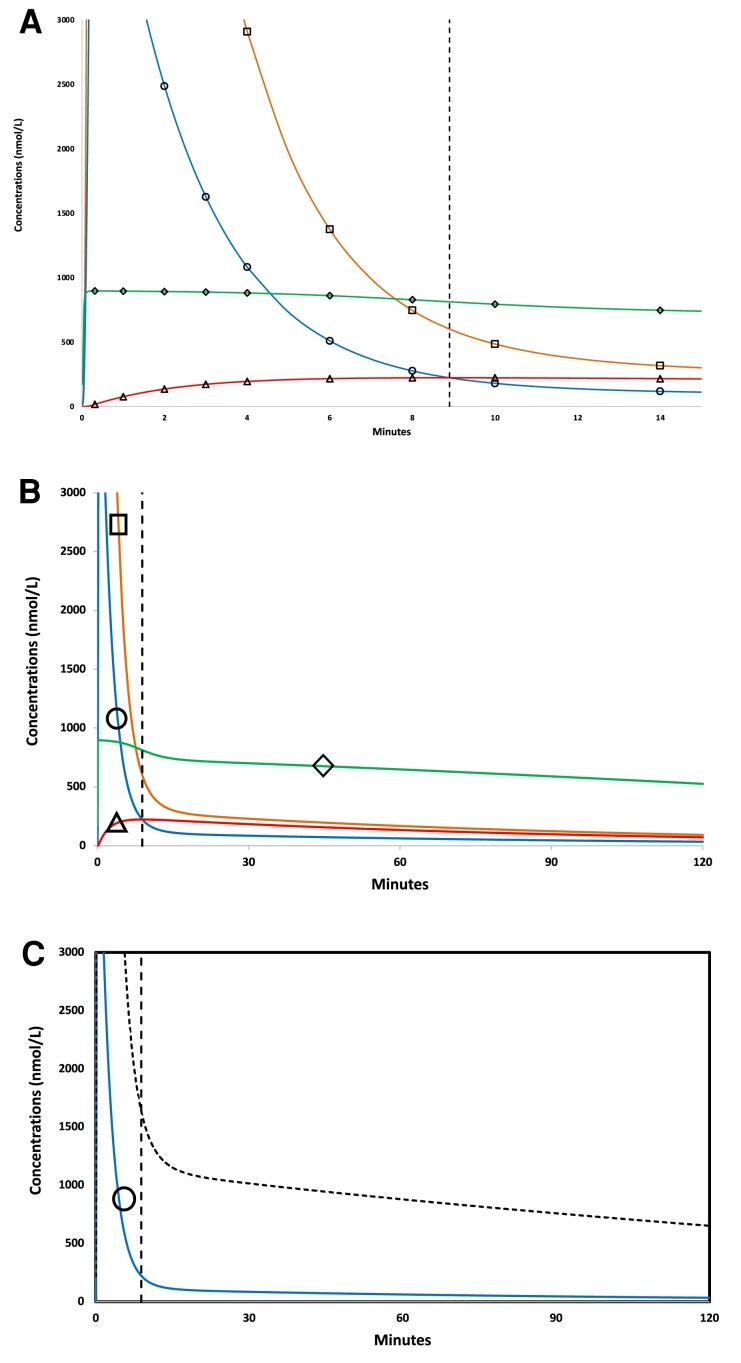
Figure 1 shows cortisol concentrations in all 4 compartments predicted by Model 4 for the 20-mg hydrocortisone bolus experiment (see “Materials and Methods”). The simulation demonstrates an abrupt increase in plasma concentrations of plasma free (X_F, blue line, open circles) and albumin-bound cortisol (X_A, orange line, open squares) within the first minute of hydrocortisone bolus (Fig. 1A). After transiently reaching peak values >5000 nmol/L (not shown, exceeds upper limit of y-axis), plasma free (X_F) and albumin-bound (X_A) cortisol concentrations rapidly decreased in tandem over the next several minutes (Fig. 1A). The simulation also illustrates saturable binding of CBG at high free cortisol concentrations, reduced rate of decline in concentrations of CBG-bound cortisol (X_C, green line, open diamonds) compared with free (X_F) and albumin-bound (X_A) cortisol, and rapid rate of increase in extravascular cortisol concentrations (X_Fe, red line, open triangles) following hydrocortisone bolus.

Figure 1.

Model 4 simulation showing time-varying cortisol concentrations for 20 mg hydrocortisone bolus. (A) Cortisol concentrations as a function of time (0-15 minutes) following IV hydrocortisone bolus (20 mg infused over 20 seconds) in all 4 compartments, including vascular (plasma) free cortisol (X_F, circle symbol, blue), vascular (plasma) albumin-bound cortisol (X_FA, square symbol, orange), vascular (plasma) CBG-bound cortisol (X_FC, diamond symbol, green), and extravascular (free) cortisol (X_Fe, red curve, triangle symbol, red). In this example a unique intersection point, where extravascular and plasma free cortisol concentrations are momentarily equal (X_F = X_Fe) occurred at T* = 8.9 minutes, indicated by dashed vertical line, and at free cortisol concentration of 223 nmol/L (X_F = X_Fe = 223 nmol/L). (B) The same data with axes expanded in cortisol concentration and time (0-120 minutes), symbols as in Panel A. (C) Model 4 predicted concentrations for 2 more commonly measured analytes: plasma free cortisol (X_F, solid line, blue) and plasma total cortisol (X_TotF, dotted line, black), which is the sum of free, albumin-bound, and CBG-bound cortisol concentrations in the vascular (plasma) compartment.

A characteristic feature of bolus simulations at all doses examined in simulation (0.1-100 mg) was the postbolus intersection point, at which time (T*) plasma free cortisol and extravascular cortisol concentrations are momentarily equal (X_F = X_Fe) and extravascular cortisol concentrations were maximal (X_Fe*). In the 20 mg bolus simulation shown in Fig. 1A, for example, the intersection point occurred at T* = 8.9 minutes (dashed vertical line) and at maximal extravascular cortisol concentration (X_Fe*) of 223 nmol/L. Figure 1B shows the longer time course (0-120 minutes) after 20 mg hydrocortisone bolus, which illustrates the monotonic decline in cortisol concentrations in all 4 compartments after T*. Plasma total cortisol (X_TotF) is typically measured in pharmacokinetic studies, often in conjunction with measured [9] or calculated [18] free cortisol (X_F). Figure 1C shows model-predicted concentrations of X_F (blue line) and X_TotF (black line), the latter of which was calculated as the sum of model-predicted X_F, X_C, and X_A (see Materials and Methods, Eqs. 1-4).

Model 4 Simulation of Cortisol Mass Following Hydrocortisone Bolus (20 mg)

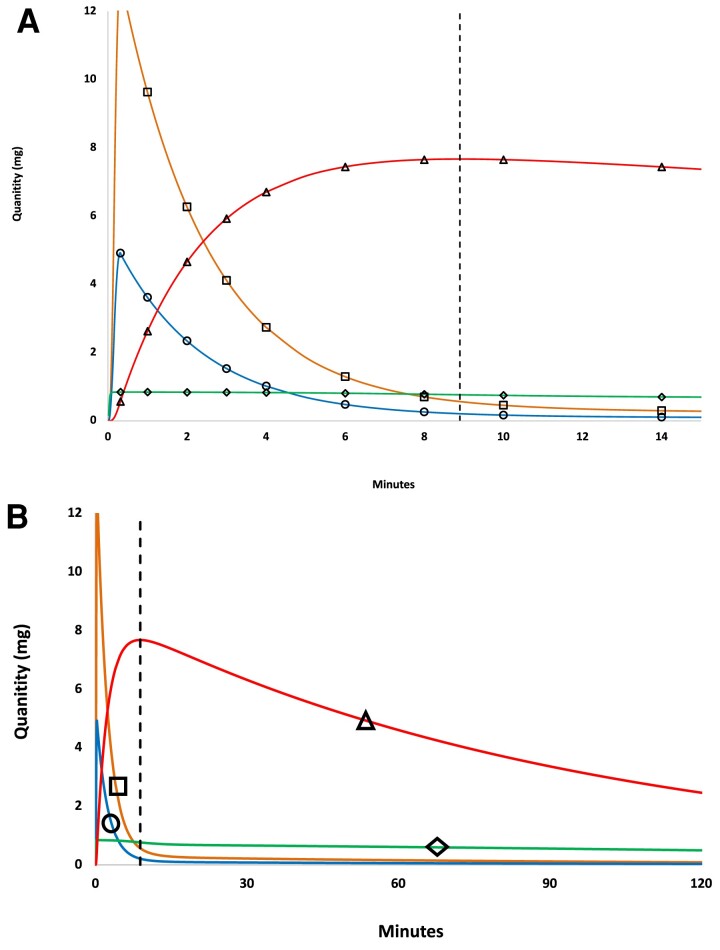
Cortisol mass (Q) in each compartment was obtained by multiplying cortisol concentrations by corresponding distribution volume (V or V_e). Figure 2A demonstrates a rapid rate of increase in extravascular cortisol mass (Q_Fe) following hydrocortisone bolus, which reached a maximum (Q_Fe*) at the intersection point (T*, dashed vertical line). Figure 2 also illustrates the Model 4 prediction that, for the 20-mg bolus simulation, extravascular cortisol mass (Q_Fe) exceeds the mass of cortisol contained in the vascular volume (Q_TotF) at most time points, and certainly at all time points after T*.

Figure 2.

Model 4 simulation showing time-varying cortisol mass for 20 mg hydrocortisone bolus. (A) Cortisol mass in all 4 compartments as a function of time, symbols and colors are as in Fig. 1. (A) Cortisol mass by compartment for 0 to 15 minutes. (B) The same data with axes expanded to 120 minutes.

Dose-dependent variation in peak extravascular cortisol concentrations (X_Fe*) and time to intersection point (T*) following hydrocortisone bolus

Model 4 predictions for variation in bolus hydrocortisone dose (0.1-100 mg) was further evaluated in simulation (Section P [14]). A good, linear (proportional) approximation between bolus dose and X_Fe* was observed in simulation (data not shown). Simulations also demonstrated a non-linear, negative correlation between bolus dose and T* as well as dose-dependent interactions with CBG and albumin concentrations (3-way interaction) (Section P, Fig. S2 [14]).

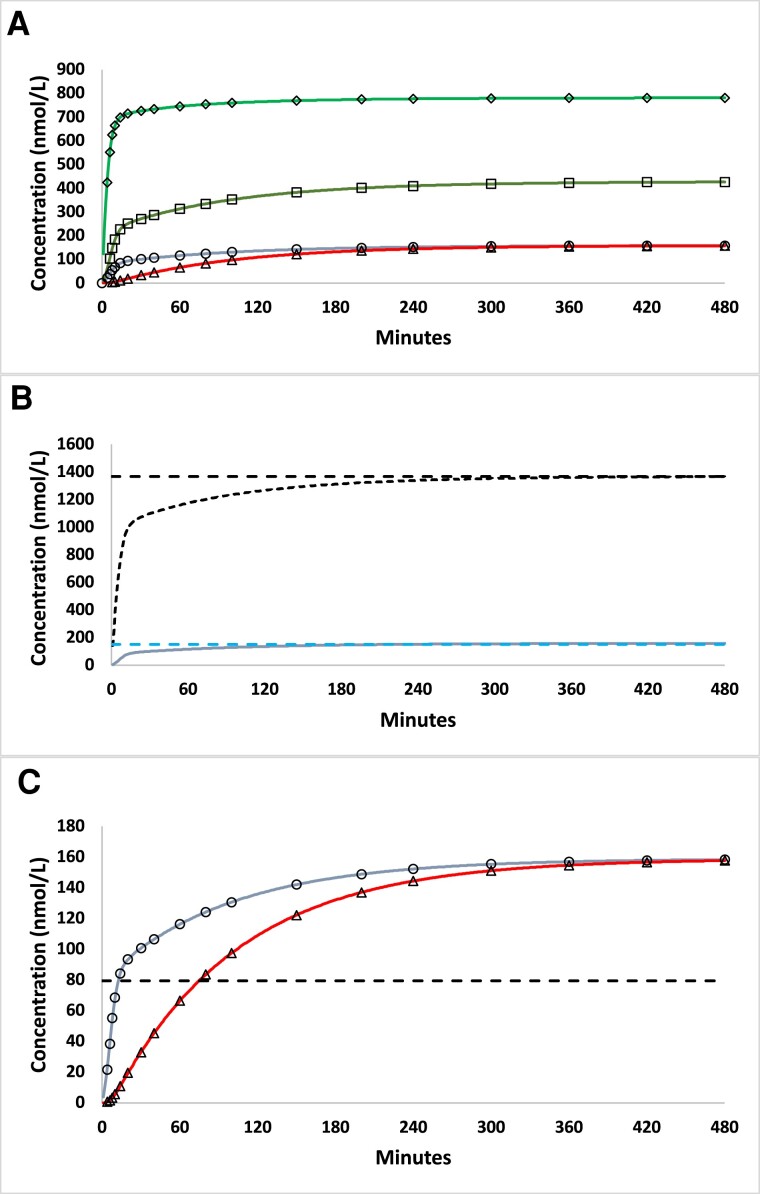
Model 4 Simulations for Continuous Hydrocortisone Infusion (8 mg/hour) in HV

Figure 3A shows the Model 4 simulation for continuous hydrocortisone infusion at a rate of 8 mg/hour, which matches experimental conditions of Prete et al [19]. Time to steady state (2.6 hours) and steady-state concentrations of plasma free cortisol (151 nmol/L) predicted by Model 4 were similar to experimental observations (≈2 hours, ≈144 nmol/L) reported in Prete et al [19, 33] (see Table 4). The simulation also illustrates the time delay related to diffusion of free cortisol between vascular and extravascular volumes. For example, the time to reach half-maximal concentrations of free cortisol (50% of steady state X_F, horizontal dashed line in Fig. 3C), was 12.6 and 75.4 minutes for X_F and X_Fe, respectively, which corresponds to a time lag ≈62 minutes. Figure 3 also illustrates the Model 4 prediction of equality of plasma free and extravascular cortisol concentrations (X_F = X_Fe) at steady state. Note as well that since the net rate of flux between vascular and extravascular compartments at steady state is 0, a corollary model prediction is that the only distribution volume involved at steady state is the vascular (plasma) volume.

Figure 3.

Model 4 simulation for continuous hydrocortisone infusion (8 mg/hour). (A) Model 4 predicted cortisol concentrations as a function of time for continuous infusion of hydrocortisone (8 mg/h) for all 4 compartments, symbols and line format as in Fig. 1. (B) Predicted concentration of vascular (plasma) total (X_TotF, black line) and free (X_F, blue line) cortisol. Steady-state cortisol concentrations (95% of asymptote) are shown by dashed lines. (C) Comparison of predicted plasma free (X_F, blue line) and extravascular (X_Fe, red line) cortisol concentrations as a function of time. The dashed horizontal line indicates the free cortisol concentration at 50% of the asymptotic, steady-state value.

Analysis of Model–Group Interaction (CBG-Deficient vs HVs) and Delineation of Model-Specific Error Types

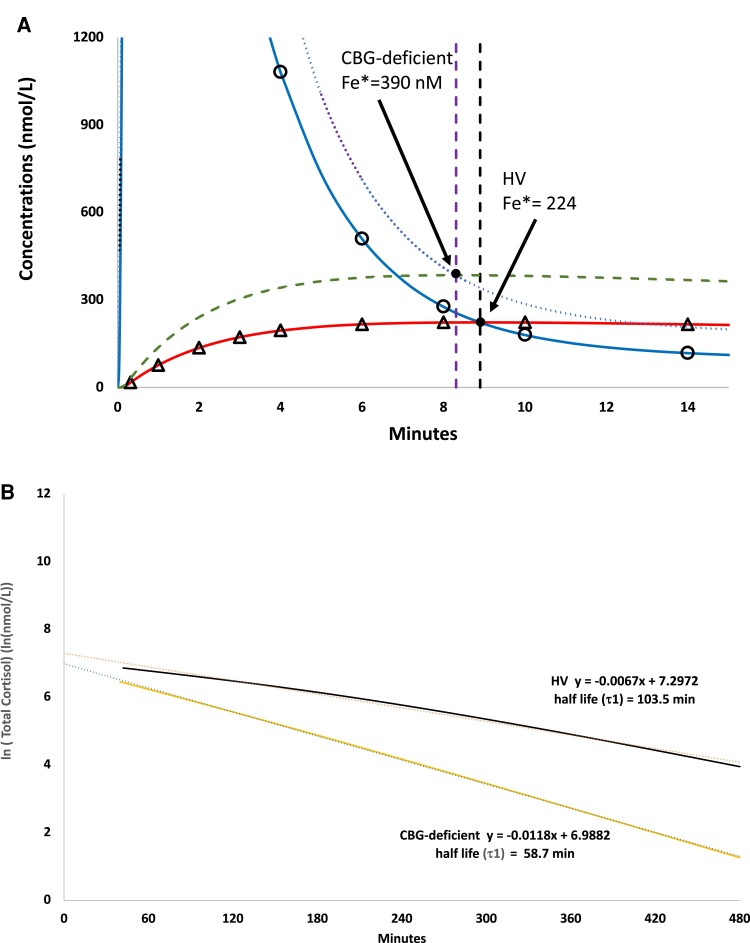
The model–group interaction observed in our study, namely significantly shorter τ₁ and significantly longer τ₃ in CBG-deficient subjects relative to HVs (Table 2), was also replicated in simulation (Fig. 4). Exposition of diffusion, protein-binding, and elimination errors by pairwise comparisons of nested models (Section S [14]) provides a plausible explanation that the observed group differences in both τ₁ and τ₃ were due to model artifact. For example, in simulation we observed that the longer τ₃ in CBG-deficient vs HV group was an artifact of diffusion error associated with Model 3 (see Fig. 4A). In additional simulation analysis, we observed that the higher X_Fe* was related to several factors that distinguished HV and CBG-deficient groups. These included decreased concentrations and binding affinity of CBG as well as decreased vascular volume (V) in the CBG-deficient group (see Section Q [14]). By contrast, the shorter τ₁ associated with CBG deficiency was an artifact of both protein-binding and elimination errors associated with application of Model 1 (see Fig. 4B and Section R [14]). A detailed discussion of these 3 types of errors that distinguish Models 1 to 4, including protein binding and elimination errors, is included elsewhere (Section S [14]). In summary, each of Models 1 to 3 are associated with 1 or more identifiable misrepresentations of physiology that were expressed as bias in parameter solutions. These sources of error were subject to interaction with relevant group differences in physiology (Table S4 [14]), which, compared with HVs, included significantly lower concentrations and cortisol-binding affinity of CBG [9, 42] and decreased vascular volume (V) (Table 2) in the CBG-deficient group. Finally, Model 4 solutions demonstrated similar rates of cortisol elimination (α₄) in HV and CBG-deficient groups (Table 2).

Figure 4.

Simulation of computer-generated cortisol concentrations for 20 mg hydrocortisone bolus obtained using Model 4 for CBG-deficient vs HV groups. (A) Model-predicted plasma free (X_F) and extravascular (X_Fe) cortisol concentrations for HV and CBG-deficient groups. For the CBG-deficient simulation, X_F and X_Fe are indicated as dotted (purple) and dashed (green) lines, respectively. For HV, X_F and X_Fe are indicated by circles (blue line) and triangles (orange line), respectively. Vertical lines indicate times to intersection point postbolus (T*) for HV (intersection (Fe* at 224 nmol/L, black) and CBG-deficient (intersection Fe* at 390 nmol/L, purple). (B) Model-predicted, log-transformed total cortisol concentrations (X_TotF) for HV and CBG-deficient groups and Model 1 half-life solutions (τ₁) for the log-transformed cortisol concentrations (terminal half-life shown in bold).

Dose-Dependent Variation in Model 1 Solutions for Cortisol Half-life (τ1)

In early pharmacokinetic studies using Model 1, the demonstration of a positive correlation between bolus dose and τ₁ contributed importantly to the recognition of the extravascular distribution volume [36–38, 49]. In pharmacokinetic studies using Model 1 recently reported by Arafah, dose-dependent variation in τ₁ in the bolus experiment was similarly observed, with significantly (P < .01) longer terminal cortisol half-life for the 25-mg (mean τ₁ = 121 minute) than the 15-mg (mean τ₁ = 109 minutes) hydrocortisone dose [28]. These dose-dependent differences in τ₁ were also reproduced in silico (Section T [14]). A plausible mechanism was suggested in simulation studies showing higher X_Fe* and Q_Fe* for the 25-mg than the 15-mg dose, which was related to expression of diffusion error in Model 1 solutions (Fig. S5, also see Section S [14]).

Discussion

The proposed 4-compartment diffusion model (Model 4) represents a novel, mechanistic mathematical formulation of cortisol disposition that includes the major determinants of plasma cortisol concentrations in vivo. By contrast, none of the contemporary Models 1 to 3 account for the distribution of cortisol in the extravascular compartment. The omission of transcompartmental cortisol flux in Models 1 to 3 was designated diffusion error and was most directly illustrated by comparing equations and parameter solutions between Model 4 and nested Model 3 (Section S [14]). In addition to diffusion error, single-compartment models were also biased by protein binding error (affecting Models 1 and 2) and elimination error (affecting Model 1). These model errors were also illustrated by our finding of ordered relationships of model-specific parameter solutions (α₁ < α₂ < α₃ < α₄ and τ₄ < τ₃ < τ₂ < τ₁, see Section M [14]). Mathematical studies also highlighted the contextual nature of model-specific parameter solutions and the inaptness of exchanging parameter solutions between models (see discussion of transposition error in Section U [14], and below). In summary, Models 1 to 3 systematically underestimate rates of cortisol elimination in vivo, while Model 4 solutions yielding shorter free cortisol half-lives are more realistic.

Adaptation of Fick's first law of diffusion to model transcompartmental cortisol flux [43, 44] was effective and, compared with first-order rate constants [35–38], parsimonious with respect to model parameterization and development of unique parameter solutions. The process of diffusion represents a time delay and smoothing function. In fact, this was further characterized mathematically, as X_Fe is a convolution integral of X_F and may be expressed in terms of an exponential probability density function (see Section M [14]). The time delay was also illustrated by the temporal lag between X_F and X_Fe in the continuous cortisol infusion experiment (Fig. 3C). Delays predicted in Model 4 simulations were also consistent with experimental observations comparing interstitial cortisol and X_F during ACTH stimulation and DEX suppression [41].

Note that the extravascular volume in the formulation of Model 4 includes both intracellular and interstitial compartments, and therefore represents the site in which the biological activities of cortisol mediated by binding to intracellular GR are initiated. Accordingly, the temporal delay between cortisol secreted or infused into the vascular compartment (X_F) and cortisol concentrations in the extravascular compartment (X_Fe) also implies a temporal delay in biological effects. With regard to clinical use of CRT, for example, our finding that hydrocortisone bolus results in more rapid increase in X_Fe than continuous hydrocortisone infusion in silico is consistent with the recommendation for an initial bolus dose of IV hydrocortisone prior to or concurrent with initiation of continuous cortisol infusion in the clinical management of adrenal crisis [15, 19]. Delays between X_F and X_Fe also imply delays in the feedback effects of cortisol associated with its pulsatile secretion by the adrenal cortex into the vascular compartment (V). Therefore, the delayed effects of feedback inhibition of the hypothalamic–pituitary–adrenal axis may be important to chronobiological aspects of ACTH and cortisol secretion in vivo, including frequency and duration of endogenous pulses of cortisol and ACTH [41, 50].

For the bolus experiment, peak extravascular cortisol concentration X_Fe* was a useful integrated measure of the magnitude of transcompartmental cortisol flux, while T* was useful in quantifying temporal dynamics of cortisol flux. For example, we observed a positive, approximately linear correlation between bolus dose (0.1-100 mg) and X_Fe* in simulation. As well, an inverse, nonlinear relationship between bolus dose and T* was also observed. Interestingly, at pharmacologic doses of hydrocortisone bolus, T* asymptotically approached a minimum value (≈8 minutes, as shown in Fig. S2 [14]) and the timing of this asymptote was sensitive to variation in serum albumin concentrations in silico. These findings suggest that in cortisol pharmacokinetic studies in humans, which typically use bolus doses in the range of 15 to 100 mg [9, 25, 28], the first cortisol measurement (10 minutes postbolus) is likely subsequent to T*. As noted above, this is a phase in which net cortisol flux (V_e→V) slows the apparent rate of decline of plasma cortisol concentrations, including X_F and X_TotF.

By contrast, at physiologic doses of hydrocortisone bolus, T* was longer (10-40 minutes) and sensitive to variation in bolus dose and CBG concentrations (Section P [14]). These findings suggest that at physiologic concentrations of X_F, normal variation in CBG and albumin concentrations significantly influence the dynamics of transcompartmental cortisol flux in vivo. As expected, several other factors were found to influence the time-varying rate of cortisol flux in simulation. These included rates of cortisol appearance and elimination, vascular volume (V) (see Fig. S3 [14]), V_e (data not shown), and permeability constant (k) (see “Materials and Methods”). Note that k is a composite parameter that incorporates terms for barrier geometry, including the surface area for diffusion (A). Therefore, variation in the permeability constant (k), and corresponding rates of cortisol flux, may be expected in clinical conditions associated with hypoperfusion or alterations in regional blood flows affecting capillary surface area.

The recognition of model-specific errors by pairwise comparisons of model equations and parameter solutions provided feasible explanations for 3 anomalous observations from the endocrine literature [9, 24, 28, 48, 51]. All 3 examples appeared to be due to modeling errors, namely, bias associated with systematic misrepresentation of physiology in the model applied to experimentally measured cortisol concentration data. The first anomaly concerns the relationship (positive correlation) between CBG concentration and τ₁, which was observed in analysis of our data (Table 2) and in simulation (Fig. S4 [14]). A similar relationship has also been reported previously in the literature [9, 51]. We conclude that this relationship was due to combined effects of protein-binding and elimination errors in Model 1 solutions. A similar mechanism likely explains the relationship between concentration of the high-affinity transport protein and τ₁ observed when comparable models (single compartment for total hormone concentration) have been applied to other hormones of the steroid/thyroid receptor superfamily [48]. The second anomaly concerns the dose-dependent variation in τ₁ reported by Arafah [28] and others [37, 52]. We conclude that these observations were not due to bona fide differences in cortisol elimination rates but rather to diffusion error in Model 1 solutions, as illustrated elsewhere (Fig. S5 [14]). As expected, diffusion error also affected solutions obtained using Model 3 (see Table 2 and Fig. 4A) and Model 2 (data not shown). The third anomaly concerns the paradoxical finding of decreased rather than increased CSR in ECIs [24], which was related to a combination of modeling errors, including transposition error (see Section U [14]).

There were several limitations to our study, including small number of study subjects, post hoc study design, and the use of a single (20 mg) bolus dose of hydrocortisone. Prospectively designed studies using cortisol infusion rates and cortisol sampling regimes optimized for numerical analysis would provide more accurate solutions and reference ranges for relevant Model 4 parameter solutions. Our objective of minimizing the number of parameters to be solved, the so-called minimal model approach [53], was appropriate for this primary stage of development of the cortisol disposition model. However, this approach necessitated several simplifying assumptions, which could be viewed as limitations. They include (1) instantaneous mixing and homogeneity of free cortisol in V and V_e, (2) treatment of cortisol in the extravascular compartment as freely diffusible; (3) use of a single term (α₄) to represent diverse enzyme activities associated with hepatic and renal elimination of free cortisol; (4) lack of accounting for other compounds circulating in the plasma volume that may compete with cortisol binding with CBG and/or albumin [54, 55]; and (5) representation of irreversible elimination of free cortisol (α) as first order rather than saturable process. Saturable kinetics of free cortisol elimination may be especially relevant at pharmacologic doses of hydrocortisone bolus associated with supraphysiologic concentrations of X_F [56, 57]. In addition, we did not account for the possibility of extra-adrenal production of cortisol through 11-β-hydroxysteroid dehydrogenase type 1 [58, 59]. Rates of extra-adrenal cortisol appearance may be substantial at pharmacologic doses of hydrocortisone bolus associated with transiently increased concentrations of free cortisone (data not shown). An advantage of the mechanistic, realistic design of the primary model described herein is its adaptability to second order modifications. For example, future modifications to Model 4 could include saturable kinetics of cortisol elimination, extra-adrenal cortisol appearance through the 11-β-hydroxysteroid dehydrogenase type 1 pathway, competition of other steroids for CBG binding [54, 55], and, in the case of the oral hydrocortisone experiment, differentiation of hepatic portal vs extrahepatic cortisol concentrations [60].

Our analysis was restricted to healthy subjects, whereas the clinical question of CRT often arises in acutely ill patients [21, 61–63]. Critical illness is associated with low CBG and albumin concentrations and high concentrations of X_F relative to X_TotF [6, 8, 64], factors which confound pharmacokinetic analysis using Models 1 to 3. The robust performance of Model 4 across HVs and CBG-deficient subjects and mechanistic design suggest that the model may be generalizable to the setting of critical illness as well. Of course, key (important) parameter values would need to be changed to reflect the changed circumstances, including lower concentrations of CBG and albumin, increased cortisol concentrations, and higher concentrations of X_F as a percent of X_TotF.

In previous studies, significantly longer cortisol half-life (7-fold longer τ₁, 3.1-fold longer τ₂, and 2.3-fold longer τ₃ obtained using Models 1-3, respectively) was observed in ECI relative to controls [18, 25, 26]. Our analysis raises the question as to whether these observations were related to absolute reductions in the rate of cortisol elimination [25], saturable kinetics of cortisol elimination [56], or diffusion error. In addition, exposition of Model 4 equations suggests that stable isotope methods may not be considered to be the gold standard method for measurement of cortisol appearance rates, at least as applied to cortisol in the context of Model 1 assumptions of X_TotF as a single compartment [25] (see Section V [14]). These considerations highlight the need for prospectively designed studies to further characterize physiologically relevant parameters of cortisol disposition in ECI and evaluate their potential significance to pathogenesis, diagnosis, and treatment of critical illness–related corticosteroid insufficiency and related conditions.

In conclusion, the proposed 4-compartment diffusion model of cortisol (Model 4) links the well-substantiated principles of the free hormone hypothesis [1, 3] to 3 chemical–physical laws generally applicable to endocrine systems, namely (1) law of mass action, (2) law of mass conservation, and (3) Fick's first law of diffusion [40]. Note that in the 4 nonlinear differential equations of Model 4 (Eqs. 1-4), it is free cortisol (rather than protein-bound cortisol) that (1) diffuses across the capillary endothelial membrane “barrier,” (2) defines the concentration gradient directly related to the direction and rate of cortisol flux, and (3) is subject to metabolic elimination, presumably as the substrate of hepatic and renal enzymes. Thus, Model 4 provides a dynamic, affirmative, and mathematical formulation of the free hormone hypothesis [1, 3]. Our findings highlight the importance of the extravascular cortisol distribution volume, which contains a substantial fraction of total body cortisol mass and contributes significantly to dynamic variation in plasma cortisol concentrations. The adaptation of Fick's first law of diffusion in conjunction with realistic systems of nonlinear differential equations are likely to be broadly applicable to endocrine systems, including but not limited to other lipophilic hormones of the steroid/thyroid receptor superfamily [1, 65]

Abbreviations

AI

adrenal insufficiency

ANOVA

analysis of variance

CBG

corticosteroid binding globulin

CRT

corticosteroid replacement therapy

CSR

cortisol secretion rate

ECI

euadrenal, critically ill patient

GR

glucocorticoid receptor

HV

healthy volunteer

IV

intravenous

RM

repeated measures

X _A

albumin-bound cortisol

X _C

CBG-bound cortisol

X _F

plasma concentration of free cortisol

X _TotF

concentration of plasma total cortisol

Disclosure Statement

The authors have nothing to disclose.

Data Availability Statement

Some or all datasets generated during and/or analyzed during the current study are not publicly available but are available from the corresponding author on reasonable request.