Abstract
Cells translate mechanical cues from the extracellular matrix (ECM) into signaling that can affect the nucleus. One pathway by which such nuclear mechanotransduction occurs is a signaling axis that begins with integrin-ECM bonds and continues through a cascade of chemical reactions and structural changes that lead to nuclear translocation of YAP/TAZ. This signaling axis is self-reinforcing, with stiff ECM promoting integrin binding and thus facilitating polymerization and tension in the cytoskeletal contractile apparatus, which can compress nuclei, open nuclear pore channels, and enhance nuclear accumulation of YAP/TAZ. We previously developed a computational model of this mechanosensing axis for the linear elastic ECM by assuming that there is a linear relationship between the nucleocytoplasmic ratio of YAP/TAZ and nuclear flattening. Here, we extended our previous model to more general ECM behaviors (e.g., viscosity, viscoelasticity, and viscoplasticity) and included detailed YAP/TAZ translocation dynamics based on nuclear deformation. This model was predictive of diverse mechanosensing responses in a broad range of cells. Results support the hypothesis that diverse mechanosensing phenomena across many cell types arise from a simple, unified set of mechanosensing pathways.
Significance
The mechanics of the extracellular microenvironment (e.g., matrix elasticity, viscosity, viscoelasticity, and viscoplasticity) affect physiological and pathological cell behaviors. A goal of mechanobiology is to identify, predict, and disrupt the molecular pathways underlying pathology. Toward this goal, we developed a computational model of a critical signaling pathway and applied it to predict diverse mechanosensing phenomena. The model lays a foundation for understanding how diverse cellular behaviors arise from a concise set of signaling steps and for potentially disrupting certain pathological mechanosensing behaviors.
Introduction
Mechanical cues from the extracellular microenvironment, such as elasticity, viscosity, and viscoelasticity of the extracellular matrix (ECM), regulate cellular behaviors such as migration, proliferation, and differentiation (1). Changes to these cues accompany pathologies such as metastasis and fibrosis and have been implicated in the development of drug resistance in chemotherapy (2). These observations motivate a range of emerging applications of mechanobiology, including concepts of mechanomedicine (3,4) and mechanochemical conversion (5).
Many different mechanotransduction pathways have been identified that can explain such phenomena, with a common theme being the force-dependent manipulation of molecules that link the ECM. This manipulation can affect nuclear signaling and gene expression through pathways that begin with members of the integrin family, whose extracellular domains can bind to the ECM (6). Through mechanochemical conversion involving focal adhesion kinase (FAK), the talin-vinculin complex, actomyosin, and a series of molecules that link the cytoskeleton to the nucleus, ECM mechanics can be transduced by integrins (7) and translated into nuclear translocation of molecular signals that affect the hippo pathway, specifically the Yes-associated protein and transcriptional coactivator with PDZ-binding motif (YAP/TAZ) (8,9).
Mathematical models of integrin-mediated intracellular signaling have reconciled many disparate cellular responses to matrix mechanics. For example, mechanosensing differences between neurons and U251 glioma cells can be explained by differences in the motor-clutch dynamics of ECM-integrin-actin linkages (10), and seemingly inconsistent trends observed in the dependence of actin flow on matrix stiffness can be explained by talin unfolding dynamics and integrin cross-talk (11,12). Clinical translation of observations like these about the role of the integrin-FAK-actomyosin-YAP/TAZ axis may someday be possible through the use of drugs that affect the different steps of the cascade, such as biogen for αvβ6 integrin, defactinib for FAK, and 4-HAP for myosin (13).
A critical need is the capacity to screen such molecules in silico to predict how such a mechanosensitive axis can modulate cellular behaviors (14), including decision-making in response to pathological mechanosignaling in disease (15). Mechanobiological models can now predict how certain cell behaviors and mechanics evolve with microenvironmental cues. Such models include the chemomechanical model of Shenoy and co-workers (16,17); the models of Deshpande, McGarry, and co-workers (18,19); the Chan-Odde molecular clutch model (20,21); and its extensions by the Roca-Cusachs groups and others (11,12,22,23,24,25) for talin-vinculin dynamics and viscous effects. Motor-clutch models predict a surprising diversity of cellular responses (e.g., cell adhesions, cell traction, and actin flows) to matrix mechanics, including matrix elasticity, viscosity, viscoelasticity, and plasticity (20,23,24,26). However, these models are not capable of predicting the responses of intracellular signals (such as YAP/TAZ nuclear translocation) to matrix mechanics.
Recently, deterministic methods such as homogenized and spatial models have been developed to study the integrin-YAP signaling axis in response to an elastic matrix (27,28). Besides, we also proposed a computational model for predicting how YAP/TAZ nuclear translocation dynamics respond to matrix elasticity (29). However, linear elasticity does not cover matrix mechanics in vivo, and we therefore extended previous computational approaches to develop a single treatment accounting for the recursive feedback between ECM mechanics, focal adhesion dynamics, and integrin-FAK-myosin-YAP/TAZ signaling. We hypothesized that a diversity of heterogeneous cellular behaviors could be predicted from a small set of mechanobiological and rate equations and tested this hypothesis by verifying the model against a range of experimental observations reported in the literature.
Materials and methods
Stochastic mechanochemical computational model
Overview of the model
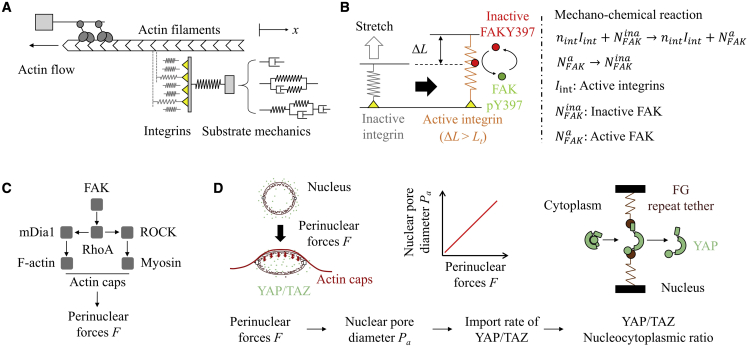
Standard motor-clutch model and its extensions are used to describe the FA-mediated mechanosensing in response to matrix elasticity, viscosity, and viscoelasticity (Fig. 1 a). Although motor-clutch models can successfully explain FA dynamics (e.g., cell traction and actin flow) on the cell-ECM interface in response to various mechanical cues, they still cannot be used to predict the dynamics of intracellular signaling. Here, we implement the motor-clutch model by treating stretch clutches as integrins, which can be activated when the elongation of stretched clutches exceeds a certain threshold (Fig. 1 b). Active integrins then can act as the enzyme to activate FAK molecules (5).
Figure 1.
Computational model for predicting YAP/TAZ nuclear translocation. (A) The extended motor-clutch model is used to simulate the focal adhesion dynamics mediated mechanosensing at the cell-ECM interface. Matrices are modeled as elastic, viscous, viscoelastic, and viscoplastic elements. (B) In the model, active integrins (i.e., bonded clutches with stretched lengths over a certain threshold) can enhance the level of FAKY397 phosphorylation at cell adhesions. This mechanochemical reaction is related to the amount of active integrins and inactive FAKY397 molecules. (C) FAKpY397 can later be fully activated by Src. Active FAK molecules can activate the Rho-mDia1/ROCK axis, which further promotes formation of intracellular stress fibers composed of F-actin and myosin (including actin caps above the nucleus) and perinuclear forces. (D) Descriptions of the dynamics of YAP/TAZ nucleocytoplasmic shuttling. Generally, perinuclear forces can induce deformation of the nucleus, which leads to a larger nuclear pore area, increasing the import rate of YAP/TAZ and ultimately changing the nucleoplasmic ratio of YAP/TAZ. To see this figure in color, go online.
Later, active FAK can activate the RhoA-mDia1/ROCK-actomyosin axis (Fig. 1 c) (30,31,32). The output of this signaling axis is the amount of actin cap filaments and, hence, the perinuclear forces above the nucleus, represented as the product of amounts of active myosin molecules and F-actin (27). Perinuclear forces are known to induce nuclear deformation, nuclear pore expansion, and unfolding of YAP/TAZ molecules through interaction with phenylalanine-glycine repeat tethers on nucleoporins (FG nups) and to enhance YAP/TAZ nuclear import (9) (Fig. 1 d). Based on previous studies (33), we modeled the normalized nuclear pore diameter as directly proportional to perinuclear forces. Finally, the effects of nuclear compression by actin cap filaments on nuclear pore opening and YAP/TAZ dynamics were modeled. The RhoA-mDia1/ROCK-actomyosin-YAP/TAZ axis in our computational model was simulated by a stochastic simulation algorithm (SSA) with a motor-clutch model in a unified framework. Because YAP/TAZ dynamics are predictive of cellular mechanosensing and other behaviors including cell differentiation and proliferation, this integrated computational model serves as a general tool to enable predictions of how perturbations to the mechanical microenvironment and intracellular signaling dynamics affect mechanosensing.
Motor-clutch model of cell adhesion
We extended our previous motor-clutch models (20,29), which link matrix elasticity and actin flow in various cell types, to explain mechanosensing and mechanoresponsiveness from the perspective of molecular bond dynamics. Elasticity-mediated cellular mechanosensing is described below. The elastic motor-clutch model considers myosin motors, actin filaments, molecular clutches, and an elastic matrix. Actin filaments are pulled by nm myosin motors, resulting in a retrograde flow that would be at a speed of V0 in the absence of cell-generated external forces. However, because of the movement of myosin motors, the speed of retrograde flow can decrease to the point at which the motors “stall” at a stall force of Fstall = nm Fm, where Fm is the maximum force that each motor can exert. When a force Fs is transmitted across all connected clutch bonds, the effective retrograde flow speed Vr reduces linearly:
| (1) |
| (2) |
where Nlink is the number of clutch bonds within an FA that are connected to transmit force from actin filaments to the matrix; xi is the elongation that clutch bond i within an FA has displaced; and xs is the displacement of the clutch’s binding site on the matrix. All such binding sites were modeled as moving together with a single displacement xs according to the matrix constitutive laws described in the next section.
The nc clutch bonds were modeled as parallel springs, each with spring constant Klink. The effective unbinding rate for these individual clutch bonds, koff, is accelerated by the force Fi on each bond according to the Bell model (20):
| (3) |
| (4) |
where Fb is the characteristic rupture force of a clutch bond and k0 is the minimum off-rate, which would exist in the absence of force. The effective binding rate, kon, is accelerated by a process called adhesion reinforcement, whereby the talin unfolding exposes cryptic vinculin binding sites, leading to integrin recruitment. This was modeled as follows:
| (5) |
where is the base on-rate and Cint is the density of integrin on the membrane. Thus, the density of integrin is determined by the force feedback in each of the clutch bonds. Following previous studies (11), we assumed that when the force exceeds a threshold force Fcr, that is , the density of integrins increases with a value of dadd. However, when the density of integrins decreases with a value of dadd. Importantly, we also used similar methods to evaluate the active bonds (i.e., active integrins) that can activate the FAK molecules (11). When the elongation of clutch exceeds a certain threshold, i.e., , the inactive clutch bond switches to the active clutch bond. Active clutch bonds then can act as the enzyme to activate FAK molecules (by promoting FAKY397 phosphorylation) as a mechanochemical reaction:
| (6) |
where Iint stands for active integrins, stands for inactive FAK molecules, and stands for active FAK molecules.
Matrix constitutive models
Four types of constitutive models were considered for the matrices.
Elastic model
The first was the elastic model, where the matrix was modeled as a linear spring, so that
| (7) |
where E is the effective spring constant of the elastic matrix.
Viscous model
To model the viscosity of cellular microenvironments, the second model was a dashpot with viscosity η, so that
| (8) |
Viscoelastic model
The third was a viscoelastic matrix modeled as a standard linear solid (SLS), for which
| (9) |
For certain constant displacement applied on the SLS, Ea + El represents the initial stiffness (short-term stiffness) of the SLS, El represents the equilibrium stiffness (long-term stiffness) of the SLS, and Ea represents the decrease of stiffness as SLS relaxes, i.e., additional stiffness. η is the matrix viscosity, and τs = η/Ea is the matrix relaxation time. Kshort and Klong represent dimensionless short-term and long-term stiffnesses of the matrix, respectively, i.e., and .
Viscoplastic model
Three different viscoplasticity models were used. The first was the Burgers viscoplastic element, for which the force-displacement relationship could be written as:
| (10) |
where E2 and (E1+E2)/E1E2 are the additional and long-term matrix stiffnesses, respectively; η1 represents the viscosity associated with viscoelastic relaxation; and η2 represents the viscosity associated with irreversible deformation. The second was the Bingham linear plastic flow model, with viscosity for viscoplasticity expressed as
| (11) |
where σ0 is the threshold stress. The third was the Norton-Hoff nonlinear plastic model, with viscosity for viscoplasticity expressed as
| (12) |
where N = 2 is exponent for nonlinear plastic flow in our model.
Conversion of matrix Young’s modulus and spring stiffness
Our extended motor-clutch model is a one-dimensional model in which the elastic matrix is modeled as an elastic spring. The model output is therefore a force (pN/nm). However, cell behaviors (e.g., cell adhesion, cell traction, and YAP/TAZ dynamics) in experiments are often expressed as a relationship to the Young’s modulus of the matrix (kPa or Pa). Thus, to compare model predictions with experiments, we used a previously described method (34) that converts spring constants to the corresponding Young’s modulus. Briefly, this approach considers a semiinfinite uncompressible elastic matrix where a circular point of adhesion of radius Sa applies a uniform shear stress. The elastic spring constant ksub of the system is the ratio between the total force exerted at the adhesion point and the displacement produced by the adhesion center. Thus, the elastic spring constant ksub can be related to the Young’s modulus E as
| (13) |
RhoA-mDia1/ROCK-actomyosin-YAP/TAZ signal transduction dynamics
A series of chemical reactions were then used to simulate the cytoplasmic signal transduction from FAK molecules to perinuclear forces and, finally, to YAP/TAZ nuclear translocation. Following the models of the Zaman group (27), the critical variables that determine the force generation are the relative amounts of active F-actin, , and myosin, . The perinuclear force F varies with these factors according to
| (14) |
The perinuclear force caused by actin cap filaments (or external forces) can promote nuclear pore deformation, and YAP/TAZ nuclear import rates are also enhanced by the low stability (i.e., easily unfolded protein and less resistance in space) of YAP/TAZ molecules (9). Our model thus first assumed that the effective nuclear pore diameter Pa varied with perinuclear forces F according to a linear relationship
| (15) |
where α is the adjustable parameter. Secondly, the nuclear import rate of YAP/TAZ, kYAP-in, was modeled as exponentially dependent on the nuclear pore diameter, while export rate kYAP-out was kept constant:
| (16) |
| (17) |
where ke is the effective stiffness of the YAP/TAZ-FG complex; KYAP and KFG are the stiffness of YAP and FG, respectively; is the base nuclear import rate in the absence of perinuclear force, and is the threshold force for YAP/TAZ unfolding. Finally, the nucleocytoplasmic ratio of YAP/TAZ (i.e., YAP/TAZ N/C ratio) is . The details of signaling dynamics can be found in the supporting material.
SSA
The integrated YAP/TAZ computational model was implemented using a Gillespie SSA. The order of events in the model is as follows. Step 1: calculate the association and disassociation rates for each clutch bond based on the current force on each bond and the integrin density on the membrane. The molecular clutch bond at the cell-ECM interface was modeled as a slip bond using the Bell model. Step 2: update all biochemical reaction rates according to amounts of each chemical species and reaction constants. Step 3: calculate the reaction times for each possible reaction in each loop:
| (18) |
where RANi is a uniformly distributed random number between 0 and 1 and ki is 1) the kinetic rate for each clutch bond (including formation, rupture, activation, and deactivation) and 2) the chemical reaction rates of cytoplasmic signal axis, e.g., Rho-ROCK/mDia1-actomyosin signals and YAP/TAZ nuclear translocation. Step 4: execute the chemical reaction (clutch bond formation or rupture, protein molecule activation or deactivation, YAP/TAZ importing or exporting from the nucleus) with the minimum ti. Step 5: advance time by the minimum ti. Step 6: calculate actin retrograde flow rate based on the current cell traction force using the linear force-velocity relationship. Step 7: advance connected bond positions by the product of the actin retrograde flow rate and time step. Step 8: calculate the matrix displacement using an elastic, viscous, viscoelastic, or viscoplastic force-displacement relationship. Step 9: calculate the cell traction, actin cap filaments, and YAP/TAZ N/C ratio. Step 10: return to step 1. Parameter values can be found in the supporting material.
Experimental methods
Hydrogel preparation and cell culture
For elastic hydrogels, 30 wt % gelatin (type A, Sigma-Aldrich, Burlington, MA, USA) aqueous solution and 4 wt % microbial transglutaminase (mTG; Pangbo, Shanghai, China) aqueous solution were mixed at prescribed concentration (gelatin aqueous solution: 10%, 10%, 15%, 10%, 10%, 15%, and 20%; mTG aqueous solution: 0.1%, 0.5%, 0.5%, 1.5%, 2%, 2%, and 2%) in Petri dishes at 37°C for 3 h to obtain hydrogels with gradient stiffnesses of 1, 5, 15, 25, 45, 65, and 125 kPa, respectively. The stiffness was determined by an atomic force microscope (Agilent Technologies, Santa Clara, CA, USA). For viscoplastic hydrogels, 3 mg/mL type I collagen (Corning, Corning, NY, USA) was self-assembled at 37°C for 40 min. To fabricate viscoplastic (irreversible deformation) hydrogels, 0.1 wt % mTG was added to cover the self-assembled collagen. After chemical cross-linking at 37°C for 5 h, the hydrogel was then washed in phosphate-buffered saline to remove unreacted molecules. To culture cells, hydrogels were soaked in phosphate-buffered saline for 24 h, and 3T3 cells were seeded onto hydrogels at a concentration of 105 cells/mL.
Western blotting analysis
FAKY397 phosphorylation was detected after 2 h of cell seeding. Total proteins were extracted with a mammalian protein extraction kit (CWBIO, Beijing, China) according to its protocol. The extracted cellular proteins were separated by SDS-polyacrylamide gel electrophoresis and transferred onto polyvinylidene fluoride membranes. After blocking with 5% bovine serum albumin at room temperature for 1 h, the membranes were incubated with anti-phospho-FAKY397 and anti-FAK antibody (Abcam, Camrbdige, UK) at 4°C overnight. Following washing with triethanolamine buffered saline and polysorbate 20, the blots were incubated with secondary antibodies (Cell Signaling, Danvers, MA, USA) at room temperature for 1 h. The relative integrated density of each protein band was determined using an Odyssey infrared imaging system (LI-COR, Lincoln, NE, USA).
Immunofluorescence staining
3T3 cells were fixed in 4% paraformaldehyde for 20 min and permeabilized in 0.5% Triton X-100 for 10 min. The cells were then blocked with 5% goat serum and incubated with the following antibodies 4°C overnight: anti-phospho-FAKY397 antibody (Abcam), anti-vinculin antibody (Cell Signaling Technology), and anti-YAP antibody (Cell Signaling Technology) at 4°C overnight. Then cells were incubated with secondary antibodies (AlexaFluor 488; Cell Signaling Technology) for 2 h at room temperature. Nuclei were counterstained with 4′,6-diamidino-2-phenylindole, and cytoplasmic cytoskeleton were stained with phalloidin (AlexaFluor 594; Invitrogen, Waltham, MA, USA). Images were taken with a confocal laser scanning microscope (FV3000, Olympus, Tokyo, Japan).
Results
YAP/TAZ response to matrix elasticity
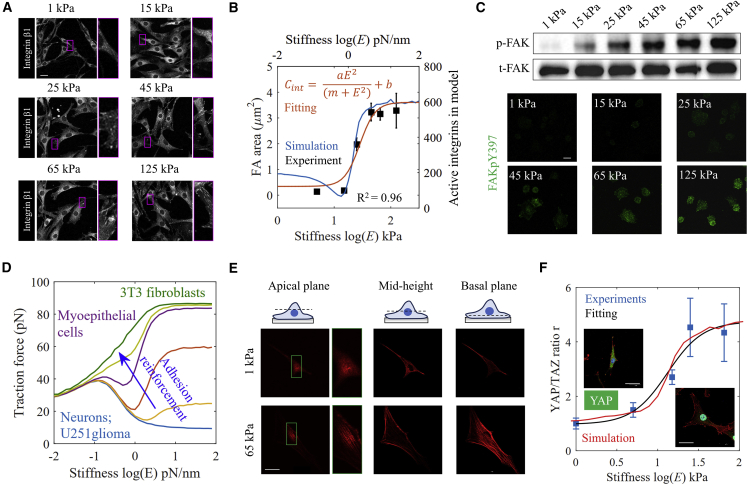
The cellular mechanosensing model begins with FA dynamics, which can be viewed as the beginning of mechanochemical signal conversion at the cell-ECM interface. This process was specifically validated using 3T3 fibroblasts cultured on matrices with stiffness across the physiological range (1–125 kPa). Quantitative immunofluorescence analysis revealed that the average area of FAs increases with increasing matrix stiffness up to a plateau (Fig. 2 a), which is well predicted by our computational model and can be approximated by a Hill-type relationship (Fig. 2 b):
| (19) |
where Cint is the normalized area of FAs (or connected integrins in model), E is the matrix stiffness (pN/nm for simulation and kPa for experiments), and m is the Hill coefficient, while a and b are fitting parameters. As shown in Fig. S1, the average number of FAs for each cell also increases with matrix stiffness. These results showed that on a stiff matrix, cells have more and larger FAs. Later, as evident from both immunostaining and quantitative Western blot analysis, phosphorylation of FAKY397 in 3T3 fibroblasts increases with increasing matrix stiffness (Fig. 2 c).
Figure 2.
YAP/TAZ response to matrix elasticity. (A) Focal adhesions on 3T3 fibroblasts cultured on matrices of different stiffnesses from 1–125 kPa. Scale bar, 30 μm. Increased cell adhesions were found in cells cultured on stiff matrices. (B) Predictions showed trends similar to those of experiments and followed a Hill-type function. Mean ± SE of n = 23 (1 kPa), 27 (15 kPa), 20 (25 kPa), 31 (45 kPa), 26 (65 kPa), and 34 (125kPa) cells from three independent experiments. (C) 3T3 fibroblasts cultured on matrices of different stiffness were immunostained for Y397-phosphorylated FAK (green). Scale bar, 30 μm. Cell lysate was analyzed by Western blot with antibodies for detecting specific FAK phosphorylation sites on Y397. Increased FAKpY397 levels were observed in cells on stiff matrices as can be identified from increased fluorescence intensity. (D) Adhesion reinforcement determines the change of traction force response to stiffness, i.e., biphasic or monotonic. (E) Cells cultured on a stiff matrix showed pronounced actin caps at the top the nucleus. Scale bar, 50 μm. (F) 3T3 fibroblasts cultured on matrices of different stiffness (1 and 65 kPa) were immunostained for YAP (green), F-actin (red), and DAPI (blue). Scale bar, 50 μm. Increased YAP N/C ratio was found in cells cultured on stiff matrices as can be identified from increased fluorescence intensity, with experiments and predictions following a Hill-type function. Mean ± SE of n = 18 (1 kPa), 21 (5 kPa), 18 (15 kPa), 24 (25 kPa), and 15 (65 kPa) cells from three independent experiments. To see this figure in color, go online.
Especially when adhesion reinforcement is considered, our computational model can predict the complex relationship between cell traction force and matrix mechanics as observed in previous studies (e.g., neuron, U251 glioma, and myoepithelial cells) and our experiments (e.g., 3T3 fibroblasts) (10,11,12,20) (Fig. 2 d). Thus, our computational model can capture integrin-mediated mechanochemical conversion at the cell-ECM interface and predict the quantitative relationship between ECM stiffness and traction force or actin flow for a broad diversity of cells.
The downstream signals of FAK are the concentration of actin cap filaments, i.e., the perinuclear forces above the nucleus (35). As observed by our experiments, actin cap filaments appear at the top of the nucleus only in cells cultured on stiff matrices (65 kPa but not 5 kPa) (Fig. 2 e). To simulate how matrix stiffness affects the YAP/TAZ N/C ratio by such perinuclear forces, we compared predictions of our model to immunofluorescence staining of YAP/TAZ N/C ratio in 3T3 fibroblasts. Experiments showed that cells cultured on the stiff matrix (65 kPa) have greater YAP/TAZ N/C ratios than those cultured on the soft matrix (5 kPa) (Fig. 2 f). Based on our computational tool, we predicted that the stiffness-YAP/TAZ N/C ratio relationship would also follow a Hill-type function (Fig. 2 f) as well, indicating that mechanosensitive variables of relevance (e.g., FA area and YAP/TAZ N/C ratio) depend upon matrix stiffness according to a Hill-type function (Eq. 19). To apply the computational model in the context of mechanomedicine, we performed a sensitivity analysis of parameters (Note S1). Results showed that talin unfolding force and nuclear deformation coefficients can effectively change the stiffness range for cell mechanosensing, while integrin density and the dynamics of ROCK only took effect on regulating YAP/TAZ N/C ratio on stiff matrices.
YAP/TAZ response to matrix viscosity
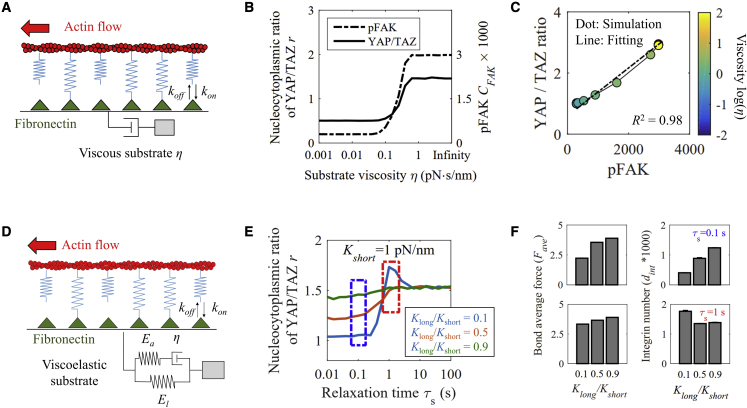
Time-dependent matrix mechanics affects the integrin-FAK-myosin-YAP/TAZ axis (36). One source of this time dependence is the viscosity (η) of the matrix. Our extended model (Fig. 3 a) predicts that the cell traction and the amount of active integrins increase with increasing viscosity (Fig. S2), with higher viscosity causing higher loading rates in clutch bonds, which promote bond reinforcement over bond disassociation. When passing the threshold force, the increased fraction of bonds increases the concentration of connected integrin molecules and intracellular tension.
Figure 3.
Cellular response to matrix viscosity and viscoelasticity. (A) Descriptions of the viscous matrix molecular clutch model. (B) Relationships between FAKpY397 or YAP/TAZ N/C ratio and viscosity followed a Hill-type function. (C) A linear relationship between FAK activation in adhesions and matrix stiffness in response to matrix viscosity was observed. (D) Schematic depicting the molecular clutch model for a viscoelastic matrix. (E) At low long-term stiffness, intermediate viscosity promotes an increased YAP/TAZ N/C ratio, but low viscosity inhibits this. (F) The bond average forces increased with the ratio of long-term stiffness to short-term stiffness. The integrin number increased with the ratio of long-term stiffness to short-term stiffness at a small relaxation time and decreased with the ratio of long-term stiffness to short-term stiffness at intermediate relaxation times. Mean ± SE of n = 10 independent simulations for each condition. To see this figure in color, go online.
Matrix viscosity now can be tuned experimentally by regulating the diffusion of ligands in the membrane (23). Our model predictions and other experimental results (23) both showed that FAKY397 phosphorylation and YAP/TAZ N/C ratio increase with increasing matrix viscosity (from 0.01 to 1 pN · s/nm), eventually reaching a saturation level (Fig. 3 b). These effects of viscosity are similar to the effects of matrix elasticity, implying that the YAP/TAZ N/C ratio increases proportionally and synergistically with FAKpY397 in elasticity and viscosity sensing, with stiffer and more viscous microenvironment yielding larger FAs due to their synergistic effects on the integrin-FAK-myosin-YAP/TAZ signaling axis (Fig. 3 c). By adjusting the molecular diffusion coefficient of vesicle membrane, a regulation of YAP/TAZ in vivo may be achieved.
YAP/TAZ response to matrix viscoelasticity
ECM proteins such as collagen and fibrin exhibit viscoelasticity with both elasticity and a resistance to cell forces that relaxes over time (37,38). These relaxation rates are controlled by cellular remodeling of the ECM but recursively affect cell behavior. For example, cells paradoxically exhibit larger FAs and higher YAP/TAZ N/C ratios on viscoelastic matrices than on elastic matrices with the same long-term stiffness and YAP/TAZ N/C ratios increasing with faster stress relaxation (37). To model such effects, we treated the matrix as a standard linear viscoelastic solid, characterized by three mechanical parameters (Fig. 3 d): a dimensionless, short-term stiffness (Kshort), the ratio of the long-term to short-term stiffness (Klong/Kshort), and the stress relaxation time constant (τs).
The predicted YAP/TAZ dynamics are diverse. As shown in Fig. S3, in the presence of bond reinforcement, cell traction force increases with Klong/Kshort only when Kshort = 1 pN/nm but has nearly no change with Klong/Kshort when Kshort = 10 pN/nm with a different relaxation time. For no bond reinforcement, cell traction force decreases with Klong/Kshort only when τs = 0.1 s. For Kshort = 1 pN/nm, three completely different responses are possible (Fig. 3 e): 1) for Klong/Kshort = 0.9, matrix viscoelasticity has negligible effect on the YAP/TAZ N/C ratio; 2) for Klong/Kshort near 0.5, the YAP/TAZ N/C ratio increases with relaxation time; or 3) for Klong/Kshort = 0.1, more interestingly, the YAP/TAZ N/C ratio is maximal at intermediate relaxation times. To explore the meaning and source of such a peak for the YAP/TAZ responses, we studied how internal model parameters vary with increasing Klong/Kshort at both fast (τs = 0.1 s) and slow (τs = 1 s) relaxation times. Simulation results showed that bond lifetimes with different relaxation times (τs = 0.1 and 1 s) both decrease with increasing Klong/Kshort (Fig. S4). So, bond lifetimes should not be the reason for such a peak. Next, we focused on two other parameters, integrin density on the membrane (dint) and average bond force (Fave). Simulation results showed that, similar to the bond lifetimes, the bond average forces have the similar trends in response to Klong/Kshort when τs = 0.1 and 1 s, i.e., with average bond force (Fave) increasing with Klong/Kshort (Fig. 3 f). However, the variation of integrin density (dint) as a function of Klong/Kshort exhibits opposite trends for fast and slow relaxation rates (Fig. 3 f), which is similar to the YAP/TAZ N/C ratio when τs = 0.1 and 1 s. This implies that the effective integrin density on the membrane may be a key factor in determining how the YAP/TAZ N/C ratio is controlled by matrix viscoelasticity and demonstrates our model platform as an in silico tool for identifying potential molecular mechanisms.
YAP/TAZ response to matrix viscoplasticity
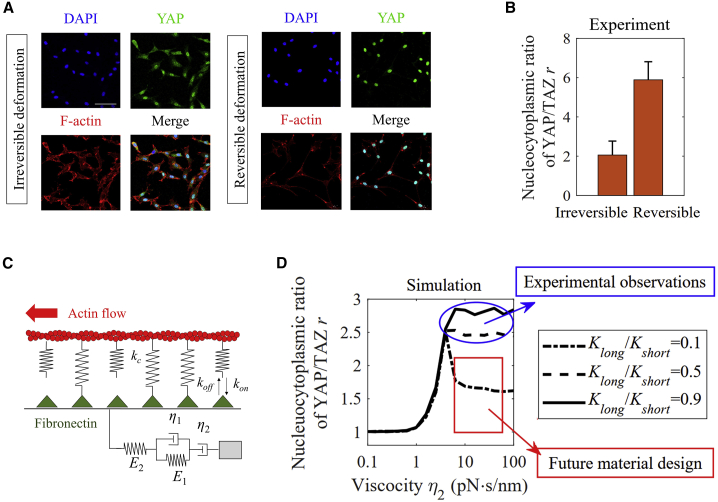
Matrix viscoplasticity, loading-rate-dependent deformation that can be partially irreversible, is central to cell-ECM interactions (39). Our experimental results have revealed that cells cultured on the matrix with reversible deformation show a larger YAP/TAZ N/C ratio (Fig. 4, a and b). To evaluate how matrix viscoplasticity affects YAP/TAZ translocation dynamics, we modeled the matrix as a four-element Burgers material with two viscous parameters: η1, a viscosity analogous to that of a (reversible) SLS, and η2, with the degree of plasticity increasing with the ratio η1/η2 (Figs. 4 c and S5).
Figure 4.
YAP/TAZ response to matrix viscoplasticity. (A and B) Experiments showed that a high degree of irreversible deformation in the matrix can decrease the YAP/TAZ N/C ratio. Mean ± SE of n = 21 (irreversible condition) and 37 (reversible condition) cells from three independent experiments. (C) A Burgers element was used to investigate the effects of irreversible deformation on cellular behavior. The mechanical parameter η2 represents the level of irreversible deformation. (D) Experiments and predictions showed that when short-term stiffness and the ratio of long-term to short-term stiffness are relatively high, the YAP/TAZ ratio increases with decreasing relative flow. However, when the ratio of long-term to short-term stiffness was relatively small, the YAP/TAZ ratio first increased and then decreased with decreasing relative flow, Kshort = 10 pN/nm and η1 = 0.1 pN · s/nm. All simulation results are the average value of 100 simulated trajectories. To see this figure in color, go online.
As shown in Fig. S6, when Kshort = 1 pN/nm, the YAP/TAZ N/C ratio shows a trend of increasing and then decreasing with irreversible deformation, which is contrary to our experiment. Thus, we later mainly focus on the condition with higher short-term stiffness, i.e., Kshort = 10 pN/nm. Simulations show that when Kshort = 10 pN/nm, the YAP/TAZ N/C ratio increases with increasing viscosity η2 at a larger Klong/Kshort, which is consistent with our experiments (Fig. 4 d). Besides, we can find that when the η2 is too small, cells cannot develop effective perinuclear forces because of the relative flow of matrix. Therefore, the YAP/TAZ N/C ratio maintains a low level and is independent of other material parameters (e.g., Klong/Kshort). However, when the η2 is large, the YAP/TAZ N/C ratio increases with Klong/Kshort because of a highly effective stiffness. Finally, users can use our model to design materials that would decrease the YAP/TAZ ratio in cells and thereby regulate cell behaviors.
YAP/TAZ response to stress-dependent viscoplasticity
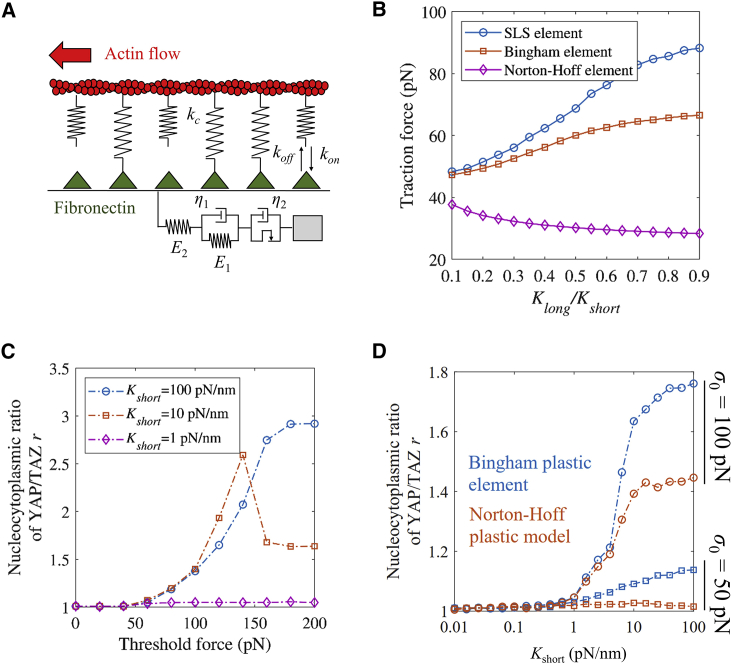
Next, we investigated the effects of stress-dependent viscoplasticity on YAP/TAZ dynamics. To achieve this goal, we used a viscoplastic model with a Bingham plastic element and a Norton-Hoff plastic element to represent the behaviors of linear and nonlinear stress-dependent viscoplasticity behaviors, respectively (Figs. 5 a and S7, a and b). For the Bingham plastic element, the degree of plasticity has no change with stress. However, for the Norton-Hoff plastic element, the degree of plasticity will increase with stress (Fig. S7 c). Also, the degree of plasticity for the Norton-Hoff plastic element is greater than that for the Bingham plastic element when the creep time is small (Fig. S7 d).
Figure 5.
YAP/TAZ response to stress-dependent matrix viscoplasticity. (A) The molecular clutch model for a stress-dependent viscoplastic matrix. (B) Traction force increased with the ratio of long-term to short-term stiffness Klong/Kshort for an SLS element and Bingham element but decreased with the ratio of long-term to short-term stiffness Klong/Kshort for a Norton-Hoff element. (C) For stress-dependent viscoplasticity, the YAP/TAZ N/C ratio showed different relationships with threshold force depending upon different short-term stiffnesses. (D) The YAP/TAZ N/C ratio increased with short-term stiffness. All simulation results are the average value of 100 simulated trajectories. To see this figure in color, go online.
Later, we investigated the effects of cell traction with different viscoplastic elements (SLS element, Bingham element, and Norton-Hoff element) by our computational model. We found that cell traction increases with Klong/Kshort with the SLS element and the Bingham element. However, the traction of the Norton-Hoff element decreases slightly with Klong/Kshort (Fig. 5 b).
Then, we investigated the roles of such linear or nonlinear stress-dependent viscoplasticity in YAP/TAZ dynamics. We found that, for the Bingham plastic model, when Kshort = 100 pN/nm, the YAP/TAZ ratio increases with threshold force (Fig. 5 c, blue line). However, when Kshort = 10 pN/nm, the YAP/TAZ N/C ratio reaches its maximal value in the intermediated threshold force (Fig. 5 c, orange line). When Kshort = 1 pN/nm, the YAP/TAZ N/C ratio is insensitive to the values of threshold force (Fig. 5 c, purple line). It implies that when the threshold force is high, cells can effectively sense the short-term stiffness. Also, cell traction and YAP/TAZ will increase with the long-term stiffness. Next, we modeled the matrix as a nonlinear strain-dependent viscoplasticity model. We found that for certain short-term stiffness, the YAP/TAZ ratio also increases with threshold force (Fig. 5 d). For a certain threshold force, the cell displays a higher YAP/TAZ N/C ratio on a linear viscoplastic matrix. This implies that for a certain stress, cells experience lower strain for the nonlinear model, with lower tension in the bonds and thus smaller cell traction and YAP/TAZ N/C ratio. Model results predict that such materials could be used to tailor cell responses, with the YAP/TAZ N/C ratio maintaining a high level with increasing Kshort only when the threshold force is large (Fig. 5 d).
Conclusions
In this study, we developed a computational model for predicting YAP/TAZ nuclear translocation in matrix mechanics sensing. Our model could predict the relationship between mechanical properties of matrices and nuclear mechanosensing for the integrin-mediated YAP/TAZ dynamics. This computational model helps us understand the heterogeneity of cellular mechanosensing behaviors and the quantitative law of mechanochemical conversion, identify some potential targets for mechanomedicines, and also design novel biomaterials through analysis of system parameters. The model predicted the complex relationship between actin flow or cell traction and stiffness in different types of cells; the Hill-type quantitative relationships between cell adhesions or YAP/TAZ N/C ratio and matrix stiffness; the effects of the time courses of both reversible and irreversible matrix deformation; the effects of drugs on these relationships; and material parameters for novel biomaterial design (Fig. 6).
Figure 6.
The computational tool may hold potential for predicting the effects of inhibitors and drugs on YAP/TAZ nuclear translocation and for calculating material parameters for biomaterial design. To see this figure in color, go online.
Accumulating evidence suggests that adhesion proteins, cytoskeleton-related proteins, and YAP/TAZ play key roles in cellular mechanosensing. This can be manifested by the elevated levels of protein activation (e.g., talin unfolding and activation, FAKY397 phosphorylation, and RhoA/ROCK activation). These activated proteins increase the assembly of structural proteins (e.g., FAs, actomyosins, and nucleoskeletal lamin-A) and, finally, enhance the YAP/TAZ transcriptional activation. The motor-clutch system may be a universal mechanism for cells to respond to different matrix mechanics.
In our model, changes to matrix mechanics initiated integrin-mediated FAK activation and a series of downstream signaling pathways that ultimately regulated YAP/TAZ dynamics. However, we still cannot exclude that there are other potential ways to affect cellular responses to matrix mechanics. For example, from the perspectives of polymer physics and systems mechanobiology, tension-mediated stabilization or degradation of polymeric proteins (e.g., lamin-A, collagenous matrix, and myosin II) could also influence the chemical rates in our model (40). Introducing these tension-mediated rates into our model would further increase the complexity of our model (e.g., the nuclear viscoplasticity changes caused by tension-mediated lamina accumulation). Our existing YAP/TAZ computational model with constant rates (not tension-mediated chemical rates) is an idealization of real and complex YAP/TAZ dynamical system in cells. Although we did not model all aspects of tension-mediated YAP/TAZ dynamics, our study may provide a basis for more detailed analysis when required.
Our model still needs to include the cross-talk between signal pathways such as the integrin-FAK-YAP/TAZ axis and the MAPK signaling axis (41). Key future directions include introducing other potential mechanics-mediated pathways (such as interleukin-1β and nuclear factor-κB signals related to cellular immunity) into our computational model. The one-dimensional nature of the model is also a known limitation, with two-dimensional molecular clutch models known to add important details, and three-dimensional models potentially adding even more. However, the computational tool here appears to capture essential biophysics of matrix-to-nucleus signal transduction, providing both sufficient detail and simplicity to identify classes of inhibitors and agonists that can be used as mechanotherapeutics.
Data accessibility
All data generated or analyzed during the study are included in this article and its supporting material. Computer codes for this study are available upon request from the authors.
Author contributions
F.X. and M.L. designed the framework. B.C. constructed the computational model. W.W. performed the experiments. All authors analyzed data and wrote the manuscript.
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China (12002262, 11972280, 12022206, and 12225208) and by funds from the Social Policy Institute and the McDonnell International Scholars Academy at Washington University in St. Louis.
Declaration of interests
The authors declare no competing interests.
Editor: Baohua Ji.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2022.11.2943.
Contributor Information
Moxiao Li, Email: moxiaoli@nuaa.edu.cn.
Feng Xu, Email: fengxu@mail.xjtu.edu.cn.
Supporting material
References
- 1.Chaudhuri O., Cooper-White J., et al. Shenoy V.B. Effects of extracellular matrix viscoelasticity on cellular behaviour. Nature. 2020;584:535–546. doi: 10.1038/s41586-020-2612-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Butcher D.T., Alliston T., Weaver V.M. A tense situation: forcing tumour progression. Nat. Rev. Cancer. 2009;9:108–122. doi: 10.1038/nrc2544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lampi M.C., Reinhart-King C.A. Targeting extracellular matrix stiffness to attenuate disease: from molecular mechanisms to clinical trials. Sci. Transl. Med. 2018;10 doi: 10.1126/scitranslmed.aao0475. eaao0475. [DOI] [PubMed] [Google Scholar]
- 4.Sheridan C. Pancreatic cancer provides testbed for first mechanotherapeutics. Nat. Biotechnol. 2019;37:829–831. doi: 10.1038/d41587-019-00019-2. [DOI] [PubMed] [Google Scholar]
- 5.Cheng B., Wan W.T., et al. Huang G. Nanoscale integrin cluster dynamics controls cellular mechanosensing via FAKY397 phosphorylation. Sci. Adv. 2020;6 doi: 10.1126/sciadv.aax1909. eaax1909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Moore S.W., Roca-Cusachs P., Sheetz M.P. Stretchy proteins on stretchy substrates: the important elements of integrin-mediated rigidity sensing. Dev. Cell. 2010;19:194–206. doi: 10.1016/j.devcel.2010.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kechagia J.Z., Ivaska J., Roca-Cusachs P. Integrins as biomechanical sensors of the microenvironment. Nat. Rev. Mol. Cell Biol. 2019;20:457–473. doi: 10.1038/s41580-019-0134-2. [DOI] [PubMed] [Google Scholar]
- 8.Totaro A., Panciera T., Piccolo S. YAP/TAZ upstream signals and downstream responses. Nat. Cell Biol. 2018;20:888–899. doi: 10.1038/s41556-018-0142-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Elosegui-Artola A., Andreu I., et al. Roca-Cusachs P. Force triggers YAP nuclear entry by regulating transport across nuclear pores. Cell. 2017;171:1397–1410.e14. doi: 10.1016/j.cell.2017.10.008. [DOI] [PubMed] [Google Scholar]
- 10.Bangasser B.L., Shamsan G.A., ., et al. Chan C.E. Shifting the optimal stiffness for cell migration. Nat. Commun. 2017;8:15313. doi: 10.1038/ncomms15313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Elosegui-Artola A., Bazellières E., et al. Roca-Cusachs P. Rigidity sensing and adaptation through regulation of integrin types. Nat. Mater. 2014;13:631–637. doi: 10.1038/nmat3960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Elosegui-Artola A., Oria R., et al. Roca-Cusachs P. Mechanical regulation of a molecular clutch defines force transmission and transduction in response to matrix rigidity. Nat. Cell Biol. 2016;18:540–548. doi: 10.1038/ncb3336. [DOI] [PubMed] [Google Scholar]
- 13.Surcel A., Schiffhauer E.S., et al. Robinson D.N. Targeting mechanoresponsive proteins in pancreatic cancer: 4-Hydroxyacetophenone blocks dissemination and invasion by activating MYH14. Cancer Res. J. 2019;79:4665–4678. doi: 10.1158/0008-5472.CAN-18-3131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lim W.A., Lee C.M., Tang C. Design principles of regulatory networks: searching for the molecular algorithms of the cell. Mol. Cell. 2013;49:202–212. doi: 10.1016/j.molcel.2012.12.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Holle A.W., Young J.L., ., et al. Van Vliet K.J. Cell-extracellular matrix mechanobiology: forceful tools and emerging needs for basic and translational research. Nano Lett. 2018;18:1–8. doi: 10.1021/acs.nanolett.7b04982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Alisafaei F., Jokhun D.S., et al. Shenoy V.B. Regulation of nuclear architecture, mechanics, and nucleocytoplasmic shuttling of epigenetic factors by cell geometric constraints. Proc. Natl. Acad. Sci. USA. 2019;116:13200–13209. doi: 10.1073/pnas.1902035116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gong Z., Wisdom K.M., ., et al. McEvoy E. Recursive feedback between matrix dissipation and chemo-mechanical signaling drives oscillatory growth of cancer cell invadopodia. Cell Rep. 2021;35:109047. doi: 10.1016/j.celrep.2021.109047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Suresh H., Shishvan S.S., et al. Deshpande V.S. Free-energy-based framework for early forecasting of stem cell differentiation. J. R. Soc. Interface. 2019;16 doi: 10.1098/rsif.2019.0571. 20190571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Buskermolen A.B.C., Suresh H., et al. Deshpande V.S. Entropic forces drive cellular contact guidance. Biophys. J. 2019;116:1994–2008. doi: 10.1016/j.bpj.2019.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chan C.E., Odde D.J. Traction dynamics of filopodia on compliant substrates. Science. 2008;322:1687–1691. doi: 10.1126/science.1163595. [DOI] [PubMed] [Google Scholar]
- 21.Bangasser B.L., Rosenfeld S.S., Odde D.J. Determinants of maximal force transmission in a motor-clutch model of cell traction in a compliant microenvironment. Biophys. J. 2013;105:581–592. doi: 10.1016/j.bpj.2013.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Adebowale K., Gong Z., et al. Chaudhuri O. Enhanced substrate stress relaxation promotes filopodia-mediated cell migration. Nat. Mater. 2021;20:1290–1299. doi: 10.1038/s41563-021-00981-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bennett M., Cantini M., et al. Salmeron-Sanchez M. Molecular clutch drives cell response to surface viscosity. Proc. Natl. Acad. Sci. USA. 2018;115:1192–1197. doi: 10.1073/pnas.1710653115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chaudhuri O., Gu L., et al. Mooney D.J. Substrate stress relaxation regulates cell spreading. Nat. Commun. 2015;6:6364. doi: 10.1038/ncomms7365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gong Z., Szczesny S.E., ., et al. Caliari S.R. Matching material and cellular timescales maximizes cell spreading on viscoelastic substrates. Proc. Natl. Acad. Sci. USA. 2018;115:2686–2695. doi: 10.1073/pnas.1716620115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Grolman J.M., Weinand P., Mooney D.J. Extracellular matrix plasticity as a driver of cell spreading. Proc. Natl. Acad. Sci. USA. 2020;117:25999–26007. doi: 10.1073/pnas.2008801117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sun M., Spill F., Zaman M.H. A computational model of YAP/TAZ mechanosensing. Biophys. J. 2016;110:2540–2550. doi: 10.1016/j.bpj.2016.04.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Scott K.E., Fraley S.I., Rangamani P. A spatial model of YAP/TAZ signaling reveals how stiffness, dimensionality, and shape contribute to emergent outcomes. Proc. Natl. Acad. Sci. USA. 2021;118 doi: 10.1073/pnas.2021571118. e2021571118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zhang C., Zhu H., et al. Lin M. Mechanics-driven nuclear localization of YAP can be reversed by N-cadherin ligation in mesenchymal stem cells. Nat. Commun. 2021;12:6229. doi: 10.1038/s41467-021-26454-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Parsons J.T., Horwitz A.R., Schwartz M.A. Cell adhesion: integrating cytoskeletal dynamics and cellular tension. Nat. Rev. Mol. Cell Biol. 2010;11:633–643. doi: 10.1038/nrm2957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Narumiya S., Tanji M., Ishizaki T. Rho signaling, ROCK and mDia1, in transformation, metastasis and invasion. Cancer Metastasis Rev. 2009;28:65–76. doi: 10.1007/s10555-008-9170-7. [DOI] [PubMed] [Google Scholar]
- 32.Higashida C., Miyoshi T., et al. Watanabe N. Actin polymerization-driven molecular movement of mDia1 in living cells. Science. 2004;303:2007–2010. doi: 10.1126/science.1093923. [DOI] [PubMed] [Google Scholar]
- 33.Liu S., Yang H., et al. Xu F. Electrostatic switching of nuclear basket conformations provides a potential mechanism for nuclear mechanotransduction. J. Mech. Phys. Solids. 2019;133:103705. [Google Scholar]
- 34.Ghibaudo M., Saez A., et al. Trichet L. Traction forces and rigidity sensing regulate cell functions. Soft Matter. 2008;4:1836–1843. [Google Scholar]
- 35.Shiu J.Y., Aires L., et al. Vogel V. Nanopillar force measurements reveal actin-cap-mediated YAP mechanotransduction. Nat. Cell Biol. 2018;20:262–271. doi: 10.1038/s41556-017-0030-y. [DOI] [PubMed] [Google Scholar]
- 36.Babaei B., Davarian A., et al. Genin G.M. Remodeling by fibroblasts alters the rate-dependent mechanical properties of collagen. Acta Biomater. 2016;37:28–37. doi: 10.1016/j.actbio.2016.03.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Chaudhuri O., Gu L., et al. Mooney D.J. Hydrogels with tunable stress relaxation regulate stem cell fate and activity. Nat. Mater. 2016;15:326–334. doi: 10.1038/nmat4489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Pryse K.M., Nekouzadeh A., Zahalak G.I. Incremental mechanics of collagen gels: new experiments and a new viscoelastic model. Ann. Biomed. Eng. 2003;31:1287–1296. doi: 10.1114/1.1615571. [DOI] [PubMed] [Google Scholar]
- 39.Nam S., Lee J., et al. Chaudhuri O. Viscoplasticity enables mechanical remodeling of matrix by cells. Biophys. J. 2016;111:2296–2308. doi: 10.1016/j.bpj.2016.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Dingal P.C.D.P., Discher D.E., Discher D.E. Systems mechanobiology: tension-inhibited protein turnover is sufficient to physically control gene circuits. Biophys. J. 2014;107:2734–2743. doi: 10.1016/j.bpj.2014.10.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zuidema A., Wang W., Sonnenberg A. Crosstalk between cell adhesion complexes in regulation of mechanotransduction. Bioessays. 2020;42 doi: 10.1002/bies.202000119. 2000119. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data generated or analyzed during the study are included in this article and its supporting material. Computer codes for this study are available upon request from the authors.