Near Infrared Light Induced Radical Polymerization in Water

Abstract

We introduce a gold nanorod (AuNR) driven methodology to induce free radical polymerization in water with near infrared light (800 nm). The process exploits photothermal conversion in AuNR and subsequent heat transfer to a radical initiator (here azobisisobutyronitrile) for primary radical generation. A broad range of reaction conditions were investigated, demonstrating control over molecular weight and reaction conversion of dimethylacrylamide polymers, using nuclear magnetic resonance spectroscopy. We underpin our experimental data with finite element simulation of the spatio‐temporal temperature profile surrounding the AuNR directly after femtosecond laser pulse excitation. Critically, we evidence that polymerization can be induced through biological tissues given the enhanced penetration depth of the near infrared light. We submit that the presented initiation mechanism in aqueous systems holds promise for radical polymerization in biological environments, including cells.

Near infrared irradiation can be sufficient to initiate radical polymerization when absorbed by gold nanorods, exploiting the photothermal effect to transfer energy to a thermal initiator molecule. A water‐soluble monomer is readily polymerized in aqueous environments affording water‐soluble polymers with tuneable molecular weights, including by irradiation through biological tissue.

Introduction

Initiating radical polymerization is perhaps the most critical step during a free radical polymerization process, as it largely dictates the conditions under which the polymerization can be conducted. Radical initiation is particularly challenging in environments where mild reaction conditions are required, such as in aqueous or biological media.[ ¹ , ² ] The initially generated radicals, often termed primary radicals, are typically generated by the decomposition of thermally responsive initiator molecules, most notably based on azo or peroxy compounds.[ ³ , ⁴ , ⁵ , ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ , ¹¹ , ¹² , ¹³ , ¹⁴ , ¹⁵ ] Alternatively, the generation of primary radicals can occur via photochemically induced initiator decomposition, most commonly in the UV range of the electromagnetic spectrum, but examples of visible light photoinitiatiors have also been reported.[ ¹⁶ , ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ , ²¹ , ²² ] Accessing longer wavelength primary radical generation beyond 550 nm is highly challenging due to the low photon energy. At these wavelengths, the energy is insufficient to directly cleave covalent bonds, requiring an alternate mechanism to initiate radical generation. Despite these challenges, it is highly desirable to induce free radical polymerization by red or near‐infrared wavelengths, due to their relatively high penetration depth in biological tissue.[ ²³ , ²⁴ , ²⁵ ] Two‐photon induced polymerization is a powerful technique to make use of near infrared (NIR) light for the initiation of polymerizations.[ ²⁶ , ²⁷ , ²⁸ , ²⁹ , ³⁰ ] However, due to the very high light intensities that this technique requires, ^[30] alternative methods with a more benign nature to biological materials are preferred. ^[31]

Some approaches to long wavelength radical polymerisation have been reported for organic solvents, employing dyes which are able to absorb NIR light and in a subsequent step transfer energy to a molecule able to generate radicals. Several groups[ ³² , ³³ , ³⁴ , ³⁵ , ³⁶ , ³⁷ , ³⁸ , ³⁹ ] have introduced NIR sensitizers, e.g. borate dyes or cyanines, combined with initiator molecules. However, no report exists describing free radical polymerization enabled by NIR in an aqueous system.

One approach to achieving NIR‐induced radical polymerisation is by exploiting the photothermal effect of gold nanorods (AuNR).[ ⁴⁰ , ⁴¹ , ⁴² , ⁴³ ] The photothermal effect is based on the conversion of radiation energy into thermal energy. The exposure of free electrons within the metal by ultrafast laser pulses increases the temperature of the electron gas. The electrons then thermalise with the lattice, establishing a new thermal equilibrium, and resulting in rapid heating of the AuNR. Subsequent external heat diffusion causes an increase in temperature of the surrounding medium. ^[41] In previous studies, Nguyen et al. described the heat transfer dynamics from AuNR to the environment, analyzing the heating of AuNR, finding that the heat transfer can be tuned to be faster by higher excitation powers. ^[44]

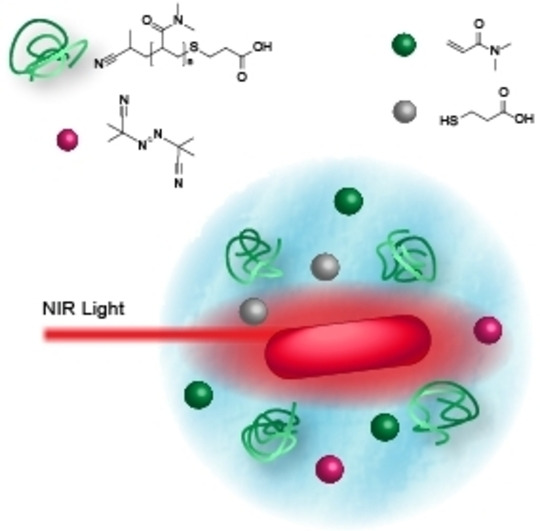
Herein, we close a critical gap in the literature by introducing a methodology to achieve free radical polymerization of a water‐soluble monomer (dimethylacrylamide, DMA) with NIR light. We do so by irradiating an aqueous solution containing the monomer, AuNR and a thermally decaying initiator. Irradiation of the solution with femtosecond (fs) laser pulses at 800 nm triggers localised heating around the AuNR, leading to the decay of the initiator and subsequent macromolecular growth. Our overarching approach is captured in Scheme 1. We carefully assess the reaction parameter space using nuclear magnetic resonance (NMR) spectroscopy and size exclusion chromatography (SEC), demonstrating the versatility of our approach.

Scheme 1.

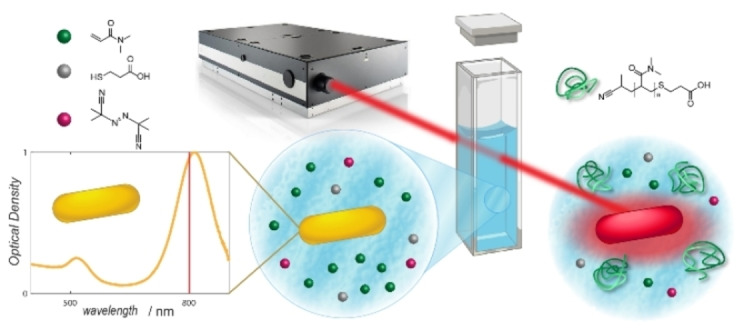
Experimental approach for NIR light induced radical polymerization of dimethylacrylamide in water. The technique exploits the photothermal effect in gold nanorods (AuNR), induced by a fs laser pulse, triggering the decomposition of the thermal initiator.

Results and Discussion

Theoretical Considerations

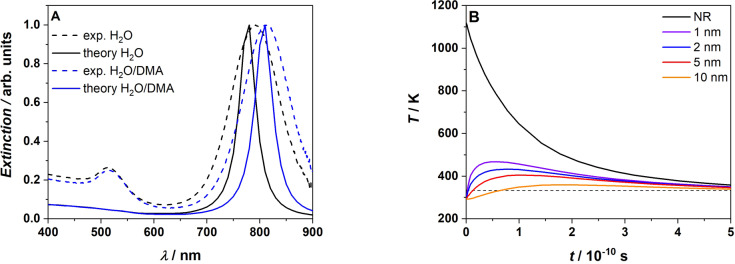
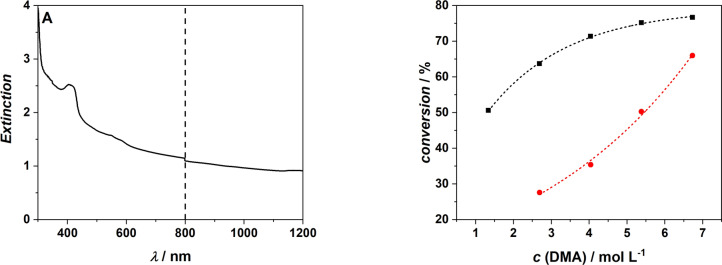
We initially explore the photo‐induced heat transfer from the AuNR theoretically, in order to estimate the expected temperature increase. The first step in quantifying the photothermal effect in AuNR is to determine the absorption cross section. The challenge of separating absorption and scattering effects experimentally meant that the absorption cross section was calculated theoretically using finite element simulations in COMSOL Multiphysics® ^[45] (for details refer to Supporting Information, Section 1). The determined spectra are presented in Figure 1(A) and were found to closely align with experimental extinction spectra as shown by the accurate predictions of the resonance peaks. The absorption cross section of an AuNR is strongly influenced by its size and the refractive index of the surrounding medium. ^[46] The absorption cross section of the AuNRs in a 50 : 50 water:dimethylacrylamide (DMA) mixture was subsequently calculated in the same fashion with the refractive index of the mixture determined by averaging the refractive index of water 1.33 ^[47] and that of DMA 1.473, ^[48] resulting in a shift of the absorption peak from 780 nm to 810 nm, as depicted in Figure 1(A). The COMSOL model only simulated the more relevant longitudinal resonance near 800 nm, thus causing the lack of the smaller absorption peak close to 520 nm that results from the transverse axis. The decreased linewidth of the NIR peaks compared with the experiment is most likely due to multiple orientations of the AuNRs with respect to the incident beam and any variation in the size and shape distributions of the AuNR in the sample.

Figure 1.

A) Simulated extinction cross section of AuNR in pure water (black solid line) and 50/50 water/DMA mixture (blue solid line) overlayed with the experimental extinction spectra in pure water (dashed black line) and 50/50 water/DMA mixture (dashed blue line). B) Temperature vs time evolution at various distances from the AuNR boundary after excititation with a 800 nm, 35 fs laser pulse. The black dashed line indicates the temperature for decomposition of AIBN initiator (60 °C), where the initiators half life is close to 10 h.

Using the calculated absorption cross sections, the temperature increase of the AuNR and surrounding medium after excitation by a 800 nm fs laser pulse was determined. Due to the short fs exposure times, and the fact that the electron gas thermalizes with the lattice on a much shorter timescale thanexternal heat diffusion, ^[49] a one temperature model—which ignores the electron gas temperature ^[50] and simulates only the temperature of the AuNR and the surrounding medium—was employed. The simulation was largely based on the method developed by Metwally and colleagues, ^[51] with the full details provided in the Supporting Information Section 1. On a general level, the simulation considers the optical power deposited on the absorption cross section, which is initially absorbed by the electron gas and transferred to the lattice resulting in a temperature increase of the AuNR. The AuNR subsequently cools as it heats the surrounding medium with a characteristic diffusion time that is dependent on its size. A thermal interface resistance—known as the Kapitza resistance ^[38] —causes a temperature discontinuity between the AuNR and the medium. In the current context, this is particularly important as it is the temperature of the medium which will initiate the polymerisation—not the temperature of the AuNR. The thermal properties of DMA, such as its heat capacity and thermal conductivity, were not available in the literature and thus the values of water alone were used. Any significant differences in the thermal properties of DMA and water introduce some error into the thermal evolution of the AuNR and medium over time, however the initial temperature of the AuNR will remain unchanged. It is also likely that the maximum temperature change within the medium will serve as a reasonable approximation.

With the maximum temperature established, the thermal evolution of the AuNR and surroundings can be deduced from the diffusion equation (Figure 1(B)). Inspection of Figure 1(B) demonstrates that in the vicinity around the AuNR, the surrounding medium experiences a significant increase in temperature. Closer to the exterior of the AuNR, the temperature increase is more significant, yet even for distances up to 10 nm, the increase is sufficient to decompose common initiators (65–80 °C) using NIR light. At a typical initiator concentration of 0.5 mmol L⁻¹, the average spacing between initiator molecules in solution is 15 nm, implying it is highly likely that multiple initiators will be within 10 nm of the 55x15 nm AuNRs employed in the current study.

Experimental Realization

To experimentally validate the theoretical predictions of the temperature increase around the AuNR, we initially focused on assessing if the polymerization activity is truly connected to the thermal heat dissipation of the AuNR after fs pulse irradiation. We employ citrate functionalized AuNR in water (55x15 nm, OD 1, absorption maximum at 800 nm). In addition to water solubility, citrate functionalized AuNR have potentially lower cytotoxicity compared to other surface‐coated AuNR such as cetyl trimethylammonium bromide (CTAB).[ ⁵² , ⁵³ , ⁵⁴ ] The water‐soluble monomer DMA was irradiated with 800 nm fs laser pulses (35 fs, 25 GW cm⁻², 1 kHz) in the presence of the thermal initiator azobisisobutyronitrile (AIBN) and AuNR (2.69 mol L⁻¹ DMA, 9 mmol L⁻¹ AIBN, 150 μL AuNR, 25 GW cm⁻²) and rapid polymer formation was observed. However, for all reactions conditions tested (variation in irradiation time, AuNR content, initiator and monomer concentration), the polymer precipitated in the aqueous system, forming a white, high molecular weight solid that could not be dissolved for characterisation (refer to Figure S2). We hypothesize that due to the relatively low primary radical concentrations generated via heat transfer of the AuNR, high molecular weight polymers are generated. As a control experiment, DMA (6.73 mol L⁻¹, H₂O) and AIBN (9 mmol L⁻¹, H₂O) were irradiated under identical conditions as the initial experiment (800 nm, 25 GW cm⁻², 1 kHz, 30 min) in the absence of AuNR. As expected, no polymerization activity was observed by size exclusion chromatography (SEC) or ¹H NMR spectroscopy. To enable the formation of soluble polymer, a water‐soluble chain transfer agent (CTA) (3‐mercaptopropionic acid) was added to the reaction solution. The addition of small concentration of CTA (10⁻² mol L⁻¹) overcame the issue of high molecular weights, generating water‐soluble polymers for further analysis. Table 1 collates the complete parameter space that was assessed in terms of the monomer concentration, AuNR content as well as CTA concentration.

Table 1.

Overview of the parameter space assessed for the NIR light‐induced free radical polymerization of dimethylacrylamide (DMA) in water mediated via gold nanorods (AuNR). The concentrations of the transfer agent 3‐mercaptopropionic acid was kept constant at 10⁻² mol L⁻¹.

Substrate	Concentration Range
N,N‐dimethylacrylamide (DMA)	0.69–6.73 mol L−1
Azobisisobutyronitrile (AIBN)	0.17–9.2 mmol L−1
AuNR	50–300 μL
3‐mercaptopropionic acid	10−2 mol L−1

The initial step to evidencing polymer formation was generating an understanding of the polymer end groups via high resolution electrospray ionization mass spectrometry (HR‐ESI‐MS) using an Orbitrap mass analyzer. Figure 2 depicts a zoom into the mass spectrum of one polymer repeat unit (for the full spectrum refer to the Supporting Information section 3.1) resulting from irradiation with 800 nm fs pulses for 30 min at a DMA concentration of 4.04 mol L⁻¹ and a AuNR content of 100 μL. This figure demonstrates that the polymer distribution is strictly transfer controlled, with some evidence of thiol‐end group cleavage (assignment P5). We did not observe any cyanoisopropyl terminated chains, which is—however—not entirely surprising in a transfer dominated polymerization, where the vast majority of chains carries a thiol‐derived chain terminus. The detailed assignments, including the isotopic pattern distributions, can be found in the Supporting Information section 3.1.

Figure 2.

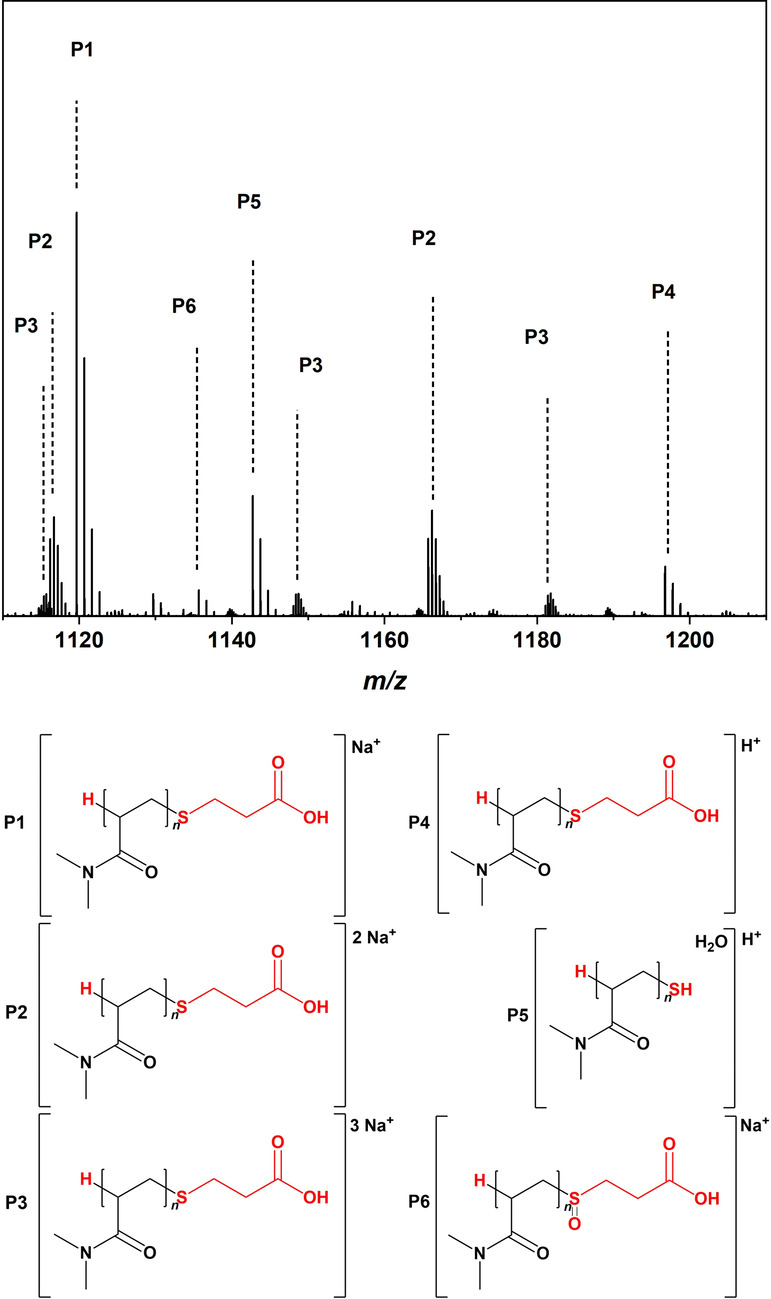
ESI‐MS spectrum obtained after the polymerization of 4.04 mol L⁻¹ DMA with 100 μL AuNR, 9 mmol L⁻¹ AIBN and 10⁻² mol L⁻¹ CTA after 30 min irradiation with 25 GW cm⁻² laser pulses at 800 nm. The irradiated solution was dissolved in 250 μL D₂O prior to direct infusion. Zoom into the repeat unit of 1110–1210 and assignment of the main species P1–P6. The full mass spectrum is depicted in the Supporting Information (Figure S3), which also contains detailed isotopic pattern simulations for each peak (Figure S4).

In the following, we explore the reaction kinetics as a function of the number of photons deposited. For a free radical polymerisation, the instantaneous degree of polymerization as a function of monomer and radical concentration can be estimated using the Mayo equation.[ ⁵⁵ , ⁵⁶ ] In our system, the monomer conversion (black: 0.69 mol L⁻¹ DMA, 50 μL AuNR, 9 mmol L⁻¹ AIBN; red: 6.73 mol L⁻¹ DMA, 50 μL AuNR, 9 mmol L⁻¹ AIBN, 25 GW cm⁻²) is presented in Figure 3, as a function of time and photon number (refer to the Supporting Information section 3.2.1 for the detailed explanation of how the monomer to polymer conversions were determined by ¹H NMR spectroscopy). We followed the monomer to polymer conversion for the highest (6.73 mol L⁻¹) and the lowest (0.69 mol L⁻¹) monomer concentration, with all other parameters kept constant. The polymerization is remarkably fast and reaches high conversions after only 5 min. At short reaction times, the increase in conversion is markedly different for both concentrations. For the high concentration, the conversion displays a sharp increase in the first 5 min and reaches its maximum of close to 65 % conversion after 15 min. For the low concentration, the conversion increases less rapidly and reaches a maximum conversion of close 45 % after 45 min. The observed behaviour is interesting, as the rate of polymerization in a conventional (thermally initiated) free radical polymerization is expected to scale directly with monomer concentration. Given that the concentrations are close to one order of magnitude apart, the observed substantial difference in the initial slope of the two conversions vs time curves is expected. The plateau region observed for both concentrations may possibly be associated with a deactivation of the AuNR surface over time.

Figure 3.

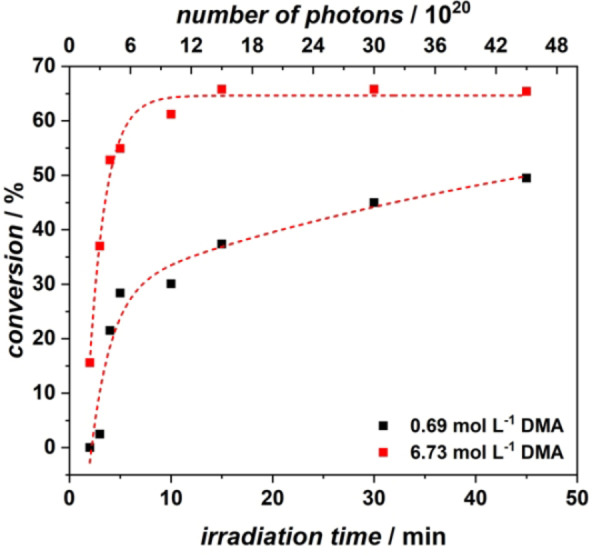
Monomer conversion as a function of reaction time or number of photons; (red) conversion for the highest monomer concentration (6.73 mol L⁻¹), (black) conversion for the lowest monomer concentration (0.69 mol L⁻¹). The lines are fits to guide the eye.

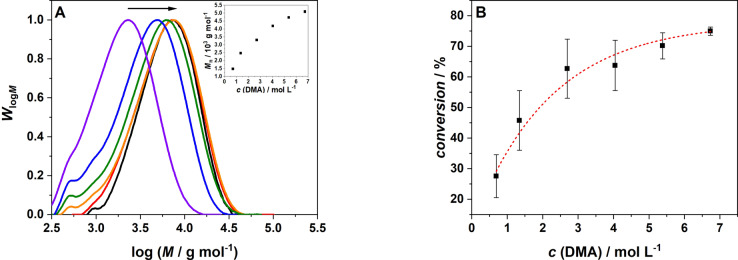
We subsequently map the degree of polymerization as a function of variable parameters, i.e., the concentration of the monomer, initiator and AuNR content (refer to Table 1). Figure 4 depicts the change in molecular weight distributions, alongside the number average molecular weight, M _n, caused by the variation of the DMA concentration after irradiation for 30 min. Varying the monomer concentration from 0.69 to 6.73 mol L⁻¹, results in a continuous shift of the molecular weight distribution to higher molecular weights. Such a behaviour is consistent with the predictions of the Mayo equation.[ ⁵⁵ , ⁵⁶ ] Increasing the monomer concentration leads to a concomitant increase of the monomer to polymer conversion (determined via ¹H NMR spectroscopy, refer to Supporting Information section 3.2). The conversion measurements were repeated in triplicate to obtain an error estimate for each data point.

Figure 4.

A) Molecular weight distribution of poly(N,N‐dimethylacrylamide) as a function of the monomer concentration: (black) 6.73 mol L⁻¹ DMA, (red) 5.38 mol L⁻¹, (orange) 4.04 mol L⁻¹, (green) 2.69 mol L⁻¹, (blue) 1.34 mol L⁻¹, (violet) 0.69 mol L⁻¹. Inset: Number average molecular weight, M _n, after 30 min irradiation as a function of the monomer concentration. B) Monomer to polymer conversion dependent on the monomer concentration with error bars (irradiation time 30 min); the dashed line serves to guide the eye only.

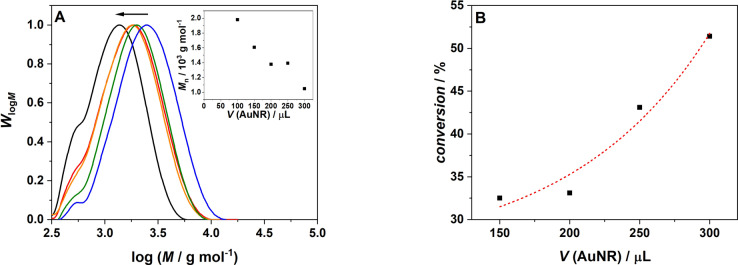
As our initiation system relies on AuNR to induce polymerization, it was critical to probe the effect of their content on the efficacy of the polymerization process. The previously mentioned control experiment revealed that in the absence of any AuNR, no polymer formation was detected. Further, we find that variation of the AuNR content in the sample (low (blue) to high (black)) results in a shift of the molecular weight distribution to lower molecular weights, which is reflected in the associated number average molecular weights, M _n. An increasing AuNR content is expected to lead to a larger portion of the reaction mixture experiencing a temperature increase and therefore to an increased radical formation. Consequently, the likelihood of chain termination increases, leading to lower molecular weight polymers, consistent with the expectations of the Mayo prediction.[ ⁵⁵ , ⁵⁶ ] Consequently, as depicted in Figure 5, the conversion increases with increasing AuNR content. Due to the increased thermal conversion in the samples with higher AuNR concentrations, more initiating radicals are generated that in turn lead to higher monomer conversions.

Figure 5.

A) Molecular weight distribution of poly‐N,N‐dimethylacrylamide dependent on the variation of the gold nanorod concentration: (black) 300 uL AuNR, (red) 250 uL AuNR, (orange) 200 uL AuNR, (green) 150 uL AuNR, (blue) 100 uL AuNR. Inset: Number average of molecular weight, M _n, after 30 min irradiation as a function of the AuNR concentration. B) Monomer to polymer conversion after 30 min irradiation as a function of the AuNR concentration; the dashed line serves to guide the eye along the data points.

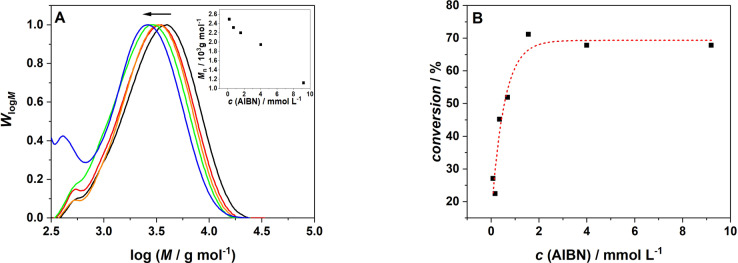
Perhaps not surprisingly, increasing the initiator (AIBN) concentration has a similar effect as increasing the AuNR content (Figure 6). As a higher AuNR content increases the probability of radical formation, so does an increase of the initiator concentration. However, the dependence of conversion on the AIBN concentration displays a specific characteristic. Commencing from a concentration of 0.17 mmol L⁻¹, an initial rapid increase of the conversion is observed, reaching its maximum close to 1.5 mmol L⁻¹. Further increasing the AIBN concentration does not lead to a further increase in conversion. Most likely—at this stage—the content of AuNR is insufficient to produce sufficient heat to activate initiator molecules beyond a specific concentration regime.

Figure 6.

A) Molecular weight distribution of poly(N,N‐dimethylacrylamide) as a function of the AIBN concentration; (black) 9.2 mmol L⁻¹ AIBN, (red) 4 mmol L⁻¹ AIBN, (orange) 1.56 mmol L⁻¹ AIBN, (green) 0.69 mmol L⁻¹ AIBN, (blue) 0.17 mmol L⁻¹ AIBN. Inset: Number average of molecular weight after 30 min as a function of the AIBN concentration. B) monomer to polymer conversion after 30 min irradiation dependent on the AIBN concentration. All experiments were conducted at an AuNR content of 50 μL; dashed line serves to guide the eye along the data points.

Interestingly, we observed that there is even polymer formation if the experiment is conducted in the absence of AIBN. We thus propose that the heat produced by the AuNR causes self‐initiation of DMA, yet the absence of AIBN and thus initiating radicals leads to less conversion compared to the experiments with AIBN.

The ability to induce polymerization at NIR wavelengths in aqueous environments makes initiation using AuNR a highly interesting and promising system for biological applications. To demonstrate that the aqueous solution system can be initiated through tissue, we placed a 1 mm thin slice of tissue (bacon) between the laser and the cuvette (refer to Scheme S1 in the Supporting Information Section 2.5.4). According to the absorption spectrum of our bacon specimen (Figure 7A), one would expect that the tissue absorbs close 90 % of the incident light (OD 1 at 800 nm). However, we recorded 10 GW cm⁻², which corresponds to an absorption of 60 %. Due to the structure of the tissue, the light diffuses after penetration. In the irradiation experiment, we can directly place the detector diode next to the slice of bacon, thus the diffusion of the laser beam is not significant. However, in the absorption spectrometer, the sample holder, where the bacon can be irradiated, and the detector are at a larger distance. Therefore, likely less incident light reaches the detector because of enhanced diffusion, resulting in a higher displayed optical density of the bacon. We compare the monomer conversion of an experiment without tissue (50 μL AuNR, 9 mmol L⁻¹ AIBN, 10⁻² mol L⁻¹ CTA, 25 GW cm⁻², black) with an experiment with tissue (50 μL AuNR, 9 mmol L⁻¹ AIBN, 10⁻² mol L⁻¹ CTA, 10 GW cm⁻², red). For each monomer concentration, the conversion of the experiment without tissue is higher in comparison to the experiment with bacon. The tissue between the laser and the sample absorbs a portion of the incident beam energy, leaving less energy for the photothermal conversion in the AuNR. Therefore, the AuNR produce less heat and thus the radical formation is decreased. We observed no polymer formation for the two lowest monomer concentrations after the insertion of the bacon. We propose that the decreased number of radicals in combination with the lower concentration of monomer molecules are insufficient to initiate polymerization.

Figure 7.

A) Extinction of 1 mm thick slice of bacon in the range of 300–1200 nm with dashed line at 800 nm to highlight the irradiation wavelength. B) Comparison of monomer to polymer conversion after 30 min irradiation of various monomer concentrations with AIBN and AuNR (black) and identically concentrated samples with a 1 mm thick slice of bacon placed in front of it, also irradiated for 30 min (red).

Conclusion

We introduce an AuNR mediated NIR polymerization of a water‐soluble monomer (DMA) in water. We underpin our experimental investigations with a careful theoretical analysis, demonstrating the heat profile generated around the AuNR dissipates within 10 nm of the surface of the AuNR, yet show experimentally that heat decay profile is sufficient to dissociate AIBN moieties within the vicinity of the AuNR into primary radicals, inducing free radical polymerization. We further show that the AuNR content, the monomer as well as the initiator concentration systematically affect the polymerization rate and the resulting number average molecular weights. We project that initiating radical polymerization via NIR light in water and through tissue opens avenues for polymerization in biological environments with high spatio‐temporal control.

Experimental Section

All experimental details can be found in the Supporting Information section.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

P. Neidinger, J. Davis, D. Voll, E. A. Jaatinen, S. L. Walden, A. N. Unterreiner, C. Barner-Kowollik, Angew. Chem. Int. Ed. 2022, 61, e202209177; Angew. Chem. 2022, 134, e202209177.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.