Abstract
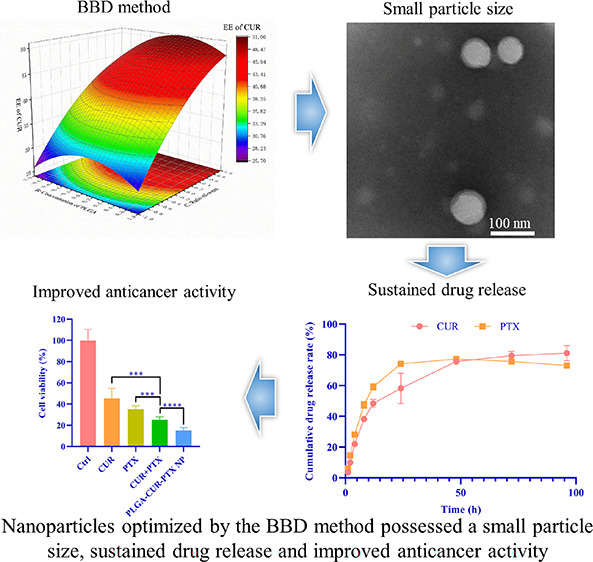
Codelivery of chemotherapeutic drugs in nanoparticles can enhance the therapeutic effects against tumors. However, their anticancer properties and physiochemical characteristics can be severely influenced by many formulation parameters during the preparation process. It is a complicated development phase to select the optimal parameters for preparation of nanoparticles based on the commonly used one single parameter method, which consumes a lot of money, time, and effort, and sometimes even fails. Therefore, the statistical analysis based on Box–Behnken design (BBD) has attracted much attention in bioengineering fields because it can illustrate the influence of parameters, build mathematical models, and predict the optimal combinational factors in a decreased number of experiments. In this study, we used a three-factor three-level BBD design to optimize the preparation of poly(lactic-co-glycolic acid) (PLGA) nanoparticles coloaded with two anticancer drugs curcumin and paclitaxel (PLGA-CUR-PTX nanoparticles). The surfactant concentration, polymer concentration, and oil–water ratio were selected as independent variables. An optimized model of the formulation for PLGA-CUR-PTX nanoparticles was validated. The optimal nanoparticles possessed a uniform spherical shape, with an average size of 99.94 nm, and the drug encapsulation efficiencies of CUR and PTX were 63.53 and 80.64%, respectively. The drug release from nanoparticles showed a biphasic release behavior, with a release mechanism via diffusion and fundamentally quasi-Fickian diffusion. The optimized nanoparticles demonstrated an enhanced cytotoxicity effect with lower IC50 values to 4T1 and MCF-7 breast cancer cell lines compared to free drugs. In summary, BBD optimization of CUR and PTX coloaded nanoparticles yielded a favorable drug carrier that holds potential as an alternative treatment for anticancer therapy.
1. Introduction
Cancer is a major public health problem worldwide, and the incidence and mortality of cancer are increasing rapidly worldwide.1,2 Chemotherapy is the classic treatment for cancer; in particular, it can be effective in treating advanced and metastatic tumors. However, many chemotherapeutic drugs face limitations in chemotherapy, such as fast plasma clearance of drugs, severe damage to normal tissues, systemic side effects, and unsatisfactory therapeutic effects.3 Therefore, it is a promising strategy to adopt combinational oncotherapy to reduce the dosage of chemotherapeutics to avoid side effects and to increase the antitumor efficiency.4 Paclitaxel (PTX) is a first-line antitumor drug, which can be used to treat a variety of cancers;5 however, it is plagued by the problems mentioned above. In the report of Madani et al., paclitaxel and methotrexate (PTX/MTX) were combined for treatment of U-87 MG and B65 cells.6 Curcumin (CUR) is extracted from the dried rhizome of Curcuma longaL., which is a safe food additive and chemosensitizer and widely used in cancer therapy.7,8 In recent years, CUR combined with MTX against glioma was reported by Mujokoro et al.; compared with CUR or MTX alone, CUR combined with MTX can decline the IC50 of CUR and MTX in U-87 MG cells.9 CUR has been considered as a safe anticancer agent without (or with only a few) therapy-related side effects in combination with chemotherapeutic drugs such as paclitaxel, doxorubicin, and cisplatin.10 For example, a study proved that CUR can potentiate the apoptotic effects of PTX in breast cancer cells through downregulating the gene expression of Bcl-2 and NF-κB.11 Thus, in this study, CUR and PTX are considered as combination therapeutic agents for antitumor therapy.
Although CUR combined with PTX is a promising strategy for cancer treatment, both drugs are confronted with the disadvantages of poor water solubility and low bioavailability, which induce unsatisfactory therapeutic effects in vitro and in vivo. To solve these problems, nanocarriers are used to coload CUR and PTX. Nanodrug carriers usually have advantages over drugs due to their nanometer size, high surface volume ratio, and good physical and chemical properties. Insoluble anticancer drugs could be encapsulated by nanoparticles to overcome the solubility and chemical stability problems of anticancer drugs and protect the anticancer drugs from being expelled and improve the circulation time of drugs in vivo.(12,13) Furthermore, nanoparticles could specifically target tumor areas. Due to increased vascular permeability and poor lymphatic drainage or transport in solid tumors, nanodrugs can accumulate in the tumor microenvironment, which is known as the enhanced permeability and retention (EPR) effect.14−16 Nanoparticles could preferentially distribute on the tumor site through the EPR effect, which led to a high drug concentration in the tumor site and a low drug concentration in the normal tissue, thus enhancing the tumor treatment effect and reducing damage of chemotherapy drugs to the normal tissue.13,17 Poly(lactic-co-glycolic acid) (PLGA) is an approved pharmaceutical excipient that can be processed into a nanodrug carrier for small-molecule drugs, proteins, and large-molecule drugs.18 PLGA has attracted extensive attention as a drug carrier due to its biodegradability, protection of drug activity, and improvement of drug bioavailability.18,19 Thus, PTX and CUR coloaded PLGA nanoparticles might be a promising strategy for increasing the antitumor efficacy and decreasing the side effects of PTX. The preparation of PLGA nanoparticles includes solvent evaporation, phase separation, spray drying, nanoprecipitation, and salting out.18 Among these methods, solvent evaporation is the most widely used method due to its simple operation, short preparation cycle, and mature technology.
Several process variables can affect the physicochemical properties of nanocarriers, such as the size, uniformity, and drug loading efficiency, and play an important role in developing a successful nanocarrier.20 The separate control variable method is a common method to optimize process parameters in nanoparticle preparation, which optimizes the formulation or process by changing one variable and keeping other parameters unchanged at a time (one-factor-at-time, OFAT method). Although this approach can achieve a solution for specific formulations, it does not achieve an optimal combination between process parameters.21 In the situation of too many process parameters, this method tends to spend considerable time, money, and effort and is not conducive to repairing errors, unable to predict the optimized process parameters, and sometimes even fails.21,22 To solve this problem, the statistical design of experiments (DoE) for optimization of nanoparticles is introduced in this study. DoE is an optimization technique method that helps to illustrate how process parameters (alone and combined) affect the product (responses). DoE can be used to optimize process variables in the preparation of nanocarriers.23,24 The DoE methods commonly used in the fabrication of nanoparticles include screening design (such as Plackett–Burman, fractional factorial design, and full factorial design) and the response surface methodology (RSM). The RSM can build mathematical models to link response values and input process parameters.25 The central composite design (CCD) and the Box–Behnken design (BBD) are the main RSM methods in the pharmaceutical fields. BBD is widely used in bioengineering processes because it has fewer factor levels and decreases the number of experiments.25,26 BBD can optimize the formulation of nanocarriers through a limited number of experiments. For instance, Shaikh et al. successfully developed PLGA nanoparticles loaded with doxorubicin (DOX-PLGA-nanoparticles) and optimized the parameters of the nanoparticle preparation process through BBD.27 The final obtained prescription has a small particle size (180.1 nm) and polydispersity index (PDI) (0.063), and the drug encapsulation efficiency is 52.29%.27 Compared with the simple OFAT approach, BBD is advantageous because the statistical evaluation can provide more accurate conclusions with a reduced number of experiments.
In this study, we developed a nanomedicine consisting of CUR and PTX coloaded into PLGA nanoparticles (PLGA-CUR-PTX nanoparticles) and achieved a combination for cancer treatment. Formulation optimization was carried out through BBD on the DoE approach. The prescription attributes of PLGA-CUR-PTX nanoparticles assessed included the particle size, PDI, encapsulation efficiency, and particle morphology. The in vitro drug release of PLGA-CUR-PTX nanoparticles was further studied. Subsequently, the inhibition effect of cancer cells was evaluated based on the optimized prescription.
2. Materials and Methods
2.1. Materials
Paclitaxel (PTX; degree of purity, ≥99%, BR) was procured from Dalian Meilun Biotechnology Co., Ltd., China; curcumin (CUR; degree of purity, 95%, HPLC) was procured from Shanghai Yuanye Biotechnology Co., Ltd., China; PLGA (LA/GA: 75/25, molecular weight: 30 kDa) was procured from Daigang Biological Engineering Co., Ltd., China; sodium cholate was procured from Sigma Aldrich, USA. Dichloromethane was procured from Sichuan Fairbest Technology Co., Ltd., China; phosphoric acid (degree of purity, 85–90%, HPLC) was procured from Macklin, China; acetonitrile was procured from Chengdu Hongben Chemical Products Co., Ltd., China; an ultrafiltration tube (molecular weight cutoff: 10 kDa) was procured from Millipore, USA; fetal bovine serum (FBS) was procured from MRC, USA; DMEM was procured from Gibco, USA.
2.2. Preparation and Optimization of CUR and PTX Coloaded PLGA (PLGA-CUR-PTX) Nanoparticles
2.2.1. Preparation of PLGA-CUR-PTX Nanoparticles
PLGA-CUR-PTX nanoparticles were developed by the emulsion solvent evaporation technique.17 In brief, certain amounts of PTX (w/w), CUR (w/w), and PLGA were dissolved in CH2Cl2 as the oil phase. Subsequently, the oil phase was poured into the water phase, which consisted of a certain amount of sodium cholate, and emulsified by an ultrasonic homogenizer (Scientz-IID, Xingzhi Biological, China) in an ice bath for 2 min at 300 W to obtain the oil-in-water (O/W) emulsion. A rotary evaporation system (RV10-autopro, IKA, Germany) was used to remove CH2Cl2 from the emulsion in a water bath at 30 °C with a vacuum of 400 mbar and a rotating speed of 120 rpm. The nanoparticle solution was obtained after 30 min of rotary evaporation. Centrifugation (2000g, 5 min) was used to remove large particles from the nanoparticle solution. The nanoparticles were centrifuged at 3260g for 15 min, using an ultrafiltration tube, and washed three times with deionized water to obtain the purified nanoparticles. Finally, the nanoparticles that agglomerated during the washing process were removed by centrifugation (2000g, 5 min), and the supernatant was taken as the final nanoparticle suspension, which was stored at 4 °C until further use.
2.2.2. Experimental Design
A Box–Behnken design (BBD) of 15 runs, three factors at three levels (33), with three replicates at the center point, was constructed to study the influence of different factor variables on the characteristics of PLGA-CUR-PTX nanoparticles. Experimental design and statistical analysis were performed by Design-Expert software (Design Expert 10.0.1, Stat-Ease, Minneapolis, MN, USA). The fitting formula of the quadratic model is generated by the software as follows.
where Y is the measured response, b0 is the constant term of the polynomial equation, b1–b3 are linear coefficients, b4–b6 are interaction coefficients of the three factors, and b7–b9 are quadratic coefficients of the observed experimental values. The main, interacting, and quadratic effects of independent variables are A, B, and C; AB, AC, and BC; and A2, B2, and C2, respectively.
In this work, three independent variables (Table 1) were chosen as follows: (A) concentration of sodium cholate (w/v, %), (B) concentration of PLGA (w/v, %), and (C) the ratio of oil volume to water volume (v/v, %). The responses to be measured (Table 2) were the (Y1) size of nanoparticles, (Y2) PDI of nanoparticles, (Y3) encapsulation efficiency of CUR, (Y4) encapsulation efficiency of PTX, and (Y5) total encapsulation efficiency. Corresponding to the independent variables, three different levels were established as the lowest (−1), the highest (+1), and central values (0) of the tested variables (Table 1). The matrix of 15 experimental formulations was constructed as represented in Table 3.
Table 1. The Independent Variables of BBD.
| levels |
|||||
|---|---|---|---|---|---|
| variables | symbol | unit | lowest (−1) | central (0) | highest (+1) |
| concentration of sodium cholate | A | % | 1.5 | 2.5 | 3.5 |
| concentration of PLGA | B | mg/mL | 15 | 20 | 25 |
| ratio of oil–water | C | % | 30 | 50 | 70 |
Table 2. The Dependent Variables of BBD.
| variables | unit | symbol | constraints |
|---|---|---|---|
| size of nanoparticles | nm | Y1 | minimize |
| PDI of nanoparticles | Y2 | minimize | |
| encapsulation efficiency of CUR | % | Y3 | maximize |
| encapsulation efficiency of PTX | % | Y4 | maximize |
| total encapsulation efficiency | % | Y5 | maximize |
Table 3. Experimental Arrangement and Resultsa.
| independent variables |
dependent variables |
|||||||
|---|---|---|---|---|---|---|---|---|
| formula | A | B | C | Y1/nm | Y2 | Y3/% | Y4/% | Y5/% |
| F1 | +1 | –1 | 0 | 76.89 ± 0.59 | 0.133 ± 0.002 | 30.07 ± 2.71 | 70.53 ± 3.59 | 43.55 ± 0.67 |
| F2 | 0 | +1 | –1 | 112.07 ± 2.16 | 0.124 ± 0.003 | 27.22 ± 7.78 | 58.23 ± 8.31 | 37.56 ± 6.10 |
| F3 | –1 | –1 | 0 | 110.13 ± 1.86 | 0.105 ± 0.009 | 50.22 ± 6.62 | 70.52 ± 5.15 | 56.99 ± 2.92 |
| F4 | 0 | 0 | 0 | 82.81 ± 6.13 | 0.111 ± 0.006 | 46.38 ± 7.03 | 67.82 ± 3.15 | 53.53 ± 4.08 |
| F5 | 0 | +1 | +1 | 119.13 ± 1.15 | 0.098 ± 0.004 | 50.82 ± 8.03 | 66.99 ± 0.99 | 56.21 ± 5.16 |
| F6 | +1 | 0 | +1 | 81.72 ± 0.68 | 0.093 ± 0.013 | 41.93 ± 4.32 | 66.65 ± 4.08 | 50.17 ± 1.95 |
| F7 | +1 | +1 | 0 | 96.24 ± 1.26 | 0.104 ± 0.020 | 34.11 ± 4.34 | 62.30 ± 3.69 | 43.50 ± 3.95 |
| F8 | 0 | –1 | +1 | 82.53 ± 1.37 | 0.131 ± 0.003 | 45.55 ± 7.17 | 73.44 ± 4.50 | 54.85 ± 4.33 |
| F9 | 0 | –1 | –1 | 92.9 ± 1.22 | 0.150 ± 0.026 | 23.07 ± 5.68 | 65.42 ± 2.00 | 37.18 ± 3.57 |
| F10 | –1 | 0 | +1 | 92.48 ± 1.33 | 0.133 ± 0.016 | 58.03 ± 7.11 | 78.36 ± 2.66 | 64.80 ± 5.30 |
| F11 | –1 | 0 | –1 | 87.54 ± 0.27 | 0.129 ± 0.019 | 53.45 ± 9.37 | 71.29 ± 3.21 | 59.40 ± 5.22 |
| F12 | 0 | 0 | 0 | 91.63 ± 1.94 | 0.246 ± 0.007 | 38.15 ± 8.11 | 68.33 ± 4.46 | 48.21 ± 4.09 |
| F13 | 0 | 0 | 0 | 108.13 ± 0.70 | 0.122 ± 0.014 | 47.97 ± 8.00 | 78.57 ± 4.37 | 58.17 ± 3.88 |
| F14 | –1 | 1 | 0 | 85.04 ± 1.94 | 0.117 ± 0.025 | 48.75 ± 10.50 | 72.66 ± 4.05 | 56.72 ± 6.29 |
| F15 | +1 | 0 | –1 | 112.03 ± 0.84 | 0.128 ± 0.027 | 15.19 ± 5.40 | 60.37 ± 8.22 | 30.25 ± 2.14 |
Notes: A, concentration of sodium cholate; B, concentration of PLGA; C, ratio of oil–water; Y1, size of nanoparticles (nm); Y2, PDI of nanoparticles; Y3, EE of CUR (%); Y4, EE of PTX (%); Y5, total EE (%). Responses are expressed as the mean ± SD (n = 3).
Variance analysis (ANOVA) was used to verify the polynomial equation generated after analysis, and the relationship between all variables and their influence on the response were predicted. Subsequently, the contour maps (2D) and response surface maps (3D) were generated by the software to understand the relationships between variables and their interactions.
2.3. Characterization of PLGA-CUR-PTX Nanoparticles
2.3.1. Nanoparticle Size and PDI Measurements
The PLGA-CUR-PTX nanoparticle (0.02 mL) suspension was diluted with pure water (2 mL), and the size and PDI of the PLGA-CUR-PTX nanoparticles were measured by dynamic light scattering (DLS) using a nanozetasizer (Nano-ZS90, Malvern, UK). Each result was measured in triplicate.
2.3.2. Drug Encapsulation Efficiency (EE) Measurements
After freeze-drying, a certain amount of PLGA-CUR-PTX nanoparticles was dissolved in 50% acetonitrile aqueous solution containing 0.05% phosphoric acid to extract CUR and PTX. The concentration of drugs in the PLGA-CUR-PTX nanoparticles was then determined by high-performance liquid chromatography (HPLC, Agilent, USA) with the following conditions: Keromasil 100-5-C18 (4.6 × 150 nm) chromatographic column; mobile phase: 0.1% phosphoric acid aqueous solution and acetonitrile (50:50, v/v); flow rate of 1 mL/min; detection wavelength of 227 nm; column temperature of 30 ± 0.1 °C; injection volume of 20 μL. The drug EE was calculated by the following equations, and each result was measured in triplicate:
2.3.3. Morphological Characterization of PLGA-CUR-PTX Nanoparticles
The shape and surface morphology of the optimized PLGA-CUR-PTX nanoparticles were examined using transmission electronic microscopy (TEM, HT7820, Hitachi, Japan). Briefly, a drop of nanoparticles was spread on a 200-mesh copper grid and dried at room temperature. Then, the sample was negatively stained by adding 1% phosphotungstic acid to the grid. The samples were examined by TEM.
2.3.4. In Vitro Drug Release Study
The in vitro release of CUR and PTX from the optimal formulation of PLGA-CUR-PTX nanoparticles was performed in phosphate-buffered saline (PBS) containing 10% ethanol and 0.5% Tween 80, using a membrane diffusion technique.28 Briefly, 1 mL of the freshly prepared nanoparticle solution corresponding to 636 μg of CUR and 374 μg of PTX was placed in a dialysis bag. Then, the dialysis bags were soaked into 50 mL of PBS containing 10% ethanol and 0.5% Tween 80 as the release media in brown bottles. The brown bottles were kept in an orbital shaker (MAXQ4000, Thermo, USA) at 37 °C and 100 rpm. At predetermined time points (1, 2, 4, 8, 12, 24, 48, 72, and 96 h), a 1 mL sample of release media was withdrawn and replaced with fresh media of an equal volume. The quantitative analysis of CUR and PTX in the release media was detected using the HPLC method. The cumulative drug release percentage was calculated, and the time–drug curve was plotted. The release experiments were performed in triplicate.
Drug release data were fitted into mathematical models of zero-order, first-order, Higuchi, and Korsmeyer–Peppas using the DD solver, an add-in of MS Excel, to build regression analysis of the mathematical expressions to explain the mechanism of drug release.29−31
2.3.5. In Vitro Antitumor Efficacy
The cytotoxicity of PLGA-CUR-PTX nanoparticles was determined in 4T1 by the MTT method. Briefly, the breast cancer cell line 4T1 was maintained in DMEM supplemented with 10% (v/v) FBS, 100 U/mL penicillin, and 100 μg/mL streptomycin and grown in a humidified incubator at 37 °C and 5% CO2. 4T1 cells were seeded in 96-well microplates with a density of 3 × 103 cells/well and incubated for 24 h. Cells were exposed concomitantly to PLGA-CUR-PTX nanoparticles (300 μg/mL) and the relative concentrations of free CUR (7.62 μg/mL), free PTX (4.83 μg/mL), and free CUR (7.62 μg/mL) + free PTX (4.83 μg/mL). The control group without drug addition was used as a negative control. Wells containing only drugs without cells were used as the blank group. After 48 h, the original culture medium was discarded, and the cells were washed twice with PBS. A solution of 100 μL of MTT (0.5 mg/mL) diluted with base medium was added to each well and incubated for 4 h. Then, the optical density (OD) values were measured at 490 nm using a microplate reader (Varioskan LUX, Thermo, USA). Cell viability was calculated according to the following formula: cell viability (%) = (ODgroups – ODblank)/(ODcontrol – ODblank) × 100%. Six parallel experiments were performed in each group. Furthermore, 4T1 cells were exposed with the blank PLGA nanoparticles without drugs in different concentrations (0–500 μg/mL) for 24 h to assess the biocompatibility of the carriers.
To determine the half maximal inhibitory concentration (IC50) for 4T1 and MCF-7 cells for 48 h, the same method was repeated using different concentrations of PLGA-CUR-PTX nanoparticles, CUR, PTX, and CUR+PTX. GraphPad Prism version 8 (GraphPad Software, San Diego, CA, USA) was used to analyze the results. To further investigate the synergistic effect of CUR and PTX, the combination index (CI) of the two drugs was calculated using the equation32 CI = H/H1 + D/D1, where H1 and D1 are the concentrations of CUR and PTX alone that kill 50% of the cell population and H and D are the concentrations of CUR and PTX in nanoparticles that give similar cell killing efficacy (50%) in combination. Values of CI at <1, =1, and >1 represent synergistic, additive, and antagonistic effects, respectively.
3. Results and Discussion
3.1. Preparation of PLGA-CUR-PTX Nanoparticles
A single emulsion solvent evaporation method was used to fabricate CUR and PTX coloaded PLGA nanoparticles. The organic mixture of PLGA, CUR, and PTX was emulsified with the aqueous phase containing sodium cholate by sonication. Finally, the PLGA-CUR-PTX nanoparticles were purified by ultrafiltration. A Box–Behnken design (BBD) of 15 runs, three factors at three levels (33), with three replicates at the center point, was constructed to study the influence of different factor variables on the size, PDI, and EE of PLGA-CUR-PTX nanoparticles. The experimental results concerning the size of the nanoparticles, PDI of the nanoparticles, and EE from all experiments are given in Table 3.
3.2. Optimization of PLGA-CUR-PTX Nanoparticles
3.2.1. Particle Size and PDI
The particle size ranged from 76.89 ± 0.59 to 119.13 ± 1.15 nm, and the mean PDI values were all less than 0.25, demonstrating the good uniformity of the prepared nanoparticles (Table 3). It is well-recognized that the suitable size of nanoparticles for antitumor therapy is less than 200 nm.33 Thus, the size of all prepared nanoparticles was beneficial to their application in antitumor therapy.
The function to predict the studied process variables affecting the size of nanoparticles (Y1) was automatically generated by Design Expert software:
The function to predict the studied process variables affecting the PDI of nanoparticles (Y2) was automatically generated by Design Expert software:
The results of the ANOVA (Table 4) showed that P for the model was higher than 0.05 for Y1 (size of nanoparticles) and Y2 (PDI of nanoparticles), indicating that the size of nanoparticles and the PDI of nanoparticle variation were not influenced by any of the factors studied.
Table 4. The ANOVA Results for All Responsesa.
| responses | sum of squares | df | mean square | F value | P value | |
|---|---|---|---|---|---|---|
| Y1 | 1528.13 | 9 | 169.79 | 0.83 | 0.6185 | not significant |
| Y2 | 0.01 | 9 | 0.00 | 0.29 | 0.9478 | not significant |
| Y3 | 2000.78 | 9 | 222.31 | 8.14 | 0.0163 | significant |
| Y4 | 379.80 | 9 | 42.20 | 2.09 | 0.2159 | not significant |
| Y5 | 1236.67 | 9 | 137.41 | 6.74 | 0.0245 | significant |
Notes: Y1, size of nanoparticles (nm); Y2, PDI of nanoparticles; Y3, EE of CUR (%); Y4, EE of PTX (%); Y5, total EE (%).
3.2.2. EE of Drugs
BBD was performed to determine the effects of the concentration of sodium cholate, the concentration of PLGA, and the ratio of oil−water on the total EE and on the EE of CUR and PTX for the optimization of nanoparticle preparation. The results of all experiments are listed in Table 3.
3.2.2.1. EE of CUR
The EE of CUR ranged from 15.19 ± 5.40 to 58.03 ± 7.01% (Table 3). The function to predict the studied process variables affecting the EE of CUR (Y3) was automatically generated by Design Expert software:
The R2 (coefficient of determination) value of the model was 0.9361. Meanwhile, the lack of fit was not significant (P = 0.5431). These values confirmed that the model was adequate for predicting the EE under any combination of values of the variables inside the experimental domain. From the equation, a positive value indicated a synergistic effect in the regression model; on the contrary, a negative value indicated an antagonistic effect.34 Factors B, C, AB, AC, BC, and A2 had a positive effect on response Y3, and A, B2, and C2 had a negative effect on the response Y3. Analysis of data by ANOVA of the proposed model indicated the significant effect of all factors on Y3 (EE of CUR) (P = 0.0163). According to the results of the statistical analysis (Tables 4 and 5), it was found that two independent process variables, namely, the concentration of sodium cholate (A) and the ratio of oil−water (C), had significant effects on the EE of CUR (P < 0.05), while another variable, the concentration of PLGA (B), had no independent impact on the EE of CUR (P > 0.05).
Table 5. ANOVA for the Surface Quadratic Model for the EE of CUR (Y3)a.
| source | sum of squares | df | mean square | F value | P value |
|---|---|---|---|---|---|
| model | 2000.78 | 9 | 222.31 | 8.14 | 0.0163 |
| A | 993.78 | 1 | 993.78 | 36.40 | 0.0018 |
| B | 18.00 | 1 | 18.00 | 0.66 | 0.4536 |
| C | 748.77 | 1 | 748.77 | 27.43 | 0.0033 |
| AB | 7.58 | 1 | 7.58 | 0.28 | 0.6207 |
| AC | 122.71 | 1 | 122.71 | 4.49 | 0.0874 |
| BC | 0.32 | 1 | 0.32 | 0.01 | 0.9180 |
| A2 | 4.09 | 1 | 4.09 | 0.15 | 0.7145 |
| B2 | 72.54 | 1 | 72.54 | 2.66 | 0.1640 |
| C2 | 34.81 | 1 | 34.81 | 1.27 | 0.3100 |
| residual | 136.51 | 5 | 27.30 | NA | NA |
| lack of fit | 80.98 | 3 | 26.99 | 0.97 | 0.5431 |
| pure error | 55.53 | 2 | 27.77 | NA | NA |
| cor total | 2137.31 | 14 | NA | NA | NA |
Notes: A, concentration of sodium cholate; B, concentration of PLGA; C, ratio of oil–water; Y1, size of nanoparticles (nm); Y2, PDI of nanoparticles.
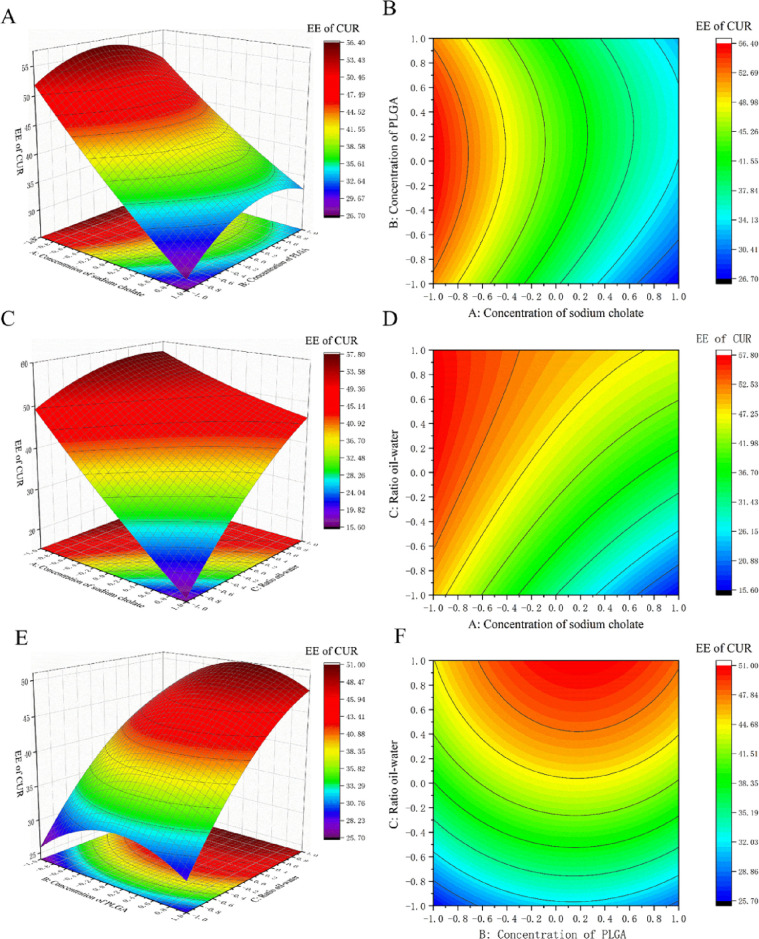
Figure 1 shows the influences of the concentration of sodium cholate, the ratio of oil−water, and the concentration of PLGA on the response variable. It clearly exhibits the response surface plots (3D) and contour plots (2D) (Figure 1), where an obvious decrease in the EE of CUR was observed with an increase in the concentration of sodium cholate from a low level to a high level with a constant ratio of oil–water. This phenomenon was similar to previous studies.35−39 This may be because sodium cholate is a surfactant with a high HLB value (HLB = 18), which usually leads to a low EE.40 On the other hand, the increase in the sodium cholate concentration can improve the solubility of hydrophobic drugs in aqueous solution and reduce the interfacial tension of the emulsion. As a result, a high concentration of sodium cholate will reduce the interfacial tension, promoting the release of drugs into the external water phase during mixing, leaving fewer drugs in the emulsion droplets and resulting in a decreased EE.39,41,42 Furthermore, an obvious increase in the EE of CUR was observed with an increase in the ratio of oil–water from a low level to a high level with a constant concentration of sodium cholate (Figure 1). This may be because increasing the ratio of the organic phase increases the viscosity of the emulsion and slows drug diffusion in the aqueous phase, thus increasing the EE of CUR.
Figure 1.
3D response surface plots and 2D contour map for PLGA-CUR-PTX nanoparticles showing the effect of (A,B) concentration of sodium cholate and concentration of PLGA, (C,D) concentration of sodium cholate and the ratio of oil–water, and (E,F) concentration of PLGA and the ratio of oil–water on the EE of CUR.
3.2.2.2. EE of PTX
The EE of PTX ranged from 58.23 ± 8.31 to 78.57 ± 4.31% (Table 3). The function to predict the studied process variables affecting the EE of PTX (Y4) was automatically generated by Design Expert software:
The results of the ANOVA test (Table 4) showed that P for the model was higher than 0.05 for Y4 (EE of PTX), indicating that the EE of PTX was not influenced by any of the factors studied.
3.2.2.3. Total EE
The total EE ranged from 30.25 ± 2.14 to 64.80 ± 5.30% (Table 3). The function to predict the studied process variables affecting the total EE (Y5) was automatically generated by Design Expert software:
Y5 = 53.30 – 8.80A + 0.18B + 7.70C + 0.05AB + 3.63AC + 0.25BC + 0.80A2 – 3.9B2 – 2.94C2 (R2 = 0.9238)
Analysis of data by ANOVA of the proposed model indicated a significant effect of all factors on Y5 (total EE), with a P value of 0.0246. The R2 value of the model was 0.9238. Meanwhile, the lack of fit was not significant (P = 0.6326). These values confirmed that the model was adequate for predicting the EE under any combination of values of the variables inside the experimental domain. Factors B, C, AB, AC, BC, and A2 had a positive effect on the response Y5, and A, B2, and C2 had a negative effect on the response Y5. According to the results of the statistical analysis (Tables 4 and 6), it was found that two independent process variables, namely, the concentration of sodium cholate (A) and the ratio of oil–water (C), had significant effects on the total EE (P < 0.05), while another variable, the concentration of PLGA (B), had no independent impact on the total EE (P > 0.05).
Table 6. ANOVA for the Quadratic Model for the Total EE (Y5)a.
| source | sum of squares | df | mean square | F value | P value |
|---|---|---|---|---|---|
| model | 1236.67 | 9 | 137.41 | 6.74 | 0.0245 |
| A | 620.08 | 1 | 620.08 | 30.40 | 0.0027 |
| B | 0.2527 | 1 | 0.25 | 0.012 | 0.9157 |
| C | 474.90 | 1 | 474.90 | 23.28 | 0.0048 |
| AB | 0.0116 | 1 | 0.01 | 0.00 | 0.9819 |
| AC | 52.62 | 1 | 52.62 | 2.58 | 0.1691 |
| BC | 0.25 | 1 | 0.25 | 0.01 | 0.9166 |
| A2 | 2.35 | 1 | 2.35 | 0.12 | 0.7481 |
| B2 | 56.40 | 1 | 56.40 | 2.77 | 0.1572 |
| C2 | 32.02 | 1 | 32.01 | 1.57 | 0.2656 |
| residual | 101.98 | 5 | 20.40 | NA | NA |
| lack of fit | 52.31 | 3 | 17.44 | 0.70 | 0.6325 |
| pure error | 49.66 | 2 | 24.83 | NA | NA |
| cor total | 1338.65 | 14 | NA | NA | NA |
Notes: A, concentration of sodium cholate; B, concentration of PLGA; C, ratio of oil–water; Y1, size of nanoparticles (nm); Y2, PDI of nanoparticles.
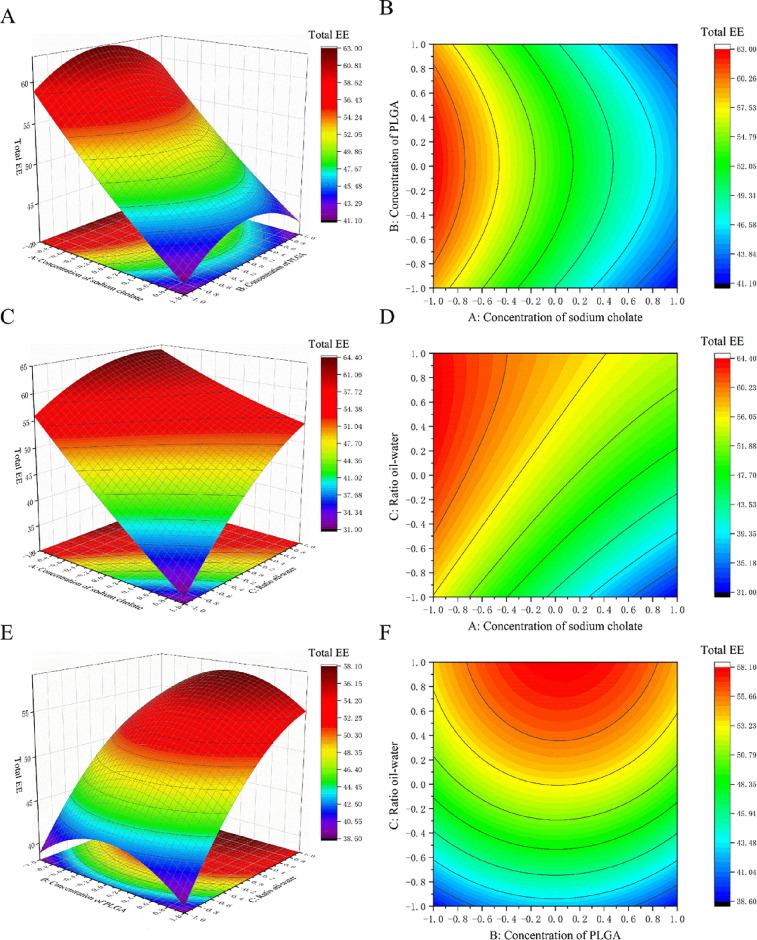
The total EE was significantly affected by both the sodium cholate concentration and the ratio of oil–water, with a higher concentration of sodium cholate leading to a lower total EE and conversely a higher oil–water ratio leading to a higher total EE (Figure 2). The effects of the surfactant concentration and the ratio of oil–water on the total EE were similar to their effect on the EE of CUR, which was probably due to the fact that the EE of the other drug PTX is not affected by any experimental factor. So, the change in the total EE is mainly caused by the change in the EE of CUR.
Figure 2.
3D response surface plots and 2D contour map for PLGA-CUR-PTX nanoparticles showing the effect of (A,B) concentration of sodium cholate and concentration of PLGA, (C,D) concentration of sodium cholate and the ratio of oil–water, and (E,F) concentration of PLGA and the ratio of oil–water on the total EE.
3.2.3. Optimal Formulation for PLGA-CUR-PTX Nanoparticles
Optimization was performed by employing the desirability method upon application of constraints to the three independent variables (A, concentration of sodium cholate; B, concentration of PLGA; C, ratio of oil–water). To obtain the maximum EE of the PLGA-CUR-PTX nanoparticles, software was used to determine the levels of the three independent variables. The levels of A, B, and C were found to be 1.5% w/v, 20.18 mg/mL, and 70% v/v, respectively. The predicted values are listed in Table 7. The optimized PLGA-CUR-PTX nanoparticles have a desirability of 0.990. The predicted levels of each variable will be used to prepare the optimized PLGA-CUR-PTX nanoparticles to confirm the prediction. The optimized response values of PLGA-CUR-PTX nanoparticles are shown in Table 7. The optimal size was 99.94 nm, the PDI was 0.101, and the optimal EE values were 63.53 (LE: 2.54%), 80.64 (LE: 1.61%), and 69.24% (LE: 4.15%) for CUR, PTX, and total drugs, respectively. This size was suitable for antitumor therapy because the optimized nanoparticles could passively target the tumor site due to the EPR effects.43 The narrow size distribution of nanoparticles indicated by a lower PDI can contribute to the high reproducibility of experiments and results. The high EE of the optimized nanoparticles can avoid the waste of drugs during the formulation process.
Table 7. The Predicted Values and the Optimized Response Values Observed for PLGA-CUR-PTX Nanoparticlesa.
| responses | predicted values | observation values |
|---|---|---|
| Y1 | 95.53 nm | 99.94 nm |
| Y2 | 0.139 | 0.101 |
| Y3 | 57.76% | 63.53% |
| Y4 | 78.57% | 80.64% |
| Y5 | 64.80% | 69.24% |
Notes: Y1, size of nanoparticles (nm); Y2, PDI of nanoparticles; Y3, EE of CUR (%); Y4, EE of PTX (%); Y5, total encapsulation efficiency (%).
3.3. Characterization of Optimized PLGA-CUR-PTX Nanoparticles
3.3.1. Size Distribution and Morphological Characterization of Optimal PLGA-CUR-PTX Nanoparticles
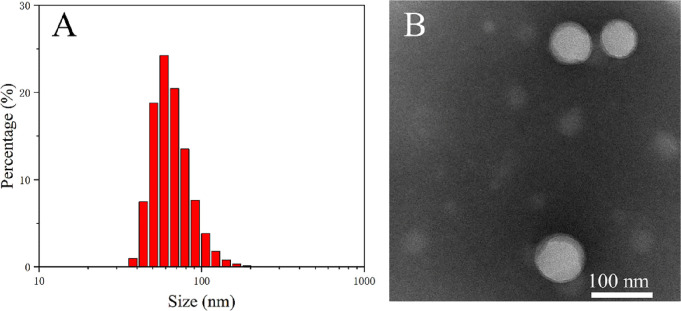
As shown in Figure 3A and Table 7, the size and PDI of the optimized nanoparticles were measured to be around 100 nm and 0.1, respectively, indicating a uniform size distribution.
Figure 3.
(A) Size distribution and (B) TEM image of optimized PLGA-CUR-PTX nanoparticles. TEM scale bar: 100 nm.
3.3.2. In Vitro Drug Release Study
The release profile of CUR and PTX from optimized PLGA-CUR-PTX nanoparticles at pH 7.4 is shown in Figure 4. The drug release profile from nanoparticles showed a biphasic release behavior, which consisted of an initial burst release (the cumulative drug release rates of CUR and PTX during the burst release period were 48.5 ± 2.57 and 59.1 ± 2.14%, respectively) within 12 h followed by controlled release in the subsequent time (the cumulative drug release rates of CUR and PTX during the controlled release period were 81.1 ± 4.97 and 73.0 ± 1.34%, respectively). The initial burst release from PLGA-CUR-PTX nanoparticles was attributed to the immediate desorption of drug molecules adsorbed onto the particle surface, and a shorter average diffusion path due to the nanoscale nanoparticles led to rapid drug molecule release.44 Thereafter, the slower release during the controlled release period was due to drug molecules resolved into the release medium from the nanoparticle core through interconnected pores and channels in the polymeric matrix.45
Figure 4.

In vitro drug release study of the optimized PLGA-CUR-PTX nanoparticles at pH 7.4 (each group represents n = 3, mean ± standard deviation).
The drug release mechanism was analyzed by different mathematical models (Table 8). Compared with the zero-order, first-order, and Higuchi models, the Korsmeyer–Peppas model was the best fit for the release behavior of CUR and PTX, with R2 values of 0.9299 and 0.8131, respectively. Based on the diffusional exponent n < 0.5, the release mechanisms of CUR (n = 0.392) and PTX (n = 0.229) were diffusion and fundamentally quasi-Fickian diffusion.46
Table 8. Release Kinetics Parameters of In Vitro CUR and PTX Release from PLGA-CUR-PTX Nanoparticles.
| the release
equations |
model coefficient (R2) |
|||
|---|---|---|---|---|
| kinetics model | CUR | PTX | CUR | PTX |
| zero-order | Mt/M∞ = 1.116 × t | Mt/M∞ = 1.096 × t | 0.3535 | –0.3298 |
| first-order | Mt/M∞ = F = 100 × [1 – exp(−0.038 × t)] | Mt/M∞ = F = 100 × [1 – exp(−0.065 × t)] | 0.8759 | 0.7237 |
| Higuchi | Mt/M∞ = F = 9.795 × t1/2 | Mt/M∞ = F = 10.035 × t1/2 | 0.8907 | 0.6076 |
| Korsmeyer–Peppas | Mt/M∞ = F = 14.994 × t0.392 | Mt/M∞ = F = 22.105 × t0.229 | 0.9299 | 0.8131 |
3.4. In Vitro Antitumor Efficacy
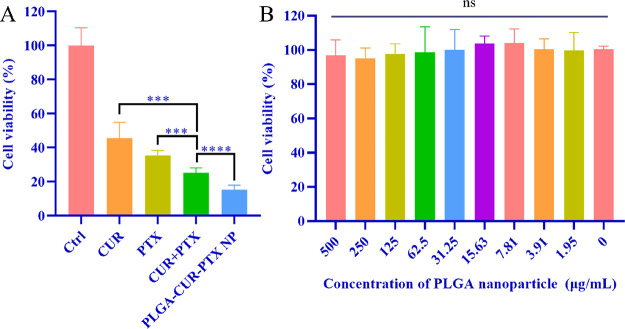
The in vitro antitumor efficacy of PLGA-CUR-PTX nanoparticles, free CUR, free PTX, and free CUR combined with free PTX in 4T1 breast cancer cells was assessed by the MTT assay (Figure 5A). The 4T1 cells were treated with different treatment groups for 48 h, and the cell activity of all groups was significantly lower than that of the control group. The cell activity of the free CUR combined with free PTX group was significantly lower than that of the free CUR group (P < 0.001) and the free PTX group (P < 0.001); moreover, the PLGA-CUR-PTX nanoparticle group further inhibited the 4T1 cell activity (P < 0.0001). As shown in Figure 5B, the cell viability was nearly 100% after incubation with nanoparticles in the concentration range of 0 to 500 μg/mL, demonstrating that the PLGA-CUR-PTX nanoparticles had superior biocompatibility.
Figure 5.
In vitro antitumor efficacy. (A) Cell viability of 4T1 breast cancer cells incubated with different treatments for 48 h. (B) Cell viability of 4T1 breast cancer cells incubated with different concentrations of blank PLGA nanoparticles for 24 h. Each group represents n = 6, mean ± standard deviation, ***P < 0.01, ****P < 0.001, ns: no significance.
The therapeutic efficacy of the drug was further investigated by measuring the IC50 of CUR, PTX, CUR+PTX, and PLGA-CUR-PTX nanoparticles on 4T1 and MCF-7 cells (Table 9). The CI values of CUR+PTX were 0.37 on 4T1 cells and 0.33 on MCF-7 cells. Moreover, the CI values were even lower for PLGA-CUR-PTX nanoparticles, with 0.17 on 4T1 cells and 0.20 on MCF-7 cells, which demonstrated the good synergistic antitumor effect of CUR and PTX. Moreover, CUR and PTX coloaded PLGA nanoparticles had the lowest IC50 values on 4T1 (CUR: 123.7 ng/mL; PTX: 66.7 ng/mL) and MCF-7 (CUR: 109.9 ng/mL; PTX: 59.37 ng/mL) cells, which were similar with the previous report.47 In this study, CUR combined with PTX could decline the IC50 of both CUR and PTX. These results demonstrated that coloading CUR and PTX in PLGA nanoparticles can improve the therapeutic effects and bioavailability of CUR and PTX.
Table 9. IC50 Values for Different Drugs and Formulations on 4T1 and MCF-7 Cells after 48 h of Incubation.
| 4T1 IC50(ng/mL) |
MCF-7 IC50(ng/mL) |
|||||
|---|---|---|---|---|---|---|
| drugs | CUR | PTX | CI50 | CUR | PTX | CI50 |
| CUR | 13,868 | 10,338 | ||||
| PTX | 420.7 | 313.8 | ||||
| CUR+PTX | 275.1 | 148.5 | 0.37 | 180.9 | 97.86 | 0.33 |
| PLGA-CUR-PTX nanoparticles | 123.7 | 66.7 | 0.17 | 109.9 | 59.37 | 0.20 |
4. Conclusions
In this study, Box–Behnken design (BBD) was used to develop and optimize CUR and PTX coloaded PLGA nanoparticles. The influence of the surfactant concentration, PLGA concentration, and the ratio of oil–water on the size, polydispersity index (PDI), and drug encapsulation efficiency were clarified, and the optimum conditions were obtained through the predictive mathematical model, in which the surfactant concentration was 1.5% w/v, the PLGA concentration was 20.18 mg/mL, and the ratio of oil–water was 70% v/v. Under this optimal condition, PLGA-CUR-PTX nanoparticles were successfully produced with a small particle size (99.94 nm) and PDI (0.101) and a high encapsulation efficiency for both CUR (63.53%) and PTX (80.64%). Coloading of CUR and PTX into PLGA nanoparticles could increase the solubility of CUR and PTX in physicochemical conditions and prolong the drug release rate. The optimized PLGA-CUR-PTX nanoparticles produced enhanced cytotoxicity with reduced IC50 values on 4T1 and MCF-7 breast cancer cells compared with the free drug combination group. Thus, the developed PLGA-CUR-PTX nanoparticles hold potential as an alternative to existing tumor chemotherapies.
Acknowledgments
This study was supported by The Science and Technology Planning Project of Sichuan Province, China (nos. 2022NSFSC1429 and 2022JDJQ0061), The National Natural Science Foundation of China (no. 22208269), The Joint Project between Luzhou Municipal People’s Government and Southwest Medical University (no. 2021LZXNYD-J17), and the Foundation of Southwest Medical University (no. 2021ZKZD012).
Author Contributions
⊥ H.H. and Z.L. contributed equally to this work.
The authors declare no competing financial interest.
References
- Sung H.; Ferlay J.; Siegel R. L.; Laversanne M.; Soerjomataram I.; Jemal A.; Bray F. Global Cancer Statistics 2020: Glonocan Estimates of Incidence and Mortality Worldwide for 36 Cancers in 185 Countrie. Ca-Cancer J. Clin. 2021, 209–249. 10.3322/caac.21660. [DOI] [PubMed] [Google Scholar]
- Siegel R. L.; Miller K. D.; Fuchs H. E.; Jemal A. Cancer statistics, 2022. Ca-Cancer J. Clin. 2022, 72, 7–33. 10.3322/caac.21708. [DOI] [PubMed] [Google Scholar]
- Jiang S.; Mou Y.; He H.; Yang D.; Qin L.; Zhang F.; Zhang P. Preparation and Evaluation of Self-Assembly Soluplus-sodium cholate-phospholipid Ternary Mixed Micelles of Docetaxel. Drug Dev. Ind. Pharm. 2019, 45, 1788–1798. 10.1080/03639045.2019.1660365. [DOI] [PubMed] [Google Scholar]
- Rawal S.; Patel M. M. Threatening Cancer with Nanoparticle Aided Combination Oncotherapy. J. Controlled Release 2019, 301, 76–109. 10.1016/j.jconrel.2019.03.015. [DOI] [PubMed] [Google Scholar]
- Abu Samaan T. M.; Samec M.; Liskova A.; Kubatka P.; Büsselberg D. Paclitaxel’s Mechanistic and Clinical Effects on Breast Cancer. Biomolecules 2019, 9, 789. 10.3390/biom9120789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madani F.; Esnaashari S. S.; Bergonzi M. C.; Webster T. J.; Younes H. M.; Khosravani M.; Adabi M. Paclitaxel/Methotrexate Co-Loaded PLGA Nanoparticles in Glioblastoma Treatment: Formulation Development and In Vitro Antitumor Activity Evaluation. Life Sci. 2020, 256, 117943. 10.1016/j.lfs.2020.117943. [DOI] [PubMed] [Google Scholar]
- Ezhilarasan D.; Lakshmi T.; Mallineni S. K. Nano-based Targeted Drug Delivery for Lung Cancer: Therapeutic Avenues and Challenges. Nanomedicine 2022, 10.2217/nnm-2021-0364. [DOI] [PubMed] [Google Scholar]
- Xiang Y.; Guo Z.; Zhu P.; Chen J.; Huang Y. Traditional Chinese Medicine as a Cancer Treatment: Modern Perspectives of Ancient but Advanced Science. Cancer Med. 2019, 8, 1958–1975. 10.1002/cam4.2108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mujokoro B.; Madani F.; Esnaashari S.; Khosravani M.; Adabi M. Combination and Co-Delivery of Methotrexate and Curcumin: Preparation and In Vitro Cytotoxic Investigation on Glioma Cells. J. Pharm. Innovation 2020, 15, 617–626. 10.1007/s12247-019-09406-3. [DOI] [Google Scholar]
- Patra S.; Pradhan B.; Nayak R.; Behera C.; Rout L.; Jena M.; Efferth T.; Bhutia S. K. Chemotherapeutic Efficacy of Curcumin and Resveratrol Against Cancer: Chemoprevention, Chemoprotection, Drug Synergism and Clinical Pharmacokinetics. Semin. Cancer Biol. 2021, 73, 310–320. 10.1016/j.semcancer.2020.10.010. [DOI] [PubMed] [Google Scholar]
- Quispe-Soto E. T.; Calaf G. M. Effect of Curcumin and Paclitaxel on Breast Carcinogenesis. Int. J. Oncol. 2016, 49, 2569–2577. 10.3892/ijo.2016.3741. [DOI] [PubMed] [Google Scholar]
- Wicki A.; Witzigmann D.; Balasubramanian V.; Huwyler J. Nanomedicine in Cancer Therapy: Challenges, Opportunities, and Clinical Applications. J. Controlled Release 2015, 200, 138–157. 10.1016/j.jconrel.2014.12.030. [DOI] [PubMed] [Google Scholar]
- Wang A. Z.; Langer R.; Farokhzad O. C. Nanoparticle Delivery of Cancer Drugs. Annu. Rev. Med. 2012, 63, 185–198. 10.1146/annurev-med-040210-162544. [DOI] [PubMed] [Google Scholar]
- Zhang J.; Wang N.; Li Q.; Zhou Y.; Luan Y. A Two-Pronged Photodynamic Nanodrug to Prevent Metastasis of Basal-Like Breast Cancer. Chem. Commun. 2021, 57, 2305–2308. 10.1039/D0CC08162K. [DOI] [PubMed] [Google Scholar]
- Zhang M.; Qin X.; Xu W.; Wang Y.; Song Y.; Garg S.; Luan Y. Engineering of A Dual-Modal Phototherapeutic Nanoplatform for Single NIR Laser-Triggered Tumor Therapy. J. Colloid Interface Sci. 2021, 594, 493–501. 10.1016/j.jcis.2021.03.050. [DOI] [PubMed] [Google Scholar]
- Zhang M.; Qin X.; Zhao Z.; Du Q.; Li Q.; Jiang Y.; Luan Y. A Self-Amplifying Nanodrug to Manipulate the Janus-Faced Nature of Ferroptosis for Tumor Therapy. Nanoscale Horiz. 2022, 7, 198–210. 10.1039/D1NH00506E. [DOI] [PubMed] [Google Scholar]
- Parveen S.; Misra R.; Sahoo S. K. Nanoparticles: A Boon to Drug Delivery, Therapeutics, Diagnostics and Imaging. Nanomedicine 2012, 8, 147–166. 10.1016/j.nano.2011.05.016. [DOI] [PubMed] [Google Scholar]
- Makadia H. K.; Siegel S. J. Poly Lactic-co-Glycolic Acid (PLGA) as Biodegradable Controlled Drug Delivery Carrier. Polymer 2011, 3, 1377–1397. 10.3390/polym3031377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gagliardi A.; Giuliano E.; Venkateswararao E.; Fresta M.; Bulotta S.; Awasthi V.; Cosco D. Biodegradable Polymeric Nanoparticles for Drug Delivery to Solid Tumors. Front. Pharmacol. 2021, 12, 601626. 10.3389/fphar.2021.601626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mora-Huertas C. E.; Fessi H.; Elaissari A. Influence of Process and Formulation Parameters on the Formation of Submicron Particles by Solvent Displacement and Emulsification-Diffusion Methods Critical Comparison. Adv. Colloid Interface Sci. 2011, 163, 90–122. 10.1016/j.cis.2011.02.005. [DOI] [PubMed] [Google Scholar]
- Singh B.; Kumar R.; Ahuja N. Optimizing Drug Delivery Systems Using Systematic ″Design of Experiments.″ Part I: Fundamental Aspects. Crit. Rev. Ther. Drug Carrier Syst. 2005, 22, 27–105. 10.1615/CritRevTherDrugCarrierSyst.v22.i1.20. [DOI] [PubMed] [Google Scholar]
- Du D.; Zhang X.; Yu K.; Song X.; Shen Y.; Li Y.; Wang F.; Zhifeng S.; Li T. Parameter Screening Study for Optimizing the Static Properties of Nanoparticle-Stabilized CO(2) Foam Based on Orthogonal Experimental Design. ACS Omega 2020, 5, 4014–4023. 10.1021/acsomega.9b03543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh B.; Kapil R.; Nandi M.; Ahuja N. Developing Oral Drug Delivery Systems Using Formulation by Design: Vital Precepts, Retrospect and Prospects. Expert Opin. Drug Delivery 2011, 8, 1341–1360. 10.1517/17425247.2011.605120. [DOI] [PubMed] [Google Scholar]
- Tavares Luiz M.; Santos Rosa Viegas J.; Palma Abriata J.; Viegas F.; Testa Moura de Carvalho Vicentini F.; Lopes Badra Bentley M. V.; Chorilli M.; Maldonado Marchetti J.; Tapia-Blácido D. R. Design of Experiments (DoE) to Develop and to Optimize Nanoparticles as Drug Delivery Systems. Eur. J. Pharm. Biopharm. 2021, 165, 127–148. 10.1016/j.ejpb.2021.05.011. [DOI] [PubMed] [Google Scholar]
- Bezerra M. A.; Santelli R. E.; Oliveira E. P.; Villar L. S.; Escaleira L. A. Response Surface Methodology (RSM) as a Tool for Optimization in Analytical Chemistry. Talanta 2008, 76, 965–977. 10.1016/j.talanta.2008.05.019. [DOI] [PubMed] [Google Scholar]
- Keskin Gündoǧdu T.; Deniz İ.; Çalışkan G.; Şahin E. S.; Azbar N. Experimental Design Methods for Bioengineering Applications. Crit. Rev. Biotechnol. 2016, 36, 368–388. 10.3109/07388551.2014.973014. [DOI] [PubMed] [Google Scholar]
- Shaikh M. V.; Kala M.; Nivsarkar M. Formulation and Optimization of Doxorubicin Loaded Polymeric Nnanoparticles Using Box-Behnken Design: Ex-Vivo Stability and In-Vitro Activity. Eur. J. Pharm. Sci. 2017, 100, 262–272. 10.1016/j.ejps.2017.01.026. [DOI] [PubMed] [Google Scholar]
- Abouelmagd S. A.; Sun B.; Chang A. C.; Ku Y. J.; Yeo Y. Release Kinetics Study of Poorly Water-Soluble Drugs From Nanoparticles: Are We Doing It Right?. Mol. Pharmaceutics 2015, 12, 997–1003. 10.1021/mp500817h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dash S.; Murthy P. N.; Nath L.; Chowdhury P. Kinetic Modeling on Drug Release from Controlled Drug Delivery Systems. Acta Pol Pharm 2010, 67, 217–223. [PubMed] [Google Scholar]
- Bahari Javan N.; Rezaie Shirmard L.; Jafary Omid N.; Akbari Javar H.; Rafiee Tehrani M.; Abedin Dorkoosh F. Preparation, Statistical Optimisation and In Vitro Characterisation of Poly (3-Hydroxybutyrate-co-3-Hydroxyvalerate)/Poly (Lactic-co-Glycolic Acid) Blend Nanoparticles for Prolonged Delivery of Teriparatide. J. Microencapsulation 2016, 33, 460–474. 10.1080/02652048.2016.1208296. [DOI] [PubMed] [Google Scholar]
- Zhang Y.; Huo M.; Zhou J.; Zou A.; Li W.; Yao C.; Xie S. DDSolver: An Add-In Program for Modeling and Comparison of Drug Dissolution Profiles. AAPS J. 2010, 12, 263–271. 10.1208/s12248-010-9185-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chou T. C.; Talalay P. Quantitative Analysis of Dose-Effect Relationships: The Combined Effects of Multiple Drugs or Enzyme Inhibitors. Adv. Enzyme Regul. 1984, 22, 27–55. 10.1016/0065-2571(84)90007-4. [DOI] [PubMed] [Google Scholar]
- Wang J.; Sui M.; Fan W. Nanoparticles for Tumor Targeted Therapies and Their Pharmacokinetics. Curr. Drug Metab. 2010, 11, 129–141. 10.2174/138920010791110827. [DOI] [PubMed] [Google Scholar]
- Avadhani K. S.; Manikkath J.; Tiwari M.; Chandrasekhar M.; Godavarthi A.; Vidya S. M.; Hariharapura R. C.; Kalthur G.; Udupa N.; Mutalik S. Skin Delivery of Epigallocatechin-3-Gallate (EGCG) and Hyaluronic Acid Loaded Nano-Transfersomes for Antioxidant and Anti-Aging Effects in UV Radiation Induced Skin Damage. Drug Delivery 2017, 24, 61–74. 10.1080/10717544.2016.1228718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arora D.; Khurana B.; Nanda S. DoE Directed Optimization, Development and Evaluation of Resveratrol Loaded Ultradeformable Vesicular Cream for Topical Antioxidant Benefits. Drug Dev. Ind. Pharm. 2020, 46, 227–235. 10.1080/03639045.2020.1716373. [DOI] [PubMed] [Google Scholar]
- Ali A.; Hassan A.; Eissa E.; Aboud H. Response Surface Optimization of Ultra-Elastic Nanovesicles Loaded with Deflazacort Tailored for Transdermal Delivery: Accentuated Bioavailability and Anti-Inflammatory Efficacy. Int. J. Nanomed. 2021, 16, 591–607. 10.2147/IJN.S276330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moolakkadath T.; Aqil M.; Ahad A.; Imam S. S.; Iqbal B.; Sultana Y.; Mujeeb M.; Iqbal Z. Development of Transethosomes Formulation for Dermal Fisetin Delivery: Box-Behnken Design, Optimization, In Vitro Skin Penetration, Vesicles-Skin Interaction and Dermatokinetic Studies. Artif. Cells, Nanomed., Biotechnol. 2018, 46, 755–765. 10.1080/21691401.2018.1469025. [DOI] [PubMed] [Google Scholar]
- Arora D.; Khurana B.; Nanda S. Statistical Development and In Vivo Evaluation of Resveratrol-Loaded Topical Gel Containing Deformable Vesicles for a Significant Reduction in Photo-Induced Skin Aging and Oxidative Stress. Drug Dev. Ind. Pharm. 2020, 46, 1898–1910. 10.1080/03639045.2020.1826507. [DOI] [PubMed] [Google Scholar]
- Patel R. R.; Chaurasia S.; Khan G.; Chaubey P.; Kumar N.; Mishra B. Cromolyn Sodium Encapsulated PLGA Nanoparticles: An Attempt to Improve Intestinal Permeation. Int. J. Biol. Macromol. 2016, 83, 249–258. 10.1016/j.ijbiomac.2015.11.084. [DOI] [PubMed] [Google Scholar]
- Elsewedy H.; Dhubiab B.; Mahdy M.; Elnahas H. Development, Optimization, and Evaluation of PEGylated Brucine-Loaded PLGA Nanoparticles. Drug Delivery 2020, 27, 1134–1146. 10.1080/10717544.2020.1797237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oseni B.; Azubuike C.; Okubanjo O.; Igwilo C.; Panyam J. Encapsulation of Andrographolide in Poly(Lactide-Co-Glycolide) Nanoparticles: Formulation Optimization and In Vitro Efficacy Studies. Front. Bioeng. Biotechnol. 2021, 9, 639409. 10.3389/fbioe.2021.639409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- El Zaafarany G.; Awad G.; Holayel S.; Mortada N. Role of Edge Activators and Surface Charge in Developing Ultradeformable Vesicles with Enhanced Skin Delivery. Int. J. Pharm. 2010, 397, 164–172. 10.1016/j.ijpharm.2010.06.034. [DOI] [PubMed] [Google Scholar]
- Davis M.; Chen Z.; Shin D. Nanoparticle Therapeutics: an Emerging Treatment Modality for Cancer. Nanosci. Technol. 2008, 7, 771–782. 10.1038/nrd2614. [DOI] [PubMed] [Google Scholar]
- Sharma D.; Maheshwari D.; Philip G.; Rana R.; Bhatia S.; Singh M.; Gabrani R.; Sharma S. K.; Ali J.; Sharma R. K.; Dang S. Formulation and Optimization of Polymeric Nanoparticles for Intranasal Delivery of Lorazepam Using Box-Behnken Design: In Vitro and In Vivo Evaluation. BioMed Res. Int. 2014, 2014, 156010. 10.1155/2014/156010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghasemian E.; Vatanara A.; Rouholamini Najafabadi A.; Rouini M. R.; Gilani K.; Darabi M. Preparation, Characterization and Optimization of Sildenafil Citrate Loaded PLGA Nanoparticles by Statistical Factorial Design. Daru, J. Pharm. Sci. 2013, 21, 68. 10.1186/2008-2231-21-68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lao L. L.; Peppas N. A.; Boey F. Y.; Venkatraman S. S. Modeling of Drug Release From Bulk-Degrading Polymers. Int. J. Pharm. 2011, 418, 28–41. 10.1016/j.ijpharm.2010.12.020. [DOI] [PubMed] [Google Scholar]
- Kim K. R.; You S. J.; Kim H. J.; Yang D. H.; Chun H. J.; Lee D.; Khang G. Theranostic Potential of Biodegradable Polymeric Nanoparticles with Paclitaxel and Curcumin Against Breast Carcinoma. Biomater. Sci. 2021, 9, 3750–3761. 10.1039/D1BM00370D. [DOI] [PubMed] [Google Scholar]