Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Dec 22;39(1):12–19. doi: 10.1021/acs.langmuir.2c02578

Role of Nanoparticles in Nanofluid Droplet Impact on Solid Surfaces

Yunus Tansu Aksoy †, Lingyue Liu ‡, Mohammad Abboud §, Maria Rosaria Vetrano †, Erin Koos ‡,*
PMCID: PMC9835883  PMID: 36548220

Abstract

graphic file with name la2c02578_0011.jpg

Splashing of a liquid droplet onto a substrate, while ubiquitous, sits at the intersection of several key fluid mechanical regions. Typically, this problem is often simplified to the transition between spreading and splashing, even for splashing on complex surfaces. Recently, there has been increased interest in using not just pure liquids but also nanofluids in applications such as spray cooling. While the addition of a few percent of nanoparticles to a Newtonian fluid does not change its apparent viscosity, the influence of the nanoparticles on the splashing transition is pronounced. We often view splashing in terms of fluid mechanics where a simple material is subjected to a complex flow and the fluid can be simply characterized by a Newtonian viscosity. For nanofluids, we have an apparently simple material in a complex flow, but the results show that the impact of the particles is nontrivial. This implies that we must now combine some of the insights we obtain from studying the rheological properties of nanosuspensions with this already complex problem.

Nanofluid Droplet Splashing

The result from the impact of a droplet on a solid substrate can be categorized as spreading, splashing, or bouncing. The specific case arises from the competition between inertia, interfacial tension, and viscous forces.1,2 These can be decomposed into the influence of several parameters: viscosity η, density ρ, surface tension σ, impact speed u0, and droplet diameter D0. In other words, the splashing threshold is characterized by Weber (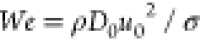Inline graphic) and Reynolds (Re = ρD0u0/η) numbers incorporating inertia, viscous stress, and surface tension. During the droplet impact, an ultrathin air film is trapped below an expanding lamella.3 Above a critical Weber number, the lamella breaks up due to the separation from the solid surface by the ambient air. Since this air film is thinner than the mean free path of air molecules, it generates a strong stress that initiate the Kelvin–Helmholtz instabilities. The lamella lift-off mechanism is explained by Mandre and Brenner4 as follows: Once the gas film ruptures, the liquid touches the substrate, then the lamella lifts off and leads to a crown. Surface wettability affects the splashing condition5 as well as the environment gas pressure since splashing can be suppressed under vacuum.6

In spite of many applications of complex fluids such as nanofluids, their effects on splashing only recently emerged. Aksoy et al.7 studied the influence of nanoparticle concentration on the splashing condition: Even a small amount of nanoparticles added to fluids affects the splashing condition. Accordingly, higher lamella spreading speed and earlier lifting than its base liquid was observed in the presence of nanofluids even at a low weight concentration as small as 0.01 wt % (Cw = 0.01 wt %). The earlier wetting of the substrate, due to the presence of nanoparticles in the liquid that modifies the contact angle, results in a larger momentum in the bulk liquid, thus pumping the fluid into the lamella. They also observed a faster lamella spreading speed which is consistent with this proposed mechanism. However, this might also depend on the nanoparticle size and type as well as the surface temperature as an inverse effect is observed by Liu et al.8 In their study, they detect drops in both spreading and receding speeds with increasing silver nanoparticle concentration up to 10 vol %.

The spreading to splashing transition, which possesses nonmonotonic behavior at different viscosity regimes, is often described by a two-piece function5,9 as shown in Figure 1a.

graphic file with name la2c02578_m002.jpg 1

where Wecrit represents the critical We number for the splashing threshold, K1 and K2 are the splashing constants, and β1 and β2 take into account the impact of viscosity. Since the presence of nanoparticles in the fluid modifies the splashing condition (the evolution of the constants is illustrated in Figure 1b), eq 1 is updated by Aksoy et al.,7 including the nanoparticle concentration Cw along with two additional constants A1 and A2:7

graphic file with name la2c02578_m003.jpg 2

Figure 1.

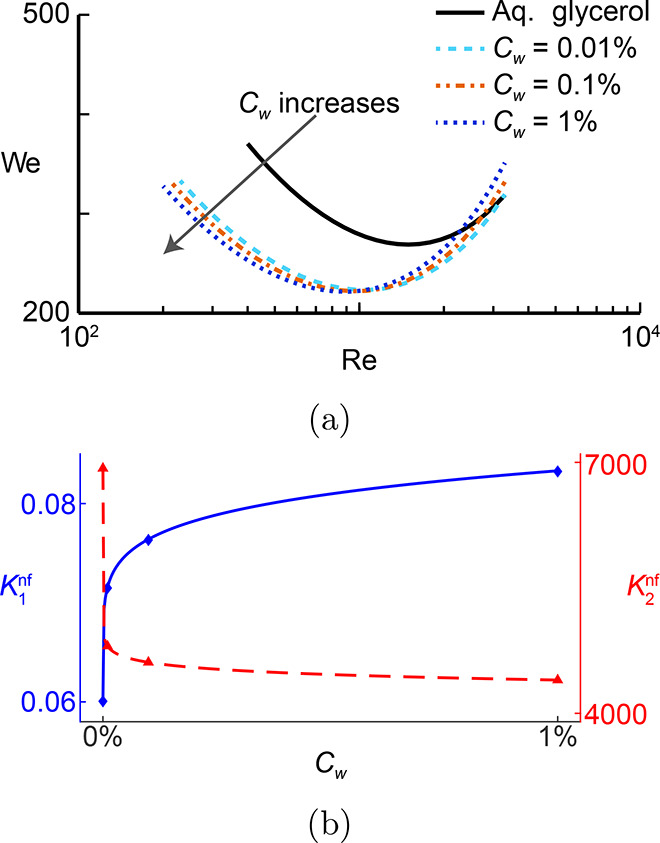
Figure 1

Open in a new tab

(a) Effect of nanoparticles on splashing on a We–Re map7 and (b) evolution of the constants in eq 1 with nanoparticle loading. Adapted with permission from ref (7). Copyright 2022 Elsevier.

This correlation was also validated for the experiments of Thoraval et al.10 for 10 nm silver nanoparticle dispersions at 52 wt %. While a change in the splashing behavior might be expected at such a high loading, the effect was also evident for the low loading of Cw = 0.01 wt %. The effect of the particles is highly nonmonotonic with fitting exponents B1 = 0.1532 and B2 = 0.038, implying that the greatest change in the splashing threshold occurs at the lowest particle concentrations.7 This is an unexpected result since any change in the fluid viscosity and interfacial tension at these low concentration is small, on the order of the measurement error.

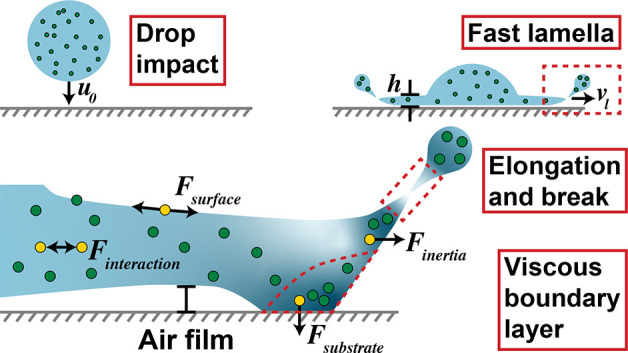
In Role of Nanoparticles, we take a closer look into each stage of splashing, giving our opinion as to where the particles play a critical role. This is summarized in the schematic of Figure 2. During the initial collision of the droplet with the substrate where the lamella forms and begins to spread (Figure 2a), the viscosity of the fluid and the surface tension play a critical role. Here, we must also consider all possible rheological changes to the fluid, such as shear thinning. As the lamella continues to spread, particle–substrate interactions may play a role. Finally, the lamella elongates and breaks into the final splash (Figure 2b). The nanoparticles can play a critical role in these later stages.

Figure 2.

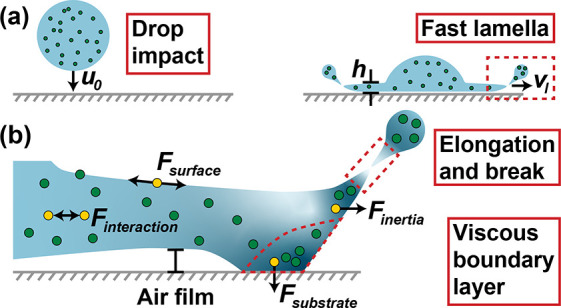
Figure 2

Open in a new tab

(a) Schematic drawing of droplet contacting substrate. The impact velocity is u0, the front expanding velocity is vl, and the thickness of the liquid film front is h. The expanding front is highlighted with red dashed lines, and (b) shows a magnified schematic of the expanding front. Key differences caused by the presence of nanoparticles are represented by yellow spheres and labels. The nanoparticle volume fraction, ranging from dilute to more concentrated, are indicated via a color gradient (light to dark, respectively). The viscous boundary layer and droplet breakup tip marked are additionally marked in red dashed lines.

Role of Nanoparticles

In the aforementioned experiments, nanofluids have shown fundamental different spreading and splashing mechanisms in comparison to their base liquids.7,10,11 The presence of nanoparticles has an impact not only on the base fluid characteristics but also on the particle interactions, which is crucial to the nanofluid flow. These parameters are often simplified into an effective viscosity and surface tension for the nanofluid so that they can be incorporated into the two-piece function shown in eq 2. There are two main issues with such a simplification, however. First, these parameters are often measured at quasi-static conditions and fail to account for changes at the high velocities present during droplet spreading and splashing. Second, the changes in viscoelastic properties of the fluids such as the interaction between the particles and the substrate or the air–liquid interface as well as changes in the elongational properties of the fluid are ignored. As described below and highlighted in Figure 2, these changes can have a pronounced influence on the rheological response and likely contribute to the observed change in the spreading–splashing transition.

Viscosity and Rheological Measurement

In the sparse suspensions present in most nanofluids, the inclusion of nanoparticles is expected to only have a minimal effect on the viscosity and it is often assumed that nanofluids behave nearly identically to their base fluids.12 Caution should be used, however, since the particles are stabilized via repulsive electrostatic or steric interactions in real systems, which increases the effective volume fraction of the particles and hence the viscosity of the system. Alternatively, attractive interactions, such as the van der Waals interactions, result in the formation of loose flocs with a higher effective volume fraction (and hence higher viscosity). Even for unstabilized nanoparticles, densely packed layers of water molecules have been found on the particle surfaces, as evidenced by their higher density.13 These varying interactions and their strength give rise to the contradictory nature of reported rheological behaviors. Both Newtonian and non-Newtonian behaviors have been reported, even for samples with same base fluid and nanoparticles (e.g., Al2O3/H2O).13 For dilute nanofluids, it is often assumed that their rheological behaviors are Newtonian with no internal microstructures.13 Collisions caused by Brownian motion or flow-induced collisions can overcome a weak repulsive barrier and give rise to a certain degree of aggregation with a resultant change in the viscosity.14,15

The difference between diffusive and adhesive dynamics is captured by the Péclet number

graphic file with name la2c02578_m004.jpg 3

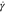where Inline graphic is the shear rate and D is the diffusion coefficient. For unstabilized suspensions, shear thinning behavior is present due to the transition from a Brownian-dominated response at low shear rates to a hydrodynamic regime at high shear rates. This transition occurs at a Péclet number around unity, corresponding to shear rates of 103 s–1, for 100 nm particles in water.16 In the hydrodynamic regime, while the arrangement of particles changes, the concentration does not. The shear thinning behavior is more pronounced for flocs that break at high shear rates (often greater than 103 s–1 even for van der Waals interactions). These high shear rates are often not captured in rheological experiments, but a 10 m/s advancing speed of the lamella and a thickness of 100 μm result in a shear rate that can easily reach 105 s–1.

At high shear rates, the shear thinning behavior is further exasperated due to the high Stokes number St = (τpu0)/dp > 1, where the particles no longer follow the flow, leading to a concentration gradient.12 As observed by Aksoy et al.,7 the splashing behavior was initialized earlier by the presence of nanoparticles and the spreading velocity vl was increased from 5.2 ± 0.2 m/s without particles to 7.3 ± 0.3 m/s with 0.1 vol % particles. This increase in the Stokes number means that the particles would be less likely to follow the spreading of the lamella in the nanofluid, leading to a concentration gradient. As shown in Figure 2b, we predict this gradient to be more pronounced at the edge of the viscous boundary layer due to the high shear rate and particle–substrate interaction and at the tip of the expanding front due to the high elongational rate. The direct influences of the concentration gradients and shear thinning behavior on splashing, however, have not been studied.

Wetting and Particle–Interface Interactions

During the splashing, air can be trapped by the droplet in two regions: at the droplet center and at the expanding front, as drawn in Figure 2. The ultrathin air film of thickness 10–100 nm is mainly responsible for the splashing.3 The stress caused by the air flow underneath the liquid film is 10 times larger than the Bernoulli stress of the air stream on top, which triggers film instability. As observed by Aksoy et al.,7 the splashing behavior is initialized earlier by the presence of nanoparticles and the lamella is observed to lift earlier for the nanofluids than for pure fluids, implying that the wetting of the substrate by the lamella occurs earlier. This wetting is affected by the interaction between particles and substrates in the viscous boundary layer, as shown in Figure 2b. The suddenly decelerated vl at the contact region due to the no-slip condition creates a viscous boundary layer where the nanoparticles in the fluid can be irreversibly adsorbed to the substrate due to van der Waals force. This adsorption, causing the particle concentration to increase as indicated by the dark blue color gradient in Figure 2b, has clear implications for the viscosity and other nanofluid material properties. A concentration gradient can further increase the local viscosity gradient, which promotes the elongation of the lamella tip. The reduction in local nanoparticle concentration can decrease the nanofluid viscosity, along with the Kelvin–Helmholtz instability force, leading to favorable separation of the droplet (onset of splashing).4

The contact angle of the nanofluid against the substrate plays a critical role in both the effective size of the viscous boundary layer and the lift off of the lamella leading to break. Even though the contact time between particles and substrate during splashing experiments is short, the adsorption of particles to the substrate can change the dynamic wetting. The influence of the nanoparticles on the static contact angle alone is complex, and both increases and decreases have been reported.17,18 Part of the reason for these conflicting reports is the complex particle–substrate, particle–fluid, and particle–particle interactions. This conclusion is reinforced by the observation that smaller particles have a larger effect on the static contact angle.18 Vafaei et al.,17 for instance, observed an increase in the contact angle from θ ≈ 0° to θ > 40° for nanoparticle concentrations as low as 3 × 10–6. This change is due to particles in the confined region of the three-phase contact line where a disordered, fluid-like bulk can exhibit solid-like crystalline arrangements of particles with enhanced spreading dynamics.19

The presence of the particles at the three-phase contact line can also result in pinning of particles at the substrate, leading to patterned surfaces.20 In the case of droplet spreading, the lamella inertia carries the fluid past this contact point, which should enhance splashing. The discussed effects can become more pronounced when nanoparticles are treated to make them hydrophobic. As they become more hydrophobic, they migrate to the three-phase contact lines and reinforce the particle concentration behavior at the viscous boundary layer.21 Hu et al.11 designed experiments to investigate the effects of the wettability properties of the nanoparticles on droplet dynamics during the receding phase, as shown in Figure 3a. Although the effect of hydrophilic particles is marginal, hydrophobic particles significantly alter the contact line pinning effect and receding breakup behavior. In fact, the maximum retraction height and vertically oscillatory relaxation time decrease due to hydrophobic particles. The possible reasons for these phenomena are that the adsorption and deposition of hydrophobic nanoparticles around the three-phase contact line give a rise to the surface roughness and the particle concentration, thus locally increasing the viscosity around that region as well. At the same time, particle deposition at the triple line can change the wettability of the local surface and bring the temporary balance of interfacial tensions at the pinning points, while the disturbance of capillary oscillation can break the balance and lead to depinning.21 This work provides a new direction to pursue for suppressing the vibration and retraction of droplets as well as offering a powerful means of exploring the mechanism of particle-induced changes to the dynamics of droplet impacts.11

Figure 3.

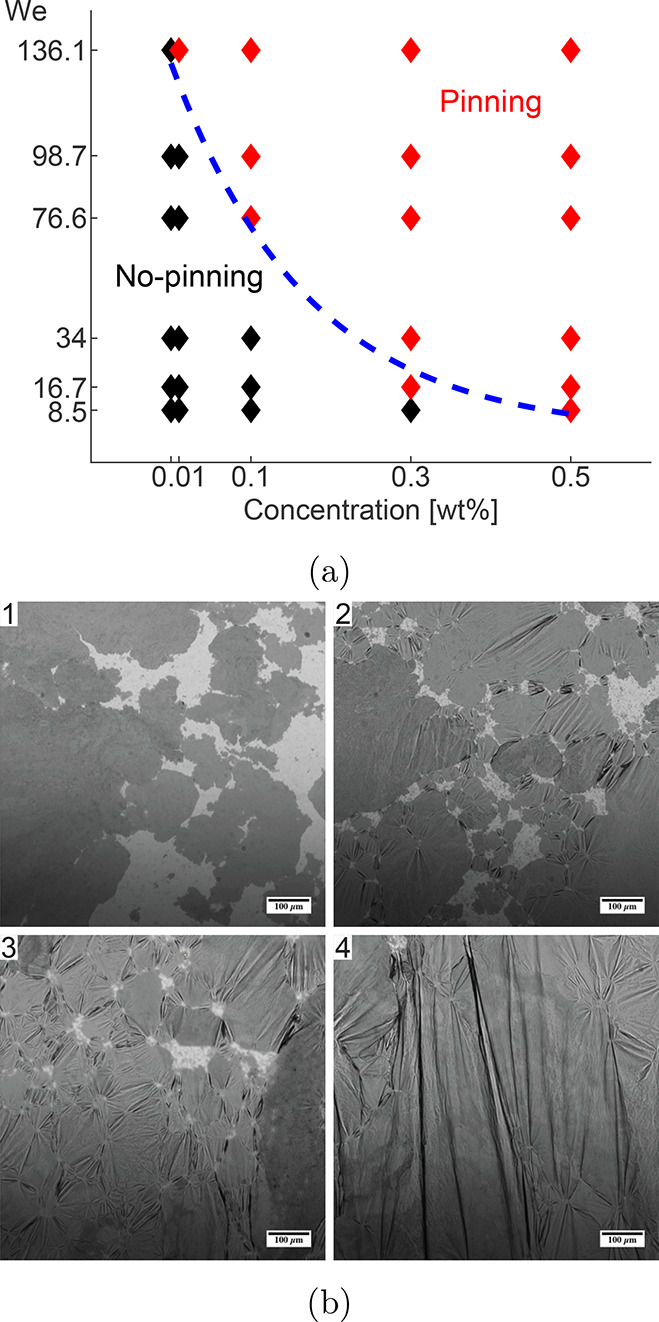
Figure 3

Open in a new tab

(a) Effect of nanoparticles on pinning of a receding droplet.11 (b) Microscopic images of carbon black particles at an oil–water interface showing the increase in wrinkling with increasing surface compression.22 (a) Adapted with permission from ref (11). Copyright 2021 Elsevier. (b) Adapted with permission from ref (22). Copyright 2013 Royal Society of Chemistry.

Naturally, the wetting behavior of the nanofluid is also influenced by the interactions at the air–water interface. The influence of nanoparticles on the surface tension has been debated with conflicting reports.11,13,23,24 Hydrophilic particles are commonly believed to have no interfacial activity when dispersed in aqueous base liquids.11 Even though hydrophobic nanoparticles tend not to stay at the interfaces, Lu et al. hypothesized that the attraction forces between them and water molecules near the surface reduce the intermolecular spacing, thus increasing the nanofluid surface tension.13 Hydrophobic nanoparticles, on the contrary, tend to gather at the interfaces; the interparticle repulsive forces are reported to cause the increase in water molecule spacing, thus reducing the surface tension.13 Contradictory to that opinion, Chinnam et al. have reported decreases in surface tension with various hydrophilic nanoparticles; the decreases are proportional to the increases in nanoparticle volume fraction and temperature.23 While conflicting reports of nanoparticles have been reported, we do not believe that the static surface tension is affected by the presence of the particle, particularly at the low volume fractions used by Aksoy et al.7 Careful measurements of the interfacial tension, however, can be hindered by the dynamics of adsorption.

For nanometer-sized particles, the energy of particle adsorption, on the order of a few kBT, is comparable to the thermal energy. The resulting spatial fluctuation increases the instability of nanoparticles at interfaces, in which case the nanoparticle wettability plays an important role.25 Adsorption of nanoparticles to the air–water interface can also increase the elasticity of the interface, leading to elastic, but brittle, surfaces that wrinkle upon compression,22 as shown in Figure 3b. This rigidity is often ignored in nanofluid splashing experiments, but its effect should be pronounced. In experiments with surfactants, Song et al.26 found a dependence of splashing on the dynamic surface tension, a measure of the surfactants’ rate of saturation. When the surfactant molecules could not replenish the air–water interface, the drop was deformed and the receding drop exhibited a high degree of fingering. Nanoparticles can also lead to a temporal change in the surface coverage, leading to similar effects in nanofluids. Such changes are not captured by static measurements of the surface tension or contact angle and necessitate additional experiments to determine the role of these time-varying behaviors on the splashing.

Elongation and Break

The final stage of splashing is the elongation and breakup of the filament into smaller droplets, as shown in Figure 2b. With the exception of ideal, Newtonian fluids, the elongational viscosity and rate dependent behavior of the fluid to an elongational flow field cannot be captured through the shear viscosity. While this final stage can be observed directly from the splashing images, it is more thoroughly characterized by separate stretching experiments. The standard elongational characterization methods are often limited to the commercially available devices such as the Capillary Breakup Extensional Rheometer (CaBER)27 and Cambridge Trimaster28 and are interpreted using simplistic fluid mechanics models that do not accurately simulate the conditions within droplet spreading and splashing.

Nevertheless, there exist several advanced liquid bridge stretching techniques that account for the advanced fluid flow mechanics of the liquid stretching, such as the ultrafast stretching of thin films into filaments, stretching between nonparallel plates, stretching between a sphere and a plate, stretching between a cone and a plate, stretching between two spheres, stretching between three spheres, cavitation and fingering instability upon stretching, single droplet dripping, dripping on a substrate, stretching in continuous jetting, and liquid-in-liquid breakup.29−35 While these methods provide a clearer insight into the elongation and breakup of a single droplet, they are predominantly performed on simple liquids and are traditionally not performed with the intention of characterizing the rheological behavior of complex liquids. Figure 4 shows high-speed-camera images of the moment right before pinch-off during dripping onto substrate demonstrating how elongation and breakup of fluids differs depending on the fluid class (such as inviscid (I), viscous (V), viscoelastic (VE), and power law (PL) fluids).36 Moreover, there has been an increasing interest in colloidal probe atomic force microscopy (CPAFM), introduced independently by Ducker et al.37 and Butt,38 allowing the direct characterization of micro- and nanoscale capillary liquid bridges. So far, the CPAFM method has been used to investigate the influences of roughness, deformability, hydrophilicity, humidity, morphology, and quantity on the capillary behavior at the nanoscale.39 CPAFM could be a better tool to investigate the breakup of microscale droplets which are analogous to the ones that form at the edges of the lamella upon splashing.

Figure 4.

Figure 4

Open in a new tab

Necking of capillary bridges of various classes of complex liquids, such as inviscid (I), viscous (V), viscoelastic (VE), and power law (PL) fluids, at moment right before pinch-off during dripping-onto-substrate rheometry. Scale bar corresponds to 0.5 mm. Reproduced with permission from ref (36). Copyright 2017 Royal Society of Chemistry.

Like the behavior in simple shear, introducing solid particles to a viscous solution affects the suspension stretching depending on the type, size, shape, and concentration of the particles. For the case of a moderate concentration of microparticles, the suspension initially behaves as a viscous liquid with dynamics determined by the bulk viscosity.40 For a fairly slow stretching, the bridge behavior during the initial stage of thinning is similar to a Newtonian liquid with a comparable viscosity and surface tension.41 When the liquid bridge decreases in width to about 5 times the microparticle diameter, its behavior is dominated no longer by the bulk microsuspension properties but by the local properties arising due to the variations of local particle concentration.40 Near pinch-off, the bridge shape becomes more irregular and an accelerated breakup occurs. As the thinning rate increases, particles migrate away from the necking area and this leads to a low viscosity Newtonian liquid breakup localized at the breakup region that is virtually unaffected by the microparticles. This accelerated thinning behavior was accurately modeled using a multiple stage one-dimensional model.42 The effects of microparticle size and concentration on the properties of the final pure liquid thread were later quantified and analyzed. The typical resulting stages of a microsuspension pinch-off are summarized in Figure 5.43 Similar results were obtained for different microsuspensions such as lycopodium grains and polytetrafluoroethylene by other researchers.44

Figure 5.

Figure 5

Open in a new tab

Typical microsuspension near pinch-off. Reproduced with permission from ref (43). Copyright 2015 AIP Publishing.

Unlike the case of microsuspensions, the addition of nanoparticles does not seem to have a generally agreed upon theory describing their effect on the elongation and breakup. The literature about stretching of nanosuspensions is scarce and divergent. The current general understanding is that at very low concentration suspensions of spherical nanoparticles have an elongation and breakup behavior similar to that of Newtonian fluids.45 On the other hand, denser hard-sphere glass colloids of particle size in the range 100–700 nm have shown a Newtonian fluid response for lower stretching speeds but exhibited a thickening behavior as the strain rate was increased, leading to a solid fracture with a large degree of dilatancy and granulation.46 Moreover, 12 nm hydrophilic fumed silica nanoparticles dispersed in an aqueous poly(ethylene oxide) solution have shown a strain hardening behavior that is qualitatively similar to thickening at a higher particle volume fraction.47 In addition, recent research on the extensional magnetorheology of ferrofluids containing 10 nm iron oxide nanoparticles–magnetite (Fe3O4) have shown that the application of a magnetic field parallel to the direction of the flow during CaBER experiments increases the extensional viscosity of the ferrofluid and eventually their breakup time, where the effect is more pronounced for higher magnetic saturation, magnetic susceptibility, and volume fraction of the nanoparticles in the ferrofluid.45,48 It is worth mentioning that similar results were obtained using human blood analogue fluids loaded with larger micrometer-sized magnetic particles.49

Research on the effect of nanoparticle stiffness on the extensional viscosity, using rod-like soft nanoparticle nanosuspensions, has concluded that the extensional viscosity is higher in flexible nanoparticles because they can arrange in complex structures such as hairpins.50 Other CaBER experiments of suspensions containing nonspherical nanomaterials such as one-dimensional and two-dimensional nanomaterials have also been performed. For instance, suspensions containing pretreated carbon nanotubes (CNTs) suspended within an epoxy resin showed an enhanced extensional viscosity due to the alignment of CNTs in the flow direction, while the addition of untreated CNTs led to local fluctuations in the diameter of the bridge and irregularities in its outer surface profile leading to a more abrupt breakup.51 CaBER experiments of graphene oxide aqueous solutions have shown a high sensitivity to deformation history, a high dependence on initial experimental conditions, and a tendency of graphene oxide flakes to migrate away from the necking area near pinch-off, while the suspension maintained a power law fluid behavior for a wide range of concentrations.52

Moving Forward

The splashing of nanoparticle-laden fluids is an area of research that is growing in importance due to heat transfer and other applications. This research sits at the intersection of fluid mechanics, colloidal science, and rheology. The underlying mechanism of splashing and the drastic effect of nanoparticles on the determination of splashing transition conditions are not yet well-understood and represent a promising area for researchers in these areas to cooperate. Indeed, it is the opinion of the authors that true progress in this field will not be made without such interdisciplinary discussions.

Since the onset of splashing in fluids is caused by the Kelvin–Helmholtz instabilities at the interface between the trapped air film and spreading lamella, the impact of the nanofluids on the size and the shape of the expanding lamella should be observed with higher resolution imaging techniques. In particular, efforts should be made to determine the location and movement of the nanoparticles. If, as we hypothesize, there is a gradient in the nanoparticle concentration, this should be made apparent through the use of (fluorescently) labeled (tracer) particles. Adding particles as tracers is typically used in the application particle image velocimetry techniques, which might possess a possible pitfall in the case of tracking the splashing in fluids without nanoparticles. The behavior of the gas film beneath the lamella should also be investigated more closely. The modification of the splashing transition condition could be due to an advanced bridging between the solid and liquid due to the presence of nanoparticles in the vicinity of the liquid/gas interface. This could possibly be investigated using interferometry, total internal refraction, or other techniques. This may mean that other shapes of substrates must be employed to better observe the lamella and air film.

The effect of the nanoparticles should be studied using differently sized particles, including non-Brownian particles, and differently shaped particles should be conducted in order to better understand the limitation of the nanoparticle effect on splashing. Although the different nanoparticle shapes such as cylindrical-like or even irregular and clumpy shapes still cause a decrease in the contact angle,11 their final effect on splashing is still unknown. The interaction between the particles and interfaces can also be modified using a combination of particle or substrate functionalization and adjustments to the bulk liquid (e.g., salinity, polarity). Finally, the volume fraction of the particles, especially in the sparse region, should be varied.

In order to clarify this phenomenon, there is a strong need to combine the fields of rheology and fluid mechanics since the possible reasons for the observed splashing transition are expected to be local. This means that the role of the nanoparticles at each stage of splashing must be broken down, as it was done here, and directly tested. This means that the non-Newtonian characteristics of the nanofluids should be investigated at high velocities and shear rates as well as under elongation. While the tools already exist to investigate the shear or elongational properties of nanofluids at low shear or stretching rates, these instruments are typically at rates several orders of magnitude lower than in the splashing experiment. This means that new apparatuses will need to be developed to properly capture the role of the nanoparticles. Naturally, simplifications in geometry will need to be made in order to accommodate these high rates. Since the nanofluid stability is one of the most significant problems, the measurement techniques should be applied in situ as much as possible, e.g., stability monitoring as proposed by Eneren et al.53

Finally, multiscale computational models can be used to confirm the changes associated with the nanoparticles on the splashing. For instance, molecular dynamics simulations of wetting kinetics can be carried out for a range of interactions. The wetting kinetics and the impact of nanoparticles on it could be simulated assuming nanosized droplets containing a limited number of nanoparticles and periodic boundary conditions. The nanoparticle interactions and their position in the simulation would give hints on the occurrence of anticipated wetting and modified splashing conditions. These could then be incorporated into better modeling of the viscous dissipation term and evaluation of the competitive forces, as in Aksoy et al.2

Acknowledgments

This work was supported by Interne Fondsen KU Leuven/Internal Funds KU Leuven (C24/18/057) in addition to support from the European Union’s Horizon 2020 research and innovation program under Marie Skłodowska-Curie Grant Agreement No. 955612 (nanoPaInt).

Biographies

graphic file with name la2c02578_0001.jpg

Yunus Tansu Aksoy has received his M.S. degree in aerospace engineering in 2015 from METU (Turkey). He completed his research master degree in 2018 at the von Karman Institute for Fluid Dynamics (Belgium). He is currently working on his Ph.D. thesis at the Department of Mechanical Engineering at KU Leuven (Belgium). His current research mainly focuses on nanofluid droplet spreading, splashing, and heat transfer.

graphic file with name la2c02578_0002.jpg

Lingyue Liu received his M.S. and B.S. degrees (2021 and 2019) in chemical and process engineering from Karlsruhe Institute of Technology (Germany), specializing in applied rheology and product design. He is currently working as a Ph.D. student in the Department of Chemical Engineering at KU Leuven (Belgium) with the guidance of Prof. Erin Koos. His research interests include nanofluids, capillary suspensions, and porous ceramic materials.

graphic file with name la2c02578_0003.jpg

Mohammad Abboud received his M.S. in micro- and nanotechnology in 2019 from METU (Turkey). His thesis was about the micromechanical characterization of nanomaterials. He is currently working on his Ph.D. thesis at the Institute of Fluid Mechanics and Aerodynamics at TU Darmstadt (Germany). His current research mainly focuses on the splashing, elongation, and breakup of nanosuspension droplets and liquid bridges under fast impact and stretching conditions.

graphic file with name la2c02578_0004.jpg

Maria Rosaria Vetrano received a Ph.D. in applied sciences at Université Libre de Bruxelles (Belgium) in 2006. From 2007 to 2012, she held the position of senior research engineer at the von Karman Institute for Fluid Dynamics (Belgium). In 2012 she applied there successfully for a professorship vacancy, and in 2015 she became an associate professor. Since 2017 she has been an associate professor in the Faculty of Engineering Science, Department of Mechanical Engineering, and she is the head of the Heat and Mass Transfer Group at KU Leuven. Her research is focused on the investigation of two-phase flow phenomena taking place at the micro- and nanoscale via the use of innovative nonintrusive measurement techniques.

graphic file with name la2c02578_0005.jpg

Erin Koos obtained her Ph.D. in mechanical engineering from the California Institute of Technology (USA). She was a postdoctoral researcher and then an independent group leader at the Karlsruhe Institute of Technology (Germany). She is a professor in the Department of Chemical Engineering of KU Leuven (Belgium) and head of the section Soft Matter, Rheology and Technology. Her research group studies the rheology, stability, and microstructure of suspensions, concentrating on systems with particle gel networks. The structure of these networks can then be used and tuned for the intelligent design of new materials.

The authors declare no competing financial interest.

References

  1. Aksoy Y. T.; Zhu Y.; Eneren P.; Koos E.; Vetrano M. R. The impact of nanofluids on droplet/spray cooling of a heated surface: A critical review. Energies 2021, 14, 80. 10.3390/en14010080. [DOI] [Google Scholar]
  2. Aksoy Y. T.; Eneren P.; Koos E.; Vetrano M. R. Spreading of a droplet impacting on a smooth flat surface: How liquid viscosity influences the maximum spreading time and spreading ratio. Phys. Fluids 2022, 34, 042106. 10.1063/5.0086050. [DOI] [Google Scholar]
  3. Liu Y.; Tan P.; Xu L. Kelvin–Helmholtz instability in an ultrathin air film causes drop splashing on smooth surfaces. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, 3280–3284. 10.1073/pnas.1417718112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Mandre S.; Brenner M. P. The mechanism of a splash on a dry solid surface. J. Fluid Mech. 2012, 690, 148–172. 10.1017/jfm.2011.415. [DOI] [Google Scholar]
  5. Almohammadi H.; Amirfazli A. Droplet impact: Viscosity and wettability effects on splashing. J. Colloid Interface Sci. 2019, 553, 22–30. 10.1016/j.jcis.2019.05.101. [DOI] [PubMed] [Google Scholar]
  6. Xu L.; Zhang W. W.; Nagel S. R. Drop Splashing on a Dry Smooth Surface. Phys. Rev. Lett. 2005, 94, 184505. 10.1103/PhysRevLett.94.184505. [DOI] [PubMed] [Google Scholar]
  7. Aksoy Y.; Eneren P.; Koos E.; Vetrano M. Spreading-splashing transition of nanofluid droplets on a smooth flat surface. J. Colloid Interface Sci. 2022, 606, 434–443. 10.1016/j.jcis.2021.07.157. [DOI] [PubMed] [Google Scholar]
  8. Liu Z.; Li S.; Pan X.; Fang H. Mechanism study on spreading dynamics of nanofluids droplet coupled with thermal evaporation. Int. J. Heat Mass Transfer 2022, 183, 122172. 10.1016/j.ijheatmasstransfer.2021.122172. [DOI] [Google Scholar]
  9. Palacios J.; Hernandez J.; Gomez P.; Zanzi C.; Lopez J. Experimental study of splashing patterns and the splashing/deposition threshold in drop impacts onto dry smooth solid surfaces. Experimental Thermal and Fluid Science 2013, 44, 571–582. 10.1016/j.expthermflusci.2012.08.020. [DOI] [Google Scholar]
  10. Thoraval M.-J.; Schubert J.; Karpitschka S.; Chanana M.; Boyer F.; Sandoval-Naval E.; Dijksman J. F.; Snoeijer J. H.; Lohse D. Nanoscopic interactions of colloidal particles can suppress millimetre drop splashing. Soft Matter 2021, 17, 5116–5121. 10.1039/D0SM01367F. [DOI] [PubMed] [Google Scholar]
  11. Hu M.; Zhou J.; Li Y.; Zhuo X.; Jing D. Effects of the surface wettability of nanoparticles on the impact dynamics of droplets. Chem. Eng. Sci. 2021, 246, 116977. 10.1016/j.ces.2021.116977. [DOI] [Google Scholar]
  12. Masoumi N.; Sohrabi N.; Behzadmehr A. A new model for calculating the effective viscosity of nanofluids. J. Phys. D: Appl. Phys. 2009, 42, 055501. 10.1088/0022-3727/42/5/055501. [DOI] [Google Scholar]
  13. Lu G.; Duan Y.-Y.; Wang X.-D. Surface tension, viscosity, and rheology of water-based nanofluids: a microscopic interpretation on the molecular level. J. Nanopart. Res. 2014, 16, 2564. 10.1007/s11051-014-2564-2. [DOI] [Google Scholar]
  14. Zhang W. In Nanomaterial: Impacts on Cell Biology and Medicine; Capco D. G., Chen Y., Eds.; Advances in Experimental Medicine and Biology 811; Springer Netherlands: Dordrecht, 2014; pp 19–43. 10.1007/978-94-017-8739-0_2. [DOI] [Google Scholar]
  15. Kovalchuk N. M.; Johnson D.; Sobolev V.; Hilal N.; Starov V. Interactions between Nanoparticles in Nanosuspension. Adv. Colloid Interface Sci. 2019, 272, 102020. 10.1016/j.cis.2019.102020. [DOI] [PubMed] [Google Scholar]
  16. Batchelor G. K. Mass transfer from small particles suspended in turbulent fluid. J. Fluid Mech. 1980, 98, 609–623. 10.1017/S0022112080000304. [DOI] [Google Scholar]
  17. Vafaei S.; Borca-Tasciuc T.; Podowski M.; Purkayastha A.; Ramanath G.; Ajayan P. Effect of nanoparticles on sessile droplet contact angle. Nanotechnology 2006, 17, 2523. 10.1088/0957-4484/17/10/014. [DOI] [PubMed] [Google Scholar]
  18. Munshi A.; Singh V.; Kumar M.; Singh J. Effect of nanoparticle size on sessile droplet contact angle. J. Appl. Phys. 2008, 103, 084315. 10.1063/1.2912464. [DOI] [Google Scholar]
  19. Wasan D. T.; Nikolov A. D. Spreading of nanofluids on solids. Nature 2003, 423, 156–159. 10.1038/nature01591. [DOI] [PubMed] [Google Scholar]
  20. Ni S.; Isa L.; Wolf H. Capillary assembly as a tool for the heterogeneous integration of micro-and nanoscale objects. Soft Matter 2018, 14, 2978–2995. 10.1039/C7SM02496G. [DOI] [PubMed] [Google Scholar]
  21. Li Y.; Zhou J.; Hu M.; Jing D. Whole Contact Line Pinning for Droplets Impacting on a Hydrophobic Surface Due to Hydrophilic TiO2 Nanoparticle Addition. Langmuir 2021, 37, 6673–6680. 10.1021/acs.langmuir.1c00523. [DOI] [PubMed] [Google Scholar]
  22. Van Hooghten R.; Imperiali L.; Boeckx V.; Sharma R.; Vermant J. Rough nanoparticles at the oil–water interfaces: Their structure, rheology and applications. Soft Matter 2013, 9, 10791–10798. 10.1039/c3sm52089g. [DOI] [Google Scholar]
  23. Chinnam J.; Das D. K.; Vajjha R. S.; Satti J. R. Measurements of the surface tension of nanofluids and development of a new correlation. International Journal of Thermal Sciences 2015, 98, 68–80. 10.1016/j.ijthermalsci.2015.07.008. [DOI] [Google Scholar]
  24. Fan H.; Striolo A. Nanoparticle effects on the water-oil interfacial tension. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics 2012, 86, 051610. 10.1103/PhysRevE.86.051610. [DOI] [PubMed] [Google Scholar]
  25. Lin Y.; Skaff H.; Emrick T.; Dinsmore A. D.; Russell T. P. Nanoparticle Assembly and Transport at Liquid-Liquid Interfaces. Science 2003, 299, 226–229. 10.1126/science.1078616. [DOI] [PubMed] [Google Scholar]
  26. Song M.; Ju J.; Luo S.; Han Y.; Dong Z.; Wang Y.; Gu Z.; Zhang L.; Hao R.; Jiang L. Controlling liquid splash on superhydrophobic surfaces by a vesicle surfactant. Science advances 2017, 3, e1602188 10.1126/sciadv.1602188. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. McKinley G. H.; Tripathi A. How to extract the Newtonian viscosity from capillary breakup measurements in a filament rheometer. J. Rheol. 2000, 44, 653–670. 10.1122/1.551105. [DOI] [Google Scholar]
  28. Vadillo D.; Tuladhar T.; Mulji A.; Jung S.; Hoath S.; Mackley M. Evaluation of the inkjet fluid’s performance using the “Cambridge Trimaster” filament stretch and break-up device. J. Rheol. 2010, 54, 261–282. 10.1122/1.3302451. [DOI] [Google Scholar]
  29. Ataei M.; Chen H.; Amirfazli A. Behavior of a liquid bridge between nonparallel hydrophobic surfaces. Langmuir 2017, 33, 14674–14683. 10.1021/acs.langmuir.7b03508. [DOI] [PubMed] [Google Scholar]
  30. Agarwal P.; Murdande R. M.; Kandaswamy A. S.; Bobji M. Dynamic stretching of a liquid bridge. International Journal of Advances in Engineering Sciences and Applied Mathematics 2019, 11, 238–243. 10.1007/s12572-020-00256-8. [DOI] [Google Scholar]
  31. Tourtit Y.; Gilet T.; Lambert P. Rupture of a Liquid Bridge between a Cone and a Plane. Langmuir 2019, 35, 11979–11985. 10.1021/acs.langmuir.9b01295. [DOI] [PubMed] [Google Scholar]
  32. Murase K.; Mochida T.; Sagawa Y.; Sugama H. Estimation on the strength of a liquid bridge adhered to three spheres. Advanced Powder Technology 2008, 19, 349–367. 10.1163/156855208X314949. [DOI] [Google Scholar]
  33. Brulin S.; Roisman I. V.; Tropea C. Fingering instability of a viscous liquid bridge stretched by an accelerating substrate. J. Fluid Mech. 2020, 899, A1. 10.1017/jfm.2020.422. [DOI] [Google Scholar]
  34. Rosello M.; Sur S.; Barbet B.; Rothstein J. P. Dripping-onto-substrate capillary breakup extensional rheometry of low-viscosity printing inks. J. Non-Newtonian Fluid Mech. 2019, 266, 160–170. 10.1016/j.jnnfm.2019.03.006. [DOI] [Google Scholar]
  35. Cramer C.; Studer S.; Windhab E. J.; Fischer P. Periodic dripping dynamics in a co-flowing liquid-liquid system. Phys. Fluids 2012, 24, 093101. 10.1063/1.4752477. [DOI] [Google Scholar]
  36. Dinic J.; Jimenez L. N.; Sharma V. Pinch-off dynamics and dripping-onto-substrate (DoS) rheometry of complex fluids. Lab Chip 2017, 17, 460–473. 10.1039/C6LC01155A. [DOI] [PubMed] [Google Scholar]
  37. Ducker W. A.; Senden T. J.; Pashley R. M. Direct measurement of colloidal forces using an atomic force microscope. Nature 1991, 353, 239–241. 10.1038/353239a0. [DOI] [Google Scholar]
  38. Butt H.-J. Measuring electrostatic, van der Waals, and hydration forces in electrolyte solutions with an atomic force microscope. Biophysical journal 1991, 60, 1438–1444. 10.1016/S0006-3495(91)82180-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Harrison A. J.; Corti D. S.; Beaudoin S. P. Capillary forces in nanoparticle adhesion: a review of AFM methods. Particulate Science and Technology 2015, 33, 526–538. 10.1080/02726351.2015.1045641. [DOI] [Google Scholar]
  40. Mathues W.; McIlroy C.; Harlen O. G.; Clasen C. Capillary breakup of suspensions near pinch-off. Phys. Fluids 2015, 27, 093301. 10.1063/1.4930011. [DOI] [Google Scholar]
  41. Alexandrou A. N.; Bazilevskii A.; Entov V.; Rozhkov A.; Sharaf A. Breakup of a capillary bridge of suspensions. Fluid Dynamics 2010, 45, 952–964. 10.1134/S001546281006013X. [DOI] [Google Scholar]
  42. McIlroy C.; Harlen O. G. Modelling capillary break-up of particulate suspensions. Phys. Fluids 2014, 26, 033101. 10.1063/1.4866789. [DOI] [Google Scholar]
  43. Zhao H.; Liu H.-F.; Xu J.-L.; Li W.-F.; Lin K.-F. Inhomogeneity in breakup of suspensions. Phys. Fluids 2015, 27, 063303. 10.1063/1.4922582. [DOI] [Google Scholar]
  44. Zou J.; Lin F.; Ji C. Capillary breakup of armored liquid filaments. Phys. Fluids 2017, 29, 062103. 10.1063/1.4984836. [DOI] [Google Scholar]
  45. Galindo-Rosales F.; Segovia-Gutiérrez J.; Pinho F.; Alves M.; de Vicente J. Extensional rheometry of magnetic dispersions. J. Rheol. 2015, 59, 193–209. 10.1122/1.4902356. [DOI] [Google Scholar]
  46. Andrade R. J.; Jacob A. R.; Galindo-Rosales F. J.; Campo-Deaño L.; Huang Q.; Hassager O.; Petekidis G. Dilatancy in dense suspensions of model hard-sphere-like colloids under shear and extensional flow. J. Rheol. 2020, 64, 1179–1196. 10.1122/1.5143653. [DOI] [Google Scholar]
  47. Khandavalli S.; Rothstein J. P. Extensional rheology of shear-thickening fumed silica nanoparticles dispersed in an aqueous polyethylene oxide solution. J. Rheol. 2014, 58, 411–431. 10.1122/1.4864620. [DOI] [Google Scholar]
  48. García-Ortiz J. H.; Galindo-Rosales F. J. Extensional Magnetorheology as a Tool for Optimizing the Formulation of Ferrofluids in Oil-Spill Clean-Up Processes. Processes 2020, 8, 597. 10.3390/pr8050597. [DOI] [Google Scholar]
  49. Nunes J. M.; Galindo-Rosales F. J.; Campo-Deaño L. Extensional Magnetorheology of Viscoelastic Human Blood Analogues Loaded with Magnetic Particles. Materials 2021, 14, 6930. 10.3390/ma14226930. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Lang C.; Hendricks J.; Zhang Z.; Reddy N. K.; Rothstein J. P.; Lettinga M. P.; Vermant J.; Clasen C. Effects of particle stiffness on the extensional rheology of model rod-like nanoparticle suspensions. Soft Matter 2019, 15, 833–841. 10.1039/C8SM01925H. [DOI] [PubMed] [Google Scholar]
  51. Ma A. W.; Chinesta F.; Tuladhar T.; Mackley M. R. Filament stretching of carbon nanotube suspensions. Rheologica acta 2008, 47, 447–457. 10.1007/s00397-007-0247-y. [DOI] [Google Scholar]
  52. Ng H. C.-H.; Corker A.; García-Tuñón E.; Poole R. J. GO CaBER: Capillary breakup and steady-shear experiments on aqueous graphene oxide (GO) suspensions. J. Rheol. 2020, 64, 81–93. 10.1122/1.5109016. [DOI] [Google Scholar]
  53. Eneren P.; Aksoy Y. T.; Zhu Y.; Koos E.; Vetrano M. R. Light extinction spectroscopy applied to polystyrene colloids: Sensitivity to complex refractive index uncertainties and to noise. Journal of Quantitative Spectroscopy and Radiative Transfer 2021, 261, 107494. 10.1016/j.jqsrt.2020.107494. [DOI] [Google Scholar]

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES