A Robust Approach for Electronic Health Record-Based Case-Control Studies with Contaminated Case Pools

Summary:

We consider analyses of case-control studies assembled from electronic health records (EHRs) where the pool of cases is contaminated by patients who are ineligible for the study. These ineligible patients, referred to as “false cases”, should be excluded from the analyses if known. However, the true outcome status of a patient in the case pool is unknown except in a subset whose size may be arbitrarily small compared to the entire pool. To effectively remove the influence of the false cases on estimating odds ratio parameters defined by a working association model of the logistic form, we propose a general strategy to adaptively impute the unknown case status without requiring a correct phenotyping model to help discern the true and false case statuses. Our method estimates the target parameters as the solution to a set of unbiased estimating equations constructed using all available data. It outperforms existing methods by achieving robustness to mismodeling the relationship between the outcome status and covariates of interest, as well as improved estimation efficiency. We further show that our estimator is root-n-consistent and asymptotically normal. Through extensive simulation studies and analysis of real EHR data, we demonstrate that our method has desirable robustness to possible misspecification of both the association and phenotyping models, along with statistical efficiency superior to the competitors.

1. Introduction

1.1. Overview

The case-control study design is one of the most frequently used study designs in biomedical research. As the name suggests, this design assembles data from two independent samples that are randomly drawn from two mutually exclusive population groups with (“cases”) or without (“controls”) the condition of interest, respectively. Despite the outcome-dependent sampling, case-control data can be analyzed using logistic regression models to assess the association between the condition of interest and some covariates as if collected prospectively (Prentice and Pyke, 1979). Readers are referred to Breslow (1996) and references therein for relevant statistical theory and applications. Recently, the case-control study design has been popularly used for clinical and translational studies based on electronic health records (EHRs), which provide a rich source of key administrative clinical data relevant to a patient’s care under a particular provider, including demographics, lab tests, prescriptions, immunization records, clinician notes, radiology and pathology reports, past medical history, etc (CMS.GOV). However, because EHRs were created mainly for billing purposes, it is often challenging to make use of them for research.

An illustrative case-control study on sepsis-related death based on Medical Information Mart for Intensive Care (MIMIC) III is described in Section 5. The goal of the study is to assess the association of sepsis-related mortality with a set of covariates. However, some of the deceased patients, who are regarded as “cases” in the analysis, actually have none of the sepsis-related billing codes. Therefore, it is likely that some cases died of reasons unrelated to sepsis, who we refer to as “false cases”. Correspondingly, we refer to sepsis-related deaths as “true cases”. Obviously, the false cases do not actually satisfy the criteria for the control selection, which is having sepsis and surviving. Hence they cannot be counted as controls but are more suitably considered as ineligible for the study that focuses on sepsis patients. In other words, being a true case, being a false case and being a control are three entirely different statuses, and false cases should always be excluded from the sample if known. On the other hand, information, e.g., the relevant billing codes about the phenotype, which is the presence or absence of sepsis in this example, is unavailable for most of the deaths in the case pool, due to incomplete records.

The above example highlights some unique analytical challenges for conducting EHR-based case-control studies, arising from contamination in the case pool and lack of phenotyping information. In this work, assuming only a small portion of the case pool have adequate phenotyping information so that their statuses of being true or false cases can be validated, as in the sepsis example, we propose an efficient yet robust method to estimate odds ratio parameters (see (3) and the following descriptions for their definition and practical importance) with the contaminated case-control data. Henceforth we refer to the subset of the case pool with validated statuses as the validation set.

1.2. Problem setup

To formulate our problem, let D denote the true status of a patient who can be a false case (D = 0), a true case (D = 1), or a control (D = 2). The “false cases” and “true cases” are collectively referred to as “candidate cases” (D ≠ 2). Let X denote a p-dimensional covariate vector whose first component is set to be constant 1.0 to capture an intercept term. We are interested in establishing the relationship between X and D given D ≠ 0, that is, whether and how the covariates are associated with the phenotype status among true cases and controls. However, the candidate case pool is contaminated by false cases (D = 0). It is known whether a patient is a control (D = 2) or a candidate case (D ≠ 2), but whether a candidate case is a false (D = 0) or true (D = 1) case is known only in a validation set which is a random subsample of the candidate case pool. Further, let S ≡ I(D ≠ 2), where I(·) is the indicator function, so that S = 1 means being a candidate case (either true or false), while S = 0 represents being a control.

Available data.

Our study sample consists of three mutually independent subsets:

1. the validation set $\left\{{\left(X_i^{\text{T}},D_i,S_i=1\right)}^{\text{T}}:i=1,\dots ,n\right\}$ of size n,

2. the nonvalidated candidate case pool $\left\{{\left(X_i^{\text{T}},S_i=1\right)}^{\text{T}}:i=n+1,\dots ,N_1\right\}$ of size N₁ − n,

3. and the control pool $\left\{{\left(X_i^{\text{T}},S_i=0\right)}^{\text{T}}:i=N_1+1,\dots ,N\right\}$ of size N₀ ≡ N − N₁,

which contain independent copies of the observations (X^T, D, S = 1)^T, (X^T, S = 1)^T and (X^T, S = 0)^T, respectively. For notational simplicity, we introduce a nonrandom indicator R ∈ {0, 1} representing whether D is known (R = 1) or not (R = 0), and write our study sample as $\left\{W_i={\left(X_i^{\text{T}},R_i{D}_i,R_i,S_i\right)}^{\text{T}}:i=1,\dots ,N\right\}$. The corresponding base observation is denoted as W = (X^T, RD, R, S)^T. Since S = 0 implies D = 2, we set R ≡ 1 for all patients with S = 0. Among the N₁ candidate cases (S = 1), only $n\equiv {\sum }_{i=1}^N{R}_i{S}_i$ of them have been validated (R = 1) and have known status D. Because the sampling was stratified on patients’ statuses of being a candidate case or a control, the realization S_i (i = 1, …, N) of the binary variable S in the study sample, as well as the sample sizes $N_1\equiv {\sum }_{i=1}^N{S}_i$ and $N_0\equiv {\sum }_{i=1}^N\left(1-S_i\right)$, is nonrandom (i.e., S_i ≡ 1 for i ∈ {1, …, N₁} while S_i ≡ 0 for i ∈ {N₁ + 1, …, N}), and the proportion τ ≡ N₁/N ∈ (0, 1) of candidate cases in the sample may not reflect the population mean η ≡ E(S) ∈ (0, 1).

Difference from the missing data problem.

The existence of unknown D values in the candidate case pool may look at first glance similar to the classical missing data setting. Nevertheless, unlike the random missingness indicators in missing data problems, whether a candidate case has been validated or not is deterministic in our framework, that is, the indicator R_i (i = 1, …, N) and the validation set size $n\equiv {\sum }_{i=1}^N{R}_i{S}_i$ are nonrandom (i.e., R_i ≡ 1 for i ∈ {1, …, n} ∪ {N₁ + 1, …, N} while R_i ≡ 0 for i ∈ {n + 1, …, N₁}). More importantly, we allow the validation set to be arbitrarily small relative to the whole sample, and thus assume the validation set size n could be asymptotically negligible compared to the whole sample size N, i.e., the ratio δ_n,N ≡ n/N is such that

$$\delta \equiv {\text{lim}}_{n,N\to \infty }{\delta }_{n,N}\in [0,\tau ).$$ (1)

Recalling τ ≡ N₁/N, the setting (1) can be expressed equivalently as ${\text{lim}}_{n,N_1\to \infty }\left(n/N_1\right)\in [0,1)$. The case with δ = 0 is a practically important and technically challenging special case. It contrasts with the classical missing data problem which requires the proportion of complete observations in the sample to be bounded away from zero (Tsiatis, 2007; Little and Rubin, 2019). In principle, (1) ensures that one can make use of all available nonvalidated candidate cases and controls in the analysis without extra effort to validate more candidate cases. Such a feature is desirable as it is often time consuming to review medical charts for patients’ true phenotype statuses.

Parameter of interest.

In this article, we aim to establish a (working) logistic regression association model using the contaminated case-control data described above. Suppose momentarily that the relationship between X and D among true cases (D = 1) and controls (D = 2) can be reflected by the following logistic regression model:

$$T(X)\equiv \text{pr}(D=1\mid X)/\text{pr}(D=2\mid X)=\text{exp}\left({\tilde{\theta }}^{\text{T}}X\right),$$ (2)

for some p-dimensional parameter vector $\tilde{\theta }\equiv {\left({\tilde{\theta }}_1,\dots ,{\tilde{\theta }}_p\right)}^{\text{T}}$. According to Prentice and Pyke (1979), the intercept term ${\tilde{\theta }}_1$ of the model (2) is unidentifiable since τ ≠ η, and the parameter that we can actually estimate from the case-control sample is θ ≡ (θ₁, …, θ_p)^T, defined as the solution to the following equation:

$$\tau E\left\{DX\overline{h}\left({\theta }^{\text{T}}X\right)\mid S=1\right\}-(1-\tau )E\left\{Xh\left({\theta }^{\text{T}}X\right)\mid S=0\right\}=0,$$ (3)

with h(x) ≡ {1 + exp(−x)}⁻¹ and $\overline{h}(x)\equiv 1-h(x)$. Owing to the fact that SD = I(D = 1) and 1 − S = I(D = 2), (3) is essentially the limit of the standard estimating equation for fitting a logistic regression model, using our contaminated case-control data but with the false cases (D = 0) excluded. Also, Prentice and Pyke (1979) showed that θ satisfies

$$\theta ={\left[{\tilde{\theta }}_1-\text{log}\{(1-\tau )\eta \}+\text{log}\{\tau (1-\eta )\},{\tilde{\theta }}_2,\dots ,{\tilde{\theta }}_p\right]}^{\text{T}},$$

which implies one can directly use the vector θ₋₁ ≡ (θ₂, …, θ_p)^T to compute the odds ratio

$$T(X)/T\left(X^{*}\right)\equiv \text{exp}\left({\tilde{\theta }}^{\text{T}}X\right)/\text{exp}\left({\tilde{\theta }}^{\text{T}}{X}^{*}\right)=\text{exp}\left\{{\theta }_{-1}^{\text{T}}\left(X_{-1}-X_{-1}^{*}\right)\right\}$$

between two individuals with covariates $X\equiv {\left(1,X_{-1}^{\text{T}}\right)}^{\text{T}}$ and $X^{*}\equiv {\left(1,X_{-1}^{* \text{T}}\right)}^{\text{T}}$, where X₋₁ and $X_{-1}^{\text{*}}$ refer to the last (p − 1) components of X and X*, respectively.

In practice, the underlying relationship between X and D given D ≠ 0 could be much more complicated than the logistic regression model. In this scenario, where (2) does not hold and the association model pr(D = 1 | X)/pr(D = 2 | X) is actually misspecified, the parameter θ, however, is still well-defined by equation (3) (under some standard regularity conditions listed in Assumption 1 of the Supporting Information). Using (2) and (3), we can establish a simple and interpretable (working) model, which allows association analysis between X and D among true cases and controls via estimation and inference of θ, as what we will do in the data analysis of Section 5. Hence, our primary goal is to estimate the parameter vector θ, whose definition (3) is in fact independent of the specific form of the association model pr(D = 1 | X)/pr(D = 2 | X). Here we emphasize that the relationship (2) is not assumed to be true anywhere throughout this paper, and all our conclusions hold valid regardless of whether the true association model is logistic or not.

1.3. Existing methods

To estimate θ in (3), the naive analysis of ignoring case contamination by treating all patients in the candidate case pool as true cases, that is, using S as D in the analysis, leads to biased estimates (Wang et al., 2021). Another straightforward strategy is to analyze the validation set and the control pool only, so that an estimator, denoted as ${\widehat{\theta }}_{\text{V}}$, is obtained by solving

$${\sum }_{i=1}^N\left\{R_i{S}_i{D}_i{X}_i\overline{h}\left({\widehat{\theta }}_{\text{V}}^{\mathrm{T}}{X}_i\right)-\left(1-S_i\right)X_{i}h\left({\widehat{\theta }}_{\text{V}}^{\mathrm{T}}{X}_i\right)\right\}=0.$$ (4)

It is noteworthy to point out that ${\widehat{\theta }}_{\text{V}}$ is in fact biased for both θ₁ and θ₋₁ defined by (3) as long as the association model pr(D = 1 | X)/pr(D = 2 | X) is not of the logistic form, since the ratio of true cases to controls in (4) is different from that in the original sample (Prentice and Pyke, 1979). In addition, even if the association model (2) is true and the last (p − 1) components of ${\widehat{\theta }}_{\text{V}}$ estimate θ₋₁ consistently, discarding nonvalidated candidate cases with R = 0 could significantly lower estimation efficiency (Wang et al., 2021). To make use of the nonvalidated candidate cases to improve estimation accuracy, Wang et al. (2021) proposed an estimating equation approach that imputes the unobserved D with an estimator of E(D | X, S = 1). However, they imposed a parametric assumption on the phenotyping model E(D | X, S = 1), violation of which could substantially degrade the performance of their estimator for θ; see Section 2 for details.

1.4. Our contributions

Motivated by the limitations of the above-mentioned methods, we devise in this article a novel estimating equation approach to estimating the parameter θ defined in (3). Similar to Wang et al. (2021), our method achieves improved estimation accuracy by employing all candidate cases even if most of them have unknown statuses D. More importantly, our estimator is robust to misspecification of both the association model pr(D = 1 | X)/pr(D = 2 | X) and the phenotyping model E(D | X, S = 1), relaxing the model assumptions required by the existing methods discussed in Section 1.3. If the form of E(D | X, S = 1) is correctly specified, our method performs analogously to that in Wang et al. (2021). Otherwise, it is still consistent and more efficient than the existing approaches which could be biased. We establish the n^1/2-consistency and asymptotic normality of our estimator without any model assumption. Further, in contrast to Wang et al. (2021) which requires δ ≡ lim_n,N→∞(n/N) > 0, we consider the more general setting (1). Our conclusions therefore remain valid for the important case with δ = 0, i.e., the validation set is much smaller than the whole sample. It allows us to improve the estimation by employing all available candidate cases even if most of them have unknown statuses D. Also, we show that, when δ = 0, our estimator is (locally) semiparametric efficient (in the sense of the theory from Tsiatis (2007)), under appropriate semiparametric models. Another advantage of our estimator is its simple form that allows straightforward implementation of estimation and inference. In summary, we develop an estimation strategy for θ as defined in (3), which can effectively accommodate possible misspecification of both the association and phenotyping models as well as a validation set that is disproportionally small relative to the whole candidate case pool.

1.5. Organization

In Section 2, we provide detailed theory on the limitations of existing methods. Section 3 introduces our unbiasedly imputed estimating equation approach and investigates its theoretical properties. Then its performance is compared with the competing methods through extensive simulation studies in Section 4. We illustrate our approach in Section 5 through a real data example. In Section 6, we conclude the article with a discussion of future directions. All technical details, along with some necessary supplements for the numerical studies in Sections 4 and 5, are deferred to Web Appendices A–H of Supporting Information.

2. Limitations of the Existing Methods

This section provides theoretical insights into the weaknesses of the existing methods mentioned in Section 1.3. Wang et al. (2021) demonstrated the loss of efficiency caused by discarding the nonvalidated candidate cases as well as the bias arising from ignoring the contamination in the candidate case pool. Moreover, Wang et al. (2021) developed an estimating equation method, which makes use of all available observations in the candidate case pool by imputing the unknown statuses D. Despite the improvement relative to other existing methods, Wang et al. (2021) relied on a parametric assumption of E(D | X, S = 1). As shown below, if this assumption is violated, their approach can also be biased.

In Wang et al. (2021), the unknown status D is imputed by its conditional expectation E(D | X, S = 1), which was estimated using a logistic working model

$$E(D\mid X,S=1)=h\left({\gamma }^{\text{T}}X\right)$$ (5)

with some p-dimensional parameter γ. Then their estimator, denoted by ${\widehat{\theta }}_{\text{PI}}$, is obtained by solving the estimating equation

$$0={\sum }_{i=1}^N\left[S_i\left\{R_i{D}_i+\left(1-R_i\right)h\left({\widehat{\gamma }}^{\text{T}}{X}_i\right)\right\}{X}_i\overline{h}\left({\widehat{\theta }}_{\text{PI}}^{\text{T}}{X}_i\right)-\left(1-S_i\right)X_{i}h\left({\widehat{\theta }}_{\text{PI}}^{\text{T}}{X}_i\right)\right],$$ (6)

$$0={\sum }_{i=1}^N{R}_i{S}_i\left\{h\left({\widehat{\gamma }}^{\text{T}}{X}_i\right)-D_i\right\}{X}_i,$$ (7)

where $\widehat{\gamma }$ is the maximum likelihood estimator of γ based on the validation set. Considering the case-control sampling and the fact that the data in the validation set are independent copies of (X^T, D, S = 1)^T, the corresponding population-level estimating equation is

$$0=E\left[\left\{\delta D+(\tau -\delta )h\left({\gamma }^{\text{T}}X\right)\right\}X\overline{h}\left({\theta }_{\text{PI}}^{\text{T}}X\right)\mid S=1\right]-(1-\tau )\left\{Xh\left({\theta }_{\text{PI}}^{\text{T}}X\right)\mid S=0\right\},$$ (8)

$$0=E\left[\left\{h\left({\gamma }^{\text{T}}X\right)-D\right\}X\mid S=1\right],$$ (9)

where θ_PI is the probability limit of ${\widehat{\theta }}_{\text{PI}}$ under standard regularity conditions. Nevertheless, substituting θ for θ_PI in the right hand side of (8), we find that

$$\begin{gathered} E\left[\left\{\delta D+(\tau -\delta )h\left({\gamma }^{\text{T}}X\right)\right\}X\overline{h}\left({\theta }^{\text{T}}X\right)\mid S=1\right]-(1-\tau )\left\{Xh\left({\theta }^{\text{T}}X\right)\mid S=0\right\} \\ =(\tau -\delta )E\left[\left\{h\left({\gamma }^{\text{T}}X\right)-D\right\}X\overline{h}\left({\theta }^{\text{T}}X\right)\mid S=1\right] \end{gathered}$$

according to the definition (3) of θ. Apparently, the constraint (9) on γ does not guarantee

$$(\tau -\delta )E\left[\left\{h\left({\gamma }^{\text{T}}X\right)-D\right\}X\overline{h}\left({\theta }^{\text{T}}X\right)\mid S=1\right]=0$$ (10)

when the working model (5) is not correct, if we exclude the trivial case where $\overline{h}\left({\theta }^{\text{T}}X\right)$ is constant almost surely or the whole candidate case pool has been validated, i.e., δ = τ. Hence, when the phenotyping model E(D | X, S = 1) is misspecified, it is possible that

$$E\left[\left\{\delta D+(\tau -\delta )h\left({\gamma }^{\text{T}}X\right)\right\}X\overline{h}\left({\theta }^{\text{T}}X\right)\mid S=1\right]-(1-\tau )\left\{Xh\left({\theta }^{\text{T}}X\right)\mid S=0\right\}\ne 0.$$

This combined with (8) implies θ ≠ θ_PI, which means ${\widehat{\theta }}_{\text{PI}}$ is inconsistent for θ.

3. Unbiasedly Imputed Estimating Equation

In this section, we introduce a general approach to constructing estimating equations that are robust to model misspecification and are unbiased for θ, as well as study the asymptotic properties of a special case with a simple form in the broad setting with either δ > 0 or δ = 0. We first elucidate the usefulness of nonvalidated candidate cases in the estimation. Inspecting the left hand side of (3), we observe that its conditional expectation given S = 1 and X does not equal zero with a positive probability, i.e.,

$$\text{pr}\left[E\left\{DX\overline{h}\left({\theta }^{\text{T}}X\right)\mid S=1,X\right\}\equiv E(D\mid S=1,X)X\overline{h}\left({\theta }^{\text{T}}X\right)\ne 0\right]>0,$$

if we exclude the trivial scenario where E(D | S = 1, X) = 0 almost surely. This indicates that the conditional distribution P(X | S = 1) indeed plays a role in the definition of θ in (3). Hence the estimation of θ can always be improved by properly utilizing the nonvalidated candidate cases, which are informative for P(X | S = 1).

3.1. General construction and a special example

To make use of the whole candidate case pool, momentarily we still assume working model (5). Besides (9), another valid estimating equation for the parameter vector γ in (5) is

$$E\left[\left\{h\left({\gamma }^{\text{T}}X\right)-D\right\}Xf(X)\mid S=1\right]=0,$$ (11)

which can be viewed as a weighted version of (9) with some weight function $f(X):{ℝ}^p\mapsto ℝ$. According to the derivation in Section 2, we know that the condition (10) is required for constructing an unbiased estimating equation for θ when D is replaced by h(γ^TX). Comparing the conditions (10) and (11), we observe that setting $f(X)\equiv \overline{h}\left({\theta }^{\text{T}}X\right)$ could ensure the condition (10) even if the working model (5) is incorrect. More generally, for an arbitrary function $g(x)\in ℝ$, we can show that

$$\begin{gathered} E\left\{g(X)X\overline{h}\left({\theta }^{\text{T}}X\right)\mid S=1\right\}=E\left[\{g(X)+D-D\}X\overline{h}\left({\theta }^{\text{T}}X\right)\mid S=1\right] \\ =E\left\{DX\overline{h}\left({\theta }^{\text{T}}X\right)\mid S=1\right\}+E\left[\{g(X)-D\}X\overline{h}\left({\theta }^{\text{T}}X\right)\mid S=1\right] \\ =E\left\{DX\overline{h}\left({\theta }^{\text{T}}X\right)\mid S=1\right\}+{\eta }^{-1}E\left[S\{g(X)-D\}X\overline{h}\left({\theta }^{\text{T}}X\right)\right]. \end{gathered}$$

The above equation indicates the key feature of a reasonable imputation function for unobserved D is making the term $E\left[S\{g(X)-D\}X\overline{h}\left({\theta }^{\text{T}}X\right)\right]$ vanish. This observation plays a critical role since it allows us to achieve a type of robust imputations that lead to unbiased estimating equations for θ without ever knowing the form of the phenotyping model E(D | X, S = 1). This idea is not only applicable in our setting, but also useful in general situations of handling nonvalidated data. We formalize this point in the next proposition.

Proposition 1: For any function $g(x):{ℝ}^p\mapsto ℝ$ satisfying

$$E\left[S\{g(X)-D\}X\overline{h}\left({\theta }^{\text{T}}X\right)\right]=0,$$ (12)

we have

$$0={\sum }_{i=1}^{N}E\left\{S_{i}g\left(X_i\right)X_i\overline{h}\left({\theta }^{\text{T}}{X}_i\right)-\left(1-S_i\right)X_{i}h\left({\theta }^{\text{T}}{X}_i\right)\right\},$$ (13)

$$0={\sum }_{i=1}^N{R}_{i}E\left[S_i\left\{g\left(X_i\right)-D_i\right\}{X}_i\overline{h}\left({\theta }^{\text{T}}{X}_i\right)\right].$$ (14)

Proposition 1 clarifies the feature of a good imputation function for the unknown values of D in the candidate case pool and provides a family of estimating equations, which are robust to misspecification of the phenotyping model E(D | X, S = 1), and are always unbiased for θ in the sense that (13) holds.

We now consider a special example where g(X) = h(α^TX) with α satisfying

$$E\left[S\left\{h\left({\alpha }^{\text{T}}X\right)-D\right\}X\overline{h}\left({\theta }^{\text{T}}X\right)\right]=0.$$ (15)

It is important here that the vector α is defined as the solution to (15) rather than the parameter vector γ of the model (5), so that the unbiasedness of our method does not require a parametric form of E(D | X, S = 1). Therefore, our method is robust to misspecification of the phenotyping model. For any vector $b={\left(b_1^{\text{T}},b_2^{\text{T}}\right)}^{\text{T}}$ with b₁, $b_2\in {ℝ}^p$, define Ψ₁(W, b) and Ψ₂(W, b) as

$${\Psi }_1(W,b)\equiv Sh\left(b_2^{\text{T}}X\right)X\overline{h}\left(b_1^{\text{T}}X\right)-(1-S)Xh\left(b_1^{\text{T}}X\right),$$

$${\Psi }_2(W,b)\equiv \left\{h\left(b_2^{\text{T}}X\right)-D\right\}X\overline{h}\left(b_1^{\text{T}}X\right).$$

Then our proposed estimator $\widehat{\beta }\equiv {\left({\widehat{\theta }}^{\text{T}},{\widehat{\alpha }}^{\text{T}}\right)}^{\text{T}}$ for the parameter $\mathit{\beta }\equiv {\left({\theta }^{\text{T}},{\alpha }^{\text{T}}\right)}^{\text{T}}\in \mathcal{B}\subset {ℝ}^{2p}$ is the solution to the following unbiasedly imputed estimating equation:

$$0={\sum }_{i=1}^N{\Psi }_n\left(W_i,\widehat{\beta }\right)\equiv {\sum }_{i=1}^N{\left\{{\delta }_{n,N}{\Psi }_1^{\text{T}}\left(W_i,\widehat{\beta }\right),R_i{S}_i{\Psi }_2^{\text{T}}\left(W_i,\widehat{\beta }\right)\right\}}^{\text{T}},$$ (16)

which is in fact the sample version of (13)–(14) with g(X) ≡ h(α^TX), and can be solved by Newton’s method. In (16), the term δ_n,N ≡ n/N is used to ensure ${\sum }_{i=1}^N{\delta }_{n,N}{\Psi }_1\left(W_i,\widehat{\beta }\right)$ and ${\sum }_{i=1}^N{R}_i{S}_i{\Psi }_2\left(W_i,\widehat{\beta }\right)$ are on the same scale, since R_iS_i is nonrandom and ${\sum }_{i=1}^N{R}_i{S}_i=n$.

3.2. Asymptotic properties of $\widehat{\beta }$

Next, we consider the asymptotic behavior of our estimator $\widehat{\beta }$. To facilitate our theoretical analysis, we first introduce some useful notation. Write

$${\Phi }_1(b)\equiv \tau E\left\{{\Psi }_1(W,b)\mid S=1\right\}+(1-\tau )E\left\{{\Psi }_1(W,b)\mid S=0\right\},$$

$${\Phi }_2(b)\equiv E\left\{{\Psi }_2(W,b)\mid S=1\right\},\Phi (b)\equiv {\left\{{\Phi }_1^{\text{T}}(b),{\Phi }_2^{\text{T}}(b)\right\}}^{\text{T}},$$

$${\Psi }_{\text{V}}(W,b)\equiv {\left\{\delta {\Psi }_1^{\text{T}}(W,b),{\Psi }_2^{\text{T}}(W,b)\right\}}^{\text{T}},{\Psi }_{\text{U}}(W,b)\equiv {\left\{{\Psi }_1^{\text{T}}(W,b),0^{\text{T}}\right\}}^{\text{T}},$$

$${\Psi }_{\text{V}}^{\prime }(W,b)\equiv \partial {\Psi }_{\text{V}}(W,b)/\partial b,{\Psi }_{\text{U}}^{\prime }(W,b)\equiv \partial {\Psi }_{\text{U}}(W,b)/\partial b,$$

$$A_{\text{V}}\equiv E\left\{{\Psi }_{\text{V}}^{\prime }(W,\beta )\mid S=1\right\},A_{\text{U}}\equiv E\left\{{\Psi }_{\text{U}}^{\prime }(W,\beta )\mid S=1\right\},$$

$$A_0\equiv E\left\{{\Psi }_{\text{U}}^{\prime }(W,\beta )\mid S=0\right\},A\equiv \partial \mathbf{\Phi }(b)/{\partial b|}_{b=\beta },$$

$$B_{\text{V}}\equiv \text{cov}\left\{{\Psi }_{\text{V}}(W,\beta )\mid S=1\right\},B_{\text{U}}\equiv \text{cov}\left\{{\Psi }_{\text{U}}(W,\beta )\mid S=1\right\},$$

$$B_0\equiv \text{cov}\left\{{\Psi }_{\text{U}}(W,\beta )\mid S=0\right\},B\equiv B_{\text{V}}+\delta (\tau -\delta )B_{\text{U}}+\delta (1-\tau )B_0,$$

$${\Omega }_n(b)\equiv {\sum }_{i=1}^N\partial {\Psi }_n\left(W_i,b\right)/\partial b.$$

We now propose the following result under the standard (and rather mild) regularity conditions specified in the Supporting Information.

Theorem 1: Under Assumption 1 in Web Appendix A of the Supporting Information, the estimator $\widehat{\beta }$ converges to β in probability, which implies $\widehat{\beta }$ is asymptotically unbiased for β. Also, it has the stochastic expansion

$$\begin{gathered} \widehat{\beta }-\beta =-{\left(nA\right)}^{-1}{\sum }_{i=1}^N{\Psi }_n\left(W_i,\beta \right)+o_p\left(n^{-1/2}\right) \\ \equiv -A^{-1}{\left\{N^{-1}{\sum }_{i=1}^N{\Psi }_1^{\text{T}}\left(W_i,\beta \right),n^{-1}{\sum }_{i=1}^N{R}_i{S}_i{\Psi }_2^{\text{T}}\left(W_i,\beta \right)\right\}}^{\text{T}}+o_p\left(n^{-1/2}\right). \end{gathered}$$ (17)

Furthermore, as n, N → ∞, the asymptotic distribution of $\widehat{\beta }$ is

$$n^{1/2}(\widehat{\beta }-\beta )\to N\left\{0,A^{-1}B{\left(A^{-1}\right)}^{\text{T}}\right\},$$ (18)

where the symbol N(·, ·) represents a multivariate normal distribution.

Remark 1 (Covariance matrix estimate): The asymptotic covariance matrix of $\widehat{\beta }$ in (18) can be estimated empirically by ${\widehat{A}}^{-1}\widehat{B}{\left({\widehat{A}}^{-1}\right)}^{\text{T}}$ with

$$\widehat{A}\equiv n^{-1}{\Omega }_n(\widehat{\beta })\text{ and }\widehat{B}\equiv {\widehat{B}}_{\text{V}}+{\delta }_{n,N}\left(\tau -{\delta }_{n,N}\right){\widehat{B}}_{\text{U}}+{\delta }_{n,N}(1-\tau ){\widehat{B}}_0\text{, where}$$

$${\widehat{B}}_{\text{V}}\equiv {\widehat{\text{cov}}}_{\text{V}}\left[{\left\{{\delta }_{n,N}{\Psi }_1^{\text{T}}(W,\widehat{\beta }),{\Psi }_2^{\text{T}}(W,\widehat{\beta })\right\}}^{\text{T}}\right],{\widehat{B}}_{\text{U}}\equiv {\widehat{\text{cov}}}_{\text{U}}\left\{{\mathit{\Psi }}_{\text{U}}(W,\widehat{\beta })\right\},{\widehat{B}}_0\equiv {\widehat{\text{cov}}}_0\left\{{\Psi }_{\text{U}}(W,\widehat{\beta })\right\}.$$

Here the notation ${\widehat{\text{cov}}}_{\text{V}}(\cdot )$, ${\widehat{\text{cov}}}_{\text{U}}(\cdot )$ and ${\widehat{\text{cov}}}_0(\cdot )$ represent the sample covariance matrix calculated based on the observed data {W_i : R_iS_i = 1, i = 1, …, N}, {W_i : (1 − R_i)S_i = 1, i = 1, …, N} and {W_i : S_i = 0, i = 1, …, N}, respectively.

Theorem 1 shows the n^1/2-consistency and asymptotic normality of $\widehat{\beta }$, which, combined with the covariance matrix estimation in Remark 1, allows us to make inference regarding θ. As a rather important special case of Theorem 1 that is significantly different from the classical missing data problem as clarified in Section 1.2, the property of $\widehat{\beta }$ when δ ≡ lim_n,N→∞(n/N) = 0 is considered in the next corollary.

Corollary 1: Let $\phi (W,b)\equiv A^{-1}{\left\{0_p^{\text{T}},{\Psi }_2^{\text{T}}(W,b)\right\}}^{\text{T}}$ and Σ ≡ cov{φ(W, β) | S = 1}, where 0_p is the p-dimensional vector of zeros. Suppose that the conditions in Theorem 1 hold and that δ = 0. Then $\widehat{\beta }$ satisfies that

$$\begin{gathered} \widehat{\beta }-\beta =-n^{-1}{\sum }_{i=1}^n\phi \left(W_i,\beta \right)+o_p\left(n^{-1/2}\right) \\ \equiv -n^{-1}{\sum }_{i=1}^n{A}^{-1}{\left[0_p^{\text{T}},\left\{h\left({\alpha }^{\text{T}}{X}_i\right)-D_i\right\}{X}^{\text{T}}\overline{h}\left({\theta }^{\text{T}}{X}_i\right)\right]}^{\text{T}}+o_p\left(n^{-1/2}\right), \end{gathered}$$ (19)

and that $n^{1/2}(\widehat{\beta }-\beta )\to N(0,\Sigma )$ in distribution as n, N → ∞.

Remark 2 (Benefits from using the nonvalidated candidate cases): Inspecting the expansion (19) of $\widehat{\beta }$, the covariance of the first part $N^{-1}{\sum }_{i=1}^N{\Psi }_1\left(W_i,\beta \right)$ in the estimating equation (16) is asymptotically negligible compared to that of the second part $n^{-1}{\sum }_{i=1}^n{\Psi }_2\left(W_i,\beta \right)$, when δ = 0. Such a result coincides with the fact that, under the setting where N increases faster than n, the conditional distribution of D given S = 1 is unrestricted and needs to be estimated with errors of order O_p(n^−1/2), while P(X | S = s), where s ∈ {0, 1}, is known up to errors of order O_p(N^−1/2) = o_p(n^−1/2). The estimation error rate o_p(n^−1/2) for P(X | S = 1) is generally unachievable without usage of the nonvalidated candidate cases. These results provide strong support to our claim that the nonvalidated candidate cases can be leveraged to improve the estimation because they provide information regarding the conditional distribution P(X | S = 1).

Remark 3 (Local semiparametric efficiency of our estimator): When δ = 0, the semiparametric model of (X^T, D, S)^T we consider is in fact asymptotically equivalent to the one given by the following class of allowable distributions:

$$\begin{gathered} \mathcal{M}\equiv \{P(X,D,S):P(X,S)\text{ is known and }P(D\mid X,S=1)\text{ is unrestricted} \\ \text{up to Assumption }1\text{ in the Supporting Information}\}\text{,} \end{gathered}$$ (20)

since the distribution P(X, S) is known up to errors of order O_p(N^−1/2) = o_P (n^−1/2), according to the arguments in Remark 2. Due to the fact that S ≡ I(D ≠ 2), the distribution P(D | X, S = 0) is trivial and the only unknown component in $\mathcal{M}$ is P(D | X, S = 1). Based on the semiparametric theory in Chapter 4 of Tsiatis (2007), we know that, as long as

$$E(D\mid X,S=1)=h\left({\alpha }^{\text{T}}X\right),$$ (21)

i.e., the true phenotyping model is indeed logistic, the efficient influence function for β, under the semiparametric model $\mathcal{M}$ defined in (20), is given by

$${\phi }_{\text{EFF}}(W,\beta )\equiv A^{-1}{\left\{0_p^{\text{T}},{\Psi }_2^{\text{T}}(W,\beta )\right\}}^{\text{T}}.$$ (22)

The proof of (22) can be found in Web Appendix G of the Supporting Information. Noticing the facts (a) that the efficient influence function φ_EFF(W, β) given in (22) equals the influence function φ(W, β) of $\widehat{\beta }$ obtained in Corollary 1, and (b) that the observations $\left\{{\left(X_i^{\text{T}},D_i\right)}^{\text{T}}:i=1,\dots ,n\right\}$ appearing in the expansion (19) can actually be viewed as a random sample drawn from the distribution P(X, D | S = 1), we know that, if (21) holds and δ = 0, our estimator $\widehat{\theta }$ attains the semiparametric efficiency bound and is (locally) semiparametric efficient for estimating θ (in the sense of the theory in Chapter 4 of Tsiatis (2007)), under the semiparametric model $\mathcal{M}$ defined by (20).

Remark 4 (Extension of our method to data with control contamination): Since the definitions of candidate cases and controls are interchangeable in the study sample, our method is directly applicable to studies with contaminated control pools. Further, by constructing imputation schemes similar to (16) for controls with unknown true statuses, our work can also be easily generalized to problems whose case and control pools are both contaminated.

4. Simulations

4.1. Basic settings

We now study the numerical performance of our method using simulated data. We consider samples of size N = 2, 500, N = 5, 000 or N = 25, 000, where the proportion of candidate cases is τ = 2/5. The validation set size is n = 100, n = 200 or n = 400. We set the covariate dimension to be p = 7 or p = 13. These multiple covariates are modeled differently in the association and phenotyping models for data generation as specified in (23) and (24) below. For example, in the phenotyping models, some covariates may have stronger nonlinear effects compared to others, leading to more severe misspecification. The results in Section 4.3 show that the existing methods, which cannot accommodate model misspecification, could yield greater biases for estimates of parameters corresponding to stronger nonlinear effects in the phenotyping models. Via varying the choices of N, n and p, we thoroughly investigate the finite-sample performance of our proposed method under a variety of simulation settings, characterized by different combinations of these three factors’ levels. The random vector X₋₁, i.e., the last (p − 1) components of the p-dimensional covariates X, is normally distributed with a zero mean and an identity covariance matrix. Recall that the first component of X is set to be one in order to include an intercept term in the model. For any positive integer d, let 0_d, 1_d and 2_d denote the d-dimensional vectors of zeros, ones and twos, respectively, for which we will omit subscripts when it does not cause confusion. Then observations for D and S are generated from one of the following two mechanisms:

$$\{\begin{array}{l}\text{pr}(D=0\mid X)/\text{pr}(D=2\mid X)=\text{exp}\left\{\rho \left(X_{-1}\right)\right\},\hfill \\ \text{pr}(D=1\mid X)/\text{pr}(D=2\mid X)=\text{exp}\left(1^{\text{T}}X/2\right);\hfill \end{array}$$ (23)

$$\{\begin{array}{l}E(S\mid X)=h\left(1^{\text{T}}X/2\right),\hfill \\ E(D\mid X,S=1)=h\left\{\rho \left(X_{-1}\right)\right\}\text{ with }h(x)\equiv {\{1+\text{exp}(-x)\}}^{-1}.\hfill \end{array}$$ (24)

The association model pr(D = 1 | X)/pr(D = 2 | X) is logistic in (23) but not logistic in (24). Here the function ρ(·) in (23)–(24) takes five different forms: ρ(x) = (a) 2^Tx, (b) (2^Tx)(1 − ω^Tx), (c) $\left(2^{\text{T}}x\right)\left(1-{\omega }^{\text{T}}x\right)+{\sum }_{j=1}^{p-1}\text{sin}\left(x_j\right)$, (d) (2^Tx)(1 − ω^Tx) − exp(−1^Tx) or (e) (2^Tx)(1−ω^Tx) − (κ^Tx)² + 2log(|1^Tx| + 1), where x ≡ (x₁, …, x_p−1)^T, $\omega \equiv {\left\{0_{(p-1)/2}^{\text{T}},1_{(p-1)/2}^{\text{T}}\right\}}^{\text{T}}/3$ and κ ≡ (1, 0, 1, 0, …, 1, 0)^T/2. In total, we use twenty (two choices of the dimension p, two choices of the mechanism generating D and S given X, and five choices of the function ρ(·)) different data generating models in our simulation study. The prevalence E(S) of candidate cases is between 0.57 and 0.68 in these models. Table S1 in the Supporting Information provides the proportion E(D | S = 1) of true cases in the candidate case pool for each of the above configurations. The parameter of interest, i.e., the last (p − 1) components θ₋₁ of θ defined by (3), equals 1/2 in (23), while its true value in (24) is approximated via Monte Carlo based on a sample {(X_i, D_i, S_i = 1) : i = 1, …, 40, 000} ∪ {(X_i, D_i, S_i = 0) : i = 1, …, 60, 000}, independent of the data used for estimation.

In the following, we compare the estimators from our unbiasedly imputed estimating equation (UIEE) (16) with those from three competing approaches: (i) validation-only estimating equation (4), which is unbiased and biased under models (23) and (24), respectively; (ii) naive estimating equation, which ignores available data for D and regards all subjects in the candidate case pool as true cases; (iii) parametrically imputed estimating equation (6)–(7) (Wang et al., 2021), which assumes a logistic regression model for E(D | X, S = 1). All the results are summarized from 500 replications. In the interest of space, we present the results with p = 7 in the Supporting Information (Appendix H, Tables S2–S3).

4.2. Results of estimation: Biases and mean squared errors

Since the full robustness to potential model misspecification is the most important superiority of our method over the existing ones, we first present results on the biases of our estimators and the three competitors (Table 1 (p = 13); Table S2 (p = 7)). Considering the estimand θ is a p-dimensional vector, for an estimator $\widehat{\mathit{\vartheta }}$ of θ, we measure its bias by the criterion

$${(p-1)}^{-1/2}\Vert E\left({\widehat{\mathit{\vartheta }}}_{-1}\right)-{\theta }_{-1}\Vert ,$$ (25)

where ∥ · ∥ represents the L₂ norm of a vector, ${\widehat{\mathit{\vartheta }}}_{-1}$ and θ₋₁ respectively denote the last (p−1) components of $\widehat{\mathit{\vartheta }}$ and θ, and the multiplier (p−1)^−1/2 is included to ensure the same scale when the parameter dimension varies. Here the intercept parameter is excluded since it is usually not of interest in case-control studies. The numbers in Tables 1 and S2 (of the Supporting Information) indicate that the biases of our method, UIEE, are always negligible (quite close to zero) under the various simulation settings, regardless of the true forms of the association and phenotyping models, substantiating that our method is fully robust to misspecification of these two underlying models, as claimed in Section 3. In contrast, the estimators from the validation-only estimating equation yield considerable biases under the model setting (24), where the association model is not logistic, while those from the parametrically imputed estimating equation is obviously biased whenever the phenotyping model takes nonlogistic forms (b)–(e). In addition, the naive approach, which does not take account of the case contamination, generates the most severe biases across all the scenarios.

Table 1.

Results of the simulations in Section 4: biases, measured by the criterion (25), of the estimators for θ₋₁ from the validation-only estimating equation (VEE), from the naive estimating equation (NEE), from the parametrically imputed estimating equation (PIEE) and from the unbiasedly imputed estimating equation (UIEE) under the models (23) and (24) with the covariate dimension p = 13. Here n is the validation set size, N is the whole sample size and ρ(x) is the function in (23)–(24).

			N = 2, 500				N = 5, 000				N = 25,000
Model	n	ρ(x)	VEE	NEE	PIEE	UIEE	VEE	NEE	PIEE	UIEE	VEE	NEE	PIEE	UIEE
(23)	100	(a)	0.02	0.35	0.00	0.00	0.02	0.35	0.01	0.01	0.02	0.35	0.01	0.01
		(b)	0.02	0.16	0.09	0.01	0.01	0.16	0.09	0.01	0.01	0.16	0.09	0.01
		(c)	0.02	0.24	0.10	0.01	0.01	0.24	0.11	0.01	0.01	0.24	0.11	0.01
		(d)	0.02	0.16	0.07	0.01	0.01	0.16	0.08	0.01	0.01	0.16	0.08	0.01
		(e)	0.02	0.19	0.10	0.01	0.01	0.19	0.11	0.01	0.01	0.19	0.11	0.01
	200	(a)	0.01	0.35	0.00	0.00	0.01	0.35	0.00	0.00	0.01	0.35	0.01	0.01
		(b)	0.01	0.16	0.08	0.01	0.01	0.16	0.09	0.01	0.01	0.16	0.09	0.00
		(c)	0.01	0.24	0.09	0.01	0.01	0.24	0.10	0.01	0.00	0.24	0.11	0.00
		(d)	0.01	0.16	0.07	0.01	0.01	0.16	0.07	0.00	0.01	0.16	0.08	0.00
		(e)	0.01	0.19	0.09	0.01	0.01	0.19	0.10	0.01	0.00	0.19	0.11	0.00
	400	(a)	0.01	0.35	0.00	0.00	0.01	0.35	0.00	0.00	0.00	0.35	0.00	0.00
		(b)	0.01	0.16	0.06	0.01	0.01	0.16	0.08	0.00	0.00	0.16	0.09	0.00
		(c)	0.01	0.24	0.07	0.01	0.01	0.24	0.09	0.00	0.00	0.24	0.11	0.00
		(d)	0.01	0.16	0.05	0.01	0.01	0.16	0.06	0.00	0.00	0.16	0.08	0.00
		(e)	0.01	0.19	0.07	0.01	0.01	0.19	0.09	0.00	0.01	0.19	0.11	0.00
(24)	100	(a)	0.14	0.41	0.02	0.02	0.18	0.41	0.01	0.01	0.23	0.41	0.01	0.01
		(b)	0.14	0.34	0.20	0.03	0.18	0.34	0.21	0.02	0.22	0.34	0.22	0.02
		(c)	0.15	0.39	0.19	0.02	0.19	0.39	0.20	0.02	0.24	0.39	0.21	0.02
		(d)	0.17	0.44	0.24	0.03	0.22	0.44	0.25	0.03	0.28	0.45	0.26	0.03
		(e)	0.12	0.32	0.18	0.03	0.16	0.32	0.20	0.02	0.21	0.32	0.21	0.03
	200	(a)	0.11	0.41	0.02	0.02	0.15	0.41	0.01	0.01	0.21	0.41	0.01	0.01
		(b)	0.11	0.34	0.19	0.02	0.15	0.34	0.21	0.01	0.22	0.34	0.22	0.01
		(c)	0.12	0.39	0.18	0.02	0.16	0.39	0.20	0.01	0.23	0.39	0.21	0.01
		(d)	0.14	0.44	0.23	0.02	0.19	0.44	0.25	0.02	0.27	0.45	0.27	0.02
		(e)	0.10	0.32	0.17	0.02	0.14	0.32	0.19	0.02	0.20	0.32	0.21	0.02
	400	(a)	0.07	0.41	0.01	0.01	0.12	0.41	0.01	0.01	0.20	0.41	0.01	0.01
		(b)	0.07	0.34	0.15	0.01	0.12	0.34	0.19	0.01	0.20	0.34	0.22	0.01
		(c)	0.07	0.39	0.14	0.01	0.13	0.39	0.18	0.01	0.21	0.39	0.21	0.01
		(d)	0.09	0.44	0.19	0.02	0.15	0.44	0.23	0.01	0.25	0.45	0.27	0.01
		(e)	0.06	0.32	0.14	0.02	0.11	0.32	0.18	0.01	0.18	0.32	0.21	0.01

Further, to provide a direct comparison of the general estimation accuracy of our method to the three competitors, Table 2 (p = 13) and Table S3 (p = 7) present the mean squared error ratios of the estimators from the validation-only estimating equation (served as a benchmark) to the other three, where a larger value indicates better performance. When computing the mean squared errors, we again exclude the intercept term and focus on the target parameter θ₋₁. UIEE appears to uniformly outperform the competitors under models (b)–(e), while yielding results slightly inferior but still fairly close to those of the parametrically imputed estimating equation under the model (a) where ρ(x) is exactly linear and the phenotyping model is of a logistic form. In Tables 2 and S3 (of the Supporting Information), we observe significant increases in the advantage of our method as the sample size N becomes larger. As discussed before Section 3.1, this improvement is owing to more precise recovery of the distribution P(X | S = 1) achieved by appropriate use of extra nonvalidated candidate cases. It also validates the claim before the assumption (1) that our UIEE method allows for an arbitrarily small δ_n,N ≡ n/N, which is between 0.004 and 0.160 under our simulation settings. Moreover, our method works well under different contamination rates {1 − E(D | S = 1)} of the candidate case pools, which are given in Table S1 of the Supporting Information. In addition, comparing the numbers across Tables 2 and S3 (in the Supporting Information), we notice, as p rises from 7 to 13, the superiority of our method, UIEE, becomes lower in most of the cases, somewhat reflecting the effect on the estimation from the increase of the covariate dimension.

Table 2.

Results of the simulations in Section 4: mean squared error ratios of the estimators for θ₋₁ from the validation-only estimating equation to those from the naive estimating equation (NEE), from the parametrically imputed estimating equation (PIEE) and from the unbiasedly imputed estimating equation (UIEE) under the models (23) and (24) with the covariate dimension p = 13. Here n is the validation set size, N is the whole sample size and ρ(x) is the function in (23)–(24).

			N = 2,500			N = 5,000			N = 25,000
Model	n	ρ(x)	NEE	PIEE	UIEE	NEE	PIEE	UIEE	NEE	PIEE	UIEE
(23)	100	(a)	0.35	3.30	3.14	0.35	3.67	3.49	0.32	4.14	3.88
		(b)	0.85	1.33	2.17	0.83	1.27	2.28	0.80	1.26	2.37
		(c)	0.50	1.25	2.46	0.47	1.18	2.61	0.42	1.11	2.70
		(d)	0.80	1.70	2.99	0.79	1.72	3.51	0.72	1.67	4.01
		(e)	0.73	1.13	1.87	0.72	1.08	1.94	0.65	0.98	1.94
	200	(a)	0.18	2.80	2.73	0.17	3.60	3.49	0.16	4.68	4.38
		(b)	0.47	1.09	2.04	0.45	0.99	2.37	0.40	0.87	2.79
		(c)	0.26	0.93	2.09	0.24	0.83	2.51	0.21	0.74	3.01
		(d)	0.44	1.31	2.46	0.42	1.26	3.33	0.37	1.13	4.41
		(e)	0.40	0.93	1.81	0.38	0.82	2.06	0.33	0.67	2.28
	400	(a)	0.09	1.85	1.82	0.08	2.71	2.65	0.08	4.49	4.27
		(b)	0.26	0.94	1.58	0.24	0.74	2.02	0.21	0.55	2.84
		(c)	0.15	0.84	1.59	0.13	0.63	2.12	0.11	0.44	3.01
		(d)	0.26	1.08	1.72	0.23	0.94	2.53	0.20	0.70	4.27
		(e)	0.23	0.85	1.51	0.21	0.63	1.85	0.17	0.42	2.35
(24)	100	(a)	0.27	2.38	2.34	0.32	3.17	3.10	0.40	4.53	4.37
		(b)	0.43	0.83	1.75	0.49	0.90	2.22	0.61	1.08	3.13
		(c)	0.33	0.93	2.05	0.39	1.03	2.76	0.50	1.29	4.02
		(d)	0.34	0.81	1.88	0.40	0.90	2.52	0.51	1.13	3.57
		(e)	0.42	0.83	1.69	0.47	0.90	2.18	0.60	1.08	2.96
	200	(a)	0.16	2.50	2.46	0.21	4.37	4.26	0.32	8.98	8.67
		(b)	0.26	0.66	2.09	0.33	0.74	3.31	0.49	0.99	5.99
		(c)	0.20	0.75	2.34	0.26	0.86	4.04	0.41	1.22	8.28
		(d)	0.21	0.64	2.25	0.28	0.75	3.86	0.42	1.05	7.53
		(e)	0.25	0.65	1.96	0.31	0.72	3.15	0.48	0.99	5.62
	400	(a)	0.09	1.88	1.86	0.13	4.38	4.29	0.26	14.81	14.42
		(b)	0.14	0.53	1.73	0.20	0.55	3.56	0.39	0.86	10.18
		(c)	0.11	0.61	1.83	0.17	0.66	4.15	0.33	1.08	13.79
		(d)	0.11	0.51	1.83	0.17	0.56	4.20	0.35	0.92	12.97
		(e)	0.13	0.53	1.58	0.19	0.53	3.21	0.38	0.84	9.32

In summary, the simulation results in Tables 1–2, as well as Tables S2–S3 of the Supporting Information, demonstrate that our method is robust to misspecification of both the association model pr(D = 1 | X)/pr(D = 2 | X) and the phenotyping model E(D | X, S = 1), and indeed improves the estimation accuracy by leveraging the nonvalidated candidate cases.

4.3. Results of inference: Confidence intervals

Next, as an illustrative example of inference, we construct 95% confidence intervals of θ₂ = 1/2 and θ₁₂ = 1/2 in the model (23) with p = 13, using the limiting distribution (18) in Theorem 1 and the covariance matrix estimate in Remark 1. We consider n = 200 or n = 400, which is large enough to ensure the asymptotic behavior given the number of covariates. The whole sample size is set to be N = 5, 000. The confidence interval lengths and coverage rates are displayed in Table 3. We can see that all the coverage rates of our method, UIEE, are close to the nominal level 95%. These results support the theoretical conclusions in Section 3 and justify our method in making inference. For comparison, we consider the 95% confidence intervals obtained from the three competing methods as well. The naive estimating equation produces extremely low coverage rates, suggesting it cannot make valid inference concerning the target parameter θ. The undercoverage issue also occurs for the parametrically imputed estimating equation in settings (b)–(e) where the phenotyping model is not of logistic form. The degenerating performance of these two methods can be attributed to their biasedness as shown in Table 1. Comparing the results for θ₂ and θ₁₂, the parametrically imputed estimating equation has much lower coverage rates, indicating more severe biases for estimating θ₁₂. This may be related to the structures of the phenotyping models in settings (b)–(e), where the presence of X₁₂, but not X₂, in the term ${\omega }^{\text{T}}{X}_{-1}\equiv {\sum }_{j=8}^{13}{X}_j/3$ in model (23) induces stronger nonlinear effects in X₁₂ in the phenotyping models. Further, the validation-only estimating equation, which is unbiased under model (23), gives satisfactory coverage rates but substantially longer interval lengths compared to UIEE. This indicates the efficiency gain of UIEE from utilizing the nonvalidated candidate cases.

Table 3.

Results of the simulations in Section 4: 95% confidence intervals of θ₂ = 1/2 and θ₁₂ = 1/2 constructed based on the unbiasedly imputed estimating equation (UIEE), the naive estimating equation (NEE), the validation-only estimating equation (VEE) and the parametrically imputed estimating equation (PIEE) under the setting (23) with p = 13 covariates and N = 5000 observations. “CIL” is the confidence interval length. “CR” is the coverage rate of the 95% confidence intervals. Here n is the validation set size and ρ(x) is the function in (23).

			VEE		NEE		PIEE		UIEE
	n	ρ(x)	CIL	CR	CIL	CR	CIL	CR	CIL	CR
θ 2	200	(a)	0.56	0.95	0.18	0.00	0.29	0.93	0.29	0.92
		(b)	0.44	0.95	0.16	0.00	0.27	0.92	0.29	0.94
		(c)	0.48	0.96	0.17	0.00	0.30	0.89	0.29	0.95
		(d)	0.42	0.94	0.16	0.00	0.24	0.88	0.23	0.95
		(e)	0.46	0.95	0.17	0.00	0.31	0.86	0.32	0.92
	400	(a)	0.40	0.96	0.18	0.00	0.25	0.94	0.25	0.95
		(b)	0.33	0.96	0.16	0.00	0.22	0.90	0.23	0.95
		(c)	0.36	0.96	0.17	0.00	0.24	0.89	0.24	0.95
		(d)	0.31	0.93	0.16	0.00	0.20	0.88	0.20	0.94
		(e)	0.34	0.94	0.17	0.00	0.24	0.84	0.25	0.93
θ 12	200	(a)	0.56	0.95	0.18	0.00	0.29	0.94	0.29	0.94
		(b)	0.41	0.95	0.16	0.17	0.27	0.58	0.26	0.95
		(c)	0.45	0.92	0.17	0.00	0.30	0.58	0.26	0.93
		(d)	0.40	0.93	0.16	0.36	0.23	0.66	0.22	0.94
		(e)	0.44	0.95	0.16	0.03	0.30	0.52	0.29	0.95
	400	(a)	0.40	0.95	0.18	0.00	0.24	0.95	0.25	0.96
		(b)	0.31	0.94	0.16	0.17	0.22	0.55	0.21	0.95
		(c)	0.33	0.93	0.17	0.00	0.24	0.50	0.22	0.94
		(d)	0.30	0.93	0.16	0.36	0.20	0.64	0.19	0.96
		(e)	0.32	0.95	0.16	0.03	0.24	0.41	0.23	0.97

5. A Data Application

In this section, we apply our method to assess risk factors associated with sepsis-related death using a subset of the data from Hou et al. (2020), which contains the records of 4,536 patients extracted from MIMIC III version 1.4. MIMIC III is a publicly available single-center critical care database that was approved by the Institutional Review Board of Beth Israel Deaconess Medical Center and the Massachusetts Institute of Technology (Johnson et al., 2016). For each patient, the data provide the vital status within 30 days along with 11 covariates of interest that include demographic variables, lab measurements and cancer status. The detailed description and summary statistics of the covariates are given in Table S4 of the Supporting Information. In the data set, some individuals actually have none of the sepsis-related billing codes, and we are concerned that some patients without sepsis might have been wrongly included in the cohort. To address such cohort contamination, we adopt a more rigorous rule for confirming sepsis statuses, requiring presence of at least three of the six common sepsis-related billing codes in the patient’s data record. Complete data for all the six codes were available for all the 3,651 survivors, among whom 810 survivors were confirmed to truly have sepsis according to our definition. We therefore used these 810 patients as controls (S = 0, or equivalently, D = 2) in our analysis of sepsis-related mortality. Among the 855 deaths, only 177 had all the six codes available (R = 1), and 68 (38.4%) were confirmed to indeed have sepsis (D = 1) while the other 109 were treated as false cases (D = 0). The sepsis statuses of the rest of 678 deaths remain ambiguous (R = 0). Our analysis included the N₀ = 810 eligible survivors (S = 0) and all the N₁ = 855 deaths (S = 1), where the n = 177 deaths with all the six codes available served as the validation set (R = 1). Our goal was to establish a logistic association model of sepsis-related death D and the 11 covariates for sepsis patients (D ≠ 0), that is, to estimate the parameter θ defined by (3) using these N = N₀ + N₁ = 1,695 observations. The two-sided t/Z-test between the groups of validated (R = 1) and nonvalidated (R = 0) deaths was conducted for each of the continuous/binary covariates, and the p-values were all above 0.05. We therefore treated the validation set as a simple random sample of all the deaths. All the continuous covariates were standardized prior to model fitting so that their scales were comparable. In the following analysis, our UIEE method can serve as a gold standard since it generates estimators guaranteed to be consistent (see Section 3), i.e., nontrivial deviation from the results of UIEE indicates bias.

We display in Figure 1 the 95% confidence intervals for the odds ratio parameter θ_j (j = 2, …, 12) in the association model (3) calculated using the four methods described in Section 4. The UIEE estimates were noticeably different from the other three sets of estimates, suggesting that the association and phenotyping models used in the three competing methods may have been misspecified. The UIEE estimates had shorter confidence intervals than those from the validation-only estimating equation, which demonstrated the efficiency improvement by accommodating the nonvalidated candidate cases. We also found that covariates “sodium max” and “aniogap max” were significant by UIEE in the sense that its confidence interval bounds for these two coefficients were clearly away from the origin (and the p-values from the Wald test were 0.001 and 0.037). These two variables were not significant by the three competing approaches, since their confidence intervals all included zero (and the p-values from the Wald test were all above 0.05). These results demonstrated the advantage of our method in terms of both accurate parameter estimation and high power for testing association.

Figure 1.

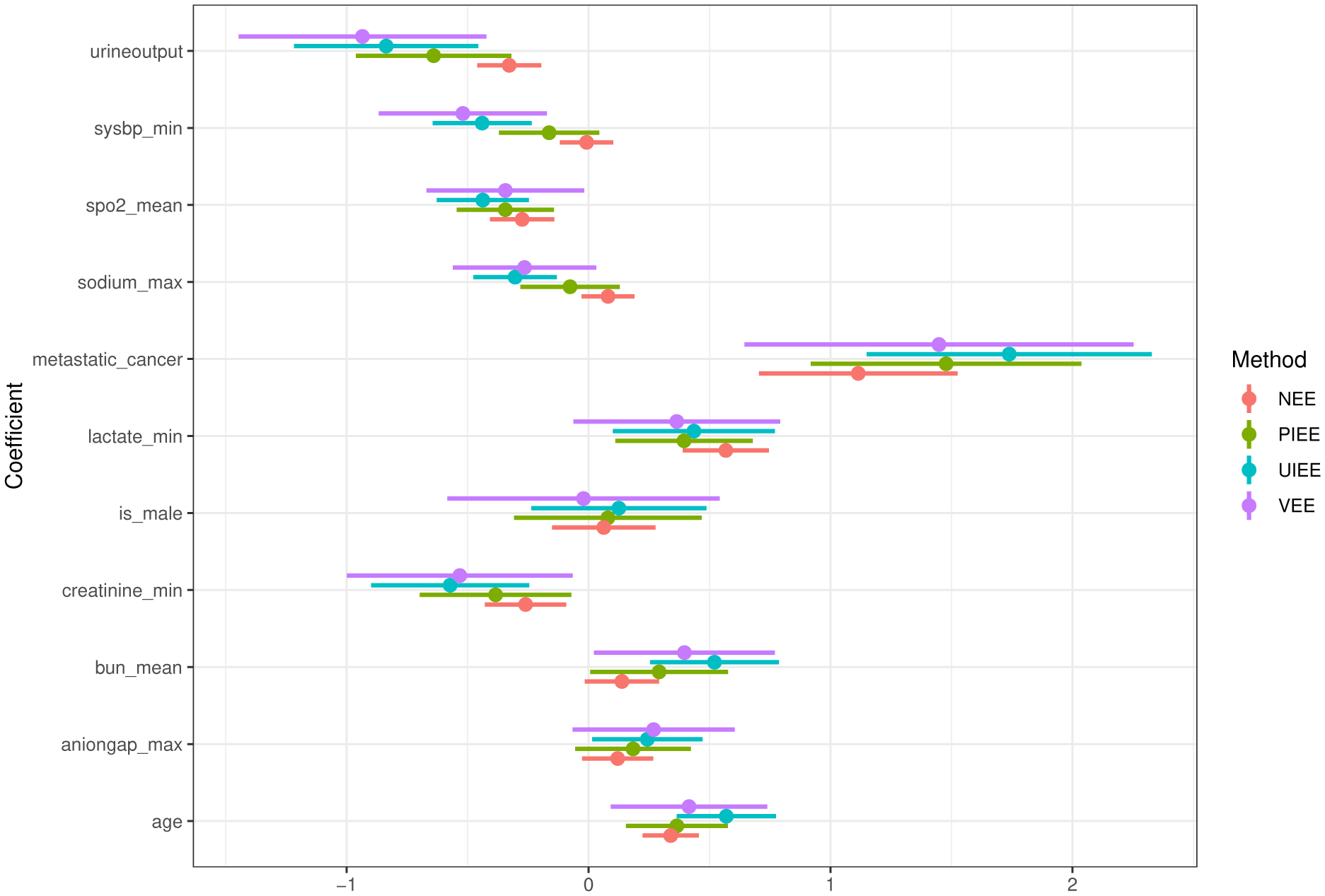
Results of the data analysis in Section 5: 95% confidence intervals of parameters in the (working) logistic regression model of vital status on eleven covariates among sepsis patients, which were calculated based on the validation-only estimating equation (VEE), the unbiasedly imputed estimating equation (UIEE), the parametrically imputed estimating equation (PIEE) and the naive estimating equation (NEE). All the continuous covariates have been standardized prior to model fitting.

6. Discussion

For analyzing case-control studies with contaminated candidate case pools and small subsets of validated cases, we proposed a general imputation strategy to accommodate non-validated candidate cases, yielding unbiased and efficient estimates for the association parameters even under misspecification of both the association and phenotyping models. The function g(X) in Proposition 1 used to impute unknown true versus false case status is key to the superior performance of our method. We envision that the estimation accuracy can be further improved by strategizing the choice of g(X) that satisfies the condition (12), for which semiparametric techniques such as dimension reduction and nonparametric smoothing may be worth considering. However, we still view the simple form of our imputation function as an advantage of our approach owing to the convenience of implementation.

In this work, the covariates considered in both the association and phenotyping models are low dimensional. In practice, EHRs contain a wealth of information for patients’ phenotype statuses, which can be leveraged to construct better imputation functions g(X) and improve the results of association analyses. Therefore, it is highly desirable to extend our method to accommodate high dimensional covariates. The challenge for studying theoretical properties of such extension is nontrivial, however, which we will pursue in future work.

Data Availability Statement

The data that support the findings in this paper are available in the Supporting Information.