Abstract
Snap-through mechanisms are pervasive in everyday life in biological systems, engineered devices, and consumer products. Snap-through transitions can be realized in responsive materials via stimuli-induced mechanical instability. Here, we demonstrate a rapid and powerful snap-through response in liquid crystalline elastomers (LCEs). While LCEs have been extensively examined as material actuators, their deformation rate is limited by the second-order character of their phase transition. In this work, we locally pattern the director orientation of LCEs and fabricate mechanical elements with through-thickness (functionally graded) modulus gradients to realize stimuli-induced responses as fast as 6 ms. The rapid acceleration and associated force output of the LCE elements cause the elements to leap to heights over 200 times the material thickness. The experimental examination in functionally graded LCE elements is complemented with computational evaluation of the underlying mechanics. The experimentally validated model is then exercised as a design tool to guide functional implementation, visualized as directional leaping.
Liquid crystal elastomers leap via thermally induced snap-through transitions facilitated by spatial programming of properties.
INTRODUCTION
The integration of soft materials into the field of robotics is one of the most compelling routes to the evolution of biomimetic systems. An important development toward this integration is material-driven locomotion, emulating the evolution of living organisms to crawl, walk, jump, and fly. Soft materials have been used to achieve crawling and walking (1–5), while only a comparatively few prior examinations have demonstrated approaches to realize leaping. Organisms such as grasshoppers (6), frogs (7, 8), and kangaroo rats (9) use stored elastic energy to launch themselves and serve as inspiration for material design. One approach to realize rapid release of stored energy is via mechanical instabilities in soft materials (10). Snap-through transitions in soft materials have been explored using gradients in crosslink density (11), light exposure (12, 13), swelling (14), and pressure (15). These previous efforts have demonstrated compelling performance but can lack a degree of freedom that is found in systems that have an intrinsic response to an applied stimulus.
Liquid crystalline elastomers (LCEs) are stimuli-responsive materials that are noted for their ability to generate large, complex deformations in response to a stimulus (16). The thermomechanical response of LCEs to heat is associated with thermotropic disruption of order, in which the material undergoes a nematic-to-isotropic transition. Alignment and retention of mesogen orientation upon polymerization have been used to prepare LCEs with distinctive deformations such as uniaxial contraction (17), bending (18), or shape morphing (19, 20). While useful in instances such as weight lifting (21) and gripping or moving objects (22), the thermomechanical deformation of an LCE can be too slow to drive motility in synthetic systems (23). Here, we explored a route to bridging the gap between snap-through instabilities and programmability of LCEs to achieve rapid actuation.
Previous demonstrations have observed snap-through in LCEs. Some of these demonstrations leverage combinations of complex through-thickness patterning of a nematic director and spatial variation of stimulus exposure to induce mechanical instabilities (24–26). The work of Jeon et al. (12), demonstrating rapid snap-through jumping in photoresponsive LCEs, is particularly relevant to this work. Others combine liquid crystalline materials with non–liquid crystalline components to bias response (27). In some cases, these snap-through events are demonstrated as routes to producing stimuli-responsive leaping. However, further advancement is necessary to develop snap-through–induced leaping with purely LCE elements that can be actuated as freestanding materials and without the need for complex spatial patterning of stimulus.
Here, LCE elements were prepared with spatial variation in the director (28–31). By integrating LCE layers in a laminate structure, a through-thickness modulus gradient was introduced in a controllable manner. The concentric packing of orientation in each of the LCEs programs a directional shape change into a cone. However, variation in the response of the LCE and the mechanical properties of the materials are shown to introduce a temporal instability that manifests as snap-through in a freestanding film. We showed that materials undergo thermally induced mechanical instabilities that result in leaping of the material to heights of over 200 times the material thickness as a result of a rapid snap-through transition that occurs in 6 ms. To elucidate the mechanics of the stimuli response, a model based on the theory of inhomogeneous plates was developed. The model was then used as a design tool to inform the experimental investigation of variables relating to the material design and geometrical constrains. The culmination of this effort was the realization of directional leaping, analogous to the motility of grasshoppers, facilitated by including “legs” of different lengths.
RESULTS
Mechanical instability in LCEs
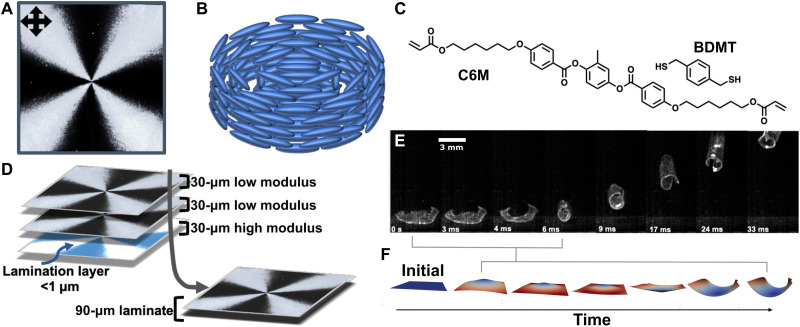
LCEs were prepared with spatial variation of the nematic director, described as a +1 topological defect. Traditionally, this patterning is used to program deformation into a cone as a result of order disruption upon heating. The brush-like pattern evident in Fig. 1A is associated with the concentric rotation of the liquid crystalline molecules around a central point (Fig. 1B). To introduce through-thickness variation in the timing and magnitude of stimuli response, we laminated several individual LCE films prepared with +1 director profiles and different moduli to create the desired modulus gradient. The laminates were prepared from 30-μm-thick LCE films of two different compositions. Each film containing a +1 topological defect was prepared as a 7-mm square. Stiffer LCEs of higher crosslink density were prepared by radical-mediated chain-transfer polymerization of 1,4-bis-[4-(6-acryloyloxyhexyloxy)benzoyloxy]-2-methylbenzene (C6M) with benzenedimethanethiol (BDMT) (Fig. 1C) in ratios of 1:0.5 acrylate:thiol, and softer LCEs of lower crosslink density were prepared from a formulation mixed at 1:0.75 acrylate:thiol. The final laminated devices were prepared by pressing the LCE films together, ensuring that defect centers and edges of the squares were aligned (Fig. 1D). To improve adhesion between the stiff and soft LCE compositions, a thin layer of C6M and photoinitiator was applied and cured by exposure to light after stacking (32). The resulting mechanical elements prepared from the LCE film layers had a stepwise gradient in modulus through the thickness. Unless otherwise noted, we used a three-layer laminate prepared from two of the softer 30-μm LCEs and one stiffer 30-μm LCE (Fig. 1D).
Fig. 1. Leaping LCEs.
(A) Birefringence associated with spatial variation of the nematic director described as a +1 topological defect is viewed in an LCE placed between crossed polarizers. (B) Nematic director in the LCE films rotates concentrically around a central point. (C) LCE films were prepared by free radical chain-transfer polymerization between the liquid crystalline monomer (C6M) and dithiol (BDMT). (D) LCE elements were prepared by stacking patterned LCEs to create elements with a modulus gradient through the thickness. The total thickness of the LCE element was 90 μm. (E) Upon heating, the laminated LCEs leap from the hot surface as a result of a snap-through event. (F) Schematic illustrates the deformation of the LCE element during snap-through.
When LCE elements were placed with the high-modulus side down on a hot surface (160°C), the film first deformed upward into a cone. Subsequently, the curvature of the LCE film inverted via mechanical instability, resulting in a snap-through deformation in the center of the element, forming an inverted cone. Figure 1E shows the leaping behavior of the LCE element as a result of this snap-through deformation, and Fig. 1F illustrates the snap-through event with simulated deformations. The force and acceleration of this transition resulted in the LCE leaping from the surface in less than 6 ms, reaching a height of over 200 times the material thickness and 2.5 times the width of the LCE element. The snap-through transition and the resulting “leap” are visualized in time-sequenced images in Fig. 1E and in movie S1.
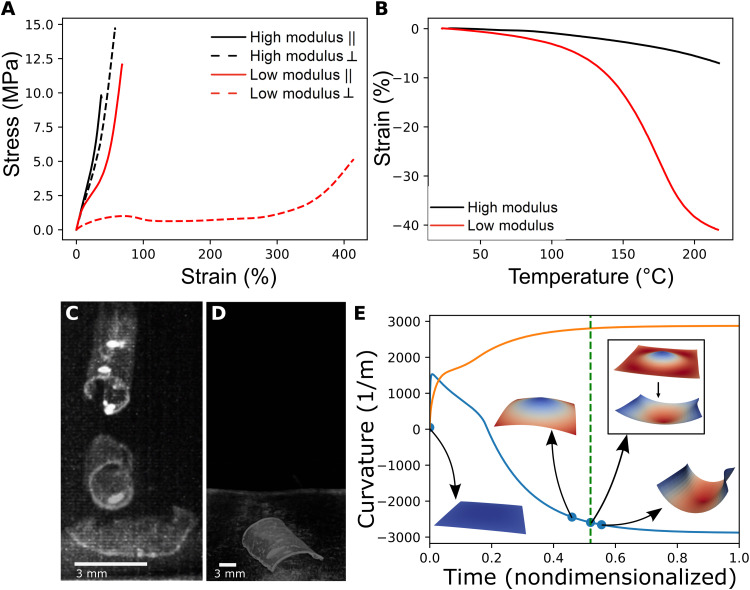
To assess the distinctive stimulus response of these LCEs, we first characterized material properties in uniaxially aligned LCEs. Notably, the modulus measured parallel to the alignment was similar for both the stiff (1:0.5) and soft (1:0.75) materials, while the moduli in the perpendicular direction differed by a factor of 5 (Table 1 and Fig. 2A). The variation in perpendicular modulus is particularly important, as the stimulus response of the LCE with a +1 topological defect will undergo out-of-plane deformation by stretching the concentrically packed mesogens along the perpendicular direction. The differences in modulus values correlated with a difference in glass transition temperature (Tg) for the two compositions, and both were attributed to a reduction in molecular weight between crosslinks (Mc) (Table 1). Furthermore, the actuation of the LCEs was characterized. Both LCEs exhibited a nematic-isotropic transition temperature (Tni; Table 1); however, the Tni for the higher-modulus LCE was more than 50°C higher than that for the lower-modulus LCE. Therefore, when subjected to thermal stimulus, the low-modulus materials generated strain in the form of contraction at a much faster rate than the high-modulus materials for a given temperature change (Fig. 2B).
Table 1. Material properties for linearly aligned model LCE.
| Composition (acrylate:thiol) | Modulus ||* (MPa) | Modulus ⊥* (MPa) | Mc† (g/mol) | Tni‡ (°C) | Tg§ (°C) | Strain rate at 160°C║ (%/°C) |
|---|---|---|---|---|---|---|
| 1:0.5 | 21 ± 0.6 | 17 ± 1 | 1000 | >225 | 22 | 0.05 |
| 1:0.75 | 18 ± 3 | 3.2 ± 0.3 | 4650 | 170 | 16 | 0.54 |
*Measured in the linear strain regime (2 to 4%) of tensile curve.
†Calculated using Mc = 3RT/E′ with E′ measured at 100°C.
‡Calculated as the inflection point of thermomechanical strain curve.
§Calculated as the peak of tanδ curve.
║Calculated as the slope of thermomechanical strain curve from 155° to 165°C.
Fig. 2. Material properties and thermomechanical response.
(A) Representative stress-strain curves for uniaxially aligned LCEs measured parallel (solid lines) and perpendicular (dashed lines) to the nematic director for high-modulus (black) and low-modulus (red) LCE films. Strain was applied at 5%/min. (B) Thermomechanical response of uniaxially aligned high-modulus (black) and low-modulus (red) LCEs as individual LCE films were held at a constant force of 0.0005 N and temperature was increased at 5°C/min. Overlaid sequence of images from high-speed recording of the response of the LCE elements when the (C) high-modulus side or (D) low-modulus side was in contact with the hot surface. (E) Evolution of curvature in the simulated LCEs for the material parameters used in experiments in the cases where the high-modulus material is placed directly on the hot surface (blue) and when the high-modulus side is up (orange).
Translating these properties to the laminated actuators, we analyzed the behavior upon placing the LCE films on a hot surface. When the high-modulus side is placed in contact with the surface at 160°C, initially, only the bottom high-modulus surface is heated and experiences strain. Although the Tni of the high-modulus material (as measured by the inflection point of the strain curve) is much higher than 160°C, the material still experiences 4% strain at this temperature. As indicated by prior literature, <5% strain is necessary to form a cone from an LCE patterned with a +1 topological defect (33). Accordingly, the response in this layer changes the configuration from a flat sheet to a conical shape. While the material could form a cone either upward or downward, the gradient in temperature biases the initial deformation to form the upward cone as dictated by the actuation of the high-modulus layer. The deformation is biased toward the upward cone partly due to the restriction of downward motion by the flat surface of the hot plate. As heat saturates, the anisotropy of modulus (crosslink density) overtakes the initial curvature and biases the final spontaneous curvature in the opposite direction. However, because the conical shape lacks smooth deformation pathways between the up and down configurations, the initial upward bias is locked in with an energy barrier. As a result, the snap-through occurs once there is a sufficient inverting spontaneous curvature (Fig. 2B), converting the stored elastic energy into kinetic energy. This snap-through is repeatable over numerous cycles in a single LCE element, provided that the element is allowed to cool back to the flat state between heat exposures (movie S13). Notably, when the low-modulus side was placed on the surface instead, the LCEs did not undergo an inversion of curvature or snap-through (Fig. 2D and movie S2).
Model development and validation
To understand better the underlying mechanics of the stimulus response reported here, a model was developed on the basis of the Föppl–von Kármán plate theory coupled to heat transfer. The model is detailed in the Supplementary Materials. To summarize the model, we computed the temperature distribution through the thickness at each time by solving the heat equation and the mechanical equilibrium using the Föppl–von Kármán plate theory with thermally induced spontaneous in-plane strain ϵm and spontaneous curvature κm. These, as well as the effective in-plane and bending modulus of the sheet, were computed from three-dimensional elasticity with thermal strain by enforcing equilibrium through the thickness of the film and are shown in Table 2. The total strain energy of the system is written in Eq. 1 where x = {x1, x2} is an element of the flat reference configuration, u = {u1, u2} is the in-plane displacement, w is the out-of-plane displacement, ϵm is the spontaneous in-plane strain, and κm is the spontaneous bending
| (1) |
Table 2. Equations used to describe the evolution of spontaneous in-plane and bending strain as a function of modulus.
| In plane | Bending | |
|---|---|---|
| Constitutive relation | ||
| Modulus | C = (E) | B = 2(E) − 1(E)2/0(E) |
| Spontaneous strain and curvature | ||
| Above, is the p-th moment through the thickness | ||
where C and B are the stretching and bending moduli, respectively, and
| (2) |
Note that the Föppl–von Kármán plate theory couples the out-of-plane displacement with the in-plane strain to account for higher-order effects of plate deformations, and this coupling is critical to the model. We computed the equilibrium configuration at each time and inferred the snap-through as a loss of stability of the equilibrium. Typical results are shown in Fig. 2E, which plots the spontaneous curvature at the center of the sheet as a function of time, and the insets show the shape.
The model predicted that as the LCE element was heated from the bottom with the high-modulus side in contact with the surface, positive curvature initially developed. Simultaneously, the system contracted due to the evolution of ϵαβ, forming an energy barrier between up and down solution variants and resulting in a bifurcation. After the initial development of positive curvature, the evolution of strain within the material caused a rapid change to net negative curvature. However, as shown in the series of simulations in Fig. 2E, the configuration of the LCE remained locked into a physical deformation with positive curvature. When a sufficiently high magnitude of negative spontaneous curvature was achieved, the positive curvature solution in the model became unstable, and the LCE inverted via snap-through to a negative curvature solution, at which point the simulation showed the physical deformation of the LCE into negative curvature. Note that, as indicated in both simulation and experiment, the inverted configuration ultimately resembles a rolled cylinder rather than the inverted cone. While the cone is a possible solution, the curled solution is a lower-energy state, particularly if the edges of the square boundary are different by as little as 1%, as would often be expected in an experimental preparation of the LCE elements. This rapid inversion in curvature is the origin of the leaping motion. Explicit analysis of the energy conversion confirmed that there is sufficient energy to result in leaping (Supplementary Materials). This scenario presents an interesting method of both inducing snap-through of a freestanding structure and having a thermally driven shape bifurcation with directional dependence. The experimental observations paralleled the computational results (Fig. 2C), thereby validating the model. Note also that the snap-through mechanism applies to LCE elements of other shapes, as demonstrated by the circle in movie S14.
Next, the simulation of the natural spontaneous in-plane strain and curvature was done for the configuration in which the high-modulus side was facing upward. Similar to the previous scenario, the system contracted monotonically as heat saturates through the thickness of the plate. As the system reached a constant temperature, the value of spontaneous in-plane strain reached a constant value. However, in this case, the coupling of the strain generation through the thickness with the evolution of temperature did not result in a bifurcation, so no curvature inversion occurred, and there was no instability. This again paralleled the experiments (Fig. 2D), further validating the model. Ultimately, when the evolution of curvature was mapped with the simulated deformation of the LCE elements as in Fig. 2E, it became plainly evident that the snap-through behavior is dependent on the initial placement of the LCE elements. For all subsequent investigation, only the configuration with the high-modulus side in contact with the hot surface was used.
Theory-led experimental examination of material and geometric variables
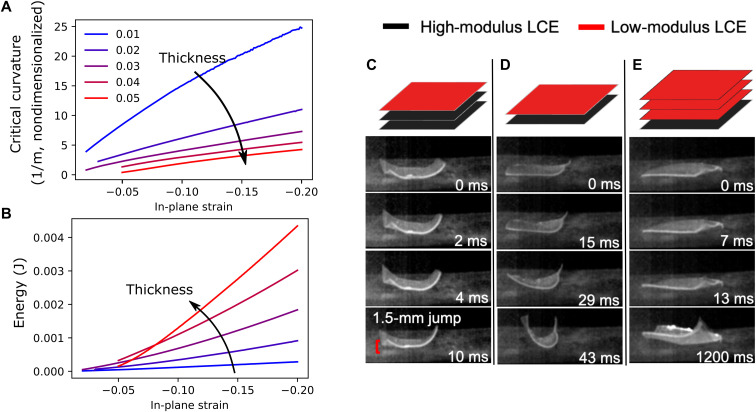
Equipped with a validated model, we considered other geometric variations of the system. One interesting adjustment was the association of the location of the point defect in the film geometry (Fig. 3A). The model predicted that as the defect center is shifted away from the center of the element, the films would still undergo snap-through. However, as the defect is shifted further from the center of the element, the model predicted that the critical curvature required for snap-through would decrease (Fig. 3B), resulting in less energy being dissipated in the snap-through event (Fig. 3C). In this theoretical analysis, either spontaneous in-plane strain or curvature was fixed to observe the individual impact of each. In practice, both evolve simultaneously, as captured in the previous section. To test these results experimentally where the curvature and in-plane strain evolve in tandem, LCE elements were prepared as described in Fig. 1D but using films where the point defect was offset from the center of the film (polarized optical microscopy images in Fig. 3, D to F). Upon actuating these materials, it was found that the offset resulted in the snap-through deformation occurring at an angle rather than the direct downward motion seen in the initial experiments. Therefore, as the defect was shifted further from the center of the film, the amount of energy was not only decreased, as predicted by the model, but also dissipated in ways that are not constructive to leaping. We saw this manifest experimentally as leaping height decreased from 2 cm (0 offset; Fig. 1 and movie S1) to 4 mm (0.1 offset; Fig. 3G and movie S3) to 1.5 mm (0.2 offset; Fig. 3H and movie S4) to no leaping (0.3 offset; Fig. 3I and movie S5) as the offset increases, confirming that the optimal location of the defect center for the maximum leaping height is in the center of the material.
Fig. 3. Spatial variation in patterning.
(A) Central point of the topological defect was offset from the center of the square films. (B and C) Model predictions indicate that the critical curvature and energy released will decrease by offsetting the center point of the director profile relative to the geometric center of the film. The equivalent elements were prepared experimentally, shown in (D) to (F) as viewed between crossed polarizers for 0.1 offset, 0.2 offset, and 0.3 offset, respectively. Materials were subjected to heat, and high-speed images (G to I) were captured of the stimuli response of the LCE patterns in (D) to (F), respectively.
A second consideration regards LCE elements with variation in the thickness. Evaluating thickness variations with our computational model, it was found that increasing the thickness of the plate decreased the critical curvature for snap-through (Fig. 4A), elucidating the trend that a thicker sheet penalizes the bending energy more than thin sheets. As a result, the sheet minimization of the bending energy causes the snap-through to occur at smaller natural curvatures. The energy released in snap-through was not as straightforward (Fig. 4B). At small spontaneous in-plane strains, a thinner sheet releases more energy than a thick sheet at snap-through. This behavior is, in part, because the snap-through for thicker sheets happens at a reduced natural curvature. At some point, the energy of the thicker plates becomes higher. Consequently, the energy release at snap-through can be controlled by tailoring the spontaneous in-plane strain and the thickness of the sheet. However, control of the physical response resulting from the snap-through is not trivial, as there are also considerations such as energy dissipation in the various cases. Exploring the complication of effects relating to thickness and modulus grading experimentally, LCEs were fabricated with variation in the layering of the two material compositions. By introducing more high-modulus material to an LCE with equivalent overall thickness to the original elements, leaping still occurred but with substantially reduced height (Fig. 4C and movie S6). When total thickness was reduced and there was equivalent depth of high- and low-modulus material incorporated through the cross section, we observed a slightly slower snap-through with no leaping (Fig. 4D and movie S7). When thickness was increased by adding an additional low-modulus layer, we saw rapid snap-through followed by slow deformation to the final stable state (Fig. 4E and movie S8). These results confirmed the complexity of the snap-through phenomenon in the LCE elements relative to the material thickness and grading of modulus. As demonstrated and discussed in previous work on active spherical caps, these studies also confirm that the snapping is proceeding nonisometrically (34, 35).
Fig. 4. Through-thickness variation.
(A) Critical curvature and (B) energy released in the snap-through event are predicted for LCE elements with varying thickness-to-width ratio as a function of spontaneous in-plane strain. Schematic of each of the three element variations and corresponding high-speed imagery of response is shown for variations of thickness and modulus gradient by combining (C) two high-modulus films and one low-modulus film, (D) one low-modulus film and one high-modulus film, and (E) three low-modulus films and one high-modulus film.
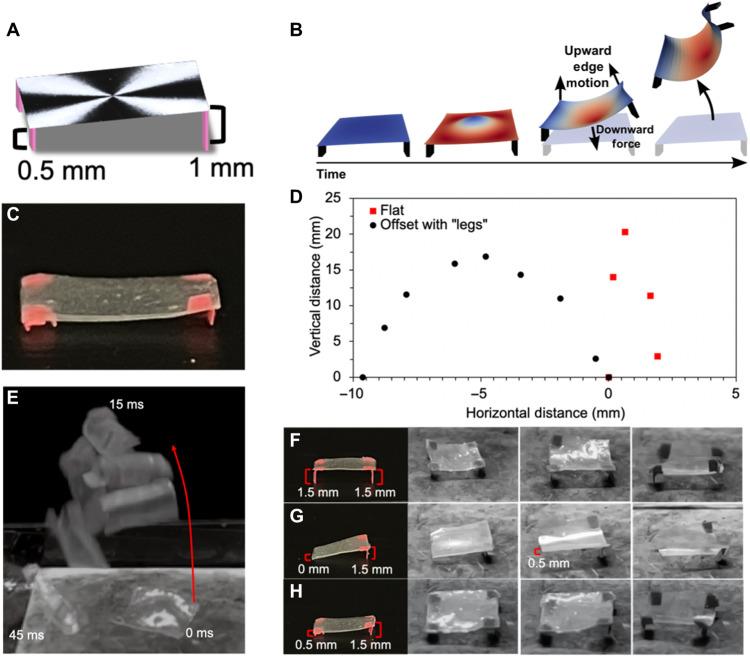
Directional LCE leaping
With this fundamental understanding of the snap-through mechanism produced in these materials, we sought to introduce directional leaping to mimic the locomotion of organisms that use stored elastic energy. Taking a bioinspired approach, materials were fabricated with legs that were longer on one edge of the material than the other (Fig. 5, A and C), giving the material a biased launching platform. The longer “back” legs offered a higher point of contact than the shorter back legs, causing the snap-through force to lift the material at an angle as depicted in Fig. 5B. The angled snap-through resulted in leaping to the left, as shown in Fig. 5 (D and E) and movie S9, and gave the LCE the ability to jump a lateral distance of 10 mm as compared to the original material that jumped approximately 2 mm laterally. We further explored the dependence of angle and leg length in relation to jumping ability and, much like defect offsets and layer variation, found that energy dissipation and curvature biases are extremely sensitive. If the legs were too long, then the material favored initial deformation to the downward stable state, likely due to a lack of surface contact to allow for upward curvature first (Fig. 5F and movie S10). This is due to gravity playing a role and breaking the symmetry of the initial bifurcation. If the angle was too steep but surface contact was allowed, then snap-through occurred, but the LCE element only left the surface on the side in contact (Fig. 5G and movie S11). Figure 5H and movie S12 show a combination of moderate angle with long legs on one side, which resulted in snap-through but immediate conversion to the second stable state with no leaping. Thus, we confirmed that through careful balance of biased launch platform and the previously discussed material properties, bioinspired directional leaping is feasible and effective.
Fig. 5. Leaping forward.
(A) To facilitate directionality, the LCE element was prepared with legs. (B) When the legs are offset in length, the model predicts that the LCE element will directionally leap. (C) LCE element was prepared with adhered legs. (D) Trajectory of the leaping of the LCE element with direct contact (red squares) is contrasted to the trajectory of the LCE element with legs (black circles). (E) Overlaid time-lapse images of the LCE with offset leaping direction upon exposure to heat. The lateral change was nearly 1 cm. (F to H) Leaping motion of the LCE elements is dependent on the difference in leg height.
DISCUSSION
We have demonstrated the ability to generate leaping as a result of thermally induced snap-through in LCEs that is dependent on a modulus gradient through the thickness of the material. Experimental results were complemented by simulation of the snap-through using theoretical considerations to elucidate strain and energy profiles. Because of a delicate dissipation of energy upon snap-through, the leaping phenomenon was shown to be dependent on material design, such as defect position and the order of stiff and soft layers. The results detailed here circumvent physical limitations that prevent rapid stimuli response of LCEs and, in so doing, open up new opportunities for these materials to enable engineered systems.
MATERIALS AND METHODS
Fabrication of alignment cells
Photopatterned cells with +1 topological defects were fabricated using glass slides coated with brilliant yellow (Sigma-Aldrich). Two slides were adhered together with 30-μm glass spacers (SPI Supplies) and NOA-68 (Norland Optical Adhesives). Assembled cells were photopatterned using a 445-nm vertically polarized laser with a q = 1/2 wave plate (BEAM Co.) and a 7-mm square mask. Each defect was exposed for 3 min with a laser intensity of 5 mW/cm2. Linearly aligned cells were fabricated using Elvamide-coated glass slides that were rubbed with velvet and adhered in antiparallel alignment with NOA-68 and 30-μm glass spacers.
Synthesis of LCEs
Liquid crystalline polymers were synthesized using C6M (Wilshire Technologies) and BDMT (Tokyo Chemical Industry). C6M and BDMT were mixed in molar ratios (acrylate:thiol) of 1:0.5 and 1:0.75. Omnirad 819 was included (0.5 weight %) for initiation of photopolymerization. Mixtures were melted at 150°C and vortexed before capillary filling into 30-μm photopatterned +1 defect or linear alignment cells at 100°C. Once filled, cells were cooled to 30°C and held for 20 min to allow for the alignment of liquid crystals. Materials were then photopolymerized with 365-nm light at 50 mW/cm2 for 5 min and subsequently removed from cells.
Lamination
Films of equivalent modulus were laminated by stacking with defect centers aligned and by pressing the films together with gentle heating at 90°C. Each 7-mm defect square of contrasting modulus was placed on a glass slide, and a spin coater was used to deposit C6M monomer and Omnirad 819 on the surface (60 s, 2000 rpm). C6M and Omnirad 819 were suspended in a solution of methanol (MeOH) and dichloromethane (DCM) [5:1 MeOH:DCM, C6M (10 mg/ml), and Omnirad 819 (0.25 mg/ml)]. Coated sides of films were pressed together with defect centers aligned, and the stacked films were heated at 90°C for 30 s before polymerization with 365-nm light at 50 mW/cm2 for 1 min. For laminated films with legs, small pieces of paper were cut to the appropriate size and attached to the bottom surface with Gorilla Super Glue.
Actuation
Films were placed with the high-modulus side in contact with a hot plate that had been preheated to 160°C. Films were left freestanding on the hot plate until snap-through occurred. Snap-through deformations were recorded using a Photron FASTCAM SA3.
Linearly aligned films were held at a constant force (0.0005 N) while temperature was ramped from 25° to 225°C (DMA 850, TA Instruments). Strain generation was measured as a function of temperature.
Cross-link density measurements
Dynamic mechanical analysis was conducted on diacrylate films using an RSA-G2 DMA (TA Instruments). The temperature was ramped from −50° to 150°C using 0.5% strain at a frequency of 1 Hz. Tg values were taken from the temperature corresponding to the maximum of tan(δ) for the material. The molecular weight between crosslinks (Mc) was calculated using the storage modulus value of the rubbery plateau at 150°C and the equation Mc = 3RTd/E′, where R is 8.314 cm3·MPa mol−1 K−1, T is the temperature, d is the density of the polymer network (1.2 g/cm3 for all materials), and E′ is the storage modulus at the corresponding temperature.
Tensile measurements
Tensile tests were conducted on linearly aligned films in both parallel and perpendicular orientation relative to the alignment. Strips were cut from the material and strained at a rate of 5%/min (RSA-G2 DMA, TA Instruments). Elastic modulus was calculated from the linear region of the stress-strain curve (2 to 4%).
Acknowledgments
Funding: This work was supported by the National Science Foundation Graduate Research Fellowship DGE 1650115 (to T.S.H.), National Science Foundation (DMR 2105369, to T.J.W.), and the U.S. Office of Naval Research through Multi-investigator University Research Initiative Grant (ONR N00014-18-1-2624, to K.K. and K.B.).
Author contributions: Conceptualization: T.J.W., C.N.B., and T.S.H. Experimental study: T.S.H. Computational study: K.K. and K.B. Supervision: T.J.W., C.N.B., and K.B. Writing—original draft: T.S.H., K.K., and T.J.W. Writing—review and editing: All authors.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper, the Supplementary Materials, or in a repository that can be found at doi.org/10.22002/stjfa-f1372.
Supplementary Materials
This PDF file includes:
Supplementary Text
Table S1
Fig. S1
References
Other Supplementary Material for this manuscript includes the following:
Movies S1 to S14
REFERENCES AND NOTES
- 1.M. Pilz da Cunha, S. Ambergen, M. G. Debije, E. F. G. A. Homburg, J. M. J. den Toonder, A. P. H. J. Schenning,A soft transporter robot fueled by light. Adv. Sci. 7,1902846 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.S. Chen, Y. Cao, M. Sarparast, H. Yuan, L. Dong, X. Tan, C. Cao,Soft crawling robots: Design, actuation, and locomotion. Adv. Mater. Technol. 5,1900837 (2020). [Google Scholar]
- 3.Z. Liu, R. Zhang, Y. Xiao, J. Li, W. Chang, D. Qian, Z. Liu,Somatosensitive film soft crawling robots driven by artificial muscle for load carrying and multi-terrain locomotion. Mater Horiz. 8,1783–1794 (2021). [DOI] [PubMed] [Google Scholar]
- 4.S. Gantenbein, K. Masania, W. Woigk, J. P. W. Sesseg, T. A. Tervoort, A. R. Studart,Three-dimensional printing of hierarchical liquid-crystal-polymer structures. Nature 561,226–230 (2018). [DOI] [PubMed] [Google Scholar]
- 5.M. P. da Cunha, M. G. Debije, A. P. H. J. Schenning,Bioinspired light-driven soft robots based on liquid crystal polymers. Chem. Soc. Rev. 49,6568–6578 (2020). [DOI] [PubMed] [Google Scholar]
- 6.E. Queathem,The ontogeny of grasshopper jumping performance. J. Insect Physiol. 37,129–138 (1991). [Google Scholar]
- 7.H. C. Astley, T. J. Roberts,Evidence for a vertebrate catapult: Elastic energy storage in the plantaris tendon during frog jumping. Biol. Lett. 8,386–389 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.H. C. Astley, T. J. Roberts,The mechanics of elastic loading and recoil in anuran jumping. J. Exp. Biol. 217,4372–4378 (2014). [DOI] [PubMed] [Google Scholar]
- 9.M. J. Schwaner, D. C. Lin, C. P. McGowan,Jumping mechanics of desert kangaroo rats. J. Exp. Biol. 221,jeb186700 (2018). [DOI] [PubMed] [Google Scholar]
- 10.M. Gomez, D. E. Moulton, D. Vella,Dynamics of viscoelastic snap-through. J. Mech. Phys. Solids 124,781–813 (2019). [Google Scholar]
- 11.Y. Kim, J. van den Berg, A. J. Crosby,Autonomous snapping and jumping polymer gels. Nat. Mater. 20,1695–1701 (2021). [DOI] [PubMed] [Google Scholar]
- 12.J. Jeon, J. C. Choi, H. Lee, W. Cho, K. Lee, J. G. Kim, J. W. Lee, K. Il Joo, M. Cho, H. R. Kim, J. J. Wie,Continuous and programmable photomechanical jumping of polymer monoliths. Mater. Today 49,97–106 (2021). [Google Scholar]
- 13.K. Korner, A. S. Kuenstler, R. C. Hayward, B. Audoly, K. Bhattacharya,A nonlinear beam model of photomotile structures. Proc. Natl. Acad. Sci. U.S.A. 117,9762–9770 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.H. Arazoe, D. Miyajima, K. Akaike, F. Araoka, E. Sato, T. Hikima, M. Kawamoto, T. Aida,An autonomous actuator driven by fluctuations in ambient humidity. Nat. Mater. 15,1084–1089 (2016). [DOI] [PubMed] [Google Scholar]
- 15.B. Gorissen, D. Melancon, N. Vasios, M. Torbati, K. Bertoldi,Inflatable soft jumper inspired by shell snapping. Sci Robot. 5,eabb1967 (2020). [DOI] [PubMed] [Google Scholar]
- 16.T. J. White, D. J. Broer,Programmable and adaptive mechanics with liquid crystal polymer networks and elastomers. Nat. Mater. 14,1087–1098 (2015). [DOI] [PubMed] [Google Scholar]
- 17.J. Küpfer, H. Finkelmann,Nematic liquid single crystal elastomers. Die Makromol. Chem. Rapid Commun. 12,717–726 (1991). [Google Scholar]
- 18.G. N. Mol, K. D. Harris, C. W. M. Bastiaansen, D. J. Broer,Thermo-mechanical responses of liquid-crystal networks with a splayed molecular organization. Adv. Funct. Mater. 15,1155–1159 (2005). [Google Scholar]
- 19.K. Fuchi, T. H. Ware, P. R. Buskohl, G. W. Reich, R. A. Vaia, T. J. White, J. J. Joo,Topology optimization for the design of folding liquid crystal elastomer actuators. Soft Matter 11,7288–7295 (2015). [DOI] [PubMed] [Google Scholar]
- 20.B. A. Kowalski, C. Mostajeran, N. P. Godman, M. Warner, T. J. White,Curvature by design and on demand in liquid crystal elastomers. Phys Rev E 97,012504 (2018). [DOI] [PubMed] [Google Scholar]
- 21.T. Guin, M. J. Settle, B. A. Kowalski, A. D. Auguste, R. V. Beblo, G. W. Reich, T. J. White,Layered liquid crystal elastomer actuators. Nat. Commun. 9,2531 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.M. Pilz da Cunha, Y. Foelen, R. J. H. Raak, J. N. Murphy, T. A. P. Engels, M. G. Debije, A. P. H. J. Schenning,Liquid crystal soft robot: An untethered magnetic- and light-responsive rotary gripper: Shedding light on photoresponsive liquid crystal actuators (Advanced Optical Materials 7/2019). Adv Opt Mater. 7,1970025 (2019). [Google Scholar]
- 23.A. Lebar, G. Cordoyiannis, Z. Kutnjak, B. Zalar, The isotropic-to-nematic conversion in liquid crystalline elastomers, in Liquid Crystal Elastomers: Materials and Applications, W. de Jeu, Ed. (Springer, 2010). [Google Scholar]
- 24.M. Ravi Shankar, M. L. Smith, V. P. Tondiglia, K. M. Lee, M. E. McConney, D. H. Wang, L. S. Tan, T. J. White,Contactless, photoinitiated snap-through in azobenzene-functionalized polymers. Proc. Natl. Acad. Sci. U.S.A. 110,18792–18797 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.C. P. Ambulo, J. J. Burroughs, J. M. Boothby, H. Kim, M. R. Shankar, T. H. Ware,Four-dimensional printing of liquid crystal elastomers. ACS Appl. Mater. Interfaces 9,37332–37339 (2017). [DOI] [PubMed] [Google Scholar]
- 26.M. Li, S. Lv, J. Zhou,Photo-thermo-mechanically actuated bending and snapping kinetics of liquid crystal elastomer cantilever. Smart Mater Struct. 23,125012 (2014). [Google Scholar]
- 27.D. Ge, K. Li,Pulsating self-snapping of a liquid crystal elastomer bilayer spherical shell under steady illumination. Int. J. Mech. Sci. 233,107646 (2022). [Google Scholar]
- 28.T. H. Ware, M. E. McConney, J. J. Wie, V. P. Tondiglia, T. J. White,Voxelated liquid crystal elastomers. Science 347,982–984 (2015). [DOI] [PubMed] [Google Scholar]
- 29.S. Ahn, T. H. Ware, K. M. Lee, V. P. Tondiglia, T. J. White,Photoinduced topographical feature development in blueprinted azobenzene-functionalized liquid crystalline elastomers. Adv. Funct. Mater. 26,5819–5826 (2016). [Google Scholar]
- 30.M. Warner,Topographic mechanics and applications of liquid crystalline solids. Annu. Rev. Condens. Matter Phys. 11,125–145 (2020). [Google Scholar]
- 31.L. T. de Haan, C. Sánchez-Somolinos, C. M. W. Bastiaansen, A. P. H. J. Schenning, D. J. Broer,Engineering of complex order and the macroscopic deformation of liquid crystal polymer networks. Angew. Chem. Int. Ed. Engl. 51,12469–12472 (2012). [DOI] [PubMed] [Google Scholar]
- 32.T. S. Hebner, H. E. Fowler, K. M. Herbert, N. P. Skillin, C. N. Bowman, T. J. White,Polymer network structure, properties, and formation of liquid crystalline elastomers prepared via thiol–acrylate chain transfer reactions. Macromolecules 54,11074–11082 (2021). [Google Scholar]
- 33.C. D. Modes, K. Bhattacharya, M. Warner,Gaussian curvature from flat elastica sheets. Proc. R. Soc. A 467,1121–1140 (2011). [Google Scholar]
- 34.M. Pezzulla, N. Stoop, M. P. Steranka, A. J. Bade, D. P. Holmes,Curvature-induced instabilities of shells. Phys. Rev. Lett. 120,048002 (2018). [DOI] [PubMed] [Google Scholar]
- 35.M. Taffetani, X. Jiang, D. P. Holmes, D. Vella,Static bistability of spherical caps. Proc. R. Soc. A 474,20170910 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.O. C. Zienkiewicz, R. L. Taylor, The Finite Element Method: Solid Mechanics (Butterworth-Heinemann, 2000), vol. 2. [Google Scholar]
- 37.D. Arndt, W. Bangerth, B. Blais, M. Fehling, R. Gassmöller, T. Heister, L. Heltai, U. Köcher, M. Kronbichler, M. Maier, P. Munch, J. P. Pelteret, S. Proell, K. Simon, B. Turcksin, D. Wells, J. Zhang,The deal.II library, version 9.3. J. Num. Math. 29,171–186 (2021). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Text
Table S1
Fig. S1
References
Movies S1 to S14