Integrated MCDM Approaches for Exploring the Ideal Therapeutic Plastic Disposal Technology: Probabilistic Hesitant Fuzzy Domain

Abstract

The probabilistic hesitant fuzzy set (PHFS) is a useful extended version of the hesitant fuzzy set (HFS), which allows decision-makers greater freedom in espousing their preferences through the use of hesitant evidence in the real DM method. As the implications for individuals and global concerns have grown, efficient clinical diagnosis of medical waste has been a major challenge, particularly in developing countries. Medical waste can be disposed of in a variety of ways. The essential thing is to decide which strategies work best. The optimal healthcare plastic waste disposal (HCPWD) option is a MCDM method involving a wide range of qualitative characteristics. The MCDM technique (ARAS) is then described, whereby the criterion weights are assessed using the recommended entropy weighted method (EWM) proportion and score function in order to increase the process utilisation. Moreover, the above-described approach is used to address a real-world problem by determining the optimal treatment option for healthcare waste (HCW) disposal. Finally, a feasibility analysis is given to support the stated viewpoint on HCPWD options being prioritised.

Introduction

Activities related to healthcare are ways to preserve health, treat patients, and save lives. However, they also produce trash, and 20% of that waste poses dangers for injury, infection, or exposure to chemicals or radiation. Although the dangers of handling hazardous medical waste and the methods for doing so are fairly well understood and covered in manuals and other literature, the International Committee of the Red Cross (ICRC) frequently encounters a lack of technical, financial, and legal support for the treatment and elimination methods advocated. Frequently, the personnel is ill-prepared to handle this task. Care professionals, workers who handle medical waste, patients and their relatives, and the local community can all be endangered by poor waste management. By approving its Constitution, any nation that is a United Nations member can join the WHO. When their application has been accepted by the World Health Assembly by a simple majority vote, other nations may be admitted as members. Upon application made on their behalf by the member or another entity responsible for their international relations, territories that are not in charge of the management of their international relations may be accepted as associate members. WHO members are divided into groups based on where they are located. Additionally, improper handling or disposal of such trash may pollute or contaminate the environment. Hazardous medical waste risks can be considerably decreased in unfavorable situations by taking sensible, practical steps. The goal of this document is to serve as a useful and practical tool for the normal management of hazardous hospital wastes. Under no circumstances does it take the place of any current national waste management laws or plans. Medical treatment and the disposal of healthcare waste (HCW) should be viewed as complementary processes. National Health Insurance (NHI) and the World Health Organization (WHO) have been collaborating to evaluate the clinical waste disposal of hospitals and laboratories in order to assess the quality of the hospitals because protecting plants and animals from medical waste is a significant social responsibility. The primary focus of hospital management is HCW. Environmental problems today are causing the spread of many different new diseases. Hospital trash is explicitly defined as human organs, infectious materials, fungi, bacteria, and viruses, as well as equipment used to clean blood vessels. As a result, these tragedies must be destroyed. The environment and human health will be negatively impacted by a range of diseases brought on by fungi, viruses, and bacteria if it is not properly disposed of. The present healthcare system concentrates on manipulating contemporary disposal techniques. Waste generally has an impact on the environment. Medical waste specifically has an impact on the environment and contains infections that cause disease in other organisms. The flora and animals as well as humans are at risk from these illnesses. In addition to being unhealthy, these medical wastes pose a direct risk of infection for hospital staff members such as doctors and nurses. The choice of medical waste discharge must be made in accordance with the climatic change and infection spread of the modern world. These days, different diseases spread in different ways; thus, this method is vital to stop that from happening. Various bacteria may emerge after hospital discharge and may impact human life. The primary purpose of the management system is to prevent the spread of infection from patient to patient, patient to hospital staff, and patient to others. This HCWT approach should be an excellent strategy to stop infectious diseases brought on by contagious microbes. In recent years, there have been hazards of waste disruption in pharmacies, medical clubs, hospitals, and basic health facilities. WHO is evaluating medical waste solutions through a number of medical organisations to solve these challenges. Therefore, a particularly secure system for disposing of medical waste is required, and not just for hospital financial reasons, but also for the protection of the public, the environment, and other living things. The “bio-medical waste management and handling” regulation was published in 1998 by the Ministry of Environment and Forestry. “Everyone shall guarantee that trash created is managed without any significant effect on human health or the environment,” reads this notification of Rule 4. The WHO published some regulations for the disposal of biomedical waste in 2018 and modified them in 2020. The nomenclature used in this manuscript is displayed in Table 1.

Table 1.

Nomenclature

DM	Decision-making
MCDM	Multi-criteria decision-making
PHFS	Probabilistic hesitant fuzzy set
HFS	Hesitant fuzzy set
PHFEs	Probabilistic hesitant fuzzy elements
ARAS	Additive ratio assessment method
CODAS	Combinative distance-based assessment
WASPAS	Weighted aggregated sum product assessment
VIKOR	VIseKriterijumska Optimizacija I Kompromisno Resenje
WHO	World Health Organization
HCPWD	Healthcare plastic waste disposal
HCW	Healthcare waste
EWM	Entropy weight method
SAW	Simple additive weight

Literature Review

The COVID-19 pandemic epidemic has made managing healthcare waste (HCW) one of the most challenging issues facing the medical community worldwide (Yu & et al., 2020). This may be because these HCWs may have come into contact with a variety of hazardous substances, including used needles and syringes, radioactive materials, dirty dressings, heavy metals, body parts, germs, diagnostic samples, blood, poisonous chemicals, medications, and medical equipment (Thakur & Ramesh, 2017). Due to the disease’s high contagiousness, there has been significant contamination of humans and other animals, including birds, mammals, and reptiles, which has caused a global disaster. Effective HCW management is essential to effectively stop the COVID-19 pandemic from spreading. To date, however, no research has focused on the best HCW disposal method selection for managing and controlling such pandemic epidemics. The primary reason for our concentration in this manner is the possibility that if HCWs are incorrectly handled and disposed of, COVID-19 could spread even more quickly and pose a serious risk to the lives of patients, healthcare workers, waste handlers, and members of society at large. Environmental damage is further exacerbated by improper healthcare waste disposal (Baghapour & et al., 2018). As a result, it is essential that all HCWs be correctly isolated at the time of generation, appropriately handled, and properly disposed (Badi & et al., 2019). Poor HCW treatment practises and unethical waste dumping tactics are frequently used in poor nations like India. Due to the infectious nature of the HCW, these inadequate HCW treatment practises and inappropriate waste disposal methods or procedures pose serious health risks and ecological degradation. With a population of almost 1.3 billion people and recent enormous developments in medical institutions, the problem of HCW management needs to be taken seriously (Minoglou & et al., 2017). According to studies from the Indian Society of Hospital Waste Management (ISHWM), a general practitioner’s clinic and hospitals are expected to produce at least 600 g of HCW per bed per day and at least 12 kg of HCW per bed per day, respectively. At least 5 to 10% of this is thought to be dangerous or infectious trash. Given the enormous number of patients in the nation, the daily generation of HCW is a sizable number that requires adequate management (Yu & et al., 2020). In order to effectively treat and dispose of hazardous and infectious wastes, efficient HCW management systems are required. In India, fewer than 50% of medical facilities use effective waste management techniques and even separate their garbage into contagious and non-infectious waste. Hospitals are solely responsible for ensuring that their HCW treatment and disposal practises will not have any negative effects on human health or the environment. According to a WHO estimate, at least 260,000 HIV infections, 2 million hepatitis C infections, and 21 million hepatitis B infections were all caused by injections with infected needles (Thakur & Ramesh, 2017). Therefore, it is crucial that HCW be properly handled and disposed of. This encourages us to create a tool for evaluating HCW disposal practises both before and after COVID-19 (Thakur & Ramesh A., 2015). Healthcare waste is defined by the World Health Organization (WHO) as waste produced by healthcare events that includes all types of resources, such as used medical instruments, injections, and toxic isotopes. According to the WHO, non-hazardous waste accounts for around 85% of HCW, and waste disposal accounts for 15%. The remaining 10%, on the other hand, is hazardous since it may contain infectious, highly contagious, and chemical waste (Patil & Shekdar, 2001). If not properly regulated or disposed of, it can constitute a threat to the environment and human health. WHO claims that improper handling of HCW has serious environmental impacts and on the general welfare evaluates healthcare waste disposal solutions using mixed decision support frameworks (Hinduja & Pandey, 2018). In Table 2, we give brief studies related to multi-criteria decision-making (MCDM) models for the study of HCWT disposal methods. One method for tackling problems is the MCDM procedure. The decision-situation maker’s and the problem scenario’s circumstances determine the decision-making procedures in all applications. Imagine that when determining the membership values, decision-makers’ judgments are based on ambiguous information. The following fuzzy theories are offered to address this fuzzy situation: The “father of fuzzy set theory” is Zadeh, who popularised the concept in 1965 (Zadeh, 1965). A development of fuzzy set theory is the hesitant fuzzy set. This hesitant fuzzy set theory has produced a wide range of operations and attributes that are used to reveal the reluctant reasoning of decision-makers. The evaluation of HCWD technologies might be regarded as a MCDM problem since HCWD systems provide capabilities for the categorisation of waste produced by healthcare institutions. A rigorous and serious approach is required to properly handle this necessary topic. Several studies have shown the significance of selecting the right waste treatment technologies (Lee & et al., 2016). Jiang and Ma (2018) used Frank t-norm and t-conorm to provide a number of PHFE procedures, and then subsequently applied those processes to a group decision-making problem with several criteria. Zhang et al. (2017) presented two normalised hesitant fuzzy prediction models based on the invertible t-norm and t-conorm and created the PHFS concept, all of which provide case studies on the PHFE Farhadinia (2015, 2017). The EWM is a well-known intelligence weighting model that has received a lot of attention (Zhi-Hong & et al., 2006). The EWM’s primary advantage over other subjective weighting approaches is that it prevents human influences from distorting the weight of measures, which improves the overall neutrality of the assessment process (Ding & et al., 2017). As a result, the EWM has been popular recently (Taheriyoun & et al., 2010). Fuzzy MCDM approaches, such as fuzzy CODAS, fuzzy VIKOR, fuzzy MULTIMOORA, fuzzy WASPAS, fuzzy ARAS, and fuzzy PROMETHEE, assess alternative ratings and weights of criteria based on the imprecision and vagueness conveyed by fuzzy numbers. Decision-makers are required to offer preferences in AHP and ANP instances. The first study on fuzzy AHP, published by Saaty (1990), used the fuzzy (AHP) to assess excavation possibilities based on a variety of decision criteria. Numerous researchers updated and implemented these strategies to tackle selection difficulties in diverse professions.

Table 2.

MCDM methods for study of HCWT disposal methods

Authors	MCDM methods for study of HCWT disposal methods
Ferreira and Teixeira (2010)	Evaluation of MCDM problem for analysing the practices of
	healthcare waste (HCW) methodology in hospitals of the
	Algae region, Portugal
Vinogradova et al. (2018)	Integrated weight finding method in MCDM problem
Hassan et al. (2018)	Evaluation of discussed healthcare waste (HCW)
	among its types of categories
Keshavarz Ghorabaee et al. (2016)	A new combination distance-based assessment (CODAS)
	method for multi-criteria decision-making
Kalantary et al. (2021)	Effect of COVID-19 pandemic on medical waste management
Brans J. P. and Vincke P. (1985)	A preference ranking organisation method,
	the PROMETHEE method for MCDM
Brauers and Zavadskas (2010)	Project management by MULTI-MOORA as
	an instrument for transition economies
Ding et al. (2017)	Fuzzy comprehensive assessment method based on the
	EWM and its application in the water environmental
	safety evaluation of the Heshangshan drinking water source area
Glaize (2019)	Healthcare decision-making applications using
	multi-criteria decision analysis
Chauhan and Singh (2016)	Hybrid MCDM method of interpretative structural modeling
	with AHP, TOPSIS
Dheeraj et al. (2022)	Probabilistic hesitant fuzzy set-based MCDM method
	with applications in portfolio selection process
Wang and Liang (2006)	Multi-criteria decision analysis by using fuzzy VIKOR
Brauers and Zavadskas (2010)	Optimisation of weighted aggregated sum product assessment
Turskis and Zavadskas (2010)	A new fuzzy additive ratio assessment method (ARAS-F),
	case study: the analysis of fuzzy multiple criteria in order
	to select the logistic centers location

In this research work, we introduce the concept of the PHFS-ARAS method of the MCDM problem to select the best HCWT disposal. This research paper is organised as follows: In Section 3, we present the definition of a probabilistic hesitant fuzzy set, its operations, and the score function found in the literature. In Section 4, we give proposed methodologies for weight finding and ranking algorithms. In Section 5, we select, suitable real-time application of HCW disposal treatment technology and evaluated by the proposed method. We describe the method for collecting the best healthcare plastic waste disposal method, as well as a comparison analysis and a sensitive analysis of the proposed methodology in Sections 6 and 7. In Section 8, we conclude the advantages of the proposed method and determine how to select the best BMW disposal treatment.

Motivation and Objective

In this study article, we aim to select the finest HCWT disposal treatment method. We have chosen the ARAS optimisation methodology from the MCDM model’s outranking method to address this issue. Additionally, we are choosing one of the MCDM model’s integrated objective weight finding methods. We are prompted to expand our chosen MCDM approaches, entropy and ARAS, in a speculative fuzzy environment by the review section in Table 2 that is mentioned above. Numerous writers from the literature have worked on the implementation of HCWT management in MCDM. And only a small number of authors have used fuzzy MCDM in this application. A few authors have also used PHF-MCDM to work on this application. The tentative fuzzy integrated weighting method has not yet been used in PHF-MCDM. We suggest PHF MCDM with a probabilistic hesitant fuzzy integrated weight technique to close this knowledge gap. Decision-makers have the opportunity to pause and experience uncertainty when presented with the values for choosing the best alternative when using the proposed weight-finding process and ranking method. In addition, the HCWT management programme has a number of hesitant and ambiguous phrases, as well as some ambiguous requirements. The membership values are assigned using a probabilistic hesitant fuzzy set that contains probabilistic hesitant fuzzy components (PHFEs). Therefore, it can be claimed that the primary motivation behind our research is the application of HCWT to PHFEs.

Contribution

This research paper’s primary goal and contribution can be summed up as follows: First and foremost, the primary contribution of this study is the novel approach to multi-criteria decision-making (MCDM) methods that we propose (probabilistic hesitant fuzzy objective weight integrated approach (PHF-Entropy) and probabilistic hesitant fuzzy additive ratio assessment method (PHF-ARAS)). The approach for obtaining weights is the second contribution. The third contribution of our work is that we are implementing the methods we have suggested for the management of HCWT, i.e. we have used the methods we have suggested to determine the optimum HCW disposal treatment procedures and also determined the weights of criteria. Our fourth contribution to our work is the comparison of our outcomes with those of existing methods to demonstrate the effectiveness of our suggested methods. In this section of the comparison, we have contrasted the PHF-ARAS ranking algorithm we have presented with well-liked fuzzy MCDM (PHF-MCDM) approaches, including PHF-CODAS, PHF-WASPAS, and PHF-VIKOR. This research paper’s fifth contribution from us is a discussion of our findings in light of various sensitivity analyses and variation problems. Instead of employing integrated weights in our suggested PHFS-Entropy method, we changed the objective weights in this section of the sensitivity analysis. The conclusion of the suggested probabilistic hesitant fuzzy multi-criteria decision-making approaches is the next step. We anticipate that the contribution of our suggested approaches will offer the finest BMW disposal treatment approach in this HCWT situation. Consequently, our work is regarded as a useful technique for choosing the appropriate treatment for BMW.

Preliminaries

Definition 1

(Torra, 2010); (Xia & Xu, 2011) Let R be the universal set. Defined by the hesitant fuzzy set (HFS) on R in finite subset of [0,1]. It is denoted by

$$G=\{\langle x,g(x)\rangle /x\in R\}$$

where g(x) ∈ [0,1] as the HFE, which denotes the element’s possible membership degree x ∈ R to the set G.In the HFS, G can be represented in terms of

$$G=\left\{〈x,\bigcup _{g\in g(x)}\{g\}〉/x\in R\right\}$$ 1

Let $g={\bigcup }_{\mathit{\text{g}}\in g}\{\mathit{\text{g}}\},g_1={\bigcup }_{{\mathit{\text{g}}}_1\in g_1}\{{\mathit{\text{g}}}_1\}\text{and}{g}_2={\bigcup }_{{\mathit{\text{g}}}_2\in g_2}\{{\mathit{\text{g}}}_2\}$ are implied to be three HFEs, then the following operations on them are identified.

$$\begin{array}{rcl}{g}^c=\bigcup _{\mathit{\text{g}}\in g}\{1-\mathit{\text{g}}\}& & \end{array}$$

$$\begin{array}{rcl}{g}_1\cup g_2& =& \bigcup _{{\mathit{\text{g}}}_1\in g_1,{\mathit{\text{g}}}_2\in g_2}\max \{{\mathit{\text{g}}}_1,{\mathit{\text{g}}}_2\};\\ g_1\cap g_2& =& \bigcup _{{\mathit{\text{g}}}_1\in g_1,{\mathit{\text{g}}}_2\in g_2}\min \{{\mathit{\text{g}}}_1,{\mathit{\text{g}}}_2\}\end{array}$$

$$\begin{array}{rcl}{g}^{\kappa }& =& \bigcup _{\mathit{\text{g}}\in g}\{{\mathit{\text{g}}}^{\kappa }\};\kappa g=\bigcup _{\mathit{\text{g}}\in g}\{1-{(1-\mathit{\text{g}})}^{\kappa }\}\kappa >0\\ & & \end{array}$$

$$\begin{array}{rcl}{g}_1\oplus g_2& =& \bigcup _{{\mathit{\text{g}}}_1\in g_1,{\mathit{\text{g}}}_2\in g_2}\{{\mathit{\text{g}}}_1+{\mathit{\text{g}}}_2-{\mathit{\text{g}}}_1{\mathit{\text{g}}}_2\};\\ g_1\otimes g_2& =& \bigcup _{{\mathit{\text{g}}}_1\in g_1,{\mathit{\text{g}}}_2\in h_2}\{{\mathit{\text{g}}}_1{\mathit{\text{g}}}_2\}\\ & & \end{array}$$

Definition 2

(He & Xu, 2019) The probabilistic hesitant fuzzy set (PHFS) was embraced, indicating that each possible value of HFE can be affiliated with a probability value that exists . The PHFS on R was defined as follows:

$$\begin{array}{rcl}{}^{\gamma }G& =& \{\langle x,{}^{\gamma }g(x)\rangle :x\in R\}\\ & =& \left\{〈x,\bigcup _{\langle \mathit{\text{g}}(x),\gamma (x)\rangle \in {}^{\gamma }g(x)}\{\langle \mathit{\text{g}}(x),\gamma (x)\rangle \}〉/x\in R\right\}\\ & & \end{array}$$ 2

A PHFEs, ^γg(x) constitute both of membership degrees x ∈R being defined by g(x) in addition to the probability of γ(x)∈ [0,1], such that ${\sum }_{{}^{\gamma }g(x)}\gamma (x)=1$ for any x ∈R.If ${}^{\gamma g}={\bigcup }_{\langle \mathit{\text{g}},\gamma \rangle \in {}^{\gamma }g}\{\langle \mathit{\text{g}},\gamma \rangle \},{}^{\gamma }{g}_1={\bigcup }_{\langle {\mathit{\text{g}}}_1,{\gamma }_1\rangle \in {}^{\gamma }{g}_1}\{\langle {\mathit{\text{g}}}_1,{\gamma }_1\rangle \}$ and ${}^{\gamma }{g}_2={\bigcup }_{\langle {\mathit{\text{g}}}_2,{\gamma }_2\rangle \in {}^{\gamma }{g}_2}\{\langle {\mathit{\text{g}}}_2,{\gamma }_2\rangle \}$ Consider the three PHFEs, the presenting some operations,

$$\begin{array}{rcl}{}^{\gamma }{g}^{\kappa }=\bigcup _{\langle \mathit{\text{g}},\gamma \rangle {\in }^{\gamma }g}\{\langle {\mathit{\text{g}}}^{\kappa },\gamma \rangle \}& & \end{array}$$

$$\begin{array}{rcl}{\kappa }^{\gamma }g=\bigcup _{\langle \mathit{\text{g}},\gamma \rangle {\in }^{\gamma }g}\{\langle 1-{(1-\mathit{\text{g}})}^{\kappa },\gamma \rangle \}& & \end{array}$$

$$\begin{array}{rcl}{}_1^{\gamma g}{\oplus }^{\gamma }{g}_2=\bigcup _{\langle {\mathit{\text{g}}}_1,{\gamma }_1\rangle {\in }^{\gamma }{g}_1,\langle {\mathit{\text{g}}}_2,{\gamma }_2\rangle {\in }^{\gamma }{g}_2}\{\langle 1-(1-{\mathit{\text{g}}}_1)(1-{\mathit{\text{g}}}_2),{\gamma }_1{\gamma }_2\rangle \}& & \end{array}$$

$$\begin{array}{rcl}{}_1^{\gamma g}{\otimes }_2^{\gamma g}=\bigcup _{\langle {\mathit{\text{g}}}_1,{\gamma }_1\rangle {\in }^{\gamma g_1},\langle {\mathit{\text{g}}}_2,{\gamma }_2\rangle {\in }^{\gamma }{g}_2}\{\langle {\mathit{\text{g}}}_1{\mathit{\text{g}}}_2,{\gamma }_1{\gamma }_2\rangle \}& & \end{array}$$

Definition 3

(Jiang & Ma, 2018) Let $\left({}^{\gamma }g(x)\right)=\left\{{\gamma }_i\left(g_i\right)/i=1,2,\dots ,\#g\right\}$ a PHFEs, the score (mean value) function is defined by:

$$S\left({}^{\gamma }g(x)\right)=\sum _{i=1}^{\#g}{\gamma }_i{g}_i\mathrm{.}$$

where γ_i is the probability of possible value ^γg(x) exhilarating $\sum _{i=1}^{\#g}{\gamma }_i=1$, # g is the number of different PHFEs in ^γg(x).

Methodology

The Entropy Weight Method

In this procedure, the analysis is set up with m indicators and n samples, and the optimum value of the i th indicator in the j th instance is noted as x_ij. The normalisation of values obtained is the first stage (Gorgij & et al., 2017). ${\tilde{D}}_{ij}$ stands for the standardised value of the i th index in the j th sample, and it is calculated based on:

$${\tilde{D}}_{ij}=\frac{x_{ij}}{{\sum }_{j=1}^n{x}_{ij}}$$ 3

The entropy value F_i is defined as follows (Liu & et al., 2010):

$$F_i=-\frac{{\sum }_{j=1}^n{\tilde{D}}_{ij}\cdot \ln {\tilde{D}}_{ij}}{\ln n}$$ 4

${\tilde{D}}_{ij}\mathrm{.}ln{\tilde{D}}_{ij}=0$ is often set when ${\tilde{D}}_{ij}$ = 0 in the actual evaluation utilising the EWM for calculating ease. $F_i\prime$ has a range of [0,1]. As more the differentiation degree of index i, the greater the amount of information that may be extracted. As a result, in the EWM, the weight w_i calculating method is (Zhi-Hong & et al., 2006).

$$w_i=\frac{1-F_i}{{\sum }_{i=1}^m\left(1-F_i\right)}$$ 5

The Proposed MCDM-ARAS Method

As previously stated proposed the ARAS approach (Turskis & Zavadskas, 2010). Forming the decision matrix and setting, the weights of criteria are the first steps in addressing decision-making issues using the ARAS approach, as they are in the other MCDM methods. Following these first steps, the remaining part of the MCDM issue solution utilising the ARAS approach may be accurately described as follows:

• Stage 1. Determine the best possible score for each criterion. The ideal performance ratings are derived as follows if the decision-maker has no priorities:

  $$x_{0j}=\left\{\begin{array}{cc}\underset{i}{\max }{x}_{ij},& j\in {\mathrm{\Delta }}_{\max }\\ \underset{i}{\min }{x}_{ij},& j\in {\mathrm{\Delta }}_{\min }\end{array}\right)$$ 6

  where x_0j indicates the j th criterion’s ideal quality performance,${\mathrm{\Delta }}_{\max }$denotes the beneficial criteria, and ${\mathrm{\Delta }}_{\min }$ means the non-beneficial criteria.
• Stage 2. Calculate the decision matrix that has been normalised. The following formula is used to obtain the normalised performance:

  $$r_{ij}=\left\{\begin{array}{cc}\frac{x_{ij}}{{\sum }_{i=1}^m{x}_{ij}},& j\in {\mathrm{\Delta }}_{\max },\\ \frac{(1/x_{ij})}{{\sum }_{i=1}^m(1/x_{ij})},& j\in {\mathrm{\Delta }}_{\min }\end{array}\right)$$ 7
• Stage 3. The following equations are used to compute the weighted normalised performance in the organisation:

  $$v_{ij}=w_j\ast r_{ij},$$ 8
• Stage 4. Evaluate each alternative’s total performance rating. To calculate total performance, use the following equation:

  $$S_i=\sum _{j=1}^n{v}_{ij}(i=0,1,2,\mathrm{...},m)$$ 9

  where S_i signifies the overall rating of the i th choice.
• Stage 5. Comparing the variant under analysis with the ideal best one, S₀, yields information about the level of alternative utility. The following equation is used to determine an alternative T_i’s utility degree K_i:

  $$Q_i=\frac{S_i}{S_0},(i=0,1,2,\mathrm{...},m)$$ 10

where S_i and S₀ are the optimality criterion values, obtained from Eq. (9) , and S₀ is the ideal alternative’s total performance.

It is obvious that the calculated values K_i are inside the range [0,1] and that they may be arranged in the required order of priorities in an increasing sequence. The utility function values can be used to calculate the complicated relative efficiency of the feasible alternative.

Case Study of HCWT Disposal

The Biomedical Sewage Treatment and Dispatching Regulations have brought healthcare plastic waste management to the forefront in India (1998). One of the most essential aspects is the choice of HCW disposal treatment. In order to describe the current application of waste disposal treatment method selection for HCW, we take into consideration the case study reported in Liu et al. (2010). We discuss five potential HCW therapy approaches that have been developed in this study work. The best treatment approach must be chosen in order to solve this issue, and the chosen treatment options must also be ranked. The current situation is being investigated based on a variety of factors, including the type and level of waste generated, how it is handled, treated, and disposed of, and some nutrition aspects. Agencies in a number of regions are failing to put in place acceptable systems owing to a lack of proper technology, economic ability, and solid waste technical programs. With the rising risks connected with this HCW disposal and flaws in the current procedure, determining the optimum methodology for the treatment of this infectious waste has become critical. In this context, utilising the ARAS approach, we suggested an MCDM technique for calculating and choosing HCW disposal options. We used the above-mentioned probabilistic hesitant fuzzy entropy and score value to evaluate the criterion weights and the suggested approach to determine the hierarchy of preferences for the HCW disposal alternatives. As shown in Fig. 1 , the explanation of HCW disposal treatment techniques and alternatives is as follows:

• Plasma pyrolysis (T₁): It is a simulation technique that uses thermal plasma to convert high-calorie plastic trash into valuable bio gas. In an oxygen-deprived atmosphere, organic compounds are broken down into gases and non-leachable solid wastes using plasma pyrolysis technology. In order to break down compounds, plasma pyrolysis makes use of a significant amount of electrons, ions, and excited molecules as well as high-energy radiation.

• Combustion (T₂): In the chemical process of combustion, an object quickly combines with oxygen to produce heat. Fuel is the term for the original substance, and oxidiser refers to the source of oxygen. Although it is typically a liquid for aeroplane propulsion, the fuel can be a solid, liquid, or gas. It is a waste-to-non-combustible-residues-and-gases conversion method that uses high temperatures. Several variables inhibit and reduce waste generation, which also depends on local circumstances. Although this method is extraordinarily successful in removing all sorts of garbage, it creates enormous volumes of harmful gases that are hazardous to public health. Hence, waste should be used or recycled wherever feasible.

• Microwave sterilisation (T₃): It is a method of sterilising garbage using humid heat and steam generated by microwave radiation. It is a radiation and disposal treatment that eliminates particles and other hazardous species like bacteria, and also all substances, infected injections, and antiseptic surgical equipment, including the thermo bio indicator. Most bacteria are destroyed by microwaves with a spectrum of around 2.45 GHz and a diameter of 12.24 NM. This is a very common misinterpretation.

• Steam disinfection (T₄): The gravity displacement autoclave and the high-speed prevacuum steriliser are the two fundamental varieties of steam sterilisers (autoclaves). It is made by exposing the chemicals to saturated high-pressure steam to neutralise them. It improves the ability of warmth to kill germs by reducing temperature and time, both of which serve to dehydrate microbe proteins. This is a very common misinterpretation.

• Chemical disinfection (T₅): It is a chemical procedure that is used to render microorganisms inactive. A chemical using NaOCl as a sanitiser is used in this therapy method. Disinfection is a process that lowers the quantity of microbes to a point where they pose no threat. Disinfection is distinct from sterilisation, which results in the removal of all live microorganisms from the thing. Chemical disinfectants are ideally suited to the treatment of liquid waste, such as blood, syringes, and other springy objects, urination, hospital sewage, and contaminated glassware, all of which must be treated first. Chemicals, on the other hand, can be used to sterilise solid waste, microorganism cultures, human fluids, and so on.

Fig. 1.

Methods for healthcare waste treatment disposal

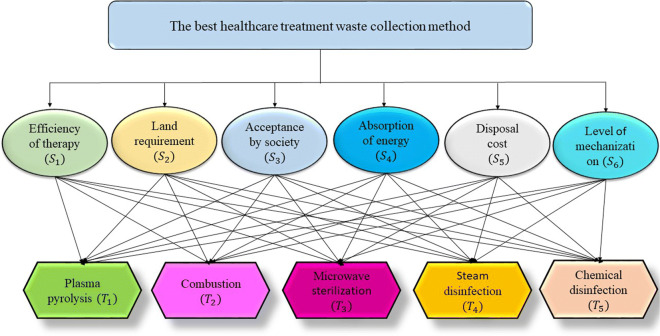
The following criteria are used to evaluate the above-mentioned options: (S₁) Efficiency of therapy, (S₂) Land requirement, (S₃) Acceptance by society, (S₄) Absorption of energy, (S₅) Disposal cost, (S₆) Level of mechanisation. The cost parameters for determining the optimum HCPWD option are (S₅) and (S₆). A group of four debate specialists from various fields has been formed. Figure 2 shows the ordered structure for Selecting the best Healthcare Treatment Waste Disposal Collection Methods approach.

Fig. 2.

Selecting the best healthcare treatment waste disposal collection method

The PHFEs in Entropy Weight Method

Now evaluate the following decision matrix, in which the elements are PHFEs:

$$\begin{array}{rcl}D=\left[\begin{array}{cccc}& S_1& S_2& \cdots S_n\\ T_1& {}^{\gamma }{g}_{11}& {}^{\gamma }{g}_{12}& {}^{\gamma }{g}_{1n}\\ T_2& {}^{\gamma }{g}_{21}& {}^{\gamma }{g}_{22}& {}^{\gamma }{g}_{2n}\\ ⋮& ⋮& ⋮& ⋮\\ T_m& {}^{\gamma }{g}_{m1}& {}^{\gamma }{g}_{m2}& {}^{\gamma }{g}_{mn}\end{array}\right]\mathrm{.}& & \end{array}$$

where ${}^{\gamma }{g}_{ij}$ (i= 1,…,m, j= 1,…,n) indicates the score of alternative T_i comparable to the criteria S_j with the weight of w_j. Then how to compare qualitative and quantitative data? Prioritising the factors (criteria) affecting the goal of DM and selecting the best alternative by using the linguistic conversion scale Table 3. Which are summarised in the PHF following definition (3) as shown in the Table 4 decision matrix.

• Step 1: Definition (5) is used to calculate the probabilistic hesitant score matrix. Table 5 shows the results.

• Step 2: The normalised matrix is created by using Eq. 3. Table 6 displays the results.

• Step 3: Utilising (4), the probabilistic hesitant EWM is determined for all the criteria (Tables 7 and 8).

  F_i = {0.089814882,0.045571813, 0.062613882,0.546841747,0.029643991, 0.079768656},where i = {1,2....6}.

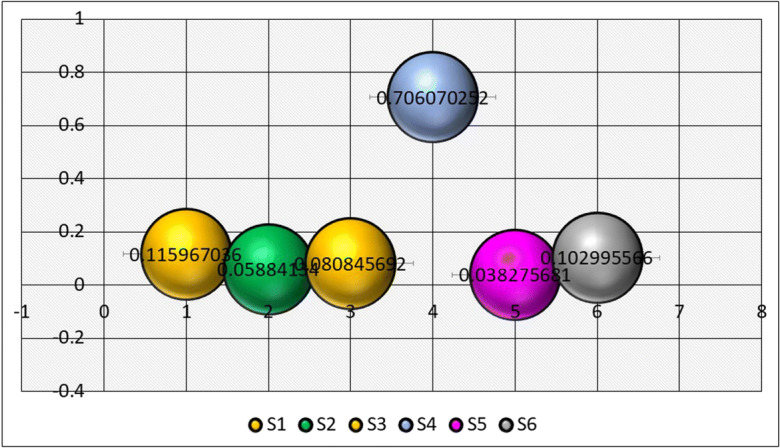
• Step 4: We compute the weights of each condition using Eq. 5, and the resultant values of the evaluation criteria are visualised in Fig. 3.

  w_i = {0.115967036,0.05884134, 0.080845692,0.706070252,0.038275681, 0.102995566}, where i = {1,2....6}.

Table 3.

Linguistic conversion scale and their corresponding PHFEs

Linguistic term	Numerical values with PHFEs
Exceptional	{〈0.8, 0.5〉,〈1.0, 0.5〉}
Very good	{〈0.7, 0.6〉,〈0.8, 0.4〉 }
Satisfactory	{〈0.5, 0.4〉,〈0.7, 0.6〉}
Average	{〈0.3, 0.7〉,〈0.5, 0.3〉}
Insufficient	{〈0.1, 0.8〉,〈0.3, 0.2〉}

Table 4.

The PHF decision matrix

S1	S2	S3
T1 {〈0.4, 0.6〉,〈0.5, 0.4〉}	{〈0.3, 0.7〉,〈0.4, 0.3〉}	{〈0.2, 0.4〉,〈0.3, 0.6〉}
T2 {〈0.6, 0.2〉,〈0.7, 0.8〉}	{〈0.8, 0.2〉,〈0.9, 0.8〉}	{〈0.2, 0.8〉,〈0.3, 0.2〉}
T3 {〈0.5, 0.5〉,〈0.6, 0.5〉}	{〈0.4, 0.2〉,〈0.3, 0.8〉}	{〈0.7, 0.6〉,〈0.8, 0.4〉}
T4 {〈0.7, 0.2〉,〈0.8, 0.8〉}	{〈0.6, 0.5〉,〈0.7, 0.5〉}	{〈0.5, 0.3〉,〈0.6, 0.7〉}
T5 {〈0.5, 0.3〉,〈0.6, 0.7〉}	{〈0.5, 0.5〉,〈0.6, 0.5〉}	{〈0.8, 0.2〉,〈0.9, 0.8〉}
S4	S5	S6
{〈0.6, 0.5〉,〈0.7, 0.5〉}	{〈0.6, 0.3〉,〈0.7, 0.7〉}	{〈0.6, 0.4〉,〈0.7, 0.6〉}
{〈0.3, 0.2〉,〈0.4, 0.8〉}	{〈0.5, 0.5〉,〈0.6, 0.5〉}	{〈0.5, 0.3〉,〈0.6, 0.7〉}
{〈0.7, 0.5〉,〈0.8, 0.5〉}	{〈0.3, 0.2〉,〈0.4, 0.8〉}	{〈0.5, 0.3〉,〈0.6, 0.7〉}
{〈0.6, 0.2〉,〈0.7, 0.8〉}	{〈0.4, 0.6〉,〈0.5, 0.4〉}	{〈0.1, 0.5〉,〈0.2, 0.5〉}
{〈0.1, 0.6〉,〈0.2, 0.4〉}	{〈0.2, 0.4〉,〈0.3, 0.6〉}	{〈0.2, 0.8〉,〈0.3, 0.2〉}

Table 5.

The PHF score matrix

	S1	S2	S3	S4	S5	S6
T1	0.44	0.33	0.66	0.65	0.67	0.66
T2	0.68	0.88	0.22	0.38	0.55	0.57
T3	0.55	0.32	0.74	0.75	0.38	0.57
T4	0.78	0.65	0.57	0.68	0.44	0.15
T5	0.57	0.55	0.26	0.14	0.26	0.22

Table 6.

Normalised PHF score matrix

	S1	S2	S3	S4	S5	S6
T1	0.181818	0.120879	0.269388	0.063725	0.291304	0.304147465
T2	0.033058	0.322344	0.089796	0.037255	0.23913	0.262672811
T3	0.227273	0.117216	0.302041	0.073529	0.165217	0.262672811
T4	0.322314	0.238095	0.232653	0.066667	0.191304	0.069124424
T5	0.235537	0.201465	0.106122	0.013725	0.113043	0.101382488

Table 7.

Efficiency performance ranking for each alternatives (S_i)

Alternatives	Si
T0	0.254212045
T1	0.182937076
T2	0.133027187
T3	0.213051806
T4	0.227615128
T5	0.092152324

Table 8.

Degree of utility for each alternatives (K_i)

Alternatives	Ki
T0	1
T1	0.719624
T2	0.523292
T3	0.838087
T4	0.895375
T5	0.362502

Fig. 3.

Weights of the criteria

The PHFE-Based ARAS Methodology

• Stage 1.Compute the optimal performance PHF score matrix for each criterion by using Eq. (6). The results are shown in Table 9.

• Stage 2 Compute the normalised PHF decision score matrix by using Eq. (7). The results are shown in Table 10.

• Stage 3 Compute the weighted normalised PHF decision matrix, using the following Eq. (8). The results are shown in Table 11.

• Stage 4 Determined the efficiency performance ranking for each alternative, using the following Eq. (9). The results are shown in Table 7.

• Stage 5 Compute the degree of utility for each alternative, using the following Eq. (10). The results are shown in Table 8.

Table 9.

Optimal performance PHF score matrix

	S1	S2	S3	S4	S5	S6
T0	0.78	0.88	0.74	0.75	3.846154	6.666667
T1	0.44	0.33	0.66	0.65	1.492537	1.515152
T2	0.68	0.88	0.22	0.38	1.818182	1.754386
T3	0.55	0.32	0.74	0.75	2.631579	1.754386
T4	0.78	0.65	0.57	0.68	2.272727	6.666667
T5	0.57	0.55	0.26	0.14	3.846154	4.545455

Table 10.

Normalised probabilistic hesitant score matrix

	S1	S2	S3	S4	S5	S6
T0	0.205263	0.243767	0.231975	0.223881	0.241785	0.291086
T1	0.115789	0.091413	0.206897	0.19403	0.093827	0.066156
T2	0.178947	0.243767	0.068966	0.113433	0.114298	0.076602
T3	0.144737	0.088643	0.231975	0.223881	0.165432	0.076602
T4	0.205263	0.180055	0.178683	0.202985	0.142873	0.291086
T5	0.15	0.152355	0.081505	0.041791	0.241785	0.198468

Table 11.

Weighted normalised probabilistic hesitant score matrix

	S1	S2	S3	S4	S5	S6
T0	0.023804	0.014344	0.018754	0.158075	0.009254	0.029981
T1	0.013428	0.005379	0.016727	0.136999	0.003591	0.006814
T2	0.020752	0.014344	0.005576	0.080092	0.004375	0.00789
T3	0.016785	0.005216	0.018754	0.158075	0.006332	0.00789
T4	0.023804	0.010595	0.014446	0.143322	0.005469	0.029981
T5	0.017395	0.008965	0.006589	0.029507	0.009254	0.020441

The options are prioritised in sorted order. To determine the proper rankings of alternatives, AS_i results are selected from highest to lowest. The degree of the alternatives’ utility, which is determined by a comparison of the variant, which is analysed with the most optimal value of T₀. The steam disinfection (T₄) alternative is the greatest in this ranking, while the chemical disinfection (T₅) alternative is the worst as shown in Fig. 4.

$$\begin{array}{rcl}{T}_4>T_3>T_1>T_2>T_5& & \end{array}$$

Fig. 4.

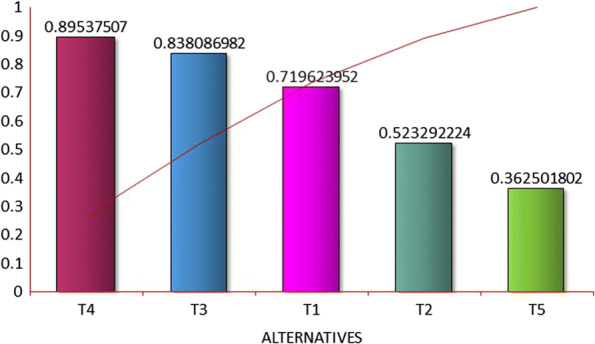
The proposed PHF-ARAS method

Comparison Analysis

The suggested method’s validity is determined by comparing the acquired findings to those obtained using PHFS-based extended CODAS, WASPAS, and VIKOR techniques for the same data set. When compared to other MCDM approaches, the ARAS method produces more realistic results and is more stable. The VIKOR and CODAS procedures are less effective at ranking the alternatives with an optimal solution because in the ARAS approach, results are averaged but criteria sorting is not really taken into account.

The evaluation of four feature-rich MCDM approaches:

WASPAS:

Problems involving multiple-criteria decision-making are straightforward and simple to solve.

VIKOR:

The decision-makers will be more prepared to accept compromise solutions if you maximise group advantages and reduce individual regret.

CODAS:

Making decisions is a useful technique for improving performance in any subject, especially one that calls for processing a lot of data and experience. Making decisions under such circumstances can frequently be challenging. The WASPAS method exploits the advantages of the additive ratio assessment (ARAS) method the best. Combining ARAS and WASPAS increases the ranking accuracy of the alternatives. In that phase, WASPAS calculates an optimal combination parameter. Because the ARAS approach is more sector-inclusive than the other MCDM methods, we use it to choose the best healthcare waste treatment collection method. Table 12 contains the results, which are visually illustrated in Fig. 5.

Table 12.

Comparison of ranking results

	WASPAS	Rank	VIKOR	Rank	CODAS	Rank	ARAS	Rank
T1	0.66686	3	0	1	− 0.13117	4	0.7196	3
T2	0.51101	4	0.401809	3	− 0.30767	5	0.5232	4
T3	0.78452	2	0.079449	2	0.109653	2	0.8380	2
T4	0.86688	1	0.580732	4	0.365326	1	0.8953	1
T5	0.35683	5	0.888539	5	− 0.03178	3	0.3625	5

Fig. 5.

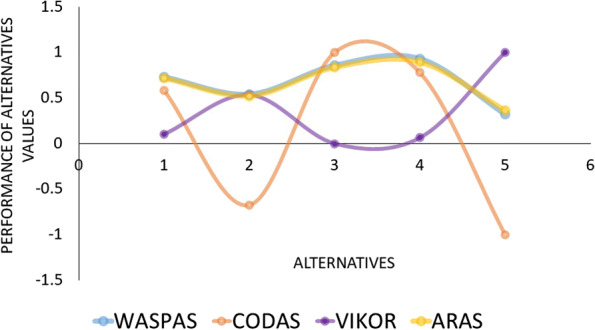
Comparison analysis

Sensitivity Analysis

Sensitivity analysis is carried out using different cases of the criteria weights. The ARAS method produces more realistic results and is more stable.

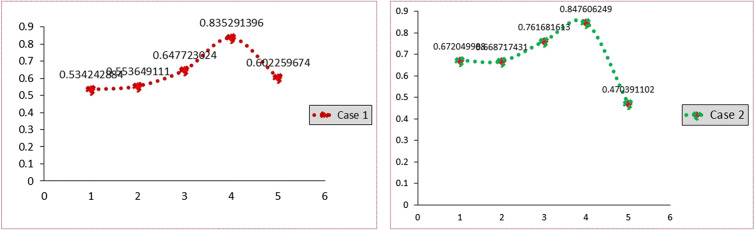
• Case 1: When it comes to successful criteria, assigning weights to both beneficial and non-beneficial criteria at equal weights is 0.1667.

• Case 2: When it comes to assigning weights for beneficial criteria, 0.25 is the weight, and for non-beneficial criteria, 0 is the weight. The ranking displayed in Table 10 indicates that T₄ is truly the greatest option and T₁ has to be the worst alternative in the creative best healthcare plastic waste disposal challenge, based on the sensitivity analysis of several conceivable settings for the fuzzy ARAS approach. When compared to two distinct circumstances, the categorisation of the options shows a high level of consistency, despite modest changes in the findings. An investigation into the validity of the proposed approaches with regard to the two cases in Table 13 was conducted. Figure 6 shows how the weighting of the criterion was changed to generate two unique situations.

Table 13.

Sensitivity analysis ranked results

Alternative	ARAS (case 1)	Rank	ARAS (case 2)	Rank
T1	0.534243	5	0.67205	3
T2	0.553649	4	0.668717	4
T3	0.647724	2	0.761682	2
T4	0.835291	1	0.847606	1
T5	0.60226	3	0.470391	5

Fig. 6.

Sensitivity analysis

Discussion and Conclusion

In this research, we have chosen an HCW disposal treatment system that will make it possible to use the five HCW disposal strategies the hospital has chosen. Based on these, we applied the MCDM approach to choose a unique HCW disposal treatment strategy for their current application. In order to deal with the complicated environment where MCDM is producing reluctant and hazy perspectives of decision-makers, we employ the hesitant fuzzy MCDM method. The reluctant opinions of decision-makers are also appreciated. The primary procedure in hospital management is trash disposal. Different kinds of new diseases are now becoming more prevalent as a result of environmental issues. Human organs, illnesses (fungi, bacterial, and viral), and equipment used to clean blood vessels are all expressly mentioned in the context of hospital waste disposal. As a result, it is essential to get rid of these medical wastes. The autoclaving disposal method that was chosen at the conclusion of this study has been looked into with regard to environmental and human health aspects. Because of this, we think autoclaving can be the best technique of disposal treatment to prevent HCW infection. In this way, it is advised to select an appropriate and secure disposal treatment system in all medical facilities, hospitals, etc. In order to address both visible and invisible criteria and select the most appropriate disposal treatment options for the bio-medical wastes of the healthcare institution, an extension of the combined objective weight (entropy) approach and ARAS is proposed in this research study. In MCDM, numerous multi-objective optimisation techniques are employed. Here, we select the ARAS approach, which is regarded as one of the top optimisation techniques. The entropy and ARAS approaches must be developed in the probabilistic hesitant fuzzy environment of this research. Additionally, these suggested methods are less sensitive because the criteria values are highly stable. By using HCW disposal treatment, the proposed tentative approach’s applicability is assessed. Based on the ranking order of alternatives, steam disinfection disposal treatment is the best disposal treatment. This ranking is based on absorption of energy, efficiency of therapy, level of mechanisation, acceptance by society, land requirements, and disposal cost risk criteria. Steam disinfection and disposal treatment reduce the risk of environmental pollution and secure human health from the effects of infections. Furthermore, patients and their attendants would be adequately informed about the advantages of using the correct HCPWD. Finally, technical advancements, government regulations, and their implementation may all be used to improve HCPWD. Moreover, we will build on the study by combining empirical and subjective data on the weight of the criterion.

Funding

This work was supported by a National Research Foundation (NRF) of Korea grant funded by the Korean Government (MSIT) Grant NRF-2022R1C1C1006671.

Data Availability

All data generated or analysed during this study are included in this published article.

Compliance with Ethical Standards

Conflict of Interest

The authors declare no competing interests.

Ethical Approval

This article does not contain any studies with human participants or animals performed by any of the authors.