Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Jan 11;23(2):652–658. doi: 10.1021/acs.nanolett.2c04497

Stability and Strength of Monolayer Polymeric C60

Bo Peng 1,*
PMCID: PMC9881160  PMID: 36630566

Abstract

graphic file with name nl2c04497_0004.jpg

Two-dimensional fullerene networks have been synthesized in several forms, and it is unknown which monolayer form is stable under ambient conditions. Using first-principles calculations, I show that the believed stability of the quasi-tetragonal phases is challenged by mechanical, dynamic, or thermodynamic stability. For all temperatures, the quasi-hexagonal phase is thermodynamically the least stable. However, the relatively high dynamic and mechanical stabilities suggest that the quasi-hexagonal phase is intrinsically stronger than the other phases under various strains. The origin of the high stability and strength of the quasi-hexagonal phase can be attributed to the strong covalent C–C bonds that strongly hold the linked C60 clusters together, enabling the closely packed hexagonal network. These results rationalize the experimental observations that so far only the quasi-hexagonal phase has been exfoliated experimentally as monolayers.

Keywords: density functional theory calculations, monolayer fullerene networks, mechanical stability, dynamic stability, thermodynamic stability

Recent attempts to synthesize layers of connected buckyballs, i.e. C60 molecules linked by carbon–carbon bonds, have obtained different arrangements of cluster cages through the formation of bonds between neighboring C60 molecules.1 The obtained allotropes include a few-layer rectangular structure in which each C60 molecule has four neighboring buckyballs and a monolayer hexagonal structure in which each C60 cage binds to six neighbors: namely, a few-layer quasi-tetragonal phase (qTP) and a monolayer quasi-hexagonal phase (qHP), respectively. Great efforts have been devoted to stabilizing the linking bonds between neighboring cluster cages by introducing magnesium atoms to form a quasi-2D fullerene network with strong intralayer covalent bonds1 because Mg atoms tend to promote covalent bonds.2,3 To aid exfoliation, the Mg ions that hold the C60 cages together can be then replaced by large organic ions, which can be removed afterward by hydrogen peroxide, leading to pure, charge-neutral fullerene networks in 2D.1,4 Unfortunately, only qHP C60 has been obtained as monolayers, while all the qTP C60 flakes are few-layers.1 These results raise doubts regarding the stability of monolayer fullerene networks.

Ever since the discovery of C60,5 the formation mechanism and stability of the fullerene molecules are far from being completely understood.6−9 When forming structural units of C60 clusters in a 2D plane, it is unclear whether ordered structures of monolayer polymeric C60 are stable under ambient conditions such as strain and temperature. Recent first-principles calculations have investigated various structural phases of monolayer C60 with different bonding characters.10−15 The mechanical stability of several phases has been confirmed.10,11,14 More recently, the thermal stability of monolayer C60 has been addressed using molecular dynamics simulations, showing that both qTP and qHP C60 monolayers can remain stable at temperatures near 800 K,16 which is partially consistent with the experimental result that monolayer qHP C60 does not decompose at 600 K.1 However, previous analyses based on mechanical and thermal stability cannot explain why the qTP monolayers have not yet been exfoliated experimentally. Furthermore, the dynamic stability of monolayer fullerene networks with respect to lattice vibrations, which indicates whether the crystal structure is in a local minimum of the potential energy surface,17−20 is still unexplored. Additionally, the thermodynamic stability of different phases, which energetically classifies the stability (especially at finite temperatures),21−33 remains unknown. Because of such knowledge gaps, several questions need to be answered to understand the phase stability of monolayer fullerene networks. (i) Are qTP and qHP C60, as pure carbon monolayers without extra Mg or organic ions to bind the C60 cages together, dynamically stable? (ii) What is their relative stability from a thermodynamic aspect? (iii) Can the calculated mechanical strength support their phase stability?

In this work, I investigate the mechanical, dynamic, and thermodynamic stability of monolayer qTP and qHP C60 by using first-principles calculations. Structural relaxation obtains two crystal structures of the quasi-tetragonal phase (denoted as qTP1 and qTP2, respectively). I show that the qTP1 monolayer, albeit being thermodynamically stable at all temperatures above 380 K, possesses low dynamic and mechanical stability due to its weak bonding perpendicular to the straight chains of C60 buckyballs. On the other hand, although qTP2 fullerene might be the ground-state structure with the lowest Gibbs free energy at 0 K and exhibits good dynamic and mechanical stability, it is only thermodynamically stable with respect to qTP1 C60 at low temperatures. Instead, monolayer qHP C60 should be experimentally accessible due to its dynamic and mechanical stability, in spite of its lowest thermodynamic stability among all three phases. In addition, qHP C60 has the highest strength under various strains (hydrostatic, uniaxial, and shear) because of the closely packed crystal structures.

First-principles calculations are performed using the Vienna ab initio simulation package (VASP) .34,35 The projector augmented wave (PAW) potential is used with C 2s22p2 valence states ,36,37 under the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof parametrization revised for solids (PBEsol) as the exchange-correlation functional.38 The crystal structures are optimized by fully relaxing the lattice constants and internal atomic coordination (for computational details, see the Supporting Information). Geometry optimization starting from the quasi-tetragonal phase consisting of only carbon atoms leads to a quasi-1D qTP monolayer (qTP1), as shown in Figure 1a. On the other hand, a two-step structural relaxation, starting from monolayer qTP Mg2C60 and then removing the Mg ions before the second relaxation, obtains a tightly bound qTP monolayer (qTP2), as shown in Figure 1b. The two-step structure relaxation mimics the experimental procedure to remove the charged ions introduced during synthesis.1,4 The computed lattice constants for all three phases are given in Table 1, which are in good agreement with previous results,10,11,15 therefore confirming the reliability of the present calculations.

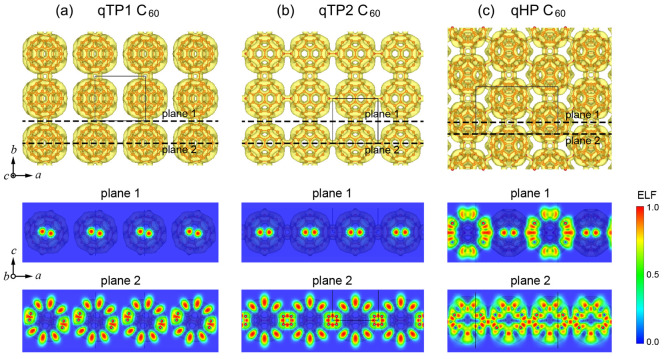
Figure 1.

Figure 1

Open in a new tab

Bond structures for (a) qTP1, (b) qTP2, and (c) qHP C60. The default isosurface level in VESTA39 is used. Maps of the ELF on the (010) plane are also present.

Table 1. Calculated Static Lattice Constants (in Å) and Cohesive Energies Ec (in eV/atom) of qTP1, qTP2, and qHP C60 Monolayers, 1D qTP C60 Chain, and 0D C60 Moleculea.

phase a b Ec
2D qTP1 10.491 9.063 –9.2582
  (10.522) (9.090)  
2D qTP2 9.097 9.001 –9.2587
  (9.132) (9.031)  
2D qHP 15.848 9.131 –9.2465
  (15.896) (9.162)  
1D 9.062   –9.2579
  (9.098)    
0D     –9.2564
Open in a new tab
a

The cohesive energy is defined as Ec = Etot/N – Eisolated, where Etot is the total energy of the crystal, N is the number of atoms in the unit cell, and Eisolated is the total energy of an isolated carbon atom. The room-temperature lattice constants calculated under the quasi-harmonic approximation are also shown in parentheses for comparison.

The bond structures at equilibrium are examined in Figure 1. The relaxed structure for qTP1 fullerene can be regarded as one-dimensional chains of C60 cages along the b direction that are linked by the nearly in-plane [2 + 2] cycloaddition bonds. In comparison, qTP2 fullerene is a two-dimensional network of C60 cages connected by the out-of-plane vertical [2 + 2] cycloaddition bonds along the a direction and the in-plane [2 + 2] cycloaddition bonds along the b direction. The major difference between qTP1 and qTP2 is the absence of the vertical [2 + 2] cycloaddition bonds along a in the former. Regarding the qHP monolayer, the C60 cages form a hexagonal network through the similar planar [2 + 2] cycloaddition bonds along the b direction and C–C single bonds along the other two directions diagonal to the rectangular unit cell.

Figure 1 also shows the maps of the electron localization function (ELF) on the (010) plane. A high value of ELF indicates strong electron localization.40−43 As shown in Figure 1a, the covalent [2 + 2] bonds along b in qTP1 fullerene lead to high electron localization there (plane 1), whereas no bonds are formed between neighboring C60 cages along a (plane 2). In contrast, the vertical [2 + 2] bonds along a in qTP2 fullerene result in high electron localization between neighboring C60 cages, as demonstrated in plane 2 of Figure 1b. For qHP C60, the hexagonal network has higher electron localization in both directions, as one can see from Figure 1c. As a result, one can expect that the hexagonal networks should stabilize and strengthen the structure of qHP C60, making it slightly more stable than qTP2 C60 while being much more stable than qTP1 C60. However, as shown below, although the mechanical and dynamic stabilities are consistent with the ELF picture, the high electron localization in qHP C60 does not guarantee its thermodynamic stability.

To confirm the mechanical stability, the elastic constants are calculated by finite differences through finite distortions of the lattice.44,45 There are different ways to define the 2D elastic constants from the computed 3D coefficients.17,46,47 Here the 2D coefficients Cij2D are renormalized by the c lattice constant (the spacing between 2D layers):17,46 i.e., Cij = c × Cij3D. The obtained 2D elastic constants (including ionic relaxations) are given in Table 2 using the Voigt notation, 1 – xx, 2 – yy, 6 – xy, and the present results agree well with previous calculations.10,11 According to Born-Huang’s lattice dynamic theory,48,49 in monoclinic crystals (qTP1 and qHP with space groups P2/m and Pc, respectively), the mechanical stability criteria are given by

graphic file with name nl2c04497_m001.jpg 1

Table 2. Elastic Properties for qTP1, qTP2, and qHP C60, with the Elastic Constants Cij, Shear Moduli G2D, Layer Moduli γ, Young’s Moduli Y2D in N/m, and Poisson’s Ratios ν (Dimensionless)a.

phase C11 C22 C12 C66 = G2D γ Ya2D Yb2D νa νb
qTP1 5.4 123.7 –1.2 –0.2 31.7 5.4 123.5 –0.010 –0.225
  (2.5) (121.3)              
qTP2 149.9 148.7 22.9 53.4 86.1 146.4 145.2 0.154 0.153
  (150.5) (141.2)   (54.5)          
qHP 150.8 186.8 22.5 60.6 95.6 148.1 183.4 0.120 0.149
  (142.4) (172.7)   (61.7)          
Open in a new tab
a

The elastic constants C11, C22, and C66 calculated from the phonon speed of sound are also shown in parentheses for comparison.

In orthorhombic crystals (qTP2 C60 with space group Pmmm), the Born stability criteria have an extra requirement in addition to eq 1

graphic file with name nl2c04497_m002.jpg 2

The elastic constants of qTP2 and qHP C60 satisfy their corresponding criteria, indicating that they are mechanically stable. Interestingly, the shear strength G2D of qTP1 C60 is negative, demonstrating its low shear resistance. The 1D chains in qTP1 C60 are prone to bending under shear deformation, which may lead to a sliding of C60 chains and even lattice instability. In addition, C11 in qTP1 fullerene is more than 1 order of magnitude lower than C22. Such weak stiffness is correlated to the weak interchain bonding effect along a, as discussed above, and the weak dynamic stability, as will be demonstrated below. In contrast, C11 and C22 are nearly the same in qTP2 fullerene because of the similar [2 + 2] cycloaddition bonds along both a and b. For qHP fullerene, the elastic constants C11, C22, and C66 are the highest among the three phases, consistent with the high electron localization in the hexagonal networks that strengthens the crystal structure.

The strength of monolayer fullerene networks is obtained from the computed elastic constants, as summarized in Table 2. The layer modulus γ is the 2D equivalent to the bulk modulus, which measures the resistance to hydrostatic stretching in 2D materials.50 The layer moduli show an increasing trend from qTP1 to qTP2 and to qHP C60. The γ value for qTP2 C60 is more than twice that of qTP1 C60, while it is slightly lower than that of qHP C60, which concurs with the bonding structures of the three fullerene networks. In general, qTP2 and qHP C60 have comparable moduli and therefore similar hardness properties, whereas qTP1 C60 has less resilience to both shear and hydrostatic strains.

The anisotropy of strength is also investigated by calculating the Young’s modulus and Poisson’s ratio. In qTP1 fullerene, the Young’s modulus Y2D along a is more than 22 times lower than that along b, indicating that qTP1 C60 is much less structurally rigid to elongations along a. In qTP2 C60, the Young’s moduli along a and b are nearly the same due to similar [2 + 2] cycloaddition bonds along both directions, showing that they have the same resilience to linear strain. Regarding the qHP monolayers, Ya2D has a value 80% that of Yb, indicating slightly weaker stiffness of the C–C single bonds in the presence of strain along a. The Poisson’s ratio ν for qTP1 C60 is negative, i.e. the qTP1 fullerene monolayers expand laterally when stretched, and |νa| is significantly lower than |νb| because of much less bond stretching under uniaxial strain. Monolayer qTP2 C60 has a nearly isotropic ν of 0.153–0.154, while νa in qHP fullerene is slightly lower than νb. These results indicate that qTP1 C60 is unable to withstand greater strains along a than those along b, which is the origin of its overall low strength.

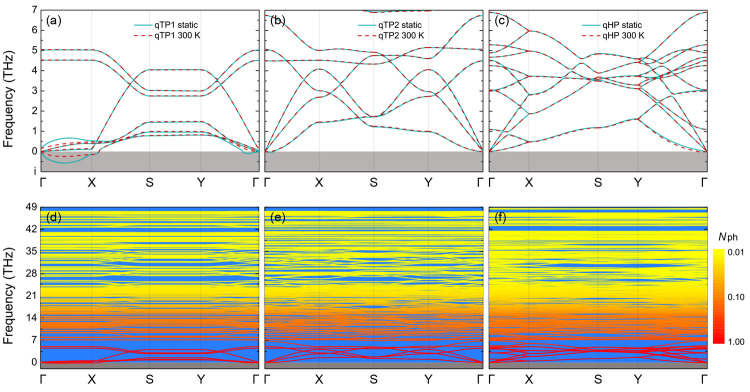
To evaluate the dynamic stability of monolayer fullerene networks, lattice dynamic properties are calculated within the harmonic approximation based on density functional perturbation theory.51−53 The phonon spectra of all three phases are gathered in Figure 2. As shown in Figure 2a, the phonon dispersion of qTP1 C60 using the static lattice constants exhibits a small imaginary frequency (<0.6i THz) along the entire Γ–X high-symmetry line. An imaginary frequency indicates a decrease in potential energy when the atoms are displaced away from their equilibrium positions, corresponding to a nonrestorative force.20 Therefore, the imaginary frequency along Γ–X implies that monolayer qTP1 C60 can be split into individual 1D chains in the presence of interchain (out-of-plane) vibrations, demonstrating its weak dynamic stability along the a direction. There is a fourth mode at Γ with nearly zero frequency in qTP1 C60, which, sometimes known as the torsional acoustic mode, is a strong indication of the (quasi-)1D nature.54,55 The thermal expansion is included by computing the Gibbs free energy under the quasi-harmonic approximation,56−58 and the room-temperature lattice constants are given in Table 1. At 300 K, the imaginary mode in qTP1 C60 remains along Γ–X, though the imaginary frequency becomes smaller (<0.2i THz). In contrast, qTP2 and qHP fullerenes are dynamically more stable, as there is no imaginary mode in Figure 2b,c using both the static and room-temperature lattice constants, indicating that these structures are a local minimum on the potential energy surface and the atoms vibrate harmonically around their equilibrium positions.

Figure 2.

Figure 2

Open in a new tab

Low-frequency phonons of (a) qTP1, (b) qTP2, and (c) qHP C60 using the static and room-temperature lattice constants. Entire phonon spectra for (d) qTP1, (e) qTP2, and (f) qHP C60 using the room-temperature lattice constants, with the phonon occupation number Nph being determined from the Bose–Einstein distribution function at 300 K.

From the phonon speed of sound, the elastic constants C11, C22, and C66 can be calculated59 (for details on the phonon group velocity, see the Supporting Information). As shown in Table 2, the calculated elastic constants are in reasonably good agreement with those computed from the finite difference method.44,45 Moreover, qHP fullerene has the highest speed of sound along b and the highest phonon frequency with four phonon branches higher than 48.4 THz throughout the entire Brillouin zone, whereas the highest phonon frequencies in qTP1 and qTP2 fullerene are lower than 47.7 THz, which is in line with the high mechanical strength in qHP C60.

To clarify the thermodynamic stability of C60 monolayers, the cohesive energy is calculated, as given in Table 1. The resulting Ec of qTP2 fullerene is 0.5 meV/atom (30 meV per formula unit) lower than that of qTP1 and 12.2 meV/atom (732 meV per formula unit) lower than that of qHP, suggesting its thermodynamic stability. However, because the energy difference between the qTP1 and qTP2 monolayers is quite small, phonons can play an important role in determining the thermodynamic stability at both 0 K and finite temperatures.21−24 The contribution of phonons can be examined by calculating the Gibbs free energy F 60−62

graphic file with name nl2c04497_m003.jpg 3

where Inline graphic finds a unique minimum value in the brackets by changing the lattice constants a and b to include thermal expansion, Etot is the total energy of the crystal, ℏ is the reduced Planck constant, ωλ is the phonon frequency at mode λ, kB is the Boltzmann constant, and T is the temperature. The second term in eq 3 is temperature-independent, corresponding to the zero point energy (ZPE) of phonons, and the last term refers to the thermally excited population of phonons, as demonstrated by the Bose–Einstein distribution Nph at 300 K in Figure 2d–f.

To quantify the relative thermodynamic stability at finite temperatures, the difference in Gibbs free energy ΔF with respect to the free energy of monolayer qTP2 C60 is plotted as a function of temperature T for all three phases, as illustrated in Figure 3. With increasing temperature, the free energy of qTP1 C60 drops faster than that of qTP2 C60 due to its smaller vibrational frequencies. According to eq 3, smaller vibrational frequencies give rise to lower free energy and higher entropy (for details on the phonon density of states and entropy, see the Supporting Information), which is similar to the case in α- and β-tin.21,22 At 150 K, monolayer qTP1 C60 becomes thermodynamically more stable than the other two phases. At 300 K, the free energy of qTP1 C60 lies 47 meV per formula unit (meV/fu) below that of qTP2 C60. At higher temperatures, the difference becomes even larger, further stabilizing the qTP1 structure from a thermodynamic perspective.

Figure 3.

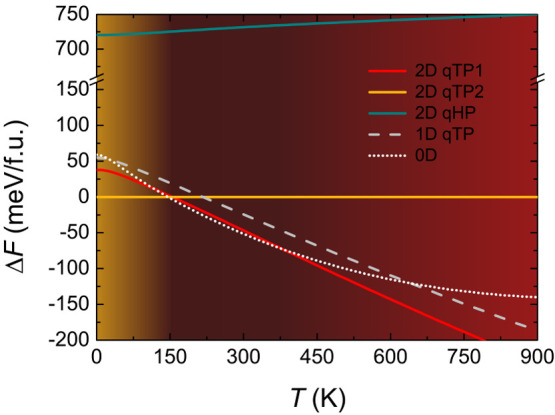
Figure 3

Open in a new tab

Relative thermodynamic stabilities of monolayer fullerene networks, a one-dimensional fullerene chain, and a zero-dimensional fullerene molecule, with the Gibbs free energy F of monolayer qTP2 C60 set to zero to compare the relative stabilities.

To further explore the thermodynamic stability of C60 in different dimensions, the monolayer qTP1 network is further isolated into a 1D qTP C60 chain and a 0D C60 molecule (for details about 1D and 3D C60, see the Supporting Information). The cohesive energies Ec of 1D qTP C60 and 0D C60 are given in Table 1. Interestingly, Ec of the 1D qTP C60 chain is higher than those of monolayer qTP1 and qTP2 C60 network by merely 0.3 and 0.8 meV/atom, respectively (18 and 48 meV/fu), whereas it is 11.4 meV/atom (684 meV/fu) lower than Ec of 2D qHP C60. The difference in Ec between the 1D qTP C60 chain and the monolayer qTP1 C60 network is even lower than the thermal fluctuation energy kBT at room temperature (26 meV), implying that 2D qTP1 C60 can be transformed into 1D chains in the presence of thermal fluctuations. Taking the finite temperature effects into account, the Gibbs free energy of the 1D qTP C60 chain and the Helmholtz free energy of the 0D C60 molecule are shown in Figure 3 as a function of temperature. The Gibbs free energy of the 1D qTP C60 chain is higher than that of 2D qTP1 C60 in the entire temperature range (0–900 K), and their free energy difference is 22 meV/fu at 300 K. On the other hand, the free energy of the 1D qTP C60 chain becomes lower than that of 2D qTP2 C60 at temperatures above 220 K. Most interestingly, the free energy of the 0D C60 molecule drops faster than those for all the other phases below room temperature and becomes lower than those of 2D qTP1 and qTP2 C60 at 120 and 150 K, respectively. However, the free energy of 2D qTP1 C60 decreases the fastest above room temperature, and consequently 2D qTP1 C60 is energetically more favored than all the other phases at temperatures above 380 K. As a result, monolayer qTP2 C60 is thermodynamically the most stable at temperatures below 150 K, the 0D C60 molecule has the lowest energy for temperatures between 150 and 380 K, and 2D qTP1 C60 is thermodynamically favored above 380 K.

Looking back at the calculated mechanical properties and stabilities, they seem in line with the experimental findings. It has been reported that fullerene monolayers can only be isolated experimentally for the honeycomb structure qHP, whereas the obtained rectangular structure qTP is few-layered.1 Although qTP2 C60 is thermodynamically favored over qTP1 C60 at low temperatures, clearly qTP1 C60 is thermodynamically more stable than the other two phases at all temperatures above 150 K. However, the thermodynamic stability of qTP1 C60 does not guarantee high dynamic stability in the presence of interchain (out-of-plane) vibrations perpendicular to the quasi-1D chains. In addition, the low moduli and strength of qTP1 C60 originating from the chain crystal structures, in addition to its low shear resistance, indicate that qTP1 C60 cannot be intrinsically resilient under deformation. Moreover, monolayer qTP1 C60 is thermodynamically less stable than the 0D C60 molecule for temperatures between 120 and 380 K. These results indicate the plausibility that the monolayer qTP1 fullerene network can be further split into individual 1D chains or 0D molecules by thermal fluctuations, interchain acoustic vibrations, or external strains. In contrast, qHP C60 is both dynamically and mechanically more stable with respect to qTP1 C60. Therefore, monolayer polymeric C60 has so far only been exfoliated from the quasi-hexagonal bulk single crystals. These results indicate that a systematic analysis of mechanical, dynamic, and thermodynamic stabilities is necessary to rationalize the experimental data.

In conclusion, I carry out first-principles calculations to evaluate the mechanical, dynamic, and thermodynamic stabilities of qTP1, qTP2, and qHP C60 monolayers, which have been so far believed to be stable. The electron localization analysis reveals that the low mechanical and dynamic stabilities in qTP1 fullerene are associated with the lack of C–C bonds connecting the adjacent C60 chains, which also limits its achievable strength. Monolayer qTP2 C60 is thermodynamically more stable at temperatures below 150 K, while thermally populated phonons hinder its thermodynamic stability with increasing temperature. The relatively high moduli of qHP fullerene indicate that it has a high strength because of the closely packed hexagonal fullerene network linked through both [2 + 2] cycloaddition bonds and C–C single bonds. This, in combination with the phonon stability, endows monolayer qHP C60 with high stability and strength.

Acknowledgments

I thank Prof. Bartomeu Monserrat and Dr. Ivona Bravić at the University of Cambridge for helpful discussions. I acknowledge support from the Winton Programme for the Physics of Sustainability and from Magdalene College Cambridge for a Nevile Research Fellowship. The calculations were performed using resources provided by the Cambridge Tier-2 system, operated by the University of Cambridge Research Computing Service (www.hpc.cam.ac.uk) and funded by the EPSRC Tier-2 capital grant EP/P020259/1, as well as with computational support from the U.K. Materials and Molecular Modelling Hub, which is partially funded by EPSRC (EP/P020194), for which access is obtained via the UKCP consortium and funded by EPSRC grant ref EP/P022561/1.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.2c04497.

  • Computational details, phonon group velocity, phonon density of states and entropy, 1D qTP C60 chains, and relative thermodynamic stabilities between 3D, 2D, 1D, and 0D C60 (PDF)

The author declares no competing financial interest.

Supplementary Material

nl2c04497_si_001.pdf (1.9MB, pdf)

References

  1. Hou L.; Cui X.; Guan B.; Wang S.; Li R.; Liu Y.; Zhu D.; Zheng J. Synthesis of a monolayer fullerene network. Nature 2022, 606, 507–510. 10.1038/s41586-022-04771-5. [DOI] [PubMed] [Google Scholar]
  2. Pontiroli D.; Aramini M.; Gaboardi M.; Mazzani M.; Gorreri A.; Riccò M.; Margiolaki I.; Sheptyakov D. Ionic conductivity in the Mg intercalated fullerene polymer Mg2C60. Carbon 2013, 51, 143–147. 10.1016/j.carbon.2012.08.022. [DOI] [Google Scholar]
  3. Tanaka M.; Yamanaka S. Vapor-Phase Growth and Structural Characterization of Single Crystals of Magnesium Doped Two-Dimensional Fullerene Polymer Mg2C60. Cryst. Growth Des. 2018, 18, 3877–3882. 10.1021/acs.cgd.8b00186. [DOI] [Google Scholar]
  4. Gottfried J. M. Molecular soccer balls connected to make a 2D material. Nature 2022, 606, 470–471. 10.1038/d41586-022-01568-4. [DOI] [PubMed] [Google Scholar]
  5. Kroto H. W.; Heath J. R.; O’Brien S. C.; Curl R. F.; Smalley R. E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. 10.1038/318162a0. [DOI] [Google Scholar]
  6. Kroto H. W. The stability of the fullerenes Cn, with n = 24, 28, 32, 36, 50, 60 and 70. Nature 1987, 329, 529–531. 10.1038/329529a0. [DOI] [Google Scholar]
  7. Kroto H. C60, fullerenes, giant fullerenes and soot. Pure Appl. Chem. 1990, 62, 407–415. 10.1351/pac199062030407. [DOI] [Google Scholar]
  8. Goroff N. S. Mechanism of Fullerene Formation. Acc. Chem. Res. 1996, 29, 77–83. 10.1021/ar950162d. [DOI] [Google Scholar]
  9. Bernal J. J.; Haenecour P.; Howe J.; Zega T. J.; Amari S.; Ziurys L. M. Formation of Interstellar C60 from Silicon Carbide Circumstellar Grains. Astrophysical Journal Letters 2019, 883, L43. 10.3847/2041-8213/ab4206. [DOI] [Google Scholar]
  10. Tromer R. M.; Ribeiro L. A.; Galvão D. S. A DFT study of the electronic, optical, and mechanical properties of a recently synthesized monolayer fullerene network. Chem. Phys. Lett. 2022, 804, 139925. 10.1016/j.cplett.2022.139925. [DOI] [Google Scholar]
  11. Yu L.; Xu J.; Peng B.; Qin G.; Su G. Anisotropic Optical, Mechanical, and Thermoelectric Properties of Two-Dimensional Fullerene Networks. J. Phys. Chem. Lett. 2022, 13, 11622–11629. 10.1021/acs.jpclett.2c02702. [DOI] [PubMed] [Google Scholar]
  12. Yuan D.; Pi H.; Jiang Y.; Zhou Y. H. L.; Jia Y.; Su G.; Fang Z.; Weng H.; Ren X.; Zhang W.. Highly in-plane anisotropic optical properties of fullerene monolayers arXiv:2207.11366, 2022; (accessed July 30, 2022)
  13. Peng B. Monolayer Fullerene Networks as Photocatalysts for Overall Water Splitting. J. Am. Chem. Soc. 2022, 144, 19921–19931. 10.1021/jacs.2c08054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ying P.; Dong H.; Liang T.; Fan Z.; Zhong Z.; Zhang J. Atomistic insights into the mechanical anisotropy and fragility of monolayer fullerene networks using quantum mechanical calculations and machine-learning molecular dynamics simulations. Extreme Mechanics Letters 2023, 58, 101929. 10.1016/j.eml.2022.101929. [DOI] [Google Scholar]
  15. Dong H.; Cao C.; Ying P.; Fan Z.; Qian P.; Su Y.. Anisotropic and high thermal conductivity in monolayer quasi-hexagonal fullerene: A comparative study against bulk phase fullerene. arXiv:2208.03982, 2022; (accessed August 30, 2022)
  16. Ribeiro L.; Pereira M.; Giozza W.; Tromer R.; Galvão D. S. Thermal stability and fracture patterns of a recently synthesized monolayer fullerene network: A reactive molecular dynamics study. Chem. Phys. Lett. 2022, 807, 140075. 10.1016/j.cplett.2022.140075. [DOI] [Google Scholar]
  17. Peng B.; Zhang H.; Shao H.; Ning Z.; Xu Y.; Ni G.; Lu H.; Zhang D. W.; Zhu H. Stability and strength of atomically thin borophene from first principles calculations. Materials Research Letters 2017, 5, 399–407. 10.1080/21663831.2017.1298539. [DOI] [Google Scholar]
  18. Malyi O. I.; Sopiha K. V.; Persson C. Energy, Phonon, and Dynamic Stability Criteria of Two-Dimensional Materials. ACS Appl. Mater. Interfaces 2019, 11, 24876–24884. 10.1021/acsami.9b01261. [DOI] [PubMed] [Google Scholar]
  19. Luo D.; Yin K.; Dronskowski R. Existence of BeCN2 and Its First-Principles Phase Diagram: Be and C Introducing Structural Diversity. J. Am. Chem. Soc. 2022, 144, 5155–5162. 10.1021/jacs.2c00592. [DOI] [PubMed] [Google Scholar]
  20. Pallikara I.; Kayastha P.; Skelton J. M.; Whalley L. D. The physical significance of imaginary phonon modes in crystals. Electron. Struct. 2022, 4, 033002. 10.1088/2516-1075/ac78b3. [DOI] [Google Scholar]
  21. Pavone P.; Baroni S.; de Gironcoli S. α ↔ β phase transition in tin: A theoretical study based on density-functional perturbation theory. Phys. Rev. B 1998, 57, 10421–10423. 10.1103/PhysRevB.57.10421. [DOI] [Google Scholar]
  22. Pavone P. Old and new aspects in lattice-dynamical theory. J. Phys.: Condens. Matter 2001, 13, 7593–7610. 10.1088/0953-8984/13/34/308. [DOI] [Google Scholar]
  23. Masago A.; Shirai K.; Katayama-Yoshida H. Crystal stability of α- and β-boron. Phys. Rev. B 2006, 73, 104102. 10.1103/PhysRevB.73.104102. [DOI] [Google Scholar]
  24. van Setten M. J.; Uijttewaal M. A.; de Wijs G. A.; de Groot R. A. Thermodynamic Stability of Boron: The Role of Defects and Zero Point Motion. J. Am. Chem. Soc. 2007, 129, 2458–2465. 10.1021/ja0631246. [DOI] [PubMed] [Google Scholar]
  25. Stoffel R. P.; Wessel C.; Lumey M.-W.; Dronskowski R. Ab Initio Thermochemistry of Solid-State Materials. Angew. Chem., Int. Ed. 2010, 49, 5242–5266. 10.1002/anie.200906780. [DOI] [PubMed] [Google Scholar]
  26. Zhang R. F.; Lin Z. J.; Mao H.-K.; Zhao Y. Thermodynamic stability and unusual strength of ultra-incompressible rhenium nitrides. Phys. Rev. B 2011, 83, 060101. 10.1103/PhysRevB.83.060101. [DOI] [Google Scholar]
  27. Deringer V. L.; Stoffel R. P.; Dronskowski R. Thermochemical Ranking and Dynamic Stability of TeO2 Polymorphs from Ab Initio Theory. Cryst. Growth Des. 2014, 14, 871–878. 10.1021/cg401822g. [DOI] [Google Scholar]
  28. Deringer V. L.; Stoffel R. P.; Dronskowski R. Vibrational and thermodynamic properties of GeSe in the quasiharmonic approximation. Phys. Rev. B 2014, 89, 094303. 10.1103/PhysRevB.89.094303. [DOI] [Google Scholar]
  29. White M. A.; Cerqueira A. B.; Whitman C. A.; Johnson M. B.; Ogitsu T. Determination of Phase Stability of Elemental Boron. Angew. Chem., Int. Ed. 2015, 54, 3626–3629. 10.1002/anie.201409169. [DOI] [PubMed] [Google Scholar]
  30. Nyman J.; Pundyke O. S.; Day G. M. Accurate force fields and methods for modelling organic molecular crystals at finite temperatures. Phys. Chem. Chem. Phys. 2016, 18, 15828–15837. 10.1039/C6CP02261H. [DOI] [PubMed] [Google Scholar]
  31. Skelton J. M.; Burton L. A.; Oba F.; Walsh A. Chemical and Lattice Stability of the Tin Sulfides. J. Phys. Chem. C 2017, 121, 6446–6454. 10.1021/acs.jpcc.6b12581. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Pallikara I.; Skelton J. M. Phase stability of the tin monochalcogenides SnS and SnSe: a quasi-harmonic lattice-dynamics study. Phys. Chem. Chem. Phys. 2021, 23, 19219–19236. 10.1039/D1CP02597J. [DOI] [PubMed] [Google Scholar]
  33. Bartel C. J. Review of computational approaches to predict the thermodynamic stability of inorganic solids. J. Mater. Sci. 2022, 57, 10475–10498. 10.1007/s10853-022-06915-4. [DOI] [Google Scholar]
  34. Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  35. Kresse G.; Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
  36. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  37. Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  38. Perdew J. P.; Ruzsinszky A.; Csonka G. I.; Vydrov O. A.; Scuseria G. E.; Constantin L. A.; Zhou X.; Burke K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. 10.1103/PhysRevLett.100.136406. [DOI] [PubMed] [Google Scholar]
  39. Momma K.; Izumi F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. 10.1107/S0021889811038970. [DOI] [Google Scholar]
  40. Becke A. D.; Edgecombe K. E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. 10.1063/1.458517. [DOI] [Google Scholar]
  41. Savin A.; Jepsen O.; Flad J.; Andersen O. K.; Preuss H.; von Schnering H. G. Electron Localization in Solid-State Structures of the Elements: the Diamond Structure. Angew. Chem., Int. Ed. Engl. 1992, 31, 187–188. 10.1002/anie.199201871. [DOI] [Google Scholar]
  42. Gatti C. Chemical bonding in crystals: new directions. Zeitschrift für Kristallographie 2005, 220, 399–457. 10.1524/zkri.220.5.399.65073. [DOI] [Google Scholar]
  43. Chen K.; Kamran S. Bonding Characteristics of TiC and TiN. Modeling and Numerical Simulation of Material Science 2013, 03, 7–11. 10.4236/mnsms.2013.31002. [DOI] [Google Scholar]
  44. Le Page Y.; Saxe P. Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress. Phys. Rev. B 2002, 65, 104104. 10.1103/PhysRevB.65.104104. [DOI] [Google Scholar]
  45. Wu X.; Vanderbilt D.; Hamann D. R. Systematic treatment of displacements, strains, and electric fields in density-functional perturbation theory. Phys. Rev. B 2005, 72, 035105. 10.1103/PhysRevB.72.035105. [DOI] [Google Scholar]
  46. Blonsky M. N.; Zhuang H. L.; Singh A. K.; Hennig R. G. Ab Initio Prediction of Piezoelectricity in Two-Dimensional Materials. ACS Nano 2015, 9, 9885–9891. 10.1021/acsnano.5b03394. [DOI] [PubMed] [Google Scholar]
  47. Pashartis C.; van Setten M.; Houssa M.; Pourtois G. On the elastic tensors of ultra-thin films: A study of ruthenium. Appl. Surf. Sci. 2022, 592, 153194. 10.1016/j.apsusc.2022.153194. [DOI] [Google Scholar]
  48. Born M.; Huang K.. Dynamical theory of crystal lattices; Clarendon Press: 1954. [Google Scholar]
  49. Wu Z.-j.; Zhao E.-j.; Xiang H.-p.; Hao X.-f.; Liu X.-j.; Meng J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 054115. 10.1103/PhysRevB.76.054115. [DOI] [Google Scholar]
  50. Andrew R. C.; Mapasha R. E.; Ukpong A. M.; Chetty N. Mechanical properties of graphene and boronitrene. Phys. Rev. B 2012, 85, 125428. 10.1103/PhysRevB.85.125428. [DOI] [Google Scholar]
  51. Baroni S.; de Gironcoli S.; Dal Corso A.; Giannozzi P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. 10.1103/RevModPhys.73.515. [DOI] [Google Scholar]
  52. Gonze X. Perturbation expansion of variational principles at arbitrary order. Phys. Rev. A 1995, 52, 1086–1095. 10.1103/PhysRevA.52.1086. [DOI] [PubMed] [Google Scholar]
  53. Gonze X. Adiabatic density-functional perturbation theory. Phys. Rev. A 1995, 52, 1096–1114. 10.1103/PhysRevA.52.1096. [DOI] [PubMed] [Google Scholar]
  54. Peng B.; Xu K.; Zhang H.; Ning Z.; Shao H.; Ni G.; Li J.; Zhu Y.; Zhu H.; Soukoulis C. M. 1D SbSeI, SbSI, and SbSBr With High Stability and Novel Properties for Microelectronic, Optoelectronic, and Thermoelectric Applications. Adv. Theory Simul. 2018, 1, 1700005. 10.1002/adts.201700005. [DOI] [Google Scholar]
  55. Lange G. F.; Bouhon A.; Monserrat B.; Slager R.-J. Topological continuum charges of acoustic phonons in two dimensions and the Nambu-Goldstone theorem. Phys. Rev. B 2022, 105, 064301. 10.1103/PhysRevB.105.064301. [DOI] [Google Scholar]
  56. Huang L.-F.; Gong P.-L.; Zeng Z. Phonon properties, thermal expansion, and thermomechanics of silicene and germanene. Phys. Rev. B 2015, 91, 205433. 10.1103/PhysRevB.91.205433. [DOI] [Google Scholar]
  57. Huang L.-F.; Lu X.-Z.; Tennessen E.; Rondinelli J. M. An efficient ab-initio quasiharmonic approach for the thermodynamics of solids. Comput. Mater. Sci. 2016, 120, 84–93. 10.1016/j.commatsci.2016.04.012. [DOI] [Google Scholar]
  58. Peng B.; Bravić I.; MacManus-Driscoll J. L.; Monserrat B. Topological semimetallic phase in PbO2 promoted by temperature. Phys. Rev. B 2019, 100, 161101. 10.1103/PhysRevB.100.161101. [DOI] [Google Scholar]
  59. Feng J.; Xiao B.; Zhou R.; Pan W.; Clarke D. R. Anisotropic elastic and thermal properties of the double perovskite slab-rock salt layer Ln2SrAl2O7 (Ln = La, Nd, Sm, Eu, Gd or Dy) natural superlattice structure. Acta Mater. 2012, 60, 3380–3392. 10.1016/j.actamat.2012.03.004. [DOI] [Google Scholar]
  60. Dove M. T.Introduction to Lattice Dynamics; Cambridge University Press: 1993. [Google Scholar]
  61. Togo A.; Oba F.; Tanaka I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 2008, 78, 134106. 10.1103/PhysRevB.78.134106. [DOI] [Google Scholar]
  62. Togo A.; Tanaka I. First principles phonon calculations in materials science. Scripta Materialia 2015, 108, 1–5. 10.1016/j.scriptamat.2015.07.021. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl2c04497_si_001.pdf (1.9MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES