Significance
Throughout the past several decades, research on metamaterials has been highly active. Metamaterials are artificial materials with amazing properties such as invisibility, field rotation, and concentration. Typically, these unique functions are achieved by the special design of material structures and one function corresponds to one specific design. As a result, a multifunctional metamaterial has never been realized. Here, we experimentally realize a multifunctional hydrodynamic metamaterial for fluid flow in a porous medium. Our system integrates the functions of the cloak, concentrator, and rotator, and achieves a continuous adjustment in both the magnitude and direction of flow with negligible disturbance to the background. Our study brings advancement to the theoretical design and the practical application of multifunctional metamaterial.
Keywords: hydrodynamic metamaterial, multifunctional metamaterial, cloak, concentrator, rotator
Abstract
Metamaterials are artificial materials that can achieve unusual properties through unique structures. In particular, their “invisibility” property has attracted enormous attention due to its little or negligible disturbance to the background field that avoids detection. This invisibility feature is not only useful for the optical field, but it is also important for any field manipulation that requires minimum disturbance to the background, such as the flow field manipulation inside the human body. There are several conventional invisible metamaterial designs: a cloak can isolate the influence between the internal and external fields, a concentrator can concentrate the external field to form an intensified internal field, and a rotator can rotate the internal field by a specific angle with respect to the external field. However, a multifunctional invisible device that can continuously tune across all these functions has never been realized due to its challenging requirements on material properties. Inside a porous medium flow, however, we overcome these challenges and realize such a multifunctional metamaterial. Our hydrodynamic device can manipulate both the magnitude and the direction of the internal flow and, at the same time, make negligible disturbance to the external flow. Thus, we integrate the functions of the cloak, concentrator, and rotator within one single hydrodynamic metamaterial, and such metamaterials may find potential applications in biomedical areas such as tissue engineering and drug release.
Transformation theory (1, 2) is a powerful and mature technique to achieve fabulous material properties by designing metamaterials (3, 4), which are a type of artificial materials whose unusual functions originate from their unique structures rather than their compositions. The theory predicts that once the dominant equation of a transport process is invariant under a certain coordinate transformation, one can tailor the medium’s transport parameters with the coordinate transformation (5–11) to achieve a desirable propagation of the corresponding physical field. Although the theory was first proposed for the design of an optical cloak (1, 2), it provides a general framework for various metamaterials in many different physics fields (12), including microwaves [5, 9, 13], acoustic waves (14, 15), elastic waves (16), thermal conduction(17–26), and hydrodynamic flows (27–30).
Besides the invisibility cloak, there are many other typical and mature metamaterial designs, such as the concentrator (26, 29) that can concentrate the external field and increase the magnitude of the internal field and the rotator (13, 30) that can rotate the internal field’s propagation direction with respect to the background field. Moreover, these devices make no disturbance to the external field, which means that similar to the cloak, they are also “invisible” to the detection of the field change. These conventional metamaterials share one common feature: one function corresponds to one specific structure, which limits their applications to multifunctional tasks. To overcome this limitation, therefore, the intelligent, reconfigurable and programmable metamaterials have become an active research field in recent years (31–36). According to the transformation theory, the cloak, concentrator, and rotator are achieved by applying compression, extension, rotation, and their combinations to the original coordinate system. Previous studies have shown that all the above transformations can be achieved by alternatively arranging distinct structures with specific patterns [19, 20, 26, 28–30], which implies the possibility of integrating all these functions into one single device and conveniently regulating both the internal field’s magnitude and direction. If experimentally realized, convenient switching among different functions will make such a device a powerful multifunctional field-regulating apparatus.
However, despite the pioneering attempts for the physical fields dominated by the Laplace equation (24, 26), they either cannot achieve continuous adjustment or the design parameters are too challenging for experimental realization. As a result, such a multifunctional metamaterial device has never been experimentally realized for any physical field. The main difficulty is that the design requires a massive variation in the transport properties of metamaterials, typically several orders of magnitude, which is difficult to achieve experimentally. In addition, a perfect impendence match between the device and the background environment is required, which is also challenging. Due to the lack of continuous tunability across a broad range of normal materials’ transport properties, such a multifunctional metamaterial has never been realized.
In hydrodynamics, metamaterials with multiple functions have potential applications in hydrodynamics and microfluidics, as well as in biomedical areas (37). In particular, with the recent development in micro/nano-devices, the exciting idea of placing biocompatible devices into the human body becomes more and more feasible. Considering the complexity of the human body, in which cells and protein fibers are distributed everywhere, in many locations, this environment can be regarded as liquid flow inside a porous medium. For example, various organs and tissues such as lungs, livers, mammary glands, and bones can all be considered porous media. However, the first crucial issue before we put any device into our body is, apparently, to make sure that they make no disturbances to the original flow and the essential functions of the body. Therefore, developing hydrodynamic multifunctional metamaterials that can manipulate the flow field inside a porous environment, and at the same time make negligible disturbance to the background, is a promising topic for the biomedical area (see Discussions for more details).
Here, we realize it in the fluid flow of a porous medium. Due to the low Reynolds number in a porous medium, the Navier–Stokes equation can be simplified into Darcy’s law, which is in the form of the Laplace equation with the permeability the dominant transport parameter. Because the Laplace equation maintains its form invariance under various coordinate transformations, we can apply the transformation theory to design hydrodynamic metamaterials in a porous medium (27), and all the mature designs such as the cloak, the concentrator, and the rotator can be applied to the hydrodynamic system described by Darcy’s law. With the progress in 3D printing (31, 38) and the optical lithography, one can conveniently construct an artificial porous-medium device with desirable permeability. Thus, the fluid flow in a porous medium provides unprecedented design freedom for metamaterials. Moreover, because of the sensitive permeability–porosity relationship, the adjustment in permeability by several orders of magnitude can be practically achieved by tuning the porosity of porous media. By tailoring the spatial distribution of porosity and permeability in the material, one can integrate different functions within one system and experimentally realize the multifunctional metamaterial.
In this study, we theoretically design and experimentally realize such a multifunctional metamaterial device, which integrates the functions of the cloak, concentrator, and rotator within one single system. Theoretically, we associate the Laplace equation’s solutions with the anisotropic permeability tensor and apply the effective medium theory to design the structure. Experimentally, we build the hydrodynamic device in both the microfluidic and macroscopic scales through optical lithography and 3D printing and then verify these functions with the fluorescence microscopy measurement.
1. Theoretical Analysis
We assume an incompressible and stationary flow with a small Reynolds number, Re = ρul/μ0 ≪ 1, where ρ, u, and μ0 are the density, flow speed, dynamic viscosity of the fluid, respectively, and l is a characteristic linear dimension. Under this condition, the Navier–Stokes equation reduces to the Stokes equation, and in a porous medium, it further reduces to the Brinkman–Stokes equation:
| (1) |
Here, is the velocity vector, μ is the effective viscosity of the flow in a porous environment, and k is the permeability, which is a rank-two tensor determined by the distribution of pores. For a small permeability, its magnitude k ≪ l2 and the term on the left-hand side is much smaller than and negligible; thus, the equation is simplified to Darcy’s law, and due to the continuity equation , we finally get Darcy’s pressure equation:
| (2) |
This equation is in the form of the Laplace equation, which is invariant under various coordinate transformations. Hence, the transformation theory can be employed to design hydrodynamic metamaterials in a porous medium.
There are three typical and mature metamaterial designs based on the transformation mapping theory: the cloak, the concentrator, and the rotator. One common property of all three is their ability to manipulate the internal field inside a shell without disturbing the background external field (12). It is achieved by tailoring the local transport property of the shell while at the same time matching its overall transport effect with the background. Because the dominant control parameter in the porous medium is the permeability tensor k, we need to match the background permeability k0 (assumed homogeneous and isotropic) with the shell’s effective permeability ke, i.e., ke = k0. Under this condition, the shell’s existence essentially makes no disturbance to the external flow field, and the shell is “invisible” to the background flow.
For a shell-shaped device, the entire space can be divided into three regions: the region inside the shell is denoted as region I, the shell itself is denoted as region II, and the region out of the shell is denoted as region III. Regions I and III are homogenous and isotropic porous medium, while region II is the functional region under our design. Due to the rotational symmetry, it is convenient to express the permeability with the polar coordinate (r, θ). The permeability tensor in different regions is written as , where j = 1, 2, and 3 indicates that regions I, II, and III, respectively, R is the rotation matrix, and diag(kr, j, kθ, j) is a diagonal matrix with the diagonal elements kr, j and kθ, j. Here, kr, j and kθ, j are the radial and tangential permeability with kθ, 1 = kr, 1 = kθ, 3 = kr, 3 = k0. To match the shell’s overall effective permeability ke, 2 with the background, we have , such that in all three regions, kr, jkθ, j = k02 is valid.
Suppose that the flow goes from the left to the right boundary with a pressure difference P0, at the top and bottom boundaries, the no-slip condition is satisfied (Darcy’s law does cause a small correction to the no-slip boundary condition, but it is negligible in most practical situations (39–41), and L is the dimension of the system in the flow direction along the x axis. With these boundary conditions and the continuity of pressure and velocity at the interface of different regions, the solution of Darcy’s pressure equation can be obtained in the polar coordinate (SI Appendix, for details):
| (3) |
where P1, P2, and P3 are the pressure distributions in regions I, II, and III, , and a and b are the inner and outer radii of the shell, respectively, with a < b. Due to the isotropic permeability, the flow’s velocity in regions I and III along the x axis depends only on the pressure gradient vx, j = k0dPj/dx. Thus, the ratio between the internal and external flow’s velocities is vx, 1/vx, 3 = (a/b)h − 1, which is determined by the parameters a, b, and h.
When h = 1, P1, P2, and P3 have the same expression, and the shell is completely transparent with respect to the background flow: The entire system can be regarded as a homogenous and isotropic porous medium. When h < 1, vx, 1/vx, 3 = (b/a)1 − h > 1, and the velocity of the internal flow is greater than that of the external flow. When h > 1, vx, 1/vx, 3 = (a/b)h − 1 < 1, and the internal flow is smaller than the outer flow. Besides the magnitude, the rotation matrix R adds another degree of freedom in manipulating the internal flow’s direction. Therefore, by designing a proper shell permeability k2 with an effective permeability ke, 2 matched to the background permeability k0, we can control both the magnitude and the direction of the internal flow while making no disturbance to the external flow.
To realize this goal, we use a chessboard-like design with two different porous media as two basic building blocks, as shown in Fig. 1B. When zoomed in, this design is anisotropic with two different building blocks specifically designed to realize different functions. When zoomed out, the entire design can be treated as a whole with an effective permeability determined by the geometrical mean of the two building blocks, which can be tuned to match the background. This is known as Keller’s theorem for physical fields satisfying the Laplace equation (25). Starting from the Cartesian coordinate in the left panel of Fig. 1B, we construct the system with two square building blocks, A and B, and the overall effective permeability is , with kA and kB being the individual permeability of each building block. We then transform the coordinate into the polar system to realize our shell device, as shown in the right panel of Fig. 1B. Each square building block now transforms into an annular block. Across each annular block, the phase changes by a constant Δφ in the azimuthal direction. In the radial direction, we have the relation lnri + 1 − lnri = Δφ with i labeling the ith layer: This relation comes from the equality between the horizontal and vertical sides of each square in the Cartesian system before the transform. Therefore, we get the effective permeability:
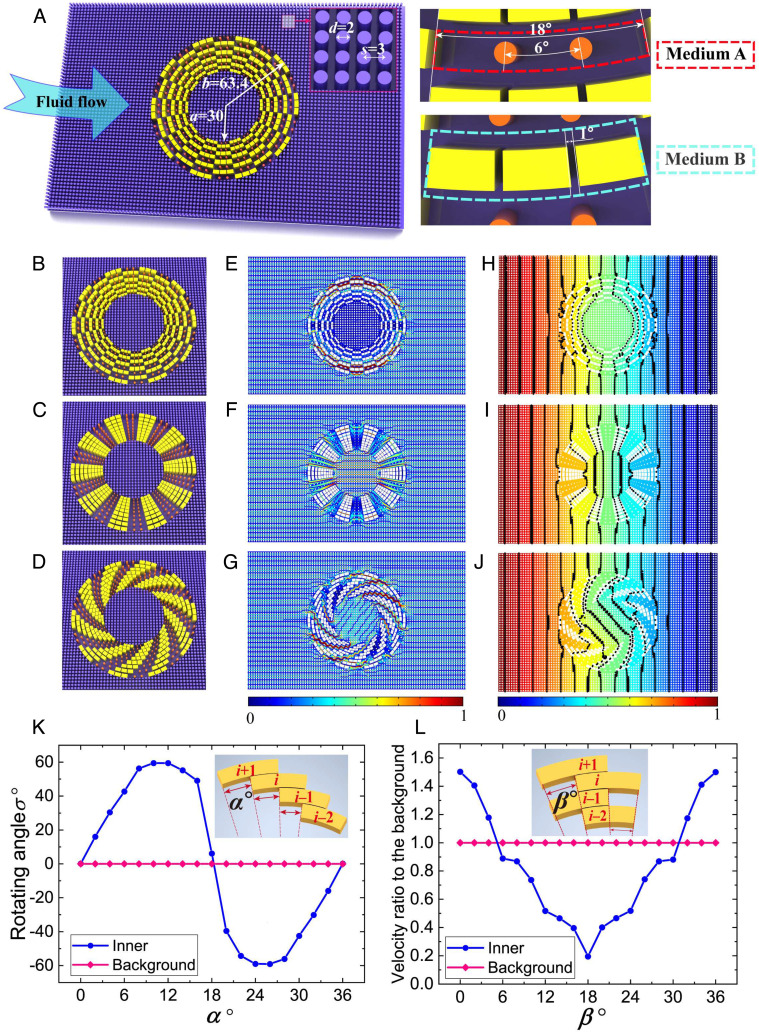
Fig. 1.
(A) The schematic graph of a shell-shaped device with inner and outer radius a and b, respectively. The entire space is divided into three regions by the shell. (B) The chessboard design based on two building blocks. The left panel shows the design in Cartesian coordinate with two building blocks denoted by black and yellow colors. The right panel shows the shell-shaped chessboard device in polar coordinate. (C-E) The configurations of the cloak, concentrator, and rotator. (F-H) The corresponding flow fields of the three devices on the left. Apparently, the cloak exhibits an inner velocity near zero, the concentrator exhibits an inner velocity higher than the background, and the rotator exhibits a significant rotation in the flow direction. At the same time, the outer streamlines remain horizontal and straight, indicating little disturbance from the device. (I-K) Corresponding pressure fields consistent with our expectation.}
| (4) |
Next, we realize the functions of the cloak, concentrator, and rotator with this chessboard design.
If the permeability is isotropic and homogeneous within each building block, we will get and thus h = 1: The device is transparent with respect to the background flow. To realize various functions, therefore, an anisotropic design within each block is required. For the cloak design in Fig. 1C, the two anisotropic building blocks can achieve the permeability tensor: with C a constant coefficient determined by the degree of diagonal anisotropy. When C > 1, we get , and the shell’s tangential permeability is larger than its radial permeability. As a result, the flow tends to go around the device along the tangential direction rather than penetrate through it radially, which is essentially a cloak. The finite element simulations in Fig. 1E and H on the right show the corresponding flow and pressure fields, which demonstrate a nice cloak performance. Note that the overall effective permeability of the shell is , which matches the background and ensures the straight streamlines outside the device.
To realize the concentrator, we fix the odd-number layers and rotate the even-number layers by Δφ and get the configuration in Fig. 1D. The tangential and radial permeabilities now become kθ, 2 = 2kAkB/(kA + kB) and kr, 2 = (kA + kB)/2, respectively. Hence, we get and thus vx, 1/vx, 3 > 1, as well as . As a result, the device behaves as a concentrator with a higher internal velocity than the background and simultaneously makes no disturbances to the background. The simulations of flow and pressure fields in Fig. 1F and I verify the concentrator performance unambiguously.
For a rotator, we progressively rotate each layer of Fig. 1D with an angle α to reach the configuration in Fig. 1. Now, a rotation matrix is introduced to the permeability tensor, . This operation does not change the overall effective permeability while only rotates the flow’s direction with an angle , with n being the total number of layers. The simulation results in Fig. 1G and J demonstrate a nice rotator performance. To summarize, theoretically we have integrated the functions of the cloak, concentrator, and rotator within one single device, and next, we will numerically and experimentally realize this powerful device.
2. Numerical Design
The previous theoretical analysis is valid for all physical fields described by the Laplace equation, such as the pressure field of hydrodynamic flow in a porous medium, the temperature field in thermal conduction, and the electrical potential in DC electrical conduction. However, due to the challenging requirements for material properties, the multifunctional metamaterial has never been realized experimentally. In this section, we numerically design a practically achievable device for the flow field inside a porous medium, as illustrated below.
Using our “shell-shaped chessboard” scheme, we can in principle manipulate the internal flow in both magnitude and direction. Correspondingly, two tuning modes between different layers are required: taking the perfectly aligned configuration in Fig. 1D as the reference, we can either progressively rotate an angle α in every layer to tune the flow direction (see Fig. 1D inset) or simultaneously rotate an angle β in every other layer to manipulate the flow magnitude (see Fig. 1L inset). To achieve better functionality, the direction and magnitude should be adjusted as much as possible and as accurately as possible: This requires a large enough layer number n and a small enough building block’s azimuthal angle Δφ. However, too many layers and too small building blocks are both practically unfavorable. To balance all requirements, we design a device with n = 9 layers and Δφ = 18° (20 blocks per revolution), as demonstrated in Fig. 2A. Although this design makes the device not orders of magnitude larger than the pore level and thus not strictly following Darcy’s law, we verify that its performance agrees well with the theoretical prediction.
Fig. 2.
(A) The exact design of the shell-shaped chessboard device. The homogeneous porous medium is formed by pillars with diameter d=2 and spacing s=3. The shell has nine layers composed by two anisotropic building blocks, A and B. The right panel shows the detailed structures of A and B. B-D Cloak, concentrator, and rotator. E-G Corresponding flow fields. H-J Corresponding pressure fields. (K) A continuous rotation across 120° achieved by our rotator (). Inset shows the tuning angle α in each layer. (L) The velocity magnitude adjusted across one order of magnitude. The maximum corresponds to concentrator and the minimum corresponds to cloak. Inset shows the tuning angle β in every other layer.
The entire system is shown in the left panel of Fig. 2A. An isotropic and homogeneous porous medium fills up the space inside (region I) and outside (region III) of the shell device: This medium is formed by pillars with diameter d = 2 and interspacing s = 3. The shell device has an inner radius a = 30 and outer radius b = 63.4 (no exact length dimensions here to give the scalable freedom according to actual needs). As proved previously, the chessboard device requires two distinct anisotropic building blocks A and B, which should be designed as simple as possible for practical convenience. As shown in the right panel of Fig. 2A, building block A is made by only two pillars and B is simply formed by three annular bricks. However, these simple building blocks can achieve multifunctions with very little disturbance to the external flow field.
To demonstrate it, we inspect the tuning power in velocity magnitude between inner (region I) and outer (region III) flow: vx, 1/vx, 3 = (a/b)h − 1, which is determined by h = kθ, 2/kr, 2. Here, kθ, 2 and kr, 2 are the overall azimuthal and radial permeability of the entire shell (region II). With our design in Fig. 2A the right panel, we can easily achieve 0.46 < h < 3.18 by turning corresponding layers, which realizes an adjustment in the velocity magnitude of 0.2 < vx, 1/vx, 3 < 1.5. To realize such an adjustment, the effective medium theory predicts a variation over two orders of magnitude between the largest and smallest transport properties in the two building blocks. Due to this challenging requirement of the broad and continuous adjustment in material property, it is very difficult to realize multifunctional metamaterial in general. In a porous medium, however, due to the permeability k’s sensitive dependence on the porosity ε, k ∝ ε3 (Kozeny–Carman equation), and our accurate control over the porosity in the shell, we can achieve such a broad adjustment in k and realize the multifunctional metamaterial.
With this simple design, we have achieved the cloak, concentrator, and rotator within one single system, as demonstrated in Fig. 2B–D. The mostly straight external streamlines in the flow field (Fig. 2E–G) and the straight pressure contours in the pressure field (Fig. 2H–J) verify its little disturbance to the background flow, due to the permeability matching with the background. Moreover, a continuous adjustment between these functions can be achieved. In Fig. 2K, our device can continuously rotate the inner flow by 120°. In Fig. 2L, the velocity magnitude can be continuously tuned by seven times, and correspondingly, the device switches from the concentrator to the cloak. During all these operations, the background flow remains stable within 10% of fluctuation, confirming very little disturbance from the device. To summarize, we have numerically designed a multifunctional metamaterial with the chessboard scheme, and next, we realize it experimentally.
3. Experimental Results
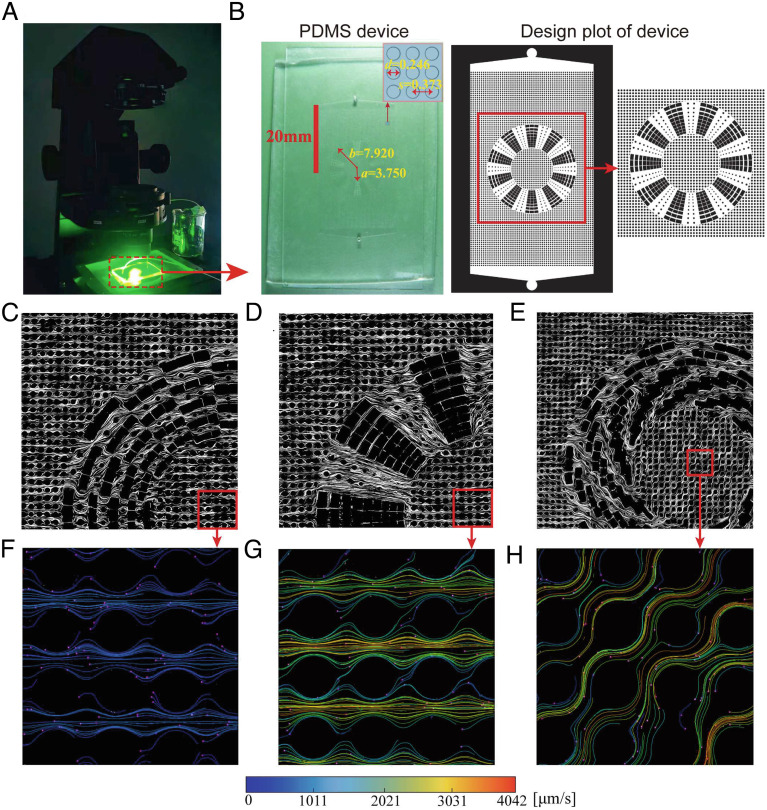
We experimentally realize the multifunctional metamaterial at microfluidic scales. As shown in Fig. 3A and B, the device is fabricated by PDMS with optical lithography, and the performance is measured by fluorescent microscopy. Following the numerical design of the last section, the homogeneous porous medium is formed by pillars with diameter d = 0.246 mm and interspacing s = 0.373 mm, and the functional shell has inner radius a = 3.750 mm and outer radius b = 7.920 mm. Due to the poor contrast of the actual PDMS system, we also show the corresponding design plot in the right panels of Fig. 3B for a better illustration.
Fig. 3.
(A) Fluorescence microscopy setup. (B) The PDMS system and its design plot. (C-E) The snapshots of the flow streamlines in the devices of the cloak, concentrator, and rotator respectively. (F-H) The corresponding flow field within the central area labeled by the red square in (C-E). The velocity magnitude is indicated by different colors, which is obtained by large statistics on particle tracking (820 particles for cloak, 1,700 for concentrator, 550 for rotator).
The measured flow fields for the cloak, concentrator, and rotator are shown in Fig. 3C–E, respectively (see also Movie S1). The streamlines are visualized by adding a very small amount of fluorescent tracer particles inside the flow (rhodamine-B-dyed PMMA particles with a radius of 2 μm and volume fraction of 5 × 10−4). Outside the shell, the straight and horizontal streamlines unambiguously confirm the little disturbance from the device and its “invisibility” to the background flow. Inside the shell, the velocity magnitude is further measured by tracking a large number of tracer particles along streamlines, as shown in Fig. 3F–H. According to the measurements, the cloak exhibits a velocity near zero, the concentrator exhibits a velocity larger than the background, and the rotator exhibits a significant rotation in the flow direction: All their performance agrees well with the numerical design.
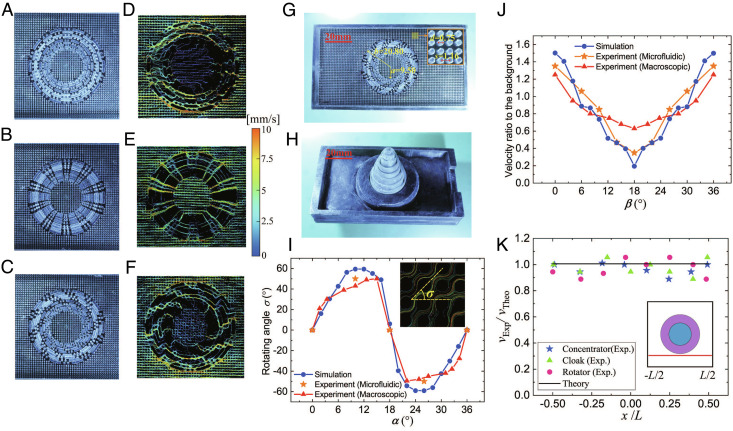
Moreover, to truly realize continuous switching among different functions, we build a millimeter-scale macroscopic system with movable layers by 3D printing (see Fig. 4G and H: d = 0.75 mm, s = 1.16 mm, a = 9.50 mm, and b = 20.80 mm). Note that the large device size is due to our printer’s limited resolution, and a much smaller device even at submillimeter scale could be achieved with a better 3D printer (31, 38). In Fig. 4G and H, we show the images of front and back sides of our device: the front side has nine movable layers, and the back side shows nine different shafts connected to the nine front layers. Each individual layer can be independently turned by the corresponding shaft to reach the desired configuration (Movie S2).
Fig. 4.
(A-C) Photographs of the cloak, concentrator, and rotator of the macroscopic device. These configurations are achieved by continuously rotating corresponding layers within one single device. (D-F) The corresponding flow fields obtained by tracking tracer particles (polystyrene particles with a radius of 10μm), and the velocity magnitudes are indicated by different colors. (G-H) The front and back sides of the actual device. (I) Comparison of the rotating angle between experiment and simulation. The blue symbols are from simulation, the orange symbols are from the microfluidic device, and the red symbols are from the macroscopic device. (J) Comparison of the velocity magnitude between experiment and simulation. (K) the velocity ratio vExp/vTheo along the red line near the cloak (see inset). The disturbances are mostly below 10%.
The three configurations of the cloak, concentrator, and rotator achieved by this single device are demonstrated in Fig. 4A–C, and the corresponding flow fields are shown in Fig. 4D–F. As expected, the cloak exhibits the smallest inner velocity, the concentrator exhibits the largest inner velocity, and the rotator exhibits a significant rotation in the flow direction (Movie S3). The comparison between the experiment and the simulation is shown in Fig. 4I and J. The rotation angle σ versus the tuning angle in each layer α is plotted in Fig. 4J, and both the microfluidic (orange symbols) and the macroscopic (red symbols) experiments agree with the simulation (blue symbols). The manipulation in the velocity magnitude is shown in Fig. 4J: the microfluidic (orange) data quantitatively agree with the simulation (blue) and the macroscopic (red) data only agree with it qualitatively. The reason is due to the limited precision of our 3D-printing equipment, which produces nonnegligible gaps between layers and leads to a nonideal performance compared to the simulation. Significant improvements can be expected with better 3D-printing equipment. To verify that our device makes negligible disturbance to background flow, in Fig. 4, we measure the velocity ratio between the experiment and the theory, vExp/vTheo, at different locations along a red line close to the cloak (see inset). Clearly, the disturbances are mostly below 10%, which is quite small, and the invisibility for flow field is achieved. Therefore, the functions of the cloak, concentrator, and rotator, as well as continuous switching among them, are realized successfully in this macroscopic device.
4. Discussions
To demonstrate that our device can indeed control living material without disturbing background environment which may find potential biomedical applications, we test our device’s control on biofilm growth. Experiment shows that our device can control the magnitude and direction of biofilm growth, while making no disturbance to the outside environment (see details in SI Appendix). Although preliminary, this result clearly shows the possibility of applying our device to living systems in the biomedical area.
Therefore, we further point out some potential applications of our hydrodynamic metamaterial in the biomedical area. In the tissue engineering area, porous media are commonly used as platforms for tissue culture, such as the biocompatible porous scaffolds that guide and support the growth of cells during tissue regeneration, either at the grafting site inside the body or in vitro. At the same time, previous studies have also shown that the growth of many tissues in human bodies is sensitive to the magnitude and direction of the fluid flow (42–44). Taking the porous bone tissue as an example, the directional fluid flow can enhance in vitro periosteal tissue growth for bones than the static culture condition (44). In addition, dynamic flows can also affect bone cell distribution, enhance cell phenotypic expression, and mineralize matrix synthesis within tissue-engineered constructs compared with the static condition (45). Therefore, the multifunctional control of the flow field by our metamaterial, coupled with its minimum disturbance to the background, makes it a good candidate to achieve the best growth conditions of cells and tissues with a negligible disturbance to the body environment. Thus our study may inspire design and optimization of 3D porous scaffolds for tissue engineering (46).
Another possible biomedical application is to design smart drug-release devices for porous environments inside the human body. Many human organs and tissues such as the lungs, livers, mammary glands, and bones are porous media. In many occasions, sustained and regulated release of medicine to their lesion regions such as tumors is required in clinical practice (47). An essential requirement of such drug delivery devices is again to make as little disturbance to the body as possible. Our device can effectively tune both flow direction and magnitude to deliver the medicine in a desired manner, while at the same time make negligible disturbance to the body. Moreover, because our device is continuously tunable, we can further tune the drug-release direction and magnitude to best match the body cycle and achieve a smart release device. Note that no matter what configuration the device changes into, minimum disturbance to the environment is always guaranteed. Therefore, our device’s multifunctional feature and minimum disturbance property make it a potential candidate for smart drug delivery devices.
Finally, we discuss the limitations of our hydrodynamic multifunctional metamaterial. Our design relies on Darcy’s law and thus cannot directly apply to the open fluid environment without a porous medium. How to achieve a more general hydrodynamic metamaterial for an open fluid environment? The previous theoretical study has proposed such a cloak by wrapping the device with a layer of material with negative permeability (27), which is impossible for common materials. However, we propose to adopt the active metamaterial design principle and use minipumps to create and modify the surrounding fluid flow, and the negative permeability could be realized. Further studies are required for this more general situation, and it is beyond the scope of this work.
5. Conclusion
To conclude, inside a porous medium, we theoretically design and experimentally realize a multifunctional metamaterial device. According to the theoretical analysis, our multifunctional device has satisfied highly challenging requirements in the material property: the maximum and minimum transport parameters differ over two orders of magnitude, and the effective parameter perfectly matches the background. As a result, a powerful hydrodynamic multifunctional metamaterial is realized, which may find applications not only in hydrodynamics but also for biomedical devices inside the human body due to its versatile functionality and little disturbance to the body environment. We further note that our study is a demonstration, and more practical systems designed for various porous media, either isotropic or anisotropic, and from microscopic to macroscopic scales can be achieved. Inspired by this work, we expect promising development in the design and application of multifunctional metamaterials in the future.
Supplementary Material
Appendix 01 (PDF)
The flow field in the microuidic device of the cloak, concentrator and rotator.
The tuning of velocity magnitude and direction in the 3D-printed device.
The flow field in the 3D-printed device of the cloak, concentrator and rotator.
Acknowledgments
We thank Ying Li, Yuhao Wang, Siyu Liu, and Xuequan Lai for the discussions and help to this study. L.X. acknowledges the financial support from NSFC-12074325, Guangdong Basic and Applied Basic Research Fund 2019A1515011171, GRF-14306518, CRF-C6016-20G, CRF-C1006-20WF, CUHK United College Lee Hysan Foundation Research Grant and Endowment Fund Research Grant, CUHK direct grant 4053354, and 4053471. X.S. acknowledges the financial support from Guangdong Basic and Applied Basic Research Foundation 2019A1515110211 and Project funded by China Postdoctoral Science Foundation 2020M672824.
Author contributions
X.S. and L.X. designed research; M.C. performed research; Z.C. and Y.W. contributed new reagents/analytic tools; M.C., X.S., J.H.Y.L., Y.L., X.X., and L.X. analyzed data; and X.S. and L.X. wrote the paper.
Competing interests
M.C., X.S., X.X. and L.X. are co-authors of a filed China patent no. 202210937497.4, which describes the methods used herein.
Footnotes
This article is a PNAS Direct Submission.
Data, Materials, and Software Availability
All study data are included in the article and/or SI Appendix.
Supporting Information
References
- 1.Pendry J. B., Schurig D., Smith D. R., Controlling electromagnetic fields. Science 312, 1780 (2006). [DOI] [PubMed] [Google Scholar]
- 2.Leonhardt U., Optical conformal mapping. Science 312, 1777 (2006). [DOI] [PubMed] [Google Scholar]
- 3.Jiang W. X., Chin J. Y., Cui T. J., Anisotropic metamaterial devices. Mater. Today 12, 26 (2009). [Google Scholar]
- 4.Zheludev N. I., Kivshar Y. S., Form metamaterials to metadevices. Nat. Mater. 11, 917 (2012). [DOI] [PubMed] [Google Scholar]
- 5.Landy N., Smith D. R., A full-parameter unidirectional metamaterial cloak for microwaves. Nat. Mater. 12, 25 (2013). [DOI] [PubMed] [Google Scholar]
- 6.Valentine J. et al. , Three-dimensional optical metamaterial with a negative refractive index. Nature 455, 376 (2008). [DOI] [PubMed] [Google Scholar]
- 7.Shalaev V. M., Transforming light. Science 384 (2008). [DOI] [PubMed] [Google Scholar]
- 8.Chen H., Chan C. T., Sheng P., Transformation optics and metamaterials. Nat. Mater. 9, 387 (2010). [DOI] [PubMed] [Google Scholar]
- 9.Schurig D. et al. , Metamaterial electromagnetic cloak at microwave frequencies. Science 314, 977 (2006). [DOI] [PubMed] [Google Scholar]
- 10.Silva A. et al. , Performing mathematical operations with metamaterials. Science 343, 160 (2014). [DOI] [PubMed] [Google Scholar]
- 11.Vakil A., Engheta N., Transformation optics using graphene. Science 332, 1291 (2011). [DOI] [PubMed] [Google Scholar]
- 12.Wegener M., Metamaterials beyond optics. Science 342, 939 (2013). [DOI] [PubMed] [Google Scholar]
- 13.Chen H. et al. , Design and experimental realization of a broadband transformation media field rotator at microwave frequencies. Phys. Rev. Lett. 102, 183903 (2009). [DOI] [PubMed] [Google Scholar]
- 14.Farhat M., Enoch S., Guenneau S., Movchan A., Broadband cylindrical acoustic cloak for linear surface waves in a fluid. Phys. Rev. Lett. 101, 134501 (2008). [DOI] [PubMed] [Google Scholar]
- 15.Zhang S., Xia C., Fang N., Broadband acoustic cloak for ultrasound waves. Phys. Rev. Lett. 106, 024301 (2011). [DOI] [PubMed] [Google Scholar]
- 16.Brun M., Guenneau S., Movchan A. B., Achieving control of in-plane elastic waves. Appl. phys. Lett. 94, 061903 (2009). [Google Scholar]
- 17.Fan C., Gao Y., Huang J., Shaped graded materials with an apparent negative thermal conductivity. Appl. Phys. Lett. 92, 251907 (2008). [Google Scholar]
- 18.Li Y. et al. , Transforming heat transfer with thermal metamaterials and devices. Nat. Rev. Mater. 1 (2021). [Google Scholar]
- 19.Narayana S., Sato Y., Heat flux manipulation with engineered thermal materials. Phys. Rev. Lett. 108, 214303 (2012). [DOI] [PubMed] [Google Scholar]
- 20.Schittny R., Kadic M., Guenneau S., Wegener M., Experiments on transformation thermodynamics: Molding the flow of heat. Phys. Rev. Lett. 110, 5 (2013). [DOI] [PubMed] [Google Scholar]
- 21.Han T. et al. , Experimental demonstration of a bilayer thermal cloak. Phys. Rev. Lett. 112, 054302 (2014). [DOI] [PubMed] [Google Scholar]
- 22.Li Y. et al. , Temperature-dependent transformation thermotics: From switchable thermal cloaks to macroscopic thermal diodes. Phys. Rev. Lett. 115, 195503 (2015). [DOI] [PubMed] [Google Scholar]
- 23.Shen X. Y., Li Y., Jiang C. R., Huang J. P., Temperature trapping: Energy-free maintenance of constant temperatures as ambient temperature gradients change. Phys. Rev. Lett. 117, 055501 (2016). [DOI] [PubMed] [Google Scholar]
- 24.Li J. et al. , Doublet Thermal Metadevice. Phys. Rev. Appl. 11, 044021 (2019). [Google Scholar]
- 25.Li Y. et al. , Thermal meta-device in analogue of zero-index photonics. Nat. Mater. 18, 48 (2019). [DOI] [PubMed] [Google Scholar]
- 26.Shen X. Y., Li Y., Jiang C. R., Ni Y. S., Huang J. P., Thermal cloak-concentrator. Appl. Phys. Lett. 109, 031907 (2016). [Google Scholar]
- 27.Urzhumov Y. A., Smith D. R., Fluid flow control with transformation media. Phys. Rev. Lett. 107, 074501 (2011). [DOI] [PubMed] [Google Scholar]
- 28.Park J., Youn J. R., Song Y. S., Hydrodynamic metamaterial cloak for drag-free flow. Phys. Rev. Lett. 123 (2019). [DOI] [PubMed] [Google Scholar]
- 29.Park J., Youn J. R., Song Y. S., Metamaterial hydrodynamic flow concentrator. Extreme Mech. Lett. 42, 101061 (2021). [Google Scholar]
- 30.Park J., Youn J. R., Song Y. S., Fluid-flow rotator based on hydrodynamic metamaterial. Phys. Rev. Appl. 12 (2019). [Google Scholar]
- 31.Feng S. et al. , Three-dimensional capillary ratchet-induced liquid directional steering. Science 373, 1344 (2021). [DOI] [PubMed] [Google Scholar]
- 32.Chen T., Pauly M., Reis P. M., A reprogrammable mechanical metamaterial with stable memory. Nature 589, 386 (2021). [DOI] [PubMed] [Google Scholar]
- 33.Bertoldi K., Vitelli V., Christensen J., Van Hecke M., Flexible mechanical metamaterials. Nat. Rev. Mater. 2, 1 (2017). [Google Scholar]
- 34.Yang S., Wang J., Dai G., Yang F., Huang J., Controlling macroscopic heat transfer with thermal metamaterials: Theory, experiment and application. Phys. Rep. 908, 1 (2021). [Google Scholar]
- 35.Jin P. et al. , Tunable hybrid thermal metamaterials with a topology transition. arXiv:2208.13638 arXiv preprint (2022). [DOI] [PMC free article] [PubMed]
- 36.Shen X. et al. , Achieving adjustable elasticity with non-affine to affine transition. Nat. Mater. 20, 1635 (2021). [DOI] [PubMed] [Google Scholar]
- 37.Sackmann E. K., Fulton A. L., Beebe D. J., The present and future role of microfluidics in biomedical research. Nature 507, 181 (2014). [DOI] [PubMed] [Google Scholar]
- 38.Dai B. et al. , Biomimetic apposition compound eye fabricated using microfluidic-assisted 3D printing. Nat. Commun. 12, 6458 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bear J., Dynamics of Fluids in Porous Media (American Elsevier Publishing, Environmental Science, New York - London - Amsterdam, 1972). [Google Scholar]
- 40.Nield D. A., The boundary correction for the Rayleigh-Darcy problem: Limitations of the Brinkman equation. J. Fluid Mech. 128, 37 (1983). [Google Scholar]
- 41.Nield D. A., Alternative model for wall effect in laminar flow of a fluid through a packed column. AIChE J. 29, 688 (1983). [Google Scholar]
- 42.O’Dea R. D., Waters S. L., Byrne H. M., A two-fluid model for tissue growth within a dynamic flow environment. Eur. J. Appl. Math. 19, 607 (2008). [Google Scholar]
- 43.Accadbled F. et al. , Influence of location, fluid flow direction, and tissue maturity on the macroscopic permeability of vertebral end plates. Spine 33, 612 (2008). [DOI] [PubMed] [Google Scholar]
- 44.Tarng Y. W. et al. , Directional fluid flow enhances in vitro periosteal tissue growth and chondrogenesis on poly-caprolactone scaffolds. J. Biomed. Mater. Res. Part A 95, 156 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Grayson W. L. et al. , Optimizing the medium perfusion rate in bone tissue engineering bioreactors. Biotechnol. Bioeng. 108, 1159 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Dias M. R., Fernandes P. R., Guedes J. M., Hollister S. J., Permeability analysis of scaffolds for bone tissue engineering. J. Biomech. 45, 938 (2012). [DOI] [PubMed] [Google Scholar]
- 47.Rattanadecho P., Keangin P., Numerical study of heat transfer and blood flow in two-layered porous liver tissue during microwave ablation process using single and double slot antenna. Int. J. Heat Mass Transfer 58, 457 (2013). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
The flow field in the microuidic device of the cloak, concentrator and rotator.
The tuning of velocity magnitude and direction in the 3D-printed device.
The flow field in the 3D-printed device of the cloak, concentrator and rotator.
Data Availability Statement
All study data are included in the article and/or SI Appendix.