Experimental reductions in subdaily flow fluctuations increased gross primary productivity for 425 river kilometers downstream

Abstract

Aquatic primary production is the foundation of many river food webs. Dams change the physical template of rivers, often driving food webs toward greater reliance on aquatic primary production. Nonetheless, the effects of regulated flow regimes on primary production are poorly understood. Load following is a common dam flow management strategy that involves subdaily changes in water releases proportional to fluctuations in electrical power demand. This flow regime causes an artificial tide, wetting and drying channel margins and altering river depth and water clarity, all processes that are likely to affect primary production. In collaboration with dam operators, we designed an experimental flow regime whose goal was to mitigate negative effects of load following on ecosystem processes. The experimental flow contrasted steady-low flows on weekends with load following flows on weekdays. Here, we quantify the effect of this experimental flow on springtime gross primary production (GPP) 90-to-425 km downstream of Glen Canyon Dam on the Colorado River, AZ, USA. GPP during steady-low flows was 41% higher than during load following flows, mostly owing to nonlinear reductions in sediment-driven turbidity. The experimental flow increased weekly GPP even after controlling for variation in weekly mean discharge, demonstrating a negative effect of load following on GPP. We estimate that this environmental flow increased springtime carbon fixation by 0.27 g C m⁻² d⁻¹, which is ecologically meaningful considering median C fixation in 356 US rivers of 0.44 g C m⁻² d⁻¹ and the fact that native fish populations in this river are food-limited.

Significance Statement.

Primary production fuels many river food webs. Extensive damming of rivers and associated changes to river flow regimes represents a pervasive change to riverine habitat, but the consequences for primary production are poorly known. Here, we compare rates of primary production below a large dam during load following hydropower operations to those during an experimental low and steady flow regime. We found nonlinear reductions in sediment transport and increases in water clarity during steady-low flows, which increased primary production. This increase occurred over both daily and weekly time scales and up to 425 km downstream from the dam. These findings show that dam management can affect photosynthetic rates, thus affecting carbon supply to food webs over large spatial extents.

Introduction

Dams regulate nearly half of the world's river volume (1), with unintended consequences for aquatic ecosystems (2, 3). Flows in regulated rivers are often designed to meet the demand or maximize the profitability of hydropower, which currently provides approximately 16% of the energy to the global power grid (4). One common flow modification consists of subdaily flow fluctuations that correspond with daily hydroelectric demand (5). Ecologists often define this management practice broadly as hydropeaking, whereas those in the energy sector reserve that term for facilities where generators are completely shut off during off-peak hours. Hereafter, we use the term “load following” to refer to the more muted subdaily changes in dam releases that result when power generation continues even during times of low electricity demand.

Load following increases river flows during times of day when electricity demand peaks. This subdaily flow variation creates an artificial daily tide that modifies physical and biological processes in the channel, and along the edges, of regulated rivers (6). Water depth and shear stress increase during the elevated portion of the load following tide, increasing turbidity and altering habitat suitability for different plant and animal species (Fig. 1). Along the river edges, the load following high tide entrains sediment (7), while the low tide exposes sessile plants (8) and early life stages of animals with limited mobility to desiccation (9, 10). Load following can increase atmospheric carbon emissions (11, 12) and decrease insect diversity, insect and fish biomass (13, 14), juvenile fish growth (15, 16), and adult fish size (17) across multiple rivers. While less is known about the effects of load following on primary production, the periodic desiccation of shoreline plants can reduce productivity of those communities 10-fold (8). In addition, larger daily discharge fluctuations for hydropower reduced downstream primary production under certain conditions (18). These findings motivated the design of a flow regime experiment, in an adaptive management context, to test how much modest modifications to the flow regime of a large, regulated river could augment ecosystem productivity while minimally affecting hydropower revenue.

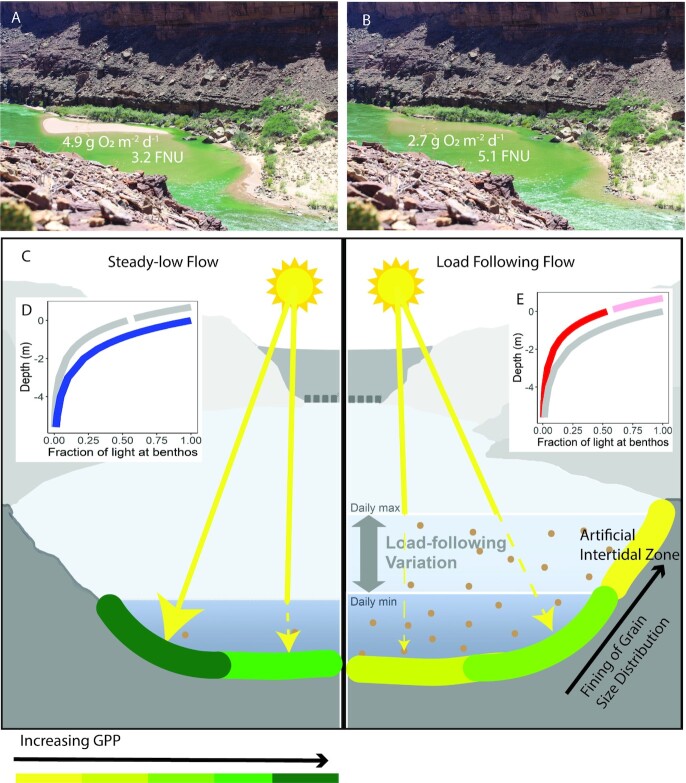
Fig. 1.

Photographs from reach B on 14 May and 16 May 2018 (river kilometer 130) show the steady-low flow (A), and the highest point of the load following flow (B). Specific turbidity and daily GPP for the reach at the time the photograph was taken is noted in white. Panel (C) shows a conceptual model for GPP in the study reaches during times when tributary inputs are low. Less turbidity, less light attenuation, and more primary production are depicted during steady-low flow conditions (left) than during load following flows (right). Finer bed grain size distribution along the river margins (19, 20) together with higher discharge result in more turbidity during load following flows. Inset panels (D) and (E) show the fraction of incident light estimated to reach the benthos from the high-water mark during steady-low (blue) and load following (red and pink) flow where gray shows the contrasting flow response in each panel. Depth indicates meters below (+) or above (-) the steady-low water line, with depths above the steady-low water line (in the artificial intertidal zone) represented in pink on panel (E). The fraction of incident light reaching the benthos was calculated as e^−Kaz, where z is water depth and Ka is the light attenuation coefficient assuming a 15º solar angle of incidence and 2,000 PFFD. Ka was estimated at the median turbidity for each flow regime (11.7 FNU, red and 8.3 FNU, blue) using the linear relationship with turbidity in the Colorado River (Figure S5a, Supplementary Material). We hypothesize that GPP in the artificial intertidal zone is low due to high disturbance associated with wetting and drying cycles. Panel (C) modified from Kennedy et al. (9).

While many studies have described how altered flow regimes affect aquatic ecosystems (2), large-scale experiments with multiple replicates of control and treatment flows are rare (21). Thus, many observational studies that aim to separate the ecological effects of load following rely on spatial comparisons. Within a single river, observational studies have compared conditions upstream vs. downstream of the dam (14), and have examined how distance downstream from the dam (22) and location relative to the discharge wave (9) affect ecosystem conditions. Observational studies have also compared conditions across rivers with different load following intensities (9, 13, 17, 22). Other observational studies have relied more on temporal comparisons within a single system by contrasting different load following intensities across different seasons (12, 18). These types of comparisons can make it difficult to separate confounding spatial and temporal covariates, highlighting the need for targeted experimental work that can directly compare different flow regimes.

An experimental flow regime enacted during the spring of 2 years (2018 to 2019) consisted of low and steady releases from Glen Canyon Dam (Arizona, USA) into the Colorado River during weekends—when demand for power is lower—with load following flows implemented during the 5 working days of the week (Fig.   2). Water releases from Glen Canyon Dam flow through > 400 river km, found mostly in Grand Canyon National Park, before entering Lake Mead. We focused inference on an ecosystem process, gross primary production (GPP), which provides nearly half of the carbon to animals in this river segment (23). GPP can be readily estimated at a daily time scale across multiple locations because of recent advances in dissolved oxygen sensors and statistical modeling (24, 25). Most GPP in the Colorado River occurs during spring (18) when tributary sediment inputs are low, turbidity is low, and variation in turbidity is mostly a function of subdaily changes in discharge that resuspend fine sediments (26, Supplementary Material). We hypothesized that steady-low flows would elevate GPP at the daily time scale due to reductions in turbidity and light attenuation. We also hypothesized that load following was causing more turbidity than would be predicted by simple linear scaling between discharge and turbidity. Thus, we predicted elevated weekly GPP in experimental flow weeks, with 2 days of steady-low flow, as compared with other weeks during the same time of year where mean discharge and bed grain size were the same. Finally, we hypothesized that turbidity reductions due to experimental flows would increase GPP the most during the springtime when rates of GPP are high and riverine turbidity is not influenced by tributary sediment inputs (i.e. when the bed grain-size distribution is coarser). To test these hypotheses, we first contrasted daily rates of GPP among steady and load following days across 11 reaches during the experimental flow regime (May and June of 2018 and 2019). Second, for three reaches with GPP estimates prior to 2018, we contrasted weekly rates of GPP before the flow experiment to weekly rates during the flow experiment. Across this same longer-term dataset, we asked how much the experimental flow affected the bed grain-size distribution by examining weekly changes in the relationship between discharge and suspended sediment (turbidity, sand, and silt-and-clay independently). Under the clear water conditions examined here, we consider these relationships as a proxy for bed grain-size distribution (26), and we examine the potential for longer-term effects of the flow regime on turbidity conditions in the river. Third, we used year-round GPP estimates together with discharge and turbidity data from three reaches with long-term data to estimate the expected effect of the experimental flow on GPP outside of the spring period investigated here.

Fig. 2.

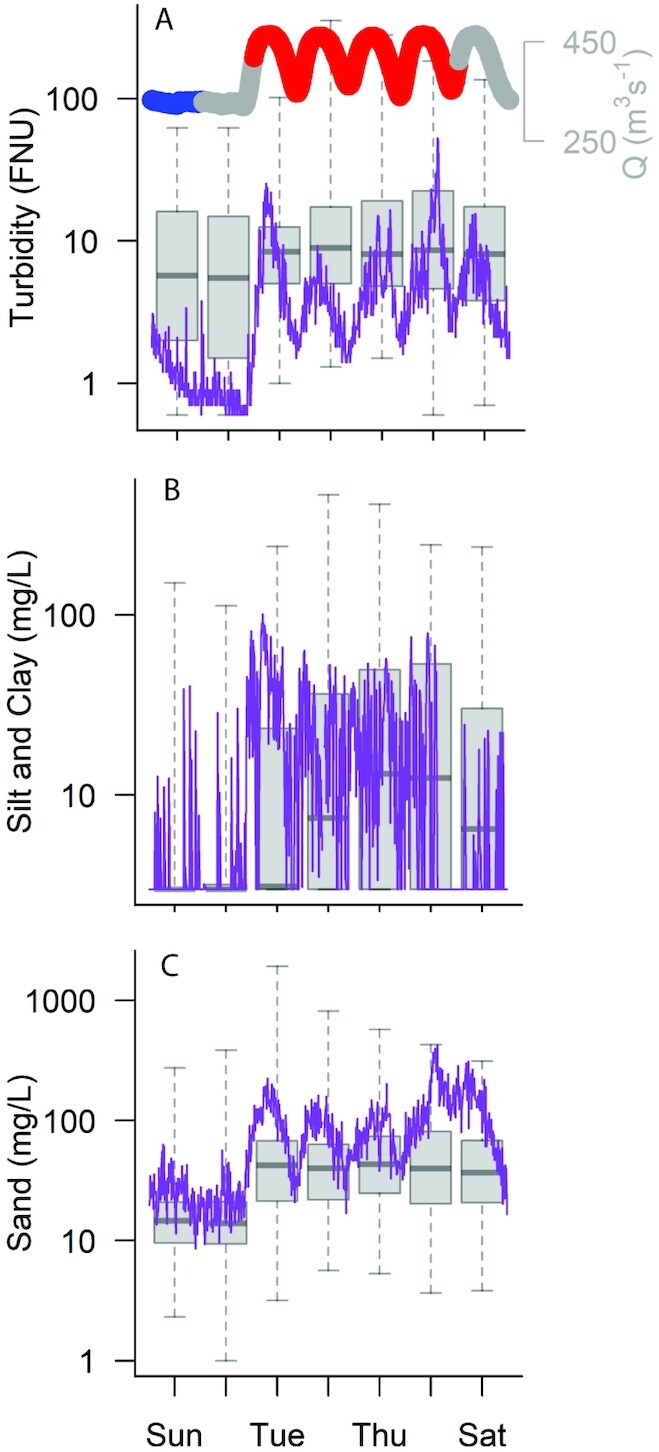
Discharge (top line) and turbidity (A), silt-and-clay (B), and sand concentrations (C) plotted in purple during the week of 2018 June 3 at the USGS Colorado River above Little Colorado River near Desert View, AZ, “A” 09383100 gaging station, 120 km below the Glen Canyon Dam. Boxplots show all turbidity (A), silt-and-clay (B), and sand (C) data available for the station during the entire experimental flow study period (May and June of 2018 and 2019). Due to transit time, steady-low flow releases from the Glen Canyon Dam reach this station very early on Sunday morning (∼2:00 MST) and last until Monday evening (∼20:00). For discharge, the modeled steady-low day of discharge is in blue, the modeled “load following” days are in red, and transition days are in gray.

Results

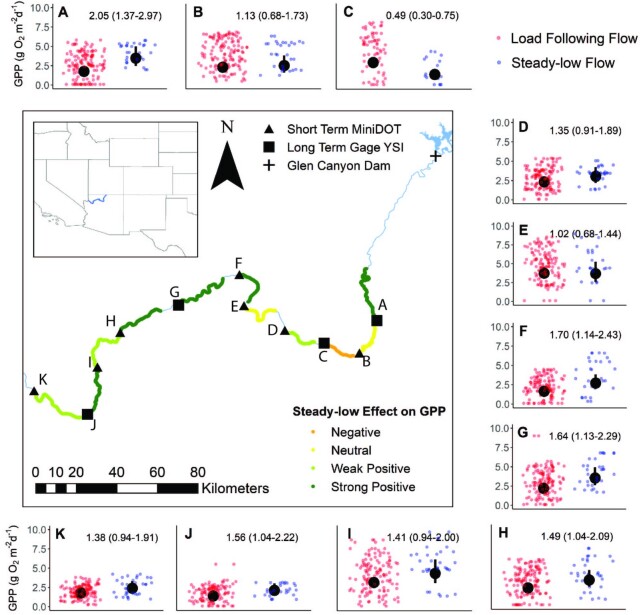
When averaging across sites, rates of GPP were 41% higher during steady-low weekend flows relative to fluctuating weekday flows. In 8 of the 11 reaches examined, GPP increased during steady-low flows (Fig. 3). When accounting for the population level effects of reach on GPP, GPP across all reaches was 3.1 ± 0.1 g O₂ m⁻² d⁻¹ during steady-low flow vs. 2.2 ± 0.1 g O₂ m⁻² d⁻¹ during hydropeaking flow, translating to a 41% increase in reach-scale GPP during the steady-low flow. Reach by reach, median steady-low flow rates of GPP ranged from 49% of hydropeaking rates (in the C reach) to 205% of hydropeaking GPP (in the A reach, Fig. 3). The fractional change in steady-low (vs. load following) GPP did not have a longitudinal pattern (Fig. 3) nor did the overall rate of GPP (Figure S1, Supplementary Material). The strongest steady-low increases in GPP occurred in reaches A, F, G, and J, with 256 river km between reaches A and J (Table S1, Supplementary Material; Fig. 3). The only decline in GPP during steady-low flows occurred in reach C. The C reach had the highest gas transfer velocity (Table S1, Supplementary Material), which complicates GPP estimation and makes modeling results from this reach less reliable. A total of two additional nearby reaches had no apparent change in GPP from hydropeaking to low and steady flow (reaches B and E). Across all reaches, gas transfer (k600) was negatively correlated with the fractional increase in GPP observed from weekday to weekend (adjusted R² = 0.56, P = < 0.001; Figure S2, Supplementary Material), however, there was no relationship between overall rate of GPP and gas transfer velocity (Figure S3, Supplementary Material).

Fig. 3.

Positive (green), neutral (yellow), or negative (orange) response of GPP rates to a shift from load following to steady-low flows in 11 reaches on the Colorado River in May and June of the 2018 and 2019 flow experiment. The length of each modeled reach is estimated based on gas transfer (80% turnover reach). The experiment maintained normal load following flow during the weekdays and adjusted to low and steady flows during the weekends. A total of 8 out of 11 reaches had elevated GPP on the weekend steady-low flow, relative to the weekday load following flow. Daily GPP estimates and modeled flow effects are plotted in separate panels for reaches A–K clockwise from the upper left to lower left. The x-axis separates GPP estimates by flow regime, with red dots representing GPP on days with load following flow and blue dots representing GPP on days with steady-low flow. Additional information about each reach and gaging station is available in the supplementary methods and Table S1 (Supplementary Material). The larger black points and ranges show the estimated median effect of load following vs. steady-low turbidity conditions with 90% credible intervals. Parameter estimates and 90% credible intervals are reported in the upper right corner and approximate the fractional change in GPP from load following to steady-low flows. Strong and weak positive effects were defined for cases where the lower end of the 90% credible interval did not drop below 1 or 0.9, respectively. A negative effect was defined when the upper end of the credible interval did not climb above 0.9, otherwise the effect was considered neutral. Inset map shows the location of the Colorado River reaches modeled here within the southwestern United States.

Steady weekend flows lowered river depth, average discharge, and water clarity. Steady-low flows lowered median water depth by 10% (from 6.3 to 5.6 m), reduced discharge by 20% (from 397 to 308 m³ s⁻¹), and lowered turbidity by 30% (from 11.7 to 8.3 FNU) across the study period (see Supplementary Results for more detail; Fig. 2). While empirical observations of light attenuation changes during the experimental flow are limited, point light measurements made near site A during the experimental flow show a 60% reduction in light intensities at a depth of 5 m when transitioning from steady-low flows to load following flows when normalized for angle of incidence (Figure S4, Supplementary Material). Independent of depth, we estimated that the turbidity reduction during steady-low flow increased the fraction of incident light reaching the bed by about 2% to 5% (Figure S5, Supplementary Material). In addition, the lower flow and concomitant turbidity reduction approximately doubled the light exposure of the shallow (0 to 0.5 m) nonintertidal benthos; Fig. 1d and e).

Silt-and-clay concentrations exerted the dominant control on turbidity during the experimental flow period examined here, but sand concentrations also contributed to turbidity during the clearest-water periods (Fig. 2b and c). Turbidity changes during periods of silt-and-clay concentration exceeding ∼10 mg L⁻¹ were driven mostly by suspended- silt-and-clay (Table S4, Supplementary Material). Median monthly sand concentrations ranged from 18 to 118 mg L⁻¹ and median monthly silt-and-clay concentrations spanned a similar range from 3 to 125 mg L⁻¹ (Table S2, Supplementary Material). The monthly average proportion of suspended sediment composed of silt-and-clay varied from 6% to 78% depending on month and reach (Table S2, Supplementary Material). Despite reductions in suspended-sediment during steady-low flow, mixed-effects models showed no clear effect of the experimental flow on the bed grain-size distribution (as measured by the ln–ln relationship between discharge and either turbidity, sand concentration, or silt-and-clay concentration; Table S3, Supplementary Material).

The flow regime together with turbidity and reach best predicted variation in daily GPP during May and June of 2018 and 2019 (Table S4, Supplementary Material). The presence of steady-low flow had a stronger but less certain positive effect on GPP, whereas turbidity values had a weaker but more certain negative effect on GPP (Table S4 and Figure S6, Supplementary Material). Inclusion of depth, month, and estimates of canyon shading (27) did not help improve model fit. Thus, the changes in water clarity due to the experimental flow were a larger control on riverine GPP than variation in canyon shading effects and monthly changes in discharge from the dam.

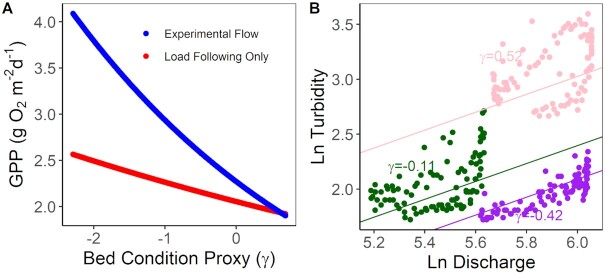
For three reaches with long-term dissolved-oxygen data (2012 to 2019; Table S1, Supplementary Material), mixed-effects modeling showed that the experimental flow elevated weekly GPP by 28% over springtime weeks with no experimental weekend steady-low flow. In addition to the experimental flow term, the best model of weekly GPP also included reach, log_e transformed mean daily discharge, and an intercept term for the previous week's log–log relationship between discharge and turbidity (hereafter γ; Table S5, Supplementary Material). This γ term, a proxy for the bed grain size, improved model fit and helped predict both the magnitude of GPP and the degree of the experimental flow effect. Coarser bed grain-size distributions (smaller values of γ) resulted in both higher GPP and a larger positive effect of the experimental flow on GPP (Fig. 4). Daily mean discharge improved model fit (Table S5, Supplementary Material), but the model predicted a large range of GPP rates even when holding daily mean discharge constant (Fig. 4). At the annual scale, the experimental flow regime tested here would have the greatest effect during spring and early summer; by elevating weekly GPP by 0.5 (0.1 to 1; May), 0.6 (0.1 to 1; June), and 0.5 (0.1 to 1; July) g O₂ m⁻² d⁻¹ (Fig. 5a). These months have highest absolute rates of GPP and the coarsest average bed grain-size distributions (Fig. 5b; Figure S7, Supplementary Material).

Fig. 4.

Panel (A) shows the average weekly mean GPP across sites A, G and J under differing bed grain size distribution conditions (γ) at a fixed daily mean discharge under experimental flows (blue) vs. load following only (red). The bed condition proxy uses the daily relationship between discharge and turbidity to infer coarser or finer bed grain size distributions (smaller and larger values of γ respectively). Panel (B) shows how daily differences in the y intercept of the ln–ln relationship between Q and turbidity are used to calculate γ. Individual points show 15-min data from a single day, with three different days depicted in three different colors. Here, γ is calculated for the day before the week begins, with lower values for γ indicating a coarser bed grain-size distribution. At γ values > 0.8 the experimental flow effect on GPP is indistinguishable relative to the load following-only scenario.

Fig. 5.

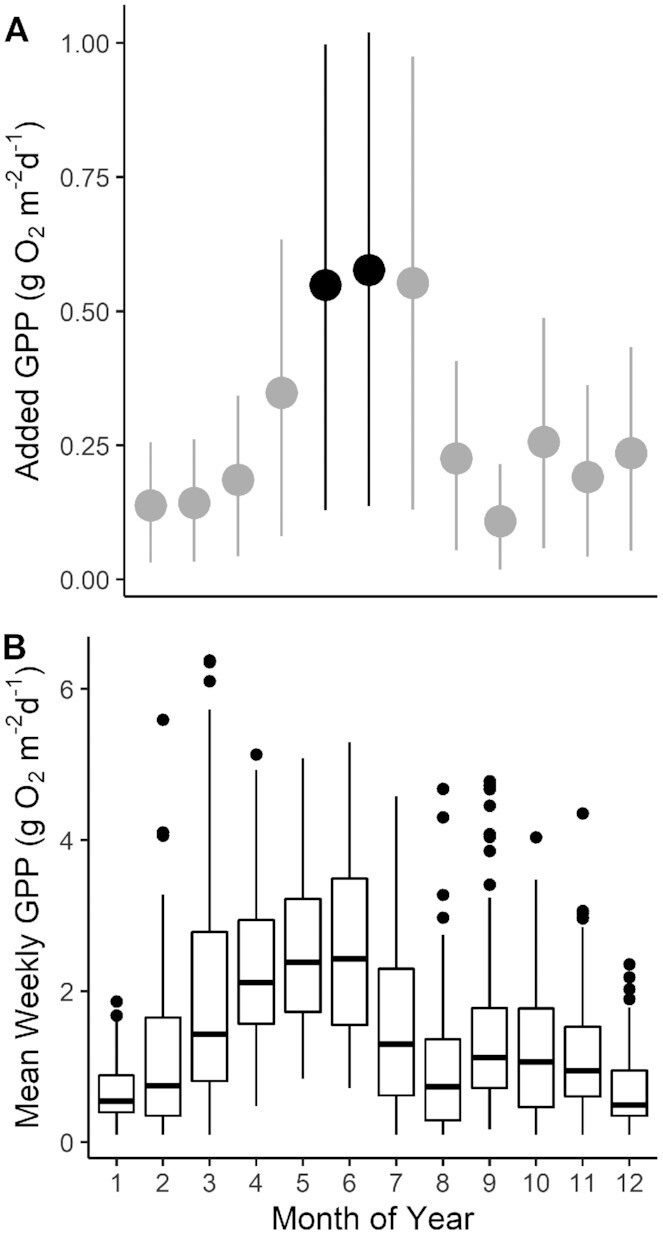
The additional weekly rate of GPP expected under the experimental flow regime during each month of the year (A) and the actual observed rates of weekly GPP (B) across 8 years in the three reaches with long-term data (reaches A, G, and J; Table S1, Supplementary Material). Actual observed rates of weekly GPP in panel (B) include 2 years of experimental flows and 6 years with no experimental flows. The experimental flow months examined in this paper are in black, extrapolated effects are in gray. In panel (A), dots indicate the model-averaged differences in the means of the posterior predictive distributions of weekly GPP under experimental vs. load following only flows; error bars indicate the 2.5% and 97.5% quantiles of the difference. In panel (B), the boxes demarcate the 25th and 75th percentiles; the horizontal lines indicate median concentrations; the whiskers extend to the largest value less than 1.5 times the interquartile range, and data extending beyond this range are plotted as individual points.

Discussion

Using experimental flows released from Glen Canyon Dam, we show that transitioning from load following to steady-low flows resulted in nonlinear reductions in turbidity and concomitant increases in primary production of the Colorado River by 41%. By examining GPP at the weekly scale and comparing years with an experimental flow to years without, we also showed that increased GPP on the weekend steady-low days did not come at the expense of GPP during the week. In other words, the clear water conditions that came with steady-low flows did not cause higher-than-normal turbidity during the following week's load following flows (Table S5, Supplementary Material). We also found no evidence that the experimental flow regime influenced the bed grain-size distribution or the overall transport of sediment (Table S3, Supplementary Material). Instead, the redistribution of turbidity from the steady-low days to the load following days affected light availability nonlinearly (Fig. 1) such that GPP was elevated on steady-low days with little effect on GPP during the load following days. Although the contrast between load following and steady-low flow tested in this study is confounded by the relationship between discharge and load following, our weekly analysis (contrasting weeks with vs. without experimental flow) separates these effects by considering weekly mean discharge as a potential control on GPP. Our results show a large springtime experimental flow effect across a variety of bed grain-size distributions even when daily mean discharge is held constant (Fig. 4). The effect of load following on GPP that is independent of daily mean discharge is likely due to Jensen's inequality, wherein the nonlinear relationship between discharge and turbidity causes higher daily mean turbidity from the diel peaks in discharge than would occur if discharge was held at the mean. The nonlinear relationship between discharge and turbidity arises from the nonlinear relations between discharge and suspended-sediment concentration and grain size in combination with the general occurrence of finer sediment at higher elevation on the channel perimeter that gets progressively inundated as discharge increases—a phenomenon that has been documented in both classic alluvial rivers and bedrock canyons (19, 20).

The increase in GPP with steady-low flow was energetically substantial. River-wide, the increase translated into the additional fixation of 0.27 g carbon (C) m⁻² d⁻¹ (from 0.87 to 1.14 g C m⁻² d⁻¹) based on the 1:1 molar ratio of oxygen produced to carbon fixed. For context, a national study of 365 rivers across the United States found that median GPP was only 0.44 g C m⁻² d⁻¹ (24). The clear water conditions below many dams (28) may further support food webs reliant on in situ primary production. For example, GPP on the river Saar increased by as much 3.5-fold across a 75-km reach with six low-head navigation dams (29). Although the Colorado River receives large amounts of terrestrial carbon inputs from flooding tributaries, macroinvertebrates derive most of their production from algae (due to higher assimilation efficiencies; (23) with diatoms, in particular, dominating the trophic basis of invertebrate production (30)). We expect that the higher GPP during steady-low flows increased secondary production of invertebrates and fishes given that production at these levels is food limited (23, 30–33).

Flow management affected GPP up to 425 km downstream from the dam (i.e. for the entire extent of our study area). This is a much greater distance than is typically considered within a dam's footprint. Nonetheless, the large spatial footprint of dam management on riverine GPP reported here fits with other broad scale geomorphic (34), biogeochemical (35), hydrological (36), and ecological effects (3, 9) that extend far downstream from the dam.

A preponderance of continuous dissolved oxygen data is supporting large-scale examinations of the patterns and controls on riverine GPP (24, 37), but it is difficult to estimate GPP from diel oxygen data in rivers below dams given the co-occurrence of both load following (e.g. variable transport times) and oxygen disequilibria. The combination of these two conditions violates both the one station modeling approach applied here and the two-station modeling approach often used to address oxygen disequilibria when water transit times remain steady (38, 39). Here, we take advantage of subdaily flow fluctuations that propagate many kilometers downstream and a rare experimental flow to examine the effects of load following on GPP. GPP methods that can accommodate both variable transit time and oxygen disequilibria have recently been developed (38), but improvements are needed to make the method more broadly applicable and to examine the geographic prevalence of the patterns we report here.

Implications for flow management

Increased GPP was an unanticipated benefit from this adaptive management flow experiment. The macroinvertebrate-production flow examined here was originally designed with the goal of increasing the diversity and production of macroinvertebrate assemblages by improving the survival of aquatic insect eggs laid on the river margins (9). While the effectiveness of the flow regime in meeting these macroinvertebrate goals is still being evaluated, we document an ecologically meaningful cobenefit of the experimental flow—a 41% increase in primary productivity to sustain aquatic and riparian food webs.

While most flow experiments quantify only a single biological variable (often freshwater fish), data collected during this experiment support study of the interaction between abiotic and biotic processes (suspended sediment dynamics and GPP), as well as work to examine effects at higher trophic levels (macroinvertebrates; ongoing work)—making it relatively unusual in the flow experiment literature (21), but see Watts et al. (40). In addition, the alteration of an overall flow regime (rather than a single punctuated flow event or a change in minimum flow magnitude) is relatively rare, constituting only 8% of 113 flow experiments in a global meta-analysis (21). The rarity of such flow experiments may arise from the relatively rigid operating constraints that some dam managers face, but such adaptive management experimentation and learning greatly improves resource outcomes over long-time scales (21, 41). The Glen Canyon Dam Adaptive Management Program designed the experimental flow regime tested here in a manner that was consistent with a complex set of operating constraints and at a 4-month net financial cost on the order of $300,000 in forgone hydropower revenue (42). This collaborative context for experimentation may make an ultimate change to dam operating policy more likely (21).

Managing Colorado River flow for lower suspended-sediment concentrations and coarser bed grain-size distributions (e.g. smaller γ) may increase primary productivity by reducing light attenuation and allowing more light to reach benthic primary producers. Sediment management and associated dam-released experimental floods have been a central theme of river management in the Grand Canyon segment of the Colorado River, with the focus largely on rebuilding and maintaining sandbars (43). Our study adds to our growing understanding of how relatively small changes in suspended sediment and associated turbidity can have large effects on ecosystem dynamics. The discharge-driven turbidity changes between flow regimes are 10 to 15 FNU, which is much lower than turbidity during storm-driven tributary floods (100 to > 1,000 FNU) when turbidity changes more as a function of changing sediment supply than discharge. Still, these small changes to turbidity at the lower end of the turbidity range can cause large differences in light attenuation. These turbidity-related differences in light availability strongly control seasonal GPP in the J reach (18) and likely canyon-wide. Small changes in turbidity affect feeding efficiency and growth of rainbow trout in the same river (44) as well as growth and survival of native fish (33, 45, 46), showing that flow-management-related changes in turbidity are emerging as a potentially useful tool for ecosystem management. Because dam-released experimental floods generally erode silt and clay from the Colorado River (26), such floods designed to build sandbars may also reduce riverine turbidity (during times not influenced by storms), thus increasing riverine GPP, although this hypothesis remains to be tested.

Global applicability of findings

The load following-related reductions in GPP we report here are likely extendable to many other regulated rivers, especially those in arid regions. GPP is often limited or colimited by light in rivers (37). Light attenuation due to water clarity and depth was recently estimated to limit primary productivity for 80% of river surface area across > 2.2 million rivers in the contiguous United States (47). While light attenuation in some rivers is driven more by colored dissolved organic matter (48), we expect that sediment-driven changes in light attenuation like those documented here are common in arid rivers draining less productive watersheds. Strong relationships between discharge and turbidity like the ones reported here are likely in many other rivers below dams given that sediment trapping behind reservoirs often, but not always, causes sediment-depleted conditions downstream. While we do not have a good sense for the global distribution of these sediment starved regulated river reaches, we know that the impoundment of rivers has caused a ∼50% reduction in sediment transport to the coast (49), suggesting the prevalence of these conditions.

A boom in small and large hydropower projects will nearly double global hydroelectric capacity in the coming decades (50, 51). Assuming completion of current and planned projects, free-flowing large rivers will decline by an additional ∼20% (50) and ∼94% of global river volume will be flow regulated, fragmented, or both (1). At the same time, a trend toward reduced load following intensity is occurring across North America (52). The regulated river ecosystems downstream of dams can have high primary productivity (28, 53–55), but the ubiquity of this phenomenon is unknown. Here, we show that flattening subdaily flow variation can measurably increase ecosystem productivity at the primary producer level. Where flexibility exists to redistribute flows within single days, dam managers may have a means to manage the overall productivity at the base of the food web.

Materials and Methods

Dissolved-oxygen data

We collected dissolved-oxygen data at 11 sites ranging from 120 to 400 km below Glen Canyon dam (Table S1, Supplementary Material; Fig. 3). Sites were far enough downstream of Glen Canyon Dam and any major tributaries to meet the assumptions of the one-station ecosystem metabolism modeling method ((56); Supplementary Methods). We selected sites to provide the best coverage of the river with respect to estimating GPP.

A total of 4 of the 11 sites were colocated with US Geological Survey (USGS) gaging stations (gages) measuring instantaneous discharge (Table S1, Supplementary Material). At these sites, temperature and dissolved oxygen have been monitored at 15-min intervals using optical Yellow Springs Instrument (YSI) Reliable Oxygen Sensor (ROX) probes continuously since at least 2012. The other 7 of the 11 sites were equipped with Precision Measurement Engineering (PME) MiniDOT loggers and recorded dissolved oxygen and temperature at 15-min intervals during the spring–fall of 2018 and 2019. Both the YSIs and the MiniDOTs were equipped with wiper units to mitigate biofouling. The MiniDOTs also had a copper plate installed around the oxygen sensor and were checked several times throughout their deployment to insure proper functionality of the wiper. PME wiper units recorded data about each wipe and these measurements were used to screen oxygen data so that data more than 2 weeks after the last effective wipe were discarded. This time period was based on a biofouling test conducted by deploying a MiniDOT with a copper plate but no wiper alongside the site A YSI in mid-April, which is typically the time of highest productivity (16). YSI oxygen sensors were field calibrated in an air saturated water bath several times yearly whereas MiniDOTs were factory calibrated and lab-checked pre and post field season. Additional calibration and quality control practices are described in the accompanying data release (57).

Turbidity and suspended-sediment data

At the four USGS gaging stations described above, turbidity (in formazin nephelometric units [FNU]) was measured using a YSI 6136 probe and false low turbidity readings were removed from the record (58). A total of 15-min concentrations of both suspended sand and silt-and-clay were measured using arrays of two to three single-frequency side-looking acoustic-Doppler profilers (59) at each station. All data collected at the USGS gaging stations (discharge, temperature, dissolved oxygen, turbidity, and suspended sediment) are available at: https://www.gcmrc.gov/discharge_qw_sediment/stations/GCDAMP. Specific gage numbers are available in the Supplementary Methods.

Light attenuation

Underwater light attenuation was opportunistically measured across a range of turbidity levels throughout Grand Canyon. Scalar and cosine-corrected quantum sensors (LiCor, Inc., LI-193SA and LI-190SZ, respectively) were used to measure photosynthetic photon flux density (PPFD; µmol quantum m⁻²s⁻¹). Because light attenuates exponentially as a function of water depth, four vertical profiles per site were used to characterize the apparent optics. For each profile, five measurements were logged at each depth at 0.5-m intervals to a depth of 5 m. Turbidity (FNU) measurements were logged every 5 min and averaged over the sampling period using a YSI as above. To reconcile for solar flux at water-surface a ratio was calculated between reciprocal measurements of underwater and surface incidence. These light-depth ratios were log_e transformed and then regressed against depth to estimate an apparent light attenuation coefficient (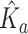) with units 1 m⁻¹. Because solar angles influence apparent optical conditions, these coefficients were normalized (K_N) using the expression

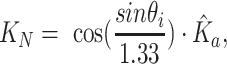where 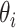is the angle-of-incidence and 1.33 is the refractive index of water. Angle-of-incidence was calculated based on spatial coordinates and solar time adjustment (27). Normalized coefficients were selected based on criteria (R² > 0.96), averaged, and then regressed against the average FNU measurement.

Modeling gas exchange

Oxygen models to estimate GPP require knowing air–water gas exchange. In the Colorado River, previous work has used the oxygen discontinuity described above (e.g. dam-induced oxygen undersaturation) to generate direct estimates of gas exchange (56). This work reported extremely high values for k₆₀₀ in rapids (up to 3,700 cm h⁻¹) and showed that reach gas exchange (measured as an exchange velocity corrected to Schmidt number of 600, k₆₀₀) values scaled best with the amount of river drop in a given reach, independent of discharge (56). Based on seven oxygen transects across different seasons, 80% oxygen turnover reaches were best estimated as the length over which the river elevation drops by 37.8 m (56). We used this relationship between river drop and oxygen turnover together with a high-resolution river-surface elevation Light Detection and Ranging (LiDAR) dataset collected in 2000 (60) to estimate the length of 80%-oxygen-turnover reaches (K_d in m) for all but the most downstream reach. In place of LiDAR data, we used a DEM layer to estimate river elevation downstream from site J (for the K reach). These reaches were used to space our dissolved-oxygen loggers for best coverage of GPP reaches. Per kilometer oxygen exchange was estimated following equation 9 in (56) as

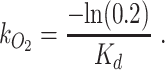We then scaled 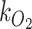to 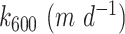based on

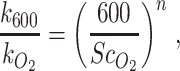where the exponentn was set to −0.5 for the turbulent river environment and the Schmidt number (Sc_O2) was calculated assuming the river temperature was 10°C and based on Wanninkhof (61).

Estimating GPP

We modeled oxygen concentrations as a means to estimate GPP using a process error model that is available in the R package streamMetabolizer (25) as model name “b_np_oipp_tr_plrckm.stan,” where “b” indicates a Bayesian model, “np” indicates nonpooling, “tr” indicates trapezoidal light, and “oipp” indicates the light process error model. This model is similar to the state–space model described by Appling and others (25), but differs in that process error is only allowed during the day and assumes lognormal error. We chose this modeling approach after preliminary comparisons showed large differences in both the modeled magnitude and subdaily timing of GPP with more traditional modeling approaches. For a subset of the data, we compared results from both b_np_oipp_tr_plrckm.stan and b_np_oipi_tr_plrckm.stan. We report the same directional effect of low and steady flows on GPP regardless of the model used (however, the absolute magnitude of the GPP estimates does change). K was fixed for all models by setting the k600_daily_sdlog to a value of 0.004 (to severely limit day to day variation in estimates of k₆₀₀, thus we effectively completely pooled k₆₀₀). As this modeling approach is Bayesian, we checked for convergence of model parameters using the Gelman–Rubin diagnostic and discarded GPP estimates from days with poor model convergence (e.g. 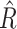> 1.1; 62). Models were run in RStan (63) through RStudio (R version 4.0.2 and 4.0.3; 64) using the streamMetabolizer package (version 11.4). Finally, we forced GPP estimates < 0.1 to equal 0.1 to best represent model sensitivity and so as to not overweight the days with the lowest GPP in our modeling efforts.

We estimated % oxygen saturation using measured river temperatures, barometric pressure readings from a weather station located in Page, Arizona (accessed from wunderground 12/16/2019; https://www.wunderground.com/history/daily/us/az/page/KPGA) corrected for the wetted surface elevation of the reach (60), and published relationships between water temperature, barometric pressure, and oxygen saturation (65).

To get depth-integrated estimates of oxygen in the water column, we assumed hydraulic continuity:

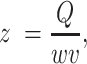where z is mean depth in m, w is wetted width in m Q is discharge in m³ s⁻¹, and v is velocity m s⁻¹). Discharge was measured at the four long-term YSI sites (Table S1, Supplementary Material) and was modeled for the other reaches using the nearest gage and assuming that the discharge wave is traveling at a speed of 8.6 km h⁻¹ (59). Using the LiDAR dataset described above, wetted width values were estimated based on wetted surface elevations for the entire 80% oxygen turnover reach and remained a constant value regardless of velocity (66). Wetted width values were corrected using a 1.04 to account for the fact that width was measured at low Q (60). River velocities (v) were estimated as

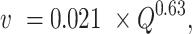where Q is river discharge in m³ s⁻¹ and v is predicted in units of m s⁻¹ following (67).

We estimated PPFD of PAR for each time point where dissolved-oxygen, temperature, and discharge measurements were available at 0.1-km intervals using a linked solar and topographic model developed for the Grand Canyon reach of the Colorado River (27). The river is canyon-bound and has little shading from riparian vegetation. While clouds and turbidity can constrain GPP (16), the light process error model we employ should accurately estimate GPP regardless of short-term fluctuations in light availability.

We cannot estimate ecosystem respiration in the Colorado River from high frequency dissolved oxygen measurements because turbulent mixing and associated bubble entrainment cause increase steady state oxygen concentrations in the river by an unknown amount above that calculated from gas saturation equation (18).

Statistical analysis

Comparison of daily GPP between steady and load following conditions during experiment flows

Flow transitions (between steady-low and load following) sometimes occurred in the middle of the day, so we selected a single day each week where water was steady and low from 4:00 to 3:45 Mountain Standard Time the following day (the time frame over which daily GPP was modeled).  The day on either side of the steady-low flow day was considered a transition day and was omitted from the analysis.  The remaining days represented the load following weekday flow. Transition days were generally intermediary in GPP (Figure S8, Supplementary Material). To summarize data and test hypotheses about potential drivers, we log_e-transformed the GPP estimates (technically the median of the posterior distribution of daily GPP) and analyzed the transformed GPP using linear mixed models (LMM) with a normal (Gaussian) error structure using the lme4 package v. 1.1–26 (68) in R (v. 4.0.2; 68). To summarize GPP under both flow conditions in each reach, we fit a model in which the intercept represented hydropeaking flows, and an indicator variable was used to indicate the steady-low flow. We chose a random effect structure that allowed both the intercept and coefficient associated with the indicator variable to vary among reaches. We then quantified the % change in GPP from load following to steady-low flow for each reach as

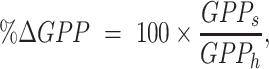where GPP_s and GPP_h are the model estimated rate of GPP during steady-low flow and load following flows, respectively. To test hypotheses regarding the role of turbidity, flow, water depth, light, and other factors as controls on daily GPP during the spring experimental flows (May and June of 2018 and 2019), we formulated a series of candidate models that were compared to each other and to the summary model (i.e. the model with flow regime as an indicator variable). The candidate models included either median daily turbidity, ln-transformed mean daily light, or median daily depth, as drivers of variation in ln-transformed GPP. All models included a reach random effect with varying intercept and allowed for the slope to vary with the random effect. We used AIC values to compare models. Turbidity was only measured at the four YSI sites. Turbidity was modeled for MiniDOT reaches following the approach used for discharge (described above), but instead of using the nearest gage we used the nearest downstream gage. This use of downstream gages for turbidity modeling was done given the strategic placement of YSIs directly above major tributaries. The exception was for modeling turbidity at the downstream-most MiniDOT (for which we used turbidity measured at site K, Table S1, Supplementary Material).

Comparison of weekly GPP between experimental flows and regular dam operations during sprint

To analyze the longer-term effect of the experimental flow on GPP, we modeled the ln-transformed weekly mean GPP at three long-term sites (A, G, and K) in the months of May and June across 8 years, two of which experienced the experimental flow (Table S1, Supplementary Material). Model estimates of GPP during weeks with regular flow (load following 7 days a week) were compared to model estimates of GPP from weeks with experimental flows (steady-low flow 2 days a week) with reach as a random effect with varying intercept.  Ln-transformed weekly GPP was also modeled as a function of ln-transformed Q, and the daily random effect intercept of the relationship between ln(Q) and ln(T) (referred to here as γ) with a separate model for each reach.

Comparison of suspended-sediment regime between experimental flows and regular dam operations

Finally, to compare the potential for scouring or accumulation of sand and/or silts-and-clays on the riverbed, we modeled the intercept of the ln–ln relationship between Q and (1) silt-and-clay concentration, (2) sand concentration, and (3) turbidity at the end of each week with reach as a random effect. This intercept can be thought of as a proxy for the grain-size distribution on the riverbed, where increasing γ reflects a greater abundance of silt and clay and/or finer sand on the riverbed. In this usage, our empirically derived γ behaves similarly to the inverse of the theoretically derived β of Rubin and Topping (69, 70). Model estimates of turbidity, silt-and-clay and sand intercepts during weeks with regular flow (load following 7 days a week) were compared to model estimates of GPP from weeks with experimental flows (steady-low flow 2 days a week) with reach as a random effect with varying intercept. Model estimates of turbidity, silt, and clay and sand intercepts at the end of the week were also modeled as a function of the respective intercepts at the beginning of the week.

Comparison of weekly GPP between experimental flows and regular dam operations across all months

To analyze the seasonality of the experimental flow effect on GPP, we modeled the ln-transformed weekly mean GPP at three long-term sites (A, G, and K) in all months across 8 years, two of which experienced the experimental flow from May to August (Table S1, Supplementary Material). This was done using two linear mixed effects models structured based on the top two models from our weekly May and June analysis but with month and year as additional random effects (Table S5, Supplementary Material). Models were fit using the rstanarm package (71). We then used the posteriors associated with both models of weekly GPP to predict weekly GPP across the entire data set under both experimental flow and nonexperimental flow conditions. These two sets of predictions were then averaged based on model weights derived from their respective AIC values. The absolute differences between the model-averaged load following and the experimental flow weekly GPP rates were then compared across months.

Authors’ Contributions

Bridget Deemer: Designed research; Performed research; Analyzed data; Wrote the paper Charles Yackulic: Designed research; Analyzed data; Wrote the paper Robert Hall: Designed research; Analyzed data; Wrote the paper Michael Dodrill: Performed research; Analyzed data; Edited paper Theodore Kennedy: Performed research; Edited paper Jeffrey Muehlbauer: Performed research; Edited paper David Topping: Contributed new analysis approaches; Edited paper Nicholas Voichick: Performed research; Edited paper Michael Yard: Performed research; Analyzed data; Edited paper

Notes

Competing Interest: The authors declare no competing interest.

Funding

Funding was provided by the Glen Canyon Dam Adaptive Management Program. Any use of trade, product, or firm names is for descriptive purposes only and does not imply endorsement by the US Government.

Data Availability

Data generated during this study are available from the USGS ScienceBase Catalog https://doi.org/10.5066/P9ZS6YLV (57).