Epistasis between promoter activity and coding mutations shapes gene evolvability

Abstract

The evolution of protein-coding genes proceeds as mutations act on two main dimensions: regulation of transcription level and the coding sequence. The extent and impact of the connection between these two dimensions are largely unknown because they have generally been studied independently. By measuring the fitness effects of all possible mutations on a protein complex at various levels of promoter activity, we show that promoter activity at the optimal level for the wild-type protein masks the effects of both deleterious and beneficial coding mutations. Mutations that are deleterious at low activity but masked at optimal activity are slightly destabilizing for individual subunits and binding interfaces. Coding mutations that increase protein abundance are beneficial at low expression but could potentially incur a cost at high promoter activity. We thereby demonstrate that promoter activity in interaction with protein properties can dictate which coding mutations are beneficial, neutral, or deleterious.

Changes in promoter activity can buffer deleterious mutations and potentiate adaptive ones.

INTRODUCTION

Mutations drive evolution through multiple effects, from altering gene expression to modifying the stability, assembly, and function of proteins, which ultimately affect cellular phenotypes and fitness. Therefore, measuring the fitness effects of mutations and identifying the underlying molecular mechanisms have been a long-standing goal in evolutionary biology (1, 2). Because of epistasis, the effects of new mutations are dependent on prior mutations, which makes their impact on fitness difficult to predict. Epistasis can take place among genes or within genes (3), including between noncoding mutations that alter different features of a gene such as its regulation, including promoter activity, and others that are coding and that alter protein activity or stability.

Regulatory and coding changes underlie phenotypic variation within and between species (4, 5). Unfortunately, both types of mutations are rarely studied simultaneously when mapping the effects of mutations on fitness, apart from a few cases (6–9) revealing that epistasis between mutations affecting the expression of a gene and coding mutations (regulatory-by-coding) is likely frequent. For instance, the relative effects of coding mutations could be amplified at low expression level, as demonstrated in the study of a short amino acid segment of the heat shock protein Hsp90 (9). Conversely, mutations that are deleterious at low expression levels could become neutral at higher expression levels or vice versa. For example, some disease-associated mutations have a higher penetrance when linked to a regulatory variant that increases their expression (10). Thus, interactions between changes in gene expression and coding mutations could represent a vast underexplored constraint on protein evolution. Here, we use deep mutational scanning (DMS) to examine how regulatory-by-coding epistasis could affect the evolutionary potential of a protein by performing a comprehensive measurement of the fitness effects of coding mutations at five levels of promoter activity in the vicinity of an expression level that is optimal for the wild-type (WT) enzyme.

RESULTS

The fitness landscape of a protein complex depends on its promoter activity level

We investigated the extent to which promoter activity affects the fitness landscape of a protein by mimicking evolutionary changes throughmutations affecting promoter activity using an inducible system. We used a metabolic enzyme that produces a metabolite that is conditionally essential for growth (Fig. 1A). The dihydrofolate reductase DfrB1 (formerly known as R67 DHFR) was first isolated as one of the factors causing trimethoprim (TMP) resistance in Enterobacteria, including Escherichia coli (11). Contrary to the monomeric FolA-type dihydrofolate reductase encoded in the E. coli main chromosome (ecDHFR) that is readily inhibited by TMP [ecDHFR inhibition constant (K_i) ~ 20 pM], DfrB1 is essentially insensitive to this antibiotic (DfrB1 K_i ~ 0.15 mM; Fig. 1B) (12, 13). The DfrB enzymes are obligate homotetramers that form a single, central active site requiring the distinct contribution from each of the four identical protomers (12, 14). DfrB enzymes are not homologous to the ubiquitous FolA-type DHFR enzymes that ecDHFR is part of (14–16). While many antibiotic resistance proteins degrade or inactivate molecules or expel them from the cell, DfrB1 is a metabolic enzyme that circumvents the inhibition of ecDHFR by duplicating the same essential enzymatic reaction: the reduction of dihydrofolate to tetrahydrofolate. The growth of E. coli can therefore be made dependent on DfrB1 activity through the inhibition of ecDHFR using TMP.

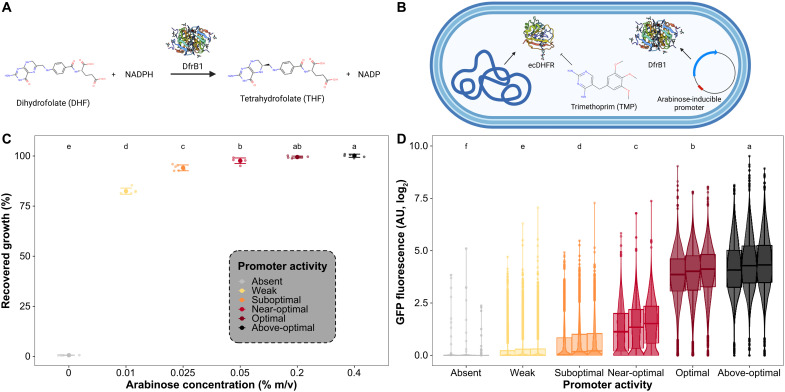
Fig. 1. Inducible DfrB1 expression connects promoter activity with fitness.

(A) DfrB1 converts dihydrofolate (DHF) to tetrahydrofolate, an essential metabolite. (B) The E. coli dihydrofolate reductase (ecDHFR) is inhibited by TMP. DfrB1 is not homologous to ecDHFR and is insensitive to TMP, and in our experiments, its transcription is modulated by an arabinose-inducible promoter. (C) Fitness function of DfrB1 promoter activity level. By inhibiting the endogenous ecDHFR with TMP (10 μg/ml), growth depends on the expression of DfrB1. Fitness is measured as a difference in growth (area under the curve) of the strain in medium with TMP relative to the same medium without TMP for a given arabinose concentration. The large dotsindicate the mean of six replicates (small dots), and error bars indicate 2.5 SEMs. Labels at the top indicate groups of recovered growth shown to be significantly different using an analysis of variance (ANOVA) and Tukey’s post hoc test (P < 0.05). (D) DfrB1-GFP expression as a function of arabinose concentration. Fluorescence of the WT DfrB1 is shown relative to the same E. coli strain but not expressing GFP. Three independent replicated cultures are shown side by side for each concentration. Labels at the top indicate groups of GFP fluorescence shown to be significantly different using an ANOVA and Tukey’s post hoc test (P < 0.05). AU, arbitrary units.

We used a plasmid whereby expression of dfrB1 is driven by an arabinose-dependent promoter (Fig. 1B). By inducing expression in 0 to 0.4% arabinose and measuring the extent of fitness recovery from ecDHFR inhibition (percentage of the growth without TMP achieved when expressing DfrB1 in media with TMP), we found that WT DfrB1 promoter activity at 0.2% arabinose completely complements the inhibition of ecDHFR. This induction level was defined as the optimal promoter activity level for WT DfrB1, and thus, we will use this arabinose concentration as the reference for most comparisons (Fig. 1C and fig. S1). Given the degree of complementation at each induction level, we refer to these levels as, starting from the highest, above-optimal (0.4% arabinose), optimal (0.2% arabinose), near-optimal (0.05% arabinose), suboptimal (0.025% arabinose), and weak (0.01% arabinose) for the WT enzyme. We measured the corresponding expression levels by fusing DfrB1 to green fluorescent protein (GFP) (Fig. 1D). E. coli populations displayed a unimodal expression level within this range of induction (median fluorescence in arbitrary units: 0% arabinose, 0.42; 0.01% arabinose, 0.74; 0.025% arabinose, 1.11; 0.05% arabinose, 2.55; 0.2% arabinose, 16.07; 0.4% arabinose, 18.85). DfrB1 therefore has a typical enzymatic fitness function as its fitness increases with promoter activity and then saturates when additional expression becomes superfluous (17).

We generated a library of all possible single-amino acid changes to the sequence of DfrB1 covering amino acid positions 2 to 78 (fig. S2). Individual mutants were combined in a pool and transferred to medium with TMP at the five arabinose concentrations defined above (fig. S3). The frequency of the mutants in the initial pool before selection and after 10 generations with TMP was measured by deep sequencing in a highly replicated fashion (tables S1 and S2). We estimated a selection coefficient (s) per DNA variant at each induction level, and then, redundant codons and replicates were aggregated (Fig. 2 and table S3). Selection coefficients are proportional to differences in growth per generation between cells with a specific DfrB1 mutation and cells with the WT DfrB1. Positive values of s indicate mutants that grow faster than the WT, negative values of s refer to mutants that grow slower than the WT, and a value of zero indicates the same growth rate as the WT (see Materials and Methods). Biological replicates were correlated across experiments, showing that the measurements are highly reproducible (fig. S4). We confirmed the deleterious effects of several previously reported catalytically inefficient mutations (figs. S5 and S6). We also validated a number of isolated mutants (n = 9) through growth curves (Spearman ρ = 0.85, P < 0.001; fig. S7). These results confirm the validity of the pooled measurements to estimate fitness effects of variants of this enzyme.

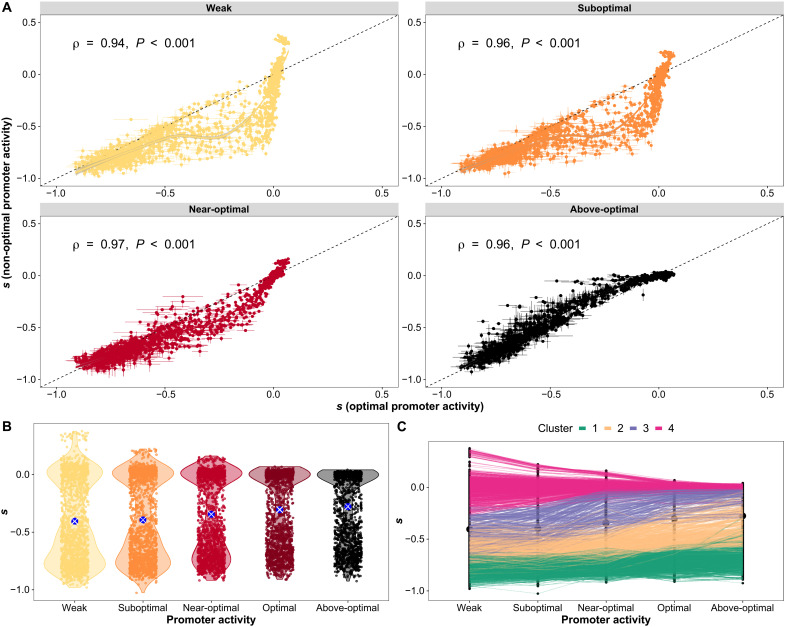
Fig. 2. Selection coefficients (s) of amino acid changes depend on promoter activity.

(A) Selection coefficient (s) of individual amino acid mutants at non-optimal levels of promoter activity compared to the optimal level for the WT, which is used as a reference point for comparisons. Spearman correlation coefficients are shown. Lines indicate LOESS regressions. Horizontal error bars indicate the SEMs observed across biological replicates at optimal promoter activity level for the WT. Vertical error bars indicate the SEMs observed across biological replicates at non-optimal promoter activity levels. (B) Distributions of s for individual mutants across promoter activity levels show reduced spread and increasing average of individual values. The larger blue dots with white crosses indicate the means of the distributions. (C) Clusters showing patterns of changes of s for individual mutants across promoter activity levels. Colored lines indicate mutants from the different clusters (k-means, k = 4). Number of mutants in each cluster: (1) 446, (2) 291, (3) 218, and (4) 581.

The selection coefficients of individual mutants are broadly correlated among promoter activity levels, revealing that most amino acid substitutions have effects that are relatively similar across promoter activity levels. However, the magnitude of these correlations when the various induction levels are compared to the optimal level for the WT (0.2% arabinose) decreases gradually as promoter activity level deviates from this reference (Fig. 2, A and B, and fig. S8A). We observe a fitness effect that depends on promoter activity for many mutations: 598 of 1458 substitutions (41%; 74 of 77 positions) measured at all five promoter activity levels showed statistically significant effects of promoter activity on selection coefficients [magnitude > 0.1, analysis of variance (ANOVA), false discovery rate (FDR) adjusted P < 0.05; fig. S8B and table S4].

To identify broad patterns of changes of individual amino acid substitutionsalong the gradient of promoter activity, we grouped the vectors of selection coefficient by similarity. Clustering using k-means identified four typical patterns (k = 4 clusters). This number of clusters is the best compromise between parsimony and interpretability (Fig. 2C; table S5; and fig. S9, A and B) because from k = 4 onward, adding more clusters does not result in a substantial decrease in the sum of squared errors. Representative centroids for each cluster are shown in fig. S9B. As one could expect, some substitutions do not have major effects on fitness (cluster 4, n = 581). At the other end of the spectrum, others are deleterious at all promoter activity levels (cluster 1, n = 446). Many variants appear to deviate from these two patterns (clusters 1 and 4), particularly between optimal (reference) and weak promoter activity levels (Spearman ρ = 0.94; Fig. 2C). Mutants in cluster 3 (n = 218) are deleterious at weak and suboptimal promoter activity, but some become neutral or near neutral at the optimal promoter activity level for the WT enzyme. Mutants from cluster 2 (n = 291) are even more deleterious at low promoter activity levels, but even if they remain deleterious, they improve in fitness as promoter activity increases, even beyond optimal induction for the WT. This gain of fitness of many mutants at above-optimal promoter activity is also visible in the relationship shown in Fig. 2A. Mutations of intermediate deleterious effects at the optimal promoter activity level are worse, as promoter activity is decreased and some are further buffered or masked at above-optimal promoter activity. Last, within cluster 4, some amino acid changes are advantageous at the lowest promoter activity level (see details below). Thus, our analyses confirm, both by statistical analysis (ANOVA for individual mutations, corrected for multiple hypothesis testing; table S4 and fig. S8B) and by machine learning (k-means clustering; table S5 and fig. S9), widespread epistasis between promoter activity level and coding mutations, with promoter activity levels having different impacts on the selection coefficient of individual mutations.

We also examined whether mutants changed fitness ranking among promoter activity levels. A change in ranking between two mutations implies that a first mutation would outcompete a second one at a given promoter activity level but that the second mutation would outcompete the first at a different promoter activity level. An ANOVA on the ranks revealed a significant interaction between genotype and promoter activity level (F = 12.15, P < 2.2 × 10⁻¹⁶), although these effects are much smaller than those associated with mutations alone (F = 666.10, P < 2.2 × 10⁻¹⁶; table S6). To validate this change in ranking, we tested a few mutants (n = 8) changing ranks in the bulk assay in individual growth curve assays. As previously, mutants with higher fitness at optimal promoter activity for WT were clearly reproduced. Mutants that were less deleterious at lower promoter activity and that changed rank in the bulk competition experiment were not as consistent with the validation cultures. For example, in the bulk competition experiment, E75R was estimated to be the second most deleterious substitution of the set considered at weak promoter activity but becomes less deleterious at optimal expression than mutations at positions 33 and 68 (K33E, K33L, K33M, and I68M). Such changes in rank would be visualized as crossing lines on fig. S10. E75R did indeed become less deleterious than K33L and K33M at optimal promoter activity level in the validation cultures, but we did not observe the expected change in rank of E75R with respect to K33E and I68M (fig. S10).This means that it is more challenging to measure precise selection coefficients for highly deleterious amino acid substitutions in bulk competition . The fact that deleterious mutations are strongly underrepresented at the final time point in bulk competition experiments increases experimental noise. Nevertheless, the differences in fitness between promoter activity levels in the individual versus bulk competition assays were strongly correlated (Spearman ⍴ = 0.82, P = 0.011; fig. S10). Overall, although changes of rank may occur, it is not the major type of expression-by-coding epistasis observed for DfrB1.

The protein structure determines which amino acid changes have effects that depend on promoter activity level

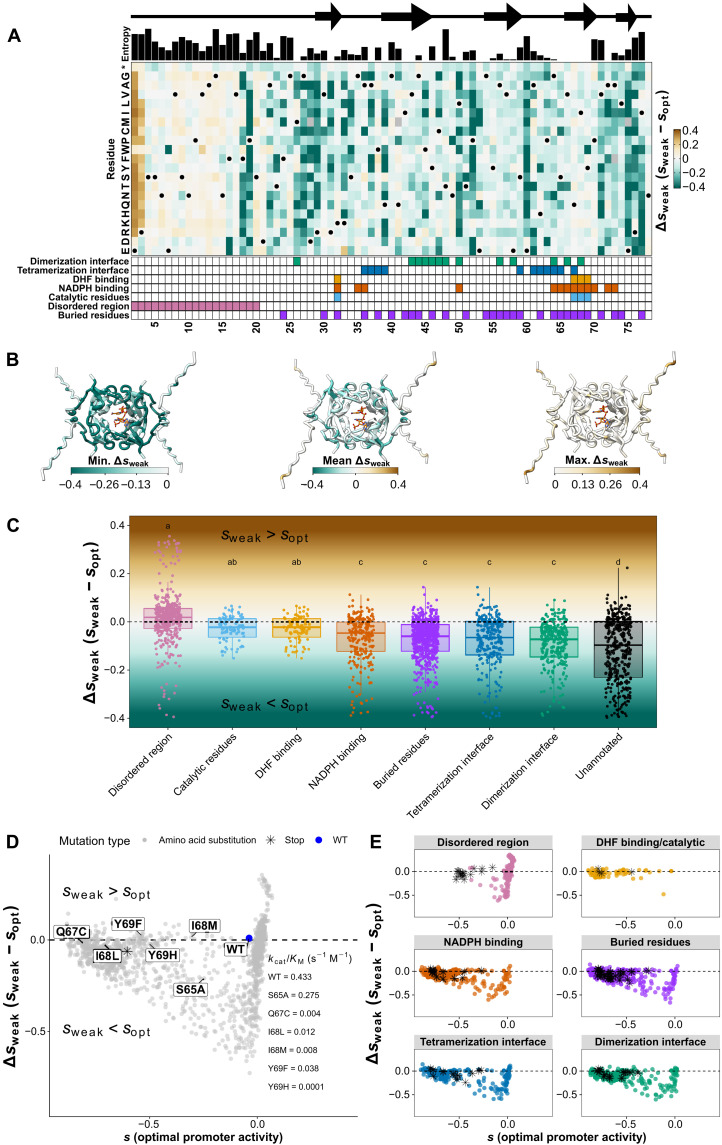
Individual amino acid mutations can alter many protein properties (18) and thus decrease the amount of functional protein complex formed, which can result from a reduction in the stability of the protein or of its tertiary assembly. The solubility of the protein can also be altered by individual mutations. For enzymes, individual amino acid changes can alter catalytic efficiency. To examine the potential underlying causes of the patterns revealed in Fig. 2, we mapped selection coefficients of all amino acid substitutions to individual protein positions (Fig. 3). Changes at conserved positions tend to be more deleterious than in nonconserved regions when considering diversity across homologs (entropy; Fig. 3, top; Spearman correlations between entropy and selection coefficients range between ρ = 0.82 and ρ = 0.83 across promoter activity levels, all with P < 4 × 10⁻²⁰). The same pattern is observed when comparing the observed selection coefficients to predictions from patterns of molecular evolution (fig. S11) (20). Selection coefficients as measured in the laboratory therefore correlate with the constraints acting on the various positions of the protein in nature, as estimated by their degree of evolutionary conservation.

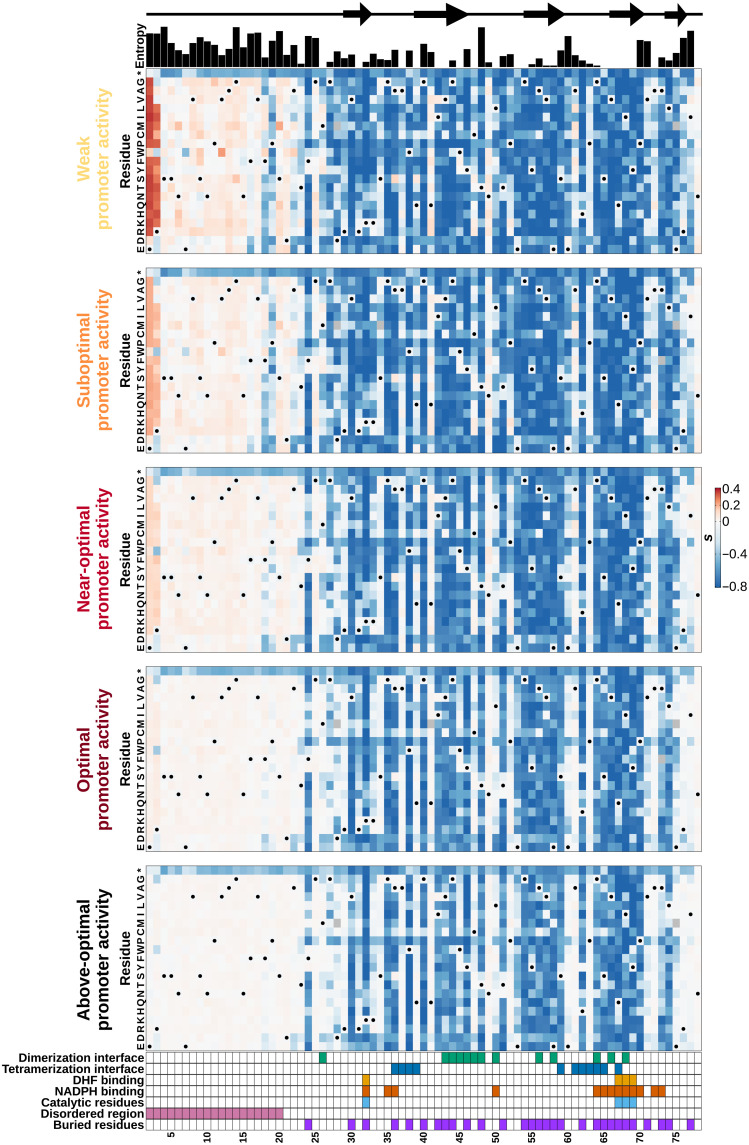
Fig. 3. The DfrB1 fitness landscape changes with promoter activity level in a very heterogeneous way along the protein sequence.

Selection coefficient (s) of individual amino acid substitutions (rows) at different positions (columns) at five promoter activity levels. Annotations above the first panel indicate the protein’s local secondary structure (arrows indicate β strands) and sequence diversity among homologs (Shannon entropy). The annotations at the bottom of the last panel highlight residues that participate in the interfaces of the DfrB1 homotetramer, which come into contact with either the substrate (DHF) or the cofactor [NADPH (reduced form of nicotinamide adenine dinucleotide phosphate)], key catalytic residues, the disordered region, and buried sites. Interfaces are labeled as dimerization and tetramerization interfaces following (20). Residues marked with a dot on the heatmaps are WT residues (WT codons and their synonymous ones).

The fitness effects of amino acid changes are heterogeneous along the length of the sequence and depend on the structural property of each segment. For instance, substitutions in the disordered region (positions 2 to 20) (15, 21) tend to have a higher selection coefficient (less negative or more positive) than the rest of the protein (P < 2.2 × 10⁻¹⁶ for all promoter activities, Wilcoxon test). Results are consistent with the higher entropy of the disordered region (P = 4.2 × 10⁻⁶, Wilcoxon test) and with results showing that the sequence essential for DfrB1 function begins between residues 16 to 26 (22). Mutants from specific protein functional sites marked at the bottom of Fig. 3 tend to be enriched in different clusters (Fig. 2C) of selection coefficients across promoter activity levels (fig. S9C). For example, substitutions in the disordered region are enriched in cluster 4 (mostly neutral) and depleted in cluster 1 (always deleterious; chi-square test, FDR adjusted P = 4.3 × 10⁻¹¹⁵). On the other hand, changes in the catalytic sites are particularly enriched in cluster 1 (chi-square test, FDR adjusted P = 4.0 × 10⁻¹⁸), while substitutions at the dimerization interface primarily belong to clusters 1 and 2 (slight recovery with higher promoter activity; chi-square test, FDR adjusted P = 3.3 × 10⁻³⁰). This enrichment of negative effects at catalytic sites is consistent with the strongly negative selection coefficients of most known catalytic mutants of DfrB1 (fig. S5). These observations show that the extent to which promoter activity level can modify the fitness effects of mutations can be explained by the various structural features of the enzyme (see more details below).

Comparison of the landscapes at the five promoter activity levels (Fig. 3) confirms a dampening of selection coefficient from weak to above-optimal promoter activity, showing that extreme fitness effects, positive as well as negative, become rarer as promoter activity level approaches the optimum for the WT. This again illustrates that the effects of different amino acid substitutions tend to be buffered at promoter activity levels near the optimum for the WT enzyme. A change of promoter activity level influences which positions of the enzyme become visible to selection, as the dampening of selection coefficients is site dependent.

To quantify the effect of promoter activity level on selection coefficients, we calculated Δs as the difference between the selection coefficients of an amino acid substitution at a given promoter activity level and at the optimal level for the WT enzyme that we use as a reference (Δs_non-opt = s_non-opt − s_opt, with s_non-opt referring to either of s_weak, s_subopt, s_near-opt, or s_above-opt). Heatmaps similar to Fig. 3 but with the Δs_non-opt scores (fig. S12A) show that (i) a majority of positions with strongly deleterious mutations are deleterious no matter the promoter activity level (Δs_non-opt around 0), (ii) the deleterious effect of some mutations is dampened at the reference promoter activity level (Δs_non-opt < 0), and (iii) some mutations are beneficial specifically at low promoter activity (Δs_non-opt > 0). The dampening of mutational effects by gene expression is dose dependent because the magnitude of Δs_non-opt becomes smaller as promoter activity level approaches the optimum, so mutational effects observed at weak promoter activity would start to be dampened even at suboptimal promoter activity (P ≤ 1.9 × 10⁻⁹ for all comparisons, Wilcoxon test for differences in means of paired samples; fig. S12B). We chose to focus on Δs_weak in the following sections because it represented the most marked decrease in promoter activity with respect to the optimum.

Low promoter activity makes some coding mutations beneficial

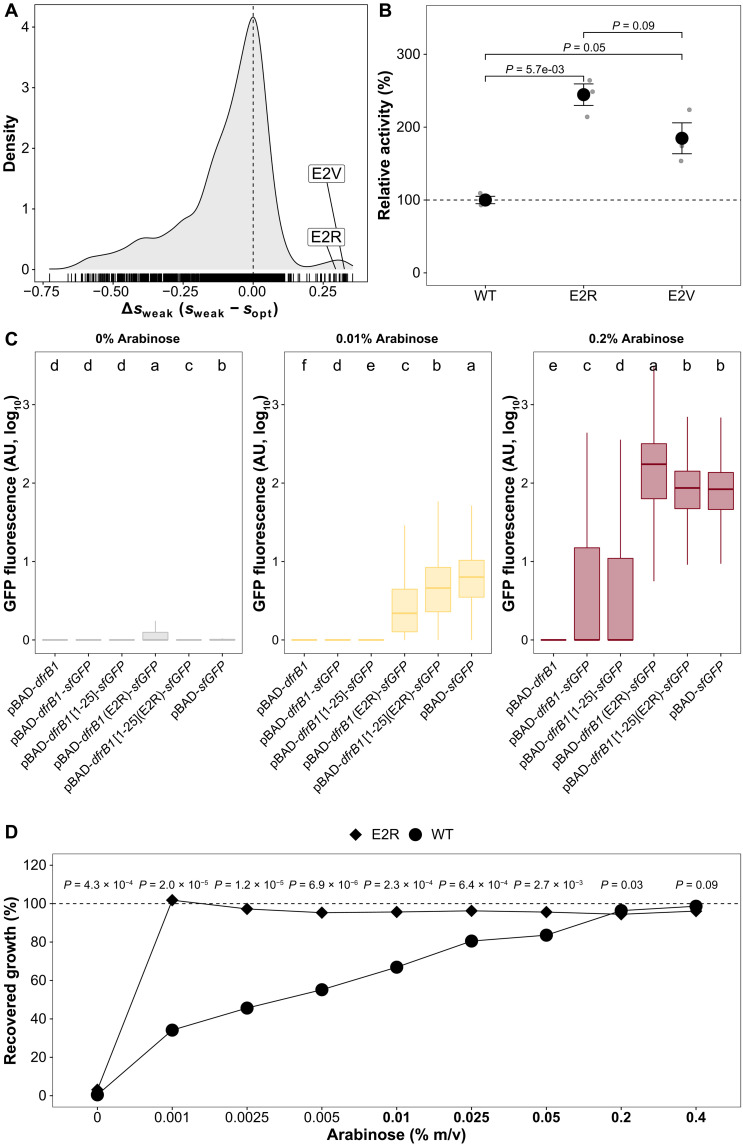
The disordered N-terminal region is distinct from the rest of the protein, as it contains beneficial amino acid changes whose effects disappear at the reference promoter activity level (Δs_weak > 0), particularly at positions 2 and 3. The E2R and E2V mutations, for instance, have extremely high values (lowest promoter activity level, s = 0.340 for E2R and s = 0.363 for E2V)(Fig. 4A). This suggests that the enzyme may be more catalytically efficient or at higher abundance than the WT when promoter activity is low. To distinguish these two possibilities, we assayed enzyme activity in cellular extracts for these two mutants. We confirmed an increase in bulk enzymatic activity for both E2R (P = 5.7 × 10⁻³, t test) and E2V (P = 0.05, t test) relative to the WT (Fig. 4B). Although only marginally significant (P = 0.09), E2R had higher activity than E2V, which corresponds to the slightly higher fitness observed for E2R in individual growth assays (fig. S7A).

Fig. 4. Mutations that are beneficial at low promoter activity lead to increases in enzyme activity through increased protein abundance.

(A) Distribution of differences in fitness effects observed for the same mutation at weak and optimal promoter activity. E2R and E2V have strongly beneficial selection coefficients at weak promoter activity, leading to positive Δs_weak. (B) Lysates from cells expressing the E2R and E2V mutants show a higher in vitro bulk activity compared to WT DfrB1. Error bars indicate the SEMs of three replicates. P values were calculated using t tests. (C) Fused DfrB1-GFP constructs have a higher protein abundance when they harbor the E2R mutation than when harboring the WT DfrB1 sequence. Data show the distributions of fluorescence intensity for 5000 cells. Labels at the top correspond to groups that show significant differences based on an ANOVA and Tukey’s post hoc test (P < 0.05). AU, arbitrary units. (D) The E2R mutation confers a higher growth recovery even at promoter activity levels far below the ones used for the bulk competition experiment. Dots indicate the average of three replicates. P values were calculated from t tests comparing growth recovery of WT DfrB1 and E2R mutant. Concentrations of arabinose in bold indicate induction levels used in the bulk competition experiment.

We next examined whether the higher observed activity of the E2R and E2V mutants could be caused by higher protein abundance. Nucleotide content and their corresponding amino acids in the first few codons of a gene are known to modulate protein expression in E. coli (23), which makes this region a target for beneficial mutations when transcription levels are low. To test the effect of amino acid changes on protein abundance, we generated GFP fusions with (i) the entire DfrB1 WT sequence with and without (ii) the most beneficial mutation (E2R), (iii) the WT disordered N-terminal region (amino acids 1 to 25), and (iv) the disordered region with the E2R mutation (fig. S13). When the E2R substitution was introduced, we observed higher protein abundance, even when only fusing the disordered fragment containing E2R to GFP, reaching more than a 10-fold expression change relative to the WT sequence (ANOVA, P < 2.2 × 10⁻¹⁶; Tukey post hoc test, all comparisons between constructs with the E2R mutation and constructs with the WT had P < 1.3 × 10⁻⁶; Fig. 4C and table S7). At the lowest promoter activity level (0.01% arabinose), the E2R mutant fused to GFP has an abundance that compares or that is slightly higher than the WT enzyme at its optimal induction level. Such a beneficial mutation at low promoter activity therefore acts by increasing protein abundance, most likely by increasing translation rate. The benefit extends to even lower promoter activity, as growth recovery is maximal for this mutant at even lower induction level (Fig. 4D). This result demonstrates that the promoter activity and coding sequence could coevolve to tune protein abundance. Thus, the optimal abundance of the protein could be achieved with lower promoter activity for the E2R and E2V mutants than for the WT. Conversely, when promoter activity approaches the optimum for the WT, the E2R and E2V mutations could lead to a decrease in fitness due to cost of producing an excess of the enzyme or other potential negative impacts. We did observe a slight significant fitness reduction for the E2R mutant at high induction levels (Fig. 4D and fig. S14). This would represent one of the few cases of changes in promoter activity that lead to a change in fitness ranking among mutants.

Masking of fitness effects is encoded in the protein structure

Unlike the individual selection coefficients at each level of promoter activity, the average Δs_weak does not correlate with the entropy measured for each position in the alignment (Fig. 5A). Instead, the positions with the strongest masking effects are those on the outside of the protein and those with no clear function (Fig. 5B, mean Δs_weak). However, strongly negative values of Δs_weak are frequent at buried positions (Fig. 5B, minimum Δs_weak), and the most strongly positive values are found in the disordered region (Fig. 5B, maximum Δs_weak). As a result, promoter activity-dependent effects are observed throughout the protein structure.

Fig. 5. Optimal promoter activity for the WT enzyme buffers mutational effects to varying degrees depending on the structural and catalytic sites.

(A) Δs for weak versus optimal promoter activity level (Δs_weak). A negative Δs_weak value indicates mutations that are more advantageous at optimal promoter activity for the WT. A positive Δs_weak value indicates mutations that are more advantageous at weak promoter activity relative to the WT. Annotations at the top (Shannon entropy) and bottom are the same as in Fig. 3. (B) Minimum, mean, and maximum Δs_weak values mapped on the DfrB1 structure. The structures were generated with AlphaFold2 to include a representation of the disordered region, which is not present in PDB: 2RK1. The molecules in the active site represent the substrate (DHF) and cofactor (NADPH) for the enzymatic reaction using the coordinates from PDB: 2RK1. For all other structural analyses, the coordinates from PDB: 2RK1 were used. (C) Δs_weak values vary with structural properties. The shaded background corresponds to the color scale from (A). Letters above box plots indicate groups with statistically significant differences as shown with an ANOVA and Tukey’s post hoc test (P < 0.05) (table S8). Positions belonging to more than one site are included in the individual distributions for all of those sites. (D) Overall landscape of selection coefficients at optimal promoter activity for the WT (s_opt, x axis) and Δs_weak (y axis). Mutants close to the horizontal dashed line have fitness effects that are independent of promoter activity. Labels indicate mutants with experimentally determined catalytic efficiency (k_cat/K_M) from the work of Strader et al. (24), also shown in figs. S5 and S6B. (E) Functional sites of the protein occupy distinct regions of the landscape. Stop codons are labeled as black asterisks. Horizontal dashed lines in (C) to (E) indicate Δs_weak = 0, that is, no promoter activity-dependent effects on fitness.

The distributions of Δs_weak for each kind of protein site show a more complete picture. Mutations that could destabilize the protein complex, such as those in buried sites and at the protein interfaces (Fig. 5C), seem to be buffered by increased promoter activity. An increase in expression level could compensate for lower stability following the law of mass action by augmenting the concentration of functional complexes. Even the sites in the disordered region with negative Δs_weak (F18 and P19; Fig. 5A and fig. S15) could be explained by interaction interfaces. AlphaFold2 (25, 26) predicts residues F18 and P19 to be in contact with W45 (fig. S15, A and B), which is known to interact with the disordered N-terminal region (27). These analyses show the sharp contrast between mutants according to their structural and enzymatic roles: those involved in catalysis having Δs_weak near 0, those in the disordered region often having positive Δs_weak, and those at interaction interfaces with more negative Δs_weak (Fig. 5C). These contrasts are reflected in the variability observed in homologous sequences, with the disordered region having higher entropy values than the interfaces and catalytic sites (Fig. 5A).

An important consideration is that Δs_weak = 0 could indicate not only mutations whose effects are not sensitive to promoter activity but also those that are completely neutral. For instance, the Q67C mutant has a catalytic efficiency reduced by 100-fold with respect to the WT DfrB1 (24) and has a Δs_weak near 0 (Δs_weak = −0.008), but the same is true for many mutations in the disordered region. We therefore mapped the effects of mutations in a two-dimensional space where Δs_weak values are plotted against s at optimal promoter activity for the WT (Fig. 5D). This representation confirms the notable difference between promoter activity-independent effects of substitutions in catalytic residues and expression-modulated effects at interaction interfaces (ANOVA, P < 2.2 × 10⁻¹⁶; Tukey post hoc test, P = 2.9 × 10⁻⁴ for the comparison between catalytic residues and the dimerization interface and P = 0.001 for the comparison between catalytic residues and the tetramerization interface; Fig. 5, C and E, and table S8). These differences remain significant when separating the data into residues that are exclusively annotated as catalytic, those that are exclusively annotated as interfaces, and those that are annotated as both catalytic and interface residues (ANOVA, P = 0.036; Tukey post hoc test, P = 0.029). Mutants with poor catalytic activity may not benefit much from change in promoter activity in this range. Of the mutants with known k_cat/K_M, only the one with a limited (36.5%) reduction in activity (S65A k_cat/K_M = 0.275; WT k_cat/K_M = 0.433) appears to be significantly improved by increasing promoter activity (S65A Δs_weak = −0.21; effect of promoter activity level on fitness, FDR adjusted P = 5.59 × 10⁻⁶; table S4). All others, with k_cat/K_M under 3% of the WT, have Δs_weak near 0 (Q67C Δs_weak = −0.018, I68L Δs_weak = −0.025, I68M Δs_weak = 0.014, Y69F Δs_weak = 0.024, and Y69H Δs_weak = −0.021). Mutations that reduce enzyme activity down to a few percent of that of the WT are therefore unconditionally deleterious in this range of promoter activity.

Slightly destabilizing mutants are masked at optimal promoter activity for the WT

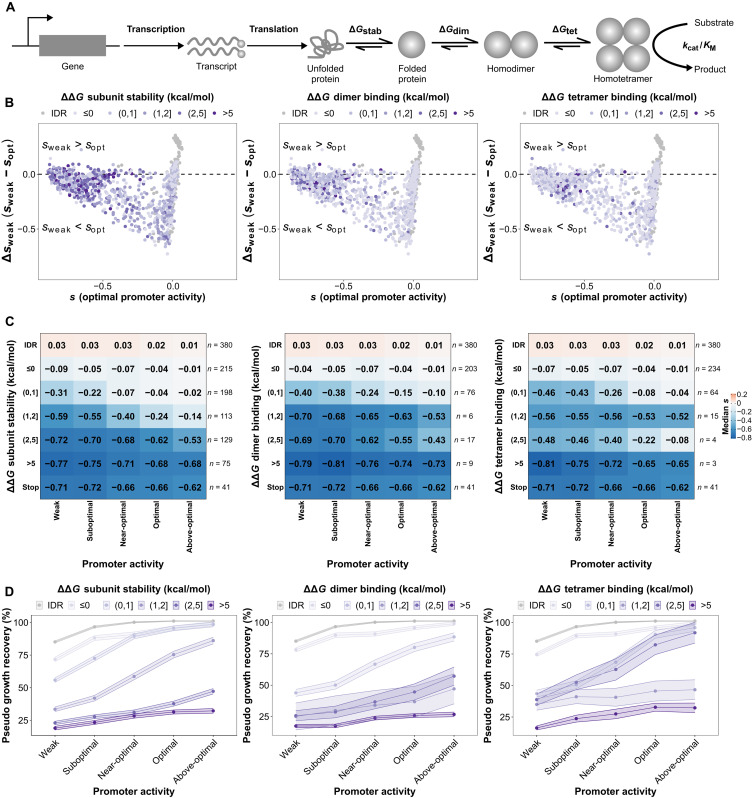
The previous analyses revealed that buried sites and binding interfaces often show mutations with effects that can be dampened by increasing promoter activity, suggesting that one of the causes of expression-dependent effects is protein destabilization. Protein destabilization would reduce the amount of protein complex formed for a given level of promoter activity by two major mechanisms: destabilizing individual protein subunits or by reducing the binding affinity at the interfaces of the homotetramer (Fig. 6A). These factors can contribute to reducing active enzyme abundance the same way changes in promoter activity or translation do. To further examine the contribution of protein destabilization to the observed Δs_weak, we computationally estimated the effects of amino acid changes on the protein and complex stability. Overall, we find a weak but significant correlation between ΔΔG of subunit stability and Δs_weak (Spearman ρ = 0.10, P = 4.3 × 10⁻⁴). We mapped destabilizing effects in the landscape of fitness effects at optimum promoter activity (s_opt) versus changes in fitness effects caused by a weak promoter activity (Δs_weak; Fig. 6B). This analysis shows that highly destabilizing mutations, especially those affecting subunit stability, cluster in the same region of the landscape in Fig. 6B as those with poor catalytic activity in Fig. 5D and stop codons in Fig. 5E, corresponding to mutations for which optimal promoter activity for the WT has limited or no masking capacity.

Fig. 6. Increased promoter activity masks slightly destabilizing mutations but not highly destabilizing ones.

(A) Mutations can affect many aspects of a gene and protein function, including its transcription rate, its translation rate and its enzymatic activity through protein stability and catalytic activity. (B) Landscape of selection coefficients at optimal promoter activity for the WT (x axis) and Δs_weak (y axis). Amino acid substitutions are represented as dots and colored according to bins of the magnitude of their destabilizing effects on subunit stability and binding affinity at the interfaces. Substitutions in the disordered region (IDR; positions 2 to 20) are also included for reference as a category of their own because they are not present in the PDB structure (2RK1), and hence, their destabilizing effects cannot be estimated. Highly destabilizing mutations cluster on the left where mutations are deleterious (negative s), and the deleteriousness tends to be independent of promoter activity level (Δs_weak around 0, horizontal dashed lines). (C) Heatmaps showing medians of measured selection coefficients for mutants with different effects on protein stability or binding affinity at the interfaces. Stop codons from the functional protein core (residues 30 to 70) are shown for comparison. Numbers of mutations considered for each bin of effects on protein stability or binding affinity at the interface are listed on the right. Increases in promoter activity lead to an increase in the median fitness of mutations with slightly destabilizing effects but not as much for those with highly destabilizing effects. (D) Pseudo growth recovery functions for mutations from the different bins of effects on protein stability and binding affinity. Dots indicate the median, and shaded ribbons indicate the SEMs.

Since the same mutation can have an effect on both protein stability and binding affinity at either of the interfaces, we looked for mutations affecting only one of these parameters at a time. For example, to focus on protein stability, we restricted further analyses to mutations causing changes between −0.5 and 0.5 kcal/mol on binding affinity at the interfaces. We did the same for mutations affecting the dimer- and tetramer-forming interfaces. We observed that higher promoter activity levels tend to improve fitness for all mutations but to a very limited extent for those with ΔΔG greater than 2 kcal/mol, both on protein stability and binding affinity at either interface, which largely behave like stop codon mutants (Fig. 6C and fig. S9C). Substitutions with highly destabilizing effects on subunit stability (P = 1.6 × 10⁻⁴⁷) and on binding affinity at the dimer (P = 8.3 × 10⁻¹⁶) and tetramer (P = 8.6 × 10⁻⁴) interfaces tend to be mostly in clusters 1 (always deleterious) and 2 (limited buffering by WT expression), as seen from the k-means analysis (P values were estimated using chi-square tests and adjusted using the Benjamini-Hochberg correction with FDR < 0.05; fig. S9C). In contrast, substitutions with weakly destabilizing effects on subunit stability (ΔΔG_stab lower than 2 kcal/mol) belong mostly to clusters 3 (strong buffering by WT expression) and 4 (mostly neutral) (fig. S9C). These observations also help explain the differences in the distribution of Δs_weak between buried and unannotated sites (Fig. 5C) because mutations in buried sites tend to be more destabilizing than mutations in exposed sites. To confirm the predominant role of protein destabilization, we trained a random forest regressor (see Materials and Methods) (28) on Δs_weak using the predicted biophysical effects of amino acid changes, structural features, changes in amino acid properties based on the differences in 57 indices from ProtScale (29), and the propensity of amino acids to be found in protein-protein interaction interfaces (table S9) (30). While the global performance was modest [R² (test set) = 0.44, R² (fivefold cross-validation) = 0.27 ± 0.031 (SEM)], it identified relative solvent accessibility, changes in hydrophobicity, and effects on subunit stability as the top features contributing to the predictions (fig. S16). Last, an ANOVA modeling selection coefficients based on expression level and bins of destabilizing effects found a statistically significant interaction between promoter activity levels and effects on subunit stability (P = 0.017; table S10). As a result from these two analyses, we conclude that the relation between destabilizing effects of mutations and promoter activity is likely nonlinear, which is illustrated in Fig. 6C. As protein destabilization increases, the improving effect of increased promoter activity on fitness decreases.

The previous section considered that protein destabilization would act by reducing protein abundance or catalytic activity, which would, in turn, reduce fitness (Fig. 6A). Fitness reduction could also come from an unstable protein through spurious interactions with other proteins (31), leading to toxic effects that would increase with promoter activity. We confirmed that expression of WT DfrB1 was not toxic in itself at any of the tested promoter activity levels in the absence of TMP (fig. S17). Although it is difficult to infer protein misfolding from the ΔΔG predictions, in principle, misfolded proteins that lead to toxicity would reduce fitness even in the absence of TMP. We therefore repeated the bulk competition experiment of the mutant library, inducing expression in 0 to 0.4% arabinose, but this time removing selection for DfrB1 activity by omitting TMP. We observed lower signal-to-noise ratio, with a lower correlation between biological replicates (fig. S18) than when TMP selected for DfrB1 activity, consistent with very little fitness differences among mutants. The distributions of selection coefficients are tightly clustered around 0, confirming the lack of detectable fitness effects of most mutations when selection is removed (figs. S19 and S20). In addition, these selection coefficients do not correlate with patterns of molecular evolution (fig. S21) and do not reflect any underlying effects on subunit stability or binding affinity (fig. S22). As a result, most of the fitness effects measured in the experiment with TMP above are therefore unlikely to come from toxic misfolding and gains of interactions but to a lowered activity or abundance of the functional tetrameric enzyme.

Our results show that the stability of the protein and of its complex would create classes of promoter activity-fitness functions different from the one observed for the WT enzyme (Fig. 1C). Because the estimated selection coefficients correlate well with growth recovery measured in growth curve assays (fig. S7), we could infer fitness functions for individual mutants with different estimated stability classes. Using the WT promoter activity-fitness function (Fig. 1C) as a reference and the selection coefficients of individual mutations (table S3), we derived a pseudo growth recovery metric (see Materials and Methods) to visualize the interaction between promoter activity level and mutational effects on protein stability and binding affinity on fitness (Fig. 6D). Growth recovery is higher as promoter activity increases, and this improvement tends to be higher for mutations with smaller effects on either protein stability or binding interfaces. Conversely, highly destabilizing mutations have fitness functions that are nearly flat, illustrating the limit of the buffering capacity of the optimal promoter activity.

DISCUSSION

By measuring how promoter activity affects the fitness effects of amino acid substitutions on a small protein complex, we find that the selection coefficients of individual amino acid substitutions are highly conditioned by the activity of the promoter, revealing rampant regulatory-by-coding epistasis. Some coding mutations become strongly advantageous at low promoter activities, some mutations are strongly deleterious at any promoter activity, and some have deleterious effects that are dampened by higher promoter activity. Coding mutations that are advantageous specifically at low promoter activity increase protein abundance. Mutations that are unconditionally deleterious tend to have a strong negative impact on the catalytic activity of the enzyme or extreme effects on its stability.

Mutations with deleterious effects that are modulated by promoter activity appear to be slightly destabilizing for the protein itself or its assembly into dimers and a tetramer. Promoter activity could therefore potentially evolve to increase the abundance of slightly underperforming enzymes. Similarly, a recent study showed that the effects on fitness of slightly destabilizing mutations in a metabolic enzyme can be compensated by a higher availability of the substrate (32). As for the highly destabilizing mutations and those affecting the catalytic sites of the enzyme, they have selection coefficients that are less likely to be buffered by increasing promoter activity within the range examined. We cannot exclude that more destabilizing mutations could also be buffered at higher promoter activity. The range of expression that we considered is from 7 to 110% of optimal expression for the WT enzyme (Fig. 1D) to mimic the range observed for naturally occurring substitutions in promoter sequences (33), which likely is representative of what is available through single-step mutations. If mutations increasing promoter activity to a much higher level are not accessible, then such coding mutations would never have a chance to be maintained, even more so because the cost of overexpression could be a substantial burden for some proteins.

Our inferences come with shortcomings. For instance, for most mutants of the catalytic sites, we have not determined experimentally how these changes affect catalytic efficiencies. However, by curating the literature, we identified many mutants whose catalytic efficiencies have been determined and those indeed remain strongly deleterious at all the levels of promoter activity that we examined (fig. S5). Similarly, computational estimations of mutational effects generally have a good agreement with experimental values but are not always as accurate (34, 35). FoldX assumes a rigid backbone, which restricts the study of misfolding induced by mutations (34). Nevertheless, our FoldX predictions agree well with the fitness estimations from our bulk competition experiment and reflect the biological effects of losses of bulk enzymatic activity.

Many biological parameters other than promoter activity can influence how much functional enzyme is produced. The total amount of protein in the cell therefore depends on the interplay and coevolution of promoter activity, translation rate, and protein stability. For instance, many combinations of transcription and translation rates can lead to the same amount of protein (36). Coding mutations that increase protein abundance, for instance, through codon usage (23), can therefore be beneficial at low promoter activity, as we observed here. Even if they produce similar steady-state amounts of proteins, combination of transcription and translation rates and protein stability are not evolutionarily equivalent because of selection on other features such as expression noise (36). In the long term, other combinations of parameters can enhance evolvability, as a more lowly expressed but more stable protein was recently shown to have access to different adaptive paths (37). Being able to measure how mutations affecting transcriptional, posttranscriptional, translational, and posttranslational regulation interact to shape fitness will help better understand how they evolve in concert.

Our results show that changes in gene regulation, such as alteration of promoter activity by mutation, could dictate which mutations will be beneficial or deleterious for a coding sequence and vice versa. Over the long term, promoter activity and protein sequences will thus coevolve. This coevolution could be disrupted when major changes occur in the environment and in the regulation of the expression level of a gene, such as in the event of gene duplication, translocation, or horizontal gene transfer. These changes could be advantageous but not necessarily optimal, for instance, in the case of drug resistance enzymes such as the one presented here. Reaching optimality could be achieved by a change in regulation of transcription, translation, or protein stability. Adaptive protein evolution could therefore occur because of suboptimal expression level or vice versa. While we focused our analyses on protein stability and the formation of a protein complex, other protein properties such as solubility could play a role in determining the optimal promoter activity for a particular variant. Overall, these results call for the joint consideration of coding and regulatory mutations in the study of protein evolution.

Although focusing on one particular protein, our results may shed light on a long-standing observation in molecular evolution. Highly expressed proteins evolve slowly (38, 39), and this is often interpreted as higher selective constraints acting on highly expressed proteins, for instance, to prevent misfolding and, potentially, misinteraction, which would be costly. We found potential misfolding to have no detectable effects for this protein, which could be the case for many other proteins as well. For such proteins, if high promoter activity buffers the effect of destabilizing mutations, then one would wrongly expect highly expressed proteins to evolve faster. However, because highly expressed proteins are costly to produce (40), their expression level may actually be below the optimal level that would be observed in the absence of metabolic cost. As a result, their fitness landscape would be more similar to the fitness landscapes that we observed at weak and suboptimal promoter activity, where purifying selection against destabilizing mutations would be more intense, thereby preserving protein sequence.

MATERIALS AND METHODS

All strains, reagents, compounds, and softwares used in this study are listed and referenced in table S11.

Strains, media, and plasmids

MC1061 is the E. coli strain used for all cloning and mutagenesis steps, whereas E. coli BL21 (DE3) is the one used for the experiments conducted in this study. Transformations with plasmids were done according to standard procedures with in-house chemically competent cells (41). Transformed bacteria were grown and selected on 2× YT + glucose medium (1.0% yeast extract, 1.6% tryptone, 0.2% glucose, 0.5% NaCl, and 2% agar) (42) with ampicillin (AMP; 100 μg/ml). For all experiments conducted in liquid medium (with the exception of the growth to measure DfrB1 activity; see below), bacteria were grown in Luria-Bertani (LB) medium (0.5% yeast extract, 1.0% tryptone, and 1.0% NaCl) (43) with AMP and with or without l(+)-arabinose (0.001 to 0.4%) and TMP [10 μg/ml in dimethyl sulfoxide (DMSO)]. To measure DfrB1 activity, bacteria were grown in Terrific broth (TB) medium (2.4% yeast extract, 1.2% tryptone, 0.4% glycerol, and 89 nM potassium phosphate).

The dfrB1 gene was expressed in bacteria from a pBAD vector that allows arabinose-controlled induction (44). pBAD-dfrB1 was constructed as follows. The pBAD vector was amplified from pBAD-chuA plasmid (45) with CLOP198-E9 and CLOP198-F9 [polymerase chain reaction (PCR) program: 5 min at 95°C; 35 cycles: 20 s at 98°C, 15 s at 61°C, and 2 min 30 at 72°C; and a final extension of 3 min at 72°C]. dfrB1 was amplified from pDNM plasmid with CLOP198-A10 and CLOP198-B10 (PCR program: 5 min at 95°C; 5 cycles: 20 s at 98°C, 15 s at 62°C, and 15 s at 72°C; 30 cycles: 20 s at 98°C, 15 s at 72°C, and 15 s at 72°C; and a final extension of 3 min at 72°C). Both PCR products were incubated for 1 hour at 37°C with 20 U of DpnIenzyme to remove parental DNA and subsequently purified on magnetic beads (Axygen AxyPrep Mag PCR Clean-Up Kit). The vector (pBAD) and insert (dfrB1), with their overlapping regions at each extremity, were then assembled by Gibson DNA assembly (46), producing pBAD-dfrB1 plasmid.

To measure the effect of mutating the second residue of DfrB1 on the expression level by cytometry, we fused GFP in 3′ of the dfrB1 gene sequence and of its mutant. The plasmid was amplified from pBAD-dfrB1 (constructed above) or from pBAD-dfrB1(E2R) (isolated from the DMS plasmid collection; see below) with CLOP273-A3/B3 (PCR program: 5 min at 95°C; 35 cycles: 20 s at 98°C, 15 s at 61°C, and 2 min 30 at 72°C; and a final extension of 3 min at 72°C). GFP was amplified from pBAD-sfGFP (47) with CLOP273-D3/F3 (PCR program: 5 min at 95°C; 5 cycles: 20 s at 98°C, 15 s at 62°C, and 20 s at 72°C; 30 cycles: 20 s at 98°C, 15 s at 72°C, and 20 s at 72°C; and a final extension of 3 min at 72°C). The PCR products corresponding to the plasmids and insert were incubated for 1 hour and 30 min at 37°C with 10 U of DpnI enzyme to remove parental DNA. Subsequently, the plasmids [pBAD-dfrB1 and pBAD-dfrB1(E2R)] and insert (sfGFP) were purified on magnetic beads (Axygen AxyPrep Mag PCR Clean-Up Kit) and assembled by Gibson DNA assembly (46), producing pBAD-dfrB1-sfGFP and pBAD-dfrB1(E2R)-sfGFP.

We also fused the GFP to a fragment corresponding only to DfrB1 first 25 residues. Vectors and the sfGFP insert were amplified from the same plasmids as above but using CLOP273-A3/C3 or CLOP273-E3/F3 primers, respectively. After DpnI digestion and magnetic beads purification, the Gibson DNA assembly produced pBAD-dfrB1[1–25]-sfGFP and pBAD-dfrB1[1-25](E2R)-sfGFP plasmids.

To insert specific mutations in the dfrB1 sequence, we performed site-directed mutagenesis based on the QuickChange Site-Directed Mutagenesis System (Stratagene, La Jolla, CA). Briefly, we amplified the pBAD-dfrB1 plasmid using pairs of primers containing the desired mutation at the center (see table S12 for the primers specific to each mutation; PCR program: 2 min at 95°C; 22 cycles: 20 s at 98°C, 15 s at 68°C, and 3 min at 72°C; and a final extension of 5 min at 72°C). The PCR products were then incubated for 1 hour and 30 min at 37°C with 6 U of Dpn I enzyme to remove parental DNA, and mutated plasmids were retrieved directly by transformation in bacteria. We used this method to generate the following mutants: pBAD-dfrB1(F24V), pBAD-dfrB1(K33E), pBAD-dfrB1(K33L), pBAD-dfrB1(K33M), pBAD-dfrB1(S59Y), and pBAD-dfrB1(I68M).

To generate a mutant in which the first methionine codon of DfrB1 is replaced by a stop codon [M1* mutant - pBAD-dfrB1(M1*)], we performed a PCR reaction using 10 ng of pBAD-dfrB1 plasmid as a template (PCR program: 5 min at 95°C; 25 cycles: 20 s at 98°C, 15 s at 59°C, and 2 min 30 at 72°C; and a final extension of 3 min at 72°C) with the nonoverlapping primers (CLOP265-A1 and CLOP259-H5) designed to incorporate a TGA stop codon on the forward primer to replace the ATG. The PCR product was then digested at 37°C for 1 hour with 10 U of DpnI. The digested PCR product was purified on magnetic beads and quantified, and ~50 ng was taken for phosphorylation using 5 U of T4 polynucleotide kinase in T4 ligase buffer for 30 min at 37°C (final reaction volume of 5 μl). Subsequently, ligation was done in a reaction volume of 10 μl by adjusting the volume of T4 ligase buffer, adding 10 U of T4 DNA ligase, and incubating for 1 hour at 22°C. Last, mutated plasmid was retrieved directly by transformation in E. coli BL21 bacteria.

For fitness validation, some of the plasmids that were used were directly isolated from the mutagenesis pools but confirmed by sequencing. Briefly, an aliquot of glycerol stock for the position of interest was diluted and plated on solid medium. Colony PCR was performed on 32 colonies to amplify the dfrB1 gene using CLOP228-C1/D1 (PCR program: 5 min at 94°C; 30 cycles: 30 s at 94°C, 30 s at 54°C, and 35 s at 72°C; and a final extension of 3 min at 72°C). Two subsequent PCR rounds were used to add specific row-column and plate barcodes (48). These PCRs are described in detail in the library sequencing section below. All pooled samples were sent to the Genomic Analysis Platform [Institut de biologie intégrative et des systèmes (IBIS), Québec, Canada] for paired-end 300-bp sequencing on a MiSeq (Illumina). After identification of individual mutations, plasmids for clones of interest were retrieved and purified from bacteria using the Presto Mini Plasmid Kit.

All PCR reactions mentioned above or described below were performed with oligonucleotides defined in table S12, using Kapa polymerase at the exception of the colony PCRs for which Taq DNA polymerase was used. The integrity of all assembled and mutagenized plasmids was confirmed by Sanger sequencing [Plateforme de séquençage et de génotypage des génomes, Centre de recherche du centre hospitalier de Québec–Université Laval (CRCHUL), Canada] using either CLOP194-G11 or CLOP196-B5 as a sequencing primer.

Deep mutational scanning

A single-site mutation library of dfrB1 was generated by a PCR-based saturation mutagenesis method plasmid with the oligonucleotides defined in (table S12). Forward oligonucleotides that have degenerate nucleotides (NNN) so each codon of dfrB1 is mutated were used in combination with a single reverse primer located in the plasmid outside the coding sequence. A first PCR to generate an amplicon containing the desired mutations was conducted following these steps: 5 min at 95°C; 35 cycles of 20 s at 98°C, 15 s at 60°C, and 30 s at 72°C; and a final extension of 1 min at 72°C. The resulting PCR product was then used as a mega primer to introduce the mutations in pBAD-dfrB1 by amplifying the whole plasmid (PCR program: 5 min at 95°C; 22 cycles: 20 s at 98°C, 15 s at 68°C, and 5 min at 72°C; and a final extension of 7 min at 72°C). The long PCR product was digested for 90 min at 37°C with 6 U of DpnI to remove parental DNA. The digestion products for individual positions were transformed into E. coli MC1061. More than a thousand colonies were retrieved from each transformation. After addition of glycerol, libraries for each position were stored separately. From the same pools of bacteria, plasmids were also extracted and purified. PCR amplification and Illumina MiSeq sequencing performed on these plasmids allowed library quality control assessment (fig. S2). In an initial round, mutagenesis of position 39 was not successful. Mutagenesis at this position was repeated separately and added to the final library after quality control.

Bulk competition assay

First, E. coli BL21 was transformed with 75 ng of each individual position mutant pool (DNA Miniprep from the DMS step above). Start and stop codon positions (positions 1 and 79) were omitted. All colonies were retrieved from each transformation plate in 5 ml of 2× YT liquid medium. Optical density at a wavelength of 600 nm (OD₆₀₀) was measured for each pool (final OD₆₀₀ between 40 and 80 after being scraped and resuspended in medium). At this step, 15% glycerol was added to the medium, and an aliquot of each pool was stored individually for further use. In parallel, pools were equally mixed at an OD₆₀₀ of 25 to generate a starting pool for the bulk competition assay. This master pool was stored for further use.

Two separate bulk competition assays were performed. Details concerning arabinose concentrations, the presence or absence of TMP, and the number of replicates are indicated in table S1. Briefly, the master pool was used to inoculate at OD₆₀₀ = 0.01 a first preculture in LB + AMP medium. After an overnight incubation at 37°C with agitation (250 rpm), cells were diluted 1:100 in fresh medium with the addition of different amounts of arabinose. Following an 18-hour incubation at 37°C (250 rpm), cells were diluted again at OD₆₀₀ = 0.025 in a final volume of 4 ml of fresh medium containing arabinose with the addition of TMP or DMSO (TMP solvent − no TMP control). Cultures were then incubated as above until OD₆₀₀ reached 0.8 (five generations). At this point, 125 μl was used to dilute back to OD₆₀₀ = 0.025 in fresh medium, and cells were grown until, once again, OD₆₀₀ reached 0.8 (another five generations). Last, at two time points (18-hour preculture = time point 0; after 10 generations = time point 10), 3 ml of the culture was used to extract plasmid DNA (fig. S3). These samples were treated as described below to prepare libraries for sequencing.

Single mutant library sequencing

Libraries for sequencing were generated as described in the work of Dionne et al. (49). Briefly, three PCR steps were done. The first one was performed directly on the small plasmid DNA preparations (4.5 ng of plasmid) corresponding to single-codon mutant libraries or to bulk competition assay samples (PCR program: 3 min at 98°C; 20 cycles: 30 s at 98°C, 15 s at 60°C, and 30 s at 72°C; and a final extension of 1 min at 72°C). The second PCR was performed to add row and column barcodes (48) for identification in a 96-well plate (PCR program: 3 min at 98°C; 15 cycles: 30 s at 98°C, 15 s at 60°C, and 30 s at 72°C; and a final extension of 1 min at 72°C). For this second PCR, the first PCR product was used as a template (2.25 μl of a 1:2500 dilution). Quantification on gel of the second PCR product using Image Lab (Bio-Rad Laboratories) allowed us to mix the libraries so each has a roughly equal amount in the final library. Mixed PCRs were purified on magnetic beads and quantified using a NanoDrop (Thermo Fisher Scientific). Last, 0.0045 ng of the purified mixed PCRs was used as template for the third PCR, which adds a plate barcode and Illumina adapters (PCR program: 3 min at 98°C; 18 cycles: 30 s at 98°C, 15 s at 61°C, and 35 s at 72°C; and a final extension of 1 min at 72°C). Each reaction for the third PCR was performed in quadruplicate and then combined. After purification on magnetic beads, libraries were quantified using a NanoDrop (Thermo Fisher Scientific) and sent to the Genomic Analysis Platform (IBIS, Québec, Canada) for paired-end 300-bp sequencing on a MiSeq (Illumina) or to the Plateforme de séquençage et de génotypage des génomes (CRCHUL, Québec, Canada) for paired-end 250-bp sequencing on a NovaSeq (Illumina). All raw data are available at SRA BioProject PRJNA842350 (accession numbers SRR19419448 and SRR19419449).

Bacterial growth curves

To measure fitness for individual WT or mutant DfrB1, growth was followed with serial OD₆₀₀ measurements in a plate reader. From an overnight preculture grown in LB + AMP medium, cells were diluted 1:100 in fresh medium with the addition of 0 to 0.4% arabinose according to the experiment. Following an 18-hour incubation at 37°C (250 rpm), cells were diluted again at OD₆₀₀ = 0.01 in a final volume of 200 μl of fresh medium containing arabinose with the addition of TMP or DMSO. The 96-well plate was incubated at 37°C in an Infinite M Nano plate reader (Tecan) for 20 hours. OD₆₀₀ measurements were taken every 15 min. The plate was agitated at 200 rpm in between measurements. Growth curves were analyzed with the Growthcurver R package (50) to calculate the area under the curve as an estimate of fitness. The percentage of recovered growth upon arabinose induction was calculated as follows

$$g=100\ast \left(\frac{{\mathrm{AUC}}_{\mathrm{TMP},\mathrm{induction}}}{{\mathrm{AUC}}_{\mathrm{noTMP},\mathrm{induction}}}\right)$$

where g refers to the recovered growth percentage and AUC refers to the area under the curve in the conditions specified by the subscript (with or without TMP).

Expression level measurement by flow cytometry

To measure GFP level by cytometry, a first preculture in LB + AMP medium was grown with bacteria containing the plasmid of interest [pBAD-sfGFP, pBAD-dfrB1-sfGFP, pBAD-dfrB1(E2R)-sfGFP, pBAD-dfrB1[1–25]-sfGFP, and pBAD-dfrB1[1-25](E2R)-sfGFP]. As for the bulk competition assay, after an overnight incubation at 37°C with agitation (250 rpm), cells were diluted 1:100 in fresh medium with the addition of different amounts of arabinose. Following an 18-hour incubation at 37°C (250 rpm), cells were diluted again at OD₆₀₀ = 0.025 in a final volume of 4 ml of fresh medium containing arabinose. Cultures were then incubated as above until OD₆₀₀ reached 0.8 (five generations). At the different time points (18-hour preculture = time point 0; after five generations = time point 5), small aliquots of cells were taken and diluted in sterile filtered water to an OD₆₀₀ = 0.05 in 200 μl. GFP fluorescent measurements and forward scatter (FSC) and side scatter (SSC) data were collected from a Guava easyCyte HT cytometer (Luminex). From the cytometry data, E. coli cells were selected on the basis of FSC and SSC. From the selected data points, the GFP fluorescence signal was measured after excitation with a blue laser (wavelength, 488 nm) and detection in the green channel (525/30 nm).

DfrB1 activity measurement

Enzymatic activity of DfrB1 and of different mutants was tested in vitro. From a 16- to18-hour 5-ml LB + AMP preculture [incubation at 37°C with agitation (230 rpm)], a 10-ml culture in TB + AMP was inoculated at OD₆₀₀ = 0.1 and incubated for 3 hours at 37°C (OD₆₀₀ = 0.7 to 1) with agitation. Induction of expression was initiated by addition of 1% arabinose, and incubation was continued at 22°C for 16 to 18 hours with agitation. After induction, cells were pelleted for 30 min at 3000 rpm (Eppendorf Centrifuge 5810 R) at 21°C, resuspended in 300 μl of lysis buffer [0.1 M KH₂PO₄-K₂HPO₄ (pH 8.0), 10 mM MgSO₄, 1 mM dithiothreitol, lysozyme (0.5 mg/ml), 5 U of deoxyribonuclease, 1.5 mM benzamidine, and 0.25 mM phenylmethylsulfonyl fluoride], and incubated for 2 hours at 30°C with vigorous shaking. Lysates were cleared by a 30-min centrifugation at 3000 rpm (Eppendorf Centrifuge 5810 R) at 21°C. In a 96-well plate, cleared lysates (20 μl) were combined with TMP (50 μg/ml), 100 μM DHF [synthesized as in (51)], and 100 μM NADPH (reduced form of nicotinamide adenine dinucleotide phosphate) in 50 mM KH₂PO₄-K₂HPO₄ (pH 7.0) in a total volume of 100 μl. Measurement of absorbance at 340 nm was taken for 5 min in a Beckman Coulter DTX880 Multimode detector plate reader. Enzyme activity was calculated using the slope for the initial 20% of substrate consumption.

Data analyses

Inferring fitness scores from sequencing data

Quality control of the MiSeq and NovaSeq sequencing data was performed using FastQC version 0.11.4 (52). Trimmomatic version 0.39 (53) was used to select reads with a minimal length from the raw data (MINLEN parameter: 299 for MiSeq reads and 250 for NovaSeq reads) and trim them to a final length (CROP parameter: 270 for MiSeq reads and 225 for NovaSeq reads). Selected reads were aligned using Bowtie version 1.3.0 (54) to the plate, row, and column barcodes to demultiplex sequences from each pool (arabinose concentration + time point). The remaining paired reads were merged with Pandaseq version 2.11 (55), and identical sequences were aggregated using vsearch version 2.15.1 (56). Last, aggregated reads were aligned to the reference sequence of DfrB1 to identify the mutant codon in each read. Stop codon TAG was removed from all analyses because it has been shown to have a lower termination efficiency than the other stop codons in E. coli (57, 58).

Raw read counts were normalized by the total number of reads in each pool (arabinose + time point). The resulting read proportions were used to calculate selection coefficients based on the end point and the starting point of each experiment using the following equation

$$s=\frac{{\log }_2\left[\frac{\frac{N_{\mathrm{mut},t10}}{\mathrm{median}(N_{\mathrm{WT},t10})}}{\frac{N_{\mathrm{mut},t0}}{\mathrm{median}(N_{\mathrm{WT},t0})}}\right]}{k}$$

where s is the selection coefficient, N is the number of reads for the corresponding mutant at a specific time point, and k is the number of generations (k = 10). Last, biases in the bimodal distributions for some samples were corrected using the mixtools R package (59) so that the second mode of the distributions would be centered at zero, the corresponding value for neutral mutations.

Because the selection coefficients were correlated with changes in growth recovery (fig. S7), we used the selection coefficients (table S3) and the growth recovery for WT at each promoter activity level (Fig. 1C) to derive a pseudo growth recovery metric that could approximate the expected growth recovery for each mutation. This metric was calculated as follows

$$\hat{g}=g_{\mathrm{WT}}\ast (1+s)$$

where ĝ is the estimated pseudo growth recovery at a given promoter activity level, g_WT is the experimentally determined growth recovery for the WT, and s is the selection coefficient of a given mutant.

Evolutionary analysis (GEMME, Evol, and jackhmmer)

A set of seven DfrB1 homologs was extracted from data published by Toulouse et al. (60). These seven sequences were then submitted to the online jackhmmer tool (www.ebi.ac.uk/Tools/hmmer/search/jackhmmer) (61) using the UniProt database as a target to look for additional homologous sequences. The resulting set of sequences was filtered with the following criteria, considering that the full-length DfrB1 sequence is 78 residues long: (i) E score < 1 × 10⁻⁶, (ii) alignment length > 50, and (ii) sequence length < 100.

Applying these filters resulted in a final set of 82 high-confidence DfrB1 homologs. These sequences were aligned with MAFFT version 7.475 (62, 63) using the iterative refinement method (64, 65). The resulting alignment was then analyzed with the Evol library from the ProDy suite version 2.0 (66) to calculate Shannon entropy at each position in the alignment as a metric of evolutionary variation. In parallel, the same MAFFT alignment was analyzed with the GEMME model (20) to obtain predictions of the fitness landscape based on the variation in the alignment.

Machine learning analyses

k-means clustering

We used k-means clustering to identify the typical patterns of expression-dependent changes in fitness effects (Fig. 2C). The k-means clustering was run using the kmeans function from the R base stats package (67) by setting the seed and using the values of k from 1 to 10 (fig. S9A) and the following parameters: iter.max = 10 and nstart = 25. k = 4 was selected as the best compromise between parsimony (based on the diminishing decrease in the sum of squared errors) and interpretability (cluster visualization in Fig. 2C). Centroids reflecting the central selection coefficients of mutants from each cluster are visualized in fig. S9B and provided in table S5. To estimate relative enrichment of mutants from specific clusters at the sites of interest, we organized the data in separate contingency tables indicating whether a particular mutant was assigned to that site and its corresponding cluster. We calculated the log₂ fold ratio of observed versus expected counts of mutants from each cluster at each site (fig. S9C). To compare whether the distribution was statistically significant from expectations, we derived contingency tables with counts of mutations from each cluster belonging to the region analyzed and to the rest of the protein. We performed chi-square tests on these contingency tables and used the Benjamini-Hochberg correction (FDR < 0.5) for multiple hypothesis testing.

Random forest regressor

A random forest regressor was trained to identify the features that better explain variation in promoter activity level–dependent Δs. Explanatory variables included in the model were as follows:

1) Relative solvent accessibility (RSA). Solvent accessibility was calculated using DSSP version 2.2.1 (68) on the biological assembly of DfrB1 present in the Protein Data Bank (PDB: 2RK1) (15). RSA was then obtained by dividing the solvent accessibility of each residue by the maximum solvent accessibility of that residue, as described by Miller et al. (69).

2) Biophysical effects of mutations. FoldX version 5.0 (34, 70) was used with the MutateX wrapper (71) to simulate all possible mutations on the biological assembly of DfrB1 (PDB: 2RK1). Effects of mutations on subunit stability and binding affinity at the dimerization and tetramerization interfaces were measured.

3) Differences in amino acid scores. Fifty-seven amino acid indices were downloaded from the ProtScale database (29) on 21 January 2019, as well as the index on propensity of each amino acid to participate in protein-protein interaction interfaces (30). For each mutation, we calculated the differences in index scores between the mutant residue and the WT residue.

All the explanatory variables were divided by their maximum values to scale them between −1 and 1. The random forest model was trained using the sklearn Python library (72, 73) with 80% of the data and tested with the remaining 20%. We used the Python rfpimp library (https://github.com/parrt/random-forest-importances; version 1.3.7) to estimate relative importances of each variable by calculating the decrease in R² of the predictions if the values of a particular feature are permuted (fig. S16A). Because of the high degree of collinearity in our set of explanatory variables, retraining the random forest with different seeds can suggest a different set of top variables. We introduced a random variable N(0, 1) as an internal control in the training set to identify which variables have significant contributions to the model. We selected the variables that have a higher relative importance than the random variable and retrained the random forest to obtain the final model. Last, we evaluated the relative importance of the variables in the final model by comparing the decrease in R² when the final model is retrained without that variable (fig. S16D).

Statistical analyses

Analyses of variance

We used two different types of ANOVAs to characterize expression-dependent changes in fitness effects of coding mutations. First, we performed an ANOVA for each mutation considering all of its replicates at all the promoter activity levels to identify mutants whose fitness effects were significantly affected by changes in gene expression. To correct for multiple hypothesis testing, we applied the Benjamini-Hochberg correction with an FDR of 0.05 using the FDRestimation R package (table S4) (74). Then, we did an ANOVA on ranks with all replicates of all mutations at all the promoter activity levels by applying the Aligned Rank Transform from the ARTool R package (75, 76) to estimate the contribution of the interaction between promoter activity level and coding mutants to fitness relative to their separate contributions (table S6).

We used ANOVAs to analyze differences in the fluorescence measured for different constructs (Fig. 4C and table S7) and differences in the distribution of Δs based on the protein sites (Fig. 5C and table S8). In both cases, we complemented the ANOVA with Tukey’s post hoc test using the agricolae R package (77).

Correction (14 August 2023): Due to a production error, the reference citations throughout the paper and Supplementary Materials did not correspond to the correct references. The reference citations have been updated. In addition, references (25–27) have been added, as they relate to the model of the protein of interest used. The PDF, Supplementary Materials, and HTML have been updated to reflect these changes.

Supplementary Materials

This PDF file includes:

Figs. S1 to S22

Legends for tables S1 to S12

Legend for data S1

References

Other Supplementary Material for this manuscript includes the following:

Table S1 to S12

Data S1