Extending the ‘one-point method’ for estimations of leaf photosynthetic capacity to a broader temperature range

Abstract

We propose a temperature-dependent scaling factor for the ‘one-point method’ to mitigate the overestimation of the maximum carboxylation capacity of photosynthesis at high temperatures.

The ‘one-point method’ (OPM) is a quick approach to estimate the maximum apparent carboxylation rate of Rubisco (Vʹ _cmax ) based on a single measurement of leaf carbon assimilation rate taken under saturating light and ambient CO ₂ , lately equal to 400 ppm ( De Kauwe et al., 2016 ). However, the OPM overestimates Vʹ _cmax at high temperatures ( Burnett et al., 2019 ). This overestimation results from the reliance of the method on a linear relationship between Vʹ _cmax and leaf respiration rates under light (R _day ), as a fixed R _day :V _cmax ratio equal to 1.5%, while these parameters have different temperature dependencies. Here, we highlight the importance of the adoption of a temperature-dependent scaling factor for the R _day :V _cmax ratio as a way to prevent the overestimation of the photosynthetic capacity at temperatures >35 °C.

The maximum carboxylation rate of Rubisco (V_cmax) is a key photosynthetic enzyme characteristic that reflects plant individual fitness. It is also a prescribed variable of global vegetation models (GVMs), which calculate primary productivity of terrestrial vegetation. This parameter is usually estimated from CO₂ response curves (A–C_i curves, where C_i is intercellular [CO₂]) (e.g. Farquhar et al., 1980—the FvCB model). Recently, the OPM was proposed as a fast alternative to standard full biochemical curve-fitting methods (De Kauwe et al., 2016). Against the gold-standard A–C_i curves, the OPM has proven to be very useful as it allows for the characterization of a large number of species and individual leaves in a short period of time (5–10 min per individual), enabling a better parameterization of highly diverse tropical vegetation communities within GVMs. Another alternative available is the rapid A–C_i technique (RACiR) (Stinziano et al., 2017), which upon any change in conditions, such as leaf temperature, requires some data processing after the measurements are taken. Apart from being fast, another advantage of the OPM is the minimization of negative effects of performing multiple full A–C_i curves on the same leaf in order to obtain the temperature dependency of photosynthetic parameters. Therefore, providing measurements are taken with the proper care and allowing enough time for stabilization of gas exchange fluxes, the OPM has the potential to significantly improve our ability to describe the carbon uptake strategies of highly diverse plant communities.

According to De Kauwe et al. (2016), Vʹ_cmax can be calculated as:

$$\begin{array}{l}V{\stackrel{´}{}}_{\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}=(A_{\mathrm{s}\mathrm{a}\mathrm{t}}+R_{\mathrm{d}\mathrm{a}\mathrm{y}})\times \frac{(C_{\mathrm{i}}+K_{\mathrm{m}})}{(C_{\mathrm{i}}-{\mathrm{\Gamma }}^{*})}\end{array}$$ (1)

Where C_i is the intercellular CO₂ concentration, Γ* is the CO₂ compensation point in the absence of mitochondrial respiration, K_m is the Michaelis–Menten constant of Rubisco, and R_day is the leaf mitochondrial respiration in the light. When R_day is not determined experimentally, the authors suggest the use of an estimated R_day ratio equal to 1.5% of Vʹ_cmax (0.015 in Equation 2).

$$\begin{array}{l}V{\stackrel{´}{}}_{\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}=\frac{A_{\mathrm{s}\mathrm{a}\mathrm{t}}}{(\frac{C_{\mathrm{i}}-{\mathrm{\Gamma }}^{*}}{C_{\mathrm{i}}+K_{\mathrm{m}}}-0.015)}\end{array}$$ (2)

However, the OPM provides an overestimation of Vʹ_cmax, especially at high temperatures above 30 °C (De Kauwe et al. 2016; Slot and Winter, 2017; Burnett et al. 2019). As the temperature dependencies of R_day and V_cmax differ considerably from each other (Wang et al. 2020), assuming a linear relationship between these parameters as a constant ratio results in the overestimation of Vʹ_cmax, as R_day peaks at a much higher leaf temperature. A better accuracy of the OPM is needed to improve its performance at higher leaf temperatures. In this sense, we propose here the adoption of a temperature-dependent scaling factor for the R_day:Vʹ_cmax ratio in order to improve predictions of Vʹ_cmax.

The temperature dependencies of both R_day and V_cmax may be defined by standard Arrhenius functions, following Kumarathunge et al. (2019) as:

$$\begin{array}{l}\frac{{R_{\mathrm{d}\mathrm{a}\mathrm{y}}}^{\mathrm{T}}}{{R_{\mathrm{d}\mathrm{a}\mathrm{y}}}^{\mathrm{R}}}=e\frac{\mathrm{E}{\mathrm{a}}_{\mathrm{R}}\times (T_{\mathrm{k}}-298.15)}{298.15\times \mathrm{R}\times T_{\mathrm{k}}}\end{array}$$ (3)

and

$$\begin{array}{l}\frac{{V_{\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}}^T}{{V_{\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}}^{\mathrm{R}}}=e\frac{E{\mathrm{a}}_{\mathrm{V}}\times (T_{\mathrm{k}}-298.15)}{298.15\times \mathrm{R}\times T_{\mathrm{k}}}\times \left[\frac{1+e{}^{(\frac{298.15\times \mathrm{\Delta }{\mathrm{S}}_{\mathrm{V}}-\mathrm{H}{\mathrm{d}}_{\mathrm{V}}}{298.15\times R})}}{1+e^{(\frac{(T_{\mathrm{k}}\times \mathrm{\Delta }{S}_V-H{d}_V}{T_k\times R})}}\right]\end{array}$$ (4)

where R_day^T and V_cmax^T are respiration and carboxylation rates at a given leaf temperature (T_k in Kelvin), R_day^R and V_cmax^R are the rates at a reference leaf temperature of 25 °C, R is the universal gas constant (8.314 J mol⁻¹ K⁻¹), Ea_R (kJ mol⁻¹) is the activation energy for respiration, and Ea_V (kJ mol⁻¹), ΔS_V (J mol⁻¹ K⁻¹), and Hd_V (kJ mol⁻¹) are respectively the activation energy, entropy, and deactivation energy of V_cmax. The adopted values for model constants are available in Supplementary Table S1.

Our new suggested model modifies Equation 2 for:

$$\begin{array}{l}V{\stackrel{´}{}}_{\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}-\mathrm{\rho }}=\frac{A_{\mathrm{s}\mathrm{a}\mathrm{t}}}{(\frac{C_{\mathrm{i}}-{\mathrm{\Gamma }}^{*}}{C_{\mathrm{i}}+K_{\mathrm{m}}}-0.015\times \mathrm{\rho })}\end{array}$$ (5)

where ρ is the temperature-dependent scaling on the R_day ratio (1.5% of Vʹ_cmax), which is calculated by dividing Equation 3 by Equation 4.

The robustness of this approach was tested using 278 unpublished A–C_i curves (12 CO₂ concentration steps) under saturating light (2000 μmol m^–2 s^–1), collected from 31 tropical species naturally occurring in savannas and Amazon rainforest in Brazil (Supplementary Table S2) using two portable gas exchange systems (LI-6800, Li-Cor Inc., Lincoln, NE, USA). Leaf temperatures were kept constant during each curve, but ranged from 25 °C to 45 °C among curves, and the leaf chamber relative humidity was not controlled. Over the whole dataset, the leaf-to-air vapor pressure deficit ranged from 1.08 kPa to 7.71 kPa (3.84 ± 1.65), while stomatal conductance ranged from 0.05 mol m⁻² s⁻¹ to 0.34 mol m⁻² s⁻¹ (0.134 ± 0.06). To estimate Vʹ_cmax and Vʹ_cmax–ρ values, we selected a single point measurement from each A–C_i curve, corresponding to ambient CO₂ concentrations (C_a) between 390 μmol mol^–1 and 410 μmol mol^–1. The Kc, Ko, and Γ* values used in Equations 2 and 3 were calculated according to the temperature dependencies listed in Bernacchi et al. (2002) and De Kauwe et al. (2016). Linear regressions were used to compare both Vʹ_cmax and Vʹ_cmax–ρ with V_cmax from full A–C_i curves (Duursma, 2015). The slopes between the two linear regressions were compared using ANOVA. Moreover, the distribution of the residuals of the regression models as a function of leaf temperature were used for method accuracy comparisons. Additionally, a multivariate sensitivity analysis was performed to investigate the role of temperature over the range values of the Arrhenius constants regarding the model outputs. All analyses we performed on R environment (R Core Team, 2020).

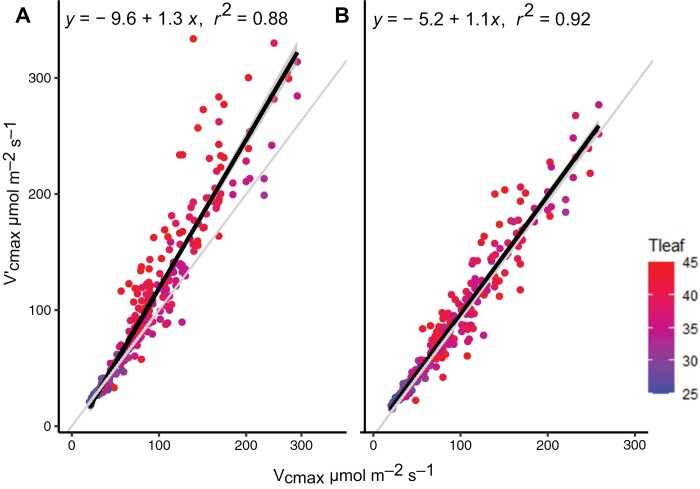
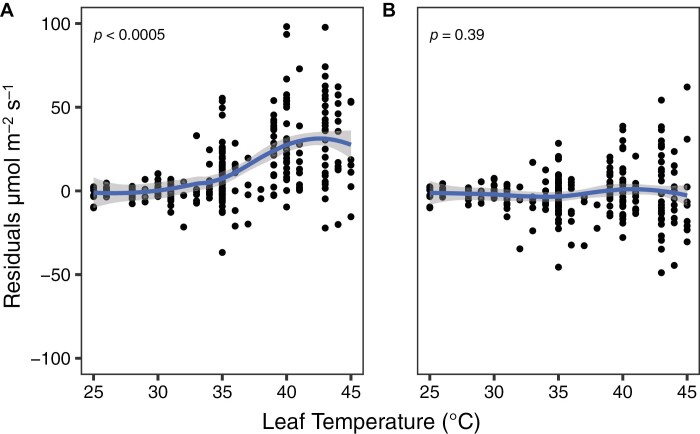
The temperature-dependent scaling factor provided a substantially better correspondence between V_cmax values from FvCB fits against the Vʹ_cmax–ρ values, when compared with Vʹ_cmax values from the original OPM (Fig. 1) (slope=1.10; r²=0.93). The ANOVA test revealed that the outputs from the two models were statistically different (P<0.005). The evaluation of the distribution of the residuals from the two regression models highlights how the overestimation of Vʹ_cmax by the original version of the OPM increases with leaf temperature (Fig. 2A), where overestimations of ~25% were observed above 35 °C. In contrast, no trend was observed for the residuals from the new model in relation to leaf temperature (Fig. 2B). The adoption of the Arrhenius temperature dependency for R_day (Equation 3) was preferred over a Q₁₀ temperature coefficient (Atkin et al., 2015), the latter resulting in an overestimation of Vʹ_cmax–ρ values of ~25% (slope=1.29, r²=0.85) (Supplementary Fig. S1), with a non-significant difference between its slope against the model using the the original OPM approach (P=0.69). The sensitivity analysis revealed that the temperature-dependent scaling factor is strongly influenced by both Ea_R and Ea_V above 25°C (Supplementary Fig. S2). As temperature increases, their relative importance decreases, while ΔS_V and the interaction among parameters become the main factors determining R_day:V_cmax.

Fig. 1.

Comparison of linear regression models between V_cmax estimated from full A–C_i curves against apparent photosynthetic capacity estimated by the ‘one-point method’ (Vʹ_cmax; Equation 2) (A), and the modified version including the temperature dependency (Vʹ_cmax–ρ; Equation 5) (B). The light gray line is the 1:1 relationship.

Fig. 2.

Residuals of maximum carboxylation rate, V_cmax, estimated from A–C_i curves estimated from apparent maximum carboxylation capacity, Vʹ_cmax (Equation 2) using the estimated R_day:V_cmax ratio (A), and using the temperature-dependent scaling factor (B) as a function of leaf temperature.

The adoption of a temperature-dependent scaling is indeed an important adjustment of the OPM, producing accurate estimations of Vʹ_cmax at high temperatures where there is proportionality of Vʹ_cmax and R_day responses to temperature (Wang et al., 2020), as demonstrated empirically in Supplementary Fig. S3. Therefore, the temperature-dependent scaling factor proposed here should allow for better determinations of the temperature response of Vʹ_cmax. However, providing reliable data for derivations of the Arrhenius constants is needed, as these constants vary among functional types of plants and species (Kumarathunge et al., 2019). Apart from the difficult task of adopting appropriate values for the Arrhenius constants for R_day and V_cmax, other aspects might be important as well. The application of biochemical models of photosynthesis often disregards the influence of g_m over estimations of Vʹ_cmax, assuming it to be large enough to cause C_i to be equal to chloroplastic CO₂ concentration (C_c). However, g_m varies with leaf temperature as a result of both enzymatic dynamics and CO₂ diffusion, resulting in an overestimation of V_cmax when assuming an infinite g_m (von Caemmerer and Evans, 2015), therefore directly impacting the R_day:V_cmax ratio. Similarly, the temperature dependency of the Γ* is assumed to be invariant among plant species, and a single function is often used to scale this parameter to a specific leaf temperature (Bernacchi et al., 2002). However, depending on the Γ* assumption, the relationship between temperature and the R_day:V_cmax ratio may change (De Kauwe et al., 2016); this is because the stoichiometry of CO₂ release by Rubisco oxygenation depends on how Γ* responds to temperature (Bernacchi et al., 2002). Therefore, a better understanding of possible variations of the temperature dependencies of both g_m and Γ* is still needed in order to improve the understanding of temperature influence on the estimations of Vʹ_cmax, irrespective of the estimation method used.

In conclusion, the inclusion of a temperature-dependent scaling factor in the ‘one-point method’ extends its applicability to leaf temperatures >35 °C. Therefore, this approach should contribute to the characterization of vegetation communities and provide data for the estimation of Arrhenius parameters without stressing leaves by performing repeated CO₂ response curves. Efforts should be directed to the understanding of the variation of temperature dependencies of the photosynthetic parameters, specifically the entropy and the activation and deactivation energies of V_cmax, R_day, and also the maximum electron transport rate (J_max).

Supplementary data

The following supplementary data are available at JXB online.

Table S1. Dataset of primary parameters and their temperature dependency used to estimate R_day and Vʹ_cmax temperature response in Equations 3 and 4.

Table S2. Species studied with the biome, their family, number of individuals (N individuals) and curves (N curves), and temperature range curves.

Fig. S1. Comparison of linear regression models between V_cmax estimated from full A–C_i curves against apparent photosynthetic capacity estimated by the ‘one-point method’.

Fig. S2. Normalized partitioning of the variation of the influence of individual coefficients over model output at a broad leaf temperature range (sensitivity analysis).

Fig. S3. Estimated R_day (R_day:V_cmax ratio) as a function of leaf temperature using the De Kauwe et al. (2016) model.

Author contributions

TCSO, TFD, and MNG: design; TCSO and MNG: data collection. TCSO: data analysis; TCSO, TFD, EV, and MNG: interpreting the analysis and results; TCSO: writing—first draft; TFD, EV, and MNG: contributing to writing.

Conflict of interest

The authors have no conflicts to declare.

Funding

This study was supported by Wageningen University and Research (WUR) to TCSO (project number 5160957987); the Partnership for Enhanced Engagement in Research program to TFD (PEER grant agreement AID-OAA-A-11-00012); the National Council for Scientific and Technological Development (CNPq) to Flávia R.C. Costa (LTER/PELD-grants #441282/2016-4, 403764/2012-2, and 558244/2009-2); and the São Paulo Research Foundation (FAPESP) (Nordeste project thematic grant NE/N012488) to J. Lloyd.

Data availability

The data supporting the findings of this study are available from the corresponding author, Tony de Oliveira, upon request.