Cross-trait assortative mating is widespread and inflates genetic correlation estimates

Abstract

The observation of genetic correlations between disparate human traits has been interpreted as evidence of widespread pleiotropy. Here, we introduce cross-trait assortative mating (xAM) as an alternative explanation. We observe that xAM affects many phenotypes and that phenotypic cross-mate correlation estimates are strongly associated with genetic correlation estimates (R² = 74%). We demonstrate that existing xAM plausibly accounts for substantial fractions of genetic correlation estimates and that previously reported genetic correlation estimates between some pairs of psychiatric disorders are congruent with xAM alone. Finally, we provide evidence for a history of xAM at the genetic level using cross-trait even/odd chromosome polygenic score correlations. Together, our results demonstrate that previous reports have likely overestimated the true genetic similarity between many phenotypes.

One-Sentence Summary:

Statistical artifacts due to non-random mating, rather than shared biology, may explain reported genetic correlations.

Methods that use summary statistics from genome-wide association studies (GWAS) to investigate genetic overlap across phenotypes have become a fundamental statistical tool across many domains of human complex trait genetics (1–5). The results of these analyses have been striking: many trait pairs, even those with limited phenotypic similarity, display nontrivial genetic correlations (for example, 0.209 [se=0.042] for attention-deficit hyperactivity disorder [ADHD] and body mass index [BMI] in (1)). These findings have been broadly interpreted as evidence for widespread pleiotropy across the phenome (6–8), and, in the case of psychiatric disorders, have raised concerns about the suitability of the existing nosology given evidence for shared genetic bases (1, 9).

Here, we consider an overlooked source of potential bias in these findings: cross-trait assortative mating (xAM), the phenomenon whereby mates display cross-correlations across distinct traits. There are several reasons to be concerned with this potential oversight: First, the single-trait linear mixed model, which genetic correlation estimators generalize, is misspecified under single-trait assortative mating (sAM) and overestimates SNP heritability (10). Second, sAM is widespread across multiple domains for which substantial genetic correlations have been observed, including anthropometric, psychosocial, and disease traits (1, 7, 8). Third, recent work has provided genetic-level evidence for a history of sAM with respect to some of these same phenotypes (11). Fourth, xAM is known to generate spurious results for other marker-based inference procedures, including Mendelian randomization (12) and association studies (13).

We set out to systematically assess the impact of xAM on genetic correlation estimates, first compiling a large atlas of cross-mate correlations across a broad array of previously-studied phenotypes utilizing two large population-based samples (n=81,394; n=746,566). We find that these phenotypic cross-mate correlations explain a major portion of empirical marker-based genetic correlation estimates for the same trait pairs (R²=74% across samples). We next demonstrate that xAM biases genetic correlation estimates and yields non-trivial estimates even among traits with uncorrelated genetic effects. We use a simulation-based approach to evaluate the extent to which empirical levels of xAM alone might plausibly explain genetic correlation estimates among previously-studied traits, finding that, for many trait pairs, substantial fractions of empirical genetic correlation estimates are congruent with expectations for etiologically independent traits subject to xAM. At the same time, we observe that particular phenotype pairs, such as schizophrenia and bipolar disorders, evidence substantially larger genetic correlation estimates than can be plausibly attributed to xAM-induced artifact. Lastly, we utilize correlations between even versus odd chromosome-specific polygenic scores (PGS) to detect genetic signatures of xAM, extending a previous approach (11). We find that cross-trait even/odd PGS correlations mirror cross-mate phenotypic correlation patterns and, through this association, explain substantial variation in empirical genetic correlation estimates.

Results

Genetic correlation estimates mirror cross-mate phenotypic correlations

We begin by quantifying the extent to which empirical genetic correlation estimates align with cross-trait spousal correlations across a broad array of phenotypes: a set of 20 previously-studied traits measured in the UK Biobank (UKB) (14) and a collection of six psychiatric disorder diagnoses ascertained from Danish civil registry data (15). We estimated cross-mate correlations for 40,697 spousal pairs within the UKB sample and 373,283 mate pairs randomly selected from the Danish population. For a pair of phenotypes Y and Z, there are three cross-mate correlation parameters: r_yy and r_zz the correlations between mates on Y and Z, respectively, and r_yz, the cross-mate cross-trait correlation; we generically denote these quantities r_mate, and present these estimates in the diagonal and sub-diagonal entries of Figs. 1A and 1B. We also compiled LD score regression (LDSC) genetic correlation estimates, denoted ${\widehat{\rho }}_{\beta ;\text{LDSC}}$, for each pair of phenotypes, which we present in the super-diagonal entries of Figs. 1A and 1B. All pairwise estimates are provided in Table S1.

Fig. 1. Cross-mate phenotypic correlation and genetic correlation estimates.

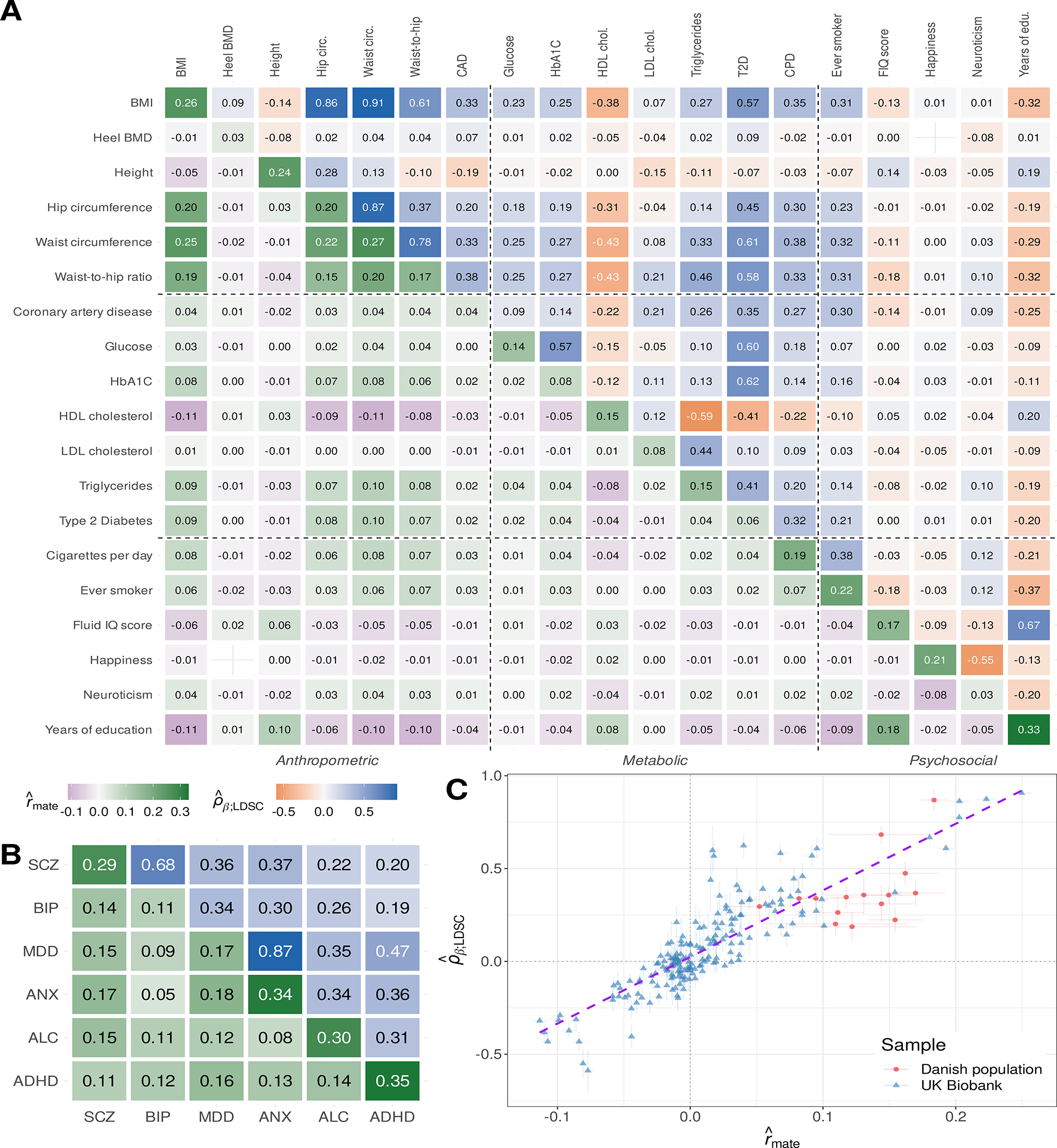
(A) Correlations among previously-studied UK Biobank (UKB) phenotypes. Diagonal and sub-diagonal heatmap entries correspond to cross-mate phenotype correlation estimates derived from 40,697 putative spouse pairs in the UKB. Super-diagonal entries correspond to empirical LD score regression (LDSC) correlation estimates among unrelated European ancestry UKB participants. (B) Cross-mate correlation and genetic correlation estimates for psychiatric disorders. Diagonal and sub-diagonal entries reflect cross-mate tetrachoric correlations among 373,283 spousal pairs sampled from the Danish population, all of which were significantly greater than zero (maximum p=1.69e-5). Super-diagonal entries are previously-reported LDSC correlation estimates (23). (C) Association between empirical cross-mate phenotypic correlation and genetic correlation estimates (meta-analytic R² ≈ 74%). Error lines indicate 95% confidence intervals and the purple dashed line displays the line of best fit across all points. All numbers have been rounded to two decimal places. The model for bone mineral density (BMD) and subjective happiness failed to converge and is omitted. ADHD: attention-deficit hyperactivity disorder; ALC: alcohol use disorders; ANX: anxiety disorders; BIP: bipolar disorders; BMI: body mass index; HDL/LDL: high/low-density lipoprotein; IQ: intelligence quotient; MDD: major depressive disorder; SCZ: schizophrenia.

Cross-mate correlation structures were diverse across the trait pairs we examined (Fig. S1). Whereas cross-mate single-trait and cross-mate cross-trait correlations were similar for some trait pairs (for example, ${\widehat{r}}_{yy}=0.26$, ${\widehat{r}}_{zz}=0.20$, and ${\widehat{r}}_{yz}=0.20$ for BMI and hip circumferences), these quantities were of opposing signs for others (for example, ${\widehat{r}}_{yy}=0.33$ and ${\widehat{r}}_{zz}=0.22$ versus ${\widehat{r}}_{yz}=-0.09$ for years of education and regular smoking). In general, cross-mate correlation structures were not consistent with sAM alone. When the cross-mate correlation r_zz for as secondary trait Z is fully mediated through sAM on Y, we expect that ${\widehat{r}}_{zz}\approx {\widehat{r}}_{yy}{\widehat{s}}_{yz}^2$; this model fit the data poorly (Fig. S2).

Estimates of ${\widehat{\rho }}_{\beta ;\mathrm{LDSC}}$ were strongly associated with r_mate estimates across both samples (Fig. 1C; meta-analytic R²=74.32%, 95% CI: 67.02%–81.62% in a linear model; R²=76.69%, 95% CI: 73.94%–79.45% in a Bayesian model accounting for heteroskedasticity and estimation error). The regression slope did not significantly differ across the UKB and psychiatric phenotypes in either model (for example, p=0.16 for a sample-by-r_mate interaction term in the linear model). The strength of this association largely persisted when excluding trait pairs with large genetic correlation estimates: considering only trait pairs with estimated genetic correlations below 0.50 in magnitude yielded R²=70.94%; further restricting to those below 0.30 in magnitude, yielded R²=67.88%. This suggests that the observed association does not merely reflect sAM on genetically homogenous factors.

Defining genetic correlation

Having established that a large degree of the variance in genetic correlation estimates can be predicted from phenotypic mating correlations, we now provide theoretical intuition as to why this might occur (see Supplementary Text for further details; (16)). We start by defining three distinct notions of genetic similarity between phenotypes. These definitions are summarized in Table 1.

Table 1.

Notions of genetic similarity and their relationship to genetic correlation estimators.

Metric of genetic similarity	Relation to shared etiology and xAM
Pleiotropy is present at a particular locus when it influences both phenotypes.	Reflects shared etiology. Substantial numbers of pleiotropic loci imply that overlapping genetic variants affect both traits, though their effects may not be consistent.
Effect correlation (ρβ) refers to the correlation between standardized genetic effects.	Reflects shared etiology. ρβ > 0 implies an overlapping set of variants (at pleiotropic loci) influence both traits with similar effects on average.
Score correlation (ρℓ) refers to the correlation between true polygenic scores.	Reflects shared etiology, or xAM-induced population structure, or both. Roughly equal to ρβ under random mating but larger than ρβ under xAM due to long-range sign-consistent LD. ρℓ > 0 does not necessarily imply biological similarity or even the existence of pleiotropic loci.
Genetic correlation estimators (${\widehat{\rho }}_{\beta }$), such as bivariate LD score regression, are commonly interpreted as estimates of the effect correlation.	Reflect shared etiology under random mating but produces estimates substantially greater than both ρβ and ρℓ under xAM, even when ρβ = 0 or in the complete absence of pleiotropy.

Under random mating, score correlations and effect correlations are equal in expectation, imply the existence of pleiotropic loci, and are well-captured by widely-used genetic correlation estimators. Under xAM, however, substantial score correlations can arise in the absence of effect correlation or even pleiotropy, and genetic correlation estimators overestimate both ρ_β and ρ_ℓ.

We consider a pair of phenotypes Y, Z, with heritable components ℓ_y, ℓ_z reflecting the additive effects of m standardized haploid variants X₁, … X_m with phenotype-specific effect vectors β_y, β_z. For simplicity, we assume that causal variants are initially unlinked and that both phenotypes have unit variance under random mating (panmixis), such that the panmictic heritabilities are $h_{y;\text{pan}}^2={\mathit{\beta }}_y^{\top }{\mathit{\beta }}_y$ and $h_{z;\text{pan}}^2={\mathit{\beta }}_z^{\top }{\mathit{\beta }}_z$.

Pleiotropy is present when a locus influences two or more phenotypes. Thus, locus X_i is pleiotropic with respect to Y and Z when both β_y;i ≠ 0 and β_z;i ≠ 0, though these effects might differ substantially in magnitude or direction. On the other hand, the correlation between effects, which we refer to as the effect correlation ρ_β, indexes the similarity of variant effects on two phenotypes:

$${\rho }_{\beta }=\mathrm{cor}\left({\mathit{\beta }}_y,{\mathit{\beta }}_z\right),$$

where the β vectors include all variants, causal or otherwise, and thus may contain elements equal to zero. A value of ρ_β > 0 implies both the existence of pleiotropic loci and that said loci have similar effects on average, and we term a pair of traits genetically orthogonal when ρ_β = 0. Effect correlation is distinct from the classical definition of genetic correlation as the correlation between the heritable components of two traits (17), which we refer to as the score correlation:

$${\rho }_{\ell }=\mathrm{cor}\left({\ell }_y,{\ell }_z\right),$$

as it reflects the correlation between the true PGS.

Within the standard linear mixed model framework, ρ_ℓ and ρ_β are equivalent and hence seldom discussed as separate quantities (though genetic correlation estimates are commonly interpreted as estimates of ρ_β (4, 18, 19)). However, traits with uncorrelated effects can unintuitively have correlated PGS. Under xAM, all causal variants affecting trait Y become correlated with all causal variants affecting trait Z, and these correlations are directionally consistent with their respective effects (see Supplementary Text (16)). As we will demonstrate in the following section, this results in non-zero score correlations in the direction of the cross-mate cross-trait phenotypic correlation, even for genetically orthogonal traits.

The impact of xAM in simulations

We ran a series of forward-time simulations using realistic genotype data to investigate the impact of xAM on multiple measures of genetic correlation. At each generation, individuals (consisting of a set of genotypes together with two phenotypes) were matched to achieve target cross-mate correlation parameters, after which we estimated genetic correlations $({\widehat{\rho }}_{\beta })$ using LDSC (denoted ${\widehat{\rho }}_{\beta ;\mathrm{LDSC}}$; (6)), Haseman-Elston regression (HE, denoted ${\widehat{\rho }}_{\beta ;\text{HE}}$; (20)), and residual maximum likelihood (REML; ${\widehat{\rho }}_{\beta ;\text{REML}}$; (18)). We also computed true score correlations (ρ_ℓ), which is possible when the true genetic effects are known. We performed sensitivity analyses to confirm that our results did not depend on simulation parameters, including the number of causal variants (Fig. S3), mate selection algorithm (Fig. S4), recombination scheme (Fig. S5), and whether causal variants with orthogonal genetic effects arose on overlapping loci (Fig. S6). We additionally investigated the impact of xAM on GWAS effect estimates and GWAS-based methods for identifying pleiotropic SNPs (Figs. S7 to S10), genetic correlation estimates for binary phenotypes subject to misdiagnosis (Fig. S11), partitioned genetic correlation estimates (Fig. S12), and genetic covariance estimators (Fig. S13).

xAM induces nonzero score correlations among genetically orthogonal traits

We confirmed that xAM induces substantial score correlations across a broad array of simulation parameters. This is perhaps most striking for traits with orthogonal effects: Fig. 2A demonstrates the increase in the true score correlation across multiple generations of xAM for a pair of traits with ρ_β = 0, r_mate = 0.5, and $h_{\text{pan}}^2=0$. Across simulation replicates, the average score correlation was 0.11 after a single generation of xAM, which increased to 0.24 after three generations.

Fig. 2. Impact of xAM on genetic correlation estimates in forward-time simulations.

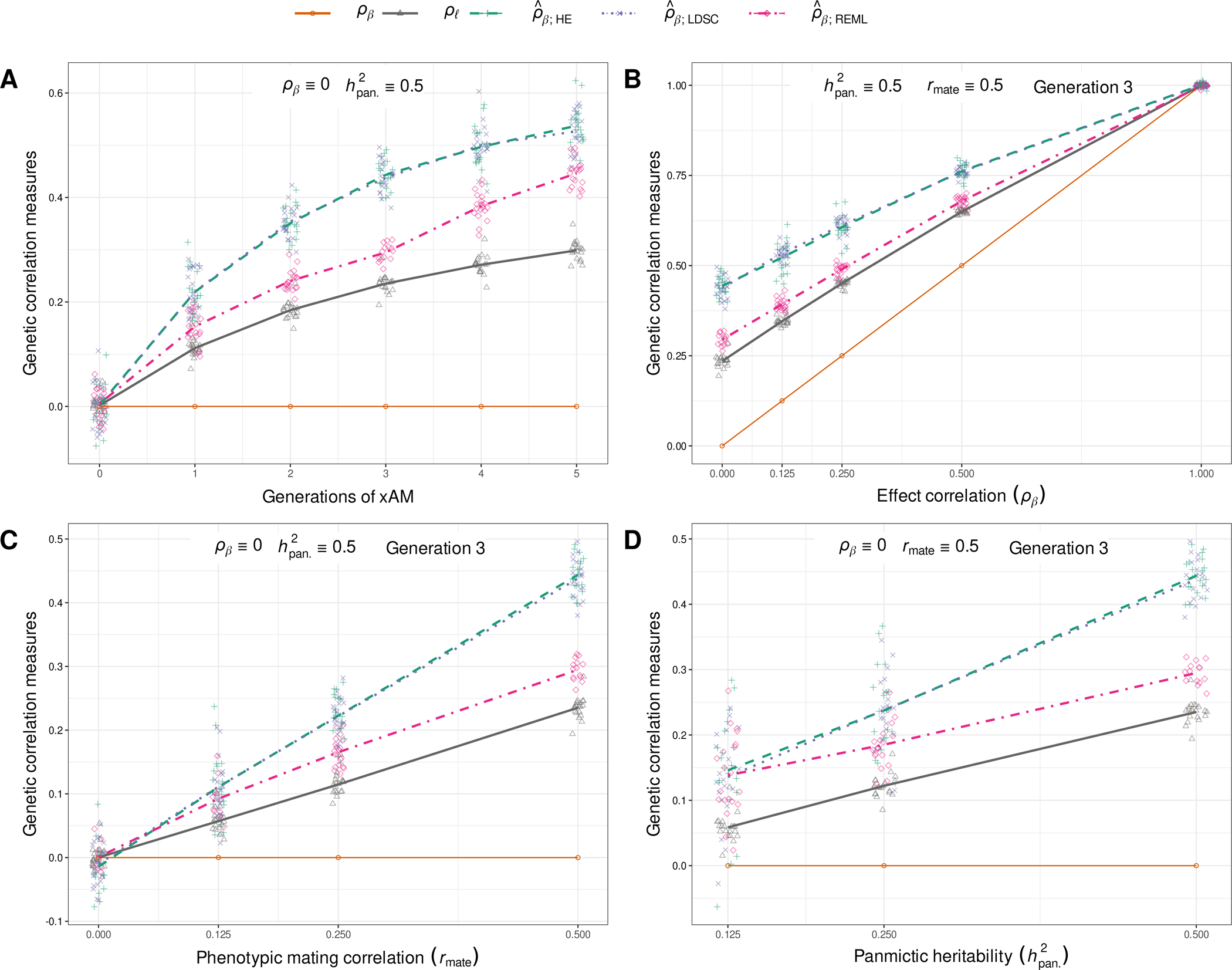
Score correlation (ρ_ℓ) and genetic correlation estimates $({\widehat{\rho }}_{\beta })$ for two phenotypes with true effect correlation ρ_β, panmictic heritabilities $h_{\text{pan}}^2$, and all cross-mate correlations set to r_mate. (A) xAM increases the true score correlation among genetically orthogonal phenotypes. HE, LDSC, and REML estimators all further overestimate ρ_β and the magnitude of this bias increases over subsequent generations. (B) After three generations of xAM, ${\widehat{\rho }}_{\beta }$ estimates are upwardly biased for genetically distinct phenotypes. (C) The impact of three generations of xAM increases with the cross-mate correlation. (D) The impact of three generations of xAM increases with the panmictic heritabilities.

Importantly, this increase in score correlation induced by xAM does not represent bias: the population-level correlation between the heritable components of the phenotypes truly does increase under xAM. On the other hand, as we demonstrate next, genetic correlation estimators become misspecified under xAM and yield biased estimates. Still, even unbiased estimates of score correlation can be driven by either shared biology, or xAM, or both, further complicating interpretation (Table 1).

Effect correlation estimates are biased upwards

For genetically orthogonal traits, after a single generation of xAM, the REML estimator yielded ${\widehat{\rho }}_{\beta }=0.15$ and the HE and LDSC estimators, which are closely related (21, 22), both yielded average estimates of ${\widehat{\rho }}_{\beta }=0.21$, all of which were greater than the true value of ρ_β=0.00. After three generations of xAM, this upward bias became more pronounced, with REML and LDSC yielding estimates of ${\widehat{\rho }}_{\beta }=0.30$ and ${\widehat{\rho }}_{\beta }=0.44$, respectively.

The quantities ρ _ℓ , and ${\widehat{\rho }}_{\beta }$ are monotonically related to ρ _β , r _mate , and $h_{\text{pan}}^2$

Many trait pairs subject to xAM will truly have correlated genetic effects. Figure 2B illustrates the relationship between ρ_β, ρ_ℓ, and ${\widehat{\rho }}_{\beta }$ for two traits with $h_{\text{pan}}^2=0.5$. Excepting the case of ρ_β=1.0 (genetically identical phenotypes), results remained consistent with the genetically orthogonal case: ρ_β was lower than ρ_ℓ, which was in turn lower than the upwardly biased ${\widehat{\rho }}_{\beta }$ estimates provided by REML, HE, and LDSC. For example, when ρ_β=0.25, LDSC yielded ${\widehat{\rho }}_{\beta }=0.62$ after three generations of xAM. We note that whereas the true effect correlation varies in Fig. 2B, the cross-mate correlations remain fixed, demonstrating that the potential for xAM-induced bias is present even when cross-mate cross-trait correlations partially reflect shared genetic bases. The impact of xAM on both ρ_ℓ and ${\widehat{\rho }}_{\beta }$ was greater for traits under stronger xAM (Fig. 2C) and for traits with greater heritabilites (Fig. 2D).

xAM biases annotation- and locus-level analyses

Partitioned genetic correlation estimators evidenced similar biases as genome-wide estimators under xAM, even when supplied with annotations directly relevant to bivariate genetic architecture. Further, this bias was greatest at regions relevant to only one of the two phenotypes (Fig. S12).

In association studies, GWAS effect estimates for SNPs causal for the focal trait were biased upwards in magnitude whereas those causal for a secondary, unrelated trait under xAM with the first were biased toward their effects on that trait (Figs. S7 to S9). These biases were asymptotically non-negligible (Fig. S9). As a result, xAM increased the likelihood of rejecting the null-hypothesis of no association at all SNPs causal for either trait, increasing both statistical power and false positives rates (Fig. S10). Eventually, all variants affecting a secondary phenotype subject to xAM with the GWAS phenotype will reach genome-wide significance as sample size becomes large. However, spurious effect estimates will remain attenuated (Figs. S7 to S9), implying that methods for identifying cross-trait heterogeneity in GWAS estimates may have the potential to differentiate trait-specific signal from xAM-induced artifacts.

xAM alone can plausibly explain substantial variance in empirical genetic correlation estimates

We next sought to quantify the extent to which empirical ${\widehat{\rho }}_{\beta }$ estimates for previously-studied trait pairs could be explained by xAM alone, assuming genetic orthogonality. We proceeded with a simulation-based approach, which we present for the UKB and psychiatric phenotypes in turn.

Within each sample we identified mate pairs and estimated phenotypic cross-mate correlations. We then used these estimates, together with empirical heritability estimates, as inputs to a forward-time simulation where separate, non-overlapping collections of causal variants were assigned to each phenotype, such that ρ_β=0.0. At each generation, we estimated the effect correlation, ρ_β, using method-of-moments. These projected effect correlation estimates, which we denote ${\widehat{\rho }}_{\text{xAM}}$, can be interpreted as expected LDSC genetic correlation estimates for genetically orthogonal traits under xAM consistent with empirical spousal correlations.

We next compared ${\widehat{\rho }}_{\text{xAM}}$ to empirical LDSC estimates derived in real data, which we denote ${\widehat{\rho }}_{\text{emp}}$. To simplify discussion, we define the ratio:

$$\widehat{\gamma }={\widehat{\rho }}_{\text{xAM}}/{\widehat{\rho }}_{\text{emp}},$$

which measures the projected LDSC effect correlation estimate due to xAM-induced artifact relative to the empirical LDSC effect correlation estimate for a given phenotype pair (Fig. 3A).

Fig. 3. Empirical and expected genetic correlations among UK Biobank phenotypes.

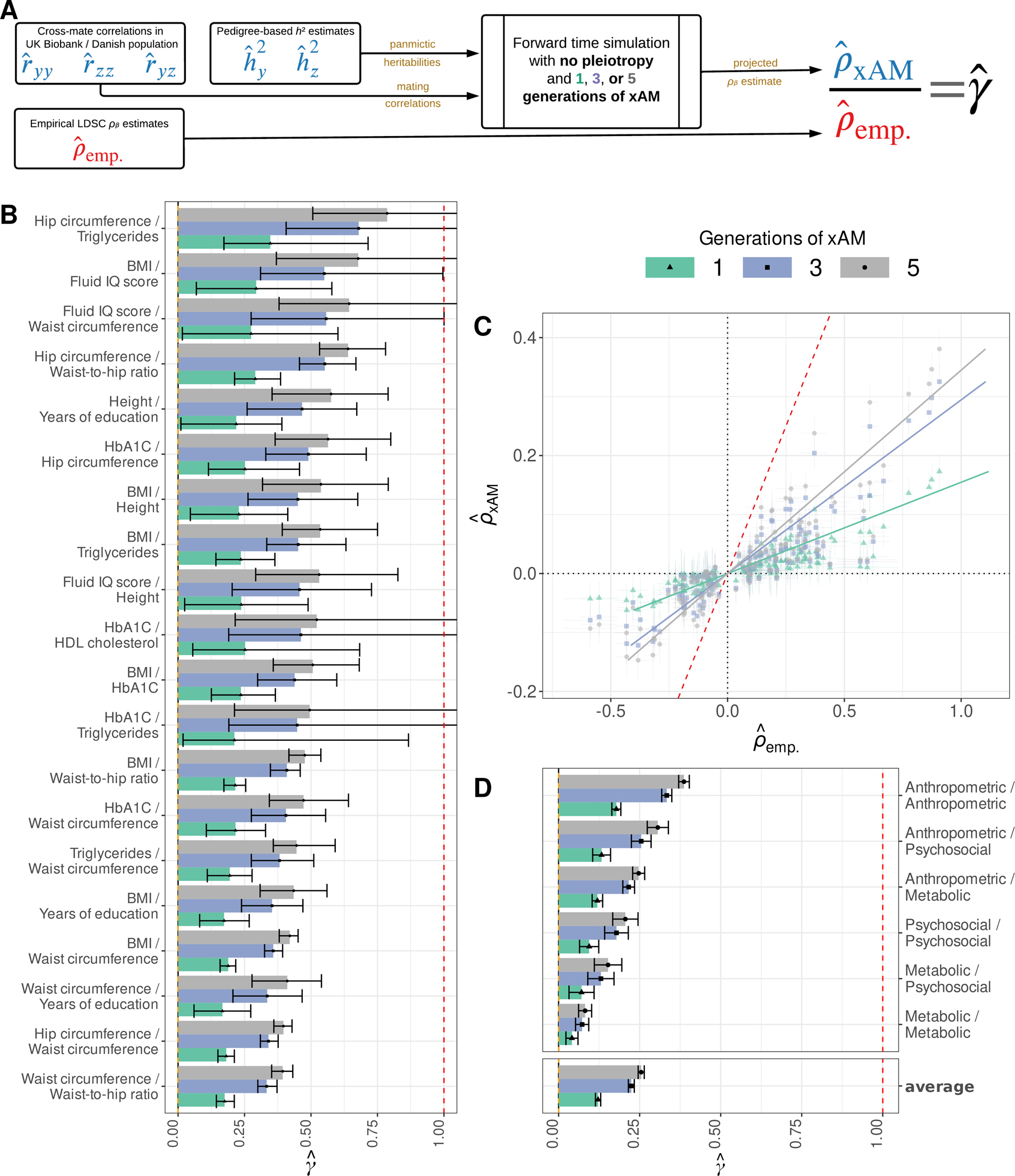
(A) We computed the expected LD score regression (LDSC) genetic correlation estimate in the absence of pleiotropy and after a given number of generations of xAM $({\widehat{\rho }}_{\text{xAM}})$, which we compared to empirical LDSC estimates $({\widehat{\rho }}_{\text{emp}})$ to obtain the ratio $\widehat{\gamma }:={\widehat{\rho }}_{\text{xAM}}/{\widehat{\rho }}_{\text{emp}}$. (B) The top 20 $\widehat{\gamma }$ estimates across previously-studied UKB phenotype pairs with nominally significant (p < 0.05) ${\widehat{\rho }}_{\text{emp}}$ values. (C) Projected versus empirical LDSC estimates for all UKB phenotypes with nominally significant genetic correlation estimates. (D) Inverse variance weighted average $\widehat{\gamma }$ estimates within and between qualitatively similar phenotypic domains. Error bars throughout represent 95% credible intervals.

Expected effect correlation estimates for UKB phenotypes in the absence of pleiotropy

We restricted our attention to 132 (of 190 possible) pairs of UKB phenotypes with nominally significant (p < 0.05) LDSC genetic correlation estimates (Table S1). We first obtained pedigree-based heritability estimates for each of the traits of interest from the literature, using estimates derived in demographically-comparable (Table S2). Together with the phenotypic mating correlations (Fig. 1A), these comprised inputs to forward time simulations used to compute ${\widehat{\rho }}_{\text{xAM}}$.

Across 132 trait pairs, 42 evidenced $\widehat{\gamma }$ values significantly greater than zero (their 95% credible intervals did not include zero) after a single generation of xAM, which increased to 74 trait pairs after three generations. Across all trait pairs (including those not significantly different from zero), the inverse variance weighted average $\widehat{\gamma }$ estimate was 0.25 (se=0.005). Figure 3B presents the first 20 pairs in descending order of $\widehat{\gamma }$ and Fig. 3C presents the raw projected and empirical effect correlation estimates across all 132 pairs (see Table S3 and Figs. S14 to S15 for detailed results spanning five generations of xAM). Finally, Fig. 3D displays average $\widehat{\gamma }$ values within and between qualitative phenotypic domains.

Expected effect correlation estimates among psychiatric disorders in the absence of pleiotropy

We next estimated ${\widehat{\rho }}_{\text{xAM}}$ for a collection of six psychiatric disorders, using correlations estimated in spousal pairs randomly selected from the Danish population (Table S4). We then compared these projections to the LDSC genetic correlation estimates reported by Grotzinger and colleagues (23).

Across all pairwise combinations of disorders, we observed an average ratio of $\widehat{\gamma }=0.29$ (se=0.016; Figs. 4A and 4B) after five generations of xAM. Some trait pairs evidenced considerably greater empirical genetic correlation estimates than might be explained by xAM alone (for anxiety disorders and major depression, $\widehat{\gamma }=0.21$, 95% CI: 0.17–0.25), whereas for other pairs this discrepancy was modest (for alcohol use disorder and schizophrenia, $\widehat{\gamma }=0.83$, 95% CI: 0.59–1.24; see Table S5 and Fig. S16 for complete results).

Fig. 4. Empirical and expected genetic correlations among psychiatric phenotypes.

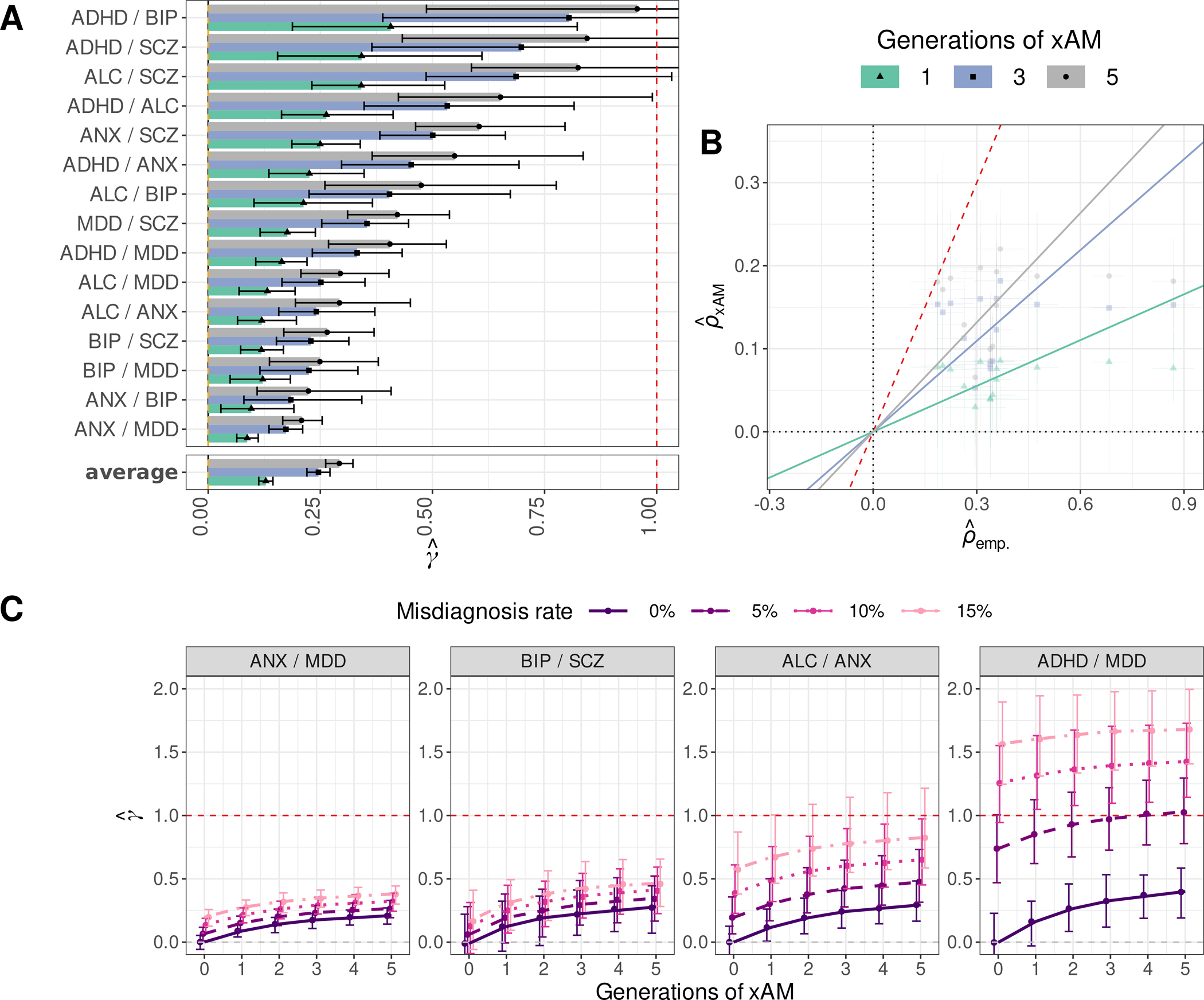
(A) Ratios $(\widehat{\gamma }:={\widehat{\rho }}_{\text{xAM}}/{\widehat{\rho }}_{\text{emp}})$ of projected LD score regression (LDSC) genetic correlation estimates under xAM alone relative to empirical genetic correlation estimates (23) for six psychiatric disorders with 95% credible intervals. (B) Projected versus empirical LDSC estimates across psychiatric phenotype pairs. (C) The potential combined impacts of bidirectional errors in diagnosis and xAM on genetic correlation estimates for selected psychiatric disorder pairs. The red dashed line corresponds to $\widehat{\gamma }=1$ across all panes.

xAM exacerbates bias due to misdiagnosis

After additional simulations demonstrated that xAM and further inflates genetic correlation estimates in the context diagnostic errors (Fig. S11), we extended our method for estimating ${\widehat{\rho }}_{\text{xAM}}$ to incorporate misdiagnosis. Results were heterogenous across disorder pairs (Fig. S17). For example, whereas moderate rates of diagnostic errors (5%) together with three generations of xAM yielded genetic correlation estimates for ADHD and major depression on par with published estimates ($\widehat{\gamma }=0.97$, 95% CI: 0.73–1.22), substantial diagnostic errors (15%) after five generations of xAM yielded estimates well below previously published estimates for bipolar disorders and major depression ($\widehat{\gamma }=0.37$, 95% CI: 0.12–0.62). Figure 4C highlights the potential impacts of xAM and diagnostic errors on four selected trait pairs and Fig. S17 presents results for all pairs.

Genetic evidence for xAM recapitulates empirical cross-mate correlations

Cross-mate phenotypic correlation estimates (r_mate) explained substantial variance in the cross-chromosome even/odd PGS correlations in a linear model (${\widehat{\rho }}_{\ell ;\text{eo}}$; R²=47.66%; Fig. 5A). This association, which is congruent with expectations under phenotypically-mediated xAM (Supplementary Text; (16)), persisted when accounting for measurement error and heteroskedasticity, and across PGS p-value thresholds (Fig. S18).

Fig. 5. Genetic level evidence consistent with xAM in the UK Biobank.

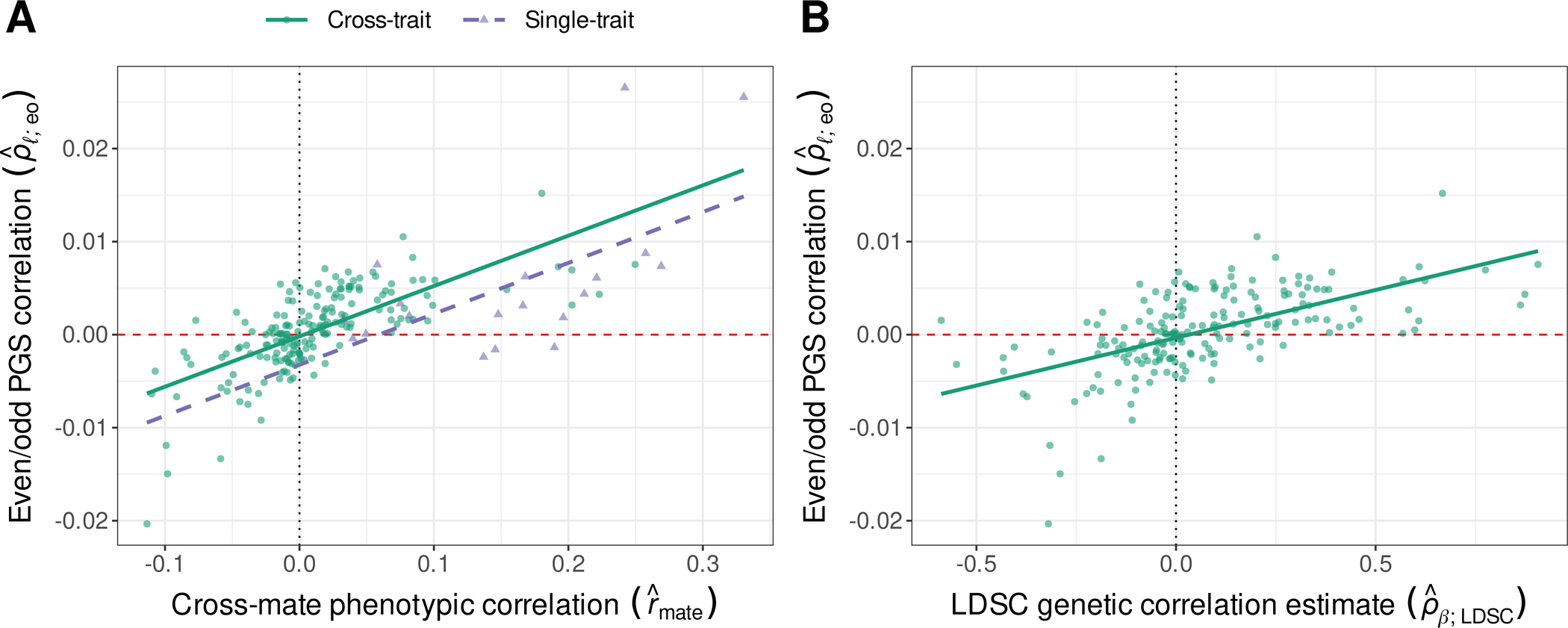
(A) Correlation between even and odd chromosome-specific polygenic scores (PGS) as a function of the cross-mate phenotypic correlation. For a single trait, the vertical axis reflects the correlation between even and odd chromosome scores ${\widehat{\ell }}_{\text{even}}$, ${\widehat{\ell }}_{\text{odd}}$ and the horizontal axis reflects the cross-mate correlation. For a pair of traits Y, Z, the vertical axis reflects a single parameter to which the correlations between ${\widehat{\ell }}_{y;\text{even}}$, ${\widehat{\ell }}_{z;\text{odd}}$ and between ${\widehat{\ell }}_{y;\text{odd}}$, ${\widehat{\ell }}_{z;\text{even}}$ are both constrained, and the horizontal axis reflects the cross-mate cross-trait correlation. (B) Cross-trait even/odd PGS correlations as a function of empirical LD score regression genetic correlation estimates.

Additionally, cross-trait even/odd chromosome PGS correlations were positively associated with empirical LDSC genetic correlation estimates (${\widehat{\rho }}_{\beta ;\text{LDSC}}$; R²=34.81%; Fig. 5B). This is consistent with the hypothesis that empirical effect correlation estimates are capturing additional structure beyond the signatures of biological overlap. Further, regressing ${\widehat{\rho }}_{\beta ;\text{LDSC}}$ on ${\widehat{\rho }}_{\ell ;\text{eo}}$ and ${\widehat{r}}_{yz}$ simultaneously revealed that the association between ${\widehat{\rho }}_{\beta ;\text{LDSC}}$ and ${\widehat{\rho }}_{\ell ;\text{eo}}$ is mediated via ${\widehat{r}}_{yz}$ (ΔR²<0.001; partial effect p=0.48 for ${\widehat{\rho }}_{\ell ;\text{eo}}$ versus p<5e-8 for ${\widehat{r}}_{yz}$). Thus, alternative sources of structure independent from xAM do not appear to explain the positive association between ${\widehat{\rho }}_{\ell ;\text{eo}}$ and ${\widehat{\rho }}_{\beta ;\text{LDSC}}$.

Discussion

Nonzero effect correlation estimates have been widely interpreted as evidence for overlapping genetic bases. It is therefore surprising that substantial variation in genetic correlation estimates can be explained by cross-mate phenotypic correlations. Given the strength of this association, the consequences of the random mating assumption implicit in all commonly used genetic correlation estimators warrant critical attention.

Our results show that cross-mate phenotypic correlations among many pairs of phenotypes are strong enough that one or more generations of xAM would substantially inflate genetic correlation estimates. Further, the correlation structures of even/odd chromosome PGS coincide with expectations after one or more generations of xAM. Wes conclude that xAM comprises a source of systematic bias in the study of genetic similarity across complex traits, one which subverts the widespread interpretation of genetic correlation as a direct index of biological similarity.

Our findings mirror recent results regarding the potential impacts of assortative mating across other areas of statistical genetics, including marker-based heritability estimation (10), and Mendelian randomization (12). Our results also complicate the interpretation of a number of multivariate analytic frameworks. For example, genomic structural equation modeling (24), which takes marker-based genetic correlation estimates as inputs, will propagate xAM induced biases. This does not mean such methods are fundamentally flawed, but instead demonstrates the importance of developing unbiased effect correlation estimators given the centrality of genetic correlation estimates in modern statistical genetics.

With this in mind, we comment on potential approaches to disentangling true effect correlation from xAM-induced artifact. First, family-based designs for addressing xAM (25) are increasingly being applied to molecular genetic data with promising results (26). Second, we conjecture that approaches aimed at characterizing effect heterogeneity across multiple phenotypes may provide a viable means for identifying trait-specific loci: though all trait-specific loci for either of two traits will achieve genome-wide significance in large sample GWAS of either trait, effect estimates will remain substantially larger at causal loci. Finally, we propose that directly modeling the dependence between genotypes and their effects will allow the differentiation of effect correlations and score correlations in samples of unrelated individuals.

There are several limitations to the current investigation. Foremost among these are the numerous assumptions about population dynamics required to model xAM, including but not limited to: panmictic heritabilities, stability of cross-mate phenotypic correlation structures over succeeding generations, stability and transmissability of environmental factors, and the extent to which mating patterns reflect social versus genetic homogamy. We proceeded under the tractable dynamical framework of two additive phenotypes subject to primary-phenotypic xAM with constant cross-mate correlations, stable non-heritable sources of variation, and no vertical transmission. Though each of these assumptions is likely untenable for particular trait pairs, thereby compromising the accuracy of our projections, we hypothesize that the qualitative phenomenon whereby xAM inflates genetic correlation estimates will persist for many traits. Nonetheless, we caution that these projections are contingent upon multiple consequential decisions. Constructing a generative model that reconciles the association between empirical mating patterns and genetic correlation estimates is an ill-posed inverse problem for which there are multiple solutions, and of which we have only explored a subset. At the same time, existing methods are only able to sidestep these decisions by making the strong (and often incorrect) assumption that mating is random.

Lastly, we remark that xAM is, in essence, a form of population structure not captured by conventional principal component or mixed-model based correction. Given the increasing evidence that existing methods fail to completely address structural factors, even in ostensibly ancestrally homogenous groups (27), a broader characterization of population structure and methods for addressing such structure will likely be necessary to generate results that are maximally clinically relevant and can be applied equitably.

Data and materials availability:

Cross-mate correlation estimates and all other results are provided in Tables S1 to S6 (16). Code used to perform simulations is publicly available (28). UK Biobank data were accessed under application 33127 and are available through the UK Biobank Access Management System. Danish data are stored in a national high performance computing facility in Denmark. Access to data may be granted upon application to Statistics Denmark in accordance with Danish Law as detailed online (29).