Competition of SARS-CoV-2 variants on the pandemic transmission dynamics

Abstract

SARS-CoV-2 has produced various variants during its ongoing evolution. The competitive behavior driven by the co-transmission of these variants has influenced the pandemic transmission dynamics. Therefore, studying the impact of competition between SARS-CoV-2 variants on pandemic transmission dynamics is of considerable practical importance. In order to formalize the mechanism of competition between SARS-CoV-2 variants, we propose an epidemic model that takes into account the co-transmission of competing variants. The model focuses on how cross-immunity influences the transmission dynamics of SARS-CoV-2 through competitive mechanisms between strains. We found that inter-strain competition affects not only both the final size and the replacement time of the variants, but also the invasive behavior of new variants in the future. Due to the limited extent of cross-immunity in previous populations, we predict that the new strain may infect the largest number of individuals in China without control interventions. Moreover, we also observed the possibility of periodic outbreaks in the same lineage and the possibility of the resurgence of previous lineages. Without the invasion of a new variant, the previous variant (Delta variant) is projected to resurgence as early as 2023. However, its resurgence may be prevented by a new variant with a greater competitive advantage.

1. Introduction

COVID-19 has spread rapidly around the world since it was first identified in Wuhan, China, in November 2019 [1]. The first discovered mutation, D614G, took over the world in July 2020 [2]. In September of the same year, with the first discovery of the B.1.1.7 (Alpha) variant in the UK [3], the evolutionary history of COVID-19 kicked off completely, and the war between humans and COVID-19 variants started officially. With the discovery of the B.1.351 (Beta) variant in South Africa [4], immune escape became a global concern [5]. However, the dominance of Beta strains was soon replaced by the B.1.617.2 (Delta) strain [6]. Just when we thought that the Delta strain had reached the peak of SARS-CoV-2 virus evolution, it was rapidly replaced by the B.1.1.529 (Omicron) strain, which has both larger transmission and immune escape ability [7], [8], [9], [10], [11]. During the evolution of Omicron subvariants, there was an improvement in both the transmission ability and the immune evasion ability of Omicron subvariants [12], [13]. BA.4/5, i.e., one Omicron subvariant, first identified in South Africa, is now the dominant strain worldwide due to its advantage of competition [14], [15].

Competition between strains is common in the real world [16], [17], [18]. Pathogens like influenza A, dengue, and meningitis are examples of infections with multiple strains that behave competitively in a population or within a single host. The competitive relationship also exists in SARS-CoV-2 variants [19], [20], [21]. Variants of SARS-CoV-2 suppress each other through competitive behavior, and variants with competitive advantage dominate, which affects the transmission dynamics of SARS-CoV-2. Competition between strains often results in the emergence of mutant strains, and these new strains have the competitive advantage in terms of transmission, which leads to epidemic outbreaks on a global scale [22], [23]. The competitive behavior between strains not only affects the evolution of the pathogen itself at the microscopic scale, but also plays a very important role in the spread of the disease in the population at the macroscopic scale [24], [25], [26], [27].

Ecologically, competition between strains is driven by cross- immunity, which leads to the complex transmission dynamics of epidemics, such as the emergence of periodic epidemic waves [28], [29], [30]. The current global epidemic of SARS-CoV-2 shows a multi-wave trend due to mutations of strains. Individuals with a history of SARS-CoV-2 infection are likely to be reinfected with the new variant due to partial cross-immunity [31]. The cross-immune protection obtained after infection with the Omicron strain is much stronger than that obtained after infection with the Delta strain [32], [33], [34], [35], [36]. However, it is unclear that how competitive mechanism driven by cross-immunity affects the transmission dynamics of SARS-CoV-2. Moreover, in contrast to the ecological study of inter-strain competition, we need to study the mathematical mechanism of competition between strains.

Several mathematical models were used to study the effect of competition between strains on epidemic dynamics. For example, Newman et al. demonstrated the threshold at which two pathogens competing for the same host can both spread in a population [37]. Girvan et al. showed that four epidemiological dynamics such as periodic epidemic outbreaks were observed during the mutation of pathogens [38]. The study of Poletto et al. addressed the role of host mobility as well as cross-immunity in shaping possible dominance regimes [39]. Previous mathematical models, however, are not applicable to the current stage of pandemic transmission due to some special characteristics of SARS-CoV-2 competing variants, such as super immune escape ability and unbalanced cross-immunity levels.

Previous mathematical models focused on the specific characteristics of SARS-CoV-2 also existed, several of which were based on variants and vaccines. For example, Barreiro et al. developed an extended interval model that includes various variants and vaccination strategies, allowing the study of the emergence and the dynamics of new COVID-19 variants [40]. Several studies modeled the impact of SARS-CoV-2 variants and vaccines on the spread of COVID-19 [41], [42], [43]. Morris et al. studied how the timing of providing the second dose would affect future epidemiological and variant evolutionary outcomes [44]. However, they did not study the impact of competition between variants on the transmission dynamics of SARS-CoV-2. Therefore, there is a lack of an epidemiological model focusing on the effect of the competition between the variants on the transmission dynamics of SARS-CoV-2.

The article is framed as follows. In Section 3.1, we proposed an epidemic model of strain co-transmission to formalize the competition between SARS-CoV-2 strains. Section 3 presented the results of fitting the real data for some countries in order to validate the accuracy of our model. In Section 4, we studied the key factors affecting the outcome of competition between SARS-CoV-2 strains. Section 5 quantified the impact of competition between strains on transmission dynamics and revealed two new possibilities for future transmission dynamics of SARS-CoV-2. Finally, in Section 6, we concluded our findings as well as limitations and presented our perspective.

2. Mathematical model of co-transmission of competing strains

We developed a mathematical model that took cross-immunity and immune escape into account. This model described the competitive relationship between Omicron and non-Omicron strains in this pandemic, where non-Omicron strains and Omicron strains were denoted by strain 1 and strain 2, respectively. The assumptions of the model are listed as follows.

• •The starting point for each country was when the first confirmed case of Omicron was reported in that country, at which point Delta strains account for more than 99% of non-Omicron strains in all countries [45], [46], thus, we ignored other strains and assumed that Delta and Omicron strains are competing with each other.
• •Since the Omicron subvariant BA.4/5 has a greater difference from previous Omicron variants, the competition was replaced by competition between Omicron subvariants when the BA.4/5 appeared.
• •Studies have shown that the effectiveness of the previous two doses of vaccine against the Omicron strain is negligible [47], [48]. Hence, we assumed that only the booster dose significantly affected the transmission of Omicron strains, while the previous two doses only limited the transmission of the non-Omicron strain. Due to loss of immunity, patients who recovered from the Delta and Omicron strains will become susceptible again. Patients who recovered from Delta strains will gain little immunity to Omicron strains and almost complete immunity to Delta strains [32], [33]. Patients who recovered from Omicron strains will gain strong cross-immunity to Delta strains and very strong immunity to Omicron strains [34], [35], [36]. Patients who recovered from Omicron strains will receive permanent immunity after the booster shot due to the hybrid immunity [35], [49].

The transfer diagram was represented by the following system of ordinary differential equations:

$$\frac{dS}{dt}=-\beta \frac{I_0}{N}S-{\beta }_1\frac{I_V}{N}S-{\alpha }_{1}S,$$$$\frac{d{S}_1}{dt}={\alpha }_1\left(S+S_0+S_V\right)-{\beta }_2\frac{I_V}{N}(S_1-{\alpha }_1{S}_V),$$$$\frac{d{E}_0}{dt}=\beta \frac{I_0}{N}S+\beta \frac{I_0}{N}{S}_V-k_1{E}_0,$$$$\frac{d{I}_0}{dt}=k_1{E}_0-\left({\delta }_1+{\gamma }_1\right)I_0$$$$\frac{d{L}_0}{dt}={\gamma }_1{I}_0-{\eta }_2{L}_0,$$$$\frac{d{S}_0}{dt}={\eta }_2{L}_0-{\beta }_1\frac{I_V}{N}{S}_0-{\alpha }_1{S}_0,$$$$\frac{d{E}_V}{dt}={\beta }_1\frac{I_V}{N}S+{\beta }_1\frac{I_V}{N}{S}_0+{\beta }_2\frac{I_V}{N}(S_1-{\alpha }_1{S}_V)-k_2{E}_V,$$$$\frac{d{I}_V}{dt}=k_2{E}_V-\left({\delta }_2+{\gamma }_2\right)I_V,$$$$\frac{d{L}_V}{dt}={\gamma }_2{I}_V-{\eta }_1{L}_V,$$$$\frac{d{S}_V}{dt}={\eta }_1{L}_V-\beta \frac{I_0}{N}{S}_V-{\alpha }_1{S}_V,$$$$\frac{dD}{dt}={\delta }_1{I}_0+{\delta }_2{I}_V,$$ (1)

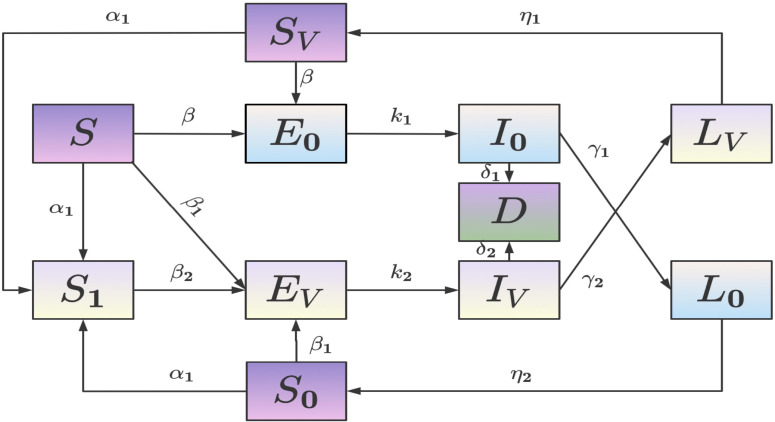
The total population $N\left(t\right)$ was defined into 11 states. Fig. 1 shows the population flow between those compartments.

Fig. 1.

Transfer diagram of the model.

$S\left(t\right)$: Susceptible people who have not received booster shots;

$S_1\left(t\right)$: Susceptible People who have received booster doses;

$E_0\left(t\right)$: People exposed to strain 1;

$I_0\left(t\right)$: People who are infected with strain 1 and are infectious;

$L_0\left(t\right)$: People who have recently been infected with strain 1 but are no longer infectious;

$S_0\left(t\right)$: People who are susceptible to strain 2 and whose most recent infection was by strain 1;

$E_V\left(t\right)$: People exposed to strain 2;

$I_V\left(t\right)$: People who are infected with strain 2 and are infectious;

$L_V\left(t\right)$: People who have recently been infected with strain 2 but are no longer infectious;

$S_V\left(t\right)$: People who are susceptible to strain 1 and whose most recent infection was by strain 2;

$D\left(t\right)$: People who died caused by infection with strain 1 or strain 2.

The relationship between the total population and each state population is:

$$N\left(t\right)=S\left(t\right)+S_1\left(t\right)+E_0\left(t\right)+I_0\left(t\right)+L_0\left(t\right)+S_0\left(t\right)+E_V\left(t\right)+I_V\left(t\right)+L_V\left(t\right)+S_V\left(t\right)+D\left(t\right).$$ (2)

where, ${\alpha }_1$  denotes the rate of booster vaccination;

$\beta$  is the transmission coefficient of the population infected by strain 1;

${\beta }_1$ is the relative transmission coefficient of the population infected by strain 2 without booster vaccination;

${\beta }_2$ is the relative transmission coefficient of the population infected by strain 2 with the booster vaccination;

$k_1$ is the rate at which exposed individuals of strain 1 become infectious;

$k_2$ is the rate at which exposed individuals of strain 2 become infectious;

${\delta }_1$ is the death rate of strain 1 infected population;

${\delta }_2$ is the death rate of strain 2 infected population;

${\gamma }_1$ is the rate of infectious loss in the population infected by strain 1;

${\gamma }_2$ is the rate of infectious loss in the population infected by strain 2;

${\eta }_1$ is the rate of loss of cross-immunity to strain 1;

${\eta }_2$ is the rate of loss of cross-immunity to strain 2.

The relative transmission coefficient ${\beta }_1$ refers to the multiplicative relationship with the transmission coefficient $\beta$. For example, strain 1 is 2–4 times more transmissive than strain 2, that is, ${\beta }_1\in [2\beta ,4\beta ]$. ${\beta }_2$ is the relative transmission coefficient of ${\beta }_1$. For example, if the effectiveness of the booster dose is 40%–60%, then ${\beta }_2\in [0.4{\beta }_1,0.6{\beta }_1]$. ${\eta }_i(i=1,2)$ is the ability of cross-immunity of one strain to another strain. ${\eta }_i=0$ denotes complete immunity to another strain while ${\eta }_i=1$ denotes recovery from one strain will not gain protection against another strain. ${\eta }_i\in (0,1)$ means limited cross-immunity to another strain. In the equation ${\eta }_i=\frac{1}{{(1-{\psi }_i)}^{-1}{T}_i}$, where ${\eta }_i$ indicates the rate of loss of immunity to another strain. ${\psi }_i$ is the limited cross-immunity to another strain acquired after recovery from infection, while $T_i$ is the length of time of loss of cross-immunity to another strain. ${\psi }_i$ and $T_i$ were selected from the references cited in Table 1.

Table 1.

Mean values of model parameters corresponding to the situation of South Korea.

Parameter	Description	Value	Range	Sources
${\alpha }_1$	Booster vaccination rate	0.0112	[$10^{-5}$, $8\times 10^{-2}$]	estimated
$\beta$	Transmission coefficient of strain 1	0.3121		estimated
${\beta }_1$	Relative transmission coefficient of strain 2	0.8715	[$2\beta$, $4\beta$]	estimated
${\beta }_2$	Transmission coefficient after immune escape	0.3123	[$0.4{\beta }_1$, $0.6{\beta }_1$]	estimated
$k_1$	Inverse of the latency period of strain 1	0.25	stable	[50]
$k_2$	Inverse of the latency period of strain 2	0.37	stable	[51], [52]
${\delta }_1$	Death rate due to strain 1	0.0798	[0.007, 0.09]	estimated
${\delta }_2$	Death rate due to strain 2	0.009	[0.001, 0.01]	estimated
${\gamma }_1$	Rate of infectious loss of strain 1 infected patients	0.2089	[0.05, 0.25]	estimated
${\gamma }_2$	Rate of infectious loss of strain 2 infected patients	0.3198	[0.2, 0.4]	estimated
${\eta }_1$	Rate of loss of cross-immunity to strain 1	$3\times 10^{-4}$	[$10^{-4}$, $8\times 10^{-4}$]	estimated
${\eta }_2$	Rate of loss of cross-immunity to strain 2	0.007	[0.005, 0.02]	estimated

3. Validate the accuracy of the model

3.1. Parameter estimation

The details of our fitting process are as follows.

• •We fit the daily new cases, the daily cumulative cases, and the proportion of competing variants, simultaneously. One data point is for the proportion of competing variants at each 14-day interval, thus we fit the proportion of competing variants for this period at the 14-day intervals. The final fit is required to correspond well to all three indicators, i.e., daily new cases, daily cumulative cases, and the proportion of competing variants at 14-day intervals.
• •The nonlinear least-squares curve fitting method is used to obtain the optimal values of parameters within a reasonable range, where the values of these parameters (${\alpha }_1,\beta ,{\beta }_1,{\beta }_2,{\delta }_1,{\delta }_2,{\gamma }_1,{\gamma }_2,{\eta }_1,{\eta }_2$) are obtained by fitting. The reasonable range refers to the parameter fluctuation range defined according to the references. We make constraints on the range of parameter values during the fitting process, i.e., the range of parameter values is consistent with the real world. In the example of the South Korean parameters, the parameters are shown in Table 1. Additionally, the parameters for other countries are shown in Table A.2 of the Appendix.
• •In each country, the starting point is the day before the first Omicron case was reported. The number of the incubation population infected by the Delta strain at this time could be calculated by $I_0\left(t\right)=k_1{E}_0\left(t-1\right)$. The initial value of $L_0$ is the cumulative number of recovered individuals from previous strains. These individuals would be converted to susceptibility to Omicron strains at a certain rate when the Omicron strain emerged. A new variant (Omicron strain) would appear on the next day, so we would know that $I_V=1$ for tomorrow, and we could also calculate $E_V$ for today. For the initial value of $S_1$, we consider that countries start vaccinating with booster shots for the Omicron strain from the first reported Omicron case, i.e., $S_1=1$ when the Omicron strain appeared. The initial value of D is the cumulative number of deaths in each country on that day, and $N$ is the total population of each country. The initial values of $S_V,L_V$, and $S_0$ are all 0 because they are generated by a new strain (Omicron strain) drive, while the new strain is not present at this time.

3.2. Fitting real data from South Korea, Denmark, and Spain

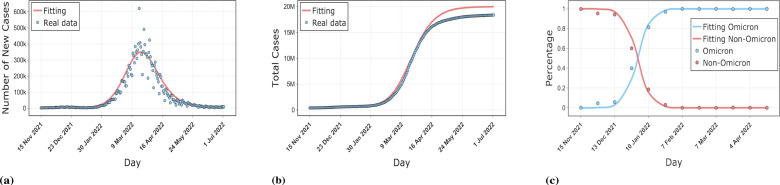
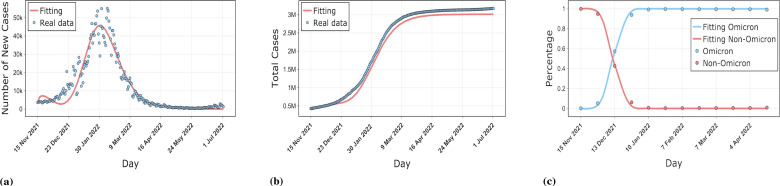
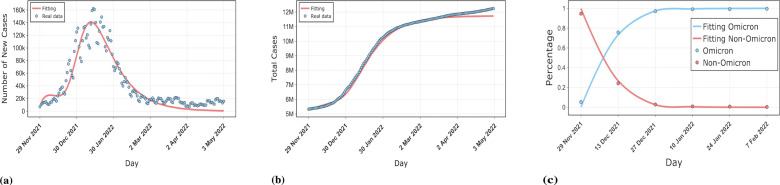
The numerical simulation results for three countries, South Korea, Denmark, and Spain, are shown in the Figs. 2,3,4. The simulations include the proportion of total patients infected with the Omicron strain, daily cases as well as cumulative cases. The results show that our model is well-fitted to the real reported data, which validates the accuracy of the model. The data was obtained from GISAID, Our World In Data and worldometer [53], [54], [55]. The starting point in time for each country simulation was from the first reported Omicron case in that country. The end date of the simulation for Spain was May 1, 2022, with a time scale of 155 days. The simulation end date for South Korea and Denmark was July 3, 2022, with a time scale of 230 days.

Fig. 2.

Comparison of our model results with real data on the epidemic in South Korea. (a) shows the fit of the model to the daily new cases. (b) shows the fit of the model to the cumulative cases. (c) shows the fit of the model to the proportion of Omicron and non-Omicron strains.

Fig. 3.

Comparison of our model results with real data on the epidemic in Denmark. (a) shows the fit of the model to the daily new cases. (b) shows the fit of the model to the cumulative cases. (c) shows the fit of the model to the proportion of Omicron and non-Omicron strains.

Fig. 4.

Comparison of our model results with real data on the epidemic in Spain. (a) shows the fit of the model to the daily new cases. (b) shows the fit of the model to the cumulative cases. (c) shows the fit of the model to the proportion of Omicron and non-Omicron strains.

3.3. Fitting the real data of BA.4/5 in South Africa

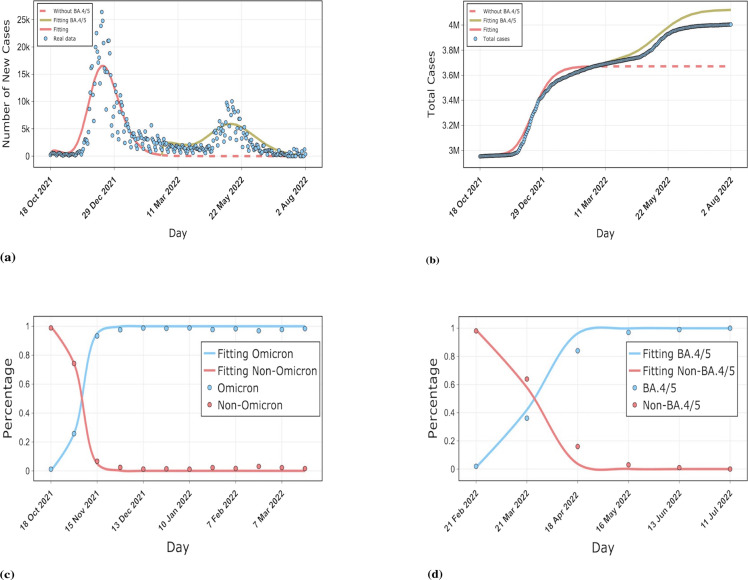
BA.4/5 quickly replaced the previous subvariant of Omicron in South Africa and caused another wave of outbreaks while other countries were still dominated by BA.1, BA.2. We fitted the reported data in South Africa by our model to estimate the burden of BA.4/5 on South Africa. The well-fitting results validate the accuracy of our model. From the simulation curve for South Africa, we can see that without the invasion of BA.4/5, the epidemic in South Africa would have been largely stabilized by the middle of March 2022. However, BA.4/5 extended the duration of the epidemic in South Africa by about 4 months, and the epidemic did not stabilize until the middle of July. As shown in Fig. 5(b), our simulation results suggest that without the invasion of BA.4/5, the final size of the South African epidemic would have been around 3.7 million, however, the emergence of BA.4/5 raised the total size of the South African epidemic to over 4.1 million. We projected that BA.4/5 would eventually cause about 400,000 extra infections in South Africa. As can be seen from Fig. 5(c), the time taken for the Omicron strain to replace the non-Omicron strain is rapid, with the Omicron sequence taking about 14 days to grow from 5% to 50%, which is supported by the study of Elliott et al. [56]. However, the BA.5 sequence went from 5% to 50% in about 28 days. The time to substitution among Omicron subvariants as well as the growth advantage was also quantified by our model, as detailed in Table A.3 of the Appendix.

Fig. 5.

Comparison of our model results with real data on the epidemic in South Africa. (a) and (b) show the fit of our model for daily new cases as well as cumulative cases, respectively. The red dashed line indicates the simulated curve of the final size that would have resulted without the invasion of the new variant BA.4/5. The dark green solid line indicates the burden on South Africa due to the BA.4/5 invasion. variant. (c) and (d) show the evolution of the Omicron strain as well as BA.4/5, respectively.(For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

4. Factors affecting competitive advantage between strains

4.1. Impact of relative transmission and immune escape ability on a strain with the competitive advantage

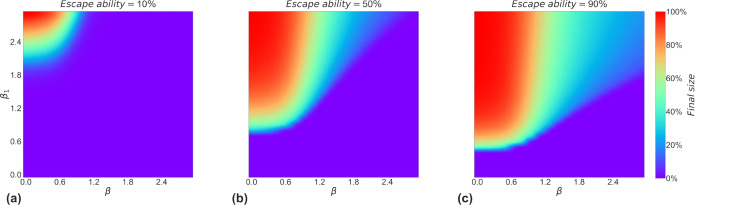
To investigate the impact of relative transmission and immune escape ability on the outcome of competition between strains, we just need to evaluate the change in the final size of the strain with a competitive advantage (strain 2). We can see from Fig. 6(a), (b) and (c) that the transmission ability is higher, the larger the final size caused by strain 2, i.e. the greater the competitive advantage. However, a strain with greater transmission ability than another strain does not mean that it will win from the competition, this is due to the initial number accumulated by the previous strain. Nevertheless, as the new strain increases its immune escape ability, the transmission ability required for it to win is decreasing. From (a) to (c) in Fig. 6, the purple part keeps decreasing, which means the mere fact that one strain is stronger than another in terms of transmission ability does not necessarily mean that it will win since the previous strain already exists at a certain size in the population. Strains with both higher relative transmission and immune escape ability are more likely to win the competition. Furthermore, as the immune escape capacity of new strains differs, a new strain with greater immune escape will have a greater chance of winning against previous strains under the same conditions of transmission ability.

Fig. 6.

Influence of relative transmission ability and immune escape on the competitive outcome of strains. (a), (b), and (c) show the final size of strain 2 at 10%, 50%, and 90% of the immune escape capacity, respectively. The color bar is around 0%, i.e., the purple area indicates that strain 2 will not outbreak, which means that the winner of the competition between strains is strain 1. The other areas indicate that strain 2 is the winner of the competition between strains.

4.2. Impact of relative transmission ability on replacement time between competing strains

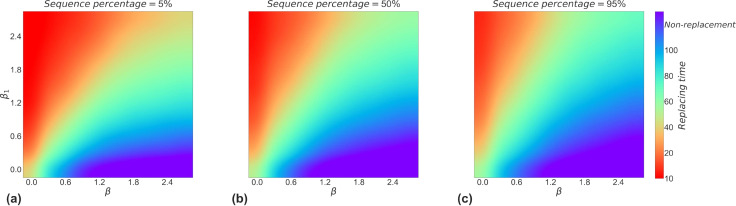
Relative transmission ability affects the intensity of competition between strains by influencing the substitution time between strains. Fig. 7 demonstrates that the strength of the relative transmission ability determines the time for one strain to replace the other, in other words, the intensity of the competition between the two strains. As the relative transmission ability increases, the time of their substitution decreases continuously, meaning that one strain is stronger in the competition. From the three heat maps, we can see that not all strains will eventually become the dominant strain when the sequence grows to 5%, while strains that reach 50% sequence will eventually grow to 95% sequence, which means that they will eventually replace another strain altogether. This may be the reason why in reality some variants appear only fleetingly, while others increasingly grow to become dominant strains.

Fig. 7.

Effect of differences in transmission ability on strain substitution time. Heat maps (a), (b), and (c) indicate the time required for a strain to reach 5%, 50%, and 95% of its sequence in the process of replacing another strain respectively. Non-replacement means that the new strain will not replace the old one during the competition process.

4.3. Impact of cross-immunity level on a strain with the competitive advantage

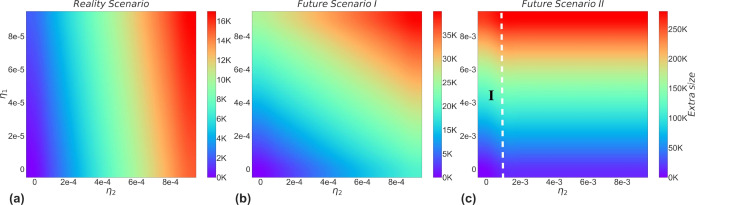
The rate of loss of cross-immunity is also an important factor influencing the competition between strains. Fig. 8 shows the impact of cross-immunity levels on strain 2 through the mechanism of competition between strains. The possible cross-immunity levels of competing strains under different scenarios both currently and future was also evaluated by us. Reality scenario means that under competitive conditions between Omicron and non-Omicron strains, the protection conferred by prior infection is less against Omicron strains, but the protection against other strains after infection with Omicron strains is strong [32], [36]. Future scenarios indicate the range of possible cross-immunization levels of future strains.

Fig. 8.

Effect of the rate of loss of cross-immunity on the extra size caused by strain 2. The extra size represents the number of infections added to the initial number of illnesses. (a), (b), and (c) show the impact of the rate of loss of cross-immunity on the competition between strains, i.e. the extra size of the outbreak caused by strain 2, in the real scenario as well as in the two possible future scenarios, respectively. Reality scenario: The size of the partial cross-immunity gained after recovery from infection with both strains is very different, and the protection gained is maintained for a longer period. Future scenario I: The difference in the size of the partial cross-immunity obtained after recovery from infection with both strains is not large and the protection obtained is maintained for a longer period. Future scenario II: The difference in the size of the partial cross-immunity obtained after recovery from infection with the two strains is small, but the protection obtained is maintained for a shorter period. The left side of the white dashed line shows that subplot (b) is part of it.

Fig. 8(a) shows that the extra size of strain 2 increases with $\eta 2$ and it is almost entirely determined by ${\eta }_2$, independent of ${\eta }_1$. The reason for this is that in the short term, people with a history of infection with other strains are likely to reinfect with Omicron strains, while people who recover from infection of Omicron strain hardly reinfect with Omicron strain, which is consistent with reality.

Fig. 8(b) shows the first scenario in the long term future time, if the emerging strain has a stronger escape capacity to natural immunity and the immunity acquired is at the same order of magnitude whether infected by previous strains or by itself, then the extra size of this strain is determined by both ${\eta }_1$, ${\eta }_2$ together. The reason for this result may be that an increase in the order of magnitude of ${\eta }_1$ means that more infected individuals of strain 1 will be brought in, and as these infected individuals recover, they will again become susceptible to strain 2. Thus ${\eta }_1$ indirectly influences the extra size of strain 2.

Fig. 8(c) shows the second scenario in the long time ahead, where the new strain has the strongest ability to escape from the previous or self-infected protection . Notably, we find that Fig. 8(c) presents the exact opposite result to Fig. 8(a), i.e., this interesting flip phenomenon where the factor determining the extra size of strain 2 changes from ${\eta }_2$ to ${\eta }_1$. The left part of the white dashed line is also the subplot Fig. 8(b). The reason for this phenomenon is that the number of recoveries from strain 1 is much less than the number of recoveries produced by strain 2 under long-term conditions, thus the number of recoveries from strain 1 who are again susceptible to strain 2 is very limited. Furthermore, because of the high recovery rate of strain 2, the effect of strain 1 on the total size of strain 2 in the later stages is minimal. In contrast, a large number of recovered individuals from strain 2 will be re-infected with strain 2 due to their strong escape ability to natural immunity.

5. Impact of competition between strains on the transmission dynamics of SARS-CoV-2

5.1. Comparing outbreak levels caused by old and new competing variants

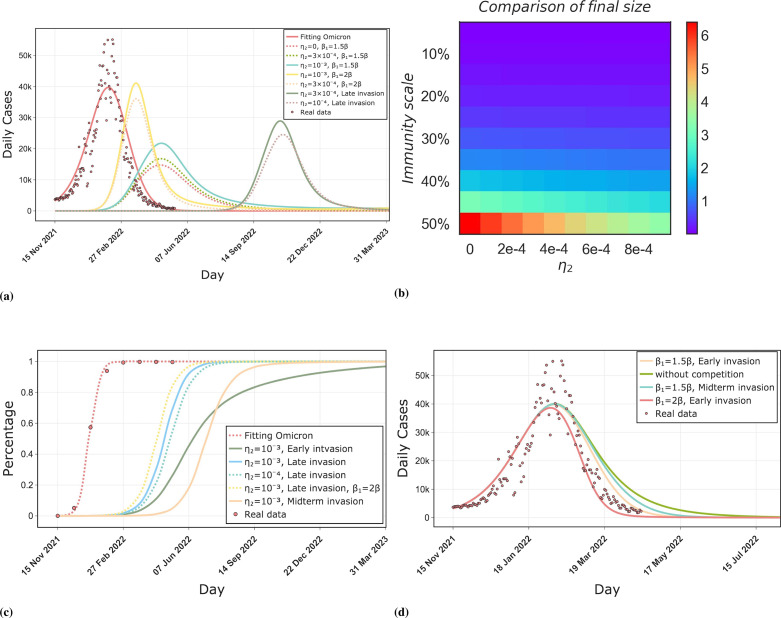
Omicron strains will not be the end of strain evolution. We simulated variants of concern (VOCs) that are likely to emerge in the future with greater transmission ability as well as immune escape. We compared it with the Omicron strain for the size, peak, duration of outbreaks. Moreover, we compared the difference in the time required for the new strain and the Omicron strain to replace the previous strain. The strength of cross-immunity and the timing of the emergence of new variants were found to significantly influenced the transmission dynamics of SARS-CoV-2 and the outcome of strain competition.

In Fig. 9(a), when ${\eta }_2=0$ means permanent immunity to the new strain is acquired after infection with the Omicron strain, therefore, the outbreak size of the new strain is minimal in this scenario. As ${\eta }_2$ increases, the outbreak size, peak, and duration of the new strain increase continuously. Relative transmission ability similarly has a significant effect on the final size and peak caused by the new strain, however, the outbreak duration decreases with increasing ${\beta }_1$ because of the rapid outbreak rate. Moreover, The timing of the invasion of a new strain has a significant effect on the dynamics of the spread of the outbreak. when a new strain invades late in Omicron transmission, the size and peak of the outbreak caused by it are significantly smaller than when it invades at the beginning of transmission. It can be seen that when the new strain invades at the beginning of Omicron transmission, under the condition ${\eta }_2=10^3,{\beta }_1=2\beta$, the size of the outbreak it causes will be larger than the size of the outbreak caused by the previous Omicron wave. When ${\eta }_2$ decreases to $3\times 10^{-4}$, the outbreak size caused by it is less than the outbreak size caused by the Omicron strain.

Fig. 9.

Comparison of outbreak levels caused by the future variant and the previous variant of SARS-CoV-2. (a) shows the size, peak, and duration of the outbreak caused by the future variant compared to the Omicron variant. We considered different values of the cross-immune protection against the new strain ${\eta }_2$ acquired after infection by previous strains and different values of the relative transmission ability ${\beta }_1$ of the new strain, as well as different time points for the emergence of the new strain. late invasion indicates that the new strain will emerge late in the transmission of the Omicron strains, with a delay of 150 days from other transmission conditions. (b) shows the ratio of the final size of the outbreak caused by the Omicron strain and the new strain. The immunity scale indicates the proportion of the population with a history of infection and cross-protection against the new strain. ${\eta }_2$ is the cross-immunization intensity. (c) shows the effect of the invasion time of the new strain, the strength of cross-immunity, and the relative transmission ability on the time of strain replacement, where Early invasion, Midterm invasion, and Late invasion represent the invasion of a new strain at 20, 90, and 170 days after the start of transmission of the previous strain, respectively, meanwhile they also represent the invasion of the new strain at the beginning of transmission, around the peak, and at the end of the last outbreak. (d) shows the effect of the timing of the emergence of a new competing variant and its relative transmission ability on the transmission dynamics of the previous strain.

Fig. 9(b) shows the ratio of the size of the previous outbreak to the size of the next outbreak caused by the new strain. The immunity scale denotes the proportion of the population with a history of previous strains infection, ${\eta }_2$ denotes cross-immune protection against the new strain acquired after being infected by a previous strain. As ${\eta }_2$ increases, the new strain will cause increasingly larger outbreaks, however, only when the immunity scale exceeds 40% the outbreak size of the new strain exceed that of previous strains.

Fig. 9(c) shows the effects of the invasion time of the new strain, the strength of cross-immunity, and the effect of relative transmission on the time of strain replacement. Three solid lines indicate that only the time of emergence of the new strain differs, all other conditions are equal. The new strain appears at the end of the transmission phase of the previous strain. It will replace the previous strain quickly since there are fewer sequences of the previous strain at this time. For previous strains such as Delta, Omicron, etc., the new strain emerges at a later stage of their transmission, hence the replacement time is relatively short. When a new strain emerges in the early or middle stage of the transmission of the previous strain, it will take longer for the new strain to reach 5% sequences due to the strong competitive effect of the previous strain. Compared to the emergence of the new strain in the middle period of the previous strain transmission (peak period), the emergence of the new strain in the early period of the previous strain transmission (Early invasion) will reach 50% sequences at a faster rate, due to the fact that in the early invasion scenario, the sequence of the previous strain is in the rising period and the base is not large enough. However, in the midterm invasion scenario, the rate of sequence growth of the new strain slows down, since at this stage the number of sequences of the previous strain reaches its peak and has a maximum base. The previous strain is the most competitive with the new strain in this period.

Fig. 9(d) shows the effect of the invasion of a competing strain on the previous strain. As can be seen, when ${\beta }_1$ was raised from $1.5\beta$ to $2\beta$, there was a significant effect on the outbreak size of the previous strain. The emergence point of the new strain also significantly affects the transmission dynamics of the previous strain due to their competition. The late invasion was not considered because it did not affect the previous strain. It can be seen that when there was no competition between strains, the duration of the previous strain was the longest. When there was a competition between strains, the earlier the new strain appeared, the shorter the duration of the previous strain would be. Invasion of a new strain significantly affects the duration as well as the peak and outbreak size of the previous strain. This provides a guide for controlling outbreaks in the future by intervening with one of the competing strains.

5.2. Ranking the susceptibility of different countries to future variants

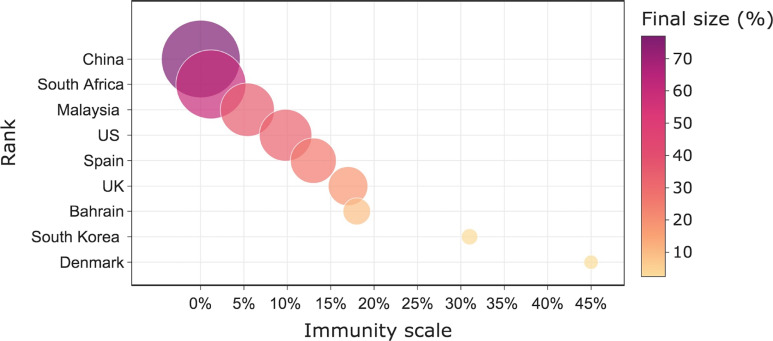
The sensitivity of nine countries to the future variant was simulated in this section. We assumed that only infections with Omicron strains from the previous outbreak would gain cross-immunity protection against the new variant. Previous infections would not protect against the new variant due to the long time interval and the strong immune escape of the new variant. Moreover, the protection gained by the infected population is the same for each country. Fig. 10 shows their sensitivity ranking. We found that the final size of the new variant in a country was negatively correlated with the scale of prior cross-immunity. This is because infected people will gain a portion of protection against the new variant due to cross-immunity, thus the final size of future variants caused in this country is strongly correlated with the number of people infected in the last wave of the outbreak. The first ranking of China means that it is the most sensitive to the next invasion of a new variant, which will have serious consequences if it is allowed spread freely. The last ranking in Denmark means that if a new variant emerges in Denmark, it will not cause a large size compared to other countries. The reason for such a large difference between countries is due to differences in the scale of the previous cross-immunization, with Denmark having a large percentage of the population infected with the Omicron strain during the Omicron period, hence it had a large cross-immunization scale. In China, however, only 0.03% of the population had the cross-immunity protection gained by the Omicron strain because of more stringent control. This result is a guide to the implementation of our future non-pharmaceutical interventions (NPIs) and other measures. Countries that are more sensitive to a new variant should be imposed stronger NPIs compared to those that are not sensitive.

Fig. 10.

Ranking the final outbreak size of countries under the free transmission of the novel variant. The immunity scale represents the proportion of the population in each country that gained cross-immune protection after the prior infection, and the final size is the proportion of the final infections resulting from the free transmission of the new variant in this country. The size of the bubbles denotes the relative size of the final size in each country. The ranking indicates the susceptibility of a country to a new variant, and from top to bottom indicates the ranking from lowest to highest, where the invasion of a new variant will cause the largest infection size in China while the smallest infection size in Denmark.

5.3. Two future scenarios caused by competition between strains

5.3.1. Recurrent outbreaks of omicron strains caused by non-permanent immunity

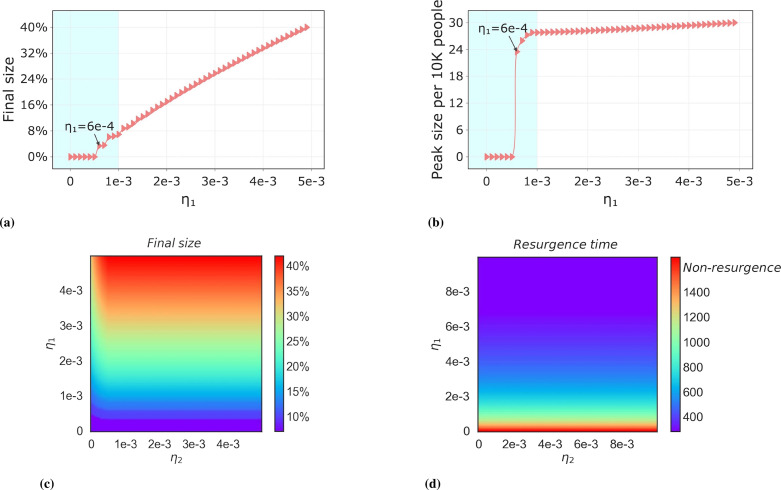
Recurrent outbreaks of the same lineage are caused by loss of immunity. The plots Fig. 11(a) and (b) indicate that the emergence of recurrent outbreaks is due to the value of ${\eta }_1$. We can see that when ${\eta }_1<6e-4$, recurrent outbreaks will not occur. The blue area indicates the recurrent outbreak of the Omicron strain in a real scenario, the range of ${\eta }_1$ is adapted to the Omicron strain period. The white area is for a future strain with a stronger ability to escape against natural immunity. Therefore, it has a higher ${\eta }_1$. The size and peak of the recurrent outbreak showed a linear relationship with ${\eta }_1$ in this area. Fig. 11(c) shows the effect of ${\eta }_1$ and ${\eta }_2$ on the recurrent outbreaks of the strain. At ${\eta }_2=0$, it means that infected by the previous strain will acquire complete immunity to the new strain, at which point the recurrent infection of the new strain is derived entirely from its immune abatement. However, as ${\eta }_2$ increases, it will affect the recurrent infections of the new strain to a lesser extent, but due to the limited number of infected individuals of the previous strain, the recurrent infections of the new strain will mainly originate from self-immunity fading for a longer period, at which point, Fig. 11(c) represents the same meaning as Fig. 11(a). Fig. 11(d) shows the time interval between the re-outbreak and the previous outbreak. The outbreak time refers to the time interval from when the initial reported case of this strain was available. The dark red area, i.e., when ${\eta }_1<6e-4$, indicates that this strain will not have a recurrent outbreak. When ${\eta }_1$ is greater than the outbreak threshold, the time interval of the outbreak decreases as ${\eta }_1$ increases.

Fig. 11.

Threshold conditions for recurrent outbreaks of the same lineage and the factors influencing them. Subplots (a), (b) represent the effect of the rate of loss of cross-immunity on the outbreak final size of the recurrent outbreak of the same lineage, where ${\eta }_1=6e-4$ is the threshold condition for the recurrent outbreak of the same lineage. The blue filler indicates the range of ${\eta }_1$ values for the current Omicron stage, in which case recurrent outbreaks of Omicron strains will result in the final size. The white filler indicates the possible scenario of recurrent outbreaks in future strains. (c), (d) show the effect of the rate of loss of immunity on the outbreak final size and specific timing of recurrent outbreaks of the same lineage. Non-resurgence represents that the same lineage strain will not resurgence.(For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

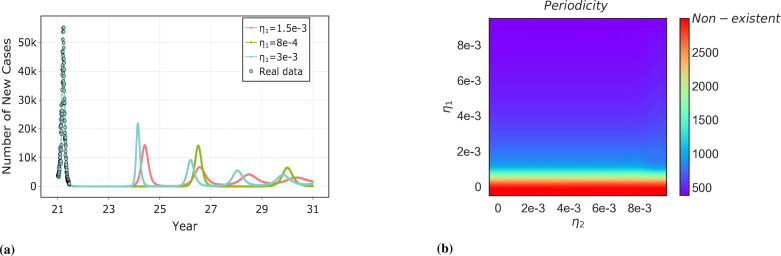
The simulation results in Fig. 12 indicate the possibility of recurrent outbreaks without the invasion of a new strain. We found that in recurrent infections with the same lineage when the strain will occur repeatedly, there is a periodic trend of outbreaks over a longer period. As ${\eta }_1$ increases, with constant immune protection, i.e., as the duration of immune protection $T$ decreases, which will result in a shorter recurrence period for recurrent strains, and periodicity correlates with the rate of loss of cross-immunity. Fig. 12(a) shows a realistic scenario of the duration of immune protection under the current Omicron period [35], [57]. The short period of recurrent outbreaks and the larger size of each outbreak can be seen when under short-term immunization conditions. Fig. 12(b) further shows the periodicity of recurrent outbreaks under all possible immune protection times $T$ and immune protection ability $\psi$, which is significantly influenced by ${\eta }_1$ and not sensitive to ${\eta }_2$, and we mention the reasons for this result in the explanation of Fig. 11.

Fig. 12.

Periodicity of recurrent outbreaks of the same lineage under long-term time. Three curves in subplot (a) indicate the periodicity of recurrent outbreaks under short-term immunization ($T=15weeks,i.e.blueline,and48weeks,i.e.redline$.) and long-term immunization ($T=90weeks,i.e.greenline$.). subplot (b) shows the effect of the rate of loss of immunity (both protection $\psi$ and duration of immunization $T$) on the periodicity of recurrent outbreaks. Non-existent indicates that there will be an absence of recurrent outbreaks of the same lineage.

5.3.2. Resurgence of the previous lineage due to partial cross-immunization

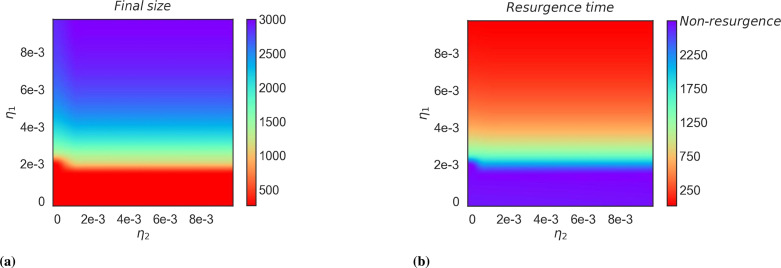
Under the condition where ${\alpha }_1$ is close to 0, which means the competitive advantage of the two strains is not related to the ability to escape immunity to the vaccine, we can see that the threshold condition for which the previous lineage will re-outbreak with ${\eta }_1$ is approximately 2e-3 in Fig. 13. Moreover, when ${\eta }_2$ is in a minimal range, the resurgence of the previous lineage will be affected, since ${\eta }_2$ has only a short-term effect on the previous lineage. While when ${\eta }_2$ is in the rest of the range, the final size of the recurrent outbreak increases with ${\eta }_1$ increases. The resurgence time is defined as the time interval from August 1, 2022 to a future date. The results of our simulations show that the previous lineage (Delta strain) will resurgence after 250 days when ${\eta }_1$ is large enough. Below the threshold condition will not occur the re-outbreak of the previous lineage. All possibilities of ${\eta }_1$ values are explored with the aim of better insights into future pandemic transmission dynamics.

Fig. 13.

Impact of the rate of cross-immunity loss on the re-outbreak of the previous strain. (a) shows the effect of the rate of cross-immunity loss on the final size of re-outbreaks from previous strains. (b) shows the effect of the rate of loss of cross-immunity on the resurgence time interval of previous strains. Non-resurgence represents the previous strain will not resurgence.

6. Conclusion and discussion

We proposed an epidemic model on the co-transmission of strains to formalize the competition between SARS-CoV-2 competing strains. It accurately fits the long-term epidemic trends in seven countries, including South Korea, Denmark, Spain, and South Africa, as well as the trends of variants. Compared with traditional transmission models such as SEIR models and deep learning techniques, it shows significant advantages in predicting long-term time series. The results are shown in Appendix A.4.

The competitive advantage of VOC currently and the factors influencing the competitive advantage among strains were quantified by our model. Through the competitive mechanism between strains, these factors have a significant impact on the transmission dynamics of SARS-CoV-2 in the future. Here are two potential future phenomena of the SARS-CoV-2 strains captured by our model. They are the invasion of a new strain and the resurgence of the previous strain, respectively.

In the first phenomenon, differences in the level of cross-immunity and the time of the invasion of a future strain will result in large differences in the size, peak, and duration of the future strain as well as the time of competing replacement. Moreover, The results of this study suggest for a future invasion of a new strain, allowing it to spread freely may result in the largest infection size in China and the smallest in Denmark due to the large difference in the previous cross-immunization scale between the two countries. This finding may help guide the implementation of future NPIs, for example, the NPIs may be relaxed in countries that are not susceptible to new strains.

In the second phenomenon, the resurgence of the same lineage and the different lineage was observed by our model. For the resurgence of the same lineage, SARS-CoV-2 will probably enter into regular circulation. The period of the cycle depends on the duration of immunization. Furthermore, the threshold conditions obtained from the numerical simulations and then, the observed phase transition phenomena are quantified in Section 5.3.1. For the resurgence of the different lineage, the resurgence of the previous variant such as the Delta variant will probably occur in the future if new variants no longer emerge. Similarly, the threshold conditions for the resurgence of the previous strain and the likely time of occurrence were evaluated in Section 5.3.2. The simulation results of two phenomena will not only benefit us to understand the consequences of a new variant invasion as well as to choose better NPIs, but also help us to determine the future transmission dynamics of SARS-CoV-2

The periodic resurgence of outbreaks due to loss of cross-immunity has been shown to be present in human coronavirus [58], [59]. However, the level of cross-immunity of SARS-CoV-2 strains differs significantly from the previous cross-immunity of coronavirus [32], [60]. Therefore, we made a very comprehensive delineation of the level of cross-immunity among SARS-CoV-2 strains and considered the possible future level of cross-immunity in our simulations. Although this scenario has not been observed among strains of SARS-CoV-2, it has also been observed in some studies through simulations [61], [62]. Nevertheless, the phenomenon of the resurgence of the previous different lineage has never been observed in the studies of SARS-CoV-2 modeling. The reason why this phenomenon has not occurred in reality may be that the emergence of a new variant prevents the resurgence of the previous different lineages.

We are in a post-epidemic era where variants of SARS-CoV-2 have still evolved to survive. Just when we were at our wits’ end about the speed of its evolution, we overlooked that as the SARS-CoV-2 variants evolved, its virulence and mortality rates reached lower levels compared to previous strains. We should take a more dialectical view of the evolution of the variants, which have increased their ability to transmission and immune escape to incredible heights, while their threat to us has decreased [63], [64]. The results of our model for future simulations give us some insight that if no more competing variants emerge, the resurgence of the strain with higher pathogenicity, such as the Delta strain, will be more frustrating. Therefore, the appearance of Omicron subvariants may be preventing the resurgence of the previous variant.

Our model has several limitations. First, we do not take into account the heterogeneity of the population. For example, the effect of age grouping on transmission dynamics is not considered by our model. Barnard et al. took age grouping into account in their simulation of medium-term dynamics of SARS-CoV-2 transmission in England in the Omicron era [65]. This consideration can bring the model closer to the real world. Second, some parameters are not in time-varying or functional form, which may be under-represented for extreme events during the long fitting time. Third, we do not consider the effect of non-pharmaceutical intervention measures on competition between strains. Fourth, our findings for some phenomena are made through numerical simulation results rather than rigorous mathematical proofs. For example, the threshold conditions we obtained for the resurgence of previous strains are solved numerically rather than analytically. Lastly, we only considered the two most dominant competing strains in each period of the competition transmission process of the strains. However, in the post-epidemic era, some other less dominant strains may also influence the whole competitive transmission process, thus the epidemiological characteristics of each variant should be modeled more carefully in future work.

CRediT authorship contribution statement

Jiaqi Chen: Conceptualization, Methodology, Software, Data curation, Writing – original draft. Changgui Gu: Writing – review & editing, Funding acquisition. Zhongyuan Ruan: Supervision, Investigation. Ming Tang: Conceptualization, Methodology, Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary material related to this article.

Data availability

Data will be made available on request.