The single-sample network module biomarkers (sNMB) method reveals the pre-deterioration stage of disease progression

ABSTRACT

The progression of complex diseases generally involves a pre-deterioration stage that occurs during the transition from a healthy state to disease deterioration, at which a drastic and qualitative shift occurs. The development of an effective approach is urgently needed to identify such a pre-deterioration stage or critical state just before disease deterioration, which allows the timely implementation of appropriate measures to prevent a catastrophic transition. However, identifying the pre-deterioration stage is a challenging task in clinical medicine, especially when only a single sample is available for most patients, which is responsible for the failure of most statistical methods. In this study, a novel computational method, called single-sample network module biomarkers (sNMB), is presented to predict the pre-deterioration stage or critical point using only a single sample. Specifically, the proposed single-sample index effectively quantifies the disturbance caused by a single sample against a group of given reference samples. Our method successfully detected the early warning signal of the critical transitions when applied to both a numerical simulation and four real datasets, including acute lung injury, stomach adenocarcinoma, esophageal carcinoma, and rectum adenocarcinoma. In addition, it provides signaling biomarkers for further practical application, which helps to discover prognostic indicators and reveal the underlying molecular mechanisms of disease progression.

Introduction

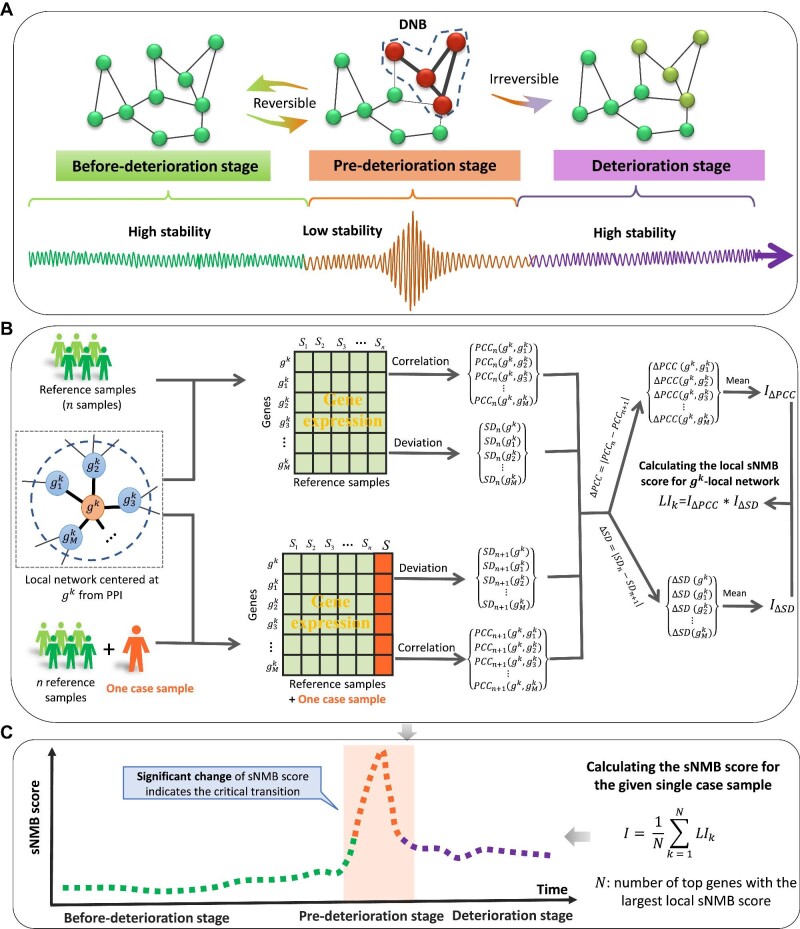
An abrupt switch to a contrasting state through a critical transition occurs in many complex systems, such as ecosystems (Beck et al., 2018; Chen et al., 2019), financial systems (Drehmann and Juselius, 2014; Huang et al., 2017), climate systems (Lenton, 2011), and infectious disease spreading (Scarpino and Petri, 2019). Similarly, the progression of many complex diseases is not always smooth but occasionally abrupt; i.e. there is a so-called critical point at which a sudden and qualitative state transition may occur (Chen et al., 2012; Liu et al., 2021). Accordingly, regardless of specific differences in clinical symptoms and biological processes, disease progression can be roughly classified into three stages, i.e. a before-deterioration stage, a pre-deterioration stage, and a deterioration stage (Figure 1A). The before-deterioration stage is viewed as a relatively healthy state with stability and high resilience. The pre-deterioration stage refers to a critical transition before switching to the onset or deterioration of symptoms and is characterized by low resilience and high susceptibility. The deterioration stage is another stable state with high resilience after the catastrophic transition to the deterioration of the disease. In contrast to the irreversible deterioration stage, the pre-deterioration stage is sensitive to perturbation and is thus usually considered to be reversible to the before-deterioration stage by appropriate intervention strategies. However, many complex diseases, such as cancers, are difficult to cure unless they are diagnosed at an early stage; i.e. missing the best time for preemptive clinical interventions results in patients having no choice but to undergo high-risk therapies. Unfortunately, because many complex diseases cause few symptoms during the early stages, the disease has already reached an advanced stage when the pathological symptoms are easily diagnosed clinically (Miller et al., 2019). Therefore, identifying the pre-deterioration stage is of great significance for preventing or delaying the occurrence of catastrophic deterioration. However, it is challenging to accurately identify the tipping point or pre-deterioration stage of complex diseases, because complex biological systems exhibit relatively little state change before approaching the catastrophic transition.

Figure 1.

Schematic illustration for identifying the pre-deterioration stage based on the sNMB score. (A) The progression of complex diseases is roughly divided into three stages, including a before-deterioration stage with high stability, an unstable pre-deterioration stage, and another deterioration stage with high stability. The pre-deterioration stage is a critical state just before disease onset or deterioration and is usually considered to be reversible to the before-deterioration stage through appropriate intervention, since it is sensitive to perturbation. (B) The sNMB score is calculated based on a single case sample and is capable of quantifying the statistical disturbance yielded from the single case sample against a group of given reference samples collected from a relatively healthy population. (C) The significant change in sNMB signals the pre-deterioration stage; i.e. the sNMB score sharply increases when the system is close to the critical point.

By exploiting the information of differential expression between the before-deterioration and pre-deterioration stages, traditional biomarkers mainly focused on distinguishing the deterioration stage rather than identifying the pre-deterioration stage, which is similar to the before-deterioration stage in terms of phenotype and gene expression. Recently, a novel concept of the dynamic network biomarker (DNB) (Chen et al., 2012) provided three statistical conditions to select a small group of relevant variables for detecting the early warning signals of the critical transition. In other words, when a biological system from a before-deterioration stage approaches the pre-deterioration stage, there appears to be a group of DNB biomolecules satisfying the following three statistical properties: (i) the correlations between DNB biomolecules rapidly increase; (ii) the correlations between DNB biomolecules and non-DNB biomolecules significantly decrease; and (iii) the standard deviations (SDs) of DNB biomolecules drastically increase. Compared with the differential information of gene expression widely used in traditional molecular biomarkers to diagnose ‘a deterioration stage’, DNB serves as a type of network-based biomarker and detects ‘a pre-deterioration stage’ by exploiting the information of differential associations. The DNB approach and its expanded versions have been employed by many research groups and applied to study a variety of biological research topics, including the detection of the cell fate decision (Richard et al., 2016), the identification of the critical stage for complex disease (Koizumi et al., 2019; Zhong et al., 2020; Huang et al., 2021), and the study of immune checkpoint blockade (Lesterhuis et al., 2017). However, the classical DNB method requires multiple samples at each time point to evaluate its three statistical indices, which generally restricts its application in most practical cases, because the availability of multiple samples for each individual is difficult to achieve in clinics. Most statistical methods fail to detect the early warning signal of critical transition when there is only a single case sample for each individual. Therefore, a novel single-sample computational approach is urgently needed to explore the criticality of complex diseases and further identify the pre-transition stage.

In recent years, network-based methods have been frequently applied to study many distinct biological questions, such as dysfunctional gene regulation (Zeng et al., 2013), combinatorial drug discovery (Guo, et al., 2021), and disease prediction (Yu et al., 2017; Liu et al., 2019; Zhang et al., 2022). Inspired by these pioneering works, we proposed a novel computational method called single-sample network module biomarkers (sNMB) to achieve the identification of the pre-deterioration stage just before disease onset or deterioration. Specifically, by exploring the differential information between the before-deterioration and pre-deterioration stages, a local sNMB score was designed to quantify the statistical disturbance caused by the single case sample against a given set of reference samples collected from a relatively healthy population (Figure 1B). The drastic increase in the sNMB score indicates the upcoming tipping point or pre-deterioration stage (Figure 1C). Clearly, this method is individual-specific and may thus benefit the determination of personalized pre-deterioration diagnosis. To validate the effectiveness of the proposed approach, it was applied to a numerical simulation and four real datasets, including stomach adenocarcinoma (STAD), esophageal carcinoma (ESCA), and rectum adenocarcinoma (READ) datasets from The Cancer Genome Atlas (TCGA) database and an acute lung injury dataset (GSE2565) from the National Center for Biotechnology Information (NCBI) Gene Expression Omnibus (GEO) database. The successful identification of the pre-deterioration stages in these datasets is consistent with the experimental observation or survival analysis. The corresponding sNMB signaling biomarkers were validated by functional analysis.

Results

Validation based on numerical simulation

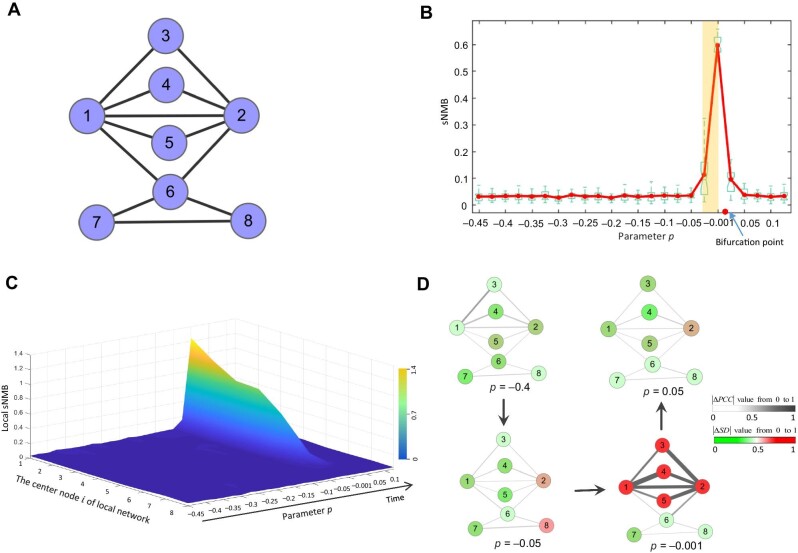
An eight-node regulatory network (Figure 2A) is employed to validate the proposed sNMB method. This regulatory network with eight variables is governed by a set of eight stochastic differential equations Eq. (S1) (Supplementary material Section A). Such a model of the regulatory network represented in the Michaelis–Menten form is often applied to study genetic regulations such as transcription, diffusion, translation, and translocation processes (Chen et al., 2009). Based on the varying parameter p ranging from −0.5 to 0.15, a numerical simulation dataset is generated. The reference samples are generated from the varying parameter p (far from the tipping point p = 0) ranging from −0.5 to −0.45. The details of the dynamical system are provided in Supplementary material Section A.

Figure 2.

Performance of the sNMB method in numerical simulation. (A) An eight-node regulatory network from which a numerical simulation dataset is generated. (B) The curve of the sNMB score abruptly increases in the vicinity of the critical point (bifurcation point p = 0). (C) The landscape of local sNMB scores in a global view is presented to exhibit the dynamic changes in local sNMB scores for eight local networks (i = 1, 2, ⋯, 8). It obviously shows that the drastic increase in sNMB scores for some local networks (i = 1, 2, ⋯, 5) centered at the DNB variables signals the upcoming critical transition. (D) An obvious change in the network structure near the tipping point (p = 0) indicates a significant difference between the single case sample of the critical stage and reference samples.

As shown in Figure 2B, an abrupt increase in the sNMB indicates the upcoming critical transition when the system is near the special parameter value p = 0, which is set as a bifurcation value in Eq. (S1) (see Supplementary material Section A for details). In addition, it can be seen from Figure 2B that the median values of sNMB also reveal the robust performance of our method in detecting the early warning signal of catastrophic transition. In addition, we analyzed the critical signals when the reference sample size (n) varies (Supplementary Figure S1), indicating that the number of reference samples within a range (usually from 3 to 100) barely affects the evolution tendency of the signal curve (e.g. abrupt increase when approaching the tipping point). In Figure 2C, the landscape of the local sNMB score for each local network in a global view is presented to exhibit the dynamic changes in the local sNMB score. It is clear that the local sNMB scores of some local networks sharply increase in the vicinity of the critical point (p = 0). As presented in Figure 2D, the dynamic evolution of a network was employed to illustrate the difference in the differential SD (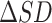) and differential Pearson correlation coefficient (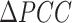) between the before-transition state and the critical point state. An obvious change in the network structure occurs near the critical point, signaling the imminent critical transition at the network level. Therefore, the numerical simulation validated that the sNMB method can accurately and effectively detect the early warning signal of a critical state transition. The source code of the numerical simulation is provided at https://github.com/zhongjiayuan/sNMB_project.

Identifying the critical state for acute lung injury

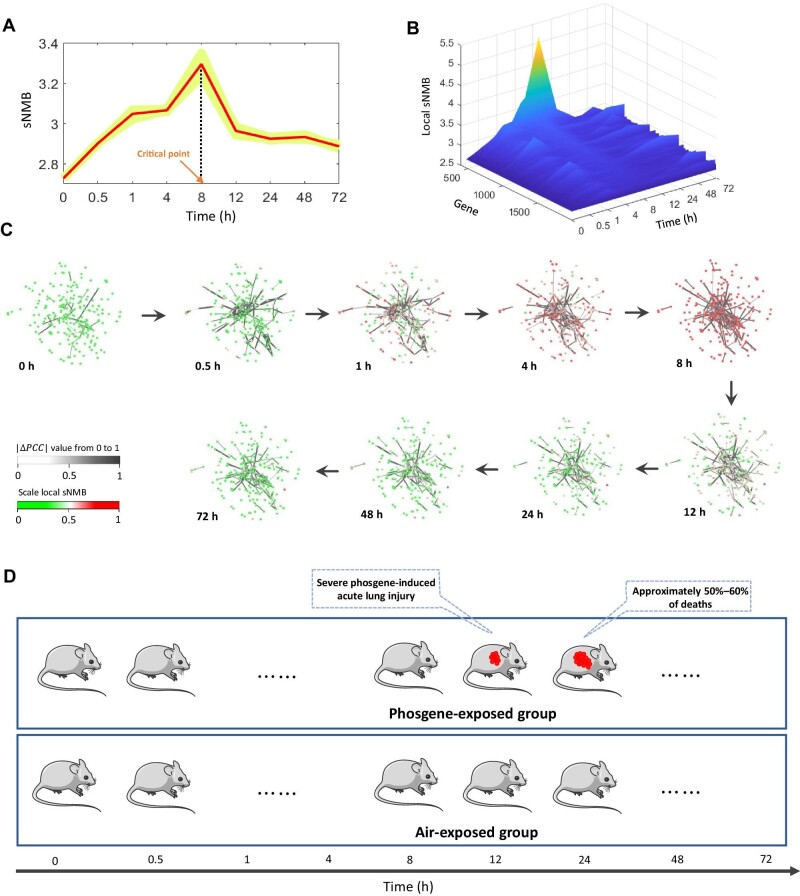
The sNMB method was applied to the microarray dataset (GSE2565) obtained from a mouse experiment of acute lung injury (Sciuto et al., 2005). In the original experiment, case group data were derived from the lung tissues of phosgene-exposed mice, while the control group data were from the air-exposed mice. For both the case and control groups, gene expression was derived from the lung tissues of six mice at nine sampling time points, i.e. 0, 0.5, 1, 4, 8, 12, 24, 48, and 72 h (Sciuto et al., 2005). The samples from the air-exposed group (control group) are regarded as the reference samples. It can be seen from the red curve in Figure 3A that the sNMB score rapidly increases and reaches a peak at 8 h, suggesting an upcoming critical transition at ∼8 h. To validate the effectiveness of the result, six resampled datasets were generated from a leave-one-out scheme. Applying the proposed sNMB method to these datasets, their sNMB scores, shown as the six yellow curves in Figure 3A, all signal the critical transition at 8 h. At the identified tipping point, the top 5% of genes with the largest local sNMB values are selected as the sNMB signaling genes for further analysis. The landscape of local sNMB scores is presented in Figure 3B, and it is observed that the peak of local sNMB values for the signaling genes appears at 8 h. Moreover, Figure 3C exhibits the dynamic evolution of signaling genes at the network level. Clearly, a notable change in the network structure occurs at 8 h, indicating an upcoming critical transition. These results are consistent with the observation in the original experiment (Figure 3D); i.e. the severe phosgene-induced acute lung injury occurred around 12 h, and ∼50%–60% of deaths were observed around 24 h (Sciuto et al., 2005).

Figure 3.

Performance of the sNMB method in acute lung injury. (A) The peak of the sNMB value presented in the red curve appears at 8 h, signaling an upcoming critical transition. To validate the significance of the result, the proposed sNMB method is applied to six resampled datasets generated from a leave-one-out scheme. The results show that six yellow curves consistently signal the critical point at 8 h. (B) The landscape exhibits a global view of the dynamic change in local sNMB scores. (C) From the dynamic evolution of signaling genes at the network level, a notable change in the network structure appears at 8 h. (D) Description of actual observations in a mouse experiment of acute lung injury. The severe phosgene-induced acute lung injury occurred around 12 h and ∼50%–60% of deaths were observed around 24 h.

Identifying the critical state for tumor diseases

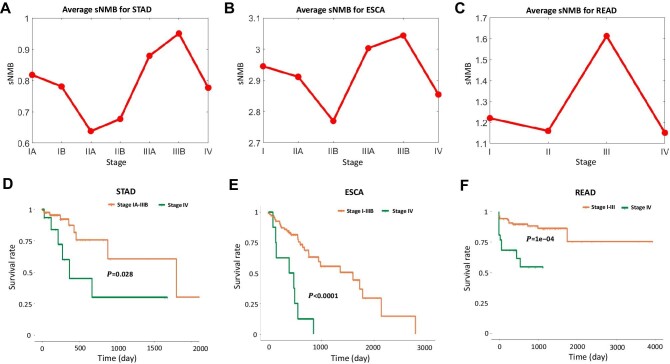
To validate the effectiveness of the sNMB method in detecting the early warning signal of the pre-deterioration stage for tumor diseases, the proposed method was applied to three tumor datasets (ESCA, READ, and STAD) from TCGA. The tumor-adjacent samples that represent the relatively healthy condition were viewed as reference samples, and then the sNMB score of each tumor sample was calculated according to the algorithm described in Materials and methods. At each stage, the mean sNMB value was adopted to quantitatively measure the pre-deterioration stage of tumor diseases. By analysis with the proposed method, the pre-deterioration stage was identified in stage IIIB for ECSA, stage III for READ, and stage IIIB for STAD (Figure 4A–C). To validate the identification of the critical stage, prognostic analysis of before-transition and after-transition samples was performed and compared through Kaplan–Meier (log-rank) survival analysis (Figure 4D–F; Supplementary Figure S2). Specifically, compared with the samples from the after-transition stage, there was usually a higher life expectancy for before-transition samples.

Figure 4.

Identification of the critical transition of tumor distant metastasis in three cancers. (A–C) Identifying the critical transition for STAD (A), ESCA (B), and READ (C). (D–F) Comparing survival curves between the before-transition stage and the after-transition stage in STAD (D), ESCA (E), and READ (F).

For ESCA, as shown in Figure 4A, a sudden increase in the sNMB score was detected in stage IIIB, after which there existed a tumor invading other adjacent structures, such as the aorta and vertebral body, and distant metastasis occurred at stage IV (Stahl et al., 2010). Figure 4D shows that there is a significant difference (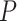 = 0.028) between the survival curves of the before-transition samples and the after-transition samples. Clearly, samples from stages I–IIIB present significantly longer survival periods than samples from stage IV. For the samples from only two stages (stages IIIB and IV) around the critical stage, the survival time of stage IIB samples was much longer than that of stage IIIA samples ( 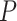= 0.0215; Supplementary Figure S3A). In addition, there was a statistically non-significant difference among the survival curves of samples from before the critical stage (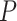= 0.295; Supplementary Figure S3B). In Figure 4B, the peak of the sNMB value appears at stage IIIB, implying an imminent critical transition of STAD after stage IIIB. References show that stage IV is a severely deteriorated stage, in which the tumor has spread to nearby tissues or metastasized to other organs and ultimately causes distant metastasis (Kwon, 2011). Figure 4E shows that there is a significant difference ( 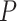< 0.0001) between the survival periods of the two groups of samples, i.e. samples from the before-transition stage (stages IA–IIIB) and samples from the after-transition stage (stage IV). It is also noted that the survival time of samples from stage IIIB was significantly longer than that of samples from stage IV (Supplementary Figure S3C). In addition, there was no significant difference (Supplementary Figure S3D) in survival curves among samples from the before-transition period (stages IA–IIIA). For READ, as shown in Figure 4C, the drastic transitions of the sNMB score appear in stage III, after which the tumor invades other parts of the human body and distant metastasis occurs at stage IV (Jessup et al., 2011). Figure 4F shows that there was a significant difference ( 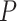= 1e−04) between the survival curves of samples from stages I–III and samples from stage IV. The before-transition samples showed a significantly longer survival time than the after-transition samples. For the samples solely from two stages (stages III and IV) around the critical state, the survival periods of stage III samples were significantly longer than those of stage IV samples (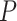= 0.0167; Supplementary Figure S3E). There was no significant difference (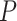= 0.819; Supplementary Figure S3F) in survival curves among samples before the critical stage (stages I–II). These results demonstrate that the sNMB score can detect the early warning signals of a critical transition of survival time, i.e. the critical transition associated with distant metastasis at stage IV can be identified by the sNMB score.

Revealing the potential signaling mechanisms during the tumor stages

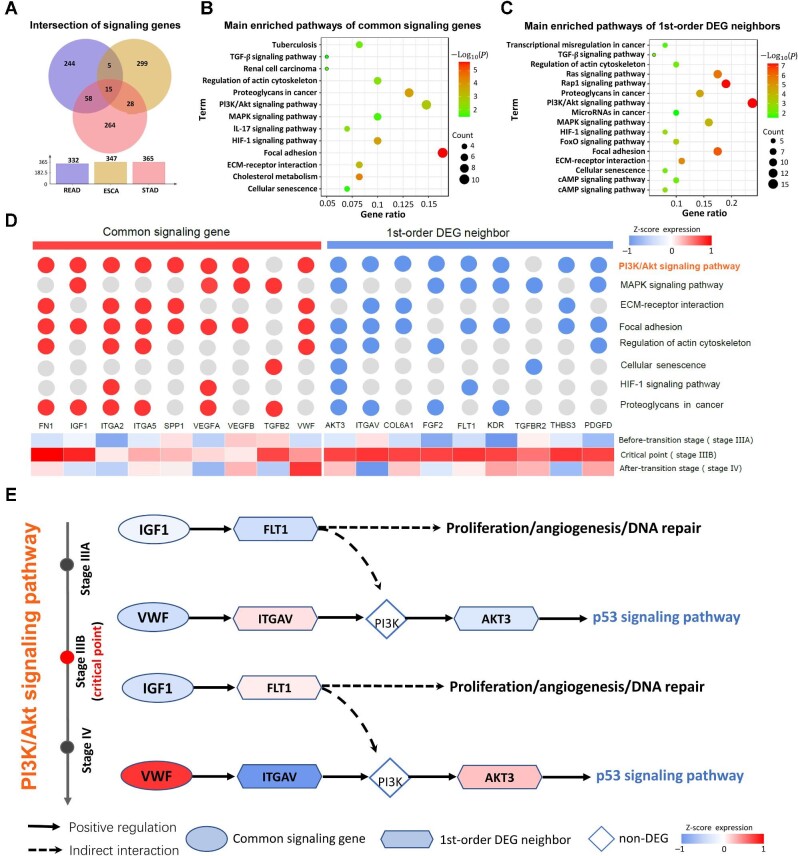
At the identified pre-deterioration stage (the critical point), the top 5% of genes with the highest local sNMB scores were selected as the signaling genes for further functional analyses. As presented in Figure 5A, there were 106 common signaling genes shared among three different tumor datasets: READ, ESCA, and STAD. To reveal the underlying signaling mechanisms, Kyoto Encyclopedia of Genes and Genomes (KEGG) pathway enrichment analysis based on the TCGA-STAD dataset was carried out for these common genes and their 1st-order neighboring differentially expressed genes (DEGs) from the protein–protein interaction (PPI) network. The 1st-order neighboring DEGs satisfy the following two conditions: (i) they are the 1st-order neighbors of common signaling genes in the PPI network and (ii) they are DEGs; i.e. from the perspective of gene expression, there are significant differences (P < 0.05) before and after the pre-deterioration stage. As shown in Figure 5B and C, the common genes and their 1st-order DEG neighbors were significantly enriched in cancer-related signaling pathways, such as the PI3K/Akt signaling pathway, the MAPK signaling pathway, extracellular matrix (ECM)–receptor interaction, and focal adhesion (Figure 5D). In addition, KEGG pathway enrichment analysis was performed for the specific signaling genes of each cancer (Supplementary Figure S4). Tumors are the result of the process of multiple hallmark changes, such as the overexpression of proliferation signals and abnormal metastasis-promoting signals (Hanahan and Weinberg, 2011). For instance, previous reports indicated that the PI3K/Akt signaling pathway was involved in tumorigenesis and tumor progression by regulating various cellular activities, including cell differentiation, proliferation, and apoptosis (Zhang et al., 2014; Huang et al., 2015). MAPK signaling is known to participate in tumor growth and progression (Roberts and Der, 2007). The ECM–receptor interaction and focal adhesion play a significant role in tumor proliferation, adhesion, and metastasis in various cancers (Wang et al., 2020). For the TCGA-STAD dataset, Figure 5D demonstrates the abnormal signals caused by the pattern of gene expression changes before and after the transition. Specifically, at the tipping point before and after metastasis, common signaling genes and their 1st-order DEG neighbors showed different regulatory patterns in the PI3K/Akt signaling pathway (Figure 5E). After the tipping point (stage IIIA), by interacting with its 1st-order DEG neighbor ITGAV, the upregulation of the upstream regulator VWF (common signaling gene) activates the key downstream factor PI3K together with upregulated FLT1 (1st-order DEG neighbor) and subsequently activates the expression of the downstream differential gene AKT3. Furthermore, the activation of AKT3 (1st-order DEG neighbor) triggers a cascade of p53 signaling pathway responses. Overall, the synergy of common signaling genes and their 1st-order neighboring DEGs may have favorable biological significance in tumor progression-related biological processes.

Figure 5.

Functional analysis of common signaling genes in different tumor datasets. (A) Venn diagrams for the intersection of signaling genes in three different cancers. There were 106 common signaling genes shared among the three datasets. (B) Dot plot of KEGG enrichment analyses for 106 common signaling genes. (C) Dot plot of KEGG enrichment analyses for 1st-order DEG neighbors in the STAD dataset. (D) The important common pathways are shared between common signaling genes and their 1st-order DEG neighbors. The common signaling genes mapping into the pathway are depicted with red circles, while their 1st-order DEG neighbors mapping into the pathway are depicted with blue circles. (E) For the TCGA-STAD dataset, the underlying signaling mechanisms involve both common signaling genes and their 1st-order DEG neighbors.

Discovering ‘dark genes’

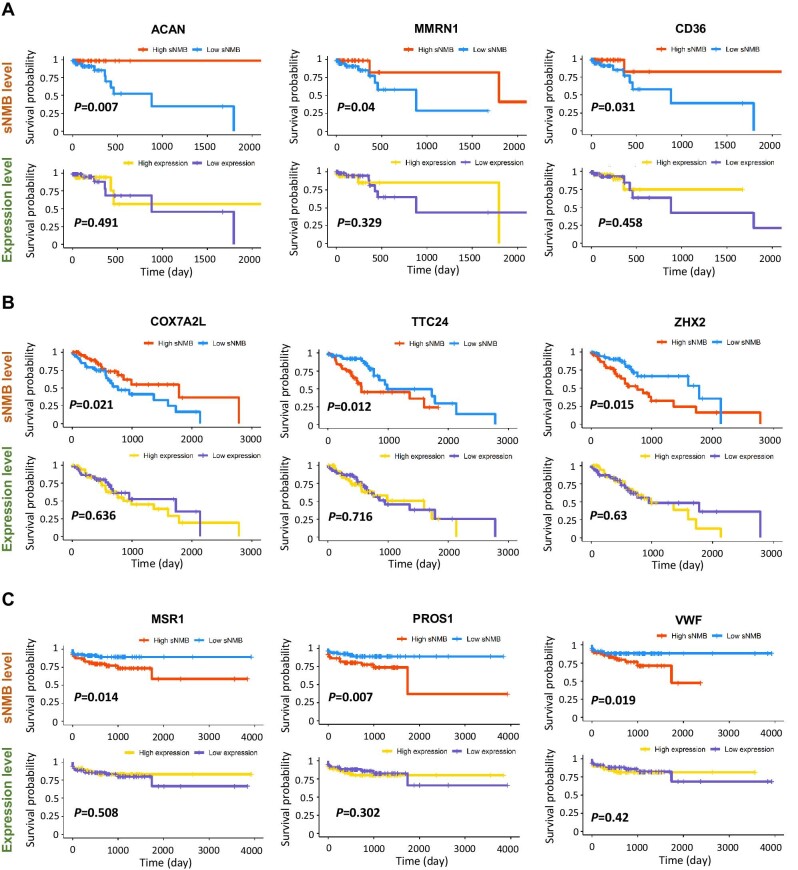
In the field of biomedicine, DEGs play a crucial role in the discovery of key regulators, drug targets, and new biomarkers. However, similar to non-coding RNAs regarded as the ‘dark matter’ in sequence, some non-DEGs may be involved in the essential biological processes of disease progression and should not be ignored. It has been reported that some dark genes’ are enriched in key functional pathways (Han et al., 2020) and perform well in prognosis (Liu et al., 2020). To discover such dark genes, the Kaplan–Meier (log-rank) survival analysis of sNMB values and that of gene expression were compared based on the signaling genes (top 5% of genes with the highest local sNMB values) that were not differentially expressed at the critical point. Figure 6 shows some dark genes for STAD, ESCA, and READ. Clearly, the dark genes perform well in prognosis and are strongly related to patient survival, not at the gene expression level but at the sNMB level. Other dark genes for the three datasets are presented in Supplementary material. These dark genes can be an indicator of patient prognosis and may be involved in the important biological processes that trigger critical deterioration. Therefore, the proposed method can help to identify new biomarkers and prognostic indicators in terms of sNMB scores.

Figure 6.

‘Dark genes’ are sensitive to the sNMB score. (A–C) Kaplan–Meier (log-rank) survival analysis of local sNMB values and gene expression for STAD (A), ESCA (B), and READ (C). The non-differential genes sensitive to the sNMB score are considered ‘dark genes’. The dark genes perform well in prognosis and are strongly related to patient survival at the sNMB level but not at the gene expression level.

Discussion

For most complex diseases, it is crucial to detect the early warning signal for sudden deterioration. However, the lack of samples in clinical and experimental practice is a general problem, which often fails most statistical approaches. Therefore, new approaches are needed to tackle the small-sample problem. In this study, the proposed single-sample method (the sNMB method) is applied to identify the tipping points or pre-deterioration stage before the occurrence of obvious symptoms and successfully identifies the pre-deterioration stage of complex diseases. Specifically, for the acute lung injury dataset, a significant change in the sNMB score indicates the critical stage of phosgene-induced acute lung injury before the deterioration into pulmonary edema. For the three tumor datasets (STAD, ESCA, and READ), the drastic transitions of the sNMB score signal the pre-disease stage before distant metastasis in stage IV. The successful detection of critical points for these biological datasets validates the effectiveness of the sNMB approach in identifying the criticality of complex diseases solely based on a single sample.

There are a few advantages to the sNMB method. First, compared with traditional biomarkers that aim to diagnose the deterioration stage based on the differential information of gene expression, the proposed method is capable of predicting the pre-deterioration stage based on the information of differential networks among biomolecules. Second, against a group of given reference samples, the sNMB method can identify the pre-deterioration stage or critical point using only a single sample, while the conventional DNB method requires multiple samples at each time point to evaluate its three statistical indices. In addition, the sNMB method not only detects general early warning signals of critical transition into the deterioration stage but also provides sNMB signaling biomarkers that are involved in key biological processes. Furthermore, by combining with dynamics prediction method (Chen et al., 2020), it may help to identify the future critical states based on omics data. Third, the sNMB method helps to reveal the dark genes, which are non-differential in their expression but sensitive to sNMB and perform well in prognosis. Finally, it should be noted that sNMB is a model-free method, which implies that the sNMB strategy does not involve feature selection or model/parameter training. In summary, we proposed a novel computational approach at the single-sample level that is helpful for elucidating the molecular mechanisms of disease progression at the network level, revealing new biomarkers (dark genes)-considered prognostic indicators, and providing a personalized pre-deterioration diagnosis.

Materials and methods

Theoretical background

The theoretical background of this study is the DNB theory. Generally, the dynamical process of a complex disease can be perceived as a time-dependent non-linear dynamical system, while sudden deterioration is regarded as a qualitative state shift at a bifurcation point (Scheffer et al., 2001). Its evolution is usually divided into three stages (Chen et al., 2012): (i) a stable normal stage with high robustness, (ii) a pre-disease stage with a high-sensitivity response to perturbations, which is a critical point just before disease onset or deterioration, and (iii) another stable disease stage with high robustness. The sNMB method is designed to detect an early warning signal of the critical transition from the before-deterioration stage to the deterioration stage. When the biological system approaches the critical point, there appears to be a group of variables defined as DNB molecules, which satisfy the following three statistical indices (Chen et al., 2012).

SD_in sharply increases, where SD_in represents the SD (coefficient of variation) for any DNB molecule;

PCC_in abruptly increases, where PCC_in represents the PCC between any two DNB molecules;

PCC_out rapidly decreases, where PCC_out represents the PCC between any DNB molecule and any non-DNB molecule.

From the properties of DNB molecules, the critical state transition of a system is actually indicated by a group of highly correlated and strongly fluctuating variables at the network level (Liu et al., 2017, 2019). Specifically, for the sub-network composed of some variables (DNB biomolecules), an obvious change in its network structure occurs when the system is close to the critical state, signaling the upcoming critical transition. By exploring the dynamic information of such a group of dominant variables at a network level, it is possible to predict the qualitative state transition. Our proposed sNMB method is designed to quantify the statistical perturbation triggered by every single sample against a group of given reference samples, which can accurately detect the early warning signals of critical transitions at the single-sample level.

Algorithm to identify the critical point based on the sNMB score

Given a set of reference samples (the samples from the normal cohort are regarded as the background, representing relatively healthy individuals), the following computational method is carried out to identify the pre-deterioration stage using only a single case sample.

[Step 1] Constructing a global template network 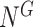by mapping the genes to the PPI network. (i) The PPI network is downloaded from the functional protein association networks (https://string-db.org). (ii) The interactions of the selected genes are incorporated by setting the threshold confidence level to 0.900. (iii) All the isolated nodes (nodes without any links to other nodes) are discarded.

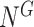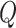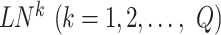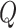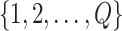[Step 2] Extracting each local network/sub-network from the global template network . Specifically, there are local networks if there are genes in the global template network 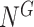. The local network 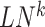is centered at a gene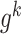, which has 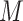first-order neighbors {, , , }.

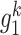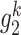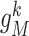[Step 3] Adding a single case sample to the reference samples. Specifically, if there exists 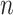samples in the reference group, then 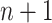mixed samples are obtained at each time point and viewed as a perturbation to 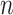reference samples. For the local network 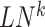, the differential local network 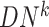is constructed by the difference in the corresponding SD and PCC between the reference and mixed samples (Figure 1B), i.e.

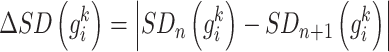(1)

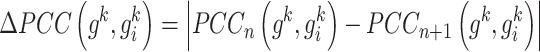(2),

where 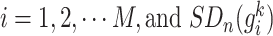and 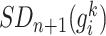represent the SD of the gene expression of gene 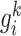based on 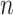reference samples and 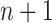mixed samples, respectively. 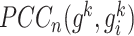and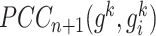 are the PCC between the center gene 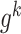and its first-order neighbor 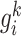based on 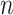reference samples and 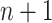mixed samples, respectively.

[Step 4] Calculating a local sNMB score for each local network. Specifically, for the local network 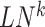centered at a gene 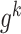, the corresponding local sNMB 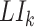is defined as follows.

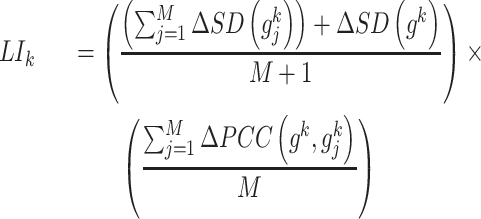(3),

where 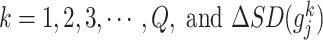and 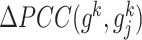are defined in Eq. (1) and Eq. (2), respectively.

[Step 5] Calculating the sNMB score for the single sample at time point 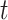. The sNMB score for the single sample is calculated based on a group of genes with the largest local sNMB score, i.e.

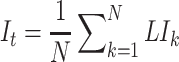(4),

where the constant 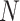is an adjustable parameter representing the number of the top 5% of genes with the largest local sNMB scores. 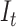is applied to quantify the overall perturbation caused by a single case sample.

According to the DNB theory, when the system approaches the critical stage, the sub-network (local network) composed of DNB molecules exhibits significant changes in terms of variance and correlation, thus resulting in significantly differential information between the pre-deterioration stage and the before-deterioration stage. Similar to previous studies (Zeng et al., 2014a,b), such a sub-network is viewed as a module, which can be utilized to detect the early warning signal of critical transition. Therefore, the composite indicator 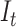would abruptly increase when the system is near the tipping point, signaling an upcoming critical transition.

Data processing and functional analysis

The proposed sNMB approach was applied to a numerical simulation and four real datasets, i.e. STAD, ESCA, and READ datasets from TCGA database (http://cancergenome.nih.gov) and an acute lung injury (GSE2565) dataset from the GEO database (http://www.ncbi.nlm.nih.gov/geo/). The tumor datasets are composed of both tumor and tumor-adjacent samples. The tumor samples are grouped into different stages according to the stage information of TCGA, and the samples lacking corresponding information are ignored. The cancer samples were grouped into seven stages (stages IA, IB, IC, IIA, IIB, IIIA, IIIB, and IV) for STAD, six stages (stages I, IB, IC, IIA, IIB, IIIA, IIIB, and IV) for ESCA, and four stages (stages I, II, III, and IV) for READ. The details of the sampling conditions are given in Supplementary Table S1. The tumor-adjacent samples that represent the relatively healthy condition are viewed as reference samples. For all these datasets, we discarded the probes without corresponding NCBI Entrez gene symbols. For each gene mapped by multiple probes, the average value was taken as its gene expression.

The analysis of pathways was performed with the KEGG database (https://www.kegg.jp). The enrichment analysis was performed by Metascape (Zhou et al., 2019) and the ClusterProfiler package (Yu et al., 2012). The functional results were based on web service tools from the Gene Ontology Consortium (http://geneontology.org) and client software from Ingenuity Pathway Analysis (IPA, http://www.ingenuity.com/products/ipa). The networks were visualized using Cytoscape.

Availability of data and materials

STAD, ESCA, and READ datasets are available from TCGA database (http://cancergenome.nih.gov). Acute lung injury dataset (GSE2565) is available from NCBI GEO database (http://www.ncbi.nlm.nih.gov/geo). The source code of the algorithm is provided at https://github.com/zhongjiayuan/sNMB_project.

Funding

This work was supported by the National Natural Science Foundation of China (12026608, 62172164, 12131020, and 12271180) and the Natural Science Foundation of Guangdong Province (2021A1515012317).

Conflict of interest

none declared.

Author contributions: P.C. and J.Z. conceived the research. J.Z. and H.L. performed the numerical simulation and real data analysis. All authors wrote the paper. All authors read and approved the final manuscript.