Simple Sensitivity Analysis for Control Selection Bias

To the Editor:

Case–control studies allow for efficient sampling schemes but are subject to bias when controls fail to represent the exposure distribution in the population from which the cases were sampled. Identifying this population, known as the study base, is often a challenge, and controls may be chosen out of convenience or to avoid other types of bias, such as exposure misclassification.¹ On the other hand, it may be straightforward to completely ascertain or randomly sample cases, as they may be enumerated in registries, hospital records, or other sampling frames.

When inappropriate control selection is suspected to have occurred, it can be informative to conduct a sensitivity analysis to investigate the possible extent of the resulting bias. In this letter, we show that a recently developed framework for simple sensitivity analysis^2–4 can be extended to this situation. We demonstrate with an example, and we provide a more detailed derivation in the eAppendix; http://links.lww.com/EDE/B670.

MacMahon et al⁵ conducted a case-control study of pancreatic cancer patients whom they compared with controls who were patients of the same physicians as the cases but who had different illnesses. After adjusting for age, cigarette smoking, and sex, they found an odds ratio of 2.7 (95% confidence interval = 1.6, 4.7) comparing drinkers of at least 3 cups per day to non-coffee drinkers.

However, soon after the study was published, multiple possible sources of bias were described.⁶ In particular, many of the control patients had gastrointestinal disorders, which the investigators failed to account for. If the controls drank less coffee than the general source population due to their illnesses, selection bias would result, exaggerating the association between coffee and pancreatic cancer.

To quantify the possible size of this bias, consider the ratio of the observable odds ratio from case–control data (OR_obs) to the odds ratio that would have been estimated had the entire study base been sampled (OR_true). For simplicity, assume that any bias from the case–control study is due to poor control selection.

It is possible to derive a bound similar to that in Smith and VanderWeele⁴ but with different definitions for the parameters resulting from the different causal structure (Figure) and estimand of interest. Specifically, if we assume that selection (S = 1) of cases (Y = 1) is independent of exposure status (A ∈{01,}) (possibly conditional on measured covariates C), but that control (Y = 0) selection is not independent of exposure without additionally conditioning on unmeasured factor(s) U, then:

$$\begin{gathered} O{R}_{\text{obs}}/O{R}_{\text{true}}\le \left\{\frac{R{R}_{U{A}_1}\times R{R}_{S_{0}U}}{R{R}_{U{A}_1}+R{R}_{S_{0}U}-1}\right\}\times \\ \left\{\frac{R{R}_{U{A}_0}\times R{R}_{S_{1}U}}{R{R}_{U{A}_0}+R{R}_{S_{1}U}-1}\right\} \end{gathered}$$

Where

$$R{R}_{U{A}_1}=\frac{\underset{u}{\max }\mathrm{Pr}(A=1\mid Y=0,u,c)}{\underset{u}{\min }\mathrm{Pr}(A=1\mid Y=0,u,c)}$$

$$R{R}_{U{A}_0}=\frac{\underset{u}{\max }\mathrm{Pr}(A=0\mid Y=0,u,c)}{\underset{u}{\min }\mathrm{Pr}(A=0\mid Y=0,u,c)}$$

$$R{R}_{S_{1}U}=\underset{u}{\max }\frac{\mathrm{Pr}(U=u\mid Y=0,S=1,c)}{\mathrm{Pr}(U=u\mid Y=0,S=0,c)}$$

$$R{R}_{S_{0}U}=\underset{u}{\max }\frac{\mathrm{Pr}(U=u\mid Y=0,S=0,c)}{\mathrm{Pr}(U=u\mid Y=0,S=1,c)}.$$

To understand these parameters, suppose that U represents a binary indicator of gastrointestinal illness that affects coffee drinking and also makes hospital visits (and therefore selection as a control) more likely. With respect to the example, $R{R}_{U{A}_1}$ describes the increased probability of drinking ≥3 cups of coffee per day in eligible controls without gastrointestinal disorders compared with those with gastrointestinal disorders, $R{R}_{U{A}_0}$ is the increased probability of no coffee drinking in eligible controls with gastrointestinal disorders compared with those without gastrointestinal disorders, $R{R}_{S_{1}U}$ is the increased probability of gastrointestinal disorders in controls who were selected for the study compared with those who were not, and $R{R}_{S_{0}U}$ is the increased probability of a healthy GI system in controls who were not selected for the study compared with those who were selected.

FIGURE.

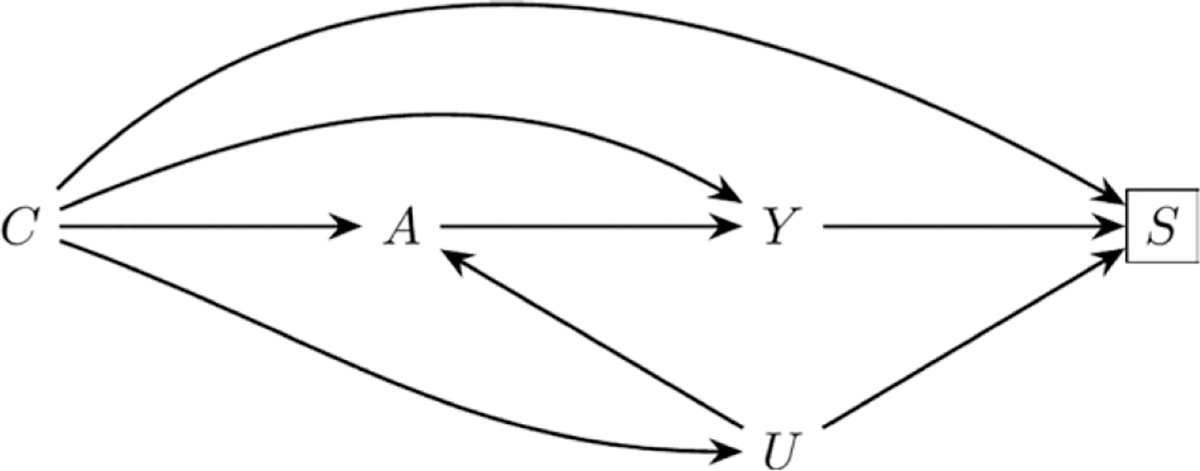
A directed acyclic graph describing a causal structure that could lead to selection bias. In the example in the text, A is coffee consumption, Y is pancreatic cancer, S is selection into the study, C is measured covariates, and U is gastrointestinal disorders.

We could propose various values for these parameters to “correct” for, or bound, selection bias. For example, suppose that among eligible controls with gastrointestinal disorders, only 5% drink at least 3 cups of coffee daily. However, among those with healthy gastrointestinal tracts, 30% drink that amount. Then $R{R}_{U{A}_1}=0.\mathrm{3/0}.05=6$ and $R{R}_{U{A}_0}=0.\mathrm{95/0}.7=1.3\text{6}$. Next suppose that among selected controls, the prevalence of gastrointestinal disorders is 0.45, but among nonselected eligible controls, it is 0.1. Assuming for the purposes of the example that gastrointestinal disorders is binary, then $R{R}_{S_{1}U}=\text{0}.\mathrm{45/0}.1=4.5$ and $R{R}_{S_{0}U}=0.\mathrm{9/0}.55=1.64$, then using these values in the formula for bound above, we would obtain 1.87. Thus we would have OR_true ≥2.7 / 1.87. = 1.44., where 2.7 was the observed odds ratio and 1.87 the bound constructed from the proposed parameters. In other words, if we assume that eligible study participants outside the hospital had a 10% prevalence of gastrointestinal disorders and those without such disorders were 6 times more likely to be heavy coffee drinkers than those with such disorders, then had they been included in the sampling frame, 1.44 is a lower bound for the estimate of the odds ratio relating coffee drinking and pancreatic cancer, conditional on sex, age, and smoking status.

We could repeat this exercise with a range of other values or allow for a more complex unmeasured factor (e.g., severe gastrointestinal disorder, mild discomfort, healthy gastrointestinal tract), as well as repeat with the lower bound of the confidence interval.

To make this type of sensitivity analysis easy to perform, we have created an online calculator available at http://selection-bias.louisahsmith.com.