Application of Bayesian approaches in drug development: starting a virtuous cycle

Abstract

The pharmaceutical industry and its global regulators have routinely used frequentist statistical methods, such as null hypothesis significance testing and p values, for evaluation and approval of new treatments. The clinical drug development process, however, with its accumulation of data over time, can be well suited for the use of Bayesian statistical approaches that explicitly incorporate existing data into clinical trial design, analysis and decision-making. Such approaches, if used appropriately, have the potential to substantially reduce the time and cost of bringing innovative medicines to patients, as well as to reduce the exposure of patients in clinical trials to ineffective or unsafe treatment regimens. Nevertheless, despite advances in Bayesian methodology, the availability of the necessary computational power and growing amounts of relevant existing data that could be used, Bayesian methods remain underused in the clinical development and regulatory review of new therapies. Here, we highlight the value of Bayesian methods in drug development, discuss barriers to their application and recommend approaches to address them. Our aim is to engage stakeholders in the process of considering when the use of existing data is appropriate and how Bayesian methods can be implemented more routinely as an effective tool for doing so.

Bayesian statistical approaches that explicitly incorporate existing data into clinical trial design, analysis and decision-making have the potential to substantially reduce the time and cost of bringing new medicines to patients in some contexts, but remain underused. This Perspective highlights the value of Bayesian methods in drug development, discusses barriers to their application and recommends approaches to address them.

Introduction

The regulatory requirement for substantial evidence of safety and efficacy to support approval by the FDA was codified into US law in 1962, with substantial evidence defined as “evidence consisting of adequate and well-controlled investigations, including clinical investigations, by experts qualified by scientific training and experience”^{1, 2}. Similar concepts are encoded in laws, regulations or guidelines in other countries. Over time, this and other regulations have generally been interpreted as requiring independent replication in two trials in the same or highly related medical conditions or patient populations, with design and analysis based on frequentist statistical methods (Box 1). Importantly, the use of frequentist methods, such as null hypothesis significance testing and reliance on p values, especially the 0.05 level of significance, has stemmed from convention and is not an explicit component of the law or any derivative regulation and guidance.

These regulatory standards are based on sound principles and have stood for decades. Nevertheless, public health needs and drug development targets have evolved, with increased focus on rare diseases and on stratified, targeted subsets of more common diseases based on improved understanding of pathophysiology of disease and developments in pharmacology, such as gene therapies and therapies targeted towards specific tumour biology. The ethical mandate to expose the fewest patients to ineffective or unsafe experimental treatments and to suboptimal control arm regimens remains. At the same time, a wealth of placebo-controlled clinical trial data has amassed, and health-care records data are both improved in quality and more readily available. Bayesian methods (Box 2) provide an intuitive yet sound quantitative and methodologically rigorous approach to incorporation of data from various sources into the design of new clinical trials, while appropriately reflecting and examining the inherent assumptions and uncertainties. This might allow the overall number of trial participants to be reduced, while maintaining the overall strength of evidence to demonstrate efficacy and safety of a new treatment. Use of such external information will not be appropriate in all contexts; for example, where the quality or relevance of external data cannot be established or where sensitivity analyses would not corroborate assumptions or reduce uncertainties on the integration of external data. There will be other circumstances, however, for which the use of high-quality external information is appropriate and has the ability to improve drug development.

Sixteen years ago, Berry³ provided an overview of Bayesian approaches in clinical trials with a plea for their expanded use and a prediction of accelerated adoption in drug development and approval by regulatory agencies. Our observation is that such progress has been minimal in mainstream development of new drugs and biologics, although many advances have been made in the review and approval of medical devices by the FDA⁴. This lack of progress has its roots in a range of factors, but, as we discuss later in this article, key factors include a lack of familiarity with these approaches and the related uncertainty about acceptance of evidence generated by using them.

Our aims with this article are thus to raise awareness of the value of Bayesian methods in drug development and for it to act as a call to involve stakeholders in the process to consider when the use of external data is appropriate and how Bayesian methods can be an effective tool for doing so. With these aims in mind, we first overview the principles of Bayesian inference and decision-making and their contrasts with the frequentist approach, and discuss various examples of the use of Bayesian approaches in clinical research. We then explore the barriers to their wider use and present a framework for deciding when Bayesian approaches may be more valuable than frequentist approaches. Finally, we provide recommendations for the incorporation of Bayesian methods in clinical drug development and regulatory decision-making.

Box 1 Frequentist statistics and clinical trials.

Frequentist statistics is a branch of statistical inference that covers a broad range of analysis approaches that are underpinned by the frequency of events occurring as a basis for probability. For example, for a fair, six-sided die, the frequency or probability or likelihood that one will roll any individual number with such a die is 1 in 6.

In the context of this article, we focus primarily on null hypothesis statistical testing, in which the null hypothesis is assumed to be true (that is, a new treatment does not work) until the data from an experiment or clinical trial are deemed sufficiently incompatible with the null hypothesis that it is reasonable to ‘reject’ that hypothesis. The ‘sufficient data’ are often captured by computing a test statistic, which is an overall measure of the treatment effect, and its corresponding p value. The more deviant that test statistic is from what is expected under the null hypothesis, the less belief we have in the null hypothesis of no treatment effect. This is often referred to as ‘proof by contradiction’. Hypothetically, if one were to execute the same clinical trial many, many times, the p value can be interpreted as the frequency (that is, probability) with which one would observe such an extreme test statistic if indeed the null hypothesis were true. Thus, when a researcher rejects the null hypothesis with a p value of <0.05, they are tacitly stating that if they had done their experiment repeatedly (analogous to the repeated roll of a die), they would expect to get their results, as encapsulated by the test statistic value, 5% of the time or less if the null hypothesis were true.

In the context of drug research and development, the frequentist approach has served regulators reasonably well in limiting the approval of ineffective drugs (avoidance of the so-called type 1 error) but is not the only way to meet the substantial evidence requirement for approval. In fact, there is another statement in the FDA’s Code of Federal Regulation: “FDA is required to exercise its scientific judgment to determine the kind and quantity of data and information an applicant is required to provide for a particular drug to meet the statutory standards.”⁵⁶ To meet this standard, regulators have sometimes relied on a single well-conducted trial with compelling results that include, but are not necessarily limited to, large effect sizes, internal consistency of primary and secondary end points, and evidence of adequate control of sources of potential bias⁵⁷. Examples of this include trials for rare diseases, trials used to establish drug effects for disease states with considerable mortality or serious morbidity, or large, long-term outcome trials such as those used for cardiovascular disease. In these circumstances, other sources of evidence external to the trial under regulatory consideration are implicitly brought to bear on decisions made by regulators, such as the strength of the biological or pharmacological rationale for beneficial drug effects, and data external to the trial programme that are relevant to the research questions of interest.

Box 2 Thomas Bayes.

The Reverend Thomas Bayes lived in the early eighteenth century and, although having very few publications in science, mathematics or probability, was known and respected well enough to be elected a member of the Royal Society. His profound contribution to probability was published posthumously in the Philosophical Transactions of the Royal Society of London in 1763: ‘An essay towards solving a problem in the doctrine of chances’⁵⁸, in reference to Abraham de Moivre’s previous seminal work Doctrine of Chances first published in 1711. At the time, mathematicians were developing notions of probability of the occurrence of an event given some assumed probability model.

Today, we talk about the frequentist approach in which we calculate the probability of an event given some hypothesized model. Most notably for this article, hypothesis testing is a bedrock of frequentist statistical inference with p values calculated as the probability that a test statistic exceeds a critical threshold (c) assuming the null hypothesis is true. In symbolic language P(T > c | H₀), which is sometimes stated colloquially as the probability of observing the data given the null hypothesis or P(D | H₀). Bayes solved the inverse probability problem; that is, what is the probability of the null hypothesis being true given the observed data, written as P(H₀ | D). This is argued to be more relevant to understanding the true state of nature. That is, it represents the philosophical perspective that we can only observe data (natural phenomena) and from that we must infer what is likely to be true (the underlying model or state of nature). Despite solving this fundamental problem in probability — a problem that Bayes’s contemporaries and subsequent mathematicians grappled with — it is worth noting that Bayes’s paper and solution did not gain notoriety or prominence for many years and was left unrecognized and underused for centuries. Excellent historical perspectives are given in The Theory That Would Not Die⁵⁹ with a deeper philosophical preference for the Bayesian approach argued in Bernoulli’s Fallacy⁶⁰.

Principles of Bayesian inference and decision-making

There are two fundamental distinctions between frequentist and Bayesian approaches. The first is shown in Fig. 1: the frequentist approach makes inferences within a single experiment, whereas the Bayesian approach synthesizes information across experiments or other sources of information to make probability statements about whether a hypothesis is likely to be true or not. Second, and more subtly, Bayesian statistics differ from frequentist statistics in the way that they provide evidence to answer research questions. Generally, frequentist approaches make inferences concerning the probability (P) of observing a test statistic with a value that exceeds a certain threshold based on the data (D), assuming some specified hypothesis (H) is true, annotated as P(D | H). This probability is called the p value. Frequentist hypothesis testing can only provide indirect answers, as one assumes that the null hypothesis is true until data that refute the hypothesis are observed in an adequate scientific experiment or clinical trial. By contrast, Bayesian statistics can be used to answer research questions directly by determining how likely the specified hypothesis is to be true given prior evidence (D₀) about the hypothesis combined with the accumulated data (D_N) from the current experiment, annotated as P(H | D₀,D_N). This provides direct evidence to answer the research question. This subtle shift in mathematical notation has enormous consequences logically and for statistical inference, as the two statistical approaches answer fundamentally different questions. Many interpret the p value — P(D | H) — as the probability that the null hypothesis is true, which it is not. To be clear, as with all conditional probabilities, P(H | D) ≠ 1 – P(D | H).

Fig. 1. Comparison between Bayesian and frequentist approaches.

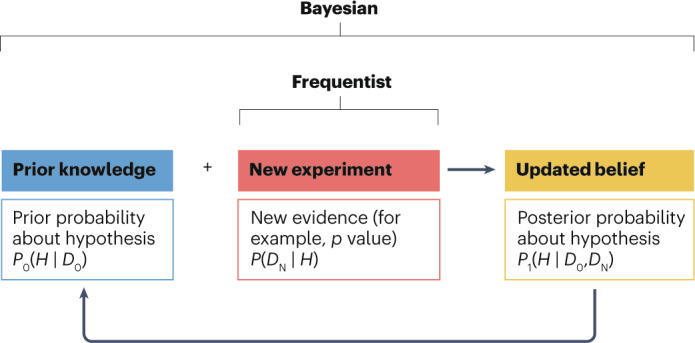
The frequentist approach evaluates evidence from a single new experiment, most often using a p value as a measure for deciding whether a hypothesis is true or false. The Bayesian approach formally and statistically quantifies prior knowledge (D₀) about a hypothesis (H) in the form of a prior probability (P₀), which is then combined with the evidence from a new experiment (D_N) to compute a posterior probability (P₁) about the veracity of that hypothesis. The posterior probability can be recycled as input to form the prior for a subsequent experiment, thereby creating a virtuous cycle of synthesizing scientific knowledge about a hypothesis.

It is worth noting that the Bayesian approach is a way of synthesizing information into a holistic analysis to evaluate the veracity of the null or alternative hypothesis as part of the inference for the current clinical trial. In that sense, it is akin to a meta-analysis. When assessing the totality of evidence using frequentist approaches, viewing each clinical trial result separately allows for an assessment of independent replication of results — an important element of the scientific process — but may also involve subjective interpretations. There are frequentist meta-analytical methods for synthesizing data across trials to make an overall inference about a hypothesis, but such analyses and resulting statistical inference are carried out separately from the current clinical trial. The same issues are present for both the Bayesian analysis and the frequentist meta-analysis, such as which historical trials should be incorporated into the analysis and what weight they should be given, but the Bayesian approach has two epistemological advantages. First, the Bayesian approach forces the discipline of stating the prior belief before the current clinical trial is done and thus is not biased by the observed results of the current trial. This prespecification can be subjective but is a key element for generating credible statistical inference. By contrast, formal frequentist meta-analyses are generally carried out after the data from the current clinical trial are known, and thus may be influenced by what has been observed in the current trial. Second, Bayesian approaches can allow for more general sources of information and subjective input (for example, based on the mechanism of action of the treatment, the idiosyncratic nature of the disease or patient population under study) for creating a prior distribution.

For readers interested in learning more, Kruschke and Liddell⁵ offer an introductory review to Bayes, and Ruberg⁶ provides a conceptual framework for comparing and contrasting frequentist and Bayesian approaches. In the remainder of this section, we overview two key aspects of Bayesian analysis — the prior and posterior distributions — and use published examples to highlight the differences between frequentist and Bayesian approaches.

Prior distributions

The first step in a Bayesian analysis plan is the definition of a prior probability distribution of the parameter for which we wish to make an inference based on the observed data, such as a treatment effect size — henceforth called the prior. This requires careful consideration of extant sources of information, such as previous clinical trials of the experimental treatment of interest, preclinical data comparing the experimental treatment with other treatments, clinical trials of other treatments in the same mechanistic class and disease state, and observational outcomes data in the patient population and disease state. There are many dimensions for deciding which prior data are used in a Bayesian analysis to make a fair or unbiased assessment of a treatment effect: the source and quality of the data (for example, controlled clinical trial or electronic medical record), how contemporaneous they are with the new experiment, the clinical setting in which the data were collected (for example, geography or community or research hospital), as well as many other features related to the patient populations involved and the administration of the treatment under consideration. Alternatively, one can define a family of prior distributions that represent a reasonable range of treatment effect possibilities, as in an example discussed below and shown in Fig. 2a.

Fig. 2. Prior distributions in Bayesian clinical trials.

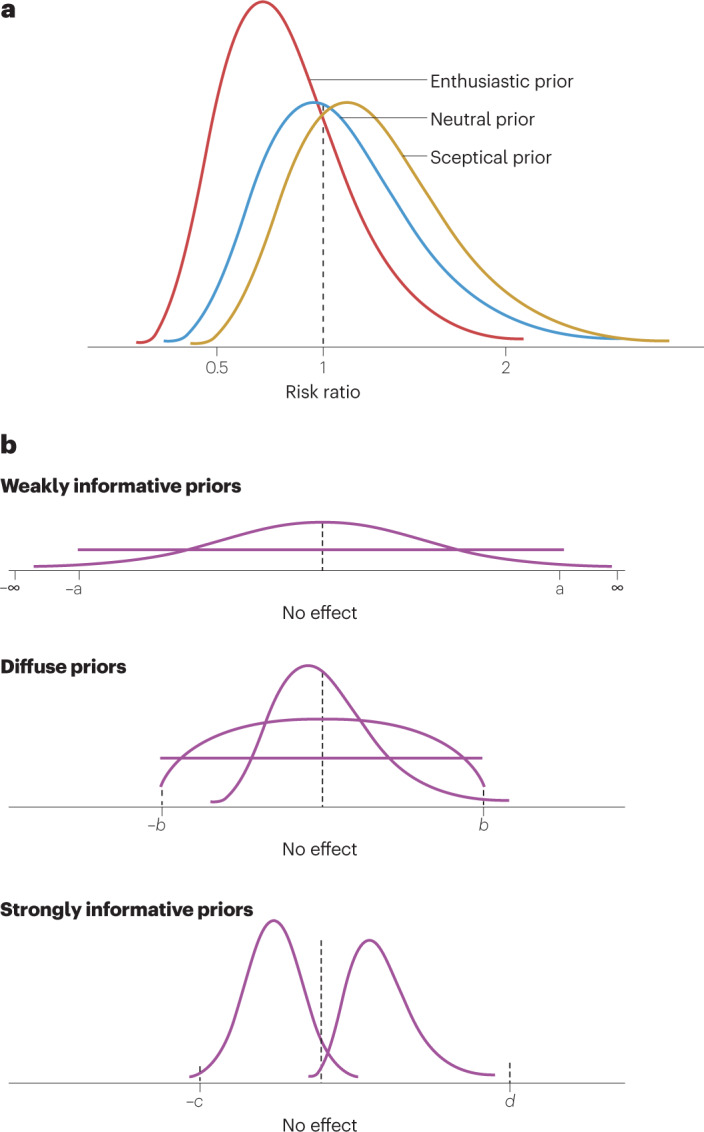
a, When using a risk ratio (RR), or any other ratio such as hazard ratio or relative risk, a value of 1 represents no difference in treatment outcomes. A neutral prior distribution (blue) reflects this and has equal probability above and below 1 (that is, the median is located at 1), conferring no preference for whether a new treatment is more effective (RR < 1) or less effective (RR > 1) than the control treatment. An enthusiastic prior (red probability distribution) is shifted to RR values <1, indicating a prior belief that the treatment effect is positive, while allowing for the possibility that the RR could be >1 (as represented by the area under the distribution curve that is above 1). A sceptical prior (gold probability distribution) is the reverse: it is shifted to the right and has greater probability of a detrimental effect (RR > 1) while allowing for the possibility that the RR is <1, as represented by the area under the probability curve for RR < 1. b, Examples of prior probability distributions for use in a Bayesian analysis. Each curve represents a distinct example of a prior distribution. The ‘no-effect’ point represents no difference in outcome between a treatment and a control. This can be a difference in treatment responses (means or proportions) that is zero or a ratio (relative risk, hazard ratio) that is 1.

Prior distributions can be symmetrical or skewed, mounded, bimodal or flat, depending on the available data or other information about the possible values of the parameter, and there are many ways to define them. For example, a treatment effect can be expressed as a difference in mean responses, difference in proportion of patients responding or some measure of relative effect such as a risk ratio (RR), relative risk, odds ratio or hazard ratio. Priors can be described in colloquial terms such as non-informative, diffuse, vague or informative, but ultimately must be defined in mathematical terms. In reality, priors exist on a continuum of information that they convey. Every prior distribution contains some information; it is only a matter of degree. For example, a uniform distribution with a wide range of possible values or a normal distribution with a very large variance relative to the treatment effect parameter of interest might be described informally as non-informative prior probability distributions, but indeed such priors convey some information about the location and range of possible values for the parameter of interest. As such, they are also known more appropriately as weakly informative priors (Fig. 2b). They are generally centred at the no-effect value of the parameter (for example, mean difference of 0 or RR of 1). So-called diffuse or vague prior probability distributions generally refer to distributions that have a wide spread of possible values but not as wide as weakly informative priors. Strongly informative priors generally are centred at a treatment parameter value that demonstrates a treatment benefit or a treatment disadvantage. When there is a considerable amount of relevant data external to the current clinical trial, such a prior distribution may be warranted or at least considered in any sensitivity analysis.

Once a prior distribution is defined, another necessary component of the subsequent Bayesian analysis is the weight given to that prior. If data used to create the prior distribution are minimal, inconsistent or only indirectly connected to the current study (for example, a different patient population, disease severity or dosing regimen), then the prior distribution may be given less weight relative to the observed data from the current clinical trial. By contrast, if the data used for creating the prior distribution are very closely related to the current clinical trial (for example, using another phase II or phase III trial of the same treatment in the same population with the same dose for the same disease state), then the prior may be given greater weight in the final analysis of the current clinical trial. The weight assigned to the prior distribution is often described as ‘borrowing’, reflecting the amount of information borrowed from previous data for the analysis of the current data.

Posterior distributions

A posterior probability distribution describes a range of likely treatment effect values as a result of the current experiment and is derived mathematically by combining information from the prior probability distribution and the newly collected data. Conceptually, it is a weighted average of what is known before the current experiment and what is observed in the current experiment, where the weights depend on the prior distribution (how informative it is) and the sample size and variability in the current experiment (small sample size and more variability carry less weight). The peak of the posterior distribution lies between the peaks of the prior distribution and the estimated distribution of the observed data. This is known as shrinkage and can be seen as a formal mechanism for guarding against the possibility of an observed random high or random low treatment effect that can occur in any individual clinical trial (Fig. 3a). Conversely, a mis-specified or biased prior can pull the observed data away from what the true treatment effect might be.

Fig. 3. Posterior distributions in Bayesian clinical trials.

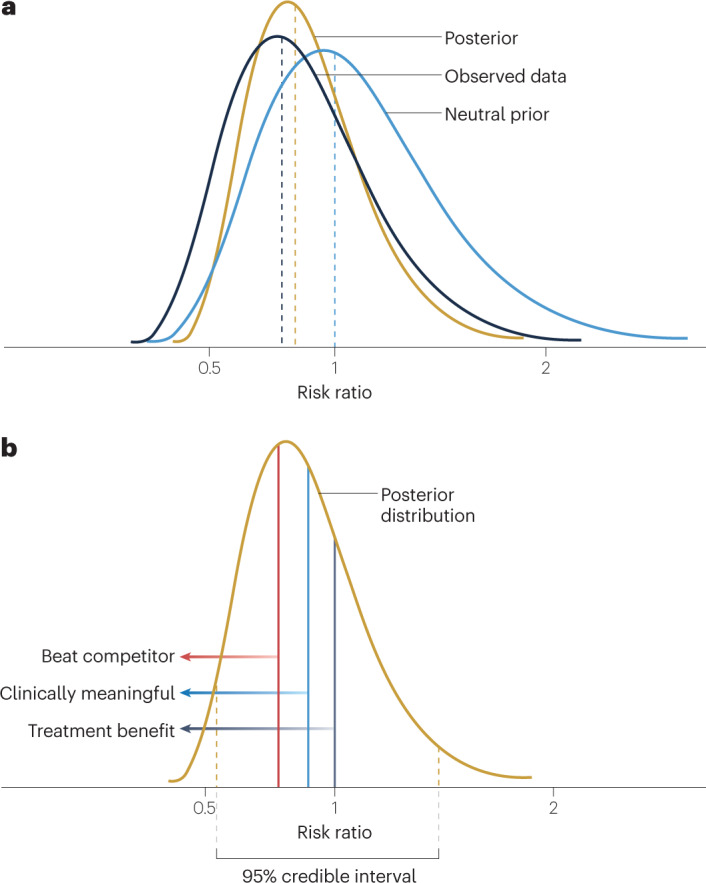
a, The posterior distribution of the treatment effect parameter is a description of the uncertainty of the treatment effect. It is derived statistically from the prior distribution of the treatment effect and the estimated probability distribution of the observed data. b, The posterior distribution of the treatment effect parameter (risk ratio in this depiction) captures the updated description of the uncertainty of the treatment effect. The 95% credible interval has upper and lower bounds such that there is a 95% probability that the true risk ratio lies between those bounds. The posterior distribution can be used to calculate direct probability statements about the risk ratio based on the area under the posterior distribution curve, as depicted by the different vertical lines. In this case, a risk ratio of <1 is indicative of a treatment benefit (dark grey line) and various other risk ratio values can be used to discern the probability of a clinically meaningful treatment effect (blue line) or a treatment effect that is superior to a competitor (red line).

There is a wide variety of Bayesian methods for combining the prior and the observed data, and some adapt the use of the prior distribution according to how consistent it is with the current experiment. What prior data or information to borrow and how much weight to give to the borrowed data that are external to the planned clinical trial are topics that require significant and careful consideration in conjunction with regulatory agencies. This is discussed in more detail subsequently.

Once the posterior distribution is defined, probability statements can be made directly relating to the treatment effect (parameter of interest) using the area under the posterior distribution curve (Fig. 3b). Most notably, a credible interval is a range of parameter values within which the unknown parameter value falls with a specified probability. For instance, if we constructed a 95% credible interval, we would say that there is a 95% probability that the value of the unknown parameter falls in this credible interval. This is distinct from a confidence interval in the frequentist paradigm. A 95% confidence interval does not mean that there is a 95% probability that the unknown parameter is contained in that interval. Instead, it must be explained in a hypothetical manner. If we were to repeat the same experiment (clinical trial) many times and to calculate the 95% confidence interval for each repeated experiment, the expected frequency with which those 95% confidence intervals contain the true unknown parameter value (treatment effect) is 95%. Unfortunately, confidence intervals are often mistakenly interpreted as credible intervals, just as p values are frequently misconstrued as the probability that the null hypothesis is true.

Unlike p values, the posterior probabilities calculated from the posterior distribution of the treatment effect can be interpreted directly as probabilities related to the treatment effect. As in Fig. 3b, the area under the curve to the left of 1 represents the probability that there is a beneficial treatment effect (that is, the null hypothesis is false). Furthermore, suppose one were to define a clinically meaningful treatment effect to be a RR of <0.85, or, for making business decisions, that a RR of <0.70 was necessary to be competitive with other available treatments. Then, the area under the distribution curve can be easily calculated and a direct probability statement can be made regarding the likelihood of these assertions about the treatment effect parameter.

Examples of application

Therapeutic hypothermia

Multiple clinical trials had demonstrated the benefit of therapeutic hypothermia in newborns with hypoxic–ischaemic encephalopathy (HIE) when initiated within 6 h of birth, but there can be practical difficulties with such a rapid intervention. Thus, there was interest in assessing the effect of initiating therapeutic hypothermia at time points up to 24 h after birth. Because this is a rare condition, enrolment was a concern and traditional frequentist approaches to designing a randomized controlled trial (RCT) based on power and resulting sample size seemed infeasible.

A Bayesian approach was therefore specified in which information would be borrowed from historical data to create three prior probability distributions for the treatment effect sizes: a sceptical prior, an enthusiastic prior and a neutral prior⁷ (Fig. 2a). The enthusiastic prior had mean RR = 0.72 based on historical data, the neutral prior had mean RR = 1.0 and the sceptical prior had mean RR = 1.10, allowing for the fact that therapeutic hypothermia may produce worse outcomes if initiated too late (Fig. 2a). For each prior, the spread of the distribution was such that 95% of the probability of the RR distribution lay in the interval 0.5–2.0. These represented plausible values for the expected outcome of the trial — 0.5 being a very positive benefit and 2.0 being a substantial detriment of therapeutic hypothermia if initiated too late after birth. The primary outcome was death or disability (predefined by specific developmental criteria) at 18–22 months of age. Newborns who met inclusion criteria were randomized to receive therapeutic hypothermia (n = 83) or non-cooling standard of care (n = 85) and rigorously followed through the planned completion of the trial.

The primary results of the trial were expressed as an estimated RR and a probability that therapeutic hypothermia initiated 6–24 h after birth resulted in better outcomes at 18–22 months than the non-cooling standard of care. That is, among newborns with HIE, the results indicated that there was a RR = 0.86 (95% credible interval: 0.58–1.29) and a 76% chance that therapeutic hypothermia reduced mortality and disability relative to the non-cooling standard of care when using a neutral prior (Fig. 2b). Furthermore, because a Bayesian analysis produces a posterior distribution of possible treatment effect sizes, other clinically meaningful questions could be answered. In this case, the authors noted that a 2% reduction in mortality or moderate–severe disability was clinically meaningful, and the Bayesian analysis inferred that there was a 64% probability that therapeutic hypothermia met that goal.

Interestingly, the authors reported the results of the frequentist analysis, which affords us the opportunity to compare the two inferential paradigms. The frequentist analysis yielded a RR of 0.81 with a 95% CI of 0.44–1.51, and although it was unreported, p ≈ 0.42 based on the width of this confidence interval, which includes RR = 1. Two comments are noteworthy here. First, the frequentist estimate of RR is smaller than the Bayesian estimate, suggesting a larger beneficial effect of therapeutic hypothermia. There is often a concern that Bayesian methods provide a shortcut or impose a lower standard of evidence for assessing a treatment effect, and this example shows that using data external to the current trial does not necessarily imply that a statistical result will be more favourable to an experimental treatment. In fact, for any single clinical trial, the observed results can vary considerably from what the true treatment effect might be. Thus, there are situations in which a neutral or conservative prior distribution shrinks a potentially random high estimate of the treatment effect from the current clinical trial to a smaller effect estimate. Furthermore, the application of a Bayesian approach that properly recognizes uncertainty in the treatment effect, as represented by a prior probability distribution, might lead to a larger sample size to generate compelling evidence than a frequentist experiment that does not reflect that same uncertainty in the design. Second, the credible interval can be interpreted directly as having a 95% probability of containing the true RR value. Although it is empirically smaller than the frequentist confidence interval, the credible interval and confidence interval are derived in fundamentally different ways and comparison of their widths is not appropriate. Nonetheless, another potential benefit of the Bayesian approach is that it incorporates additional information into the inference, although a smaller credible interval is not always guaranteed.

The choice of a prior is perhaps one of the most controversial and troubling aspects of Bayesian analysis for those steeped in the frequentist paradigm. This is why the authors of the HIE research prespecified three possible prior distributions at the start of their study. Although some view having a range of priors as a drawback of the Bayesian approach, others view it as an advantage, as different individuals or institutions can make decisions based on what is relevant to their circumstances or perspective. Of course, in regulated clinical development of a new treatment, the sponsor would be required to prespecify the prior, with regulatory agreement, for the primary analysis and interpretation of the clinical trial, with a range of prior distributions that includes sceptical and enthusiastic for sensitivity analyses.

Vaccines for COVID-19

In early 2020, severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infection became a global pandemic, and the resulting coronavirus disease 2019 (COVID-19) subsequently affected many millions of people. There was an urgent need for a safe and effective vaccine. The worldwide community of health officials and regulators discussed and debated what would constitute an effective vaccine, and the FDA issued a guidance in June 2020 that stated, “the primary efficacy endpoint point estimate for a placebo-controlled efficacy trial should be at least 50%, and the statistical success criterion should be that the lower bound of the appropriately alpha-adjusted confidence interval around the primary efficacy endpoint point estimate is >30%.”⁸ That is, a sponsor could demonstrate a highly statistically significant vaccine effect with a very large trial, say p < 0.001, but that effect may not be meaningful from a public health perspective for containing the spread of the virus. Thus, there was a need to quantify the level of confidence that the true vaccine effect is sufficiently large.

Pfizer and BioNTech sponsored a trial of their BNT162b2 mRNA vaccine for prevention of COVID-19. For the phase III portion of their clinical programme, the primary efficacy analysis was based on the Bayesian posterior probability that vaccine efficacy was >30%. The success criterion was explicitly defined as P(vaccine efficacy > 30%) >98.6%. That is, regardless of any p value calculation, the study success criterion was a 98.6% probability that the true vaccine efficacy (VE) was greater than the public health minimum requirement of 30% (Box 3). This illustrates that a Bayesian analysis requires a probability statement for decision-making that is directly related to the magnitude of the treatment effect, unlike the arbitrary, yet conventional, p value < 0.05. The prior distribution for VE was centred at 30%, which was considered pessimistic given other data and/or information on the vaccine from earlier phases, and encompassed a very broad range of possible VE values, including the potential for an increase in infection rates from the vaccine. Thus, the prespecified statistical analysis plan for the phase III trial described the prior as “minimally informative”.

There were more than 43,000 patients randomized and 36,523 evaluable for efficacy at the time the first results were published⁹. The results from the study that were used for an emergency use authorization application to the FDA noted that the Bayesian posterior probability for the true VE exceeding the predefined lower limit of 30% was >99.99%, far exceeding the 98.6% success criterion. In this situation, the dataset is very large and the observed vaccine effect so dramatic that the prior distribution had minimal impact on the decision about vaccine efficacy. That is, almost any reasonable prior distribution would have led to the same conclusion. It is worth noting that with these very compelling data, the frequentist analysis of the data would also have come to the same conclusion. Of course, the vaccine was rapidly authorized by regulators, and the Bayesian approach was in no way seen as a shortcut or a lowering of the evidentiary bar for approval. In fact, one of the advantages of the Bayesian approach is that it provided an easily communicated way to quantify the level of certainty that the vaccine would be a considerable public health benefit. Further benefits to using a Bayesian approach are elucidated in other examples discussed below.

Box 3 Decision-making based on Bayesian approaches.

When using Bayesian inference to make decisions, probability statements are often constructed to express the likelihood of achieving some clinically meaningful effect size (CM). If T is the desired minimum probability, or threshold, of that effect size, then a decision rule can be expressed as P(true effect > CM) > T, where the probability P is derived from the Bayesian posterior probability distribution. The choice of CM and T depend on the disease state, the degree of unmet medical need, the patient population and so on. One can define a low value for CM but a high probability threshold T in order to be highly confident that a new treatment is minimally effective. Conversely, one can define a high CM value but allow for a lower T value about such a large effect. Any combination of CM and T can be chosen so long as they create desirable operating characteristics in the context of the decision to be made.

One desirable operating characteristic in drug development is to maintain a low probability of a false positive finding, known as a type 1 error. In a frequentist drug development programme, phase III trials are designed with a significance level of 0.05 or less to control the type 1 error. The success of the phase III trial and the effectiveness of the new treatment culminate by observing a p value lower than the planned significance level in at least one trial, and most often in two. If two phase III trials with a planned significance level of 0.05 produce what appear to be conflicting results, say p = 0.02 and p = 0.09, the frequentist decision is generally that the drug development programme failed to replicate results, and the demonstration of a treatment effect is insufficient.

By contrast, for a Bayesian drug development programme, information is continually updated as the posterior distribution of treatment effect from one phase or trial is used as partial input for the subsequent trials. The output from the final phase III trial is then a single posterior probability of a positive treatment effect derived from all trials. An important question is: what is the posterior probability threshold T for deciding whether that development programme demonstrated substantial evidence? This is a topic beyond the scope of this article, but we give it brief consideration here.

Suppose a larger value for the treatment effect represents a treatment benefit. Regulatory authorities generally work from the assumption that the treatment effect is zero, consistent with the frequentist perspective, and want to evaluate a Bayesian decision rule of the form: P(true effect > 0) > T. However, the Bayesian perspective allows for some non-zero probability that the null hypothesis is false. This conflict is ‘resolved’ by the selection of an appropriate posterior probability threshold T in the decision rule. That is, mathematical calculations or simulations are done assuming that the null hypothesis is true and then calibrating the posterior probability T from the Bayesian analysis such that the decision rule P(true effect > 0) > T is achieved with an acceptably low probability, say 0.05. Although this combination of perspectives may be philosophically at odds with each other, perhaps it represents a bridge between frequentist and Bayesian thinking and a step forwards in the use of more Bayesian analysis.

Under this construct for statistical decision-making, the value of T is generally quite large, indicating a high level of confidence that the true treatment effect exceeds zero. This single posterior probability may give more insight into the treatment effect and resolve the apparent discrepancy noted above when two p values are on opposite sides of 0.05 (ref. ¹³).

The Bayesian approach is quite common inside pharmaceutical companies when making go/no-go decisions about advancing a new treatment. Furthermore, such decision criteria are quite commonly used in interim analysis of large or long-term clinical trials to make decisions about whether to continue a trial or to invoke a prespecified change in an adaptive trial.

In the Pfizer–BioNTech phase III COVID-19 vaccine study, a stopping rule was defined for the theoretical possibility that the vaccine efficacy (VE) would be small relative to the placebo⁹. At any of four interim analyses, if the probability of meeting the success criteria at the end of the trial was <5%, then the trial was to be stopped for futility. Conversely, the statistical analysis plan stated a decision rule that if P(VE > 30%) > 99.5% at any of the four interim analyses, then the study could be stopped and declared a success. Just as the frequentist approach requires adjusted significance levels to be <0.05 to declare a positive treatment effect at an interim analysis, the Bayesian approach generally uses a higher threshold probability at the interim analyses (99.5%) than at the final analysis (98.6%) as a success criterion. Although a full Bayesian analysis does not require an adjustment to the interim posterior probability threshold as the frequentist approach requires adjusted significance levels, this is usually done to meet regulatory needs. A discussion of the related mathematical and philosophical concepts is beyond the scope of this article.

Examples of how Bayesian methods are being used effectively

The goal of discussing selected examples in this section is to demystify and normalize the use of Bayesian methods in various scenarios and demonstrate that the risk of using these approaches may not be as high as perceived by some stakeholders, and the advantages may be relevant for efficient drug development. Additional examples of the use of Bayesian approaches in the regulatory setting have been described elsewhere^{10, 11}.

Generating substantial evidence

In many cases, having multiple studies to demonstrate drug efficacy and safety is required by regulators because of the scientific value of replication. There are several ways to undertake a multiple-study drug development programme, including conducting studies in parallel or in sequence. When carrying out clinical studies in sequence, which is natural and most common in drug development, Bayesian methods could provide a beneficial approach for generating substantial evidence of the treatment effect at reduced cost and time of development without sacrificing scientific credibility.

In the case of phase II studies that are carried out as a precursor to phase III, valuable data on the dose, the patient population and the posterior distribution of the treatment effect size on a primary response variable of interest can be used as a prior for phase III planning. Compared with phase II data, the phase III data will be generated on the same treatment, with a highly similar patient population, by the same sponsor, in a nearly contemporaneous time frame, often involving some of the same investigative sites. Thus, the phase II data can often be highly relevant for creating a prior for phase III, even if aspects such as the inclusion and exclusion (I/E) criteria change, or the treatment formulations change slightly. Such refinements in phase III can be easily handled by using discounting factors (that is, less weight or less borrowing of prior information) in the Bayesian analysis that are mutually agreeable to sponsor and regulator. In general, the degree to which the sample size of phase III studies can be reduced while maintaining suitably high power is directly related to the quantity and quality of the phase II data¹² as well as the amount of borrowing of that information, which can be mathematically defined in the Bayesian analysis. Marked changes from phase II to phase III in any of the clinical trial design factors would result in larger discounting of the phase II data. Ruberg et al.¹³ present an example of this approach with further details and considerations.

When phase III studies are carried out sequentially — either two identical phase III studies carried out in sequence to defer cost and risk of development or phase III studies carried out in different disease states or patient populations (for example, sacubitril–valsartan in heart failure for reduced ejection fraction and subsequently in heart failure for preserved ejection fraction) — borrowing data and or information from initial phase III studies to form priors can also reduce the sample size, cost and time for subsequent clinical trials using a Bayesian approach, without reducing the quality of the inference about a beneficial treatment effect on the primary outcome. This potential reduction in sample size has further implications, especially in the evaluation of safety.

First, it is worth noting that even with the use of prior information and Bayesian approaches, some situations may still require large sample sizes — although smaller than without the use of prior information — in phase III for demonstration of a beneficial treatment effect, thereby creating a sufficient safety database to assess the benefit–risk trade-off of the new treatment. However, in other situations, the Bayesian approach, although still providing credible evidence of a treatment effect, can result in fewer patients being exposed in clinical trials and thus less overall evidence about the efficacy and safety of an investigational product. From an efficacy perspective, there may be less opportunity to assess the treatment on secondary end points or in subgroups of patients that may be of interest. Having fewer patients in phase III RCTs is particularly important in the context of safety assessments of a new treatment. Even in some traditional drug development programmes, an evaluation of efficacy requires smaller sample sizes, but phase III RCTs are designed with very large sample sizes and over-powered to create a large enough safety database. Whether it be a traditional frequentist drug development programme or one using a Bayesian paradigm, when fewer patients are needed to demonstrate a beneficial treatment effect, a sound alternative is to collect additional safety data outside the context of such complex and expensive efficacy trials. For example, simpler trials could be designed with fewer visits, fewer efficacy and quality of life procedures, less restrictive I/E criteria and so on to build the safety database. These simpler trials might also be more reflective of clinical practice and provide better insight into the safety issues with a new treatment under more normal conditions of use. Thus, a Bayesian approach could confirm the benefits of the new treatment in smaller — but more complex and expensive — trials while the entire clinical development programme can be used in more efficient ways to build better evidence regarding the safety of the new treatment.

Second, a Bayesian approach may also be helpful in synthesizing information across a drug development programme, which is often not powered to test statistical hypotheses about specific adverse events. Small numbers of unexpected adverse events are occasionally reported in a trial, and determination of whether such events are a true treatment effect or a spurious finding is difficult. Although evaluating unexpected adverse events is inevitably post hoc, most often sponsors and regulators make intuitive judgements regarding their prior belief of a causal link between the treatment and the unexpected safety finding. Although defining a prior in a post hoc way may seem contradictory, a Bayesian approach may help to formalize understanding of different perspectives and quantify the level of posterior belief for the treatment effect on such adverse events. Thus, a Bayesian analysis could be a more informative way of describing the potential risks of a new treatment based on the accumulation of safety data across a drug development programme. Such quantification is generally not suited for a frequentist null hypothesis significance testing approach, and p values are often not relevant in such situations.

Furthermore, the use of Bayesian methods has the potential to result in a more appropriate use of evidence generated in clinical trials. In particular, evidence from a trial for which a conventional frequentist hypothesis test fails to reach statistical significance still contributes towards a calculation that a treatment effect of particular magnitude has (or has not) been established rather than the trial simply being viewed as ‘failed’, as is often done in both a regulatory and an academic context. Certainly, some phase III trial and academic study ‘failures’ represent false negative findings, and Bayesian approaches can create a scientific basis to consider how evidentiary standards for ‘success’ are framed, giving an opportunity to tailor those requirements to each therapeutic setting. A recent re-analysis of a failed trial in the treatment of paediatric cardiac arrest with therapeutic hypothermia (p = 0.14) used a Bayesian approach to calculate a posterior probability of therapeutic benefit of 94%¹⁴. The authors argue that the results presented this way are in stark contrast to the original study conclusion that stated that therapeutic hypothermia did not confer a significant benefit¹⁵.

Lastly, for treatments given conditional or accelerated approval, subsequent phase III commitments for confirmatory trials could use the trial that is the basis for accelerated or conditional approval to form an appropriate prior for the confirmatory trial. Such post-approval commitments for additional trials tend to be more difficult to complete in the presence of the already marketed product, and a Bayesian approach could, under appropriate circumstances, be a low-risk regulatory approach to avoid large, expensive and potentially wasteful trials.

Supplementing data with an external control group

Bayesian augmented control designs allow researchers to reduce the number of participants required for a trial by incorporating, or borrowing, information on control groups from historical studies or, in rare diseases, well-designed natural history studies, without sacrificing power to detect an effect. The method used to borrow historical controls can vary across study types, and rigorous assessment of the external source is required to reduce bias¹⁶. For instance, bias can occur if the historical control sample is dissimilar to the current trial’s control arm or if the standard of care in medical practice has evolved over time. Thus, an important part of any study design is to be comfortable that the chosen design and the incorporation of historical data into the statistical analysis can result in reasonably unbiased estimates of treatment effect.

Bayesian augmented control designs have been employed effectively in early-stage oncology trials. In these studies, data on members of the control group are borrowed from other trials with similar demographics and disease characteristics. Ultimately, this method allowed for a new trial to use 15–20% fewer participants than would be required for a standalone clinical trial with a full, concurrent control group¹⁷. This same approach could be used in phase III trials to create an even larger impact on the efficiency of clinical drug development¹⁸, including borrowing control data from studies in other therapeutic areas.

Acceptance of this method has grown. The FDA has accepted trials using Bayesian augmented control designs into the Complex Innovative Design Program (see Related links). It would be beneficial to write a publication to describe innovative trial designs and share lessons on important points to consider in advance of trial results coming out. Publishing these studies would allow others to learn more about the implementation of innovative designs, expanding the field’s knowledge and experience. Additionally, it would help to develop best practices for investigations, to clarify assumptions related to the relevance of data from one source to another and to open discussion surrounding methods of adjustment to address deviations between data from the current trial and previously collected data.

Bayesian hierarchical models

Both Bayesian and frequentist hierarchical models are helpful because they allow us to assess different sources of variation in the data and account for variables at multiple levels of analysis^{19, 20} (Box 4). For instance, we can examine how a person’s symptoms change throughout a trial as well as differences that may occur at a group level. These methods also allow for borrowing of external data, under certain assumptions. This can be particularly helpful when investigating treatment effects across subgroups.

Using a Bayesian hierarchical modelling approach involves creating submodels that use both prior information and the available data to estimate the parameters of the posterior distribution. The hierarchical model is created by combining these submodels, and the overall model accounts for uncertainty present at all levels. Further, in the process of creating a Bayesian hierarchical model, the researcher quantifies their assumptions and priors and makes them explicit in the model. This increases transparency compared with models focused on a single level of analysis, where such assumptions may be used implicitly to interpret statistical results. Bayesian hierarchical models have been used in a wide variety of drug development contexts, such as investigating subgroup findings and establishing drug safety.

Box 4 Bayesian hierarchical models.

Bayesian hierarchical models allow us to examine sources of variation at various levels of analysis. At the top of the hierarchy is the overall treatment effect in the population of patients defined by the inclusion and exclusion criteria for a clinical trial. That overall treatment effect may be built upon subdivisions of the data that are nested in a way to make a hierarchical schema (see figure). The groupings at each level share some common attributes, and the relationship within and between groupings can be used to make more precise inference about a treatment effect that may differ between groups. In the schema shown in the figure, level 2 may include further subdivision of patients into refined subgroups.

Hierarchies can be quite general and represent many different scenarios of clinical interest. For example, level 1 in the schema may represent different subgroups of patients defined by phenotypic, genotypic or genomic factors. The hierarchical model allows for an overall treatment effect estimate but also a distinct treatment effect estimate in each subgroup. In practice, the subgroup treatment effect estimates will differ from the overall treatment effect estimate, and the fundamental question is whether such differences represent true heterogeneity of the treatment effect or merely random fluctuations due to sampling variability and the variability of the clinical outcome of interest. As described in the therapeutic hypothermia for hypoxic–ischaemic encephalopathy example in the main text, the Bayesian approach ‘shrinks’ the observed subgroup treatment effect estimates towards the overall treatment effect estimate, depending on the prior and how much weight is given to that prior. The FDA’s Impact Story on using innovative statistical approaches has some practical examples from actual clinical trials to describe this in more detail (see Related links).

Other hierarchical models may include different studies at level 1 with the same or different treatments at level 2. This approach was taken in the early 2000s for what is arguably the first FDA approval of a new treatment — a combination of pravastatin plus aspirin — using a Bayesian approach to estimate the treatment effect as the primary efficacy analysis⁶¹. Various models were examined to account for differences between studies, and prior distributions for all parameters in the model were defined explicitly. The result was that pravastatin–aspirin combination was superior to placebo, and in fact, the effects were synergistic (the effect of the combination exceeds the additive effect of pravastatin plus the effect of aspirin) based on a posterior probability of 0.9999 of the synergistic effect.

As another illustration of a Bayesian hierarchical model, we may be interested in the effect of a treatment on a certain outcome for which we have a model that describes the probability of a patient having that outcome (overall treatment effect). But the effect of the treatment depends on a patient’s compliance with the treatment regimen, for which we may have a different model describing the probability or extent to which the patient adheres to the treatment regimen (level 1 of the hierarchy). Such a model can be used to estimate the posterior distribution of each model parameter — the probability of treatment adherence and, subsequently, probability statements about the treatment effect.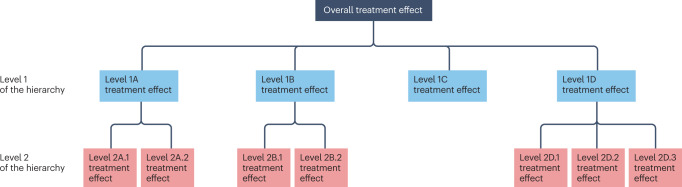

Investigating subgroup findings

The safety or efficacy of a drug may differ for subgroups of participants. This is a vexing problem in clinical development as the analysis of multiple subgroups can lead to spurious or false positive findings²¹, which are sometimes referred to as ‘random highs’ or ‘random lows’ in response (see the FDA’s Impact Story on using innovative statistical approaches in Related links). That is, when clinical trial data are partitioned in many ways, to create many subgroups, there are more likely to be larger or smaller treatment effects within individual subgroups than the expected true effect in such a subgroup. Bayesian hierarchical models offer one approach to examining findings in a subgroup of people with similar demographic or clinical traits by using prior information or biological mechanisms to produce more reliable conclusions.

These subgroup investigations can take two forms: purely descriptive (for example, age, gender, ethnicity) where there is a basis to postulate that these do not modify effects; or investigations of whether drug effects are truly heterogeneous across subgroups as a step towards personalized medicine. Bayesian hierarchical models account for individual differences in the subgroup of interest at one level and borrow strength from the full model, which can decrease spurious findings and lead to more accurate treatment effect estimates¹⁹. However, for appropriate use, the assumptions must be plausible, and researchers must be careful in making assumptions about consistency across subgroups based on insufficient information.

Bayesian hierarchical models have been effectively used to investigate treatment effects in subgroups of patients with non-small-cell lung cancer (NSCLC). For instance, the Biomarker-integrated Approaches of Targeted Therapy for Lung Cancer Elimination (BATTLE) project — which was “the first completed prospective, biopsy-mandated, biomarker-based, adaptively randomized study in pretreated lung cancer patients” — used a Bayesian hierarchical model to examine the effectiveness of several targeted therapies for patients with NSCLC according to their biomarker status²². Patients were initially randomized equally to four treatments. As clinical outcome data accumulated over the course of the trial, a Bayesian hierarchical model was used to assess subgroups of patients with specific biomarker signatures to identify the treatment that was most likely to be beneficial for biomarker-specific patients based on a Bayesian posterior probability of the treatment effect. Randomization probabilities were adapted accordingly so that subsequent patients were more likely to get the most effective treatment according to their biomarker signature.

The Bayesian hierarchical model approach identified subgroups in which the treatments would be effective better than independent analyses conducted in each subgroup²³. Further, in combination with other approaches, such as adaptive design, Bayesian hierarchical models can reduce sample size and allow faster completion of clinical trials²⁴. The success criterion for the trial was prespecified as a Bayesian posterior probability of >80% that a study treatment achieved a 30% disease control rate (DCR) at 8 weeks after randomization, and the overall DCR at this point was 48.6%. The study was considered a success in “establishing a new paradigm for personalizing therapy for patients with NSCLC.”²²

Drug and vaccine safety

Bayesian hierarchical models have also been used to examine the safety of an experimental intervention. For instance, results from a measles–mumps–rubella–varicella (MMRV) vaccine trial were re-analysed using this approach²⁵. This Bayesian hierarchical model accounted for adverse events at three separate levels, including type of adverse event, the body system affected and all of the body systems together, which allowed information across different subgroups, or body systems, to be borrowed, to increase power. However, it also demonstrated that assignment to subgroups, in this case body systems, could alter outcomes, suggesting that subgroups should be identified on the basis of expert knowledge, not just by relying on statistical correlation. Furthermore, assessing the safety of a treatment can be a vexing multiple inference problem owing to the many types of adverse event that occur in clinical trials. Using hierarchical models to account for multiplicity issues related to drug safety assessments has also been proposed²⁶.

Extrapolation

Extrapolation refers to an approach whereby information obtained from one or more subgroups of the patient population is applied to make inferences for another population or subgroup. This can reduce the number of patients in the latter group that need to be exposed to generate conclusions of the same scientific rigour. When there are data from prior trials and it is determined to be relevant, Bayesian methods could be applied to allow prior knowledge to be included in future studies.

Extrapolation has been successfully achieved in various contexts, including extrapolation across species of infectious bacteria, across body systems and across age groups. Extrapolation can be relevant when one wants to apply information from a well-studied population or body site to one that is less studied. For example, data from studies with ambulatory boys with Duchenne muscular dystrophy could be extrapolated to inform design and analysis of studies in those who are non-ambulatory. Although extrapolation techniques exist in both Bayesian and frequentist frameworks, Bayesian methods can be used to extrapolate from a source population to a target population by directly using data from the source population to inform the prior distribution. Quantifying the extent to which treatment effects in the source population apply to a target population is complex. A Bayesian approach has the possibility to address uncertainties related to the use of data from a source population by building an appropriate prior in which the treatment effect distribution reflects that uncertainty. Bayesian methods can explicitly quantify the uncertainty of extrapolation and also allow for source information to be down-weighted, thereby allowing the data from the target population to be weighted more heavily in the creation of the posterior distribution²⁷.

Extrapolation from adult to paediatric populations is often of interest, and regulatory guidances exist^{28, 29}, including an FDA guidance for medical devices that explicitly describes the use of Bayesian hierarchical models²⁹. Although no such FDA guidance exists for therapeutic treatments, Bayesian methods have been used to successfully extrapolate from adult populations to paediatric populations. For example, Gamalo-Siebers et al.³⁰ used several types of Bayesian model to extrapolate from information learned about the efficacy of the Crohn’s disease therapy rituximab in adults to provide insight into the efficacy of the drug in paediatric populations. They found that borrowing data from adults led to more precise drug efficacy estimates for children and advised that confidence in the Bayesian estimates of the treatment effect can be increased with proper planning — clearly stated assumptions, evaluating model fit, justification of priors, compatibility of the target (paediatric) and reference (adult) populations and more. The resulting reduction in sample size, which directly affects the cost and duration of a trial, can lead to greater efficiency in development and approval of medications for paediatric populations.

Decision-making for an ongoing clinical trial

Bayesian methods can be used in several ways to facilitate the workings of an ongoing clinical trial, including interim clinical trial monitoring and decision-making, utility analysis and sample size re-estimation. A Bayesian approach to monitoring trial progression can be helpful to assess accumulating data and make modifications, such as modifying or stopping the trial for safety or efficacy reasons, altering sample sizes or altering randomization procedures to favour certain arms of the study³¹ (Box 3). An emerging and promising use of Bayesian methods for ongoing clinical trials is in the design and analysis of master protocols, which include basket, umbrella and platform trials³². Such protocols often involve adaptive features and Bayesian decision rules for futility or advancing an experimental treatment for confirmatory clinical trials³³. Because the Bayesian approach offers such flexibility, it is important to discuss these options with regulators and other involved parties to ensure satisfactory evidence is collected.

The Bayesian adaptive approach was used successfully to compare the efficacy and safety of dulaglutide and sitagliptin for treating type 2 diabetes mellitus³⁴. In the first part of this study (phase II), the researchers aimed to determine whether dulaglutide was effective and, if so, the optimal dosage of dulaglutide. In this trial, randomization probabilities were adapted based on biweekly interim analyses using Bayesian decision rules regarding the probability that dulaglutide was superior to placebo and non-inferior to sitagliptin. Patient data were analysed every 2 weeks to adjust the randomization probabilities to the seven dulaglutide dose levels that were studied. Bayesian probabilities were also used to assess whether the phase II portion of the trial should be terminated for futility. The Bayesian interim analyses ultimately helped to select the optimal doses of dulaglutide to pursue in the second part of this study (phase III), which was highly successful. The Bayesian approach allowed for seamless integration of data across the phases of the study for making statistical inference about the treatment effect.

Another emerging trial design and analysis paradigm that may have great potential for rare diseases is the small sample, sequential, multiple assignment, randomized trial (snSMART). In such designs, patients who do not benefit sufficiently from their initial randomized study treatment are re-randomized (that is, crossed over) to other treatments in the study, which can be different treatments or different doses of the same treatment. Data from both randomization stages of the design are combined to estimate the treatment effect of all treatments involved. An example of such a design is a randomized multicentre study for isolated skin vasculitis (ARAMIS) comparing the efficacy of three drugs: azathioprine, colchicine and dapsone³⁵. Newly developed methods using Bayesian joint stage models of such designs^{36, 37} have demonstrated the possibility of reducing sample sizes by 15–60% while maintaining the validity of the inference about a treatment effect.

Barriers to widespread adoption of Bayesian analyses

Bayesian methods to incorporate external data require acceptance from various stakeholders, including sponsors, regulators, statisticians and clinicians. Although some of the barriers to gaining acceptance are technical, others are social, stemming from a lack of confidence or comfort with these approaches and insufficient Bayesian education. Furthermore, we acknowledge that some obstacles are present across various stakeholders, whereas others lead to unique challenges for specific groups. Below, we highlight some existing barriers and discuss ways to reduce them.

Historically, Bayesian methods have been underused in drug development because these methods were computationally intensive, and computers did not have enough power to run the necessary calculations. However, this issue has largely been resolved with advances in statistical theory and computational technology, thereby eliminating at least one barrier to implementation of Bayesian methods.

Drug development is a complex, costly and time-consuming enterprise, and so it is prudent to avoid approaches that are perceived as risky because inappropriate risk can jeopardize the years of work that precede clinical trials. Consequently, two key (and related) barriers to the use of Bayesian methods in clinical trials are the lack of acceptance and familiarity with these methods among regulators and industry sponsors, and the lack of experience and guidance about how to use them, especially in confirmatory phase III trials. At present, there appears to be a vicious cycle in which regulators may be reluctant to accept new methods that are not well established, which may lead industry sponsors to be hesitant about trying new methods owing to uncertainty surrounding regulatory acceptance. Disrupting this cycle presents a challenge, but we can examine comparable instances in clinical trial history to inform a solution.

The use of adaptive designs for clinical trials is a prime example of sponsors creating comfort with new methods and building confidence among regulators and other stakeholders. Although adaptive designs were increasingly discussed in the biostatistics literature during the 1960s, they were rarely used in practice because sponsors and regulators had little knowledge and experience with the methods or their application. Adaptive designs are now more widely accepted as an alternative to traditional fixed clinical trial designs^{38, 39} (although some may argue that adaptive designs are still underused). However, it took many years of discussions and negotiations to create the confidence and comfort necessary for adaptive designs to become normalized, including the issuance of regulatory guidances^{40, 41}.

Therefore, one motivation for this article is to facilitate discussions about the use of Bayesian approaches, and especially conversations to discuss the interpretation of outputs of both frequentist and Bayesian analyses. Decades of experience with frequentist hypothesis testing and the use of the conventional level of p < 0.05 for declaring statistical significance have created a common understanding among researchers and a level of comfort with using p values to make decisions. By contrast, Bayesian analyses do not enjoy a long, collective history and understanding among the same scientists, and there is no established convention for what constitutes substantial evidence of a treatment effect based on Bayesian posterior probabilities or distributions. As this format is unfamiliar to most, understanding such outputs and the differences with p values will be necessary for the more widespread adoption of Bayesian methods.

Although a guidance for the use of Bayesian statistics in medical device clinical trials was published by the FDA in 2010 (ref. ⁴) and 2016 (ref. ²⁹), there is no comparable guidance for drugs and biologics. Increasing familiarity and confidence in Bayesian methods may also help to address this lack of regulatory guidance. When sponsors propose the use of Bayesian methods, more upfront planning is required, including discussion of the use of prior knowledge and external data, selection of a prior distribution and definition of a posterior probability threshold for concluding whether a treatment is effective. Without established precedents or guidances, these additional discussions between sponsors and regulators are more time-consuming and may strain the already limited resources within regulatory agencies, creating a structural barrier to the use of Bayesian approaches that is unrelated to scientific utility or appropriateness. These negotiations could become less time-consuming and resource-intensive as stakeholders become more familiar and practised with Bayesian methods. Similar to adaptive designs, we expect that increases in familiarity will enable the successful use of Bayesian methods in ways that require less upfront work and could facilitate the development of guidance from regulatory agencies.

Training biases within academia and insufficient experiences present another challenge to the more widespread use of Bayesian methods. Many statisticians are taught frequentist methods more thoroughly than Bayesian or other biostatistical methods, leading frequentist methods to become more normalized and acceptable. Non-statistician academics are even less familiar with Bayesian approaches and are prone to rely on frequentist methods. These training biases also extend to clinicians. Even though clinicians typically rely on prior knowledge when examining a single patient, they are often taught to interpret population-level trials through a frequentist lens. This barrier can be reduced by creating comfort and building confidence with Bayesian approaches in this group.

Similar barriers are present in the industry. The Drug Information Association Bayesian Scientific Working Group surveyed organizations and found that insufficient practical knowledge was a hurdle to adopting Bayesian approaches⁴². This issue is not unique to large or small companies. Although Bayesian methods are more commonly used for internal decision-making purposes, they may be viewed sceptically by regulatory affairs professionals within companies running clinical trials, who may be reluctant to take on the regulatory risk of using these approaches instead of commonly used frequentist ones. This sense that Bayesian methods have a low level of acceptance may prevent their consideration within sponsor organizations even before discussions with regulators might occur.

Although lack of familiarity is a key barrier to the adoption of Bayesian approaches, there are many knowledgeable statisticians and researchers who understand the Bayesian approach mathematically and philosophically yet prefer the frequentist inferential approach. Their perspective is that the perceived weaknesses of the Bayesian approach — such as the subjectivity of the prior and the potential for over-optimism, the difficulty of defining a posterior probability threshold for decision-making, assumptions and modelling approaches — outweigh the benefits. This article is not meant to ‘convert’ such thoughtful statisticians and scientists, but instead to create an opening for Bayesian inference in our scientific quest to uncover the truth about the cause-and-effect relationship between a new treatment and a clinical outcome, or at least to quantify the probability that such a cause-and-effect relationship exists.

Finally, the role of payers cannot be ignored. Payers create economic models that examine the costs of specific events and the probability that these events occur. In reality, these questions align well with Bayesian approaches. The probability of a treatment benefit or a treatment harm can be coupled with the savings achieved by the benefits and the additional costs caused by the harms to build a realistic economic model for evaluation by payers⁴³. However, given the limited use of Bayesian methods for approvals, payers’ unfamiliarity may drive concerns that products approved using Bayesian methods are not as well-studied or as validated as those using other methods. This lack of familiarity, coupled with other pressures faced by payers, may lead to additional scrutiny about the validity of trial data, even if the FDA and other international regulators approved it.

Overall, although each group of stakeholders has varying motivations and concerns, the lack of familiarity with Bayesian approaches is a common underlying theme that must be addressed for a large contingent of stakeholders before these methods are used more often.

Framework for deciding when Bayesian approaches may work

When approaching clinical development, there is no right or wrong answer about whether to use frequentist or Bayesian methodology. These two approaches actually coexist (explicitly or implicitly) as shown in Fig. 1. All statistical methods — frequentist and Bayesian — require assumptions and models, the veracity of which we can never fully know. Thus, there is undoubtedly some level of subjectivity, and subsequently bias, in all of our analyses. Information external to the current experiment can be combined with data from the current experiment to make decisions in both the Bayesian and frequentist frameworks. However, the incorporation of prior knowledge is inherent to a Bayesian approach and results in a probability format or statement that is very useful and natural for decision-making.

Here, we present a framework to help decide whether to use Bayesian or frequentist methods (Fig. 4). This decision should not be the first step; instead, we argue that the researcher should first consider the research question of interest and the totality of evidence needed for the decision-makers about that question. Second, the researcher should determine whether external information relevant to the research question exists. For instance, when planning a phase III confirmatory study, high-quality, relevant information could be external data from a previously run well-controlled phase II study with a population that is similar to that of the planned phase III study. This is not to say that the phase III prior should be taken directly from the phase II posterior probability distribution of the treatment effect. One must consider not only the similarity or differences in the populations being studied, but also different geographical locations of the study, changes in formulation or dose that can occur between phases, changes in the primary efficacy outcome, generally longer durations of phase III trials and more. Furthermore, sponsors pick the winners from phase II studies for further study in phase III. Thus, there is a natural bias or tendency for compounds that progress into phase III to be the result, in part, of the random high bias^{44, 45}. Each of these factors need careful, objective consideration, and the degree of difference between phase II and phase III studies should be captured in the down-weighting of the phase II data for use as a phase III prior¹³. Conversely, there may be limited data on the efficacy response to a new treatment as it may have been studied in relatively few patients in phases I and II, and thus, minimal information to borrow about the new treatment effect. This should not deter the researcher from exploring what might be a wealth of placebo or other active control data across many trials in the same or similar disease settings or with a treatment having a similar mechanism of action, as noted above. There are other forms of high-quality, relevant prior knowledge that may exist from other drugs in the same mechanistic class or in the same disease state. Observational data from electronic medical records, medical claims databases or other such real-world settings can be helpful but must be used cautiously owing to their uncontrolled nature and potential for considerable bias. Additionally, expert opinion, albeit subjective, can be used to synthesize disparate sources and types of preclinical and clinical data to assist in the formation of a prior distribution.

Fig. 4. Recommended stepwise process for deciding whether a frequentist or Bayesian approach is most applicable for design, analysis and interpretation for the test of an experimental hypothesis.

Information may consist of quantitative data, qualitative knowledge such as theories about a biological mechanism, or other subjective inputs such as expert opinion.

Next, the researcher should evaluate whether the external data can be explicitly included in ways that result in the best summary of the totality of evidence and reasonably unbiased estimates of treatment effects (Fig. 4). If external data are appropriate, researchers should determine which method, Bayesian or frequentist, is most suitable for the circumstance, including additional sensitivity analyses to ‘stress test’ the impact of assumptions on conclusions. If there is not sufficient prior knowledge, then frequentist methods, or weakly informative priors, will most likely be appropriate¹⁴. Although the results of analyses based on frequentist approaches and Bayesian approaches with weakly informative priors may result in very similar conclusions, we advocate for the use of the Bayesian approach as its posterior probabilities make direct statements about the hypothesis of interest. Furthermore, Bayesian approaches are generally more suited for adaptive and other complex innovative designs, handling missing data, complex modelling and more.

Recommendations for action

Bayesian methodology is an important and underused tool to combine and interpret the totality of evidence needed to demonstrate the safety and efficacy of a drug while making full and quantitative use of prior knowledge. When there is a sound scientific basis to do so, there are benefits to public health where medicines can be brought forward more expeditiously, providing early access to patients and requiring fewer subjects to participate in clinical trials, without compromising decision-making rigour. For this to be successful, we recommend the following actions.

Increase communication and knowledge exchange

Industry groups and regulators should publish their findings using Bayesian approaches and generally communicate them more regularly to the broader audience involved in drug development. This will allow for research teams, as well as others, to gain experience and familiarity with Bayesian methods. Initially, a Bayesian analysis may be a supplemental description of the trial results, as in the case of a phase II trial for the potential Alzheimer disease therapy donanemab⁴⁶. In the assessment of cognitive and functional decline among patients with Alzheimer disease, researchers reported a p value of 0.04 for rejecting the null hypothesis of no treatment effect and supplemented the finding by noting a Bayesian posterior probability of 76% that the slowing of cognitive and functional decline estimated in the trial met a prespecified clinically meaningfully threshold. A similar phase II Alzheimer disease study of lecanemab used a Bayesian analysis as the primary analysis, reporting a 64% probability that the treatment effect achieved a clinically meaningful threshold⁴⁷. The successful phase III trial of lecanemab reverted to a frequentist paradigm to demonstrate a beneficial treatment effect — quoting a p value of <0.001 for the primary efficacy outcome⁴⁸ — perhaps illustrating the reluctance to implement the Bayesian paradigm across the full drug development programme.

Create transparency

Designing studies with Bayesian approaches can be intensive and can require advanced methods, including simulations. Transparency in design and analysis is necessary for more widespread adoption of Bayesian methods. Guidance from the International Council for Harmonisation of Technical Requirements for Pharmaceuticals for Human Use (ICH)-E9 Statistical Principles for Clinical Trials states that “The extent to which the procedures in the protocol are followed and the primary analysis is planned a priori will contribute to the degree of confidence in the final results and conclusions of the trial.”⁴⁹ In the Bayesian framework, the entire decision-making framework is prespecified by the explicit incorporation of the prior and therefore may be considered a more holistic approach. In the frequentist paradigm, inferences from the current study are interpreted subjectively in the context of external data and/or information, which can allow for post hoc, hidden biases to seep into decision-making. Following these guidelines when creating, conducting and publishing work would increase confidence in both the research and Bayesian methods more generally.

Publicly sharing computational algorithms could increase understanding of how to implement Bayesian approaches. Further, sharing code reduces the possibility of Bayesian approaches being viewed as a ‘black box’, as it allows others to become familiar with the processes and calculations involved. Regulators should provide support for such activities, and sponsors should demonstrate that they are prudently using Bayesian methods by being more open about their use.

Create institutional structures that build confidence

With increasing use of Bayesian methods, concerns about deviating from tradition will be less of a barrier. To reduce such concerns further, public conversations on the use of Bayesian methods should occur more often. An FDA advisory committee could be created, which advises and ultimately leads to development of specific guidance on how to determine relevant prior distributions and use Bayesian methods in drug development trials. International health authorities have developed guidance for sponsors on defining relevant non-inferiority margins^{50, 51} that rely on the Bayesian framework for evaluating historical data, and the same should occur for the use of Bayesian frameworks in other clinical trial settings. In medical device development, for which each generation of a device is often very similar to the previous generation, Bayesian methods for the next-generation device clinical trials have used data from clinical trials on the previous generation of the device to make approval decisions with established guidance from the FDA^{4, 29}. The sequential nature of device development has given the device industry a head start on the use of Bayesian methods for design and analysis of clinical trials, but undoubtedly there are lessons to be learned from such sequential development that can be applied to the development of new treatments. A similar guidance for the use of Bayesian methods in drug development would provide much-needed clarity to industry and FDA staff. Lastly, principles and standards for reporting Bayesian design and analysis approaches have emerged and can be a basis to establish further common ground upon which confidence and clarity is built⁵².

Build and maintain capabilities

Education of regulators and clinical staff on Bayesian approaches is also crucial for more widespread acceptance. Provision of more training and mentoring opportunities for these stakeholders to learn about Bayesian methods would increase familiarity and lead to greater adoption of Bayesian methods, when appropriate. For example, postdoctoral fellowships at the FDA and industry courses explicitly designed for the use of Bayesian methods in clinical drug development could help to accomplish these goals.

Foster open-mindedness

Researchers and the pharmaceutical industry should look for opportunities to include external data and to use Bayesian methods in drug development, developing sound proposals that avoid the introduction of significant biases and examine assumptions explicitly and comprehensively. For instance, researchers could include Bayesian analyses more often as supplemental analyses in their publications, as in recent cardiovascular⁵³ and Alzheimer disease⁴⁶ studies. Regulators will need to keep an open mind about this approach, so that trials using Bayesian approaches become normalized and accepted.

Conclusion

A central tenet of our work is that public health needs and drug development targets have evolved to the extent that the frequentist mindset towards drug development is not optimal in all circumstances. Specifically, in cases where relevant knowledge, scientific understanding and data have already been amassed or are hard to ignore, the need to undertake two prospective fully powered trials for a frequentist hypothesis test might represent an excessive burden for patients and sponsors, and perhaps overkill for regulatory decision-making.

More broadly, we argue that researchers could benefit from considering Bayesian thinking when proposing and designing any new study, be it a laboratory experiment or a clinical trial. There must be some prior knowledge that justifies the expense and effort of conducting a study and some level of belief that the study may be successful in meeting its objectives. Researchers do not pull experiments or clinical trials out of thin air, but instead use the accumulated knowledge of the scientific community to create a hypothesis and inform subsequent study design. Wacholder et al.⁵⁴ state: “Investigators already informally use prior probability to decide whether to launch a study, which genes to study and how to interpret the results. We believe that formally developing prior probabilities before seeing study results can, in itself, lead to a substantial improvement in interpreting study findings over the current scientific practice.” Additionally, in difficult experimental situations, such as clinical research on rare diseases and paediatric diseases, a mindset to quantitatively and explicitly use all available evidence has the potential to offer a sounder basis for decision-making. Although the focus in this article is on clinical drug development, the body of Bayesian work across all phases of drug development, including health economics, is growing as well as the number of examples of its successful use⁵⁵.

As demonstrated above, drug development using Bayesian methods already occurs, with Bayesian methods being used in key analyses and in the interpretation of trial results, including one of the most consequential clinical trials of our times for establishing the efficacy of a COVID-19 vaccine⁹. There are no regulatory requirements to use frequentist methods, although they are mainly considered the default approach for pivotal studies and, as such, are the dominant approach in current regulatory review and approval. Bayesian methods could be the basis of the primary analyses and conclusions for a clinical trial, with frequentist approaches being considered as sensitivity analysis to the primary Bayesian approach, as with the therapeutic hypothermia trial for HIE⁷ and the Pfizer–BioNTech COVID-19 vaccine trial⁹. Such a reversal in thinking is constrained only by our conventions and traditions.

Although not a panacea, Bayesian methods have epistemological and interpretational advantages over frequentist methods because they directly address the probability of the veracity of the research hypothesis of interest, instead of providing indirect evidence through a p value. Bayesian approaches bring a level of rigour beyond frequentist approaches in that they require prespecification of data and analysis methods for the entire decision-making process, in contrast to frequentist results derived from a single experiment that may be integrated with previous scientific data in a post hoc fashion. To harness the full power of Bayesian approaches, there must be stakeholder agreement on when and how it is appropriate to include prior knowledge in analyses and on the totality of evidence needed to support marketing authorization by a regulatory agency. By educating a wide variety of stakeholders and informing them of the potential benefits of using Bayesian methods, we hope to promote discussions on what is considered “substantial evidence of safety and efficacy” to support approval in different settings, as well as how data sources and methods could be used to meet the totality of evidence required. Put simply, evolutions in science, drug development, pharmacology, data accessibility and data analysis methodology should be matched by a similar evolution and advances in inferential methods, most notably by careful and explicit use of existing knowledge and data. We believe that the widespread adoption of Bayesian approaches has the potential to be the single most impactful tool for accelerating the development of new medicines, reducing exposure of clinical trial participants to suboptimal control arms and providing earlier access to high-quality treatments for patients.

Peer review

Peer review information

Nature Reviews Drug Discovery thanks Emmanuel Lesaffre, Philip Pallmann, Benjamin Saville and the other, anonymous, reviewer for their contribution to the peer review of this work.

Competing interests

S.J.R. is a consultant to the Pharmaceutical Research and Manufacturers of America (PhRMA) and several pharmaceutical companies. F.B. is employed at Leuven University and at Sanofi, where he is a stockholder. Most of the work on this manuscript was completed while employed at Merck KGaA. R.H. is an independent consultant to the pharmaceutical industry. P.H. is a stockholder in Pfizer and Merck and works as an adviser to Blackstone, which invests in many pharmaceutical companies. T.I. is an employee of Janssen Pharmaceutical Companies of Johnson & Johnson and a stockholder. L.L. is an employee of the University of North Carolina, Chapel Hill and has an Intergovernmental Personnel Act (IPA) Assignment with the FDA. She is an expert statistical consultant with the Center for Drug Evaluation and Research. G.L. is employed by a startup health-care data company, N-Power Medicine, but performed work on this manuscript as an employee of Genentech. She is a Roche shareholder. J.M. is a Pfizer stockholder and is retired but performed most of his work on this manuscript while employed by PhRMA. R.M. is retired but performed most of his work on this manuscript while employed by PhRMA. He is a board director of KSQ corporation, a privately held biotech company.