Abstract
Following the explosive growth of global data, there is an ever-increasing demand for high-throughput processing in image transmission systems. However, existing methods mainly rely on electronic circuits, which severely limits the transmission throughput. Here, we propose an end-to-end all-optical variational autoencoder, named photonic encoder-decoder (PED), which maps the physical system of image transmission into an optical generative neural network. By modeling the transmission noises as the variation in optical latent space, the PED establishes a large-scale high-throughput unsupervised optical computing framework that integrates main computations in image transmission, including compression, encryption, and error correction to the optical domain. It reduces the system latency of computation by more than four orders of magnitude compared with the state-of-the-art devices and transmission error ratio by 57% than on-off keying. Our work points to the direction for a wide range of artificial intelligence–based physical system designs and next-generation communications.
An unsupervised photonic generative neural network enables high-throughput image transmission.
INTRODUCTION
Because of the prevailing development of intelligent society, the transmission of images becomes a fundamental demand in various fields in daily life (1–3). For example, an instant play of one single Blu-ray movie requires a transmission throughput of several gigabits per second. The transmission links require satisfying the throughput of a large number of such terminals simultaneously, which brings extreme challenges for image transmission (4–7). In addition, because image transmission usually requires high throughput and visualization quality, pre- and postprocessing, such as compression and error correction with large operation numbers are essential in image transmission (8–10).
However, although nowadays more than 95% of digital information globally is transmitted through optical fibers (11), image processing remains to base themselves mainly on electronic processors (12, 13). For instance, in an optical fiber communication (OFC) system for image transmission, it includes preprocessing (compression, encryption, and antinoise encoding), electro-optic modulation (EOM), transmission, optical-to-electronic conversion (OEC), and postprocessing (decompression, decryption, and error correction decoding) to reconstruct messages from the received signals (14). Different modulation and demodulation schemes, including pulse amplitude modulation (PAM), phase-shift keying, and on-off keying (OOK), are used to encode and decode the digital signal. The EOM and OEC in an OFC system are usually done by Mach-Zehnder modulators and photodetectors, while the pre- and postprocessing are mostly implemented with digital signal processors (5, 6, 15). Processing the transmitted massive optical image signals, such as encryption and compression, has placed critical burdens on current electronic computing platforms. The gap in the operating frequency between the state-of-the-art electronic circuits and the fiber transmission lines is orders of magnitude due to the limited drift velocity of electrons, therefore becoming one of the most time-consuming parts in high-throughput transmission (4, 7, 16–18).
The recent surge of intelligent photonic computing is considered promising to provide a solution to overcome the electronic bottleneck by processing the images directly in the photonic domain (19–23). Diffractive neural networks (24, 25), coherent nanophotonic circuits (26), convolutional accelerators (27, 28), fiber computing (29–31), and other optoelectronic devices (32–36) successfully realize parallel photonic neural networks and increase the computational efficiency substantially. However, the existing all-optical neural networks are mainly focused on classification tasks, for example, the recognition of handwritten digits and letters. The processing in image transmission requires not only feature extraction and image clustering but also reconstruction after compression and encryption. The recent development of electronic generative models has proved their capability in photorealistic image generation, which is promising for high-quality image transmission (37, 38). In particular, the variational autoencoder (VAE) model can controllably transform between large-scale datasets and low-dimensional representations (the latent space), which finds applications in data encoding and generation (38). Although optoelectronic generative models have been reported, existing photonic intelligent processors are incapable of all-optical end-to-end generative neural networks and, hence, fail in achieving ultralow-latency complicated image processing in transmission (36, 39).
Here, we propose an unsupervised photonic VAE, named photonic encoder-decoder (PED), for end-to-end processing in image transmission. To the best of our knowledge, PED is the first demonstration of all-optical generative neural networks. The end-to-end learned PED structure enables it to encode the optical input information into a compressed and encrypted optical latent space (OLS) for transmission and decode the transmitted distorted signals from the encrypted domain to the reconstructed images optically. The elaborately designed diffractive neurons directly manipulate the information in the optical domain without loss and distortion caused by the convertors to increase the transmission precision. Modeling the transmission noise as the variations in the OLS and constraining it with the probability distribution entitle the PED to learn an optimal coding scheme to maximize its noise resilience. In our prototype optical system, the PED decreases the system latency of image transmission by more than four orders of magnitude compared with the state-of-the-art central processing unit (CPU). On benchmarking datasets, PED experimentally achieves 57% reduction in transmission error ratio (ER) than OOK, one of the mainstream methods with the lowest ER. In addition, the PED increases the transmission throughput by two orders of magnitude than PAM-8 and 87 times than the conventional compression method discrete cosine transform (DCT), as we demonstrate in medical images.
RESULTS
Modeling of the PED
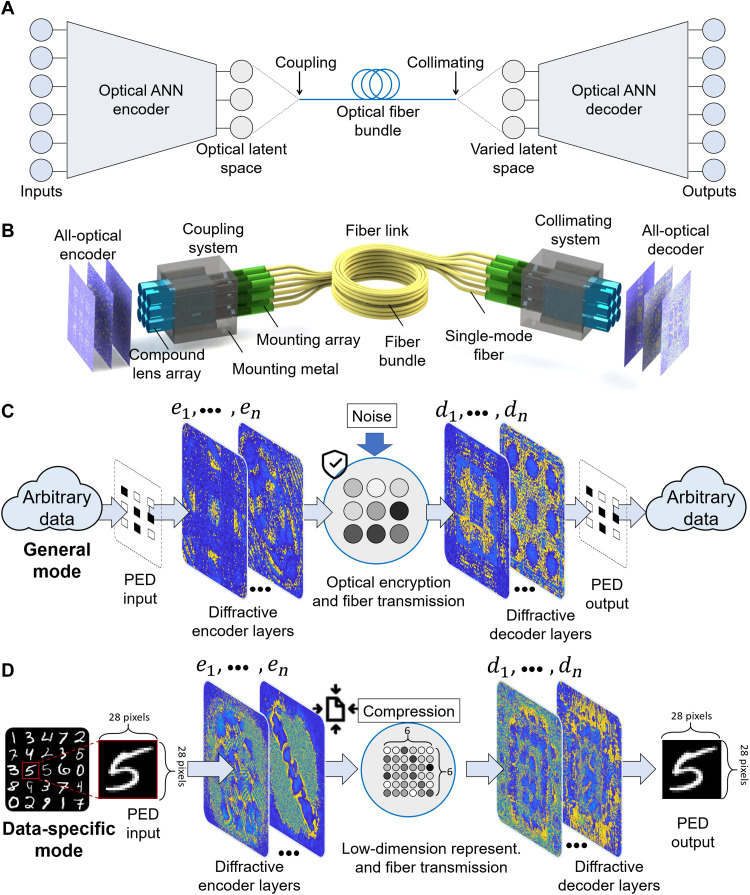
In the proposed PED architecture (Fig. 1A), the input messages are encoded into an OLS with an optical artificial neural network encoder and are later correspondingly coupled into the single-mode fiber bundle. The noise during transmission is modeled as the variation in the OLS in a VAE-based architecture. An optical artificial neural network decoder decodes the transmitted latent space representations, i.e., the combination of the Gaussian speckles after the collimating lenses, for the faithful reconstruction of input messages. Because the OLS highly encrypts the input messages, it prevents tapping and guarantees the security of transmission.
Fig. 1. Image transmission using the PED neural network architecture.
(A) The PED, implemented with photonic VAE, is used for end-to-end designing of an image transmission system, which comprises the optical neural network of an encoder and a decoder and transmits the OLS with an optical fiber bundle. ANN, artificial neural network. (B) System design of the PED. It couples the light-field output by the encoder into fiber bundles and decodes the information by the decoder all-optically. (C) General mode: The PED allows optically encrypting the digital inputs and reducing the transmission error with a non–data-specific pretrained coding architecture. (D) Data-specific mode: The PED compresses the grayscale inputs into low-dimensional representations with the encoder and reconstructs them with its decoder for high-throughput image transmission. en (n = 1, 2) is the n-th layer of the encoder, and dn (n = 1, 2) is the n-th layer of the decoder.
Figure 1B is the system design of the all-optical PED, establishing the encoding-transmission-decoding flow without the requirement of any analog-digital/digital-analog and opt-electrical conversions by carrying out all processes in the analog optical field, which notably improves the speed and efficiency of communication. As depicted in Fig. 1B, after an all-optical encoder composed of trainable diffractive layers, the PED passively couples the light field into a fiber bundle through a lens array and decodes the OLS with an all-optical decoder back to the original data. Every lens in the lens array couples one corresponding area of the optical field to one single-mode fiber in the fiber bundle. The coupling efficiency depends on the light field and the characteristics of the fibers and lens. The light field in the fiber can be considered as a linear superposition of different spatial frequencies with respective coupling coefficients (see Materials and Methods for the modeling of the coupling process). In addition, PED is naturally compatible with most existing OFC systems as they both use single-mode fiber bundles for transmission, which are already buried underground over the world (see details about the compatibility in note S5).
The PED allows two operation modes: general and data-specific modes, as shown in Fig. 1 (C and D, respectively). The general mode provides fundamental secure and noise-resistant transmission for arbitrary images optically. When some prior information is obtained, not necessarily labels, the data-specific mode additionally allows notable compression to improve the transmission throughput.
The latent space of the VAE architecture is a hyperspace representation of inputs that is subject to a continuous distribution function (38). In the PED, we generate and evaluate the OLS by dividing the output plane of the encoder into subregions and sum the low-frequency component of the optical field at each subregion by coupling it into a single-mode optical fiber. Different subregions correspond to different single-mode fibers of the fiber bundle. The number of subregions, which corresponds to the number of optical fibers for spatial multiplexing, determines the dimensionality of the OLS. After transmission, the OLS is collimated into the optical decoder to reconstruct the inputs.
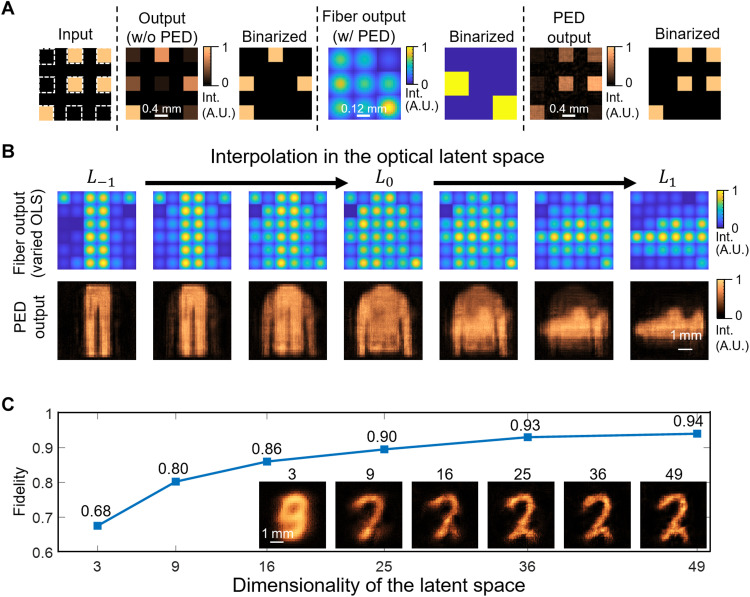
In the general mode, Fig. 2A shows an example of the PED transmission results under a signal-to-noise ratio (SNR) of 9 dB. The SNR usually depends on the transmission situations (see an example of optical fiber transmission in note S2). The input data are coded into binary blocks as bits (the first column), and the transmission noise deteriorates the input bit codes and generates incorrect bit codes after binarization (the second and third columns). During PED-based communication, messages are encrypted by the encoder into the OLS as a complex optical field for transmission, where the same amount of transmission noise is introduced. The intensity of the optical field and its binarized result are shown in the fourth and fifth columns of Fig. 2A. By modeling the transmission noise as the variation of the OLS during the unsupervised training of the PED, the decoder reconstructs the correct bit code from a distorted OLS (Fig. 2A, sixth and seventh columns).
Fig. 2. Modeling of the PED.
(A) OLS in the general mode: The encoder encrypts the inputs into their OLS representations, where the decoder can correct the bit error induced by the transmission noise and reduce the bit ER. Numerical results of the general mode are shown here. A.U., arbitrary units. (B) OLS in the data-specific mode: The OLS representations of inputs (the fiber outputs) are imposed by a continuous Gaussian distribution function, where the interpolation is uniform, while the reconstructions assemble around the original items. Numerical results of the data-specific mode are shown here. (C) Reconstruction quality (fidelity) improves with the increasing of the OLS dimensionality rapidly when the compression ratio is large and turns gradually when the OLS dimensionality is adequate. Numerical examples of the reconstructed digit “2” at different OLS dimensionality are displayed.
Furthermore, the OLS allows unsupervised compression when some prior information of the transmission messages is obtained, which is common in data centers and factories. Figure 2B demonstrates an example in the data-specific mode over fashion products, i.e., the Fashion-MNIST,a Modified National Institute of Standards and Technology (MNIST)–like fashion product database (40). The PED encoder maps the 28 × 28 input image (a shirt here) into a hyper-point L0 in a 36-dimensional OLS, and the decoder reconstructs the input faithfully from the compressed and encrypted OLS (see the complete inputs, outputs, and masks in fig. S1). The variation during training allows the PED to obtain a continuous and noise-resistant OLS, as depicted in Fig. 2B. We interpolate between different hyper-points in the OLS, such as L−1, L0, and L1, to which the PED encoder maps a pair of trousers, a shirt, and a sneaker, respectively. The interpolation step is uniform between each image, whereas the PED outputs remain close to these fashion products around each hyper-point instead of reconstructing inexistent items. It shows that the unsupervised OLS can correctly reconstruct the items even disturbed by distinct transmission noise, implying the exceeding robustness of the PED transmission.
The compression ratio, which depends on the dimensionality of the OLS, influences the reconstruction quality as shown in Fig. 2C. The image fidelity (correlation) of the transmission outputs, averaged over the MNIST testing dataset (10k images, 28 × 28 grayscale pixels each) under different OLS dimensions, is displayed. The results demonstrate that the transmission performance improves with the increasing OLS dimensionality rapidly when the compression ratio is huge and gradually improves when the dimensionality is adequately large. Example results of the transmitted digit “2” under different OLS dimensionalities are shown. As the quantitative accuracy is finite, the PED can implement full precision because the analog signal theoretically has infinite precision. Figure S13 shows some examples of reconstruction images by the PED whose reconstruction fidelity is 1.00.
General mode for secure and high-accuracy image transmission
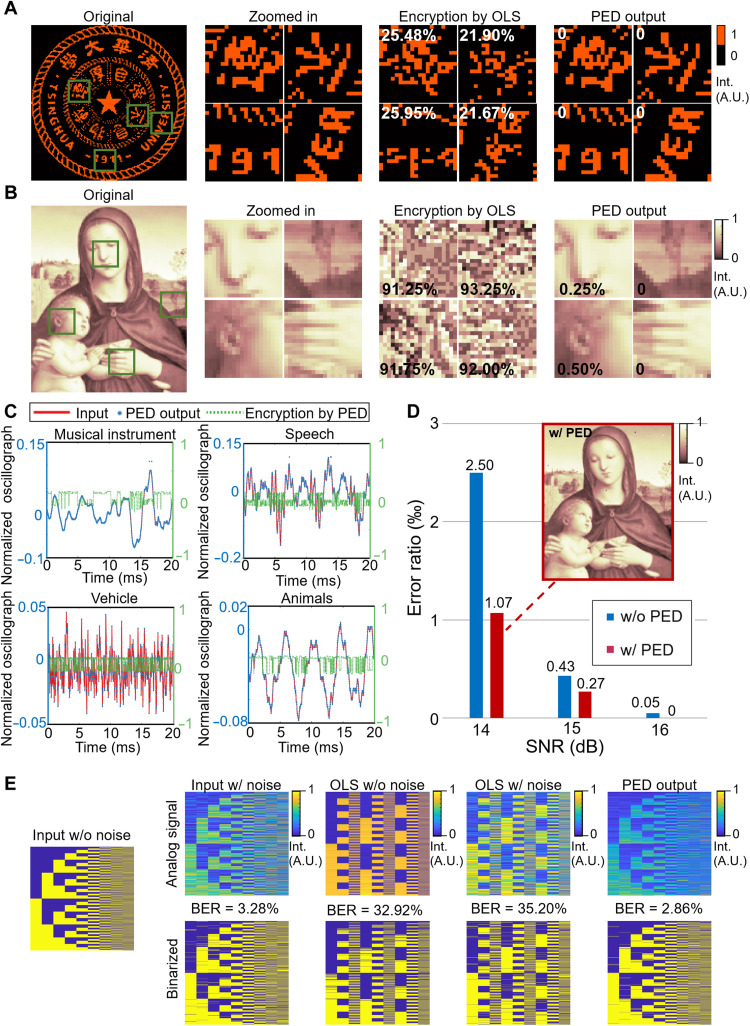
Arbitrary images are encoded into binary bits and transmitted on the basis of OOK in the general mode, while applying a pretrained non–data-specific PED provides photonic encryption for image transmission as the encoder embeds the information into the OLS. High precision can be achieved simultaneously with the noise-resistant coding scheme optimized by the PED. To facilitate the evaluation of PED performance, we capture the output intensity of each layer to reuse the spatial light modulator (SLM), named optoelectronic PED. Optoelectronic and all-optical PED have comparable performance, as proved in fig. S5 (see Materials and Methods for the details of experimental modeling and setup). Figure 3A displays the experimental results of encryption by the PED over a binary image (the logo of Tsinghua University). Bits (3 × 3) are transmitted in each frame, as shown in Fig. 2A, and arranged back into the image. The information transmitted in fiber bundles, which may potentially be eavesdropped, is distorted into an unrecognizable image with the ER orders of magnitude higher than the reconstructed image (25.48, 21.90, 25.95, and 21.67% and 0, 0, 0, and 0, relatively). The letters (“VER”), digits (“191”), and Chinese characters are effectively encrypted beyond recognition. The OLS produces the coupling relationship between all latent values, which makes interception with only some of the channels relatively impossible.
Fig. 3. Experimental results of PED for the general mode.
(A to C) Experimental encrypted transmission of binary images, grayscale images, and audios. All successfully distort the information in OLS and reconstruct after decoders. (D) Experimental ER of the PED under different transmission noise levels. We encode the grayscale image (a 150 × 125 painting) into binary bits and transmit it with simulated noise. PED reduces the ER by more than 57% (relatively) compared with OOK (one of the existing methods that are most robust to transmission noise). One example of the face is shown at 14 dB. (E) Experimental denoising results of the general mode on all 512 instances. We transmit all coding instances (512 images) to calibrate and test the global encryption and denoising capability of PED at a noise level of 9 dB. The same level of noise is added in both the OOK and the OLS. The PED encrypts the information with the bit ER (BER) of 35.20% and reconstructs it to the BER of 2.86%. After coding, it reduces the BER by 12.80% (relatively) with respect to OOK.
Besides effective encryption on characters, the PED shows exceeding encryption performance over natural grayscale images, such as the painting exhibited in Fig. 3B, i.e., a 150 × 125 image with 256 grayscale levels. Each grayscale pixel is encoded in one frame that has nine binary bits. We do not change the number of bits in each frame according to the image because the grayscale depth of the image may not always be prior information under real transmission situations. The PED experimentally achieves an ER of only 0.26% in reconstruction, while the ER in OLS is 90.56% on the whole image. Zoomed-in features are shown in Fig. 3B, where all details are unrecognizable in OLS, including the facial details, the hair and ear of the child, fingers, and plants in the background, with the ER encrypted to 91.25, 93.25, 91.75, and 92.00% and reconstructed to 0.25%, 0, 0.50%, and 0, respectively.
We also display the experimental performance of the PED over various media, such as audio (Fig. 3C). We use four classes of audios (instrument, speech, animal, and vehicle) in the Google AudioSet (41), from which 20 ms each is selected and tested in a pretrained non–data-specific PED. The input (the red line) and the PED output (the blue dots) coincide well, while the information in the OLS (the green dotted line) acutely changes. The overall ER of OLS is 88.69% (3129 of 3528), and the output audio reduces it to 0.14% (5 of 3528).
Another important purpose of coding in an image transmission system is to resist transmission noise, which is realized with a PED by transmitting trained OLS. We use additive white Gaussian noise channels to test the performance of the PED based on different transmission distances (see note S2 for the modeling of transmission noise). Each grayscale pixel with a maximum grayscale depth of 512 is encoded into nine bits in one frame. We train the PED over all 29 instances with random noise, as shown in Fig. 3E (each line for one instance). The SNR is 9 dB for both with and without the PED, which can also be inferred from the error of the input (the second column) and the OLS (the fourth column). The threshold is grid-searched during calibration, such as Fig. 3E, and fixed during practical communications, such as Fig. 3D. We demonstrate the transmission of a grayscale painting (“Madonna and Child with Book,” cropped and resized into 150 ×125 pixels), and each grayscale pixel of the transmitted image is encoded into nine bits in one frame. The variance in the OLS dexterously models the transmission noise during training, which notably increases the anti-transmission noise ability of the model under different SNRs, i.e., different transmission distances or systems. We compare the PED with OOK (Fig. 3D), forward error correction (FEC; table S1), and QAM-16 (quadrature amplitude modulation; table S3). OOK is one of the most noise-robust modulation methods in existing optical communications that is widely used in today’s intensity modulation and direct detection systems, while FEC is one of the most commonly used error correction methods nowadays in digital electronic processors. QAM-16 is a coherent modulation that is commonly used in long-distance OFCs. The PED decreases the ER by 57.20, 37.21, and 100% (relatively) at 14, 15, and 16 dB, respectively, compared with OOK. The all-optical multilayer PED also achieves two orders of magnitude lower bit ER than QAM-16 (table S3) and similar error rates to FEC when reducing the latency and energy consumption by orders of magnitude.
As the noise level increases, the effect of the PED first rises and subsequently decreases because when the SNR is high, the experimental error of the PED dominates the results, while the PED may be unable to correct the OLS if it diverges from the ground truth too much when the SNR is quite low. Both the quantitative evaluation of the ER and the appearance of the images are distinctly improved compared with OOK at a large range of SNRs (one example at 14 dB is shown in Fig. 3D).
Data-specific mode for high-throughput image transmission
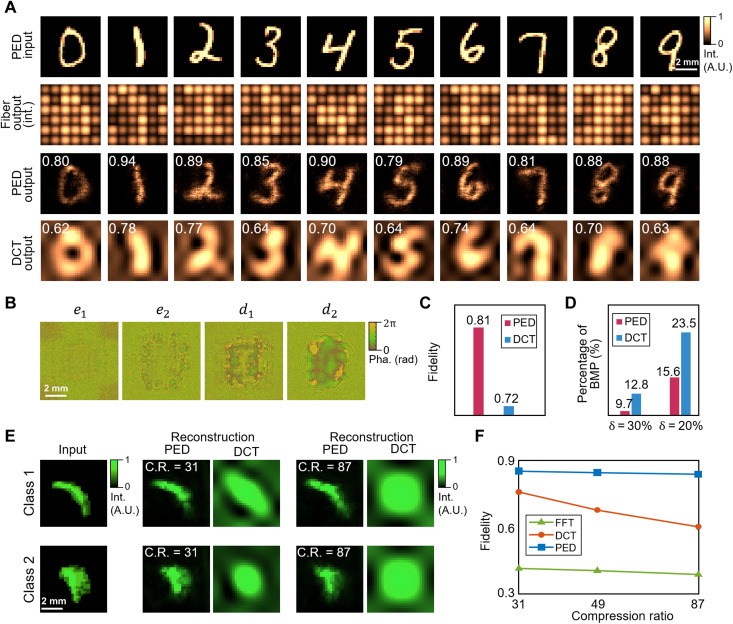
When applied in situations with some prior information of the transmission images, such as some unlabeled examples of the images, the PED allows extra compression in addition to secure transmission after unsupervised data-specific learning. Figure 4A shows an example of the PED trained to transmit the images of handwritten digits using the MNIST training set, where both the encoder and decoder are implemented with diffractive neural networks. The input digits with a size of 28 ×28 are transmitted by transforming into the OLS representations with a dimensionality of 6 × 6. Figure 4A displays the experimental results of transmitting 10 example digits, i.e., 0, 1, …, 9, from the test set (the first row). The OLS representations of the input images are generated by experimentally coupling the optical fields at different subregions of the encoder output plane with single-mode fibers and combining them. As the single-mode fiber transmits only the fundamental mode inside, it decreases the dimensionality of the transmission information. The transmission noise is modeled by setting the SNR to 24 dB with the phase noise obeying an additive Gaussian distribution (see note S2 for an example of noise modeling). After the transmission, the fiber outputs (the second row) are decoded by the decoder to reconstruct the inputs (the third row). Figure 4B displays the phase patterns of the encoder and decoder that PED uses in the task of Fig. 4A. Each layer includes 400 × 400 optical neurons.
Fig. 4. Experimental results of PED for the data-specific mode.
(A) Inputs, i.e., handwritten digits from 0 to 9, 28 ×28 grayscale pixels each (the first row), are optically transformed by the encoder and transmitted using their OLS representations. The OLS with a dimensionality of 6 × 6 is obtained by fiber coupling the optical field of different subregions on the encoder output plane, where the transmission noise is included as the variation of the OLS representations (the second row). Both amplitude noise (24 dB) and phase noise in transmission are simulated in the fiber link. The optical fields of fiber outputs are optically decoded by the decoder to reconstruct the input handwritten digits (the third row), demonstrating superior performance than DCT compression under the same compression ratio (the fourth row). Their reconstruction fidelities are labeled on each corner. Experimental results are shown here. (B) Phase masks of the diffractive layers of the PED in this task. en (n = 1, 2) is the n-th layer of the encoder, and dn (n = 1, 2) is the nth layer of the decoder. (C and D) The experimental reconstruction fidelity and percentage of bad matching pixels (BMP) of the PED and DCT averaged over the MNIST test dataset (10k images). (E) Experimental reconstruction of the PED compared with DCT at different compression ratios over the projected adrenal CT images from MedMNIST (42). C.R., compression ratios. (F) Experimental reconstruction fidelity of the PED, DCT, and FFT (fast Fourier transform) at different compression ratios. The PED surpasses the other two mainstream methods notably overall demonstrated compression ratios.
We exhibit the comparisons with the DCT compression (the fourth row), with the reconstruction fidelities labeled on each corner. The results demonstrate that the PED successfully encrypts the inputs for optical transmission and reconstructs the input digits from their low-dimensional OLS representations at a high compression ratio. Compared with the transmission results using DCT compression, the proposed PED reconstructs input digits with notably improved quality under the same compression ratio. The average fidelity of the experimental PED results over the MNIST testing set with 10k images is 0.81, whereas the transmission with DCT compression only achieves 0.72 (Fig. 4C). We also calculate the percentage of bad matching pixels, which is a common evaluation index for reconstructions (Fig. 4D), in which the PED outperforms DCT over both thresholds, indicating the advantage of PED in both details (smaller threshold) and outlines (larger threshold). We further validate the PED on the transmission of a medical dataset: adrenal computed tomography (CT) images (42). Because medical images usually require frequent transmission between departments and clouds and normally have prior information, we choose clinically collected CT images to inspect the practical performance of the PED. The original binary three-dimensional (3D) CT images are projected by one axis to generate a 28 × 28 grayscale 2D image for each adrenal gland. Figure 4E displays the experimental results of the PED over two examples from normal and pathological classes, respectively, under different compression ratios. When the compression ratio is 31 and 87, the corresponding dimensionality of the OLS is 25 and 9. The PED successfully reconstructs the shape and features of the adrenal gland (the second and fourth columns), while the DCT fails to retain any details at such high compression ratios (the third and fifth columns). The reconstruction quality of the PED remains stably high even at a quite huge compression ratio (87 times), and different classes can be easily distinguished after compression and reconstruction, which is unfulfillable to DCT (the fifth column). It not only demonstrates the powerful capability in transmission and compression of the PED but also indicates its potential to do intelligent computations such as disease diagnosis and semantic comprehension during transmission. We compare the PED with DCT and fast Fourier transform (FFT), which are one of the most widely used compression methods in image processing. The fidelity of the reconstructed image after transmission by the PED, DCT, and FFT is 0.86, 0.77, and 0.43 when the compression ratio is 31; 0.85, 0.69, and 0.42 when the compression ratio is 49; and 0.85, 0.61, and 0.40 when compression ratio is 87, respectively, as depicted in Fig. 4F. The PED notably outperforms mainstream compression methods DCT and FFT experimentally. Taking the adrenal images as an example, the PED improves the transmission throughput by orders of magnitude than PAM-8 and QAM-512, and ~87 times than DCT.
Besides, the PED corrects the errors in the input images after encoding and decoding. It is especially helpful when the error accumulates during long-distance transmission and plenty of optical-electrical conversions, resulting in noisy input when transmitted to downstream links. Therefore, we further demonstrate the PED dealing with noisy input in fig. S3. It shows the experimental results of transmitting 10 examples of MNIST handwritten digits, i.e., 0, 1, …, 9 (the first row), with additive Gaussian noise. The encoder encrypts and extracts the information before the coupling system subsamples the light field into a 6 × 6 OLS. The transmission noise in the fiber bundle, with the SNR of 24 dB and additive Gaussian phase noise, is modeled as the variation in OLS (the second row). The PED achieves comparable reconstruction performance (the third row) as in Fig. 4A because the lossy compression with the PED entitles the PED to powerful denoising capability. The results prove that the PED is qualified for a wide range of transmission distances and multilevel transmission.
DISCUSSION
By effectively extracting features from the original images, PED achieves orders of magnitude higher throughput compared with existing methods in image transmission. On the medical dataset, PED improves the transmission throughput by 232.3 times, 77.4 times, and 87.1 times compared with PAM-8, QAM-512, and DCT when achieving the same transmission fidelity experimentally (see note S3 for calculation details). In the general mode, because the PED solves the bottleneck of system latency by all-optical processing, its bit rate theoretically achieves 24.6 Tbit/s (see note S4 for calculation details). In addition, adjusting the parameters in the network helps further improve the performance of PED. We analyze the four main parameters that influence the performance of the PED, which are the layer number of the encoder/decoder (fig. S7A), the diffractive distance between the layers (fig. S7B), the diffractive distance after the last layer in the encoder/decoder (fig. S7C), and the pixel size, i.e., size of neurons (fig. S7D). The performance of the PED improves notably when the layer number of the PED decoder increases from 1 to 2 and grows gradually when the layer number continues to increase for both general and data-specific modes. For the distance between the diffractive masks, 15 cm achieves the best performance for both general and data-specific modes. The performance of the PED increases as the diffractive distance after the last layer of the encoder/decoder increases in the range of 10 to 50 cm. The PED shows better performance with smaller pixel sizes in the range of 10 to 25 μm.
Simultaneously, the all-optical PED experimentally improves the computation latency by five orders of magnitude than the state-of-the-art CPU (Intel, CA, Intel Core i7 6500U CPU @2.5 GHz). In addition, we calculate the end-to-end system latency of PED in a fiber communication system, including computation, opt-electronic conversions, and analog-to-digital converters (fig. S11), and the PED improves the system latency by more than four orders of magnitude than the state-of-the-art CPU. It shows that the PED optimizes the time-consuming bottleneck that restricts the improvement of throughput instead of some parts that are fast enough already. Even when compared with the state-of-the-art graphics processing unit (GPU) with ultra-high computing speed (~47 TOPS/S) (43), PED remains to achieve one order of magnitude improvement in system latency (see note S3 for calculation and measurement details). We note that the commercial image communication systems can only achieve a computing speed much lower than this example with the state-of-the-art CPU or GPU considering the cost. Therefore, the actual improvement may be higher.
Compared with existing optical neural networks, the PED extends the application beyond decision-making tasks to notably wider generative scopes. Figure S4 demonstrates applications of the PED as a universal unsupervised optical generative model in style transferring and human action video enhancement. Because decision tasks and labeled images are only a small portion in real life, the demonstration of an unsupervised generative photonic model with ultra-high speed and the ability of parallel computation will be capable of revolving plenty of application fields, including augmented reality, edge computing, and virtual reality.
In conclusion, we propose an unsupervised PED for OFC. It not only provides an end-to-end learned processor for image processing in OFC, including encoding, encryption, compression, and decoding all optically but also improves the communication quality by processing in the optical domain directly. Two modes of the PED have introduced: the general mode for arbitrary image coding and encryption and the data-specific mode for notably high throughput. The transmission ER experimentally decreases by 57% by the PED, as demonstrated on a benchmarking dataset. The PED widens the transmission throughput by two orders of magnitude than PAM-8 and 87 times than DCT over displayed medical images. The all-optical PED reduces the system latency by more than four orders of magnitude compared with the state-of-the-art CPU.
By codesigning the encoder, decoder, and fiber system all in the optical domain, our work makes inherent connections between the unsupervised learning architecture and the physical model of fiber communication systems, inspiring the next-generation all-optical communication systems with higher throughput, accuracy, and data security. We believe that the proposed generative photonic computing system and the end-to-end unsupervised photonic learning method will facilitate a wide range of artificial intelligence applications, including 6G, medical diagnosis, robotics, and edge computing.
MATERIALS AND METHODS
PED modeling and training details
We use a VAE architecture to establish the PED, which is one of the most mainstream unsupervised generative models with various application scopes (38). The encoder-decoder structure perfectly matches the OFC process, and its ability to reconstruct data from a low-dimensional domain enables the PED to compress and encrypt the transmitted information. In addition, the VAE provides better performance in noise resistance due to the variation in latent space when training. The loss function of the PED for optimization can be described as
where lKLD is the Kullback-Leibler divergence that guarantees the distribution in the OLS close enough to the ideal distribution, i.e., Gaussian distribution; lMSE is the mean square error between the PED output and the input; and lOP is a penalty term. To prevent the middle results from changing fiercely between the diffractive layers to make the images sick or sensitive to noise, we use an optical penalty term in the loss, similar to what many electronic deep neural networks do (44). lOP is usually composed of an l1- or l2-norm between the middle results and the ideal output; α, β, and γ are constant coefficients that balance these losses.
We use the optical fields in the fibers to characterize the high-dimensional latent values in the optical networks. The all-optical PED encodes the information in both the amplitude and phase domains. During training, the phase and amplitude are calculated on the basis of the optical field in front of the coupling lens array with corresponding complex coupling coefficients. For experimental convenience, we also establish the model of optoelectronic PED. It allows the PED to achieve comparable performance with only one phase modulator. The output of each diffractive layer is captured with a sensor, and the measured intensity is fed back to reuse the diffractive system. In this way, the optoelectronic PED achieves nonlinearity from the sensor but loses phase information to encode. Figure S5 presents the comparison of the performance between the all-optical and optoelectronic PED on both general and data-specific modes. The all-optical and optoelectronic PED achieves tantamount results in the reconstruction fidelity and noise resistance. In addition, the latency of this reusing architecture in optoelectronic PED has been proved ultra-low (45). Therefore, the optoelectronic PED provides a convenient way to validate the all-optical PED. More details for the experimental implementation in Figs. 3 and 4 are included in the “Experimental setup” section below.
During training, the proposed OLS complies with the assumption of a biased Gaussian distribution because the intensity of the optical signals is nonnegative. The deviation is set as a constant instead of learning during training to mimic the real fiber communication situations. Adjusting the deviation to different values helps the PED handle different noise levels. The phase masks for the general and data-specific modes are shown in fig. S6.
Experimental setup
The system design and experimental setup are shown in fig. S2. We use a single-mode 532-nm laser (Changchun New Industries Optoelectronics Tech. Co., Ltd., MGL-III-532-200 mW) to generate the collimating incident light. A cascaded beam expander system is used to expand the diameter of the beam to ~25 mm. We use an amplitude-modulation SLM (HOLOEYE Photonics AG, HES6001) to generate the grayscale input and a phase-only SLM (Meadowlark Optics Inc., P1920-400-800-PCIE) as the diffractive layer in the optical neural network. It has a frame rate of up to 714 Hz. The pixel size of the optical neurons that we use in the PED is 18.4 μm. A 4f system is placed between the two SLMs to conjugate the input image onto the phase modulation plane. The diffractive distance between the second SLM and the sensor is 300 mm. We use a scientific complementary metal-oxide semiconductor (Tucsen Photonics Co. Ltd., Dhyana 400BSI) to measure the intensity output from the optical neural network. In the optoelectronic PED, the multilayer network is realized by iteration with this system. The coupling of the fiber is measured in sequence by one fiber to mimic the effect of the array (fig. S2C). An equivalent experiment of all-optical PED is demonstrated in fig. S15, which shows similar exceeding performance to optoelectronic PED. The long-distance transmission noise is simulated according to the SNR as modeled in the Supplementary Materials. We use the single-mode fiber (Daheng Optics, DH-FSM450-FC) at 532 nm.
Adaptive training of the PED
The layers in the PED should be aligned precisely, or the signal cannot be processed with the correct corresponding weights. In an integrated all-optical PED shown in Fig. 1B, it is aligned with the high-resolution microscope and fixed with bonding, which has submicrometer alignment precision. For evaluation setup with commercial devices, the alignment precision depends on the precision of the translation stages (Daheng Optics, GCM-930602 M), which provides an alignment error below 6 μm in PED. The PED has the robustness to small misalignment errors and, for larger alignment errors, we use adaptive training to correct some of the errors in the experimental system. By retraining the last few diffractive layers with experimental middle outputs over a small scale of the training dataset, adaptive training achieves distinct improvement on the test dataset. Because of the leverage of reconfigurable equipment in the setup, we can easily change the weight in the PED after adaptive training.
General mode
Because the training and testing datasets are the same and the scale is small, we go through the whole dataset (512 instances). The noise is randomly added in each training epoch. Adaptive training fine-tunes the decoder masks for several epochs over data with random noise.
Data-specific mode
We experimentally test the output of the encoder on a small part of the training dataset (~3%) and fine-tune the decoder with this small amount of training data.
Modeling of the coupling in the PED
The corresponding lenses in the microlens array divide the light-field output from the encoder into m areas, where m is the dimensionality of the OLS. Each lens Fourier transfers the corresponding area to its frequency domain on its Fourier plane. Given single-mode fibers with a proper numerical aperture, only the low frequencies are coupled into the fibers. The light in the fiber is a combination of light with different incident angles with corresponding complex coupling coefficients. The coupling efficiency is based on the data because the nonplanar wavefront affects the coupling. Figure S8 (A and B) gives an example of the modulated light field on the front focal plane and the results after coupling by the lens array. Light with different incident angles has different complex coupling coefficients.
In this work, we simulate the complex coupling coefficients at different incident angles with the finite-difference time-domain (FDTD) method (fig. S8C). In this way, any complicated incident wavefront can be decomposed into components from different angles to add up.
We take the vertical incidence as an example to verify the FDTD simulation with theoretical predictions. We use the Gaussian approximation of the zeroth-order Bessel function. The electric field of the fundamental mode on the edge is (46)
where r is the radial coordinate and ω0 is the radius of the single-mode field. The coupling efficiency is usually defined as (46)
where Eif is the electric field of the incident light on the back focal plane and Eff is the electric field on the fiber edge. The FDTD simulation corresponds well with the theoretical result in this example.
Acknowledgments
We thank F. Bao, H. Xie, Y. Guo, and Y. Jin for their helpful discussions.
Funding: This work is supported by the Project of NSFC (nos. 62088102, 62275139, and 62125106), the National Key Research and Development Program of China (no. 2021ZD0109902), the National Natural Science Foundation of China (no. 62071271), the Beijing Municipal Natural Science Foundation (no. JQ21012), and the Project of MOST (nos. 2020AA0105500 and 2021ZD0109901).
Author contributions: Q.D., X.L., and L.F. initiated and supervised the project. Y.C., X.L., and J.W. conceived the research and method. Y.C. and T.Z. designed the simulation and experiment and conducted the experiments. Y.C. and T.Z. built the experimental system. Y.C., X.L., and J.W. analyzed the results. Y.C., H.Q., J.W., X.L., L.F., and Q.D. prepared the manuscript with input from all authors. All authors discussed the research.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Supplementary Materials
This PDF file includes:
Notes S1 to S6
Figs. S1 to S15
Tables S1 to S3
Legends for movies S1 and S2
References
Other Supplementary Material for this : manuscript includes the following:
Movies S1 and S2
REFERENCES AND NOTES
- 1.A. Voulodimos, N. Doulamis, A. Doulamis, E. Protopapadakis, Deep learning for computer vision: A brief review. Comput. Intell. Neurosci. 2018, 2018, 7068349 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.S. Li, L. D. Xu, S. Zhao, The internet of things: A survey. Inf. Syst. Front. 17, 243–259 (2015). [Google Scholar]
- 3.Y. Wang, Z. Su, N. Zhang, R. Xing, D. Liu, T. H. Luan, X. Shen, A survey on metaverse: Fundamentals, security, and privacy. arXiv:2203.02662 [cs.CR] (5 Mar 2022). [Google Scholar]
- 4.P. Winzer, Scaling optical fiber networks: Challenges and solutions. Opt. Photonics News 26, 28–53 (2015). [Google Scholar]
- 5.L. Wanhammar, DSP integrated circuits, in Academic Press Series in Engineering, (Academic Press, 1999), pp. 1–29. [Google Scholar]
- 6.K. Kikuchi, Fundamentals of coherent optical fiber communications. J. Light. Technol. 34, 157, 179 (2016). [Google Scholar]
- 7.D. J. Richardson, Beating the electronics bottleneck. Nat. Photonics 3, 562–564 (2009). [Google Scholar]
- 8.S. Dhawan, A review of image compression and comparison of its algorithms. Int. J. Electron. Commun. Technol. 2, 22, 26 (2011). [Google Scholar]
- 9.M. Rabbani, P. W. Jones, in Digital Image Compression Techniques (SPIE Press, 1991), p. 240. [DOI] [PubMed] [Google Scholar]
- 10.M. M. P. Petrou, C. Petrou, in Image Processing: The Fundamentals (John Wiley & Sons, ed. 2, 2010). [Google Scholar]
- 11.P. Bayvel, Kuen Charles Kao (1933–2018): Engineer who proposed optical fibre communications that underpin the Internet. Nature 563, 326 (2018). [DOI] [PubMed] [Google Scholar]
- 12.P. Sharma, M. Singh, A review of the development in the field of fiber optic communication systems. Int. J. Emerg. Technol. Adv. Eng. 3, 113–119 (2013). [Google Scholar]
- 13.D. A. Morero, M. A. Castrillon, A. Aguirre, M. R. Hueda, O. E. Agazzi, Design tradeoffs and challenges in practical coherent optical transceiver implementations. J. Light. Technol. 34, 121–136 (2016). [Google Scholar]
- 14.G. P. Agrawal, in Fiber-Optic Communication Systems (John Wiley & Sons, ed. 4, 2011). [Google Scholar]
- 15.L. R. Rabiner, B. Gold, in Theory and Application of Digital Signal Processing (Prentice-Hall, 1975). [Google Scholar]
- 16.O. Ishida, K. Takei, E. Yamazaki, Power efficient DSP implementation for 100G-and-beyond multi-haul coherent fiber-optic communications, in Proceedings of the 2016 Optical Fiber Communications Conference and Exhibition (OFC) (IEEE, 2016). [Google Scholar]
- 17.K. Roberts, I. Roberts, DSP: A disruptive technology for optical transceivers, in Proceedings of the 2009 35th European Conference on Optical Communication (ECOC) (IEEE, 2009). [Google Scholar]
- 18.E. M. Ip, J. M. Kahn, Fiber impairment compensation using coherent detection and digital signal processing. J. Light. Technol. 28, 502–519 (2010). [Google Scholar]
- 19.A. S. Raja, S. Lange, M. Karpov, K. Shi, X. Fu, R. Behrendt, D. Cletheroe, A. Lukashchuk, I. Haller, F. Karinou, B. Thomsen, K. Jozwik, J. Liu, P. Costa, T. J. Kippenberg, H. Ballani, Ultrafast optical circuit switching for data centers using integrated soliton microcombs. Nat. Commun. 12, 5867 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.A. E. Willner, S. Khaleghi, M. R. Chitgarha, O. F. Yilmaz, All-optical signal processing. J. Light. Technol. 32, 660–680 (2014). [Google Scholar]
- 21.L. Yan, A. E. Willner, X. Wu, A. Yi, A. Bogoni, Z.-Y. Chen, H.-Y. Jiang, All-optical signal processing for ultrahigh speed optical systems and networks. J. Light. Technol. 30, 3760–3770 (2012). [Google Scholar]
- 22.M. P. Fok, Z. Wang, Y. Deng, P. R. Prucnal, Optical layer security in fiber-optic networks. IEEE Trans. Inf. Forensics Secur. 6, 725–736 (2011). [Google Scholar]
- 23.A. Sludds, S. Bandyopadhyay, Z. Chen, Z. Zhong, J. Cochrane, L. Bernstein, D. Bunandar, P. B. Dixon, S. A. Hamilton, M. Streshinsky, A. Novack, T. Baehr-Jones, M. Hochberg, M. Ghobadi, R. Hamerly, D. Englund, Delocalized photonic deep learning on the internet’s edge. Science 378, 270–276 (2022). [DOI] [PubMed] [Google Scholar]
- 24.C. Liu, Q. Ma, Z. J. Luo, Q. R. Hong, Q. Xiao, H. C. Zhang, L. Miao, W. M. Yu, Q. Cheng, L. Li, T. J. Cui, A programmable diffractive deep neural network based on a digital-coding metasurface array. Nat. Electronics 5, 113–122 (2022). [Google Scholar]
- 25.X. Lin, Y. Rivenson, N. T. Yardimci, M. Veli, Y. Luo, M. Jarrahi, A. Ozcan, All-optical machine learning using diffractive deep neural networks. Science 361, 1004–1008 (2018). [DOI] [PubMed] [Google Scholar]
- 26.Y. Shen, N. C. Harris, S. Skirlo, M. Prabhu, T. Baehr-Jones, M. Hochberg, X. Sun, S. Zhao, H. Larochelle, D. Englund, M. Soljačić, Deep learning with coherent nanophotonic circuits. Nat. Photonics 11, 441–446 (2017). [Google Scholar]
- 27.J. Feldmann, N. Youngblood, M. Karpov, H. Gehring, X. Li, M. Stappers, M. le Gallo, X. Fu, A. Lukashchuk, A. S. Raja, J. Liu, C. D. Wright, A. Sebastian, T. J. Kippenberg, W. H. P. Pernice, H. Bhaskaran, Parallel convolutional processing using an integrated photonic tensor core. Nature 589, 52–58 (2021). [DOI] [PubMed] [Google Scholar]
- 28.X. Xu, M. Tan, B. Corcoran, J. Wu, A. Boes, T. G. Nguyen, S. T. Chu, B. E. Little, D. G. Hicks, R. Morandotti, A. Mitchell, D. J. Moss, 11 TeraFLOPs per second photonic convolutional accelerator for deep learning optical neural networks. Nature 589, 44–51 (2021). [DOI] [PubMed] [Google Scholar]
- 29.J. Liu, Q. Wu, X. Sui, Q. Chen, G. Gu, L. Wang, S. Li, Research progress in optical neural networks: Theory, applications and developments. PhotoniX 2, 5 (2021). [Google Scholar]
- 30.M. Li, H.-S. Jeong, J. Azaña, T.-J. Ahn, 25-terahertz-bandwidth all-optical temporal differentiator. Opt. Express 20, 28273–28280 (2012). [DOI] [PubMed] [Google Scholar]
- 31.E. Cohen, D. Malka, A. Shemer, A. Shahmoon, Z. Zalevsky, M. London, Neural networks within multi-core optic fibers. Sci. Rep. 6, 1–14 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.F. Ashtiani, A. J. Geers, F. Aflatouni, An on-chip photonic deep neural network for image classification. Nature 606, 501–506 (2022). [DOI] [PubMed] [Google Scholar]
- 33.D. Brunner, M. C. Soriano, C. R. Mirasso, I. Fischer, Parallel photonic information processing at gigabyte per second data rates using transient states. Nat. Commun. 4, 29080 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.B. J. Shastri, A. N. Tait, T. Ferreira de Lima, W. H. P. Pernice, H. Bhaskaran, C. D. Wright, P. R. Prucnal, Photonics for artificial intelligence and neuromorphic computing. Nat. Photonics 15, 102–114 (2021). [Google Scholar]
- 35.J. Feldmann, N. Youngblood, C. D. Wright, H. Bhaskaran, W. H. P. Pernice, All-optical spiking neurosynaptic networks with self-learning capabilities. Nature 569, 208–214 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.C. Huang, S. Fujisawa, T. F. de Lima, A. N. Tait, E. C. Blow, Y. Tian, S. Bilodeau, A. Jha, F. Yaman, H.-T. Peng, H. G. Batshon, B. J. Shastri, Y. Inada, T. Wang, P. R. Prucnal, Silicon photonic-electronic neural network for fibre nonlinearity compensation. Nat. Electron. 4, 837–844 (2021). [Google Scholar]
- 37.I. J. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, Y. Bengio, Generative adversarial networks. Commun. ACM 63, 139–144 (2020). [Google Scholar]
- 38.M. Welling, Auto-encoding variational bayes. arXiv:1312.6114 [stat.ML] (20 December 2013). [Google Scholar]
- 39.C. Wu, X. Yang, H. Yu, R. Peng, I. Takeuchi, Y. Chen, M. Li, Harnessing optoelectronic noises in a photonic generative network. Sci. Adv. 8, eabm2956 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.H. Xiao, K. Rasul, R. Vollgraf, Fashion-MNIST: A novel image dataset for benchmarking machine learning algorithms. arXiv:1708.07747 [cs.LG] (25 August 2017).
- 41.J. F. Gemmeke, D. P. W. Ellis, D. Freedman, A. Jansen, W. Lawrence, R. C. Moore, M. Plakal, M. Ritter, Audio set: An ontology and human-labeled dataset for audio events, in Proceeedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (IEEE, 2017). [Google Scholar]
- 42.J. Yang, R. Shi, D. Wei, Z. Liu, L. Zhao, B. Ke, H. Pfister, B. Ni, MedMNIST v2: A large-scale lightweight benchmark for 2D and 3D biomedical image classification, arXiv:2110.14795 [cs.CV] (27 October 2021). [DOI] [PMC free article] [PubMed]
- 43.Nvidia. Inference Platforms for HPC Data Centers | NVIDIA Deep Learning AI; www.nvidia.cn/deep-learning-ai/inference-platform/hpc/.
- 44.C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, A. Rabinovich, Going deeper with convolutions, in Proceeedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (IEEE, 2015). [Google Scholar]
- 45.T. Zhou, X. Lin, J. Wu, Y. Chen, H. Xie, Y. Li, J. Fan, H. Wu, L. Fang, Q. Dai, Large-scale neuromorphic optoelectronic computing with a reconfigurable diffractive processing unit. Nat. Photonics 15, 367–373 (2021). [Google Scholar]
- 46.C. Ruilier, A study of degraded light coupling into single-mode fibers. Proc. SPIE 3350, 319–329 (1998). [Google Scholar]
- 47.B. Rahmani, D. Loterie, G. Konstantinou, D. Psaltis, C. Moser, Multimode optical fiber transmission with a deep learning network. Light Sci. Appl. 7, 69 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.A. Splett, C. Kurtske, K. Petermann, Ultimate transmission capacity of amplified optical fiber communication systems taking into account fiber nonlinearities, in Proceedings of the 1993 19th European Conference on Optical Communication (ECOC) (IEEE, 1993). [Google Scholar]
- 49.J. Hecht, in Understanding Fiber Optics (Laser Light Press, 2015). [Google Scholar]
- 50.V. J. Urick, J. D. Mckinney, K. J. Williams, in Fundamentals of Microwave Photonics (Wiley, 2015). [Google Scholar]
- 51.S. Xing, G. Li, Z. Li, N. Chi, J. Zhang, Study of efficient photonic chromatic dispersion equalization using MZI-based coherent optical matrix multiplication. arXiv:2206.10317 [physics.optics] (20 May 2022).
- 52.P. Poggiolini, G. Bosco, A. Carena, V. Curri, Y. Jiang, F. Forghieri, The GN-model of fiber non-linear propagation and its applications. J. Light. Technol. 32, 694–721 (2014). [Google Scholar]
- 53.P. Poggiolini, The GN model of non-linear propagation in uncompensated coherent optical systems. J. Light. Technol. 30, 3857–3879 (2012). [Google Scholar]
- 54.B. Goebel, R. J. Essiambre, G. Kramer, P. J. Winzer, N. Hanik, Calculation of mutual information for partially coherent Gaussian channels with applications to fiber optics. IEEE Trans. Inf. Theory 57, 5720–5736 (2011). [Google Scholar]
- 55.T. Fehenberger, A. Alvarado, G. Böcherer, N. Hanik, On probabilistic shaping of quadrature amplitude modulation for the nonlinear fiber channel. J. Light. Technol. 34, 5063–5073 (2016). [Google Scholar]
- 56.C. Haffner, W. Heni, Y. Fedoryshyn, J. Niegemann, A. Melikyan, D. L. Elder, B. Baeuerle, Y. Salamin, A. Josten, U. Koch, C. Hoessbacher, F. Ducry, L. Juchli, A. Emboras, D. Hillerkuss, M. Kohl, L. R. Dalton, C. Hafner, J. Leuthold, All-plasmonic Mach-Zehnder modulator enabling optical high-speed communication at the microscale. Nat. Photonics 9, 525–528 (2015). [Google Scholar]
- 57.A. Forouzmand, M. M. Salary, G. Kafaie Shirmanesh, R. Sokhoyan, H. A. Atwater, H. Mosallaei, Tunable all-dielectric metasurface for phase modulation of the reflected and transmitted light via permittivity tuning of indium tin oxide. Nanophotonics 8, 415–427 (2019). [Google Scholar]
- 58.C. Caillaud, P. Chanclou, F. Blache, P. Angelini, B. Duval, P. Charbonnier, D. Lanteri, G. Glastre, M. Achouche, Integrated SOA-PIN detector for high-speed short reach applications. J. Light. Technol. 33, 1596–1601 (2015). [Google Scholar]
- 59.B. J. Puttnam, G. Rademacher, R. S. Luís, Space-division multiplexing for optical fiber communications. Optica 8, 1186–1203 (2021). [Google Scholar]
- 60.Z. Wang, L. Chang, F. Wang, T. Li, T. Gu, Integrated photonic metasystem for image classifications at telecommunication wavelength. Nat. Commun. 13, 2131 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.C. Schüldt, I. Laptev, B. Caputo, Recognizing human actions: A local SVM approach, in Proceedings of the 17th International Conference on Pattern Recognition, 2004. ICPR 2004 (ICPR) (IEEE, 2004). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Notes S1 to S6
Figs. S1 to S15
Tables S1 to S3
Legends for movies S1 and S2
References
Movies S1 and S2