Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Jan 30;145(6):3276–3282. doi: 10.1021/jacs.2c11450

Resolving Molecular Heterogeneity with Single-Molecule Centrifugation

Yi Luo †,‡,§, Jeffrey Chang ∥, Darren Yang †,‡,§, J Shepard Bryan IV ⊥,#, Molly MacIsaac †,‡,§, Steve Pressé ⊥,#,, Wesley P Wong †,‡,§,*
PMCID: PMC9936575  PMID: 36716175

Abstract

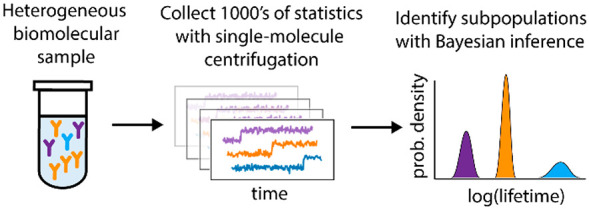
graphic file with name ja2c11450_0005.jpg

For many classes of biomolecules, population-level heterogeneity is an essential aspect of biological function—from antibodies produced by the immune system to post-translationally modified proteins that regulate cellular processes. However, heterogeneity is difficult to fully characterize for multiple reasons: (i) single-molecule approaches are needed to avoid information lost by ensemble-level averaging, (ii) sufficient statistics must be gathered on both a per-molecule and per-population level, and (iii) a suitable analysis framework is required to make sense of a potentially limited number of intrinsically noisy measurements. Here, we introduce an approach that overcomes these difficulties by combining three techniques: a DNA nanoswitch construct to repeatedly interrogate the same molecule, a benchtop centrifuge force microscope (CFM) to obtain thousands of statistics in a highly parallel manner, and a Bayesian nonparametric (BNP) inference method to resolve separate subpopulations with distinct kinetics. We apply this approach to characterize commercially available antibodies and find that polyclonal antibody from rabbit serum is well-modeled by a mixture of three subpopulations. Our results show how combining a spatially and temporally multiplexed nanoswitch-CFM assay with BNP analysis can help resolve complex biomolecular interactions in heterogeneous samples.

Population heterogeneity of biomolecules often bears functional significance; for example, antibodies produced by the immune system are highly polyclonal, with each subpopulation exhibiting distinct binding properties.1−3 In bulk assays of heterogeneous populations, only ensemble-averaged properties are observed. To characterize subpopulations directly, it is necessary to use techniques capable of interrogating single molecules. Recently developed approaches for single-molecule manipulation have led to many mechanistic insights in biology, from the action of molecular motors during transcription and replication, to the dynamic strength of receptor–ligand interactions.4−8 However, the limited throughput of traditional one-molecule-at-a-time methods makes it difficult to fully resolve samples that are highly heterogeneous such as polyclonal antibodies. While recent advances in multiplexed single-molecule methods9−15 allow statistics on many different molecules to be collected, sufficient information must also be collected for each molecule, and a suitable analysis framework is needed to interpret this data. In this work, we demonstrate that by combining highly multiplexed single-molecule centrifuge force microscopy (CFM)14−16 with DNA Nanoswitches17−20 and Bayesian Non-Parametric (BNP) inference,21−29 we can resolve and characterize the unbinding kinetics of distinct subpopulations in a polyclonal antibody sample.

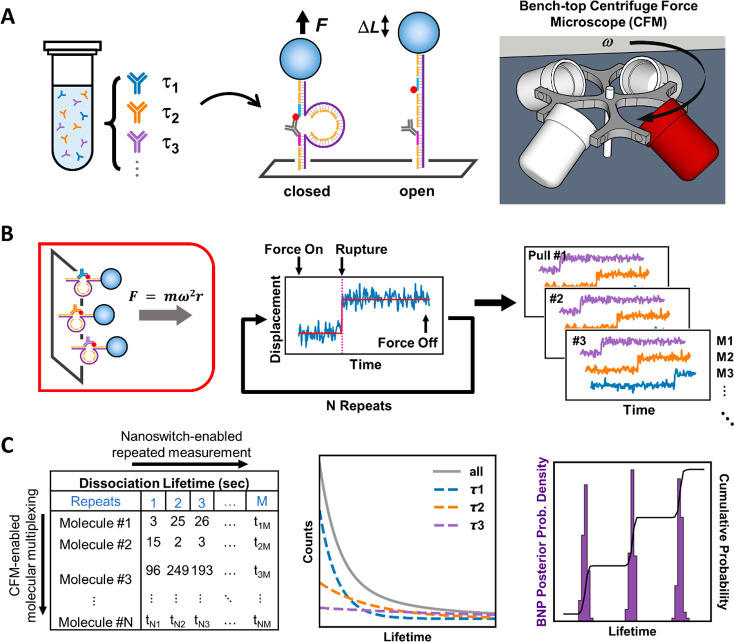
The key to resolving heterogeneity is to collect enough single-molecule statistics—both in terms of the number of molecules interrogated, and the number of statistics collected per molecule—to enable precise characterization of subpopulation fractions and their corresponding molecular properties. Accordingly, we have developed an experimental method with sufficiently high throughput along both dimensions [Figure 1C]. To measure properties of hundreds of individual molecules in parallel, we use the Centrifuge Force Microscope (CFM) [Figure 1A],14,15 an inexpensive and easy-to-use instrument capable of performing highly multiplexed9−12,30 single-molecule force spectroscopy. To collect multiple statistics for a given molecule, we use programmable DNA nanoswitches,17,18 nanomechanical devices31−33 that link together receptor–ligand pairs.34−36 Of particular note, the nanoswitch enables repeated measurements across multiple binding-unbinding cycles. Nanoswitches also provide a unique molecular signature which can be used to filter out aberrant statistics. Together, the CFM and the DNA nanoswitch allow hundreds of molecules to be individually, repeatedly interrogated [Figure 1C].

Figure 1.

Figure 1

Open in a new tab

Schematic description of the assay. (A) Heterogeneous samples can contain multiple subpopulations with distinct unbinding kinetics (left). We mount pairs of antibody and antigen molecules into a DNA nanoswitch construct so that binding and unbinding can be seen by a change in DNA length (middle). The constructs are placed in a benchtop Centrifuge Force Microscope (CFM, right). (B) The CFM applies a centrifugal force on the antibody–antigen bond (left), leading to rupture events with a distinct signature (middle). By simultaneously tracking all the beads in the field of view, many pairs of molecules can be measured at once; with repeated pulls, multiple statistics can be collected per molecular pair (right). (C) Transition times are determined from bead trajectories and collated into a table (left). Collectively, the unbinding kinetics are multiexponential, but the individual subpopulations are single-exponential (middle). With Bayesian nonparametric analysis, the separate subpopulations can be resolved (right).

We use antibody–antigen binding to demonstrate that this method can resolve molecular heterogeneity. Antibody–antigen interactions are central to immune function and widely applied in molecular detection, diagnosis, and therapeutics.37−39 The issue of heterogeneity is important for antibodies because the immune system naturally produces polyclonal antibodies.2,3,40 Many therapeutics and reagents are also polyclonal.41,42

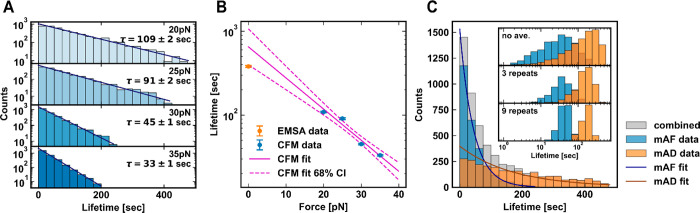
To validate our assay, we first measured a homogeneous interaction between a monoclonal antibody and its cognate antigen. We chose fluorescein and its monoclonal antibody (mAF) (Invitrogen 31242) as the test system. We tethered together single pairs of fluorescein and mAF molecules on a DNA nanoswitch construct [Figure 1A]; next, we immobilized the constructs on a flow cell surface to allow a stretching force to be applied with the CFM [Figure 1B, Figure S3] (see Section S1 for methods). Bond rupture of individual antibody–antigen pairs can be observed by tracking bead motion under the microscope [Figure S4, Figure S5]. We applied a constant stretching force of 30pN for a duration until most pairs within the field of view ruptured; subsequently, we reduced the stretching force to zero to allow relaxation and rebinding before repeating the force cycle [Figure 1B]. After 20 force cycles, we collected 2642 individual unbinding events of 341 validated single antibody–antigen pairs from a single field of view. Collectively, the unbinding times show a clear single-exponential distribution with a time constant of 45 ± 1 s [Figure 2A].

Figure 2.

Figure 2

Open in a new tab

Validation of the CFM for homogeneous samples. (A) Unbinding lifetime distribution of the interaction between fluorescein and monoclonal antifluorescein (mAF), with y-axis on a log scale. The fit line and characteristic lifetime τ show results from a maximum likelihood estimation using a truncated exponential model. (B) Dependence of mAF unbinding lifetime on force as measured by CFM, with the best-fit line (magenta) based on the Bell–Evans model: τ ∝ exp (−F/F0). An independent zero force lifetime was measured by EMSA (orange). (C) Unbinding lifetime distribution of fluorescein and monoclonal antifluorescein (mAF), and DIG and monoclonal anti-DIG (mAD). Shown in gray is the combined data, representative of ensemble-averaged kinetics in a mixed sample. The inset shows the narrowing of the two distributions by taking per molecule averaged lifetimes (x-axis on log scale, y-axis normalized counts). The top panel contains the same data as in the main plot but with the x-axis on a log scale. The middle and lower panels show the average of a random subset of 3 and 9 data points per molecular pair, respectively, for all molecular pairs with at least that many statistics collected (the number of molecular pairs measured for the 3 repeat data was Nmolecular pairs = 288 and 319 for mAF and mAD, respectively; correspondingly, for 9 repeats, Nmolecular pairs = 171 and 106).

Next, to assess the force-dependence of the unbinding rate, we repeated the experiment under additional constant stretching forces of 20pN, 25pN, and 35pN. For each stretching force, > 2300 unbinding events were measured from >293 validated pairs of molecules [Table 1]. In all cases we observe clear single-exponential unbinding kinetics [Figure 2A]. We found that the mean lifetime varies exponentially with force [Figure 2B], as described by the Bell–Evans model,7,8 indicating that the underlying interaction is homogeneous and can be well-modeled as a single-bond interaction. A linear fit of the log lifetime vs force yields a characteristic force scale of 12 ± 6 pN, or an equivalent transition state length scale of 0.3 ± 0.2 nm, roughly the dimensions of a small molecule such as fluorescein. The extrapolated equilibrium unbinding time of 600 ± 300 s agrees well with an independent bulk electrophoretic mobility shift assay (380 ± 50 s) [Figure S1].

Table 1. Statistics for Monoclonal Datasets Collected.

  Nmolecular pairs Nevents Lifetime (s)
mAF 20pN 405 4273 109 ± 2
mAF 25pN 349 2300 91 ± 2
mAF 30pN 341 2642 45 ± 1
mAF 35pN 293 2847 33 ± 1
mAD 30pN 415 2385 259 ± 11
Open in a new tab

For comparison, we also measured the binding strength of a second monoclonal antibody–antigen pair, digoxygenin (DIG) and anti-DIG (mAD) (Invitrogen 700772). The unbinding kinetics of mAF and mAD under a stretching force of 30pN are presented in Figure 2C; both have single exponential decay kinetics, but the mAD interaction has a longer lifetime of 259 ± 11 s [Table 1].

Although the population-level unbinding kinetics of these particular monoclonal antibodies are distinguishable, this distinction would be less clear if fewer statistics were available, or if the two underlying time constants were more similar. The challenge of discriminating between two subpopulations is exasperated by the broad, exponential shape of their lifetime distributions, as shown in Figure 2C. Crucially, discrimination between subpopulations can be improved by averaging across the repeated measurements of each molecular pair. This per-molecule-averaging reduces the width of the lifetime distribution, as illustrated in the inset of Figure 2C. Compared to the case with no averaging, the two peaks are more easily distinguished after averaging as few as 3 lifetime measurements per molecular pair. The variation in per-molecule-averaged lifetime is further reduced by averaging over 9 repeats [Figure 2C lower inset; Figure S5]. Thus, the ability to make repeated measurements can enable multiple species with similar lifetimes to be more easily distinguished.

To characterize how well this approach could discriminate subpopulations, we next considered mixtures of two distinct monoclonal antibodies. A handmade mixture of monoclonal antibodies is conceptually similar to polyclonal antibodies generated from the natural immune response. At the ensemble level, the unbinding kinetics of a mixed sample is a sum of exponentials, illustrated by the gray curve in Figure 1C. However, at the single-molecule level, the unbinding statistics obtained from a given molecular pair should be distributed monoexponentially. The rate constant is identical for all molecular pairs in the same subpopulation but differs between subpopulations. To more confidently infer which subpopulation a molecular pair belongs to, we take the average of the repeated statistics per molecule; to determine the subpopulation fractions, we count the number of molecular pairs assigned to each subpopulation. These two capabilities are enabled by greater throughput of our assay at the molecule and population level, respectively.

The task of parameter fitting to heterogeneous samples is more difficult than for homogeneous samples. It is necessary to infer a separate population fraction pk and average lifetime τk for each subpopulation of the mixture; furthermore, each molecular pair has a latent (unobserved) variable for which subpopulation it is in. To infer these parameters from our data set, we developed a nonparametric Bayesian model and sampled the posterior distribution with a Monte Carlo method, detailed in Section S2. The model assumes that, for all beads in the same subpopulation, the rupture time is distributed monoexponentially, as we verified with monoclonal samples.

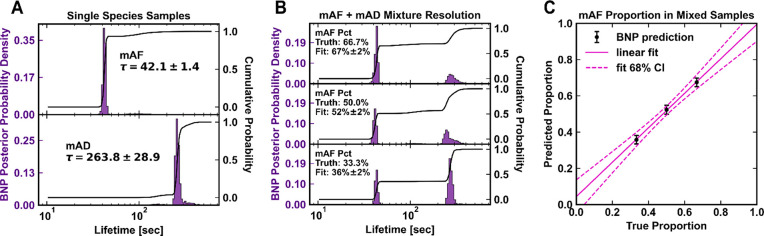
We first tested this analysis method with the unmixed mAF and mAD data sets [Figure 3A]. The inferred lifetimes agreed with a simpler maximum-likelihood fit to a monoexponential. Interestingly, the mAF data set exhibits a small (∼5%) fraction of molecular pairs with an ∼3-fold longer average lifetime, a subpopulation which is hidden in population-level histograms [Figure 2C].

Figure 3.

Figure 3

Open in a new tab

Validation of Bayesian Non-Parametric (BNP) inference with known samples of mAF and mAD for pure samples (A) and handmade binary mixtures (B). The inferred lifetime posterior is shown in dark purple. The distribution is a histogram of Monte Carlo samples of the lifetime [Figure S8, second row], weighted by the subpopulation fraction of that lifetime [Figure S8, first row] (see Section S2). The width of a peak represents its statistical uncertainty; the integrated area its population fraction. Solid line shows the cumulative probability; the inferred mAF proportion is the integrated area of the leftmost peak. (C) Correlation between true mAF proportion and inferred mAF proportion.

Next, we created mixed samples of mAF and mAD at molecular ratios of 2:1, 1:1, and 1:2. As shown in Figure 3B and 3C, Bayesian analysis correctly recovers the mixing proportion and lifetime of each species, validating our approach for two-part mixtures with a known ground truth.

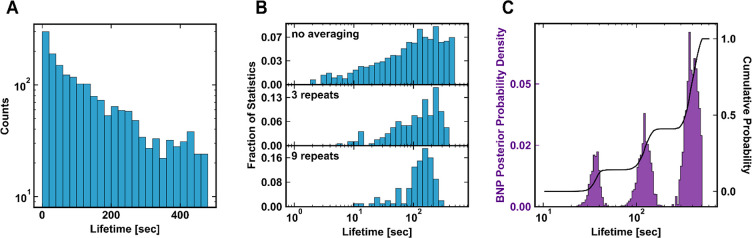
Finally, to test these experimental and analysis techniques, we characterized a polyclonal anti-FITC antibody (pAF, Invitrogen A-889) of unknown composition. The data collected from this sample show clear signs of heterogeneity: the ensemble unbinding kinetics exhibit a nonexponential pattern [Figure 4A], and the per-molecule-averaged distribution of lifetimes does not approach a normal distribution [Figure 4B].

Figure 4.

Figure 4

Open in a new tab

Demonstration of the CFM and BNP approach for an unknown polyclonal anti-FITC sample. (A) Population-level unbinding statistics of the polyclonal antibody. The nonexponential kinetics indicates heterogeneity. (B) Histogram of the per-molecule average lifetime. (C) Posterior distribution of lifetime inferred from Bayesian nonparametric analysis, as in Figure 3.

These results indicate that the polyclonal sample contains multiple molecular species with distinct off-rates. However, unlike the artificial binary mixture, the polyclonal sample confers no a priori information about the number of subpopulations. Our nonparametric inference method accounts for this because it is general enough to encompass an arbitrary number of subpopulations.22,27,28 The number of significant subpopulations, K, converges onto a final value (or distribution of values) based on the data set (see Section S2). We find that the final value(s) of K is robust to the initialization [Figure S6] but does depend slightly on a hyperparameter, the concentration parameter of the Dirichlet prior [Figure S7].

Results of Bayesian inference on the polyclonal anti-FITC sample are plotted in [Figure 4C]. We find that three components are necessary to explain the observed unbinding kinetics. The posterior mean and standard deviation for each parameter is listed in Table 2.

Table 2. BNP Inferred Parameters for pAF Dataset.

  τ1 (sec) τ2 (sec) τ3 (sec) p0 p1 p2
mean 35.451 119.566 400.079 0.140 0.266 0.594
std 4.186 17.970 54.083 0.032 0.067 0.075
Open in a new tab

The task of resolving components in a mixture of exponentials is a classic example of an ill-conditioned statistical fitting problem and many methods have been proposed.22,23,43−47 Compared to other situations involving multiexponential decays in biophysics,28,48 our single-molecule assay has the key difference that all statistics from a given molecular pair are known to originate from the same mixture component, i.e. from the same monoexponential distribution, provided that the multiple decay times observed arise purely from static heterogeneity. In Section S3, we discuss how this extra information reduces the uncertainty in predicted lifetimes. This approach for improving resolution could be applicable in other areas of single-molecule biophysics.

We note that if two components have very similar off-rates, then more repetitions are required to sufficiently resolve them, since the width of the per-molecule averaged lifetime distribution decreases in proportion to √N [Figure 2C, Figure S5]. If two molecular species have identical off-rates but are otherwise distinct (e.g., differ in sequence or post-translational modification), it is not possible to distinguish them with our current assay. Limitations like this are intrinsic to any method which characterizes molecules based on their functional binding strength, rather than by genotypic or structural criteria. Interestingly, however, if two species differed in the force-dependence of kinetics, then it could be possible to resolve them by varying the force. Such an experiment would give two properties (equilibrium off-rate and force-dependence) by which subpopulations can be distinguished. Further distinguishing properties such as binding epitope or protein stability can be obtained by repeating CFM pulls under different buffer conditions.

Several applications could benefit from resolving the heterogeneity of polyclonal antibodies. These include characterizing the immune response to a vaccine or measuring the binding affinity distribution of a molecular detection reagent. Population-averaged measures, such as an effective KD or IC50, do not reveal which molecular species in a mixture are responsible for activity.40 Advances in proteomics make it possible to identify the sequences of the most prominent species in a polyclonal antibody;3 however, further biophysical description still requires separate cloning, expression, purification, and assay of each species. In contrast, our assay directly measures functional properties of each molecule, which could complement information about sequence and structure.

In summary, by combining temporally and spatially multiplexed single-molecule force spectroscopy with nonparametric Bayesian analysis, we have developed a powerful yet accessible method to directly assay biophysical properties and resolve molecular heterogeneity at the single-molecule level. As we demonstrated for polyclonal antibodies, our approach enables the rapid and accurate resolution of multiple functional subpopulations within a heterogeneous mixture—a capability that should enable new insights into the immune response and vaccine development. We expect this approach will impact fields ranging from immunology to nanotechnology by providing the ability to accurately characterize molecular heterogeneity at a functional and single-molecule level within both natural and synthetic samples.

Acknowledgments

W.P.W. thanks NIH NIGMS (R35GM119537). S.P. thanks NIH NIGMS (R01GM130745) and NIH NIGMS (R01GM134426). Support from the National Science Foundation Graduate Research Fellowship Program (to J.C.) is gratefully acknowledged.

Glossary

Abbreviations

CFM

centrifuge force microscope

BNP

Bayesian Nonparametric analysis

mAF

monoclonal antifluorescein

mAD

monoclonal antidigoxigenin.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.2c11450.

  • Nanoswitch construction and preparation, CFM experiment and data processing, Bayesian nonparametric method, discussion of how per-molecule information aids in resolution. (PDF)

Author Contributions

○ Y.L., J.C., and D.Y. contributed equally to this paper.

The authors declare the following competing financial interest(s): D.Y. and W.P.W. are inventors on patent applications covering aspects of this work.

Supplementary Material

ja2c11450_si_001.pdf (3MB, pdf)

References

  1. Kabat E. A. Structure and Heterogeneity of Antibodies. Acta Haematol. 2004, 36 (3–4), 198–238. 10.1159/000209100. [DOI] [PubMed] [Google Scholar]
  2. Abbott W. M.; Snow M.; Eckersley S.; Renshaw J.; Davies G.; Norman R. A.; Ceuppens P.; Slootstra J.; Benschop J. J.; Hamuro Y.; Lee J. E.; Newham P. Characterization of the complex formed between a potent neutralizing ovine-derived polyclonal anti-TNFα Fab fragment and human TNFα. Biosci. Rep. 2013, 33 (4), e00060 10.1042/BSR20130044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Wine Y.; Boutz D. R.; Lavinder J. J.; Miklos A. E.; Hughes R. A.; Hoi K. H.; Jung S. T.; Horton A. P.; Murrin E. M.; Ellington A. D.; Marcotte E. M.; Georgiou G. Molecular deconvolution of the monoclonal antibodies that comprise the polyclonal serum response. Proc. Natl. Acad. Sci. U. S. A. 2013, 110 (8), 2993–2998. 10.1073/pnas.1213737110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bustamante C.; Cheng W.; Mejia Y. X. Revisiting the Central Dogma One Molecule at a Time. Cell 2011, 144 (4), 480–497. 10.1016/j.cell.2011.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Greenleaf W. J.; Woodside M. T.; Block S. M. High-resolution, single-molecule measurements of biomolecular motion. Annu. Rev. Biophys. Biomol. Struct. 2007, 36, 171–190. 10.1146/annurev.biophys.36.101106.101451. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Neuman K. C.; Nagy A. Single-molecule force spectroscopy: optical tweezers, magnetic tweezers and atomic force microscopy. Nat. Methods 2008, 5 (6), 491–505. 10.1038/nmeth.1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Merkel R.; Nassoy P.; Leung A.; Ritchie K.; Evans E. Energy landscapes of receptor-ligand bonds explored with dynamic force spectroscopy. Nature 1999, 397 (6714), 50–53. 10.1038/16219. [DOI] [PubMed] [Google Scholar]
  8. Evans E. Probing the relation between force--lifetime--and chemistry in single molecular bonds. Annu. Rev. Biophys. Biomol. Struct. 2001, 30, 105–128. 10.1146/annurev.biophys.30.1.105. [DOI] [PubMed] [Google Scholar]
  9. Sitters G.; Kamsma D.; Thalhammer G.; Ritsch-Marte M.; Peterman E. J. G.; Wuite G. J. L. Acoustic force spectroscopy. Nat. Methods 2015, 12 (1), 47–50. 10.1038/nmeth.3183. [DOI] [PubMed] [Google Scholar]
  10. De Vlaminck I.; Henighan T.; van Loenhout M. T. J.; Pfeiffer I.; Huijts J.; Kerssemakers J. W. J.; Katan A. J.; van Langen-Suurling A.; van der Drift E.; Wyman C.; Dekker C. Highly Parallel Magnetic Tweezers by Targeted DNA Tethering. Nano Lett. 2011, 11 (12), 5489–5493. 10.1021/nl203299e. [DOI] [PubMed] [Google Scholar]
  11. Ribeck N.; Saleh O. A. Multiplexed single-molecule measurements with magnetic tweezers. Rev. Sci. Instrum. 2008, 79 (9), 094301 10.1063/1.2981687. [DOI] [PubMed] [Google Scholar]
  12. Kim S.; Blainey P. C.; Schroeder C. M.; Xie X. S. Multiplexed single-molecule assay for enzymatic activity on flow-stretched DNA. Nat. Methods 2007, 4 (5), 397–399. 10.1038/nmeth1037. [DOI] [PubMed] [Google Scholar]
  13. Otten M.; Ott W.; Jobst M. A.; Milles L. F.; Verdorfer T.; Pippig D. A.; Nash M. A.; Gaub H. E. From genes to protein mechanics on a chip. Nat. Methods 2014, 11 (11), 1127–1130. 10.1038/nmeth.3099. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Halvorsen K.; Wong W. P. Massively Parallel Single-Molecule Manipulation Using Centrifugal Force. Biophys. J. 2010, 98 (11), L53–L55. 10.1016/j.bpj.2010.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Yang D.; Ward A.; Halvorsen K.; Wong W. P. Multiplexed single-molecule force spectroscopy using a centrifuge. Nat. Commun. 2016, 7 (1), 11026. 10.1038/ncomms11026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Yang D.; Wong W. P.. Repurposing a Benchtop Centrifuge for High-Throughput Single-Molecule Force Spectroscopy. In Single Molecule Analysis; Peterman E. J. G., Ed.; Methods in Molecular Biology; Springer: New York: New York, NY, 2018; Vol. 1665, pp 353–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Halvorsen K.; Schaak D.; Wong W. P. Nanoengineering a single-molecule mechanical switch using DNA self-assembly. Nanotechnology 2011, 22 (49), 494005. 10.1088/0957-4484/22/49/494005. [DOI] [PubMed] [Google Scholar]
  18. Koussa M. A.; Halvorsen K.; Ward A.; Wong W. P. DNA nanoswitches: a quantitative platform for gel-based biomolecular interaction analysis. Nat. Methods 2015, 12 (2), 123–126. 10.1038/nmeth.3209. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hansen C. H.; Yang D.; Koussa M. A.; Wong W. P. Nanoswitch-linked immunosorbent assay (NLISA) for fast, sensitive, and specific protein detection. Proc. Natl. Acad. Sci. U. S. A. 2017, 114 (39), 10367–10372. 10.1073/pnas.1708148114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Shrestha P.; Yang D.; Tomov T. E.; MacDonald J. I.; Ward A.; Bergal H. T.; Krieg E.; Cabi S.; Luo Y.; Nathwani B.; Johnson-Buck A.; Shih W. M.; Wong W. P. Single-molecule mechanical fingerprinting with DNA nanoswitch calipers. Nat. Nanotechnol. 2021, 16 (12), 1362–1370. 10.1038/s41565-021-00979-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Dykstra R. L.; Laud P. A Bayesian Nonparametric Approach to Reliability. Ann. Stat. 1981, 9 (2), 356–367. 10.1214/aos/1176345401. [DOI] [Google Scholar]
  22. Hines K. E.; Bankston J. R.; Aldrich R. W. Analyzing Single-Molecule Time Series via Nonparametric Bayesian Inference. Biophys. J. 2015, 108 (3), 540–556. 10.1016/j.bpj.2014.12.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Landowne D.; Yuan B.; Magleby K. L. Exponential Sum-Fitting of Dwell-Time Distributions without Specifying Starting Parameters. Biophys. J. 2013, 104 (11), 2383–2391. 10.1016/j.bpj.2013.04.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Li C.; Rana S.; Phung D.; Venkatesh S. Dirichlet Process Mixture Models with Pairwise Constraints for Data Clustering. Ann. Data Sci. 2016, 3 (2), 205–223. 10.1007/s40745-016-0082-z. [DOI] [Google Scholar]
  25. Li M.; Meng H.; Zhang Q. A nonparametric Bayesian modeling approach for heterogeneous lifetime data with covariates. Reliab. Eng. Syst. Saf. 2017, 167, 95–104. 10.1016/j.ress.2017.05.029. [DOI] [Google Scholar]
  26. Sgouralis I.; Whitmore M.; Lapidus L.; Comstock M. J.; Pressé S. Single molecule force spectroscopy at high data acquisition: A Bayesian nonparametric analysis. J. Chem. Phys. 2018, 148 (12), 123320. 10.1063/1.5008842. [DOI] [PubMed] [Google Scholar]
  27. Sgouralis I.; Madaan S.; Djutanta F.; Kha R.; Hariadi R. F.; Pressé S. A Bayesian Nonparametric Approach to Single Molecule Förster Resonance Energy Transfer. J. Phys. Chem. B 2019, 123 (3), 675–688. 10.1021/acs.jpcb.8b09752. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Tavakoli M.; Jazani S.; Sgouralis I.; Heo W.; Ishii K.; Tahara T.; Pressé S. Direct Photon-by-Photon Analysis of Time-Resolved Pulsed Excitation Data using Bayesian Nonparametrics. Cell Rep. Phys. Sci. 2020, 1 (11), 100234. 10.1016/j.xcrp.2020.100234. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Fazel M.; Jazani S.; Scipioni L.; Vallmitjana A.; Gratton E.; Digman M. A.; Pressé S. High Resolution Fluorescence Lifetime Maps from Minimal Photon Counts. ACS Photonics 2022, 9 (3), 1015–1025. 10.1021/acsphotonics.1c01936. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Urbanska M.; Lüdecke A.; Walter W. J.; van Oijen A. M.; Duderstadt K. E.; Diez S. Highly-Parallel Microfluidics-Based Force Spectroscopy on Single Cytoskeletal Motors. Small Weinh. Bergstr. Ger. 2021, 17 (18), 2007388 10.1002/smll.202007388. [DOI] [PubMed] [Google Scholar]
  31. Pfitzner E.; Wachauf C.; Kilchherr F.; Pelz B.; Shih W. M.; Rief M.; Dietz H. Rigid DNA beams for high-resolution single-molecule mechanics. Angew. Chem., Int. Ed. Engl. 2013, 52 (30), 7766–7771. 10.1002/anie.201302727. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Wang X.; Ha T. Defining single molecular forces required to activate integrin and notch signaling. Science 2013, 340 (6135), 991–994. 10.1126/science.1231041. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Kim D.; Sahin O. Imaging and three-dimensional reconstruction of chemical groups inside a protein complex using atomic force microscopy. Nat. Nanotechnol. 2015, 10 (3), 264–269. 10.1038/nnano.2014.335. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Kim J.; Zhang C.-Z.; Zhang X.; Springer T. A. A mechanically stabilized receptor–ligand flex-bond important in the vasculature. Nature 2010, 466 (7309), 992–995. 10.1038/nature09295. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Kilchherr F.; Wachauf C.; Pelz B.; Rief M.; Zacharias M.; Dietz H. Single-molecule dissection of stacking forces in DNA. Science 2016, 353 (6304), aaf5508. 10.1126/science.aaf5508. [DOI] [PubMed] [Google Scholar]
  36. Kostrz D.; Wayment-Steele H. K.; Wang J. L.; Follenfant M.; Pande V. S.; Strick T. R.; Gosse C. A modular DNA scaffold to study protein–protein interactions at single-molecule resolution. Nat. Nanotechnol. 2019, 14 (10), 988–993. 10.1038/s41565-019-0542-7. [DOI] [PubMed] [Google Scholar]
  37. Darwish I. A. Immunoassay Methods and their Applications in Pharmaceutical Analysis: Basic Methodology and Recent Advances. Int. J. Biomed. Sci. IJBS 2006, 2 (3), 217–235. [PMC free article] [PubMed] [Google Scholar]
  38. Landegren U.; Vänelid J.; Hammond M.; Nong R. Y.; Wu D.; Ullerås E.; Kamali-Moghaddam M. Opportunities for Sensitive Plasma Proteome Analysis. Anal. Chem. 2012, 84 (4), 1824–1830. 10.1021/ac2032222. [DOI] [PubMed] [Google Scholar]
  39. Lu R.-M.; Hwang Y.-C.; Liu I.-J.; Lee C.-C.; Tsai H.-Z.; Li H.-J.; Wu H.-C. Development of therapeutic antibodies for the treatment of diseases. J. Biomed. Sci. 2020, 27 (1), 1. 10.1186/s12929-019-0592-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Stevens F. J.; Bobrovnik S. A. Deconvolution of antibody affinities and concentrations by non-linear regression analysis of competitive ELISA data. J. Immunol. Methods 2007, 328 (1–2), 53–58. 10.1016/j.jim.2007.08.007. [DOI] [PubMed] [Google Scholar]
  41. Ascoli C. A.; Aggeler B. Overlooked benefits of using polyclonal antibodies. BioTechniques 2018, 65 (3), 127–136. 10.2144/btn-2018-0065. [DOI] [PubMed] [Google Scholar]
  42. Lipman N. S.; Jackson L. R.; Trudel L. J.; Weis-Garcia F. Monoclonal Versus Polyclonal Antibodies: Distinguishing Characteristics, Applications, and Information Resources. ILAR J. 2005, 46 (3), 258–268. 10.1093/ilar.46.3.258. [DOI] [PubMed] [Google Scholar]
  43. Smith M. R.; Cohn-Sfetcu S.; Buckmaster H. A. Decomposition of Multicomponent Exponential Decays by Spectral Analytic Techniques. Technometrics 1976, 18 (4), 467–482. 10.1080/00401706.1976.10489479. [DOI] [Google Scholar]
  44. Livesey A. K.; Brochon J. C. Analyzing the Distribution of Decay Constants in Pulse-Fluorimetry Using the Maximum Entropy Method. Biophys. J. 1987, 52 (5), 693–706. 10.1016/S0006-3495(87)83264-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Bajzer Z.; Myers A. C.; Sedarous S. S.; Prendergast F. G. Padé-Laplace method for analysis of fluorescence intensity decay. Biophys. J. 1989, 56 (1), 79–93. 10.1016/S0006-3495(89)82653-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Bajzer Ž.; Therneau T. M.; Sharp J. C.; Prendergast F. G. Maximum likelihood method for the analysis of time-resolved fluorescence decay curves. Eur. Biophys. J. 1991, 20 (5), 247–262. 10.1007/BF00450560. [DOI] [PubMed] [Google Scholar]
  47. Zhou Y.; Zhuang X. Robust Reconstruction of the Rate Constant Distribution Using the Phase Function Method. Biophys. J. 2006, 91 (11), 4045–4053. 10.1529/biophysj.106.090688. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Yang H.; Luo G.; Karnchanaphanurach P.; Louie T.-M.; Rech I.; Cova S.; Xun L.; Xie X. S. Protein Conformational Dynamics Probed by Single-Molecule Electron Transfer. Science 2003, 302 (5643), 262–266. 10.1126/science.1086911. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja2c11450_si_001.pdf (3MB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES