Toward real-world automated antibody design with combinatorial Bayesian optimization

Summary

Antibodies are multimeric proteins capable of highly specific molecular recognition. The complementarity determining region 3 of the antibody variable heavy chain (CDRH3) often dominates antigen-binding specificity. Hence, it is a priority to design optimal antigen-specific CDRH3 to develop therapeutic antibodies. The combinatorial structure of CDRH3 sequences makes it impossible to query binding-affinity oracles exhaustively. Moreover, antibodies are expected to have high target specificity and developability. Here, we present AntBO, a combinatorial Bayesian optimization framework utilizing a CDRH3 trust region for an in silico design of antibodies with favorable developability scores. The in silico experiments on 159 antigens demonstrate that AntBO is a step toward practically viable in vitro antibody design. In under 200 calls to the oracle, AntBO suggests antibodies outperforming the best binding sequence from 6.9 million experimentally obtained CDRH3s. Additionally, AntBO finds very-high-affinity CDRH3 in only 38 protein designs while requiring no domain knowledge.

Graphical abstract

Highlights

• •AntBO is a sample-efficient combinatorial Bayesian optimization tool for antibody design
• •Provides an easy interface to benchmark optimization methods for antibody design
• •Utilizes trust region to design antibodies with favorable developability scores
• •Consistently outperforms baseline approaches, including experimentally known CDRH3s

Motivation

Designing antibody sequences that bind to an antigen of interest is a fundamental problem in therapeutics design. In addition to the binding toward the target antigen, the antibodies of clinical interest should have favorable biophysical (i.e., developability) properties. The simulation of antigen-antibody binding affinity is a complex process that requires a model to generate a structure of antibody and antigen from their respective sequences and then simulate the binding affinity. We view this intricate process as a black-box oracle that takes a pair of antibody and antigen sequences as an input and returns their binding affinity. The design process to find an optimal antibody sequence is essentially a combinatorial search in the antibody sequence space to find an instance that maximizes the target function of a black oracle (e.g., a function that determines binding affinity). The combinatorial nature of the antibody sequence space makes it impossible to query the oracle function exhaustively, both computationally and experimentally. Therefore, we need a computationally efficient mechanism to search for an antibody sequence that maximizes the oracle’s output to achieve strong affinity with an antigen and has desired biophysical properties.

Khan et al. develop AntBO, a combinatorial Bayesian optimization tool for antibody design. AntBO provides a sample-efficient strategy for an in silico design of antibodies with a diverse range of favorable developability properties on various antigens of interest, including a lethal SARS-CoV pathogen.

Introduction

Antibodies or immunoglobulins (Igs) are utilized by the immune system to detect, bind, and neutralize invading pathogens.¹ From a structural perspective, these are mainly large Y-shaped proteins that contain variable regions, enabling specific molecular recognition of a broad range of molecular surfaces of foreign proteins called antigens.^2,3,4,5 As a result, antibodies are a rapidly growing class of biotherapeutics.⁶ Monoclonal antibodies now constitute five of the ten top-selling drugs.^7,8,9 Antibodies are also used in molecular biology research as affinity reagents due to their ability to detect low concentrations of target antigens with high sensitivity and specificity.¹⁰

A typical antibody structure consists of four protein domains: two heavy and two light chains connected by disulfide bonds. Each heavy chain (VH) includes three constant domains and one variable domain (Fv region), while a light chain (VL) possesses one constant and one variable domain.^3,4,11 Antibodies selectively bind antigens through the tip of their variable regions, called the Fab domain (antigen-binding fragment), containing six loops, three on the light and three on the heavy chain, called complementarity-determining regions (CDRs).^4,12,13 The interacting residues at the binding site between antibody and antigen are called the paratope on the antibody side and the epitope on the antigen side.^4,12,13 The base of an antibody is called the fragment crystallizable (Fc) region that reacts with the Fv region. Despite many studies focusing only on Fv regions of antibodies and CDRH3 loops, it has been shown that the Fc region is also important for antibody design. The Fc region is connected to developability parameters such as aggregation, half-life, and stability, which are crucial for antibody success in clinical trials.¹⁴

The main overarching goal in computational antibody design is to develop CDR regions that can bind to selected antigens (such as pathogens, tumor neoantigens, or therapeutic pathway targets) since the CDR regions mainly define the binding specificity.^3,15,16 In particular, the CDRH3 region possesses the highest sequence and structural diversity, conferring a crucial role in forming the binding site.^2,4,5 For this reason, the highly diverse CDRH3 is the most extensively re-engineered component in monoclonal antibody development. In this article, we refer to the design of the CDRH3 region as an antibody design.

When a candidate antibody-antigen complex structure is already known, structural methods predicting affinity change upon mutation at the interaction site^17,18,19,20 are useful in generating antibodies with higher affinity. As recent examples,²¹ combine structural modeling and affinity scoring function to get a 140-fold affinity improvement on an anti-lysozyme antibody. In contrast to other affinity-based scoring functions,²² use an ensemble machine learning (ML) strategy that utilizes the affinity change induced by single-point mutations to predict new sequences with improved affinity. mCSM-AB2²³ uses graph-based signatures to incorporate structural information of antibody-antigen complexes and combine it with energy inference using FoldX²⁴ to predict improvements in binding energy. Finally, two other generalized methods derived from the protein-protein interaction problem have been used on antibody affinity prediction: TopNetTree²⁵ combines a convolutional neural network (CNN) with gradient-boosting trees, and GeoPPI²⁶ uses a graph neural network instead of the CNN. However, there is still a high discrepancy between the results of affinity prediction methods.^27,28

In practice, the development of antibodies is a complex process that requires various tools for building a structural model for different parts of the antibody,²⁹ generating structures from antigen sequences,³⁰ and docking them.³¹ Moreover, the combinatorial nature of all possible CDRH3 sequences makes it impractical to query any antigen-antibody simulation framework exhaustively. For a sequence of length $n$ consisting of naturally occurring amino acids (AAs) $\left(m=20\right)$, there are $m^n$ possible sequences. Thus, even with a modest size of $n=11$, this number becomes too large to search exhaustively. In reality, the search space is even larger since CDR sequence lengths can be up to 36 residues,³² and designed proteins are not restricted to naturally occurring AAs.³³ Furthermore, not all CDRH3 sequences are of therapeutic interest. A CDRH3 can have a strong binding affinity to a specific target but may cause problems in manufacturing due to its unstable structure or show toxicity to the patient. Antibodies should be evaluated against typical properties known as developability scores for such reasons.³⁴ These scores measure properties of interest, such as whether a CDRH3 sequence is free of undesirable glycosylation motifs or the net charge of a sequence is in a prespecified range.^35,36

Recently, Robert et al.¹³ proposed Absolut!, a computational framework for generating antibody-antigen binding datasets that has been used to stress test and benchmark different ML strategies for antibody-antigen binding prediction.¹³ Absolut! is a deterministic tool that provides an end-to-end simulation of antibody-antigen binding affinity using coarse-grained lattice representations of proteins. We can use Absolut! to evaluate all possible binding conformations of an arbitrary CDRH3 sequence to an antigen of interest and return the optimal binding conformation. To be of real-world relevance, Absolut! preserves more than eight levels of biological complexity present in experimental datasets¹³: antigen topology; antigen aa composition; physiological CDRH3 sequences; a vast combinatorial space of possible binding conformations; positional aa dependencies in high-affinity sequences; a hierarchy of antigen regions with different immunogenicity levels; the complexity of paratope-epitope structural compatibility; and a functional binding landscape that is not well described by CDRH3 sequence similarity. Moreover, Absolut! demonstrates three examples where different ML strategies showed the same ranking in their performance compared with experimental datasets. Importantly, ML conclusions reached on Absolut!-generated simulated data transfer to real-world data.¹³ However, the combinatorial explosion of CDRH3 sequence space makes it unrealistic to exhaustively test every possible sequence, either experimentally or using Absolut! Therefore, the problem of antibody-antigen binding design demands a sample-efficient solution to generate the CDRH3 region that binds an arbitrary antigen of interest while respecting developability constraints.

Bayesian optimization (BO)^37,38,39,40 offers powerful machinery for aforementioned issues. BO uses Gaussian processes (GPs)⁴¹ as a surrogate model of a black box oracle that incorporates the prior belief about the domain in guiding the search in the sequence space. The uncertainty quantification of GPs allows the acquisition maximization step to trade off exploration and exploitation in the search space. (The idea of exploration is to eliminate the region of search space that does not contain the optimal solution with a high probability. The exploitation guarantees that the search finds optimal sample points with a high probability. BO uses GP as a surrogate model that introduces mean and variance estimates with every data point. As BO encounters new data points in a local search to maximize the acquisition function, it checks if two points have the exact mean estimate and selects the one with the highest variance, thereby exploring the space. When data points have the same variance, BO chooses the one with the highest mean estimate thus exploiting the solution.) This attractive property of BO enables us to develop a sample-efficient solution for antibody design. In this article, we introduce AntBO—a combinatorial BO framework for in silico design of a target-specific antibody CDRH3 region. Our framework uses Absolut!’s binding energy simulator as a black-box oracle. In principle, AntBO can be applied to any sequence region. Here, we consider CDRH3, since this is the primary region of interest for antibody engineering.^4,5,42,43 In addition, the Absolut! framework currently only allows CDRH3 binding simulation.

Our key contributions are as follows.

• $•$ The AntBO framework utilizes biophysical properties of CDRH3 sequences as constraints in the combinatorial sequence space to facilitate the search for antibodies suitable for therapeutic development.

• $•$ We demonstrate the application of AntBO on 159 known antigens of therapeutic interest. Our results demonstrate the benefits of AntBO for in silico antibody design through diverse developability scores of discovered protein sequences.

• $•$AntBO substantially outperforms the very-high-affinity sequences available from a database of 6.9 million experimentally obtained CDRH3s, with several orders of magnitude fewer protein designs.

• $•$Considering the enormous costs (time and resources) of wet-lab antibody-design-related experimentation, AntBO can suggest very-high-affinity antibodies while making the fewest queries to a black-box oracle for affinity determination. This result serves as a proof of concept that AntBO can be deployed in the real world where sample efficiency is vital.

Results

Formulating antibody design as a black-box optimization with CDRH3 developability constraints

To design antibodies of therapeutic interest, we want to search for CDRH3 sequences with a high affinity toward the antigen of interest that satisfies specific biophysical properties, making them ideal for practical applications (e.g., manufacturing, improved shelf life, higher concentration doses). These properties are characterized as “developability scores.”³⁵ In this work, we use the three most relevant scores identified for the CDRH3 region.^35,44 First, the net charge of a sequence should be in the range $\left[-\mathrm{2,2}\right]$. It is specified as a sum of the charge of individual residues in a primary aa sequence. Consider a sequence $\mathbf{x}=\left\{x_1,\dots ,x_n\right\}$, and let $\mathbb{I}[.]$ be the indicator function that takes value 1 if the conditions are satisfied and 0 otherwise; then, the charge of a residue is defined as $C\left(x_i\right)=\mathbb{I}\left[x_i\in \left\{R,K\right\}\right]+0.1\cdot \mathbb{I}\left[x_i=H\right]-\mathbb{I}\left[x_i\in \left\{D,E\right\}\right]$ and that of the sequence as ${\sum }_{i}C\left(x_i\right)$, where R stands for arginine, K for lysine, H for histidine, D for aspartic acid, and E for glutamate. Second, any residue should not repeat more than five times in a sequence $\mathbb{I}\left[\text{count}\left(x_i\right)\le 5\mid \forall i\in \left[0,\mathrm{n}-1\right]\right]$. Lastly, a sequence should not contain a glycosylation motif—a subsequence of form N-X-S/T except when X is a proline.

The binding affinity of an antibody and an antigen simulated as an energy score comes with several challenges. The energy score is not directly accessible as a closed-form expression that can return binding energy as a function of an input sequence without enumerating all possible binding structures. A vast space of CDRH3 sequences makes it computationally impractical to exhaustively search for an optimal sequence. Therefore, we pose the design of the CDRH3 region of antibodies as a black-box optimization problem. Specific to our work, a black box refers to a tool that can take an arbitrary CDRH3 sequence as an input and return an energy score that describes its binding affinity toward a prespecified antigen. The high cost of lab experiments expects the antibody design method to suggest a sequence of interest in the fewest design steps. To simulate such a scenario, we want a sample-efficient solution that makes a very small prespecified number of calls to an oracle and suggests antibody sequences with very high affinity.

To formally introduce the problem, consider the combinatorial space $\mathcal{X}$ of protein sequences of length $n$, for 20 unique aas, the cardinality of space is $\left|\mathcal{X}\right|=20$. We can consider a black-box function $f$ as a mapping from protein sequences to a real-valued antigen specificity $f:\mathcal{X}\to \mathbb{R}$ where an optimum protein sequence under developability constraints is defined as

$$\begin{array}{l}{\mathbf{x}}^{\ast }=\arg \underset{\mathbf{x}\in \mathcal{X}}{\min }f\left(\mathbf{x}\right)\\ \mathrm{s}.\mathrm{t}.CDRH3\mathit{-}Developable\left(\mathbf{x}\right)\end{array}\text{,}$$ (Equation 1)

where $CDRH3\mathit{-}Developable:X\to \left\{\mathrm{0,1}\right\}$ is a function that takes a sequence of aas and returns a Boolean value for whether constraints introduced in formulating antibody design as a black-box optimization with CDRH3 developability constraints are satisfied (1) or unsatisfied (0). An example of an unsatisfied CDRH3 sequence is shown in Figure 1C.

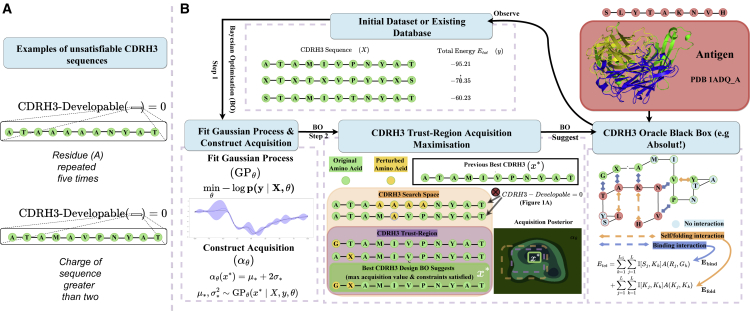
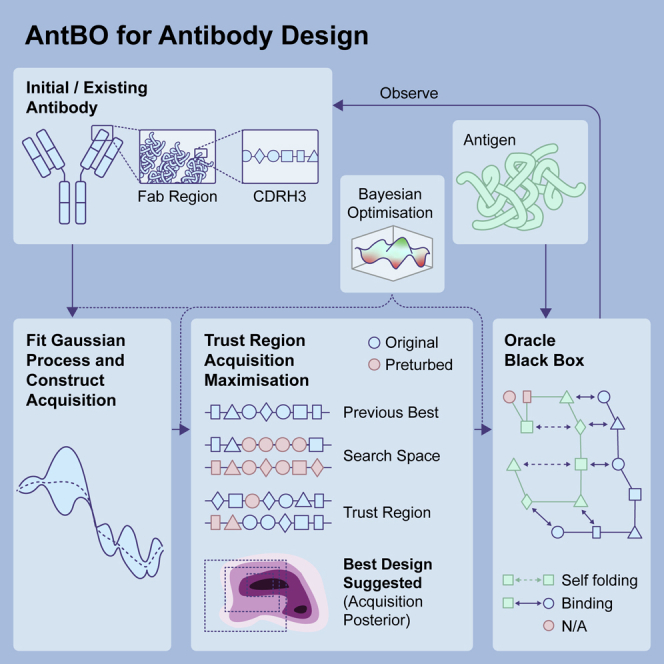
Figure 1.

AntBO iteratively proposes a CDRH3 sequence and requests its affinity to Absolut! before adapting its posterior with the affinity of this sequence

(A and B) The performance of AntBO or other optimization tools is measured as the highest affinity achieved and how fast it reaches high affinity.

(A) The demonstrative example of two CDRH3 sequences not satisfying the developability criterion is discarded in the overall optimization procedure.

(B) Overall optimization process of AntBO for antibody design: from a predefined target antigen structure (discretized from its known PDB structure), binding affinities of antibody CDRH3 sequences to the antigen are simulated using Absolut! as an in silico surrogate for costly experimental measurements. AntBO treats Absolut! as a black-box to be optimized for ${\mathbf{E}}_{\text{bind}}$ and can suggest high-affinity CDRH3 protein designs within a trust region of acceptable sequences.

Combinatorial BO for antibody design

Our goal is to search for an instance (antibody sequence) in the input space ${\mathbf{x}}^{\ast }\in \mathcal{X}$ that achieves an optimum value under the black-box function $f$. In a typical setting, the function $f$ has properties such as (1) high evaluation cost, (2) no analytical solution, and (3) may not be differentiable. To circumvent these issues, we use BO to solve the optimization problem. BO typically goes through the following loop: we first fit a GP on a random set of data points at the start. Next, we optimize an acquisition function that utilizes the GP posterior to propose new samples that improve over previous observations. At last, these new samples are added to data points to refit a GP and repeat the acquisition maximization, as shown in Figure 1. We have provided a brief introduction to BO in the STAR Methods section method details. For a comprehensive overview of BO, we refer to readers to Snoeck et al.,⁴⁵ Shahriari et al.,⁴⁶ Hernández-Lobato et al.,⁴⁷ Frazier,⁴⁸ Cowen-Rivers et al.,⁴⁹ Antoine et al.,⁵⁰ and Garnett.⁵¹

Kernels to operate over antibody sequences

To build a GP surrogate model, we need a kernel function to measure a correlation between pairs of inputs. Since, in our problem, the input space is categorical, we need a kernel that can operate on sequences. We investigate three choices of kernels. Firstly, a transformed overlap kernel (TK) that uses hamming distance with a length-scale hyperparameter for each dimension. Secondly, a protein BERT kernel (protBERT) that uses pretrained BERT model⁵² to map a sequence to a continuous Euclidean space and uses radial basis function (RBF) kernel to measure correlation. Lastly, the fast string kernel (SSK) defines the similarity between two sequences by measuring a number of common substrings of order $l$. The details are discussed in the STAR Methods section kernels.

CDRH3 trust region acquisition maximization

The combinatorial explosion of antibody design space makes it impractical to use standard methods of acquisition maximization. Several recent developments have proposed the use of discrete optimization algorithms for the combinatorial nature of problem.^{53,54,55,56,57} However, their application to antibody design requires a mechanism to restrict the search to sequences with feasible biophysical properties. We next introduce our method, which utilizes crucial biophysical properties to construct a trust region (TR) in the combinatorial sequence space, thus allowing us to extend the combinatorial BO machinery to antibody design.

At each iteration $t$ of the search step, we define a trust region CDRH3-TR around the previous best point ${\mathbf{x}}^{\ast }$ that includes all points satisfying antibody design constraints introduced in formulating antibody design as a black-box optimization with CDRH3 developability constraints and differ in at most $L_t$ indices from ${\mathbf{x}}^{\ast }$. We then run CDRH3-TR acquisition maximization,

$$\text{CDRH}3-{\text{TR}}_{L_t}\left({\mathrm{x}}^{\ast }\right)=\left\{\mathrm{x}|\mathit{CDRH}3\mathit{-}\mathit{Developable}\left(\mathrm{x}\right),\sum _i\delta \left({\mathrm{x}}_i,{\mathrm{x}}_i^{\ast }\right)\le L_t\right\}\text{,}$$ (Equation 2)

where $\delta \left(.,\text{.}\right)$ is the Kronecker delta function. To perform a search, we start with the previous best ${\mathbf{x}}^{\ast }$ and, next, sample a neighbor point ${\mathbf{x}}_{\text{Neigh}.}^{\ast }$ contained within CDRH3-TR by selecting a random aa and perturbing it with a new aa. We store the sequence if it improves upon the previous suggestions. The value of $L_t$ is restricted in the range $\left[d_{\min },d_{\max }\right]$, where $d_{\min }$ and $d_{\max }$ are the minimum and maximum size of TR that we treat as a hyperparameter. When $L_t$ reaches $d_{\min }$, we restart the optimization using GP-upper-confidence bound (UCB) principle.⁵⁸ It has been noted in several works^59,60 that introducing $L_t$ promises theoretical convergence guarantees. Figure 1 illustrates this process. Algorithm 1 outlines the pseudocode of AntBO. The details of acquisition function are presented in the STAR Methods section.

Algorithm 1. Antibody Bayesian Optimisation (AntBO).

Input: Objective function $f:X\to \mathbb{R}$, number of evaluations $N$, alphabet size of categorical variable $K$.

Randomly sample an initial dataset ${\mathcal{D}}_1={({\mathbf{x}}_i,f({\mathbf{x}}_i\left)\right)}_{i=1}^M$

for $i=1,\dots ,N$ do

 Fit a GP surrogate $g$ on ${\mathcal{D}}_i$

 Construct a $\mathtt{C}\mathtt{D}\mathtt{R}\mathtt{H}3-{\mathtt{T}\mathtt{R}}_{L_i}\left({\mathbf{x}}^{\ast }\right)$ around the best point ${\mathbf{x}}^{\ast }=\arg {\min }_{\mathbf{x}\in {\mathcal{D}}_i}g\left(\mathbf{x}\right)$ using Equation 2 in the main document.

 Optimise constrained acquisition,

  ${\mathbf{x}}_{i+1}=\arg {\min }_{\mathbf{x}\in TR\left({\mathbf{x}}^{\ast }\right)}\alpha \left(\mathbf{x}|{\mathcal{D}}_i\right)$

 Evaluate the black-box $f\left({\mathbf{x}}_{i+1}\right)$

 Update the dataset ${\mathcal{D}}_{i+1}={\mathcal{D}}_i\cup \left({\mathbf{x}}_{i+1},f\left({\mathbf{x}}_{i+1}\right)\right)$

Output: The optimum sequence ${\mathbf{x}}^{\ast }$

Evaluation setup and baseline methods

We use Absolut! for simulating the energy of the antibody-antigen complex. We indicate our framework (AntBO’s) kernel choice directly in the label, e.g., AntBO SSK, AntBO TK, and AntBO ProtBERT. We compare AntBO with several other combinatorial black-box optimization methods such as HEBO,⁴⁹ COMBO,⁶¹ TuRBO,⁶² LamBO,⁶³ random search (RS), and genetic algorithm (GA). We introduce the same developability criteria defined as in the CDRH3 trust region in all the methods for a fair comparison. We also run AntBO TK without a hamming distance criterion, which is by omitting ${\sum }_i\delta \left({\mathbf{x}}_i,{\mathbf{x}}_i^{\ast }\right)\le L_t$ term in Equation 2 of the trust region, and label it as AntBO NT. The trust region size $L_t$ is the distance of the best-seen sequence from the random starting sequence. The criterion restricts the local optimization within a certain radius $L_t$ from the starting sequence. Removing the distance criterion $d_{\max }$ allows a local search to reach the maximum possible value and lets the optimization process explore distant regions in the search space. For an explanation of the algorithms, including the configuration of hyperparameters, we refer to readers to STAR Methods section baseline approaches. For the primary analysis in the main article, we use twelve core antigens identified by their PDB ID and a chain of an antigen. Our choice of antigens is based on their interest in several studies.^13,64 We also evaluate our approach on the remaining 147 antigens in the Absolut! antibody-antigen binding database. The results for those are provided in Figures S3, S4, and S5.

AntBO is sample efficient compared with baseline methods

Precise wet-lab evaluation of an antibody is a tedious process and comes with a significant experimental burden because it requires purifying both antibody and antigen and testing their binding affinity.^31,65 We, therefore, first investigate the sample efficiency of all optimization methods. We ran experiments with a prespecified budget of 200 function calls and reported the convergence curve of protein designs versus minimum energy (or binding affinity) in Figure 2. The experimental validation we substitute here by Absolut!-based in silico proof is expensive and time consuming. Therefore, budgeting of optimization steps is a vital constraint.⁶⁵ In Figure 3, we compare AntBO with baseline methods and various binding affinity categories very high, super, and super+ (determined from 6.9 M experimentally obtained murine CDRH3s available from the Absolut! database). We normalize the energy score by the super+ threshold. Core antigen experiments are run with ten random seeds and the remaining antigens with three. We report the mean and $95\%$ confidence interval of the results.

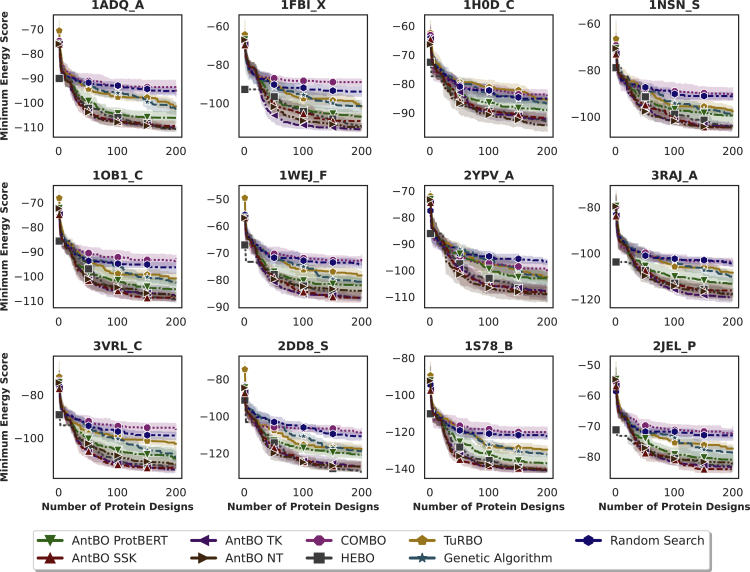
Figure 2.

AntBO is a sample-efficient solution for antibody design compared with existing baseline methods

AntBO with the transformed overlap kernel can find binding antibodies while outperforming other methods. It takes around 38 steps to suggest an antibody sequence that surpasses a very-high-affinity sequence from the Absolut! 6.9 M database and about 100 to outperform a super+ affinity sequence. We run all methods with 10 random seeds and report the mean and $95\%$ confidence interval for the 12 antigens of interest.¹³ The title of each plot is a PDB ID followed by the chain of an antigen. For extended results on the remaining 147 antigens, we refer to readers to Figures S3, S4, and S5. To understand the AntBO optimization, we also report the 3D visualization for an antigen 1ADQ_A in Figure S2.

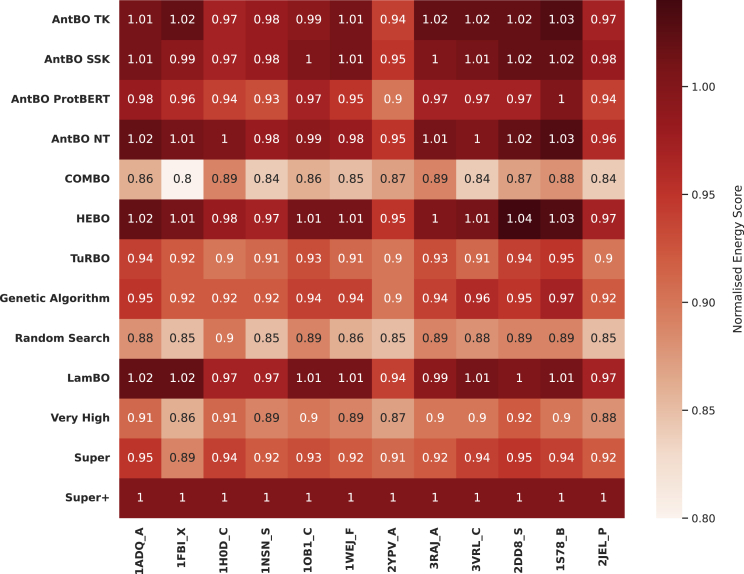
Figure 3.

We compare the binding energy threshold of different categories (low, high, very high, super, super+) obtained from the Absolut! 6.9M database and the average binding affinity of a sequence designed using AntBO methods and the baselines

The energycan scores are normalized by the threshold of the super+ category. We observe AntBO outperforms the best sequence in a majority of antigens and emerges as the best method in finding high-binding-affinity sequences in under 200 evaluations.

We observe that AntBO TK achieves the best performance with regards to (w.r.t.) to minimizing energy (maximizing affinity), typically reaching high affinity within 200 protein designs, with no prior knowledge of the problem. AntBO TK can search for CDRH3 sequences that achieve significantly better affinity than very-high-affinity sequences from the experimentally obtained Absolut! 6.9 M database. In the majority of antigens, AntBO TK outperforms the best-evaluated CDRH3 sequence by Absolut! We noticed that for the S protein chain of 1NSN, the P protein chain of 2JEL, and on a few other antigens (figures reported in the supplemental information), AntBO gets close to the best experimental sequence known for that antigen but does not outperform its affinity. We attribute this result to the complexity of the 3D lattice representation of an antigen that might require more sequence designs to explore the antibody optimization landscape. We wish to study this effect in future work. For some antigens, such as 1H0D, the binding affinity decreases in smaller factors when compared with other antigens, such as 1S78. This observation shows that some antigens are difficult to bind, while there are more possible improvements for others.³⁴ We make a similar observation in which transfer learning from one antigen to another differed across different pairs.

We found for a majority of antigens that AntBO TK outperforms AntBO ProtBERT. This finding contradicts our assumption that a transformer trained on millions of protein sequences would provide us with a continuous representation that can be a good inductive bias for GPs. We believe this could be associated with specific characteristics of antibody sequences that differ from a large set of general protein sequences. Consequently, there is a shift in distribution between the sequences used for training the protein BERT model and the sequences we encounter in exploring the antibody landscape. This finding also demonstrates that AntBO can reliably search in combinatorial space without relying on deep-learning models trained on enormous datasets. However, we want to remark that AntBO ProtBERT performs on par with other baselines.

We next investigate the average number of protein designs AntBO TK takes to get to various levels of binding affinity across all antigens. For this purpose, we take five affinity groups from existing works^13,64: low affinity (5%), high affinity (1%), very high affinity (0.1%), super (0.01%), and super+ (the best known binding sequence taken from the 6.9 M database.) and report the average protein designs needed to suggest a sequence in the respective classes for 188 antigens. Table 1 describes the performance of AntBO TK and other baselines. We observe that AntBO TK reaches a very-high-affinity class in around $\sim 38$ protein designs, super in around 50 designs, and only 85 to outperform the best available sequence. This sample efficiency of AntBO TK demonstrates its superiority and relevance in the practical world.

Table 1.

AntBO consistently ranks as the best method in designing high-affinity-binding antibodies while making minimum calls to the black-box oracle

Method affinity	Low			High			Very high			Super			Super+
	Top 5%			Top 1%			Top 0.1%			Top 0.01%			Best
	# $\downarrow$	% $\uparrow$	Score $\downarrow$	# $\downarrow$	% $\uparrow$	Score $\downarrow$	# $\downarrow$	% $\uparrow$	Score $\downarrow$	# $\downarrow$	% $\uparrow$	Score $\downarrow$	# $\downarrow$	% $\uparrow$	Score $\downarrow$
AntBO TK	20	100	0.2	29	100	0.29	${41}^{\ast }$	${99}^{\ast }$	$0.{42}^{\ast }$	${58}^{\ast }$	${96}^{\ast }$	$0{\text{.}}^{\ast }$	${97}^{\ast }$	${55}^{\ast }$	$1.{76}^{\ast }$
AntBO SSK	21	100	0.21	30	100	0.3	46	100	0.46	64	96	0.67	94	48	1.94
AntBO ProtBERT	24	100	0.24	37	97	0.39	60	88	0.69	84	73	1.14	121	24	5.02
AntBO NT	19	100	0.19	28	99	0.29	43	98	0.44	61	95	0.64	111	52	2.15
COMBO	44	92	0.48	56	56	0.97	67	15	4.44	99	3	39.47	–	–	–
HEBO	${15}^{\ast }$	${100}^{\ast }$	$0.{15}^{\ast }$	${25}^{\ast }$	${100}^{\ast }$	$0.{25}^{\ast }$	50	100	0.5	74	97	0.75	130	56	2.33
TuRBO	34	100	0.34	65	99	0.65	109	79	1.37	124	40	3.11	112	1	134.4
Genetic algorithm	34	100	0.34	70	99	0.7	111	92	1.21	140	56	2.48	141	4	33.79
Random search	37	100	0.37	71	78	0.9	84	23	3.61	99	3	39.6	–	–	–
LamBO	19	100	0.19	32	100	0.32	55	100	0.55	73	94	0.78	101	51	1.99

Here, we analyze the required number of successful trials to reach various binding affinity categories. We report a number of protein designs needed to reach low, high, very high, and super affinity (top 5%, 1%, 0.1%, and 0.01% quantiles from the Absolut! 6.9 M database, respectively). We denote by super+ the number of designs required to outperform the best CDRH3 in the 6.9 M database. The various binding categories are taken from existing works.^13,64 We collectively report three scores for every affinity class across all respective methods (10 trials and 12 antigens). For a given method, let $\mathbf{T}\mathbf{E}$ be a matrix of size $\left[12\times \mathrm{10,200}\right]$ (where each trial lasts 200 iterations) of all trial affinities; $\mathbb{I}\left(\mathbf{T}{\mathbf{E}}_i\le c\right)$ be an indicator function that returns 1 if for a given trial $i$ a method finds any $\mathbf{T}\mathbf{E}$ better than the affinity category $c$’s value; and $\mathcal{F}$ as a function that returns minimum samples required to reach affinity category $c$; if the trial did not reach the affinity category, it returns 0. The first column (# $\uparrow$) outlines the average number of protein designs ${\sum }_i^N\mathcal{F}\left({\mathbf{T}\mathbf{E}}_i,c\right)/N$ required to reach the respective affinity quantile value $c$. The second column (% $\uparrow$) is the proportion of trials ${\sum }_i^N\mathbb{I}\left({\mathbf{T}\mathbf{E}}_i\le c\right)/N$ that output a protein design better than the given affinity category $c$, given as a percentage. Ideally, the best method would attain the lowest value in the first column and a value of 100% in the second column, showing that it reaches the affinity category in all trials and does so in the lowest number of samples on average. Due to the importance of both measurements, in the third column (Score $\downarrow$), we report the ratio of the two values to get an estimate of overall performance, where we penalize the reported mean samples required to reach an affinity category by the percentage of failed trials to reach that affinity category. The penalized ratio balances the probability of designing a super+ sequence and required evaluations. The categories in which no samples by a method reach the affinity class are denoted by $-$. The asterisk ∗ symbol indicates the best performing method. Our results demonstrate that AntBO TK is the superior method that consistently takes fewer protein designs to reach important affinity categories.

Visualization of trajectory for antigen 1ADQ_A

Figure S2 shows the trajectory of protein designs for an antigen 1ADQ_A for every ten steps. We observe that AntBO first explores sequences with different binding structures, later converges into regions of sequence space that contain antibodies of the same binding mode, and iteratively improves binding affinity by mutations that preserve the binding structure. We provide the sequence trajectories of all antigens in our codebase under the directory “results_data/”. The instructions for the 3D visualization of the trajectory are also provided in the codebase.

AntBO suggests antibodies with favorable developability scores

AntBO iteratively designs antibodies that improve (over previous suggestions) to reach an optimal binding sequence. The antibody sequences we encounter in the iterative refinement process compose a trajectory on the binding affinity landscape. To understand the search mechanism of AntBO, here, we investigate the developability scores of 200 CDRH3 designs found along the above trajectory on the binding affinity landscape. This analysis helps us understand how optimizing energy affects the biophysical properties of antibody sequences. The developability scores we used in CDRH3-TR are a few of many other biophysical properties. As noted in formulating antibody design as a black-box optimization with CDRH3 developability constraints, more scores can be added as constraints. However, finding an optimum sequence also adds an extra computational cost. Here, in addition to charge, we report hydrophobicity (HP) and the instability index, which have been used in other studies for assessing downstream risks of antibodies.^13,42 A smaller instability index value means the sequence has high conformational stability, and in practical scenarios, it is desired to have a score of less than 40. CDRH3 regions tend to aggregate when developing antibodies, making it impractical to design them. This phenomenon is due to the presence of hydrophobic regions. A low value of HP means a sequence has a lesser tendency to aggregate. We use the Biopython⁶⁶ package to compute HP and instability scores. We next discuss the analysis of developability parameters for severe acute respiratory syndrome coronavirus (SARS-CoV) antigen. The results on the remaining core antigens are provided in Figures S6, S7, and S8.

Case study: Application of AntBO for SARS-CoV antibody design

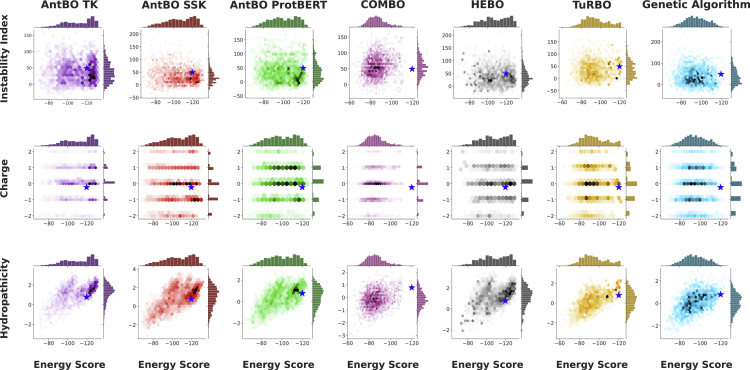
The spike (S) protein of the SARS-CoV (PDB: 2DD8) is responsible for the entry of the virus into the host cell, making it an important therapeutic target for the effective neutralization of the virus. Figure 4 demonstrates that AntBO can design antibodies for SARS-CoV with diverse developability parameters. On the top of each plot is a histogram of binding affinity of 200 designs and a right histogram of developability scores. The hexagon discretizes the space with the binding affinity on the vertical axis and the developability score on the horizontal axis. The color of hexagons shows a subspace frequency within a specific binding affinity range and the respective developability score. We observe that the distribution of three developability scores varies across all methods, showing the distinction between their designed sequences. Interestingly, the performance on developability scores, which were not included in constraints, demonstrates that the AntBO methods can identify sequences with diverse developability parameters. This observation suggests that our approach is suitable for exploring sequences toward high affinity and selecting candidates in a desired developability region. To understand how the spread of scores compares with experimentally known sequences, we take a set of super+ (top 0.01% annotated using the Absolut! 6.9 M database) and report their average developability score, which is denoted by the star ($\star$) symbol in the hexagram plots. We observe that the spread of scores of AntBO methods is close to the mean of super+. Thus, we can conclude AntBO is a more practically viable method for antibody design.

Figure 4.

AntBO can design antibodies that achieve diverse developability scores, demonstrating that it is a viable method to be practically investigated

We analyze the developability scores of 200 proteins designed by each method averaged across all 10 random seeds to simulate the diversity of suggested proteins across a single trial. Here, we report developability scores for S protein from the SARS-CoV virus (PDB: 2DD8). The landscape of designed sequences suggested during the optimization process for each method is shown with their binding affinity and three developability scores (hydropathicity, charge, and instability). We also take super+ (top 0.01%) sequences from the Absolut! 6.9 M database and report their mean developability scores denoted by a star ($\star$) in the plots. Interestingly, we observe a positive correlation between hydropathicity increasing with energy. While other methods have a larger charge spread, we see AntBO favorably suggesting the most points with a neutral charge. We observe the spread of developability scores of AntBO methods is close to the average score of super+ sequences. Overall, we conclude that energetically favorable sequences still explore a diverse range of developability scores and that the protein designs of AntBO are more stable than other methods.

Knowledge of existing binders benefits AntBO in reducing the number of calls to black-box oracle

The optimization process of AntBO starts with a random set of initial points used in fitting the GP surrogate model. This initialization scheme includes the space of non-binders, allowing more exploration of the antibody landscape. Alternatively, we can start with a known set of binding sequences to allow the surrogate model to better exploit the local region around the good points in finding an optimum binding sequence. We hypothesize that the choice of initial data points dictates the tradeoff between exploration and exploitation of the protein landscape. To investigate the question, we study the effect of different initialization schemes on the number of function evaluations required to find very-high-affinity sequences. We create three data point categories: losers, mascotte, and heroes. In the losers, all data points are non-binders; in the mascotte, we use half non-binders and half low binders; and finally, in the heroes, we take a proportion of six non-binders, six low binders, and eight high binders. The threshold of categories is obtained using the Absolut! database.¹³

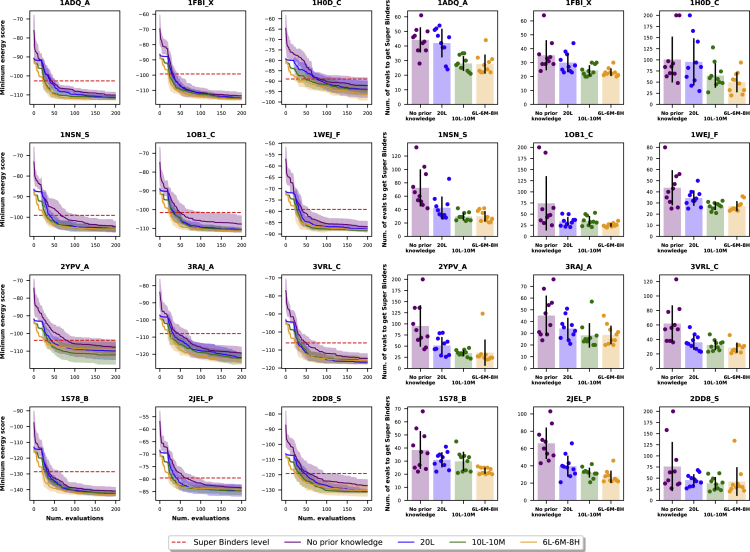
For each of the 12 core antigens, Figure 5 reports the convergence plot and the histogram of an average number of evaluations across 5 trials required to reach the super affinity category. When starting with the known sequence, AntBO exploits prior knowledge of the landscape, limiting the search technique to find an optimal design in the vicinity of available binders. Interestingly, we observe that when using prior information of binders for some antigens, such as 2YPV_A and 3RAJ_A, AntBO requires more sequence designs to reach the super affinity category. We hypothesize that this phenomenon can be attributed to the complexity of antigen structure that, in turn, can benefit from more exploration of the antibody sequence landscape.

Figure 5.

Effect of different initial class distributions on BO convergence

Experiments are run for three sets of initial points varying with the amount of binder (top 1%) and non-binders (remaining sequences): losers 20L (with only non-binders), mascotte 10L-10M (half non-binders and half low binders), and heroes 6L-6M-8H (six non-binders, six low binders, and eight high binders). The top is the BO convergence plot with a horizontal line denoting the energy threshold to reach the super binder level. The bottom figures show the histogram of the number of antibody designs required to reach super binding affinity class averaged across 5 trials. We find that for the majority of antigens, prior knowledge of binders helps in reducing the number of evaluations.

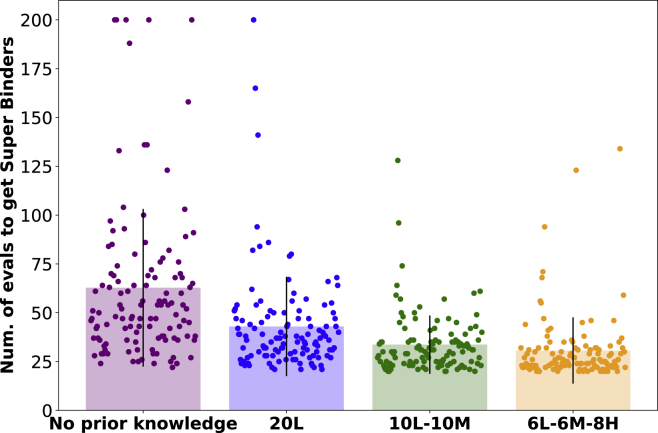
Figure 6 further reports the histogram of a number of antibody designs averaged across both 5 trials and 12 core antigens. We observe that the overall required number of calls to the black-box oracle to reach the super binding affinity category decreases when information on known antibody binding sequences is made available to AntBO as training data for the GP surrogate model. We can interpret the initialization as prior domain knowledge that aids the antibody design process by reducing the computational cost of evaluating the black-box oracle.

Figure 6.

AntBO benefits from the knowledge of a prior binding sequence in arriving at super binders

The average number of antibody designs reduces when information about known binders is made available to GP surrogate model. On the y axis, we report the average number of iterations required across all antigens to reach the super binding affinity class (outperforming the best sequence in the Absolut! database), and on the x axis, we have three affinity classes, namely losers 20L (with only non-binders), mascotte 10L-10M (half non-binders and half low binders), and heroes 6L-6M−8H (six non-binders, six low binders, and eight high binders).

Discussion

General computational approaches for antibody discovery

Several computational approaches have been developed to support antibody design^14,16 either using physics-based antibody and antigen structure modeling^29,67,68 and docking^69,70 or using ML methods to learn the rules of antibody-antigen binding directly from sequence or structural datasets.¹⁴ (1) Paratope and epitope prediction tools consider either sequence or structure of both antigen or antibody to predict the interacting residues.^{12,28,71,72,73,74,75,76,77,78} Knowledge of the paratope and epitope does not directly inform affinity but helps priorities important residues to improve affinity. (2) Binding prediction tools, often inspired by protein-protein interaction (PPI) prediction tools,⁷⁹ predict the compatibility between an antibody and an antigen sequence or structure. The compatibility criterion is decided by either using clustering to predict sequences that bind to the same target,^80,81 using a paratope-epitope prediction model,⁵ or using a ranking of binding poses to classify binding sequences.⁸² However, predicting antibody binding mimics the experimental screening for antibody candidates but does not directly help to get high affinity and specific antibody sequences. (3) Affinity prediction tools specifically predict affinity improvement following mutations on antibody or antigen sequences. Our work particularly focuses on the affinity prediction problem because it is a major time and cost bottleneck in antibody design.

Small size of available experimental datasets limiting the application of ML methods

Available experimental datasets

The experimental datasets describing the antibody binding landscape can be categorized in four ways. (1) Structures of antibody-antigen complexes provide the most accurate description of the binding mode of an antibody and the involved paratope and epitope residues,⁸³ which helps to prioritize residues that can modulate binding affinity. Structures do not directly give an affinity measurement but can be leveraged with molecular docking and energy tools to infer approximate binding energy. Only $\sim 1200$ non-redundant antibody-antigen complexes are known so far.⁸³ (2) Sequence-based datasets contain the results of qualitative screenings of thousands of antibodies (either from manually generated sequence libraries or from ex vivo B cells).⁶⁵ Typically, millions of sequences can be inserted into carrier cells expressing the antibody on their surface. Following repeated enrichment steps for binding to the target antigen, a few thousand high-affinity sequences can be obtained,⁴² and newer experimental platforms will soon allow reaching a few million. As of yet, however, sequencing datasets can only label sequences with binder or non-binder or low-affinity, medium-affinity, and high-affinity classes. (3) Affinity measurements are very time consuming because they require the production of one particular antibody sequence as protein before measuring its physicochemical properties (including other in-vitro-measurable developability parameters). Affinity measurements are precise and quantitative, either giving an affinity reminiscent of the binding energy or down to an association and dissociation constant. As an example, the AB-bind database only reports in total 1,100 affinities on antibody variants targeting 25 antigens,⁸⁴ and a recent cutting-edge study⁴² measured the affinity of 30 candidate antibodies, showing the experimental difficulty in obtaining the affinity measurement of many antibodies. Finally, (4) in (and ex) vivo experiments describe the activity of injected antibodies, including in vivo developability parameters^35,85 such as half-life, and toxicity, including off-targets. In vivo experiments are restricted to lead candidates due to their high cost and cannot be performed when screening for antibody leads. Although qualitative (sequencing) datasets inform on initial antibody candidates, increasing the activity and specificity of antibody candidates requires many steps to further improve their affinity toward the antigen target while keeping favorable developability parameters. It is the most tedious and time-consuming step. However, upcoming methods may reveal more quantitative affinity measurements at high throughput.⁸⁶

Generative models for sampling antibody candidates

Generative ML architectures have been leveraged to generate antibody candidates from sequence datasets. Specifically, an autoregressive model,⁸⁷ a variational autoencoder,⁸⁸ or a generative adversarial network (GAN)⁸⁹ has been used for generating aa sequences of antibodies^{64,90,91,92,93,94}. Amimeur et al.⁹⁰ also incorporate therapeutic constraints to avoid sampling a non-feasible sequence at inference. Ingraham et al.,⁹⁵ Koga et al.,⁹⁶ and Cao et al.⁹⁷ additionally include information of a backbone structure. Recently, Jin et al.⁴⁴ proposed an iterative refinement approach to redesign the 3D structure and sequence of antibodies for improving properties such as the neutralizing score. The generative modeling paradigm can increase the efficient design of antibodies by prioritizing the next candidates to be tested experimentally.

Due to the current small size of datasets, the application of ML methods for improving antibody affinity has been minimal. Further, the generalizability of such approaches is difficult to assess, and there is a lack of generative models that can be conditioned for affinity. Here, we set out to leverage the maximal information on antibody sequence affinity from the minimal number of experimental, iterative measurements using BO to generate an informed prediction on potential higher-affinity sequences. We use the Absolut! simulator as a black-box oracle to provide a complex antibody-antigen landscape that recapitulates many layers of the experimental complexity of antibody-antigen binding.

Combinatorial methods for protein engineering

Methods on protein engineering^98,99,100 use evolutionary methods to explore the combinatorial space of protein sequences. They use directed evolution—an iterative protocol of mutation and selection followed by a screening to identify sequences with improved diversity and functional properties. However, the approach suffers from high experimental costs due to inefficient screening methods. To overcome the experimental hurdle, Yang et al.³³ propose an ML pipeline for protein engineering. The central theme is to utilize the measurements of known protein sequences to train an ML model that can further guide the evolution of protein sequences. A concurrent work⁶³ introduces LamBO—a multiobjective BO framework for designing molecular sequences. LamBO utilizes a deep kernel for fitting GPs. Specifically, it does optimization in the latent space of a denoising autoencoder. We want to remind the readers AntBO with protBERT uses a deep kernel in the latent space of pretrained BERT for training GPs. However, the acquisition maximization is done in the input space. The major limitation is that none of these methods have been investigated for antibody design due to limited data on antibody specificity.

AntBO: A sample-efficient solution for computationally favorable antibody design

A list of therapeutically relevant developability parameters is considered vital for designing antibodies.^14,42 These parameters include solubility, charge, aggregation, thermal stability, viscosity, immunogenicity (i.e., the antibody should not induce an immune response, which might also induce its faster clearance by the body), glycosylation motifs, and the in vivo half-life. Although the whole antibody sequence can be modified to improve developability, the CDRH3 region also seems to have a critical impact on them beyond only affinity and antigen recognition.¹⁰¹ Therefore, it is crucial to include developability constraints in CDRH3 design. Interestingly, many parameters can be calculated in advance from the antibody sequence according to experimentally validated estimators,¹⁴ allowing for defining boundaries of the search space according to development needs. Our proposed AntBO framework utilizes the developability parameters to construct a trust region of feasible sequences in the combinatorial space, thus allowing us to search for antibodies with desired biophysical properties.

Our findings across several antigens demonstrate the efficiency of AntBO in finding sequences outperforming many baselines, including the best CDRH3 obtained from the Absolut! 6.9 M database. AntBO can suggest very-high-affinity sequences with an average of only 38 protein designs and a super binding sequence within 100 designs. The versatility of Absolut! allows defining binder/non-binder levels based on user requirements. In the future, an interesting investigation would be measuring the performance of AntBO as a function of different binder definitions.¹³ We also wish to investigate our framework for improved structure prediction with other docking simulation models and perform experimental validations.

Limitations of the study

We want to remark to the readers that AntBO is the first framework showcasing different flavors of combinatorial BO for the antibody design problem. The potential limitations of AntBO in its current scope are (1) AntBO sequentially designs antibodies suggesting one sequence per evaluation step. To achieve a more efficient experimental scenario, AntBO can be adapted to a batch scenario, allowing us to design more sequences in fewer evaluations. (2) Another limitation is that the current binding simulation framework Absolut! utilizes 3D lattice representation based on prespecified inter-aa distances and 90° angles. Such a representation is highly restrictive in many configurations where antibodies can bind to an antigen of interest. We wish to address this in future work, building on a more realistic framework combining docking such as FoldX²⁴ with structure prediction tools like AbodyBuilder²⁹ and Alpha-Fold Multimer.¹⁰² (3) In the current work, we only design the CDRH3 region, which is identified as the most variable chain for an antibody, and ignore the folding of other CDR loops that can affect the binding specificity. The above-discussed limitations are promising research questions to extend AntBO that we wish to study in future work.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Absolut 6.9M	Robert, Philippe A., et al.13	https://archive.sigma2.no/pages/public/datasetDetail.jsf?id=10.11582/2021.00063
Software and algorithms
AntBO	This paper	https://doi.org/10.5281/zenodo.7344859
GPyTorch	Gardner, Jacob, et al.103	https://github.com/cornellius-gp/gpytorch
Pytorch	Paszke, Adam, et al.104	https://pytorch.org/
Absolut	Robert, Philippe A., et al.13	https://github.com/csi-greifflab/Absolut
Casmopolitan	Wan, Xingchen, et al.60	https://github.com/xingchenwan/Casmopolitan
COMBO	Oh, Changyong, et al.61	https://github.com/QUVA-Lab/COMBO
TurBO	Eriksson et al., 201962	https://github.com/rdturnermtl/bbo_challenge_starter_kit/tree/master/example_submissions/turbo

Resources availability

Lead contact

All requests for additional information and resources should be directed to a Lead Contact, Haitham Bou-Ammar (haitham.ammar@huawei.com).

Materials availability

This study did not generate new unique reagent.

Method details

Introduction to BO and GP

Gaussian Processes

A GP is defined as a collection of random variables, where a joint distribution of any finite number of variables is a Gaussian.⁴¹

Let $f:\mathcal{X}\to \mathbb{R}$ be a continuous function, then the distribution over function $f$ is specified using a GP, that is, $f\left(\mathbf{x}\right)\sim GP\left(\mu \left(\mathbf{x}\right),\mathbf{K}\left(\mathbf{x},{\mathbf{x}}^{\prime }\right)\right)$, where $\mu \left(\mathbf{x}\right)=\mathbb{E}\left[f\left(\mathbf{x}\right)\right]$ is a mean function and $\mathbf{K}\left(\mathbf{x},{\mathbf{x}}^{\prime }\right)=\mathbb{E}\left[\left(f\left(\mathbf{x}\right)-\mu \left(\mathbf{x}\right)\right)\left(f\left({\mathbf{x}}^{\prime }\right)-\mu \left({\mathbf{x}}^{\prime }\right)\right)\right]$ is a covariance matrix. The standard choice for a mean function is a constant zero $\mu \left(\mathbf{x}\right)=0$,⁴¹ and the entries of a covariance matrix are specified using a kernel function. By definition, kernel function $\mathbf{k}:\mathcal{X}\times \mathcal{X}\to \mathbb{R}$ maps a pair of input to a real-valued output that measures the correlation between a pair based on the closeness of points in the input space. As $\mathcal{X}$ is combinatorial, we need particular kernels to get a measure of correlation, which we introduce in section kernels to operate over antibody sequences.

GP prediction

Consider $\mathbf{X}={\left({\mathbf{x}}_i,{\mathbf{y}}_i\right)}_{i=1}^N$ be a set of training data points and ${\mathbf{X}}^{\ast }={\left({\mathbf{x}}_i^{\ast },{\mathbf{y}}_i^{\ast }\right)}_{i=1}^N$ be a set of test data points. To fit a GP, we parameterise kernel hyperparameters and maximise the marginal log likelihood (MLL) using the data. Specifically, we define $\mathbf{K}\left(\mathbf{X},\mathbf{X}\right)$ as a covariance matrix of training samples, $\mathbf{K}\left(\mathbf{X},{\mathbf{X}}^{\ast }\right)$ and $\mathbf{K}\left({\mathbf{X}}^{\ast },\mathbf{X}\right)$ are covariance matrix of train-test pairs and vice versa, and $\mathbf{K}\left({\mathbf{X}}^{\ast },{\mathbf{X}}^{\ast }\right)$ is a covariance matrix of test samples. The final posterior distribution over test samples is obtained by conditioning on the train and test observation as,

$$\begin{array}{l}{\mathit{f}}^{\ast }|{\mathbf{X}}^{\ast },\mathbf{X},\mathit{y}\sim \mathcal{N}(\mathbf{K}\left({\mathbf{X}}^{\ast },\mathbf{X}\right)\mathbf{K}{\left(\mathbf{X},\mathbf{X}\right)}^{-1}\mathit{y}\text{,}\\ \mathbf{K}\left({\mathbf{X}}^{\ast },{\mathbf{X}}^{\ast }\right)-\mathbf{K}\left({\mathbf{X}}^{\ast },\mathbf{X}\right)\mathbf{K}{\left(\mathbf{X},\mathbf{X}\right)}^{-1}\mathbf{K}\left(\mathbf{X},{\mathbf{X}}^{\ast }\right))]\end{array}$$

GP training

We fit the GP by optimising the negative MLL using Adam.¹⁰⁵ The kernel functions in GPs come with hyperparameters that are useful to adjust the fit of a GP; for example, in an SE kernel described above, we have a lengthscale hyperparameter that acts as a filter to tune the contribution of various frequency components in data. In a standard setup, the optimum value of the hyperparameter is obtained by minimising the negative marginal log likelihood,

$$\begin{array}{c}-\log \mathrm{p}\left(\mathrm{y}|\mathrm{X},\theta \right)=0.5\log \left|\left({\mathrm{K}}_{\theta }\left(\mathrm{X},\mathrm{X}\right)+{\sigma }^2\mathrm{I}\right)\right|\\ +0.5y^T\left({\mathrm{K}}_{\theta }\left(\mathrm{X},\mathrm{X}\right)\right)+0.5N\log \left(2\pi \right)\end{array}$$

where $\theta$ is the set of kernel hyperparameters and $|.|$ is the determinant operator.

Kernels

Transformed overlap kernel (TK)

TK defines the measure of similarity as $k\left(\mathbf{x},{\mathbf{x}}^{\prime }\right)=\exp \left(\frac{1}{L}{\sum }_{i=1}^L{\theta }_i\delta \left(x_i,x_i^{\prime }\right)\right)$ where ${\left\{{\theta }_i\right\}}_{i=1}^L$ are the lengthscale parameters that learn the sensitivity of input dimensions allowing GP to learn complex functions.

ProteinBERT kernel (ProtBERT)

We utilise a deep kernel for protein design based on the success of transformer architecture BERT. The ProteinBERT⁵² model is a transformer neural network trained on millions of protein sequences over 1000s of GPUs. Such large-scale training facilitates learning of the representation space that is expressive of the higher-order evolutionary information encoded in protein sequences. We use the encoder of the pre-trained ProteinBERT model followed by a standard RBF kernel to measure the similarity between a pair of inputs.

Fast string kernel (SSK)¹⁰⁶

Let ${\Sigma }^l$ be a set of all possible ordered sub-strings of length $l$ in the alphabet, $\mathbf{x}$ and ${\mathbf{x}}^{\prime }$ be a pair of antibody sequences, then the correlation between the pair is measured using a kernel $k_{\theta }\left(.,\text{.}\right)$ is defined as,

$$\begin{array}{cc}{k}_{\theta }\left(\mathbf{x},\mathbf{x}\right)& =\sum _{\mathbf{y}\in {\Sigma }^l}{\varphi }_{\mathbf{y}}^{\theta }\left(\mathbf{x}\right){\varphi }_{\mathbf{y}}^{\theta }\left({\mathbf{x}}^{\prime }\right)\text{,}\\ {\varphi }_{\mathbf{y}}^{\theta }\left({\mathbf{x}}^{\prime }\right)& ={\theta }_m^{\left|\mathbf{y}\right|}\sum _{1\le i_1<,\dots ,\le i_k\le \left|\mathbf{x}\right|}{\theta }_g^{i_{\left|\mathbf{y}\right|}-i_1+1}{\mathbb{I}}_{\mathbf{y}}\left[\left({\mathbf{x}}_{i_1}^{\prime },\dots ,{\mathbf{x}}_{i_{\left|\mathbf{y}\right|}}^{\prime }\right)\right]\end{array}$$

where ${\mathbf{x}}_{i_j}^{\prime }$ is a length $j$ subsequence of sequence ${\mathbf{x}}^{\prime }$, $\theta ={\theta }_m,{\theta }_g$ are kernel hyperparameters, ${\theta }_m,{\theta }_g\in \left[\mathrm{0,1}\right]$ control the relative weighting of long and non-contiguous subsequences, ${\mathbb{I}}_{\mathbf{y}}\left[\mathbf{x}\right]$ is an indicator function set to 1 if strings $\mathbf{x}$ and $\mathbf{y}$ match otherwise 0, and ${\varphi }_{\mathbf{y}}^{\theta }\left(\mathbf{x}\right)$ measures the contribution of subsequence $\mathbf{y}$ to sequence $\mathbf{x}$.

Acquisition function

BO relies on the criterion referred to as acquisition function to draw new samples (in our problem protein sequences) from the posterior of GP that improve the output of the black box (binding energy). The most commonly used acquisition function is expected improvement (EI).¹⁰⁷ EI aims to search for a data point that provides expected improvement over already observed data points. Suppose we have observed $N$ data points ${\mathcal{D}}_n=\left\{\left({\mathbf{x}}_1,f\left({\mathbf{x}}_1\right)\right),\dots ,\left({\mathbf{x}}_n,f\left({\mathbf{x}}_n\right)\right)\right\}$ then the EI is defined as an expectation over ${\mathcal{D}}_n$ under the GP posterior distribution as ${\alpha }_{\text{EI}}\left(\mathbf{x}\right)={\mathbb{E}}_{\left(.|{\mathcal{D}}_n\right)}\left[\min \left(\mathbf{f}\left(\mathbf{x}\right)-\mathbf{f}\left({\mathbf{x}}^{\ast }\right),0\right)\right]$, where ${\mathbf{x}}^{\ast }=\arg {\min }_{\mathbf{x}\in {\mathcal{D}}_n}f\left(\mathbf{x}\right)$. There are several other choices of acquisitions we refer to readers to.^45,51,108

Implementation details

We use Python for the implementation of our framework. We run all our experiments on a Linux server with 87 cores and 12 GB of GPU memory. We have outlined the hyperparameter used for all the methods in Table S1. For BERT we use a pre-trained “prot_bert_bfd” model available from.⁵² We package AntBO as software that comes with an easy interface to introduce a new optimisation algorithm and a black box oracle function. Thus, it offers a platform to investigate new ideas and benchmark them quickly across other methods. We next provide the details of the software.

Software

The framework’s architecture can be seen in part (a) of Figure S1. The dataloader, execution, and summarise layer are abstracted and integrated with the training, leaving only the optimizer for developers to design. The developers could also optionally include Gaussian Process, Neural Network or an arbitrary model to use with the optimiser. The platform has three important features that facilitate training.

$•$ Distributed training: Multiple CPU processes for data sampling in a parallel environment, especially useful in low data efficiency algorithms such as deep reinforcement learning. Multiple CPU processes are also utilised to evaluate the binding energy with Absolut, which speeds up the evaluation time. Multiple GPU training for an algorithm that supports the neural network.

$•$ Real-time visualisation: Update the training results of the optimizer in real-time. Our framework offers visualisation of the training graph, minimum binding energy obtained so far per iteration, and the corresponding sequence for the minimum binding energy and antigen docking visualisation.

$•$ Gym environment: Our framework offers a highly reusable gym environment containing the objective function evaluator via Absolut!. Developers could set the antigen to evaluate and CDRH3 sequences to bind, and the environment returns the binding energy of the corresponding CDRH3 sequences. The gym environment has two options, SequenceOptim and BatchOptim. For SequenceOptim, the agent fills a character in each step until all characters for the CDRH-3 are filled, when the episode stops. For each step, the reward is zero until the last step of the episode, when the CDRH-3 sequences will be evaluated, and the negative binding energy is returned as a reward. The binding energy is negative; hence lower negative binding energy represents a higher reward. For BatchOptim, each episode only has one step, in which the agent inputs the list of CDRH3 sequences of the antigens into the environment and the reward returns are a list of binding energy corresponding to the CDRH-3 sequences. SequenceOptim is useful for seq2seq optimisation, and BatchOptim is useful for combinatorial optimisation.

Baseline approaches

In this section, we discuss details of all the baseline approaches we use for comparison.

Random search

Given a computational budget of $s$ black-box function evaluations in a constrained optimisation setting, random search (RS) samples $s$ candidates that satisfy the specified constraints and evaluate the black-box function at those samples. The best candidate is the one with the minimum cost.

BO methods

HEBO

The Heteroscedastic and Evolutionary Bayesian Optimisation solver (HEBO⁴⁹) is the winning solution of the NeurIPS 2020 black-box optimisation (BBO) challenge.¹⁰⁹ HEBO is designed to tackle BBO problems with continuous or categorical variables, dealing with categorical values by transforming them into one-hot encodings. Efforts are made on the modeling side to correct the potential heteroscedasticity and non-stationarity of the objective function, which can be hard to capture with a vanilla GP. To improve the modeling capacity, parametrised non-linear input and output transformations are combined to a GP with a constant mean and a Matérn-3/2 kernel. When fitting the dataset of observations, the parameters of the transformations and of the GP are learned together by minimising the negative marginal likelihood using Limited-memory BFGS (LBFGS) optimiser. When it comes to the suggestion of a new point, HEBO accounts for the imperfect fit of the model and for the potential bias induced by choice of a specific acquisition function by using a multi-objective acquisitions framework, looking for a Pareto-front solution. Non-dominated sorting genetic algorithm II (NSGA-II), an evolutionary method that naturally handles constrained discrete optimisation, is run to jointly optimise the Expected Improvement, the Probability of Improvement, and the Upper Confidence Bound. The final suggestion is queried from the Pareto front of the valid solutions found by NSGA-II that is run with a population of 100 candidate points for 100 optimisation steps.

HEBO results presented in this paper are obtained by running the official implementation by⁴⁹ at https://github.com/huawei-noah/HEBO/tree/master/HEBO.

TuRBO

To tackle the optimisation of high-dimensional black-box functions, BO solvers face the difficulty of finding good hyperparameters to fit a global GP over the entire domain, as well as the challenge of directly exploring an exponentially growing search space.⁶² introduces local BO solvers to alleviate the above issues. The key idea is to use local BO solvers in separate subregions of the search space, leading to a trust region BO algorithm (TuRBO). A TR is a hyperrectangle characterised by a center point and a side length $L$ similar to what we describe in Section CDRH3 trust region acquisition maximisation. A local GP with constant mean and Matérn-5/2 ARD kernel fits the points lying in the TR better to capture the objective function’s behavior in this subdomain. The GP fit is obtained by optimising the negative MLL using Adam.¹⁰⁵ The size of the TR is adjusted dynamically as new points are observed. The side length $L$ is doubled (up to $L_{\max }$) after ${\tau }_{\text{succ}}$ consecutive improvements of the observed black-box values and is halved after ${\tau }_{fail}$ consecutive failures to find better point in the TR. The TR is terminated whenever $L$ shrinks to an $L_{\min }$ value, and a new TR is initialised with a side size of $L_{\text{init}}$. The next point to evaluate is selected using the Thompson Sampling strategy, which ideally consists of drawing a function $f$ from the GP posterior and finding its minimiser. However, it is impossible to draw a function directly over the entire TR; therefore, a set of $\min \left(100d,5000\right)$ candidate points covering the TR is used instead. Function values are sampled from the surrogate model’s joint posterior at these candidate points. The candidate point achieving the lowest sample value is acquired. Our experiments only acquire suggested points that fulfill the developability constraints.

In our experiments, we rely on the TuRBO implementation provided in the BBO challenge¹⁰⁹ codebase at https://github.com/rdturnermtl/bbo_challenge_starter_kit/tree/master/example_submissions/turbo.

COMBO

To adapt the BO framework for combinatorial problems,⁶¹ proposed to represent each element of the discrete search space as a node in a combinatorial graph. Then a GP surrogate model is trained for the task of node regression using a diffusion kernel over the combinatorial graph. However, the graph grows exponentially with the number of variables, making it impractical to compute its diffusion kernel. To address this issue, the authors express the graph as a cartesian product of subgraphs. This decomposition allows the computation of a graph diffusion kernel as a cartesian product of kernels on subgraphs. The efficient computation of diffusion kernel is done using Fourier transform. The hyperparameters of the GP model, such as kernel scaling factors, signal variance, noise variance, and constant mean value, are obtained using 100 slice sampling steps at the beginning and ten slice sampling iterations afterward. Once we obtain the GP fit, it remains to optimise an acquisition function over the combinatorial space, which is done by applying a breadth-first local search (BFLS) from 20 starting points selected from 20,000 evaluated random vertices. Since COMBO does not support constraints on the validity of the suggested sequences, we modify the acquisition optimisation to incorporate the CDRH3-TR introduced in 2. We use the default hyperparameters that we provide in Table S1 and add constraints handling to the official implementation by⁶¹ at https://github.com/QUVA-Lab/COMBO.

Genetic algorithm

Genetic algorithms (GAs) are inspired by Charles Darwin’s theory of natural selection. The idea is to use probabilistic criteria to draw new population samples from the current population. This sampling is generally done via crossover and mutation operations.¹¹⁰ Overall the primary operations involved in GA are: encoding schemes, crossover, mutation, and selection, respectively.¹¹¹ For encoding, we use a general ordinal encoding scheme that assigns a unique integer to each AA—inspired from binary encoding where each gene represents integer 0–1 or hexadecimal that represents integer 0–15 (or 0–9, A-F).¹¹² Specific to our work, we express each gene by a letter of CDRH3 sequences ranging from (0–19). For selection, we use the elitism mechanism,¹¹³ which preserves a few best solutions in the current population to the next population. Our mutation operator is inspired by the most commonly used bit flipping mutation¹¹⁴ that flips a bit of each gene with a given probability. Instead, we randomly replace a gene from 0–19 as our range is different. Finally, for crossover, we use a uniform crossover, which suggests unbiased exploration and better recombination.¹¹¹ The pseudocode of a GA is illustrated in Algorithm 11.8.2 (Algorithm 2).

Algorithm 2. Genetic Algorithm.

Input: Black box function $f:X\to \mathbb{R}$, Constraint function $C:X\to \mathrm{0,1}$, Maximum number of iterations $N_{iter}$, Population size $N_{pop}$, Number of elite samples $N_{elite}$, Crossover probability $p_c$, Mutation probability $p_m$

Output: Best performing sample.

1$P^0=rejectionSampling\left(C\right)$ // Sample initial population

2$F^0\leftarrow f\left(P^0\right)$ // Evaluate initial population

  for $i=1,\dots ,N_{iter}$ do

3 $P^{i+1}=\left[\right]$ // Initialise next population with an empty list

4 $Q^i=\left[\right]$ // initialise list of parents

  for $j=1,\dots ,N_{elite}$ do

5 $p^j\leftarrow$ sample with $j^{th}$ highest fitness from $P^i$ // Get sample with the next highest fitness

6 $P^{i+1}\leftarrow P^{i+1}\cup p^j$ // Add this sample to the next population

7 $Q^i\leftarrow Q^i\cup p^j$// Add this sample to the list of parents

  for $j=N_{elite}+1,\dots ,N_{pop}$ where $j$ increases in steps of 2 do

8 $q_1,q_2\sim Q^i$ // Randomly sample two parents

9   $constraint\_satisfied=False$

  while not $constraint\_satisfied$ do

10 ${\eta }_1,{\eta }_2=crossover\left(q_1,q_2,p_c\right)$ // Perform crossover to generate two offsprings

11 ${\eta }_1,{\eta }_2\leftarrow mutate\left({\eta }_1,p_m\right),mutate\left({\eta }_2,p_m\right)$ // Mutate both offsprings

12 $constraint\_satisfied=C\left({\eta }_1\right)\wedge C\left({\eta }_2\right)$ // Check that both offsprings satisfy all constraints

13 $P^{i+1}\leftarrow P^{i+1}\cup {\eta }_1\cup {\eta }_2$ // Add offsprings to new population

14 $F^{i+1}\leftarrow f\left(P^{i+1}\right)$ // Evaluate new population

Absolut! a binding affinity computation framework

Absolut!¹³ is a state-of-the-art in silico simulation suite that considers biophysical properties of antigen and antibody to create a simulation of feasible bindings of antigen and antibody. Although Absolut! is not able to directly generate antibody-antigen bindings at the atomic resolution, and therefore to predict antibody candidates directly. However, using Absolut!, we can develop methods in the simulation world and later employ the best method in the complex real-world scenario, with the knowledge that this method already performed well on the levels of complexity already embedded into Absolut! datasets. This feature of Absolut! makes it an ideal black-box candidate for the antibody design problem. However, we note that AntBO is, in principle, agnostic to the choice of the black-box oracle used and can be adapted to other in silico or experimental oracles provided they can compute or determine binding affinity or any other criteria relevant for antibody design. Absolut! performs the computation of binding affinity in three main steps, i) antibody-antigen lattice representation, ii) discretisation of antigen and iii) binding affinity computation. We next introduce the main steps of binding affinity computation in Absolut!

Discretisation of antigen

The Absolut! suite utilises Latfit^115,116 to transform a PDB structure of an antigen into a 3D lattice coordinates position. The PDB structure represents each residue in a protein sequence using 3D coordinates. The Latfit maps these coordinates to a discretised lattice position by optimising dRMSD (Root-Mean-Square Distance) between the original PDB structure and many possible lattice reconstitutions of the same chains. Specifically, for a sequence of length $n$, Latfit first assigns a lattice position to a starting residue and then enumerates all neighboring sites to select the one with the best dRMSD to the PDB coordinate of the next residue. The generated nascent lattice structures are rotated to better match the original PDB before adding the next AA. This process is repeated sequentially, and at each step, Latfit keeps track of $s$ best structures of length $K$ to find the best position of the next residue.

Antibody-antigen binding representation

Absolut! uses the Ymir¹¹⁷ framework to represent the protein structures as a 3D lattice model. A protein’s primary structure is a sequence of amino acids (AA). In a 3D lattice structure, each AA can occupy a single position, and the consecutive AAs occupy the neighboring sites. This layout form only permits a fixed inter-AA distance with joint angles of 90°.

The structure of the protein is specified with the help of a starting position in the grid and a sequence of relative moves (straight (S), up (U), down (D), left (L), right (R)) that determine the next AA position. The first step is to define a coordinate system with the starting point as an observer and the next move relative to the observer to specify the sequence of moves. There is also a possibility of backwards (B) for the first move that is not allowed for other positions to prevent any collision.

Computation of antibody-antigen binding affinity

In this stage, the lattice structure of two proteins is used to compute their binding affinity. Since the structure of the antibody is not known apriori for a specific antigen, all possible foldings of CDRH3 are generated recursively using the algorithm proposed in¹¹⁷ and stored in the memory. As the number of possibilities of folding grows combinatorially with the length of a sequence, Absolut! restricts the size of the CDRH3 sequence to 11 and limits the search to structures with a realistic minimum of contact points (10) to the target antigen.

After we obtain the lattice structure of an antigen and the list of pre-computed structures for the CDRH3 sequences, the binding affinity of one structure is described as a summation of three terms, a) binding energy the interaction between residues of antibody and residues of antigen, b) antibody folding energy the interactions within the residues of antibody, and c) antigen folding energy the interaction within the residues of antigen. Since the antigen structure is fixed apriori, the third term is constant and can be ignored.

Consider a pair of lattice positions and residues of an antigen sequence $\left(\mathbf{S},\mathbf{R}\right)$ and of an antibody sequence $\left(\mathbf{G},\mathbf{K}\right)$. The binding energy ${\mathbf{E}}_{\text{bind}}$ is defined as a sum of all interaction potential,

$${\mathbf{E}}_{\text{bind}}=\sum _{k=1}^{L_G}\sum _{j=1}^L\mathbb{I}\left(S_j,K_k\right)\mathcal{A}\left(R_j,G_k\right)$$ (Equation 3)

and the folding energy ${\mathbf{E}}_{\text{fold}}$ of an antibody is defined as a sum of intra-bonds between its AAs,

$${\mathbf{E}}_{\text{fold}}=\sum _{j=1}^L\sum _{k=1}^L\mathbb{I}\left(K_j,K_k\right)\mathcal{A}\left(K_j,K_k\right)$$ (Equation 4)

where $\mathcal{A}\left(.,\text{.}\right)$ is an interaction potential of residues determined via Miyazawa-Jernigan interaction potential¹¹⁸ and $\mathbb{I}\left(a,b\right)$ is an indicator function that takes the value 1 if $a$ and $b$ are non-covalent neighbors in the lattice otherwise 0. For the evaluation of an arbitrary CDRH3 sequence, the pre-computed structures are filled one by one with residues of CDRH3, and their total energy is computed as ${\mathbf{E}}_{\text{total}}={\mathbf{E}}_{\text{fold}}+{\mathbf{E}}_{\text{bind}}$, this step is known as exhaustive docking. The best structure is then selected using the minimum total energy criterion. Absolut! does this computation for sequences of length 11; if the CDRH3 is of size greater than 11, the same process is repeated for all subsequences of length 11 with a stride of 1 from left to right. Altogether, the total energy of an antibody-antigen structure determines its stabililty, and the binding energy is the term that represents the energy score (binding affinity), that aims to be minimized in this work.

Visualisation tools

We use open source python package matplotlib¹¹⁹ and seaborn library built on top of matplotlib for the purpose of data visualisation in the paper. For the visualisation in Figure 1 we use an open-source online tool draw.io. For the graphical abstract we thank to the service of 10creative.co.uk.

Quantification and statistical analysis

In all convergence plots reported across all methods we run experiments with 10 random seeds and report the mean and $95\%$ confidence interval for the 12 antigens of interest.¹³ For the analysis of remaining antigens reported in supplemental materials we run experiments with 5 seeds. All relevant details are explained in the caption of figures.

Published: January 3, 2023

Data and code availability

• $•$ This paper analyzes existing, publicly available data. These accession numbers for the datasets are listed in the key resources table.

• $•$ The code of our software AntBO and other used resources are open source on https://github.com/huawei-noah/HEBO/tree/master/AntBO. The DOI is listed in the key resources table.

• $•$ Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.