Summary
Sex-biased admixture can be inferred from ancestry-specific proportions of X chromosome and autosomes. In a paper published in the American Journal of Human Genetics, Micheletti et al.1 used this approach to quantify male and female contributions following the transatlantic slave trade. Using a large dataset from 23andMe, they concluded that African and European contributions to gene pools in the Americas were much more sex biased than previously thought. We show that the reported extreme sex-specific contributions can be attributed to unassigned genetic ancestry as well as the limitations of simple models of sex-biased admixture. Unassigned ancestry proportions in the study by Micheletti et al. ranged from ∼1% to 21%, depending on the type of chromosome and geographic region. A sensitivity analysis illustrates how this unassigned ancestry can create false patterns of sex bias and that mathematical models are highly sensitive to slight sampling errors when inferring mean ancestry proportions, making confidence intervals necessary. Thus, unassigned ancestry and the sensitivity of the models effectively prohibit the interpretation of estimated sex biases for many geographic regions in Micheletti et al. Furthermore, Micheletti et al. assumed models of a single admixture event. Using simulations, we find that violations of demographic assumptions, such as subsequent gene flow and/or sex-specific assortative mating, may have confounded the analyses of Micheletti et al., but unassigned ancestry was likely the more important confounding factor. Our findings underscore the importance of using complete ancestry information, sufficiently large sample sizes, and appropriate models when inferring sex-biased patterns of demography. This Matters Arising paper is in response to Micheletti et al.,1 published in American Journal of Human Genetics. See also the response by Micheletti et al.,2 published in this issue.
Keywords: admixture, Americas, genetic ancestry, mathematical models, population genetics, sex bias, slave trade
Introduction
In the paper “Genetic consequences of the transatlantic slave trade in the Americas,” Micheletti et al. conducted an ambitious study that integrated genetic evidence of admixture in the Americas with historic documents of the transatlantic slave trade to the Americas.1 A central component of their study was to estimate sex-biased contributions of Africans, Europeans, and Native Americans to the gene pools of contemporary populations in the Americas. Using ancestry proportions from X chromosomes and autosomes, Micheletti et al. inferred sex biases that are consistent with the directionality established by previous studies (e.g., female-biased African contributions and male-biased European contributions).1 However, the reported ratios of female and male contributions were markedly larger than previous estimates.3,4,5,6,7,8,9 For example, they reported that African women contributed approximately 15 times as much as African men to the gene pool in Central America, and European men contributed approximately 71 times as much as European women to the gene pool in Cabo Verde (Table 1 in Micheletti et al.).1 Importantly, these unusually large numbers were directly repeated by various news outlets.10,11,12 Although there is no question that sex-biased admixture occurred, we find that the extreme sex ratios reported by Micheletti et al. are questionable.
There are three major reasons to question their claims of such strong sex-biased admixture in the Americas. First, inconsistencies in the results, which we describe below, suggest that Micheletti et al. may have improperly implemented a population genetics model for estimating sex biases of a recent single admixture event, leading to misestimates of sex bias. Second, some geographic regions have substantial amounts of unassigned genetic ancestry in the study by Micheletti et al. As will be shown below, this unassigned ancestry can create false patterns of sex-biased admixture. Third, the applied models assume a single admixture event followed by random mating with no subsequent population growth or gene flow. However, admixture in the Americas was more complex than a single pulse admixture event,13,14,15,16,17,18,19 and violations of these simplifying assumptions may have confounded the analyses of Micheletti et al.1
Here, we set out to identify which of the above three issues most likely confounded the analyses of Micheletti et al.1 Using the model by Goldberg and Rosenberg,8 we re-estimated sex ratios from X chromosomal and autosomal ancestry proportions reported by Micheletti et al.1 As we still observed unexpectedly large sex ratios and cases of model failure (i.e., negative sex ratios), we systematically explored the consequences of unassigned ancestry, model sensitivity, small sample sizes, and violations of simplifying demographic assumptions on the magnitude of estimated sex-biased admixture. We found that violations of demographic assumptions can lead to misestimations of sex biases, but unassigned genetic ancestry was likely the primary confounding factor in the analyses of Micheletti et al.1 Furthermore, we found that the models are highly sensitive to small changes in the inferred mean ancestry proportions, complicating the interpretation of results. Thus, the large sex ratios reported by Micheletti et al. are most likely the result of unassigned ancestry in their study and the sensitivity of the applied models. Altogether, we caution against over-interpreting models when genetic ancestries do not add up to 100%.
Material and Methods
Population genetic models for estimating sex-biased admixture
Here, we briefly describe two models that were applied by Micheletti et al. to infer sex-biased admixture from X chromosomal and autosomal ancestry proportions.1 We start with a description of an equilibrium model that assumes an infinite number of generations since admixture, and then we describe a model developed by Goldberg and Rosenberg that considers a more recent admixture event.8
The equilibrium model for estimating the sex-biased admixture using X chromosomal and autosomal ancestry proportions is easily derived by noticing the sex-specific inheritance of the X chromosome. Females contribute two-thirds of the X chromosomes and males one-third, while females and males contribute an equal number of autosomes.7 In the limit of infinite generations since the admixture event, the equilibrium sex ratio for ancestry S1 is
| (Equation 1) |
where and are the female and male contributions from S1 and and are the observed ancestry proportions of X chromosomes and autosomes in the admixed population (H) coming from S1, respectively. A sex ratio greater than one (sf/sm > 1) implies female-biased admixture, whereas a sex ratio between zero and one (0 < sf/sm < 1) implies male-biased admixture. For a detailed derivation of Equation 1, see the supplemental information.
Goldberg and Rosenberg proposed a model that captures the dynamics of sex-specific contributions for the first few generations after a single admixture pulse.8 Their model is based on the observation that the X chromosomal ancestry proportion in males depends only on the X chromosomal ancestry proportion in females in the previous generation, leading to an oscillation of the X chromosomal ancestry proportion during the first few generations after admixture. This oscillation of X chromosomal ancestry proportions implies a time dependence during the early generations after admixture that also applies to inferred sex ratios. However, after approximately ten generations of random mating within the admixed population, the expected X chromosomal ancestry proportions in females and males converge to an equilibrium value (Figure 2 in Goldberg and Rosenberg).8 Thus, the sex ratio under this dynamic model converges to Equation 1. For more details, see the original publication by Goldberg and Rosenberg.8 Both models implicitly assume a constant population size, no gene flow, random mating, no genetic drift, and no selection after initial admixture.
Additional simulations of American admixture
To evaluate whether the analyses of Micheletti et al. were confounded by violations of demographic assumptions, we simulated different demographic scenarios after initial admixture. Specifically, we simulated exponential population growth of the admixed population, subsequent gene flow into the admixed population, and sex-specific assortative mating. For each scenario, we simulated diploid individuals with a single 100 Mb autosome, 100 Mb sex chromosomes (X and Y), and 20 kb mtDNA using SLiM v3.7.1.20
Prior to admixture, African (S1), European (S2), and Native American/East Asian (S3) ancestries were simulated as three continental ancestries according to the Gravel 2011 demographic model.21 Initial American admixture was then simulated 15 generations ago as a three-way admixture of S1, S2, and S3 with the admixture proportions 1/6, 1/3, and 1/2, respectively (proportions taken from Browning et al.13). Initial contributions from S1 and S3 were female biased, with ratios of 2 and 1.25 females to 1 male, respectively. Initial contributions from S2 were male biased, with a ratio of 2 males to 1 female. Note that the proportions and sex biases used do not necessarily represent historical realities. Instead, they are used to quantitatively assess the effect of different demographic scenarios when inferring sex-biased admixture.
A single-pulse admixture scenario was simulated as the null model. Additional simulations incorporated exponential growth of the admixed population, constant gene flow from the source populations into the admixed population, and/or sex-specific assortative mating. First, exponential growth of the admixed population was simulated at a rate of r = 0.05. Second, constant gene flow from all three source populations into the admixed population was simulated at migration rates m1 = 0.05, m2 = 0.025, and m3 = 0.01, with the same sex biases as used during the initial admixture. Third, we simulated sex-specific assortative mating with S2 females being asymmetrically more likely to mate with S2 males. This was achieved by replacing a non-S2 male mating with an S2 female with an S2 male in 40% of the cases (i.e., p = 0.4). In this mating scheme, female contributions from the different populations remain unchanged, but S2 males contribute more than expected under a random mating scheme (Table S3). We also simulated a more extreme case of sex-specific assortative mating with p = 0.9.
Simulated X chromosomes and autosomes were LD pruned using plink222 before estimating ancestry proportions using ADMIXTURE.23 Simulated mtDNA and Y chromosomes in admixed individuals were assigned to different ancestries based on proximity to ancestral haplogroup clusters. A detailed description of the simulations can be found in supplemental information.
Re-estimation of sex ratios based on ancestry proportions and haplogroup frequencies from Micheletti et al.
Micheletti et al. appear to have miscalculated sf/sm ratios, i.e., they miscalculated sex ratios when using the model of Goldberg and Rosenberg (see results and discussion).1,8 To assess the impact of this on the results of Micheletti et al., we implemented the model by Goldberg and Rosenberg8 to re-estimate sex ratios based on the ancestry proportions in Table S9 of Micheletti et al.1 Since the model by Goldberg and Rosenberg also requires knowing the fraction of sampled females and males, we inferred those for each broad region from Tables S2 and S10 in Micheletti et al.1 (Table S1 in our paper). mtDNA and Y chromosome haplogroup imbalances were inferred from reported haplogroup frequencies in Table S8 in Micheletti et al.1 (Table S2 in our paper). Note that there are inconsistencies between the reported Native American ancestry proportions in Table 1 of Micheletti et al. and Table S9 of Micheletti et al., as well as internal inconsistences between ancestry proportions reported for granular and broad regions in their Table S9.1 Here, we chose to use the numbers found in the “ancestry composition by broad region” section of Table S9 in Micheletti et al.,1 as more significant digits were reported there.
Table 1.
Re-estimation of sex bias reveals the confounding effects of unassigned ancestry
|
African |
European |
Native American |
Unassigned ancestry |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Region | HX | HA | mt/Y | HX | HA | mt/Y | HX | HA | mt/Y | ||||||||
| Guianas | 1.73 | 1.71 | 0.650 | 0.598 | 1.27 | 0.22 | 0.23 | 0.122 | 0.154 | 0.32 | – | – | 0.039 | 0.043 | – | 0.189 | 0.205 |
| United States | 1.47 | 1.48 | 0.756 | 0.710 | 1.35 | 0.33 | 0.33 | 0.206 | 0.248 | 0.25 | – | – | 0.029 | 0.023 | 3.05 | 0.009 | 0.019 |
| British Caribbean | 1.88 | 1.86 | 0.824 | 0.749 | 1.52 | 0.04 | −0.03 | 0.119 | 0.184 | 0.09 | – | – | 0.014 | 0.013 | 1.74 | 0.043 | 0.054 |
| Latin Caribbean | 13.3 | 10.3 | 0.237 | 0.186 | 1.24 | 1.11 | 1.11 | 0.531 | 0.522 | 0.21 | 3.78 | −4.08 | 0.155 | 0.100 | 43.66 | 0.077 | 0.192 |
| C. South America | 4.62 | −5.56 | 0.182 | 0.123 | 1.62 | 0.92 | 0.93 | 0.632 | 0.640 | 0.34 | 2.26 | −2.44 | 0.115 | 0.064 | – | 0.071 | 0.173 |
| N. South America | 17.2 | 10.5 | 0.139 | 0.109 | 1.03 | 0.44 | 0.47 | 0.430 | 0.489 | 0.09 | 3.38 | −3.80 | 0.363 | 0.231 | 15.64 | 0.068 | 0.171 |
| Central America | 15.6 | 10.9 | 0.106 | 0.083 | 0.55 | 1.12 | 1.12 | 0.321 | 0.315 | 0.13 | 28.0 | 15.7 | 0.507 | 0.392 | 3.47 | 0.066 | 0.210 |
| Cabo Verde | 22.6 | −81.4 | 0.593 | 0.442 | 2.50 | 0.01 | 0.05 | 0.351 | 0.504 | 0.09 | – | – | 0.002 | 0.004 | – | 0.054 | 0.050 |
X chromosomal (HX) and autosomal (HA) ancestry proportions from Table S9 in Micheletti et al.1 were used to infer ratios of female to male ancestry contributions for each admixed population after 15 generations of random mating (sf/sm). Subscripts indicate whether sex ratios refer to the original miscalculated values reported by Micheletti et al. () or the re-estimated sex ratios from our study (, see Table S4 for all generations). Ratios of female to male contributions were not calculated when ancestry proportions were below 0.05. refers to ratios of mtDNA and Y chromosome haplogroup frequencies inferred from Table S8 of Micheletti et al.1 Unexpectedly large sex ratios and model failure occur more often when there are large fractions of unassigned ancestry—especially when the amount of unassigned ancestry differs between X chromosomes and autosomes. There are also multiple situations where the direction of sex bias from X chromosomal and autosomal data is discordant with the direction inferred from mtDNA and Y chromosome haplogroups.
Computation of confidence intervals for sex ratios
As we shall see, the models are highly sensitive to small changes in inferred mean ancestry proportions. For this reason, reporting sex ratios with confidence intervals is preferable over point estimates. A general approach for computing confidence intervals of sex bias estimates involves bootstrapping individual-level ancestry proportions (e.g., obtained using ADMIXTURE23). Given m individuals in the dataset, m individuals are resampled n times with replacement, and for each resampling step, mean ancestry proportions and corresponding sex biases are calculated. From the obtained distribution of sex biases, confidence intervals are inferred, e.g., 2.5% and 97.5% percentile. This approach was used to compute 95% confidence intervals of sex bias estimates from simulations. We dynamically set the number of bootstrap samples (n) to equal the sample size (m). However, we always did at least 500 and at most 10,000 bootstrap resamples.
Results and discussion
Re-estimating sex ratios based on summary statistics from Micheletti et al
Micheletti et al. reported sex ratios for 15 generations after admixture in their Table 1.1 However, their implementation of the model of Goldberg and Rosenberg8 appears to be flawed for two reasons. First, the sex ratios reported by Micheletti et al. do not match expectations under the model of Goldberg and Rosenberg, as their implementation of the model does not converge to the expected equilibrium value after approximately 15 generations of random mating (compare g = 15 and g = inf in Table S9 in Micheletti et al.).1 For example, Micheletti et al. inferred that African women contributed approximately 22 times as much as African men to the gene pool of Cabo Verde after 15 generations of mating, but an equilibrium sex ratio of approximately 81 African females to males was reported in Table S9.1 Second, in some cases, the models are misspecified for the reported ancestry proportions, i.e., they yield non-sensical negative sex ratios, but only positive sex ratios are reported in Table 1 of Micheletti et al. and Table S9 of Micheletti et al.1 For instance, given the reported African ancestry proportions in Cabo Verde, the equilibrium model yields a non-sensical sex ratio of approximately negative 81 African females to one male instead of the positive 81 reported by Micheletti et al. in Table S9.1 For these reasons, we re-estimated sex ratios after 15 generations of random mating in admixed populations using the ancestry proportions reported in Table S9 in Micheletti et al.1 and the model by Goldberg and Rosenberg.8
In regions for which Micheletti et al. assigned almost all of the ancestry, such as the United States, the originally reported numbers are reasonable (Table 1). However, unexpectedly large sex ratios, instances of model failure (negative sex ratios), and impossible scenarios like female-biased contributions from all three ancestral populations are observed for geographic regions with substantial amounts of unassigned ancestry. These issues appear to be especially problematic if the amount of unassigned ancestry differs between X chromosomes and autosomes (e.g., in Central America and the Latin Caribbean). We therefore caution against interpreting the sf/sm values observed in Table 1 as the actual ratios of female to male contributions.
False patterns of sex bias arising from unassigned ancestry
Because many of the irregularities in Micheletti et al. are observed when ancestry estimates do not sum to 100%,1 we give an example to illustrate how unassigned ancestry can create false patterns of sex bias. We consider a scenario with no underlying sex biases where S1 contributes 75% of the genetic ancestry to the admixed population and S2 contributes 25%. We suppose that ancestries are inferred accurately, but 5% of X chromosomal and 10% of autosomal data of each ancestry cannot be unambiguously assigned, i.e., in total, 10% of the X chromosomal and 20% of the autosomal ancestry are left unassigned (these are approximately the proportions of unassigned ancestry for the Latin Caribbean populations in Micheletti et al.1). Then, for S1, the inferred observed X chromosomal ancestry proportion is and the autosomal ancestry proportion is . Similarly, for S2, the inferred X chromosomal and autosomal ancestry proportions are and , respectively. In this case, Equation 1 falsely implies female-biased admixture for S1 (1.6 females to one male), and the model is not specified for the observed ancestry proportions for S2. Note that unassigned ancestry can also create false patterns of male-biased admixture depending on the distribution of missing ancestry. For these reasons, sex ratios from Micheletti et al. reported for the broad regions of the Latin Caribbean, central South America, northern South America, and Central America should be questioned, as 6%–8% X chromosomal and 17%–21% autosomal DNA ancestry were left unassigned (Table 1).1 Because inferred sex ratios depend on relative X chromosomal and autosomal ancestry proportions, these imbalances between unassigned amounts of X chromosomal and autosomal ancestry further contribute to misestimates of sex bias.
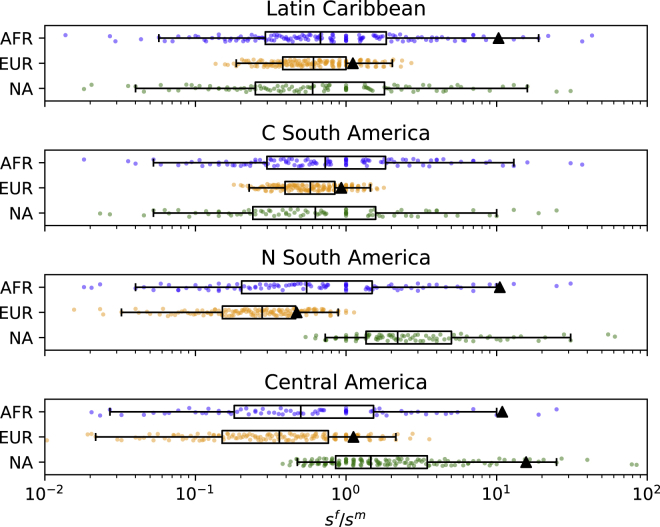
Given the potentially significant confounding effect of unassigned ancestry in the study by Micheletti et al., we distributed the unassigned ancestry in 1% increments to the three source ancestries—African, European, and Native American—such that ancestry proportions sum to 100%. This was done for the geographic regions of the Latin Caribbean, central South America, northern South America, and Central America. Sex ratios were then re-estimated for each possible combination of ancestry proportions using the equilibrium model (Equation 1). Figure 1 shows that wide ranges of sex ratios are possible, given the amounts of unassigned ancestry in these four regions. African contributions (blue) could have been either female- or male-biased based in all four regions. In contrast to this, male-biased European contributions (orange) are persistently indicated, as most of the possible sf/sm values are smaller than one. For Native American contributions (green), it is not possible to definitively say whether they were female or male biased in the Latin Caribbean and central South America, while most ways of distributing the unassigned ancestry suggest female-biased contributions in northern South America and Central America (Figure 1). Interestingly, mean African and Native American ancestry proportions reported by Micheletti et al. yield extreme sex ratios that are in the tails of the distributions of possible sf/sm values (black triangles) or lead to model failure (no black triangle shown). Thus, sf/sm values reported by Micheletti et al. are unlikely to represent true values, illustrating the confounding effects of unassigned ancestry in their study.
Figure 1.
A wide range of sex ratios is plausible in geographic regions with substantial amounts of unassigned ancestry
Missing ancestry in the study by Micheletti et al. for the Latin Caribbean, central South America, northern South America, and Central America was distributed in 1% increments such that ancestry proportions add up to 100%. Corresponding sex ratios were then computed using the equilibrium model (Equation 1). Ancestry proportions that led to model failure were discarded. The boxes represent the inter-quartile range, with the median sex ratio indicated by the line spanning the box. The whiskers represent the range between the 2.5th and 97.5th percentile. Note that the x axis is logarithmic to show the full range of possible sex ratios but that sf/sm < 0.1 and sf/sm > 10 are improbable. The clustering of the sex ratios is due to increments of 0.01 that were used for distributing unassigned ancestry. Black triangles correspond to sex ratios estimated from mean ancestry proportions reported by Micheletti et al. (Table 1). If no black triangle is shown, model failure was observed.
Sensitivity of models to small differences in ancestry proportions
As delineated above, many cases of model failure (i.e., negative sex ratios) are observed based on the data of Micheletti et al. For this reason, we conducted a sensitivity analysis of the equilibrium model, to better understand the conditions that lead to model misspecification. Using two examples, we show that the models are highly sensitive to small differences in inferred ancestry proportions and that the models are only specified for a narrow range of ancestry proportions. For both examples, we use the equilibrium model (Equation 1), but the analyses described below also hold for the dynamic model developed by Goldberg and Rosenberg.8 The models’ sensitivity implies that slight differences in inferred ancestry proportions can lead to qualitatively different results or model failure, exacerbating the problem of unassigned ancestry.
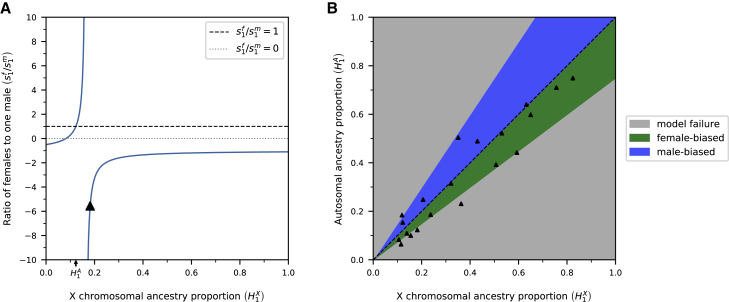
First, we assume that the true observed autosomal ancestry proportion for S1 is 0.123 (the autosomal African ancestry proportion in central South America reported by Micheletti et al.1), and the observed X chromosomal ancestry proportion is 0.130. In this case, Equation 1 yields a sex ratio of 1.412 females to 1 male. However, if the X chromosomal ancestry proportion were observed to be 0.120, the sex ratio would be 0.864 females to 1 male. Thus, slight differences in observed ancestry proportions can change the conclusion from female-biased contributions to male-biased contributions, a qualitatively different interpretation (Figure 2A).
Figure 2.
Estimates of sex-biased admixture from X chromosomes and autosomes are highly sensitive to small differences in ancestry proportions
sf/sm refers to the ratio of female to male contributions, X chromosomal ancestry proportions are represented by HX, and autosomal ancestry proportions are represented by HA.
(A) Presuming an autosomal ancestry of 0.123 (i.e., the autosomal African ancestry proportion in central South America reported by Micheletti et al.1), X chromosomal ancestry proportions must be in the interval [0.082, 0.164] under a demographic model of a single admixture event. X chromosome-related ancestries outside of this range cause negative sex ratios (i.e., model failure). The black triangle indicates the sex ratio inferred based on the ancestry proportions reported by Micheletti et al. for African ancestry in central South America (Table 1).
(B) Exploration of parameter space for different combinations of autosomal and X chromosomal ancestry proportions. Scenarios that yield female-biased sex ratios (sf/sm > 1) are colored green, male-biased sex ratios (0 < sf/sm < 1) are colored blue, and model failures (sf/sm < 0) are colored gray. Black triangles indicate ancestry proportions reported by Micheletti et al. (Table 1). Most cases of model failure are observed when inferred ancestry proportions are small (black triangles in gray area). No triangle is shown when either the X chromosomal or autosomal ancestry proportion was below 0.05.
Second, we consider the two scenarios when only one sex from S1 contributes to the admixed population. Again, we suppose a true autosomal ancestry proportion of 0.123 for S1 (the autosomal African ancestry proportion in central South America reported by Micheletti et al.1). If S1 contributes only females, the expected X chromosomal ancestry proportion for S1 would be 0.164 (Equation S8), yielding a sex ratio of plus infinity. Due to a singularity of the equilibrium model at this point (Figure 2A), the model is highly sensitive, and inferred sex ratios can vary significantly. Contrarily, if S1 contributes only males, the expected X chromosomal ancestry proportion would be 0.082 (Equation S9), yielding a sex ratio of 0. Therefore, plausible X chromosomal ancestry proportions under the demographic model of a single admixture event would be in the interval [0.082, 0.164] in this example. For values outside of these demographically possible limits, a model of a single admixture event is misspecified, yielding negative sex ratios. This was the case for the X chromosomal ancestry proportion inferred by Micheletti et al. (0.182),1 leading to a non-sensical negative sex ratio (black triangle in Figure 2A). In such cases, models accounting for more complex demographics should be considered.
Figure 2B shows that the equilibrium model (Equation 1) is specified for only a narrow range of observed ancestry proportions, which becomes narrower when the estimated ancestry proportions are close to zero. When Micheletti et al. inferred small ancestry proportions, the combinations of X chromosomal and autosomal ancestry proportions often lead to model failure (black triangles in gray areas in Figure 2B). Furthermore, some of the combinations of X chromosomal and autosomal ancestry proportions inferred by Micheletti et al. are close to regions of the parameter space where the models are most sensitive to small changes in ancestry proportions (black triangles close to the border between the green area and the gray area in Figure 2B). Thus, some of the cases of model failure and large sex ratios observed based on the data of Micheletti et al. may be partially attributed to the sensitivity of the models, especially when small ancestry contributions were inferred (Table 1; Figure 2B).
Effects of small sample sizes on the inference of sex bias
The above-demonstrated sensitivity of the models also implies that sample sizes may be a confounding factor due to sampling errors. While Micheletti et al. generally had large sample sizes for most geographic regions (i.e., >1,500), sample sizes were less than 300 for both Cabo Verde and the Guianas.1 To evaluate what sample sizes are necessary to confidently infer sex-biased admixture, we simulated sex-biased American admixture 15 generations ago (see material and methods). We sampled between 100 and 30,000 random individuals and computed mean ancestry proportions as well as corresponding sex ratios with confidence intervals for 15 generations after admixture, i.e., the model by Goldberg and Rosenberg.8
Generally, confidence intervals of sex ratios are a function of the sample size as well as the level of inferred ancestry proportions. For small sample sizes and low inferred ancestry proportions, the confidence intervals are large, precluding any statement about the extent of sex bias (Figure 3). This is because the models exhibit greater sensitivity to slight changes in ancestry proportions if inferred ancestry proportions are low (Figure 2B). Sample sizes of 1,000 or greater are sufficient to guarantee reasonable confidence intervals for ancestries that made medium or large (i.e., ) contributions to the admixed population (i.e., S2 and S3), while sample sizes of 5,000 or greater are required to yield reasonably narrow confidence for ancestries that made only small contributions (i.e., S1 component is 1/6; Figure 3). Thus, for Cabo Verde and the Guianas sampling uncertainty and presumably large confidence intervals preclude any definitive statement regarding sex-biased admixture in the study by Micheletti et al.
Figure 3.
Large sample sizes are required to confidently estimate the extent of sex-biased admixture using X chromosomal and autosomal ancestry proportions
Admixture in the Americas was simulated as three-way combinations of source population 1 (S1; blue), source population 2 (S2; orange), and source population 3 (S3; green) with female-biased contributions from S1 and S3 (i.e., 2 and 1.25 females to 1 male, respectively) and male-biased contributions from S3 (i.e., two males to one female). The simulated admixture proportions were 1/6, 1/3, and 1/2 for S1, S2, and S3, respectively. The crosses indicate the simulated sex ratio (sf/sm), filled circles indicate mean estimates, and error bars represent 95% confidence intervals.
Complications arising from violations of demographic assumptions
Micheletti et al. applied models for estimating sex bias that assume constant population size, no subsequent gene flow, and random mating after initial admixture.8 However, admixture in the Americas as a consequence of the European colonization and the transatlantic slave trade was more complex than a single admixture event.13,14,15,16,17,18,19 Here, we used simulations to evaluate whether violations of these demographic assumptions may have confounded the analyses of Micheletti et al. The following analyses are based on sample sizes of 10,000 individuals. Inferred sex ratios under different demographic scenarios for 15 generations after admixture are listed in Table 2.
Table 2.
Evaluation of the effect of different demographic scenarios on the sex ratios inferred from X chromosomal and autosomal ancestry proportions
|
S1 |
S2 |
S3 |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Demography | sf/sm | HX | HA | mt/Y | sf/sm | HX | HA | mt/Y | sf/sm | HX | HA | mt/Y |
| Simulated parameters (single pulse) | 2.00 | 0.1852 | 0.1667 | 2.00 | 0.50 | 0.2963 | 0.3333 | 0.50 | 1.25 | 0.5200 | 0.5000 | 1.25 |
| Single pulse | 2.02 (1.73–2.37) | 0.1828 (0.1797–0.1859) | 0.1644 (0.1624–0.1664) | 1.70 (1.57–1.84) | 0.54 (0.49–0.59) | 0.2974 (0.2937–0.3011) | 0.3305 (0.3280–0.3330) | 0.48 (0.46–0.51) | 1.19 (1.12–1.26) | 0.5198 (0.5158–0.5238) | 0.5051 (0.5025–0.5078) | 1.33 (1.28–1.38) |
| Population growth | 2.56 (2.15–3.06) | 0.1861 (0.1830–0.1891) | 0.1624 (0.1604–0.1644) | 1.37 (1.27–1.47) | 0.38 (0.34–0.41) | 0.286 (0.2824–0.2896) | 0.3369 (0.3344–0.3394) | 0.60 (0.57–0.63) | 1.39 (1.31–1.48) | 0.5280 (0.5240–0.5319) | 0.5007 (0.4980–0.5033) | 1.21 (1.17–1.26) |
| Gene flow | 1.78 (1.58–2.00) | 0.3475 (0.3422–0.3527) | 0.3179 (0.3143–0.3216) | 1.61 (1.52–1.70) | 0.42 (0.37–0.47) | 0.2378 (0.2335–0.2421) | 0.2758 (0.2725–0.2790) | 0.43 (0.41–0.46) | 1.13 (1.04–1.23) | 0.4147 (0.4097–0.4199) | 0.4063 (0.4027–0.4099) | 1.21 (1.16–1.26) |
| Population growth + gene flow | 1.64 (1.46–1.85) | 0.3089 (0.3043–0.3136) | 0.2858 (0.2825–0.2891) | 1.76 (1.66–1.87) | 0.55 (0.49–0.61) | 0.2636 (0.2595–0.2677) | 0.2922 (0.2891–0.2953) | 0.37 (0.35–0.39) | 1.08 (1.00–1.17) | 0.4274 (0.4227–0.4322) | 0.4220 (0.4187–0.4252) | 1.51 (1.44–1.59) |
| Sex-specific assortative mating (40%) | 2.96 (2.42–3.66) | 0.1671 (0.1642–0.1700) | 0.1436 (0.1416–0.1454) | 4.48 (3.92–5.12) | 0.39 (0.36–0.42) | 0.3755 (0.3715–0.3793) | 0.4403 (0.4375–0.4430) | 0.28 (0.27–0.29) | 1.85 (1.71–2.00) | 0.4574 (0.4534–0.4614) | 0.4162 (0.4135–0.4188) | 4.97 (4.60–5.39) |
| Sex-specific assortative mating (40%) + gene flow | 2.76 (2.33–3.27) | 0.2826 (0.2780–0.2873) | 0.2446 (0.2414–0.2479) | 3.94 (3.60–4.32) | 0.31 (0.28–0.34) | 0.3303 (0.3259–0.3348) | 0.4009 (0.3975–0.4042) | 0.23 (0.22–0.24) | 1.76 (1.59–1.95) | 0.3871 (0.3823–0.3919) | 0.3545 (0.3513–0.3578) | 3.18 (2.96–3.42) |
| Sex-specific assortative mating (40%) + gene flow + population growth | 2.30 (1.98–2.70) | 0.2829 (0.2782–0.2877) | 0.2502 (0.2469–0.2534) | 3.42 (3.16–3.70) | 0.41 (0.38–0.45 | 0.3422 (0.3376–0.3468) | 0.3971 (0.3937–0.4005) | 0.23 (0.22–0.24) | 1.46 (1.33–1.61) | 0.3748 (0.3702–0.3795) | 0.3527 (0.3496–0.3561) | 2.99 (2.78–3.22) |
| Sex-specific assortative mating (90%) | 7.63 (−335–364) | 0.0947 (0.0922–0.0972) | 0.0719 (0.0705–0.0733) | 30.1 (22.3–41.8) | 0.51 (0.49–0.54) | 0.6678 (0.6633–0.6724) | 0.7478 (0.7452–0.7504) | 0.19 (0.19–0.20) | −336 (−395–463) | 0.2375 (0.2336–0.2414) | 0.1803 (0.1780–0.1825) | 29.0 (23.7–35.9) |
For each scenario, the initial admixture of S1, S2, and S3 was simulated with admixture proportions 1/6, 1/3, and 1/2, respectively. S1’s and S3’s contributions were female biased with ratios of 2 females and 1.25 females to 1 male, and S2’s contributions were male biased with a ratio of 2 males to 1 female. Additionally, exponential population growth was simulated at a rate of r = 0.05, constant gene flow from the source populations into the admixed population was modeled at population-specific rates of m1 = 0.05, m2 = 0.025, and m3 = 0.01, and sex-specific assortative mating was simulated according to the mating scheme shown in Table S3 with p = 0.4 and p = 0.9. The expected X chromosomal and autosomal proportions for a single admixture event with the above parameterization are shown in the first row of this table (computed using Equations 5, 12, and 13 in Goldberg and Rosenberg8). Confidence intervals are given in parentheses for each point estimate.
Recent analyses have shown that admixed populations in the Americas experienced population expansion after admixture.13 In our simulations, exponential growth of the admixed American population at a rate of r = 0.05 did not affect the sex ratios inferred from X chromosomal and autosomal data nor mtDNA and Y chromosome haplogroup imbalances. Differences between simulated and estimated sex ratios are due to the sensitivity of the models (Table 2). This suggests that population growth alone cannot have caused the large sex ratios estimated by Micheletti et al.
Constant, sex-biased gene flow
Historically, admixture in the Americas involved continuous gene flow as opposed to a single admixture event.19 Although our simulations show that constant gene flow from source populations into an admixed population changes estimates of sex bias, it does not yield as extreme sf/sm values as reported by Micheletti et al.1 Note that these effects are weaker when population growth is also present (Table 2).
We also investigated whether an additional constant gene flow model from Goldberg and Rosenberg8 better fits the data of Micheletti et al. In regions with nearly complete ancestry assignments, this model yields a range of smaller sf/sm values that consistently indicate sex biases in one direction (e.g., United States). However, in geographic regions with substantial unassigned ancestry, either female or male sex bias fits the data (e.g., European ancestry in Central America; Figure S1). For these reasons, constant gene flow after initial admixture likely contributed to the extreme sex ratios reported by Micheletti et al., but unassigned ancestry appears to be the more important confounding factor.
Sex-specific assortative mating
Given well-established historical accounts, random mating did not happen in the Americas or was even prevented through anti-miscegenation laws.14,15,16,17,18 These appalling laws and other social norms led to sex-specific assortative mating. To evaluate the effect of sex-specific assortative on sex ratios inferred from X chromosomal and autosomal data by Micheletti et al., we performed simulations in which S2 females were asymmetrically more likely to mate with S2 males (Table S3).
In concordance with theory,24 our simulations show that sex-specific assortative mating confounds estimates of sex biases from X chromosomal and autosomal ancestry proportions (Table 2). Extreme sex-specific assortative mating (i.e., a non-S2 male is rejected 90% of the time as a mating partner of an S2 female and replaced with an S2 male (p = 0.9)) can cause model failure, but it also leads to extreme mitochondrial and Y chromosome haplogroup imbalances. If sex-specific assortative mating was a major factor confounding the estimates of sex bias from X chromosomal and autosomal ancestry proportions by Micheletti et al., it should also be reflected in mtDNA and Y chromosome haplogroup imbalances, which is not the case (see Table 1 in Micheletti et al. and Table S8 in Micheletti et al.).1 Furthermore, sex-specific assortative mating (p = 0.4), constant gene flow, and population growth do not enhance each other in ways that lead to model failure, given the current parameterization (Table 2). For these reasons, although sex-specific assortative mating may have contributed to the extreme sex ratios, it appears that unassigned ancestry was a more important confounding factor in the study by Micheletti et al.
Conclusions
The racist legacy of the slave trade has undoubtedly left its mark in the genomes of admixed individuals in the Americas. However, our findings suggest that the extreme sex biases reported by Micheletti et al. are questionable.
Substantial amounts of unassigned ancestry were likely the primary confounding factor in the study by Micheletti et al. (Table 1). This is because artificial deviation of the observed ancestry proportions from the true ancestry proportions can create false patterns of sex-biased admixture, explaining the observed exorbitant sex ratios and cases of model failure (i.e., negative sex ratios). The problem of unassigned ancestry is further exacerbated if different amounts of X chromosomal and autosomal ancestry are missing. Unassigned ancestry arises when genomic windows have multiple competing ancestries with low posterior probabilities. Low posterior probabilities are oftentimes observed in admixed individuals with Native American ancestry due to the lack of good reference panels.25,26,27 This conservative approach to assigning ancestry is justified when reporting ancestries to consumers but leads to problems when ancestry proportions are applied to estimate magnitudes of sex-biased admixture.
While population genetic models provide the theoretical background for inferring sex bias of past admixture events from X chromosomal and autosomal data, their real-world applicability is limited due to their sensitivity. This limitation can partially be addressed by providing confidence intervals, which can be obtained by bootstrapping individual ancestry proportions as described in material and methods. For the present analyses based on the data from Micheletti et al.,1 we were unfortunately not able to improve the interpretability of their results with confidence intervals because 23andMe’s consent and privacy guidelines limit the availability of individual-level genotype data.1 This underscores the importance of open data-sharing policies.28 Overall, we caution that inference methods of sex-biased admixture that use X chromosomal and autosomal data perform poorly when ancestry proportions do not add up to 100% and that reconstructing recent human history from genetic data requires both accurate data and appropriate models.
Acknowledgments
The authors thank Tomas Bruna and members of the Center for Integrative Genomics at Georgia Tech for their helpful suggestions and critiques. We also thank two anonymous reviewers for their thoughtful and constructive comments that helped to improve the manuscript. This work was supported by an NIGMS MIRA grant to J.L. (R35GM133727). This research was supported in part through research cyberinfrastructure resources and services provided by the Partnership for an Advanced Computing Environment (PACE) at Georgia Institute of Technology, Atlanta, Georgia, USA.
Declaration of interests
The authors declare no competing interests.
Published: February 2, 2023
Footnotes
Supplemental information can be found online at https://doi.org/10.1016/j.ajhg.2022.12.012.
Supplemental information
Based on the data provided in Table S8A of Micheletti et al.
Mean ancestry proportions were taken from Table S9 in Micheletti et al. For each broad region of the Americas estimates of sex-bias were calculated for generations 2 to 15 following admixture, as well generation infinity. Negative or extreme sex ratios indicate model failure. Within generation 15 after admixture, the model of Goldberg and Rosenberg converges to the equilibrium (g = inf) model
Data and code availability
The code and all data needed to reproduce the results presented in this study are available at https://github.com/LachanceLab/sex_biased_admixture. The referenced supplemental tables from the study by Micheletti et al. are available at https://doi.org/10.1016/j.ajhg.2020.06.012.
References
- 1.Micheletti S.J., Bryc K., Ancona Esselmann S.G., Freyman W.A., Moreno M.E., Poznik G.D., Shastri A.J., 23andMe Research Team. Beleza S., Mountain J.L., et al. Genetic consequences of the transatlantic slave trade in the Americas. Am. J. Hum. Genet. 2020;107:265–277. doi: 10.1016/j.ajhg.2020.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Micheletti S.J., Ancona Esselmann S.G., Bryc K., Mountain J.L. Response to Pfennig and Lachance. Am. J. Hum. Genet. Am. J. Hum. Genet. 2023;110 doi: 10.1016/j.ajhg.2022.12.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kayser M., Brauer S., Schädlich H., Prinz M., Batzer M.A., Zimmerman P.A., Boatin B.A., Stoneking M. Y chromosome STR haplotypes and the genetic structures of U.S. populations of African, European, and Hispanic ancestry. Genome Res. 2003;13:624–634. doi: 10.1101/gr.463003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Parra E.J., Marcini A., Akey J., Martinson J., Batzer M.A., Cooper R., Forrester T., Allison D.B., Deka R., Ferrell R.E., Shriver M.D. Estimating African American admixture proportions by use of population-specific alleles. Am. J. Hum. Genet. 1998;63:1839–1851. doi: 10.1086/302148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Parra E.J., Kittles R.A., Argyropoulos G., Pfaff C.L., Hiester K., Bonilla C., Sylvester N., Parrish-Gause D., Garvey W.T., Jin L., et al. Ancestral proportions and admixture dynamics in geographically defined African Americans living in South Carolina. Am. J. Phys. Anthropol. 2001;114:18–29. doi: 10.1002/1096-8644(200101)114:1<18::AID-AJPA1002>3.0.CO;2-2. [DOI] [PubMed] [Google Scholar]
- 6.Bryc K., Durand E.Y., Macpherson J.M., Reich D., Mountain J.L. The genetic ancestry of african americans, latinos, and european Americans across the United States. Am. J. Hum. Genet. 2015;96:37–53. doi: 10.1016/j.ajhg.2014.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lind J.M., Hutcheson-Dilks H.B., Williams S.M., Moore J.H., Essex M., Ruiz-Pesini E., Wallace D.C., Tishkoff S.A., O’Brien S.J., Smith M.W. Elevated male European and female African contributions to the genomes of African American individuals. Hum. Genet. 2007;120:713–722. doi: 10.1007/s00439-006-0261-7. [DOI] [PubMed] [Google Scholar]
- 8.Goldberg A., Rosenberg N.A. Beyond 2/3 and 1/3: the complex signatures of sex-biased admixture on the X chromosome. Genetics. 2015;201:263–279. doi: 10.1534/genetics.115.178509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Patin E., Lopez M., Grollemund R., Verdu P., Harmant C., Quach H., Laval G., Perry G.H., Barreiro L.B., Froment A., et al. Dispersals and genetic adaptation of Bantu-speaking populations in Africa and North America. Science. 2017;356:543–546. doi: 10.1126/science.aal1988. [DOI] [PubMed] [Google Scholar]
- 10.Genetic Impact of African Slave Trade Revealed in DNA Study.“ BBC News. 24 July 2020. https://www.nytimes.com/2020/07/23/science/23andme-african-ancestry.html. Accessed 24 May 2022.
- 11.Kenneally C. The New York Times; 2020. DNA Study from 23andMe Traces Violent History of American Slavery.https://www.nytimes.com/2020/07/23/science/23andme-african-ancestry.html Accessed 24 May 2022. [Google Scholar]
- 12.Kaur H. CNN; 2020. 23andMe DNA Study Offers Insight into the Horrific Story of the Trans-Atlantic Slave Trade.https://www.cnn.com/2020/07/26/us/dna-transatlantic-slave-trade-study-scn-trnd/index.html Accessed 24 May 2022. [Google Scholar]
- 13.Browning S.R., Browning B.L., Daviglus M.L., Durazo-Arvizu R.A., Schneiderman N., Kaplan R.C., Laurie C.C. Ancestry-specific recent effective population size in the Americas. PLoS Genet. 2018;14:10073855–e1007422. doi: 10.1371/journal.pgen.1007385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pascoe P. Oxford University Press; 2009. What Comes Naturally: Miscegenation Law and the Making of Race in America. [Google Scholar]
- 15.Hartman S.V. Oxford University Press; 1997. Scenes of Subjection: Terror, Slavery, and Self-Making in Nineteenth-Century America. [Google Scholar]
- 16.Wallenstein P. Race, Marriage, and the Law of Freedom: Alabama and Virginia, 1860s-1960s: Personal Liberty and Private Law. Chic. Kent. Law Rev. 1994;70:371. [Google Scholar]
- 17.Pokorak J.J. Rape as a badge of slavery: the legal history of, and remedies for, prosecutorial race-of-victim changing disparities. Nev. Law J. 2006;7:1. [Google Scholar]
- 18.Jennings T. “Us colored women had to go though a plenty”: sexual exploitation of African-American Slave women. J. Wom. Hist. 1990;1:45–74. [Google Scholar]
- 19.Jordan I.K., Rishishwar L., Conley A.B. Native American admixture recapitulates population-specific migration and settlement of the continental United States. PLoS Genet. 2019;15:e1008225. doi: 10.1371/journal.pgen.1008225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Haller B.C., Messer P.W. SLiM 3: forward genetic simulations beyond thewright–fisher model. Mol. Biol. Evol. 2019;36:632–637. doi: 10.1093/molbev/msy228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gravel S., Henn B.M., Gutenkunst R.N., Indap A.R., Marth G.T., Clark A.G., Yu F., Gibbs R.A., 1000 Genomes Project. Bustamante C.D. Demographic history and rare allele sharing among human populations. Proc. Natl. Acad. Sci. USA. 2011;108:11983–11988. doi: 10.1073/pnas.1019276108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chang C.C., Chow C.C., Tellier L.C., Vattikuti S., Purcell S.M., Lee J.J. Second-generation PLINK: rising to the challenge of larger and richer datasets. GigaScience. 2015;4:7. doi: 10.1186/s13742-015-0047-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Alexander D.H., Novembre J., Lange K. Fast model-based estimation of ancestry in unrelated individuals. Genome Res. 2009;19:1655–1664. doi: 10.1101/gr.094052.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Goldberg A., Rastogi A., Rosenberg N.A. Assortative mating by population of origin in a mechanistic model of admixture. Theor. Popul. Biol. 2020;134:129–146. doi: 10.1016/j.tpb.2020.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Durand E., Do C., Mountain J., Macpherson J.M. Ancestry composition: a novel, efficient pipeline for ancestry deconvolution. bioRxiv. 2014:010512. doi: 10.1101/010512. Preprint at. [DOI] [Google Scholar]
- 26.Maples B.K., Gravel S., Kenny E.E., Bustamante C.D. RFMix: a discriminative modeling approach for rapid and robust local-ancestry inference. Am. J. Hum. Genet. 2013;93:278–288. doi: 10.1016/j.ajhg.2013.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Baran Y., Pasaniuc B., Sankararaman S., Torgerson D.G., Gignoux C., Eng C., Rodriguez-Cintron W., Chapela R., Ford J.G., Avila P.C., et al. Fast and accurate inference of local ancestry in Latino populations. Bioinformatics. 2012;28:1359–1367. doi: 10.1093/bioinformatics/bts144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Powell K. How a field built on data-sharing became a Tower of Babel. Nature. 2021;590:198–201. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Based on the data provided in Table S8A of Micheletti et al.
Mean ancestry proportions were taken from Table S9 in Micheletti et al. For each broad region of the Americas estimates of sex-bias were calculated for generations 2 to 15 following admixture, as well generation infinity. Negative or extreme sex ratios indicate model failure. Within generation 15 after admixture, the model of Goldberg and Rosenberg converges to the equilibrium (g = inf) model
Data Availability Statement
The code and all data needed to reproduce the results presented in this study are available at https://github.com/LachanceLab/sex_biased_admixture. The referenced supplemental tables from the study by Micheletti et al. are available at https://doi.org/10.1016/j.ajhg.2020.06.012.