Direct observation of aggregative nanoparticle growth: Kinetic modeling of the size distribution and growth rate

Abstract

Direct observations of solution-phase nanoparticle growth using in situ liquid transmission electron microscopy (TEM) have demonstrated the importance of “non-classical” growth mechanisms, such as aggregation and coalescence, on the growth and final morphology of nanocrystals at the atomic and single nanoparticle scales. To date, groups have quantitatively interpreted the mean growth rate of nanoparticles in terms of the Lifshitz-Slyozov-Wagner (LSW) model for Ostwald ripening, but less attention has been paid to modeling the corresponding particle size distribution. Here we use in situ fluid stage scanning TEM to demonstrate that silver nanoparticles grow by a length-scale dependent mechanism, where individual nanoparticles grow by monomer attachment but ensemble-scale growth is dominated by aggregation. Although our observed mean nanoparticle growth rate is consistent with the LSW model, we show that the corresponding particle size distribution is broader and more symmetric than predicted by LSW. Following direct observations of aggregation, we interpret the ensemble-scale growth using Smoluchowski kinetics and demonstrate that the Smoluchowski model quantitatively captures the mean growth rate and particle size distribution.

Recent advances in in situ TEM techniques have allowed direct observation of solution-phase nanoparticle growth,^1–10 facilitating the first direct quantitative tests of classical coarsening models.^11–13 Many researchers have demonstrated that in addition to simple monomer attachment, non-classical growth mechanisms such as aggregation,^{4, 7, 9, 14} coalescence,^{1, 3, 5} and oriented attachment^{2, 4} affect the growth route and final morphology of single nanoparticles. Atomic-scale in situ TEM observations of solution-phase nanocrystal growth have elucidated non-classical growth mechanisms such as oriented attachment² and have provided new explanations for the origin of defects in nanoparticles formed by aggregation.³ While these direct observations of nanocrystal growth on the atomic and nanoscale have greatly increased our fundamental knowledge of nanoparticle growth mechanisms, the functional behavior of single nanoparticles is well known to change with their size, shape, and from that of the entire nanoparticle ensemble.^15–18 The particle size distribution (PSD) often dictates important functional properties such as size and shape-dependent plasmonic response,^19–21 magnetic response,^22–24 and catalytic activity.^{25, 26} Besides size and shape dependence, interparticle interactions in a nanoparticle ensemble, such as aggregation, can affect nanoparticle functional behavior, such as plasmon coupling,¹⁸ and can also affect transport phenomena, such as heat transfer from nanoparticle ensembles during phase transitions.¹⁶ Although researchers have demonstrated the importance of non-classical growth pathways on the single nanoparticle and atomic scales, a fundamental investigation of the effect of aggregation on the ensemble-scale properties of nanoparticles, such as the mean growth rate and PSD, has not been undertaken with in situ liquid cell electron microscopy.

Previous studies of nanoparticle ensemble growth employed in situ spectroscopy techniques to determine the PSD and mean growth rate.^27–31 In situ spectroscopy techniques can discern time dependent nanoparticle ensemble properties; however, they lack real time direct observations at the nanoscale, making it difficult to establish the effect of specific nanoparticle interactions. Cryo-TEM quenching studies of nanoparticle growth allow for time dependent measurements of ensemble properties,^32–34 but the growth mechanisms and ensemble properties must be inferred from the size and morphology of the nanoparticles ex situ, and interparticle interactions cannot be directly observed due to temporal resolution limits of the technique. Aggregative nanoparticle growth mechanisms have been inferred through ex situ TEM observations of bimodal PSDs;^{35, 36} however, drying artifacts such as capillary driven nanoparticle aggregation³⁷ during preparation of liquid nanoparticle aliquots for TEM analysis limit these techniques’ ability to directly observe aggregation of nanoparticles. In situ liquid cell electron microscopy provides a means for directly observing the effect of aggregation and other interparticle interactions on the nanoparticle ensemble properties while simultaneously observing their morphology in real time.

Different research groups have demonstrated via in situ TEM that the mean growth rate of nanoparticles was consistent with the LSW model for Ostwald ripening, i.e. the mean nanoparticle radius, <r> ~ t^1/3.^{1, 9} Simultaneously, however, the same groups also observed particle aggregation and coalescence.^{1, 3, 4, 6, 9} Since the LSW model explicitly omits particle aggregation,³⁸ these observations beg the question: how can the mean growth rate be consistent with Ostwald ripening despite clear evidence of aggregation? In this Letter, we measure the mean growth rate and PSD of an ensemble of silver nanoparticles grown by in situ electron beam reduction via STEM imaging, and demonstrate that the nanoparticle ensemble properties can be interpreted using Smoluchowski aggregation kinetics. Although our observed mean growth rate is consistent with the LSW model, we show that the ensemble-scale mean growth rate is ~20% larger than for individual (non-aggregating) nanoparticles and that the corresponding PSD is broader and more symmetric than predicted by LSW. Instead we interpret the nanoparticle growth using Smoluchowski aggregation kinetics and conclude that the growth mechanism is dependent on the length scale, where individual nanoparticles grow by monomer attachment and the ensemble grows by aggregation. These results suggest that care must be taken when quantitatively interpreting growth dynamics in terms of Ostwald ripening in processes where aggregation or other interparticle interactions can occur, such as heterogeneous nanoparticle catalyst deactivation,^{25, 39, 40} shape controlled synthesis of nanoparticles,^{33, 41, 42} and biomineralization of nanocrystals.^{34, 43, 44}

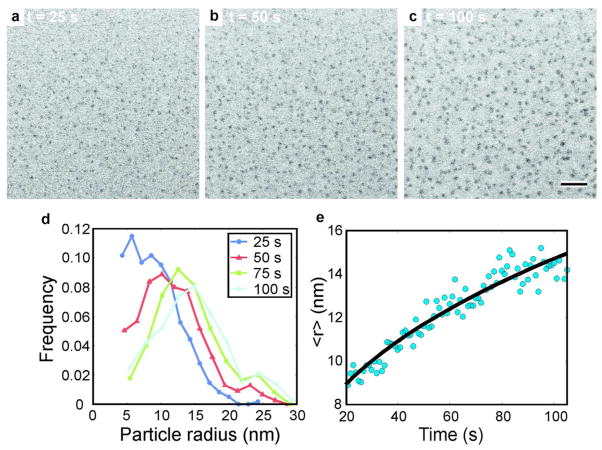
Our experimental apparatus was similar to that used in previous studies.^{8, 10, 45} We grew silver nanoparticle ensembles of 300–500 particles from a dilute aqueous silver nitrate precursor by electron beam irradiation via scanning transmission electron microscopy (STEM) (see Figure S1). Nucleation and growth is thought to occur via reduction of the silver ions by aqueous electrons, followed by subsequent monomer attachment to the nanoparticle surfaces.⁸ Figures 1a–c show a representative time series of silver nanoparticles growing from solution over a time period of 75 seconds, where each second of the movie is approximately one STEM scan (cf. Movie S1). STEM image series were acquired at relatively low magnification (M = 100,000 x) and electron beam current (i_e = 20 pA) to obtain the most representative image series of the nanoparticle ensemble and to mitigate electron beam-liquid interactions. While these imaging conditions lowered the signal to noise ratio of the images, the STEM imaging parameters were chosen to create a relatively low electron dose rate⁸ to minimize the effect of confounding beam induced imaging artifacts such as bubbling,⁴⁶ nanoparticle charging,^{45, 47} and nanoparticle dissolution,⁴⁸ enabling more reproducible beam induced nanoparticle growth. Following standard methods, the projected area of each individual nanoparticle was measured in each image and each radius approximated as $r\approx {\left(\frac{A}{\pi }\right)}^{1/2}$ (cf. Figure S2 and Methods). To reduce artifacts in the nanoparticle detection, post processing of each STEM image series was performed to correlate nanoparticle positions between subsequent frames—only nanoparticles that had radii r > ~ 5 nm and existed for 60% or more of the movie frames were included in the analysis.⁴⁹ During the first 20 s of imaging, the nanoparticles were too small to accurately detect. After 25 seconds of irradiation the mean nanoparticle radius was ~9 nm (Figure 1a), and the ensemble PSD indicated that the nanoparticles were polydisperse with radii ranging up to a maximum of ~20 nm (Figure 1d). During growth the nanoparticles were mobile on the silicon nitride window surface; measurements of various particle trajectories indicated that the nanoparticles diffused by Brownian motion (Figure S3). The nanoparticle mobility was greatly hindered compared to the vigorous Brownian motion predicted for nanoparticles by the Stokes-Einstein relation, likely due to their vicinity to the window surface.⁵⁰ The mobile nanoparticles collided and separated with neighboring particles multiple times during the growth period. Individual nanoparticles always grew with time, and were never observed to dissolve. After 100 seconds of imaging (Figure 1c) the mean nanoparticle radius increased by ~60% to 15 nm (Figure 1f), and the PSD showed that the maximum nanoparticle radius increased to almost 30 nm. The mean nanoparticle radius fit a power law function of the following form, <r> = Kt^<β>, where linear regression yielded a mean growth exponent of <β> = 0.31 ± 0.01. We emphasize that this growth is consistent with previous in situ TEM studies that have reported growth exponents of 1/3 for growth of platinum nanoparticles¹ and 0.32 for growth of zinc oxide nanoparticles,⁹ and is likewise consistent with the LSW model prediction of <β> = 1/3 for Ostwald ripening.³⁸

Figure 1.

(a)–(c) Time lapsed series of BF-STEM images showing growth of an ensemble of silver nanoparticles starting at 25 seconds from the initial irradiation (20 pA beam current). The scale bar in (c) is 200 nm. (d) Particle size distribution (PSD) of the ensemble for various times; the PSD’s are normalized by their total integral to yield a probability density function. (e) Mean nanoparticle radius as a function of time. The black line is the result of a power law fit of the form <r> = Kt^<β>, where linear regression yielded <β> = 0.31 ± 0.01.

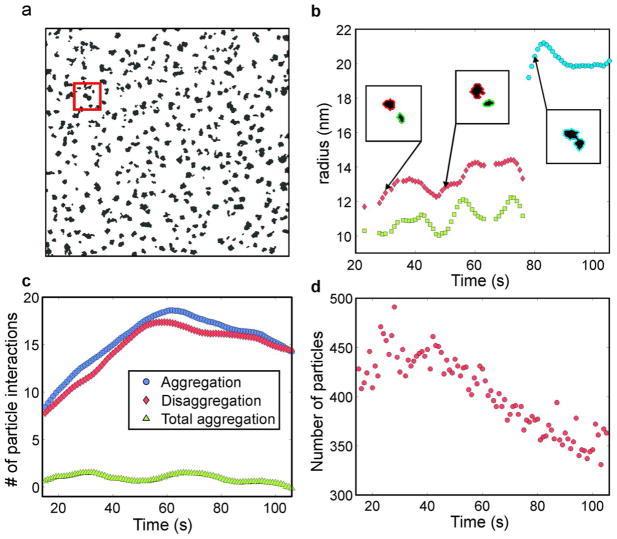
Although the mean growth exponent is consistent with Ostwald ripening, our qualitative and quantitative observations indicate that many of the nanoparticles aggregated during the growth process. Non-spherical nanoparticle morphologies revealed that numerous particles were in fact nanoparticle aggregates (e.g. red box, Figure 2a), which are formed when nanoparticles growing by monomer attachment collide to form a single aggregate (Figure 2b). No nanoparticle coalescence was observed after aggregation. Observations of nanoparticle diffusion by Brownian motion (Figure S3) and power-law growth of the mean nanoparticle radius (Figure 1e) suggest that the aggregation was diffusion limited.^{51, 52} We measured the number of aggregation and disaggregation events between each time lapse image,⁵³ and found that the net aggregation rate (i.e. the difference of aggregation and disaggregation frequencies) was approximately constant with time at 0.9 aggregation events per second (Figure 2c). The key point is that aggregation caused a substantial decrease in the total number of nanoparticles over the growth time, with the number of particles decreasing ~30% over 85 seconds of growth (Figure 2d). Again, we emphasize that this decrease in the number of particles is qualitatively consistent with prior observations by Liu and co-workers, who observed the number of ZnO nanoparticles to decrease monotonically after ~20 seconds of in situ electron beam stimulated growth, apparently as a result of aggregation, coalescence, and Ostwald ripening.⁹

Figure 2.

(a) Black and white rendering of the BF-STEM image at t = 105 s, where nanoparticles are in black, showing the morphology of individual nanoparticles and aggregates obtained through nanoparticle tracking. (b) Growth of silver nanoparticles (marked in red box in Figure 2a) by monomer attachment and aggregation. Insets show the particle morphologies at various time points before and after aggregation, which occurred at t = 78 s. Data are filtered using a 5 second running filter to reduce noise. (c) Number of particle interactions (aggregation, disaggregation) as a function of time. The data are filtered using a 20 second running filter to reduce noise. (d) Number of nanoparticles in the ensemble as a function of time.

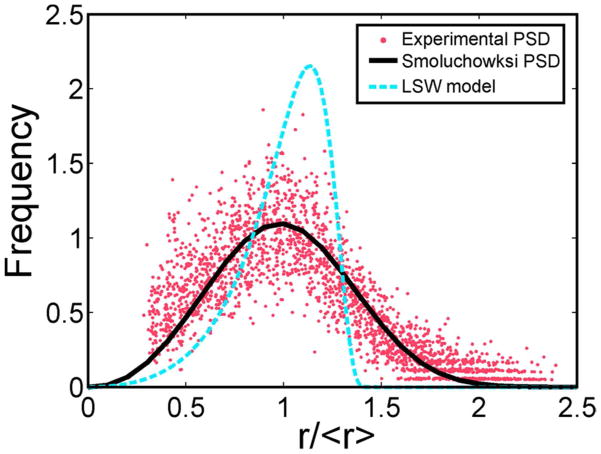
Although previous groups have interpreted the mean growth exponent in terms of the LSW model for Ostwald ripening, less attention has been paid to quantitatively modeling the corresponding PSD. Comparison of our experimentally measured PSD with the LSW prediction indicates that the LSW model actually provides a poor representation of the PSD (Figure 3). The experimental PSD for all growth times between 15 – 105 s (Figure 3, red points) is broader and more symmetric about r/<r> = 1 compared to the LSW PSD (Figure 3, dashed blue line), which peaks to the right of r/<r> = 1 due to the preferential growth of larger particles in Ostwald ripening. Approximately 10% of the nanoparticles at any time had radii greater than the distinct cutoff in the LSW PSD at r/<r> = 1.5. The distinct differences between the LSW and experimental PSDs suggest that Ostwald ripening was not the dominant mechanism for growth on the ensemble scale. Direct observations also revealed that each nanoparticle radius grew monotonically with time (cf. Figures 1a–c), which is in direct conflict with an Ostwald ripening mechanism that would cause particles above a critical radius to grow at the expense of particles below the critical radius. Since our image analysis technique can only resolve nanoparticles > 5 nm, we can only conclude that nanoparticles larger than this are not growing by Ostwald ripening.

Figure 3.

The scaled nanoparticle PSD measured for all times from t = 15 – 105 s. The dashed blue curve is the LSW PSD (sum of squared errors SSE = 1550), and the solid black curve is the Smoluchowski PSD with <β_PSD> = <β> = 0.31 (SSE = 78). Nanoparticle radii are normalized to the respective mean nanoparticle radius for that time.

In short, the mean growth exponent is consistent with the LSW model, but the shape of the experimental PSD and qualitative observations of the nanoparticle growth are not. Since we and others (cf. Figure 2 and refs^{1, 3, 4, 6, 9}) observe aggregation events, we hypothesize that aggregation drives growth of the nanoparticles on the ensemble scale. To quantitatively model the effect of aggregation on the ensemble properties we employ Smoluchowski coagulation kinetics, a classical model that describes the time evolution of an ensemble of particles as they aggregate.⁵⁴ A characteristic analytical PSD can be derived for a system of aggregating particles from Smoluchowski kinetics assuming that (1) particles only collide by Brownian motion, (2) the collisions are homogenous in space and uncorrelated, and (3) the collision rate is independent of time.^{54, 55} The BF STEM images (Figures 1a–c), aggregation kinetics (Figure 2c), and observed Brownian motion of the nanoparticles (Figure S3) suggest that these assumptions are reasonable for our nanoparticle ensembles. Similar to the LSW model, Smoluchowski kinetics predicts power law growth of the mean particle radius; however, unlike Ostwald ripening the value of the growth exponent depends on the mechanism for diffusion of the particles.⁵⁵ If the particles are assumed to be 2-dimensional clusters diffusing by Brownian motion, a scaling analysis of the Stokes-Einstein diffusivity equation yields a predicted Smoluchowski growth exponent <β> = 1/3, coincidentally equivalent to the LSW prediction for Ostwald ripening (see Supplementary Material). For this model the growth exponent can be determined by fitting the experimental PSD with the Smoluchowski PSD; if the growth exponent determined by the PSD fit (β_PSD) is consistent with the experimental growth exponent then the nanoparticle ensemble is likely growing by aggregation.^{55, 56} We fit the Smoluchowski PSD to the experimental PSD at each time, and the time averaged growth exponent was <β_PSD> = 0.29 ± 0.05, which is indeed consistent with the observed mean growth exponent of <β> = 0.31 (see Figure S4). Importantly, the Smoluchowksi PSD captured the qualitative features of the experimental PSD’s for all times with the experimentally determined growth exponent (i.e. <β_PSD> = <β> = 0.31). The Smoluchowski PSD was consistent with the near-symmetric shape of the experimental PSD about r/<r> = 1 and the extended tail on the right side of the PSD (solid black line, Figure 3). Consistency between the time averaged Smoluchowski fitting parameter, <β_PSD>, the mean growth exponent, <β>, and the exponent predicted from Smoluchowski aggregation by Brownian motion, along with the excellent agreement between the Smoluchowski and experimental PSD shown in Figure 3, all strongly corroborate the idea that aggregative growth controls the shape of the PSD and the mean growth exponent.

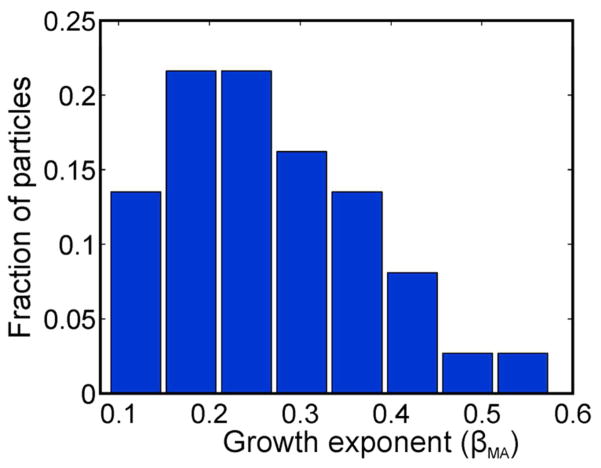
While aggregative growth seems to be the dominant mechanism for growth on the ensemble scale, it was clear that each nanoparticle grew by monomer attachment (cf. Figures 1a–c). This raises a natural question: Is the mean growth exponent simply a result of the average of each individual nanoparticle’s growth exponent? To address this question we measured the growth trajectories of 37 nanoparticles that did not aggregate during the growth period. The mean of their growth exponents was <β_MA> = 0.26 ± 0.11 (median = 0.22), ~20% smaller than the mean growth exponent, with 70% of the nanoparticles growing at a rate slower than the mean growth exponent (Figure 4). By separating aggregative growth from growth by monomer attachment we see that aggregation expedited growth on the ensemble scale causing the observed growth exponent. Surprisingly, the growth mechanism here is dependent on the length scale, where growth on the nanometer scale occurs by monomer attachment, and growth on the ensemble scale occurs by aggregation.

Figure 4.

Histogram of the growth exponents of 37 nanoparticles growing only by monomer attachment. The mean of the growth exponents is <β_MA> = 0.26 ± 0.11, the median is 0.22.

In summary, we used in situ liquid STEM imaging to grow and directly observe nanoparticle ensembles that exhibited power law growth. While the mean growth exponent suggested Ostwald ripening was the dominant growth mechanism, direct observations of aggregation of nanoparticles and the shape of the PSD did not agree with the LSW model. The significant amount of nanoparticle aggregation suggested that the ensemble was growing by aggregation. We demonstrated that the Smoluchowski PSD describes the experimental PSDs both qualitatively and quantitatively, where the time averaged growth exponent, <β_PSD>, was consistent with the experimentally determined growth exponent and the scaling estimate derived for aggregation by Brownian motion. The mean growth exponent was ~20% larger than for nanoparticles growing by monomer attachment alone, suggesting a length scale dependence of the growth mechanism. We conclude that the observed mean growth rate and PSD shape are a result of aggregation, shedding light on previous unexplained observations of aggregative nanoparticle growth quantitatively consistent with the LSW model.^{1, 9} While our system doesn’t contain any stabilizing ligands or capping agents as is typical for lab scale wet syntheses, we expect our direct observations of aggregative nanoparticle growth will lend better quantitative understanding of ex situ syntheses, as numerous reports have shown that aggregative nanoparticle growth occurs even in the presence of ligands and capping agents.^{1, 3, 4, 6, 35, 57} This in situ STEM method for quantitatively modeling aggregative nanoparticle growth is a first step in allowing researchers to accurately predict and tune nanoparticle size distributions in lab-scale syntheses based on physical theories instead of empirical observations. These results indicate that researchers should consider kinetic models, such as the Smoluchowski model, to quantitatively model ensemble properties of nanoparticles where significant aggregation or other non-classical growth mechanisms are observed. Likewise, our observations of length-scale dependent nanoparticle growth emphasize the need to quantify and correlate the contributions of growth mechanisms at different length scales to help tune the overall properties of functional nanostructures,⁵⁸ biomineralized nanocrystals,^{34, 43, 44} heterogeneous catalysts,^{25, 39, 40} and other complex nanoscale ensembles formed by non-classical growth mechanisms.^{33, 41, 42 1, 4, 6, 58}

METHODS

In situ nanoparticle growth experiments

In situ nanoparticle growth experiments were performed on a JEOL 2100F spherical aberration corrected transmission electron microscope, operated in scanning (STEM) mode. A continuous flow fluid stage (Hummingbird Scientific, WA, USA) held a thin layer of liquid precursor, approximately 800 nm thick (see Figure S1). For all experiments, the liquid precursor was 0.1 mM AgNO₃ (Fisher Scientific). Ensemble scale nanoparticle growth movies were acquired with a STEM beam current of 20 pA, dwell time of 5 μs, and magnification of M = 100,000, resulting in a STEM frame scan time of 1.3 seconds. We used a freeware frame grabber to capture movies of the ensemble growth at a frame rate of 1 frame per second. Further details of the experimental apparatus and methods are included in a previous publication.⁸

Image analysis methods

We located and tracked the trajectories of the moving nanoparticles in a video sequence of in situ liquid STEM images. We applied our own image segmentation method to extract outlines of nanoparticles for each time frame of the video; see Figure S2 for an example.⁵³ The outlines were associated over different time frames to track growth trajectories of individual nanoparticles, identifying shape changing events such as nucleation, growth, and aggregation. Each trajectory is a sequence of temporally changing outlines of the same nanoparticles and their interactions; see Figure S2 for an example of nanoparticle aggregation. This analysis counts an aggregate as a single particle, and defines an aggregation event as two or more particles merging into one particle.

A growth trajectory of a nanoparticle is mathematically represented by a time varying function of a changing particle outline,

$$\mathbf{\varphi }(\mathbf{r},t)=\mathbf{B}\times \mathbf{r}(t)+\mathbf{\epsilon }(t)$$ (1)

where ϕ is the vector of the pixel locations on the outline of a nanoparticle, B is a basis function matrix, r is the location of a small number of the landmark points on the particle outline, and ε(t) is the measurement noise.