Kernel Ordinary Differential Equations

Abstract

Ordinary differential equation (ODE) is widely used in modeling biological and physical processes in science. In this article, we propose a new reproducing kernel-based approach for estimation and inference of ODE given noisy observations. We do not assume the functional forms in ODE to be known, or restrict them to be linear or additive, and we allow pairwise interactions. We perform sparse estimation to select individual functionals, and construct confidence intervals for the estimated signal trajectories. We establish the estimation optimality and selection consistency of kernel ODE under both the low-dimensional and high-dimensional settings, where the number of unknown functionals can be smaller or larger than the sample size. Our proposal builds upon the smoothing spline analysis of variance (SS-ANOVA) framework, but tackles several important problems that are not yet fully addressed, and thus extends the scope of existing SS-ANOVA as well. We demonstrate the efficacy of our method through numerous ODE examples.

1. Introduction

Ordinary differential equation (ODE) has been widely used to model dynamic systems and biological and physical processes in a variety of scientific applications. Examples include infectious disease (Liang and Wu 2008), genomics (Cao and Zhao 2008; Chou and Voit 2009; Ma et al. 2009; Lu et al. 2011; Henderson and Michailidis 2014; Wu et al. 2014), neuroscience (Izhikevich 2007; Zhang et al. 2015, 2017; Cao, Sandstede, and Luo 2019), among many others. A system of ODEs take the form,

$$\frac{dx(t)}{dt}=\left(\begin{array}{c}\frac{d{x}_1(t)}{dt}\\ ⋮\\ \frac{d{x}_p(t)}{dt}\end{array}\right)=\left(\begin{array}{c}{F}_1(x(t))\\ ⋮\\ F_p(x(t))\end{array}\right)=F(x(t)),$$ (1)

Where $x(t)={\left(x_1(t),\dots ,x_p(t)\right)}^{\top }\in {ℝ}^p$ denotes the system of p variables of interest, F = {F₁, …, F_p} denotes the set of unknown functionals that characterize the regulatory relations among x(t), and t indexes time in an interval standardized to $\mathcal{T}=[0,1]$. Typically, the system (1) is observed on discrete time points {t₁, …, t_n} with measurement errors,

$$y_i=x\left(t_i\right)+{ϵ}_i,i=1,\dots ,n,$$ (2)

where $y_i={\left(y_{i1},\dots ,y_{ip}\right)}^{\top }\in {ℝ}^p$ denotes the observed data, ${ϵ}_i={\left({ϵ}_{i1},\dots ,{ϵ}_{ip}\right)}^{\top }\in {ℝ}^p$ denotes the vector of measurement errors that are usually assumed to follow independent normal distribution with mean 0 and variance ${\sigma }_j^2$, j = 1, …, p, and n denotes the number of time points. Besides, an initial condition $x(0)\in {ℝ}^p$ is usually given for the system (1).

In a biological or physical system, a central question of interest is to uncover the structure of the system of ODEs in terms of which variables regulate which other variables, given the observed noisy time-course data ${\left\{y_i\right\}}_{i=1}^n$. Specifically, we say that x_k regulates x_j, if F_j is a functional of x_k. In other words, x_k controls the change of x_j through the functional F_j on the derivative dx_j/dt. Therefore, the functionals F = {F₁, …, F_p} encode the regulatory relations of interest, and are often assumed to take the form,

$$\begin{gathered} F_j(x(t))={\theta }_{j0}+\sum _{k=1}^p{F}_{jk}\left(x_k(t)\right)+\sum _{k\ne l,k=1}^p\sum _{l=1}^p{F}_{jkl}\left(x_k(t),x_l(t)\right), \\ j=1,\dots ,p, \end{gathered}$$ (3)

where ${\theta }_{j0}\in ℝ$ denotes the intercept, and F_jk and F_jkl represent the main effect and two-way interaction, respectively. Higher order interactions are possible, but two-way interactions are the most common structure studied in ODE (Ma et al. 2009; Zhang et al. 2015).

There have been numerous pioneering works studying statistical modeling of ODEs. However, nearly all existing solutions constrain the forms of F. Broadly speaking, there are three categories of functional forms imposed. The first category considers linear functionals for F. For instance, Lu et al. (2011) studied a system of linear ODEs to model dynamic gene regulatory networks. Zhang et al. (2015) extended the linear ODE to include the interactions to model brain connectivity networks. The model of Zhang et al. (2015), other than differentiating between the variables that encode the neuronal activities and the ones that represent the stimulus signals, is in effect of the form,

$$\begin{gathered} F_j(x(t))={\theta }_{j0}+\sum _{k=1}^p{\theta }_{jk}{x}_k(t)+\sum _{k\ne l,k=1}^p\sum _{l=1}^p{\theta }_{jkl}{x}_k(t)x_l(t), \\ j=1,\dots ,p, \end{gathered}$$ (4)

whereas the model of Lu et al. (2011) is similar to (4) but focuses on the main-effect terms only. In both cases, F_j takes a linear form. Dattner and Klaassen (2015) further extended the functional F_j in (4) to a generalized linear form, but without the interactions, that is,

$$F_j(x(t))={\theta }_{j0}+{\psi }_j{(x(t))}^{\top }{\theta }_j,j=1,\dots ,p,$$ (5)

where ${\theta }_{j0}\in ℝ,{\theta }_j\in {ℝ}^d$, and ${\psi }_j(x)={\left({\psi }_{j1}(x),\dots ,{\psi }_{jd}(x)\right)}^{\top }\in {ℝ}^d$ is a finite set of known basis functions. The second category considers additive functionals for F. Particularly, Henderson and Michailidis (2014), Wu et al. (2014), and Chen, Shojaie, and Witten (2017) considered the generalized additive model for F_j,

$$\begin{gathered} F_j(x(t))={\theta }_{j0}+\sum _{k=1}^p{F}_{jk}\left(x_k(t)\right) \\ ={\theta }_{j0}+\sum _{k=1}^p\left\{\psi {\left(x_k(t)\right)}^{\top }{\theta }_{jk}+{\delta }_{jk}\left(x_k(t)\right)\right\}, \\ j=1,\dots ,p, \end{gathered}$$ (6)

where ${\theta }_{j0}\in ℝ$, ${\theta }_{jk}\in {ℝ}^d$, $\psi (x)={\left({\psi }_1(x),\dots ,{\psi }_d(x)\right)}^{\top }\in {ℝ}^d$ is a finite set of common basis functions, and ${\delta }_{jk}\in ℝ$ is the residual function. Different from Dattner and Klaassen (2015), the residual δ_jk is unknown. The functional F_j in (6) takes an additive form. Finally, there is a category of ODE solutions focusing on the scenario where the functional forms for F are known (González, Vujačić, and Wit 2014; Zhang, Cao, and Carroll 2015; Mikkelsen and Hansen 2017).

These works have laid a solid foundation for statistical modeling of ODE. However, in plenty of scientific applications, the forms of the functionals F are unknown, and the linear or additive forms on F can be restrictive. Besides, it is highly nontrivial to couple the basis function-based solutions with the interactions. We give an example in Section 2.1, where a commonly used enzyme network ODE system involves both nonlinear functionals and two-way interactions. Such examples are often the rules rather than the exceptions, motivating us to consider a more flexible form of ODE. Moreover, the existing ODE methods have primarily focused on sparse estimation, but few tackled the problem of statistical inference, which is challenging due to the complicated correlation structure of ODE.

In this article, we propose a novel approach of kernel ordinary differential equation (KODE) for estimation and inference of the ODE system in (1) given noisy observations from (2). We adopt the general formulation of (3), but we do not assume the functional forms of F are known, or restrict them to be linear or additive, and we allow pairwise interactions. As such, we consider a more general ODE system that encompasses (4)–(6) as special cases. We further introduce sparsity regularization to achieve selection of individual functionals in (3), which yields a sparse recovery of the regulatory relations among F, and improves the model interpretability. Moreover, we derive the confidence interval for the estimated signal trajectory x_j(t). We establish the estimation optimality and selection consistency of kernel ODE, under both low-dimensional and high-dimensional settings, where the number of unknown functionals p can be smaller or larger than the number of time points n, and we study the regime-switching phenomenon. These differences clearly separate our proposal from the existing ODE solutions in the literature.

Our proposal is built upon the smoothing spline analysis of variance (SS-ANOVA) framework that was first introduced by Wahba et al. (1995), then further developed in regression and functional data analysis settings by Huang (1998), Lin and Zhang (2006), and Zhu, Yao, and Zhang (2014). We adopt a similar component selection and smoothing operator (COSSO) type penalty of Lin and Zhang (2006) for regularization, and conceptually, our work extends COSSO to the ODE setting. However, our proposal considerably differs from COSSO and the existing SS-ANOVA methods, in multiple ways. First, unlike the standard SS-ANOVA models, the regressors of kernel ODE are not directly observed and need to be estimated from the data with error. This extra layer of randomness and estimation error introduces additional difficulty to SS-ANOVA. Second, we employ the integral of the estimated trajectories in the loss function to improve the estimation properties (Dattner and Klaassen 2015). The use of the integral and the inclusion of the interaction terms pose some identifiability question that we tackle explicitly. Third, we establish the estimation optimality and selection consistency in the RKHS framework, which is utterly different from Zhu, Yao, and Zhang (2014), and requires new technical tools. Moreover, our theoretical analysis extends that of Chen, Shojaie, and Witten (2017) from the finite bases setting of cubic splines to the infinite bases setting of RKHS. Finally, for statistical inference, we derive the confidence bands to provide uncertainty quantification for the penalized estimators of the signal trajectories in the ODE model. Our solution builds on the confidence intervals idea of Wahba (1983). But unlike the classical methods focusing on the fixed dimensionality p (Wahba 1983; Opsomer and Ruppert 1997), we allow a diverging p that can far exceed the sample size n. In summary, our proposal tackles several crucial problems that are not yet fully addressed in the existing SS-ANOVA framework, and it is far from a straightforward extension. We believe the proposed kernel ODE method not only makes a useful addition to the toolbox of ODE modeling, but also extends the scope of SS-ANOVA-based kernel learning.

The rest of the article is organized as follows. We propose kernel ODE in Section 2, and develop the estimation algorithm and inference procedure in Section 3. We derive the consistency and optimality of the proposed method in Section 4. We investigate the numerical performance in Section 5, and illustrate with a real data example in Section 6. We conclude the paper with a discussion in Section 7, and relegate all proofs and some additional numerical results to the Supplementary Appendix.

2. Kernel Ordinary Differential Equations

2.1. Motivating example

We consider an enzymatic regulatory network as an example to demonstrate that nonlinear functionals as well as interactions are common in the system of ODEs. Ma et al. (2009) found that all circuits of three-node enzyme network topologies that perform biochemical adaptation can be well approximated by two architectural classes: a negative feedback loop with a buffering node, and an incoherent feedforward loop with a proportioner node. The mechanism of the first class follows the Michaelis–Menten kinetic equations (Tzafriri 2003),

$$\begin{gathered} \frac{d{x}_1(t)}{dt}=c_1\frac{x_0\left\{1-x_1(t)\right\}}{\left\{1-x_1(t)\right\}+C_1}-{\tilde{c}}_1{c}_2\frac{x_1(t)}{x_1(t)+C_2}, \\ \frac{d{x}_2(t)}{dt}=c_3\frac{\left\{1-x_2(t)\right\}{x}_3(t)}{\left\{1-x_2(t)\right\}+C_3}-{\tilde{c}}_2{c}_4\frac{x_2(t)}{x_2(t)+C_4}, \\ \frac{d{x}_3(t)}{dt}=c_5\frac{x_1(t)\left\{1-x_3(t)\right\}}{\left\{1-x_3(t)\right\}+C_5}-c_6\frac{x_2(t)x_3(t)}{x_3(t)+C_6}, \end{gathered}$$ (7)

where x₁(t), x₂(t), x₃(t) are three interacting nodes, such that x₁(t) receives the input, x₂(t) plays the diverse regulatory role, and x₃(t) transmits the output, x₀ is the initial input stimulus, and c₁, …, c₆, C₁, …, C₆, ${\tilde{c}}_1$, ${\tilde{c}}_2$ denote the catalytic rate parameters, the Michaelis–Menten constants, and the concentration parameters, respectively. See Figure 1(a) for a graphical illustration of this ODE system. In this model, the functionals F₁, F₂, F₃ are all nonlinear, and both F₂ and F₃ involve two-way interactions. It is of great interest to estimate F_j’s given the observed data, to verify model (7), and to carry out statistical inference of the unknown parameters. This example, along with many other ODE systems with nonlinear functionals and interaction terms motivate us to consider a general ODE system as in (3).

Figure 1.

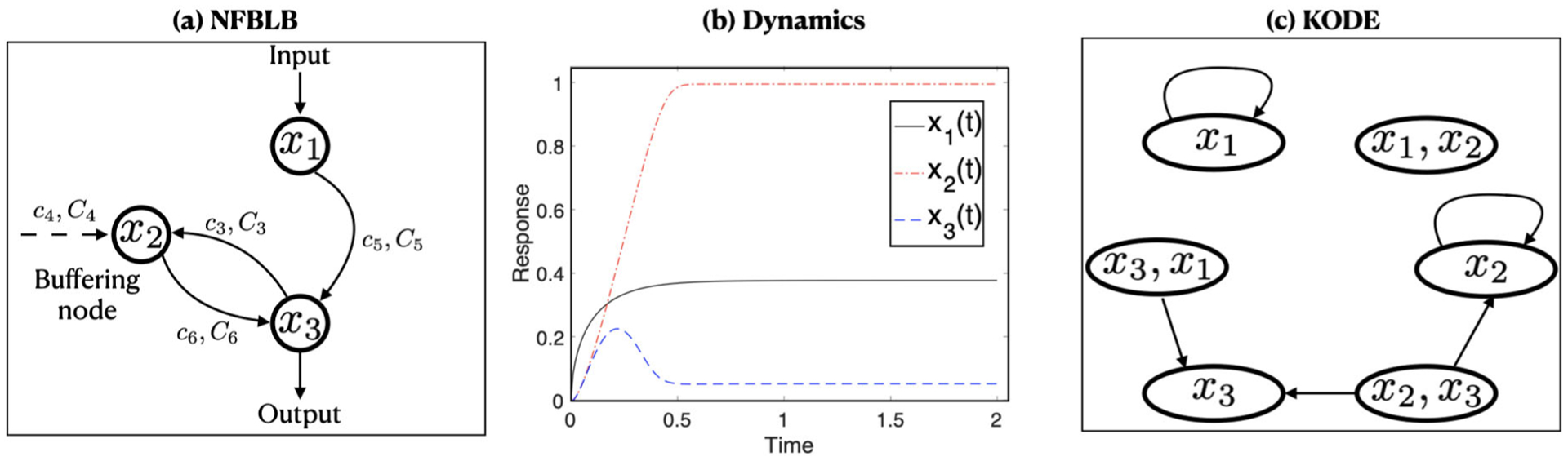
(a) Diagram of the NFBLB regulatory network following (7). (b) Phase dynamics for the three nodes x₁, x₂, x₃ over time [0, 1], with a random input x₀ uniformly drawn from [0.5, 1.5]. (c) Illustration of the NFBLB network in terms of the interactions in KODE.

2.2. Two-Step Collocation Estimation

Before presenting our method, we first briefly review the two-step collocation estimation method, which is commonly used for parameter estimation in ODE, and is also useful in our setting. The method was first proposed by Varah (1982), then extended to various ODE models. In the first step, it fits a smoothing estimate,

$$\begin{gathered} {\widehat{x}}_j(t)=\underset{z_j\in \mathcal{F}}{\text{arg min}}\left\{\frac{1}{n}\sum _{i=1}^n{\left\{y_{ij}-z_j\left(t_i\right)\right\}}^2+{\lambda }_{nj}{J}_1\left(z_j\right)\right\}, \\ j=1,\dots ,p, \end{gathered}$$

where J₁(·) is a smoothness penalty in the function space $\mathcal{F}$, and z_j is a function in $\mathcal{F}$ that we minimize over. In the second step, it solves an optimization problem to estimate the model parameters ${\theta }_{j0}\in ℝ$ and ${\theta }_j={\left({\theta }_{j1},\dots ,{\theta }_{jp}\right)}^{\top }\in {ℝ}^p$, for j = 1, …, p. Particularly, Varah (1982) considered the derivative $d{\widehat{x}}_j(t)/dt$ and the following minimization,

$$\underset{{\theta }_{j0},{\theta }_j}{\text{min}}{\int }_0^1{\left(\frac{d{\widehat{x}}_j(t)}{dt}-{\theta }_{j0}-\sum _{k=1}^p{\theta }_{jk}{\widehat{x}}_k(t)\right)}^{2}dt,j=1,\dots ,p.$$

Wu et al. (2014) developed a similar two-step collocation method for their additive ODE model (6), and estimated the model parameters ${\theta }_{j0}\in ℝ$ and ${\theta }_{jk}={\left({\theta }_{jk1},\dots ,{\theta }_{jkd}\right)}^{\top }\in {ℝ}^d$, for j, k = 1, …, p, with a standardized group ℓ₁-penalty,

$$\begin{gathered} \underset{{\theta }_{j0},{\theta }_{jk}}{\text{min}}{\int }_0^1{\Vert \frac{d{\widehat{x}}_j(t)}{dt}-{\theta }_{j0}-\sum _{k=1}^p{\theta }_{jk}^{\top }\psi \left({\widehat{x}}_k(t)\right)\Vert }_2^{2}dt \\ +{\tau }_{nj}\sum _{k=1}^p{\left[{\int }_0^1{\left\{{\theta }_{jk}^{\top }\psi \left({\widehat{x}}_k(t)\right)\right\}}^{2}dt\right]}^{1/2}. \end{gathered}$$

They further discussed adaptive group ℓ₁ and regular ℓ₁-penalties. Meanwhile, Henderson and Michailidis (2014) considered an extra ℓ₂-penalty.

Alternatively, in the second step, Dattner and Klaassen (2015) proposed to focus on the integral ${\int }_0^t{g}_j(\widehat{x}(u))du$, rather than the derivative $d{\widehat{x}}_j(t)/dt$, and they estimated the model parameters ${\theta }_{j0}\in ℝ$ and ${\theta }_j={\left({\theta }_{j1},\dots ,{\theta }_{jd}\right)}^{\top }\in {ℝ}^d$, for j = 1, …, p, in (5) by,

$${\underset{{\theta }_{j0},{\theta }_j}{\text{min}}\sum _{j=1}^p{\int }_0^1\{{\widehat{x}}_j(t)-{\theta }_{j0}-{\theta }_j^{\top }{\int }_0^t{\psi }_j\widehat{x}(u)\text{)}du\}}^{2}dt.$$

They found that this modification from the derivative to integral leads to a more robust estimate and also an easier derivation of the asymptotic properties. Chen, Shojaie, and Witten (2017) adopted this idea for their additive ODE model (6), and estimated the parameters ${\theta }_{j0}\in ℝ$, ${\tilde{\theta }}_j\in ℝ$, and ${\theta }_{jk}={\left({\theta }_{jk1},\dots ,{\theta }_{jkd}\right)}^{\top }\in {ℝ}^d$, for j, k = 1, …, p, by

$$\begin{gathered} \underset{{\theta }_{j0},{\tilde{\theta }}_j,{\theta }_{jk}}{\text{min}}\frac{1}{2n}\sum _{i=1}^n{\left\{y_{ij}-{\theta }_{j0}-b_j{t}_i-\sum _{k=1}^p{\theta }_{jk}^{\top }{\int }_0^{t_i}\psi \left({\widehat{x}}_k(u)\right)du\right\}}^2 \\ +{\tau }_{nj}\sum _{k=1}^p{\left[\frac{1}{n}\sum _{i=1}^n{\left\{{\theta }_{jk}^{\top }{\int }_0^{t_i}\psi \left({\widehat{x}}_k(u)\right)dt\right\}}^2\right]}^{1/2}. \end{gathered}$$

2.3. Kernel ODE

We build the proposed kernel ODE within the smoothing spline ANOVA framework; see Wahba et al. (1995) and Gu (2013) for more background on SS-ANOVA. Specifically, let ${\mathcal{H}}_k$ denote a space of functions of $x_k(t)\in \mathcal{X}$ with zero marginal integral, where $\mathcal{X}\subset ℝ$ is a compact set. Let {1} denote the space of constant functions. We construct the tensor product space as

$$\mathcal{H}=\left\{1\right\}\oplus \sum _{k=1}^p{\mathcal{H}}_k\oplus \sum _{k=1,k\ne l}^p\sum _{l=1}^p\left({\mathcal{H}}_k\otimes {\mathcal{H}}_l\right).$$ (8)

We assume the functionals F_j, j = 1, …, p, in the ODE model (3) are located in the space of $\mathcal{H}$. The identifiability of the terms in (3) is assured by the conditions specified through the averaging operators: ${\int }_{\mathcal{T}}{F}_{jk}\left(x_k(t)\right)dt=0$ for k = 1, …, p. Let· $\parallel \cdot {\parallel }_{\mathcal{H}}$ denote the norm of $\mathcal{H}$, and ${\mathcal{P}}^k{F}_j$ and ${\mathcal{P}}^{kl}{F}_j$ denote the orthogonal projection of F_j onto ${\mathcal{H}}_k$ and ${\mathcal{H}}_k\otimes {\mathcal{H}}_l$, respectively. We consider a two-step collocation estimation method, by first obtaining a smoothing spline estimate $\widehat{x}(t)={\left({\widehat{x}}_1(t),\dots ,{\widehat{x}}_p(t)\right)}^{\top }$, where

$$\begin{gathered} {\widehat{x}}_j(t)=\underset{z_j\in \mathcal{F}}{\text{arg min}}\left\{\frac{1}{n}\sum _{i=1}^n{\left\{y_{ij}-z_j\left(t_i\right)\right\}}^2+{\lambda }_{nj}{\Vert z_j(t)\Vert }_{\mathcal{F}}^2\right\}, \\ j=1,\dots ,p, \end{gathered}$$ (9)

then estimating $F_j\in \mathcal{H}$ and ${\theta }_{j0}\in ℝ$ by the following penalized optimization,

$$\begin{gathered} \underset{{\theta }_{j0},F_j}{\text{min}}\frac{1}{n}\sum _{i=1}^n{\left\{y_{ij}-{\theta }_{j0}-{\int }_0^{t_i}{F}_j(\widehat{x}(t))dt\right\}}^2 \\ +{\tau }_{nj}\left(\sum _{k=1}^p{\Vert {\mathcal{P}}^k{F}_j\Vert }_{\mathcal{H}}+\sum _{k\ne l,k=1}^p\sum _{l=1}^p{\Vert {\mathcal{P}}^{kl}{F}_j\Vert }_{\mathcal{H}}\right). \end{gathered}$$ (10)

Our proposal deals with the integral ${\int }_0^{t_i}{F}_j(\widehat{x}(u))du$, rather than the derivative $d{\widehat{x}}_j(t)/dt$, which is in a similar spirit as Dattner and Klaassen (2015). Besides, it involves two penalty functions, $J_1\equiv \parallel \cdot {\parallel }_{\mathcal{F}}^2$ in (9), and $J_2\left(F_j\right)\equiv {\sum }_{k=1}^p{\Vert {\mathcal{P}}^k{F}_j\Vert }_{\mathcal{H}}+{\sum }_{k=1}^p{\sum }_{l=1}^p{\Vert {\mathcal{P}}^{kl}{F}_j\Vert }_{\mathcal{H}}$ in (10), with λ_nj and τ_nj as two tuning parameters. We next make some remarks about this proposal.

For the functionals, the formulation in (10) is highly flexible, nonlinear, and incorporates two-way interactions. Meanwhile, it naturally covers the linear ODE in (4) and (5), and the additive ODE in (6) as special cases. In particular, if $\mathcal{H}$ is the linear functional space, $\mathcal{H}=\left\{1\right\}\oplus {\sum }_{k=1}^p\left\{x_k-1/2\right\}\oplus {\sum }_{k\ne l}[\{x_k-1/2\}\otimes \left\{x_l-1/2\right\}]$ with the input space $\mathcal{X}={[0,1]}^p$, then any F of the form in (4) belongs to $\mathcal{H}$. If $\mathcal{H}$ is spanned by some known generalized functions, $\mathcal{H}={\psi }_{j1}(x)\oplus \cdots \oplus {\psi }_{jp}(x)$, then any F in (5) belongs to $\mathcal{H}$. If $\mathcal{H}$ is the additive functional space, $\mathcal{H}=\left\{1\right\}\oplus {\sum }_{k=1}^p{\mathcal{H}}_k$ with the ℓ₂-norm, then for F_jk, (x_k(t)) = ψ(x_k(t))^⊤θ_jk, the penalty on the main effects becomes ${{\sum }_{k=1}^p\Vert {\mathcal{P}}^k{F}_j\Vert }_{\mathcal{H}}={{\sum }_{k=1}^p\left[{\int }_0^1{\left\{\psi {\left(x_k(t)\right)}^{\top }{\theta }_{jk}\right\}}^{2}dt\right]}^{1/2}$, which is exactly the same as the ODE model of Chen, Shojaie, and Witten (2017).

For the penalties, the first penalty function J₁ is the squared RKHS norm corresponding to the RKHS $\{\mathcal{F},\parallel \cdot {\parallel }_{\mathcal{F}}\}$. It is for estimating ${\widehat{x}}_j$, and $\mathcal{F}$ does not have to be the same as $\mathcal{H}$. The second penalty function J₂ is a sum of RKHS norms on the main effects and pairwise interactions. This penalty is similar as the COSSO penalty of Lin and Zhang (2006). But as we outline in Section 1, our extension is far from trivial. We also note that, we do not impose a hierarchical structure for the main effects and interactions, in that if an interaction term is selected, the corresponding main effect term does not have to be selected (Wang et al. 2009). This is motivated by the observation that, for example, in the enzymatic regulatory network example in Section 2.1, the interaction terms x₁(t)x₃(t) and x₂(t)x₃(t) both appear in the ODE regulating x₃(t), but the main effect terms x₁(t) and x₂(t) are not present.

Theorem 1.

Assume that the RKHS $\mathcal{H}$ can be decomposed as in (8). Then there exists a minimizer of (10) in $\mathcal{H}$ for any tuning parameter τ_nj ≥ 0. Moreover, the minimizer is in a finite-dimensional space.

Theorem 1 is a generalization of the well-known representer theorem (Wahba 1990). The difference is that, unlike the smoothing splines model as studied in Wahba (1990), the minimization of (10) involves an integral in the loss function, and the penalty is not a norm in $\mathcal{H}$ but a convex pseudo-norm. A direct implication of Theorem 1 is that, although the minimization with respect to F_j is taken over an infinite-dimensional space in (10), the solution to (10) can actually be found in a finite-dimensional space. We next develop an estimation algorithm to solve (10).

3. Estimation and Inference

3.1. Estimation Procedure

The estimation of the proposed kernel ODE system consists of two major steps. The first step is the smoothing spline estimation in (9), which is standard and the tuning of the smoothness parameter λ_nj is often done through generalized cross-validation (see, e.g., Gu 2013). The second step is to solve (10). Toward that end, we first propose an optimization problem that is equivalent to (10), but is computationally easier to tackle. We then develop an estimation algorithm to solve this new equivalent problem.

Specifically, we consider the following optimization problem, for j = 1, …, p,

$$\begin{gathered} \underset{{\theta }_{j0},{\theta }_j,F_j}{\text{min}}\frac{1}{n}\sum _{i=1}^n{\left\{y_{ij}-{\theta }_{j0}-{\int }_0^{t_i}{F}_j(\widehat{x}(t))dt\right\}}^2 \\ +{\eta }_{nj}\left(\sum _{k=1}^p{\theta }_{jk}^{-1}{\Vert {\mathcal{P}}^k{F}_j\Vert }_{\mathcal{H}}^2+{\theta }_{jkl}^{-1}\sum _{k=1,k\ne l}^p\sum _{l=1}^p{\Vert {\mathcal{P}}^{kl}{F}_j\Vert }_{\mathcal{H}}^2\right) \\ +{\kappa }_{nj}\left(\sum _{k=1}^p{\theta }_{jk}+\sum _{k=1,k\ne l}^p\sum _{l=1}^p{\theta }_{jkl}\right), \end{gathered}$$ (11)

subject to θ_k ≥ 0, θ_kl ≥ 0, k, l = 1, …, p, k ≠ l, where ${\theta }_j={\left({\theta }_{j1},\dots ,{\theta }_{jp},{\theta }_{j12},\dots ,{\theta }_{j1p},\dots ,{\theta }_{jp1},\dots ,{\theta }_{jp(p-1)}\right)}^{\top }\in {ℝ}^{p^2}$ collects the parameters to estimate, and η_nj, κ_nj≥0 are the tuning parameters, j = 1, …, p. Comparing (11) to (10), we introduce the parameters θ_jk and θ_jkl to control the sparsity of the main effect and interaction terms in F_j. This is similar to Lin and Zhang (2006). The two optimization problems (10) and (11) are equivalent, in the following sense. Let ${\kappa }_{nj}={\tau }_{nj}^2/\left(4{\eta }_{nj}\right)$. Then we have,

$${\eta }_{nj}{\theta }_{jk}^{-1}{\Vert {\mathcal{P}}^k{F}_j\Vert }_{\mathcal{H}}^2+{\kappa }_{nj}{\theta }_{jk}\ge 2{\eta }_{nj}^{1/2}{\kappa }_{nj}^{1/2}{\Vert {\mathcal{P}}^k{F}_j\Vert }_{\mathcal{H}}={\tau }_{nj}{\Vert {\mathcal{P}}^k{F}_j\Vert }_{\mathcal{H}},$$

where the equality holds if ${\theta }_{jk}={\eta }_{nj}^{1/2}{\kappa }_{nj}^{-1/2}{\Vert P^k{F}_j\Vert }_{\mathcal{H}}$. A similar result holds for ${\theta }_{jkl}={\eta }_{nj}^{1/2}{\kappa }_{nj}^{-1/2}{\Vert P^{kl}{F}_j\Vert }_{\mathcal{H}}$. In other words, if $\left({\widehat{\theta }}_{j0},{\widehat{F}}_j\right)$ minimizes (10), then $\left({\widehat{\theta }}_{j0},{\widehat{\theta }}_j,{\widehat{F}}_j\right)$ minimizes (11), with ${\widehat{\theta }}_{jk}={\eta }_{nj}^{1/2}{\kappa }_{nj}^{-1/2}{\Vert {\mathcal{P}}^k{\widehat{F}}_j\Vert }_{\mathcal{H}}$, and ${\theta }_{jkl}={\eta }_{nj}^{1/2}{\kappa }_{nj}^{-1/2}{\Vert {\mathcal{P}}^{kl}{F}_j\Vert }_{\mathcal{H}}$, for any k, l = 1, …, p, k ≠ l. Meanwhile, if $\left({\widehat{\theta }}_{j0},{\widehat{\theta }}_j,{\widehat{F}}_j\right)$ minimizes (11), then $\left({\widehat{\theta }}_{j0},{\widehat{F}}_j\right)$ minimizes (10).

Next, we devise an iterative alternating optimization approach to solve (11). That is, we first estimate θ_j0 given fixed F_j and θ_j, then estimate the functional F_j given fixed θ_j0 and θ_j, and finally estimate θ_j given fixed θ_j0 and F_j.

For given ${\widehat{F}}_j$ and ${\widehat{\theta }}_j$, we have that,

$${\widehat{\theta }}_{j0}={\overline{y}}_j-{\int }_{\mathcal{T}}\overline{T}(t){\widehat{F}}_j(\widehat{x}(t))dt,$$

where T_i(t) = 1{0 ≤ t ≤ t_i}, $\overline{T}(t)=\frac{1}{n}{\sum }_{i=1}^n{T}_i(t)$ and ${\overline{y}}_j=n^{-1}\sum _{i=1}^n{y}_{ij}$.

For given ${\widehat{\theta }}_{j0}$ and ${\widehat{\theta }}_j$, the optimization problem (11) becomes,

$$\begin{gathered} \underset{F_j}{\text{min}}\{\frac{1}{n}\sum _{i=1}^n{\left[\left(y_{ij}-{\overline{y}}_j\right)-{\int }_{\mathcal{T}}\left\{T_i(t)-\overline{T}(t)\right\}{F}_j(\widehat{x}(t))dt\right]}^2 \\ +{\eta }_{nj}\left(\sum _{k=1}^p{\widehat{\theta }}_{jk}^{-1}{\Vert {\mathcal{P}}^k{F}_j\Vert }_{\mathcal{H}}^2+{\widehat{\theta }}_{jkl}^{-1}\sum _{k=1,k\ne l}^p\sum _{l=1}^p{\Vert {\mathcal{P}}^{kl}{F}_j\Vert }_{\mathcal{H}}^2\right)\}. \end{gathered}$$ (12)

Let $K_j(\cdot ,\cdot ):\mathcal{X}\times \mathcal{X}\mapsto ℝ$ denote the Mercer kernel generating the RKHS ${\mathcal{H}}_j$, j = 1, …, p. Then K_kl ≡ K_kK_l is the reproducing kernel of the RKHS ${\mathcal{H}}_k\otimes {\mathcal{H}}_l$. Let $K_{{\theta }_j}=\sum _{k=1}^p{\widehat{\theta }}_{jk}{K}_k+{\sum }_{k\ne l}{\widehat{\theta }}_{jkl}{K}_{kl}$. By the representer theorem (Wahba 1990), the solution ${\widehat{F}}_j$ to (12) is of the form,

$${\widehat{F}}_j(\widehat{x}(t))=b_j+\sum _{i=1}^n{c}_{ij}{\int }_{\mathcal{T}}{K}_{{\theta }_j}(\widehat{x}(t),\widehat{x}(s))\left\{T_i(s)-\overline{T}(s)\right\}ds$$ (13)

for some $b_j\in ℝ$ and $c_j=\left(c_{1j},\dots ,c_{nj}\right)\in {ℝ}^n$. Write $y_j={\left(y_{1j},\dots ,y_{nj}\right)}^{\top }\in {ℝ}^n$ and ${\overline{y}}_j={\left({\overline{y}}_j,\dots ,{\overline{y}}_j\right)}^{\top }\in {ℝ}^n$. Let B be an n × 1 vector whose ith entry is $B_i={\int }_{\mathcal{T}}\left\{T_i(t)-\overline{T}(t)\right\}dt$, i = 1, …, n. Let Σ be an n × n matrix whose (i, i′)th entry is ${\Sigma }_{i{i}^{\prime }}={\int }_{\mathcal{T}}{\int }_{\mathcal{T}}\left\{T_i(s)-\overline{T}(s)\right\}{K}_{{\theta }_j}(\widehat{x}(t),\widehat{x}(s))\left\{T_{i^{\prime }}(t)-\overline{T}(t)\right\}\mathit{\text{dsdt}}$, i, i′ = 1, …, n. Plugging (13) into (12), we obtain the following quadratic minimization problem in terms of {b_j, c_j},

$$\underset{b_j,c_j}{\text{min}}\frac{1}{n}{\Vert \left(y_j-{\overline{y}}_j\right)-\left(B{b}_j+\Sigma c_j\right)\Vert }_2^2+{\eta }_{nj}{c}_j^{\top }\Sigma c_j,$$

which has a closed-form solution. Consider the QR decomposition B = [Q₁ Q₂][R 0]^⊤, where $Q_1\in {ℝ}^{n\times 1}$, $Q_2\in {ℝ}^{n\times (n-1)}$, and [Q₁ Q₂] is orthogonal such that B^⊤Q₂ = 0_1×(n−1). Write W_j = Σ+ nη_njI_n, where I_n is the n × n identity matrix. Then the minimizers are,

$$\begin{gathered} c_j=Q_2{\left(Q_2^{\top }{W}_j{Q}_2\right)}^{-1}{Q}_2^{\top }\left(y_j-{\overline{y}}_j\right), \\ {b}_j=R^{-1}{Q}_1^{\top }\left(y_j-{\overline{y}}_j-W_j{c}_j\right). \end{gathered}$$

Following the usual smoothing splines literature, we tune the parameter η_nj in (12) by minimizing the generalized cross-validation criterion (GCV, Wahba et al. 1995),

$$\text{GCV}=\frac{{\Vert A_j\left({\eta }_{nj}\right)\left(y_j-{\overline{y}}_j\right)-\left(y_j-{\overline{y}}_j\right)\Vert }^2}{{\left[n^{-1}tr\left\{I_n-A_j\left({\eta }_{nj}\right)\right\}\right]}^2},$$

where the smoothing matrix $A_j\left({\eta }_{nj}\right)\in {ℝ}^{n\times n}$ is of the form,

$$A_j\left({\eta }_{nj}\right)=I_n-n{\eta }_{nj}{Q}_2{\left(Q_2^{\top }{W}_j{Q}_2\right)}^{-1}{Q}_2^{\top }.$$ (14)

For given ${\widehat{\theta }}_{j0}$ and ${\widehat{F}}_j$, θ_j is the solution to a usual ℓ₁-penalized regression problem,

$$\underset{{\theta }_j}{\text{min}}\left\{{\left(z_j-G{\theta }_j\right)}^{\top }\left(z_j-G{\theta }_j\right)+n{\kappa }_{nj}\left(\sum _{k=1}^p{\theta }_{jk}+\sum _{k\ne l,k=1}^p\sum _{l=1}^p{\theta }_{jkl}\right)\right\},$$ (15)

subject to θ_k ≥ 0, θ_kl ≥ 0, k, l = 1, …, p, k ≠ l where the “response” is $z_j=\left(y_j-{\overline{y}}_j\right)-(1/2)n{\eta }_{nj}{c}_j-B{b}_j$, the “predictor” is $G\in {ℝ}^{n\times p^2}$, whose first p columns are Σ^kc_j with k = 1, …, p, and the last p(p − 1) columns are Σ^klc_j with k, l = 1, …, p, k ≠ l, and ${\Sigma }^k=\left({\Sigma }_{i{i}^{\prime }}^k\right),{\Sigma }^{kl}=\left({\Sigma }_{i{i}^{\prime }}^{kl}\right)$ are both n × n matrices whose (i, i′)th entries are ${\Sigma }_{i{i}^{\prime }}^k={\int }_{\mathcal{T}}{\int }_{\mathcal{T}}\{T_i(s)-\overline{T}(s)\}{K}_k(\widehat{x}(t),\widehat{x}(s))\left\{T_{i^{\prime }}(t)-\overline{T}(t)\right\}\mathit{\text{dsdt}}$, and ${\Sigma }_{i{i}^{\prime }}^k={\int }_{\mathcal{T}}{\int }_{\mathcal{T}}\{T_i(s)-\overline{T}(s)\}{K}_{kl}\widehat{x}(t),\widehat{x}(s))\left\{T_{i^{\prime }}(t)-\overline{T}(t)\right\}\mathit{\text{dsdt}}$, respectively, where i, i′ = 1, …, n, j = 1, …, p. We employ Lasso for (15) in our implementation, and tune the parameter κ_nj using 10-fold cross-validation, following the usual Lasso literature.

We repeat the above optimization steps iteratively until some stopping criterion is met; that is, when the estimates in two consecutive iterations are close enough, or when the number of iterations reaches some maximum number. In our simulations, we have found that the algorithm converges quickly, usually within 10 iterations. Another issue is the identifiability of ${\mathcal{P}}^k{F}_j^{\prime }s$ and ${\mathcal{P}}^{kl}{F}_j^{\prime }s$ in (11) in the sense of unique solutions. We introduce the collinearity indices ${\mathcal{C}}_{jk}$ and ${\mathcal{C}}_{jkl}$ to reflect the identifiability. Specifically, let $\mathcal{W}$ denote a p² × p² matrix, whose entries are $\text{cos}\left({\mathcal{P}}^k{F}_j,{\mathcal{P}}^{k^{\prime }}{F}_j\right)$, $\text{cos}\left({\mathcal{P}}^k{F}_j,{\mathcal{P}}^{k^{\prime }{l}^{\prime }}{F}_j\right)$, $\text{cos}\left({\mathcal{P}}^{kl}{F}_j,{\mathcal{P}}^{k^{\prime }}{F}_j\right)$, $\text{cos}\left({\mathcal{P}}^{kl}{F}_j,{\mathcal{P}}^{k^{\prime }{l}^{\prime }}{F}_j\right)$, j, k, l = 1, …, p. Then ${\mathcal{C}}_{jk}^2$ and ${\mathcal{C}}_{jkl}^2$ are defined by the diagonals of ${\mathcal{W}}^{-1}$. When some ${\mathcal{C}}_{jk}$ and ${\mathcal{C}}_{jkl}$ are much larger than one, then the identifiability issue occurs (Gu 2013). This is often due to insufficient amount of data relative to the complexity of the model we fit. In this case, we find that increasing η_nj and κ_nj in (11) often helps with the identifiability issue, as it helps reduce the model complexity.

We summarize the above estimation procedure in Algorithm 1.

3.2. Confidence Intervals

Next, we derive the confidence intervals for the estimated trajectory ${\widehat{x}}_j\left(t_i\right)$. This is related to post-selection inference, as the actual coverage probability of the confidence interval ignoring the preceding sparse estimation uncertainty can be dramatically smaller than the nominal level. Our result extends the recent work of Berk et al. (2013) and Bachoc, Leeb, and Pötscher (2019) from linear regression models to nonparametric ODE models, while our setting is more challenging, as it involves infinite-dimensional functional objects.

Let ${\widehat{\theta }}_j$ denote the estimator of θ_j obtained from Algorithm 1. Denote $\mathcal{M}\equiv \{1,\dots ,p,(1,2),\dots ,(1,p),\dots ,(p,1),\dots ,(p,p-1)\}$, and denote $M_j\subseteq \mathcal{M}$ as the index set of the nonzero entries of the sparse estimator ${\widehat{\theta }}_j$. Note that M_j is allowed to be an empty set. Let ${\widehat{\theta }}_{M_j}$ be the least squares estimate with M_j as the support that minimizes the unpenalized objective function in (15), that is, (z_j − Gθ_j)^⊤ (z_j − Gθ_j). Plugging this estimate ${\widehat{\theta }}_{M_j}$ into (13) gets the corresponding estimate of the functional F_j as,

$${\widehat{F}}_{j,{\widehat{\theta }}_{M_j}}(\widehat{x}(t))=b_j+\sum _{i=1}^n{c}_{ij}{\int }_{\mathcal{T}}{K}_{{\widehat{\theta }}_{M_j}}(\widehat{x},\widehat{x}(s))\left\{T_i(s)-\overline{T}(s)\right\}ds.$$

For a nominal level α ∈ (0, 1) and i = 1, …, n, define $c_0\left({\widehat{x}}_j\left(t_i\right)\right)$ as the smallest constant satisfying that,

$${\mathbb{P}}_{n,F_j,{\sigma }_j}\left[\underset{M_j\subseteq \mathcal{M}}{\text{max}}{\sigma }_j^{-1}\mid {\left\{{\tilde{A}}_{M_j}\right\}}_{i\cdot }\left(y_j-{\overline{y}}_j\right)\right)\mid \le c_0\left({\widehat{x}}_j\left(t_i\right)\right)]\ge 1-\alpha ,$$ (16)

where ${\left\{{\tilde{A}}_{M_j}\right\}}_{i.}={\left\{A_{M_j}\right\}}_{i.}/{\Vert {\left\{A_{M_j}\right\}}_{i.}\Vert }_{l_2},{\left\{A_{M_j}\right\}}_{i.}$ is the ith row of $A_{M_j}$, $A_{M_j}$ is the smoothing matrix as defined in (14) with the corresponding ${\widehat{\theta }}_{M_j}$, and ${\sigma }_j^2$ is the variance of the error term ϵ_ij in (2). We then construct the confidence interval $\text{CI}\left({\widehat{x}}_j\left(t\right)\right)$ for the prediction of true trajectory x_j(t) following model selection as,

$$\begin{gathered} \text{CI}\left({\widehat{x}}_j\left(t_i\right)\right)={\int }_{\mathcal{T}}\left\{T_i(t)-\overline{T}(t)\right\}{\widehat{F}}_{j,{\widehat{\theta }}_{M_j}}(\widehat{x}(t))dt \\ \pm c_0\left({\widehat{x}}_j\left(t_i\right)\right){\sigma }_j\Vert {\left\{A_{M_j}\right\}}_{i.}\Vert , \end{gathered}$$ (17)

for any i = 1, …, n and j = 1, …, p.

Next, we show that the confidence interval in (17) has the desired coverage probability. Later we develop a procedure to estimate the cutoff value $c_0\left({\widehat{x}}_j\right)$ in (16) given the data.

Theorem 2.

Let $M_j\subseteq \mathcal{M}$ be the index set of the nonzero entries of the sparse estimator ${\widehat{\theta }}_j$. Then the choice of $c_0\left({\widehat{x}}_j\left(t_i\right)\right)$ in (16) does not depend on F_j, and $\text{CI}\left({\widehat{x}}_j\left(t_i\right)\right)$ in (17) satisfies the coverage property, for any i = 1, …, n and j = 1, …, p, in that,

$$\underset{F_j\in \mathcal{H},{\sigma }_j>0}{\text{inf}}\mathbb{P}\left\{{\int }_{\mathcal{T}}\left\{T_i(t)-\overline{T}(t)\right\}\mathbb{E}\left[{\widehat{F}}_{j,{\widehat{\theta }}_{M_j}}(\widehat{x}(t))\right]dt\in \text{CI}\left({\widehat{x}}_j\left(t_i\right)\right)\right\}\ge 1-\alpha .$$

A few remarks are in order. First, the coverage in Theorem 2 is guaranteed for all sparse estimation and selection procedures. As such, $\text{CI}\left({\widehat{x}}_j\right)$ in (17), following the terminology of Berk et al. (2013), is a universally valid post-selection confidence interval. Second, if we replace $c_0\left({\widehat{x}}_j\left(t_i\right)\right)$ in (17) by z_α/2, that is, the α/2 cutoff value of a standard normal distribution, then $\text{CI}\left({\widehat{x}}_j\left(t_i\right)\right)$ reduces to the “naive” confidence interval. It is constructed as if M_j were fixed a priori, and it ignores any uncertainty or error of the sparse estimation step. This naive confidence interval, however, does not have the coverage property as in Theorem 2, and thus is not a truly valid confidence interval. Finally, data splitting is a commonly used alternative strategy for post-selection inference. But it is not directly applicable in our ODE setting, because it is difficult to split the time series data into independent parts.

Next, we devise a procedure to compute the cutoff value $c_0\left({\widehat{x}}_j\left(t_i\right)\right)$.

Proposition 1.

The value $c_0\left({\widehat{x}}_j\left(t_i\right)\right)$ in (16) is the same as the solution of t ≥ 0 satisfying,

$${\mathbb{E}}_U\mathbb{P}\left(\underset{M_j\subseteq \mathcal{M}}{\text{max}}\left|{\left\{{\tilde{A}}_{M_j}\right\}}_{i.}V\right|\le t/U\mid U\right)=1-\alpha ,$$

where V is uniformly distributed on the unit sphere in ${ℝ}^n$, and U is a nonnegative random variable such that U² follows a chisquared distribution χ²(n).

Following Proposition 1, we compute $c_0\left({\widehat{x}}_j\left(t_i\right)\right)$ as follows. We first generate N iid copies of random vectors V₁, …, V_N uniformly distributed on the unit sphere in ${ℝ}^n$. We then calculate the quantity, $c_v={\text{max}}_{M_j\subseteq \mathcal{M}}\left|{\left\{{\tilde{A}}_{M_j}\right\}}_{i.}{V}_v\right|$ for ν = 1, …, N. Let D_U denote the cumulative distribution function of U, and $D_{{\chi }^2}$ denote the cumulative distribution function of a χ²(n) distribution. Then $D_U(t)=D_{{\chi }^2}\left(t^2\right)$. We next obtain $c_0\left({\widehat{x}}_j\left(t_i\right)\right)$ by searching for c that solves $N^{-1}\sum _{i=1}^N{D}_U\left(c/c_i\right)=1-\alpha$, using, for example, a bisection searching method.

Finally, we estimate the error variance ${\sigma }_j^2$ in (17) using the usual noise estimator in the context of RKHS (Wahba 1990); that is, ${\widehat{\sigma }}_j^2={\Vert A_{M_j}\left(y_j-{\overline{y}}_j\right)-\left(y_j-{\overline{y}}_j\right)\Vert }^2/tr\left(I-A_{M_j}\right)$.

We also remark that, the inference on the prediction of the trajectory x_j(t) following model selection as described in Theorem 2 amounts to the inference on the estimation of the integration ${\int }_0^t{F}_j(x(s))ds$. This type of inference is of great importance in dynamic systems (Izhikevich 2007; Chou and Voit 2009; Ma et al. 2009). Our solution takes the selected model as an approximation to the truth, but does not require that the true data generation model has to be among the candidates of model selection. We note that, it is also possible to do inference on the individual components of F_j directly; for example, one could construct the confidence interval for F_jk in (3). But this is achieved at the cost of imposing additional assumptions, including the requirement that the true data generation model is among the class of pairwise interaction model as in (3), and the orthogonality property as in Chernozhukov, Hansen, and Spindler (2015), or its equivalent characterization as in Zhang and Zhang (2014); Javanmard and Montanari (2014). For nonparametric kernel estimators, the orthogonality property is shown to hold if the covariates x_j’s are assumed to be weakly dependent (Lu, Kolar, and Liu 2020). It is interesting to further investigate if such a property holds in the context of kernel ODE model under a similar condition of weakly dependent covariates. We leave this as our future research.

4. Theoretical Properties

We next establish the estimation optimality and selection consistency of kernel ODE. These theoretical results hold for both the low-dimensional and high-dimensional settings, where the number of functionals p can be smaller or larger than the sample size n. We first introduce two assumptions.

Assumption 1.

The number of nonzero functional components is bounded, that is, ({k : F_jk ≠ 0} ∪ {1 ≤ l ≠ k ≤ p : F_jkl ≠ 0}) is bounded for any j = 1, …, p.

Assumption 2.

For any $F_j\in \mathcal{H}$, there exists a random variable B, with $\mathbb{E}(B)<\infty$, and

$$\left|\frac{\partial F_j(x)}{\partial x_k}\right|\le B{\Vert F_j\Vert }_{L_2},\text{ almost surely}.$$

Assumption 1 concerns the complexity of the functionals. Similar assumptions have been adopted in the sparse additive model over RKHS when F_jkl = 0 (see, e.g., Koltchinskii and Yuan 2010; Raskutti, Wainwright, and Yu 2011). Assumption 2 is an inverse Poincaré inequality type condition, which places regularization on the fluctuation in F_j relative to the ℓ₂-norm. The same assumption was also used in additive models in RKHS (Zhu, Yao, and Zhang 2014).

We begin with the error bound for the estimated trajectory $\widehat{x}(t)$ uniformly for j = 1, …, p. This is a relatively standard result, which is needed for both analyzing the error of the functional estimators in kernel ODE, and establishing the selection consistency later.

Theorem 3 (Optimal estimation of the trajectory).

Suppose that $x_j(t)\in \mathcal{F},j=1,\dots ,p$, and the RKHS $\mathcal{F}$ is embedded to a β₁th order Sobolev space, β₁ > 1/2. Then the smoothing spline estimate from (9) satisfies that, for any j = 1, …, p,

$$\underset{{\lambda }_{nj}\ge 0}{\text{min}}{\int }_{\mathcal{T}}{\left\{{\widehat{x}}_j(t)-x_j(t)\right\}}^{2}dt=O_p\left(n^{-\frac{2{\beta }_1}{2{\beta }_1+1}}\right),$$

which achieves the minimax optimal rate.

Next, we derive the convergence rate for the estimated functional F_j. Because the trajectory $\widehat{x}$ is estimated, to establish the optimal rate of convergence, it requires extra theoretical attention, which is related to recent work on errors in variables for lasso-type regressions (Loh and Wainwright 2012; Zhu, Yao, and Zhang 2014). The proof involves several tools for the Rademacher processes (van der Vaart and Wellner 1996), and the concentration inequalities for empirical processes (Talagrand 1996; Yuan and Zhou 2016).

Theorem 4 (Optimal estimation of the functional).

Suppose that $F_j\in \mathcal{H}$, j = 1, …, p, where $\mathcal{H}$ satisfies (8), and the RKHS ${\mathcal{H}}_j$ is embedded to a β₂th order Sobolev space, β₂ > 1. Suppose Assumptions 1 and 2 hold. Then, as long as F_j is not a constant function, the KODE estimate ${\widehat{F}}_j$ from (10) satisfies that, for any j = 1, …, p,

$$\begin{gathered} \underset{{\tau }_{nj}\ge 0}{\text{min}}{\int }_{\mathcal{T}}{\left\{{\widehat{F}}_j(x(t))-F_j(x(t))\right\}}^{2}dt \\ =O_p\left({\left(\frac{n}{\text{log}n}\right)}^{-\frac{2{\beta }_2}{2{\beta }_2+1}}+\frac{\text{log}p}{n}+n^{-\frac{2{\beta }_1}{2{\beta }_1+1}}\right), \end{gathered}$$

which achieves the minimax optimal rate.

This theorem is one of our key results, and we make a few remarks. First, there are three error terms in Theorem 4, which are attributed to the estimation of the interactions, the Lasso estimation, and the measurement errors in variables, respectively. Particularly, the error term $O_p\left(n^{-2{\beta }_1/\left(2{\beta }_1+1\right)}\right)$ arises due to the unobserved x(t), which is instead measured at discrete time points and is subject to measurement errors. Since this error term achieves the optimal rate, it fully characterizes the influence of the estimated $\widehat{x}(t)$ on the resulting estimator ${\widehat{F}}_j$. Moreover, β₁ and β₂ measure the orders of smoothness for estimating x_j and F_j, respectively. They can be different, which makes it flexible when choosing kernels for the estimation procedure. For instance, if there is prior knowledge that x(t) is smooth, we may then choose β₁ > β₂, and the resulting estimator ${\widehat{F}}_j$ achieves a convergence rate of $O_p\left({(n/\text{log}n)}^{-2{\beta }_2/\left(2{\beta }_2+1\right)}+\text{log}p/n\right)$. It is interesting to note that this rate is the same as the rate as if x(t) were directly observed and there were no integral involved in the loss function, for example, in the setting of Lin and Zhang (2006).

Second, there exists a regime-switching phenomenon, depending on the dimensionality p with respect to the sample size n. On one hand, if it is an ultrahigh-dimensional setting, that is, $p>\text{exp}\left[{\left\{n{(\text{log}n)}^{2{\beta }_2}\right\}}^{\frac{1}{2{\beta }_2+1}}\right]$, then the minimax optimal rate in Theorem 4 becomes $O_p\left(\text{log}p/n+n^{-2{\beta }_1/\left(2{\beta }_1+1\right)}\right)$. Here, the first rate O_p(log p/n) matches with the minimax optimal rate for estimating a p-dimensional linear regression when the vector of regression coefficients has a bounded number of nonzero entries (Raskutti, Wainwright, and Yu 2011). Hence, we pay no extra price in terms of the rate of convergence for adopting a nonparametric modeling of F_j in (3), when compared with the more restrictive linear ODE model in (4) (Zhang et al. 2015). On the other hand, if it is a low-dimensional setting, that is, $p\le \text{exp}\left[{\left\{n{(\text{log}n)}^{2{\beta }_2}\right\}}^{\frac{1}{2{\beta }_2+1}}\right]$, then the optimal rate becomes $O_p\left({(n/\text{log}n)}^{-2{\beta }_2/\left(2{\beta }_2+1\right)}+n^{-2{\beta }_1/\left(2{\beta }_1+1\right)}\right)$. Here, the first rate $O_p\left({(n/\text{log}n)}^{-2{\beta }_2/\left(2{\beta }_2+1\right)}\right)$ is the same as the optimal rate of estimating F_j as if we knew a priori that F_j comes from a two-dimensional tensor product functional space, rather than the p-variate functional space $\mathcal{H}$ in (8); see also Lin (2000) for a similar observation.

Third, the optimal rate in Theorem 4 is immune to the “curse of dimensionality”, in the following sense. We introduce p(p − 1) pairwise interaction components to $\mathcal{H}$ in (8), and henceforth, for each x_j(t), j = 1, …, p, it requires to estimate a total of p² functions. A direct application of an existing basis expansion approach, for instance, Brunton, Proctor, and Kutz (2016), leads to a rate of $O_p\left(n^{-O\left(1/p^2\right)}\right)$. This rate degrades fast when p increases. By contrast, we proceed in a different way, where we simultaneously aim for the flexibility of a nonparametric ODE model by letting $\mathcal{H}$ obey a tensor product structure as in (8), while exploiting the interaction structure of the system. As a result, our optimal error bound $O_p\left({(n/\text{log}n)}^{-2{\beta }_2/\left(2{\beta }_2+1\right)}\right)$ does not depend on the dimensionality p.

Finally, the incorporation of the integral, ${\int }_0^{t_i}{F}_j\left(\widehat{x}(t)\right)dt$, in the loss function in (10) makes the estimation error of ${\widehat{F}}_j$ depend on the convergence of $\mathbb{E}{\int }_{\mathcal{T}}{\left\{{\widehat{x}}_j(t)-x_j(t)\right\}}^{2}dt$. As a comparison, if we use the derivative instead of the integration, then the estimation error would depend on the convergence of the derivative, $\mathbb{E}{\int }_{\mathcal{T}}{\left\{d{\widehat{x}}_j(t)/dt-d{x}_j(t)/dt\right\}}^{2}dt$ (Wu et al. 2014). However, it is known that the derivative estimation in the reproducing kernel Hilbert space has a slower convergence rate than the function estimation (Cox 1983). That is, $\mathbb{E}{\int }_{\mathcal{T}}{\left\{d{\widehat{x}}_j(t)/dt-d{x}_j(t)/dt\right\}}^{2}dt$ converges at a slower rate than $\mathbb{E}{\int }_{\mathcal{T}}{\left\{{\widehat{x}}_j(t)-x_j(t)\right\}}^{2}dt$. This demonstrates the advantage of working with the integral in our KODE formulation, and our result echoes the observation for the additive ODE model (Chen, Shojaie, and Witten 2017).

Next, we establish the selection consistency of KODE. Putting all the functionals {F₁, …, F_p} together forms a network of regulatory relations among the p variables {x₁(t), …, x_p(t)}. Recall that, we say x_k is a regulator of x_j, if in (3) F_jk is nonzero, or if F_jkl is nonzero for some l ≠ k. Denote the set of the true regulators and the estimated regulators of x_j(t) by

$$S_j^0=\left\{1\le k\le p:F_{jk}\ne 0,\text{ or }{F}_{jkl}\ne 0\text{ for some}1\le l\ne k\le p\right\},$$

$${\widehat{S}}_j=\{1\le k\le p:{\Vert {\widehat{F}}_{jk}\Vert }_{\mathcal{H}}\ne 0,\text{ or }{\Vert {\widehat{F}}_{jkl}\Vert }_{\mathcal{H}}\ne 0\text{ for some }1\le l\ne k\le p\},$$

respectively, j = 1, …, p. We need some extra regularity conditions on the minimum regulatory effect and the design matrix, which are commonly adopted in the literature of Lasso regression (Zhao and Yu 2006; Ravikumar, Wainwright, and Lafferty 2010). In the interest of space, we defer those conditions to Section S.1.6.2 of the Appendix. The next theorem establishes that KODE is able to recover the true regulatory network asymptotically.

Theorem 5 (Recovery of the regulatory network).

Suppose that $F_j\in \mathcal{H}$, j = 1, …, p, where $\mathcal{H}$ satisfies (8), and the RKHS ${\mathcal{H}}_j$ is embedded to a β₂th order Sobolev space, with β₂ > 1. Suppose Assumption 1, and Assumptions 3, 4, 5 in the Appendix hold. Then, the KODE correctly recovers the true regulatory network, in that, for all j = 1, …, p,

$$\mathbb{P}\left({\widehat{S}}_j=S_j^0\right)\to 1,\hspace{1em}\text{ as }n\to \infty .$$

5. Simulation Studies

5.1. Setup

We study the empirical performance of the proposed KODE using two ODE examples, the enzyme regulatory network in Section 5.2, and the Lotka–Volterra equations in Section 5.3. For a given system of ODEs and the initial condition, we obtain the numerical solutions of the ODEs using the Euler method with step size 0.01. The data observations are drawn from the solutions at an evenly spaced time grid, with measurement errors. To implement KODE, we fit the smoothing spline to estimate x_j(t) in (9) using a Matérn kernel, $K_{\mathcal{F}}\left(x,x^{\prime }\right)=(1+\sqrt{3}\parallel x-x^{\prime }\parallel /v)\text{exp}\left(-\sqrt{3}\Vert x-x^{\prime }\Vert /v\right)$, where the smoothing parameter λ_nj is chosen by GCV, and the bandwidth ν is chosen by 10-fold cross-validation. We compute the integral ${\int }_0^{t_i}{F}_j(\widehat{x}(t))dt$ in (10) numerically with independent sets of 1000 Monte Carlo points. We compare KODE with linear ODE with interactions in (4) (Zhang et al. 2015), and additive ODE in (6) (Chen, Shojaie, and Witten 2017). Due to the lack of available code online, we implement the two competing methods in the framework of Algorithm 1, using a linear kernel for (6), and using an additive Matérn kernel for (6). We evaluate the performance using the prediction error, plus the false discovery proportion and power for edge selection of the corresponding regulatory network. Furthermore, we compare with the family of ODE solutions assuming a known F (Zhang, Cao, and Carroll 2015; Mikkelsen and Hansen 2017) in Section S2.1 of the Appendix. We also carry out a sensitivity analysis in Section S2.2 of the Appendix to study the robustness of the choice of kernel function and initial parameters.

5.2. Enzymatic Regulatory Network

The first example is a three-node enzyme regulatory network of a negative feedback loop with a buffering node (Ma et al. 2009, NFBLB). The ODE system is given in (7) in Section 2.1. Figure 1(a) shows the NFBLB network diagram consisting of the three interacting nodes: x₁ receives the input, x₃ transmits the output, and x₂ plays a regulatory role, leading a negative regulatory link to x₃. We note that, although biological circuits can have more than three nodes, many of those circuits can be reduced to a three-node framework, given that multiple molecules often function as a single virtual node. Moreover, despite the diversity of possible network topologies, NFBLB is one of the two core three-node topologies that could perform adaption in the sense that the system resets itself after responding to a stimulus; see Ma et al. (2009) for more discussion of NFBLB. For the ODE system in (7), we set the catalytic rate parameters of the enzymes as c₁ = c₂ = c₃ = c₅ = c₆ = 10, c₄ = 1, the Michaelis–Menten constants as C₁ = ⋯ = C₆ = 0.1, and the concentration parameters of enzymes as ${\tilde{c}}_1=1$, ${\tilde{c}}_2=0.2$. These parameters achieve the adaption as shown in Figure 1(b). The output node x₃ shows a strong initial response to the stimulus, and also exhibits strong adaption, since its post-stimulus steady state x₃ = 0.052 is close to the prestimulus state x₃ = 0. The input $x_0\in {ℝ}^3$ is drawn uniformly from [0.5, 1.5], with the initial value x(0) = 0, and the measurement errors are iid normal with mean zero and variance ${\sigma }_j^2$. The time points are evenly distributed, t_i = (i − 1)/20, i = 1, …, n. In this example, p = 3, and for each function x_j(t), j = 1, 2, 3, there are p² = 9 functions to estimate, and in total there are 27 functions to estimate under the sample size n = 40.

Figure 2 reports the true and estimated trajectory of x₃(t), with 95% upper and lower confidence bounds, of the three ODE methods, where we use the tensor product Matérn kernel for KODE in (10). The noise level is set as σ_j = 0.1, j = 1, 2, 3, and the results are averaged over 500 data replications. It is seen that the KODE estimate has a smaller variance than the additive and linear ODE estimates. Moreover, the confidence interval of KODE achieves the desired coverage for the true trajectory. In contrast, the confidence intervals of additive and linear ODE models mostly fail to include the truth. This is because there is a discrepancy between the additive and linear ODE model specifications and the true ODE model in (7), and this discrepancy accumulates as the course of the ODE evolves.

Figure 2.

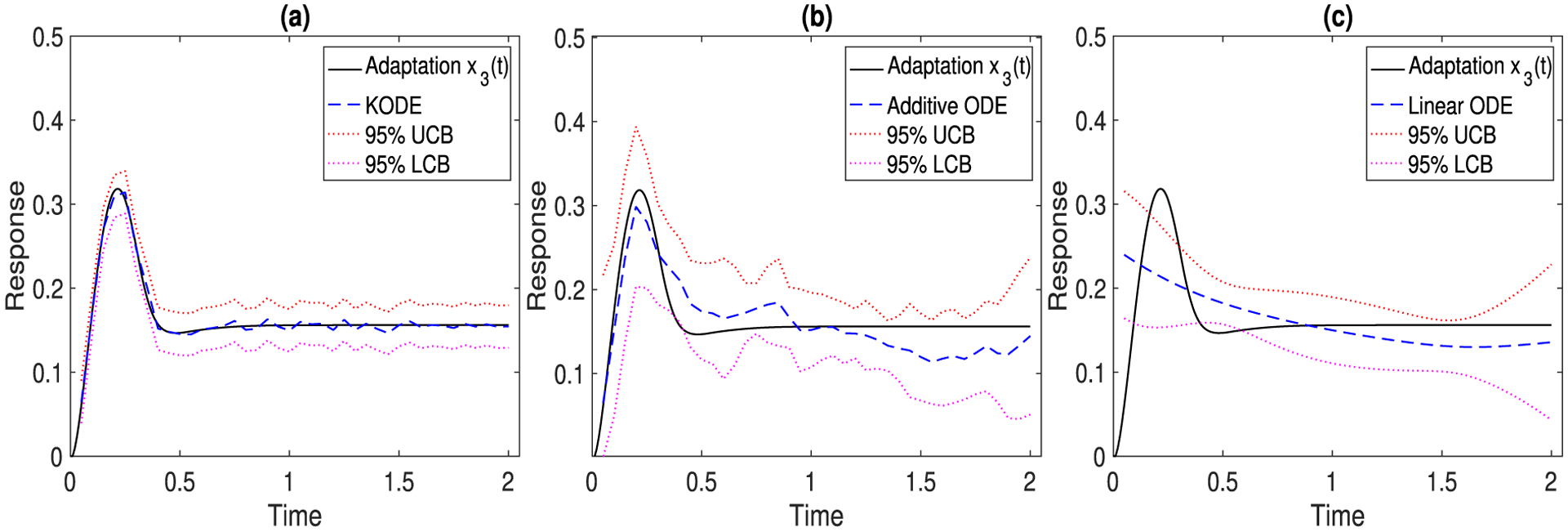
The true (black solid line) and the estimated (blue dashed line) trajectory of x₃(t), with the 95% upper and lower confidence bounds (red dotted lines). The results are averaged over 500 data replications. (a) KODE; (b) additive ODE; (c) linear ODE.

Figure 3 reports the prediction and selection performance of the three ODE methods, with varying noise level σ_j ∈ {0.01, 0.02, …, 0.1}, j = 1, 2, 3. The results are averaged over 500 data replications. The prediction error is defined as the squared root of the sum of predictive mean squared errors for x₁(t), x₂(t), x₃(t) at the unseen “future” time point t = 2. The false discovery proportion is defined as the proportion of falsely selected edges in the regulatory network out of the total number of edges. The empirical power is defined as the proportion of selected true edges in the network. It is seen that KODE clearly outperforms the two alternative solutions in both prediction and selection accuracy. Moreover, we report graphically the sparse recovery of this regulatory network in Section S2.3 of the Appendix.

Figure 3.

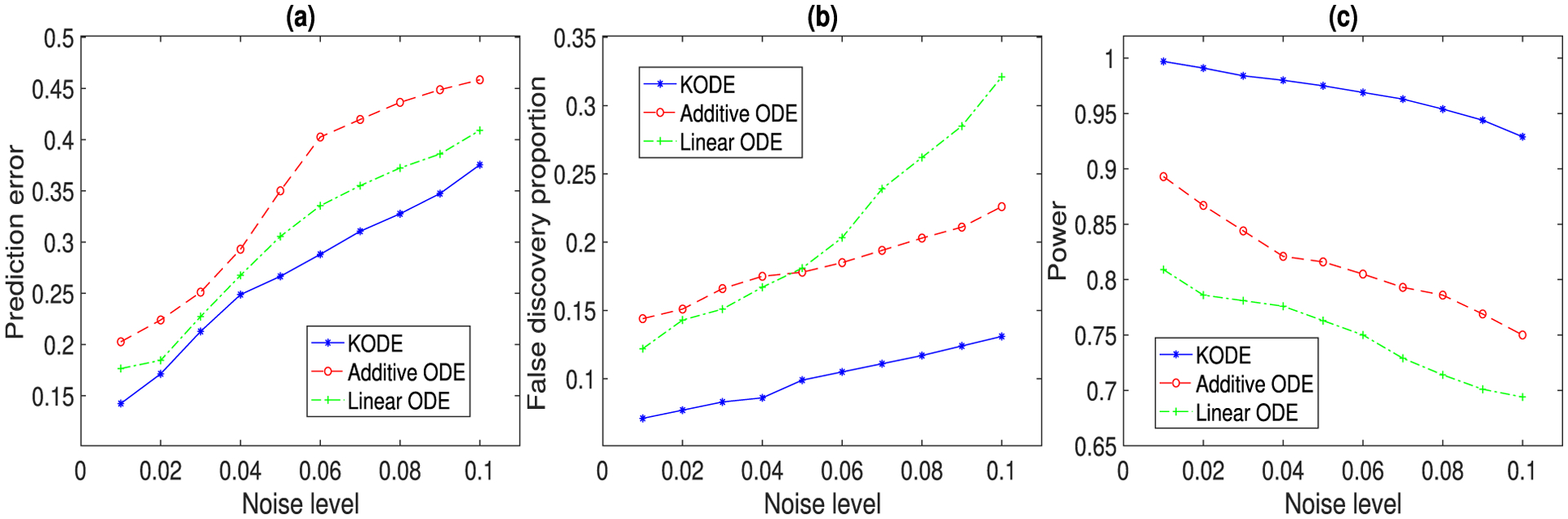
The prediction and selection performance of three ODE methods with varying noise level. The results are averaged over 500 data replications. (a) Prediction error; (b) false discovery proportion; (c) empirical power.

5.3. Lotka–Volterra Equations

The second example is the high-dimensional Lotka–Volterra equations, which are pairs of first-order nonlinear differential equations describing the dynamics of biological systems in which predators and prey interact (Volterra 1928). We consider a 10-node system,

$$\frac{d{x}_{2j-1}(t)}{dt}={\alpha }_{1,j}{x}_{2j-1}(t)-{\alpha }_{2,j}{x}_{2j-1}(t)x_{2j}(t),\frac{d{x}_{2j}(t)}{dt}={\alpha }_{3,j}{x}_{2j-1}(t)x_{2j}(t)-{\alpha }_{4,j}{x}_{2j}(t),$$ (18)

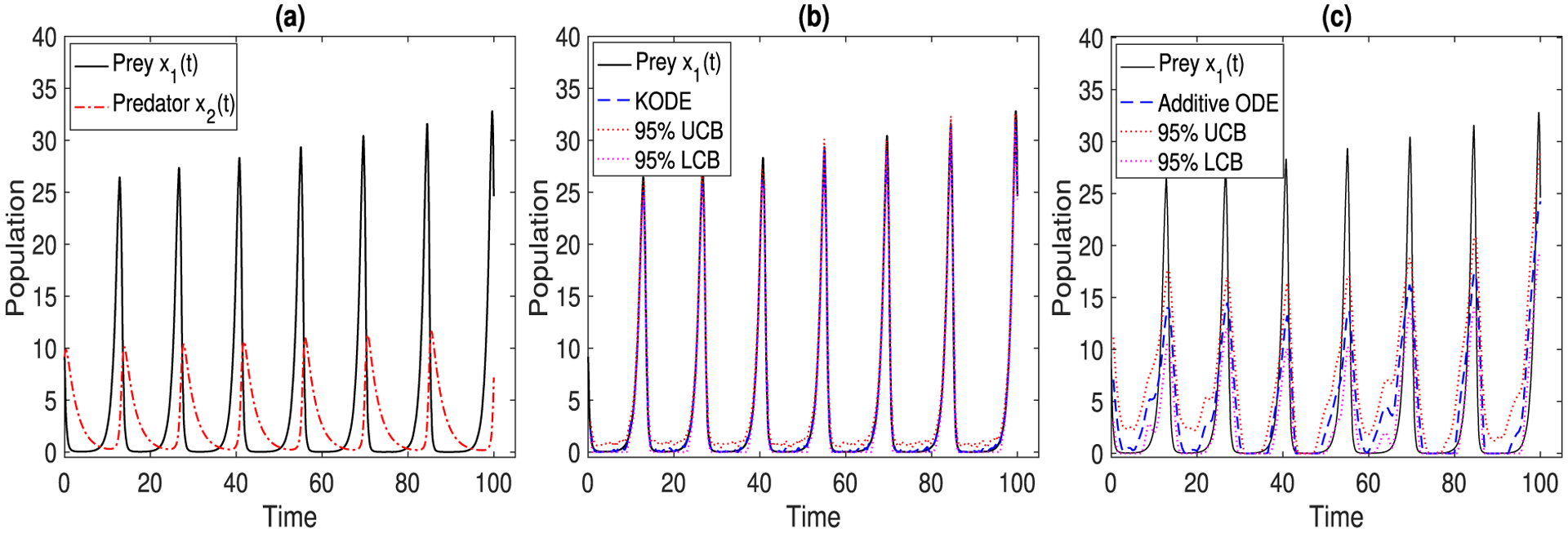
where α_1,j = 1.1 + 0.2(j − 1), α_2,j = 0.4 + 0.2(j − 1), α_3,j = 0.1 + 0.2(j − 1), and α_4,j = 0.4 + 0.2(j − 1), j = 1, …, 5. The parameters α_2,j and α_3,j define the interaction between the two populations such that dx_2j−1(t)/dt and dx_2j(t)/dt are nonadditive functions of x_2j−1 and x_2j, where x_2j−1 is the prey and x_2j is the predator. Figure 4(a) shows an illustration of the interaction between x₁(t) and x₂(t). The input $x_0\in {ℝ}^{10}$ is drawn uniformly from [5, 15]¹⁰, with the initial value x_2j−1(0) = x_2j(0), and the measurement errors are iid normal $N\left(0,{\sigma }_j^2\right)$, where σ_j again reflects the noise level. The time points are evenly distributed in [0, 100] with n = 200. In this example, p = 10, and for each function x_j(t), j = 1, …, 10, there are p² = 100 functions to estimate, and in total there are 1000 functions to estimate under the sample size n = 200.

Figure 4.

(a) The true trajectories of the prey x₁(t) and the predator x₂(t). (b) The estimated trajectory ${\widehat{x}}_1(t)$ (blue dashed line), with the 95% upper and lower confidence bounds (red dotted lines), by KODE. (c) By additive ODE. The results are averaged over 500 data replications.

Figure 4(b) and (c) report the estimated trajectory of x₁(t), with 95% upper and lower confidence bounds, of KODE and additive ODE, where the noise level is set as σ_j = 1, j = 1, …, 10. The confidence interval of KODE achieves a better empirical coverage for the true trajectory compared to that of additive ODE. For this example, we use the linear kernel for KODE in (10), since the functional forms in (18) are known to be linear. For this reason, we only compare KODE with the additive ODE method. Moreover, in the implementation, the estimates ${\widehat{F}}_j\left(\widehat{x}(t)\right)$ are thresholded to be nonnegative to ensure the physical constraint that the number of population cannot be negative. Figure 5 reports the prediction and selection performance of the two ODE methods, with varying noise level σ_j ∈ {1, 2, …, 10}, j = 1, …, 10. All the results are averaged over 500 data replications. It is seen that the KODE estimate achieves a smaller prediction error, and a higher selection accuracy, since KODE allows flexible nonadditive structures, which results in significantly smaller bias and variance in functional estimation as compared to the additive modeling.

Figure 5.

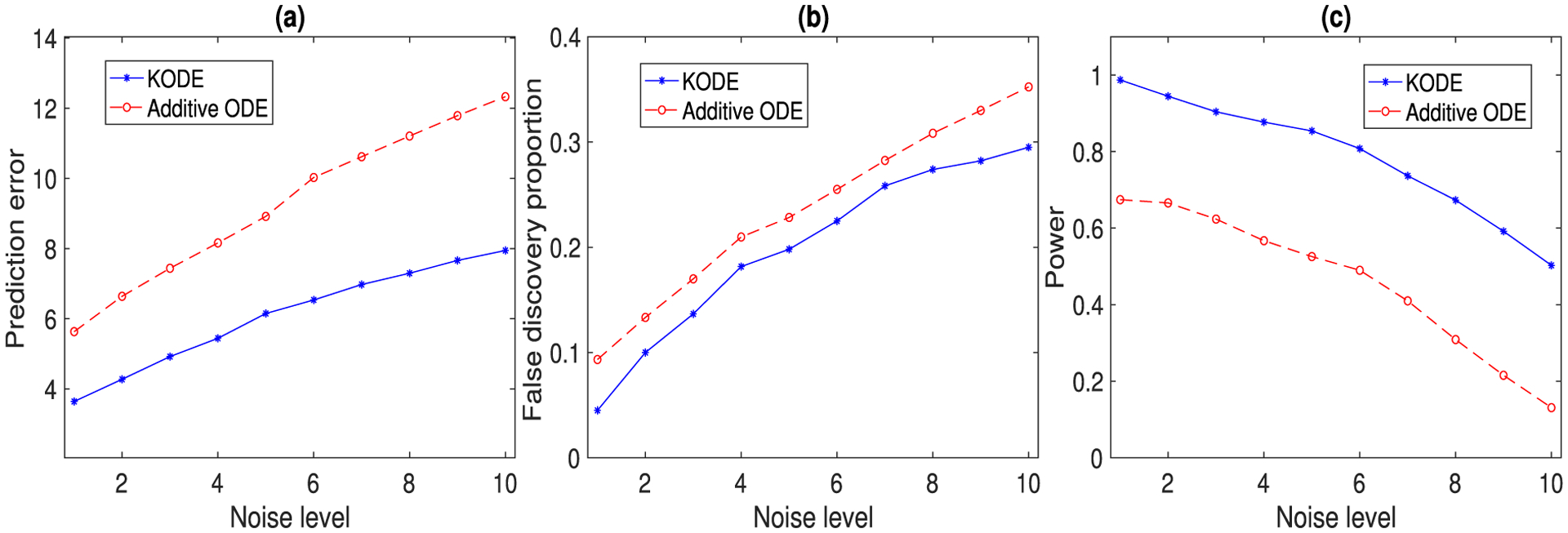
The prediction and selection performance of two ODE methods with varying noise level. The results are averaged over 500 data replications. (a) Prediction error; (b) false discovery proportion; (c) empirical power.

6. Application to Gene Regulatory Network

We illustrate KODE with a gene regulatory network application. Schaffter, Marbach, and Floreano (2011) developed an open-source platform called GeneNetWeaver (GNW) that generates in silico benchmark gene expression data using dynamical models of gene regulations and nonlinear ODEs. The generated data have been used for evaluating the performance of network inference methods in the DREAM3 competition (Marbach et al. 2009), and were also analyzed by Henderson and Michailidis (2014); Chen, Shojaie, and Witten (2017) in additive ODE modeling. GNW extracts two regulatory networks of E.coli (E.coli1, E.coli2), and three regulatory networks of yeast (yeast1, yeast2, yeast 3), each of which has two dimensions, p = 10 nodes and p = 100 nodes. This yields totally 10 combinations of network structures. Figures 6(a) and (b) show an example of the 10-node and the 100-node E.coli1 networks, respectively. The systems of ODEs for each extracted network are based on a thermodynamic approach, which leads to a nonadditive and nonlinear ODE structure (Marbach et al. 2010). Besides, the network structures are sparse; for example, for the 10-node E.coli1 network, there are 11 edges out of 90 possible pairwise edges, and for the 100-node E.coli1 network, there are 125 edges out of 9900 possible pairwise edges. Moreover, for the 10-node network, GNW provides R = 4 perturbation experiments, and for the 100-node network, GNW provides R = 46 experiments. In each experiment, GNW generates the time-course data with different initial conditions of the ODE system to emulate the diversity of gene expression trajectories (Marbach et al. 2009). Figures 6(c)–(f) show the time-course data under R = 4 experiments for the 10-node E.coli1 network. All the trajectories are measured at n = 21 evenly spaced time points in [0, 1]. We add independent measurement errors from a normal distribution with mean zero and standard deviation 0.025, which is the same as the DREAM3 competition and the data analysis done in Henderson and Michailidis (2014) and Chen, Shojaie, and Witten (2017).

Figure 6.

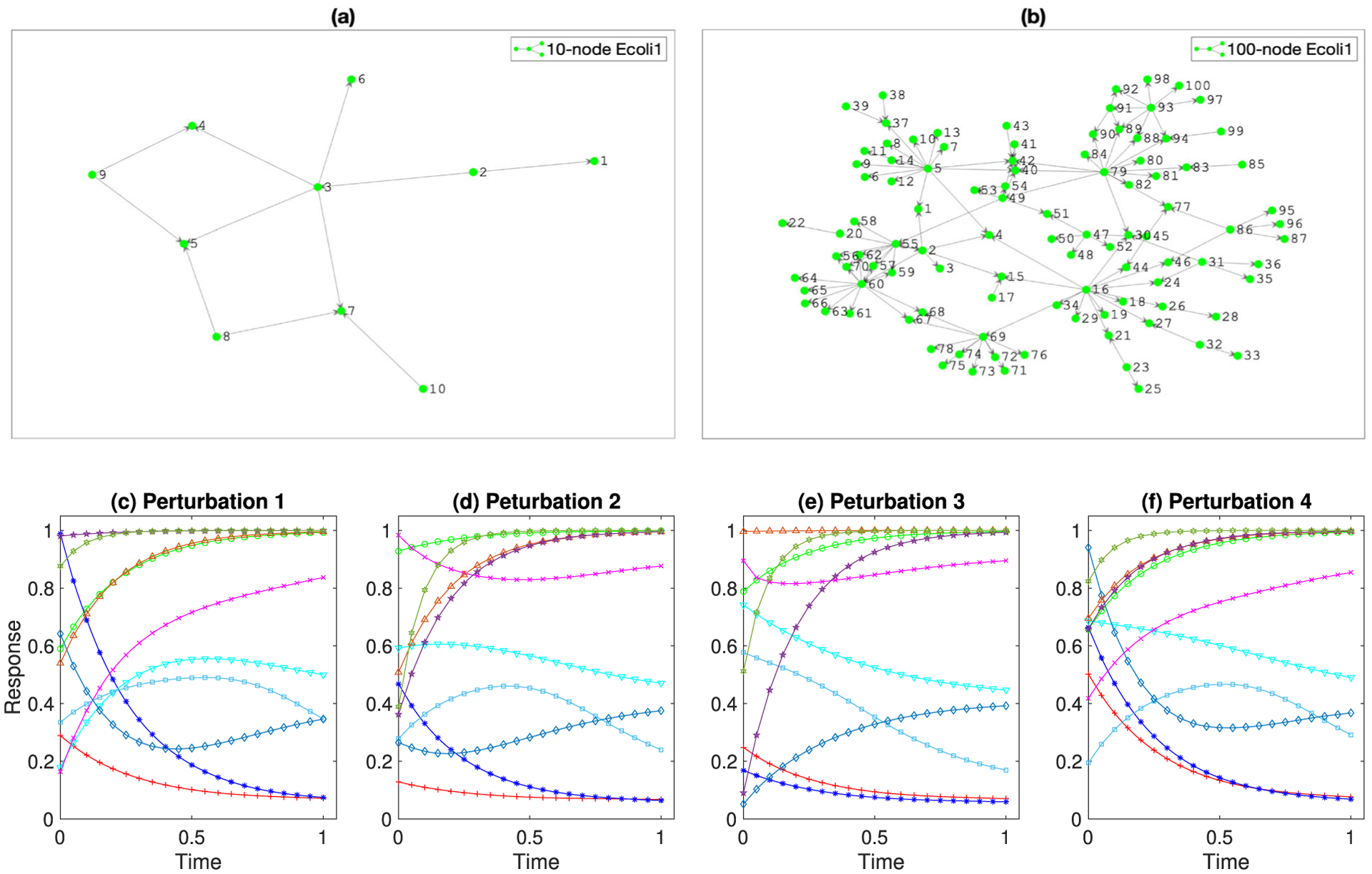
(a) The 10-node E.coli1 network. (b) The 100-node E.coli1 network. (c–f) Four perturbation experiments for the 10-node E.coli1 network, where each experiment corresponds to a different initial condition of the ODE system.

The kernel ODE model we have developed focuses on a single experiment data, but it can be easily generalized to incorporate multiple experiments. Specifically, let $\{y_{ij}^{(r)};i=1,\dots ,n,j=1,\dots ,p,r=1,\dots ,R\}$ denote the observed data from n subjects for p variables under R experiments, with unknown initial conditions $x^{(r)}(0)\in {ℝ}^p$, r = 1, …, R. Then we modify the KODE method in (9) and (10), by seeking $F_j\in \mathcal{H}$ and ${\theta }_{j0}\in ℝ$ that minimize

$$\frac{1}{Rn}\sum _{r=1}^R\sum _{i=1}^n{\left\{y_{ij}^{(r)}-{\theta }_{j0}-{\int }_0^{t_i}{F}_j\left({\widehat{x}}^{(r)}(t)\right)dt\right\}}^2+{\tau }_{nj}\left(\sum _{k=1}^p{\Vert {\mathcal{P}}^k{F}_j\Vert }_{\mathcal{H}}+\sum _{k\ne l,k=1}^p\sum _{l=1}^p{\Vert {\mathcal{P}}^{kl}{F}_j\Vert }_{\mathcal{H}}\right),$$ (19)

where ${\widehat{x}}^{(r)}(t)={\left({\widehat{x}}_1^{(r)}(t),\dots ,{\widehat{x}}_p^{(r)}(t)\right)}^{\top }$ is the smoothing spline estimate obtained by,

$${\widehat{x}}_j^{(r)}(t)=\underset{z_j\in \mathcal{F}}{\text{arg min}}\left\{\frac{1}{n}\sum _{i=1}^n{\left(y_{ij}^{(r)}-z_j\left(t_i\right)\right)}^2+{\lambda }_{nj}{\Vert z_j(t)\Vert }_{\mathcal{F}}^2\right\},j=1,\dots ,p,r=1,\dots ,R.$$

Algorithm 1 can be modified accordingly to work with multiple experiments.

We again compare KODE with the additive ODE (Chen, Shojaie, and Witten 2017) and the linear ODE (Zhang et al. 2015), adopting the same implementation as in the simulations. Since we know the true edges of the generated gene regulatory networks, we use the area under the ROC curve (AUC) as the evaluation criterion. Table 1 reports the results averaged over 100 data realizations for all ten combinations of network structures. It is clearly seen that KODE outperforms both alternative methods in all cases. We further report graphically the sparse recovery of the 10-node E.coli1 network in Section S2.4 of the Appendix. This example shows that our proposed KODE is a competitive and useful tool for ODE modeling. In addition, it also shows that the proposed method can scale up and work with reasonably large networks. For instance, for the network with p = 100 nodes, there are p² = 10,000 functions to estimate, and the sample size is n = 21 with R = 46 perturbations.

Table 1.

The area under the ROC curve, and the 95% confidence interval, for 10 combinations of network structures from GNW.

	p = 10			p = 100
	KODE	Additive ODE	Linear ODE	KODE	Additive ODE	Linear ODE
E.coli1	0.582	0.541	0.460	0.711	0.677	0.640
	(0.577, 0.587)	(0.535, 0.547)	(0.453, 0.467)	(0.708, 0.714)	(0.672, 0.682)	(0.637, 0.643)
E.coli2	0.662	0.632	0.562	0.685	0.659	0.533
	(0.658, 0.666)	(0.625, 0.639)	(0.555, 0.569)	(0.681, 0.689)	(0.652, 0.666)	(0.527, 0.539)
Yeast1	0.603	0.541	0.436	0.619	0.589	0.569
	(0.599, 0.607)	(0.536, 0.546)	(0.430, 0.442)	(0.616, 0.622)	(0.581, 0.597)	(0.562, 0.576)
Yeast2	0.599	0.562	0.536	0.606	0.588	0.541
	(0.595, 0.603)	(0.555, 0.570)	(0.530, 0.542)	(0.603, 0.609)	(0.582, 0.594)	(0.536, 0.546)
Yeast3	0.612	0.569	0.487	0.621	0.613	0.609
	(0.608, 0.616)	(0.564, 0.573)	(0.481, 0.493)	(0.617, 0.625)	(0.607, 0.619)	(0.605, 0.613)

NOTE: The results are averaged over 100 data replications. Boldface indicates the method with larger AUC.

7. Conclusion and Discussion

In this article, we have developed a new reproducing kernel-based approach for a general family of ODE models that learn a dynamic system from noisy time-course data. We employ sparsity regularization to select individual functionals and uncover the underlying regulatory network, and we derive the post-selection confidence interval for the estimated signal trajectory. Our proposal is built upon but also extends the smoothing spline analysis of variance framework. We establish the theoretical properties of the method, while allowing the number of functionals to be either smaller or larger than the number of time points.

In numerous scientific applications, ODE is often employed to understand the regulatory effects and causal mechanisms within a dynamic system under interventions. Our proposed KODE method can be applied for this very purpose. There are different formulations of causal modeling for dynamic systems in the literature. We next consider and illustrate with two relatively common scenarios, one regarding dynamic causal modeling (DCM) under experimental stimuli (Friston, Harrison, and Penny 2003), and the other about kinetic modeling that is invariant across heterogeneous experiments (Pfister, Bauer, and Peters 2019).

The first scenario concerns DCM that infers the regulatory effects within a dynamic system under experimental stimuli (Friston, Harrison, and Penny 2003). Specifically, the DCM characterizes the variations of the state variables $x\left(t\right)={\left(x_1(t),\dots ,x_p(t)\right)}^{\top }\in {ℝ}^p$ under the stimulus inputs $u\left(t\right)={\left(u_1(t),\dots ,u_p(t)\right)}^{\top }\in {ℝ}^q$ via a set of ODEs, dx(t)/dt = F(x(t), u(t)), where the functional F is modeled by a bilinear form,

$$F_j(x(t),u(t))={\theta }_{j0}+\sum _{k=1}^p{\theta }_{jk}^{(1)}{x}_k(t)+\sum _{l=1}^q{\theta }_{jl}^{(2)}{u}_l(t)+\sum _{k=1}^p\sum _{l=1}^q{\theta }_{jkl}^{(1,2)}{x}_k(t)u_l(t),j=1,\dots ,p.$$ (20)

In this model, ${\theta }_{jk}^{(1)}\in ℝ$ reflects the strength of intrinsic connection from x_k(t) to x_j(t), ${\theta }_{jl}^{(2)}\in ℝ$ reflects the effect of the lth input stimulus u_l(t) on x_j(t), and ${\theta }_{jkl}^{(1,2)}\in ℝ$ reflects the influence of u_l(t) on the directional connection between x_k(t) and x_j(t), j, k = 1, …, p, l = 1, …, q. Note that ${\theta }_{jk}^{(1)}$ and ${\theta }_{kj}^{(1)}$ can be different, and thus the effect from x_k(t) to x_j(t) and that from x_j(t) to x_k(t) can be different. Similarly, ${\theta }_{jkl}^{(1,2)}$ and ${\theta }_{kjl}^{(1,2)}$ can be different. As such, model (20) encodes a directional network, and under certain conditions, a causal network. DCM has been widely used in biology and neuroscience (see, e.g., Friston, Harrison, and Penny 2003; Zhang et al. 2015, 2017; Cao, Sandstede, and Luo 2019).

We can combine the proposed KODE with the DCM model (20) straightforwardly. Such a combination allows us to estimate and infer the causal regulatory effects under experimental stimuli without specifying the forms of the functionals F. This is appealing, as there have been evidences suggesting that the regulatory effects can be nonlinear (Buxton et al. 2004; Friston et al. 2019). More specifically, we model F such that,

$$F_j(x(t),u(t))={\theta }_{j0}+\sum _{k=1}^p{F}_{jk}^{(1)}\left(x_k(t)\right)+\sum _{l=1}^q{F}_{jl}^{(2)}\left(u_l(t)\right)+\sum _{k=1}^p\sum _{l=1}^q{F}_{jkl}^{(1,2)}\left(x_k(t),u_l(t)\right),j=1,\dots ,p.$$ (21)

Similar as the tensor product space defined in (8), let ${\mathcal{H}}_k^{(1)}$ and ${\mathcal{H}}_l^{(2)}$ denote the space of functions of x_k(t) and u_l(t) with zero marginal integral, respectively. We impose that the functionals F_j, j = 1, …, p in (21) are located in the following space,

$$\mathcal{H}=\left\{1\right\}\oplus \sum _{k=1}^p{\mathcal{H}}_k^{(1)}\oplus \sum _{l=1}^q{\mathcal{H}}_l^{(2)}\oplus \sum _{k=1}^p\sum _{l=1}^q\left({\mathcal{H}}_k^{(1)}\otimes {\mathcal{H}}_l^{(2)}\right).$$

Parallel to (20), the functions $F_{jk}^{(1)}$, $F_{jl}^{(2)}$ and $F_{jkl}^{(1,2)}$ in (21) capture the regulatory effects, and together, they encode a directional network. Moreover, Algorithm 1 of KODE is directly applicable to estimate $F_{jk}^{(1)}$, $F_{jl}^{(2)}$, and $F_{jkl}^{(1,2)}$. As we have shown in our simulations, the DCM model (21) based on KODE should outperform (20) that is based on linear ODE.

The second scenario concerns learning the causal structure of kinetic systems by identifying a stable model from noisy observations generated from heterogeneous experiments. Pfister, Bauer, and Peters (2019) proposed the CausalKinetiX method, where the main idea is to optimize a noninvariance score to identify a causal ODE model that is invariant across heterogeneous experiments. Again, we can combine the proposed KODE with CausalKinetiX to learn the causal structure, while balancing between predictability and causality of the ODE model, and extending from a linear ODE model to a more flexible ODE model. We refer to this integrated method as KODE-CKX.

More specifically, consider R heterogeneous experiments, which stem from interventions such as manipulations of initial or environmental conditions. Following Algorithm 1 of KODE, we obtain ${\widehat{\theta }}_j^{(r)}$ for each experiment r ∈ {1, …, R}, and j = 1, …, p. Let $M_j^{(r)}\subseteq \mathcal{M}$ denote the index set of the nonzero entries of the sparse estimator ${\widehat{\theta }}_j^{(r)}$. We propose the following four-step procedure to score each model $M_j^{(r)}$. In the first step, we obtain the smoothing spline estimate ${\widehat{x}}_j^{(r)}(t)$ by (9) using the data from the rth experiment. In the second step, we apply Algorithm 1 to compute ${\widehat{F}}_j^{(r)}$, by setting κ_nj = 0, restricting ${\theta }_j\in M_j^{(r)}$, and using the data from all other experiments except for the rth experiment. Here leaving out the rth experiment is to ensure a good generalization capability. In the third step, we estimate the signal trajectory under the derivative constraint,

$${\tilde{x}}_j^{(r)}(t)=\underset{z_j\in \mathcal{F}}{\text{arg min}}\left\{\frac{1}{n}\sum _{i=1}^n{\left\{y_{ij}-z_j\left(t_i\right)\right\}}^2+{\lambda }_{nj}{\Vert z_j(t)\Vert }_{\mathcal{F}}^2\right\},\text{ such that }{\tilde{x}}_j^{(r)}\left(t_i\right)={\widehat{F}}_j^{(r)}\left({\widehat{x}}_j^{(r)}\left(t_i\right)\right),$$ (22)

for i = 1, …, n, j = 1, …, p. In the last step, similar as CausalKinetiX, we obtain for each model $M_j^{(r)}\subseteq \mathcal{M}$ the noninvariance score,

$$\text{NS}\left(M_j^{(r)}\right)\equiv \frac{1}{R}\sum _{r=1}^R\frac{{\text{RSS}}_B^{(r)}-{\text{RSS}}_A^{(r)}}{{\text{RSS}}_A^{(r)}},$$

where ${\text{RSS}}_A^{(r)}=n^{-1}{{\sum }_{i=1}^n\left\{y_{ij}^{(r)}-{\widehat{x}}_j^{(r)}\left(t_{ij}\right)\right\}}^2$, and ${\text{RSS}}_B^{(r)}=n^{-1}{{\sum }_{i=1}^n\left\{y_{ij}^{(r)}-{\tilde{x}}_j^{(r)}\left(t_{ij}\right)\right\}}^2$ are the residual sums of squares based on ${\widehat{x}}_j^{(r)}(t)$ and ${\tilde{x}}_j^{(r)}(t)$, respectively. Due to the additional constraint in (22), ${\text{RSS}}_B^{(r)}$ is always larger than ${\text{RSS}}_A^{(r)}$. Following Pfister, Bauer, and Peters (2019), the model $M_j^{(r)}\subseteq \mathcal{M}$ with a small score $\text{NS}\left(M_j^{(r)}\right)$ is predictive and invariant. Such an invariant ODE model allows researchers to predict the behavior of the dynamic system under interventions, and it is closely related to the causal mechanism of the underlying dynamic system from the structural casual model and modularity perspective (Rubenstein et al. 2018; Pfister, Bauer, and Peters 2019). Compared to CausalKinetiX, our proposed KODE-CKX further extends the linear ODE to a general class of nonlinear and nonadditive ODE.

To verify the empirical performance of KODE-CKX and to compare with CausalKinetiX, we consider the 100-node E.coli1 gene regulatory network example in Section 6. Figure 7 compares the models with the smallest noninvariance score from KODE-CKX and CausalKinetiX, respectively, based on 100 data replications. Comparing Figures 7(a) and (b), it is seen that in the majority of cases, KODE-CKX is able to recover the causal parents, and it outperforms CausalKinetiX by achieving a smaller number of false discoveries. Here, the measurement errors were drawn from a normal distribution with mean zero and standard deviation 0.025, the same setup as in Section 6. We next further evaluate the performance of the two methods when we vary the standard deviation of the measurement errors. Figure 7(c) reports the AUC averaged over 100 data replications. It is seen again that, for all noise levels, KODE-CKX performs better than CausalKinetiX.

Figure 7.

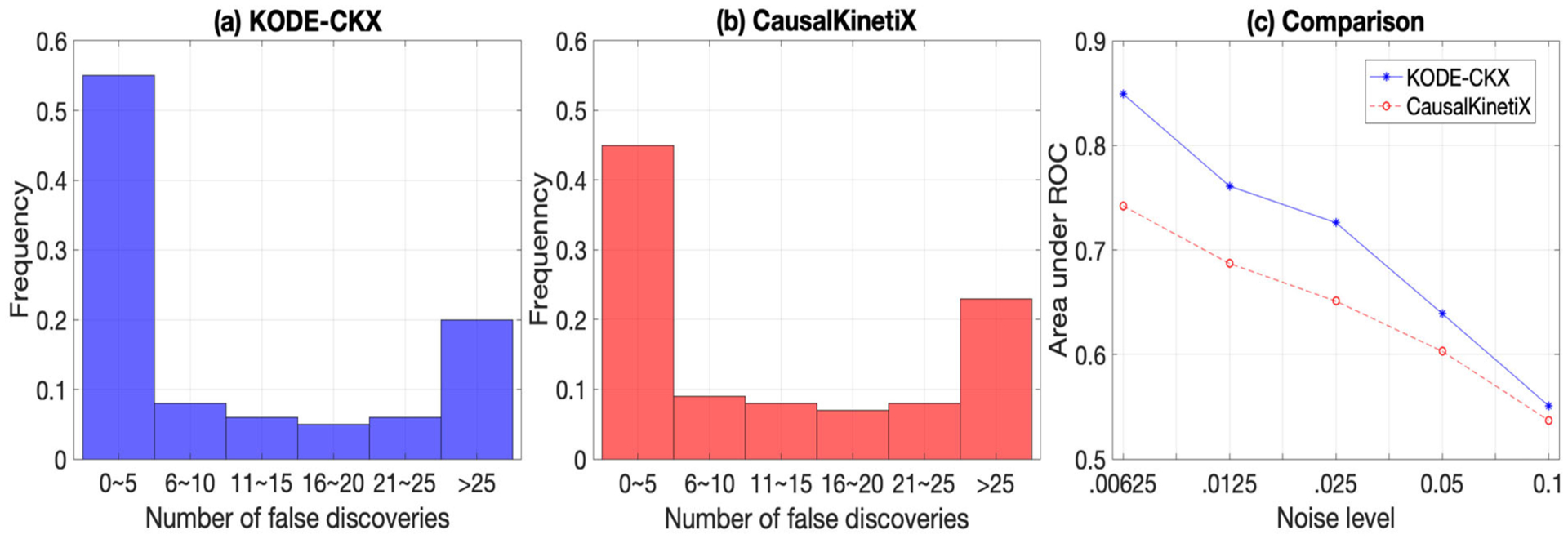
The selection performance of KODE-CKX and CausalKinetiX. The results are averaged over 100 data replications. (a) Number of false discoveries in the estimated model based on KODE-CKX; (b) number of false discoveries in the estimated model based on CausalKinetiX; (c) area under ROC under different noise levels.

In summary, our proposed KODE is readily applicable to numerous scenarios to facilitate the understanding of the regulatory causal mechanisms within a dynamic system from noisy data under interventions.