Curvature gradient drives polarized tissue flow in the Drosophila embryo

Significance

Much is known about how genetic prepatterning of the embryo defines the initial instructions for morphogenesis, but how these instructions are deployed in a specific mechanical and geometrical environment is unknown. In our manuscript, we use Drosophila embryos to explore how genetics, mechanics, and geometry interact to drive polarized (directional) tissue flow. Through a combination of experimental and modeling approaches, we show that previously proposed mechanisms cannot account for the tissue flows observed during the early stages of Drosophila morphogenesis. Instead, we reveal a mechanism whereby polarized flows arise from the interaction between myosin-driven tissue contraction and the curvature of the tissue imposed by the shape of the egg.

Abstract

Tissue flow during morphogenesis is commonly driven by local constriction of cell cortices, which is caused by the activation of actomyosin contractility. This can lead to long-range flows due to tissue viscosity. However, in the absence of cell-intrinsic polarized forces or polarity in forces external to the tissue, these flows must be symmetric and centered around the region of contraction. Polarized tissue flows have been previously demonstrated to arise from the coupling of such contractile flows to points of increased friction or adhesion to external structures. However, we show with experiments and modeling that the onset of polarized tissue flow in early Drosophila morphogenesis occurs independent of adhesion and is instead driven by a geometric coupling of apical actomyosin contractility to tissue curvature. Particularly, the onset of polarized flow is driven by a mismatch between the position of apical myosin activation and the position of peak curvature at the posterior pole of the embryo. Our work demonstrates how genetic and geometric information inherited from the mother interact to create polarized flow during embryo morphogenesis.

Morphogenesis is the process by which organisms develop from a simple fertilized egg to an adult with complex form and function. This process depends keenly on the dynamics of the underlying biological tissues, which itself arises from cellular attributes such as cell–cell adhesion, cortical tension, osmotic pressure, elasticity, and viscosity, all of which can be passively and actively controlled in space and time (1, 2). Tissue-scale effects can arise as a result of local changes to these cellular attributes. For example, tissue invagination emerges from apical constriction of well-defined groups of cells (3) such as in the mesoderm or endoderm of Caenorhabditis elegans (4, 5), Drosophila (6), sea urchin (7), or ascidians (8, 9). Similarly, apical constriction has been shown to drive cell shape changes during vertebrate development (10).

Tissue flows are ubiquitous in animal development, especially during embryogenesis and organogenesis. Tissue flow may be symmetric or polarized (asymmetric and vectorial) depending on the pattern and polarity of internal active stresses and on the existence of external polarized active stress acting on the tissue (2). When no external polarized force exists, flow is intrinsically symmetric. Cells may converge toward a group of constricting cells such as on either side of the Drosophila mesoderm (11). Alternatively, anisotropic forces driving cell division can give rise to local divergent flow due to bipolar cell displacement (12, 13) or tissue extension (14). These two types of symmetric flows may coexist, perpendicular to each other, during the process of so-called convergent extension. During this process, cell intercalation causes local divergent flow and perpendicular convergence due to junction shrinkage along one axis and junction extension along the perpendicular axis (15–22). In contrast, the emergence of polarized flow depends upon the presence of an external acting force. For instance, contraction of the hinge at the proximal end of the developing Drosophila pupal wing and anchoring of the wing at its distal tip drive polarized tissue flow and global extension of the wing (13, 23, 24). Similarly, a supracellular tensile ring in the posterior of chick epiblast drives nonlocal polarized rotational flows in the whole embryonic field during primitive streak formation (25).

During early Drosophila morphogenesis, a single layer of epithelial cells is formed by the simultaneous cellularization of the 6,000 nuclei composing the syncytial blastoderm (26). Subsequently, at the onset of gastrulation, this initially static tissue begins to flow and thereby initiates the process of axis elongation along the antero-posterior axis (15, 16). Most notably, the tissue in the posterior of the embryo, called the endoderm, undergoes a polarized flow toward the dorsal-anterior side of the embryo (17, 27) (Movie S1 and Fig. 1A). This sharp onset of polarized flow makes the Drosophila embryo a powerful system to study the physical mechanisms that drive tissue flow.

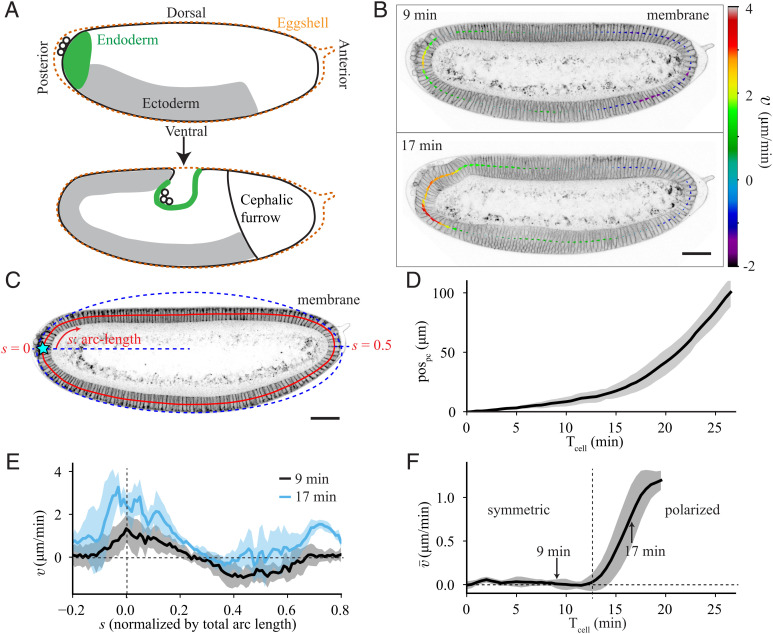
Fig. 1.

Quantification of tissue flow during early Drosophila morphogenesis. (A) Cartoons of Drosophila embryo (Top) at an early stage, during cellularization, and (Bottom) approximately 30 min later. (B) Sagittal plane of an embryo imaged with membrane marker GAP43::mScarlet at 9 min and 17 min after the cellularization front passes the nuclei in the dorsal posterior (T_cell = 0). The arrows show the tangential velocity of the tissue along the midline, extracted using particle image velocimetry. (C) Two-photon image of the sagittal plane of an embryo imaged with GAP43::mScarlet. The red line denotes the midline of the epithelium. The arc-length (s) increases in the clockwise direction and is normalized to the total length of the midline. The blue dashed line represents an elliptical fit to the apical surface of the epithelium used to determine the location of s = 0 at the posterior pole (Materials and Methods). (D) Quantification of the pole cell position (pos_pc, defined in Materials and Methods) as a function of time after T_cell = 0, averaged over 6 embryos. (E) Spatial profile of tangential tissue velocity ($v$) along the midline at the same times as in C, averaged over 5 embryos. (F) Spatial average of the tangential velocity ($\overline{v}$) as a function of time. Vertical dashed line marks the onset of polarized flow. Average performed over 5 embryos. All scale bars are 50 μm. Error bars represent the SD.

It is so far unclear what creates this early polarized flow in the Drosophila embryo. One possibility is that it might be coupled to and dependent on other processes during early Drosophila morphogenesis, such as mesoderm invagination on the ventral side (11), germband extension along the lateral side (17), or the cephalic furrow in the anterior (28). Indeed, existing studies have shown that most of the embryonic tissue flow can be accurately predicted from the pattern of nonmuscle Myosin-II (hereafter myosin) localization and polarization (29). However, earlier studies revealed that an additional force arising near the posterior pole must contribute to driving tissue flows, as evidenced by gradients of cell shape (17, 27) and mechanical stresses (17), as well as genetic and mechanical perturbations (17, 30). For instance, blocking endoderm invagination (as in a Torso mutant) entirely blocks whole-embryo elongation (17). Moreover, the early polarized flow of the endoderm is independent of the abovementioned processes, as demonstrated by embryos with simultaneously blocked mesoderm invagination [twist, snail (31)], germband extension, and cephalic furrow formation [eve (32)] (Movie S2 and SI Appendix, Fig. S1 A and B). Hence, the question remains as to what causes the first polarized tissue flow of the Drosophila epithelium and initiation of axis elongation.

Results

Drosophila Morphogenesis Begins with Symmetric Tissue Flow That Becomes Polarized.

To understand what drives tissue flow in early Drosophila morphogenesis, we first quantified the flow to determine how it evolves in time. To do so, we performed live imaging of Drosophila embryos using a two-photon microscope to capture the sagittal plane that cuts through the center of the embryo (Fig. 1 B and C and Materials and Methods). We tracked the position of the pole cells (pos_pc) to quantify the motion of the posterior tissue (Movie S3 and Materials and Methods), which revealed that there is an initially slow flow of the posterior, which speeds up over time (Fig. 1D).

We also quantified the spatial profile of the flow in the epithelium by performing particle image velocimetry on subsequent frames and extracting the velocity of the flow tangential to the midline of the epithelium ($v$; Fig. 1 B and C and Materials and Methods). At each time, the tangential velocity (Fig. 1E) can be spatially averaged to give a single value that describes the global polarity of the flow ($\overline{v}$; Fig. 1F). If there is as much clockwise (positive) flow as counterclockwise (negative) flow, the average is zero, and the flow is considered symmetric (as at T_cell = 9 min). If there is more clockwise flow than counterclockwise flow, the average will be positive, indicating that the flow is polarized (as at T_cell = 17 min). Averaging the velocity revealed that there are two distinct phases of flow: a symmetric flow for approximately the first 12 min after the cellularization front passes the nuclei (T_cell = 0, Materials and Methods), followed by the onset of polarized flow with average velocity that increases in time (Fig. 1F).

When we performed the same quantifications on embryos mutant for eve, twist, and snail (hereafter ets), which have blocked mesoderm invagination, germband extension, and cephalic furrow formation (Movie S2 and SI Appendix, Fig. S1 A and B), we still saw this transition to polarized flow (SI Appendix, Fig. S1 C and D). The timing of the transition was even slightly earlier in ets embryos than in wildtype, likely due to the lack of ventral pulling from the mesoderm invagination, as evidenced by the increased flow in the ventral-anterior region of the embryo (−0.2 < s < 0; SI Appendix, Fig. S1 E and F). This clearly demonstrates that the polarized flow does not depend on myosin polarization in the germband or on geometric constraints imposed by the cephalic furrow as previously predicted (28, 29). This led us to two main questions: What physical mechanisms drive tissue flow in the early Drosophila embryo? And what mechanism is involved in the transition from symmetric to polarized flow?

Symmetric and Polarized Tissue Flows Arise from Basal and Apical Myosin, Respectively.

Myosin is known to be a common tissue-intrinsic driver of flow in many biological tissues (1, 33). We therefore imaged the myosin distribution in the embryo as a function of time to determine its impact on tissue flow. In wildtype embryos (Fig. 2 A, Top row), there are two distinct populations of myosin: one on the apical side of the cells and the other on the basal side.

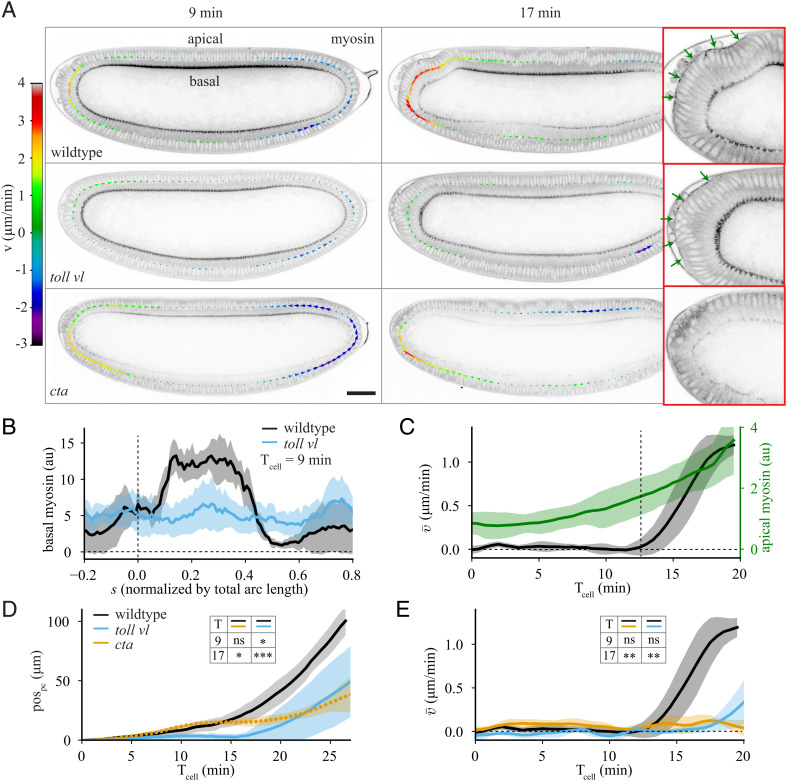
Fig. 2.

Impact of apical and basal myosin on tissue flow. (A) Sagittal plane of an embryo imaged with Myosin-II (myosin) marker spaghetti squash (sqh)::GFP at 9 min and 17 min after T_cell = 0 for (Top) wildtype, (Middle) toll vl mutant, and (Bottom) cta mutant embryos. The arrows show the tangential velocity of the tissue along the midline. The panels on the right show a zoomed view of the posterior at T_cell = 17 min with apical myosin indicated with green arrows. (B) Spatial profile of basal myosin intensity at T_cell = 9 min for wildtype (black) and toll vl mutant (blue) embryos. Average performed over 5 wildtype and 6 toll vl mutant embryos. (C) Average of apical myosin over the posterior of the embryo (−0.1 < s < 0.15; green) and spatial average of the tangential velocity as a function of time (black) for 5 wildtype embryos. Vertical dashed line marks the onset of polarized flow. (D) pos_pc as a function of time for wildtype, toll vl, and cta embryos. Average performed over 6 wildtype, 7 toll vl, and 7 cta embryos. (E) Spatial average of the tangential velocity as a function of time. Average performed over 5 wildtype, 6 toll vl, and 5 cta embryos. All scale bars are 50 μm. Error bars represent the SD. Insets in D and E show results of two-tailed unpaired t tests comparing wildtype, toll vl, and cta at T_cell = 9 and 17 min. ns, not significant; *P <0.05; **P < 0.01; ***P < 0.001.

During the symmetric phase of flow, there is no apical myosin activation, but there is a strong accumulation of basal myosin (Fig. 2 A, Top Left), associated with the process of cellularization (26). The progression of the furrow canal is known to depend on the contractility of this pool of basal myosin (34–36). It is, however, likely that the mechanical impact of this basal myosin contraction is lower than that of apical myosin due to the very high density of the actin network that decreases actin network deformation/contraction (37). Cellularization completes first on the ventral side of the embryo, causing more basal myosin dorsally than ventrally (Fig. 2B), which coincides with the center of the domain of symmetric tissue flow (SI Appendix, Fig. S2A). This led us to the hypothesis that nonuniformity of basal myosin could drive the symmetric phase of tissue flow.

To test this hypothesis, we used a mutation that removes the dorsal–ventral specification of the embryo, and leads the entire embryo to act as ventrolateral tissue (38) (toll  ^rm9/toll^rm10 hereafter toll vl; Fig. 2 A, Middle row). This makes the embryo rotationally symmetric about its anterior–posterior axis (SI Appendix, Fig. S2B), which in turn removes the dorsal–ventral difference in basal myosin (Fig. 2B and Movie S5). In toll vl embryos, the posterior tissue does not always flow dorsally but instead is significantly more likely than wildtype to flow toward the ventral or lateral directions (SI Appendix, Fig. S2C and Movie S4). To quantify the flow in the imaging plane, we analyzed only embryos that flow dorsally. Tracking the pole cells in these mutants revealed that the early, symmetric flow is almost completely halted (Fig. 2D), confirming that the symmetric flow observed is driven by the increased activation of basal myosin on the dorsal side of the embryo. These results coincide well with previous work from Streichan et al. (29), who showed that twist mutant embryos, which have a strong reduction in DV asymmetry of basal myosin, show a strong reduction of tissue movement towards the dorsal side of the embryo during early stages of morphogenesis.

We next considered what drives the polarized flow that occurs following the symmetric phase of flow. Around the time where the transition occurs, the levels of basal myosin begin to decrease and there is a localized accumulation of apical myosin in the dorsal posterior (Fig. 2 A, Top Right and Fig. 2C). To test whether the polarized flow requires this posterior pool of apical myosin, we strongly downregulated all apical myosin in the embryo using a mutation in the gene encoding for the G protein Gɑ_12/13 (known as Concertina (Cta) in Drosophila), which is required specifically for medial apical myosin recruitment (39, 40) (Fig. 2 A, Bottom Row and Movie S5). Quantifying the flow by pole cell tracking (Fig. 2D) and by averaging epithelial velocity (Fig. 2E) showed that the symmetric flow is similar to wildtype but that the polarized flow is strongly suppressed.

Based on these observations, we concluded that the symmetric phase of flow requires the nonuniformity of basal myosin and the polarized flow requires apical myosin. Since polarized tissue flow is normal in ets mutants in which mesoderm invagination and germband extension are blocked, we concluded that apical myosin is required strictly in the posterior region of the embryo and not in other adjacent tissues. It is known that the main effect of myosin accumulation is to drive contraction of the acto-myosin network inside cells (1, 33). We therefore decided to investigate whether the observed flow dynamics arise solely due to tissue contraction driven by these two different pools of myosin.

Myosin-Driven Tension-Based Model Explains the Symmetric Flow.

To gain mechanistic insights into the process driving the flow, we decided to test our hypotheses using a combination of experiments and modeling. Our aim was to understand the embryo flow dynamics on the tissue scale. We therefore chose to use a model that considers collective cellular behavior rather than individual cellular processes. Because the strain rates measured during this phase of development do not surpass approximately 1/50 min⁻¹ (SI Appendix, Fig. S3 A and B), we neglected elastic stresses, which are expected to relax much faster, on the time scale of approximately 2 to 5 min (41). Finally, we focused on the flow within a sagittal section of the embryo, which we described by a continuous, thin 1D membrane. These simplifications allowed us to compare our sagittal observations of embryos in two-photon microscopy to a model of a 1D thin active fluid (42, 43) (SI Appendix), which takes into account tissue viscosity (describing pushing and pulling forces that locally arise from flows compressing and extending the tissue, respectively), friction with the vitelline membrane (part of the eggshell that surrounds the embryo), and myosin-driven spatially-dependent active tension (equation (1) in Fig. 3A).

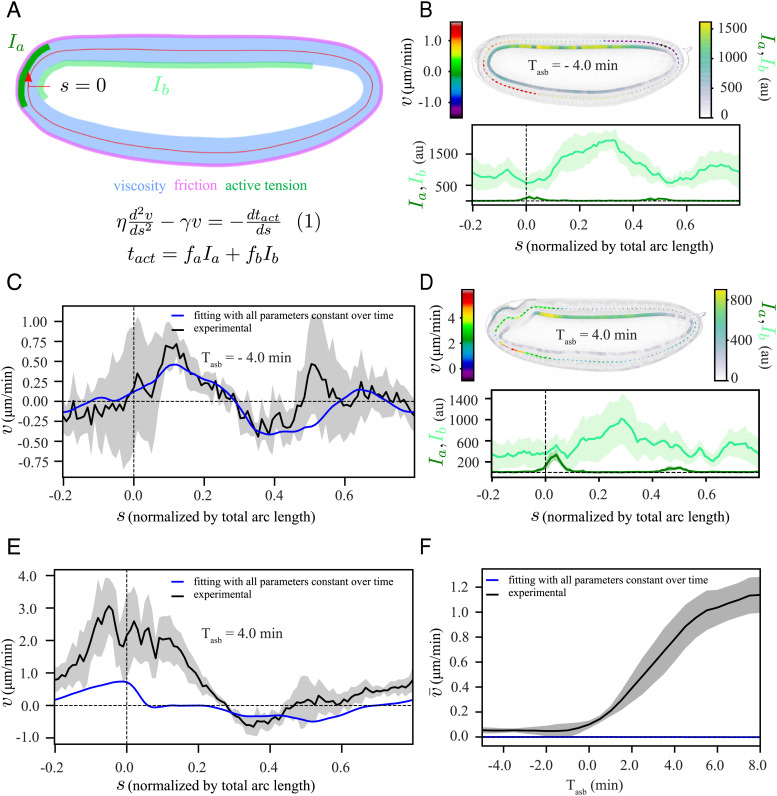
Fig. 3.

A model based on an active tension mechanism explains the symmetric flow. (A) Schematic representation of our modeling framework, equation (1), in which the epithelium is considered as a viscous fluid ($\eta ,$ blue) with homogeneous friction ($\gamma ,$ pink) with the surroundings, along with domains of apical myosin (I_a, dark green) and basal myosin (I_b, light green) as contractile elements. The tissue is approximated by a 1D continuous membrane, positioned along the midline of the epithelium (red line). At any given position, s, the tangential component of the velocity ($v$) fulfills equation (1). (B and D) (Top): a representative time frame with a heatmap of $v$, I_a and I_b, (Bottom): the corresponding spatial profiles of I_a and I_b. (B) from the symmetric phase at T_asb = −4 min; (D) from the polarized phase at T_asb = 4 min. (C and E) Simultaneous fit (blue) of equation (1) to the experimentally measured $v$ (black) for time points between T_asb = −5 min and T_asb = 8 min, with all parameters constant over time (SI Appendix). (C) T_asb = −4 min, (E) T_asb = 4 min. (F) Temporal profile of spatially averaged velocity ($\overline{v}$) in experiment (black) and from our simultaneous fit (blue). The shaded regions associated with experimental data are the SD, computed over six embryos.

This type of model is effective for making quantitative comparisons as well as qualitative predictions. To quantitatively compare our model to the data, we solved equation (1) for velocity, using the measured apical and basal myosin intensities (both in symmetric and polarized phase of flow, Fig. 3 B and D respectively) as input to the equation. By fitting to the measured velocity field, we extracted the values of three relevant physical parameters (SI Appendix). The first parameter is a hydrodynamic length scale $l_H=\sqrt{\eta /\gamma }$, which reflects the ratio between viscosity, $\eta$, and friction with the surroundings, $\gamma$. The other two parameters are conversion factors that relate myosin intensity to active tension (f_a for apical myosin and f_b for basal myosin), which are divided by viscosity $\eta$. The resulting ratios, r_a and r_b, reflect tissue contraction rates for apical and basal myosin, respectively. To build qualitative intuition, we also performed simulations of a simplified model without basal myosin on an elliptic representation of the embryo (hereafter elliptic model), using values of the relevant physical parameters from our fitting (SI Appendix).

We then used this model to test our hypothesis that the nonuniform contraction of basal myosin is what drives the observed symmetric flow. To simplify our modeling studies, we chose to use ets instead of wildtype embryos. ets embryos behave similarly to wildtype at early times but do not have a mesoderm invagination (SI Appendix, Fig. S1), which is a separate complex process of flow and deformation that we do not model explicitly. We first averaged the data over all ets embryos where, to decrease embryo-to-embryo variation, we aligned the embryos to the time at which each transitioned to polarized flow (T_asb = 0; SI Appendix, Fig. S4). We performed a fit of the model given by equation (1) to the data with l_H, r_a, and r_b as free parameters and found that we could reproduce the symmetric flow (Fig. 3C). However, this model could not reproduce the later polarized flow (Fig. 3E) because the spatially averaged velocity is always strictly zero for this simple model (Fig. 3F). Nonzero average flow is not possible because equation (1) contains only tissue-intrinsic, symmetric forces and a homogeneous friction force, none of which can lead to polarized flow. Thus, an additional mechanism is required for driving the polarized flow.

Localized Friction or Adhesion Is not Responsible for Polarized Flow.

During the polarized phase of flow, the dorsal-posterior activation of apical myosin (Figs. 2A and 3D) leads to bending of the epithelium. This causes the anterior end of the apical myosin domain to come into close contact with the eggshell (30), which could create a localized domain with higher friction. This close contact could also lead to adhesion between the epithelium and the eggshell due to the presence of the adhesion protein alpha-Integrin (Scab), which is expressed in this region (44). Intuitively, this configuration could lead to asymmetric contraction of the myosin patch since one end is able to move more freely than the other. Adhesion of the anterior end of the apical myosin domain has even been shown to be crucial to the anterior wave propagation of the endoderm invagination slightly later in development (30). To test whether the polarized flow that we observe could be created by such an asymmetric friction, we accordingly updated our model by including a domain (G) that translocates with the anterior end of the myosin domain, where friction is increased by a factor g (see equation (2) in Fig. 4A).

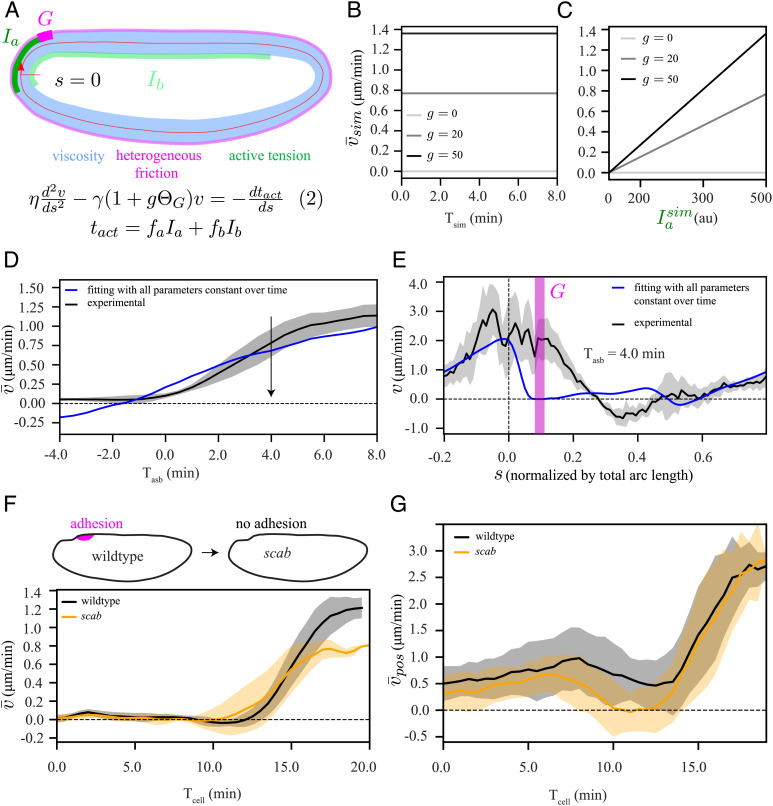
Fig. 4.

Adhesion (or heterogeneous friction)-active tension coupling based model cannot explain the polarized flow. (A) Schematic representation of our model, equation (2), which is similar to equation (1) in Fig. 3A, but with an additional domain G (magenta) of localized increase in friction by a factor g. (B and C) Elliptic model simulation (SI Appendix, Fig. S5 A and B): (B) temporal profile of the spatially averaged velocity (${\overline{v}}_{\mathit{sim}}$) when myosin intensity ($I_{\mathit{sim}}^a$) is constant over time, shown for three different values of g, (C) Dependence of ${\overline{v}}_{\mathit{sim}}$ on temporal increase in $I_{\mathit{sim}}^a$, shown for three different values of g. (D) Experimentally measured temporal profile of spatially averaged velocity $\overline{v}$ (black) and fit of equation (2) (blue), using the same procedure as described in Fig. 3. (E) Spatial fit curve corresponding to panel D at a representative time point during the asymmetric phase (T_asb = 4 min). Chi-squared analysis to evaluate the quality of the fit to the data are reported in Fig. 5I. We also performed a single-sided t test to verify whether the velocity goes to zero in the domain G. The results are shown in SI Appendix, Fig. S5D. (F, Top) Schematic diagram of scab knockout, (Bottom) temporal profile of $\overline{v}$ for wildtype (black) and scab (orange). (G) Temporal profile of spatially averaged velocity ${\overline{v}}_{\mathit{pos}}$, where average was performed only over a posterior domain from s = −0.1 to s = 0.15, for wildtype (black) and scab (orange). The shaded regions associated with experimental data are the SD, computed over six embryos. To compare the wildtype and scab conditions in F and G, we performed two-tailed student t test. The results are shown in SI Appendix, Fig. S5H.

To build intuition for the effect of this new term in the model, we performed simulations using our elliptic model (SI Appendix, Fig. S5 A and B). We obtained polarized flow, though the average velocity remained constant in time unless the amount of localized friction g (Fig. 4B) or the myosin intensity (Fig. 4C) changed over time. The latter could be a possibility as our observed data shows apical myosin increasing over time (Fig. 2C).

To test the localized-friction model against the experimental data, we performed detailed fits of the measured velocity to solutions of equation (2) using the measured time-dependent apical and basal myosin patterns, where we included the additional fit parameter g, which we restricted to be positive. While we found that this reproduced the observed overall increase in the spatially average velocity (Fig. 4D), it failed to predict the observed spatial velocity profile at individual time points (Fig. 4E, corresponding fitting with a time-dependent localized friction g resulted in a similar outcome SI Appendix, Fig. S5 C and D). This is because the model predicts that, for positive values of g, the velocity in region G should be negative (counter clockwise) or go to zero in the case of infinite friction (as shown using our elliptic model in SI Appendix, Fig. S5F), while experimentally we observed positive (clockwise) flow.

We also experimentally tested the contributions of alpha-Integrin-mediated adhesion to polarized flow by generating a CRISPR knock-out of scab (44) (Movie S6). We found that the movement of the posterior tissue is almost identical for wildtype and scab embryos (SI Appendix, Fig. S5G); however, the average velocity after symmetry breaking is reduced for scab mutants (Fig. 4F). To reduce the impacts of any unintended effects of the mutation on other parts of the embryo (SI Appendix, Fig. S5H), we also computed a spatially averaged velocity over only the posterior domain of the epithelium (${\overline{v}}_{\mathit{pos}}$; Fig. 4G). This analysis confirmed that the onset of polarized flow in scab mutant embryos is similar to wildtype, thus indicating that alpha-Integrin is not required for the onset of polarized flow. Taken together, our combined study of modeling and experiment ruled out adhesion (or localized friction) as a mechanism for the onset of polarized flow.

Interaction of Tissue Curvature with Active Moment Can Explain the Polarized Flow.

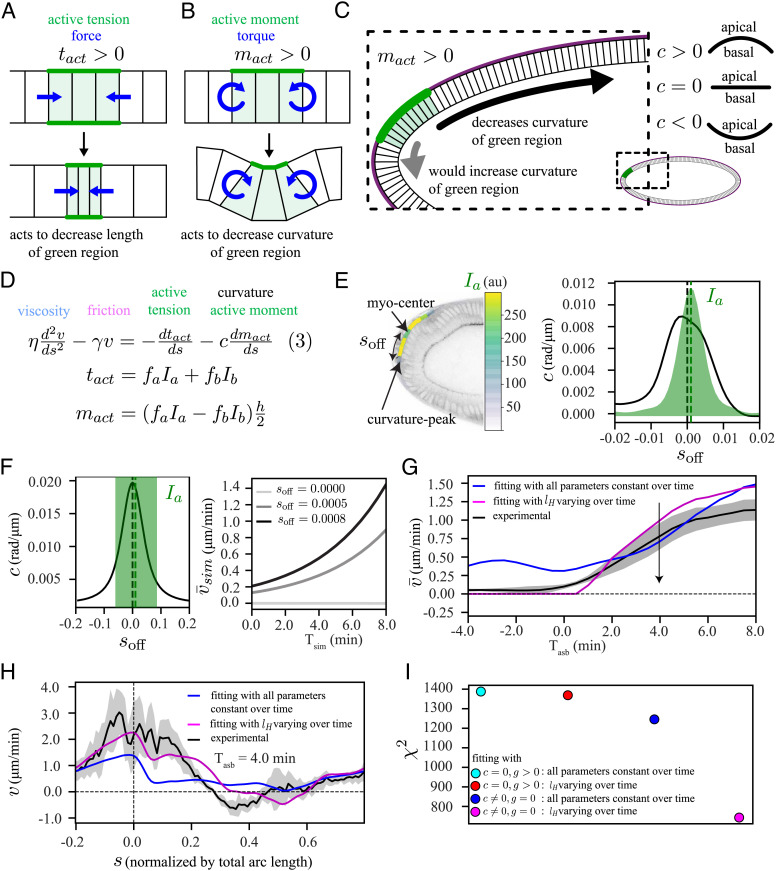
Polarized forces, and thus polarized flow, can be created by the interaction of a curvature gradient with an active moment, following from the theory of active surfaces (45) (SI Appendix). Active moments are created when apical and basal myosin tensions differ. When myosin (and therefore active tension) is present at similar levels apically and basally in a region of tissue, this acts to contract this region, which in turn exerts forces on the surrounding tissue (Fig. 5A). When the levels of apical and basal myosin differ in a region of tissue, an active moment is present that causes this region to exert torques on neighboring tissue, which acts to increase or decrease the curvature of this region (Fig. 5B).

Fig. 5.

A curvature-active moment coupling based model can explain the polarized flow. (A) Active tension (t_act, green) exerts forces (blue arrows) to contract the green region. (B) Active moment (m_act, green) exerts torques (blue arrows) to decrease the curvature of the green region. (C) Positive active moment (m_act > 0) interacts with the eggshell to drive the tissue in a direction that allows the green region to decrease its curvature (black arrow), with sign convention c > 0 (convex) and c < 0 (concave). (D) Model equation (3), equation (1) with a curvature-active-moment coupling term. (E) Experimental mismatch ($s_{\mathit{off}}$) between curvature-peak and apical myosin center. (F) Elliptic model simulation (SI Appendix, Fig. S6 A and B): (Left) illustration of $s_{\mathit{off}}.$ (Right) temporal profile of the spatially averaged velocity (${\overline{v}}_{\mathit{sim}}$) with constant myosin intensity ($I_{\mathit{sim}}^a)$, for three different values for $s_{\mathit{off}}$. (G) Experimental temporal profile of spatially averaged velocity $\overline{v}$ (black) and two fit (using the procedure in Fig. 3) curves to equation (3). (blue) All parameters constant, (magenta) all parameters but the hydrodynamic length (l_H) constant. (H) Spatial fit curves corresponding to panel G at a representative time point during the polarized phase (T_asb = 4 min). (I) Chi-square values (${\chi }^2$) summed over all time points. Model with locally increased friction, all parameters constant (cyan) or only varying l_H (red). Model with curvature-active-moment, all parameters constant (blue) or only varying l_H (magenta). The shaded regions associated with experimental data are the SD, computed over six embryos.

We therefore hypothesized that polarized flow could arise because the dorsal-posterior apical myosin patch creates an active moment that interacts with the curvature gradient in this region. The emergence of polarized flow can be most clearly explained in the limit where the yolk pressure is so high that it presses the epithelium against the eggshell. In this case, the epithelium is forced to have the same curvature as the eggshell everywhere. Since the region with the apical myosin patch has a positive active moment, it will act to decrease its own curvature, which happens only if it moves away from the pole, creating polarized flow (Fig. 5C).

To test whether this effect could explain our observations, we added coupling between the active moment and the epithelium curvature to our continuum model by including a new force term, as shown in equation (3) (Fig. 5D and SI Appendix). This term follows directly from the theory of active surfaces (45) and includes no new fit parameters. The resulting flow depends critically on the position of the domain of apical myosin activation, relative to the curvature profile of the embryo. A simple quantity to consider is the offset between the center of the apical myosin domain and the position of peak epithelial curvature at the posterior pole (henceforth called myosin-curvature offset, s_off, Fig. 5E). Simulating equation (3) using our elliptic model (SI Appendix, Fig. S6 A and B) created polarized flow where the average velocity increased as s_off increased (Fig. 5F) even when we held the myosin intensity constant over time.

To further test our hypothesis, we fit equation (3) to the experimentally measured velocity profile, using measured myosin and curvature data. Fitting with all physical parameters held constant over time reproduced the substantial increase of the polarized flow with time but also predicted some polarized flow at times before symmetry breaking (blue curve Fig. 5 G and H). We found that this early polarized flow in the blue fit curve arises due to the active moment created by basal myosin (SI Appendix, Fig. S6C). This suggested that there must be something that prevents polarized flow at early stages. It has previously been observed that the amount of friction changes over time during the early phase of cellularization in the Drosophila embryo (41). Moreover, tissue deformations and folding that occur during gastrulation alter the distance between epithelium and eggshell in certain regions, which could further affect the friction. Accordingly, we performed fitting allowing the overall homogeneous friction, γ, to change over time. This modified fit captured the experimentally observed transition from symmetric to polarized flow and the spatial velocity patterns (magenta curves, Fig. 5 G and H). This fit suggested a large increase of the hydrodynamic length l_H around the time of symmetry breaking, i.e., a large decrease in friction with the eggshell (SI Appendix, Fig. S6D). However, this increase in l_H decreased drastically when we consider that the region expressing apical myosin can only be compressed by a finite amount (SI Appendix, Figs. S6 E and F and S7). Comparing fitting accuracies using chi-squared analysis, we found that the curvature-active-moment model, equation (3), could consistently explain the measurements better than the tension-with-heterogeneous-friction model, equation (2) (Fig. 5I). This supports the idea that coupling between curvature and active moment can act as a driver for the polarized flow observed in the early embryo.

Changing Embryo Curvature and Active Moment Alters the Flow, Consistent with the Model.

To further test the predictions of the model, we performed targeted perturbations to parameters that are essential for flow in the model: the curvature of the embryo and the location of the apical myosin domain with respect to the curvature peak (s_off).

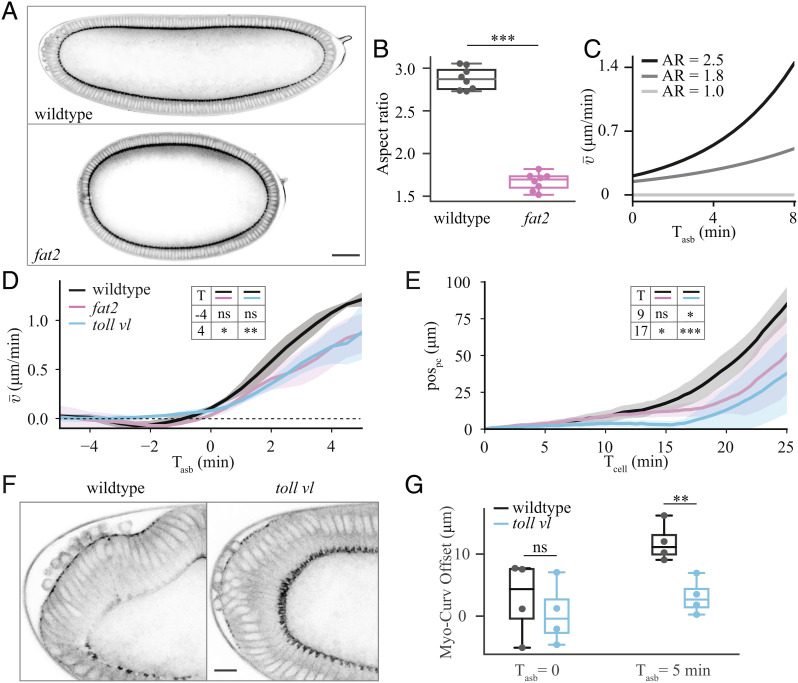
To alter the curvature of the embryo, we took advantage of the fact that there is an adhesion molecule, Fat2, present in the maternal follicular epithelium that is needed to shape embryo geometry. We therefore used UAS-fat2-RNAi, traffic jam(tj)-GAL4 mothers to produce embryos with an altered shape (46–48) (hereafter fat2 embryos) that are significantly shortened along the anterior–posterior axis and, as a result, are much rounder (Fig. 6 A and B and Movie S7). In this condition, the embryo itself is neither genetically mutant for fat2 maternally nor zygotically, only its shape is affected since the fat2-RNAi is expressed exclusively in the somatic follicle cells in the egg chamber. To explore the expected impact of changing the aspect ratio on the flow dynamics, we performed simulations based on equation (3) using our elliptic model with varying aspect ratios. The simulations predicted that decreasing the embryo’s aspect ratio should decrease the rate at which the spatially averaged velocity increases during the phase of polarized flow (Fig. 6C). Experimentally, we observed a wide variation in the average velocity profile for individual fat2 embryos (SI Appendix, Fig. S8A). But, when the embryos were aligned with respect to the onset of polarized flow, we observed the predicted decrease in the average velocity (Fig. 6D). This decreased velocity was confirmed by tracking of the position of the posterior tissue (Fig. 6E) and by averaging the velocity in only the posterior of the embryo (SI Appendix, Fig. S8B).

Fig. 6.

Experimental perturbations to challenge model predictions. (A) Sagittal section of wildtype (Top) and fat2 (Bottom) embryos at T_cell = 0, imaged for sqh::GFP. (Scale bar, 50 μm.) (B) Quantification of aspect ratio, defined as the length of the major embryo axis divided by the maximal height of the embryo for eight wildtype and eight fat2 embryos. (C) Average velocity of tissue flow resulting from simulations using our elliptic model with different aspect ratios (AR). In the simulations (SI Appendix, Fig. S5E), the position and extent of the myosin domain was initialized consistent with the experimental data. (D) Experimental spatially-averaged tangential velocity as a function of time after symmetry breaking for 5 wildtype, 4 fat2, and 6 toll vl embryos. (E) Pole cell position (pos_pc) as a function of time for 6 wildtype, 5 fat 2, and 7 toll vl embryos. (F) View of the posterior of a wildtype (Left) and toll vl (Right) embryo imaged for sqh::GFP. (Scale bar, 10 μm.) (G) Quantification of the offset between the position of maximum curvature and the center of the patch of posterior myosin (Myo-Curv Offset) for 4 wildtype and 4 toll vl embryos. Comparisons in B, D, E, and G performed using two-tailed unpaired t tests. ns, not significant; *P < 0.05; **P < 0.01; ***P < 0.001.

To verify that the decreased average flow speed was not due to lower myosin levels, we quantified myosin intensity using lightsheet microscopy (SI Appendix, Fig. S8D and Materials and Methods). We found that the onset of myosin recruitment at the cortex was delayed by approximately 4 min in fat2 embryos compared to wildtype (SI Appendix, Fig. S8E), consistent with the delay in the fast phase of flow seen in Fig. 6E. Since we compare the speed of flow to theoretical predictions with time aligned to symmetry breaking, this delay does not affect our conclusions. We found that the size of the expression domain varied from embryo to embryo but found no significant difference in average domain size between wildtype and fat2 embryos (SI Appendix, Fig. S8F). Finally, we found that the average intensity of myosin levels in the expression domain of fat2 embryos were not significantly different from wildtype (SI Appendix, Fig. S8G), indicating that the altered geometry of the embryo, and not the difference in myosin intensity, is responsible for the altered dynamics.

Next, we altered the position of the apical myosin domain using the toll vl mutant embryos described previously. Because the toll vl mutation removes dorsal–ventral polarity, the domain of apical myosin becomes more centered on the posterior pole of the embryo compared to the dorsal–posterior localization in wildtype (Fig. 6 F and G). The difference becomes increasingly significant over time. According to our prediction, decreasing the myosin-curvature offset, s_off, is expected to decrease the average velocity (Fig. 5G). Once the individual embryos (SI Appendix, Fig. S8C) were aligned with respect to the onset of polarized flow, this decrease in the average velocity was confirmed experimentally (Fig. 6 D and E and SI Appendix, Fig. S8B).

In addition to the decrease in average velocity, there is a large delay (approximately 5 min) in the onset of polarized flow in toll vl embryos (Fig. 2E). This delay likely occurs for two reasons. If the apical myosin patch were perfectly centered on the posterior pole, it would not flow at all until it was displaced slightly in any direction by some other effect. This would also explain why toll vl embryos tend to flow in directions other than dorsally as normally seen in wildtype (SI Appendix, Fig. S2 C, Movie S4). Additionally, toll vl embryos lack the dorsal–ventral asymmetry in basal myosin that, in wildtype embryos, leads the myosin patch to shift away from the pole even before the onset of polarized flow. This initial shift increases the speed of polarized flow arising from the myosin-curvature offset in wildtype. There is, in a sense, a feedback based on the initial position of the apical myosin patch and the initial flow. The larger the offset, the more polarized flow, which increases the offset, and so on until the domain of myosin reaches the region of lowest curvature on the dorsal side of the embryo.

We performed two further tests to assess whether the observed change in flow results from the changed position of myosin with respect to the curvature peak. First, we extracted parameters from wildtype fitting (SI Appendix, Fig. S9 A and B) and used the myosin and curvature profiles measured in toll vl to predict flow using model equation (3). This prediction yielded a good match to the experimentally measured flows in toll vl embryos and confirmed the decrease in the average velocity (SI Appendix, Fig. S9 C and D). Second, we quantified flow dynamics in capicua mutant embryos, whose apical myosin domain is larger but more centered on the posterior pole than in wildtype embryos (SI Appendix, Fig. S8 H and I and Movie S8). In capicua embryos, we observed a slowed and delayed increase in average velocity despite a larger domain of apical myosin (SI Appendix, Fig. S8 J and K), which was also predicted by simulations using our elliptic model (SI Appendix, Fig. S8L).

Taken together, these experimental perturbations deeply and broadly challenge the predictions of the model. While each of the mutations discussed in this section may have unintended effects on other aspects of development, the combination of multiple mutations that each modify orthogonal pathways provides strong evidence that the agreement with our model is not based on unintended secondary effects. We therefore conclude that the model given in equation (3) accurately captures the features that are necessary for driving the onset and evolution of polarized flow in early Drosophila morphogenesis. Overall, our results show that an initially symmetric flow, driven by a nonuniform pool of basal myosin, transitions to polarized flow as a result of the activation of apical myosin in a domain of the embryo that experiences a curvature gradient.

Discussion

We have identified two distinct phases of tissue flow in the early Drosophila embryo, where an initially symmetrically deforming tissue transits to a polarized flow. While previous work has studied flow-generating mechanisms during morphogenesis, we showed that this polarized flow can neither be explained by forces emerging from other tissues such as the germband and mesoderm (SI Appendix, Fig. S1) nor by a myosin-adhesion coupling. Our work revealed instead that a coupling between tissue curvature and an active moment, generated by a difference in apical and basal myosin intensity, is responsible for driving the polarized flow. We also demonstrated the importance of spatially varying curvature, with an offset between the curvature peak and the domain of the active moment for early polarized movement.

This system is an ideal example for how organized multicellular dynamics that occur during morphogenesis emerge from genetic and geometric blueprints inherited from the mother. Beyond simply fulfilling inherited instructions, the offset between the patterns of cell contractility and tissue curvature is also amplified by the very flow it induces. This illustrates that interactions between genetic and geometric information update this information as a result of morphogenesis. Thus, information is not simply inherited, it is constantly modified.

While the mechanism that we report accurately describes the onset of polarized flow, it is not sufficient to explain later stages of morphogenesis, in particular the wave of deformation toward the anterior that follows as reported in Bailles et al. (30). Indeed, directly following our phase of investigation (at T_cell $\approx$ 27 min) dynamically regulated alpha-Integrin/Scab-dependent adhesion between the epithelium and the vitelline membrane in the dorsal posterior (30) begins to play a role in the expansion of the invagination toward the embryo anterior (Movie S6). This alpha-Integrin/Scab-dependent adhesion also dynamically feeds back on apical myosin, triggering a wave of activation and tissue deformation. Additionally, it has been shown that later phases of tissue progression toward the anterior (T_cell $\approx$ 30 min) depend on the process of convergent extension, driven by myosin polarization in the lateral ectoderm (15–17). Our experiments with scab mutant embryos (Fig. 4, SI Appendix, Fig. S5, and Movie S6) and eve, twist, and snail mutant embryos (SI Appendix, Fig. S1 and Movie S2), however, show that these effects do not have any impact on the onset of polarized flow discussed here.

To keep our model as simple as possible while still revealing the mechanisms required to achieve the observed flow, we restricted our investigation to the 1D tangential flow in the sagittal plane of the epithelium and made several simplifying assumptions. Quantitative comparisons of the model to our data suggested that contraction of the tissue in the primordium is limited by elastic resistance, which for simplicity, we modeled by a local increase in viscosity (SI Appendix, Fig. S7). This is consistent with the fact that, due to the incompressibility of the cytoplasm, there is a limit to cell deformation upon contraction (Movie S1). We also compared our experimental results to a simple, purely elastic model (SI Appendix). However, for a complete understanding of tissue flow, deformation, and folding, explicit consideration of the interaction between elasticity and viscosity, and a full 3D modeling approach will be necessary. This would open the way to addressing for example how tissue flow progresses along the dorsal midline during later stages of embryo development.

Morphogenetic processes are both self-organized and dependent on initial conditions to deterministically guide future processes (2). In in vitro synthetic systems, such initial conditions are engineered to drive robust organoid development (49, 50), but in vivo they are inherited from previous developmental stages. During development, heredity is classically associated with genomic heredity. Yet, as we show here, structural or geometric heredity (e.g., egg size and shape) is also essential to drive tissue flow and morphogenesis. It will be interesting to investigate further how the interplay between genetic and geometric heredity guide developmental processes in other systems.

Materials and Methods

Fly Strains and Genetics.

Details of the fly lines used are provided in the SI Appendix.

Sample Preparation.

Flies were kept in a cage at 25 °C with the exception of GAL4 lines which were kept at 18 °C. Embryos were collected using apple cider plates smeared with yeast paste. Embryos were transferred to a mesh basket, rinsed with water, dechorionated with 2.6% bleach for 1 min, and then rinsed copiously with water before being transferred back to clean agar. Embryos in the early stages of cellularization were visually selected and aligned laterally. They were then transferred to a glass coverslip coated with homemade glue. A drop of Halocarbon 200 Oil (Polysciences; for DIC experiments) or 1× phosphate buffered saline (prepared from Dulbecco’s phosphate buffered saline (eurobio); for two photon experiments) was placed on the embryos to keep them from drying during imaging.

Brightfield Imaging.

For quantifying the direction of tissue rotation in toll vl mutants (SI Appendix, Fig. S2C), embryos were imaged at 21 °C on a Zeiss Axiovert 200M inverted microscope using a 20×-0.75 numerical aperture (NA) objective. Images were acquired once per minute for 2 to 3 h.

Lightsheet Imaging.

Comparing the myosin expression of wildtype and fat2 embryos (SI Appendix, Fig. S8 D–G) required 3D imaging on a lightsheet microscope instead of 2D two photon imaging since the fat2 embryos were too round to reliably align to consistently capture the myosin domain. Experiments were performed using a Zeiss Z.1 lightsheet microscope with a 20×/0.1 W UV-Vis detection objective and two LSFM 10×/0.2 illumination objectives. Embryos were mounted perpendicularly in a 1-mm capillary in 1% (w/w) low melting temperature agarose (Fisher BioReagents) and were suspended in a water-filled cuvette so that the posterior pole of the embryo faced the imaging objective. The water was kept at 23 °C during imaging. Illumination was provided by a 561 nm laser for mScarlet and 488-nm laser for GFP. Every 30 s, a z-stack of 105-µm total depth with a step size of 1.5 µm was acquired.

Two Photon Imaging.

For all other experiments, embryos were imaged at 23.5 to 24.5 °C using a Nikon A1R MP+ multiphoton microscope with a 25×-1.10 NA water-immersion objective. Illumination was provided by a pulsed 1,040-nm laser (Coherent) for mScarlet and a tunable wavelength pulsed laser (Coherent) set to 920 nm for GFP. Images were acquired once every 30 s with 2× line averaging.

Data Analysis.

Pole cell tracking.

We selected a central pole cell and manually tracked its coordinates over time in FIJI. As the selected pole cell began to invaginate, we tracked the position radially outward from it near the vitelline membrane to record only its tangential movement (Movie S3). The position is defined as $po{s}_{\mathit{pc}}=\sqrt{(x-x_o{)}^2+(y-y_o{)}^2}$, where (x_o,y_o) is the position at T_cell = 0.

Image analysis.

The two photon images were processed using custom python scripts to align and segment the embryos and to extract the apical and basal myosin as well as tangential tissue velocity profiles. See SI Appendix for a full description of the procedure.

Supplementary Material

Appendix 01 (PDF)

Movie S1.

Time-lapse of early Drosophila morphogenesis in a wildtype embryo. Imaged in the sagittal plane on a two-photon microscope labeled with GAP43::mScarlet (top) and sqh::GFP (bottom).

Movie S2.

Tissue dynamics in wildtype and ets embryos. Time-lapse of myosin activation in a wildtype (top) and eve, twist, snail embryo (bottom) synchronized with respect to the time when the cellularization front passes the nuclei in the dorsal posterior.

Movie S3.

Tracking of pole cells in a wildtype embryo. Time-lapse of tissue dynamics in an embryo labeled for cell membrane maker GAP43::mScarlet. The green dot shows the position used to calculate pole cell movement over time (as in Fig. 1D).

Movie S4.

Direction of flow in toll vl embryos. Time-lapse of three toll vl mutant embryos that flow indifferent directions. The top embryo flows dorsally, the middle embryo flows laterally, and the bottom embryo flows ventrally.

Movie S5.

Tissue dynamics in wildtype, toll vl, and cta embryos. Time-lapse of myosin activation in a wildtype (top), toll vl (middle), and cta (bottom) embryos synchronized with respect to the time when the cellularization front passes the nuclei in the dorsal posterior.

Movie S6.

Tissue dynamics in wildtype and scab knockout embryos. Time-lapse of myosin activation in a wildtype (top) and scab knockout (bottom) embryos synchronized with respect to the time when the cellularization front passes the nuclei in the dorsal posterior.

Movie S7.

Tissue dynamics in wildtype and fat2 embryos. Time-lapse of myosin activation in a wildtype (top) and fat2 (bottom) embryos synchronized with respect to the time when the cellularization front passes the nuclei in the dorsal posterior.

Movie S8.

Tissue dynamics in wildtype and cic embryos. Time-lapse of myosin activation in a wildtype (top), and cic (bottom) embryos synchronized with respect to the time when the cellularization front passes the nuclei in the dorsal posterior.

Data, Materials, and Software Availability

The raw image files are available in BioStudies repository (51). The datasets generated and analyzed during the current study are available at https://www.ebi.ac.uk/biostudies/studies/S-BIAD602. The computer code used to perform data analysis, simulations, and model fitting is available at https://github.com/HiBandan/modelTissueFlow.