Simulation of ligand dissociation kinetics from the protein kinase PYK2

Abstract

Early-stage drug discovery projects often focus on equilibrium binding affinity to the target alongside selectivity and other pharmaceutical properties. The kinetics of drug binding are ignored but can have significant influence on drug efficacy. Therefore, increasing attention has been paid on evaluating drug-binding kinetics early in a drug discovery process. Simulating drug-binding kinetics at the atomic level is challenging for the long time scale involved. Here, we used the transition-based reweighting analysis method (TRAM) with the Markov state model to study the dissociation of a ligand from the protein kinase PYK2. TRAM combines biased and unbiased simulations to reduce computational costs. This work used the umbrella sampling technique for the biased simulations. Although using the potential of mean force from umbrella sampling simulations with the transition-state theory over-estimated the dissociation rate by three orders of magnitude, TRAM gave a dissociation rate within an order of magnitude of the experimental value.

Graphical Abstract

The contents of this page will be used as part of the graphical abstract of html only. It will not be published as part of main.

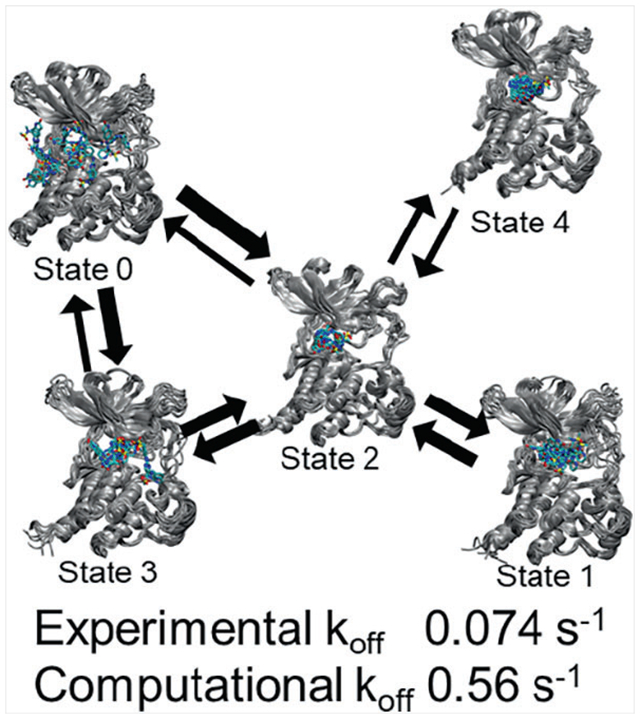
Using the transition-based reweighing analysis method (TRAM), we showed that the dissociation of an inhibitor from the bound state (4) of the PYK2 protein kinase went through an intermediate state (2) to two pre-dissociated states (0 and 3) before complete dissociation. We also found a mis-trapped bound state (1) that bound to PYK2 with a higher energy than the true bound state. The model predicted a dissociation rate within an order of magnitude of experiment.

1 |. INTRODUCTION

The binding affinity of a ligand with its target receptor is an important determinant of its potency and, in combination with other pharmaceutical properties, determines its potential as a candidate drug for modifying the effect of that receptor for therapeutic purposes. Consequently, a wide range of computational techniques have been developed for estimating the binding free energy of ligands with their receptors or at least screening potential drug candidates in order to prioritize candidates for synthesis. These span a spectrum from computationally inexpensive techniques such as docking that give a score that reflects binding affinity^1–5 to more rigorous and computationally expensive techniques such as alchemical free energy simulations.^6–9 On the other hand, the kinetics and mechanism of drug binding have received less attention until recently. The concept of long residence time was first emphasized.^10–12 Long residence time could lead to a larger therapeutic window, an increased duration of action, or less frequent dosing. Later, we surveyed the literature¹³ and found that the role of drug-binding kinetics could go well beyond the concept of long residence time. For example, a fast dissociation rate, or short residence time, is important in reducing the toxicity of the drug memantine for treating Alzheimer’s disease.¹⁴ Meanwhile, the association rate of engineered antibodies was found to correlate better than the dissociation rate with the ability of the antibodies to neutralize the respiratory syncytial virus.¹⁵

To find drug candidates with therapeutically useful drug-binding kinetics, molecular dynamics simulations can be useful. However, accurately determining kinetic rates from atomistic molecular dynamics simulations is challenging because the processes of interest often occur on a time scale beyond what can be simulated directly. A number of methods are specifically designed to determine rates using a large number of short, unbiased simulations conducted in parallel. These include the weighted ensemble method,^16–19 milestoning,^20,21 and transition path sampling.^22,23 Recently, the weighted ensemble method has been used to identify four separate pathways for the dissociation of benzene from the L99A mutant of T4 lysozyme,²⁴ and mile stoning has been used to characterize the dissociation of the anticancer drug imatinib from the Abl protein kinase.²⁵ The weighted ensemble method has also been modified to function better with higher-dimensional progress coordinates, by incorporating a complex hierarchical binning strategy to create WExplore,²⁶ or by abandoning binning altogether in favor of cloning and merging walkers based on a distance matrix in REVO.²⁷ REVO has further been applied to ligand dissociation.²⁸

Some approaches, such as umbrella sampling,²⁹ apply biasing potentials to encourage sampling of configuration space higher in free energy along a pre-defined reaction coordinate. The need to choose a specific reaction coordinate or progress coordinate in order to define the structural changes whose rates are to be studied suffers some drawbacks. An incorrect choice of reaction or progress coordinate can lead to failure to sample relevant degrees of freedom, to slow convergence, or to incorrect estimates of free energy barrier heights.³⁰ In studying drug-binding kinetics, the reaction coordinate is often not simply a variable describing the distance of the ligand from the binding pocket, but also includes many degrees of freedom of the protein that can couple with ligand dissociation. In addition, it is necessary to perform some form of post-processing to remove the effects of the biasing potential and recover the unbiased ensemble. The weighted histogram analysis method (WHAM)^31,32 provides one way to do this. This recovers a potential of mean force along the reaction coordinate, from which free energy barriers for conformational transitions can then be estimated. It is more difficult to remove the effect of the biasing potential from estimates of kinetic rates. However, methods for doing this have been developed. For example, based on methods for determining kinetic rates from replica exchange simulations,³³ the dynamic histogram analysis method (DHAM)^34,35 has been developed as a means for determining transition rates between bins in terms of the reaction coordinate. These transition rates for the biased ensemble can then be extrapolated to an unbiased ensemble using either data from unbiased simulations or models for extrapolation. A similar method, the discrete transition-based reweighting analysis method (dTRAM),³⁶ likewise estimates transition rates between bins in a biased ensemble and can be shown to become identical to WHAM in the limit when samples are statistically independent and drawn from a global equilibrium distribution. The xTRAM method³⁷ is closely related to dTRAM and makes fewer assumptions about the dynamics, but is not a maximum likelihood method and therefore may not perform as well statistically.

These methods can also be used to enhance the performance of the Markov state analysis.^38–42 Markov state analysis uses large numbers of short simulations to extract information on the mechanisms and rates of structural changes associated with long-time dynamics. The structures from the simulations are clustered into a set of discrete states, and the transition probability matrix between these states is computed. The assumption is made that the probability of transitioning to another discrete state depends only on the current state and not on the past evolution of the system. Although the assumption of Markovian behavior does not always hold, this can be overcome by incorporating some history-dependent information into the analysis.^43,44 Markov state analysis does not require a pre-selected reaction or progress coordinate and can work with powerful methods for dimension reduction that can identify complex pathways.^40,45,46

However, a challenge for Markov state analysis is that it can require a large number of simulations to obtain reliable results. The transition-based reweighting analysis method (TRAM),⁴⁷ a generalization of dTRAM, was introduced to augment unbiased simulations with biased simulations (umbrella sampling simulations in this work) so that the computational costs for studying long-time dynamics can be substantially reduced. The biased simulations help to sample events that are not easily accessed by unbiased simulations, such as simulating the bound ligand climbing up the activation barrier to reach the transition state. The details were described in the paper by Wu et al.⁴⁷ Briefly, after performing biased and unbiased simulations, one can compute the count matrix with elements $c_{\text{ij}}^{\text{k}}$ counting the transitions from configuration state i to j in ensemble k. (In our application, k labels an unbiased ensemble or an ensemble generated within an umbrella-sampling window.) The probability of transition from configuration state i to state j for ensemble k, $p_{\text{ij}}^{\text{k}}$, can then be computed from the count matrix by

$$p_{\text{ij}}^{\text{k}}=\frac{c_{\text{ij}}^{\text{k}}+c_{\text{ji}}^{\text{k}}}{\text{exp}\left[f_{\text{j}}^{\text{k}}-f_{\text{i}}^{\text{k}}\right]{\nu }_{\text{j}}^{\text{k}}+{\nu }_{\text{i}}^{\text{k}}}$$ (1)

after the Lagrange multipliers ${\nu }_{\text{i}}^{\text{k}}$ and the local free energy for each state $f_{\text{i}}^{\text{k}}$ have been solved from a set of nonlinear algebraic equations as described in Wu et al. The probability matrix for configurational transitions for the unbiased ensemble can then be used in a Markov state model in the usual way to calculate equilibrium and kinetic properties. This method was applied to the dissociation of benzamidine from trypsin, correctly predicting the dissociation rate within a factor of two. In another application, the method was applied to the binding of cyclic peptide analogs of the transactivation domain of p53 to MDM2.⁴⁸ In that case, both binding and dissociation rates determined using TRAM came closer to the experimental values than those evaluated using conventional Markov analysis. Although the binding rate determined using TRAM came within an order of magnitude of the experimental value, the dissociation rate was off by a factor of about 300.

It is useful to point out that TRAM is designed specifically for estimating the transition rates in a Markov State Model between microstates defined separately from any reaction coordinate used for the underlying biased simulations. The unbiased simulations are performed without pre-defined reaction coordinates; they can sample high-dimensional configurational space beyond that covered by the biased simulations. It is also useful to point out that although rates can be estimated from biased simulations alone using techniques such as DHAM, this requires assuming a rate model, which would necessitate additional validation. By including unbiased simulations, no rate model needs to be assumed. In the application of TRAM to the benzamidine/trypsin system, at least 5% of the data had to come from unbiased simulations in order to reliably estimate the dissociation rate.

We have been applying various computational techniques to study the dissociation of ligands from protein kinases. In one study of the dissociation of three ligands from focal adhesion kinase (FAK), steered molecular dynamics correctly rank-ordered their dissociation rates and identified a two-step mechanism for ligand unbinding.⁴⁹ An expansion of this study to 14 ligands showed a strong correlation between the time necessary for a ligand to exit the binding site in a SMD simulation with the experimental dissociation rate. Furthermore, free energy surfaces for dissociation were derived for three of the ligands using umbrella sampling, with the center of mass of the ligand relative to the protein as a reaction coordinate. Although the free energy surfaces further supported the two-step mechanism of dissociation, the estimated barrier heights did not rank-order the experimental dissociation rates properly, and absolute dissociation rates estimated from Eyring’s equation were approximately six orders of magnitude too high.⁵⁰

In this work, we use TRAM to simulate the dissociation of a ligand from the protein kinase PYK2. Biased simulations are performed by using the umbrella sampling technique, placing windows along trajectories obtained from τ-random acceleration molecular dynamics (τ-RAMD) that enhanced the identification of the dissociation path.⁵¹ TRAM then combines the results of biased and unbiased molecular dynamics simulations to estimate dissociation rate by transition-path theory. The computed rate is within an order of magnitude of experiment. By coarse-graining, the Markov states into a small number of macrostates, we obtain useful insights into the molecular mechanism of ligand dissociation.

2 |. MATERIALS AND METHODS

2.1 |. Unbiased molecular dynamics and umbrella sampling simulations

Table 1 presents a summary of the molecular dynamics simulations used in this work. Initial configurations were extracted from τ-RAMD simulations of PYK2 in complex with ligand 1, previously reported by Berger et al.⁵¹ The structure of ligand 1 is shown in Figure 1. In these random acceleration molecular dynamics (RAMD) simulations, the solvated protein-ligand system was subjected to molecular dynamics simulation with a force of predetermined magnitude and random direction applied to the ligand. If the center of mass of the ligand did not move sufficiently, the random direction of the force was changed and the simulation was continued. In this way, a total of 60 trajectories comprising a total of approximately 5.7 ns of simulation were accumulated, in which different possible exit paths for the ligand were explored.⁵¹

TABLE 1.

Summary of molecular dynamics simulations

Type	Number	Duration	Total duration	Manner in which initial configurations selected
Umbrella	421	10 ns	4.21 μs	1 Å apart, within 15 Å of bound state
Unbiased	5	200 ns	1 μs	All from bound state
Unbiased	13	100 ns	1.3 μs	5 Å apart, 10–15 Å from bound state

FIGURE 1.

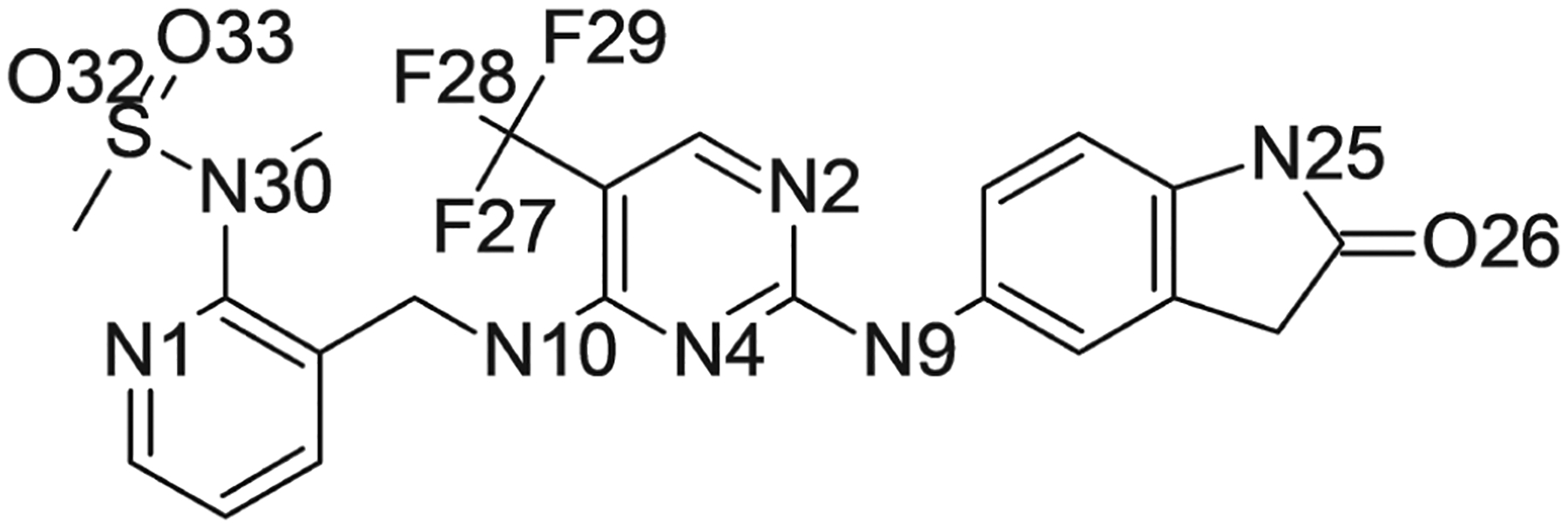
Structure of ligand 1. Nitrogen, oxygen, and fluorine atoms are labeled with the names used in the simulations reported in this work

In the present work, initial configurations for longer MD simulations were extracted from these trajectories using a protocol similar to that used for our previous simulations of FAK in complex with ligands.⁵⁰ The first frame from the first trajectory was identified as an initial configuration, and subsequently additional frames were identified if the ligand center of mass was at least 1 Å from any previous center of mass and less than 15 Å from the initial configuration. (This protocol is similar to that used for our previous simulations of FAK in complex with a ligand⁵⁰; the latter condition was imposed in order to limit sampling of configurations with the ligand far away from the binding site.) Each configuration was solvated in a cubic box of TIP3P water⁵² and 150 mM sodium chloride. They were then simulated in explicit solvent using the same force field as in the previous work, which consisted of an AMBER ff14SB force field for the protein,⁵³ and a GAFF force field for the ligand.⁵⁴ Glu 617 was protonated as was done in the original τ-RAMD simulations.⁵¹ The particle mesh Ewald method was used for the treatment of electrostatics.⁵⁵ The simulation protocol consisted of heating gradually to 300 K over 600 ps under harmonic restraints of 1.0 kcal/mol/Ų, relaxing those restraints over an additional 400 ps, and performing MD simulation at constant pressure and temperature either with or without an additional biasing potential for the duration specified in Table 1. Both umbrella and unbiased simulations were carried out using NAMD^56,57 and the colvars module within NAMD was used to impose the umbrella potential in umbrella simulations.⁵⁸

Umbrella sampling simulations use a harmonic biasing potential centered on the ligand center of mass in the initial configuration of the form

$$U(\text{x})=U_{\text{FF}}(\text{x})+\frac{k}{2}{\left({\text{r}}_{\text{CM}}-{\text{r}}_{\text{CM},0}\right)}^2$$ (2)

where U_FF(x) is the potential given by the force field, r_CM is the center of mass of the ligand after alignment of the protein backbone with the initial configuration, and r_CM,0 is the center of mass in the initial configuration. (These positions are shown in Figure 2.) The force constant k of the harmonic restraint was 2.0 kcal/molŲ. The first 1 ns of each of the simulations with an umbrella potential was discarded, and the remaining part of each trajectory was used to construct a three-dimensional histogram of the center of mass of the ligand relative to the protein with a bin size of 0.5 Å in each dimension. The histograms were then combined into a free energy surface using the weighted histogram analysis method.^31,32 As with our previous work using FAK, the resulting free energy surfaces were then visualized using VMD to determine the location of free energy basins and saddle points corresponding to transition states. This was done by visualizing the isosurface of constant free energy for increasing free energy levels until energy basins connected with each other. The standard error of the free energy surface was also determined, by calculating three separate free energy surfaces using the parts of each umbrella trajectory from 1–4, 4–7, and 7–10 ns and then calculating the SE of the free energy for each bin. This was then visualized by coloring contours of the free energy surface according to the calculated SE. (The free energy surface and its standard error were also evaluated using MBAR⁵⁹; similar results were obtained.) The three-dimensional free energy surface was also used to produce a one-dimensional potential of mean force in terms of the distance of the ligand center of mass from its position in the reference structure, by integrating the probability over all bins corresponding to a given center of mass distance and converting to a free energy.

FIGURE 2.

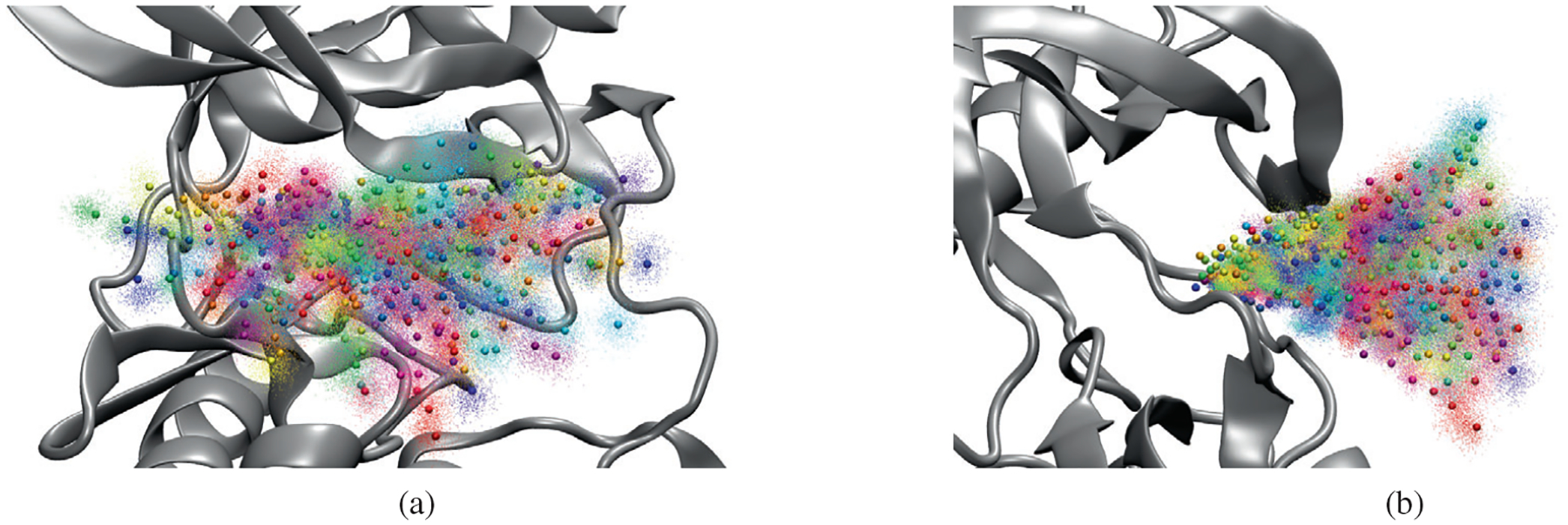
Positions of umbrella potential centers (spheres) and sampled ligand center of mass positions (points) in umbrella sampling simulation of ligand 1 dissociation from PYK2. Different colors correspond to different umbrella windows. (A) View from front; (B) view from side

2.2 |. TRAM analysis

In order to obtain more precise estimates of the dissociation rate of ligand 1, the umbrella and unbiased trajectories were combined and subjected to the transition-based reweighting analysis method (TRAM).⁴⁷ This method estimates Markov state models^38–42 for both biased and unbiased thermodynamic states while simultaneously correcting for the use of biasing potentials. The combined trajectories were discretized by first selecting input features consisting of the minimum heavy-atom distance between the ligand and each protein residue as well as internal dihedrals within the ligand for each rotatable bond. These features were then projected using Time-lagged Independent Component Analysis (TICA)⁴⁶ with a lag time of 5 ns onto a subspace containing 95% of the kinetic variance (resulting in a total of 80 TICA dimensions) and then discretized into either 50 or 100 clusters using k-means clustering. TRAM was then applied to construct Markov state models for both biased and unbiased thermodynamic states with a Markov lag time of either 1, 2, or 5 ns; each Markov model included only those clusters which were sampled in the corresponding trajectories. This was done by first constructing an initial guess for the relative free energy of each thermodynamic state using MBAR⁵⁹ and then iterating the TRAM equations until the relative free energies converged to within 1.0 × 10⁻² kcal/mol. A summary of the parameters used for TRAM is shown in Table 2.

TABLE 2.

Principal parameters for Markov state model analysis using TRAM

Parameter	Value
Initially selected features	Minimum distance of ligand from each residue, selected ligand dihedrals
TICA lag time	5 ns
Number of TICA dimensions	80
Number of clusters (microstates)	50 or 100
MSM lag time	1, 2, or 5 ns

In order to estimate the dissociation rate from the Markov model for the unbiased state, the clusters were divided into two macrostates based on the average distance of the ligand center of mass from its original position over all the frames in each cluster. Those clusters with a mean ligand center of mass distance of less than 10 Å were considered to belong to the bound state, whereas those with a mean ligand center of mass distance of 10 Å or greater were considered to belong to the unbound state. The mean first passage time between the two states was then determined and its reciprocal was taken to be an estimate of the dissociation rate.

One of the Markov state models obtained using TRAM was coarse-grained using PCCA+⁶⁰ in order to create a smaller, more comprehensible model that could be interpreted to gain more insight into the mechanism of dissociation of ligand 1. The Markov model with 50 clusters and an MSM lag time of 2 ns was used; this model was chosen because the probability estimates in the 50-cluster model were likely to be more accurate, and of the 50-cluster models, a lag time of 2 ns produced the most accurate estimate of the dissociation rate. PCCA+ is a method for using the Markov model to combine the clusters originally defined using k-means clustering into larger macrostates such that the transitions between macrostates are slow compared to the transitions within them. It allows for ‘fuzzy” or “soft” macrostates, in which each cluster can belong to multiple macrostates to a fractional extent given by a “membership grade” for each cluster and each macrostate. These “fuzzy” macrostates can then be reduced to “crisp” macrostates by identifying for each cluster the macrostate to which it belongs to the greatest extent. The coarse-grained transition matrix for the unbiased thermodynamic state was recalculated from the original transition matrix estimated by TRAM for that state using the following equation:

$$p_{\text{AB}}=\frac{\sum _{\text{j}\in \text{B}}\sum _{\text{i}\in \text{A}}{w}_{\text{i}}{p}_{\text{ij}}}{\sum _{\text{i}\in \text{A}}{w}_{\text{i}}}$$ (3)

This equation gives the coarse-grained transition probability p_AB for transitions between macrostates A and B in terms of the original transition probabilities p_ij for transitions from cluster i to cluster j which belong to the macrostates according to the crisp memberships, as well as the stationary distribution w_i for the original Markov model. This ensured that the coarse-grained transition matrix satisfied the mathematical properties needed for stochasticity, whereas using the fuzzy membership grades for this calculation did not necessarily do so. Both the application of TRAM to produce fine-grained Markov models and the application of PCCA+ to reduce the Markov model were performed using PyEMMA.⁶¹

From each macrostate identified by PCCA+, a random sample of 100,000 frames was selected for structural analysis. Using this sample, a Ramachandran analysis was carried out on residues 566–580, covering the activation loop. A hydrogen bond analysis was carried out searching for potential hydrogen bonds between ligand 1 and the protein; hydrogen bonds were defined as involving either nitrogen, oxygen or fluorine as donors or acceptors, with a donor-acceptor distance of 3.5 Å or less and an angular deviation of 20° from straightness. A contact analysis was performed by calculating for each non-hydrogen atom in the protein the fraction of frames in which that atom was within 4 Å of one of the non-hydrogen atoms in the ligand. These analyses were performed using VMD.⁶²

3 |. RESULTS

3.1 |. Free energy surface for exit of ligand 1 from PYK2 binding site

The three-dimensional free energy surface for the center of mass of ligand 1 from the active site of PYK2 gives a sense of the possible pathways for ligand dissociation and the location and nature of activation barriers. Figure 3 shows this surface as a series of contour surfaces in relation to the protein; saddle points in the surface indicate the position of the ligand center of mass in the transition state. The use of a large number of τ-RAMD simulations to define centers for the umbrella potentials allowed for sampling a much larger space of possible ligand positions, and estimating a more complete free energy surface, compared to our previous work with FAK in which we used a steered MD simulation for this purpose and where the free energy was well estimated only near this pathway. As with FAK, the lowest free energy basin corresponds to the bound state. Figure 3 shows several contour surfaces. The top panel displays contour at 12.5 and 13.0 kcal/mol. The 12.5 kcal/mol contour revealed two free energy basins, a larger one surrounding the bound state, and a smaller one nearby. At 13.0 kcal/mol, these two basins can be connected. The bottom panel shows how several basins not connected by the contour at 15.0 kcal/mol become connected at 15.5 kcal/mol. At these contours, two pathways of dissociation are evident: one towards the activation loop shown on the right side of the figure, the other away from the linker connecting the N- and C-terminal lobes of the kinase domain, shown on the left side of the figure. The estimated standard error of the free energy surface is approximately 0.5–1 kcal/mol.

FIGURE 3.

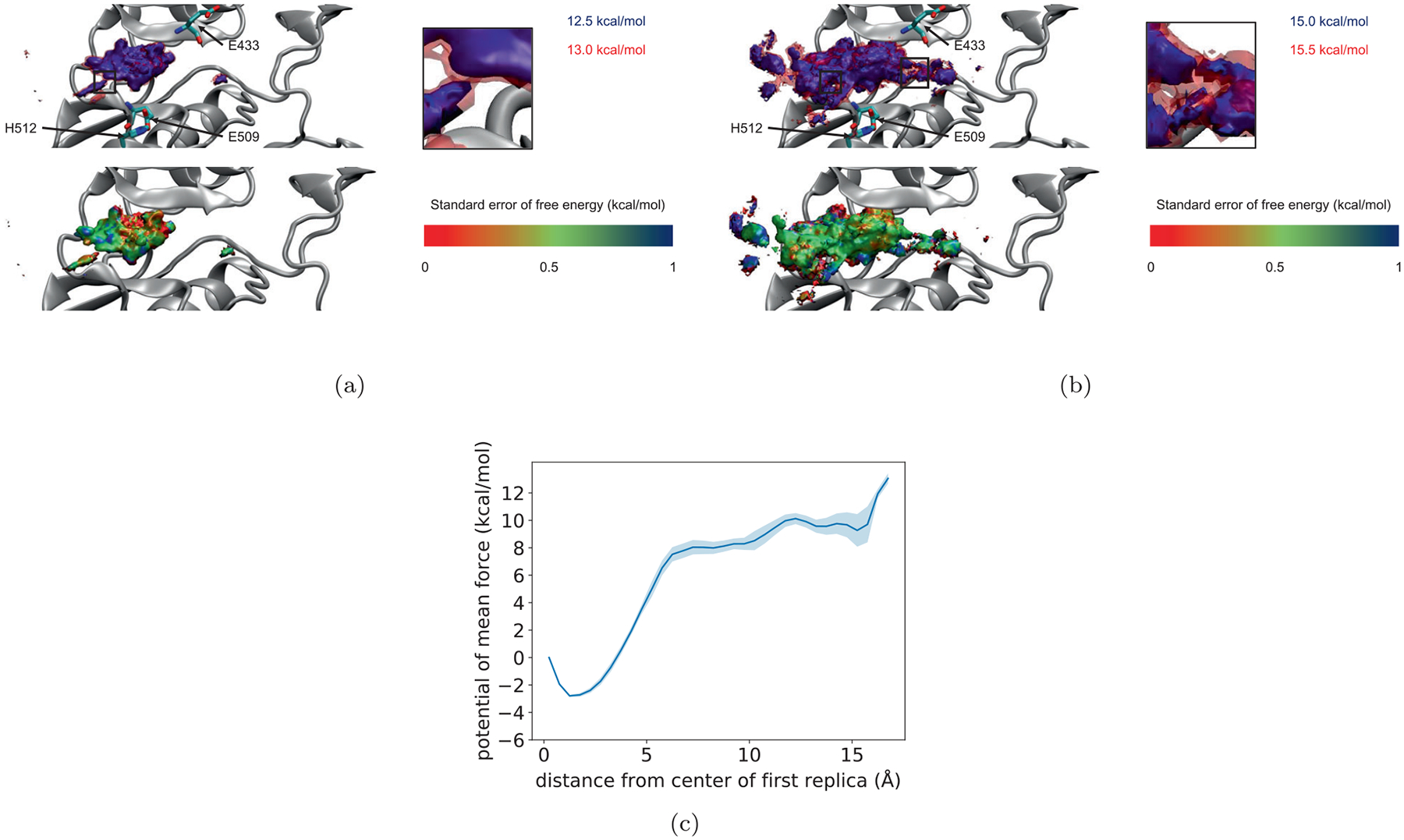
Contour plots of the free energy surface of the center of mass of ligand 1 relative to PYK2 as determined from umbrella sampling simulations, together with standard error of free energy surface as determined from dividing umbrella trajectories into thirds (see text). (A) The top panel shows two contours just before and just after the two states on the left can be connected. The bottom panel shows the lower contour colored by its SE. (B) As in (A), but for the contours just before and just after the two states on the right are also connected. In both cases, insets show close up views of the region of connection. (C) One dimensional potential of mean force as a function of the distance of the ligand center of mass from the binding site

The one-dimensional potential of mean force shown in Figure 3C contains a large well at 2 Å, corresponding to the bound state, but does not show a distinct transition state, unlike the one-dimensional PMFs calculated for the exit of various ligands from FAK.⁵⁰ This is likely because this PMF results from integrating out the other two degrees of freedom and combining the two pathways, which have transition states with the ligand at different distances from its original position. This shows the benefits of constructing a three-dimensional free energy surface described above.

3.2 |. Estimating the dissociation rate of ligand 1 from simulation

One way to estimate the dissociation rate of ligand 1 is to use Eyring’s transition state equation^63,64:

$$k_{\text{d}}=\frac{\kappa k_{\text{B}}T}{h}\text{exp}\left[-\frac{\Delta {\text{G}}^{‡}}{k_{\text{B}}T}\right]$$ (4)

where ΔG^‡ is the transition state free energy, T is the temperature and κ the transmission coefficient (the fraction of reactions that proceed to products after reaching the transition state). From Figure 3, ΔG^‡ is about 15.25 kcal/mol. Assuming the transmission coefficient κ to be 1 gives a dissociation rate of approximately 48:4 s⁻¹, which is about three orders of magnitude larger than the experimental dissociation rate. One approach to resolving this discrepancy would be to perform additional simulations to estimate κ. Since κ is always less than 1, incorporating an estimated value into Eyring’s equation should bring the calculated rate closer to the experimental value. However, we instead tried to estimate the dissociation rate using a more accurate approach than transition-state theory.

The construction and use of Markov models offers an alternative, more rigorous approach to the estimation of dissociation rates from MD simulation data, and the use of TRAM allows for including data from biased simulations, such as the umbrella sampling simulations performed here. Table 3 shows the dissociation rates calculated using TRAM for different choices of the number of microstates and Markov model lag time. All of the estimates are within 1–2 orders of magnitude of the experimental value, except for the estimate obtained from a 100-cluster Markov model with a 5 ns lag time, which is off by a factor of approximately 400. This is likely because the larger number of clusters, together with the long lag time, reduces the number of frames available for the estimation of transition probabilities and therefore results in a statistically less accurate estimate of the dissociation rate.

TABLE 3.

Comparison between estimates of the dissociation rate of ligand 1 obtained using TRAM and experimental dissociation rate from ref. 65

Number of clusters	MSM lag time (ns)	koff (s−1)
50	1.0	1.39
50	2.0	0.56
50	5.0	0.80
100	1.0	0.33
100	2.0	0.17
100	5.0	33.44
Experimental		0.074±0.025

The consistency of the dissociation rate estimates also suggests that the Markov models have converged as a function of the MSM lag time. As an additional test to verify convergence of the Markov model, Figure S1 in the supporting information shows a plot of the implied timescales of the unbiased state Markov model as a function of the MSM lag time for both 50 and 100-cluster models. In both cases, the longest timescales appear to have converged by an MSM lag time of 2 ns.

3.3 |. Mechanism of ligand 1 dissociation from PYK2

While the original Markov state models yielded relatively accurate estimates of the dissociation rate, they contained too many microstates to be easily interpreted in terms of a structural mechanism for dissociation. Consequently, the models were coarse-grained using PCCA+ in order to reduce the number of states and produce a less complex and more easily interpreted model. A five-state model constructed using PCCA+ is shown in Figure 4 as a kinetic network, together with renderings of a random selection of 10 frames from each macrostate. The corresponding stationary probabilities and relative free energies of the macrostates are shown in Table 4. In this model, dissociation proceeds via a two-step mechanism, in which the system passes from the bound state (macrostate 4) to an intermediate state (macrostate 2) and then to one of two dissociated states (macrostates 0 and 3). Macrostate 0 appears similar to the dissociation pathway exiting the linker connecting the N- and C-terminal lobes shown in the free energy contour in Figure 3. Macrostate 3 resembles the dissociation pathway towards the activation loop. Macrostate 2, the intermediate state, is the central state within the network and includes configurations in which the ligand has departed from the binding site but is still interacting with both domains of the protein.

FIGURE 4.

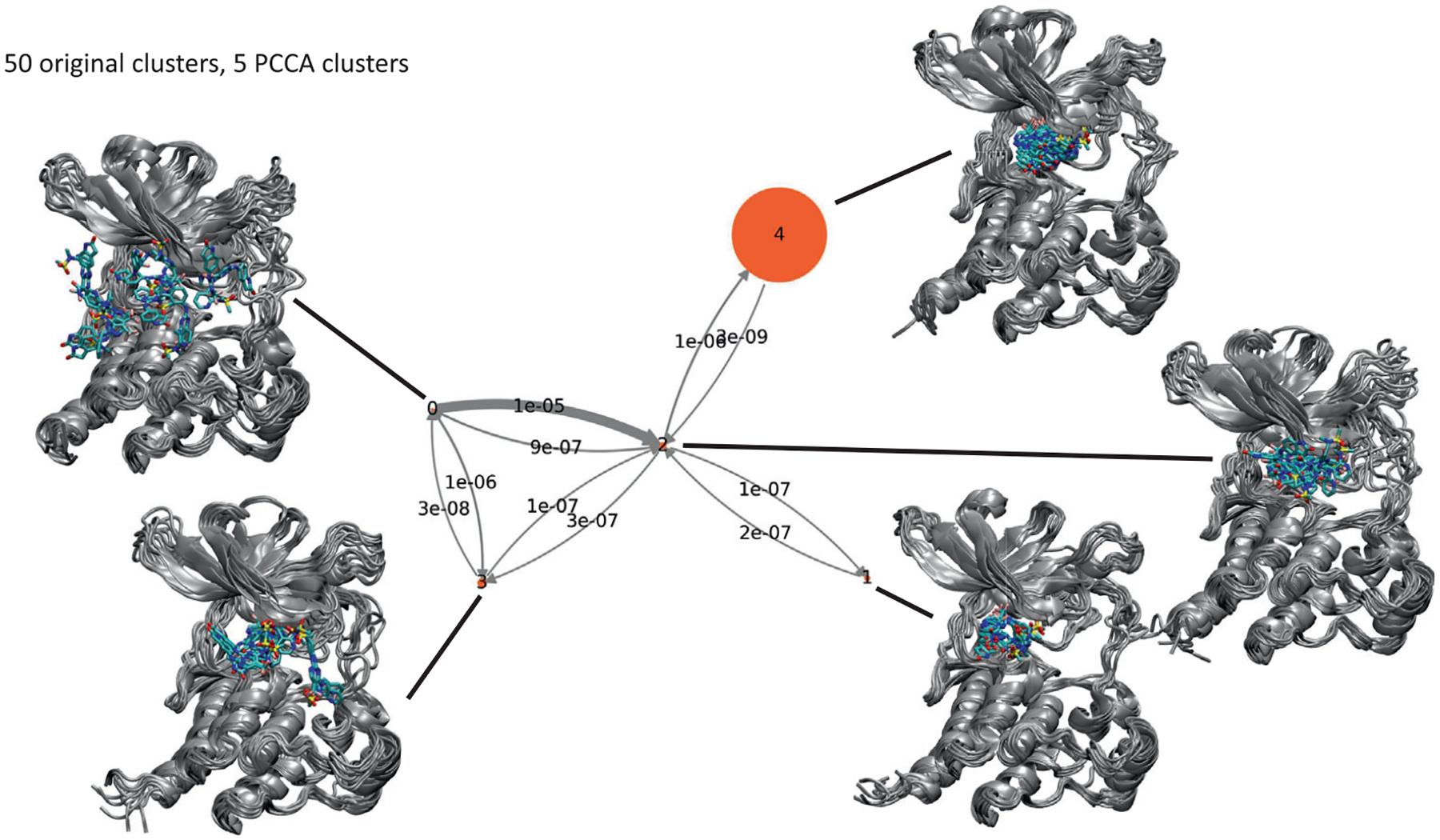
Network illustrating transition probability matrix for unbiased state of TRAM model originally constructed using 50 clusters and an MSM lag time of 2 ns, condensed down to 5 macrostates using PCCA. Each state is illustrated using a superposition of 10 frames randomly chosen from the corresponding macrostate. The area of each disk is proportional to the corresponding stationary population (shown in Table 4) and the thickness of each arrow is proportional to the corresponding transition probability

TABLE 4.

Probabilities from the stationary distribution and corresponding relative free energies for the five macrostates shown in the network model of Figure 4

Macrostate	Number of frames	Stationary probability	Relative free energy (kcal/mol)
0	1,567,191	1.9 × 10−4	5.1
1	131,576	2.0 × 10−3	3.7
2	2,974,824	3.0 × 10−3	3.5
3	292,842	6.2 × 10−3	3.0
4	145,647	9.9 × 10−1	0.0

Macrostate 1 appears to represent a state in which the ligand occupies the binding site, similar to the bound state, but containing configurations in which the ligand adopts an alternative bound conformation distinct from the conformation shown in the main bound state with lower free energy. In this alternative conformation, the sulfonamide moiety points away from the binding site, rather than facing towards the N-terminal domain or activation loop as it does in the crystal structures or in the main bound state. Macrostate 1’s free energy is higher than the bound state, macrostate 4, by about 3 kcal/mol. The conformations of the ligand within macrostate 1 appears less varied than those in macrostate 4, which would suggest reduced conformational entropy which would in turn contribute partially to the higher free energy of macrostate 1. Similar mis-bound state was observed in an earlier simulation of the binding/unbinding pathways between p-nitrocatechol sulfate and the protein phosphatase YopH⁶⁶ As in this study, the mis-bound state and the bound state could not interconvert without the ligand first moving out a little from the binding site.

We also analyzed and compared protein-ligand interactions in the macrostates. Figure 5 shows the parts of the protein surface that are contacted by ligand 1 while Table 6 shows contacts on a residue basis in each macrostate, and Table 5 shows the occupancy of hydrogen bonds between ligand and protein. The contact analysis illustrates how macrostate 2 (the intermediate state) dissociates in opposite directions to reach macrostate 0 and 3; the table of contacts by residue also points to contacts with residues 429–439 in the N-terminal domain, residues 502–512 in the linker, and residues 553 and 556 in the C-terminal domain, many of which are hydrophobic in nature. In the bound state (macrostate 4), two classic hydrogen bonds formed between the inhibitor and the backbone of the linker connecting the N- and C-terminal lobes using N2 and N9 of the ligand and residue Y505 of the protein. The sulfonamide provides additional hydrogen bonds with the backbone of E433 and E509. The oxindole moiety adds hydrogen bond interactions with the side chains of Y505 and H512. The intermediate state (macrostate 2) keeps the hydrogen bonds in the bound state except those formed by the oxindole moiety. On the other hand, the sulfonamide moiety extends its interactions to include the backbone NH group of E509. Although not found with at least 1% occupancy in the bound state, this sulfonamide-NH interaction occurs with greater than 1% occupancy in all the other four macrostates. The dissociated macrostate 0 loses most of the hydrogen bond interactions occuring in the bound state. Instead, it uses the oxindole to interact with the side chain of E509, and the middle ring to interact with the side chain of N517. The other dissociated state (macrostate 3) loses the interactions in the bound state except the interactions between the sulfonamide and the protein. In some frames of macrostate 3, the oxindole moiety of ligand 1 makes contact with F435 while there is a salt bridge interaction between the sulfonamide moiety and R586 and a hydrophobic contact between the pyridine ring and V584. Figure 6 shows example frames demonstrating these interactions. The figure also shows key atoms in the protein forming hydrogen bonds in macrostate 2, including interactions between the sulfonamide moiety and the backbone of E433.

FIGURE 5.

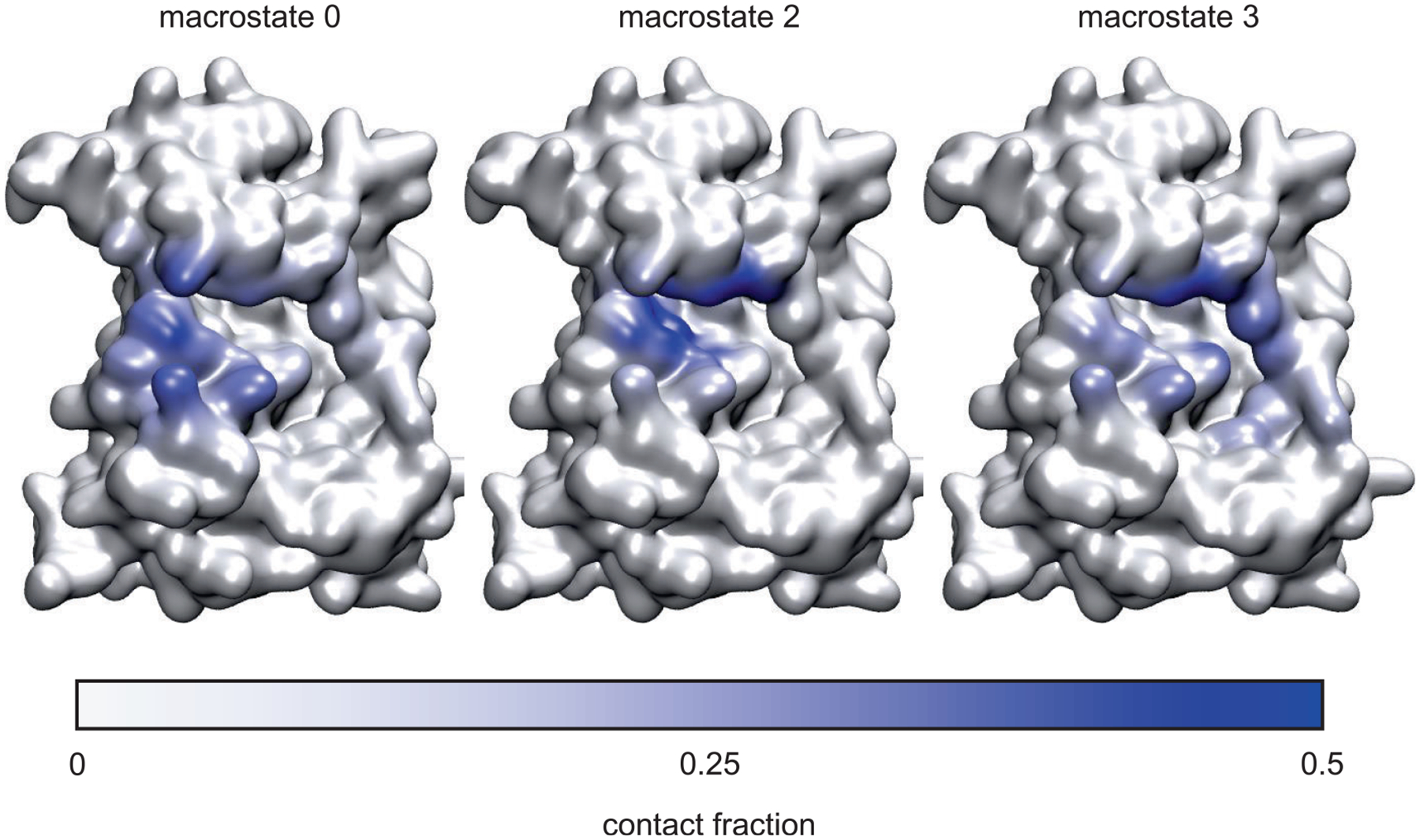
Molecular surface representation of PYK2, colored according to the fraction of contacts between each non-hydrogen atom and ligand 1, for macrostates 0, 2, and 3 in the 5-state network model shown in Figure 4. Contacts were defined as any pair of non-hydrogen atoms within 4 Å

TABLE 6.

Percentage of frames in which ligand 1 is in contact with residues for each macrostate in the 5-state network model shown in Figure 4. Contacts were defined as any pair of non-hydrogen atoms within 4 Å, and residues are listed if they made contact with the ligand at least 5% of the time in at least one macrostate

Residue	0	1	2	3	4
R429	40.3	11.6	22.0	15.1	12.3
I430	22.9		11.4	8.9	0.2
L431	44.7	98.0	93.9	65.3	97.7
G432	15.9	82.2	76.1	58.1	94.9
E433	17.9	66.1	76.0	72.9	94.4
G434	9.9	20.9	40.2	50.5	53.1
F435	10.5		1.8	46.2	1.6
V439	4.2	78.3	73.8	45.4	92.8
E441	23.6	0.3	4.4	1.1	2.8
N453	8.3
A455	1.0	94.9	66.6	5.3	92.8
K457		29.0	49.5	9.1	81.8
V487		25.6	19.1		7.2
M502	0.2	95.6	63.7	3.0	85.7
E503	1.1	95.3	63.2		73.0
L504	22.3	77.8	50.8	7.1	45.9
Y505	15.4	99.4	74.1	11.7	75.3
P506	54.3	80.0	52.4	21.6	33.7
Y507	41.6	18.2	11.6	13.5	4.6
G508	24.0	93.0	74.2	24.8	66.6
E509	19.9	87.7	63.7	20.2	63.6
G511	7.4		0.5
H512	44.5	11.0	17.0	30.0	17.9
Y513	14.9			0.2
E515	10.0			0.4
R516	45.7	9.4	13.4	22.3	4.3
N517	15.0
D549	0.2			8.8
R553	14.5	65.5	50.2	38.8	44.8
N554		4.7	12.2	2.1	3.3
L556	2.9	92.4	69.8	11.6	69.6
P560	6.7
D567		12.1	8.5	9.6	9.2
S583	4.0			11.7
V584	7.3		0.3	35.0
T585	5.0			1.9
R586	4.5			22.0
L587	0.5			10.0
P588	1.0			14.9
W591	1.0			15.5

TABLE 5.

Occupancy of hydrogen bonds between ligand 1 and the protein in each of the five macrostates shown in the network model of Figure 4. Only hydrogen bonds present in more than 1% of frames are shown. Hydrogen bonds were defined by distance and angle criteria of 3.5 Å between donor and acceptor and angle of 20° deviation from straightness. Names for atoms in ligand 1 are as shown in Figure 1

Donor	Acceptor	Macrostate
				0	1	2	3	4
E509	N	Ligand 1	O32	1.01	3.24	1.43	1.07
Ligand 1	N25	E509	OE1	1.16				1.59
N517	ND2	Ligand 1	N2	4.74
Ligand 1	N9	N517	OD1	1.86
Y505	N	Ligand 1	N2		47.80	27.89		28.21
Ligand 1	N9	Y505	O		32.09	11.63		6.72
E433	N	Ligand 1	O32		1.81	2.52	3.35	6.80
E433	N	Ligand 1	O33			1.41	3.44	1.23
Ligand 1	N9	E433	O				2.90
Ligand 1	N25	E509	OE2					2.32
H512	ND1	Ligand 1	O26					1.12

FIGURE 6.

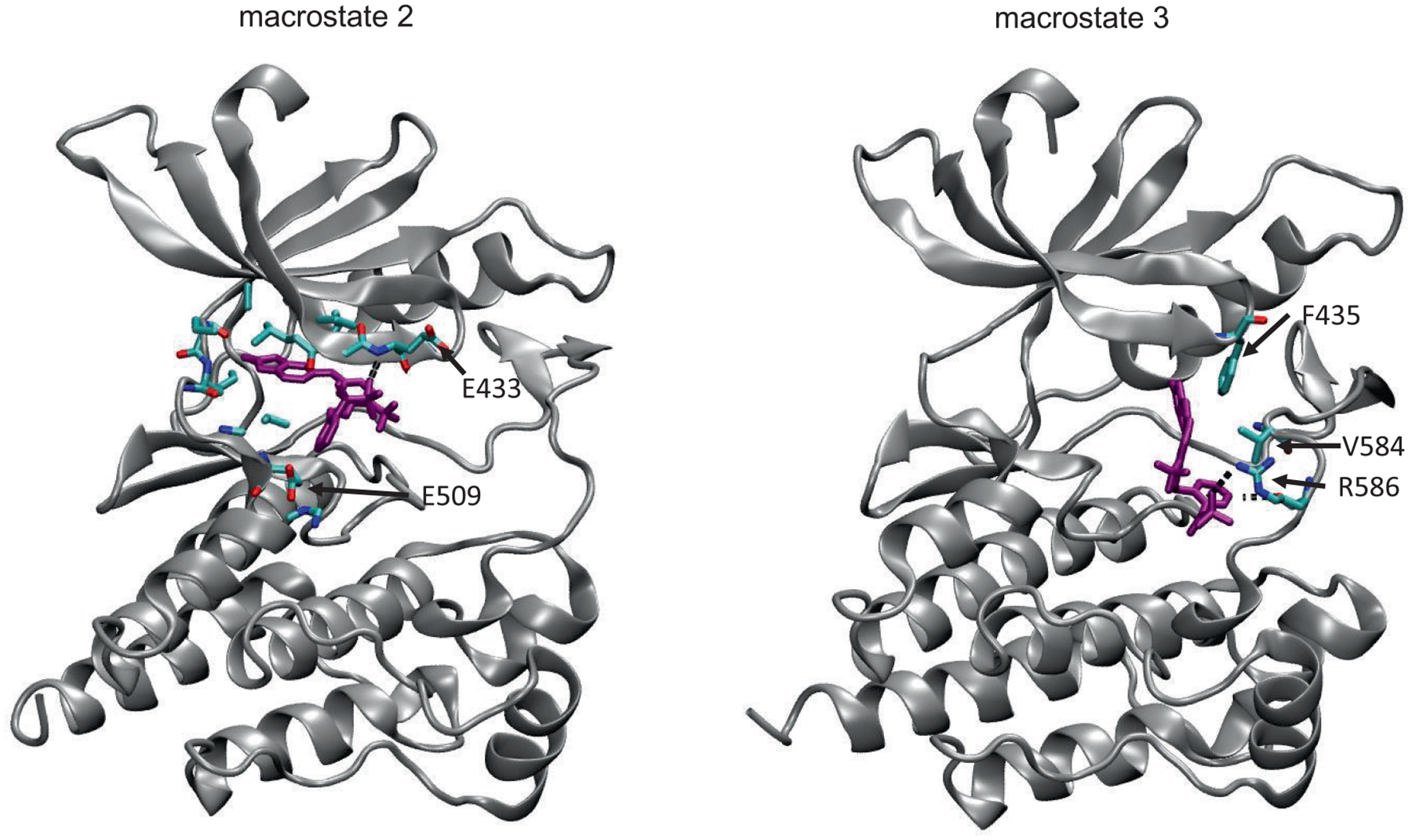
Example frames from macrostate 2, showing the atoms that form hydrogen bonding interaction between sulfonamide moiety of ligand 1 and backbone of E433, and from macrostate 3, demonstrating interaction of ligand 1 with F435, V584, and R586

The renderings from each macrostate shown in Figure 4 also suggest variations in the backbone conformation of the activation loop in each macrostate. To investigate this further, Ramachandran plots were constructed for the residues in the activation loop for each macrostate, as shown in Figure 7. These plots show differences in the backbone conformation of the DFG motif and the activation loop. Modi and Dunbrack⁶⁷ have developed a classification scheme for conformations of the DFG motif based largely on the backbone dihedral angles of the aspartate and phenylalanine residues in the motif, as well as those of the immediately preceding residue. For PYK2, these residues are G566, D567, and F568. In the crystal structure, they are all in β-sheet regions of the plot, and similar configurations can be found in all five macrostates. These configurations do not correspond directly to any of the Dunbrack classifications, but macrostates 1 and 3 contain configurations with D567 in the left-handed α-helical conformation, corresponding to the “BLBminus” conformational state in the “DFGin” group described in that paper. Other residues in the activation loop also show differences. For example, L570 shows variations in the balance between β-sheet and left handed α-helical regions depending on the macrostate, while S571, I574, and D578 show increases in the α-helical region of the plot in some macrostates. These differences suggest a role for backbone conformational changes in the activation loop in modulating ligand binding, particularly the exit of ligand 1 through macrostate 3.

FIGURE 7.

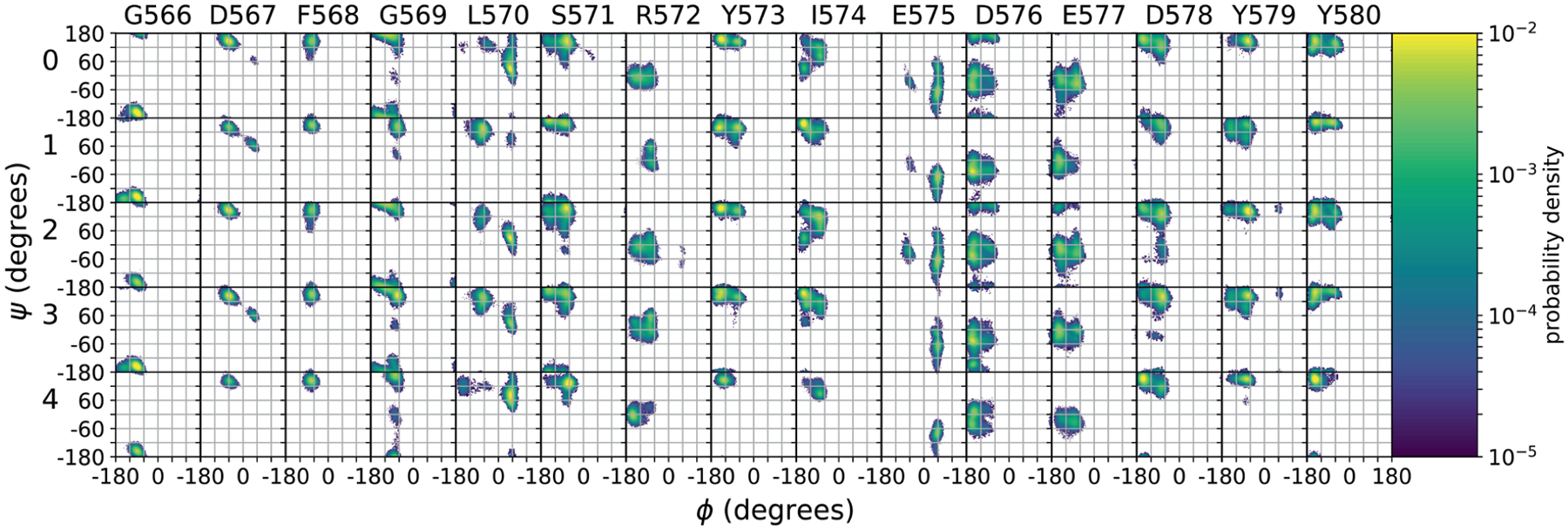
Ramachandran angle distributions for amino acid residues in the PYK2 activation loop (residues 566–580) for the five macrostates shown in the network model of Figure 4

4 |. DISCUSSION

4.1 |. Assessment of barrier heights and dissociation rates

A principal goal of this work was to identify methods for more accurately calculating the absolute dissociation rate of ligands from protein kinases. While the free energy surface produced by umbrella sampling provided useful insights into the mechanism of dissociation of ligand 1 from PYK2, the dissociation rate estimated by applying Eyring’s equation to the barrier height turned out to be three orders of magnitude too fast. Similarly, our previous attempt to use umbrella sampling to estimate the dissociation rates of three ligands from FAK yielded dissociation rates too fast by several orders of magnitude, and did not entirely get the ordering right.⁵⁰ By contrast, TRAM gave estimates of the dissociation rate that came within an order of magnitude of the experimental rate.

The improved success of the TRAM-based method reported here can be attributed to several factors. The umbrella sampling method requires a reaction coordinate to be defined beforehand. In this work, the reaction coordinate was defined by the center of mass of the ligand placed along trajectories obtained by τ-RAMD simulations. The choice of the coordinates of the center of mass of the ligand relative to the protein made it possible to portray the free energy surface in three dimensions and to locate basins and transition states relative to the protein, but coupled motion with protein conformational change was not described well. This can result in barrier heights that are too low or too high.³⁰ The Markov state analysis works in a much higher dimensional space and consequently can identify better reaction coordinates that describe a more complex pathway for ligand unbinding. The determination of the dissociation rate using TRAM is also based on a more rigorous transition path theory, compared to the approximate determination of the rate from the Eyring equation using the barrier height derived from umbrella sampling.

4.2 |. Mechanism of ligand dissociation

The umbrella sampling simulations and the Markov state model were consistent in showing two pathways for the dissociation of ligand 1 from PYK2. The Markov state analysis showed a clear intermediate state (macrostate 2) bridging the bound state and the two dissociation states (macrostates 0 and 3). Multiple pathways of dissociation were also observed in previous simulations, such as the dissociation of benzene from the binding site of the L99A mutant of T4 lysozyme,^24,68 and the dissociation of a hexapeptide from the insulin receptor tyro-sine kinase.⁶⁹ In addition, macrostate 1 from the Markov state model suggests that ligand 1 can bind to PYK2 with a pose having higher free energy and this pose can only be interconverted with the pose having the lowest free energy by the ligand first moving out a little from the binding site. This phenomenon was also observed in a previous simulation of the binding/unbinding between p-nitrocatechol sulfate and the protein phosphatase YopH.⁶⁶

As Badaoui et al.⁷⁰ used umbrella sampling and string methods to study the dissociation of several ligands from another protein kinase, cyclin dependent kinase 2 (CDK2), it is useful to compare their dissociation mechanisms to ours. In their method, an initial dissociation pathway is constructed by performing biased simulations using a biasing potential based on a periodically updated list of interatomic distances. The finite temperature string method is then used to obtain the potential of mean force along this pathway. Their method identified only one dissociation pathway for each ligand, whereas in this work two separate dissociation pathways for ligand 1 with different barrier heights are described. That said, the dissociation pathway of ligand 18 K they describe involves the ligand moving forward and out of the binding site in a similar manner to the dominant pathway obtained here, whereas the dissociation pathway for ligand 62 K appears to be more similar to the sideways pathway, interacting with Val163 in the activation loop of CDK2. Structural differences between ligands 1 and ligands 18 and 62 K of CDK2 mean that they do not form analogous hydrogen bonds during dissociation. For example, an amine group attached to a thiazole ring in ligand 18 K makes and breaks hydrogen bonds with the backbone oxygen atoms of Glu81 and His84 in CDK2 during dissociation. However, ligand 1 only has a trifluoromethyl group in a similar position to the thiazole ring, so cannot make hydrogen bonds with the analogous backbone oxygen atoms of E503 or P506 in PYK2. The sulfonamide group of ligand 62 K also makes and breaks a hydrogen bond with the backbone oxygen atom of His84, but the oxindole group of ligand 1, which is in the same position, does not make a similar hydrogen bond, likely because this would require the oxindole ring to flip over so that atom N25 is facing the peptide backbone.

4.3 |. Comparison with WExplore and REVO

It is interesting to compare our approach with WExplore²⁶ and REVO,²⁷ which have also recently been used to study long-timescale ligand unbinding processes, have a similar computational expense, and also do not require single progress coordinates. These WExplore and REVO methods are extensions of the weighted ensemble method^16,18 that are designed to encourage sampling in a high dimensional space of progress coordinates. Like the weighted ensemble method, they are based on running multiple unbiased simulations (“walkers”) simultaneously and cloning or merging them to balance resources in sampling relevant space. In recent applications of these approaches to studying drug-dissociation kinetics, simulations were all started in the bound state. As the simulations discovered previously unexplored space, new trajectories were spawned in the newly discovered space. Repeating this process gradually generated dissociation pathways. In our approach here, we first used trajectories from random-accelerated molecular dynamics (RAMD) to map out preliminary dissociation pathways. As RAMD applied random artificial forces to speed up dissociation, it did not give actual time scale. We used TRAM to quantify kinetics afterwards. As noted above, TRAM also works in a high-dimensional space. In unpublished work, we also used the fluctuation amplification of specific traits (FAST) method⁷¹ to discover dissociation pathways from the bound state without applying artificial forces. The idea was similar to the recent application of WExplore or REVO to studying drug-dissociation kinetics in that dissociation pathways was gradually discovered by spawning more trajectories in previously unexplored space, starting from the bound state. The dissociation pathways can then be used in TRAM as described in this paper. However, WExplore and REVO discover pathways and obtain kinetics simultaneously without the need to divide the two processes into separate steps. Furthermore, WExplore and REVO do not assume Markovian behavior and could be useful for studying systems that do not follow Markovian kinetics.

5 |. CONCLUSION

Although umbrella-sampling simulations along with transition-state theory over-estimated the dissociation rate of a ligand from PYK2 by three orders of magnitude, using the results together with TRAM gave results within an order of magnitude of experiment. TRAM combines biased and unbiased trajectories in the Markov state model to provide better estimates of rates with more manageable computational costs. Our simulations suggested that the dissociation of the ligand took two dominant paths moving in opposite directions, one towards the activation loop. Coarse graining the Markov states helped to gain deeper insight into the mechanism of ligand dissociation. The dissociation went through an intermediate state in which the interactions between the oxindole ring of the ligand and the protein occurring in the bound state were lost. Differences in the structures of the activation loop in the coarse-grained Markov states suggested the activation loop might play a role in influencing ligand dissociation.

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.