The Length of the ROC Curve and the Two Cutoff Youden Index within a Robust Framework for Discovery, Evaluation, and Cutoff Estimation in Biomarker Studies Involving Improper ROC Curves

Abstract

During the early stage of biomarker discovery, high throughput technologies allow for simultaneous input of thousands of biomarkers that attempt to discriminate between healthy and diseased subjects. In such cases, proper ranking of biomarkers is highly important. Common measures, such as the area under the ROC curve (AUC), as well as affordable sensitivity and specificity levels, are often taken into consideration. Strictly speaking, such measures are appropriate under a stochastic ordering assumption, which implies, without loss of generality, that higher measurements are more indicative for the disease. Such an assumption is not always plausible and may lead to rejection of extremely useful biomarkers at this early discovery stage. We explore the length of a smooth ROC curve as a measure for biomarker ranking, which is not subject to directionality. We show that the length corresponds to a ϕ divergence, is identical to the corresponding length of the optimal (likelihood ratio) ROC curve, and is an appropriate measure for ranking biomarkers. We explore the relationship between the length measure and the AUC of the optimal ROC curve. We then provide a complete framework for the evaluation of a biomarker in terms of sensitivity and specificity through a proposed ROC analogue for use in improper settings. In the absence of any clinical insight regarding the appropriate cutoffs, we estimate the sensitivity and specificity under a two-cutoff extension of the Youden index and we further take into account the implied costs. We apply our approaches on two biomarker studies that relate to pancreatic and esophageal cancer.

1. Introduction

The most common statistical tool for the evaluation of continuous classifiers that attempt to discriminate between two distinct classes is the Receiver Operating Characteristic (ROC) curve ([1]). It has been a commonplace strategy to evaluate the discriminating ability of various kinds of classifiers such as blood-based tests, urine-based tests, imaging, cognitive tests etc. Typically, in many biostatistical applications biomarkers attempt to discriminate between a non-diseased and a diseased group. An underlying assumption in many ROC studies is that the density ratio is monotone. This implies the traditional setting found in the literature where the higher the marker score, the greater the suspicion for the disease (or the mathematically equivalent claim that the lower the marker score the higher the suspicion for the disease). In such cases the marker scores comply with the stochastic ordering assumption of the form X < Y, where X is the random variable that refers to the scores of the non-diseased group and Y is the random variable that refers to the marker scores of the diseased group. Under this scenario we have concavity of the ROC curve and an appropriate and popular summary measure of the discriminatory ability of a continuous marker is the area under the ROC curve (AUC) which is equal to the probability P(X < Y). The popular Mann-Whitney test-statistic ([2]) is simply a two-sided test of the null hypothesis that states that the AUC is equal to 0.5. In cases where the density ratio is not monotone we obtain non-concave (also known as improper) ROC curves. When concavity is severely violated then the use of typical ROC analysis may be very misleading. In some cases, improper ROCs indicate differences in terms of scale apart from differences in terms of location. The vast clinical literature that deals with biomarkers focuses on the traditional settings. However, it may be the case that in many applications there are biomarkers of great promise that exhibit improper ROC curves. They may yield an AUC that is very close to 0.5, potentially misleading a researcher to dismiss such biomarkers as uninformative, in spite of their potentially high discriminatory ability. As we will see in the discussion to follow, it may be the case that a marker is perfect and yet its AUC is equal to 0.5. As a result, when traditional measures such as the AUC are blindly applied in large lists of candidate biomarkers, then potentially excellent biomarkers that are not monotone are doomed to be missed. Modern high-throughput technologies allow us to simultaneously assay hundreds or even thousands of markers, a practice quite common in cancer research. This situation illustrates a need for a robust statistical framework that can reveal all useful markers whether they are monotone or not. Once these are discovered then it is of interest to evaluate them with clinically appealing measures such as the sensitivity and specificity tradeoffs, that need to be redefined for non-monotone markers. Finally, once the useful markers have been identified clinical interest lies in determining decision making cutoffs.

One example of the aforementioned setting refers to assays that involve blood-based biomarkers for the detection of pancreatic cancer. Pancreatic ductal adenocarcinoma (PDAC) is the third leading cause of cancer-related mortality in both men and women in the United States. Overall, PDAC is associated with a dire prognosis and a 5-year survival rate of approximately 8%, which makes PDAC the most deadly of cancers by organ site ([3]). The diagnosis of PDAC at an early stage is uncommon and usually incidental, with the majority of patients (∼85%) presenting with locally-advanced or metastatic disease ([4]). Currently, no individual marker has adequate performance characteristics for detecting early stage PDAC in asymptomatic individuals. High throughput technologies like mass-spectrometry and protein microarrays are commonly used for biomarker discovery, often providing a very large set of candidates that initially need to be ranked based on some criterion. Common criteria are the area under the ROC curve or the sensitivity/specificity at a (clinically affordable level. While these criteria enjoy a broad acceptance in both statistical and clinical literature, they fail to capture biomarkers that are of improper behavior. Selection based on the AUC, initially studied by [5], implicitly assumes stochastic ordering of the two distributions (i.e., healthy versus diseased) of biomarker scores. There are cases, however, in which this single-directionality assumption is severely violated. For example, plasma tumor antigen levels may be associated with immune complex formation, leading to depletion of the free autoantibodies against the antigen as well as the antigen itself, which may serve as cancer biomarkers ([6]). Using conventional statistical techniques for discriminatory ability rankings might eliminate further consideration of promising or even excellent biomarkers without allowing researchers to question and explore them further. An additional example is studies associating lung cancer with levels of pro-surfactant protein B (ProSFTPB) ([7]), for which both non-detectable (very low) and higher levels of ProSFTPB are being associated with the disease.

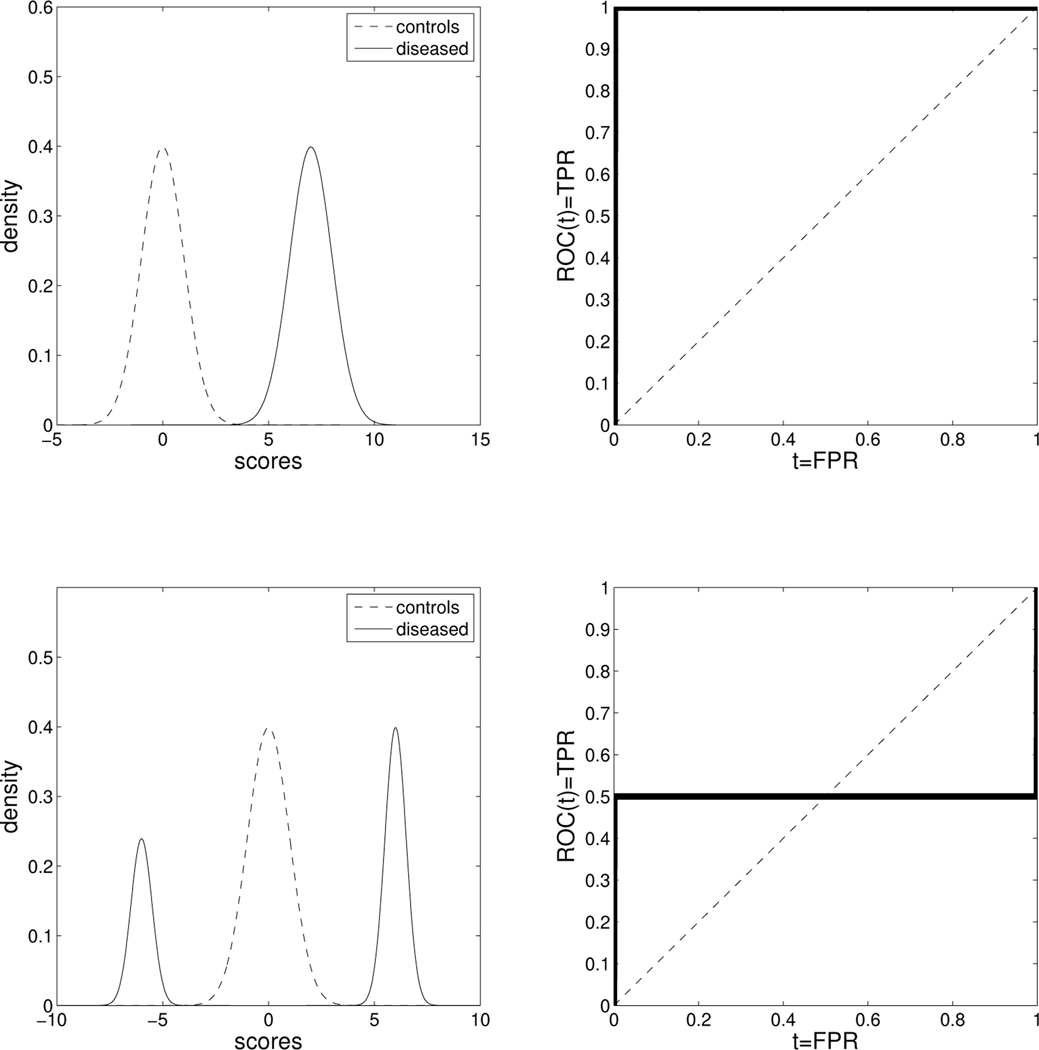
When a stochastic ordering does not hold, we cannot rely on the regular definitions of the sensitivity and specificity for ranking the candidate biomarkers. The notion of sensitivity and specificity needs to be extended to take into account this improper behavior. When stochastic ordering is violated, the AUC can be equal to 0.5, even when the underlying biomarker is perfect. The partial AUC (pAUC) can also be subject to that artifact. In Figure 1 we provide such an example, which also is discussed in [8]. Some authors have considered alternative criteria to capture such biomarkers in similar situations. Parodi (2008) [9] et al. propose the area between the ROC curve and the reference diagonal (named as ABCR). It is defined as $ABCR={\int }_0^1|ROC(t)-t|dt$ and can be easily shown to be equal to ${\int }_{-\infty }^{\infty }\left|F_Y(z)-F_X(z)\right|f_X(z)dz$. Even though such a measure does manage to attribute discriminatory ability to markers that may be rejected by the AUC, it is still a hostage of directionality. For example, consider the two perfect markers shown in Figure 1. The ABCR for the upper panels is equal to 0.5 while for the lower panels it is equal to 0.25. Another interesting measure discussed in the same paper is the TNRC which is a useful measure to detect improper markers. We note that all these criteria refer to the two-sample problem which is also the focus of this paper.

Figure 1.

Upper panels: An example of a perfect biomarker where the densities of the controls and the diseased (left) comply with a traditional framework, under which the stochastic ordering X < Y holds, and the corresponding ROC curve is in the right panel. Corresponding metrics: AUC = 1, pAUC(t₁, t₂; t₂ > t₁) = t₂ − t₁, area between the ROC and the reference diagonal= 0.5, proposed length= 2. Lower panels: An example of a perfect biomarker in which the stochastic ordering X < Y cannot be assumed. Corresponding metrics: AUC = 0.5, pAUC(t₁, t₂;t₂ > t₁) = 0.5(t₂ − t₁), area between the ROC and the reference diagonal= 0.25, proposed length = 2 (the proposed length is immune to directionality and characterizes the underlying biomarker as perfect in both cases, as opposed to all other measures.)

When the stochastic ordering assumption is violated, essential differences between the two groups are frequently implied in terms of dispersion. As a result, goodness-of-fit tests, such as the Kolmogorov Smirnov and the two-sample extension of the Anderson Darling test, might provide useful alternatives ([10], [11]). Another measure proposed in [12] is the projected length of the ROC curve. Even though this measure is immune to directionality and can be linearly transformed to attain an interpretation as a probability, it is geometrically difficult to visualize. In addition, its asymptotic behavior is not yet thoroughly studied.

One measure that was very recently studied under a binormal setting is the length of the ROC curve ([13]). Therein, the utility of the length of the binormal model-based ROC curve as an accuracy index is discussed. In this paper, we study its use as a measure for ranking biomarkers in a general setting that involves discrimination of cases and controls that includes non-monotone biomarkers under general parametric as well as non-parametric frameworks. The length successfully captures useful markers, which would have been rejected using traditional measures. We illustrate that the length of the ROC is directly related to a ϕ divergence and we provide a test statistic for inference. We show that the length of the common ROC curve is identical to the length of the optimal, likelihood ratio-based, ROC curve. In other words, the length does not change when one applies the likelihood ratio transformation to the marker values. As we discuss, this is true for any ϕ divergence. Hence, a ϕ divergence reflects the potential discriminatory ability of a biomarker. Among possible ϕ divergences one might employ for inference, the length has the advantage of being geometrically appealing to practitioners. Furthermore, we apply isoperimetric methods to explore its relationship to the AUC of the optimal ROC curve. In other words, given the length of an ROC curve we obtain lower and upper bounds of the AUC of the optimal (likelihood ratio) ROC. We study the asymptotic behavior of the estimated length and its related test statistic assuming a general parametric family. Furthermore, in a non-parametric framework we estimate the length using kernel-densities and explore its statistical properties via bootstrap and permutation tests. Based on simulations, we observe that when the stochastic ordering assumption is violated, then the test based on the length outperforms traditional tests, such as the Wilcoxon, the t-test, and the Kolmogorov-Smirnov test.

Once the initial ranking is done, interest lies in clinically relevant measures that will provide insights regarding the performance of a selected biomarker. While the traditional ROC curve is the most popular statistical tool for the evaluation of a biomarker, it should be avoided when it is improper. We present an appropriate analogue of the ROC graph that visualizes the sensitivity and specificity in the ROC space under a framework that uses two cutoff points. We define an optimal ROC curve, under the notion of a unimodal likelihood ratio ordering, which defines a dispersion ordering. This optimal ROC curve is identical to the generalized ROC curve (gROC) first introduced in [14]. A parametric estimator has been considered in [15] and its Youden index in [16]. Optimality of the gROC under the normality assumption has been shown in [17]. In this paper, we show that the gROC is the optimal ROC under the assumption of a unimodal density ratio. We further discuss the notions of sensitivity and specificity in the presence of two cutoffs which we estimate based on an extension of the Youden index initially discussed in [18] and provide inferences around them that can also accommodate costs.

This paper is organized as follows: In Section 2 we present the proposed measure for biomarker ranking. We discuss its properties and provide results that relate the length of the ROC curve to the length and area of the optimal (likelihood ratio transformed) ROC curve. In addition, we explore the estimation and statistical inference based on this measure. In Section 3 we explore the appropriate ROC analogous when two cutoffs are considered and discuss the conditions under which the two-cutoff ROC is optimal. We present an example that illustrates the fact that a common ROC curve does not reveal the discriminatory ability of an improper marker and the appropriateness of using the length as a measure of discriminatory ability. In Section 4 we discuss estimation and inference for the sensitivity and specificity of such markers under different parametric and non-parametric settings. In Section 5 we discuss our simulations and in Section 6 we employ our approaches in two data sets related to cancer.

2. Length of the ROC Curve and ϕ Divergence

Let Y denote a continuous biomarker score in a study of n₀ healthy individuals and n₁ patients of the diseased group. Denote with $f_0(\cdot )$ and $f_1(\cdot )$ the densities of the healthy and the diseased group, respectively. Also denote the corresponding cumulative distribution functions as $F_0(\cdot )=1-S_0(\cdot )$ and $F_1(\cdot )=1-S_1(\cdot )$. We assume that the two distributions have common support. The traditional ROC curve is defined as $ROC(t)=S_1\left(S_0^{-1}(t)\right)$, $t\in (0,1)$. The length of a differentiable ROC curve, $l_{ROC}$, is given by the following two equivalent expressions:

$$l_{ROC}={\int }_0^1\sqrt{1+{\left(\frac{dgROC(t)}{dt}\right)}^2}dt={\int }_{-\infty }^{+\infty }\sqrt{{\left(\frac{dFPR(c)}{dc}\right)}^2+{\left(\frac{dTPR(c)}{dc}\right)}^2}dc$$ (1)

where FPR = S₀(c) and TPR = S₁(c) for a given cutoff c. Using the result in [1] (pg. 70), $\frac{dgROC(t)}{dt}=\frac{f_1\left(S_0^{-1}(t)\right)}{f_0\left(S_0^{-1}(t)\right)}$ we obtain

$$l_{ROC}={\int }_{-\infty }^{+\infty }\sqrt{1+{\left(\frac{f_1(x)}{f_0(x)}\right)}^2}{f}_0(x)dx={\int }_{-\infty }^{+\infty }\sqrt{f_1^2(x)+f_0^2(x)}dx.$$ (2)

We see that $\sqrt{2}\le l_{ROC}<2$. The minimum value, $\sqrt{2}$, is attained if and only if the distribution of the diseased is identical to that of the non-diseased, which implies a non-informative marker. The quantity $l_{ROC}-\sqrt{2}$, the difference between the length of the ROC curve and the length of a non-informative marker, is a ϕ divergence and is equivalent to the perimeter divergence measure studied by [19], as it is simply equal to the difference in perimeter of the set underneath the ROC curve between the marker studied and a non-informative marker. As shown in [19], the square root of this divergence is a metric divergence.

The following theorem shows that the length (and the corresponding divergence measure) remains the same when one considers the likelihood ratio ROC curve based on the marker Y, which is the length of the ROC curve associated with the random variable $W=\frac{f_1(Y)}{f_0(Y)}$. It is well known that the likelihood ratio ROC is concave and is the optimal ROC one can construct based on a given marker.

Theorem 1

Denote the length of the ROC curve obtained by using the untransformed Y by $l_{ROC}^Y$ and the length of the likelihood ratio ROC curve by $l_{ROC}^W$ (obtained by using the transformation $W=\frac{f_1(Y)}{f_0(Y)}$. Then $l_{ROC}^W=l_{ROC}^Y$.

Proof:

The proof follows from the fact that the likelihood ratio of the likelihood ratio equals the likelihood ratio (see [1], pg. 94), that is $\frac{g_1(w)}{g_0(w)}=w$, where g₀ and g₁ denote the densities of W for the healthy and diseased respectively. Let $\varphi (u)=\sqrt{1+u^2}$. We have

$$l_{ROC}^W=E_{G_0}\varphi \left(\frac{g_1(W)}{g_0(W)}\right)=E_{G_0}\varphi (W)=E_{F_0}\varphi \left(\frac{f_1(Y)}{f_0(Y)}\right)=l_{ROC}^Y\square .$$ (3)

We note here that it is evident from the proof that the above result is valid for all ϕ divergences. Thus, one can argue that ϕ divergences are well suited for making fair comparisons between markers based on a single ROC summary measure, as they are invariant to the optimal (likelihood ratio) transformation of the marker values. This is especially obvious in the case when no directionality of disease is assumed by the researchers. The length has the advantage of being a geometrically appealing measure. Moreover, we can relate the length to the AUC of the optimal (likelihood ratio) ROC. If the likelihood ratio and its distribution were known, then the AUC of the optimal ROC could be computed directly. This is almost never the case in practice. However, one can use the following theorem, which provides bounds on the AUC of the optimal ROC curve, given the length of the original ROC curve. These bounds can be used by practitioners to assess biomarkers.

Theorem 2

Let $l_{ROC}^Y=l$ and denote the AUC of the optimal ROC by AUC^W. Then 2a) For $\sqrt{2}\le l\le \frac{\pi }{2}$ we have

$$\frac{1}{2}+\frac{\left(l^2-2\right)}{4(l-1)}<AU{C}^W\le \frac{1}{2}+S,$$ (4)

where S equals the area of a circular segment with chord length equal to $\sqrt{2}$ and corresponding arc length equal to l. 2b) For $\frac{\pi }{2}<l<2$ we have

$$\frac{1}{2}+\frac{\left(l^2-2\right)}{4(l-1)}<AU{C}^W<1-\frac{{(4-2l)}^2}{4(4-\pi )}.$$ (5)

Proof:

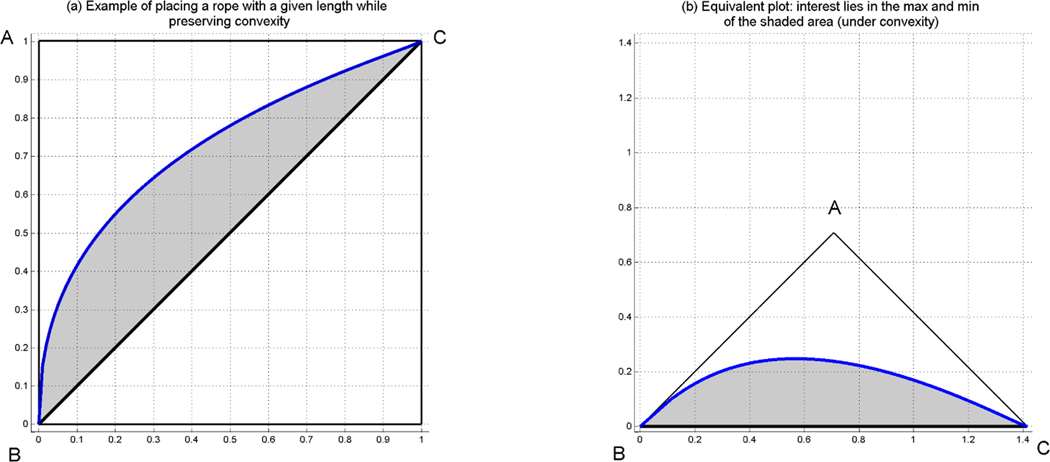
Note that we are dealing here with isoperimetric problems. Since the likelihood ratio ROC curve is concave, and as we have shown earlier has length l, we consider the mathematically equivalent problems of maximizing and minimizing the area among all convex sets within the right isosceles triangle ABC (see Figure 2) formed by a rope of length l tied to the edges B and C.

Figure 2.

Geometric representation of the problem of finding the max and min area under the curve, when assuming convexity for a given length of the rope (ROC). Under convexity, it is enough to study the area between the reference diagonal and the rope. Hence, we only can focus on the right panel (b), which is equivalent to the left panel (a).

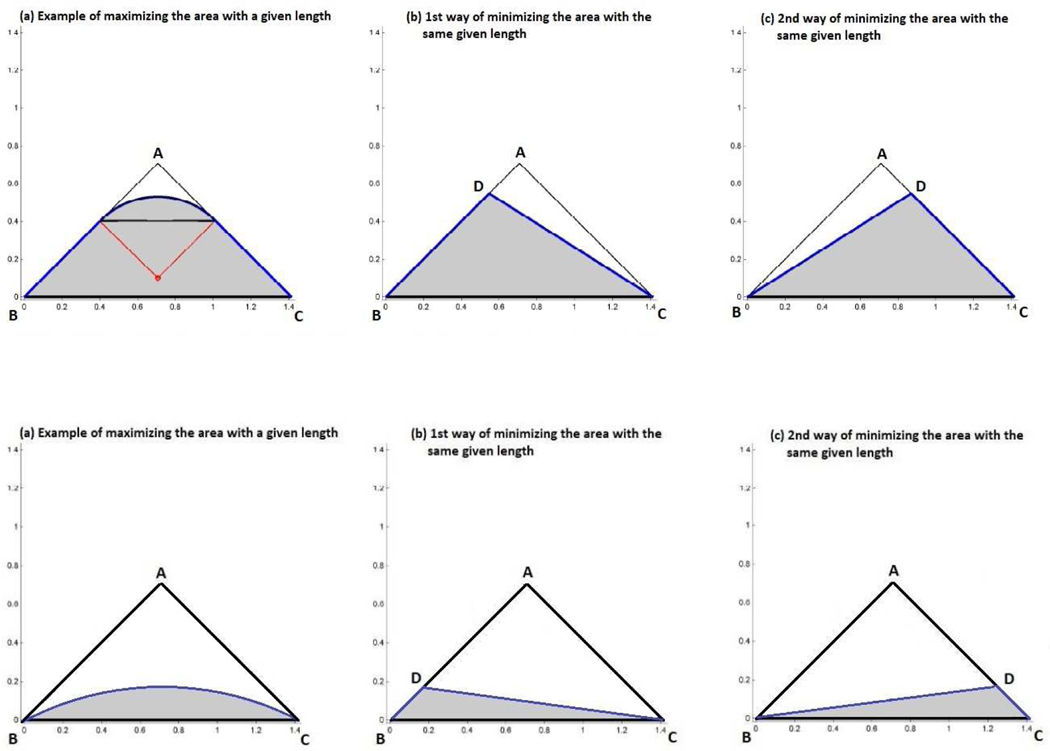
The maximization of the area given the rope’s length, l, is a variant of the famous Dido problem, and is dealt with in [20] (pg. 4, 5, and 292) using methods of optimal control. Although the maximization problem is typically formulated without the convexity constraint, its solution forms a convex set, and hence is the solution to our problem. It turns out that if the rope length, l, does not exceed π/2, then the solution is to place the rope so as to form a partially circular region (see Figure 3). The area of the convex set formed can be found numerically (the solution coincides with that of the Dido problem, since, in this case, the circular arc stays within the triangle ABC). When l is larger than π/2, we lay the rope on the two sides AB and AC, moving along the sides an equal distance until we have enough rope remaining to draw the arc of a quarter circle inside the triangle ABC. It can be shown that the distance we need to move up on each side equals $\frac{(2l-\pi )}{(4-\pi )}$, and the quarter circle arc corresponds to a circle with radius equal to $\frac{(4-2l)}{(4-\pi )}$. The area of the maximizing convex set is then computed using elementary geometry. The corresponding optimal ROC curve in this case is not attained in our framework, due to our assumption that the densities for diseased and non-diseased have common support. An ROC curve in our setting, however, can be infinitely close to the optimal one.

Figure 3. Upper panels:

Geometric representation of the maximum area for a given length when the length is larger than $\frac{\pi }{2}$ (panel (a)), and the minimum area for the same given length (panels (b) and (c)). Both panels (b) and (c) correspond to the same area. All three panels correspond to the same length. Lower panels: Geometric representation of the maximum area for a given length when the length is smaller than $\frac{\pi }{2}$ (panel (a)), and the minimum area for the same given length (panels (b) and (c)). Both panels (b) and (c) correspond to the same area. All three panels correspond to the same length.

There are two solutions to the minimization problem, which yield a lower bound for AUC^W. One is the triangle BCD, with the length of CD, let $\gamma$, equal to $\frac{\left(l^2-2\right)}{2(l-1)}$. The other is a triangle symmetric to the above around a line passing through point A and perpendicular to BC. These two solutions, along with the corresponding minimum area, are obtained by considering the dual problem of maximizing the perimeter of a given area. We spare the reader of the mathematical details of the minimization problem and provide the related Theorem in Web Appendix A □.

Table 1 gives the lower and upper bounds of the optimal (likelihood ratio) ROC for select values of the length.

Table 1.

Attained lower and upper bounds of the AUC for some given values of the length.

length	lower bound of AUC	upper bound of the AUC
$\sqrt{2}$	0.50000	0.50000
1.65	0.77788	0.85729
1.75	0.85417	0.92719
1.85	0.91838	0.97379
1.95	0.97434	0.99709
2.00	1.00000	1.00000

Inference on the length of the ROC curve is rather straightforward, if we assume that the distributions of diseased and non-diseased belong to the same parametric family, with density f(x;θ), where θ is an M × 1 parameter vector. Let $f\left(x;{\theta }_0\right)=f_0(x)$ and $f\left(x;{\theta }_1\right)=f_1(x)$ denote the densities of the non-diseased and diseased populations, respectively.

The quantity $l_{ROC}-\sqrt{2}$ can be written as an (h, ϕ) divergence measure (see [21]). Since the two distributions have densities, an (h, ϕ) divergence is defined as

$$D_{\varphi }^h\left({\theta }_0,{\theta }_1\right)=\underset{\text{Λ}}{\int }{h}_{\alpha }\left({\int }_{-\infty }^{+\infty }{\varphi }_{\alpha }\left(\frac{f\left(x;{\theta }_1\right)}{f\left(x;{\theta }_0\right)}\right)f\left(x;{\theta }_0\right)dx-{\varphi }_{\alpha }(1)\right)d_{\eta }(\alpha ),$$ (6)

where $h={\left(h_{\alpha }\right)}_{\alpha \in \text{Λ}}$ and $\varphi ={\left({\varphi }_{\alpha }\right)}_{\alpha \in \text{Λ}}$ are real valued C² functions, with $h_{\alpha }(0)=0$ and η is a σ-finite measure on the measurable space (Λ, β). Furthermore, for every α, either ${\varphi }_{\alpha }$ is convex and $h_{\alpha }$ is increasing or ${\varphi }_{\alpha }$ is concave and h_α is decreasing. The divergence measure $l_{ROC}-\sqrt{2}$ is obtained by letting Λ = 1, η a point mass at 1, $h_1(u)=u$, and ${\varphi }_1(t)=\sqrt{1+t^2}$.

Let ${\widehat{\theta }}_0$ and ${\widehat{\theta }}_1$ be the maximum likelihood estimators of θ₀ and θ₁, and consider the divergence statistic

$${\widehat{l}}_{ROC}-\sqrt{2}={\int }_{-\infty }^{+\infty }\sqrt{1+{\left(\frac{f\left(x;{\widehat{\theta }}_1\right)}{f\left(x;{\widehat{\theta }}_0\right)}\right)}^2}f\left(x;{\widehat{\theta }}_0\right)dx-\sqrt{2}$$ (7)

We obtain the following result, presented as a theorem, to test the null hypothesis H₀ : θ₁ = θ₀.

Theorem 3

Under the null hypothesis H₀ : θ₁ = θ₀, and assuming $\frac{n_0}{n_0+n_1}\to \lambda \in (0,1)$

$$\frac{4\sqrt{2}{n}_0{n}_1}{n_0+n_1}\left({\widehat{l}}_{ROC}-\sqrt{2}\right)\to {\chi }_M^2$$ (8)

Proof:

The proof is an immediate consequence of the Corollary 2.(b) in [21] □.

The theorem above allows us to test, within a parametric framework, whether a marker is informative. It is a divergence-based test of the equality of two distributions within a parametric family and is closely related to the likelihood ratio test. We explore the power and size of this test in our simulation studies where we consider also randomization (permutation based) versions of it under different parametric assumptions (results are presented in Web Appendix C and discussed in our simulation section). If the null hypothesis is rejected, then the following theorem, which is an immediate consequence of Corollary 2.(a) in [21], allows the construction of a confidence interval for the length of the ROC curve.

Theorem 4

Under the alternative hypothesis $H_A:{\theta }_1\ne {\theta }_0$, assuming $\frac{n_0}{n_1+n_0}\to \lambda \in (0,1)$

$$\sqrt{\frac{n_0{n}_1}{n_0+n_1}}\left({\widehat{l}}_{ROC}-l_{ROC}\right)\to N\left(0,\lambda {\mathbf{t}}^T{I}^{-1}\left({\theta }_1\right)\mathbf{t}+(1-\lambda ){\mathbf{s}}^T{I}^{-1}\left({\theta }_0\right)\mathbf{s}\right),$$ (9)

where $I\left({\theta }_1\right)$ and $I\left({\theta }_0\right)$ are the Fisher information matrices associated with θ₁ and θ₀, and the elements of the M × 1 vectors t and s are given by

$$t_i={\int }_{-\infty }^{+\infty }\frac{\left(\frac{f\left(x;{\theta }_1\right)}{f\left(x;{\theta }_0\right)}\right)}{\sqrt{1+{\left(\frac{f\left(x;{\theta }_1\right)}{f\left(x;{\theta }_0\right)}\right)}^2}}\frac{df\left(x;{\theta }_1\right)}{d{\theta }_{1i}}dx$$

$$s_i={\int }_{-\infty }^{+\infty }\left[\sqrt{1+{\left(\frac{f\left(x;{\theta }_1\right)}{f\left(x\mid ;{\theta }_0\right)}\right)}^2}\frac{df\left(x;{\theta }_0\right)}{d{\theta }_{0i}}-\frac{\left(\frac{f\left(x;{\theta }_1\right)}{f\left(x;{\theta }_0\right)}\right)}{\sqrt{1+{\left(\frac{f\left(x;{\theta }_1\right)}{f\left(x;{\theta }_0\right)}\right)}^2}}\frac{df\left(x;{\theta }_0\right)}{d{\theta }_{0i}}\frac{f\left(x;{\theta }_1\right)}{f\left(x;{\theta }_0\right)}\right]dx$$

Theorems 3 and 4 assume a common parametric family for the two distributions and are well suited for modeling data sets with large sample sizes using flexible parametric families, which is typically not the case in biomarker discovery. An alternative is to obtain smooth nonparametric estimates for the two distributions and estimate the length of the ROC curve based on equation (2). Testing can then be performed using a randomization test and bootstrap confidence intervals for the length can be obtained.

It should finally be noted that the length of the empirical ROC curve cannot be used for statistical inference, since it can easily be seen that, in the absence of ties, the length of the empirical ROC equals 2. So, in practice the length is estimated either by plugging in estimates of the parameters involved when assuming a parametric family or by first obtaining smooth nonparametric estimates of the densities involved. Further note, that under the classical binormal setting, in the case of equal variances knowledge of the AUC implies knowledge of the length of the ROC and vice versa.

3. The ROC with two cutoffs

Under the usual setting where it is assumed that the higher the measurement the more likely the existence of disease, the common ROC analysis plots the sensitivity $Se(c)=TPR=1-F_1(c)=S_1(c)$ over the false positive rate $1-Sp(c)=FPR=1-F_0(c)=S_0(c)$ for all possible cutoffs c, with $c\in (-\infty ,+\infty )$. In the case where we consider very high and very low measurements as indicative of the disease, while measurements of the healthy are considered to lie in a bounded interval, let (c₁, c₂), then a proper analogous to an ROC plot can be considered that may be more appropriate to assess the biomarker’s performance. In this case the sensitivity, the specificity, and the false positive rates are defined as follows:

$$Se\left(c_1,c_2\right)=F_1\left(c_1\right)+S_1\left(c_2\right)Sp\left(c_1,c_2\right)=F_0\left(c_2\right)-F_0\left(c_1\right)Fp\left(c_1,c_2\right)=F_0\left(c_1\right)+S_0\left(c_2\right),$$

where c₁ < c₂. To perform an ROC analysis one can plot two surfaces in the unit cube, one that refers to the sensitivity and one that refers to the specificity for all $c_1<c_2,c_i\in (-\infty ,+\infty )$, i = 1,2 (see Figures 4 and 5). Proceeding further, one can construct an equivalent definition, analogous to the one in the common settings in which $ROC(t)=S_1\left(S_0^{-1}(t)\right)$, $t\in (0,1)$. In our case, since we have two cutoffs, there is the implication that for different pairs of c₁ and c₂ we may get the exact same sensitivity and specificity. Observe that by setting the false positive rate equal to an argument $t\in (0,1)$ we derive:

$$Fp\left(c_1,c_2\right)=t\Rightarrow c_2=S_0^{-1}\left(t-F_0\left(c_1\right)\right),F_0\left(c_1\right)<t<1$$ (10)

and by substitution to the sensitivity we derive:

$$Se\left(t;c_1\right)=F_1\left(c_1\right)+ROC\left(t-F_0\left(c_1\right)\right),F_0\left(c_1\right)<t<1.$$ (11)

Obviously, as $c_1\to -\infty$ we obtain the classical ROC setting. Note that as $t\to 0Se\left(t,c_1\right)\to 1$. Formula (11) above implies that for a given cutoff c₁ we can plot a projection of the sensitivity surface on the unit rectangle for all $t^{\prime }\in \left(0,1-F_0\left(c_1\right)\right)$ where $t^{\prime }=1-t$ expresses the specificity. One could derive this plot by scanning c₁ restricted on a straight line parallel to the c₂–axis (i.e. taking an infinitely thin slice) of the sensitivity surface. It can be easily shown (since the derivative of the ROC curve equals the density ratio evaluated at the t-th upper quantile of the healthy distribution) that the derivative of the sensitivity w.r.t. c₁ is

$$\frac{dSe\left(t;c_1\right)}{d{c}_1}=f_0\left(c_1\right)\left\{r\left(c_1\right)-r\left(S_0^{-1}\left(t-F_0\left(c_1\right)\right)\right)\right\}.$$ (12)

If one is interested in forcing desired sensitivity levels to derive the corresponding specificity values, then using the argument t* to avoid confusion, we get:

$$Se\left(c_1,c_2\right)=t^{*}\Rightarrow c_2=F_1^{-1}\left(F_1\left(c_1\right)+1-t^{*}\right)F_1\left(c_1\right)<t^{*}<1$$ (13)

and by substitution to the specificity we derive:

$$Sp\left(t^{*};c_1\right)=F_0\left(F_1^{-1}\left(F_1\left(c_1\right)+1-t^{*}\right)\right)-F_0\left(c_1\right),F_1\left(c_1\right)<t^{*}<1.$$ (14)

Similar expressions for given c₂ can be also derived. Given two cutoffs we utilize the dominant generalized ROC curve (gROC):

$$\begin{array}{l}gROC(t)=\underset{F_0\left(c_1\right)+S_0\left(c_2\right)=t}{\sup }\left\{F_1\left(c_1\right)+S_1\left(c_2\right)\right\}\\ =\underset{c_1\le F_0^{-1}(t)}{\sup }Se\left(t;c_1\right)=\underset{c_1\le F_0^{-1}(t)}{\sup }\left\{F_1\left(c_1\right)+ROC\left(t-F_0\left(c_1\right)\right)\right\}t\in (0,1).\end{array}$$ (15)

The above ROC curve was first introduced in [14]. They refer to it as the generalized ROC (gROC) curve. We follow this terminology even though one could hypothesize that a generalized ROC would, in principle, refer to settings with more than two cutoff points. Whereas considering more than two cutoff points may be useful in general classification problems with multimodal distributions, we find it hard to imagine practitioners entertaining this idea when dealing with biomarkers.

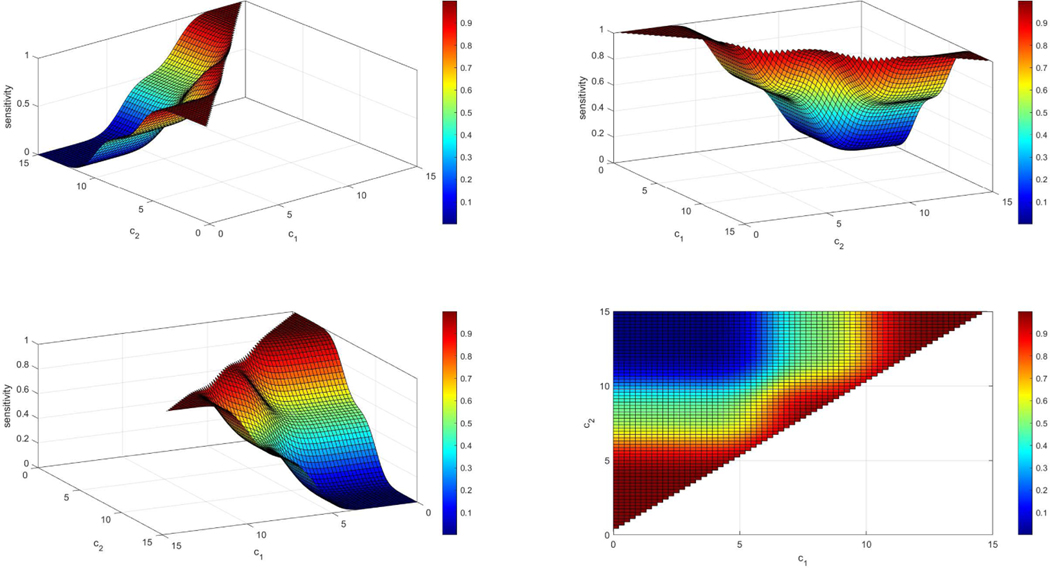
Figure 4.

Example of a sensitivity surface when the density of the controls is N(8,1) and the density of the cases is a two component normal mixture: 0.5N(6, 1) + 0.5N(10, 1). The sensitivity plot is given under four different angles (panels above) for better visualization. We observe that when c₁ is very small and c₂ is very large then the sensitivity yields very low values since the mass of both densities is low below c₁ and beyond c₂. In addition, if c₁ is very close to c₂ then we expect that almost all individuals that are diseased will be categorized as such since it is very likely that they will not be between c₁ and c₂ and thus the sensitivity for those cutoffs is very high (red regions).

Figure 5.

Example of a specificity surface when the density of the controls is N(8, 1) and the density of the cases is a two component normal mixture: 0.5N(6, 1) + 0.5N(10, 1). The specificity plot is given under four different angles (panels above) for better visualization. We observe that when c₁ is very small and c₂ is very large then the specificity yields very high values as expected since most healthy individuals will lie within (c₁, c₂). In addition, if c₁ is very close to c₂ then we expect that almost all individuals that are healthy will be categorized as diseased and since it is very likely that they will not be between c₁ and c₂ and thus the specificity for those cutoffs is very low (blue regions).

It is easily seen that $gROC(t)\to 0$ as $t\to 0$, $gROC(t)\to 1$ as $t\to 1$ and is non-decreasing. Furthermore, by observing that $Se(t;-\infty )=ROC(t)$ and $Se\left(t;F_0^{-1}(t)\right)=1-ROC(1-t)$, we have that $gROC(t)\ge ROC(t)$ and $gROC(t)\ge 1-ROC(1-t)$. We note here that $1-ROC(1-t)$ is the appropriate ROC curve in the case where smaller measurements are indicative of the disease.

The two cutoff ROC curve is optimal under the assumption that the density ratio $r(y)=\frac{f_1(y)}{f_0(y)}$ is unimodal in the sense that there exists y* (possibly −∞ or +∞) such that r(y) is strictly decreasing in $\left(-\infty ,y^{*}\right)$ and strictly increasing in ($y^{*}=+\infty$). This is easy to see since the ROC curve based on the density (likelihood) ratio transformed measurements results in a two cutoff decision rule. The assumption of a unimodal density ratio is a dispersion ordering of the two distributions involved (the distribution of healthy individuals is less dispersed than the distribution of the diseased) and is closely related to the uniform conditional variability ordering studied in [22]. Note that in the case of a multimodal density ratio one would need to consider more than two cutoffs to define an optimal ROC.

We note that when $y^{*}=-\infty$ then we have an increasing density ratio and $gROC(t)=ROC(t)$ for 0 < t < 1, whereas when $y^{*}=+\infty$ then we have a decreasing density ratio and $gROC(t)=1-ROC(1-t)$ for 0 < t < 1. Also, when y* is a real number and $r(-\infty )=r(\infty )$ (as is the case with two Normal distributions with the variance of the diseased greater than the variance of the healthy) for each t we obtain two cutoffs that are real numbers. In this case, by setting the expression in equation (16) equal to 0, we obtain the unique solution for the lower cutpoint, $c_1^{*}(t)$, that satisfies

$$r\left(c_1\right)=r(S_0^{-1}\left(t-F_0\left(c_1\right)\right).$$ (16)

Obviously the second cutoff equals $c_2^{*}(t)=S_0^{-1}\left(t-F_0\left(c_1^{*}\right)\right)$. Thus $gROC(t)=F_1\left(c_1^{*}(t)\right)+S_1\left(c_2^{*}(t)\right)$. A straightforward application of the envelope theorem (see for example [23], pg. 603–609) yields

$$\frac{dgROC(t)}{dt}=r\left(c_1^{*}(t)\right)=r\left(c_2^{*}(t)\right)$$ (17)

Furthermore, the Youden index of gROC(t), which is commonly used to select cutoff points in an ROC setting, is given by

$$\underset{0<t<1}{\sup }|gROC(t)-t|=\underset{0<t<1}{\sup }(gROC(t)-t),$$ (18)

since, in this case, gROC(t) is the optimal ROC curve and thus concave. It is easy to see that maximization of $gROC(t)-t$ leads to selecting the two cutoff points that satisfy

$$\frac{dgROC(t)}{dt}=r\left(c_1^{*}(t)\right)=r\left(c_2^{*}(t)\right)=1$$ (19)

This method of obtaining cutoffs can be extended to the situation where costs are available. For example, as discussed in [1] (pg. 31,32,72), denote by C the cost of performing the test, $C_D^{(1)}$ and $C_D^{(0)}$ the costs of treatment and morbidity for diseased subjects that test positive and negative respectively, $C_{\overline{D}}^{(1)}$, the cost of work-up, stress and unnecessary treatment for the non-diseased that test positive. Then minimization of the overall cost of disease per subject in the population in the presence of testing leads to selecting the two cutoff points that satisfy

$$\frac{dgROC(t)}{dt}=r\left(c_1^{*}(t)\right)=r\left(c_2^{*}(t)\right)=\left(\frac{1-\rho }{\rho }\right)\frac{C_{\overline{D}}^{(1)}}{C_D^{(0)}-C_D^{(1)}},$$ (20)

where ρ denotes disease prevalence. In the following section we discuss, among other things, the estimation of cutoffs in various settings and the associated inference.

Example:

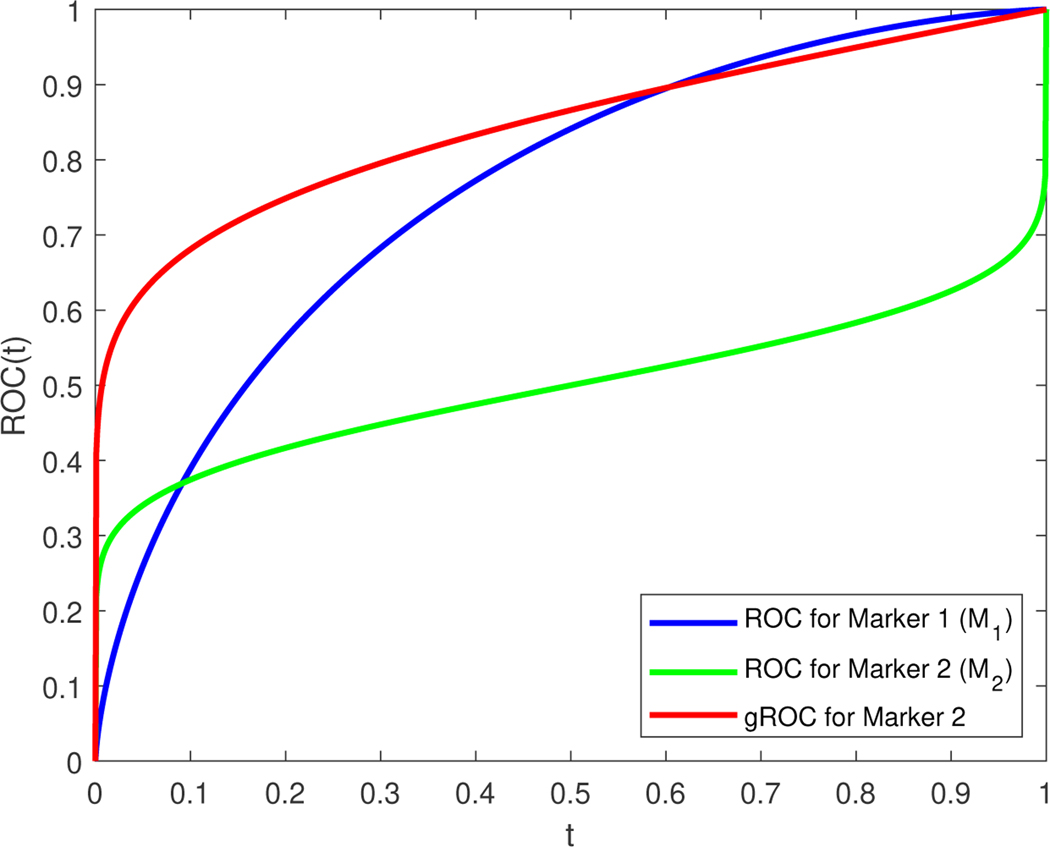
Consider two markers M₁ and M₂ that both follow a standard normal distribution for the non-diseased population. Assume the measurements of the diseased population for the first marker, M₁, follow a N(1, 1²) distribution, whereas the measurements of the diseased population for the second marker, M₂, follow a N(0, 4²) distribution (see Figure 6 for the discussion that follows). The ROC curves for these two markers are: $RO{C}_1(t)=\text{Φ}\left(1+{\text{Φ}}^{-1}(t)\right)$ (with AUC₁ = 0.76025 and length $l_{RO{C}_1}=1.5465$) and $RO{C}_2(t)=\text{Φ}\left(\frac{1}{4}{\text{Φ}}^{-1}(t)\right)$ (with AUC₂ = 0.5000 and length $l_{RO{C}_2}=1.6701$). By examining the two ROC curves one will be tempted to conclude that M₁ is superior to M₂. The same conclusion would follow by comparing the two AUCs. However, whereas ROC₁(t) is the optimal curve for M₁, ROC₂(t) is not the optimal curve for M₂. The density ratios for the two markers are $r_1(y)=e^{\frac{1}{2}(2y-1)}$ and $r_2(y)=\frac{1}{4}{e}^{\frac{15}{32}{y}^2}$. Since an ROC curve is invariant to monotone transformations, the optimal curve (likelihood ratio ROC) for M₁ is based on the measurements themselves whereas the optimal curve for M₂ is the curve based on the squared values of the measurements, which here yields $gRO{C}_2(t)=1-G\left(\left(G^{-1}(1-t)\right)/16\right)$, where G is the cdf of a ${\chi }_1^2$ distribution. We have $AU{C}_{gRO{C}_2}=0.8440$, $l_{gRO{C}_2}=1.6701$. Note that the length of the optimal ROC for the second marker is the same as that of ROC₂. By comparing the two markers based on their optimal ROC curves one would conclude that the second marker is superior, which is the conclusion one would arrive at when using the length as a summary measure.

Figure 6.

ROC curves for the hypothetical example with markers M₁ and M₂. Both ROC curves are illustrated and would tempt us to consider M₁ as an overall better biomarker. The gROC of marker 2 is presented as well showing its potential in actually outperforming M₁. The gROC of M₂ and the ROC of M₂ have exactly the same length that is larger than the length of M₁.

To obtain cutoffs based on the Youden index criterion we simply set the density ratios to one and thus obtain a single cutoff for M₁ (c = 0.5) and two cutoffs for M₂ (c₁ = −1.71972 and c₂ = +1.71972). For M₁ this results in a false positive rate of 0.308538 and a sensitivity equal to 0.691462. For M₂, using two cutoffs, the false positive rate is 0.0854834 and the sensitivity is equal to 0.667246.

4. Estimation and inference for the sensitivity and specificity of the selected markers

In a given set of the top candidates, both proper and improper ROC curves might appear. For those biomarkers that exhibit proper ROC curves, well defined and studied measures are available in the literature in order to evaluate them. For the evaluation of those biomarkers that exhibit an improper ROC curve, caution is required. The AUC bounds of the optimal ROC curve for a given marker (see Theorem 2) provide a rough indication of the discriminatory potential of the marker. Obviously, the full potential of the marker can be assessed by using the likelihood ratio transformation (see also [24]). However, in practice the likelihood ratio is not known. Martínez-Camblor et al. (2018) ([17]) explore functional transformations to deal with this problem but as they note this practice can produce classification regions with no practical interpretation. An alternative would be to consider nonparametric estimation of the density ratio under the assumption of unimodality, but we leave this as the goal of future research. Furthermore, given a large number of candidate biomarkers to be ranked, exploring a suitable functional transformation for each would be a daunting task. We present below a simplified framework with which we can estimate the sensitivity, specificity, Youden-based optimal cutoffs (possibly modified to account for costs), and the appropriate construction of confidence intervals. Below we explore parametric and non-parametric approaches.

4.1. Normality assumption

4.1.1. Estimation and inference for the sensitivity and specificity when given a pair of cutoffs

For given cutoffs of an improper marker the corresponding sensitivity and specificity under the normality assumption (binormal setting) we have:

$$Se\left(c_1,c_2\right)=\text{Φ}\left(\frac{c_1-{\mu }_1}{{\sigma }_1}\right)+\text{Φ}\left(\frac{{\mu }_1-c_2}{{\sigma }_1}\right),Sp\left(c_1,c_2\right)=\text{Φ}\left(\frac{c_2-{\mu }_0}{{\sigma }_0}\right)-\text{Φ}\left(\frac{c_1-{\mu }_0}{{\sigma }_0}\right)$$

and the estimated sensitivity and specificity for given c₁, c₂ are given by plugging in maximum likelihood estimates of the corresponding means and variances: ${\widehat{\mu }}_0$, ${\widehat{\sigma }}_0$, ${\widehat{\mu }}_1$, and ${\widehat{\sigma }}_1$. For the construction of the underlying confidence intervals, one can simply apply the delta method: $Var(\widehat{S}e)\approx \left(\frac{\partial Se}{\partial {\mu }_1},\frac{\partial Se}{\partial {\sigma }_1}\right){\text{Σ}}_1{\left(\frac{\partial Se}{\partial {\mu }_1},\frac{\partial Se}{\partial {\sigma }_1}\right)}^{\prime }$ where an estimate of the 2 × 2 diagonal covariance matrix ${\text{Σ}}_1$ can be derived by using $Var\left({\widehat{\mu }}_0\right)=\frac{{\widehat{\sigma }}_1^2}{n_1}$ and $Var\left({\widehat{\sigma }}_1\right)=\frac{{\sigma }_1^2}{2\left(n_1-1\right)}$. The partial derivatives can be derived in closed form. A similar expression is derived for $Var(\widehat{S}p)$, for which the involved partial derivatives also can be derived in closed form. In order for the proposed confidence intervals to avoid exceeding the bounds of (0,1), following the ideas presented in [25], we first transform the sensitivity using ${\text{Φ}}^{-1}(\cdot )$, then derive based on the delta method a 95% confidence interval for the transformed sensitivity, and finally back transform the endpoints of that confidence interval with $\text{Φ}(\cdot )$. Thus, the proposed confidence interval is: $\text{Φ}\left({\text{Φ}}^{-1}(\widehat{S}e)\pm 1.96\sqrt{Var\left({\text{Φ}}^{-1}(\widehat{S}e)\right)}\right)$, where $Var\left({\text{Φ}}^{-1}(\widehat{S}e)\right)\approx \left(\frac{\partial {\text{Φ}}^{-1}(Se)}{\partial {\mu }_1},\frac{\partial {\text{Φ}}^{-1}(Se)}{\partial {\sigma }_1}\right){\text{Σ}}_1{\left(\frac{\partial {\text{Φ}}^{-1}(Se)}{\partial {\mu }_1},\frac{\partial {\text{Φ}}^{-1}(Se)}{\partial {\sigma }_1}\right)}^{\prime }$. The derivation for the corresponding confidence interval of the specificity is similar.

4.1.2. Estimation and inference for the sensitivity and specificity when the pair of cutoffs is estimated

In the absence of any clinical insight regarding where to locate the two cutoff points, we can estimate them under the optimization of some clinically relevant criterion. Such a criterion is the Youden index initially suggested in [26] for the single cutoff setting and extended to the dual cutoff framework given in [18]:

$$J={max}_{c_1,c_2:c_1<c_2}\left(Se\left(c_1,c_2\right)+Sp\left(c_1,c_2\right)-1\right)$$ (21)

Under the normality assumption, the pair of cutoffs can be derived in closed form by:

$$J=ma{x}_{c_1}\left(\text{Φ}\left(\frac{c_1-{\mu }_1}{{\sigma }_1}\right)+\text{Φ}\left(\frac{{\mu }_0-c_1}{{\sigma }_0}\right)\right)+ma{x}_{c2}\left(\text{Φ}\left(\frac{{\mu }_1-c_2}{{\sigma }_1}\right)+\text{Φ}\left(\frac{c_2-{\mu }_0}{{\sigma }_0}\right)-1\right)$$ (22)

To maximize J, we need to separately maximize both terms of (22), which are both equivalent to the maximization of the regular Youden index in the common single cutoff setting of the binormal case. Hence, under the necessary assumption that σ₀ < σ₁, the pair of cutoffs can be derived in closed form by:

$$c_{1,2}^{*}=\frac{{\sigma }_0^2{\mu }_1-{\sigma }_1^2{\mu }_0\pm {\sigma }_0{\sigma }_1\sqrt{{\left({\mu }_0-{\mu }_1\right)}^2+\left({\sigma }_0^2-{\sigma }_1^2\right)\log \left(\frac{{\sigma }_0^2}{{\sigma }_1^2}\right)}}{{\sigma }_0^2-{\sigma }_1^2}$$ (23)

We note that in the binormal setting the density ratio is unimodal and the two cutoffs are obtained by solving equation (19). The estimated cutoffs can be derived by simply plugging in (23), the maximum likelihood estimates of the means and variances. After the pair of cutoffs is estimated, then the corresponding sensitivity and specificity (at the estimated pair of cutoffs) are correlated, as opposed to the previous section where the cutoffs were given. Following the ideas in [25] we denote ${\delta }_e={\text{Φ}}^{-1}\left(Se\left(c_1^{*},c_2^{*}\right)\right)$ and ${\delta }_p={\text{Φ}}^{-1}\left(Sp\left(c_1^{*},c_2^{*}\right)\right)$. We can derive the estimates ${\widehat{\delta }}_e$ and ${\widehat{\delta }}_p$ by simply plugging in the maximum likelihood estimates of the means and variances i.e., ${\widehat{\mu }}_0$, ${\widehat{\sigma }}_0$, ${\widehat{\mu }}_1$, ${\widehat{\sigma }}_1$). Then, based on the delta method we derive: $Var\left({\widehat{\delta }}_e\right)\approx \left(\frac{\partial {\widehat{\delta }}_e}{\partial {\mu }_0},\frac{\partial {\widehat{\delta }}_e}{\partial {\sigma }_0},\frac{\partial {\widehat{\delta }}_e}{\partial {\mu }_1},\frac{\partial {\widehat{\delta }}_e}{\partial {\sigma }_1}\right)\text{Σ}\left(\frac{\partial {\widehat{\delta }}_e}{\partial {\mu }_0},\frac{\partial {\widehat{\delta }}_e}{\partial {\sigma }_0},\frac{\partial {\widehat{\delta }}_e}{\partial {\mu }_1},\frac{\partial {\widehat{\delta }}_e}{\partial {\sigma }_1}\right)$, where Σ is the diagonal matrix $\text{Σ}=diag\left\{Var\left({\widehat{\mu }}_0\right),Var\left({\widehat{\sigma }}_0\right),Var\left({\widehat{\mu }}_1\right),Var\left({\widehat{\sigma }}_1\right)\right\}$ and $Var\left({\widehat{\mu }}_0\right)=\frac{{\sigma }_0^2}{n_0}$, $Var\left({\widehat{\sigma }}_0\right)=\frac{{\widehat{\sigma }}_0^2}{2\left(n_0-1\right)}$, $Var\left({\widehat{\mu }}_1\right)=\frac{{\sigma }_1^2}{n_1}$, and $Var\left({\widehat{\sigma }}_1\right)=\frac{{\sigma }_1^2}{2\left(n_1-1\right)}$. The corresponding estimates, and thus $\widehat{\sum }$, can be derived by simply plugging in the maximum likelihood estimates of the means and variances. The expression is similar for $Var\left({\widehat{\delta }}_p\right)$. The covariance can be derived by: $Cov\left({\widehat{\delta }}_e,{\widehat{\delta }}_p\right)\approx \left(\frac{\partial {\widehat{\delta }}_e}{\partial {\mu }_0},\frac{\partial {\widehat{\delta }}_e}{\partial {\mu }_0},\frac{\partial {\widehat{\delta }}_e}{\partial {\mu }_1},\frac{\partial {\widehat{\delta }}_e}{\partial {\sigma }_1}\right)\text{Σ}{\left(\frac{\partial {\widehat{\delta }}_p}{\partial {\mu }_0},\frac{\partial {\widehat{\delta }}_p}{\partial {\mu }_0},\frac{\partial {\widehat{\delta }}_p}{\partial {\mu }_1},\frac{\partial {\widehat{\delta }}_p}{\partial {\sigma }_1}\right)}^{\prime }$. All partial derivatives can be found in closed form. An approximate joint confidence region for (${\delta }_e$, ${\delta }_p$) can be obtained by the ellipse defined by $(\mathbf{x}-\mathbf{a}{)}^{\prime }{\widehat{\text{Σ}}}^{-1}(\mathbf{x}-\mathbf{a})=q$, where $\mathbf{a}=\left({\widehat{\delta }}_e,{\widehat{\delta }}_p\right)$ and q is the 95%th percentile of a ${\chi }_2^2$. To derive a joint confidence region of the estimated sensitivity and specificity within the ROC space, we back-transform the elliptical confidence region by applying $\text{Φ}(\cdot )$ on its coordinates, and hence derive an egg-shaped confidence region for (Se, Sp). Marginal Wald type 95% confidence intervals for the sensitivity and specificity can be also derived within the ROC space by $\text{Φ}\left({\widehat{\delta }}_e\pm 1.96\sqrt{Var\left({\widehat{\delta }}_e\right)}\right)$ and $\text{Φ}\left({\widehat{\delta }}_p\pm 1.96\sqrt{Var\left({\widehat{\delta }}_p\right)}\right)$, respectively. Based on the Bonferroni correction, once the marginal confidence intervals are derived, we also can proceed with rectangular confidence regions that are more easily communicated to clinicians. By constructing the rectangle with sides based on $\text{Φ}\left({\widehat{\delta }}_e\pm 2.24\sqrt{Var\left({\widehat{\delta }}_e\right)}\right)$ and $\text{Φ}\left({\widehat{\delta }}_p\pm 2.24\sqrt{Var\left({\widehat{\delta }}_p\right)}\right)$ that correspond to adjusted 97.5% marginal confidence intervals, we obtain a 95% confidence rectangular region for the (Se, Sp). However, such a rectangular region does not accommodate the implied correlation of the estimated sensitivity and specificity at the Youden-based cutoffs, and for that reason it consistently provides a larger area compared to the egg-shaped proposed region previously described. This is observed in our simulation studies (Web Appendix C). In case normality is violated, transformations to normality might be useful alternatives for a selected marker. A discussion about the Box-Cox transformation ([27]) in this setting is given in the Web Appendix B.

4.2. Estimation and inference using kernel density estimates

4.2.1. Estimation and inference for the sensitivity and specificity when given a pair of cutoffs

When no parametric assumptions can be justified by the data at hand, then we need to proceed non-parametrically. In such a case, we employ the kernel density estimate of the form:

$${\widehat{f}}_0(y)=\frac{1}{n_0{h}_0}\sum _{i=1}^{n_0}K\left(\frac{y-Y_{0i}}{h_0}\right),$$ (24)

where h₀ is the bandwidth for which one can use a simple plug-in expression like the one given by Silverman’s rule ([28]): $h_0=0.9min\left(sd\left(Y_0\right),iqr\left(Y_0\right)/1.34\right)n_0^{-0.2}$, where $Y_{0i}$, $i=1,\dots ,n_0$ are the marker scores for the healthy group. Similarly for ${\widehat{f}}_1(y)$. Given the cutoffs we obtain for the sensitivity and specificity: $\widehat{S}e\left(c_1,c_2\right)={\widehat{F}}_1\left(c_1\right)+1-{\widehat{F}}_1\left(c_2\right)$, $\widehat{S}p\left(c_1,c_2\right)={\widehat{F}}_0\left(c_2\right)-{\widehat{F}}_0\left(c_1\right)$ where ${\widehat{F}}_0(x)={\int }_{-\infty }^x{\widehat{f}}_0(z)dz$, and similarly for ${\widehat{F}}_1(y)={\int }_{-\infty }^y{\widehat{f}}_1(z)dz$. A common choice that we employ in practice is the normal kernel. This allows us to write ${\widehat{F}}_0(y)=\frac{1}{n_0}\sum _{i=1}^{n_0}\text{Φ}\left(\frac{y-Y_{0i}}{h_0}\right)$ and ${\widehat{F}}_1(y)=\frac{1}{n_1}\sum _{j=1}^{n_1}\text{Φ}\left(\frac{y-Y_{1i}}{h_1}\right)$. From standard kernel theory (see [29] and [30]) it can be shown that kernels are asymptotically equivalent to empirical estimates (Theorem 2.1. of [31]), and thus we have:

$$Var\left(\widehat{S}e\left(c_1,c_2\right)\right)\sim \frac{1}{n_1}{F}_1\left(c_1\right)\left(1-F_1\left(c_1\right)\right)+\frac{1}{n_1}{F}_1\left(c_2\right)\left(1-F_1\left(c_2\right)\right)-\frac{F_1\left(c_1\right)\left(1-F_1\left(c_2\right)\right)}{n_1}.$$

Similarly for the specificity. An estimate can be derived by simply plugging in the estimated kernel-based distribution functions. Using the delta method we have $Var\left({\text{Φ}}^{-1}\left(\widehat{S}e\left(c_1,c_2\right)\right)\right)=\frac{\partial {\text{Φ}}^{-1}\left(\widehat{S}e\left(c_1,c_2\right)\right)}{\partial \widehat{S}e\left(c_1,c_2\right)}\times Var\left(\widehat{S}e\left(c_1,c_2\right)\right)$, and thus the proposed 95% confidence interval for the sensitivity is given by $\text{Φ}\left({\text{Φ}}^{-1}\left(\widehat{S}e\left(c_1,c_2\right)\right)\pm 1.96\sqrt{Var\left({\text{Φ}}^{-1}\left(\widehat{S}e\left(c_1,c_2\right)\right)\right)}\right)$. Similarly for the specificity. For a joint confidence interval, one can readily obtain a rectangular region based on the Bonferroni adjustment, since the estimated sensitivity and specificity are uncorrelated, as the cutoffs are given.

4.2.2. Estimation and inference for the sensitivity and specificity when the pair of cutoffs is estimated

Since the kernel based cutoffs cannot be derived in closed form, a numerical procedure is needed to obtain the estimates of the optimal pair of cutoffs, ${\widehat{c}}_1^{*}$ and ${\widehat{c}}_2^{*}$. Once the corresponding $\widehat{S}e\left({\widehat{c}}_1^{*},{\widehat{c}}_2^{*}\right)$ and $\widehat{S}p\left({\widehat{c}}_1^{*},{\widehat{c}}_2^{*}\right)$ are derived, then we consider again: ${\widehat{\delta }}_e={\text{Φ}}^{-1}\left(\widehat{S}e\left({\widehat{c}}_1^{*},{\widehat{c}}_2^{*}\right)\right)$, ${\widehat{\delta }}_p={\text{Φ}}^{-1}\left(\widehat{S}p\left({\widehat{c}}_1^{*},{\widehat{c}}_2^{*}\right)\right)$. To derive estimates of $Var\left({\widehat{\delta }}_e\right)$ and $Var\left({\widehat{\delta }}_p\right)$ and $Cov\left({\widehat{\delta }}_e,{\widehat{\delta }}_p\right)$, we employ the following bootstrap scheme:

• Step 1: Calculate the bandwidths h₀ and h₁ based on the scores of the healthy and diseased group respectively. Derive the corresponding estimates of the cutoffs using the kernel density estimates ${\widehat{f}}_0$ and ${\widehat{f}}_1$. Obtain numerically the Youden-based optimal pair of cutoffs (${\widehat{c}}_1^{*}$, ${\widehat{c}}_2^{*}$) as well as $\widehat{S}p\left({\widehat{c}}_1^{*},{\widehat{c}}_2^{*}\right)$ and $\widehat{S}e\left({\widehat{c}}_1^{*},{\widehat{c}}_2^{*}\right)$.

• Step 2: Sample with replacement from the scores of the healthy and diseased group separately, let $Y_0^{(b)}$ and $Y_1^{(b)}$.

• Step 3: Set $Y_{0i}^{(s)}=Y_{0i}^{(b)}+e_{0i}$, where $e_{0i}\sim N\left(0,h_0^2\right)$, and $Y_{1i}^{(s)}=Y_{1i}^{(b)}+e_{1i}$, where $e_{1i}\sim N\left(0,h_1^2\right)$. Using $Y_0^{(s)}$ and $Y_1^{(s)}$ obtain numerically the Youden-based optimal pair of cutoffs (${\widehat{c}}_1^{*}$, ${\widehat{c}}_2^{*}$), as well as $\widehat{S}p\left({\widehat{c}}_1^{*},{\widehat{c}}_2^{*}\right)$ and $\widehat{S}e\left({\widehat{c}}_1^{*},{\widehat{c}}_2^{*}\right)$.

• Step 4: Use the ${\text{Φ}}^{-1}(\cdot )$ transformation and derive the current (for the current bootstrap sample) ${\text{Φ}}^{-1}\left(\widehat{S}p\left({\widehat{c}}_1^{*},{\widehat{c}}_2^{*}\right)\right)$ and ${\text{Φ}}^{-1}\left(\widehat{S}e\left({\widehat{c}}_1^{*},{\widehat{c}}_2^{*}\right)\right)$.

• Step 5: Repeat Steps 2 and 4 B times, and based on these B estimates derive the bootstrap-based estimates of $Var\left({\text{Φ}}^{-1}\left(\widehat{S}p\left({\widehat{c}}_1^{*},{\widehat{c}}_2^{*}\right)\right)\right)$, $Var\left({\text{Φ}}^{-1}\left(\widehat{S}e\left({\widehat{c}}_1^{*},{\widehat{c}}_2^{*}\right)\right)\right)$ and the underlying $Cov\left({\text{Φ}}^{-1}\left(\widehat{S}p\left({\widehat{c}}_1^{*},{\widehat{c}}_2^{*}\right)\right),{\text{Φ}}^{-1}\left(\widehat{S}e\left({\widehat{c}}_1^{*},{\widehat{c}}_2^{*}\right)\right)\right)$.

• Step 6: Construct the 95% elliptical confidence region for $\left({\text{Φ}}^{-1}\left(Sp\left(c_1,c_2\right)\right),{\text{Φ}}^{-1}\left(Se\left(c_1,c_2\right)\right)\right)$ and then construct the egg-shaped confidence region in the ROC space by transforming back the coordinates of the elliptical confidence region using ${\text{Φ}}^{-1}(\cdot )$.

In practice, we use B = 400 bootstrap samples. An approximate joint confidence region for (${\delta }_e$, ${\delta }_p$) can be obtained as described in the previous sections, using the construction of an ellipse defined by $(\mathbf{x}-\mathbf{a}{)}^{\prime }{\widehat{\text{Σ}}}^{-1}(\mathbf{x}-\mathbf{a})=q$, where q is the 95%th percentile of a ${\chi }_2^2$. The resulting joint confidence region of a = (Se, Sp) in the ROC space is obtained by back-transforming. Note that in Step 3 we add a generated error term to the bootstrapped sample of each group. Alternatively, one could simply proceed with the drawn bootstrap samples instead. However, as we point out later in our simulation study, we find the presented smooth bootstrap scheme to perform better than a regular bootstrap algorithm that would not involve the addition of these error terms. Such a finding is in-line with similar conclusions under a different ROC setting presented in [32].

5. Simulations

To evaluate our approaches, we consider Monte Carlo simulations under various scenarios. Our simulations refer to the evaluation of the following:

• The size and the power of the test statistic related to the proposed length of the ROC curve (thoughout our simulations the significance level considered is a = 0.05).

• The coverage of the egg-shaped versus the rectangular confidence region, when the two underlying cutoffs are estimated by the data.

In our simulations we have generated data from normal distributions, gamma distributions, as well as a mixture of normals to explore the robustness of our approaches. In terms of sample size, we considered scenarios with (n₀, n₁) = (50,50),(100,100),(200,200), and (500,500). All tables of our simulation results are given in Web Appendix C.

5.1. Size and power of the proposed test based on the length of the ROC curve

Regarding the size and power of the proposed test, we consider both traditional scenarios in which the stochastic ordering X < Y holds (or traditional setting), as well as scenarios in which this assumption is violated (or non-traditional setting). In both cases we compare the size and power of our statistic to the well-known Wilcoxon (Mann-Whitney), t-test, and the Kolmogorov-Smirnov test (KS). For the traditional setting, we consider 12 different scenarios in terms of distributions for each sample size: 6 related to normal distributions and 6 to gamma distributions. We observe that, in terms of size, our test provides satisfactory performance, just as the competing well-known tests (see Tables 1-2 of the Web Appendix). In terms of power, for the normal related scenarios, we observe that the t-test and the Wilcoxon test exhibit the best performances, as expected. However, even though our performance is inferior, as anticipated, the differences compared to the traditional tests are not dramatic. For example, after applying a Box-Cox transformation our test exhibits almost equivalent performance with the Kolmogorov Smirnov test, even in the gamma-related scenarios. Our performance is even better if we assume normality, and the generated data are indeed normally distributed. This is not a surprise, as we can accommodate such an assumption. We observe that the Box-Cox based length-test works similarly well in all scenarios, in spite of the estimated extra parameter. Regarding our kernel based approach, we observe nice size performance, as well as satisfactory power performance throughout.

Regarding the non-traditional scenarios, we consider two settings for the power. One that refers to two underlying normal distributions with unequal variances, and one that refers to two gammas (the selected parameters are given in the Web Appendix). Under the non-traditional scenarios, the differences are dramatic in favor of our methods. More specifically, we observe that the t − test and the Wilcoxon test completely collapse, as expected. The KS test is dramatically outperformed by our approaches throughout, even in the cases for which we do not make any distributional assumption (see Tables 1-2 of the Web Appendix). Furthermore, even in cases for which we make the wrong distributional assumptions, since a gamma model does not lie in the Box-Cox family, we still observe better performance in favor of our test (see Table 2 of the Web Appendix).

5.2. Coverage and areas of egg-shaped and rectangular confidence regions of the sensitivity and the specificity

For this setting we consider both cutoffs to be unknown, and we estimate them based on the extension of the Youden index. Thus, we compare the approaches of egg(normal), egg(BC), and egg(kernels), depending on our underlying assumption of the distribution of the two groups. We compare these confidence regions in terms of coverage and area to their rectangular counterparts: rect(normal), rect(BC), and rect(kernels). We observe that the rectangular regions are more conservative throughout, and that they are outperformed by the proposed egg-shaped confidence regions in terms of their area. The reason is that the egg-shaped regions take into account the underlying correlation of the estimated pair of sensitivity and specificity, whereas the rectangular confidence regions do not. All relevant results are presented in Table 3. We observe that a smooth bootstrap ([32], [33]) scheme is more preferable in attaining the desired coverage as opposed to a traditional bootstrap based algorithm.

5.3. A note on bandwidth selection

As pointed out by a referee different kernel based strategies may provide improved results with regards to our non-parametric strategy. This is true as presented in the vast literature regarding bandwidth selection when kernel density estimates are involved. For our methods and simulations, we have used a simple closed form bandwidth [28]. Other more sophisticated bandwidths used in kernel density estimation are available in the literature. A standard textbook that contains such strategies is given by [29] among others. Another kernel technique of interest is presented in [34] and is based on diffusion. We have compared the latter with the standard plug-in bandwidth of Silverman’s rule previously discussed in section 4. Our comparisons are focused on the bias, the standard error, and the MSE that relate to the estimation of the length of the ROC curve. We have considered our aforementioned gamma related scenarios as well as the bimodal mixture (for the values of the parameters considered see Web Appendix C) and used 1000 Monte Carlo iterations. Our results are presented in Table 4 of the Web Appendix C where we compare the two kernel strategies. We observe that for the gamma related scenarios the diffusion is the clear winner while results are similar in the bimodal setting. Generally, the optimal bandwidth strongly depends on the underlying setting. For that reason, inferences based on smoothed estimations are generally complex. Further comparisons with cross validation bandwidths are also of interest but such issues lie beyond the scope of this study and are left for future research.

6. Applications

6.1. Pancreatic Cancer

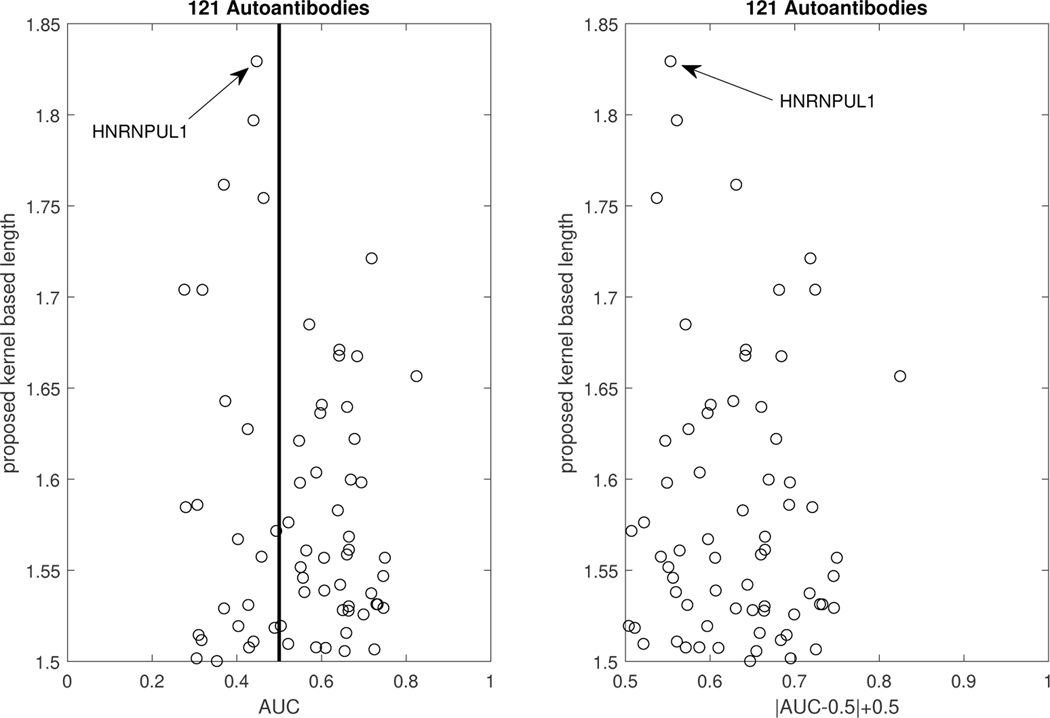
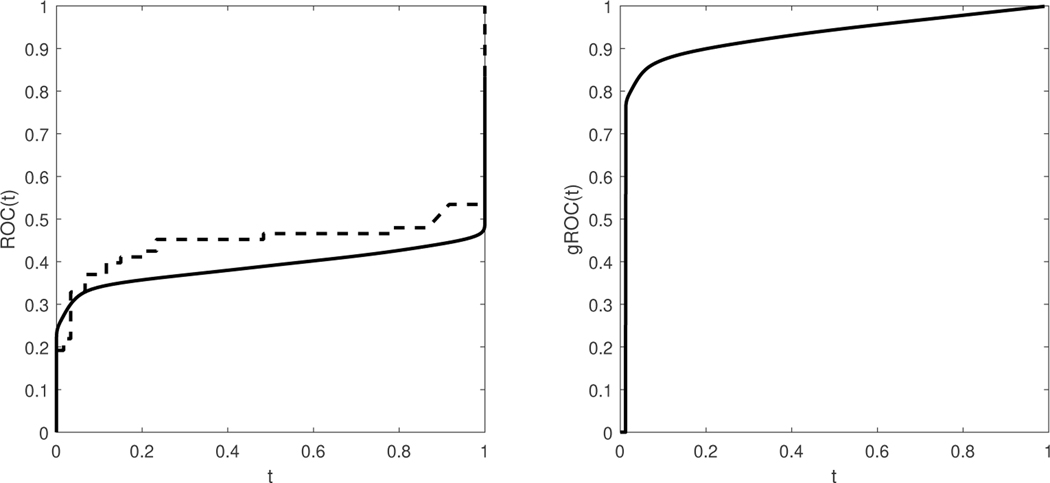
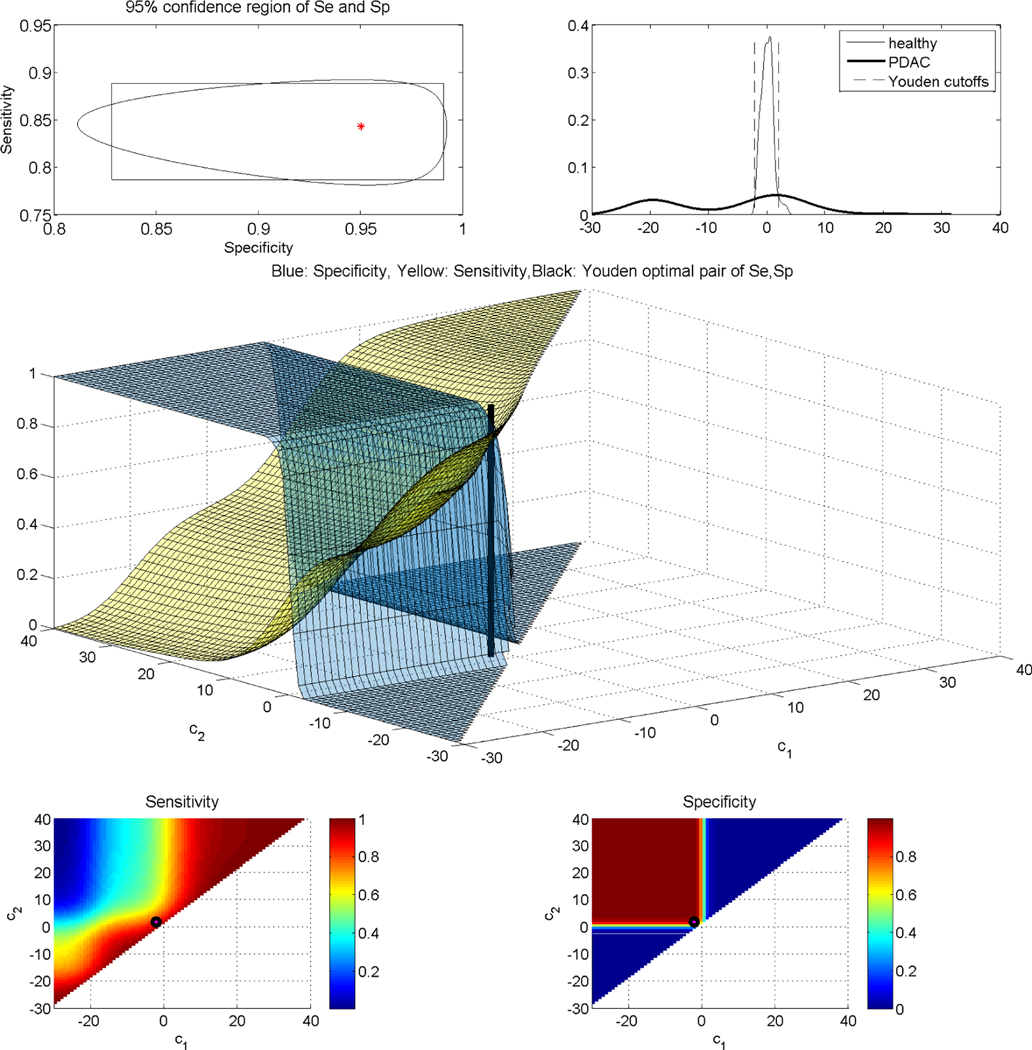
We investigated the contribution of autoantibodies as potential circulating biomarkers for PDAC early detection using a case-control study design. To assess autoantibody levels in early stage PDAC patient samples, we used microarray slides coated with a nitrocellulose-surface and spotted with 121 proteins, previously described as tumor-associated antigens across different solid tumor types from multiple prior studies ([35], [6], [36]). We tested three independent plasma sample sets: set 1 consisted of stages IB to IIB PDAC cases (n = 10), healthy controls (n = 10), and chronic pancreatitis cases (n = 10); set 2 consisted of early-stage (IA to IIA) PDAC cases (n = 42), healthy controls (n = 50), and chronic pancreatitis cases (n = 50); and set 3 consisted of resectable PDAC cases (n = 21) and benign pancreatic cyst cases (n = 14). Plasma samples were individually hybridized, and immunoglobulin G reactivity against each spotted antigen was quantified using an indirect immunofluorescence protocol. In our analysis, we consider the performance of the autoantibodies for group separation of the healthy versus the PDAC patients, after merging the data of all three sets. This suggests a total sample size for the control group of n₀ = 60, and a sample size for the PDAC group of n₁ = 73. In Figure 7, we plot the AUC of all 121 autoantibodies versus the kernel-based length, and we observe that the highest length is achieved by the autoantibody HNRNPUL1. The empirical and the kernel-based estimates of the traditional ROC of HNRNPUL1 are shown in Figure 8. The empirical AUC of that autoantibody with the corresponding 95% confidence interval is 0.4468(0.3392,0.5544). For the kernel-based length, we derive an estimate of 1.8255 with a 95% confidence interval of (1.7846–1.8748). We note that, based on Theorem 2, a length of 1.8255 corresponds to an area under the optimal ROC curve between 0.9035 and 0.9645, which implies that the marker has high potential. We provide the estimated kernel-based dominant generalized ROC (gROC) curve in Figure 8 which is obtained by simply using the ratio of the kernel based estimators. Its AUC equals to 0.9154. We have to stress that in theory the gROC is the optimal ROC under the condition of a unimodal likelihood ratio and thus not always optimal. Moreover, the estimation of the gROC is computationally intensive, especially if one wants to obtain the gROC estimates for a large number of biomarker candidates. On the other hand, estimates of the length are computationally trivial to obtain and at the same time it provides estimated bounds of the optimal and unknown optimal AUC. the theoretical gROC is not always the optimal ROC and is computationally intensive. The surfaces of the sensitivity and specificity of HNRNPUL1 are given in Figure 9. This plot helps an investigator visualize on the original scale of the marker the tradeoff of the sensitivity and specificity for various pairs of c₁ and c₂. The top panel of Figure 9 provides the egg-shaped confidence region around the Youden-based optimal pair of sensitivity and specificity. Remember that a perfect marker always yields a length of 2, while a useless one would yield a length of $\sqrt{2}$. The kernel density estimates for the healthy and the PDAC group are presented in Figure 9. We observe a bimodality for the PDAC-group related density that extends to the right and to the left of the estimated density of the controls. Namely, PDAC patients do exhibit either very high or very low measurements of this autoantibody compared to the healthy group. The reason is that the increase of tumor antigen levels in the plasma is associated with immune complex formation, leading to the depletion of free autoantibodies against the antigen ([6]).

Figure 7.

Scatterplot of the AUCs and proposed lengths of all 121 autoantibodies.

Figure 8.

Left Panel: Traditional ROC curves for the top performing autoantibody: dashed line refers to the empirical, and solid line refers to the kernel-smoothed based one. The corresponding AUCs and 95% CIs are 0.4468(0.3392, 0.5544) and 0.3892(0.3055,0.4730), respectively. The estimated kernel-based length with the corresponding 95% CI is 1.8255 (1.7846–1.8748). Right panel: The corresponding kernel-based estimated gROC. The area under this kernel based estimate of gROC is 0.9154.

Figure 9.

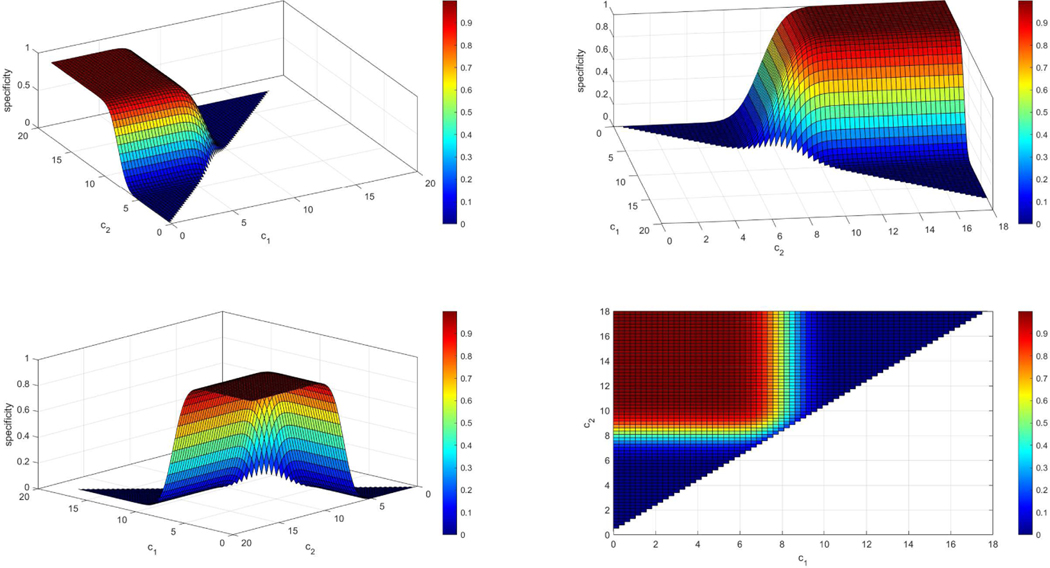
Top left: Egg shaped 95% confidence region for the sensitivity and specificity at the Youden-based estimated cutoffs. Top right: Underlying kernel densities of the healthy and the diseased. Middle: Surfaces of sensitivity and specificity along with the estimated Youden-based optimal pair of cutoffs. Bottom left: Contour plot of the surface of sensitivity for all possible cutoffs, along with the estimated Youden-based optimal pair of cutoffs (black dot). Bottom right: Contour plot of the surface of specificity for all possible cutoffs, along with the estimated Youden-based optimal pair of cutoffs (black dot).

We proceed by further evaluating this autoantibody in terms of sensitivity and specificity. As there are no available clinical insights regarding the underlying cutoffs, we estimate them by the data at hand. In this data set, as the diseased group exhibits bimodality, we do not proceed with the parametric-based approaches, but with our kernel-based approaches throughout. The kernel-based estimated cutoffs are derived to be (−2.1336, 1.8944) and are visualized in Figure 9. The underlying Youden-based sensitivity and specificity, along with their marginal 95% confidence intervals, are 0.8429(0.7946, 0.8831) and 0.9502(0.8498, 0.9880). The corresponding egg-shaped and rectangular 95% confidence regions are given in the first panel of Figure 9, in which we observe that the area of the egg-shaped region is 0.0151, and smaller than the rectangular one that yields an area of 0.0164. The surfaces of the sensitivity and specificity within the ROC space, which now is the unit cube, are given in Figure 9 (middle panel). A contour plot of those are given in the bottom two panels of Figure 9. By those figures, it is evident that the specificity achieved based on the Youden-based cutoffs is impressively large for any pair of cutoffs for which c₁ < −2.1336, c₂ > 1.8944. In the contour plots of Figure 9, we also visualize by a dot the corresponding pair of the Youden-based optimal pair of cutoffs. Overall, our results show a very promising performance of this autoantibody, which would have been rejected had we relied on the traditional empirical-based AUC.

6.2. Esophageal squamous cell carcinoma

Esophageal squamous cell carcinoma (ESCC) is an aggressive form of cancer with poor prognosis [37]. Biomarker discovery for its early detection is important since esophageal cancer is usually detected only after an advanced stage. Su et al. (2011) ([37]) focus on profiling global gene expression and their study revealed 159 genes that showed statistically significant difference between cases and controls based on fold-changes. Out of those 116 are derived to be up-regulated while 43 down-regulated. Their study involves 53 cases and 53 controls, and their data are publicly available from Affymetrix U133A expression arrays. These data are also discussed in [18] where it is also pointed out that non-monotone (or ‘non-traditional’) markers are also available in this data set.

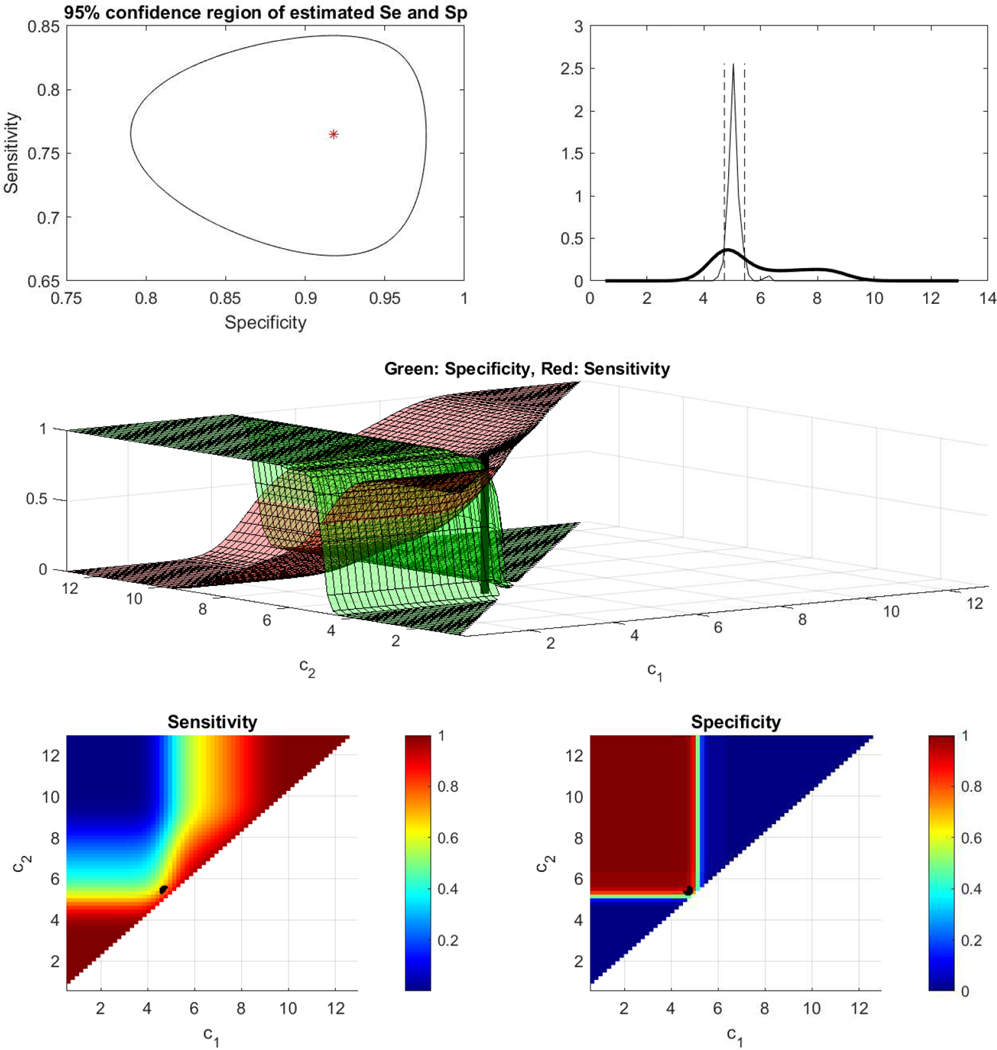
For probe 209644 the empirically estimated AUC is 0.5421 (0.4175–0.6667). This indicates that probe 207039 would be discarded as uninformative. By employing the proposed approaches, we derive the length of the ROC that corresponds to this marker to be 1.6518 and statistically significant (95% CI is 1.5938–1.7403). The two cutoff Youden yields a pair of Spec and Sens equal to (0.8754, 0.6659). In addition, the area under the gROC for this marker is 0.8238. The sensitivity and specificity surfaces along with the confidence region around their Youden based optimized values are given in Figure 10.

Figure 10.

ESCC data (probe 207039).Top left: Egg shaped 95% confidence region for the sensitivity and specificity at the Youden-based estimated cutoffs. Top right: Underlying kernel densities of the healthy and the diseased. Middle: Surfaces of sensitivity and specificity along with the estimated Youden-based optimal pair of cutoffs. Bottom left: Contour plot of the surface of sensitivity for all possible cutoffs, along with the estimated Youden-based optimal pair of cutoffs (black dot). Bottom right: Contour plot of the surface of specificity for all possible cutoffs, along with the estimated Youden-based optimal pair of cutoffs (black dot).

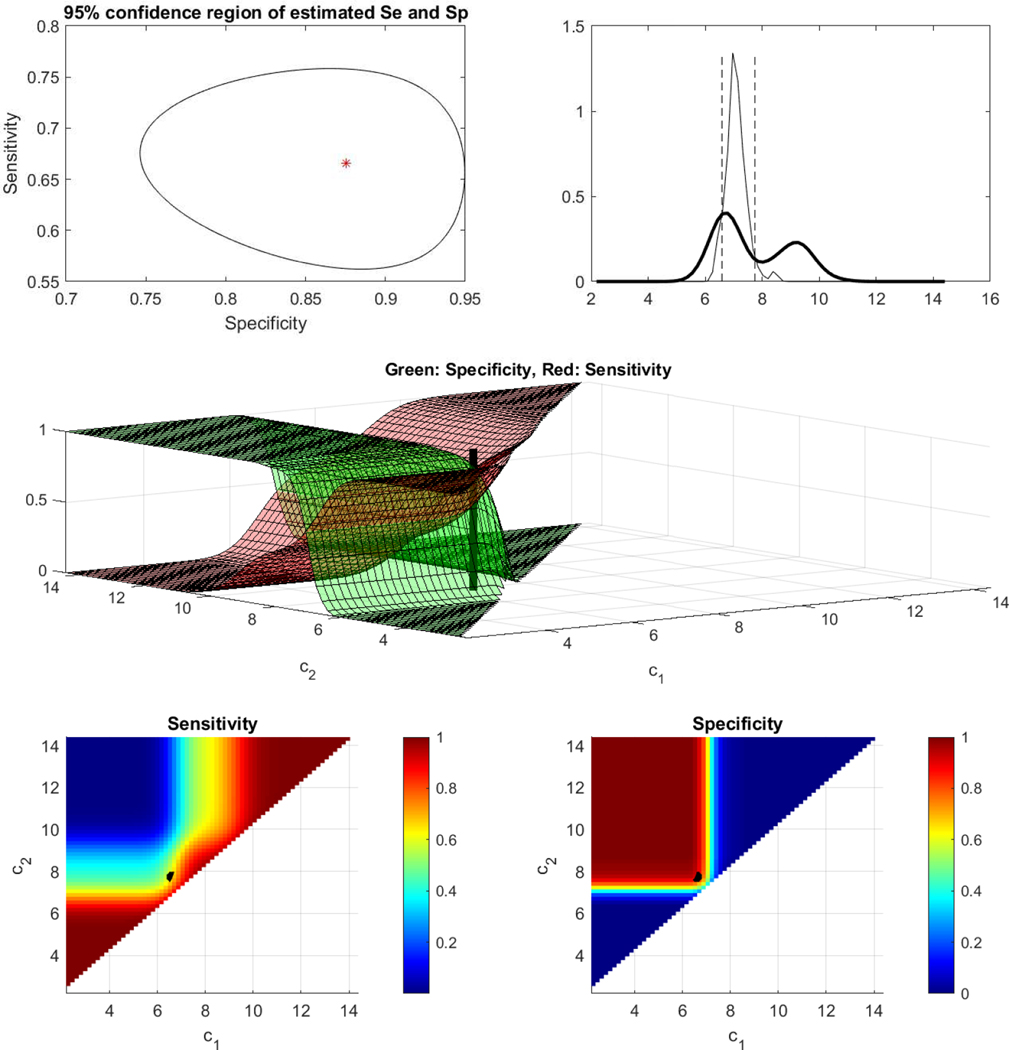
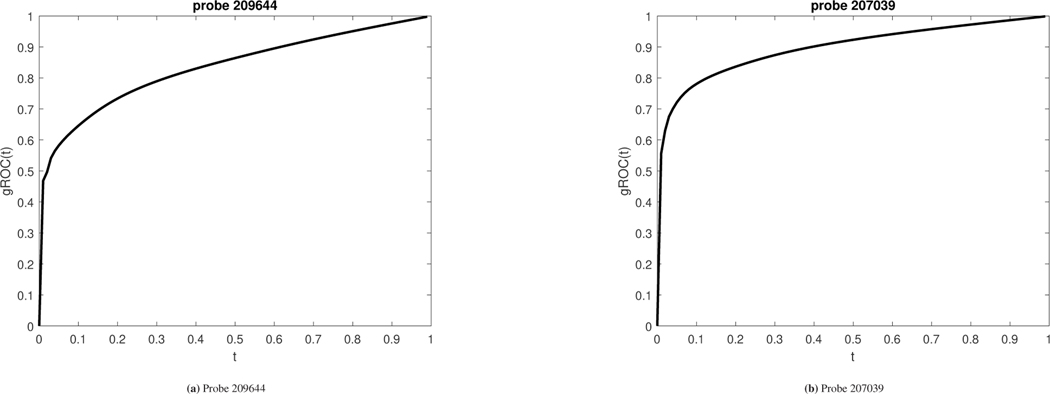
Results are analogous for probe 207039. The empirical AUC is equal to 0.5180(0.3963–0.6397). Namely, this marker too was discarded as uninformative while in fact the length of its ROC is equal to 1.7442 and statistically significant with a 95% CI (1.6807–1.8101). The two cutoff analysis results to a pair of (Spec, Sens) equal to (0.9180, 0.7648). The area under the gROC of this marker is equal to 0.8858 which implies a potentially promising marker that would have been missed with traditional ROC methodology. The sensitivity and specificity surfaces along with the confidence region around their Youden based optimized values are given in Figure 11. The corresponding gROCs for both probes are shown in Figure 12.

Figure 11.

ESCC data (probe 209644). Top left: Egg shaped 95% confidence region for the sensitivity and specificity at the Youden-based estimated cutoffs. Top right: Underlying kernel densities of the healthy and the diseased. Middle: Surfaces of sensitivity and specificity along with the estimated Youden-based optimal pair of cutoffs. Bottom left: Contour plot of the surface of sensitivity for all possible cutoffs, along with the estimated Youden-based optimal pair of cutoffs (black dot). Bottom right: Contour plot of the surface of specificity for all possible cutoffs, along with the estimated Youden-based optimal pair of cutoffs (black dot).

Figure 12.

gROCs for both probes discussed in the application that refers to the esophageal data. Left panel: gROC for probe 209644 with an area under it equal to 0.8238. The two cutoff Youden-based sensitivity and specificity are derived to be (0.8754, 0.6659). The area under the usual empirical ROC estimate is 0.5421 (0.4175–0.6667) which implies that this marker would have been discarded as uninformative in spite of its discriminatory ability. Right panel: gROC for probe 207039 with an area under it equal to 0.8858. The two cutoff Youden-based sensitivity and specificity are derived to be (0.9180, 0.7648). The area under the usual empirical ROC estimate is 0.5185 (0.3963–0.6397) which implies that this marker would have been discarded as uninformative in spite of its discriminatory ability.

7. Discussion

Nowadays, high throughput technologies allow for the simultaneous input of hundreds of markers. Hence, there is a crucial need of proper biomarker ranking. Traditional measures involve the AUC, as well as affordable levels of sensitivity and specificity that may be ill posed under a potential improper behavior of a biomarker, implying a severe violation of the underlying stochastic ordering assumption of the healthy and cancer patients.

In this paper we explore the properties of the length of the ROC curve both under a parametric and a non-parametric setting. We illustrate that the length of the ROC can be expressed as a ϕ−divergence and for parametric models we study its asymptotic distribution. We provide a link of the length of the ROC with the area of the optimal ROC. Namely, given the length, we provide the upper and lower bounds of the AUC of the optimal ROC which reveals the full potential of a marker. We focus on settings where the density ratio is unimodal and thus the gROC is optimal. For cutoff derivation we explore the two cutoff Youden index and illustrate that under this context the sensitivity and the specificity are surfaces that can be visualized in the unit cube to reveal the usual sens/spec tradeoff. We further provide joint confidence regions for the achieved sensitivity and specificity. We provide both parametric and non-parametric frameworks.

Our approaches can have a broad application in the biomarker field as they may be safely applied to any candidate list, ensuring that all four kinds of markers will be captured: 1) markers of the usual monotone ordering (i.e. the higher the marker score the greater the suspicion of the disease), 2) markers of the reverse ordering (the lower the marker score the greater the suspicion of the disease), 3) a non-monotone behavior which is commonplace in many mundane tests and may sometimes be present in cancer biomarkers. That is, very high and very low scores tend to correspond to diseased individuals while the healthy scores tend to lie in a zone in between. Finally, 4) more complex non-monotone behaviors than in case (3) that could imply more than two cutoffs (when the density ratio has two or more modes). We note that under a biomarker setting, it is hard to think of plausible situations where more than two cutoffs are necessary. Regarding case (3) above, we have illustrated three examples of such markers in our application section. The non-monotone behavior of HNRNPUL1 can be explained biologically. For example, we have previously observed that, with tumor development and progression, elevated levels of antigen in the plasma lead to the formation of circulating immune complexes, which deplete plasma of free autoantibodies against the antigen ([6]). This could explain the improper behavior of autoantibodies against the protein HNRNPUL1, implying that very high and very low measurements are indicative of cancer. We have observed that immune complexes for HNRNP family members can be identified in the plasma of cancer patients, and that their levels are, similarly, either elevated or decreased in patients, compared to matched controls. These results suggest that autoantibodies and immune complexes for the same antigen may exhibit an inverse relationship, leading to the improper behavior which is the focus of our paper. Based on previously discussed traditional biomarker ranking approaches, an improper behavior of the autoantibody HNRNPUL1, in terms or recognizing early PDAC stages, would naively lead to its rejection as uninformative. In this paper, we provide a complete framework to discover and then evaluate such promising biomarkers. Our approaches fill in an essential literature gap, which may have caused the rejection of very useful biomarkers of this nature.

There are several points for future research. One practical topic that needs to be further investigated is the efficiency of different versions of bandwidth especially since this setting may involve bimodal densities. Further comparisons based on other measures can also be of interest. One such measure is the overlap coefficient (OVL) discussed in [38], [39], [40], and [41]. Graphically, the OVL is the area between the densities of the non-diseased and the diseased group when those are plotted on the same axes and is related to Kullback-Leibler divergence ([42]). An interesting measure that can be used in conjunction with our approaches is the TNRC (see [9]) to classify which of the detected markers are improper. As discussed above, it is important to note that our approach may reveal markers for which the use of more than two cutoffs is suggested. A smooth graph of the density ratio could be used for revealing such markers. A graph suggesting a monotone density ratio indicates a proper ROC curve whereas a graph suggesting a unimodal density ratio indicates the need of two cutoffs. Other type of configurations may indicate the necessity of more than two cutoffs which, as stated above, is hard to justify when dealing with biomarkers.