Triage of in vivo burn injuries and prediction of wound healing outcome using neural networks and modeling of the terahertz permittivity based on the double Debye dielectric parameters

Abstract

The initial assessment of the depth of a burn injury during triage forms the basis for determination of the course of the clinical treatment plan. However, severe skin burns are highly dynamic and hard to predict. This results in a low accuracy rate of about 60 - 75% in the diagnosis of partial-thickness burns in the acute post-burn period. Terahertz time-domain spectroscopy (THz-TDS) has demonstrated a significant potential for non-invasive and timely estimation of the burn severity. Here, we describe a methodology for the measurement and numerical modeling of the dielectric permittivity of the in vivo porcine skin burns. We use the double Debye dielectric relaxation theory to model the permittivity of the burned tissue. We further investigate the origins of dielectric contrast between the burns of various severity, as determined histologically based on the percentage of the burned dermis, using the empirical Debye parameters. We demonstrate that the five parameters of the double Debye model can form an artificial neural network classification algorithm capable of automatic diagnosis of the severity of the burn injuries, and predicting its ultimate wound healing outcome by forecasting its re-epithelialization status in 28 days. Our results demonstrate that the Debye dielectric parameters provide a physics-based approach for the extraction of the biomedical diagnostic markers from the broadband THz pulses. This method can significantly boost dimensionality reduction of THz training data in artificial intelligence models and streamline machine learning algorithms.

1. Introduction

Approximately 416,000 patients were treated for burn injuries in emergency departments across the USA in 2018 [1]. Burn injuries can result in significant skin necrosis and deep tissue damage. They have a tremendously deleterious impact on individual health, causing significant pain and a negative influence on mental health, quality of life, the ability to return to work, and subsequent mortality [2]. The initial assessment of the severity of a burn injury is paramount because it forms the basis for all subsequent clinical treatment plans [3]. There are three categories of burns: superficial, partial-thickness (PT), and full-thickness (FT). PT burns are further divided into superficial partial-thickness (SPT) and deep partial-thickness (DPT) subcategories. SPT burns only affect the papillary dermis, causing pain, blisters, and weeping, and generally do not require surgical intervention. DPT burns, on the other hand, extend into the reticular dermis, partially destroying the dermal appendages and potentially requiring surgery to aid in healing and prevent infection and scarring. Also, PT burns are dynamic and potentially can progress to FT status. In addition, the skin alterations caused by the PT burns are highly dynamic, leading to a low accuracy rate of only 60 - 75 $\mathrm{\%}$ in the diagnosis of PT burns (i.e., differentiation between SPT and DPT) in the acute post-burn period [4,5]. The clinical diagnosis of the intermediate burns, which is mainly a subjective evaluation task [6], can be further improved by utilizing noninvasive imaging devices, in addition to computer-aided burn depth determination softwares [7–12].

Over the past two decades, terahertz time-domain spectroscopy (THz-TDS) has emerged as a promising tool for biosensing applications in general [13–36] and the assessment of skin and monitoring burn injuries in particular [37–54]. The first demonstrations of the utility of the THz-TDS technique for diagnosing the severity grade of cutaneous burn injuries were limited to point-spectroscopy measurements, not accounting for the heterogeneity and the spatial variations in burns. Furthermore, the THz spectroscopy setups were bulky, expensive and required cumbersome optical alignments, making them unsuitable for real-world clinical use. To address this challenge, we have designed and fabricated a handheld imaging device, named the PHASR (Portable HAndheld Spectral Reflection) Scanner, for fast reflection imaging of in vivo burn injuries using the THz-TDS technique [55]. The PHASR Scanner is compact and portable and provides high-speed broadband (0.1 to about 2 THz) spectroscopic imaging measurements. We have shown that the resolution of the images obtained using the PHASR Scanner is diffraction-limited [56]. We have also implemented numerical feature extraction and machine learning techniques to automatically estimate the severity grade of in vivo burn injuries using the PHASR Scanner measurements [53,54,57]. However, previous works have not investigated the dynamics and macroscopic changes of the dielectric functions of the skin burn tissue. There are three main physical changes in burn injuries that can alter their THz reflectivity: 1) swelling of the burned tissue, which is largely caused by water and is highly correlated with THz reflectivity [44]; 2) dermal adnexal structures that contribute to THz scattering and are correlated with burn severity and THz reflectivity measurements [40]; and 3) changes in the chemical structure and dielectric permittivity of biomolecules like proteins and collagen fibers due to heat exposure, which can also affect THz reflectivity but is difficult to isolate from the other two sources of THz signal contrast. These macroscopic alterations are hypothesized to be responsible for the contrast in THz-TDS measurements of burns with different depths [38,58,59]. Several variations of the Debye model of dielectric relaxations have been used to describe the complex permittivity of water and other polar liquids at THz frequencies [60–65]. In addition, because liquid water is the main constituent of most biological tissues, the double Debye theory has been employed successfully to explain the interaction of THz radiation with various biological tissue types, including the human skin [66,67], human blood [68], breast cancer tissue [69], basal cell carcinoma [70], and brain gliomas [71]. One of the acute features of cutaneous thermal injuries is the swelling of the involved tissue caused by a fluid shift from the circulating plasma or the interstitial edema predominantly composed of water [72]. Therefore, in this work, we also employ the double Debye theory to investigate the mechanisms of dielectric relaxations in cutaneous burn injuries to explain the origin of contrast observed between the refractive indices of burns of different depths.

In the following, we explain our experimental design to obtain the THz-TDS images of the burns using the PHASR Scanner. We describe our methodology for the measurement and numerical modeling of the complex permittivity of burn injuries in vivo using a collocated reflection measurement geometry. The extracted empirical double Debye parameters used to explain the measured dielectric permittivities are utilized to create artificial neural network (NN) algorithms capable of automatically diagnosing the burn severity group and predicting the re-epithelialization status of the wounds in 28 days. The Debye parameters provide a feature extraction strategy based on the complex dielectric function of the tissue instead of using purely numerical features. Combined with the NN models, they can predict the outcome of the wound healing process with an accuracy rate of 93 $\mathrm{\%}$ and estimate the severity group of the burns with an average accuracy rate of 84.5 $\mathrm{\%}$ . Our technique additionally serves to reduce the number of input variables of the NN models from all frequency-dependent components of the reflection coefficient or index of refraction of a sample to only 5 Debye parameters, which represents a significant boost in dimensionality reduction. This unique feature is exceptionally critical in processing large data sets obtained over large clinical trials.

2. Method

2.1. Burn protocol

The burn protocol and the induction procedure used in this study are reviewed and approved by the Institutional Animal Care and Use Committee (IACUC) at Stony Brook University and are described in detail elsewhere [73]. In summary, forty burns were created on the dorsum of two Landrace pigs using two standardized models, including a metallic brass bar ( $N=10$ ) and a hot water scald ( $N=30$ ) device, which represent the sources of many of the clinically-relevant burn injuries [74]. Each burn was approximately 2.54 cm in diameter and 4 cm apart from the adjacent burn sites. We varied both the device temperature and exposure time to create burns of different severities. The percentage depth of the burned dermis and the re-epithelialization rate of the burn wounds were measured histologically and used to assign the severity label of each burn as the ground truth. The percentage of burn depth was assessed by measuring the deepest point of injury in the dermis using Hematoxylin $\mathrm{\&}$ Eosin (H $\mathrm{\&}$ E) staining of four- or eight-mm punch biopsies, which were extracted within twenty-four hours post-induction of the burns. Burns with a partially-damaged dermis formed the partial-thickness (PT) burns group. Burns with an entirely-damaged dermis create the full-thickness (FT) burns category. Burn injuries are highly dynamic during the inflammatory period, and their severity can change over the next few days post-burn onset. Therefore, we also measured the re-epithelialization rate of the burns twenty-eight days post induction to deterministically identify which burn wounds were fully-healed and which required a surgical intervention. The re-epithelialization rate was calculated on each punch biopsy obtained on Day 28 by measuring the width of the new epidermis and dividing by the total width of the section. If a burn was fully-re-epithelialized on Day 28, it was included in the fully-healed (FH) group, while all other burns were accounted for in the not-healed (NH) category. Table 1 provides a summary of the different abbreviated labels used to denote various burn severity and wound healing outcome categories, along with the criteria used to select each category and the number of observations (i.e., the total number of burns or healthy samples belonging to each category).

Table 1. Burn labels’ abbreviations, categorization criteria, and number of samples in each burn severity and wound healing group.

Tissue Type	Group Label	Categorization Criteria	Number of Samples
Healthy	H	Not burned	8
Partial-Thickness	PT	Percentage depth of burned dermis on Day 0 < 100 $\mathrm{\%}$	25
Full-Thickness	FT	Percentage depth of burned dermis on Day 0 $\ge$ 100 $\mathrm{\%}$	15
Fully-Healed	FH	Re-epithelialization rate on Day 28 = 100 $\mathrm{\%}$	22
Not-Healed	NH	Re-epithelialization rate on Day 28 <100 $\mathrm{\%}$	18

2.2. THz-TDS measurements

We used the PHASR Scanner, a collocated, telecentric imaging device, to obtain the in vivo THz-TDS measurements [55]. Figure 1(a) shows the schematic configuration of the optical and mechanical components inside the scanner housing. The beam is raster scanned across the aperture of the f- $\theta$ lens by a mirror mounted on a gimbal composed of a goniometer and a rotational stage in a heliostat configuration. Importantly, the f- $\theta$ lens design is customized such that a collimated beam passing through the front focus at a deflection angle of $\theta$ is focused at a distance of $f\times \theta$ from the lens optical axis [75]. Consequently, the focus is always parallel to the optical axis of the lens and is perpendicular to the target plane. In this perpendicular trajectory, the reflection coefficient of a tissue is independent of the polarization of light and is obtained following the Fresnel equation given by,

$$r_{\text{tissue}}=\frac{E_{\text{tissue}}}{E_i}=\frac{{\tilde{n}}_{\text{w}}-{\tilde{n}}_{\text{tissue}}}{{\tilde{n}}_{\text{w}}+{\tilde{n}}_{\text{tissue}}},$$ (1)

where $E_{\text{tissue}}$ and $E_i$ are the Fourier spectrum of the reflected and incident beams at the interface of imaging window and tissue, $\tilde{n}=n-i\kappa$ is the complex refractive index as a function of frequency, where $n$ is the refractive index and $\kappa$ is the extinction coefficient, ${\tilde{n}}_{\text{w}}$ represents the complex refractive index of the imaging window, which is measured separately in transmission geometry. Because $E_i$ is not available directly, we can use an additional reference measurement from a material with known optical properties such as the ambient air. Dividing the reflection coefficient of tissue given by Eq. (1) with that of the reference air results in

$$R=\frac{r_{\text{tissue}}}{r_{\text{air}}}=\frac{E_{\text{tissue}}}{E_{\text{air}}}=\frac{({\tilde{n}}_{\text{w}}-{\tilde{n}}_{\text{tissue}})({\tilde{n}}_{\text{w}}+{\tilde{n}}_{\text{air}})}{({\tilde{n}}_{\text{w}}+{\tilde{n}}_{\text{tissue}})({\tilde{n}}_{\text{w}}-{\tilde{n}}_{\text{air}})},$$ (2)

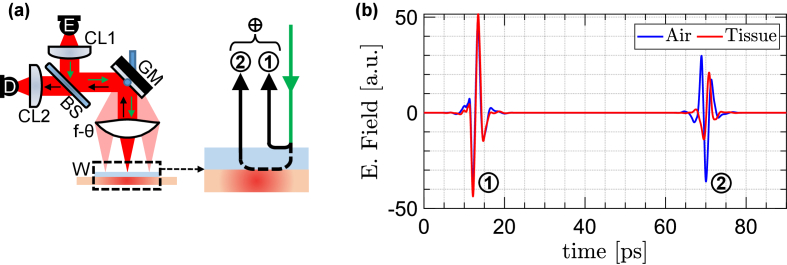
Fig. 1.

(a) the schematic configuration of the optical and mechanical components inside the PHASR Scanner housing. (b) example THz-TDS traces of a burn and air samples.

Because ${\tilde{n}}_{\text{w}}$ and ${\tilde{n}}_{\text{air}}$ are known in advance, Eq. (2) can be rearranged to calculate the complex refractive index of the tissue according to

$${\tilde{n}}_{\text{tissue}}=\frac{(1-R)n_w^2+(1+R)n_{\text{w}}}{1-R+(1+R)n_{\text{w}}}.$$ (3)

Figure 1(b) shows example THz-TDS traces of a burn and air samples. All acquired pulses are processed by wavelet denoising implemented as level-based hard-thresholding, explained in detail elsewhere [54]. The first reflections in Fig. 1(b), marked as ①, were originated from the interface of air and the imaging window. These reflections were used to calibrate the phase information and accounting for any phase distortions caused by mechanical system drifts. In addition, wavelet denoising was used to remove any ringing or baselines that may result from the first reflections. The second reflections, marked as ②, were originated from the interface of the imaging window and sample. Knowing the thickness of the imaging window, we were able to estimate the location of the second reflections from the tissue interface. We used a Blackman window around the second reflections with a 20-ps time width around the peak of the THz pulse. Fourier transform of the windowed burn and air pulses yield the $E_{\text{tissue}}$ and $E_{\text{air}}$ to be used for calculating $R$ . In calculating $R$ by dividing $E_{\text{tissue}}$ with $E_{\text{air}}$ , we use Wiener deconvolution to prevent large spectral value artifacts caused by the ill-posed deconvolution implementation [54].

2.3. Double Debye model

The double Debye (DD) dielectric relaxation theory has be used for explaining the permittivity of water in the THz frequency range. The complex dielectric permittivity as a function of frequency described by the DD model is given by,

$${\hat{\epsilon }}_r^{DD}={\epsilon }_{\mathrm{\infty }}+\frac{{\epsilon }_s-{\epsilon }_2}{1+j\omega {\tau }_1}+\frac{{\epsilon }_2-{\epsilon }_{\mathrm{\infty }}}{1+j\omega {\tau }_2}.$$ (4)

The ${\epsilon }_s$ represents the static low-frequency permittivity, ${\epsilon }_{\mathrm{\infty }}$ is the permittivity at the high frequency limit, ${\tau }_1$ and ${\tau }_2$ are the relaxation times of the slow and fast processes, respectively, and ${\epsilon }_2$ represents the intermediate permittivity, describing the transition between these two processes. Following Eq. (3), the measured dielectric permittivity of a burn tissue is given by,

$${\hat{\epsilon }}_r^{\text{measured}}={\tilde{n}}_{\text{tissue}}^2={(n_{\text{tissue}}-i{\kappa }_{\text{tissue}})}^2,$$ (5)

Therefore, the Debye parameters of a burn tissue can be obtained by fitting Eq. (4) to the measured values obtained by Eqs. (3, 5) using an optimization procedure intended to minimize the sum of the squared residuals given by,

$$\text{{SSR}}=\sum _{k=1}^N{({\hat{\epsilon }}_r^{\text{measured}}(k)-{\hat{\epsilon }}_r^{\text{DD}}(k))}^2.$$ (6)

In this work, we used the nonlinear least squares function in MATLAB, choosing the Levenberg-Marquardt algorithm [76]. All the five Debye parameters were optimized in our implementation. The boundary values of each parameter during optimization, i.e., the lower and upper limits, were chosen based on the previously published ranges of the DD parameters in the literature [69,70]. Additionally, we set the initial value of each parameter to the average of its lower and upper bounds.

2.4. Neural network

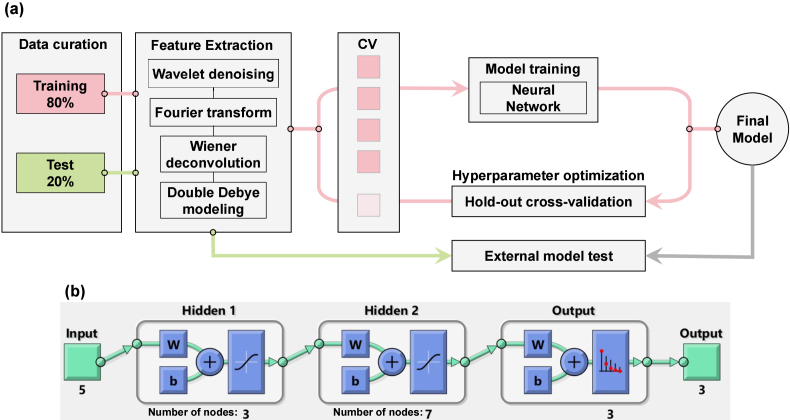
We developed two multi-layer fully-connected neural network (NN) models to address two different tasks: one for estimating the depth of burn injuries in the healthy (H), partially-thickness (PT), and full-thickness (FT) groups, and another for predicting the healing outcome of burn wounds in the fully-healed (FH) and not-healed (NH) groups. The machine learning pipeline is depicted in Fig. 2(a). Each THz-TDS measurement (examples shown in Fig. 1(b)) underwent wavelet denoising in the time domain, followed by a Fourier transform and Wiener deconvolution using reference air measurements. The Wiener deconvolution produced the $R$ values required to calculate the refractive index and dielectric permittivity of the burns using Eqs. (3) and (5). The DD parameters were then obtained by fitting Eq. (4) to the measured dielectric permittivity values. These four steps formed the signal processing and feature extraction block in the machine learning pipeline. In previous work, we demonstrated that rough-surface and Mie scattering can cause significant spectral artifacts in THz-TDS measurements of chemical and biological samples [77–79]. To address this issue, we implemented a spatial averaging approach to mitigate artifacts caused by skin appendages and rough surface scattering in tissue spectra. We divided each image into all possible 5 $\times$ 5-pixel regions of interest (ROI) over the entire field of view of each sample and used the average of the 25 pixels at each ROI as a single observation. This resulted in 300, 556, and 569 observations from the H, PT, and FT categories, respectively. The DD parameters obtained at each ROI, along with labels assigned to each burn based on the histological assessment of punch biopsies, were used to train the NN models. For each classification task, we randomly selected 80 $\mathrm{\%}$ of the observations for training the model and reserved the remaining 20 $\mathrm{\%}$ as the test set. During the training process, we optimized the NN hyperparameters, including the number of layers and the number of nodes at each layer. We performed this optimization using brute-force search over a range of possible values for each parameter (number of layers: 2-4, nodes at each layer: 2-20) to minimize the error of a 5-fold cross-validation (CV) on the training set. This involved dividing the entire training set into a 4:1 ratio for five trials, using 4/5 of the training set to train the model and calculating its error on the remaining 1/5. We then found the combination of number of layers and number of nodes per layer that yielded the least cross-validation error based on the average classification error of those five folds. The best hyperparameters were used to train the model over the entire training set, and this final model was tested using the 20 $\mathrm{\%}$ of observations that were set aside before training. It is worth noting that the final performance of the model may be affected by the distribution of observations into the 80 $\mathrm{\%}$ training set and the 20 $\mathrm{\%}$ test set. This means that choosing different observations in each partition could yield different model performance values. To avoid this bias, it is common to repeat the training and testing process multiple times and report the mean and standard deviation of the model’s performance over those random trials. Therefore, we repeated this process over one hundred iterations, with different observations randomly included in the training and test groups at each iteration. In the Results section, we will evaluate the performance of the models based on the mean and standard deviation across these hundred trials.

Fig. 2.

(a) the machine learning pipeline, (b) the architecture of a three-layer feed-forward fully-connected neural network.

Figure 2(b) shows an example NN architecture used for classifying burns into the H, PT, and FT groups. It can be seen that the input block in this architecture consists of the five DD parameters. The two hidden layers have three and seven nodes, respectively, and a sigmoid activation function is used at the output of each hidden layer. As previously mentioned, the number of layers and number of nodes per layer in this example were determined by brute-force search to minimize the 5-fold cross-validation loss on the training set. The parameters $W$ and $b$ in Fig. 2(b) represent the weight and bias vectors of each layer, which are adjusted by stochastic gradient descent optimization based on the output loss function. We also used the SoftMax activation function on the final output layer to calculate the probability of an observation belonging to each burn severity or wound healing group. Given the limited number of observations and features (only five DD parameters per observation), using deeper NN models or more complex algorithms, such as those commonly used for computer vision tasks, was not justified in this case.

To evaluate the performance of the models on the test set, we used receiver operating characteristic (ROC) curves. These curves were generated using the predicted probability of each observation belonging to each burn severity or wound healing group. An ROC curve plots the true positive rate (TPR) against the false positive rate (FPR) at different thresholds chosen from the predicted probabilities [80]. A higher ROC-AUC (area under the curve) value indicates better predictive performance by the model [81].

3. Results and discussion

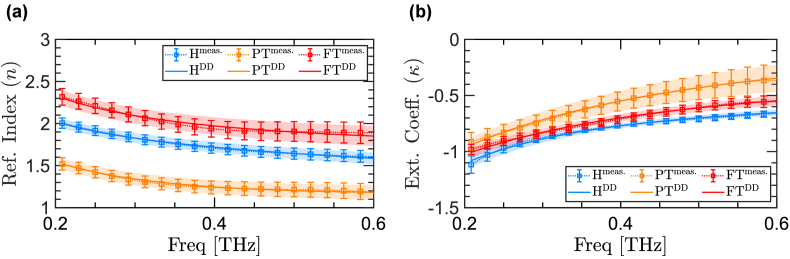
Figure 3 compares the refractive indices of three representative burn samples from H (blue), PT (orange), and FT (red) groups. Here, the dashed lines with error bars show the mean and standard deviation of the refractive indices measured over the entire field-of-view of the scanner. In contrast, the solid lines with error regions show the mean and standard deviation of the DD model fitted to each measurement. Figure 3(a) shows the real part of the refractive indices, $n$ , over the frequency range of 0.2 - 0.6 THz, while Fig. 3(b) compares the imaginary part of the refractive indices (i.e., the extinction coefficient ( $\kappa$ )) of the three representative burns. First, it can be noticed that there is great agreement between the measured and the numerically-modeled refractive indices in both real and imaginary parts. In particular, the Pearson correlation coefficient between the measurements and the fitted model is 1, 0.99, and 0.98 for H, PT, and FT samples, respectively. Second, the origin of the difference between the refractive indices of the healthy sample and the burn tissues with different severity grades can be explained based on the variations in the water content of the tissue, in addition to the intactness of the skin adnexa, whose effect on the THz spectra has been studied in our prior work [40]. Recent studies have proposed several signal processing techniques using cepstral [82] and wavelet domain analysis [78] for mitigating such granular scattering effects. Additionally, rough surface scattering can impact broadband THz measurements from skin [51,83], which can also be addressed using wavelet domain signal processing techniques [77,84].

Fig. 3.

(a) the refractive index and (b) the extinction coefficient of three representative samples from H, PT, and FT groups.

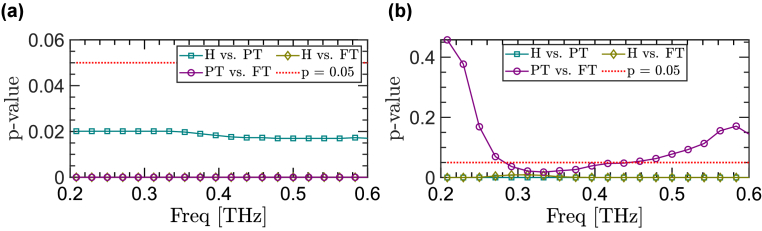
To further investigate the contrast between the THz dielectric function of different samples, Fig. 4 shows the statistical significance of the differences between the refractive indices in both real and imaginary parts by plotting the p-values as a function of frequency. Here, we used the Kruskal–Wallis analysis of variance (ANOVA) to determine the statistical significance. The Kruskal–Wallis test is a nonparametric method which, unlike the analogous one-way (ANOVA), does not assume that the residuals form a normal distribution. In this analysis, we have set the level of significance to $\alpha =0.05$ . Therefore, any p-value below 0.05 indicates a statistically-significant difference between the two groups. It can be seen in Fig. 4(a) that the difference between the real refractive indices among each pair of the three groups, i.e., H versus PT, H versus FT, and PT versus FT, is statistically significant over all the frequency components of the reliable bandwidth of measurements. In addition, Fig. 4(b) shows that the difference in extinction coefficients between the H and PT groups and also the H and FT groups is statistically significant over all frequencies. However, the p-value of the difference between PT and FT samples is less than 0.05 only over the spectral range between 0.28 and 0.42 THz.

Fig. 4.

The p-values of the statistical significance of the difference between (a) the real refractive indices and (b) the extinction coefficients of representative healthy and burn samples as a function of frequency.

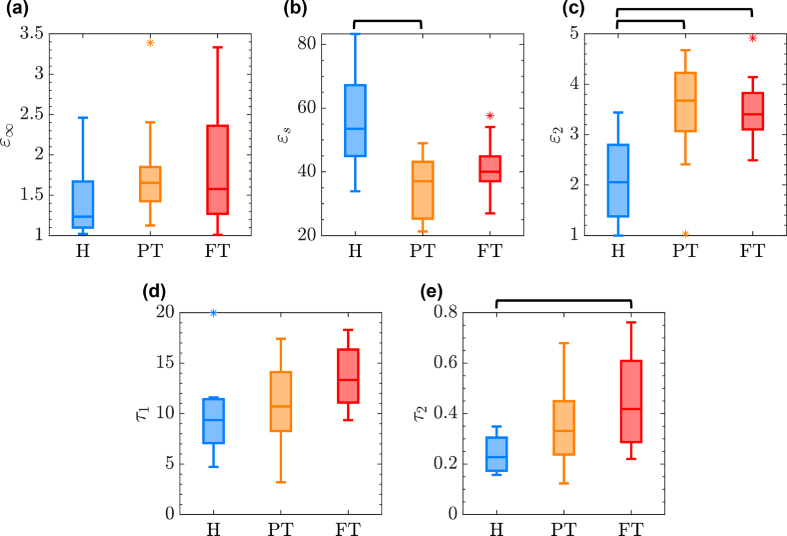
To further investigate the utility of the DD parameters in describing the difference among the burns of different severity and the healthy control samples, Fig. 5 provides the distribution of DD parameters over the entire sample set using box plots. The specific DD parameters whose distributions are shown by the box-plot diagrams are given on the y-axes in Fig. 5(a-e). Here, the blue, orange, and red boxes are associated with H, PT, and FT groups, respectively. The horizontal line within each box indicates the median of the double Debye parameter in each group, while the bottom and top edges of each box indicate the ${25}^{th}$ and ${75}^{th}$ percentiles. The whiskers extend to the data points within the 1.5 times the interquartile range from either edge of the box. The outliers outside this range are plotted individually using the * symbol. We performed further statistical significance testing over each of DD parameters to differentiate between the groups. We observed that the difference in the ${\epsilon }_s$ is only significant (i.e., p-value<0.05) between H and PT groups. On the contrary, ${\epsilon }_2$ provides a statistically-significant difference between both H and PT groups, and H and FT groups. Finally, the difference in the ${\tau }_2$ is only significant between H and FT categories. We observed that ${\epsilon }_{\mathrm{\infty }}$ and ${\tau }_1$ cannot differentiate between various categories. Results in Fig. 5 confirm that there is no single DD parameter that can separate between the burns of different severity and the healthy samples. Therefore, in our classification models, we use all these five parameters as inputs to the NN algorithms for identification of the best combination that can achieve accurate burn diagnosis.

Fig. 5.

the distribution of five DD parameters including (a) ${\epsilon }_{\mathrm{\infty }}$ , (b) ${\epsilon }_s$ , (c) ${\epsilon }_2$ , (d) ${\tau }_1$ , and (e) ${\tau }_2$ within each group over the entire sample set. The horizontal back lines over each sub-plot shows a statistically-significant (p<0.05) difference between any two groups using a specific parameter. For example, the horizontal line between H and PT groups in (b) means that the difference between the ${\epsilon }_s$ values of all samples in H and PT categories is statistically significant.

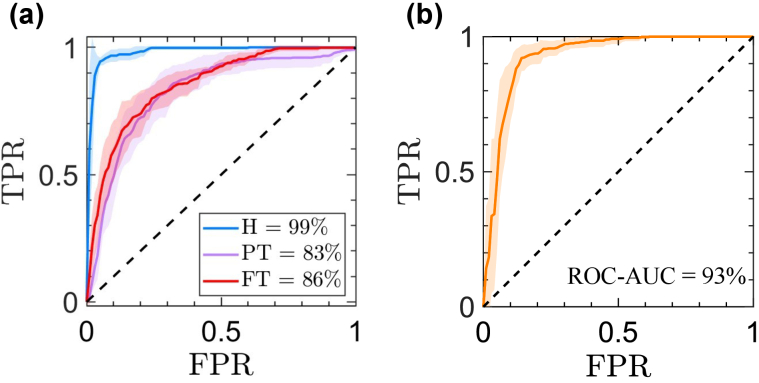
Figure 6 provides the ROC curves obtained using the two NN models, one for classification of the samples into H, PT, and FT categories, Fig. 6(a), and one for classification of the samples into FH and NH categories, Fig. 6(b). The solid lines and error regions in Fig. 6 represent the mean and standard deviation of the ROC curves obtained over 100 random iterations. The average ROC-AUC obtained for accurate diagnosis of each severity group of the burn injuries is included in the legends of Fig. 6(a-b). We obtained the ROC-AUC values of 99 $\mathrm{\%}$ , 83 $\mathrm{\%}$ , and 86 $\mathrm{\%}$ in recognition of H, PT, and FT groups (one-versus-all recognition), respectively. In addition, the ROC-AUC value of predicting the burn healing outcome was 93 $\mathrm{\%}$ , corresponding to accuracy, sensitivity, and specificity rates of 88 $\mathrm{\%}$ , 87 $\mathrm{\%}$ , and 90 $\mathrm{\%}$ , respectively.

Fig. 6.

The ROC curves obtained using the two NN models, for (a) classification of the samples into H, PT, and FT categories and (b) classification into FH and NH categories.

It can be noticed that the THz-TDS measurements can predict the final result of the healing process with a higher ROC-AUC value of 93 $\mathrm{\%}$ compared to the diagnosis of the burn severity group with the average ROC-AUC value of 84.5 $\mathrm{\%}$ between the PT and FT burns. It has been indicated in the literature that the biopsies obtained in the first 24-hours post-burn period can underestimate the severity of the burns [85]. This can be either because of the burn wound progression over the inflammatory cascade of the tissue or the inability of the H $\mathrm{\&}$ E staining to reveal the functional cell damage [85]. Further improvements might be obtained by using other biopsy staining methodologies. Therefore, the re-epithelialization rate of the burns obtained four weeks post-burn is a more reliable histological assessment for training machine intelligence algorithms. It also should be noted that predicting the wound healing outcome is a binary classification task, whereas estimation of the burn depth is a multi-class supervised machine learning problem (the number of classes is three in this work). Defining a multi-class modeling problem can result in a smaller number of observations within each group, affecting the accuracy, sensitivity, and specificity rates of diagnosis, especially when limited measurements are available. Therefore, similar to other automatic medical diagnosis applications, including more observations helps to validate and improve the reported accuracy, sensitivity, and specificity rates. As a result, expanding the available experimental data set is warranted for future studies. Overall, the reported accuracy rates are all above 83 $\mathrm{\%}$ , which promises a robust feature extraction strategy for diagnosis of the burn injuries that can be explained based on physical models instead of using purely numerical feature extraction techniques, which are harder to interpret.

4. Conclusion

In this paper, we have provided a methodology for calculating the physical THz spectroscopic features of in vivo burn injuries in the form of DD parameters. We have shown that the optimized DD models agree well with the real and imaginary parts of the refractive indices measured using our THz PHASR Scanner. Moreover, we demonstrated that although no single Debye parameter can provide a statistically-significant differentiation between the burns of different severities and healthy samples, the five DD parameters obtained using this strategy can be used for creating diagnostic NN models for automatic estimation of the severity grade of the in vivo burn injuries. In particular, we formed one NN model based on using the DD parameters for classification of the burns according to their depth of injury into H, PT, and FT groups. The ground-truth burn depth was estimated based on the histological assessment of punch biopsies collected from the burn sites in the acute post-burn period, i.e., within 24-hours of the burn induction. The other NN model was trained to predict the final healing outcome of the burn injuries into NH and FH groups. To accomplish this task, THz-TDS measurements obtained 24-hours post burn were used for predicting the wound healing status, which was determined histologically based on the re-epithelialization rate of the wounds twenty-eight days post burn.

Future directions include investigation of other histological staining techniques to determine the ground-truth for burn depth more reliably. In addition, THz-TDS measurements can be collected longitudinally post-burn to assess the utility of DD parameters in capturing the dynamics of burn conversion.

Funding

National Institute of General Medical Sciences10.13039/100000057 (GM112693).

Disclosures

MHA discloses intellectual property owned by the University of Washington, US Patent No. US9295402B1 [86]. Other authors declare no conflicts of interest.

Data availability

Data underlying the results presented in this paper are not publicly available at this time but can be obtained from the corresponding author.