Abstract
DNA methylation (DNAm) has been suggested to play a critical role in post-traumatic stress disorder (PTSD), through mediating the relationship between trauma and PTSD. However, this underlying mechanism of PTSD for African Americans still remains unknown. To fill this gap, in this article, we investigate how DNAm mediates the effects of traumatic experiences on PTSD symptoms in the Detroit Neighborhood Health Study (DNHS) (2008–2013) which involves primarily African Americans adults. To achieve this, we develop a new mediation analysis approach for high-dimensional potential DNAm mediators. A key novelty of our method is that we consider heterogeneity in mediation effects across subpopulations. Specifically, mediators in different subpopulations could have opposite effects on the outcome, and thus could be difficult to identify under a traditional homogeneous model framework. In contrast, the proposed method can estimate heterogeneous mediation effects and identifies subpopulations in which individuals share similar effects. Simulation studies demonstrate that the proposed method outperforms existing methods for both homogeneous and heterogeneous data. We also present our mediation analysis results of a dataset with 125 participants and more than 450,000 CpG sites from the DNHS study. The proposed method finds three subgroups of subjects and identifies DNAm mediators corresponding to genes such as HSP90AA1 and NFATC1 which have been linked to PTSD symptoms in literature. Our finding could be useful in future finer-grained investigation of PTSD mechanism and in the development of new treatments for PTSD.
Keywords: Clustering, Difference of convex, DNA methylation, High-dimensional mediators, Linear structural equation modeling, Variable selection
1. Introduction
Post-traumatic stress disorder (PTSD) is a serious mental health disorder that people may develop after they experience or witness a traumatic event, such as a natural disaster, a serious accident, a war, or sexual violence. People suffering from PTSD have symptoms such as disturbing thoughts, nightmares related to the events, mental or physical distress to trauma-related cues, attempts to avoid trauma-related cues, and negative alterations in thinking and feeling (Morrison et al. 2019). As shown in Roberts et al. (2011) and Himle et al. (2009), the prevalence of PTSD is higher in African Americans (AAs) than whites. This is possibly due to that PTSD is an adversity-related mental disorder and that AAs are more likely to encounter socially adverse experiences of discrimination and isolation which have a profound impact on mental health (Hudson et al. 2013; Cacioppo et al. 2015). However, research for the course of PTSD among AAs is very limited.
As suggested by Rusiecki et al. (2013) and Morrison et al. (2019), DNA methylation (DNAm), an epigenetic mechanism associated with the regulation of gene expression, plays a critical role in the pathophysiology of the PTSD. Since DNAm is a reversible process (Ramchandani et al. 1999), uncovering the role of DNAm in the pathophysiology of PTSD may facilitate the development of new potential treatments for PTSD (Rusiecki et al. 2013). For example, the epigenetics literature suggests that DNAm could mediate the effect of traumatic events on depression (Zhao et al. 2013; Dempster et al. 2014; Januar et al. 2015; Lei et al. 2015; Vangeel et al. 2015; van der Knaap et al. 2015; Turecki and Meaney 2016; Tyrka et al. 2016; Schuster et al. 2017; Gao et al. 2019). In particular, Peng et al. (2018) discover that DNAm levels at two cytosine-phosphate-guanine (CpG) probes mediate the effects from childhood trauma to depressive symptoms. Rutten et al. (2018) also observe that DNAm mediates the relationship between combat trauma and PTSD symptoms.
Moreover, according to Dickstein et al. (2010), heterogeneity occurs in the course of PTSD. For example, Kim et al. (2019b) observe gender differences in risk of PTSD, indicating a potential mechanism that yields heterogeneity across subjects in the effects of trauma. This motivates us to develop a heterogeneous model. In addition, Heinzelmann and Gill (2013) suggest that epigenetics may play a key role in the heterogeneous responses to trauma and differential risk of PTSD. Furthermore, Orcutt, Erickson, and Wolfe (2004) and Dickstein et al. (2010) reveal distinct trajectories of PTSD symptoms. This is crucial since finding all the prototypical patterns of adaptation to trauma could help us identify biomarkers and risk factors for PTSD. Nevertheless, to the best of our knowledge, heterogeneity in the mediation effects of the DNAm between traumatic events and PTSD symptoms has not been investigated so far.
In fact, heterogeneous mediation effects could arise frequently due to factors such as demographic and genetic characteristics, medical history, lifestyle, and unobserved attributes of subjects. Mediators in different subpopulations could vary or have different effects on the outcome. For example, as illustrated in Figure 1, high pressure on subjects could mediate the effects from the exposure of competitive environments to the performance of subjects. Yet, high pressure may have positive effects on performance of subjects in some subpopulation but negative effects for subjects in another subpopulation. This heterogeneity among subjects likely comes from stress tolerance and the ability to turn pressure into power, which may vary greatly across different groups of people.
Figure 1.

A heterogeneous mediation example.
In this case, it could be infeasible to identify the true mediator in a homogeneous model, since opposite effects could be canceled out. Recently, several mediation methods have been studied for heterogeneous mediation effects (Qin and Hong 2017; Dyachenko and Allenby 2018). However, they either require prespecified subpopulations or only focus on a single mediator variable.
In this article, we aim to investigate the high-dimensional heterogeneous mediation effects of DNAm variation on the relationship between trauma exposures and PTSD symptoms using the Detroit Neighborhood Health Study (DNHS) data (Uddin et al. 2010). The DNHS is a representative longitudinal cohort study involving primarily African Americans. In addition, we propose a novel mediator selection method which can identify subgroups of subjects and select mediators in each subgroup simultaneously for high-dimensional potential mediators. We refer to this new method as “the proposed method” in the rest of this article.
Note that the goal of our study is not to compare differences in PTSD risk by race and thus an interaction between race and trauma is not needed in our model. Rather, AAs’ higher prevalence of PTSD is a motivation for us to examine the mediation effects in a sample from this population. Hence, the focus of this article is to investigate the mediation mechanism in a predominantly AA sample (the DNHS data). On the other hand, in fact, there are few non-AA subjects in the DNHS dataset, indicating that it is inappropriate to use this dataset to compare racial differences in PTSD.
Our numerical studies show that the proposed method outperforms existing homogeneous methods in terms of mediation effect estimation and mediator selection. More importantly, the proposed method identifies meaningful DNAm mediators which are not selected by the homogeneous mediation methods on the DHNS data. Specifically, the selected DNAm CpG probes correspond to genes including HSP90AA1, SMARCA4, and NFATC1 which are indeed associated with PTSD risk (Raabe and Spengler 2013; Kuan et al. 2017; Criado-Marrero et al. 2018; Breen et al. 2019; Kim et al. 2019a, 2019b). These DNAm mediators can be highly informative in future development of novel interventions for PTSD. In addition, our data analysis shows the potential heterogeneity in mediation effects of DNAm on PTSD risk, which suggests finer-grained comparisons in future PTSD research.
The remainder of this article is organized as follows.
In Section 2, we describe details of the DNHS data which we analyze in this article. In Section 3, we propose the heterogeneous mediation method and illustrate the implementation of the proposed method.
Section 4 provides numerical studies through simulations. In Section 5, we apply the proposed method to the DNHS dataset. Finally, we conclude this study with discussion in Section 6.
2. DNHS Data
Our work is motivated by the Detroit Neighborhood Health Study (DNHS) where samples are collected between 2008 and 2013 from predominantly African American (AA) adults living in Detroit, Michigan. Studies suggest that DNA methylation (DNAm) could play a crucial role as mediators in the underlying relationship between traumatic events and PTSD (Dempster et al. 2014; Vangeel et al. 2015; Tyrka et al. 2016; Gao et al. 2019). Our work was further inspired by initial joint analysis of expression and EWAS data in GRRN genes (Vukojevic et al. 2014; Palma-Gudiel et al. 2015; Kim et al. 2019a; Wani et al. 2021), to find potential functional significance, and the DNHS is one of the few available datasets with both of these data types (Uddin et al. 2010).
In this article, in order to understand the underlying mechanism of PTSD in AAs, we conduct mediation analysis of DNAm on the relationship between trauma exposures and PTSD symptoms. One significant impact of identifying true mediators is that the occurrence of PTSD can be potentially intervened through the DNAm mediators. This is especially important for PTSD patients in the DNHS since the independent variables such as the previous trauma experience and adverse events cannot be altered after.
The DNHS is comprised of five survey waves where a total of 2081 participants have completed a 40-minute telephone survey. The survey includes questions on participants’ neighborhoods, mental and physical health status, social support, exposure to traumatic events, PTSD symptoms, and various demographics characteristics. All participants have been offered an opportunity to provide a blood specimen for genetic testing of DNA. In particular, the DNHS measures the PTSD symptom severity of participants through the widely used self-report PTSD Checklist, Civilian Version (PCL-C) (Blanchard et al. 1996; Grubaugh et al. 2007). The PCL-C set contains 17 items corresponding to key symptoms of PTSD. Participants indicate how much they have been bothered by each symptom using a 5-point (1–5) scale in reference to their worst traumatic experience. To access the overall severity, we calculate the average of the 17 items and treat the average PCL-C score as a representative of the PTSD symptom severity for each participant.
The DNHS also records the types of traumatic or stressful events that each participant has experienced. In our survey, we have specific questions such as “Have you experienced exposure to a war zone in the military or as a civilian?” to understand the exact nature of trauma exposures. Thus, a trauma exposure of a subject provides information of a certain type of trauma. We calculate the total number of trauma exposures (i.e., how many different types of traumas a subject experienced) and use it as a trauma feature characterizing overall trauma severity for each subject. Here we use the total number of experienced event types since many studies have used it as a measure of severity of trauma, for example, Lee and Park (2018), Irish et al. (2013), Harte, Vujanovic, and Potter(2015), Farley, Minkoff, and Barkan (2001), and Kessler et al. (2017).
The blood specimens in the DNHS are processed according to Weckle et al. (2015), and the DNA Mini Kit (Qiagen, Germantown, MD) is used to extract genomic DNA from peripheral blood. The extracted DNA samples are bisulfite-converted using the Zymo EZ-96 DNA methylation kit (Zymo Research, Irvine, CA). The converted samples are then profiled through the Illumina Infinium 450 K DNA methylation array (Illumina, San Diego, CA) according to manufacturer protocols. Specifically, we assess the methylation levels of more than 450,000 CpG sites which cover 99% of reference sequence (RefSeq) genes. More detailed explanation of the processing procedures are provided in Kim et al. (2019b), Ward-Caviness et al. (2020), Wolf et al. (2018), Ratanatharathorn et al. (2017), and Uddin et al. (2018).
There are several existing studies on the DNHS data from various aspects. Uddin et al. (2010) find that Detroit residents have PTSD prevalence more than twice of the corresponding prevalence in the entire United States, and that a person’s immune-related functions are related to genes with relatively lower levels of methylation. McClure et al. (2018) assess the association between environmental stressors and the Great Recession, while Horesh et al. (2015) and Kim et al. (2019b) reveal gender differences in PTSD. Moreover, Chang et al. (2012), Ratanatharathorn et al. (2017), Uddin et al. (2018), and Nevell et al. (2014) study genetic factors associated with the risk of PTSD in the DNHS. However, none of them have conducted mediation analysis for relationship between traumatic exposures and PTSD symptoms on the DNHS data.
In this article, we use the baseline wave in DNHS for our mediation analysis. In total, there are 125 subjects in the DNHS who have available PTSD measurements, trauma type numbers, and DNAm data. This sample size is relatively small. In fact, many existing studies on PTSD-related mediation analysis have around one hundred participants (Kearney et al. 2013; Ruhlmann et al. 2019; Kelly et al. 2019; Demir et al. 2020; van der Vleugel et al. 2020; Kwon, Lee, and Lee 2021). A relatively small sample size could be a challenge for existing statistical methods, which motivates us to develop more powerful statistical methods to identify mediators. The demographic characteristics of these DNHS participants are summarized in Table 1. The study participants are predominantly (88.8%) African-American (AA). In addition, of the 125 participants, 64.8% are female, and 43.2% are current smoking, referring to any cigarette smoking in the past 30 days. The age of DNHS participants has a wide range from 20 to 89 years with a median of 53 years.
Table 1.
Key demographic characteristics.
| Gender | Race | |||
|---|---|---|---|---|
| Female | Male | AA | EA | Other |
| 81 | 44 | 111 | 13 | 1 |
| Median age (range) | Current smoking | |||
| No | Yes | Missing | ||
| 53 (20–89) | 70 | 54 | 1 |
NOTE: “AA” represents African American. “EA” represents European American. “Current smoking” refers to any cigarette smoking in the past 30 days.
Studies show that the pathophysiology of PTSD is associated with DNAm in glucocorticoid receptor regulatory network (GRRN) genes (Rusiecki et al. 2013). Therefore, we screen DNAm CpG probes via an expression quantitative trait methylation (eQTM) analysis on GRRN-annotated DNAm CpG probes and 53 expressed GRRN genes. Here these 53 genes correspond to 1680 GRRN-annotated probes. For each probe, we examine whether the probe is significantly correlated with expression levels of the corresponding gene at a significance level of 0.05. If it is significant, we select that probe; otherwise, the probe is not selected. That is, we choose the CpG probes in probe-gene pairs with significant p-values. Through this, we identify 144 CpG probes significantly correlated with the GRRN genes. For mediation analysis, we treat the PCL-C score as a dependent variable, the total number of trauma exposures as an independent variable, and the 144 DNAm CpG probes as potential mediators. Our aim is to select key mediators between the independent and dependent variables from the 144 DNAm CpG probes. We introduce our proposed method in the following section and provide the analysis results of the DNHS data in Section 5.
3. Heterogeneous Mediation Analysis Method
In this section, we propose a heterogeneous mediator selection approach inspired by Tang, Xue, and Qu (2020) to achieve subpopulation identification, mediator selection in each subpopulation, and mediation effect estimation for heterogeneous data simultaneously. Statistically, to the best of our knowledge, this is the first work which considers heterogeneous mediation effects for high-dimensional potential mediators without pre-specifying subgroups. In addition, we do not assume the subgroup membership depending on observed covariates.
Moreover, to select mediators instead of variables in each subpopulation, we propose a new mediation penalty which jointly penalizes the effect from the independent variable to a mediator (independent-mediator effect) and the effect from the mediator to the outcome (mediator-outcome effect). Essentially, the proposed mediation penalty encourages selection of mediators with large mediation effects. Before introducing the details of the proposed method, we first discuss related existing methods in the following section.
3.1. Existing Mediation Analysis methods
Traditional mediation analysis has been conducted via linear regression models (Baron and Kenny 1986). As an extension, causal mediation analysis imposes “no unmeasured confounding” assumptions and defines direct and indirect effects under a counterfactual framework with potential outcomes (Rubin 1974; Robins and Greenland 1992; Pearl 2001; Imai, Keele, and Tingley 2010a).
Methods of multiple mediators have been developed in recent years (Imai, Keele, and Yamamoto 2010b; Boca et al. 2013; Serang et al. 2017; Jirolon et al. 2020). To account for high-dimensional mediators, Zhao and Luo (2016) consider mediation pathway selection for a large number of causally dependent mediators, and present a sparse mediation model using a regularized structural equation model (SEM). In addition, Van Kesteren and Oberski (2018) develop an exploratory coordinate-wise mediation filter approach, and Zhang et al. (2016) propose a high-dimensional mediation analysis (HIMA) approach for DNA methylation. Moreover, Zhou, Wang, and Zhao (2020) develop estimation and inference procedures for mediation effects under a high-dimensional linear mediation model. However, these methods are all under the homogeneous model framework.
To investigate heterogeneous mediation effects, Qin and Hong (2017) develop a weighting method to identify and estimate site-specific mediation effects, using an inverse-probability-of-treatment weight (Rosenbaum 1987) and ratio of-mediator-probability weighting (Hong, Deutsch, and Hill 2015). This method assumes the heterogeneity caused by the variation of sites. However, the method is not applicable in general, since the potential mechanism resulting in subpopulations is usually unknown. Dyachenko and Allenby (2018) propose a Bayesian mixture model which combines likelihood functions based on two different outcome models to incorporate heterogeneity. Nevertheless, only a single mediator variable is considered and the mixture model requires a prespecified number of subgroups.
3.2. Notations and Assumptions
In this section, we introduce notations and assumptions for the proposed method. Let Xi be an independent variable (e.g., treatment or exposure), Zi be a r × 1 vector of pretreatment confounders (e.g., race or gender), Mi = (Mi1, …, Mip)T be potential mediators, and Yi be the outcome for the ith subject (1 ≤ i ≤ N). Throughout the article, we make the stable unit treatment value assumption (SUTVA) (Rubin 1980); that is, the potential outcomes of one subject are unaffected by the assignment of treatments to other subjects, which is a standard assumption for causal inference. Without loss of generality, we also assume that the outcome and all the covariates are centered. We suppose that the entire population can be partitioned into H nonempty subgroups, where mediators and mediation effects within each subgroup are homogeneous. Denote the index set for subjects in the hth subgroup by (h) for h = 1, …, H.
3.3. Proposed Subgroup Linear Structural Equations Modeling Framework
We consider the heterogeneous mediation problem under the following subgroup linear structural equations modeling (LSEM) with p potential mediators and r pretreatment confounders:
| (1) |
| (2) |
for subject i ∈ 𝒮(h), where bh, δi, , , and . Here, βh represents the direct effect from the independent variable Xi (e.g., trauma) to the outcome variable Yi (e.g., PTSD) in the hth subgroup, represents the joint mediation (indirect) effect of the treatment, bh is the parameter relating the treatment to the potential mediators, and δi ~ N (0, Σ) and εi ~ N(0, σ 2) are random errors, where δi is independent of Xi and Zi, and εi is independent of Xi, Zi, and Mi. We acknowledge that the LSEM imposes strong assumptions about the linearity and distribution of variables, indicating the results based on the proposed subgroup LSEM should be considered exploratory and instructive for generation of potential hypotheses.
We illustrate the relationship of variables in the LSEM for the hth subgroup without the pretreatment confounders Zi in Figure 2. The arrow with βh represents the direct effects from the independent variable Xi to the response Yi, while the arrow with θh represents effects from mediators Mi to the response Yi in model (2). The direct effect βh and indirect effects could vary across different subgroups.
Figure 2.

Mediation structure.
In this article, we assume that the potential mediators are uncausally correlated (Jirolon et al. 2020). That is, the mediators could be conditionally dependent given the independent variable and observed pretreatment confounders, but are not in any prespecified causal order. For instance, it is possible that there exist an unmeasured covariate U affecting multiple mediators like two mediators M1 and M2 in Figure 3(a), where X denotes the independent variable and Y denotes the outcome. Since M1 and M2 are not causally ordered, they are defined as “uncausally correlated.” In contrast, M1 and M2 in Figure 3(b) are causally ordered, that is, a change in M2 causes a change in M1.
Figure 3.

Different situations with two mediators.
In addition, we assume that P(Xi = x|Zi = z) > 0 for all x and z if Xi is discrete, and that fX(x|Zi = z) > 0 for all x and z if Xi is continuous, where fX is the conditional density function of Xi. We also suppose that the effects of pretreatment confounders Zi on each mediator and the outcome are homogeneous across all the subgroups in (1) and (2). Moreover, we assume that the mediator models and the outcome model in (1) and (2) are sparse; that is, most true values in bh and θh are zero for each h.
Under the proposed model and the assumptions, the sequential ignorability assumption in Jirolon et al. (2020) holds for each subgroup in the parametric model in (1) and (2). Moreover, the natural indirect effects δj(t) on the eighth page of Jirolon et al. (2020) for the jth mediator is identical to bh,jθh,j for subjects from the hth subpopulation, where bh,j and θh,j are the jth element in bh and θh in Equations (1) and (2), respectively. In the following proposition, we have shown that parameters in (1) and (2) are identifiable, which implies that the indirect effects are identifiable under the parametric model. Thus, we aim to estimate the causal quantity bh,jθh,j under the proposed model.
To state the proposition, we introduce some notations. Let C = (C1, …, Cn)T be a vector consisting of all subgroup labels, and Θ be a vector collecting all elements in Γ, γ and bh, βh, θh for h = 1, … H. Since the group-specific parameters, bh, βh and θh, are different across subgroups, we consider the identifiability problem on the set , , and for any h ≠ h′}.
Proposition 1. Under the nondegeneracy Condition 1, for any (Θ, C), (Θ′, C′) ∈ 𝒜, under the proposed model in Equations (1) and (2), if the distribution of the observable variables satisfies f(Xi, Mi, Yi, Zi; Θ, C) = f(Xi, Mi, Yi, Zi; Θ′, C) for 1 ≤ i ≤ N, then (Θ, C) and (Θ′, C′) are the same up to a permutation of subgroups.
This proposition states that our model is parametrically identifiable up to a permutation of subgroups. The proof of the Proposition is provided in Section S.1 of supplementary materials. Due to page limit, the nondegeneracy Condition 1 is also in Section S.1 of supplementary materials.
To determine the subgroup membership of each subject, we evaluate how well each subject fits each subpopulation by the loss function
for the ith subject and the hth subpopulation, where and Θ2 = (γ, ΓT). We propose to group subjects and identify the subgroup label of each subject through finding a smallest Li,h for the ith subject among all subgroups (h = 1, …, H), since a smaller loss function indicates better fitness and greater likelihood of the sample. Let Θ1 = (Θ11, …, Θ1H).
Then, the loss function for all the subjects is
| (3) |
which is a sum of all within-cluster loss.
In the proposed method, we do not prespecify or assume which variables determine the subgroup membership. Instead, these classes are identified in a completely data-driven manner, which is one of the key advantages of our method. We do not impose assumptions on which variables cause or determine the heterogeneity, since the heterogeneity of mediation effects could have complicated reasons. Essentially, analogous to a clustering algorithm, our model aggregates individuals into several classes where the individuals share similar mediation effects within each class but have different effects across classes. In addition, our proposed subgroup identification is different from that in the individualized-multi-directional method (IMDM) (Tang, Xue, and Qu 2021). We provide a comparison of the two methods in Section S.5.1 of the supplementary materials.
3.4. Mediation Regularization for Sparsity
In this section, we propose a new mediation penalty. As mentioned in Section 3.3, under the proposed subgroup LSEM in (1) and (2), the mediation effect of the jth mediator in the hth subgroup is bh,jθh,j. To identify mediators with large mediation effects in each subgroup, we consider bh,j and θh,j jointly for each 1 ≤ j ≤ p, and propose a two-dimensional joint mediation penalty
| (4) |
where c0 is a constant to adjust the shrinkage. We plot the mediation penalty with p = 1 and c0 = 0.5 in Figure 4. As shown in Figure 4, the penalty tends to shrink small values toward zero, and the shrinkage gradually levels off as |θh,1| or |bh,1| increases.
Figure 4.

Mediation penalty with p = 1 and c0 = 0.5.
The high-dimensional mediation analysis proposed by Zhang et al. (2016) adopts the minimax concave penalty (MCP) (Zhang 2010) for variable selection in the outcome model. Compared with the traditional Lasso (Tibshirani 1996), MCP, and smoothly clipped absolute deviation (SCAD) penalties (Fan and Li 2001), the proposed mediation penalty selects mediators instead of covariates in the sense that the pm(bh, θh) penalizes bh and θh jointly rather than separately. Schaid and Sinnwell (2020) also jointly consider each pair of coefficients in the mediator and outcome model for each mediator using a group Lasso penalty. Compared to the group Lasso penalty, the proposed joint mediation penalty tends to be flat, and the corresponding shrinkage gradually levels off as the coefficients in each pair increase; which can relax the rate of penalization for large coefficients and large mediation effects. Thus, the proposed penalty could reduce the bias due to joint shrinkages.
Intuitively, we need a relatively small shrinkage for bh,j when θh,j is large; otherwise it is hard to select the jth mediator when bh,j is small but θh,j and the mediation effect bh,jθh,j are large. However, this property does not hold for penalty functions such as |θh,j| + |bh,j| and the pathway Lasso penalty in Zhao and Luo (2016) penalizing bh and θh jointly via |θh,jbh,j| (1 ≤ j ≤ p). Specifically, with a penalty of |θh,j| + |bh,j|, the shrinkage of bh,j does not depend on θh,j; and with a penalty of |θh,jbh,j|, the shrinkage on bh,j increases as θh,j increases. In contrast, our joint mediation penalty in (4) has the desired property since the shrinkage on bh,j in pm(bh, θh) gradually levels off as θh,j increases and vice versa, as shown in Figure 4. On the other hand, the proposed mediation penalty will not induce a strong shrinkage for θh,j if bh,j = 0. In Figure 4, even if bh,1 = 0, the rate of penalization on θh,1 will still decrease as θh,1 itself increases, which is analog to the SCAD penalty imposed on a single coefficient θh,1.
3.5. Fusion Penalty for Cross-Group Information
In general, it is possible that not every mediator has different mediation effects across subgroups. We use the following between-group fused Lasso penalty (Tibshirani et al. 2005)
| (5) |
to shrink similar between-group effects together, where λ0 is a tuning parameter. Specifically, the between-group penalty pb(Θ1) encourages mediators to share the same parameter across different subgroups when the corresponding effects are similar. In this way, we can borrow information across subgroups in estimating the mediation effects.
Consequently, the objective function of the proposed method is
| (6) |
where
| (7) |
is a within-group penalty, pSCAD,λ1,a(·) is the SCAD penalty with tuning parameters λ1 and a, is a l1 penalty with tuning parameter λ2 for pretreatment confounders to avoid over-fitting, and Γj denotes the jth row of Γ. Through minimizing f(Θ1, Θ2) in (6), we not only incorporate the heterogeneity of mediation effects in subjects, but also combine cross-group information for similar effects. Moreover, in the objective function f(Θ1, Θ2), we penalize not only θh but also the direct effect βh in the outcome model in Equation (2) since otherwise the estimation obtained by minimizing the objective function could falsely transfer the effects of mediators Mi to the effect of Xi. In the following section, we provide an algorithm to obtain the minimizer of the objective function.
3.6. Implementation
In this section, we propose an effective algorithm to minimize the objective function in Equation (6). Note that our objective function is nonconvex, since the within-group penalty pw in (7) is not convex and the loss function in (3) involves minimization. To tackle this challenge, we decompose our objective function as a difference of two convex functions and solve the optimization problem based on the difference of convex (DC) algorithm (Le Thi Hoai and Tao 1997; Shen, Pan, and Zhu 2012), which is shown to converge to a stationary point under regularity conditions (Abbaszadehpeivasti, de Klerk, and Zamani 2021). Also, we use a smooth approximation of the between-group fused Lasso penalty.
Specifically, we rewrite the objective function as a difference of two functions
| (8) |
where ν is a vector consisting of all parameters bh, βh, θh, γ, Γ (for h = 1, …, H) in models (1) and (2),
| (9) |
and . It can be shown that pd(Θ1h) + pw(Θ1h) is convex for each 1 ≤ h ≤ H, since the corresponding Hessian matrix is block-diagonal and each diagonal block is positive-definite. This implies that f1(ν) is a convex function. In addition, since the maximum of convex functions is still convex, f2(ν) is also a convex function.
Based on this DC decomposition on f, we iteratively construct a sequence of convex approximations for f(ν). We first calculate the subdifferential of f2(ν) in the following:
where Fik(ν) = ∑1≤h≤H,h≠k Li,h (Θ1h, Θ2), J(ν) = {1 ≤ k ≤ H: Fik (ν) = max1≤k≤H Fik(ν)}, and “co” stands for the convex hull. At the mth iteration, given the previous estimate ν(m−1), we replace f2(ν) in (8) by its affine minorization: , where μ(m−1) ∈ ∂f2 (v(m−1)). then, is an upper convex approximating function for f (ν) at the mth iteration. Through this, we convert the nonconvex objective function into a convex relaxation via a tangent approximation of f2(ν).
In addition, since the between-group fused Lasso pb(Θ1) in f1(ν) is non-smooth and non-separable, we approximate it by a smooth function. Specifically, we reformulate the fused Lasso as where D is a difference operator corresponding to the differences in pb(Θ1). That is, the pb(Θ1) is equivalent to the maximum of the maximization problem for ηTDν. Hence, we let , where ρ is a positive smoothing parameter. This function approximates pb(ν) as ρ → 0 (Nesterov 2005). Let η* =S(Dν/ρ), where
Then we have , which is convex and differentiable in ν (Chen et al. 2012). In our implementation, we choose ρ = 10−4 following Chen et al. (2012).
Consequently, at the mth iteration, we replace the f2(ν) and pb(ν) in (8) by and , respectively, and obtain
| (10) |
where
We solve the minimization problem in Equation (10) through the gradient descent algorithm (Curry 1944) with the back-tracking line search (Shi 2004; Stanimirović and Miladinović 2010) for the step size. The above algorithm can be summarized in Algorithm 1. We also provide an expanded version of this algorithm in Section S.2 of the supplementary materials.

To determine the tuning parameters and the number of subgroups H, we propose the following Bayesian information criterion (BIC) type criterion:
| (11) |
where dfM(λ, H) and dfY(λ, H) are numbers of nonzero estimated coefficients in mediator models and the outcome model, respectively, λ = (λ0, λ1, λ2), , and . Here, , , , , , and are the estimates of bh, Γ, βh, θh, γ, and Ci, respectively, based on H subgroups and tuning parameters λ. Recall that the between-group fused Lasso penalty pb(Θ1) in (5) encourages shared parameters for similar effects across different subgroups. In dfM and dfY, the shared parameters are counted without multiplicity.
We select the optimal tuning parameters and the optimal number of subgroups through minimizing BIC(λ, H), incorporating information from both the mediator models and the outcome model. In the implementation for the following sections, we mainly tune λ0, λ1, and H using a grid search to minimize the BIC. We do not tune λ2 since it is for penalization of the pretreatment confounders, which are not involved in our simulations and real data application.
4. Simulated Data Experiments
In this section, we investigate the performance of the proposed method compared with existing homogeneous mediation methods via simulation studies. We simulate data following models in (1) and (2) with r = 0. The proposed method is implemented based on Algorithm 1 with c0 = 10 and a = 3.7. We apply the “HIMA” package (https://cran.r-project.org/web/packages/HIMA/index.html) in R to implement the high-dimensional mediation analysis (HIMA) method (Zhang et al. 2016) for comparison, which is a homogeneous mediation approach. Our results are summarized based on 100 replications.
To evaluate the performance of each method, we calculate the average of all individuals’ mediator false negative rates (FN) and the average of all individuals’ mediator false positive rates (FP) for mediator selection as follows:
Where , , and are estimators of θhj, bhj, and Ci, respectively. Specifically, the FN and FP represent proportions of unselected true mediators and selected noises, respectively. A method with smaller FN+FP selects more accurate mediators. In practice, the FP and FN may have different costs. For example, in scenarios such as a pregnancy test or a COVID-19 test, FN costs much more than FP. However, in other scenarios such as criminal conviction or identifying spam emails, FP costs much more than FN. Given specific application context and background information, we may assign different weights to FP and FN, respectively. Since simulation studies do not involve any real situations, we treat them equally and just use FN+FP as an evaluation criterion.
We also evaluate each method via the mean-squared-errors (MSE) of mediation effects in an average of all individuals as . For the proposed method, we also report the proportion of replications where the number of subgroups is correctly selected via the BIC(λ, H) in (11), which we refer to as the correct rate of subgroup number selection. Moreover, we compute the misclassification rate of subjects based on the proposed method for evaluation of subgroup identification.
We consider the following three settings, where the nonzero coefficients in bh and θh share the same signal strengths bhs and θhs, respectively, for 1 ≤ h ≤ H. For the sensitivity of the proposed approach to misspecification, we investigate situations without heterogeneity in the first setting, which involves a homogeneous underlying true model with only one subpopulation. In contrast, Settings 2 and 3 assume heterogeneous true models with two subpopulations. In addition, we consider high-dimensional situations in Setting 3.
Setting 1. Let N = 200, H = 1, n1 = 200, and p = 30. True coefficients in the model are illustrated in Figure 5 with β1 = 0.5, b1s = 1, and θ1s = 0.2, 0.3, or 0.4. As shown in Figure 5, we have four true mediators with mediation effects θ1s. In addition, we generate Xi and εi from a standard normal distribution and δi ~ N(0, Ip×p) for each i = 1, …, N.
Figure 5.

True coefficients for the homogeneous Setting 1. The “X” denotes the independent variable, “Mi” denotes the ith mediator, and “Y” denotes the dependent variable. The value above each arrow represents the true coefficient for the corresponding effect.
Setting 2. We proceed similarly as in Setting 1 except that H = 2, n1 = 50, and n2 = 150. True coefficients in the model are illustrated in Figure 6 with β1 = 0.5, b1s = 1, β2 = −0.5, b2s = −1, θ1s = 0.5, 1, or 4 and θ2s = −0.5, −1, or − 4. As shown in Figure 6, we have three true mediators in each subgroup.
Figure 6.
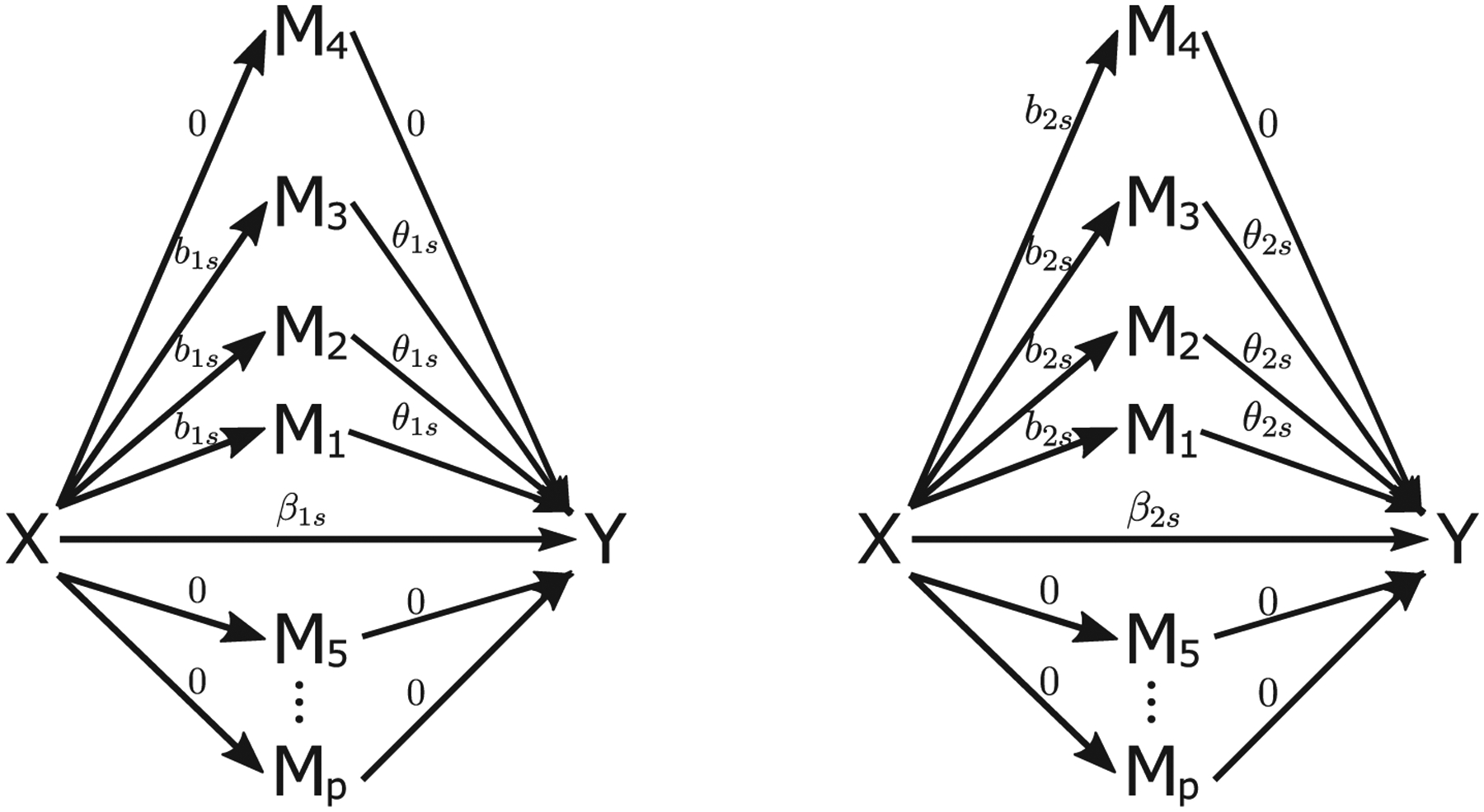
True coefficients for the heterogeneous Settings 2 and 3 with two subpopulations (left and right). The p is 30 and 150 under Settings 2 and 3, respectively. The “X” denotes the independent variable, “Mi” denotes the ith mediator, and “Y” denotes the dependent variable. The value above each arrow represents the true coefficient for the corresponding effect.
Setting 3. We investigate a high-dimensional case proceeding similarly as in Setting 2 except that N = 100, n1 = 30, n2 = 70, p = 150, β1 = 1, β2 = −1, θ1s = 0.5, 0.8, 1, or 4 and θ2s = −0.5, −0.8, −1, or −4. The covariance matrix of δi has an autoregressive structure of order 1, that is, AR(1), with diagonal 1 and off-diagonal parameter ρ.
Tables 2–4 provide the results of the proposed method and the HIMA method, and show that the proposed method produces smaller overall FN+FP totals than the HIMA method across all the settings, indicating that the proposed method selects mediators more accurately. Moreover, the proposed method produces smaller MSE of mediation effects, implying that the proposed method is also more effective in estimation of mediation effects.
Table 2.
FN, FP, FN+FP, and MSE under Setting 1.
| θ 1s | Method | FN | FP | FN+FP | MSE |
|---|---|---|---|---|---|
| 0.2 | Proposed | 0.046 | 0.002 | 0.048 | 0.002 |
| HIMA | 0.570 | 0.000 | 0.570 | 0.003 | |
| 0.3 | Proposed | 0.000 | 0.000 | 0.000 | 0.002 |
| HIMA | 0.100 | 0.000 | 0.100 | 0.002 | |
| 0.4 | Proposed | 0.000 | 0.000 | 0.000 | 0.002 |
| HIMA | 0.005 | 0.000 | 0.005 | 0.001 |
NOTE: “HIMA” stands for the high-dimensional mediation analysis method. The “θ1s” represents the signal strength in θ1.
Table 4.
FN, FP, FN+FP, and MSE under Setting 3.
| (θ1s, θ2s) | Method | FN | FP | FN+FP | MSE | |
|---|---|---|---|---|---|---|
| ρ = 0 | (0.5, −0.5) | Proposed | 0.530 | 0.001 | 0.531 | 0.004 |
| HIMA | 0.890 | 0.001 | 0.891 | 0.006 | ||
| (0.8, −0.8) | Proposed | 0.220 | 0.000 | 0.220 | 0.005 | |
| HIMA | 0.967 | 0.001 | 0.967 | 0.013 | ||
| (1,−1) | Proposed | 0.143 | 0.001 | 0.144 | 0.007 | |
| HIMA | 0.977 | 0.001 | 0.977 | 0.021 | ||
| (4,−4) | Proposed | 0.092 | 0.001 | 0.093 | 0.068 | |
| HIMA | 0.963 | 0.000 | 0.964 | 0.314 | ||
| ρ = 0.2 | (0.5, −0.5) | Proposed | 0.554 | 0.001 | 0.555 | 0.003 |
| HIMA | 0.917 | 0.001 | 0.917 | 0.006 | ||
| (0.8, −0.8) | Proposed | 0.269 | 0.001 | 0.270 | 0.006 | |
| HIMA | 0.983 | 0.001 | 0.984 | 0.013 | ||
| (1,−1) | Proposed | 0.259 | 0.001 | 0.260 | 0.009 | |
| HIMA | 0.977 | 0.000 | 0.977 | 0.021 | ||
| (4,−4) | Proposed | 0.161 | 0.001 | 0.162 | 0.093 | |
| HIMA | 0.957 | 0.000 | 0.957 | 0.312 |
NOTE: “HIMA” stands for the high-dimensional mediation analysis method. The “θ1s” and “θ2s” represent the signal strength in θ1 and θ2, respectively, and “ρ” is a correlation parameter.
In particular, under the homogeneous Setting 1, the proposed method still outperforms the homogeneous HIMA method. For example, when θ1s = 0.2, the FN+FP of the proposed is only 8.8% of that of the HIMA as shown in Table 2. This is likely due to the advantage of the proposed mediation penalty, and that the proposed method correctly identifies the number of subgroups in most situations as shown in Table 5. Moreover, the proposed method falsely un-selects 4.6% of true mediators and falsely selects just 0.2% of noises (variables that are not mediators), even when the mediation effect of each true mediator is as small as 0.2. In addition, under this situation, the MSE of mediation effects is only 0.002, indicating that the proposed method performs consistently well even when there is no heterogeneity and the effect size is small.
Table 5.
Correct rate of subgroup number selection and misclassification rate for different settings.
| (θ1s, θ2s) | Correct rate of subgroup number selection | Misclassification rate | |
|---|---|---|---|
| Setting 1 | (0.2,–) | 0.76 | – |
| (0.3,–) | 1.00 | – | |
| (0.4,–) | 1.00 | – | |
| Setting 2 | (0.5, −0.5) | 0.99 | 0.13 |
| (1,−1) | 1.00 | 0.11 | |
| (4,−4) | 0.92 | 0.10 | |
| (0.5, −0.5) | 0.66 | 0.17 | |
| Setting 3 | (0.8, −0.8) | 0.68 | 0.14 |
| ρ = 0 | (1,−1) | 0.72 | 0.13 |
| (4,−4) | 0.62 | 0.12 | |
| (0.5, −0.5) | 0.59 | 0.17 | |
| Setting 3 | (0.8, −0.8) | 0.69 | 0.15 |
| ρ = 0.2 | (1,−1) | 0.62 | 0.15 |
| (4,−4) | 0.66 | 0.14 |
NOTE: “Correct rate of subgroup number selection” represents the proportion of replications where the number of subgroups is correctly selected via the proposed method. “Misclassification rate” is the average proportion of subjects who are misclassified by the proposed method.
In addition, the proposed method also performs much better than the HIMA when there are two subgroups with opposite mediation effects in Settings 2 and 3, that is, with positive mediation effects in one subgroup and negative mediation effects in the other. In this case, the homogeneous HIMA method usually fails to identify true mediators. For instance, the FN of the HIMA is as high as 0.957 when (θ1s, θ2s) = (0.5, −0.5) as shown in Table 3, while the corresponding FN of the proposed method is only 0.031.
Table 3.
FN, FP, FN+FP, and MSE under Setting 2.
| (θ1s, θ2s) | Method | FN | FP | FN+FP | MSE |
|---|---|---|---|---|---|
| (0.5, −0.5) | Proposed | 0.031 | 0.007 | 0.038 | 0.004 |
| HIMA | 0.963 | 0.004 | 0.968 | 0.025 | |
| (1,−1) | Proposed | 0.002 | 0.000 | 0.002 | 0.006 |
| HIMA | 0.943 | 0.003 | 0.946 | 0.099 | |
| (4,−4) | Proposed | 0.001 | 0.000 | 0.001 | 0.058 |
| HIMA | 0.790 | 0.002 | 0.792 | 1.514 |
NOTE: “HIMA” stands for the high-dimensional mediation analysis method. The “θ1s” and “θ2s”represent the signal strength in θ1 and θ2, respectively.
Moreover, we explore high-dimensional scenarios in Setting 3 to mimic the case of the DNHS data. In this setting, we also consider the situations where the error terms in the mediator models in (1) are correlated, that is, the correlations among mediators may not just come from the independent variable. In all the high-dimensional cases, the proposed method produces smaller FN+FP and smaller MSE than the HIMA method illustrated in Table 4. For example, when (θ1s, θ2s) = (4, −4) and ρ = 0.2, the FN+FP of the proposed method is only 16.7% of that of the HIMA method, and the MSE is only 29.8% of that of the HIMA.
In Table 5, we provide the correct rates of subgroup number selection and the misclassification rates under various settings. We observe that the proposed method correctly determines the number of subgroups in most situations, especially in Settings 1 and 2 where there are more samples. In addition, the proposed method groups most subjects correctly across different settings due to the low misclassification rates.
In summary, our simulation studies show that the proposed method achieves higher mediator selection accuracy and mediation effect estimation accuracy than the existing homogeneous mediation method across all the settings. One reason is that the proposed method adopts the mediation penalty in (4) which considers effects in mediator models and outcome models jointly, and encourages selection of mediators with large mediation effects. In addition, the proposed method allows heterogeneity among subjects, and thus can identify mediators with heterogeneous mediation effects, which is especially powerful for mediators with opposite effects in different subgroups. We investigate more simulations for larger-scale cases, with different initial values, various coefficients, moderators, and under non-normality of the independent variable in Sections S.3.1, S.3.2, S.3.4–S.3.6 of supplementary materials, respectively.
5. DNHS Case Study
In this section, we investigate how DNA methylation mediates the effects of traumatic experiences on development of PTSD based on the DNHS data. Specifically, we apply the proposed method to study the mediation effects of DNAm variation of GRRN genes on PTSD symptom severity. In this study, we use the baseline wave of the DNHS data for our mediation analysis. We treat the total number of trauma exposures as an independent variable, DNAm CpG probes that are significantly correlated with the GRRN genes as potential mediators, and the average PCL-C score as the outcome variable. There are 125 subjects and 144 selected DNAm CpG probes after screening. Our main objective is to identify key DNAm CpG probes from all the potential mediators.
To evaluate the performance of the proposed method compared with existing methods, we randomly split the data into a training set (90% of all samples) and a testing set (10% of all samples) for 100 times. The training sets in the 100 replications are repeated random subsamples (90%) of the complete data. For the proposed method, to identify the subgroup label of the ith subject in the testing set, we calculate the average prediction error of mediators , where is the predicted value for Mi based on estimated parameters and in the hth subgroup. Then the ith subject is labeled with a specific subgroup that minimizes . For each method, we train the model on the training data, and calculate the prediction root-mean-squared errors (PRMSEs) for the mediators and the outcome variable in the testing set; that is, and , respectively, where 𝒯 denotes the index set of subjects in the testing set and |𝒯| is the testing sample size.
We provide mean PRMSE for each method based on 100 replications in Table 6. The proposed method produces much smaller prediction errors for both the mediators and the outcome variable compared to the existing high-dimensional mediation analysis (HIMA) method, indicating that the proposed method is more accurate in terms of prediction. Note that, in both methods, we use all the potential mediators to calculate the prediction errors of mediators, and then take an average of the errors over the mediators.
Table 6.
The DNHS data results by the proposed method and the high-dimensional mediation analysis (HIMA) method.
| Method | NS | Mediator | Outcome |
|---|---|---|---|
| Proposed | 6 | 0.455 | 1.235 |
| HIMA | 0 | 4.309 | 2.774 |
NOTE: Here “NS” represents the mean number of selected mediators. The “Mediator” represents average prediction error for mediators, and “Outcome” represents average prediction error for the outcome variable based on 100 replications.
For the subgroup identification in the DNHS data, we apply the proposed method to all the samples. The proposed method selects four DNAm probes, and identifies three subgroups consisting of 60, 26, 39 subjects, respectively. We provide the estimated coefficients of the four DNAm probes in the three subgroups in Figure 7. Although the size of some estimated coefficients are small, the estimated mediation effect size here is comparable to the findings from other studies for DNA methylation (Tobi et al. 2018), and thus the mediation effects are still non-ignorable. For example, the mediation effect from trauma to PCL score through cg01277438 is 0.02 × 0.94 ≈ 0.02 for the subgroup in Figure 7(c). Note that the range of the trauma measurement is from 0 to 14 with mean 4.0. If the trauma variable takes its average value 4.0, the influence of this trauma value on PCL score through the mediator cg01277438 is about 0.08. Moreover, if the trauma variable takes its maximum value 14, the influence of this trauma value on the PCL score through the mediator cg01277438 is about 0.28, which is 25% of the standard deviation 1.1 of the PCL score.
Figure 7.

Estimated coefficients for the selected four mediators in the three subgroups identified by the proposed method based on all samples.
Specifically, the four DNAm probes identified by the proposed method correspond to NFATC1, HSP90AA1, SMARCA4, and CREBBP genes, among which HSP90AA1, SMARCA4, and NFATC1 are indeed related to PTSD based on existing literature (Raabe and Spengler 2013; Kuan et al. 2017; Criado-Marrero et al. 2018; Breen et al. 2019; Kim et al. 2019a, 2019b). In addition, we apply the HIMA method to each of the three subgroups on the four mediators. At a 0.05 significance level, the HIMA method shows that three (“cg11789371,” “cg03738979,” and “cg01277438”) of the four selected mediators are significant, after controlling the false discovery rate (FDR) via the Benjamini–Hochberg procedure (Benjamini and Hochberg 1995). However, the HIMA method cannot identify any mediator when all potential mediators and samples are used. This confirms that the subgroups and mediators selected by the proposed method are useful in scientific findings.
Furthermore, we find common patterns in subgroup identification across the analyses of the 100 random split datasets and the whole dataset, which are provided in Section S.4.1 of supplementary materials. Also, we investigate the racial make-up of the three identified subgroups. The results are provided in Table 13 in Section S.4.2 of supplementary materials, showing that the subjects are not grouped based on race since each subgroup contains both AAs and European Americans.
In summary, the proposed method produces smaller prediction errors than the homogeneous mediation method. Moreover, the proposed method identifies important mediators which cannot be detected by existing methods. In addition, our method shows heterogeneous mediation among subjects in the DNHS data.
6. Discussion
Our main contribution is to advance the understanding of the underlying mechanism of PTSD using the DNHS data. Specifically, we conduct a mediation analysis for DNA methylation on the relationship between traumatic events and PTSD symptoms based on the DNHS data. The identification of DNAm mediators presents new statistical challenges due to the heterogeneous nature of PTSD among patients and the high-dimensional structure of the DNAm data. To address these challenges, we develop a heterogeneous mediation model with multiple mediators, incorporating heterogeneity among subjects. Moreover, we propose a novel mediation penalty to incorporate effects in the mediator models and the outcome model jointly for high-dimensional data. Our numerical studies show that the proposed method selects true mediators more accurately than the existing homogeneous high-dimensional mediation analysis method.
In the DNHS case study, we identify meaningful DNAm mediators using the proposed method, which has important impact in practice since it would advance development of new personalized treatments for PTSD. In fact, recent studies have shown that successful PTSD treatments are reflected by significant DNAm changes (Yehuda et al. 2013; Vinkers et al. 2019). Our finding could also suggest future biomedical research on the selected mediators and corresponding genes for further biological verification. In particular, the selected DNAm CpG probes correspond to genes such as HSP90AA1, SMARCA4, and NFATC1, which have been reported in literature that they are associated with the PTSD (Raabe and Spengler 2013; Kuan et al. 2017; Criado-Marrero et al. 2018; Breen et al. 2019; Kim et al. 2019a, 2019b).
In addition, the subgroup identification by the proposed method for the DNHS dataset with predominantly African-American subjects indicates potential heterogeneity in the underlying DNAm profiles which mediate risk for PTSD. This is an important discovery, as it could help us to uncover important genetic complexities which have been ignored for treatment and prevention of this debilitating mental disorder.
In this article, we mainly consider the detection of heterogeneous mediators and estimation of corresponding mediation effects. We have not developed statistical inference for the heterogeneous mediation effects, which is a limitation of this article. It would be of great interest to investigate the statistical inference on these mediation effects in the future; for example, constructing de-biased estimators of subpopulation mediation effects for confidence intervals or hypothesis testing. A de-biasing procedure can also reduce the bias for mediation effects incurred from regularization. One possible way is to control the bias of estimators for parameters in both mediator and outcome models, and then use multiplication of each pair of de-biased estimates to estimate the mediation effects of the corresponding mediator.
Moreover, the proposed model in Equations (1) and (2) implies that there is no unmeasured confounders. However, to our best knowledge, it is unclear whether there are any common factors impacting both methylation and PTSD symptoms, as the exact biological processes underlying the development of PTSD remain elusive, which is a study limitation given the current state of science. We provide more discussion on the proposed model regarding exposure–mediator interactions, latent subpopulations, and moderated mediation and mediated moderation in Sections S.5.2–S.5.4 of supplementary materials, respectively.
Furthermore, our use of cross-sectional rather than longitudinal methylation measurements in the DNHS data application can be considered a study limitation, since the mediation assumption cannot be verified in cross-sectional data. However, it is consistent with the majority of existing epigenetic work relevant to PTSD published to date. In fact, many methylation studies are actually cross-sectional (King et al. 2014; Young et al. 2016; Joehanes et al. 2016; Alghanim et al. 2017; Nakatochi et al. 2017; Christiansen et al. 2021), and the majority of epigenetic PTSD studies to date have used a similar study design (Kuan et al. 2017; Hossack et al. 2020; Sheerin et al. 2021; Young et al. 2021; Qi et al. 2021). As a future work, we expect the proposed method can be extended to longitudinal data when such data become available.
In addition, the number of subject in the DNHS study is relatively small, and thus readers should be cautious when directly using the results that the DNHS dataset provides. In the future, with more date collected, we will apply the proposed method to a larger dataset. More discussion on the limitations of the DNHS data is provided in Section S.5.5 of supplementary materials.
Supplementary Material
Funding
We would like to acknowledge support for this project from the National Institutes of Health grants R01MD011728, R01DA022720, and RC1MH088283; and from the National Science Foundation grants DMS-1821198 and DMS-1952406.
Footnotes
Supplementary Materials
The supplementary materials provide an expanded version of Algorithm 1, proofs, and additional results for simulations, real data analyses, and discussion.
References
- Abbaszadehpeivasti H, de Klerk E, and Zamani M (2021), “On the Rate of Convergence of the Difference-of-Convex Algorithm (DCA),” arXiv preprint arXiv:2109.13566 [Google Scholar]
- Alghanim H, Antunes J, Silva DSBS, Alho CS, Balamurugan K, and McCord B (2017), “Detection and Evaluation of DNA Methylation Markers Found at SCGN and KLF14 loci to Estimate Human Age,” Forensic Science International: Genetics, 31, 81–88. [DOI] [PubMed] [Google Scholar]
- Baron RM, and Kenny DA (1986), “The Moderator–Mediator Variable Distinction in Social Psychological Research: Conceptual, Strategic, and Statistical Considerations,” Journal of Personality and Social Psychology, 51, 1173–1182. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, and Hochberg Y (1995), “Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing,” Journal of the Royal Statistical Society, Series B, 57, 289–300. [Google Scholar]
- Blanchard EB, Jones-Alexander J, Buckley TC, and Forneris CA (1996), “Psychometric Properties of the PTSD Checklist (PCL),” Behaviour Research and Therapy, 34, 669–673. [DOI] [PubMed] [Google Scholar]
- Boca SM, Sinha R, Cross AJ, Moore SC, and Sampson JN (2013), “Testing Multiple Biological Mediators Simultaneously,” Bioinformatics, 30, 214–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breen MS, Bierer LM, Daskalakis NP, Bader HN, Makotkine I, Chattopadhyay M, Xu C, Grice AB, Tocheva AS, Flory JD, Buxbaum JD, Meaney MJ, Brennand K, and Yehuda R (2019), “Differential Transcriptional Response Following Glucocorticoid Activation in Cultured Blood Immune Cells: A Novel Approach to PTSD Biomarker Development,” Translational Psychiatry, 9, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cacioppo JT, Cacioppo S, Capitanio JP, and Cole SW (2015), “The Neuroendocrinology of Social Isolation,” Annual Review of Psychology, 66, 733–767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang S-C, Koenen KC, Galea S, Aiello AE, Soliven R, Wildman DE, and Uddin M (2012), “Molecular Variation at the SLC6A3 Locus Predicts Lifetime Risk of PTSD in the Detroit Neighborhood Health Study,” PloS One, 7, e39184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Lin Q, Kim S, Carbonell JG, and Xing EP (2012), “Smoothing Proximal Gradient Method for General Structured Sparse Regression,” The Annals of Applied Statistics, 6, 719–752. [Google Scholar]
- Christiansen C, Castillo-Fernandez J, Domingo-Relloso A, Zhao W, Moustafa JE-S, Tsai P-C, Maddock J, Haack K, Cole S, Kardia S, Molokhia M, Suderman M, Power C, Relton C, Wong A, Kuh D, Goodman A, Small KS, Smith JA, Tellez-Plaza M, Navas-Acien A, Ploubidis GB, Hardy R, and Bell JT (2021), “Novel DNA Methylation Signatures of Tobacco Smoking with Trans-Ethnic Effects,” Clinical Epigenetics, 13, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Criado-Marrero M, Rein T, Binder EB, Porter JT, Koren III J, and Blair LJ (2018), “Hsp90 and FKBP51: Complex Regulators of Psychiatric Diseases,” Philosophical Transactions of the Royal Society B: Biological Sciences, 373, 20160532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curry HB (1944), “The Method of Steepest Descent for Non-linear Minimization Problems,” Quarterly of Applied Mathematics, 2, 258–261. [Google Scholar]
- Demir Z, Böge K, Fan Y, Hartling C, Harb MR, Hahn E, Seybold J, and Bajbouj M (2020), “The Role of Emotion Regulation as a Mediator between Early Life Stress and Posttraumatic Stress Disorder, Depression and Anxiety in Syrian Refugees,” Translational Psychiatry, 10, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dempster EL, Wong CC, Lester KJ, Burrage J, Gregory AM, Mill J, and Eley TC (2014), “Genome-Wide Methylomic Analysis of Monozygotic Twins Discordant for Adolescent Depression,” Biological Psychiatry, 76, 977–983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickstein BD, Suvak M, Litz BT, and Adler AB (2010), “Heterogeneity in the Course of Posttraumatic Stress Disorder: Trajectories of Symptomatology,” Journal of Traumatic Stress, 23, 331–339. [DOI] [PubMed] [Google Scholar]
- Dyachenko TL, and Allenby GM (2018), “Bayesian Analysis of Heterogeneous Mediation,” Georgetown McDonough School of Business Research Paper, (2600140). [Google Scholar]
- Fan J, and Li R (2001), “Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties,” Journal of the American Statistical Association, 96, 1348–1360. [Google Scholar]
- Farley M, Minkoff JR, and Barkan H (2001), “Breast Cancer Screening and Trauma History,” Women & Health, 34, 15–27.11785855 [Google Scholar]
- Gao Y, Yang H, Fang R, Zhang Y, Goode EL, and Cui Y (2019), “Testing Mediation Effects in High-Dimensional Epigenetic Studies,” Frontiers in Genetics, 10, 1195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grubaugh AL, Elhai JD, Cusack KJ, Wells C, and Frueh BC (2007), Screening for PTSD in ‘Public-Sector Mental Health Settings: The Diagnostic Utility of the PTSD Checklist,” Depression and Anxiety, 24, 124–129. [DOI] [PubMed] [Google Scholar]
- Harte CB, Vujanovic AA, and Potter CM (2015), “Association between Exercise and Posttraumatic Stress Symptoms among Trauma-Exposed Adults,” Evaluation & the Health Professions, 38, 42–52. [DOI] [PubMed] [Google Scholar]
- Heinzelmann M, and Gill J (2013), “Epigenetic Mechanisms Shape the Biological Response to Trauma and Risk for PTSD: A Critical Review,” Nursing Research and Practice, 2013, 417010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Himle JA, Baser RE, Taylor RJ, Campbell RD, and Jackson JS (2009), “Anxiety Disorders among African Americans, Blacks of Caribbean Descent, and Non-Hispanic Whites in the United States,” Journal of Anxiety Disorders, 23, 578–590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hong G, Deutsch J, and Hill HD (2015), “Ratio-of-Mediator-Probability Weighting for Causal Mediation Analysis in the Presence of Treatment-by-Mediator Interaction,” Journal of Educational and Behavioral Statistics, 40, 307–340. [Google Scholar]
- Horesh D, Lowe SR, Galea S, Uddin M, and Koenen KC (2015), “Gender Differences in the Long-Term Associations between Posttraumatic Stress Disorder and Depression Symptoms: Findings from the Detroit Neighborhood Health Study,” Depression and Anxiety, 32, 38–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hossack MR, Reid MW, Aden JK, Gibbons T, Noe JC, and Willis AM (2020), “Adverse Childhood Experience, Genes, and PTSD Risk in Soldiers: A Methylation Study,” Military Medicine, 185, 377–384. [DOI] [PubMed] [Google Scholar]
- Hudson DL, Puterman E, Bibbins-Domingo K, Matthews KA, and Adler NE (2013), “Race, Life Course Socioeconomic Position, Racial Discrimination, Depressive Symptoms and Self-rated Health,” Social Science & Medicine, 97, 7–14. [DOI] [PubMed] [Google Scholar]
- Imai K, Keele L, and Tingley D (2010a), “A General Approach to Causal Mediation Analysis,” Psychological Methods, 15, 309–334. [DOI] [PubMed] [Google Scholar]
- Imai K, Keele L, and Yamamoto T (2010b), “Identification, Inference and Sensitivity Analysis for Causal Mediation Effects,” Statistical Science, 25, 51–71. [Google Scholar]
- Irish LA, Gabert-Quillen CA, Ciesla JA, Pacella ML, Sledjeski EM, and Delahanty DL (2013), “An Examination of PTSD Symptoms as a Mediator of the Relationship between Trauma History Characteristics and Physical Health Following a Motor Vehicle Accident,”Depression and Anxiety, 30, 475–482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Januar V, Ancelin M-L, Ritchie K, Saffery R, and Ryan J (2015), “BDNF Promoter Methylation and Genetic Variation in Late-Life Depression,” Translational Psychiatry, 5, e619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jirolon A, Baglietto L, Birmeli E, Alarcon F, and Perduca V (2020), “Causal Mediation Analysis in Presence of Multiple Mediators Uncausally Related,” The International Journal of Biostatistics, 17, 191–221. [DOI] [PubMed] [Google Scholar]
- Joehanes R, Just AC, Marioni RE, Pilling LC, Reynolds LM, Mandaviya PR, Guan W, Xu T, Elks CE, Aslibekyan S, Moreno-Macias H, Smith JA, Brody JA, Dhingra R, Yousefi P, Pankow JS, Kunze S, Shah SH, McRae AF, Lohman K, Sha J, Absher DM, Ferrucci L, Zhao W, Demerath EW, Bressler J, Grove ML, Huan T, Liu C, Mendelson MM, Yao C, Kiel DP, Peters A, Wang-Sattler R, Visscher PM, Wray NR, Starr JM, Ding J, Rodriguez CJ, Wareham NJ, Irvin MR, Zhi D, Barrdahl M, Vineis P, Ambatipudi S, Uitterlinden AG, Hofman A, Schwartz J, Colicino E, Hou L, Vokonas PS, Hernandez DG, Singleton AB, Bandinelli S, Turner ST, Ware EB, Smith AK, Klengel T, Binder EB, Psaty BM, Taylor KD, Gharib SA, Swenson BR, Liang L, DeMeo DL, O’Connor GT, Herceg Z, Ressler KJ, Conneely KN, Sotoodehnia N, Kardia SLR, Melzer D, Baccarelli AA, van Meurs JBJ, Romieu I, Arnett DK, Ong KK, Liu Y, Waldenberger M, Deary IJ, Fornage M, Levy D, and London SJ (2016), “Epigenetic Signatures of Cigarette Smoking,” Circulation: Cardiovascular Genetics, 9, 436–447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kearney DJ, Malte CA, McManus C, Martinez ME, Felleman B, and Simpson TL (2013), “Loving-Kindness Meditation for Posttraumatic Stress Disorder: A Pilot Study,” Journal of Traumatic Stress, 26, 426–434. [DOI] [PubMed] [Google Scholar]
- Kelly MM, DeBeer BB, Meyer EC, Kimbrel NA, Gulliver SB, and Morissette SB (2019), “Experiential Avoidance as a Mediator of the Association between Posttraumatic Stress Disorder Symptoms and Social Support: A Longitudinal Analysis,” Psychological Trauma: Theory, Research, Practice, and Policy, 11, 353–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kessler RC, Aguilar-Gaxiola S, Alonso J, Benjet C, Bromet EJ, Cardoso G, Degenhardt L, de Girolamo G, Dinolova RV, Ferry F, Florescu S, Gureje O, Haro JM, Huang Y, Karam EG, Kawakami N, Lee S, Lepine J-P, Levinson D, Navarro-Mateu F, Pennell BE, Piazza M, Posada-Villa J, Scott KM, Stein DJ, Have MT, Torres Y, Viana MC, Petukhova MV, Sampson NA, Zaslavsky AM, and Koenen KC (2017), “Trauma and PTSD in the WHO World Mental Health Surveys,” European Journal of Psychotraumatology, 8, 1353383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim G, Aiello A, Koenen K, Galea S, Wildman D, and Uddin M (2019a), “27. Differential Methylation at Glucocorticoid-Relevant Regulatory Regions Associated with PTSD in African Americans,” Biological Psychiatry, 85, S11–S12. [Google Scholar]
- Kim GS, Smith AK, Xue F, Michopoulos V, Lori A, Armstrong DL, Aiello AE, Koenen KC, Galea S, Wildman DE, and Uddin M (2019b), “Methylomic Profiles Reveal Sex-Specific Differences in Leukocyte Composition Associated with Post-traumatic Stress Disorder,” Brain, Behavior, and Immunity, 81, 280–291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King WD, Ashbury JE, Taylor SA, Tse MY, Pang SC, Louw JA, and Vanner SJ (2014), “A Cross-Sectional Study of Global DNA Methylation and Risk of Colorectal Adenoma,” BMC Cancer, 14, 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuan P, Waszczuk M, Kotov R, Marsit C, Guffanti G, Gonzalez A, Yang X, Koenen K, Bromet E, and Luft B (2017), “An Epigenome-Wide DNA Methylation Study of PTSD and Depression in World Trade Center Responders,” Translational Psychiatry, 7, e1158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwon A, Lee HS, and Lee S-H (2021), “The Mediation Effect of Hyperarousal Symptoms on the Relationship between Childhood Physical Abuse and Suicidal Ideation of Patients with PTSD,” Frontiers in Psychiatry, 12, 613735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Thi Hoai A, and Tao PD (1997), “Solving a Class of Linearly Constrained Indefinite Quadratic Problems by DC Algorithms,” Journal of Global Optimization, 11, 253–285. [Google Scholar]
- Lee SY, and Park CL (2018), “Trauma Exposure, Posttraumatic Stress, and Preventive Health Behaviours: A Systematic Review,” Health Psychology Review, 12, 75–109. [DOI] [PubMed] [Google Scholar]
- Lei M-K, Beach SR, Simons RL, and Philibert RA (2015), “Neighborhood Crime and Depressive Symptoms among African American Women: Genetic Moderation and Epigenetic Mediation of Effects,” Social Science & Medicine, 146, 120–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacQueen J (1967), “Some Methods for Classification and Analysis of Multivariate Observations,” in Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability (vol. 1), pp. 281–297. Oakland, CA, USA. [Google Scholar]
- McClure E, Feinstein L, Ferrando-Martínez S, Leal M, Galea S, and Aiello AE (2018), “The Great Recession and Immune Function,” RSF: The Russell Sage Foundation Journal of the Social Sciences, 4, 62–81. [PMC free article] [PubMed] [Google Scholar]
- Morrison FG, Miller MW, Logue MW, Assef M, and Wolf EJ (2019), “DNA Methylation Correlates of PTSD: Recent Findings and Technical Challenges,” Progress in Neuro-Psychopharmacology and Biological Psychiatry, 90, 223–234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakatochi M, Ichihara S, Yamamoto K, Naruse K, Yokota S, Asano H, Matsubara T, and Yokota M (2017), “Epigenome-Wide Association of Myocardial Infarction with DNA Methylation Sites at Loci Related to Cardiovascular Disease,” Clinical Epigenetics, 9, 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nesterov Y (2005), “Smooth Minimization of Non-smooth Functions,” Mathematical Programming, 103, 127–152. [Google Scholar]
- Nevell L, Zhang K, Aiello AE, Koenen K, Galea S, Soliven R, Zhang C, Wildman DE, and Uddin M (2014), “Elevated Systemic Expression of ER Stress Related Genes is Associated with Stress-Related Mental Disorders in the Detroit Neighborhood Health Study,” Psychoneuroendocrinology, 43, 62–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orcutt HK, Erickson DJ, and Wolfe J (2004), “The Course of PTSD Symptoms among Gulf War Veterans: A Growth Mixture Modeling Approach,” Journal of Traumatic Stress: Official Publication of The International Society for Traumatic Stress Studies, 17, 195–202. [DOI] [PubMed] [Google Scholar]
- Palma-Gudiel H, Córdova-Palomera A, Leza JC, and Fañanás L (2015), “Glucocorticoid Receptor Gene (NR3C1) Methylation Processes as Mediators of Early Adversity in Stress-Related Disorders Causality: A Critical Review,” Neuroscience & Biobehavioral Reviews, 55, 520–535. [DOI] [PubMed] [Google Scholar]
- Pearl J (2001), “Direct and Indirect Effects,” in Proceedings of the Seventeenth Conference on Uncertainty in Artificial Intelligence, pp. 411–420. [Google Scholar]
- Peng H, Zhu Y, Strachan E, Fowler E, Bacus T, Roy-Byrne P, Goldberg J, Vaccarino V, and Zhao J (2018), “Childhood Trauma,” DNA Methylation of Stress-Related Genes, and Depression: Findings from Two Monozygotic Twin Studies,” Psychosomatic Medicine, 80, 599–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qi R, Luo Y, Zhang L, Weng Y, Surento W, Xu Q, Jahanshad N, Li L, Cao Z, Lu GM, and Thompson PM (2021), “Decreased Functional Connectivity of Hippocampal Subregions and Methylation of the NR3C1 Gene in Han Chinese Adults who lost their Only Child,” Psychological Medicine, 51, 1310–1319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin X, and Hong G (2017), “A Weighting Method for Assessing between-site Heterogeneity in Causal Mediation Mechanism,” Journal of Educational and Behavioral Statistics, 42, 308–340. [Google Scholar]
- Raabe FJ, and Spengler D (2013), “Epigenetic Risk Factors in PTSD and Depression,” Frontiers in Psychiatry, 4, 80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramchandani S, Bhattacharya SK, Cervoni N, and Szyf M (1999). DNA Methylation is a Reversible Biological Signal,” Proceedings of the National Academy of Sciences, 96, 6107–6112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratanatharathorn A, Boks MP, Maihofer AX, Aiello AE, Amstadter AB, Ashley-Koch AE, Baker DG, Beckham JC, Bromet E, Dennis M, Garrett ME, Geuze E, Guffanti G, Hauser MA, Kilaru V, Kimbrel NA, Koenen KC, Kuan P-F, Logue MW, Luft BJ, Miller MW, Mitchell C, Nugent NR, Ressler KJ, Rutten BFF, Stein MB, Vermetten E, Vinkers CH, Youssef NA, VA Mid-Atlantic MIRECC Workgroup, PGC PTSD Epigenetics Workgroup, Uddin M, Nievergelt CM, and Smith AK (2017),“Epigenome-Wide Association of PTSD from Heterogeneous Cohorts with a Common Multi-site Analysis Pipeline,” American Journal of Medical Genetics Part B: Neuropsychiatric Genetics, 174, 619–630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts AL, Gilman SE, Breslau J, Breslau N, and Koenen KC (2011), “Race/Ethnic Differences in Exposure to Traumatic Events, Development of Post-traumatic Stress Disorder, and Treatment-Seeking for Post-traumatic Stress Disorder in the United States,” Psychological Medicine, 41, 71–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robins JM, and Greenland S (1992), “Identifiability and Exchangeability for Direct and Indirect Effects,” Epidemiology, 3, 143–155. [DOI] [PubMed] [Google Scholar]
- Rosenbaum PR (1987)’, “Model-based Direct Adjustment,” Journal of the American Statistical Association, 82, 387–394. [Google Scholar]
- Rubin DB (1974), “Estimating Causal Effects of Treatments in Randomized and Nonrandomized Studies,” Journal of Educational Psychology, 66, 688–701. [Google Scholar]
- — (1980), “Randomization Analysis of Experimental Data: The Fisher Randomization Test Comment,” Journal of the American Statistical Association, 75, 591–593. [Google Scholar]
- Ruhlmann LM, Gallus KL, Beck AR, Goff BSN, and Durtschi JA (2019), “A Pilot Study Exploring PTSD Symptom Clusters as Mediators between Trauma Exposure and Attachment Behaviors in Married Adults,” Journal of Couple & Relationship Therapy, 18, 65–84. [Google Scholar]
- Rusiecki JA, Byrne C, Galdzicki Z, Srikantan V, Chen L, Poulin M, Yan L, and Baccarelli A (2013), “PTSD and DNA Methylation in Select Immune Function Gene Promoter Regions: A Repeated Measures Case–Control Study of US Military Service Members” Frontiers in Psychiatry, 4, 56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutten BP, Vermetten E, Vinkers CH, Ursini G, Daskalakis NP, Pishva E, de Nijs L, Houtepen LC, Eijssen L, Jaffe AE, Kenis G, Viechtbauer W, van den Hove D, Schraut KG, Lesch K-P, Kleinman JE, Hyde TM, Weinberger DR, Schalkwyk L, Lunnon K, Mill J, Cohen H, Yehuda R, Baker DG, Maihofer AX, Nievergelt CM, Geuze E, and Boks MPM (2018), “Longitudinal Analyses of the DNA Methylome in Deployed Military Servicemen Identify Susceptibility Loci for Post-traumatic Stress Disorder,” MolecularPsychiatry, 23, 1145–1156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaid DJ, and Sinnwell JP (2020), “Penalized Models for Analysis of Multiple Mediators,” Genetic Epidemiology, 44, 408–424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuster R, Kleimann A, Rehme M-K, Taschner L, Glahn A, Groh A, Frieling H, Lichtinghagen R, Hillemacher T, Bleich S, and Heberlein A (2017), “Elevated Methylation and Decreased Serum Concentrations of BDNF in Patients in Levomethadone Compared to Diamorphine Maintenance Treatment,” European Archives of Psychiatry and Clinical Neuroscience, 267, 33–40. [DOI] [PubMed] [Google Scholar]
- Serang S, Jacobucci R, Brimhall KC, and Grimm KJ (2017), “Exploratory Mediation Analysis via Regularization,” Structural Equation Modeling: A Multidisciplinary Journal, 24, 733–744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheerin CM, Lancaster EE, York TP, Walker J, Danielson CK, and Amstadter AB (2021), “Epigenome-Wide Study of Posttraumatic Stress Disorder Symptom Severity in a Treatment-Seeking Adolescent Sample,” Journal of Traumatic Stress, 34, 607–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen X, Pan W, and Zhu Y (2012), “Likelihood-based Selection and Sharp Parameter Estimation,” Journal of the American Statistical Association, 107, 223–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi Z-J (2004), “Convergence of Line Search Methods for Unconstrained Optimization,” Applied Mathematics and Computation, 157, 393–405. [Google Scholar]
- Stanimirović PS, and Miladinović MB (2010), “Accelerated Gradient Descent Methods with Line Search,” Numerical Algorithms, 54, 503–520. [Google Scholar]
- Tang X, Xue F, and Qu A (2020), “Individualized Multidirectional Variable Selection,” Journal of the American Statistical Association, 116, 1280–1296. [Google Scholar]
- Tang X, Xue F, and Qu A (2021), “Individualized Multidirectional Variable Selection,” Journal of the American Statistical Association, 116, 1280–1296. [Google Scholar]
- Tibshirani R (1996), “Regression Shrinkage and Selection via the Lasso,” Journal of the Royal Statistical Society, Series B, 58, 267–288. [Google Scholar]
- Tibshirani R, Saunders M, Rosset S, Zhu J, and Knight K (2005), “Sparsity and Smoothness via the Fused Lasso,” Journal of the Royal Statistical Society, Series B, 67, 91–108. [Google Scholar]
- Tobi EW, Slieker RC, Luijk R, Dekkers KF, Stein AD, Xu KM, Biobank-based Integrative Omics Studies Consortium, Slagboom PE, van Zwet EW, Lumey L, and Heijmans BT (2018), “DNA Methylation as a Mediator of the Association between Prenatal Adversity and Risk Factors for Metabolic Disease in Adulthood,” Science Advances, 4, eaao4364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turecki G, and Meaney MJ (2016), “Effects of the Social Environment and Stress on Glucocorticoid Receptor Gene Methylation: A Systematic Review,” Biological Psychiatry, 79, 87–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyrka A, Parade S, Welch E, Ridout K, Price L, Marsit C, Philip N, and Carpenter L (2016), “Methylation of the Leukocyte Glucocorticoid Receptor Gene Promoter in Adults: Associations with Early Adversity and Depressive, Anxiety and Substance-Use Disorders,” Translational Psychiatry, 6, e848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uddin M, Aiello AE, Wildman DE, Koenen KC, Pawelec G, De Los Santos R, Goldmann E, and Galea S (2010), “Epigenetic and Immune Function Profiles Associated with Posttraumatic Stress Disorder,” Proceedings of the National Academy of Sciences, 107, 9470–9475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uddin M, Ratanatharathorn A, Armstrong D, Kuan P-F, Aiello AE, Bromet EJ, Galea S, Koenen KC, Luft B, Ressler KJ, Wildman DE, Nievergelt CM, and Smith A (2018), “Epigenetic Meta-Analysis Across Three Civilian Cohorts Identifies NRGL and HGS as Blood-based Biomarkers for Post-traumatic Stress Disorder,” Epigenomics, 10, 1585–1601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Knaap LJ, Oldehinkel AJ, Verhulst FC, van Oort FV, and Riese H (2015), “Glucocorticoid Receptor Gene Methylation and HPAAxis Regulation in Adolescents: The TRAILS Study,” Psychoneuroendocrinology, 58, 46–50. [DOI] [PubMed] [Google Scholar]
- van der Vleugel BM, Libedinsky I, de Bont PA, de Roos C, van Minnen A, de Jongh A, van der Gaag M, and van den Berg D (2020), “Changes in Posttraumatic Cognitions Mediate the Effects of Trauma-Focused Therapy on Paranoia,” Schizophrenia Bulletin Open, 1, sgaa036. [Google Scholar]
- Van Kesteren E-J, and Oberski DL (2018), “Exploratory Mediation Analysis with Many Potential Mediators,” arXiv preprint arXiv:1810.06334 [Google Scholar]
- Vangeel E, Van Den Eede F, Hompes T, Izzi B, Del Favero J, Moorkens G, Lambrechts D, Freson K, and Claes S (2015), “Chronic Fatigue Syndrome and DNA Hypomethylation of the Glucocorticoid Receptor Gene Promoter 1F Region: Associations with HPA Axis Hypofunction and Childhood Trauma,” Psychosomatic Medicine, 77, 853–862. [DOI] [PubMed] [Google Scholar]
- Vinkers CH, Geuze E, van Rooij SJ, Kennis M, Schür RR, Nispeling DM, Smith AK, Nievergelt CM, Uddin M, Rutten BP, Vermetten E, and Boks MP (2019), “Successful Treatment of Posttraumatic Stress Disorder Reverses DNA Methylation Marks,” Molecular Psychiatry, 26, 1264–1271. [DOI] [PubMed] [Google Scholar]
- Vukojevic V, Kolassa I-T, Fastenrath M, Gschwind L, Spalek K, Milnik A, Heck A, Vogler C, Wilker S, Demougin P, Peter F, Atucha E, Stetak A, Roozendaal B, Elbert T, Papassotiropoulos A, and de Quervain DJF (2014), “Epigenetic Modification of the Glucocorticoid Receptor Gene is Linked to Traumatic Memory and Post-traumatic Stress Disorder Risk in Genocide Survivors,” Journal of Neuroscience, 34, 10274–10284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wani AH, Aiello AE, Kim GS, Xue F, Martin CL, Ratanatharathorn A, Qu A, Koenen K, Galea S, Wildman DE, and Uddin M (2021), “The Impact of Psychopathology, Social Adversity and Stress-Relevant DNA Methylation on Prospective Risk for Posttraumatic Stress: A Machine Learning Approach,” Journal of Affective Disorders, 282, 894–905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward-Caviness CK, Pu S, Martin CL, Galea S, Uddin M, Wildman DE, Koenen K, and Aiello AE (2020), “Epigenetic Predictors of All-cause Mortality are Associated with Objective Measures of Neighborhood Disadvantage in an Urban Population,” Clinical Epigenetics, 12, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weckle A, Aiello AE, Uddin M, Galea S, Coulborn RM, Soliven R, Meier H, and Wildman DE (2015), “Rapid Fractionation and Isolation of Whole Blood Components in Samples Obtained from a Community-Based Setting,” Journal of Visualized Experiments, 105, e52227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf EJ, Maniates H, Nugent N, Maihofer AX, Armstrong D, Ratanatharathorn A, Ashley-Koch AE, Garrett M, Kimbrel NA, Lori A, Va Mid-Atlantic Mirecc Workgroup, Aiello AE, Baker DG, Beckham JC, Boks MP, Galea S, Geuze E, Hauser MA, Kessler RC, Koenen KC, Miller MW, Ressler KJ, Risbrough V, Rutten BPF, Stein MB, Ursano RJ, Vermetten E, Vinkers CH, Uddin M, Smith AK, Nievergelt CM, and Logue MW (2018), “Traumatic Stress and Accelerated DNA Methylation Age: A Meta-Analysis,” Psychoneuroendocrinology, 92, 123–134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yehuda R, Daskalakis NP, Desarnaud F, Makotkine I, Lehrner A, Koch E, Flory JD, Buxbaum JD, Meaney MJ, and Bierer LM (2013), “Epigenetic Biomarkers as Predictors and Correlates of Symptom Improvement Following Psychotherapy in Combat Veterans with PTSD,” Frontiers in Psychiatry, 4, 118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young GP, Pedersen SK, Mansfield S, Murray DH, Baker RT, Rabbitt P, Byrne S, Bambacas L, Hollington P, and Symonds EL (2016), “A Cross-Sectional Study Comparing a Blood Test for Methylated BCAT 1 and IKZF 1 Tumor-Derived DNA with CEA for Detection of Recurrent Colorectal Cancer,” Cancer Medicine, 5, 2763–2772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young RM, Lawford B, Mellor R, Morris CP, Voisey J, McLeay S, Harvey W, Romaniuk M, Crawford D, Colquhoun D, Young RM, Dwyer M, Gibson J, O’Sullivan R, Cooksley G, Strakosch C, Thomson R, Voisey J, and Lawford B (2021), “Investigation of C-Reactive Protein and AIM2 Methylation as a Marker for PTSD in Australian Vietnam Veterans,” Gene, 803, 145898. [DOI] [PubMed] [Google Scholar]
- Zhang C-H (2010), “Nearly Unbiased Variable Selection under Minimax Concave Penalty,” The Annals of Statistics, 38, 894–942. [Google Scholar]
- Zhang H, Zheng Y, Zhang Z, Gao T, Joyce B, Yoon G, Zhang W, Schwartz J, Just A, Colicino E, Vokonas P, Zhao L, Lv J, Baccarelli A, Hou L, and Liu L (2016), “Estimating and Testing High-Dimensional Mediation Effects in Epigenetic Studies,” Bioinformatics, 32, 3150–3154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao J, Goldberg J, Bremner JD, and Vaccarino V (2013), “Association between Promoter Methylation of Serotonin Transporter Gene and Depressive Symptoms: A Monozygotic Twin Study,” Psychosomatic Medicine, 75, 523–529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y, and Luo X (2016), “Pathway Lasso: Estimate and Select Sparse Mediation Pathways with High-Dimensional Mediators,” arXiv preprint arXiv:1603.07749 [Google Scholar]
- Zhou RR, Wang L, and Zhao SD (2020), “Estimation and Inference for the Indirect Effect in High-Dimensional Linear Mediation Models,” Biometrika, 107, 573–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


