Antigen presentation dynamics shape the antibody response to variants like SARS-CoV-2 Omicron after multiple vaccinations with the original strain

Abstract

The Omicron variant of SARS-CoV-2 is not effectively neutralized by most antibodies elicited by two doses of mRNA vaccines, but a third dose increases anti-Omicron neutralizing antibodies. We reveal mechanisms underlying this observation by combining computational modeling with data from vaccinated humans. After the first dose, limited antigen availability in germinal centers (GCs) results in a response dominated by B cells that target immunodominant epitopes that are mutated in an Omicron-like variant. After the second dose, these memory cells expand and differentiate into plasma cells that secrete antibodies that are thus ineffective for such variants. However, these pre-existing antigen-specific antibodies transport antigen efficiently to secondary GCs. They also partially mask immunodominant epitopes. Enhanced antigen availability and epitope masking in secondary GCs together result in generation of memory B cells that target subdominant epitopes that are less mutated in Omicron. The third dose expands these cells and boosts anti-variant neutralizing antibodies.

Graphical abstract

Yang et al. investigate why three doses of mRNA COVID vaccines elicit improved antibody breadth against a mutated strain (e.g., the Omicron variant), compared with two doses. Their modeling results and clinical data show that antigen presentation dynamics and epitope masking play key roles in determining the humoral recall response.

Introduction

The emergence of viral mutants that escape from vaccine-imprinted immune memory is a major challenge for the development of vaccines against highly mutable viruses. In less than 2 years since effective vaccines became available, several SARS-CoV-2 variants of concern have emerged and spread. The Omicron (BA.1) variant harbors 32 mutations in the spike protein that enables it to escape from the majority of known monoclonal antibodies.^{1 , 2 , 3} Individuals vaccinated with two doses of mRNA vaccines encoding the spike protein of the original Wuhan strain have much lower neutralizing antibody titers against Omicron compared with the original strain. However, a third dose (booster) of the same vaccine significantly increases protection against Omicron.^{4 , 5 , 6 , 7}

After the booster, the peak neutralization titer increases roughly 3-fold against the wild-type (WT) Wuhan strain compared with the peak value after the second dose, but increases 20- to 30-fold against Omicron.^{8 , 9 , 10 , 11} Thus, the booster shot increased the breadth of the resulting neutralizing antibodies in addition to restoring antibody titers that waned over time. The increase in breadth after the third dose has been attributed to the rise of antibodies targeting diverse epitopes in the receptor-binding domain (RBD), some of which are relatively conserved between the Wuhan and Omicron strains.^{8 , 12}

Many immunodominant epitopes on the SARS-CoV-2 spike protein lie in the ACE2 binding interface region.^{8 , 9 , 13 , 14} Several human germline heavy chain genes exhibit high affinities for these epitopes.¹⁵ Antibodies that develop from these germlines are highly enriched in response to both infection¹⁶ and two doses of mRNA vaccination.¹⁷ The Omicron variant is highly mutated in the epitopes targeted by these antibodies, and therefore it can effectively evade the immune response generated after two doses of mRNA vaccines.⁹

Some of the Omicron-neutralizing antibodies that develop after the third vaccine dose must target relatively conserved epitopes. These antibodies must be subdominant because they are not present in large titer after the second vaccine dose. Immunodominance during interclonal competition of germinal center (GC) B cells is not well understood. It is thought to be shaped by a combination of factors that include the frequency and affinity of naive B cells,^{18 , 19 , 20 , 21} antigen availability in the lymph node,^{22 , 23} re-activation of pre-existing memory B cells,^{20 , 24} and epitope masking by pre-existing antibodies.^{25 , 26 , 27 , 28 , 29 , 30}

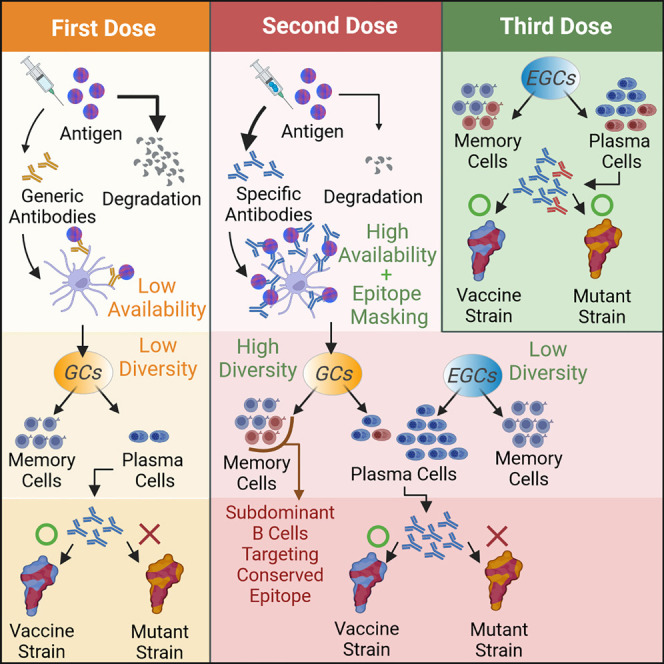
In this paper, we studied the mechanisms that underlie how repeated doses of the vaccine that encodes for the Wuhan strain’s spike change the immunodominance hierarchy of the resulting antibody response. We first developed an in silico model that integrates the processes that occur in GCs with the expansion and differentiation of memory B cells outside the GC (extra germinal centers or EGCs). We explicitly consider antigen presentation dynamics in lymph nodes after the first and subsequent shots of homologous vaccines. Our results show that antigen availability on follicular dendritic cells (FDCs) in GCs differs markedly between the first and second shots, and this difference plays a key role in the diversity of memory B cells generated. Limited antigen availability in GCs after the first shot results in a memory response restricted to B cells that target immunodominant epitopes, which are heavily mutated in an Omicron-like strain. In secondary GCs seeded after the second dose, higher levels of antigen are available on FDCs because antibodies generated after the first dose enable effective antigen transport to FDCs. The increased antigen availability leads to an increase in memory B cells that target subdominant epitopes that are relatively conserved in an Omicron-like strain.

We also investigate the role of epitope masking by circulating antibodies in secondary GCs. These antibodies are mainly derived from memory cells generated after the first dose and can block the dominant epitopes more effectively than subdominant epitopes. By incorporating experimental data on epitope mapping of serum antibodies, our in silico results show that considering the degree of overlap between RBD epitopes is important to understand the role of epitope masking in polyclonal response to vaccines.

In response to the third dose, the existing memory B cells that target subdominant epitopes expand and differentiate into plasma cells, leading to production of antibodies that confer better protection against emergent variants. These predictions from the in silico model are consistent with our analyses of new and existing data obtained from individuals vaccinated with three shots of mRNA vaccines. Taken together, our results show that antigen availability on FDCs and epitope masking are two distinct factors that affect affinity maturation in secondary GCs. Clinically observed changes in immunodominance hierarchy upon receiving the third shot of COVID mRNA vaccines cannot be explained by accounting for only one of these effects. These insights shed new light on fundamental aspects of the nature of the recall response that are directly relevant to vaccine design. Our results also explain several recent observations linking different vaccine regimens to protection from Omicron.^{31 , 32}

In silico model for the humoral immune response

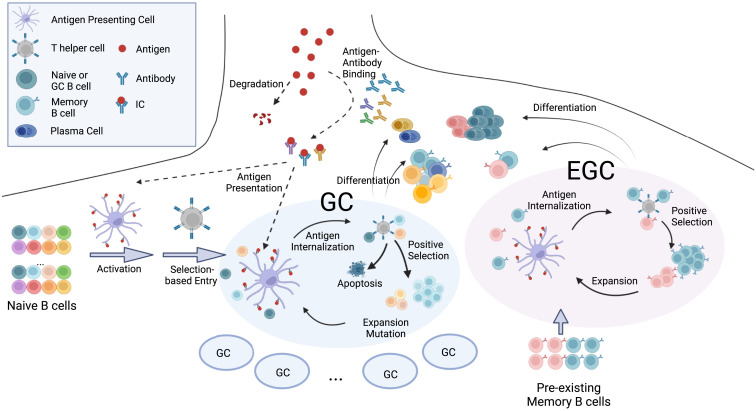
Our model incorporates four main aspects of the B cell and antibody responses: (1) antigen presentation on FDCs, (2) activation of naive B cells and entry into GCs, (3) affinity maturation in GCs and export of memory and plasma cells, and (4) expansion of memory B cells and differentiation into plasma cells in EGCs (Figure 1 ). A set of differential equations that extends a previous study³³ models antigen capture and transport. Stochastic agent-based models are used to simulate GC and EGC processes.^{20 , 24 , 34} We consider four general classes of B cells: naive B cells, GC B cells, memory B cells, and plasma cells. At each incremental time step in the simulations, the probabilities of actions such as activation, selection, proliferation, mutation, differentiation, and apoptosis are calculated for the B cells, and these actions are then executed accordingly. A total of 200 separate GCs are simultaneously simulated to mimic a secondary lymphoid organ.³⁵ The simulation is repeated 10 times for each vaccine dose. The average quantities thus calculated could be considered to be the typical population-level response. Descriptions of the computational model and the simulation algorithm are outlined below (see STAR Methods for further details of the model, Tables S1 and S2 for parameters used, and Table S3 for detailed simulation algorithm). Parameter sensitivity analysis was performed for several key parameters, while the values for the other parameters were chosen to be consistent with experimental observations, as described in Table S2.

Figure 1.

Schematic depiction of the in silico model

The model integrates antigen presentation dynamics with processes in GCs and EGCs. Circulating antibodies help present antigen on FDCs. GC entry; GC B cell selection, replication, and mutation; and differentiation of GC B cells into memory and plasma cells are considered. In the EGC, pre-existing memory cells undergo selection, proliferation, and differentiation without mutations. See also Figure S1. The figure was created with Biorender software.

Model for antigen presentation

Although mRNA vaccines induce antigen production in vivo, the protein production rate decreases rapidly and exponentially.³⁶ So, we model vaccination as injection of a bolus of antigen.³³ Soluble and immune complex (IC) forms of the antigen rapidly reach dynamic equilibrium, with their relative amounts determined by the pre-existing antibody concentrations and equilibrium constants for antibody-antigen binding. The soluble antigen decays quickly, but ICs are transported to FDCs where they decay with a much longer half-life. Upon immunization with a new antigen, small numbers of low-affinity circulating immunoglobulin (Ig)M antibodies are available to bind antigen. For subsequent immunizations, higher-affinity antibodies generated by earlier GC/EGC processes are available to form ICs. The differential equations that describe IC formation and antigen presentation are coupled to the agent-based simulation of GC and EGC processes (parameters used, Table S1; simulation methods in STAR Methods).

Model for naive B cells and WT and variant strains

We model the distribution of germline-endowed affinities of naive B cells as an exponential distribution between K _d = 10⁻⁶ M and 10⁻⁸ M, where K _d is the dissociation constant. This is because a minimum affinity of about K _d = 10⁻⁶ M is required for activation,³⁷ and rare naive B cells with ∼100-fold higher affinities can be found for antigens like SARS-CoV-2.^{38 , 39} In our coarse-grained model, we group the few dominant epitopes on an antigen into a single “dominant” epitope and group the subdominant epitopes into a single “subdominant” epitope. The “dominant” epitope is targeted by a greater number of naive B cells, and their affinities exhibit a longer high-affinity tail compared with the “subdominant” epitope (Figure S1A; STAR Methods, Equations 2, 3, 4, and 5; parameters in Table S2).

Most immunodominant neutralizing epitopes on the SARS-CoV-2 spike protein are highly mutated in the Omicron variant (compared with WT),² while some subdominant epitopes are relatively conserved.⁴⁰ It has been suggested that mutations in the Omicron variant emerged to escape from immune pressure.⁴¹ Therefore, in our model, the dominant epitope is less conserved. Each B cell has different affinities for the WT and the variant because the initial affinity and the effects of the mutations depend on the antigen (Figure S1B, STAR Methods, Equations 6 and 7). The effect of mutations on binding affinities for the WT and the variant are drawn from correlated log-normal distributions so that ∼5% of affinity-affecting mutations are beneficial for each strain and most mutations are deleterious (Figure S1C).^{42 , 43} The level of correlation between the WT and variant distributions determines the fraction of mutations that will be beneficial for binding to both strains (Figure S1D). We chose parameters so that about 72% and 19% of beneficial mutations increase affinities toward both strains for B cells that target subdominant and dominant epitopes, respectively. Our qualitative results are robust to changes in these parameters within reasonable ranges. Details of the simulation methods are in STAR Methods.

Model for GC entry of naive B cells

Naive B cells continuously enter 200 GCs after activation and selection.^{44 , 45} At each time step, naive B cells internalize different amounts of antigen based on their binding affinity for the WT antigen and its availability.^{24 , 37 , 46} Then, they stochastically get activated and compete for T helper cells for selection signals that allow GC entry.^{47 , 48 , 49} The probabilities for these entry events are determined by the amounts of internalized antigen (STAR Methods, Equations 10, 11, 12, and 13). The effect of memory B cell participation in GCs is studied by varying the fraction of pre-existing memory B cells added to the pool of naive B cells.

Selection stringency is an important factor in shaping B cell competition dynamics and thus the diversity of the response.⁵⁰ We studied the effects of changing the level of selection stringency and alternative models for antigen internalization to test the robustness of our qualitative results (STAR Methods, Equation 10 and 14).

Model for affinity maturation in GCs

For positive selection, GC B cells require activation by antigen capture^{51 , 52} followed by selection by T helper cells.⁵³ In our model, GC B cells internalize antigen and are stochastically activated in the same way as the naive B cells. To model the competition for limited amount of T cell help, the birth rate of an activated GC B cell is determined by two factors: the amount of antigen it has captured relative to the average amount captured by all activated GC B cells, and the ratio between the number of T helper cells and activated B cells (STAR Methods, Equations 15 and 16). The number of T cells at a given time point is determined by a model that recapitulates a clinical observation in SARS-CoV-2 vaccinated subjects (STAR Methods, Equation 17).⁵⁴ All GC B cells also stochastically undergo apoptosis with a constant death rate (STAR Methods, Equation 18).⁵⁵ The use of birth-death model implicitly treats the cyclical migration between the light and dark zones. Many previous studies have used similar models and shown that they recapitulate the qualitative aspects of GC dynamics.^{20 , 43 , 56 , 57 , 58} In our model, GC B cells that receive a stronger selection signal from T helper cells will statistically undergo a greater number of birth events in a given time. Therefore, our model is qualitatively consistent with experimental findings, which shows that GC B cells that receive stronger selection signals proliferate a greater number of times in one cycle.⁵⁹

With a probability, p ₁, each positively selected B cell exits the GC. It can differentiate into a plasma cell with probability p ₂, or become a memory cell. As discussed later, we studied varying p ₁ and p ₂. The remaining positively selected cells proliferate once. During a birth event, one of the two daughter cells mutates.⁶⁰ A mutation leads to apoptosis (probability 0.3), no affinity change (probability 0.5), or a change in the mutation state of a randomly selected residue (probability 0.2).⁴³ Details of the simulation methods are in STAR Methods.

Model for EGC processes

Upon the second and third vaccination, an EGC response develops. EGCs select and expand pre-existing memory B cells without introducing mutations.⁶¹ The number of memory B cells peaked 1 week after the second dose in vaccinated subjects.⁵⁴ Thus, although some memory B cells may continue to be generated in EGCs, in the simulation we terminate the EGC after 6 days. The selection process is identical to that in the GCs, except that the number of T cells is assumed to be equal to the peak value to account for the fast kinetics of the EGC. Proliferating cells in the EGC are assumed to differentiate into plasma cells with a high probability of 0.6, consistent with the observation that ∼60% of newly proliferating memory cells are short-lived plasma cells.⁶²

Results

Limited antigen availability after the first vaccine dose leads mostly to memory B cells that are descendants of naive B cells with high germline-endowed affinities for dominant epitopes

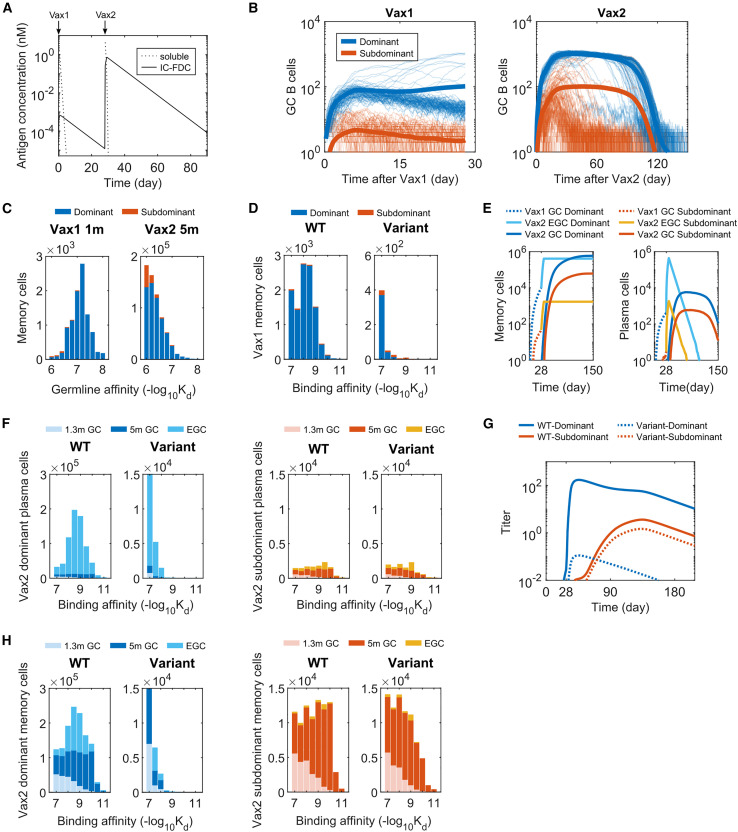
Our simulations show that after the first vaccine dose (Vax 1) only a small amount of antigen gets deposited and retained on FDCs (Figure 2 A). This is because soluble antigen decays rapidly and IgM antibodies with relatively low affinity for the new antigen form immune complexes. These results are consistent with images of antigen retention on FDCs in mouse and monkey lymph nodes after a first vaccine dose.^{22 , 33 , 63} In the first week after immunization, many naive B cells are activated and about 70 distinct cells enter each simulated GC (Figure S2A), a result consistent with observations in mice.^{33 , 64}

Figure 2.

B cell and antibody responses after Vax 1 and Vax 2

(A) Concentrations of soluble antigen and immune complexes on FDCs. Vax 1 was administered on day 0 and Vax 2 on day 28.

(B) Number of GC B cells that target dominant and subdominant epitopes after Vax 1 (left panel) and Vax 2 (right panel). Ten independent simulations of 200 GCs were performed for each case, and the bold curves show the mean values per GC. The other curves represent individual dynamic trajectories in 100 randomly selected GCs.

(C) Histograms showing the distribution of WT-binding affinities of the germline B cell ancestors of GC-derived memory cells at 1 month after Vax 1 (left panel) and 5 months after Vax 2 (right panel).

(D) Histograms showing the distribution of binding affinities of memory B cells against the WT and the variant at 1 month after Vax 1.

(E) Number of memory cells (left panel) and plasma cells (right panel) from GCs and EGCs after Vax 1 and Vax 2. Memory cells generated from Vax1 are expanded in the EGC and differentiate into plasma cells. New memory B cells and plasma cells are also generated from Vax 2 GCs. The plasma cells are short-lived and decay at a constant rate.

(F) Histograms showing the distribution of binding affinities of plasma cells for the dominant (left panels) and subdominant (right panels) epitopes of the WT and the variant strains after Vax 2. GC-derived cells at 1.3 months and 5 months after vaccination and EGC-derived cells are shown. EGCs only last for six days, so no plasma cells are generated from EGCs between 1.3 and 5 months. Since plasma cells are short-lived, the data for a given time point shows all cells generated until that time.

(G) Antibody titers after Vax 1 and Vax 2 that target the dominant and subdominant epitopes of the WT and the variant strains. Titers are calculated as the antibody concentrations divided by K_d.

(H) Histograms showing the distribution of binding affinities of memory cells for the dominant (left panels) and subdominant (right panels) epitopes of the WT and the variant strains after Vax 2. All histograms show distributions in terms of numbers of cells from 200 GCs, averaged over 10 simulations. See also Figures S2–S4.

Given the low antigen availability, the probability of low-affinity GC B cells capturing enough antigen to become activated and receive survival signals from T helper cells is low, consistent with experimental observations.^{37 , 51} Consequently, B cells in early GCs with low germline affinities have a low frequency of proliferation. GC B cells also develop deleterious mutations more frequently than beneficial ones,⁴² which further reduces their chance of being positively selected. Since the default for GC B cells is to undergo apoptosis,⁵⁵ in many simulated GCs the B cell population begins to decline, which makes it even more unlikely that beneficial affinity-increasing mutations will evolve. Thus, many GCs eventually collapse (Figure 2B). In some GCs, however, B cells with high affinity evolve through mutations, and they can continue to proliferate, affinity mature, and generate memory B cells despite low antigen availability. We find that ∼75% of these memory B cells generated after Vax 1 originate from B cells with high germline affinities (${-logK}_d\ge 7$) even though they make up a small fraction (∼0.06%) of naive B cells (Figure 2C). High germline affinities are critical because they allow the B cells to proliferate frequently in the early GC, enabling them to acquire rare beneficial mutations. These cells predominantly target dominant epitopes (Figures 2B and 2C). The genetic diversity in GCs is also limited as a small number of high-affinity B cells quickly dominate (Figure S2B).^{65 , 66} Thus, the memory response after Vax 1 is dominated by a small number of expanded clones (Figure S2C), consistent with data from vaccinated humans.¹⁷ Since these B cells target immunodominant epitopes that are highly mutated in the variant, they exhibit limited cross-reactivity (Figures 2D and S2D).

Many observed neutralizing class 1/2 antibodies against WT SARS-CoV-2 that target dominant epitopes differ by only one or two mutations from the corresponding germline ancestors.^{15 , 67 , 68 , 69} Our results suggest that this is because the GC response after Vax 1 is dominated by a few expanded clones that originate from naive B cells characterized by relatively high germline affinity for the dominant epitopes. One or two mutations are sufficient for these B cells to successfully mature in GCs.

We chose a particular set of parameters (Table S2) to obtain the results shown in the main text, but we tested the robustness of this finding by varying the following key simulation parameters: the parameter that determines the relative importance of antigen availability for positive selection of GC B cells; parameters that characterize the naive B cell repertoire and stringency of affinity-based selection. Our qualitative findings are robust across a wide range of these parameter values (Figures S3A–S3D). Our results are also robust to using an alternative model for the selection of GC B cells (STAR Methods Equation 14, Figure S3E).

Expansion and differentiation of existing memory B cells that target dominant epitopes control the antibody response after the second dose, while increased antigen availability in secondary GCs elicits memory B cells that target subdominant epitopes

After the second vaccine dose (Vax 2), the memory and plasma cell responses are determined by processes that occur in newly formed secondary GCs and in EGC compartments. Our choice of simulation parameters that characterize the relative numbers of plasma and memory cells that exit from the GCs and EGCs (p₁ and p₂ from the section “ Model for affinity maturation in GCs ”) was informed by data from mice and humans. These data suggest that many short-lived plasma cells are rapidly produced in EGCs which then quickly decay, while GCs produce a relatively small number of plasma cells over longer times.^{8 , 54 , 70} The number of EGC and GC-derived memory B cells appear to be of similar orders of magnitude since the numbers of RBD-targeting memory cells are similar between ∼1 month and ∼5 months after Vax 2.^{8 , 54} Our qualitative results are robust to parameter variations over wide ranges (Figures S3A–S3F).

Since EGCs select and expand the memory B cells generated in response to Vax 1 in an affinity-dependent manner (Figure 2E), most of the plasma cells that differentiate from them target the dominant epitopes and have low cross-reactivity to the variant (Figures 2F, S2D, and S2E). Therefore, the WT antibody titer rapidly increases but not the variant titer (Figure 2G). The number of plasma cells derived from secondary GCs is small compared with EGC-derived plasma cells (Figures 2E and 2F) and has a limited contribution to the overall antibody titer after Vax 2, an observation consistent with original antigenic sin.⁷¹ That is, the antibody response to secondary immunization is dominated by the recall of previously generated responses.

After Vax 2, soluble antigen rapidly forms ICs with pre-existing high-affinity antibodies before it decays to low levels (Figure 2A). Thus, we find a large difference in antigen availability after primary and secondary immunization, consistent with lymph node imaging of rhesus macaques.⁶³ In the first week after immunization, a similar number of B cells joins the GCs as in Vax 1 (Figure S2A). The high amounts of antigen available on FDCs now allow lower affinity B cells that target subdominant epitopes to internalize antigen, proliferate, acquire beneficial mutations, and compete with higher-affinity cells for survival signals from helper T cells. Unlike Vax 1 GCs, this effect prevents secondary GC B cells from being completely dominated by high-affinity B cells that target dominant epitopes (Figures 2B and S2B), and diverse memory B cells exit from the GCs (Figure S2C). Since low-affinity naive B cells are much more common, they often ultimately outcompete the rare high-affinity naive B cells to take over GCs (Figure 2C). Only ∼7% of memory B cells descend from naive cells with high affinities after Vax 2 ($-log{K}_d\ge 7)$, in contrast to ∼75% after Vax 1. By 5 months after Vax 2, large numbers of GC-derived memory B cells are produced, and they have higher affinities toward WT than the EGC-derived clones because of affinity maturation over time (Figure 2H). Notably, by 5 months after Vax 2, some subdominant epitope-targeting memory B cells also develop high affinities toward the variant (Figures 2H and S2F).

We also studied the role of memory B cell re-entry into secondary GCs. We added different fractions of existing memory B cells to the naive B cell pool after Vax 2. We find that more memory B cell re-entry into GCs decreases the output of memory B cells that target subdominant epitopes (Figure S4A). This is because most of the existing memory cells target dominant epitopes, and high-affinity memory B cells have a high chance of dominating the GC once they enter (Figure S4B). These findings suggest that limiting memory B cell re-entry into the secondary GCs promotes the generation of memory B cells that target subdominant epitopes, and may be a mechanism that evolved to confer protection against future variants that may emerge.^{27 , 72} Similar effects could result from alternative mechanisms such as the early export of predominantly low-affinity GC B cells as memory cells.⁷³

Memory B cells generated in GCs after the second dose are expanded and differentiated in EGCs after the third vaccine dose to drive improved variant neutralization

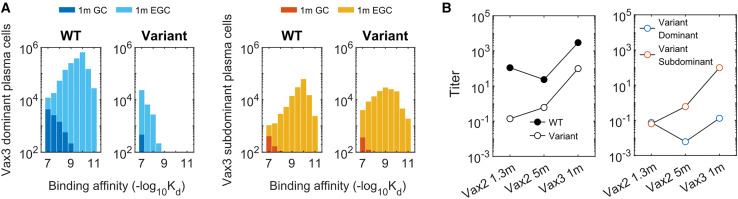
After the third vaccine dose (Vax 3), existing memory B cells expand in the EGC and differentiate into plasma cells. A number of high-affinity memory B cells generated after Vax 2 target subdominant epitopes that are relatively conserved between the WT and variant strains (Figure 2H). These cells differentiate into plasma cells with high affinity for the variant (Figure 3 A). Thus, the antibody titer against the variant increases after Vax 3 (Figure 3B). The fold-change in titer from 1.3 months post Vax 2 to 1 month post Vax 3 is greater for the variant than for the WT, consistent with serum responses in vaccinated humans.^{8 , 10} The breakdown of antibody titers based on epitope specificity shows that the variant-binding titer is driven by the subdominant epitope-targeting antibodies, while the WT-binding titer is still driven by the dominant epitope-targeting antibodies (Figure 3B). The greater fold-change in variant-binding titer is therefore explained by the large increase in the number of subdominant memory B cells that emerge from Vax 2 GCs compared with that from Vax 1 GCs. Note that our results showing that neutralizing antibodies for the variant after Vax 3 are drawn from the existing memory pool after Vax 2 are consistent with clinical data showing that antibody sequences that neutralize Omicron after the third dose were present in the memory compartment after the second dose.⁸

Figure 3.

B cell and antibody responses after Vax 3

(A) Histograms showing the distribution of binding affinities of plasma cells targeting the dominant and subdominant epitopes of the WT and variant strains 1 month after Vax3. Almost all of the plasma cells at this point are derived from the EGC. A substantial response to the subdominant epitope of the variant emerges. All histograms show distributions in terms of numbers of cells from 200 GCs, averaged over 10 simulations.

(B) Comparison of antibody titers against the WT and the variant (left panel) and the epitope specificity of the variant-targeting antibodies (right panel) at 1.3 months after Vax 2, 5 months after Vax 2, and 1 month after Vax 3. The titer for antibodies targeting the subdominant epitope of the variant increases monotonically after 1.3 months post Vax 2 because it has a very low value at early times. Titers are calculated as the antibody concentrations divided by K_d.

Analysis of sera from vaccinated humans is consistent with in silico predictions

We explored the veracity of our in silico predictions by analyzing data on sera obtained from individuals vaccinated with COVID-19 mRNA vaccines. Muecksch et al. sampled B cells from five uninfected individuals after the first, second, and third doses of the Moderna or Pfizer-BioNTech vaccines.⁸ The samples were collected an average of 2.5 weeks, 1.3 and 5 months, and 1 month after the first, second, and third doses, respectively. We grouped sequences of 1370 B cells into clonal families and constructed a phylogenetic tree for each clonal family using MATLAB’s seqlinkage function. If a phylogenetic tree contained two or more identical IGH sequences at the same time point or at different time points, we assumed that these clones were expanded in EGCs. The basis for this method is that EGCs expand memory cells with little to no mutations (Figure S5A). This method is conservative, as there is a low rate of mutation in EGCs.⁶² For this reason and because of under-sampling, we can identify only a small fraction of EGC-derived B cells. However, when tested against simulated data, we found the precision of our method for identifying EGC clones to be very high. From the simulation data in Figures 2 and 3, we randomly sampled B cells from different time points as was done in experiments. We then applied the method described above, and found our identification method has a sensitivity of ∼0.3 and a precision of ∼0.9 for finding the EGC B cells (Figure S5B). Bayesian analysis agrees with these estimates (STAR Methods, Figure S5B). Sequences that were not EGC-derived were considered to be derived from GCs. Thus, we classified the sequences of B cells obtained after Vax 2 and Vax 3 as either EGC-derived or GC-derived. The GC-derived cells were further classified as clones if clonally related sequences were observed and otherwise as singlets.

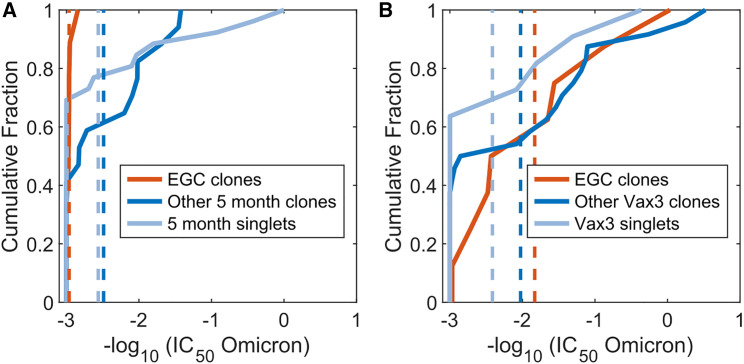
To test the in silico results against clinical data, we determined the neutralization activity of antibodies derived from the sequences classified as EGC-derived and GC-derived. We combined existing data⁸ with new measurements of neutralization activities for some of the sequences that our analyses identified as EGC-derived. The new measurements were carried out using the methods described before.^{8 , 74 , 75} The neutralization activities (half maximal inhibitory concentration [IC₅₀]) of 112 antibodies derived from B cells were measured against the Omicron RBD. Nine EGC-derived B cells were identified from samples collected after Vax 2. Other B cells sampled 5 months after Vax 2 were labeled as GC-derived clonal families or singlets. The EGC-derived clones have a much higher IC₅₀ than the likely GC-derived clones or singlets in terms of the mean and the maximum (Figure 4 A), indicating their low potency. The geometric mean of the GC-derived clones and singlets is 341 ng/mL, which is much lower than the 919 ng/mL for EGC clones (p = 0.00027). This result agrees with the in silico prediction that GC-derived B cells exhibit better Omicron neutralization titers than the EGC-derived B cells after Vax 2 (Figures 2H, S2E, and S2F). We note that five of the nine EGC-derived B cells after Vax 2 also did not neutralize the WT (Table S4).

Figure 4.

Omicron neutralization potency of monoclonal antibodies that are inferred to originate in EGCs and GCs, derived from vaccinated humans

(A) The cumulative distributions of Omicron neutralization titers (IC₅₀) of B cells and their antibodies sampled after Vax 2. Based on the sequence analysis (see text), the B cells have been classified as those identified to be derived from EGCs (red curves), other clonal families (blue curves), or singlets (light blue curves). Dashed lines indicate mean values. Because the EGCs are short-lived and the distributions were identical, EGC B cells collected 5 months after Vax 2 were combined with EGC B cells collected 1.3 months after Vax 2.

(B) Similar data as in (A) for cells sampled 1 month after Vax 3. A statistical comparison of the distributions shown in (A) and (B) is noted in the text. See also Figure S5.

Eight EGC-derived B cells were identified after Vax 3. Figure 4B shows that the IC₅₀ of EGC clones improved from a geometric mean of 919 ng/mL after Vax 2 to 68 ng/mL after Vax 3 (p = 0.0035, STAR Methods). Comparing Figures 4A and 4B shows that the geometric mean of IC₅₀ values for EGC-derived antibodies after Vax 3 is more similar to the GC-derived ones after Vax 2 (341 ng/mL) than the EGC-derived clones after Vax 2 (919 ng/mL). This is consistent with our in silico predictions (Figure 2, Figure 3), which show that the EGCs formed after Vax 3 expand the subdominant and cross-reactive memory B cells generated after Vax 2.

Epitope masking by polyclonal antibodies amplifies the increase in subdominant responses, but increased antigen availability plays a key role

Circulating antibodies can mask their corresponding epitopes, promoting the evolution of GC B cells that target other epitopes. Several experiments have shown that injection of high-affinity monoclonal antibodies along with the immunogen in mice^{25 , 26 , 27 , 28} and humans²⁹ abrogates de novo affinity maturation to the target epitopes. However, while some studies have also observed enhanced subdominant response upon repeated vaccinations in animals, the role of epitope masking by vaccine-induced polyclonal antibodies in this response is less conclusive.^{26 , 28} It has been speculated that masking of dominant epitopes by circulating antibodies may drive the diversity increase of memory B cells upon repeated mRNA vaccinations.^{8 , 76 , 77} By combining mathematical modeling with available clinical observations, we aimed to clearly understand the effects of epitope masking in the context of SARS-CoV-2 vaccination in humans.

Given the reported serum RBD-targeting antibody concentrations and affinities after mRNA vaccination,^{78 , 79} the extent to which antibodies mask their corresponding epitopes can be calculated assuming dynamic equilibrium.⁸⁰ Such a calculation suggests that epitope masking will not be important after Vax 1 because of low antibody titer, but by 2 weeks after Vax 2, antibodies will mask ∼99% of the epitopes (Figure S6A). If the dominant and subdominant epitopes do not overlap, then epitope masking selectively lowers the effective dominant epitope concentrations by ∼100-fold. In our simulations, this causes subdominant B cells to monopolize the secondary GC response (Figures S6B and S6C), consistent with the observations in experimental studies that used monoclonal antibodies to block immunodominant epitopes.

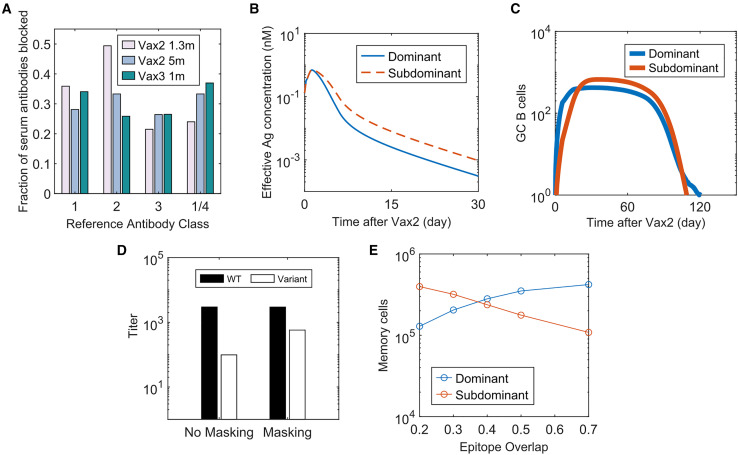
However, antibodies developed after mRNA vaccination are highly polyclonal and target many overlapping epitopes. Class 1 and 2 antibodies that dominate early neutralizing antibody responses bind to the ACE2 binding motif.^{2 , 81} Class 3 and 4 neutralizing antibodies target relatively conserved peripheries of the RBD and are subdominant.^{2 , 8} Yet, reanalysis of data from Muecksch et al.⁸ shows that each of the reference class 1, 2, 3, and 1/4 neutralizing antibodies interfere with 20%–50% of the polyclonal antibodies across all time points (Figure 5 A). These data suggest that serum polyclonal antibodies will likely partially block both dominant and subdominant epitopes due to overlap between epitopes.

Figure 5.

Role of epitope masking on immunodominance hierarchy

(A) Fraction of antibodies derived from human serum responses that blocked the binding of four reference antibodies (class 1, 2, 3, and 1/4) that target different regions of the SARS-CoV-2 RBD. Data from Muecksch et al. were reanalyzed.⁸

(B) Epitope-dependent effective antigen concentrations when there is epitope masking with 30% of epitope overlap.

(C) Number of GC B cells that target dominant and subdominant epitopes after Vax 2 with 30% epitope overlap.

(D) Comparison of antibody titers at 1 month after Vax 3 between simulations with no epitope masking (“No Masking”) and epitope masking with 30% of epitope overlap (“Masking”). Titers are calculated as the antibody concentrations divided by K_d.

(E) Number of dominant and subdominant memory B cells at 5 months Vax 2 when the degree of epitope overlap is varied in simulations. See also Figure S6.

Therefore, we studied an epitope masking model where a fraction of antibodies targeting dominant epitopes can also block subdominant epitopes, and vice versa. When this fraction (epitope overlap) is 30%, the antigen availability advantage for subdominant B cells is relatively small (Figure 5B). But even this moderate effect amplifies the subdominant B cell response from the secondary GCs (Figure 5C). Compared with the case without epitope masking, the antibody titer for the variant further increases after Vax 3, without much difference in the WT titer (Figure 5D). Thus, our model suggests that epitope masking from polyclonal responses can enhance targeting of subdominant epitopes that moderately overlap with immunodominant epitopes. Thus, epitope masking likely plays a significant role in the observed increase in class 3 and 4 neutralizing antibodies (that bind to the RBD periphery) after Vax 3.⁸

However, well-conserved, but subdominant, epitopes also exist on the ACE2 binding motif that are targeted by class 1 and 2 antibodies, and antibodies that target these epitopes can neutralize Omicron well.⁴⁰ These subdominant epitopes overlap significantly with the epitopes targeted by immunodominant class 1 and 2 antibodies because antibody footprints typically cover most of the ACE-2 binding motif.^{81 , 82} Our calculations show that the promotion of subdominant epitope-targeting by epitope masking decreases with an increase in the degree of overlap between dominant and subdominant epitopes (Figure 5E). Thus, if epitope masking was the only mechanism underlying increased Omicron neutralization after Vax 3, Omicron-neutralizing subdominant class 1 and 2 antibodies should be rare. However, analysis of 43 Omicron-neutralizing antibodies isolated from humans after Vax 3 showed that 63% of them were class 1/2 antibodies.⁸³ These antibodies were derived mostly from subdominant germlines that were rarely observed 1.3 months after Vax 2, but they became more prevalent after Vax 3 and were significantly mutated.⁸³ These observations suggest their development in secondary GCs. Meanwhile, class 1/2 antibodies derived from immunodominant germlines dominated the early antibody response after Vax 2, as expected.⁸³ Since these immunodominant antibodies likely also significantly mask the epitopes targeted by subdominant class 1/2 antibodies, epitope masking alone cannot explain the rise of the latter in secondary GCs. Increased antigen availability on FDCs after Vax 2 (see earlier sections) likely plays a key role in promoting their emergence.

Discussion

We studied the effects of repeated immunization with a WT vaccine on antibody responses to a highly mutated variant, such as the Omicron strain of SARS-CoV-2. Our findings shed new light on fundamental aspects of the humoral immune response, and can guide the design of vaccination strategies that aim to elicit broadly protective responses against mutable viruses.

After Vax 1, the limited antigen availability during GC reactions strongly promotes the dominance of the B cells that have high germline affinity or can acquire high affinity via a small number of mutations (Figure 2D). Such B cells likely target the immunodominant epitopes that are highly mutated in the variant. Upon receiving Vax 2, memory B cells generated by GCs after Vax 1 are rapidly expanded and they differentiate into plasma cells that secrete antibodies (Figures 2E and 2F). Thus, the antibodies produced after Vax 2 largely target immunodominant epitopes, and so Omicron-neutralizing titers are low (Figure 2G). These in silico results are consistent with data showing the dominant antibodies produced after the first two doses have few mutations.⁸

After Vax 2, higher amounts of antigen are displayed on FDCs. This increased antigen availability allows memory B cells that target subdominant epitopes to emerge despite their lower germline affinities (Figures 2B and 2C). These epitopes are relatively conserved between the WT and Omicron strains. After Vax 3, these memory B cells are expanded in EGCs, resulting in increased Omicron-neutralizing antibody titers (Figure 3B). This is consistent with data showing that the Omicron-neutralizing antibodies present after Vax 3 existed in the memory pool after Vax 2.⁸ Importantly, our in silico predictions are consistent with our analyses of sequence and neutralization data that we obtained from vaccinated individuals (Figure 4).

In addition to the effects of increased antigen availability, epitope masking in secondary GCs can further promote B cell response against the subdominant epitopes. However, the effects of epitope masking in the context of vaccine-induced polyclonal responses in humans is more complex than in past studies using monoclonal antibodies in mice^{25 , 26 , 27 , 28} since the overlap between epitopes targeted by polyclonal antibodies must be considered. Our in silico model incorporates the analysis of serum antibody epitope mapping data. Our findings indicate that epitope masking is likely to enhance the class 3 and 4 B cell response in secondary GCs, but the observation of Omicron-neutralizing subdominant class 1 and 2 antibodies in large numbers after Vax 3⁸³ cannot be explained only by epitope masking. Instead, this observation suggests that increased antigen availability on FDCs and epitope masking work together to promote the emergence of subdominant responses upon boosting.

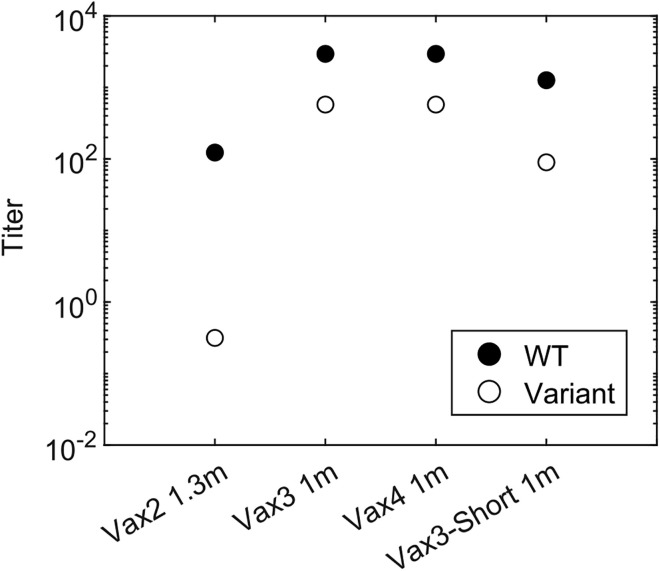
Regev-Yochay et al. reported that a fourth dose of an mRNA vaccine restored the antibody titer against Omicron to a level similar to the peak response after Vax 3, but unlike Vax 3 it did not further boost the titer compared with the previous dose.³² Results from our model are consistent with this finding (Figure 6 ). The mechanistic explanation is that GCs formed after Vax 3 do not benefit further from increased antigen availability compared with the GCs formed after Vax 2. Moreover, antibodies that target subdominant epitopes are available in higher titers soon after Vax 3 and they can mask these epitopes. Therefore, masking immunodominant epitopes confers less of an advantage to the subdominant B cells in GCs formed after Vax 3 compared with those formed after Vax 2. Thus, similar or fewer subdominant GC B cells develop after Vax 3. However, overall antibody titer after the fourth dose is still similar to Vax 3 because both GC and EGC-derived memory cells generated after Vax 3 are expanded.

Figure 6.

Comparison of antibody titers for different vaccination regimens

Antibody titer elicited by different vaccination regimens. “Vax4” refers to the case when a second booster dose was given 5 months after Vax3. “Vax3-Short” refers to the case when Vax 3 was given 1.3 months after Vax 2 instead of the standard 5-month interval. To study how epitope masking may affect the second booster (Vax 4), all cases were simulated with epitope masking and 30% epitope overlap. Titers are calculated as the antibody concentrations divided by K_d.

Although memory B cells participating in secondary GCs can help protect against closely related variants, our results show that these memory B cells can limit epitope diversification and adversely impact the ability to protect against variants that differ more significantly from the WT strain. This is because the affinity advantage of memory cells can allow them to dominate GCs. We note also that higher antigen availability and epitope masking may underlie recent observations in mice showing that memory B cells are not highly represented in secondary GCs.^{27 , 72}

Our results provide mechanistic insights into the effects of the timing of booster shots on the ability to develop variant-neutralizing antibodies. A group of subunit vaccine ZF2001 recipients who received Vax 3 only 1 month after Vax 2 were less likely to develop Omicron-neutralizing antibodies than the group with a 4-month interval (56% vs. 100%).³¹ Our model predicts (Figure 6) that when Vax 3 is given 1.3 months after the second dose (“Vax3-Short”), the subdominant epitope-targeting antibody titer is low. Most of the memory cells that have high affinities 1.3 months after Vax 2 are EGC-derived and thus target the dominant epitope (Figure 2H). Also, even subdominant GC-derived memory B cells have a relatively low affinity toward the variant due to limited time for affinity maturation (Figure 2G). As a result, receiving Vax 3 1.3 months after Vax 2 will mostly expand B cells with low cross-reactivity. But 4 months after Vax 2, more affinity maturation allows B cells with higher affinity for subdominant epitopes to develop, which is consistent with the observation that the number of mutations increases significantly between 1.3 months and 5 months after Vax 2.⁸ The memory B cells available 4 months after Vax 2 can be expanded in EGCs after Vax 3 to result in better Omicron-neutralizing capability.

Our results may also have implications for efforts to elicit broadly neutralizing antibodies (bnAbs) against HIV by sequential immunization with variant antigens.^{24 , 84 , 85} This approach aims to focus the B cell response on a conserved target epitope. Higher antigen availability and masking of the conserved epitope after booster shots will likely promote the evolution of off-target responses in secondary GCs, consistent with observations in macaques.⁸⁵ These effects may be especially significant when the conserved target epitope is quite distinct from the diverse variable regions, as is the case for some epitopes targeted by bnAbs against HIV and the conserved epitope in the stem of influenza’s spike.^{86 , 87}

The purpose of our in silico study is not detailed quantitative fitting of experimental data, but rather obtaining new mechanistic insights that we tested against clinical data. To achieve this, we adopted a simplified model that focuses on the most important aspects of the humoral immune response but omitted details that are unlikely to affect qualitative outcomes. The simplification is necessary because adding these details would increase the number of parameters and associated uncertainties without enhancing mechanistic understanding. Nonetheless, the congruence between our predictions and existing and new clinical data reported in this paper suggest that our model captures much of the relevant biology.

One interesting question is whether the different peptide epitopes presented by people with different HLA haplotypes may influence T helper cell responses, and thus affect B cell immunodominance. BCRs with different binding specificities bind to different surface epitopes on the spike protein, but if binding is sufficiently strong, regardless of B cell epitope specificity, the whole spike protein is internalized. Thus, diverse peptides derived from the entire spike protein are available for presentation by individuals with any given haplotype. The main difference between the B cells with different specificities is the amounts of antigen they internalize. Therefore, we used the amount of antigen internalized to model the competition between B cells for T cell help without considering the individual helper T cell epitopes. Consistent with this view, the B cell immunodominance observed after receiving COVID vaccines is similar among diverse individuals in the population,^{10 , 13} despite the variability of HLA subtypes and helper T cell epitope immunodominance.⁸⁸ In addition, better Omicron responses are consistently observed after the third dose in a diverse group of individuals.¹⁰

We hope that our results and mechanistic insights will motivate other fundamental studies into how the humoral immune response is influenced by antigen presentation dynamics. For example, it will be interesting to explore whether strategies to modulate antigen availability such as slow antigen delivery and immunization with immune complexes or particulate immunogens may help mitigate unwanted immunodominance hierarchies.^{22 , 89 , 90}

Limitations of the study

This study presents a potential mechanism for how B cell immunodominance is shaped, and shows that it is consistent with the analysis of clinical data. However, it does not exclude the possibility that features not included in the model may also play a role in shaping B cell immunodominance, especially through non-linear interactions with each other. For example, some of the details that are omitted by our model but can potentially influence B cell immunodominance include the existence of non-neutralizing epitopes and non-native epitopes,³⁸ the role of T cell signal strength on differentiation fates of naive and GC B cells,⁹¹ and mechanisms that control the GC lifetimes other than antigen availability.⁹²

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
Dulbecco’s Modified Eagle Medium (DMEM)	GIBCO	Cat#11995-065
Critical commercial assays
Luciferase Cell Culture Lysis 5X Reagent	Promega	Cat#E1531
Protein A biosensor	ForteBio	Cat#18-5010
Bio-Layer Interferometer	ForteBio	Octet RED96e
Nano-Glo Luciferase Assay System	Promega	Cat#N1110
Deposited data
Simulation data	This paper; Mendeley Data	https://doi.org/10.17632/39bb2273yz.1
Antibody Sequences in Figure 4	Muecksch et al.8	https://doi.org/10.17632/39bb2273yz.1
Experimental models: Cell lines
293T cells	ATCC	Cat# CRL-3216
HT1080Ace2 cells cl.14	Schmidt et al.75	https://doi.org/10.1084/jem.20201181
Recombinant DNA
pSARS-CoV-2-SΔ19(R683G)_Omicron BA.1	Wang et al.74	https://doi.org/10.1038/s41586-021-03696-9
pCR3.1 SARS-CoV SΔ19(R683G)	Schmidt et al.75	https://doi.org/10.1084/jem.20201181
Software and algorithms
ForteBio	Wang et al.74	https://doi.org/10.1038/s41586-021-03696-9
MATLAB	Mathworks	https://www.mathworks.com/products/matlab.html
Simulation and analysis algorithm in MATLAB	This paper; Mendeley Data	https://doi.org/10.17632/39bb2273yz.1

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Arup K. Chakraborty (arupc@mit.edu).

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

Cell lines

293T cells were obtained from ATCC (stock number CRL-3216; Homo sapiens; female, embryonic kidney). HT1080Ace2 cl14 cells (Homo sapiens; male, fibrosarcoma) were derived from stocks purchased from ATCC as previously described.⁷⁵ The cells were cultured as previously described.⁹³

Method details

Simulation details for antigen dynamics

Table S1 describes the reactions that govern antigen dynamics and the differential-algebraic equations derived from the reactions that are solved in the simulations. The values of initial conditions and parameters are also shown, with notes on how they were selected. The following species are involved in the dynamics: soluble antigen (Ag), soluble antibody (Ig), soluble immune complex (IC), immune complex on follicular dendritic cell (IC-FDC), and plasma cell (PC).

The simulation progresses in time steps of 0.01 day, and the concentrations are updated at each step. Since the on-rate for antigen and antibody binding is very fast (order of $k_a={10}^{11}{\mathrm{M}}^{-1}\mathrm{d}\mathrm{a}{\mathrm{y}}^{-1}$),³⁷ we assume that fast equilibrium is maintained between Ag, Ab, and IC. Thus, the equilibrium concentrations [Ag], [Ig], and [IC] can be calculated. Then, the concentrations of all species except for the PCs are updated to account for Ag decay, IC deposition on FDC, Ig production by plasma cells, IC-FDC consumption, and Ig decay, based on the differential equations described in Table S1. The PC concentration is updated based on their stochastic production and apoptosis from B cell dynamics involving GCs and EGCs. Each simulation models 200 GCs and 1 EGC simultaneously, and all the PCs derived from them contribute to the Ig kinetics. After all of the concentrations are updated at each step, the mean antibody association constant $K_a$ for the WT and the variant are updated. The governing equation is derived using the product rule as follows:

$$\begin{array}{cc}& \frac{d{K}_a}{dt}=\frac{1}{\left[Ig\right]+\left[IC\right]}\left[\frac{d\left(K_a(\left[Ig\right]+\left[IC\right]\right))}{dt}-K_a\frac{d\left(\left[Ig\right]+\left[IC\right]\right)}{dt}\right]\\ & =\frac{1}{\left[Ig\right]+\left[IC\right]}\left[\left\{K_a\left(-d_{Ig}\left[Ig\right]-k_{deposit}\left[IC\right]\right)+K_a^{PC}\left(k_{Ig}\left[PC\right]\right)\right\}-K_a\left(-d_{Ig}\left[Ig\right]-k_{deposit}\left[IC\right]+k_{Ig}\left[PC\right]\right)\right]\\ & =\frac{\left(K_a^{PC}-K_a\right)k_{Ig}\left[PC\right]}{\left[Ig\right]+\left[IC\right]}\end{array}$$ (Equation 1)

$K_a$ and $K_a^{PC}$ are the mean association constants of the existing antibodies and PCs, respectively, and $k_{Ig}$ is the rate of antibody production per plasma cell. The other parameters are described in Table S1. The derivation makes use of the fact that the change in total antibody titer, $K_d\left(\left[Ig\right]+\left[IC\right]\right)$, can be obtained from the consumption and production of the antibody species.

For Vax 1, the initial concentrations for IC, IC-FDC, and PC are set to zeros and the initial concentration for Ag is set to 10 nM to represent a bolus injection of antigen. There will be only a small number of weakly-binding antibodies to the new immunogen, so $\left[Ig\right]$ and $K_a=1/K_d$ are initially set to small values. These values and other parameters in Table S1 are picked from reasonable physiological ranges based on the literature.^{33 , 63 , 78 , 79} While there are uncertainties about the true underlying biological values, the physical significances of these initial values and parameters are in determining the level of antigen availability in the lymph node. In our model, the antigen availability depends on the reference antigen concentration $C_0$ because antigen capture by B cells depends on the normalized antigen availability $\frac{C}{C_0}$, where $C$ is the amount of antigen in the lymph node. Thus, by changing $C_0$, we can study the effect of changing antigen availability in the system. As mentioned in the main figures and shown in Figure S4A, we tested the robustness of the results on varying $C_0$.

For Vax 2, Vax 3, and Vax 4, the initial concentrations of the species are set to the values determined by response to the previous vaccination.

Simulation details for B cells and 2-epitope model

As described in the main text, the dynamics of B cells are simulated with an agent-based model. Each B cell is an agent that has the following properties: type, lineage, target epitope, mutational state, and binding affinities. At each time point, the B cells stochastically undergo different actions based on their properties and the conditions of the simulation. The details of the model are described below, and the simulation algorithm is summarized in Table S3. Table S2 summarizes the parameters used in the simulations. It shows which equations the parameters appear in, their descriptions, values, and notes about how those values were selected.

Each simulation models 200 GCs simultaneously. Each GC is associated with a pool of naive B cells that have not yet entered the GC. The number of total naïve B cells in humans is estimated^{94 , 95} to be about $1\times {10}^{10}$, and the frequency of SARS-CoV-2 RBD-specific naïve B cells³⁹ is about 1 in $3\times {10}^4$. Thus, we assume that the number of naïve B cells for each GC is $N_{naive}=\left(1\times {10}^{10}\right)/\left(3\times {10}^4\right)/200\cong 2000$ cells. These naïve B cells have germline-endowed WT-binding affinities, whose possible values are $E_k=6+0.2k\left(k=0...10\right)$. These affinities correspond to $-{\log }_{10}{K}_d$. The distribution of the naïve B cells over the possible values is determined by three parameters: $E_1^h,d{E}_{12},p$. Higher-affinity B cells should be rarer, so the frequency of B cells is determined analogously to a truncated geometric distribution (see Figure S1A for the schematics). The frequency of naïve B cells that target the dominant and subdominant epitopes are as follows:

$$f_{dominant}\left(E_k\right)=N_{naive}\left(1-p\right)\frac{e^{{-r}_1\left(E_k-E_0\right)}}{\sum _k{e}^{{-r}_1\left(E_k-E_0\right)}}$$ (Equation 2)

$$f_{subdominant}\left(E_k\right)=N_{naive}p\frac{e^{{-r}_2\left(E_k-E_0\right)}}{\sum _k{e}^{{-r}_2\left(E_k-E_0\right)}}$$ (Equation 3)

$p$ is the fraction of naïve B cells that target the subdominant epitope, and $r_1$, $r_2$ in the exponents are specified by the parameters $E_1^h$ and $d{E}_{12}$ from the following relationships.

$$f_{dominant}\left(E_1^h\right)/\left(1-p\right)=1$$ (Equation 4)

$$f_{subdominant}\left(E_1^h-d{E}_{12}\right)/p=1$$ (Equation 5)

That is, $E_1^h$ and $E_1^h-d{E}_{12}$ are the affinities at which the frequency of naïve B cells that target the dominant and subdominant epitopes respectively would be 1 cell per GC, before adjusting for the total frequency (Figure S1A). For each GC, the exact number of naive B cells that have germline affinity equal to $E_k$ is determined by stochastically rounding up or rounding down $f_{dominant}(E_k$) and $f_{subdominant}\left(E_k\right)$ to the nearest integer, using the fractional part as the probability of rounding up. Very high-affinity naive B cells have precursor frequencies of less than 1 per GC (Figure S1A), so they will exist only for some of the GCs.

Each naive B cell also has a germline-endowed binding affinity against the variant strain. Immunization with the WT strain will recruit naive B cells with high WT-binding affinities; even the naive B cells with the lowest WT-binding affinity in the pool ($E_0=6$) still represents the top 1 in $\sim 3\times {10}^4$ of all naïve B cells in the human repertoire. The binding affinity of these naïve B cells against the variant will likely be lower. Thus, we assume that all naïve B cells have germline binding affinity of $-{\log }_{10}{K}_d=6$ against the variant, equal to the lowest value of binding affinity against the WT, and that required for GC entry.³⁷

During affinity maturation, the affinities of B cells change as they accumulate mutations. To account for mutations, each naïve B cell is represented as a string of 0’s with length $n_{res}$, and an affinity-affecting mutation to a GC B cell changes the value of one randomly selected residue from 0 to 1 or from 1 to 0. Each residue that has a value of 1 changes the binding affinity towards the WT and the variant by pre-determined amounts. These amounts, which are analogous to the fitness landscape of the B cell, are drawn from a correlated probability distribution. Figure S1B schematically shows how the affinities are determined for GC B cell, $i$. The binding affinities against the WT and the variant are determined as

$$E_i^{wt}=E_i^{0,wt}+\sum _{j=1}^{n_{res}}{\delta }_{i,j}{s}_{i,j}^{wt}$$ (Equation 6)

$$E_i^{var}=E_i^{0,var}+\sum _{j=1}^{n_{res}}{\delta }_{i,j}{s}_{i,j}^{var}$$ (Equation 7)

where $E_i^{0,wt}$ and $E_i^{0,var}$ are the germline affinities towards the WT and the variant, respectively; ${\delta }_{i,j}\in \left\{\mathrm{0,1}\right\}$ is the mutational state of residue $j$; and $s_{i,j}^{wt}$ and $s_{i,j}^{var}$ are the effects of the mutation at residue $j$ on the binding affinities against the WT and the variant, respectively. $s_{i,j}^{wt}$ and $s_{i,j}^{var}$ are sampled from the following shifted log-normal distribution, independently for each residue $j$, at the initiation of the simulation.

$${[s}_{i,j}^{wt},s_{i,j}^{var}]\sim e^{N\left(\mu ,{\sigma }^2\mathrm{\Sigma }\right)}-ϵ$$ (Equation 8)

The parameters $\mu ,\sigma ,ϵ$ are chosen to fit experimentally determined distribution, where ∼5% of affinity-affecting mutations are beneficial while most of the mutations are strongly deleterious (Figure S1C).^{42 , 43} The covariance has the form

$$\mathrm{\Sigma }=\left[\begin{array}{cc}1& \rho \\ \rho & 1\end{array}\right]$$ (Equation 9)

where $\rho$ represents the level of conservation of an epitope between the WT and variant. As $\rho$ increases, mutations that are beneficial for binding both strains become more common (Figure S1D). We choose $\rho =0.95$ for the subdominant epitope and $\rho =0.4$ for the dominant epitope. For B cells that target the subdominant and dominant epitope, respectively 72% and 19% of mutations that are beneficial for binding the WT are also beneficial for binding the variant, and vice versa. Since B cells are selected in GCs based on their WT-binding affinities, an increase in variant-binding affinities mainly occurs through the accumulation of mutations that increase affinities against both strains. Hence, B cells that target the subdominant epitope are more likely to develop high cross-reactivity for the variant than those that target the dominant epitope.

Simulation details for germinal center entry of naive B cells

At each time step, the amount of antigen captured by naive B cells is determined based on their WT-binding affinities and the effective antigen concentration in the lymph node, $C\text{.}$ For B cell $i$, this amount, $A_i$, is determined as follows:

$$A_i={\left(\frac{C}{C_0}{10}^{\left(\min \left(E_i^{WT},10\right)-E_0\right)}\right)}^K$$ (Equation 10)

$E_i^{WT}$ is the WT-binding affinity of B cell $i$. The amount of antigen captured increases with $E_i^{WT}$, but saturates at affinities higher than $E_i^{WT}=10$ because of the affinity ceiling.⁹⁶ A similar model of antigen capture has been used in several previous studies.^{20 , 24 , 56 , 97} B cells can see both the soluble antigen and the antigen presented on FDCs, but the latter is known to be about 2 orders of magnitude more potent at activating B cells due to multivalent presentation.⁹⁸ Therefore, the effective antigen concentration $C$ is calculated as $C=0.01\left(\left[Ag\right]+\left[IC\right]\right)+\left[IC-FDC\right]$. The parameter $K$ determines how much a given difference in concentration or affinity changes the amount of antigen internalized by a B cell. If $K$ is large, then even a small difference in concentration or affinity results in large difference in the amount of antigen internalized, which in turn affects the probability of activation and positive selection by T helper cells. Thus, $K$ represents the stringency of selection. We studied varying $K$ to test the robustness of the results, since stringency of selection is known to affect the diversity of B cells that develop in GCs⁵⁰ (Figure S3D).

Naive B cells that capture enough antigen can be activated.³⁷ In our simulation, whether B cell $i$ is activated at each time step is determined probabilistically as follows:

$$\mathrm{Pr}\left(\mathrm{B}\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}i\mathrm{i}\mathrm{s}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}\right)=\min \left(A_i,1\right)$$ (Equation 11)

The entry of activated naive B cells to GCs is limited by competition for positive selection by helper T cells, and B cells that have internalized greater amounts of antigen have better chances of successfully entering GCs.^{48 , 49} Thus, the rate of entry for an activated B cell $i$, ${\lambda }_i$, and the probability that it enters GC during a time step are given as follows:

$${\lambda }_i=\frac{\frac{N_{\mathit{max}}}{N_{activated}}\frac{A_i}{⟨A⟩}}{1+\frac{N_{\mathit{max}}}{N_{activated}}\frac{A_i}{⟨A⟩}}$$ (Equation 12)

$$\mathrm{Pr}\left(\mathrm{B}\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}i\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{G}\mathrm{C}\right)=1-e^{-{\lambda }_{i}dt}$$ (Equation 13)

$N_{activated}$ is the total number of activated B cells, $⟨A⟩$ is the average amount of antigen captured by all activated B cells, and $N_{\mathit{max}}$ is the capacity for entry that represents the limited amount of T cell help. $N_{\mathit{max}}$ is selected so that about ten distinct naive B cells will enter the GC per day, consistent with the literature.⁶⁴ The assumption that $N_{\mathit{max}}$ is fixed is conservative because higher antigen availability is known to increase naive B cell recruitment to GCs,²³ which would only further strengthen our finding that secondary GCs produce more diversity. When a naive B cell enters GC, it simultaneously proliferates twice, so that a total of 4 identical B cells are added to the GC.

Alternative model for antigen capture

According to Equation 10, the amount of antigen captured by B cells continues to increase with antigen concentration and B cell affinity. However, it is possible that the amount of antigen captured plateaus when antigen concentration and B cell affinity are very high.⁴⁶ Therefore, we studied how using an alternative model where antigen capture saturates at high affinities and antigen concentrations affects our findings. Under this model, the amount of antigen captured is determined as:

$$A_i=\frac{\left(H+1\right)\frac{C}{C_0}{10}^{\left(\min \left(E_i^{WT},10\right)-E_0\right)}}{H+\frac{C}{C_0}{10}^{\left(\min \left(E_i^{WT},10\right)-E_0\right)}}$$ (Equation 14)

When $H\to \infty$, this formulation becomes equivalent to Equation 10 with K = 1. For a finite value of $H$, $A_i$ saturates to $H+1$ when $\frac{C}{C_0}{10}^{\left(\min \left(E_i^{WT},10\right)-E_0\right)}\gg H$. When $H$ is smaller and antigen availability is higher, the affinity at which saturation will occur will be lower, making the selection of B cells permissive. We studied the effect of varying $H$ on our findings (Figure S4E).

Simulation details for GCs

Each simulation models 200 GCs simultaneously. Plasma cells generated from all GCs collectively determine antibody production, which affects antigen transport and epitope masking, and memory B cells generated from all GCs seed the EGC upon subsequent vaccination. The birth, death, mutation, and differentiation of GC B cells occur stochastically at each time step. The model implicitly treats migration between GC light zone and dark zone, but such a model has been shown to recapitulate qualitative GC dynamics well.^{20 , 56 , 99 , 100}

GC B cells capture antigen and become stochastically activated in the same way as the naive B cells. Activated GC B cells compete for positive selection signals from helper T cells. The rate of positive selection for a GC B cell $i$, ${\beta }_i$, and the probability that it gets positively selected during a time step are given as:

$${\beta }_i={\beta }_{\mathit{max}}\frac{\frac{N_T}{N_{activated}}\frac{A_i}{⟨A⟩}}{1+\frac{N_T}{N_{activated}}\frac{A_i}{⟨A⟩}}$$ (Equation 15)

$$\mathrm{Pr}\left(\mathrm{G}\mathrm{C}\mathrm{B}\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}i\mathrm{i}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{l}\mathrm{y}\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d}\right)=1-e^{{-\beta }_{i}dt}$$ (Equation 16)

where ${\beta }_{\mathit{max}}$ is the maximum rate of positive selection, $N_{activated}$ is the number of activated GC B cells, and $N_T$ is the number of helper T cells. Thus, $\frac{N_T}{N_{activated}}$ represents the physical availability of helper T cells to GC B cells, and $\frac{A_i}{⟨A⟩}$ represents the competitive advantage of B cell $i$ compared with other activated GC B cells. B cells internalize the whole spike protein despite binding to potentially different surface epitopes. Thus, each B cell that internalize antigen present diverse peptides derived from the protein to helper T cells. The main difference between the B cells is the amount of antigen they present. Therefore, we model the competition based on the amount of antigen without considering individual T cell epitopes, similar to previous models of affinity maturation.^{20 , 24 , 57 , 97}

Clinical data from SARS-CoV-2 vaccinated subjects showed that the number of CD4⁺ T cells peaked about 2 weeks after vaccination and decayed with a half-life of ∼47 days.⁵⁴ For simplicity, we model $N_T$ as simple linear growth up to $t_0=14days$, followed by first-order decay afterward with rate $d_T$ as follows:

$$N_T\left(t\right)=\{\begin{array}{c}\frac{t}{t_0}{N}_{T0}\left(t<t_0\right)\\ N_{T0}{e}^{-d_T\left(t-t_0\right)}\left(t>t_0\right)\end{array}$$ (Equation 17)

$N_{T0}$ is the peak level of non-dimensionalized T cell availability, and is chosen to give a mean peak GC size of ∼1000 cells/GC.

A positively selected B cell exits a GC with a probability $p_1$, and then differentiates into a PC with a probability $p_2$ or into a memory cell with a probability $1-p_2$. The remaining selected B cells proliferate once and one of the daughter cells mutates, as described in the main text.

At the end of the time step, all GC B cells are subject to stochastic apoptosis with a rate $\alpha$. The probability of apoptosis is given as:

$$\mathrm{Pr}\left(\mathrm{G}\mathrm{C}\mathrm{B}\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}i\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{o}\mathrm{e}\mathrm{s}\mathrm{a}\mathrm{p}\mathrm{o}\mathrm{p}\mathrm{t}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{s}\right)=1-e^{-\alpha dt}$$ (Equation 18)

Similarly, plasma cells from both GCs and EGCs also undergo stochastic apoptosis at a rate $d_{PC}$, so that the probability of apoptosis is given as:

$$\mathrm{Pr}\left(\mathrm{P}\mathrm{C}i\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{r}\mathrm{g}\mathrm{o}\mathrm{e}\mathrm{s}\mathrm{a}\mathrm{p}\mathrm{o}\mathrm{p}\mathrm{t}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{s}\right)=1-e^{-d_{PC}dt}$$ (Equation 19)

Clinical sample collection and analysis methods

Data used in Figure 4 are derived from B cell sequences reported in Table S2 of Muecksch et al., which contains sequences of B cells isolated from SARS-CoV-2 mRNA-vaccinated subjects.⁸ Phylogenetic trees were generated from these B cell clonal families using MATLAB’s seqlinkage function. EGC-derived B cells were identified by applying the classification method described in the main text and in the next section. Then, using the monoclonal antibodies that correspond to these B cells based on the protein sequences (reported in Table S3 of Muecksch et al.), the WT and Omicron-neutralizing activity (IC₅₀) of these sequences were measured, except for three antibodies for which both values were already reported in the Tables S4 and S5 of Muecksch et al. The measurements were performed as previously described.^{8 , 74 , 75} We additionally measured the neutralization activity of 26 randomly-selected singlets that were found 5 months after Vax 2, to compare with the EGC-derived antibodies. Table S4 describes the neutralization activities of the EGC-derived antibodies used in this study.

The statistical analyses to compare the neutralization activity of EGC- and GC-derived antibodies were performed based on the logarithm of IC₅₀ data. We used the two-sample t test to calculate the statistical significance (p value) of the difference in the mean values between the two groups. The degrees of freedom were conservatively estimated using the smaller sample size of the two samples, so that it was given as one less than the number of sequences in the smaller group. The analysis was performed to compare Vax 2 EGC-derived cells with Vax 2 GC-derived cells, and to compare Vax 2 EGC-derived cells with Vax 3 EGC-derived cells.

Sensitivity and precision of the Inference of EGC-derived memory cells

A B cell was identified as EGC-derived if it satisfied at least one of the two conditions below.

• (1)Criteria 1: At least one other identical sequence was sampled at the same time
• (2)Criteria 2: At least one identical sequence was sampled at an earlier time

Assume that after secondary immunization, the sets of unique memory B cell sequences derived from GC and EGC are ${\mathbb{S}}_{GC}=\left\{s_1^{GC},\dots ,s_K^{GC}\right\}$ and ${\mathbb{S}}_{EGC}=\left\{s_1^{EGC},\dots s_K^{EGC}\right\}$, respectively. Without the loss of generality, let the number of GC-derived memory B cells that have sequences $s_1^{GC},\dots ,s_K^{GC}$ to be $m_1>\dots >m_K$ for GC-derived cells. Similarly, let the number of EGC-derived memory B cells that have sequences $s_1^{EGC},\dots s_K^{EGC}$ to be $n_1>\dots >n_K$ for EGC-derived cells. $K$ is a sufficiently large number. If the actual number of GC-derived unique sequences is smaller than $K$, then $n_i$ will be zero for some large values of $i$. The same is true for EGC-derived sequences.

The sequences $s_1^{EGC},\dots s_K^{EGC}$ must be identical to the sequences derived from the GC of the primary immunization. Let the numbers of B cells from the prime GC that correspond to these sequences be $l_1,\dots ,l_K$.

Suppose that total of $S$ sequences are sampled each after the secondary immunization and the primary immunization. Let these sequences be $\mathbb{S}=\left\{s_1,\dots s_S\right\}$ and ${\mathbb{S}}_p=\left\{s_{1,p},\dots s_{S,p}\right\}$, respectively. Based on the two criteria, a B cell $i$ sampled after secondary immunization is labeled as EGC-derived if and only if

$$s_i\in {\mathbb{S}}_{\setminus i}\cup {\mathbb{S}}_p$$

where ${\mathbb{S}}_{\setminus i}=\left\{s_1,..,s_{i-1},s_{i+1},\dots ,s_S\right\}$ is defined as the set of sequences in $\mathbb{S}$ excluding $s_i$.

The sensitivity, or true positive rate, of the classification is defined as the following expected value:

$$TPR=\mathrm{{\rm E}}\left[\frac{n_{TP}}{n_{TP}+n_{FN}}\right]$$

where $n_{TP}$ and $n_{FN}$ are the number of true positives and false negative in the labeled samples. A true positive sample is an EGC-derived sequence labeled as EGC-derived, and false positive is an EGC-derived sequence labeled as GC-derived.

An equivalent definition for sensitivity is the probability that an EGC-derived sequence will be labeled correctly as EGC-derived. That is,

$$\mathrm{T}\mathrm{P}\mathrm{R}=\mathrm{Pr}\left(s_i\in {\mathbb{S}}_{\setminus i}\cup {\mathbb{S}}_p|s_i\in {\mathbb{S}}_{EGC}\right)$$ (Equation 20)

Let $\sum _{j=1}^K{n}_j=N$, $\sum _{j=1}^K{m}_j=M$, $\sum _{j=1}^K{l}_j=L$. Then, the sensitivity can be calculated as

$$\begin{array}{cc}TPR& =1-\mathrm{Pr}\left(s_i\notin {\mathbb{S}}_{\setminus i}\cup {\mathbb{S}}_p|s_i\in {\mathbb{S}}_{EGC}\right)\\ & =1-\sum _{j=1}^K\mathrm{Pr}\left(s_j^{EGC}\notin {\mathbb{S}}_{\setminus i}\cup {\mathbb{S}}_p|s_i=s_j^{EGC}\right)\mathrm{Pr}\left(s_i=s_j^{EGC}|s_i\in {\mathbb{S}}_{EGC}\right)\\ & =1-\sum _{j=1}^K\mathrm{Pr}\left(s_j^{EGC}\notin {\mathbb{S}}_{\setminus i}\cup {\mathbb{S}}_p|s_i=s_j^{EGC}\right)\mathrm{Pr}\left(s_j^{EGC}\notin {\mathbb{S}}_p|s_i=s_j^{EGC}\right)\mathrm{Pr}\left(s_i=s_j^{EGC}|s_i\in {\mathbb{S}}_{EGC}\right)\\ & =1-\sum _{j=1}^K\begin{array}{c}\frac{{\mathcal{C}}_{S-1}^{N+M-n_j}}{{\mathcal{C}}_{S-1}^{N+M}}\frac{{\mathcal{C}}_S^{L-l_j}}{{\mathcal{C}}_S^L}\frac{n_j}{N}\end{array}\\ & \triangleq 1-\sum _{j=1}^K\frac{n_j}{N}Q\left(n_j,S\right)Q^{\prime }\left(l_j,S\right)\end{array}$$ (Equation 21)

where $Q\left(n_j,S\right)=\frac{\left(N+M-S+1\right)}{\left(N+M\right)}\frac{\left(N+M-S\right)}{\left(N+M-1\right)}\dots \frac{\left(N+M-n_j-S+2\right)}{\left(N+M-n_j+1\right)}$, $Q^{\prime }\left(l_j,S\right)=\frac{\left(L-S\right)}{L}\frac{\left(L-S-1\right)}{\left(L-1\right)}\dots \frac{\left(L-S-l_j+1\right)}{\left(L-l_j+1\right)}$

$Q\left(n_j,S\right)$ decreases with $n_j$ and $S$. Thus, the sensitivity will be high if most B cells belong to largely expanded sequences, and if the sampling number is large. $Q^{\prime }\left(l_j,S\right)$ decreases with $l_j$ and $S$. Thus, the sensitivity will be high if for the values of $j$ such that $n_j$ is large, $l_j$ is also large.

The precision, or positive predictive value, of the classification is defined as

$$PPV=\mathrm{{\rm E}}\left[\frac{n_{TP}}{n_{TP}+n_{FP}}\right]$$

where $n_{FN}$ is the number of false positives, or GC-derived B cells labeled as EGC-derived. An equivalent definition for precision is the probability that an EGC-labeled B cell is a true EGC-derived B cell.

$$PPV=\mathrm{Pr}\left(s_i\in {\mathbb{S}}_{EGC}|s_i\in \left({\mathbb{S}}_{prev}\cup {\mathbb{S}}_{\setminus i}\right)\right)$$ (Equation 22)

Using Bayes’ rule,

$$\begin{array}{cc}PPV& =\frac{\mathrm{Pr}\left(s_i\in \left({\mathbb{S}}_{prev}\cup {\mathbb{S}}_{\setminus i}\right)|s_i\in {\mathbb{S}}_{EGC}\right)\mathrm{Pr}\left(s_i\in {\mathbb{S}}_{EGC}\right)}{\mathrm{Pr}\left(s_i\in \left({\mathbb{S}}_{prev}\cup {\mathbb{S}}_{\setminus i}\right)\right)}\\ & =\frac{\mathrm{Pr}\left(s_i\in \left({\mathbb{S}}_{prev}\cup {\mathbb{S}}_{\setminus i}\right)|s_i\in {\mathbb{S}}_{EGC}\right)\mathrm{Pr}\left(s_i\in {\mathbb{S}}_{EGC}\right)}{\mathrm{Pr}((s_i\in \left({\mathbb{S}}_{prev}\cup {\mathbb{S}}_{\setminus i}\right)|s_i\in {\mathbb{S}}_{EGC}))\mathrm{Pr}(s_i\in {\mathbb{S}}_{EGC})+\mathrm{Pr}((s_i\in \left({\mathbb{S}}_{prev}\cup {\mathbb{S}}_{\setminus i}\right)|s_i\in {\mathbb{S}}_{GC}\left)\right)\mathrm{Pr}(s_i\in {\mathbb{S}}_{GC})}\\ & =\frac{TPR\left(\frac{N}{N+M}\right)}{TPR\left(\frac{N}{N+M}\right)+\left(1-\sum _{j=1}^K\frac{m_j}{N}Q\left(m_j,S\right)\right)\left(\frac{M}{N+M}\right)}\end{array}$$ (Equation 23)

Assuming that $N$ and $M$ are similar, high precision is reached if the values of $Q\left(m_j,S\right)$ are large for the GC-derived B cells. Since $Q\left(m_j,S\right)$ increases with decreasing $m_j$, precision is high if many GC-derived sequences have similar sizes.

We applied this analysis to the data from simulations to find the sensitivity and precision of the method. We also tested the analysis against Monte-Carlo sampling of sequences from the simulations. For this, we sampled equal numbers of memory B cells from 1 month after Vax 1 and 5 months after Vax 2. Then we applied the labeling method and calculated the number of true positives, false negatives, and false positives. This was repeated 1000 times to calculate the mean sensitivity and precision.

Epitope masking

When epitope masking is considered in the simulations, B cells can only see free antigen. The total amount of antigen in a lymph node is $\left[Ag\right]+\left[IC\right]+\left[IC-FDC\right]={\left[Ag\right]}_{tot}$. Let us use subscripts 1 and 2 to denote antibodies that target the dominant and subdominant epitopes, respectively, and let $q$ be the epitope overlap. The effective concentration and mean binding affinity of the antibodies that cover the dominant epitope are ${\left[I{g}_1\right]}_{eff}=\left[I{g}_1\right]+q\left[I{g}_2\right]$ and $\frac{1}{K_{d1,eff}}=\left(\frac{\left[I{g}_1\right]}{K_{d,1}}+\frac{q\left[I{g}_2\right]}{K_{d,2}}\right)/{\left[I{g}_1\right]}_{eff}$, respectively. Using these values, the free antigen concentration for the dominant epitope, ${\left[Ag\right]}_{tot,1}$, can be calculated from the following equilibrium.

$$K_{d1,eff}=\frac{{\left[Ag\right]}_{tot,1}{\left[I{g}_1\right]}_{eff}}{{\left[Ag\right]}_{tot}-{\left[Ag\right]}_{tot,1}}$$ (Equation 24)

Here, we used the fact that typically ${\left[I{g}_1\right]}_{eff}\gg {\left[Ag\right]}_{tot}$ to approximate the free antibody concentration. Finally, to calculate the effective free antigen concentration for the dominant epitope, $C_{eff,1}$, we must adjust for the fractions of the free antigen that are soluble or on FDC as follows:

$$C_{eff,1}={\left[Ag\right]}_{tot,1}\left\{0.01\frac{\left[Ag\right]+\left[IC\right]}{{\left[Ag\right]}_{tot}}+\frac{\left[IC-FDC\right]}{{\left[Ag\right]}_{tot}}\right\}$$ (Equation 25)

The effective free antigen concentration for the subdominant epitope can be calculated similarly. Note that although ICs are tethered to FDC, we treat them as free antigen unless it is additionally covered by serum antibody, similar to the computational model from a previous study.⁸⁰ In the experimental part of this study, mice were immunized with 4-hydroxy-nitrophenyl coupled to chicken gamma globulin (NP-CGG) along with NP-specific antibodies so that the ICs were deposited on FDCs. These ICs on FDCs elicited NP-specific serum response, suggesting that the NP epitope was not blocked by the tethering of IC to FDC.

Quantification and statistical analysis

For GC simulations, 200 GCs were simulated simultaneously to mimic a lymph node. The B cells from all GCs were pooled from each simulation before analysis. The stochastic simulation was repeated 10 times using unique seeds for the random number generator in MATLAB. The mean values are reported in Figures 2, 3, 5, and 6. Two-sample t test was used to compare the EGC- and GC-derived antibody IC₅₀ mean values in Figure 4 and calculate the p value.

Published: March 6, 2023

Data and code availability

• •Simulation data have been deposited at Mendeley Data:https://doi.org/10.17632/39bb2273yz.1 and are publicly available.
• •All original code has been deposited at Mendeley Data:https://doi.org/10.17632/39bb2273yz.1 and is publicly available.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.