Abstract
Fluorescence lifetime imaging captures the spatial distribution of chemical species across cellular environments employing pulsed illumination confocal setups. However, quantitative interpretation of lifetime data continues to face critical challenges. For instance, fluorescent species with known in vitro excited-state lifetimes may split into multiple species with unique lifetimes when introduced into complex living environments. What is more, mixtures of species, which may be both endogenous and introduced into the sample, may exhibit 1) very similar lifetimes as well as 2) wide ranges of lifetimes including lifetimes shorter than the instrumental response function or whose duration may be long enough to be comparable to the interpulse window. By contrast, existing methods of analysis are optimized for well-separated and intermediate lifetimes. Here, we broaden the applicability of fluorescence lifetime analysis by simultaneously treating unknown mixtures of arbitrary lifetimes—outside the intermediate, Goldilocks, zone—for data drawn from a single confocal spot leveraging the tools of Bayesian nonparametrics (BNP). We benchmark our algorithm, termed BNP lifetime analysis, using a range of synthetic and experimental data. Moreover, we show that the BNP lifetime analysis method can distinguish and deduce lifetimes using photon counts as small as 500.
Significance
We introduce a method of Bayesian nonparametrics lifetime analysis to infer lifetimes and photon ratios in a single confocal spot. The Bayesian nonparametrics lifetime analysis method is capable of learning a wide range of lifetimes from below the instrumental response function to comparable to the laser interpulse window.
Introduction
Amid a number of fluorescence microscopy techniques (1,2,3,4,5,6,7,8), fluorescence lifetime imaging microscopy (FLIM) has extensively contributed to our understanding of subcellular structures and processes (9,10,11,12,13,14,15,16). In FLIM experiments within a biological sample, multiple biomolecules may be labeled with unique fluorophores characterized by different lifetimes (17,18,19,20). To deduce how these labels are spatially distributed, a single (confocal) spot within the sample is exposed to either modulated (21,22) or pulsed (23,24) excitation with the excitation spot eventually scanned across the sample. Here, we focus on pulsed illumination since it provides time-stamped photon arrivals (and helps reduce phototoxicity). A train of such illumination pulses is shown in Fig. 1 a.
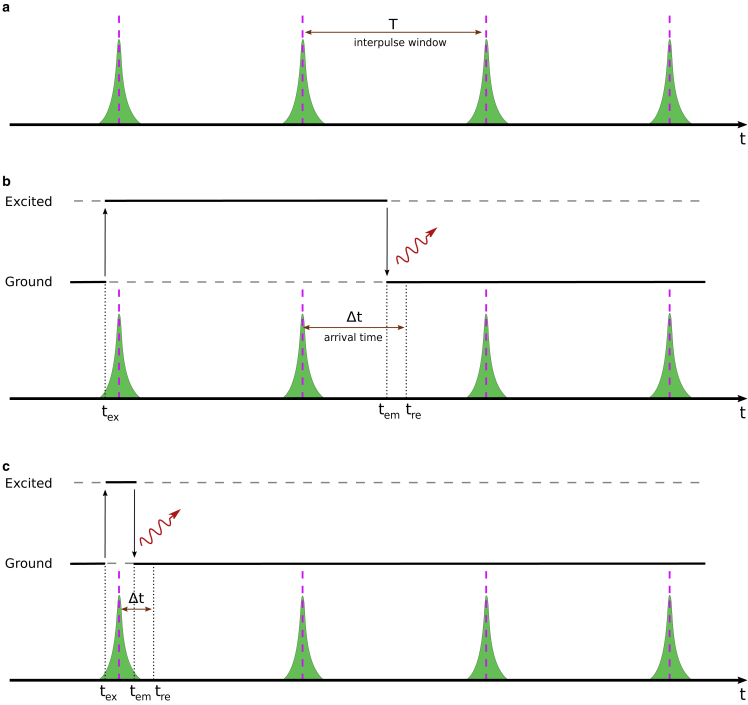
Figure 1.
A cartoon representation of laser pulses, designated by green spikes, and fluorophore excitation and emission. (a) A train of laser pulses with interpulse window . The pink dashed lines represent the pulse centers. (b) Fluorophores can be excited during laser pulses and may emit photons after multiple pulses due to long excited-state lifetimes compared with the interpulse windows. Indeed, even lifetimes on par with the interpulse time can appear after the subsequent pulse with probability . (c) For fluorophores with lifetimes shorter than the IRF, an excited fluorophore might emit photons even before the excitation pulse is complete. Here, , and , respectively, stand for excitation, emission times, and the recorded photon arrival time. The difference between emission and recorded times arises from the stochastic delay in detectors that, combined with the finite breadth of the laser pulse, is termed the IRF.
Once excited by a pulse, fluorophores emit photons whose arrival times at the detector are recorded and used to infer lifetimes and corresponding photon ratios across species for each spot (25,26,27). By photon ratios, we mean the probability (weight) that any given photon will be emitted by each species within the confocal area probed. The photon ratio is itself related to the product of concentration of the species and excitation cross section.
To deduce weights (photon ratios) and lifetimes present from photon arrival time data, analysis methods employ either model free techniques, such as phasors (26,28) and deep learning (29,30), or model-based techniques, such as least-squares (31,32), compressed sensing (33), maximum likelihood (34,35), and Bayesian methods (27,36,37,38,39).
However, existing analysis methods are optimized for two well-separated lifetimes typically longer than the instrument response function (IRF) (see Fig. 1) but otherwise much shorter than the interpulse window. This regime of lifetimes can be difficult to control in vivo, as lifetimes invariably drift in response to the local environment chemistry whose composition may further split apparent single lifetimes into multiple different lifetimes (40,41,42). In addition, existing lifetime analysis methods, starting from the single spot/pixel, face several other key challenges including 1) requiring the number of lifetime components as input otherwise often truncated for simplicity to two species (29,30,33,34,35,36,37,38); 2) require high photon budgets due to information averaging arising from data preprocessing, e.g., data binning (31,32,43); and 3) provide full uncertainty over the estimated parameters originating from unavoidable sources of stochasticity including random excitation times introduced by the IRF’s finite breadth and exponential waiting times for excited-state lifetimes (29,30,31,32,33,34,35).
To address these challenges, we begin by considering photon arrival times. These photon arrival times are essentially a mixture of temporal data points generated from multiple different sources, namely fluorophore species, characterized by their lifetimes. As such, mathematically, the output of a pulsed excitation experiment may be conceptualized as generating data drawn from a mixture model where the ultimate goal of an analysis method would be to classify the arrival times into multiple categories corresponding to the underlying fluorophore species. More broadly, such classification tasks fall within the purview of clustering algorithms. For instance, K-means (44) is perhaps the simplest and most popular clustering algorithm classifying a set of input data points into a given number, , of clusters.
However, as the number of lifetime components is inherently unknown in photon arrival analysis, we need to evoke more sophisticated clustering algorithms.
To be precise, to correctly propagate inherent uncertainties, we work within a Bayesian paradigm where our inference is informed by sources of uncertainty including intrinsic stochasticity in the photon arrival times, finite breadth of IRF, and finite interpulse time. Moreover, we further specialize working within a Bayesian nonparametric (BNP) paradigm to accommodate the unknown number of fluorophore species.
In particular, within BNPs, we leverage Dirichlet processes (45,46,47,48,49) to allow inference over the number of species warranted by the data while rigorously propagating uncertainty from all the existing sources throughout the problem.
The Dirichlet process formally allows us to place priors on an infinite number of putative species that could be warranted by the data (45,46,47,48,49). As we will see, as we collect data, weights associated to species contributing to the data will increase, while the weights ascribed to other species will reduce to negligible values (see Fig. 2).
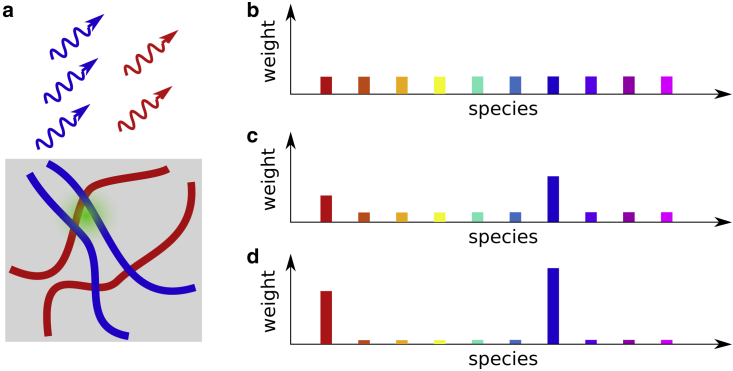
Figure 2.
The Dirichlet process for lifetime analysis. (a) A spot within a sample is illuminated with a green laser that, in turn, leads to photons from red and blue fluorophore species staining different structures within the sample. The set of collected photon arrival times from this experiment is modeled with a Dirichlet process with the first 10 species, represented by 10 different colors, shown. (b) When no photon arrival times have yet been collected, the weights ascribed to all species coincide with the prior value (often it is reasonable to assume uniform). (c) When 500 photon arrival times have been collected, the weights start differing from the nominal prior value, and, in this cartoon, the blue and red species gain more weights. (d) At 5000 photon arrival times, most of the weights are ascribed to the blue and red species, while the rest tend toward negligible values.
Here, building upon our previous work (27,39), we propose a BNP lifetime analysis (BNP-LA) method. This method leverages the Dirichlet process along with an accurate likelihood model, informed by features such as IRF and pulsed excitation (see Fig. 1, b–c), to simultaneously address all the following challenges: it is capable of dealing with a broad range of lifetimes ranging from values smaller than the IRF width to comparable to the interpulse time while addressing the challenges 1–3 above.
Before moving on to the results, a word on nomenclature is warranted. “Species” here is defined as it normally is in the FLIM literature, i.e., as exponential components (1,2). We thus inherit all advantages and disadvantages of this definition. This nomenclature is historically motivated by the fact that many fluorophore lifetime histograms are beautifully fit to a single exponential (36,39). As such, we may be (incorrectly) inclined to assume that a species is a chemically distinct molecule. Indeed, we need to be careful as there exist cases where the lifetime may differ from exponential (50,51,52) and be, say, bi-exponential. This is the case where two radiative pathways are available for de-excitation. In this case, the literature would define these as two “species.”
Materials and methods
In this section, we illustrate our likelihood model formulation and inverse strategy. We begin with the likelihood for a set of given photon arrival times
| (1) |
where is the likelihood for the th photon arrival time. The indicator parameter allocates photons to different species, and and , respectively, denote the inverse of the lifetime and the th photon arrival time. The bars over parameters denote the set of parameters for all photons, for example .
The likelihood for the th photon arrival time, assuming the photon is from a species indicated by , can be derived by considering that is the sum of three random variables (also see Eq. 13): 1) the time the fluorophore spent in the excited state sampled from an exponential distribution; 2) the stochastic time added due to the IRF sampled from a Gaussian distribution; and 3) the number of pulses over which the fluorophore remains excited sampled from a categorical distribution. As such, the likelihood is given by a convolution of the distributions arising from these three contributions (39):
| (2) |
where , and are, respectively, the maximum number of pulses after which photon emissions might occur, the interpulse window, the offset, and the IRF variance. This likelihood has been previously derived and employed within a parametric framework with a known number of lifetime components (39). Here, we go beyond the parametric framework and use this likelihood in conjunction with a Dirichlet process to obtain a posterior within a nonparametric Bayesian paradigm where the number of lifetime components is one of the unknowns.
We now proceed to derive our nonparametric posterior. The posterior is the joint probability over all unknowns we wish to learn including the weight over each species denoted by symbol for the th species, inverse of the corresponding lifetimes (i.e., the rate) denoted by for the th species, and the indicator parameters for each photon designated by and assigning the th photon to one of the species. We collect all these parameters into , where, formally, within the nonparametric framework. Next, the posterior over , proportional to the product of the likelihood and priors over these parameters, reads
| (3) |
where denotes the corresponding priors. This posterior, however, assumes a nonstandard form, and we cannot jointly sample all parameters. Therefore, we invoke a Gibbs sampling strategy for which we can sample individual parameters from the full conditional posteriors (53,54,55,56,57,58,59,60). That is, the posterior of the parameter of interest conditioned on the remaining parameters. The Gibbs sampling strategy of BNP-LA is as follows:
-
1)
Sample the indicator parameters from their full conditional posterior given by
| (4) |
where is the prior over the indicator parameters.
-
2)
Sample weights using their corresponding full conditional posterior
| (5) |
where denotes the prior over weights.
-
(3)
Sample the inverse of the lifetimes employing their full conditional posterior given as
| (6) |
where is the prior distribution over the lifetime inverse.
Now, for the sake of computational convenience, we opt for conjugate priors whenever possible such that those conditional posteriors assume analytical forms allowing for direct sampling. As such, we put a categorical prior distribution over the indicator parameters
| (7) |
leading to a closed form full conditional distribution that can be directly sampled. For weights, we select a Dirichlet process prior
| (8) |
conjugate to the categorical distribution. Here, is a positive hyper-parameter, which we set to one. This results in a standard closed form distribution
| (9) |
where denotes the Kronecker delta. There are two approaches that can be employed to draw samples from the distribution in Eq. 9: slice sampling and finite truncation (46,47,48,49). Here, we opt for finite truncation due its computational efficiency. This approach sets an upper limit on the number of species by assuming a finite, but large, value for , facilitating sampling from the above Dirichlet distribution. Finally, for the inverse of lifetimes, we use a gamma prior to guarantee positive values:
| (10) |
Since the likelihood of Eq. 2 does not have an associated conjugate prior, even with a choice of gamma prior, we must use Metropolis-Hastings (61,62,63,64,65) to numerically draw samples. Here, samples are proposed also using a gamma proposal distribution,
| (11) |
to avoid negative proposals. The proposed values are then accepted with probability
| (12) |
Using the Gibbs sampling strategy described above, we build a chain of samples by iteratively sweeping the set of parameters. Finally, the generated chain can be used for the subsequent numerical analyses.
Results
Our BNP-LA method’s main objective is to learn the lifetimes and their corresponding weights given a set of photon arrival times. As the BNP-LA method operates within the Bayesian framework, to learn these parameters, we work with a posterior, which is proportional to the product of the likelihood and priors over these parameters (see materials and methods). However, our nonparametric posterior does not attain a standard form, and we cannot deal with that analytically. Therefore, we develop a numerical strategy to efficiently sample our posterior (see materials and methods). The results presented in this section are thus histograms of samples drawn from the BNP-LA posterior.
Here, we use both synthetic and experimental data to evaluate the performance of our BNP-LA analysis package. We first use synthetic data to benchmark our method with 1) a decreasing interpulse window (see Fig. 3) where photon detections occurring after pulses following the one inducing excitation become increasingly probable; 2) multiple lifetimes smaller than the width of IRF distribution, and lifetimes with subnanosecond differences (see Figs. 4 and 5); 3) photon counts (see Fig. 5); 4) a range of different weights associated to species due to variations in photon counts across species (see Fig. 6); and 5) more than two lifetimes (see Fig. 7). In addition, we compare parametric and nonparametric analyses (see Fig. 7), revealing that, for the same amount of data, nonparametrics reveals the number of species and their associated uncertainty.
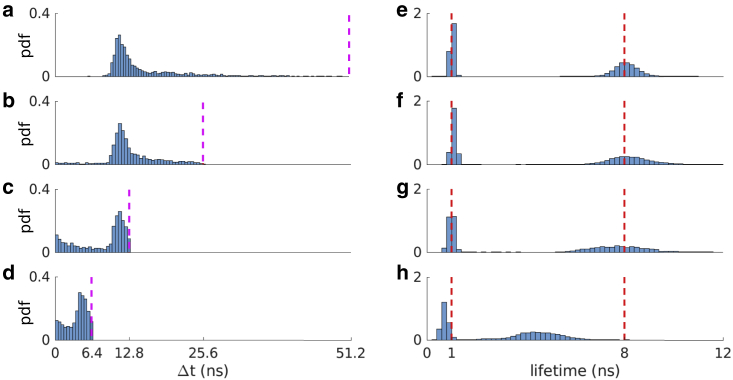
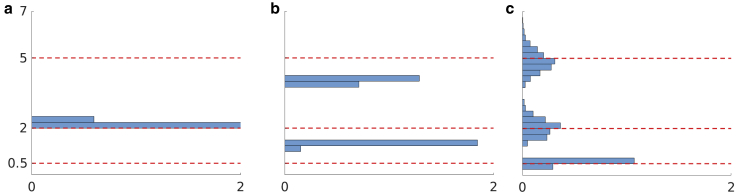
Figure 3.
Interpulse window effect on lifetime estimation. (a–d) Histograms of photon arrival data generated with two lifetimes of 1 and 8 ns and interpulse times of 51.2, 25.6, 12.8, and 6.4 ns, respectively. Pink dashed lines represent the interpulse window. PDF stands for probability density function, which is obtained by normalizing the area under histograms to unity. (e–h) Marginal posterior of lifetimes corresponding to each generated data. Red dashed lines represent ground truths. We retain the same convention throughout the article.
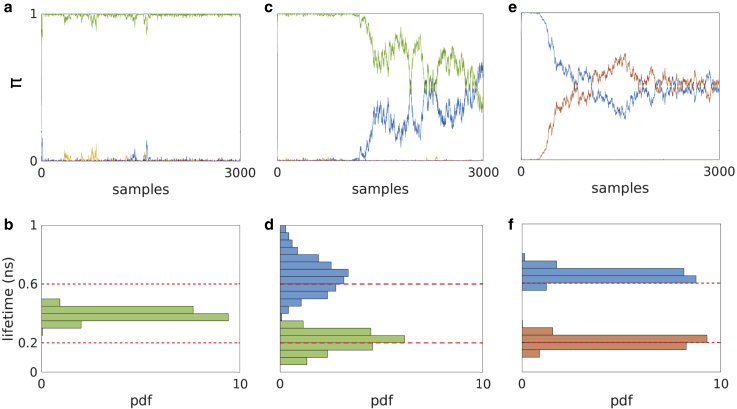
Figure 4.
Picking out two lifetimes smaller than the IRF width ( ns) as we increase the number of photons in the analysis. (a) Plot of sampled photon ratios from the posterior using just 500 photons in the analysis, where only the component shown in green has a nonnegligible photon ratio (i.e., no other species appreciably contributes photons). (b) Lifetime histogram corresponding to the green component contributing more than 0.95 photon ratio in (a). (c) Plot of sampled photon ratios from the posterior using 1000 photons, where the green and blue components have nonnegligible photon ratios (i.e., again, no other species appreciably contributes photons). (d) Histogram of lifetime samples corresponding to the green and blue components contributing a more than 0.95 photon ratio after 1500 samples in (c). (e) Plot of sampled photon ratios using 5000 photons, where the red and blue components have nonnegligible photon ratios. (f) Histogram of lifetime samples from the posterior corresponding to the blue and red components contributing more than 0.95 to the photon ratio after 1500 samples, as before, in (e). We note that the two (ground-truth) species become apparent only beyond 500 photons incorporated into the analysis.
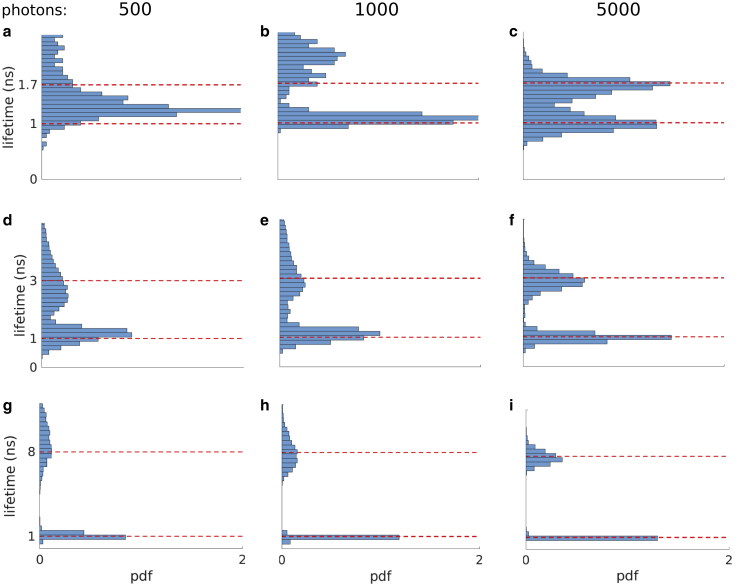
Figure 5.
Robustness test against lifetimes and photon counts. (a–c) Marginal posteriors of lifetimes for 1 and 1.7 ns with subnanosecond difference using different photon counts. (d–f) Marginal posterior of lifetimes of 1 and 3 ns using different photon counts. (g–i) Marginal posterior of lifetimes of 1 and 8 ns (close to interpulse window) using different photon counts.
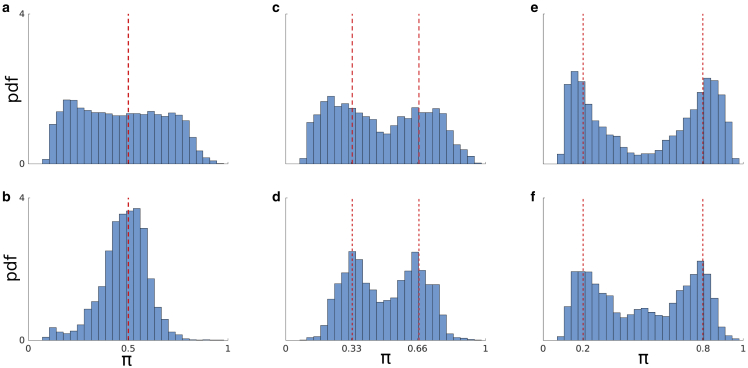
Figure 6.
Robustness test against lifetime weights, shown by , and photon counts. (a and b) Marginal posterior for the two weights found (when the ground truth is for 1/2 each) when 1000 and 5000 total photon counts are considered in the analysis, respectively. (c and d) Similar to above except for when the ground truth of the weights is 1/3 and 2/3. (e and f) Same as above except for weights of 1/5 and 4/5.
Figure 7.
Parametric versus nonparametric analysis. Here, we use simulated data with three lifetimes of 0.5, 2, and 5 ns containing 30,000 photons to compare Bayesian parametric algorithms with our nonparametric BNP-LA. (a) Resulting lifetime histogram from a parametric sampler with a single lifetime. (b) Resulting lifetime histogram from a parametric sampler with two lifetimes. (c) Resulting lifetime histogram from our BNP-LA algorithm without a priori specification of the number of lifetime components.
Next, we employ experimental data to evaluate the robustness of our method in estimating lifetimes over a wide range, e.g., short lifetimes falling within the width of the IRF, with short interpulse windows and different photon counts (see Fig. 8). Moreover, employing experimental data containing lifetimes of 0.6, 2.3, and 4.6 ns, we will show that BNP-LA can distinguish and deduce three lifetime species using as few as 30,000 photons (see Fig. 9).
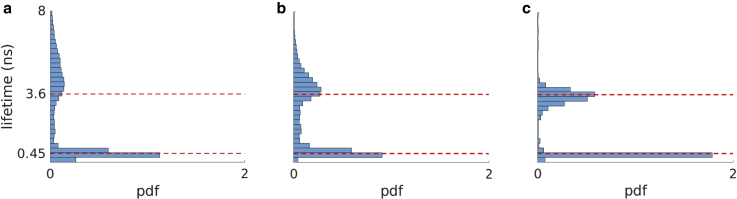
Figure 8.
Experimental data with two lifetimes including a lifetime (0.45 ns) below IRF width (0.66 ns). (a–c) Marginal posterior of lifetimes for 500, 1000, and 5000 photons, respectively.
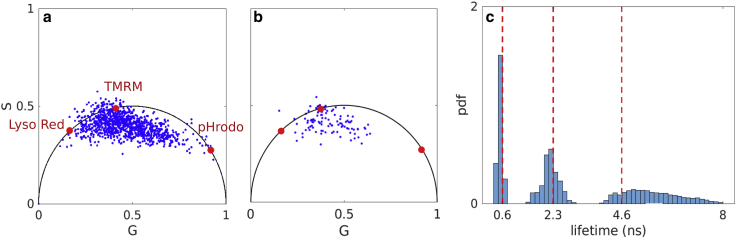
Figure 9.
Experimental data containing three fluorophore species, namely Lyso red, TMRM, and pHrodo with lifetimes of 4.6, 2.3, and 0.6 ns, respectively. (a) For illustrative purposes, we show the resulting phasor plot for an FLIM image of pixels. Here, we only used pixels containing more than 200 photons with a total photon count of 330,000. The red dots represent the three fluorophore species on the universal circle (26,28). The corresponding lifetimes are used as ground truth. (b) Results using a phasor plot for multiple pixels containing 30,000 total photons (which is the same number we analyze) highlighting the data efficiency of BNP-LA. (c) Marginal posterior of lifetimes from the BNP-LA method using 30,000 photons. The red dashed lines show lifetimes obtained using the phasor technique with 330,000 photons.
Synthetic data
Here, we first illustrate how we simulate our data and then describe our BNP-LA analysis. To generate synthetic photon arrival time traces, for each photon, we would first need to sample the species being excited, then sample the stochastic excited-state lifetime from an exponential, and finally add to this lifetime a stochastic IRF time due to both finite size of laser pulses, i.e., laser pulses are not infinitely narrow, and detector delay. As such, we first sample the fluorophore species leading to the th photon detection ( for fluorophore species) from a categorical distribution, then an excited-state lifetime from an exponential distribution, and then add to this the IRF time sampled from a normal distribution.
To be clear, the categorical distribution is an extension of the Bernoulli distribution with more than two options (species); the mean of the exponential distribution for each individual species that we use in the simulation to sample lifetimes is set to that species’ lifetime; and the Gaussian used in sampling the IRF time has a mean and standard deviation of 10.4 and 0.66 ns, respectively (similar to values in our experimental data that we will see shortly) (7). We also assume a value for the interpulse window of ns, again inspired by values from our experimental data.
In cases when the interpulse window is not much larger than both lifetimes and the IRF offset, the data generated as described above can lead to photon arrival times larger than the interpulse window. As such, to guarantee photon arrival times smaller than the interpulse window, we have to introduce a third term as follows,
| (13) |
for the th photon arrival time. Here, gives the integer part of its argument.
Now, in order to test BNP-LA against different interpulse windows (for which the third term in Eq. 13 becomes increasingly important), we simulate data, as described above, using two lifetimes of 1 and 8 ns and interpulse windows of 51.2, 25.6, 12.8, and 6.4 ns (see Fig. 3, a–d).
We start by describing results using the largest interpulse window as this is the easiest case since we can safely ascribe arriving photons as having been generated from the excitation pulse immediately preceding the photon arrival. In this case, the resulting weights ascribed to two lifetimes are nonnegligible and add up to more than 0.9. The histogram of the lifetimes pertaining to these wights is shown in Fig. 3 e. Here, our method infers both small and large lifetimes with standard deviations of 0.01 and 0.35 ns, respectively. Next, in Fig. 3, f and g, we consider the more difficult case of decreased interpulse windows. This, in turn, leads to larger uncertainties over lifetimes, although the means of the histograms still coincide with true values. Finally, Fig. 3 h shows the resulting lifetimes corresponding to the data in Fig. 3 d with an interpulse window 6.4 ns. Here, again, two important weights are found associated to two lifetimes. However, our method begins under-estimating the lifetime with the ground truth (8 ns) larger than the interpulse window. To develop an intuition as to why the method begins to fail (as it should) for increasingly small windows, we consider infinitely small interpulse windows. In this case, the photon arrival times are essentially uniform over that window, and no information can be extracted from a flat distribution. Conversely, as the interpulse window duration increases, this uniform distribution in arrival times begin acquiring some shape that, loosely speaking, any method can begin leveraging to deduce lifetimes.
Next, we continue by considering the challenging case of multiple lifetimes whose value is smaller than the width of the IRF (in shorthand, “lifetimes below the IRF”). We do so by generating photon traces involving 500, 1000, and 5000 photons with two lifetimes of 0.2 and 0.6 ns, both below the IRF, and similar weights (photon ratios) of 0.5. We then show how many photons are needed to start discerning that we have two lifetimes present. To do so, we first consider the weights sampled by our BNP-LA algorithm associated to each species and report them as the number of lifetime components those lifetimes associated to weights with nonnegligible values (see Figs. 2 and 4). Here, we start by describing the results for the trace containing 500 photons. When these data are analyzed, the BNP-LA method (incorrectly) ascribes weight to a single lifetime component represented in green in Fig. 4 a. The resulting lifetime histogram has a peak close to the average lifetimes of the two (ground truth) components present in the data (see Fig. 4 b). Increasing the photon budget in the analysis to 1000 and then 5000, our method begins attributing nonnegligible weights to two lifetimes with weights whose sum is larger than 0.95 (see Fig. 4, c–f). We also note that the uncertainties over the estimated lifetimes decrease with increasing photon counts.
After demonstrating our method for lifetimes below the IRF, we proceed to assess its performance over a range of lifetimes, namely lifetimes with subnanosecond differences (but not necessarily below the IRF), lifetimes comparable to the interpulse window ( ns), and lifetimes in the intermediate range. To do so, we analyzed synthetic photon traces containing 500, 1000, and 5000 photons.
In Fig. 5, a–c, we start by considering lifetimes with subnanosecond difference (lifetimes of 1 and 1.7 ns). Using 500 photons, only a single lifetime is appreciably warranted by the data with a weight much larger than the other lifetimes (see Fig. 5 a). However, upon reaching 1000 and 5000 collected photons, BNP-LA begins ascribing important weight to two lifetimes adding up to more that 0.9 (Fig. 5, b and c). Next, we examine larger lifetime gaps in Fig. 5, d–i. In these cases, the BNP-LA method attributes nonnegligible weights to two lifetimes even for data sets with as few as 500 photons (Fig. 5, d and g). At larger photon counts, as expected, our method recovers sharper histograms while accurately recovering both lifetimes with less than an 8 difference between the histograms’ means (posteriors’ means) and ground-truth values (Fig. 5, e–f and h–i).
Now that we have benchmarked our BNP-LA algorithm using a wide range of lifetimes, we continue by evaluating our algorithm in learning the lifetime weights, designated by . To be clear, the weights associated to different lifetimes are proportional to the photon ratios from those lifetimes. In order to perform such an evaluation, we simulate data sets with two lifetimes of 1 and 3 ns containing 1000 and 5000 photons (the first and second rows in Fig. 6) and weights of (0.5, 0.5), (0.33, 0.66), and (0.2, 0.8) for data sets used in Fig. 6, a–f, respectively. As we now see, only weights associated to two lifetimes were found to contribute nonnegligibly. Fig. 6 represents histograms over these weights. As expected, cases with 500 photons have larger uncertainty (Fig. 6, a and b), with the uncertainty decreasing as the photons considered in the analysis mount.
Finally, in Fig. 7, we show that our nonparametric method is capable of dealing with data sets containing more than two lifetime components and compare the results with parametric samplers assuming one and two species a priori. As such, we generate data with three lifetimes of 0.5, 2, and 5 ns. These traces are now, naturally, longer (contain more photons) as the inference task is more difficult. In particular, we find that we need about 30,000 photons to analyze these data, though the exact number of photons required is specific to a number of parameters (including how well separated the lifetimes are). The BNP-LA method returned three nonnegligible weights adding up to with corresponding mean posterior lifetimes of 0.5, 2, and 5 ns (see Fig. 7 c). As expected, the resulting lifetime histograms exhibit more uncertainty for larger lifetimes, as measured by a wider posterior, on account of more photon emissions occurring beyond the pulse subsequent to the one resulting in excitation.
We also analyzed this data set using a parametric version of our sampler while assuming one or two lifetime components such as in (36,37). The resulting lifetime histograms are, respectively, depicted in Fig. 7, a and b. In both cases, the learned lifetimes are incorrect, and the histogram peaks coincide with averages of the lifetimes present within the data.
Experimental data
We now continue by benchmarking our BNP-LA method on experimental data. We start with a data set acquired using only two fluorophores, namely calcein and MitoTracker, with lifetimes of 3.6 and 0.45 ns, respectively. Here, the shorter lifetime falls below the IRF, where the IRF parameters as well as the interpulse window are the same as what were used for the simulations. In Fig. 8, a–c, we analyze photon traces from this data set containing 500, 1000, and 5000 photons, respectively. Our BNP-LA method returns two nonnegligible weights adding up to for all the cases. The corresponding lifetime histograms show that the BNP-LA method deduces both lifetimes including the lifetime below the IRF even for as few as 500 photons.
Finally, we test our method by employing an experimental data set containing three fluorophore species, i.e., Lyso red, TMRM, and pHrodo, characterized by lifetimes of 4.6, 2.3, and 0.6 ns, respectively. These ground-truth values are obtained by using 330,000 photons with commonly employed phasor plots (26) (see Fig. 9 a).
Next, we process a trace of 30,000 photons from this data set using both our BNP-LA method and the phasor technique (see Fig. 9, b and c). Using only 30,000 photons, it is difficult to extrapolate the three lifetimes from the phasor plot (Fig. 9 b). However, analysis by our method results in three major weights adding up to , indicating the presence of three lifetime components within the input data. Fig. 9 c illustrates the lifetime histogram corresponding to these three weights. The histogram peaks match the values we use as ground truth. Here, for reasons identical to synthetic data, uncertainty increases with larger lifetimes.
Discussion
Fluorescence lifetime experiments provide a means to probe subcellular processes and structures. For instance, these techniques have been essential in cancer diagnosis (66,67) and monitoring the effect of drugs on cancer cells (67). However, quantitative assessment of FLIM data remains a challenge, as the number of fluorescent lifetime species and their associated lifetimes may vary within a biological sample due to exposure to variable chemical environments (41,42).
These issues immediately require the development of methods capable of learning the number of unique species, as well as their associated lifetimes and photon ratios. Ideally, such methods would be robust in treating lifetimes irrespective of what numerical value they ultimately attain in experiments, whether they are shorter than the width of the IRF, on par with the interpulse time, or similar to each other.
Here, we put forward a BNP-LA method capable of enumerating lifetime components using as few photons as 500 from a single confocal spot while simultaneously deducing the corresponding lifetimes over a wide range from below the IRF to the interpulse window. BNP-LA does so by leveraging tools, such as Dirichlet processes, from the BNP paradigm.
We benchmark BNP-LA using both synthetic and experimental data over a broader range of conditions than was previously accessible. That is, we benchmarked our method against lifetimes shorter than the IRF width, comparable to the interpulse window, and lifetimes with subnanosecond gaps with different photon ratios.
In terms of computational cost, the scaling growth is linear with the number of photons, while the exact absolute cost depends on the number of iterations required for the sampler to converge, which is, in turn, related to the number of lifetimes and how close they are. For instance, for typical lifetimes in Figs. 4 and 8, the computation took less than 1 min on a regular scientific desktop for cases involving 5000 photons. We expect this value to vary depending on the exact CPU specifications.
Although here we only assume Gaussian IRFs, BNP-LA can be extended to consider non-Gaussian IRFs by modifications to the likelihood in Eq. 2. Furthermore, BNP-LA can be used to construct a pixel-by-pixel spatial map of species distributions over a large field of view by independently analyzing data obtained from individual confocal spots across a specimen.
While we have advanced LA, there are questions neither we nor any existing methods can address. Answering these questions may inspire alternatives to lifetime experiments. For instance, we cannot learn lifetimes when arrival times far exceed the interpulse window; as a corollary, we cannot avoid posterior broadening for larger lifetimes, e.g., lifetimes comparable to the interpulse window; we cannot determine whether two exponential components coincide with the same chemical species or two different chemical species; we cannot distinguish chemical species with small lifetime differences, e.g., as of the current date of publication is less than approximately 0.2 ns, from the number of photons we typically analyze (far higher photon counts would then introduce high computational costs, which may require greater resources not yet available). Additionally, we can only quantify photon ratios and not concentrations nor absorption cross sections, as the latter two quantities always appear as one (a product of both fundamental quantities) in the likelihood (39).
More broadly, our method uses few photons to draw inferences. From this follow two consequences: 1) our method may help improve spatial resolution by allowing for the analysis of data obtained using small pinholes that otherwise provide too few photons for other methods, and 2) we may reduce sample photodamage by lowering the power of illumination.
Author contributions
S.P. conceived and supervised the project. M.F. designed the algorithm, wrote the codes, and performed simulations. The experimental data were provided by A.V., L.S., E.G., and M.A.D. M.F. wrote the manuscript with help from S.P. All the authors reviewed and commented on the manuscript.
Acknowledgments
S.P. acknowledges support from NIH grants R01GM134426 and R01GM130745. Image and data acquisition were made possible through access to the Laboratory for Fluorescence Dynamics, a shared resource center supported by the National Institutes of Health (grant no. P41GM103540 to L.S., A.V., and E.G.). This study was supported in part by funds from the National Science Foundation (grant nos. DMS1763272 and 1847005 to M.A.D.) and a grant from the Simons Foundation (594598 QN to M.A.D.).
Declaration of interests
Authors declare no competing interests.
Editor: Dylan Myers Owen.
Data and code availability
The experimental data used in this work are available upon reasonable request from the corresponding author. The software package along with the simulated data used in Fig. 4 are available at https://github.com/MohamadFazel/BNP-LA.
References
- 1.Becker W. Fluorescence lifetime imaging–techniques and applications. J. Microsc. 2012;247:119–136. doi: 10.1111/j.1365-2818.2012.03618.x. [DOI] [PubMed] [Google Scholar]
- 2.Datta R., Heaster T.M., et al. Skala M.C. Fluorescence lifetime imaging microscopy: fundamentals and advances in instrumentation, analysis, and applications. J. Biomed. Opt. 2020;25:1–43. doi: 10.1117/1.JBO.25.7.071203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lippincott-Schwartz J., Patterson G.H. Development and use of fluorescent protein markers in living cells. Science. 2003;300:87–91. doi: 10.1126/science.1082520. [DOI] [PubMed] [Google Scholar]
- 4.Garini Y., Young I.T., McNamara G. Spectral imaging: principles and applications. Cytometry A. 2006;69:735–747. doi: 10.1002/cyto.a.20311. [DOI] [PubMed] [Google Scholar]
- 5.Schermelleh L., Ferrand A., et al. Drummen G.P.C. Super-resolution microscopy demystified. Nat. Cell Biol. 2019;21:72–84. doi: 10.1038/s41556-018-0251-8. [DOI] [PubMed] [Google Scholar]
- 6.Lelek M., Gyparaki M.T., et al. Zimmer C. Single-molecule localization microscopy. Nat. Rev. Methods Primers. 2021;1:39. doi: 10.1038/s43586-021-00038-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fazel M., Wester M.J. Analysis of super-resolution single molecule localization microscopy data: a tutorial. AIP Adv. 2022;12:010701. [Google Scholar]
- 8.Lerner E., Cordes T., et al. Weiss S. Toward dynamic structural biology: two decades of single-molecule Förster resonance energy transfer. Science. 2018;359:1133. doi: 10.1126/science.aan1133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Weber G. Resolution of the fluorescence lifetimes in a heterogeneous system by phase and modulation measurements. J. Phys. Chem. 1981;85:949–953. [Google Scholar]
- 10.Bastiaens P.I., Squire A. Fluorescence lifetime imaging microscopy: spatial resolution of biochemical processes in the cell. Trends Cell Biol. 1999;9:48–52. doi: 10.1016/s0962-8924(98)01410-x. [DOI] [PubMed] [Google Scholar]
- 11.Sameni S., Syed A., et al. Digman M.A. The phasor-FLIM fingerprints reveal shifts from OXPHOS to enhanced glycolysis in Huntington Disease. Sci. Rep. 2016;6:34755. doi: 10.1038/srep34755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chanoca A., Burkel B., et al. Otegui M.S. Using fluorescence lifetime microscopy to study the subcellular localization of anthocyanins. Plant J. 2016;88:895–903. doi: 10.1111/tpj.13297. [DOI] [PubMed] [Google Scholar]
- 13.Hato T., Winfree S., et al. Dagher P.C. Two-photon intravital fluorescence lifetime imaging of the kidney reveals cell-type specific metabolic signatures. J. Am. Soc. Nephrol. 2017;28:2420–2430. doi: 10.1681/ASN.2016101153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Saari H., Lisitsyna E., et al. Vuorimaa-Laukkanen E. FLIM reveals alternative EV-mediated cellular up-take pathways of paclitaxel. J. Control. Release. 2018;284:133–143. doi: 10.1016/j.jconrel.2018.06.015. [DOI] [PubMed] [Google Scholar]
- 15.Davis R.T., Blake K., et al. Lawson D.A. Transcriptional diversity and bioenergetic shift in human breast cancer metastasis revealed by single-cell RNA sequencing. Nat. Cell Biol. 2020;22:310–320. doi: 10.1038/s41556-020-0477-0. [DOI] [PubMed] [Google Scholar]
- 16.Perinbam K., Chacko J.V., et al. Siryaporn A. A shift in central metabolism accompanies virulence activation in Pseudomonas aeruginosa. mBio. 2020;11 doi: 10.1128/mBio.02730-18. e02730-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Suhling K., Siegel J., et al. Davis D.M. Imaging the environment of green fluorescent protein. Biophys. J. 2002;83:3589–3595. doi: 10.1016/S0006-3495(02)75359-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tregidgo C., Levitt J.A., Suhling K. Effect of refractive index on the fluorescence lifetime of green fluorescent protein. J. Biomed. Opt. 2008;13:031218. doi: 10.1117/1.2937212. [DOI] [PubMed] [Google Scholar]
- 19.Okabe K., Inada N., et al. Uchiyama S. Intracellular temperature mapping with a fluorescent polymeric thermometer and fluorescence lifetime imaging microscopy. Nat. Commun. 2012;3:705. doi: 10.1038/ncomms1714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hao L., Li Z.-W., et al. Mao Z.-W. Monitoring mitochondrial viscosity with anticancer phosphorescent Ir III complexes via two-photon lifetime imaging. Chem. Sci. 2019;10:1285–1293. doi: 10.1039/c8sc04242j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ankri R., Basu A., et al. Michalet X. Single-photon, time-gated, phasor-based fluorescence lifetime imaging through highly scattering medium. ACS Photonics. 2020;7:68–79. doi: 10.1021/acsphotonics.9b00874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Štefl M., James N.G., et al. Jameson D.M. Applications of phasors to in vitro time-resolved fluorescence measurements. Anal. Biochem. 2011;410:62–69. doi: 10.1016/j.ab.2010.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gratton E., Breusegem S., et al. Barry N. Fluorescence lifetime imaging for the two-photon microscope: time-domain and frequency-domain methods. J. Biomed. Opt. 2003;8:381–390. doi: 10.1117/1.1586704. [DOI] [PubMed] [Google Scholar]
- 24.Michalet X., Weiss S., Jäger M. Single-molecule fluorescence studies of protein folding and conformational dynamics. Chem. Rev. 2006;106:1785–1813. doi: 10.1021/cr0404343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Clegg R.M., Holub O., Gohlke C. Vol. 360. Elsevier; 2003. Methods in Enzymology; p. 509. [DOI] [PubMed] [Google Scholar]
- 26.Digman M.A., Caiolfa V.R., et al. Gratton E. The phasor approach to fluorescence lifetime imaging analysis. Biophys. J. 2008;94:14–L16. doi: 10.1529/biophysj.107.120154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tavakoli M., Jazani S., et al. Pressé S. Direct photon-by-photon analysis of time-resolved pulsed excitation data using bayesian nonparametrics. Cell Rep. Phys. Sci. 2020;1:100234. doi: 10.1016/j.xcrp.2020.100234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ranjit S., Malacrida L., et al. Gratton E. Fit-free analysis of fluorescence lifetime imaging data using the phasor approach. Nat. Protoc. 2018;13:1979–2004. doi: 10.1038/s41596-018-0026-5. [DOI] [PubMed] [Google Scholar]
- 29.Wu G., Nowotny T., et al. Li D.D.-U. Artificial neural network approaches for fluorescence lifetime imaging techniques. Opt. Lett. 2016;41:2561–2564. doi: 10.1364/OL.41.002561. [DOI] [PubMed] [Google Scholar]
- 30.Smith J.T., Yao R., et al. Intes X. Fast fit-free analysis of fluorescence lifetime imaging via deep learning. Proc. Natl. Acad. Sci. USA. 2019;116:24019–24030. doi: 10.1073/pnas.1912707116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Verveer P.J., Squire A., Bastiaens P.I. Global analysis of fluorescence lifetime imaging microscopy data. Biophys. J. 2000;78:2127–2137. doi: 10.1016/S0006-3495(00)76759-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Pelet S., Previte M.J.R., et al. So P.T.C. A fast global fitting algorithm for fluorescence lifetime imaging microscopy based on image segmentation. Biophys. J. 2004;87:2807–2817. doi: 10.1529/biophysj.104.045492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Yao R., Ochoa M., et al. Intes X. Net-FLICS: fast quantitative wide-field fluorescence lifetime imaging with compressed sensing–a deep learning approach. Light Sci. Appl. 2019;8:26. doi: 10.1038/s41377-019-0138-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bajzer Ž., Therneau T.M., et al. Prendergast F.G. Maximum likelihood method for the analysis of time-resolved fluorescence decay curves. Eur. Biophys. J. 1991;20:247–262. doi: 10.1007/BF00183269. [DOI] [PubMed] [Google Scholar]
- 35.Maus M., Cotlet M., et al. Seidel C.A. An experimental comparison of the maximum likelihood estimation and nonlinear least-squares fluorescence lifetime analysis of single molecules. Anal. Chem. 2001;73:2078–2086. doi: 10.1021/ac000877g. [DOI] [PubMed] [Google Scholar]
- 36.Rowley M.I., Coolen A.C.C., et al. Barber P.R. Robust Bayesian fluorescence lifetime estimation, decay model selection and instrument response determination for low-intensity FLIM imaging. PLoS One. 2016;11:0158404. doi: 10.1371/journal.pone.0158404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kaye B., Foster P.J., et al. Needleman D.J. Developing and testing a Bayesian analysis of fluorescence lifetime measurements. PLoS One. 2017;12:0169337. doi: 10.1371/journal.pone.0169337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wang S., Chacko J.V., et al. Yuan M. Nonparametric empirical Bayesian framework for fluorescence-lifetime imaging microscopy. Biomed. Opt Express. 2019;10:5497–5517. doi: 10.1364/BOE.10.005497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Fazel M., Jazani S., et al. Pressé S. High resolution fluorescence lifetime maps from minimal photon counts. ACS Photonics. 2022;9:1015–1025. doi: 10.1021/acsphotonics.1c01936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Stringari C., Cinquin A., et al. Gratton E. Phasor approach to fluorescence lifetime microscopy distinguishes different metabolic states of germ cells in a live tissue. Proc. Natl. Acad. Sci. USA. 2011;108:13582–13587. doi: 10.1073/pnas.1108161108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Blacker T.S., Mann Z.F., et al. Duchen M.R. Separating NADH and NADPH fluorescence in live cells and tissues using FLIM. Nat. Commun. 2014;5:3936. doi: 10.1038/ncomms4936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Blacker T.S., Duchen M.R. Investigating mitochondrial redox state using NADH and NADPH autofluorescence. Free Radic. Biol. Med. 2016;100:53–65. doi: 10.1016/j.freeradbiomed.2016.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Le Marois A., Labouesse S., et al. Heintzmann R. Noise-Corrected Principal Component Analysis of fluorescence lifetime imaging data. J. Biophotonics. 2017;10:1124–1133. doi: 10.1002/jbio.201600160. [DOI] [PubMed] [Google Scholar]
- 44.Ahmed M., Seraj R., Islam S.M.S. The k-means algorithm: a comprehensive survey and performance evaluation. Electronics. 2020;9:1295. [Google Scholar]
- 45.Ferguson T.S. A Bayesian analysis of some nonparametric problems. Ann. Statist. 1973;1:209. [Google Scholar]
- 46.Neal R.M. Markov chain sampling methods for Dirichlet process mixture models. J. Comput. Graph Stat. 2000;9:249. [Google Scholar]
- 47.Gelfand A.E., Kottas A., MacEachern S.N. Bayesian nonparametric spatial modeling with Dirichlet process mixing. J. Am. Stat. Assoc. 2005;100:1021–1035. [Google Scholar]
- 48.Teh Y.W. Encyclopedia of Machine Learning. Vol. 1063. 2010. Dirichlet process; p. 280. [Google Scholar]
- 49.Sgouralis I., Pressé S. An introduction to infinite HMMs for single-molecule data analysis. Biophys. J. 2017;112:2021–2029. doi: 10.1016/j.bpj.2017.04.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Włodarczyk J., Kierdaszuk B. Interpretation of fluorescence decays using a power-like model. Biophys. J. 2003;85:589–598. doi: 10.1016/S0006-3495(03)74503-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Remington J.M., Philip A.M., et al. Kohler B. On the origin of multiexponential fluorescence decays from 2-aminopurine-labeled dinucleotides. J. Chem. Phys. 2016;145:155101. doi: 10.1063/1.4964718. [DOI] [PubMed] [Google Scholar]
- 52.Lyvers D.P., Moazzezi M., et al. Drachev V.P. Cooperative bi-exponential decay of dye emission coupled via plasmons. Sci. Rep. 2018;8:9508. doi: 10.1038/s41598-018-27901-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kilic Z., Sgouralis I., Pressé S. Generalizing HMMs to continuous time for fast kinetics: hidden Markov jump processes. Biophys. J. 2021;120:409–423. doi: 10.1016/j.bpj.2020.12.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Moyer C., Kilic Z., et al. Pressé S. Inferring gene expression models from snapshot RNA data. bioRxiv. 2022 doi: 10.1101/2022.05.28.493734. Preprint at. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Saurabh A., Niekamp S., et al. Pressé S. Modeling non-additive effects in neighboring chemically identical fluorophores. J. Phys. Chem. B. 2022 doi: 10.1021/acs.jpcb.2c01889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Bryan J.S., 4th, Sgouralis I., Pressé S. Diffraction-limited molecular cluster quantification with Bayesian nonparametrics. Nat. Comput. Sci. 2022;2:102–111. doi: 10.1038/s43588-022-00197-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Safar M., Saurabh A., et al. Presse S. Single photon smFRET. III. application to pulsed illumination. bioRxiv. 2022 doi: 10.1101/2022.07.20.500892. Preprint at. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Saurabh A., Safar M., et al. Pressé S. Single photon smFRET. II. application to continuous illumination. bioRxiv. 2022 doi: 10.1101/2022.07.20.500888. Preprint at. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Saurabh A., Safar M., et al. Pressé S. Single photon smFRET. I. theory and conceptual basis. bioRxiv. 2022 doi: 10.1101/2022.07.20.500887. Preprint at. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Von Toussaint U. Bayesian inference in physics. Rev. Mod. Phys. 2011;83:943–999. [Google Scholar]
- 61.Metropolis N., Rosenbluth A.W., et al. Teller E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953;21:1087–1092. [Google Scholar]
- 62.Hastings W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 1970;57:97. [Google Scholar]
- 63.Jazani S., Sgouralis I., et al. Pressé S. An alternative framework for fluorescence correlation spectroscopy. Nat. Commun. 2019;10:3662. doi: 10.1038/s41467-019-11574-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Fazel M., Wester M.J., et al. Lidke K.A. High-precision estimation of emitter positions using Bayesian grouping of localizations. Nat. Commun. 2022;13:7152–7211. doi: 10.1038/s41467-022-34894-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Fazel M., Wester M.J., et al. Lidke K.A. Bayesian multiple emitter fitting using reversible jump Markov chain Monte Carlo. Sci. Rep. 2019;9:13791. doi: 10.1038/s41598-019-50232-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Ouyang Y., Liu Y., et al. Wu M. FLIM as a promising tool for cancer diagnosis and treatment monitoring. Nano-Micro Lett. 2021;13:133. doi: 10.1007/s40820-021-00653-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Pascua S.M., McGahey G.E., et al. Digman M.A. Caffeine and cisplatin effectively targets the metabolism of a triple-negative breast cancer cell line assessed via phasor-FLIM. Int. J. Mol. Sci. 2020;21:2443. doi: 10.3390/ijms21072443. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The experimental data used in this work are available upon reasonable request from the corresponding author. The software package along with the simulated data used in Fig. 4 are available at https://github.com/MohamadFazel/BNP-LA.