Optimal biomechanical parameters for measuring sclerotic chronic graft-versus-host disease

Abstract

Skin biomechanical parameters (dynamic stiffness, frequency, relaxation time, creep, and decrement) measured using a myotonometer (MyotonPRO) could inform management of sclerotic disease. To determine which biomechanical parameter(s) can accurately differentiate sclerotic chronic graft-versus-host disease (cGVHD) patients from post-hematopoietic cell transplant (post-HCT) controls, 15 sclerotic cGVHD patients and 11 post-HCT controls were measured with the myotonometer on 18 anatomic sites. Logistic regression and two machine learning algorithms, LASSO regression and random forest, were developed to classify subjects. In univariable analysis, frequency had the highest overfit-corrected area under the receiver operating characteristic curve (AUC 0.91). Backward stepwise selection and random forest machine learning identified frequency and relaxation time as the optimal parameters for differentiating sclerotic cGVHD patients from post-HCT controls. LASSO regression selected the combination of frequency and relaxation time (overfit-corrected AUC 0.87). Discriminatory ability was maintained when only the sites accessible while the patient is supine (12 sites) were used. We report the distribution of values for these highly discriminative biomechanical parameters, which could inform assessment of disease severity in future quantitative biomechanical studies of sclerotic cGVHD.

INTRODUCTION

Chronic graft-versus-host disease (cGVHD) occurs in 30–40% of patients after allogeneic hematopoietic cell transplantation (HCT), and is the leading cause of non-relapse mortality in patients surviving more than two years after transplant (Arai et al., 2015; Socie et al. 1999). Among cGVHD patients, 20% develop sclerosis within 3 years of initial systemic treatment for cGVHD, resulting in significant disability (Inamoto et al., 2013). However, the lack of quantitative and objective measurements of skin activity has restricted the advancement of treatment options for sclerotic disease (Socie et al., 2014).

The MyotonPRO, a handheld myotonometer that measures soft tissue biomechanical parameters through a noninvasive mechanical impulse, has promise in sclerotic cGVHD management (Baker et al., 2021; Dellalana et al., 2019; Vain, 2012). The device simultaneously extracts five biomechanical parameters, dynamic stiffness, oscillation frequency, relaxation time, creep, and decrement. It has shown high inter-operator reliability to measure dynamic stiffness in healthy controls and sclerotic cGVHD patients (Chen et al., 2019; Dellalana et al., 2019). While a previous study demonstrated the dynamic stiffness parameter’s ability to differentiate sclerotic patients from healthy volunteers, it did not examine other available parameters and lacked post-HCT controls (Chen et al., 2018).

With the advent of new diagnostic technologies and quantitative methods, an effective coupling of data to statistical methods, including machine learning, could enhance informed decision-making. Application of traditional regression models and machine learning algorithms in the setting of skin biomechanical parameters has the potential to differentiate sclerotic cGVHD patients from post-HCT controls with greater accuracy.

In this cross-sectional study of myotonometry measurements in cGVHD patients and post-HCT controls, we investigated the diagnostic ability of all five available biomechanical parameters in univariable analysis and explored the diagnostic impact of combinations of parameters selected by stepwise regression and machine-learning algorithms. We also evaluated whether a convenient supine-only protocol maintains the diagnostic accuracy of total body measurements.

RESULTS

A total of 15 sclerotic cGVHD patients and 11 post-HCT controls were included in this study. Patient characteristics are summarized in Table 1 and Table 2. The median time from HCT was 1686 days (1^st-3^rd quartile: 1169–2575 days) for sclerotic cGVHD patients and 910 days (1^st-3^rd quartile: 335–2507 days) for controls. Subjects were measured with a myotonometer, the MyotonPRO, on 18 anatomic sites (Figure 1). Two cGVHD patients were measured only on the 12 sites that could be measured with the patient in the supine position due to discomfort when laying in the prone position. The distribution of parameter values for each anatomic site are shown in Figure 2. Correlation across bilateral sites was high for all five biomechanical parameters (Table 3). For each subject, we calculated the parameter averages over all 18 measured sites and over the 12 supine sites. For the averages across all 18 measured sites, sclerotic cGVHD patients displayed significant increases in frequency (p=0.033) and stiffness (p=0.043), and decreases in relaxation time (p=0.001) and creep (0.002) compared to post-HCT controls (Figure 3). For the averages across the 12 supine sites, sclerotic cGVHD patients had significant increases in frequency (p=0.033) and decreases in relaxation time (p=0.001) and creep (p=0.002).

Table 1.

Demographic and clinical characteristics of 15 sclerotic cGVHD patients.

cGVHD Subjects (n=15)	Subject ID	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	Summary1
Demographics2	Age	55	52	40	28	72	59	47	47	71	60	14	65	60	35	70	55 [40–65]
	Race	C	C	C	C	C	C	C	C	C	C	C	C	C	C	C	100% C
	Sex	M	M	M	F	M	M	M	F	F	M	M	M	M	M	M	80% M
	BMI	24	24	27	14	31	17	23	34	21	20	22	33	18	23	32	23 [20–31]
Disease Characteristics3	Disease Histology	AML	MDS	MM	HL	ALL	AML	NHL	ALL	AML	MDS	AML	AML	NHL	ALL	CLL	33% AML 20% ALL 13% NHS 13% MDS 7% MM 7% HL 7% CLL
Transplant Characteristics4	Transplant Source	BM	PB	PB	PB	PB	PB	PB	BM	PB	PB	PB	PB	PB	PB	-	12/14 PB 2/14 BM
cGVHD Characteristics at Study Entry5	NIH Score BSA Involvement	3	3	2	3	2	3	1	2	1	2	3	1	2	1	-	4/14 NIH 1 5/14 NIH 2 5/14 NIH 3
	NIH Score Skin Feature	3	3	3	3	3	3	3	3	2	3	3	2	3	3	2	80% NIH 3 20% NIH 2
MyotonPRO Session	Days from HCT6	1676	4604	1084	1908	1169	2030	2575	4429	1256	1119	1339	3660	1061	1686	2132	1686 [1169–2575]

¹Values are shown as median [interquartile range] for continuous variables and n (%) for categorical variables

²Demographics: C: Caucasian, M: Male, F: Female

³Disease characteristics: AML: acute myeloid leukemia, ALL: acute lymphoblastic leukemia, CLL: chronic lymphoblastic leukemia, MDS: myelodysplastic disorder, MM: multiple myeloma, NHL: non-Hodgkin’s lymphoma, HL: Hodgkin’s lymphoma

⁴Transplant characteristics: PB: peripheral blood, BM: bone marrow

⁵NIH Score BSA involvement: 1: 1–18%, 2:19–50%, 3: >50%; NIH Score Skin Feature: 2: superficial sclerosis, 3: deep sclerosis

⁶Days from HCT: days between hematopoietic cell transplantation and MyotonPRO measurement session

Table 2.

Demographic and clinical characteristics of 11 post-HCT controls

Post-HCT Controls (n=11)	Subject ID	16	17	18	19	20	21	22	23	24	25	26	Summary1
Demographics2	Age	66	25	71	52	65	59	59	65	62	63	57	62 [57–65]
	Race	C	C	C	C	C	C	C	C	AA	C	AA	82% C 18% AA
	Sex	M	F	M	F	M	M	M	M	M	F	M	73% M
	BMI	26	40	26	43	31	24	27	26	36	45	35	31 [26–40]
Disease Characteristics3	Disease Histology	MF	AA	AML	MDS	NHL	AML	CLL	MDS	AML	AML	ALL	36% AML 18% MDS 9% ALL 9% MF 9% AA 9% NHL 9% CLL
Transplant Characteristics4	Transplant Source	PB	BM	PB	CB	PB	PB	PB	PB	-	PB	PB	8/10 PB 1/10 BM 1/10 CB
MyotonPRO Session	Days from HCT5	329	1785	1301	3276	910	411	2507	4046	857	335	148	910 [335–2507]

¹Values are shown as median [interquartile range] for continuous variables and n (%) for categorical variables

²Demographics: C: Caucasian, AA: African American, M: Male, F: Female

³Disease characteristics: AML: acute myeloid leukemia, ALL: acute lymphoblastic leukemia, CLL: chronic lymphoblastic leukemia, MDS: myelodysplastic disorder, MF: primary myelofibrosis, AA: aplastic anemia, NHL: non-Hodgkin’s lymphoma

⁴Transplant characteristics: PB: peripheral blood, BM: bone marrow, CB: cord blood

⁵Days from HCT: days between hematopoietic cell transplantation and MyotonPRO measurement session

Figure 1.

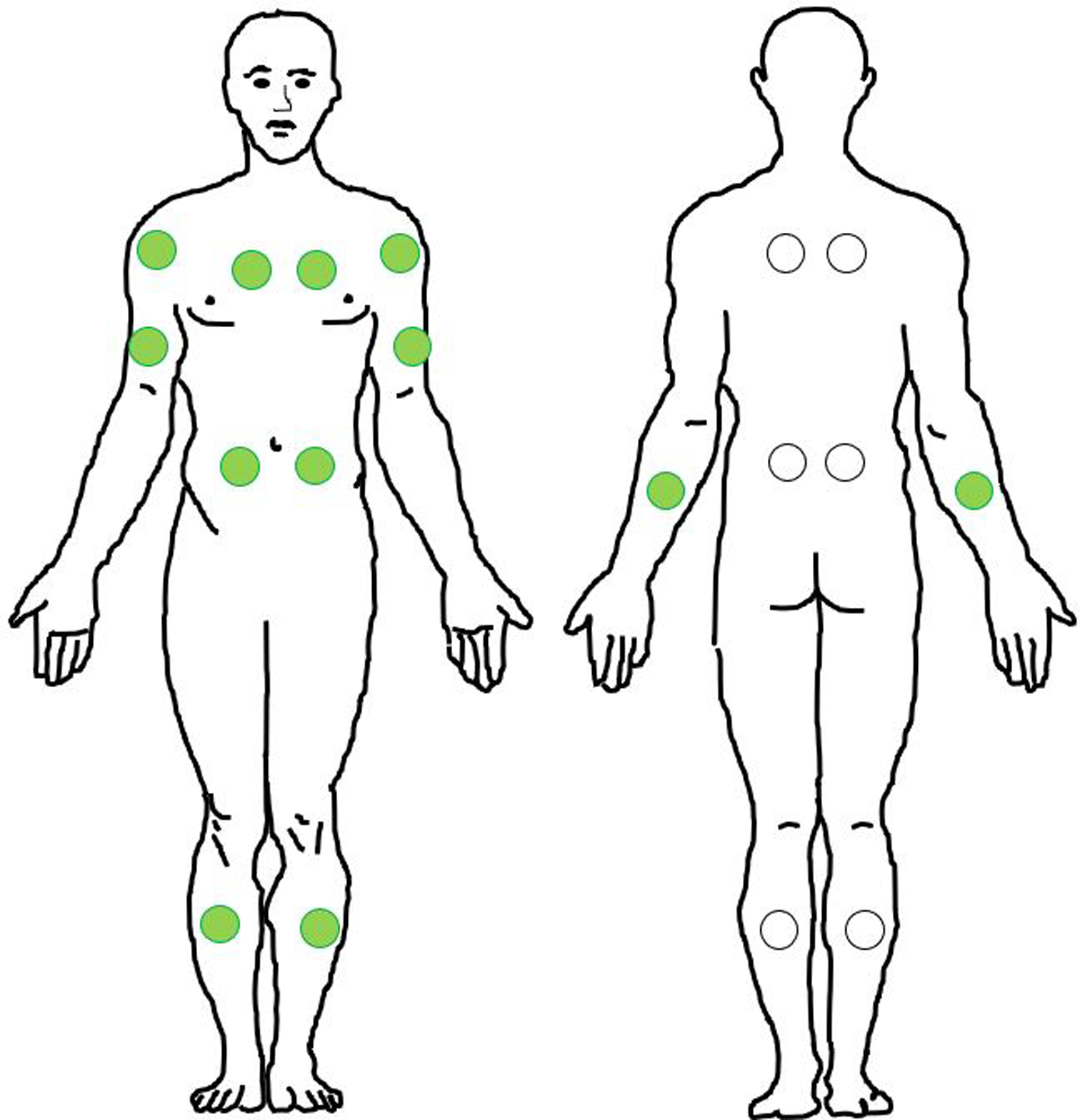
18 measured sites. Green circles represent the 12 sites that are measured in the supine position.

Figure 2.

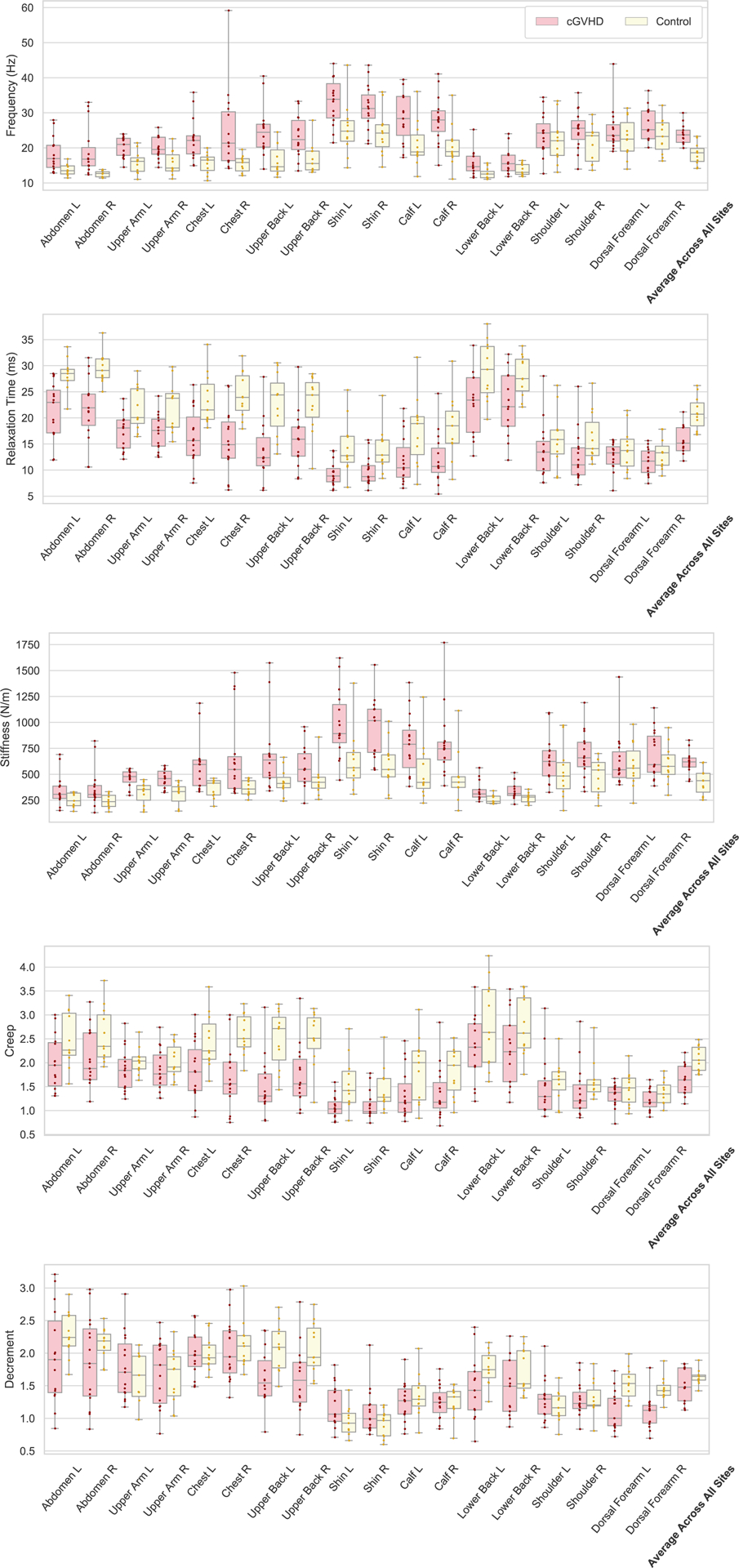
Box and whisker plots of the parameter values by site, in sclerotic cGVHD patients and post-HCT controls. Sites are displayed in descending order of the frequency AUCs shown in Figure 4. Bilateral sites are displayed next to each other. The bottom and top boundaries of each box represent the 25^th and 75^th quartiles, the horizontal line within the box represents the median, the whiskers represent the minimum and maximum values.

Table 3.

Spearman’s correlation coefficients between left and right-side parameter measurements for all five biomechanical parameters, in sclerotic cGVHD patients and post-HCT controls.

	Frequency	Relaxation Time	Stiffness	Creep	Decrement
Sclerotic cGVHD	0.812	0.879	0.859	0.847	0.838
Post-HCT Controls	0.868	0.915	0.955	0.842	0.843

Figure 3.

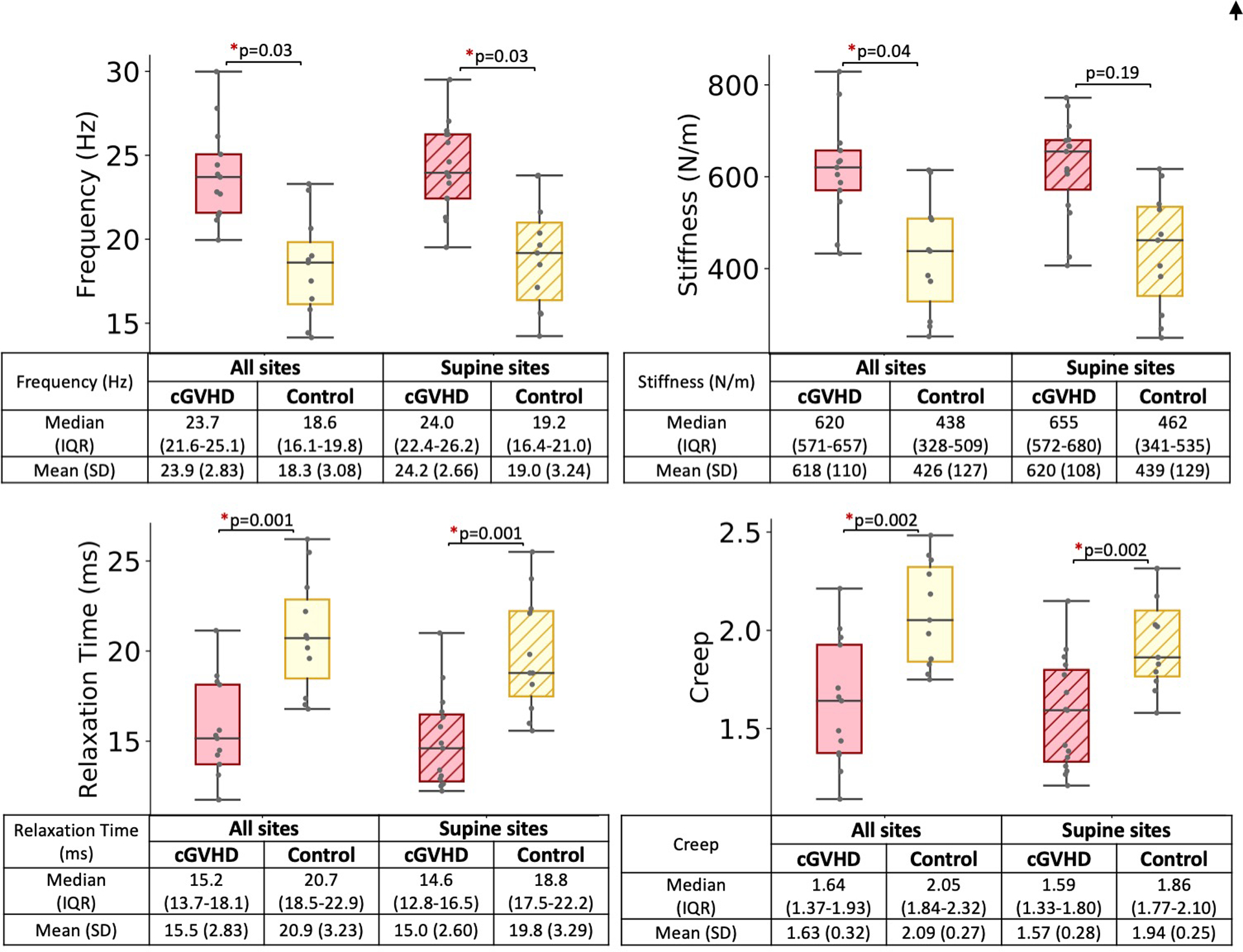
Sclerotic cGVHD patients (pink boxes) had increased stiffness and frequency, and decreased relaxation time and creep compared to post-HCT controls (yellow boxes). Sclerotic cGVHD patients and post-HCT controls were compared by Wilcoxon rank-sum test, using averages across 18 sites (solid boxes, cGVHD n=13, post-HCT n=11) and averages across 12 supine sites (diagonal pattern, cGVHD n=15, post-HCT =11), *p<0.05. Frequency and stiffness (Top row) values are expected to be higher for sclerotic skin than healthy skin, while relaxation time and creep (Bottom row) values are expected to be lower for sclerotic skin. Logarithmic decrement (overall: p=0.209, supine: p=0.209) not shown.

Abbreviations: Q1-Q3, 25^th – 75^th percentile; SD, standard deviation.

Univariable analysis

For each parameter, averages across all sites and averages across supine sites were used to develop univariable logistic regressions that modeled the diagnosis of sclerotic cGVHD as a dichotomous variable. For parameter averages over all 18 measured sites, the univariable overfit-corrected areas under the receiver operating characteristic curve (AUCs) for frequency, relaxation time, stiffness, and creep were 0.91, 0.89, 0.88, and 0.86, respectively (Table 4). For parameter averages across the 12 supine sites, the overfit-corrected AUCs for frequency, relaxation time, stiffness, and creep were 0.87, 0.87, 0.84, and 0.76, respectively.

Table 4.

Univariable and bivariable logistic regression AUCs (with and without overfit correction) and 95% confidence intervals for averages across all measured sites (sclerotic cGVHD n=13, post-HCT controls n=11) and averages across 12 supine sites (sclerotic cGVHD n=15, post-HCT controls n=11).

Parameter(s)	Across all 18 measured sites				Across 12 supine sites
	AUC (95% CI)	AUC with overfit correction	P-value		AUC (95% CI)	AUC with overfit correction	P-value
Frequency	0.909 (0.786–1.000)	0.910	0.014		0.873 (0.725–1.000)	0.873	0.011
Relaxation Time	0.888 (0.756–1.000)	0.890	0.011		0.873 (0.737–1.000)	0.874	0.011
Stiffness	0.874 (0.734–1.000)	0.875	0.012		0.842 (0.692–0.993)	0.840	0.012
Creep	0.860 (0.711–1.000)	0.862	0.014		0.767 (0.581–0.953)	0.763	0.026
Decrement	0.615 (0.361–0.869)	0.594	0.184		0.576 (0.347–0.804)	0.503	0.497
Frequency and Relaxation Time	0.916 (0.801–1.000)	0.890	-		0.879 (0.732–1.000)	0.851	-

Backward stepwise selection

Backward stepwise selection using the Akaike Information Criterion (AIC) was applied to a starting multivariable logistic regression model that consisted of all five biomechanical parameters. The final model for averages across all sites consisted of the single parameter frequency, while the final model for averages across supine sites consisted of the single parameter relaxation time.

Machine learning models and bivariable logistic regression

Regression with least absolute shrinkage and selection operator (LASSO) is a machine learning algorithm that performs autonomous variable selection to create reduced models, which can include either a single parameter or a combination of parameters. For both averages across all sites and averages across supine sites, LASSO regression selected the combination of frequency and relaxation time as the most important variables in differentiating sclerotic cGVHD patients from post-HCT controls (overfit-corrected AUC 0.87 for averages across all sites, 0.78 for averages across supine sites) (Table 5).

Table 5.

LASSO regression coefficients and AUCs of 10 repeats of 3-fold cross-validation for averages across all 18 measured sites (sclerotic cGVHD n=13, post-HCT controls n=11) and averages across 12 supine sites (sclerotic cGVHD n=15, post-HCT controls n=11).

LASSO regression models for averages across all 18 measured sites
Rep	AUC without overfit correction [95% CI]	AUC with overfit correction [95% CI]	Parameters selected by model
			Frequency	Relaxation Time	Stiffness	Creep	Decrement
1	0.909 [0.786, 1]	0.871 [0.641, 0.998]	1.722	−0.050	-	-	-
2	0.909 [0.786, 1]	0.871 [0.641, 0.998]	1.592	−0.030	-	-	-
3	0.909 [0.786, 1]	0.871 [0.641, 0.998]	1.300	-	-	-	-
4	0.909 [0.786, 1]	0.871 [0.641, 0.998]	1.456	−0.008	-	-	-
5	0.909 [0.786, 1]	0.871 [0.641, 0.998]	1.592	−0.030	-	-	-
6	0.909 [0.786, 1]	0.871 [0.641, 0.998]	1.524	−0.019	-	-	-
7	0.909 [0.786, 1]	0.871 [0.641, 0.998]	1.904	−0.076	-	-	-
8	0.909 [0.786, 1]	0.871 [0.641, 0.998]	1.040	-	-	-	-
9	0.909 [0.786, 1]	0.871 [0.641, 0.998]	1.383	-	-	-	-
10	0.909 [0.786, 1]	0.871 [0.641, 0.998]	1.592	−0.030	-	-	-
LASSO regression models for averages across 12 supine sites
Rep	AUC without overfit correction [95% CI]	AUC with overfit correction [95% CI]	Parameters selected by model
			Frequency	Relaxation Time	Stiffness	Creep	Decrement
1	0.873 [0.725, 1]	0.778 [0.429, 0.978]	1.161	−0.139	-	-	-
2	0.873 [0.725, 1]	0.778 [0.429, 0.978]	0.970	−0.014	-	-	-
3	0.873 [0.725, 1]	0.778 [0.429, 0.978]	1.040	−0.061	-	-	-
4	0.867 [0.721, 1]	0.777 [0.429, 0.978]	1.627	−2.367	−0.542	1.500	−0.095
5	0.873 [0.725, 1]	0.778 [0.429, 0.978]	1.005	−0.038	-	-	-
6	0.873 [0.725, 1]	0.778 [0.429, 0.978]	1.161	−0.139	-	-	-
7	0.873 [0.725, 1]	0.778 [0.429, 0.978]	1.040	−0.061	-	-	-
8	0.873 [0.725, 1]	0.778 [0.429, 0.978]	1.161	−0.139	-	-	-
9	0.873 [0.725, 1]	0.778 [0.429, 0.978]	0.923	-	-	-	-
10	0.873 [0.725, 1]	0.778 [0.429, 0.978]	1.040	−0.061	-	-	-

A random forest classification algorithm ranked the five biomechanical parameters by their importance in differentiating sclerotic cGVHD from post-HCT controls. 10 of 10 iterations (Table 6) identified frequency as the most important variable, followed by relaxation time, consistent with both logistic regression and LASSO regression models.

Table 6.

MyotonPRO biomechanical parameters in descending order of feature importance (1=most important, 5=least important) selected by random forest models (10 iterations) for averages across all sites (cGVHD n=13, control n=11) and averages across supine sites (cGVHD n=15, control n=11). Note the conserved order apart for position of stiffness and creep.

Averages across all sites
Parameter	Feature Importance
Frequency	1
Relaxation time	2
Stiffness	4
Creep	3
Decrement	5
Averages across supine sites
Parameter	Feature Importance
Frequency	1
Relaxation time	2
Stiffness	3
Creep	4
Decrement	5

The overfit-corrected AUCs from bivariable logistic regressions of frequency and relaxation time for averages across all sites and averages across supine sites were 0.89 and 0.85, respectively (Table 4).

Analysis of anatomic sites

LASSO regression was performed on each anatomic site. Combinations of parameters determined by LASSO as the most important variables for each site are shown in Table 7. Additional univariable analyses examined the discriminatory ability of each of the five biomechanical parameters for individual anatomic sites (Table 8). Both frequency and relaxation time trended towards higher discriminatory ability in the shin, upper back, chest, upper arm, and abdomen (Figure 4). Stiffness demonstrated higher discriminatory ability in the chest, shin, and upper arm, while creep had higher discriminatory ability in the chest and upper back. Decrement had high discriminatory ability in the dorsal forearm (Table 8).

Table 7.

Representative¹ combinations for parameters selected by LASSO regression as the most important variables in differentiating sclerotic cGVHD patients from post-HCT controls for each site.

	Frequency	Relaxation Time	Stiffness	Creep	Decrement	AUC with overfit correction [95% CI]
Abdomen L	+	+	+		+	0.884 [0.674, 0.996]
Abdomen R	+	+			+	0.902 [0.737, 0.999]
Upper Arm L	+		+			0.773 [0.431, 0.981]
Upper Arm R	+		+			0.773 [0.422, 0.983]
Chest L	+	+		+	+	0.801 [0.437, 0.992]
Chest R		+				0.829 [0.546, 0.992]
Upper Back L	+				+	0.840 [0.533, 0.994]
Upper Back R	+				+	0.756 [0.358, 0.987]
Shin L		+			+	0.855 [0.606, 0.992]
Shin R		+	+		+	0.761 [0.407, 0.978]
Calf L	+					0.741 [0.404, 0.964]
Calf R	+	+	+	+	+	0.780 [0.411, 0.986
Lower Back L		+	+		+	0.812 [0.445, 0.988]
Lower Back R	+		+	+	+	0.740 [0.327, 0.979]
Shoulder L	+	+	+	+	+	0.725 [0.381, 0.955]
Shoulder R	+	+	+	+	+	0.757 [0.392, 0.981]
Dorsal Forearm L		+			+	0.782 [0.427, 0.985]
Dorsal Forearm R	+				+	0.846 [0.559, 0.995]
Average across all sites	+	+				0.871 [0.641, 0.998]
Average across supine sites	+	+				0.778 [0.429, 0.978]

¹Representative: out of 10 repetitions, the most commonly selected combination of parameters for each site is shown.

Table 8.

Area under the receiver operating characteristic curve (AUC) of univariable analyses of each of the five parameters for individual sites. Overfit-corrected AUCs under 0.8 are shaded light-grey, AUCs under 0.7 are shaded dark-grey.

	Frequency		Relaxation Time		Stiffness		Creep		Decrement
	AUC (95% CI)	Overfit-corrected AUC	AUC (95% CI)	Overfit-corrected AUC	AUC (95% CI)	Overfit-corrected AUC	AUC (95% CI)	Overfit-corrected AUC	AUC (95% CI)	Overfit-corrected AUC
Abdomen L	0.824 (0.665, 0.983)	0.825	0.873 (0.737, 1)	0.871	0.661 (0.437, 0.884)	0.652	0.739 (0.543, 0.936)	0.728	0.661 (0.436, 0.885)	0.628
Abdomen R	0.939 (0.845, 1)	0.949	0.873 (0.725, 1)	0.878	0.745 (0.550, 0.941)	0.743	0.758 (0.567, 0.949)	0.753	0.606 (0.376, 0.836)	0.572
Upper Arm L	0.861 (0.715, 1)	0.852	0.788 (0.610, 0.966)	0.778	0.855 (0.702, 1)	0.848	0.667 (0.452, 0.882)	0.627	0.600 (0.373, 0.827)	0.543
Upper Arm R	0.824 (0.656, 0.992)	0.818	0.776 (0.593, 0.959)	0.766	0.842 (0.693, 0.992)	0.833	0.648 (0.431, 0.866)	0.607	0.582 (0.350, 0.814)	0.493
Chest L	0.861 (0.718, 1)	0.853	0.836 (0.675, 0.998)	0.828	0.812 (0.642, 0.983)	0.801	0.779 (0.599, 0.958)	0.769	0.491 (0.260, 0.722)	0.398
Chest R	0.812 (0.645, 0.979)	0.810	0.885 (0.755, 1)	0.884	0.812 (0.646, 0.978)	0.804	0.873 (0.730, 1)	0.874	0.588 (0.359, 0.817)	0.51
Upper Back L	0.851 (0.697, 1)	0.852	0.877 (0.739, 1)	0.877	0.779 (0.594, 0.965)	0.777	0.877 (0.731, 1)	0.877	0.799 (0.622, 0.976)	0.795
Upper Back R	0.821 (0.648, 0.995)	0.819	0.818 (0.624, 1)	0.815	0.727 (0.515, 0.939)	0.706	0.825 (0.632, 1)	0.824	0.773 (0.583, 0.963)	0.768
Shin L	0.8 (0.609, 0.991)	0.788	0.836 (0.662, 1)	0.829	0.824 (0.643, 1)	0.815	0.818 (0.639, 0.997)	0.811	0.733 (0.533, 0.933)	0.718
Shin R	0.788 (0.595, 0.98)	0.779	0.824 (0.661, 0.987)	0.816	0.861 (0.719, 1)	0.853	0.770 (0.584, 0.956)	0.762	0.664 (0.443, 0.884)	0.639
Calf L	0.782 (0.593, 0.97)	0.771	0.764 (0.563, 0.964)	0.747	0.782 (0.583, 0.980)	0.762	0.721 (0.510, 0.932)	0.7	0.582 (0.349, 0.814)	0.514
Calf R	0.818 (0.633, 1)	0.808	0.800 (0.611, 0.989)	0.788	0.861 (0.690, 1)	0.857	0.752 (0.553, 0.95)	0.738	0.491 (0.251, 0.731)	0.399
Lower Back L	0.804 (0.623, 0.986)	0.801	0.776 (0.586, 0.966)	0.773	0.790 (0.605, 0.975)	0.786	0.657 (0.427, 0.888)	0.628	0.713 (0.492, 0.935)	0.692
Lower Back R	0.685 (0.465, 0.906)	0.665	0.755 (0.556, 0.955)	0.75	0.783 (0.593, 0.973)	0.781	0.699 (0.484, 0.914)	0.671	0.678 (0.453, 0.904)	0.649
Shoulder L	0.594 (0.360, 0.828)	0.517	0.655 (0.428, 0.881)	0.607	0.673 (0.449, 0.896)	0.627	0.630 (0.398, 0.862)	0.554	0.567 (0.334, 0.799)	0.504
Shoulder R	0.691 (0.478, 0.904)	0.681	0.752 (0.561, 0.942)	0.741	0.776 (0.595, 0.956)	0.779	0.733 (0.528, 0.938)	0.706	0.515 (0.279, 0.751)	0.422
Dorsal Forearm L	0.594 (0.350, 0.838)	0.545	0.570 (0.323, 0.817)	0.515	0.503 (0.260, 0.746)	0.433	0.618 (0.370, 0.866)	0.568	0.824 (0.663, 0.985)	0.832
Dorsal Forearm R	0.685 (0.465, 0.905)	0.671	0.648 (0.427, 0.870)	0.618	0.594 (0.367, 0.821)	0.555	0.673 (0.458, 0.887)	0.650	0.915 (0.788, 1)	0.918
Average across 18 sites	0.909 (0.786, 1)	0.910	0.888 (0.756, 1)	0.890	0.874 (0.734, 1)	0.875	0.860 (0.711, 1)	0.862	0.615 (0.361, 0.869)	0.594

Figure 4.

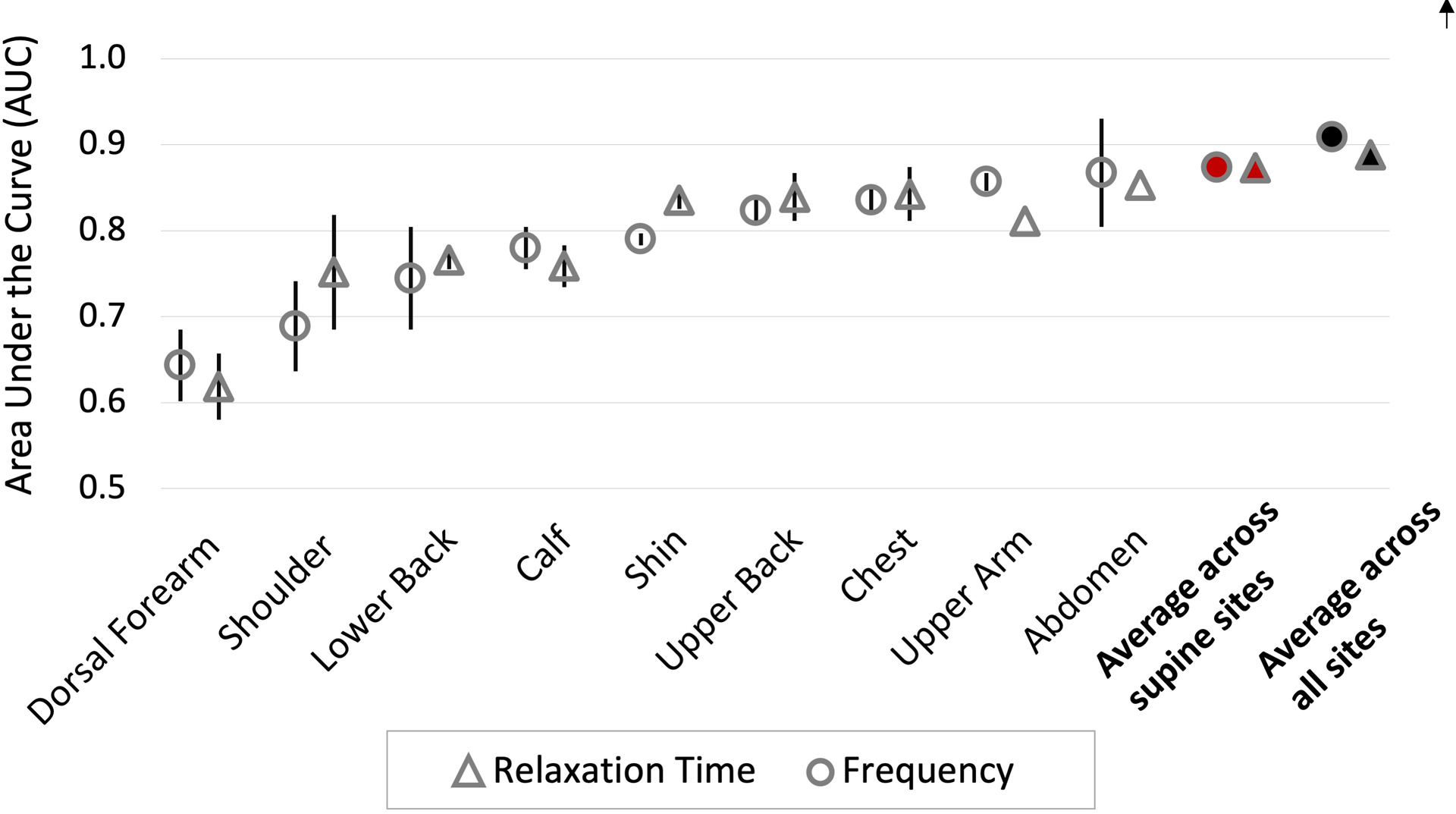
Area under the receiver operating characteristic curve (AUC) of univariable analyses of frequency and relaxation time for individual anatomic sites (frequency = open circles, relaxation time = open triangles), averages across 12 supine sites (red-filled markers, cGVHD n=15; controls n=11), and across all 18 measured sites (black-filled markers, cGVHD n=13; controls n=11). Markers represent the averages of the left and right anatomic sites’ AUCs. Error bars represent the ranges between the left and right AUCs.

Correlation between biomechanical parameters

Spearman’s correlation (r) between frequency and relaxation time was −0.94 for both averages across all sites and averages across supine sites (Table 9). High correlation (absolute value of r close to 1) between frequency and relaxation time suggests presence of redundant information provided by the two parameters. Similarly, stiffness was highly correlated with frequency (r 0.95 for both averages across all sites and averages across supine sites) and negatively correlated with relaxation time (r −0.93 and −0.94, for averages across all sites and averages across supine sites, respectively).

Table 9.

Spearman’s correlation coefficient matrix between the MyotonPRO biomechanical parameters using parameter averages in all study patients (combined sclerotic cGVHD and post-transplant control) for averages across all sites (n=24) and averages across supine sites (n=26). Higher absolute value of Spearman’s correlation coefficient represents greater correlation between two parameters.

Averages across all sites
	Frequency	Relaxation time	Stiffness	Creep	Decrement
Frequency	1	−0.94	0.95	−0.86	−0.28
Relaxation time	−0.94	1	−0.93	0.94	0.41
Stiffness	0.95	−0.93	1	−0.82	−0.22
Creep	−0.86	0.94	−0.82	1	0.54
Decrement	−0.28	0.41	−0.22	0.54	1
Averages across supine sites
	Frequency	Relaxation time	Stiffness	Creep	Decrement
Frequency	1	−0.94	0.95	−0.87	−0.10
Relaxation time	−0.94	1	−0.94	0.94	0.15
Stiffness	0.95	−0.94	1	−0.87	−0.04
Creep	−0.87	0.94	−0.87	1	0.32
Decrement	−0.10	0.15	−0.04	0.32	1

DISCUSSION

Objective measurement of skin sclerosis is an unmet need for many sclerosing diseases including cGVHD and systemic sclerosis (Carpenter et al., 2015; Odell et al., 2020). The myotonometer is a promising potential response measure instrument, but many questions must be answered prior to clinical implementation (Table 10). The device has demonstrated high inter-operator reliability in measuring stiffness in healthy controls and sclerotic cGVHD patients (Chen et al., 2019; Dellalana et al., 2019). A recent longitudinal study in sclerotic cGVHD patients showed that stiffness measurements over time correlated with clinically important changes in disease (Baker et al., 2021). Our previously published cross-sectional analysis of myotonometry measurements lacked post-HCT controls and only evaluated the discriminatory ability of the stiffness parameter (Chen et al., 2018). By investigating all five available parameters using logistic regression and machine learning models, the present study found that measuring frequency and relaxation time offer the highest diagnostic yield in differentiating sclerotic cGVHD patients from post-HCT controls.

Table 10.

Topics of investigation required for the myotonometer to serve as a valid response measure instrument in the management of sclerotic cGVHD.

Topics of investigation	Relevant Studies
1. Intra- and inter-operator reliability	Dellalana LE, Chen F, Vain A, Gandelman JS, Põldemaa M, Chen H, et al. Reproducibility of the durometer and myoton devices for skin stiffness measurement in healthy subjects. Skin Res Technol. 2019; 25(3):289–93.
2. Ability to discriminate obvious sclerotic patients from healthy patients	Chen F, Dellalana LE, Gandelman JS, Vain A, Jagasia MH, Tkaczyk ER. Non-invasive measurement of sclerosis in cutaneous cGVHD patients with the handheld device Myoton: a cross-sectional study. Bone Marrow Transplant. 2018; 54(4):616–19.
3. Ability to discriminate obvious sclerotic patients from post-HCT controls without signs of clinical sclerosis	Current study
4. Determination of the optimal parameter or combination of parameters for question 3	Current study
5. Selection of an efficient clinical protocol which future studies and clinical practice can use for patient-level investigation	Chen F, Dellalana LE, Gandelman JS, Vain A, Jagasia MH, Tkaczyk ER. Non-invasive measurement of sclerosis in cutaneous cGVHD patients with the handheld device Myoton: a cross-sectional study. Bone Marrow Transplant. 2018; 54(4):616–19. Current study found that a supine-only protocol maintained discriminatory ability.
6. Determination of whether individual sites are more or less useful than averages across sites, as well as how individual sites correlate with the clinical appreciation of sclerosis at or near those sites	Current study provides the typical ranges of parameter values that may be used to design future studies.
7. Consistency of longitudinal measurements with clinical response	Baker LX, Chen F, Ssempijja Y, Byrne M, Kim TK, Vain A, et al. Longitudinal tracking of skin dynamic stiffness to quantify evolution of sclerosis in chronic graft-versus-host disease [e-pub ahead of print]. Bone Marrow Transplant; doi:10.1038/s41409-020-01158-w
8. Ability to detect subclinical disease	Future study

While all models placed importance on frequency and relaxation time, whether these parameters should be used alone or in combination requires further consideration. Possible redundant information between frequency and relaxation time, suggested by the high Spearman’s correlation, may limit the added explanatory value provided by the inclusion of the second parameter. Accordingly, with overfit correction, bivariable frequency and relaxation time did not outperform either univariable frequency or univariable relaxation time analyses. Similarly, backward elimination selected single-parameter models (frequency for averages across all sites, relaxation time for averages across supine sites) over models with combinations of parameters. In contrast, the LASSO algorithm, which also had the ability to select either a single variable or a combination of variables, favored models using the combination of frequency and relaxation time over single-variable models. An independent data set is needed to validate and compare the classification performance of frequency, relaxation time, and the combination of the two parameters.

This study also informs the development of future myotonometer measurement protocols. Because the AUCs of the parameter averages across the 12 supine sites did not differ significantly from those across all 18 measured sites, an expedient supine-only measurement protocol may be implemented to reduce measurement time and improve patient experience, while maintaining diagnostic accuracy. Additionally, the dorsal forearm, which had previously been found to have low interobserver repeatability (Dellalana et al., 2019), exhibited the lowest AUCs for both frequency and relaxation time in the present study. Thus, the dorsal forearm may be omitted or substituted with another site, such as the volar forearm, in future measurement protocols. Lastly, we report the distribution of values of biomechanical parameters for sclerotic cGVHD patients and post-HCT controls, which could inform the design of future myotonometer studies.

This study has several limitations. Of the 11 post-HCT controls, three subjects were measured within 12 months of HCT (Table 2) and could have had subclinical cGVHD at the time of measurement. In addition, the myotonometer does not distinguish between cGVHD changes in the skin, changes in subcutaneous tissue, and changes in fascia and skeletal muscle (Hu et al., 2018; Oda et al., 2009). The measurements represent contributions from all underlying soft tissue layers and the proportional contribution of each layer is unknown. Our study design lacked an independent validation data set. While boot-strapping was used to generate confidence intervals, an independent validation set is required to assess model accuracy. Finally, the device’s ability to differentiate clinically sclerotic sites from clinically normal sites is an important question precluded by our study design. For clinical implementation, a future study that follows patients before clinical signs of sclerosis, through the subsequent appearance of sclerosis is required.

In conclusion, this study shows that a brief clinical protocol measuring the frequency and relaxation time of patients’ skin can effectively differentiate sclerotic cGVHD patients from post-HCT controls. A larger follow-up study is needed for model validation.

MATERIALS & METHODS

Data collection

The study protocol was approved by the Institutional Review Board at Vanderbilt (IRB# 170456) and the Department of Veterans Affairs Tennessee Valley Healthcare System (IRB# 1170055). 15 sclerotic cGVHD patients (NIH Skin Features Score 2–3) and 11 post-HCT controls were recruited. All participants provided written informed consent. Subjects underwent MyotonPRO measurement by a single observer (JFC) according to our previously published protocol (Chen et al., 2018). Each subject was measured on 9 anatomic sites bilaterally over completely relaxed muscles (shin over tibialis anterior, dorsal forearm over extensor digitorum, upper arm over biceps brachii caput longum, shoulder over medial deltoideus, chest over pectoralis major, abdomen over rectus abdominus, calf over gastrocnemius caput laterale, upper back over medial trapezius, and lower back over erector spinae), resulting in 18 total measurement sites. Each measurement session lasted ~20 minutes. Two of the cGVHD patients were measured only on the 12 sites that could be measured with the patient in the supine position (bilateral shin, dorsal forearm, upper arm, shoulder, chest, and abdomen) due to discomfort when laying in the prone position. These supine-only measurement sessions lasted ~10–15 minutes.

Statistical analysis

For each subject, we calculated the parameter averages over all 18 measured sites and over the 12 supine sites. The Wilcoxon rank sum test was performed to compare the distributions of parameter averages between sclerotic cGVHD patients and post-HCT controls. Spearman’s correlation coefficient was calculated for each pair of the parameters. We evaluated the discriminatory ability of the parameters using: (1) univariable logistic regression for each parameter, (2) backward stepwise selection on the 5-parameter logistic regression model, (3) bivariable logistic regression consisting of frequency and relaxation time, (4) LASSO regression, and (5) random forest. The AUC was used to compare model performances. Overfit-corrected AUCs were calculated from Bootstrap 0.632+ method with 100 bootstrap replications (Efron and Tibshirani, 1997). All analyses were completed using R, version 3.6.1.

Backward stepwise selection was performed by eliminating one parameter at a time from the full 5-parameter model to minimize the AIC. The AIC assesses the models’ goodness of fit while penalizing model complexity. A smaller AIC value suggests a simpler model with better fit. The final model is reached when the elimination of any remaining parameter no longer reduced the AIC.

LASSO is a machine learning algorithm that extends standard logistic regression models by enabling variable selection in the fitting process (Friedman et al., 2010). All variables were standardized prior to LASSO regression. The R package glmnet was applied to build a LASSO regression (Friedman et al., 2021). Each analysis consisted of 10 repetitions of 3-fold cross validation. The 3-fold cross-validation selected the tuning parameters and determined which of the 5 biomechanical properties, alone or in combination, best indicated the diagnosis of sclerotic cGVHD.

Random forest is an ensemble learning algorithm that uses sets of classification or regression trees to evaluate the potential variables and rank them according to their relative strength in predicting the outcome (Strobl et al., 2009). The R package randomForest was applied to build the random forest classification algorithm (Breiman et al., 2018). Random forest analysis ranked the five biomechanical parameters by their importance in differentiating sclerotic cGVHD from post-HCT controls.

Abbreviations:

cGVHD

chronic graft-versus-host disease

AUC

area under the receiver operating characteristic curve

HCT

hematopoietic cell transplantation

NIH

National Institutes of Health

LASSO

least absolute shrinkage and selection operator

ICC

intraclass correlation coefficient

Data availability statement:

Datasets related to this article can be found at http://dx.doi.org/10.17632/6mdy96dkxz.1, an open-source online data repository hosted at Mendeley Data (Baker et al., 2021).