Abstract
Extracellular physiological recordings are typically separated into two frequency bands: local field potentials (LFPs, a circuit property) and spiking multi-unit activity (MUA). There has been increased interest in LFPs due to their correlation with fMRI measurements and the possibility of studying local processing and neuronal synchrony. To further understand the biophysical origin of LFPs, we asked whether it is possible to estimate their time course based on the spiking activity from the same or nearby electrodes. We used Signal Estimation Theory to show that a linear filter operation on the activity of one/few neurons can explain a significant fraction of the LFP time course in the macaque primary visual cortex. The linear filter used to estimate the LFPs had a stereotypical shape characterized by a sharp downstroke at negative time lags and a slower positive upstroke for positve time lags. The filter was similar across neocortical regions and behavioral conditions including spontaneous activity and visual stimulation. The estimations had a spatial resolution of ~1 mm and a temporal resolution of ~200 ms. By considering a causal filter, we observed a temporal asymmetry such that the positive time lags in the filter contributed more to the LFP estimation than negative time lags. Additionally, we showed that spikes occurring within ~10 ms of spikes from nearby neurons yielded better estimation accuracies than nonsynchronous spikes. In sum, our results suggest that at least some circuit-level local properties of the field potentials can be predicted from the activity of one or a few neurons.
Keywords: local field potentials, neuronal circuits, signal estimation theory, spike trains, computational neuroscience, biophysical models
1. INTRODUCTION
The brain is usually studied at multiple scales from molecules to systems. How signals at one scale relate to those at other scales is poorly understood. Of particular importance towards understanding how perception and action are orchestrated by neuronal signals is to characterize how the activity of neuronal circuits consisting of tens to thousands of neurons arises from their component units and their interactions. A major challenge towards achieving this goal is the experimental difficulty of recording simultaneously from multiple nearby neurons and the theoretical efforts required to characterize biophysically realistic neural networks.
The extracellular voltage recorded extracellularly through microwires is typically separated into two frequency bands (Logothetis, 2002): the multi-unit spiking activity (MUA) and the local field potentials (LFPs) (Figure 1A). MUA represents a weighted sum of the action potentials of neurons within a radius of about 200 μm around the electrode tip (Holt and Koch, 1999; Gold et al., 2006). Low-pass filtering the extracellular signal (with a corner frequency of about 100–300 Hz) yields the local field potential (LFP). The biophysical nature of the MUA signal is much better understood than the origins of the LFP. The LFPs are thought to reflect the activity of large numbers of neurons in a sphere of one to several millimeters around the recording electrode ((Mitzdorf, 1985; Juergens et al., 1999); see however (Katzner et al., 2009)). Current-source density analyses and simultaneous recordings of spikes and LFPs have suggested that LFPs are more strongly correlated with EPSPs, afterpotentials and dendritic spikes than with the output action potentials of the surrounding neurons (Haberly and Shepherd, 1973; Mitzdorf, 1985; Logothetis, 2002). This has led to the notion that LFPs represent the input to and local processing within a given brain area.
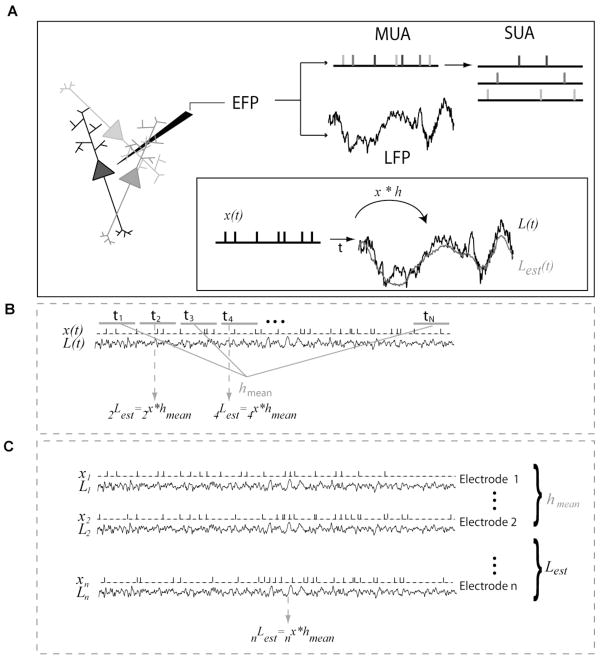
Figure 1. LFP estimation method.
(A) The extracellular field potential (EFP) is typically separated into two frequency bands: the local field potentials (LFP) and the multi-unit spiking activity (MUA). The MUA signal can in turn be separated into multiple single-unit activity (SUA) clusters through spike sorting. Except for Figure S9 all the Figures in this manuscript use MUA. An estimate, Lest(t), of the LFP, L(t), was obtained from the spike train, x(t), by convolving the spike train with a Wiener-Kolmogorov filter (see text for details). The filter h was computed using half of the recorded LFP and spike train (labeled “trial-specific filter” in Figure 3A). The estimation accuracy was quantified by computing the correlation coefficient (r) between the LFP and the estimate in the remaining half of the recordings. (B) Construction of a general filter for the estimation of all LFPs collected with a given electrode in V1 (labeled “electrode-specific” filter in Figure 3B). Several four-minute time series of spontaneous activity (“trials”) were simultaneously collected with 8 to 16 electrodes placed in V1 of seven monkeys. For each electrode, half of the trials (odd-numbered trials) were selected for the construction of a general filter hmean. The LFPs of the remaining half of the trials collected with the same electrode were then estimated by convolving the general filter with the corresponding spike trains (see text for details). (C) In a similar fashion to (B), we considered the LFP estimation using a single general filter for all electrodes recorded from a given monkey. For this purpose, half of the electrodes were randomly selected to construct a general filter (labeled “monkey-specific” filter in Figure 3C). The LFPs recorded from all the remaining electrodes were then estimated by convolving the general filter with each spike train.
Many approaches have been followed to compare spikes and LFPs (e.g. (O’Keefe and Recce, 1993; Fries et al., 2001; Laurent, 2002; Pesaran et al., 2002; Bedard et al., 2004; Kreiman et al., 2006; Belitski et al., 2008; Montemurro et al., 2008; Nauhaus et al., 2008; Rasch et al., 2008) among others). Here we asked whether it is possible to estimate the time course of LFPs from spiking activity. At first glance, the large differences in terms of the spatial scales and biophysical origin between the two signals might suggest that this would be a challenging task. We use methods from Signal Estimation Theory (Poor, 1994) to show that a linear filter operation on the activity of one or a few neurons can explain a significant fraction (but not all) of the LFP time course. The estimations have a spatial scale of ~1mm and a temporal scale of ~200ms. The linear filter estimation extrapolates across cortical regions and behavioral conditions. We also show that spikes that temporally coincide within ~10 ms with spikes from nearby neurons lead to better estimations. Taken together, these results suggest that the activity of individual neurons can be related to at least some of the circuit level properties of local field potentials.
2. METHODS
2.1 Electrophysiological recordings and data processing
Electrophysiological data recorded from seven anesthetized monkeys (Macaca mulatta) are included in the present study. Detailed description of the surgical methods and recording setup are described elsewhere (Rasch et al., 2008). Briefly, simultaneous recordings of neuronal activity were made from primary visual cortex (V1) using 8 to 16 electrodes configured in 4 × 4 or 8 × 2 matrices in a grid of 1 to 2 mm. We study data recorded during spontaneous activity (labeled “spont” throughout the text) and data recorded while the monkey was shown a commercial movie (labeled “stim” throughout the text). In the spontaneous condition, the V1 data studied here (7 monkeys, 109 electrodes) were recorded during periods when the input screen was blank for about 4 minutes. Multiple segments of spontaneous activity were recorded within each session. From each session we considered five segments of spontaneous activity. Unless described otherwise in the text, all electrodes recorded in each session were included in the analyses. This resulted in 545 (5 × 109) recorded time series of four minutes length, which we refer to as “trials” throughout the manuscript. In three sessions (two anesthetized monkeys), four electrodes were simultaneously placed in the LGN. In the visual stimulation condition (6 monkeys, 84 electrodes, 420 “trials”), a 4 to 6 minute movie segment was shown to the monkey. The movie frames, synchronized to the monitor refresh rate (60 Hz), encompassed 7 to 12 degrees of the visual field (Rasch et al., 2008). The analyses for the “spont” and “stim” conditions are based on 4-min segments where we discarded the initial and final 30 seconds to avoid potential non-stationarities. Examples of the power spectral density for the LFP recordings and the spike trains are shown in Figure S1. The LFP power spectral densities show a power law decay similar to those reported in other studies (e.g. (Henrie and Shapley, 2005; Nauhaus et al., 2008) among many others) and the log-log plots can be fitted with a line of slope close to 2 ((Milstein et al., 2009); Figure S1). For comparison purposes, in Section 3.2 and Figure 4A we show results obtained based on recordings from awake monkey inferior temporal cortex during passive viewing conditions from the study reported in (Kreiman et al., 2006).
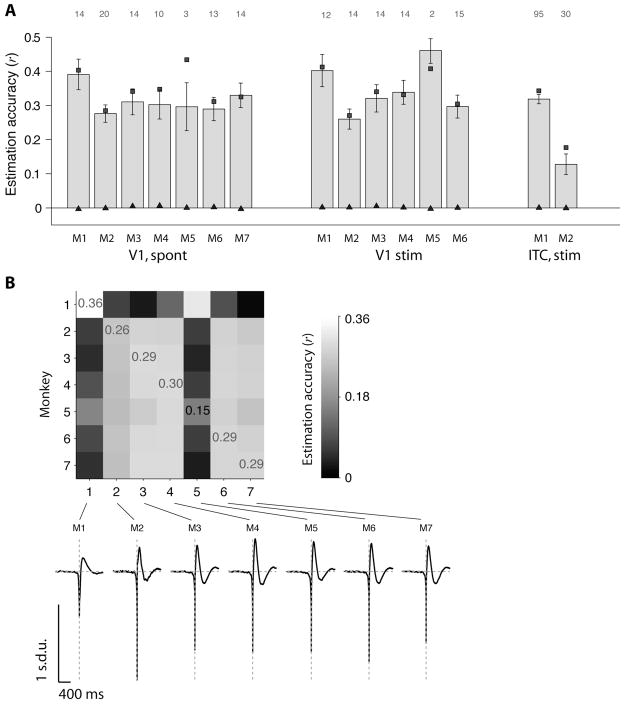
Figure 4. Linear estimation of LFPs across monkeys, stimuli and locations.
(A) Average estimation accuracies for all electrodes in V1 under spontaneous activity in 7 monkeys (left), all electrodes in V1 during visual stimulation in 6 monkeys (middle) and all electrodes in inferior temporal cortex (ITC) during visual stimulation in 2 monkeys (right). The V1 visual stimulation consisted of natural movies (see Methods). The ITC visual stimulation consisted of static grayscale images presented for 100 ms during passive viewing (Kreiman et al., 2006). Each bar indicates the mean estimation accuracy averaged over all the electrodes in each monkey (using “electrode-specific” filters; see Figure 1B). The error bars denote one SEM. The number of electrodes averaged in each case is indicated above each column. The conventions are the same as in Figure 3; the squares indicate the reconstruction accuracy and the triangles show the estimation accuracies expected by chance.
(B) Estimation accuracies computed across monkeys (V1 data, spontaneous activity). Entry in row i, column j indicates the estimation accuracy obtained when the W-K filter was computed using all the electrodes recorded in monkey i and the estimation accuracy was computed using the spike trains and LFPs from monkey j. Note that the LFP estimate for a given electrode is always computed here using the spike train from the same electrode (using Eq. 2). The W-K filter is computed using data from a different monkey (using Eq. 8). The values reported correspond to the average across all electrodes in monkey j. We indicate the estimation accuracies for the diagonal entries for reference. The bottom part shows the W-K filters for each monkey.
The data preprocessing steps are described in detail in (Rasch et al., 2008). Briefly, electrode signals were decimated to 7 KHz. The 7-KHz signal was low-pass filtered with a cutoff frequency of 220 Hz and resampled at 500 Hz to obtain the local field potentials (LFPs). Spike times were detected by applying a threshold to the high-pass filtered 7-KHz signal (fourth-order Butterworth, cutoff frequency 500 Hz). Except when noted otherwise, the detection threshold was applied at 5 standard deviations of the noise component of the multi-unit activity (MUA) signal. In Figure S9, we examined the dependence of the estimation accuracies on the spike detection threshold. In Figure S9, we also performed spike sorting using the algorithm described in (Quian Quiroga et al., 2004) to compare the performance MUA against single-unit activity (SUA).
2.2 Linear estimation of time-varying signals from spike trains
We asked whether we could infer the time course of the local field potentials from the spike trains recorded from one cell or a small number of cells near the LFP electrode. One possible approach to this problem is to apply methods of Signal Estimation Theory (Poor, 1994). Such methods have been used in Neurobiology by several groups (Bialek et al., 1991; Rieke et al., 1993; Gabbiani and Koch, 1996; Kreiman et al., 2000) to study the transmission of information by peripheral sensory neurons. Here we analyzed the data using the following algorithm (Bialek et al., 1991; Gabbiani and Koch, 1996) (see the scheme in Figure 1A). Let
| (1) |
be the spike train obtained after subtracting the mean firing rate x0 (where ti are the spike occurrence times). Except in Figure S9B, x(t) contains spikes from multi-unit activity. A linear estimate, Lest(t), of the local field potential, L(t), given the spike train was obtained by convolving x(t) with a filter, h(t),
| (2) |
where T is the duration of the LFP recording and τ is the integration variable spanning the convolution period. The Wiener-Kolmogorov (W-K) filter, h(t), is chosen in such a way as to minimize the mean squared error, ε2, between the LFP and its estimate:
| (3) |
where the integration is over the LFP recording duration T. An explicit formula for this filter is given by (Poor, 1994):
| (4) |
where fc is the cutoff frequency of the LFP, PLx is the Fourier transform of the cross-correlation between the LFP and the spike train and Pxx is the Fourier transform of the spike train autocorrelation.
We considered 3 types of W-K filters: (i) “trial-specific” filters, (ii) “electrode-specific” filters and (iii) “monkey-specific” filters (Figure 1). For the “trial-specific” filter, each trial was divided into two segments of equal length. The first segment was used to estimate the W-K filter according to Eq. 4. The second segment was used to estimate the LFP according to Eq. 2. The performance of the filter in this test is labeled “estimation accuracy” throughout the text (see below for the computation of the estimation accuracy). We compared this estimation accuracy against the “reconstruction accuracy” obtained by using the same segment to compute the W-K filter and to reconstruct the LFP time course. The reconstruction accuracies are reported in the figures as black squares and likely contain some amount of overfitting. All the conclusions in this manuscript are based on the estimation accuracies where the data used to compute the filter are separate from the data used to estimate the LFP. For the “electrode-specific” filter, we used half of the trials recorded from each electrode (odd-numbered trials) to compute the W-K filter and used the remaining half of the trials (even-numbered trials) to estimate the LFPs (Figure 1B). Unless stated otherwise, throughout the text we report the estimation accuracies obtained by the “electrode-specific” filters. As described in the Results section below, we observed that the W-K filters were very similar across electrodes and recording conditions. Therefore, we also evaluated the performance of a “monkey-specific” filter where the data from half of the electrodes were used to compute the W-K filter and the data from the remaining half of the electrodes were used to estimate the LFP (Figure 1C).
The W-K filter in Eq. 4 will not be causal in general (i.e., h(t) ≠ 0 for t > 0). Imposing the causality constraint on the filter h requires solving the causal Wiener-Hopf equation (Poor, 1994). Since h has a finite support in the time domain, causality can also be implemented by introducing a delay in the filter (Bialek et al., 1991). In the present study we used this second method to impose causality (see Section 3.7 and Figure 8).
Figure 8. Causal filters.
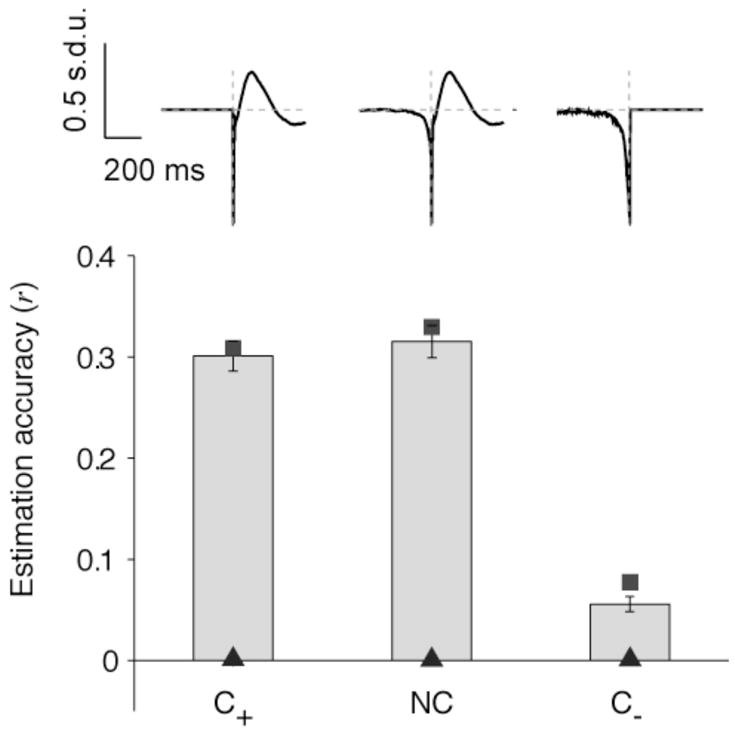
Mean estimation accuracies (“electrode-specific” filters, V1, spontaneous activity) for three different filters: NC (non causal filter, as used in Figures 2–7), C+ (only has information for positive time lags; hC+(α) = 0 for α < 0)) and C− (only has information about negative time lags; hC−(α) = 0 for α > 0)). The conventions are the same as in Figure 3. Error bars denote one SEM (n=88 electrodes). The squares indicate the mean reconstruction accuracy. The triangles indicate the mean estimation accuracies under the null hypothesis (generating a Poisson spike train with the same number of spikes). All the LFP estimation accuracies shown here are statistically significant compared with the estimations obtained under the null hypothesis (p<0.01, two-sample Kolmogorov-Smirnov test). The estimations obtained with NC and C+ are statistically indistinguishable (p>0.1) and there is a significant difference between the estimations obtained with either NC or C+, and C− (p<0.01).
2.3 Data Analysis
All the data were analyzed using MATLAB (Mathworks, Natick, MA). The spike occurrence times were resampled at 500 Hz together with the LFPs. Estimates of the LFP and spike train power spectra were obtained with a fast Fourier transform algorithm and Bartlett windowing using nfft=2048. As expected, the estimation accuracies, and in particular the reconstruction accuracies, depend on nfft (Figure S2A). Small values of nfft do not capture enough information of the LFP time course and very large values lead to overfitting. Throughout the text, we use nfft=2048.
The same analysis was performed to obtain estimates of the cross-correlation between spike trains and LFPs. The cutoff frequency of the LFP was estimated by fitting the squared gain of the low-pass (Butterworth) filter transfer function to the power spectrum of the LFP, L(t). The optimal W-K filter, h(t), was obtained by deconvolving the cross-correlation of the spike train and the LFP with the power spectrum of the spike train according to Eq. 4. The LFP estimations (Lest(t)) were obtained by computing the convolution of the W-K filter and the spike train, x(t), (see Eq. 2) in the frequency domain with the use of a fast Fourier transform.
2.4 Performance measures
Since the filter h is derived by minimizing the mean squared error between the LFP and the estimated LFP (see Eq. 3), a natural measure for the quality of the estimations is the mean squared error, ε2. Another commonly used performance measure is the Pearson’s correlation coefficient (denoted by r throughout the manuscript). Given that in this case both L(t) and Lest(t) are normalized so that they have zero mean and standard deviation one, a linear relationship exists between the mean squared error and the correlation coefficient: ε2= 2(1 − r) (see Supplementary Material for the derivation of this expression and Figure S1F). Throughout the text we report the r values and refer to them as the “estimation accuracy”.
In order to assess the statistical significance of the estimations, we compared the results against a null hypothesis where no correlation existed between the temporal structure of the LFPs and the spike trains. Under the null hypothesis, we generated random spike trains with the same mean firing rate as the experimental spike trains but with spike times governed by a Poisson process (xrand(t)). We then followed the same procedure in Eq. 4 to compute the optimum W-K filter to estimate the LFP time course from the random spike train, hrand:
| (5) |
with . If the spike trains convey no information about the LFP time course, we would expect the correlation between the estimated LFP and the actual LFP obtained from the experimental spike trains to be close to the correlations obtained from the random spike trains. We repeated this procedure 50 times; the average estimation accuracies obtained under the null hypothesis are shown as black triangles throughout the figures. To assess the statistical significance of the LFP estimations, we performed two-tailed t-tests, comparing the estimation accuracies obtained under the null hypothesis against those obtained with the actual spike trains.
3 RESULTS
3.1 Linear LFP estimations based on single trials
We considered 545 spontaneous activity “trials” recorded from V1 (109 electrodes, 7 monkeys), of approximately 4 minutes length (we discarded the first and last 30 seconds to avoid any potential border effects). To estimate the LFP from the spike train, we computed a linear filter that minimizes the difference between the LFP and its estimate (Eqs. 2–4 and Figure 1A). To avoid overfitting the data, the estimation filter h was constructed (as described in Sections 2.2 and 2.3) with the first half of the LFP and spike train of each trial. The estimation, Lest(t), was computed by convolving h with the second half of each spike train. Therefore, there was no overlap between the data used to compute the filter and the data used to test the filter by estimating the LFP time course and measuring the correlation between L(t) and Lest(t) (Section 2.4).
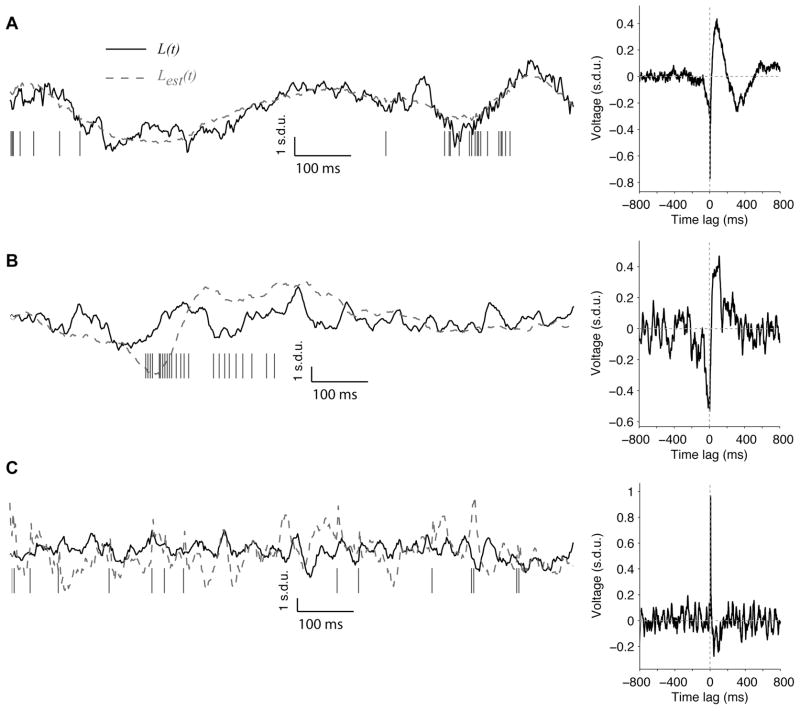
Three one-second segments of typical LFP traces and their estimations are shown in Figure 2. These 3 examples illustrate the range of estimation accuracies from good (Figure 2A; where the estimation captures, to a large degree, the overall structure of the LFP time course) to poor (Figure 2C; where the estimate is only weakly correlated with the actual LFP). We show another example electrode in Figure S3A and we show more data segments for the electrode illustrated in Figure 2A in Figure S3B. We quantified the accuracy of the LFP estimation by computing the Pearson correlation coefficient between the estimation and the actual LFP (referred to as the “estimation accuracy” (r) throughout the manuscript; see Section 2.4). In the examples shown in Figure 2, r has a value of 0.61 (A), 0.29 (B) and 0.01 (C). On the right in Figure 2, we show the corresponding W-K filters for time lags between −800 ms and +800 ms (the actual number of points in the W-K filter was nfft+1 (2049) but there were only small deviations from 0 outside the ±800 ms range). As illustrated by the examples in Figure 2, wider W-K filters tended to yield higher estimation accuracies. Typical features of the W-K filter include a sharp downstroke for tens of ms for negative time lags followed by a slower upstroke lasting more than 100 ms for positive time lags (see also the example W-K filters in Figures 3C, 4B, 8, S3, S7, S9).
Figure 2. Examples of linear estimation of LFPs.
(A–C) Three examples of LFP estimations in 3 different electrodes recording V1 spontaneous activity. A random one-second sample is shown for each electrode; the firing rates and estimation accuracies are computed using a 240-second recording. The solid line shows the actual LFP and the dashed line shows the estimated LFP. The vertical ticks show the action potentials (MUA). On the right, we show the Wiener-Kolmogorov filter for each electrode (hmean). We only show the W-K filter for time lags between −800 ms and +800 ms; the number of points in the W-K filter was nfft+1 (nfft=2048). These examples illustrate the range of estimation levels that we observed (A: r=0.61, firing rate=46 Hz; B: r=0.29, firing rate=10 Hz; C: r=0.01, firing rate 13 Hz). More data segments for the electrode in 2A are shown in Figure S3B.
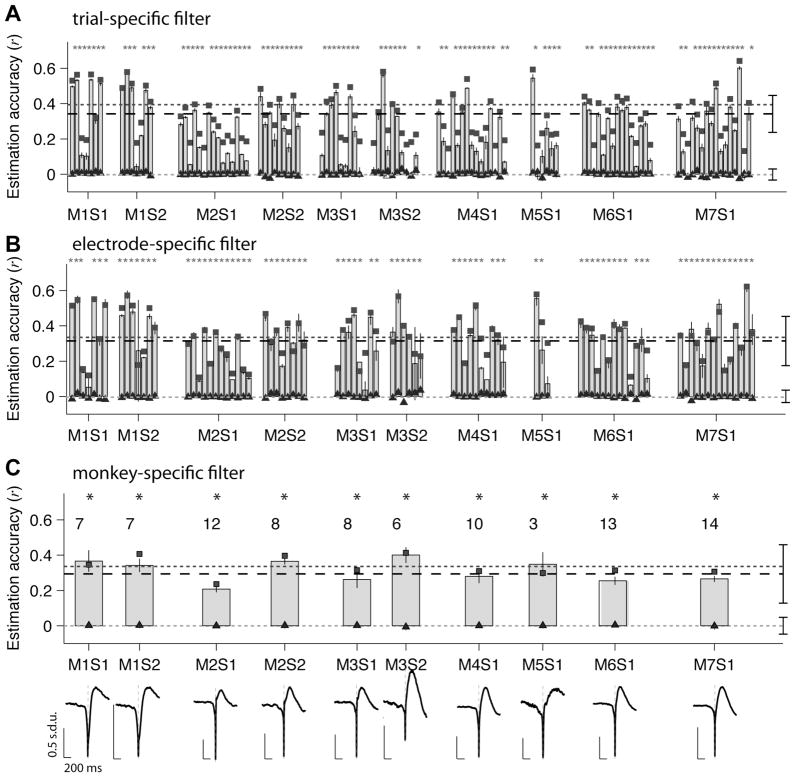
Figure 3. Linear estimation of LFPs for all electrodes.
(A) LFP time course estimations based on “trial-specific” W-K filters (see text and Figure 1A). Each 4-minute trial was split into two segments: one of these was used to build the W-K filter and the other segment was used to compute the LFP estimate. Each vertical bar reports the mean estimation accuracy (labeled “r” throughout the text) for all test trials in one electrode and error bars represent one SEM (5 “trials”). The data are blocked according to recording session (S) and monkey (M). The black squares represent the mean reconstruction accuracy obtained when the same data were used to compute the filter and reconstruct the LFP (see Methods). The triangles indicate the estimation accuracy obtained under the null hypothesis using random spike trains with the same firing rates (see Section 2.4). The “*” indicates statistical significance (p<0.01) based on a two-tailed t-test comparing the estimation accuracies against the null hypothesis. The dashed line indicates the average estimation accuracy (r̄) across all electrodes and all monkeys (r̄ = 0.36±0.15, n=109). The dark gray dotted line indicates the average reconstruction accuracy (average of the black squares, (r̄ = 0.39±0.12, n=109)). The light gray dotted line indicates the average estimation accuracy under the null hypothesis (average of the triangles, r̄ rand = 0.001±0.035, n=109).
(B) LFP time-course estimations based on “electrode-specific” W-K filters (see text and Figure 1B). For each electrode, half of the trials were used to compute the W-K filter and the spike trains in the remaining trials were used to estimate the LFP (Figure 1B). Each bar shows the estimation accuracy for a different electrode averaged over the trials used to estimate the LFP (error bars denote one SEM). The conventions are the same as in part (A). Only those electrodes with firing rate >5 spikes/s and CV>1 are shown here and in subsequent figures (n=88 electrodes out of the total of 109 electrodes; see Figure S4).
(C) LFP time course estimations based on “monkey-specific” filters (see text and Figure 1C). For each monkey, the data from half of the electrodes were used to compute the W-K filter and the spike trains from the remaining electrodes were used to estimate the LFP. For each recording session, here we show the average estimation accuracy across all the electrodes used to estimate the LFP (error bars denote one SEM). The conventions are the same as in part (A). The number of electrodes recorded in each session is indicated above each bar. The monkey-specific W-K filters are shown for each recording session.
Figure 3A shows the estimation accuracy for each one of the 109 electrodes recorded from V1 during spontaneous activity after averaging across all “trials” (5 trials). We found that r varies significantly across trials and electrodes. Whereas the estimation accuracy for some trials is higher than 0.6, it is almost zero for others (see the overall distribution in Figure S2B). Overall, most of the electrodes (95 of the 109 electrodes) yielded a statistically significant estimation accuracy compared to the null hypothesis obtained by creating a Poisson spike train with the same mean firing rates (p<0.01, two-tailed t-test, see Section 2.4). The average estimation accuracy across V1 was 0.36 ± 0.15 (mean±S.D., 109 electrodes, dashed line in Figure 3A). On average, the estimations obtained under the null hypothesis led to a correlation of r̄ rand = 0.001±0.035 (mean±S.D., 109 electrodes, triangles and bottom dotted line in Figure 3A). Despite the variability across trials and electrodes, we found that the estimations were highly significant (two sample Kolmogorov-Smirnov test comparing the distribution in Figure S2B against the corresponding distribution obtained under the null hypothesis, p < 10−10).
To gain further insight into what contributes to the variability in the estimation accuracies across trials and across electrodes, we plotted the estimation accuracy as a function of basic properties of the spike trains and LFPs (Figure S4). The estimation accuracy increased with higher firing rates (correlation coefficient = 0.49, Figure S4A, S4D), with the total power of the LFP signal (correlation coefficient = 0.44, Figure S4B, S4E) and also with the coefficient of variation (CV) of the interspike interval distribution (correlation coefficient = 0.59, Figure S4C, Figure S4F). It should be noted that these relatively large CV values are based on MUA and not SUA. Based on Figure S4, subsequent analyses in the manuscript focused on those electrodes that had a firing rate of at least 5 spikes/s and a CV of at least 1 (88 out of the 109 electrodes).
Given the intrinsic noise in the spike trains and LFPs, we were interested in estimating an upper bound for the estimation accuracy r. For this purpose, we asked how well this linear algorithm performs when estimating the LFP time course by reconstructing the LFP measured in one electrode (LFP1) from the LFP recorded from a nearby electrode, LFP2 (Figure S6A). Since the recordings were performed simultaneously, two electrodes that are nearby are likely to be measuring a similar signal from slightly different places. As expected, the LFP-LFP estimation decreased with the distance between the two electrodes (Figure S6C). For a distance of 1 mm (the smallest distance available in our data set), the mean LFP-LFP estimation was 0.55±0.05 (mean±S.D., n=109 electrodes; cf. 0.36 for the spike-LFP estimation accuracy with a distance of 0 mm).
3.2 Towards a general function to map spikes into LFPs
Is the map between spikes and LFPs specific to each trial/electrode or is there a general filter that can extrapolate across different trials or even different recording electrodes? We asked whether we could find a general filter that, when applied to a spike train in V1 recorded from a given electrode, would give us an estimate of the corresponding LFP recorded from the same electrode. We addressed this question in three steps, with increasing degrees of extrapolation. First, we constructed an “electrode-specific” filter to predict the LFPs of all the trials recorded from a given electrode after computing the W-K filter using different trials recorded from the same electrode (Figure 1B; one filter per electrode as opposed to one filter per trial as used in the previous Section). Second we constructed a “monkey-specific” filter to predict the LFPs of all the trials and electrodes of each monkey after computing the W-K filter using different electrodes recorded from the same monkey and same brain region (Figure 1C; one W-K filter per monkey). Finally, we assessed whether a W-K filter computed from all the electrodes in a given monkey could be used to estimate the LFPs recorded in a different monkey. Note that in all cases, the LFP estimate for a given electrode was computed from the spike trains recorded from the same electrode (using Eq. 2). The extrapolation refers to the way in which the W-K filter is computed (using Eq. 4 and data from different trials, different electrodes or different monkeys).
We constructed the “electrode-specific” filter for a given electrode by minimizing the sum of the mean squared errors in the estimations of individual trials recorded from that electrode (see Figure 1B–C). We find the filter (hmean) that minimizes
| (7) |
where N is half of the total number of trials for the electrode, Lj is the LFP corresponding to trial j and, xj is the spike train of trial j with the mean subtracted. The minimization of the error leads to an expression for the Fourier transform of the filter (see Supplementary Material for a derivation of this expression),
| (8) |
where j P Lx and j Pxx are the cross power spectrum and power spectrum respectively of the LFP and spike train in trial j. In a similar fashion, we constructed a single “monkey-specific” filter for each monkey by using Eqs. 7 and 8 but summing over all the trials and electrodes used to construct the filter (half of the electrodes for each monkey, see below).
In both cases (“electrode-specific” W-K filter and “monkey-specific” W-K filter), we estimated the LFP in each trial by convolving the spike train in the same trial with hmean (instead of using the filter h computed for each trial as in the previous Section). When building an “electrode-specific” W-K filter, we used different trials to compute the filter and to compute the estimation: we picked half of the trials for a given electrode to build the filter according to Eq. 8 and used the remaining trials from the same electrode to predict the LFP time course (Figure 1B). When building a “monkey-specific” W-K filter, we used different electrodes to compute the filter and to compute the estimation (Figure 1C): we randomly picked half of the electrodes to build the filter according to Eq. 8 and used the remaining electrodes to predict the LFP time course.
Using “electrode-specific” filters, the mean estimation accuracy was r = 0.31±0.14 (Figure 3B, dashed-line). Using “monkey-specific” filters the mean estimation accuracy was, r = 0.30±0.16 (Figure 3C, dashed-line). As expected, the mean estimation accuracy in this case is lower than the values reported in Figure 3A. Yet, it is remarkable that a general linear filter can achieve a rather accurate estimation of the LFP time course. The distribution of LFP estimations were highly significant compared to those obtained using Poisson spike trains with the same mean rate (p < 10−6 (“electrode-specific” filters) and p < 10−4 (“monkey-specific” filters), two sample Kolmogorov-Smirnov test). The shape of each of the “monkey-specific” W-K filters is shown in Figure 3C.
The properties of the Wiener-Kolmogorov filter in the context of encoding time-varying signals by spike trains have been studied using idealized neuron models (Gabbiani, 1996; Gabbiani and Koch, 1996). Using an integrate-and-fire model, assuming a linear filter, neglecting the refractory period and assuming an exponentially-distributed spike threshold, it has been shown that the spike-triggered average (STA) of the signal yields an estimation filter that converges onto the W-K optimal filter in the limit of low firing rates (Gabbiani and Koch, 1996). This result also holds for experimental recordings (Wessel et al., 1996). We therefore quantified how well we could estimate the LFP time course using Eq. 2 from a filter built by computing the spike-triggered average of the LFP instead of the optimal Wiener-Kolmogorov filter. Figure S7A-B compares the shape of the STA with the shape of the average “electrode-specific” optimal W-K filter. The STA shows a sharp negativity for negative time lags and an upswing for positive time lags. This stereotypical structure of the STA is common across V1 electrodes and resembles the shape of the optimal filter hmean. The STA yielded a good estimate of the LFP time course (Figure S7C). As expected, this estimate was slightly worse than the one obtained using the optimal W-K filter. Thus, to a coarse approximation and in the limit of low-firing rates, we can think of the W-K filter as the average LFP surrounding a spike.
3.3 Spontaneous activity versus visual stimulation
The results presented thus far correspond to recordings during spontaneous activity. We asked whether the linear estimation of LFPs from spike trains would extend to conditions where V1 neurons are activated by visual input (as opposed to spontaneous firing). To examine the influence of visual stimulation on the spike-LFP relationship, we repeated the analyses in recordings form 84 electrodes in V1 while the anesthetized monkeys were shown commercial movies (see Methods). Consistent with the previous findings, we could also linearly estimate the LFP time course during visual stimulation (Figure 4A). The shape of the WK filter for the visual stimulation condition was similar to the corresponding shape during spontaneous activity. The mean estimation accuracy during the stimulation condition was 0.32 ± 0.13 using “electrode-specific” filters. Furthermore, there was a strong correlation between the estimation accuracies during spontaneous activity and those during stimulus-driven activity (Figure S5, correlation coefficient = 0.64).
Given the similarity across conditions (spontaneous actiivty versus visual stimulation) for a given monkey, we asked whether the LFP estimations could extrapolate across monkeys. Using the same approach described by Eqs. 7–8, we computed the W-K filter using all the recordings from a given monkey (Eqs. 7–8) and used this filter to estimate the LFPs recorded in a different monkey (Eq. 2). Figure 4B shows that the W-K filter from one monkey can be used to estimate the LFPs recorded from the same area (V1) in a different monkey (in all cases, the LFP estimate for a given electrode is based on the spike trains from the same electrode). This observation is due to the stereotypical shape of the W-K filters across monkeys (Figure 4B bottom).
Is the relationship between spikes and LFPs specific to a given brain area or is there a universal mapping between these two scales of neural analysis? We addressed this question by considering physiological recordings from the macaque monkey inferior temporal cortex (ITC) described in (Kreiman et al., 2006). During the ITC recordings, awake monkeys passively viewed a stream of grayscale objects. Using the same approach as in Figure 3, the mean correlation between the estimated LFP and the actual LFP for 125 ITC electrodes was r̄ = 0.27±0.17. Given the similarity between the V1 W-K filters and the ITC W-K filters, we asked whether we could use the V1 W-K filters to estimate the ITC LFPs based on the ITC spike trains. Using the general filter computed with the V1 data to estimate the ITC LFP from the ITC spike trains, we obtained a mean estimation accuracy of r̄ = 0.25±0.12. In other words, using a general filter computed with data from V1, we obtained an estimation accuracy of 0.30 in the remaining half of the V1 electrodes and an estimation accuracy of 0.25 in the ITC data. This shows a remarkable degree of extrapolation and suggests a general relationship between spikes and LFPs across different neocortical areas.
In contrast to the extrapolation across conditions (spontaneous activity and stimulus-driven activity in V1; Figure 4A), monkeys (Figure 4B), neocortical areas (V1 and ITC; Figure 4A), the W-K filter showed a poor performance in the lateral geniculate nucleus (LGN) recordings. In three recording sessions in two monkeys, 8 additional electrodes were simultaneously positioned in the (LGN). Using 95 trials recorded from the LGN, we estimated the LGN LFPs from the LGN spiking activity as described in Section 3.1–2. Figure S8 shows the estimation accuracy over all LGN trials using “electrode-specific” filters (cf. Figure 3B). The algorithm performed substantially worse when trying to estimate LGN LFPs than when trying to estimate V1 LFPs: the average estimation accuracy for the LGN was r̄ = 0.03. We observed that the spike-triggered average (STA) of the LFP was essentially flat and noisy in the LGN, which further indicates the lack of a clear relationship between spikes and LFPs in the LGN.
3.4 Frequency analysis
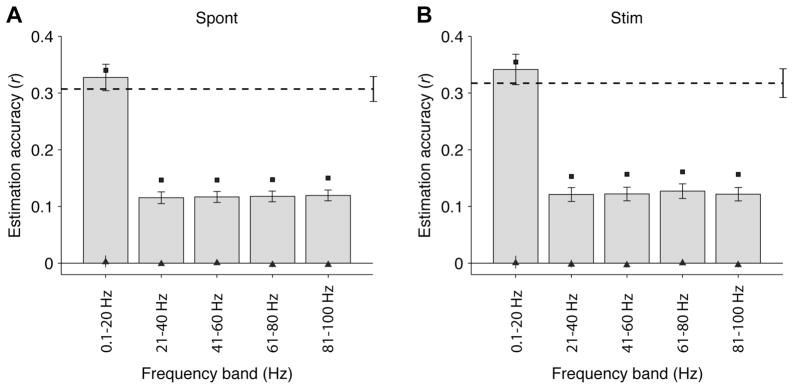
The results presented above quantify the estimation of the entire LFP time course. We asked whether there were differences in the estimation accuracy across different LFP frequency bands. For this purpose, we filtered the LFP into different frequency bands between 0.1 and 100 Hz and computed a separate W-K filter to estimate the different frequency components (Figure 5). The estimation accuracies were statistically significant compared to the null hypothesis for all frequency bands (p < 0.01, based on a two-sample Kolmogorov-Smirnov test). The lower frequency band (i.e., 0.1 – 20 Hz) yielded the best estimation accuracy (p<10−5 for the spontaneous condition and p<10−5 for the stimulation condition, based on a two sample Kolmogorov-Smirnov test comparison against the null hypothesis).
Figure 5. Frequency dependence.
Mean estimation accuracies for five different frequency bands between 0.1 and 100 Hz for all V1 trials during spontaneous activity (A, n=88) and visual stimulation (B, n=71). We filtered the LFPs in the corresponding frequency band, we computed the W-K filters and we estimated the LFPs by convolving the “electrode-specific” filters with each spike train (see Section 3.2). The horizontal dashed lines represent the mean estimation accuracy for the unfiltered LFPs (see Figure 3B). The conventions are the same as in Figure 3. Error bars denote one SEM. The black squares correspond to the reconstruction accuracies and the triangles indicate the chance performance levels. The LFP estimations are significantly better than the ones obtained under the null hypothesis (triangles) at all frequency bands (p<0.01, based on a two-sample Kolmogorov-Smirnov test) and the 0.1 to 20 Hz frequency band yielded significantly higher estimation accuracies than all other frequency bands (p<0.01, based on a two-sample Kolmogorov-Smirnov test).
These observations suggest that the spiking activity contains more information about low frequencies of the LFP than about high frequencies. This result is consistent with the results reported in (Rasch et al., 2008). Rasch et al. showed that spikes seem to be locked at the onset of low frequency oscillations in the LFP and that the spike-LFP coherence level is higher for low frequencies than for high frequencies. Indeed, the spike-LFP coherence (Pesaran et al., 2002) can be used as a measure of the error in the estimations. High coherence in a given frequency band translates into small LFP estimation errors (for further details about the relationship between W-K filtering and spike-LFP coherence, see Supplementary Material).
3.5 Robustness of the estimations to spike time jitter
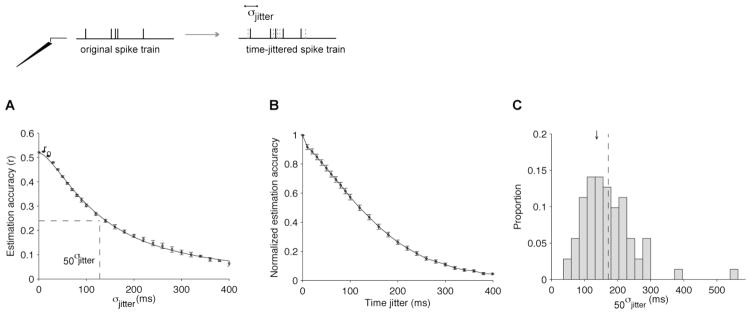
Intuitively, the possibility of estimating the LFP time course from the spike train depends on the temporal structure of the spike train. This is further emphasized by the poor LFP estimations when using the null model consisting of a spike train with the same mean rate but random spike times. To further investigate the robustness of the LFP estimates to spike time distortions, we re-computed the W-K filter after adding temporal jitter to the spike trains. We created synthetic spike trains from the experimental ones by randomly jittering the spike times. The LFP was then estimated from these synthetic spike trains. For each spike train, the spike times were moved from their actual occurrence times by a random amount taken from a zero-mean Gaussian distribution with a standard deviation σjitter.
The robustness of the estimations to time jittering was evaluated by plotting the mean estimation accuracy as a function of σjitter and computing the amount of temporal distortion required to cause a 50% drop in the estimation accuracy (50σjitter, Figure 6). The value of 50σjitter σn was obtained by fitting the following equation: , where r0 is the mean estimation accuracy when σjitter = 0, and 50σjitter and n are free parameters. Figure 6A shows the mean estimation accuracy (r̄) as a function of σjitter for an example electrode in V1. To compare the decrease in r with time jitter across electrodes, we normalized the estimation accuracy by r0 (Figure 6B). The distribution of 50σjitter for all V1 electrodes is shown in Figure 6C; the mean value was 172 ± 89 ms.
Figure 6. Robustness to spike time jitter.
(A) Example electrode showing the mean estimation accuracy as a function of the spike time jittering for an example electrode in V1 (spontaneous activity). For each value of σjitter, we randomly shifted each spike train by an amount taken from a gaussian distribution with mean=0 and standard deviation σjitter (see scheme at the top). We show the mean estimation accuracy averaged across all test trials. Error bars indicate one SEM. “r0” denotes the estimation accuracy obtained for σjitter=0. The continuous line indicates a fit with the following function: where 50σjitter and n are free parameters.
(B) For each electrode, we repeated the procedure described in (A) and normalized r by dividing it by r0 (“Normalized estimation accuracy”). We show the mean normalized estimation accuracy across all electrodes (n=88) using the “electrode-specific” filters.
(C) Distribution of 50σjitter for all V1 electrodes recorded during spontaneous activity (n=88). The black arrow shows the position of the example from part (A). The dashed vertical line indicates the mean value: the mean value of 50σjitter was 172 ± 89 ms (mean±SD). Bin size = 25 ms.
The robustness of the LFP estimate to time jitter was strongly correlated with the width of the optimal W-K filter. We found a linear relationship between the width of the optimal filter and 50σjitter (slope = 0.35, correlation coefficient = 0.64). The relatively long values of 50σjitter are consistent with the higher values of r̄ at low frequencies described in the previous Section (Figure 5).
3.6 Dependence on distance between spike trains and LFP electrode
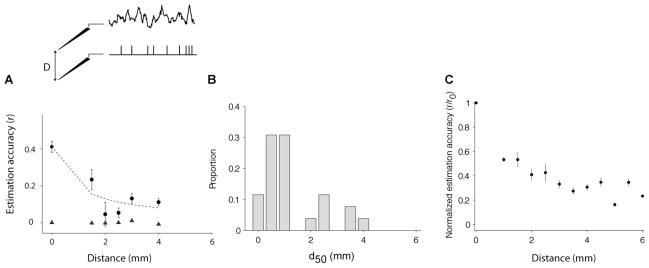
Spikes constitute a measure of activity within a small vicinity of the electrode, on the order of 200 μm (see e.g. (Holt and Koch, 1999; Logothetis, 2002)). In contrast, LFPs measure neural activity within a larger area ((Mitzdorf, 1985; Kruse and Eckhorn, 1996; Juergens et al., 1999; Logothetis, 2002; Kreiman et al., 2006; Belitski et al., 2008; Liu et al., 2008; Nauhaus et al., 2008); see however (Katzner et al., 2009)). Because recordings were performed simultaneously with multiple electrodes, we were able to study the spatial resolution of the relationship between spikes and LFPs by considering spiking activity and LFPs recorded from separate electrodes. For this purpose, we considered two electrodes separated by a distance D and we used the spike train in one electrode to estimate the LFP in the other electrode according to Eqs. 2–4. In Figure 7, the estimation accuracy is plotted as a function of the distance between the spike electrode tip and the LFP electrode tip (D = 0 corresponds to the case where LFPs and spikes were recorded from the same electrode as discussed in the previous Sections). Figure 7A shows the results of this analysis for an example recording session where electrodes spanned a distance of up to 4 mm. We fitted the function where D50 is a free parameter (dotted line in Figure 7A). We show the distribution of D50 values in Figure 7B. To compare the decrease in r with distance across electrodes, we normalized the estimation accuracy by r0 (Figure 7C). The estimation accuracy decreases by approximately 50% when the two electrodes are 1 mm apart (this is the minimum electrode distance in these data). Beyond 1 mm, we found a weak dependence of the estimation accuracy with distance. This significant drop with distance was also observed when we considered only the 0.1 to 20 Hz frequency band of the LFP.
Figure 7. Dependence on LFP-spike distance.
(A) Example electrode showing the estimation accuracy as a function of the distance D between the spike train and the LFP (see scheme at the top). Here the spike train and the LFP were simultaneously recorded using different electrodes, separated by the distance given in the x-axis (Distance = 0 corresponds to the estimations reported so far where the spike train and the LFP were recorded from the same electrode). For each spike-LFP pair, we repeated the procedure described in Figure 1B to compute the W-K filter and estimate its performance. Error bars denote one SEM. The triangles show the estimation accuracy obtained under the null hypothesis (generating a Poisson spike train with the same number of spikes). The dashed line corresponds to a fit using the following function: . (B) Distribution of D50 values for the 65 electrodes where we obtained a reliable fit (p<0.01 in a Chi2 goodness-of-fit test). Bin size = 0.5 mm. (C) We followed the procedure in (A) and normalized r by r0 for all the V1 electrodes recorded during spontaneous activity (n=88). The estimation accuracies were binned according to the spike-LFP distance using a bin size of 0.5 mm. Error bars correspond to one SEM. The mean estimation accuracy decreases by about 50% when the distance between the LFP and spike train location is 1 mm. We did not have any electrode pair with Distance < 1 mm in these data.
3.7 Causal Filters
In the analyses presented thus far, at any given time point t, both the spikes before t and the spikes after t contribute to the estimate of the LFP (see Eq. 2 and the shape of the W-K filters in Figure 2 and Figure 3). We conjectured that there may be a temporal asymmetry such that the LFP estimate at time t using those spikes before t may yield a different estimation accuracy than those occuring after t. To evaluate this possibility, we constructed two different causal filters and compared their performance to the estimation accuracies from the non-causal (NC) filter used in the previous Sections.
In the first case (C+), we constructed a filter that was set to 0 for negative time lags (i.e., hC+(α) = 0 for α < 0). In the second case (C−), we constructed a filter that was set to 0 for positive time lags (i.e., hC−(α) = 0 for α > 0). In both cases, after imposing the causality constraint the estimates were computed as in Section 3.2. Figure 8 shows r̄ for the three different filters, NC, C+ and C−, for 88 V1 electrodes during spontaneous activity. We found that the predictions computed with NC and C+ were statistically indistinguishable (p>0.1 two-sample Kolmogorov-Smirnov test). In contrast, the LFP estimations using the C− filter were significantly worse than those based on either NC or C+ (Figure 8, p<0.01). The estimations based on C− were still significantly better than chance (p<0.01, two-sample Kolmogorov-Smirnov test).
3.8 Estimations based on multiple temporally clustered spike trains
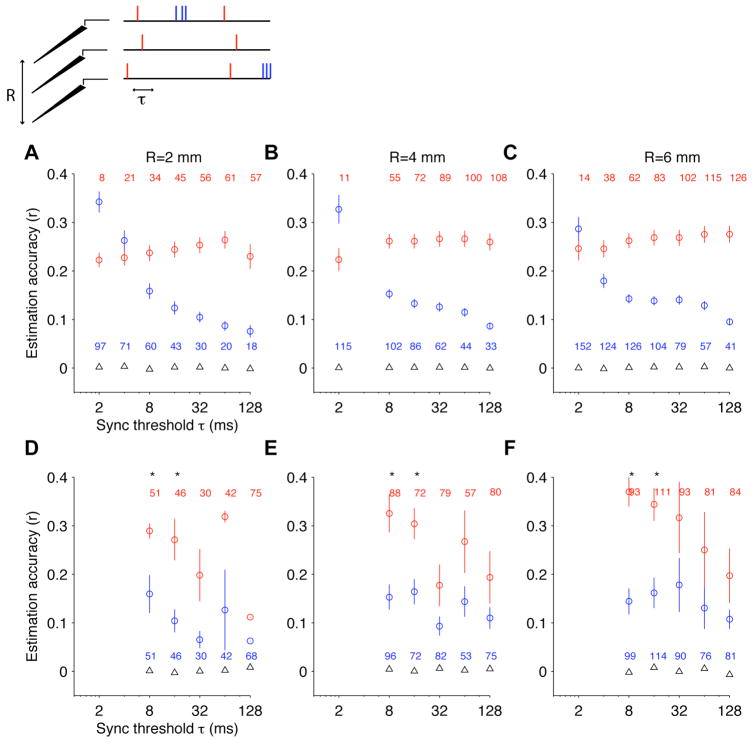
It has long been assumed that local field potentials reflect the synchronous activity of ensembles of neurons (e.g. (Mitzdorf, 1985; Fries et al., 2001; Pesaran et al., 2002; Berens et al., 2008)). Based on this assumption, we hypothesized that spikes clustered in the time dimension (i.e. co-occurring within short time windows) across multiple electrodes could show an enhanced contribution to the LFP time course than isolated spikes (i.e. those spikes that do not co-occur with other spikes within short time windows). To test this hypothesis we considered an electrode recording LFPs and all simultaneously recorded spike trains from nearby electrodes within a sphere of radius R. For a given time window τ, we separated those spike times that coincided within τ ms with spikes in any other electrode within the sphere (“time-clustered” spikes) and those spikes that occurred more than τ ms away from spikes in any other electrode within this sphere (“time-isolated” spikes). We used the same procedure in Eqs. 2–4 to estimate the W-K filter and the LFP based on these two types of spike models. In Figure 9A–C we show that, overall, the “time-clustered” spikes (red circles) yielded higher estimation accuracies than the “time-isolated” spikes for all values of R and most values of τ. In those cases where the “time-isolated” spikes yielded better estimation accuracies, we noted that there was a wide discrepancy in the number of “time-isolated” and “time-clustered” spikes (e.g. τ=2 ms in Figure 9A). Given the correlation between estimation accuracy and firing rate (Figure S4A), we repeated the analysis restricting to those values of R, τ and those trials where the number of spikes for the “time-isolated” spikes was within 20% of the number of spikes in the “time-clustered” spikes (Figure 9D–F). We observed that “time-clustered” spikes yielded a significantly higher estimation accuracy for τ=8 and τ=16 ms (we could not test this hypotheses for smaller values of τ because in those cases there were always many more spikes in the “time-isolated” condition; see Figure 9A–C). Overall, spikes that are temporally clustered with nearby spikes within ~10 ms contain more information about the LFP time course than isolated spikes.
Figure 9. LFP estimation from time-clustered spikes.
For each LFP recording site, we considered all the spike trains recorded within a sphere of radius R (R=2 mm in A,D; R=4 mm in B,E; R=6 mm in C,F). For each spike, we asked whether there were spikes recorded from other electrodes within a distance R of the LFP and within τ ms (x-axis). We built a model spike train that contains all the spikes within R mm of the LFP and within τ ms of any nearby spike (“temporally-clustered spikes”, red spikes in the scheme on top and red circles in A–F) and a separate model spike train that contains all the spikes within R mm of the LFP but without other spikes within τ ms (“isolated spikes”, blue spikes in the scheme on top and blue circles in A–F). These model spike trains were used to estimate the LFP using Eqs. 2–4. Here we report the estimation accuracies as a function of τ for different values of R for the two types of spike train models. The numbers indicate the average firing rates for the corresponding circles. The triangles indicate the estimation accuracy obtained under the null hypothesis. (D–F) Part of the differences between temporally clustered spikes and isolated spikes in A–C are due to the different firing rates between the two models. To control for the number of spikes, in D–F we only considered those values of R, τ and those trials where the number of spikes for the red circles was within 20% of the number of spikes for the blue circles.
4. DISCUSSION
There has been increased interest recently in local field potentials (e.g. (Fries et al., 2001; Logothetis, 2002; Pesaran et al., 2002; Mehring et al., 2003; Bedard et al., 2004; Kreiman et al., 2006; Kraskov et al., 2007; Nir et al., 2007; Belitski et al., 2008; Nauhaus et al., 2008) among others) due to the correlation between LFPs and functional imaging measurements (Logothetis, 2002; Kayser et al., 2004; Mukamel et al., 2005), the use of LFPs as a measure of local synchrony (Fries et al., 2001; Womelsdorf et al., 2007) and the potential use of LFPs for prosthetic applications (Pesaran et al., 2002; Mehring et al., 2003). Additionally, understanding the biophysical origins of LFPs could provide insights into the computations performed in local cortical circuits.
The biophysics underlying the generation of local field potentials (LFPs) is not clearly understood. Although several pieces of evidence suggest that the spatial extent of the LFPs is larger than the spatial extent of the spiking signals (Mitzdorf, 1985; Kruse and Eckhorn, 1996; Juergens et al., 1999; Logothetis, 2002; Bedard et al., 2004; Kreiman et al., 2006; Logothetis et al., 2007; Nauhaus et al., 2008; Katzner et al., 2009), the exact quantitative limits remain unclear. Additionally, current source density analyses and simultaneous recordings of LFPs and spikes have suggested that the LFPs are better understood in terms of synaptic potentials, afterpotentials and other membrane potentials that show a slower temporal resolution than spikes themselves (Mitzdorf, 1985; Kamondi et al., 1998). In spite of the large differences in spatial and temporal scales, our observations show that a linear filter operation on the spiking activity of one or a few neurons can explain a significant fraction of the variations in the LFP time course.
The shape of the W-K filter was highly stereotypical (e.g. Figure 2, 3, 4B, 8, S3, S7, S9; see also the spike-triggered average LFP in Figure S7A): a sharp downstroke for negative time lags was followed by a slower upstroke for positive time lags. This shape is remarkably similar to the waveform shape in extracellular action potentials (see e.g. the experimental recordings as well as the computational simulations in Figure 1 in (Gold et al., 2006)). The biophysics of the signals that give rise to the extracellular action potential have been characterized in multiple studies (Koch, 1999). For example, the simulations in (Gold et al., 2006) show that this prototypical shape can be generated by combining well-known channels, most prominently fast inactivating Na+ channels and a variety of slower K+ channels. While it is dangerous to extrapolate from the waveform of an extracellular action potential to the W-K filter in our study, it is tempting to speculate that part of the linear estimation that we report here might be accounted for by (weighted) linear and temporally-smoothed averaging over many transmembrane potentials.
For an individual neuron, there can be strong non-linearities in the generation of action potentials from the incoming synaptic currents and the integration of subthreshold dendritic events (Koch, 1999). The linear relationship that we report here concerns the estimation of an average over large numbers of dendritic events across many neurons. Furthermore, there is a topographical organization in V1 whereby neurons in the vicinity of the electrode registering the spiking activity may share similar properties. It is possible that this topography plays an important role in the structure of the LFP signal. If this conjecture holds, then we might expect that the relationship between spikes and LFPs may be more complex in areas that do not show such a strong topography as V1.
The local spiking activity analyzed here in the form of multi-unit activity (MUA) consists of action potentials derived from multiple neurons. The exact number of neurons in the MUA is not known. However, in contrast with the LFPs, the spatial extent of the MUA decays rapidly with distance (e.g. (Kreiman et al., 2006)) suggesting that the MUA has a spatial extent of ~200 μm and that the number of components is unlikely to be larger than hundreds of neurons. Additionally, we performed spike sorting on the MUA (Figure S9). Even with the best available methods for spike sorting, we cannot guarantee that the SUA consists only of a single neuron but the SUA signal is unlikely to consist of more than a few neurons (Lewicki, 1998). The small difference in the estimation accuracies using different spike cut-off thresholds (Figure S9A) as well as the small difference in the estimation accuracies between SUA and MUA (Figure S9B) further supports the idea that part of the LFP time course can be understood from highly local spiking signals. Therefore, it seems unlikely that the current estimation accuracies based on linear filtering are a consequence of the averaging of a noisy signal over tens to hundreds of neurons in the MUA. Carrying the argument to the extreme, even a single neuron might carry significant amounts of information about the LFP, a macroscopic property of the local circuit (see also (Katzner et al., 2009)).
We chose to use a linear filter because this transformation provides the simplest possible insights into the nature of the relationship between spikes and LFPs. It is conceivable that more complex non-linear operations can account for an even higher fraction of the LFP time course. We emphasize that there remains a significant fraction of the LFP time course that is not accounted for by our linear estimates. The values reported throughout the text correspond to the mean estimation accuracies. There are cases where the correlation between the linear estimate and the LFP was as high as ~0.6 (see the distribution in Figure 3 and Figure S2B). This value is close to the best estimation accuracy of the LFP time course in one electrode from the LFP signal in a nearby electrode.
How generic is the map between spikes and LFPs? Several pieces of evidence argue that at least part of the LFP time course can be explained by a rather general linear function of the local spike trains. First, the estimation accuracies were quite stationary over time: for a given electrode, a filter computed in one trial performed quite well on a separate trial. Second, the estimations extrapolated across electrodes for a given monkey and even across monkeys (Figure 4). Thirdly, we also showed that a W-K filter computed using spikes and LFPs recorded from primary visual cortex could estimate the LFP time course in inferior temporal cortex using the inferior temporal cortex spikes (see Section 3.3; we further note that these are recordings performed in different labs, different behavioral conditions and using different tasks).
The generality of the linear W-K filter used here seems to break down outside of neocortex. First, the linear W-K filter did not work well when we attempted to estimate the LFP time course in LGN (Figure S8) or in the human hippocampus (not shown). It seems that outside of neocortex, the relationship between these two signals is more complicated and might require non-linear operations, extensive recordings from more nearby units or building more complex models that incorporate other aspects of the circuit architecture. The LFP in the LGN during spontaneous activity may be generated or governed by modulatory inputs that are less related to the spiking of cells. Another non-exclusive possibility is that the special geometry of neocortex, with 6 layers and a columnar architecture is an important component of the linear relationship between spikes and LFPs. As noted above, it is possible that topography also plays a role in the relationship between spikes and LFPs. These observations constrain future development of biophysical models of the origin of local field potential signals.
When we used causal filters (Figure 8) we noted a significant asymmetry: the LFP estimations based on a filter that was constrained to be zero for negative time lags (C+) were significantly higher than those estimations based on a filter that was constrained to be zero for positive time lags (C-). Furthermore, the estimations based on the C+ filter were almost as high as the ones obtained when using the non-causal filter (Figure 8). The possibility of linearly estimating the time course of the local field potentials from spike trains during spontaneous activity extrapolates to conditions of visual stimulation (Figure 4A). We also observed that the linear estimation holds in another brain area (inferior temporal cortex) under a passive viewing task in awake monkeys (see Section 3.3; (Kreiman et al., 2006)). Therefore, the basic map between spikes and LFPs holds for different brain areas (V1, ITC), stimulation conditions (spontaneous activity, visual stimulation) and behavioral states (anesthesia, awake). The estimation accuracies and, in particular, the estimation accuracies for different frequency bands may show a strong dependence on the experimental conditions. Several investigators have noted that the stimulus, task and behavioral state of the animal (e.g. attention, short-term memory) can influence the relationship between spikes and LFPs (Fries et al., 2001; Pesaran et al., 2002; Liu and Newsome, 2005; Buschman and Miller, 2007; Womelsdorf et al., 2007; Belitski et al., 2008). In particular, there are many cases where spikes and LFPs (or particular frequency bands of the LFPs) can be decorrelated (Kreiman et al., 2006; Belitski et al., 2008; Berens et al., 2008).
It has been assumed that LFPs may reflect synchronous activity across ensembles of local neurons (e.g. (Fries et al., 2001; Laurent, 2002; Logothetis, 2002; Womelsdorf et al., 2006; Montemurro et al., 2008)). Our observation that temporally-clustered spikes yield better estimation accuracies than temporally-isolated spikes (Figure 9) seems to be compatible with the idea that LFPs may reflect computations that are local both in space as well as in the time domain. However, the estimation accuracies were robust to significant amounts of spike time jittering (Figure 6). More research is necessary to further our understanding of the biophysical signals that give rise to the LFPs, how many neurons are involved and how exactly neuronal events across local ensembles give rise to the field potential.
As in other systems, a multi-scale analysis of neuronal circuits provides rich insights that cannot be achieved by focusing on a single level only. Many efforts in Neuroscience aim to understand perception and behavior using only macroscopic signals such as BOLD measurements. As emphasized elsewhere (Logothetis, 2008), it is not always trivial to interpret these measurements without a detailed understanding of the underlying architecture and cellular function. Other efforts in Neuroscience correlate perception and behavior with the activity of single neurons. Circuits of neurons may show emergent properties that are not always easy to visualize by looking at individual neurons without studying their interactions (Koch and Segev, 1989). The combination of spikes and LFPs provides an ideal resolution to understand the relationship between individual neurons and local neuronal circuits.
Supplementary Material
Figure S1: LFP and spike train power spectral densities
Figure S2: Dependence on nfft and distribution of estimation accuracies.
Figure S3: Example LFP estimates
Figure S4: Correlation between estimation accuracy and firing rate, CV and LFP power
Figure S5: Correlation between estimation accuracy for spontaneous activity and stimulus-driven activity
Figure S6: LFP estimations from nearby LFP recordings
Figure S7: LFP estimations using the spike-triggered average
Figure S8: Estimations in the LGN
Figure S9: Estimations based on SUA versus MUA
Acknowledgments
We would like to thank Fabrizio Gabbiani and Ulf Knoblich for comments on the manuscript and helpful discussions. We thank Stefano Panzeri, Rodrigo Quiroga and Alberto Mazzoni for help with the spike sorting (Figure S9). The V1 data used throughout the manuscript were recorded in the Logothetis lab. The inferior temporal cortex data shown in the last two columns of Figure 4A were recorded by Chou Hung and James DiCarlo. This research was sponsored by the Whitehall Foundation, the Klingenstein Fund and the Children’s Hospital Boston Faculty Development Award.
References
- Bedard C, Kroger H, Destexhe A. Modeling extracellular field potentials and the frequency-filtering properties of extracellular space. Biophys J. 2004;86:1829–1842. doi: 10.1016/S0006-3495(04)74250-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belitski A, Gretton A, Magri C, Murayama Y, Montemurro MA, Logothetis NK, Panzeri S. Low-frequency local field potentials and spikes in primary visual cortex convey independent visual information. J Neurosci. 2008;28:5696–5709. doi: 10.1523/JNEUROSCI.0009-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berens P, Keliris GA, Ecker AS, Logothetis NK, Tolias AS. Comparing the feature selectivity of the gamma-band of the local field potential and the underlying spiking activity in primate visual cortex. Front Syst Neurosci. 2008;2:2. doi: 10.3389/neuro.06.002.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bialek W, Steveninck R, Warland D. Reading a neural code. Science. 1991;252:1854–1857. doi: 10.1126/science.2063199. [DOI] [PubMed] [Google Scholar]
- Buschman TJ, Miller EK. Top-down versus bottom-up control of attention in the prefrontal and posterior parietal cortices. Science. 2007;315:1860–1862. doi: 10.1126/science.1138071. [DOI] [PubMed] [Google Scholar]
- Fries P, Reynolds J, Rorie A, Desimone R. Modulation of oscillatory neuronal synchronization by selective visual attention. Science. 2001;23:1560–1563. doi: 10.1126/science.1055465. [DOI] [PubMed] [Google Scholar]
- Gabbiani F. Coding of time varying signals in spike trains of linear and half-wave rectifying signals. Network: Computation in Neural Systems. 1996;7:61–85. doi: 10.1080/0954898X.1996.11978655. [DOI] [PubMed] [Google Scholar]
- Gabbiani F, Koch C. Coding of time varying signals in spike trains of integrate and fire neurons with random threshold. Neural Computation. 1996;8:44–66. [Google Scholar]
- Gold C, Henze DA, Koch C, Buzsaki G. On the origin of the extracellular action potential waveform: A modeling study. J Neurophysiol. 2006;95:3113–3128. doi: 10.1152/jn.00979.2005. [DOI] [PubMed] [Google Scholar]
- Haberly L, Shepherd G. Current-density analysis of summed evoked potentials in opposum prepyriform cortex. Journal of Neurophysiology. 1973;36:789–803. doi: 10.1152/jn.1973.36.4.789. [DOI] [PubMed] [Google Scholar]
- Henrie JA, Shapley R. LFP power spectra in V1 cortex: the graded effect of stimulus contrast. J Neurophysiol. 2005;94:479–490. doi: 10.1152/jn.00919.2004. [DOI] [PubMed] [Google Scholar]
- Holt GR, Koch C. Electrical interactions via the extracellular potential near cell bodies. Journal of Computational Neuroscience. 1999;6:169–184. doi: 10.1023/a:1008832702585. [DOI] [PubMed] [Google Scholar]
- Juergens E, Guettler A, Echhorn R. Visual stimulation elicits locked and inducd gamma oscillations in monkey intracortical and EEG-potentials but not in human EEG. Experimental Brain Research. 1999;129:247–259. doi: 10.1007/s002210050895. [DOI] [PubMed] [Google Scholar]
- Kamondi A, Acsady L, Buzsaki G. Dendritic spikes are enhanced by cooperative network activity in the intact hippocampus. J Neurophysiol. 1998;18:3919–3928. doi: 10.1523/JNEUROSCI.18-10-03919.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katzner S, Nauhaus I, Benucci A, Bonin V, Ringach DL, Carandini M. Local origin of field potentials in visual cortex. Neuron. 2009;61:35–41. doi: 10.1016/j.neuron.2008.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kayser C, Kim M, Ugurbil K, Kim DS, Konig P. A comparison of hemodynamic and neural responses in cat visual cortex using complex stimuli. Cereb Cortex. 2004;14:881–891. doi: 10.1093/cercor/bhh047. [DOI] [PubMed] [Google Scholar]
- Koch C. Biophysics of Computation. New York: Oxford University Press; 1999. [Google Scholar]
- Koch C, Segev I. Methods in neuronal modeling: from synapses to networks. Cambridge, Mass: MIT Press; 1989. [Google Scholar]
- Kraskov A, Quian Quiroga R, Reddy L, Fried I, Koch C. Local Field Potentials and Spikes in the Human Medial Temporal Lobe are Selective to Image Category. Journal of Cognitive Neuroscience. 2007;19:479–492. doi: 10.1162/jocn.2007.19.3.479. [DOI] [PubMed] [Google Scholar]
- Kreiman G, Krahe R, Metzner W, Koch C, Gabbiani F. Robustness and Variability of Neuronal Coding by Amplitude Sensitive Afferents in the Weakly Electric Fish Eigenmannia. Journal of Neurophysiology. 2000;84:189–204. doi: 10.1152/jn.2000.84.1.189. [DOI] [PubMed] [Google Scholar]
- Kreiman G, Hung C, Quian Quiroga R, Kraskov A, Poggio T, DiCarlo J. Object selectivity of local field potentials and spikes in the inferior temporal cortex of macaque monkeys. Neuron. 2006;49:433–445. doi: 10.1016/j.neuron.2005.12.019. [DOI] [PubMed] [Google Scholar]
- Kruse W, Eckhorn R. Inhibition of sustained gamma oscillations (35–80 Hz) by fast transient responses in cat visual cortex. Proc Natl Acad Sci U S A. 1996;93:6112–6117. doi: 10.1073/pnas.93.12.6112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurent G. Olfactory Network Dynamics and the coding of multidimensional signals. Nature Reviews Neuroscience. 2002;3:884–895. doi: 10.1038/nrn964. [DOI] [PubMed] [Google Scholar]
- Lewicki MS. A review of methods of spike sorting: the detection and classification of neural action potentials. Network: Computation and Neural Systems. 1998;9:R53–R78. [PubMed] [Google Scholar]
- Liu H, Agam Y, Madsen JR, Kreiman G. Stationarity of the neural code for vision. Society for Neuroscience Annual Meeting; Washington: SFN; 2008. [Google Scholar]
- Liu J, Newsome WT. Correlation between speed perception and neural activity in the middle temporal visual area. J Neurosci. 2005;25:711–722. doi: 10.1523/JNEUROSCI.4034-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis N, Kayser C, Oeltermann A. In vivo measurements of cortical impedance spectrum in monkeys: implications for signal propagation. Neuron. 2007;55:809–823. doi: 10.1016/j.neuron.2007.07.027. [DOI] [PubMed] [Google Scholar]
- Logothetis NK. The neural basis of the blood-oxygen-level-dependent functional magnetic resonance imaging signal. Philos Trans R Soc Lond B Biol Sci. 2002;357:1003–1037. doi: 10.1098/rstb.2002.1114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis NK. What we can do and what we cannot do with fMRI. Nature. 2008;453:869–878. doi: 10.1038/nature06976. [DOI] [PubMed] [Google Scholar]
- Mehring C, Rickert J, Vaadia E, Cardosa de Oliveira S, Aertsen A, Rotter S. Inference of hand movements from local field potentials in monkey motor cortex. Nature Neuroscience. 2003;6:1253–1254. doi: 10.1038/nn1158. [DOI] [PubMed] [Google Scholar]
- Milstein J, Mormann F, Fried I, Koch C. Neuronal shot noise and Brownian 1/f2 behavior in the local field potential. PLoS One. 2009;4:e4338. doi: 10.1371/journal.pone.0004338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitzdorf U. Current source-density method and application in cat cerebral cortex: investigation of evoked potentials and EEG phenomena. Physiological Reviews. 1985;65:37–99. doi: 10.1152/physrev.1985.65.1.37. [DOI] [PubMed] [Google Scholar]
- Montemurro MA, Rasch MJ, Murayama Y, Logothetis NK, Panzeri S. Phase-of-firing coding of natural visual stimuli in primary visual cortex. Curr Biol. 2008;18:375–380. doi: 10.1016/j.cub.2008.02.023. [DOI] [PubMed] [Google Scholar]
- Mukamel R, Gelbard H, Arieli A, Hasson U, Fried I, Malach R. Coupling between neuronal firing, field potentials, and FMRI in human auditory cortex. Science. 2005;309:951–954. doi: 10.1126/science.1110913. [DOI] [PubMed] [Google Scholar]
- Nauhaus I, Busse L, Carandini M, Ringach DL. Stimulus contrast modulates functional connectivity in visual cortex. Nat Neurosci. 2008 doi: 10.1038/nn.2232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nir Y, Fisch L, Mukamel R, Gelbard-Sagiv H, Arieli A, Fried I, Malach R. Coupling between neuronal firing rate, gamma LFP, and BOLD fMRI is Related to Inter-Neuronal Correlations. Current Biology. 2007;17:1275–1285. doi: 10.1016/j.cub.2007.06.066. [DOI] [PubMed] [Google Scholar]
- O’Keefe J, Recce M. Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus. 1993;3:317–330. doi: 10.1002/hipo.450030307. [DOI] [PubMed] [Google Scholar]
- Pesaran B, Pezaris J, Sahani M, Mitra P, Andersen R. Temporal structure in neuronal activity during working memory in macaque parietal cortex. Nature Neuroscience. 2002;5:805–811. doi: 10.1038/nn890. [DOI] [PubMed] [Google Scholar]
- Poor HV. An introduction to signal detection and estimation. Springer-Verlag; 1994. [Google Scholar]
- Quian Quiroga R, Nadasdy N, Ben-Shaul Y. Unsupervised spike sorting with wavelets and superparamagnetic clustering. Neural Computation. 2004;16:16161–11687. doi: 10.1162/089976604774201631. [DOI] [PubMed] [Google Scholar]
- Rasch M, Gretton A, Murayama Y, Maass W, Logothetis NK. Inferring spike trains from local field potentials. Journal of Neurophysiology. 2008;99:1461–1476. doi: 10.1152/jn.00919.2007. [DOI] [PubMed] [Google Scholar]
- Rieke F, Bodnar DA, Andersen R. Coding efficiency and information rates in sensory neurons. Europhys Lett. 1993;22:151–156. [Google Scholar]
- Wessel R, Koch C, Gabbiani F. Coding of time-varying electric field amplitude modulations in a wave-type electric fish. Journal of Neurophysiology. 1996;75:2280–2293. doi: 10.1152/jn.1996.75.6.2280. [DOI] [PubMed] [Google Scholar]
- Womelsdorf T, Fries P, Mitra PP, Desimone R. Gamma-band synchronization in visual cortex predicts speed of change detection. Nature. 2006;439:733–736. doi: 10.1038/nature04258. [DOI] [PubMed] [Google Scholar]
- Womelsdorf T, Schoffelen JM, Oostenveld R, Singer W, Desimone R, Engel AK, Fries P. Modulation of neuronal interactions through neuronal synchronization. Science. 2007;316:1609–1612. doi: 10.1126/science.1139597. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1: LFP and spike train power spectral densities
Figure S2: Dependence on nfft and distribution of estimation accuracies.
Figure S3: Example LFP estimates
Figure S4: Correlation between estimation accuracy and firing rate, CV and LFP power
Figure S5: Correlation between estimation accuracy for spontaneous activity and stimulus-driven activity
Figure S6: LFP estimations from nearby LFP recordings
Figure S7: LFP estimations using the spike-triggered average
Figure S8: Estimations in the LGN
Figure S9: Estimations based on SUA versus MUA