Abstract
Like human infants, songbirds acquire their song by imitation and eventually generate sounds that result from complicated neural networks and intrinsically nonlinear physical processes. Signatures of low-dimensional chaos such as subharmonic bifurcations have been reported in adult and developing zebra finch song. Here, we use methods from nonlinear dynamics to test whether adult male zebra finches (Taenopygia guttata) use the intrinsic nonlinear properties of their vocal organ, the syrinx, to insert subharmonic transitions in their song. In contrast to previous data on the basis of spectrographic evidence, we show that subharmonic transitions do not occur in adult song. Subharmonic transitions also do not arise in artificially induced sound in the intact syrinx, but are commonly generated in the excised syrinx. These findings suggest that subharmonic transitions are not used to increase song complexity, and that the brain controls song in a surprisingly smooth control regimen. Fast, smooth changes in acoustic elements can be produced by direct motor control in a stereotyped fashion, which is a more reliable indicator of male fitness than abrupt acoustic changes that do not require similarly precise control. Consistent with this view is the presence of high fidelity at every level of motor control, from telencephalic premotor areas to superfast syringeal muscles.
Introduction
Natural behavior involves strong interactions among nervous system, morphology, and environment that can constrain neural control but also provides opportunities for rich complexity in behavior (Chiel and Beer, 1997). The central control of learned vocal behavior is an excellent system in which to study this interaction because vocal organs are highly nonlinear devices whose intrinsic properties can give rise to complex acoustic features (Fee et al., 1998).
Many songbirds learn their song from adult conspecifics and practice through sensorimotor error correction to refine their own song into a highly stereotyped, so-called crystallized song (Konishi, 1965; Tchernichovski et al., 2001). Any attempt to understand the neural basis of song and relate neural instruction to song characteristics depends crucially on understanding the translation of neural patterns into song, but it remains unclear as to how neural patterns of firing are decoded into sound in the peripheral sound producing system. To generate stereotyped song, the avian vocal organ, the syrinx, must translate neural patterns into sound reliably and predictably, even in an internal environment where mechanical perturbations may occur. This translation involves many biophysical processes, such as muscle contraction (Elemans et al., 2008a), flow induced oscillation of vibrating structures (Goller and Larsen, 1997; Fee et al., 1998, Larsen and Goller, 1999), filtering (Nowicki, 1987; Riede et al., 2006) and, possibly, acoustic feedback (Laje et al., 2001; Laje and Mindlin, 2005; Hatzikirou et al., 2006), which themselves or in their interactions are intrinsically nonlinear (Wilden et al., 1998; Fitch et al., 2002; Mindlin and Laje, 2005).
In zebra finch song, the occurrence of various phenomena related to low-dimensional chaos (LDC) has been reported to arise from oscillatory dynamics in the syrinx and has been suggested as a mechanism for enhancing acoustic complexity without complex neural control (Fee et al., 1998). However, it remains unclear how to control nonlinear phenomena reliably to produce stereotyped song. Specifically period doubling, a type of subharmonic transition where the frequency of the uttered sound abruptly changes to half its previous value, has been suggested to enable rapid pitch changes in song syllables in adults (Fee et al., 1998) and during vocal learning in juveniles (Tchernichovski et al., 2001). In a regimen where subharmonic transitions occur, small variations in neural control signals could result in abrupt, large pitch changes. However, this abrupt nature might be expected to compromise the stereotyped repeatability of the song. It also contrasts with gradual pitch adjustments (Andalman and Fee, 2009; Sober and Brainard, 2009) that require a control regimen where pitch changes smoothly with its control parameters. To evaluate these divergent mechanisms of central motor control, understanding the origin of nonlinear transitions in bird-song is necessary.
In this study, we test whether zebra finches make use of nonlinear characteristics of their vocal organ to insert subharmonic transitions into song. To separate neural contribution from the intrinsic properties of the syrinx, we also investigate the occurrence of complex spectral features in artificially induced sounds in in situ, denervated, and excised syrinx preparations.
Materials and Methods
Identification of subharmonic transitions using topology analysis
The theory of nonlinear dynamics established that the long-term behavior of a dynamical system depends on the geometry of the underlying attractor (Strogatz, 1994). In voiced sound production by vertebrates, the most common low-dimensional attractors are the fixed point (a constant value), limit cycle (any periodic oscillation, such as pure tones and harmonic stacks), torus (e.g., amplitude modulated sounds), and chaotic attractor (“noisy” sounds) (Wilden et al., 1998; Fitch et al., 2002). The attractors underlying voiced sound leave characteristic signatures in spectrograms and therefore spectrographic evidence has been used to identify phenomena of LDC in the vocalizations of the zebra finch (Fee et al., 1998) and several other bird species (Nowicki and Capranica, 1986; Fletcher, 2000; Baker and Logue, 2003; Beckers and ten Cate, 2006; Zollinger et al., 2008), as well as frogs (Suthers et al., 2006), humans, and other mammals (Fachini et al., 2003; Herzel et al., 1995; Mann et al., 2006; Riede et al., 2000; Svec et al., 1996; Titze et al., 1993; Tokuda et al., 2008; Tyson et al., 2007), and one insect (Benko and Perc, 2007). Although spectrographic representation of sound is indeed helpful in identifying potential candidates, only more detailed analysis, such as close-return (CR) plots and phase-space embedding, allow unambiguous identification (Titze et al., 1993; Herzel et al., 1995; Svec et al., 1996; Fletcher, 2000; Riede et al., 2000; Fachini et al., 2003; Mann et al., 2006; Tyson et al., 2007; Tokuda et al., 2008).
By changing the system’s driving parameters, the stability of one attractor can be transferred to a qualitatively different one: for instance, in a period doubling bifurcation the system abandons a limit cycle for a related limit cycle with twice the period. In the context of vocalizations, this bifurcation would abruptly change the frequency of the uttered sound to half its previous value. A more detailed description of period doubling bifurcations and their phase-space relations is included as supplemental material (available at www.jneurosci.org as supplemental material).
Candidates for subharmonic transitions (e.g., period doubling or tripling) were identified by visually screening spectrograms of crystallized song from 130 adult male zebra finches (Taenopygia guttata) from different laboratories and gene pools. We screened 5–10 full motifs of each individual and recorded the number of syllables per motif (excluding introductory notes). Syllables were defined as continuous sounds, separated by a silent period (Tchernichovski et al., 2001). The song syllables contained two types of fast frequency transitions: abrupt frequency jumps within periods of relative constant frequency and transitions within fast frequency sweeps <50 ms in duration. Therefore, we scored all syllables for these features. Syllables were further classified according to whether the frequencies before or after the jump or near the beginning or end of the frequency sweep were harmonically related. Thus, we scored the syllables for content of (1) frequency modulation (FM) sweeps <50 ms, (2) FM sweeps <50 ms connecting harmonically related frequencies, (3) instantaneous jumps between harmonically related frequencies, and (4) instantaneous jumps between non-harmonically related frequencies. An FM sweep was defined as a continuous frequency modulated energy band in the spectrogram, the duration of which was measured from the time signal (Elemans et al., 2008c). We took extra care to omit recordings that contained multiple animals by listening and comparing multiple motifs. The identified syllables that contained FM sweeps <50 ms connecting harmonically related frequencies or instantaneous jumps between harmonically related frequencies were subjected to further analysis.
To get a first indication whether the segment contained a real subharmonic transition, we calculated a CR plot of the entire segment. From such plots, it is easy to identify the location and the period of a potential periodic orbit, which here would be a periodic oscillation in the recorded time series, related to a voiced sound. For a time series x(t), the CR plot is based on the observation that the difference |x(t) − x(t+T)| remains smaller than a given threshold ε when x(t) is near a periodic orbit of period T (Gilmore, 1998). The CR plot contains a mesh plot as a function of time t and period T (Fig. 1c), where the pixel (t,T) is plotted black when |x(t) − x(t+T)| < ε (for an example, see Fig. 1C,E). Close-return segments appear as horizontal line segments in this plot and represent segments in the time series with a definite period. If the CR plot shows an abrupt start or end of a line segment as a harmonically related segment continues, then we have a potential subharmonic transition. If the lines in the CR plot are modulated, we do not have a potential subharmonic transition. The cutoff value ε was determined by eye and individually for each plot. The chosen value was the result of a trade-off between increasing visibility of fainter strokes (higher cutoff) and avoiding noise (lower cutoff).
Figure 1. Zebra finch song contains many features that superficially resemble subharmonic transitions.
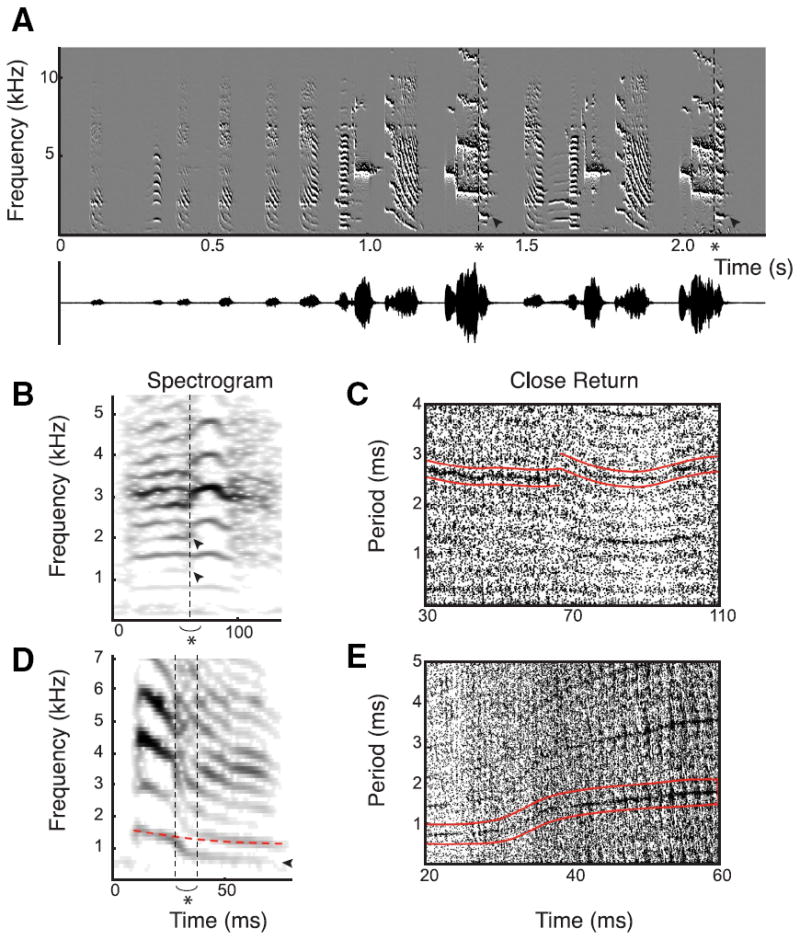
A, Spectral derivative plot and oscillogram of typical zebra finch song demonstrating candidate period doublings at asterisk. These candidates tested negative with topological tools (for the tools, see Fig. 2). The song also contains several fast frequency sweeps of 60 – 80 ms duration. B, C, Spectrogram (B) and CR plot (C) of song syllable with an apparent period halving at asterisk. Arrowheads show frequencies that disappear suggesting a period halving candidate. It is evident in the CR plot that, although the period on the left (bounded by red lines) changes to around half its value, the upper line is clearly not continuous. Alternative explanations could be the two independently acting sources, or a nonlinear phenomenon more complex than a period doubling. For the construction of the CR plot, ε = 0.0005, which is 4.3% of the root mean square value. D, E, Spectrogram (D) and CR plot (E) of a very fast frequency modulation in ~10 ms. Although the frequency ratio before and after (dashed vertical lines) the modulation is ~2, the CR plot shows a smooth change in periodicity (red lines). For the construction of the CR plot, ε = 0.0005, which is 8.8% of the root mean square value.
The doubling of the period in a nonlinear system yields waveforms before and after the bifurcation that are topologically related to each other (Gilmore, 1998). Therefore, we extracted segments of the time series before and after the presumed bifurcation and checked whether the topological organization of the corresponding orbits was compatible with a period doubling bifurcation (see supplemental material, available at www.jneurosci.org as supplemental material). Only the candidates that passed the CR plot criteria were subjected to this analysis. The orbits were reconstructed from the time series x(t) by time-delayed embedding in a three-dimensional phase-space, as follows: [x(t), x(t − τ), x(t − 2τ)], with τ typically in the order of one-tenth of the period T.
In three dimensions, the topological organization is represented by a set of integers and rational fractions, which provide information about the topological organization of periodic orbits. These indices are independent of coordinate system changes and also remain invariant under control parameter variation (Gilmore, 1998). The orbits in a specific bifurcation are constrained to have a specific set of topological indices. Any departure from these values should cast serious doubt on the identity of the bifurcation. The topological organization of the orbits in the specific bifurcation we study in this work (period doubling between period 1 and period 2) is completely described by the linking number (LN). The LN is half the sum of the signed crossings between the two orbits. The period-1 and period-2 orbits in a period doubling bifurcation should rotate the same odd number of half turns around each other, which result in an odd LN between the orbits. For a more detailed explanation, see the supplemental material (available at www.jneurosci.org as supplemental material).
Induced vocalizations
Subjects
For induced vocalization experiments, six male zebra finches were used. All zebra finches were housed in 45 × 45 × 52 cm group cages on a 12 h light/dark cycle and provided with food and water ad libitum. Experiments were performed at the University of Utah (Salt Lake City, UT). All experiments were conducted in accordance with the Institutional Animal Care and Use Committee of the University of Utah.
Surgical procedures
We quantified nonlinear phenomena and oscillation onset conditions during gas-induced vocalizations in four preparations: syrinx in situ (P1), syrinx in situ immediately after syringeal denervation (P2), 1–2 d after denervation (P3), and on an in vitro preparation of the excised syrinx (P4). Six male zebra finches were anesthetized with an intramuscular injection of chloropent (3.4 μl/g). Two cannulae (silastic tube; total length, 10 cm; outer diameter, 2.16 mm; inner diameter, 1.02 mm) (Dow-Corning) were inserted bilaterally in the anterior thoracic air sac to control flow through the syrinx. Phonation was induced by forcing moisturized air through these air sac cannulae with a mass-flow/pressure controller (type MC, Alicat Scientific). Pressure was slowly ramped up from 0–2 kPa (relative to atmospheric pressure) and back down again over a period of 20 s (preparation P1). To avoid neuromuscular control of the vocal organ, we denervated the syringeal muscles by cutting the tracheosyringeal nerves bilaterally. Phonation was again induced in our experimental setup (preparation P2). The cannulae were then plugged and connected on the back so that the bird could recover from anesthesia and to allow it to move about unhindered in its cage.
After 24–48 h, the birds were anesthetized again with an intramuscular injection of chloropent (3.4 μl/g) and phonation was induced in our experimental setup (preparation P3). Then birds were killed by an overdose of Isoflurane (Abbott), and the syrinx was removed. The syrinx was placed in a Sylgard covered Petri dish. Silastic tubing was prepositioned with insect pins to ensure a natural position for the syrinx. The bronchi and trachea were connected to silastic tubing with the smallest amount of fast-curing dental impression medium possible. The trachea and non-vibrating parts of the bronchi with attached cannulae were embedded in 3% agarose in avian saline buffer. Extra care was taken to prevent any fluid from loading the vibrating structures. The relative humidity or air was increased locally by placing moist Kim-wipes close to the syrinx preparation. A mass-flow/pressure controller was connected to the bronchial cannulae (type MC, Alicat Scientific) and tracheal cannula (type MC altered for vacuum, Alicat Scientific). Bronchial pressure was set to +0.5 kPa and tracheal pressure slowly ramped from 0 to –2 kPa (re atmospheric pressure) and then back down over a 20 s period (preparation P4), following the protocol of Fee et al. (1998).
Experimental setup and data analysis
Sound was recorded in the near-field, 2–4 cm from the beak opening with a microphone (type 40AG, preamplifier type 26AK, power module 12AD, G.R.A.S., Denmark). The mass-flow/pressure controllers measured pressure and flow. In addition, supplied air pressure was measured before the cannula connection, 10 cm from the air sac, with a 3.5F Mikro-Tip catheter pressure transducer (SPR524, Millar Instruments) connected to a preamplifier and pressure control unit (PCU-2000, Millar Instruments). Sound pressure, pressure, and flow signals were low-pass filtered at 10 kHz (Instrumentation Amplifier 410, Brownlee Precision) and digitized at 30 kHz with an A/D board (PCI-6251, National Instruments). The set-up was controlled with custom written software in Labview (National Instruments).
To extract the phonation onset parameters, sound was high-pass filtered at 300 Hz and the onset threshold level of sound amplitude was set at the mean plus 4–6 times the SD of a 1 s silent segment before the pressure ramp. Pressure and flow signals were divided into 100 ms bins with 20 ms shifts. Bronchial pressure (pB), tracheal pressure (pT), bronchial flow (UB) and tracheal flow (UT) were evaluated at the time of phonation onset and presented as gauge pressures, i.e., relative to atmospheric pressure. The onset pressures presented in Figure 5 are defined as the bronchial-tracheal pressure gradient (pB−pT), where pT is assumed to be zero (atmospheric pressure) for P1, P2, and P3. To determine flow, we used the bronchial flow measurement for P1, P2, and P3, and the tracheal flow measurement for P4.
Figure 5. Spectrum complexity and sound onset parameters of induced sound production in four experimental preparations.
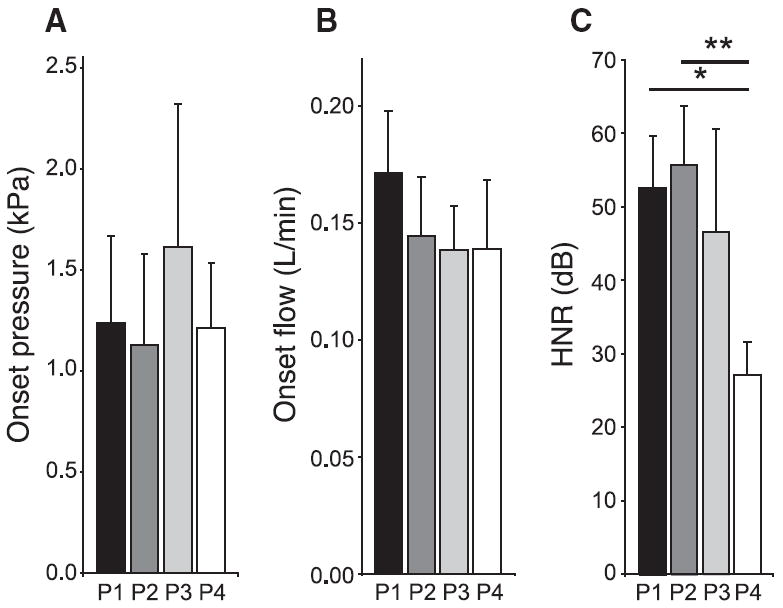
A, B, Both pressure (A) and flow (B) at the onset of sound production do not differ significantly across experimental preparations. C, Two-tailed paired t tests show that the HNR is significantly decreased in the excised preparation (P4) compared with in situ (P1, *p < 0.05) and to the 24 – 48 h denervated syrinx (P3, **p < 0.01), which means that the amount of spectrum complexity increases significantly in the excised syrinx. N = 6, except for P4, where N = 4. Preparation P1, in situ phonation; preparation P2, in situ phonation after lesion of the bilateral tracheosyringeal branches of the hypoglossal nerve; preparation P3, in situ phonation 24 – 48 h after lesion; and preparation P4, excised in vitro preparation.
Calculation of spectral complexity
We chose the harmonic-to-noise ratio (HNR) as a proxy for spectrum complexity (Tokuda et al., 2002). The HNR is a measure of the relative amplitude of peaks in the spectrum (usually due to harmonic components) relative to the background noise level, where the background noise level is obtained by smoothing the spectrum. The HNR is then the largest difference between the original spectrum and the background noise spectrum, in decibels. A spectrum with high peaks against a low-level background noise (for instance a very clear harmonic spectrum) has a very high HNR, while a signal with a very dense spectrum (either with very close peaks, very low peaks, or noisy) has a very low HNR.
We calculated a windowed version of the HNR, since the peak-broadening in the spectrum due to the quite common frequency modulations in our signals could bias the regular HNR calculation toward spuriously low values. Sound signals were bandpass filtered (100 – 9000 Hz) and then windowed into 350 ms non-overlapping segments. The HNR was calculated for every segment in a signal and then averaged across segments. The background noise level was estimated by a 100-point-moving average from the original spectrum of the segment. All calculations were performed with custom written software in C.
Statistics
Data means were compared using two-tailed paired t tests in JMP software (SAS).
Results
Adult song
We studied the crystallized song motifs of 130 adult male zebra finches from different laboratories and searched for subharmonic transitions, such as period doubling (Fig. 1A) and halving. Visual screening of spectrograms revealed other acoustic features that superficially resemble subharmonic transitions, such as two-voice phenomena (Fig. 1B,C) or fast frequency modulations (Fig. 1D,E). The motifs of the 130 animals contained 5.3 ± 1.6 syllables per motif and a total of 693 syllables. Of all syllables, 154 (22.2% of total) contained a fast frequency sweep (<50 ms), an average of 1.2 ± 1.3 per motif. Of the syllables containing a fast frequency sweep (<50 ms), only 17 (2.5% of total) contained a fast frequency sweep connecting two harmonically related frequencies. These latter frequency modulations could resemble period doublings when the frequency ratio before and after the modulation is around two (Fig. 1D). Instantaneous jumps between nonharmonically related frequencies were found in 52 syllables (7.5% of total). Instantaneous jumps between harmonically related frequencies were found in only 14 syllables (2.0% of total) in 11 birds. These latter syllables and the syllables with a fast frequency sweep connecting two harmonically related frequencies contained our prime candidates for subharmonic transitions and these 31 syllables (4.5% of total) were subjected to further investigation.
For the 31 syllables containing a candidate, we calculated a CR plot to identify the location and the period of the potential periodic orbit (Gilmore, 1998). Close-return segments appeared as horizontal line segments and represent segments in the time series with definite period. A potential subharmonic could be recognized by the abrupt start or end of a line segment, while a harmonically related segment continued. Figure 1B shows a period halving candidate, where it is evident from the CR plot (Fig. 1C) that, although the period on the left changes to around half its value, the upper line is not continuous. Alternatively, this sound feature could arise from contributions of the two bilateral sound sources. For all 17 syllables that contained a fast frequency sweep (<50 ms) connecting two harmonically related frequencies, the corresponding CR plot (Fig. 1 E) showed smooth changes in periodicity, which clearly indicates that the modulation does not arise from a period doubling.
For the remaining 14 syllables, where the CR plot supported a subharmonic transition, we extracted the time series that contained the candidate and quantified support for a transition by determining topological parameters of the embedded signals (Fig. 2). We calculated a topological index, the LN, which provides information about the topological organization of periodic orbits that is independent of coordinate system changes and, importantly, remains invariant under control parameter variation (Gilmore, 1998). Orbits in a specific bifurcation are constrained to have a specific set of topological indices. For a real period doubling bifurcation, the period-1 and period-2 orbits should rotate an odd number of half turns around each other, resulting in an odd LN between the orbits (either positive or negative). Any departure from these values should cast serious doubt on the identity of the bifurcation. For a period doubling bifurcation between period 1 and period 2, the topological organization is completely described by the LN. Therefore, the bifurcation is strongly supported by an odd LN and can be discarded by an even LN. See Material and Methods and supplemental material (available at www.jneurosci.org as supplemental material) for a more detailed description of the topological program.
Figure 2. False candidate for period doubling in zebra finch song.
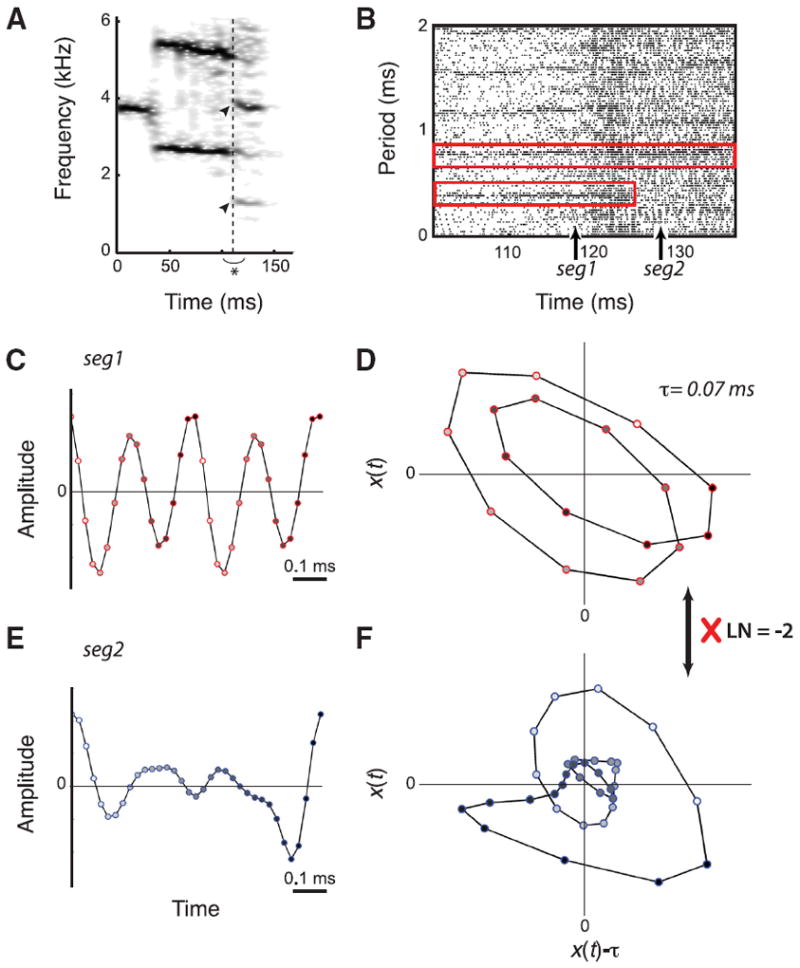
A, Sound spectrogram of song syllable (detail from Fig. 1 A, first asterisk) shows new spectral components (arrowheads) starting at ~130 ms (dashed vertical line) at half the frequency spacing. B, The CR plot shows that the signal periodicity suddenly jumps from ~0.4 to 0.8 ms, which is a strong indication for a period doubling. Upward arrows indicate the location of the extracted segments seg1 and seg2 for the topological analysis. ε = 0.007, which is 8.3% of the RMS value. C, E, Time series of the extracted segments: period-1 segment (seg1) (C) and period-2 segment (seg2) (E). The change in face color of the markers from white to black indicates time progression. D, F, The corresponding embedded orbits with time-delay τ = 0.07 ms. The calculated topological index needs to be an odd integer to support true period doubling. The linking number between the two orbits is an even integer (LN = −2). Therefore, the topological index does not support a real period doubling.
The 14 candidates that were supported by the CR plot failed to conform with the topological requirements. Figure 2 shows the analysis of an example candidate where both the spectrogram (Fig. 2A) and CR plot (Fig. 2B) support a period doubling. First, the waveforms are isolated (Fig. 2C) and embedded (Fig. 2D). From the embedded time series of the period-1 and period-2 orbits, we calculated the topological index LN. The linking number for these orbits was LN = −2, which is not an odd integer. The waveforms of this identified transition did, therefore, not relate to each other in the correct manner and the identified transition was not an actual period doubling. None of the 14 candidates found in adult male song of 11 birds tested positive as an actual period doubling or halving bifurcation. Therefore our data show that subharmonic bifurcations are absent or very rare in zebra finch song.
We could only confirm one identified candidate for a subharmonic transition, though not in song but in the contact call of one male. This single instance was the only call observed in screened files that contained a potential subharmonic bifurcation and presented a strong case for an actual period doubling (Fig. 3). From the embedded time series (Fig. 3D) of the period-1 and period-2 orbits, we calculated the linking number: LN = −7, which is consistent with the hypothesis that the identified transition is an actual period doubling.
Figure 3. The only real period doubling found in the contact call of an adult male zebra finch.
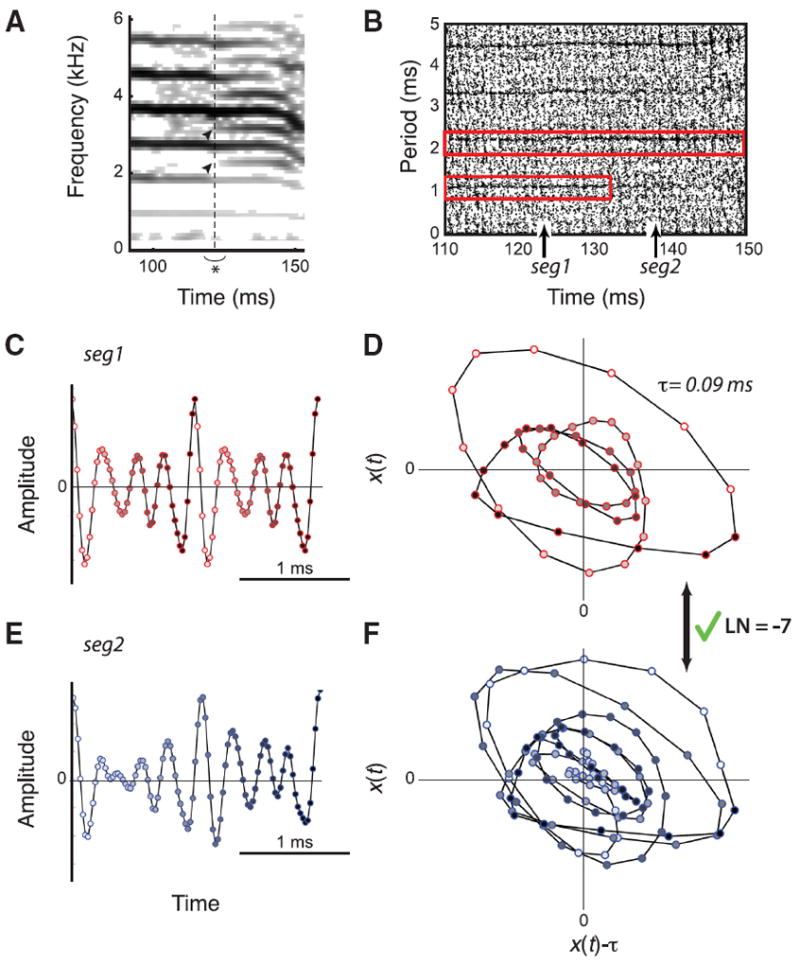
A, Spectrogram of sound signal. Visual inspection shows new spectral components (arrowheads) starting at ~12 ms (dashed vertical line) at half the frequency spacing. B, The CR plot shows that the periodicity of the signal suddenly jumps from ~1 to ~2 ms, which is a strong indication for a period doubling. Upward arrows indicate the location of the extracted segments seg1 and seg2 for the topological analysis. ε = 0.001, which is 7.8% of the RMS value. C, E, Time series of the extracted segments: period-1 segment (seg1) (C) and period-2 segment (seg2) (E). The change in face color of the markers from white to black indicates time progression. D, F The corresponding orbits with time-delay τ = 0.09 ms. The linking number between period-1 and period-2 orbits is an odd integer LN = −7. This value is indicative of a real period doubling.
Induced sound production
Gas-induced sound production in an in vitro preparation has confirmed many phenomena associated with low-dimensional chaos previously observed in zebra finch song (Fee et al., 1998). However, we did not find positive cases of period doubling in zebra finch song, which raises the possibility that the nonlinear phenomena caused by nonlinear intrinsic properties of the syrinx may be restrained by either neural or mechanical constraints. Also, the oscillatory behavior of in vitro preparations may deviate from the in vivo situation, and therefore, it is necessary to know whether sound production in the isolated syrinx has a larger tendency to demonstrate complex phenomena.
We performed a series of experiments where we recorded induced sound production by the syrinx. To separate the contributions of neuromuscular control, the suspension of the syrinx in vivo and the intrinsic properties of the syrinx, we quantified complex phenomena and oscillation onset conditions during gas-induced vocalizations by controlling airflow and pressure in the syrinx in the following four preparations: in situ (Fig. 4A, preparation P1); in situ immediately after syringeal denervation (Fig. 4 B, preparation P2); 24 – 48 h after denervation (Fig. 4C, preparation P3); and on an in vitro preparation of the excised syrinx (Fig. 4D, preparation P4).
Figure 4. The spectrum complexity increases from in situ to an excised preparation.
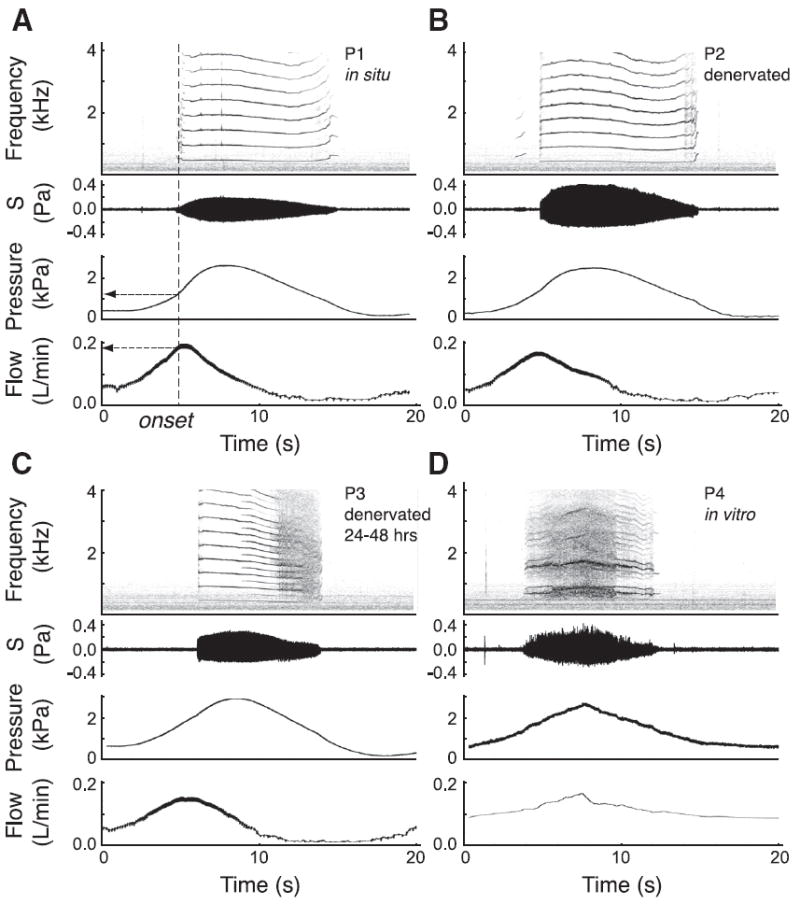
Typical run of each preparation, with sound spectrogram, sound amplitude, pressure and flow traces. A–D, Preparation P1, in situ phonation (A); preparation P2, in situ phonation after lesion of the bilateral tracheosyringeal branches of the hypoglossal nerve (B); preparation P3, in situ phonation 24 – 48 h after lesion (C); and preparation P4, excised in vitro preparation (D). A pressure ramp of 2 kPa gauge pressure was imposed in each case except for P4 where suction was applied on the trachea (compare with Fee et al., 1998). The dashed vertical line indicates the phonation onset for P1 with corresponding onset pressure and onset flow (arrows).
Sound could be induced readily in each preparation (Fig. 4). The measured oscillation onset conditions for sound production by the labia, such as phonation onset values for bronchial pressure (Fig. 5A) and flow (Fig. 5B), did not change significantly within the four preparations P1 to P4. This suggests that the in vitro preparation is representative for the in situ situation in respect to these dynamical conditions. Any apparent change in muscle tension caused by denervation does not alter onset pressure and flow appreciably, even after 24–48 h (Figs. 4B,C, 5A,B).
Visual inspection of the spectrograms showed an apparent increase in signal complexity with reduced neuromuscular control (Fig. 4B,C) and in the excised preparation (Fig. 4D), as exemplified by the sudden appearance and/or disappearance of new spectral components, more dense regions, periodic windows within noisy regions, peak broadening and frequency jumps. In the spectrogram of induced sound production in the in vitro preparation (Fig. 4D), we see many bifurcation candidates and as such confirm the data by Fee et al. (1998) that the excised syrinx exhibits rich nonlinear behavior. Initial analyses of subharmonic phenomena in the sound signals using low-dimensional topological tools (Linking Number) showed that some apparent period doublings tested negative. This could be either due to the occurrence for instance of more complex phenomena, two-source interaction, or the vocal tract filtering effects obscuring the topological fingerprint. Thus, to quantify complexity in the spectrum we abandoned the low-dimensional topological tools and changed to a more generic measure, the HNR (Tokuda et al., 2002). The HNR values were significantly lower in the in vitro preparation (P4) compared with both in situ situations, before (P1) and after the nerve cut (P2) (Fig. 5C). This means that the amount of complex acoustic phenomena is significantly higher in the in vitro preparation.
Discussion
We show that true subharmonic transitions are either absent or very rare in adult zebra finch song. This result, based on songs from 130 individual birds and through the use of topological tools, contradicts previous suggestions based on spectrographic evidence in 12 individuals (Fee et al., 1998). Although subharmonic transitions do not occur during spontaneous song, complex acoustic phenomena are clearly present in the excised syrinx (supporting data in Fee et al., 1998) and significantly more frequent than in the in vivo situation. These findings indicate that although phenomena of LDC can arise from the intrinsically nonlinear dynamics of isolated sound producing structures, LDC is not used to enhance vocal complexity in zebra finch song.
Neuronal control does not prevent nonlinear phenomena, but apparently the in situ conditions counteract their presence. We propose two mechanisms that may explain why nonlinear acoustic phenomena do occur in vitro, but do not in situ. First, the syrinx is held in place by the bronchi and trachea as well as through connective tissue attachments to the interclavicular air sac and esophagus, which add structural stability (King, 1989). These stabilizing attachments are no longer present in the excised syrinx. When mounting the syrinx, its in situ length along the bronchiotracheal axis cannot be recreated precisely, but this length must influence tension in the syrinx. A departure from the in situ tension might increase the occurrence of LDC, but would also likely alter onset air pressure and airflow of phonation, which we did not observe (Fig. 5), suggesting an alternative explanation is required. Second, in contrast with excised larynx preparations in humans (Svec et al., 1999, Tokuda et al., 2008), and dogs (Jiang et al., 2003), where subglottal and supraglottal pressures are comparable to the in vivo situation, in excised syrinx experiments the suprasyringeal pressure conditions are changed. Labial oscillations are induced by a bronchiotracheal pressure gradient, which during normal phonation is defined by elevated pressure in the bronchi and air sacs relative to that in the trachea. A similar gradient is presented by suction at the tracheal end to induce phonation in the excised syrinx preparation (this study and Fee et al., 1998). Applying only positive pressure on the bronchial side does not induce labial oscillations in vitro, probably because the surrounding air sac is not present. However application of suction changes the suprasyringeal forces acting on the labia (Lous et al., 1998; Elemans et al., 2008b) and may alter the flow separation point on the labia (Pelorson et al., 1994; Lous et al., 1998) and suprasyringeal acoustic feedback (Laje et al., 2001; Laje and Mindlin, 2005; Hatzikirou et al., 2006). Therefore, this difference possibly contributes to the more frequent occurrence of complex acoustic phenomena in the artificially induced sounds of the excised syrinx.
In songbirds, rapid acoustic transitions or spectral signatures that resemble subharmonics can result from switching between one and two-voiced sounds (Suthers, 1990; Goller and Cooper, 2004), or from a 180° out-of-phase to a synchronous oscillation regimen of the two sound sources, or from interaction between the left and right sides (Nowicki and Capranica, 1986; Laje and Mindlin, 2005) in the bipartite songbird syrinx. However, coupling between the left and right sound generators in the zebra finch syrinx is an unlikely source of LDC because LDC is present when phonation is induced in vitro on one side (Fee et al., 1998) and both sides (this study). Although suggested that period doublings are a component of song learning (Tchernichovski et al., 2001), our data indicate that such bifurcations are rare in zebra finch song. The provided example for a period doubling in this earlier study (zebra finch B6, training day 14 in Tchernichovski et al., 2001) shows a spectrum with well defined peaks that are in fact not harmonically related (peaks at 646, 1421, 2067, 2864, 3488, 4306, 4952, 5727, 6373, and 7019 Hz). This vocalization can therefore not be a subharmonic transition of the previously uttered sound and may result from switching from one to two voice-sound production (Suthers, 1990; Goller and Cooper, 2004). From this we conclude that the role, if any, of subharmonic transitions in vocal learning trajectories needs to be reconsidered.
Zebra finch song is characterized by a high degree of acoustic and temporal stereotypy (Chi and Margoliash, 2001; Tchernichovski et al., 2001; Hahnloser et al., 2002; Glaze and Troyer, 2007). Such stereotypy requires accurate and precise control, which we expect is an important indicator of adult male fitness. Because simply crossing a period doubling bifurcation does not require accurate control, it is more difficult to infer demanding control from this kind of acoustic phenomena. To our knowledge, it is also unknown whether LDC is a salient acoustic feature of song. We, therefore, do not know whether these acoustic features are selected against or favored by female choice, which could be tested by exploring responses to manipulated songs in females.
We suggest that rapid acoustic transitions in zebra finch song, such as the unverified candidates for subharmonic transitions, are produced by direct muscular control. Recent evidence on the very rapid contraction kinetics (twitch halftimes of 3.7 ms) of syringeal muscles in zebra finches provides strong support that acoustic transitions in the order of milliseconds can be effected via direct central motor control of the vocal organ (Elemans et al., 2008a). Many of the subharmonic candidates or rapid transitions we observed in song were very fast, but smooth modulations (Fig. 1D), which is consistent with expected movements effected by superfast muscle contractions. Neuromuscular control does not seem to play a major role in avoiding unwanted bifurcations during song, because the HNR did not decrease significantly after neuromuscular control was eliminated (Fig. 5C).
Throughout life, adult songbirds are thought to be capable of small pitch-shifts for specific syllables reducing error during song (Tumer and Brainard, 2007; Sober and Brainard, 2009), using the anterior forebrain pathway (Andalman and Fee, 2009). These frequency shifts are small [a maximum of ~3% for Bengalese finch in Sober and Brainard (2009) and 15% for zebra finch in Andalman and Fee (2009)] and, most importantly, continuous (Tumer and Brainard, 2007; Andalman and Fee, 2009; Sober and Brainard, 2009). Were period doublings to occur, the possibility for small continuous changes in pitch would require an alternative mechanism of syringeal control. Furthermore, error signals are only useful to the extent that they can be converted to an appropriate motor action (articulatory gesture) that addresses the error (Derégnaucourt et al., 2004). Therefore to provide a useful error signal, the translation of motor output to produced sound (motor pathway) must be reflected in the translation of auditory feedback to error with the sensory target (auditory pathway). This implies that when the syrinx is operated in a regimen where period doublings occur, a useful error signal must mirror their presence.
Understanding the neural basis of song requires a more detailed knowledge of how neural patterns of firing are decoded into sound in the peripheral sound producing system (Suthers and Margoliash, 2002; Suthers and Zollinger, 2004). On the basis of the results of this study, we conclude that the song motor system in zebra finches does not have to account for nonlinearities found in the excised syrinx and can operate the syrinx in a regimen where abrupt changes in fundamental frequency and dense spectra are avoided. This implies that the brain controls song in a smooth regimen, which further implies that it is justified to link neural patterns to song characteristics using linear correlation methods. In the case of the zebra finch, motor proficiency to avoid and thus identify instances of nonlinearities does not appear to be required because nonlinearities do not occur in the physiological parameter space in vivo. We suggest that most rapid acoustic transitions in zebra finch song are effected by direct superfast muscular control. Consistent with this view is the presence of high temporal precision at every level of motor control, from telencephalic premotor areas (Chi and Margoliash, 2001; Hahnloser et al., 2002; Glaze and Troyer, 2007) to extremely fast syringeal muscles (Elemans et al., 2008a).
Supplementary Material
Acknowledgments
This study was funded by National Institutes of Health Grants DC04390 and DC06876 to F.G. and G.B.M. We thank B. Cooper, J. Raksin, and J. Whittington for providing zebra finch recordings; and S. Bottjer, J.M. Ratcliffe, S.A. White, and especially H. Mehaffey and two reviewers for comments on previous versions of the manuscript.
References
- Andalman AS, Fee MS. A basal ganglia-forebrain circuit in the songbird biases motor output to avoid vocal errors. Proc Natl Acad Sci U S A. 2009;106:12518–12523. doi: 10.1073/pnas.0903214106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker MC, Logue MD. Population differentiation in a complex bird sound: a comparison of three bioacoustical analysis procedures. Ethology. 2003;109:223–242. [Google Scholar]
- Beckers GJL, ten Cate C. Nonlinear phenomena and song evolution in Streptopelia doves. Dong Wu Xue Bao. 2006;52:482–485. [Google Scholar]
- Benko TP, Perc M. Singing of Neoconocephalus robustus as an example of deterministic chaos in insects. J Biosci. 2007;32:797–804. doi: 10.1007/s12038-007-0081-5. [DOI] [PubMed] [Google Scholar]
- Chi Z, Margoliash D. Temporal precision and temporal drift in brain and behavior of zebra finch song. Neuron. 2001;32:899–910. doi: 10.1016/s0896-6273(01)00524-4. [DOI] [PubMed] [Google Scholar]
- Chiel HJ, Beer RD. The brain has a body: adaptive behavior emerges from interactions of nervous system, body and environment. Trends Neurosci. 1997;20:553–557. doi: 10.1016/s0166-2236(97)01149-1. [DOI] [PubMed] [Google Scholar]
- Derégnaucourt S, Mitra PP, Fehér O, Maul KK, Lints TJ, Tchernichovski O. Song development: in search of the error signal. Ann NY Acad Sci. 2004;1016:364–376. doi: 10.1196/annals.1298.036. [DOI] [PubMed] [Google Scholar]
- Elemans CP, Mead AF, Rome LC, Goller F. Superfast muscles control sound production in songbirds. PLoS One. 2008a;3:e2581. doi: 10.1371/journal.pone.0002581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elemans CP, Zaccarelli R, Herzel H. Biomechanics and control of vocalization in a non-songbird. J R Soc Interface. 2008b;5:691–703. doi: 10.1098/rsif.2007.1237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elemans CPH, Heeck K, Muller M. Spectrogram analysis of mechanical events in sound production of animals. J Bioacoustics. 2008c;18:183–212. [Google Scholar]
- Facchini A, Bastianoni S, Marchettini N, Rustici M. Characterization of chaotic dynamics in the vocalization of Cervus elaphus corsicanus (L) J Acoust Soc Am. 2003;114:3040–3043. doi: 10.1121/1.1624071. [DOI] [PubMed] [Google Scholar]
- Fee MS, Shraiman B, Pesaran B, Mitra PP. The role of nonlinear dynamics of the syrinx in the vocalisations of a songbird. Nature. 1998;395:67–71. doi: 10.1038/25725. [DOI] [PubMed] [Google Scholar]
- Fitch WT, Neubauer J, Herzel H. Calls out of chaos: the adaptive significance of nonlinear phenomena in mammalian vocal production. Anim Behav. 2002;63:407–418. [Google Scholar]
- Fletcher NH. A class of chaotic bird calls? J Acoust Soc Am. 2000;108:821–826. doi: 10.1121/1.429615. [DOI] [PubMed] [Google Scholar]
- Gilmore R. Topological analysis of chaotic dynamical systems. Rev Mod Phys. 1998;70:1455–1529. [Google Scholar]
- Glaze CM, Troyer TW. Behavioral measurements of a temporally precise motor code for birdsong. J Neurosci. 2007;27:7631–7639. doi: 10.1523/JNEUROSCI.1065-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goller F, Cooper BG. Peripheral motor dynamics of song production in the zebra finch. Ann NY Acad Sci. 2004;1016:130–152. doi: 10.1196/annals.1298.009. [DOI] [PubMed] [Google Scholar]
- Goller F, Larsen ON. A new mechanism of sound generation in songbirds. Proc Natl Acad Sci U S A. 1997;94:14787–14791. doi: 10.1073/pnas.94.26.14787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hahnloser RH, Kozhevnikov AA, Fee MS. An ultra-sparse code underlies the generation of neural sequences in a songbird. Nature. 2002;419:65–70. doi: 10.1038/nature00974. [DOI] [PubMed] [Google Scholar]
- Hatzikirou H, Fitch WT, Herzel H. Voice instabilities due to source-tract interactions. Acta Acust Acust. 2006;92:468–475. [Google Scholar]
- Herzel H, Berry D, Titze I, Steinecke I. Nonlinear dynamics of the voice: signal analysis and biomechanical modeling. Chaos. 1995;5:30–34. doi: 10.1063/1.166078. [DOI] [PubMed] [Google Scholar]
- Jiang JJ, Zhang Y, Ford CN. Nonlinear dynamics of phonation in excised larynx experiments. J Acoust Soc Am. 2003;144:2198–2205. doi: 10.1121/1.1610462. [DOI] [PubMed] [Google Scholar]
- King AS. Functional anatomy of the syrinx. In: King AS, McLelland J, editors. Form and function in birds. New York: Academic; 1989. pp. 105–192. [Google Scholar]
- Konishi M. The role of auditory feedback in the control of vocalization in the white-crowned sparrow. Z Tierpsychol. 1965;22:770–783. [PubMed] [Google Scholar]
- Laje R, Mindlin GB. Modelling source-source and source-filter acoustic interaction in birdsong. Phys Rev E. 2005;72:036218. doi: 10.1103/PhysRevE.72.036218. [DOI] [PubMed] [Google Scholar]
- Laje R, Gardner TJ, Mindlin GB. Continuous model for vocal fold oscillations to study the effect of feedback. Phys Rev E. 2001;64:056201. doi: 10.1103/PhysRevE.64.056201. [DOI] [PubMed] [Google Scholar]
- Larsen ON, Goller F. Role of syringeal vibrations in birds vocalizations. Proc R Soc Lond B Biol Sci. 1999;266:1609–1615. [Google Scholar]
- Lous NJC, Hofmans GC, Veldhuis RNJ, Hirschberg A. A symmetrical two-mass vocal-fold model coupled to vocal tract and trachea, with application to prosthesis design. Acta Acust Acust. 1998;84:1135–1150. [Google Scholar]
- Mann DA, O’Shea TJ, Nowacek DP. Nonlinear dynamics on manatee vocalizations. Marine Mammal Sci. 2006;22:548–555. [Google Scholar]
- Mindlin GB, Laje R. The physics of bird song. Berlin: Springer; 2005. [Google Scholar]
- Nowicki S. Vocal tract resonances in oscine bird sound production: evidence from birdsongs in a helium atmosphere. Nature. 1987;325:53–55. doi: 10.1038/325053a0. [DOI] [PubMed] [Google Scholar]
- Nowicki S, Capranica RR. Bilateral syringeal interaction in vocal production of an oscine bird sound. Science. 1986;231:1297–1299. doi: 10.1126/science.3945824. [DOI] [PubMed] [Google Scholar]
- Pelorson X, Hirschberg A, van Hassel RR, Wijnands APJ. Theoretical and experimental study of quasisteady-flow separation within the glottis during phonation. Application to a modified two-mass model. J Acoust Soc Am. 1994;96:3416–3431. [Google Scholar]
- Riede T, Herzel H, Mehwald D, Seidner W, Trumler E, Böhme G, Tembrock G. Nonlinear phenomena in the natural howling of a dog-wolf mix. J Acoust Soc Am. 2000;108:1435–1442. doi: 10.1121/1.1289208. [DOI] [PubMed] [Google Scholar]
- Riede T, Suthers RA, Fletcher NH, Blevins WE. Songbirds tune their vocal tract to the fundamental frequency of their song. Proc Natl Acad Sci U S A. 2006;103:5543–5548. doi: 10.1073/pnas.0601262103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sober SJ, Brainard MS. Adult birdsong is actively maintained by error correction. Nat Neurosci. 2009;12:927–931. doi: 10.1038/nn.2336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strogatz SH. Nonlinear dynamics and chaos. Cambridge, MA: Perseus Books; 1994. [Google Scholar]
- Suthers RA. Contributions to birdsong from the left and right sides of the intact syrinx. Nature. 1990;347:473–477. [Google Scholar]
- Suthers RA, Margoliash D. Motor control of birdsong. Curr Opin Neurobiol. 2002;12:684–690. doi: 10.1016/s0959-4388(02)00386-0. [DOI] [PubMed] [Google Scholar]
- Suthers RA, Zollinger SA. Producing song. The vocal apparatus. Ann NY Acad Sci. 2004;1016:109–129. doi: 10.1196/annals.1298.041. [DOI] [PubMed] [Google Scholar]
- Suthers RA, Narins PM, Lin WY, Schnitzler HU, Denzinger A, Xu CH, Feng AS. Voices of the dead: complex nonlinear vocal signals from the larynx of an ultrasonic frog. J Exp Biol. 2006;209:4984–4993. doi: 10.1242/jeb.02594. [DOI] [PubMed] [Google Scholar]
- Svec JG, Schutte HK, Miller DG. A subharmonic vibratory patterns in normal vocal folds. J Speech Hear Res. 1996;39:135–143. doi: 10.1044/jshr.3901.135. [DOI] [PubMed] [Google Scholar]
- Svec JG, Schutte HK, Miller DG. On pitch jumps between chest and falsetto registers in voice: data from living and excised human larynges. J Acoust Soc Am. 1999;106:1523–1531. doi: 10.1121/1.427149. [DOI] [PubMed] [Google Scholar]
- Tchernichovski O, Mitra PP, Lints T, Nottebohm F. Dynamics of the vocal imitation process: how a zebra finch learns its song. Science. 2001;291:2564–2569. doi: 10.1126/science.1058522. [DOI] [PubMed] [Google Scholar]
- Titze IR, Baken RJ, Herzel H, Titze IR. Evidence of chaos in vocal fold vibration. In: Titze IR, editor. Vocal fold physiology. San Diego: Singular Publishing Group; 1993. pp. 143–188. [Google Scholar]
- Tokuda I, Riede T, Neubauer J, Owren MJ, Herzel H. Nonlinear analysis of irregular animal vocalizations. J Acoust Soc Am. 2002;111:2908–2919. doi: 10.1121/1.1474440. [DOI] [PubMed] [Google Scholar]
- Tokuda IT, Horácek J, Svec JG, Herzel H. Bifurcations and chaos in register transitions of excised larynx experiments. Chaos. 2008;18:013102. doi: 10.1063/1.2825295. [DOI] [PubMed] [Google Scholar]
- Tumer EC, Brainard MS. Performance variability enables adaptive plasticity of “crystallized” adult birdsong. Nature. 2007;450:1240–1244. doi: 10.1038/nature06390. [DOI] [PubMed] [Google Scholar]
- Tyson RB, Nowacek DP, Miller PJ. Nonlinear phenomena in the vocalizations of North Atlantic right whales (Eubalaena glacialis) and killer whales (Orcinus orca) J Acoust Soc Am. 2007;122:1365–1373. doi: 10.1121/1.2756263. [DOI] [PubMed] [Google Scholar]
- Wilden I, Herzel H, Peters G, Tembrock G. Subharmonics biphonation and deterministic chaos in mammal vocalisation. Bioacoustics. 1998;9:171–196. [Google Scholar]
- Zollinger SA, Riede T, Suthers RA. Two-voice complexity from a single side of the syrinx in northern mockingbird Mimus polyglottos vocalizations. J Exp Biol. 2008;211:1978–1991. doi: 10.1242/jeb.014092. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


