The Hodgkin-Huxley Heritage: From Channels to Circuits

Abstract

The Hodgkin-Huxley studies of the action potential, published 60 years ago, are a central pillar of modern neuroscience research, ranging from molecular investigations of the structural basis of ion channel function to the computational implications at circuit level. In this Symposium Review, we aim to demonstrate the ongoing impact of Hodgkin’s and Huxley’s ideas. The Hodgkin-Huxley model established a framework in which to describe the structural and functional properties of ion channels, including the mechanisms of ion permeation, selectivity, and gating. At a cellular level, the model is used to understand the conditions that control both the rate and timing of action potentials, essential for neural encoding of information. Finally, the Hodgkin-Huxley formalism is central to computational neuroscience to understand both neuronal integration and circuit level information processing, and how these mechanisms might have evolved to minimize energy cost.

Introduction

A series of papers published in The Journal of Physiology in 1952 revolutionized our understanding of neuronal function: Alan Hodgkin and Andrew Huxley used the experimental data from a sequence of papers on voltage-dependent conductances in the squid giant axon (Hodgkin et al., 1952; Hodgkin and Huxley, 1952a–c) to propose a model that accurately predicted the shape of the action potential (Hodgkin and Huxley, 1952d). This provided the first quantitative description of the electrical events underlying action potential generation. However, their model was influential far beyond the generation of action potentials. It created a conceptual basis for at least three levels of research in neuroscience. First, at a molecular level, the Hodgkin-Huxley model established a framework in which to describe the structural and functional properties of ion channels, including the mechanisms of ion permeation, selectivity, and gating. Second, at a cellular level, the model predicted not only the action potential itself, but also the conditions that control the timing of action potential onset, including threshold and refractory periods. Finally, at a circuit level, the predictive success of the Hodgkin-Huxley formalism made it an exemplar of how to use data-based modeling in scientific research and paved the way for the now-thriving field of computational neuroscience.

In this Symposium Review, we aim to show how the Hodgkin-Huxley model inspired and continues to inspire neuroscientific research. With a focus on sodium channels, we will first discuss how the Hodgkin-Huxley model continues to influence research on the structure and function of ion channels. We will then discuss the control of action potential timing and synchronization in neuronal information processing, and finally examine the Hodgkin-Huxley model from the perspective of computational neuroscience.

Structure of voltage-gated sodium channels

Voltage-gated sodium channels initiate action potentials in nerve, muscle, and other excitable cells. The sodium current that initiates the nerve action potential was discovered by Hodgkin and Huxley using the voltage-clamp technique in their landmark series of papers in 1952. They described sodium selectivity, voltage-dependent activation, and fast inactivation, and they developed a quantitative model for action potential generation that has endured for many decades (Hodgkin et al., 1952; Hodgkin and Huxley, 1952a–d).

Following Hodgkin and Huxley, in the 1960s, Hille, Armstrong, and others introduced the idea that the sodium and potassium currents are conducted by specific ion channels (Chandler and Meves, 1965; Moore et al., 1967; Hille, 1968; Armstrong, 1971), and many investigators used the voltage-clamp technique to further define the functional properties of sodium channels and develop conceptual models for their function through the 1960s and 1970s. Studies of ion selectivity, saturation, and block of sodium permeation led to a detailed model of the ion selectivity filter of the sodium channel and its function in sodium selectivity (Hille, 1971, 1972, 1975). The four-barrier, three-site model envisaged partial dehydration of Na⁺ through interaction with a high-field-strength site containing a carboxyl side chain at the extracellular end of the pore, followed by rehydration in the lumen of the pore and escape into the intracellular milieu. Hille (1977) also established that local anesthetics and related drugs that act on sodium channels bind to a receptor site in the pore of the channel, which can be accessed either through the open activation gate at the intracellular end of the pore or, for small hydrophobic drugs, through a membrane access pathway.

Armstrong and Bezanilla (1973) used high-resolution electro-physiological recording methods to detect the transmembrane movement of the gating charges, the “electrically charged particles” associated with sodium channels that respond to changes in electrical field and drive the rapid activation of the channels as predicted by Hodgkin and Huxley (Hodgkin and Huxley, 1952d). Armstrong and colleagues (1973) also made key insights into the process of fast sodium channel inactivation, showing that it is mediated by protein components on the intracellular surface of the sodium channel, which were hypothesized to fold into the pore and block it during inactivation. These studies established enduring conceptual models of sodium channel function (for review, see Hille, 2001), but there was no information on the actual structure of ion channel proteins at that time.

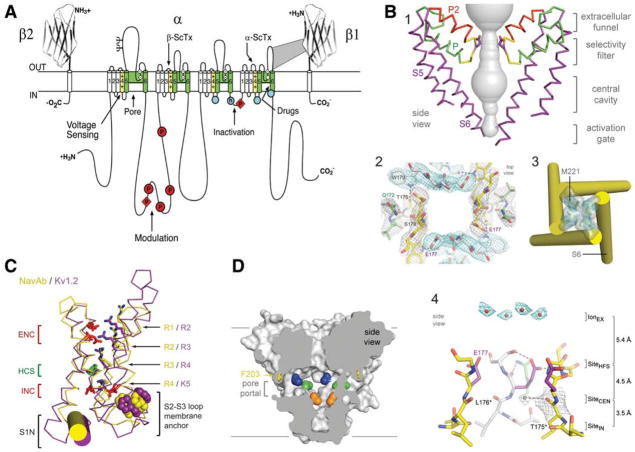
Sodium channels were identified and purified in active form from mammalian brain using specific neurotoxins as molecular probes (Beneski and Catterall, 1980; Catterall, 1984; Hartshorne and Catterall, 1984). They were found to consist of a large α subunit of 260 kDa and smaller β subunits of 30–40 kDa. The complex of purified α and β subunits was shown to be sufficient for reconstitution of neurotoxin- and voltage-dependent activation of sodium conductance characteristic of voltage-gated sodium channels (Tamkun et al., 1984; Hartshorne et al., 1985). Cloning and sequencing cDNA encoding the α subunits established their primary structures and showed that mRNA encoding the α subunit is sufficient for expression of functional sodium channels (Noda et al., 1984, 1986; Goldin et al., 1986). Sodium channel α subunits are composed of ~2000 aa residues organized in four homologous domains, and each contains six transmembrane segments (Fig. 1 A). Later biochemical analyses and cDNA cloning showed that sodium channel β subunits are composed of an N-terminal extracellular Ig-like fold, a single transmembrane segment, and a short intracellular segment (Fig. 1 A) (Isom et al., 1992, 1995). These subunits modulate the kinetics and voltage dependence of sodium channel activation and inactivation and serve as cell adhesion molecules to localize and immobilize sodium channels.

Figure 1.

Structure of voltage-gated sodium channels. A, Primary structures of the subunits of mammalian voltage-gated sodium channels. Cylinders represent β-helical segments. Bold lines represent the polypeptide chains with length approximately proportional to the number of amino acid residues. The extracellular domains of the β1 and β2 subunits are shown as Ig-like folds. Ψ, sites of probable N-linked glycosylation; P in red circles and diamonds, sites of protein phosphorylation by PKA and PKC, respectively; green, pore-lining segments; white circles, the outer (EEEE) and inner (DEKA) rings of amino residues that form the ion selectivity filter and the tetrodotoxin binding site; yellow, S4 voltage sensors; h in blue circle, inactivation particle in the inactivation gate loop; blue circles, sites implicated in forming the inactivation gate receptor. Sites of binding of α- and β-scorpion toxins (ScTx) and a site of interaction between α and β1 subunits are also shown. B, Architecture of the Na_VAb pore. 1, Conformation of the pore-lining S5 and S6 segments and the P loop, containing the conserved P helix and the P2 helix unique to Na_V channels. Glu177 side-chains, purple; pore volume, gray. 2, Top view of the ion selectivity filter. Symmetry-related subunits are colored white and yellow; P-helix residues are colored green. Hydrogen bonds between Thr175 and Trp179 are indicated by gray dashes. Electron densities from Fo–Fc omit maps are contoured at 4.0 σ(blue and gray). 3, The closed activation gate at the intracellular end of the pore illustrating the close interaction of Met221 residues in closing the pore. 4, Side view of the selectivity filter. Glu177 (purple) interactions with Gln172, Ser178, and the backbone of Ser180 are shown in the far subunit. Fo–Fc omit map at 4.75 σ (blue); putative cations or water molecules (red spheres, Ion_EX). Electron density around Leu176 (gray; Fo–Fc omit map at 1.75 σ) and a putative water molecule is shown (gray sphere). Na ⁺-coordination sites: Site_HFS, Site_CEN, and Site_IN. C, Voltage-sensing module. Structures of Na_VAb (yellow) and K_v1.2 (purple) are overlapped. ENC, extracellular negative cluster; HCS, hydrophobic constriction site; INC, intracellular negative cluster. R1–R4, gating charges of Na_VAb; R2–K5 conserved gating charges of K_v1.2. D, Membrane access to the central cavity in Na_VAb. Side view through the pore module illustrating fenestrations (portals) and hydrophobic access to central cavity. Phe203 side chains, yellow sticks. Surface representations of Na_VAb residues aligning with those implicated in drug binding and block: Thr206 (blue), Met209 (green), Val213 (orange). Membrane boundaries, gray lines. Electron density from an Fo–Fc omit map is contoured at 2.0 σ.

Extensive structure–function studies have revealed the primary functional components of sodium channels (for review, see Catterall, 2000). Each domain of the α subunit is composed of two functional modules—a voltage-sensing module consisting of the S1–S4 segments and a pore-forming module consisting of the S5 and S6 segments, and the P loop between them (Fig. 1 A). Voltage-dependent activation of the channel depends on gating charges located in the S4 segments. Sodium is selectively conducted through the outer selectivity filter formed by the P loops and the inner pore lined by the S6 segments. After a few milliseconds, sodium channels are inactivated. Fast inactivation is mediated by the intracellular loop connecting domains III and IV, which folds into the channel structure and blocks the pore like a hinged lid (Fig. 1 A).

The two-dimensional map of sodium channel structure and function (Fig. 1A) can now be visualized in three-dimensions based on x-ray crystallographic studies of an ancestral bacterial sodium channel, Na_VAb from Arcobacter buzleri (Payandeh et al., 2011), which was captured in a closed-pore conformation with four activated voltage-sensors at 2.7 Å resolution (Fig. 1 B–D). The pore has a wide outer vestibule and a narrow intracellular activation gate in the closed conformation (Fig. 1 B1,B3). The Na_VAb selectivity filter is short, ~4.6 Å wide, and water-filled, with four acidic side-chains surrounding the narrowest part of the ion conduction pathway (Fig. 1 B2,B4). This unique structure presents an outer high-field-strength anionic coordination site formed by Glu177 residues, which confers Na ⁺-selectivity through partial dehydration via direct interaction with glutamate side-chains, followed by central and inner coordination sites formed by backbone carbonyls of Leu176 and Thr175 (Payandeh et al., 2011). The selectivity filter is sized to coordinate a sodium ion with two planar waters of hydration at the high-field-strength site and four planar waters of hydration at the central and inner sites. Unexpectedly, fenestrations are observed in the sides of the pore module (Fig. 1 D), and these portals are large enough for the entry of small, hydrophobic physiological regulators or pore-blocking drugs to the receptor site for local anesthetic, antiarrhythmic, and antiepileptic drugs (Payandeh et al., 2011). These fenestrations may represent the pathway through which small hydrophobic drugs reach their receptor site, as predicted in the Modulated Receptor Hypothesis (Hille, 1977).

The arginine gating charges, located at intervals of 3 aa residues in the S4 segments (Bezanilla, 2000; Catterall, 2000), make multiple hydrophilic interactions within the voltage-sensor of Na_VAb, including unanticipated hydrogen bonds to protein backbone carbonyls (Fig. 1C). These hydrophilic interactions stabilize the gating charges in the transmembrane environment and catalyze its outward movement during voltage-dependent activation. A hydrophobic constriction site (HCS) serves to separate the extracellular and intracellular components of the voltage sensor (1C). The voltage-sensing module in Na_VAb is in an activated state, in which three of the gating charges (R1–R3) have moved outward through the HCS and are neutralized by interaction with the extracellular negative cluster of amino acid side chains (Fig. 1C). Gating charge R4 remains on the intracellular side of the HCS, interacting with the intracellular negative cluster (Fig. 1C). Combining the structure of Na_VAb with experimental analysis of voltage sensor movement by disulfide cross-linking of substituted cysteine residues and molecular modeling with the Rosetta Membrane algorithm defined a series of voltage-sensor conformations from resting to activated states. These states are characterized by progressive outward movement of the S4 segment through the voltage sensor catalyzed by exchange of ion pair interactions with the intracellular negative-charge cluster for interactions with the extracellular negative-charged cluster (Yarov-Yarovoy et al., 2012). Comparison to previous open-pore potassium channel structures (Long et al., 2005, 2007) suggests that the voltage-sensor domains and the S4–S5 linkers dilate the central pore by pivoting together around a hinge at the base of the pore module, which opens the pore with an iris-like motion (Payandeh et al., 2011; Yarov-Yarovoy et al., 2012).

Their simple homotetrameric structure leaves bacterial Na_V channels without the fast inactivation gate found in mammalian Na_V channels (Payandeh et al., 2011). However, bacterial Na_V channels are thought to undergo an inactivation process similar to the slow inactivation in mammalian sodium channels, which follows prolonged depolarization, is very slowly reversed, and has a different molecular mechanism from that of fast inactivation (Rudy, 1978). X-ray crystallographic studies of a second crystal form of Na_VAb have captured it in a slow-inactivated state (Payandeh et al., 2012). In this structure, two of the S6 segments have collapsed toward the axis of the pore and two have moved outward, resulting in a strikingly asymmetric dimer-of-dimers conformation at the selectivity filter, central cavity, and activation gate (Payandeh et al., 2012). Only subtle rolling movements of the voltage-sensing module around the pore module are observed during slow inactivation (Payandeh et al., 2012). This slow-inactivated structure has a major conformational change at the drug receptor site in the central cavity (Payandeh et al., 2011), which may be responsible for the increase in affinity for drug binding to the inactivated state of sodium channels (Hille, 1977).

Altogether, these new structures of a bacterial ancestor of mammalian sodium channels have given substantial new insights into the three-dimensional structures of the functional components of sodium channels.

Mechanisms of sodium channel inactivation

In the model for sodium channel gating of Hodgkin and Huxley (1952d), one mode of inactivation accurately described the behavior of sodium channels on the time scale of an action potential. Subsequent work showed that the physical correlate of the inactivation h-gate was the linker between domains III and IV (DIII, DIV) of the voltage-gated sodium channel α subunit (Vassilev et al., 1988; Stühmer et al., 1989). Subsequent studies have shown that an inactivation particle composed of the amino acid sequence isoleucine-phenylalanine-methionine-threonine (IFMT) in this linker folds into the pore and blocks it through interactions with amino acid residues in the S4–S5 linkers in DIII and DIV and the intracellular end of the S6 segment in DIV (Catterall, 2000). This amino acid sequence is arrayed on a pair of turns in the secondary structure of this segment, positioned just before a rigid α helix (Catterall, 2000). This segment is thought to pivot on a pair of glycine residues upstream of the IFMT motif, allowing the inactivation gate to close like a hinged lid and place the inactivation particle firmly over the intracellular mouth of the pore, where it binds to keep the gate closed (Catterall, 2000). Fast inactivation by a single gate, structurally contained within the α sub-unit, defines sodium currents in the squid giant axon as well as in nerve, muscle, and endocrine cells from invertebrates to mammals.

Some neurons, however, have a second mode of rapid inactivation, suggestive of an additional gate (Raman and Bean, 1997). These channels stop passing current within milliseconds of depolarization because of a gate that plugs the pore, acting as an open-channel blocker. This gate is distinct from classical fast inactivation, since it reopens with moderate repolarization (Raman and Bean, 2001). Further distinguishing this gating process from the original Hodgkin-Huxley formalism, blocked channels cannot fast-inactivate, nor can they deactivate until they have reopened to expel the blocking particle. Thus, classical m-gate activation and h-gate inactivation are not independent of block by a b-gate. This behavior is analogous to blockade of K channels by quaternary ammonium ions (Armstrong, 1971) and sodium channels by several exogenous blocking compounds (Yeh and Narahashi, 1977; Cahalan and Almers, 1979; Armstrong and Croop, 1982; O’Leary et al., 1994). Like these compounds, the blocking protein itself does not directly sense the membrane voltage but is displaced in a voltage-dependent manner by inwardly permeating sodium ions (Aman and Raman, 2010). Because of this voltage-dependent unblock, current flows upon repolarization, generating a resurgent sodium current that facilitates repetitive firing (Raman and Bean, 1997, 1999). To date, resurgent current has been identified in >15 classes of neurons (Do and Bean, 2003; Afshari et al., 2004; Cummins et al., 2005; Enomoto et al., 2006; Leão et al., 2006; Castelli et al., 2007a,b; Mercer et al., 2007; Gittis and du Lac, 2008; Kim et al., 2010; Ding et al., 2011).

Of molecular interest is the identity of this second gate. Studies in excised patches and α-subunit null mice suggest that it is a separate protein, physically associated with the sodium channel (Grieco et al., 2002; Grieco and Raman, 2004). Sodium channels with open-channel block thus resemble K_V1 and BK channels, which rely on β subunits to confer inactivation (Rettig et al., 1994; Xia et al., 1999). Sodium channel α subunits likewise associate with β subunits. All four known Na_Vβ subunits have a single transmembrane segment, a large extracellular N terminus, and a short cytoplasmic tail of 35–45 aa (Isom et al., 1992, 1995; Morgan et al., 2000; Yu et al., 2003). The cytoplasmic tail of Na_Vβ4 contains a 10 aa insert just after the transmembrane segment, enriched in positively charged residues that surround an aromatic residue. A 20 aa peptide including this sequence, KKLITFILKKTREKKKECLV, is reminiscent of peptides that block sodium channels (Tang et al., 1996). Indeed, when applied intracellularly to sodium channels from which the endogenous blocking protein has been enzymatically removed, a synthetic β4 peptide of this sequence precisely replicates the native kinetics of open-channel block upon depolarization and unblock upon repolarization. The β4 peptide also induces resurgent-like current in neurons that lack a native blocking protein (Grieco et al., 2005). The subunit is expressed heavily in the cerebellum and brainstem, but sparsely in the cortex and hippocampus, broadly matching the distribution of resurgent sodium current. Thus, Na_Vβ4 has emerged as a good candidate for the endogenous open-channel blocker of sodium channels.

This subunit is not sufficient to generate resurgent current, however: expressing Na_Vβ4 with α subunits in HEK cells does not reconstitute open-channel block (Chen et al., 2008; Aman et al., 2009), suggesting either that additional proteins and/or sub-unit modifications are necessary, or that Na_Vβ4 is not the blocking protein. In cultured cerebellar granule neurons, however, siRNA-mediated knockdown of Na_Vβ4 removes native resurgent current and disrupts repetitive firing; both features are restored by the β4 peptide (Bant and Raman, 2010). Thus, in some neurons, Na_Vβ4 expression is indeed necessary for normal resurgent current. Examining the sequences of the Na_Vβ4 subunit across species reveals conservation of the FxxKK sequence central to the β4 peptide. In fact, five distinct β4 peptides representing 13 species share this motif and generate resurgent-like current, which is disrupted by mutation of the phenylalanine or lysine pair (Lewis and Raman, 2011). Nevertheless, given the variable properties of resurgent current across cells (Aman and Raman, 2007), it seems unlikely that all neurons express the same blocking protein. Defining the structural requirements for a b-gate sets the stage for identifying other β-like subunits that act as open-channel blockers and modulate sodium currents and neuronal firing patterns.

The cellular dynamics of excitability

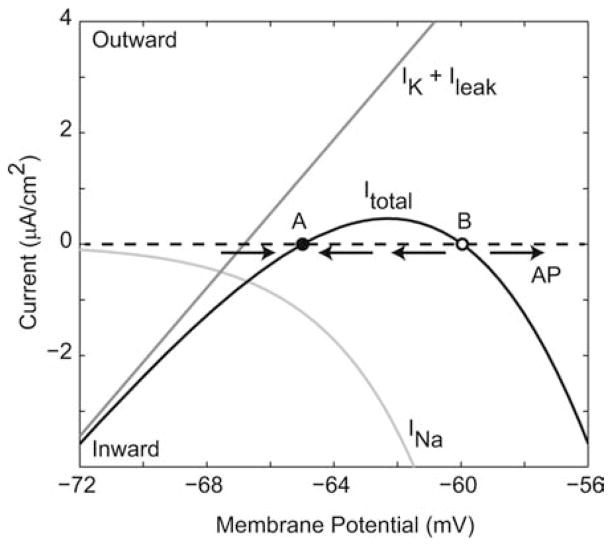
In providing a quantitative description of the electrical responses of squid giant axon, the Hodgkin-Huxley model also gave rise to the modern nonlinear dynamical understanding of action potential generation. A patch of excitable axon membrane has four dynamical quantities: voltage, sodium activation (m), sodium inactivation (h), and potassium activation (n). One can understand excitability by separating the time scales of sodium and potassium channel kinetics (Fig. 2), since near rest, the former is much faster than the latter. If the membrane potential is perturbed from rest, for example, by injecting a stimulus current pulse, then on a short time scale, the conductance of the sodium channel population will follow its steady-state dependence on voltage, while the conductance of the potassium channel population is essentially fixed. The total membrane current is the sum of leak, potassium, and sodium currents. The graph of total current versus membrane potential (IV curve) passes through zero at two locations, a stable fixed point (A; Fig. 2, filled circle) corresponding to the resting potential, and an unstable fixed point (B; Fig. 2, open circle). For small perturbations around A, the effect of membrane current will be to restore the membrane potential toward A, i.e., the curve crosses the axis at A with a positive slope. If the membrane potential exceeds the unstable fixed point B, though, it is driven increasingly positive, since the IV curve has a negative slope at B, and an action potential is initiated.

Figure 2.

The nature of excitability in the Hodgkin-Huxley model. The total membrane current (I_total) [the sum of steady-state sodium current (I_Na) and the resting-conductance potassium and leak currents (I_K + I_leak)], crosses zero at two points, A (resting potential) and B (threshold). See explanation in the main text. In Hodgkin-Huxley terminology, this could be expressed as $I_{\text{total}}={\overline{g}}_K{n}_{\infty }^4(-65)[V-E_K]+{\overline{g}}_{\text{Na}}{m}_{\infty }^3(V)h_{\infty }(V)[V-E_{\text{Na}}]+g_{\text{leak}}[V-E_{\text{leak}}]$. If the membrane potential is perturbed only a little from rest, the direction of membrane current is such that it is attracted back to A, while if it exceeds the unstable fixed point B, then the membrane potential has a positive derivative, driving it further away from B, and an action potential (AP) is generated.

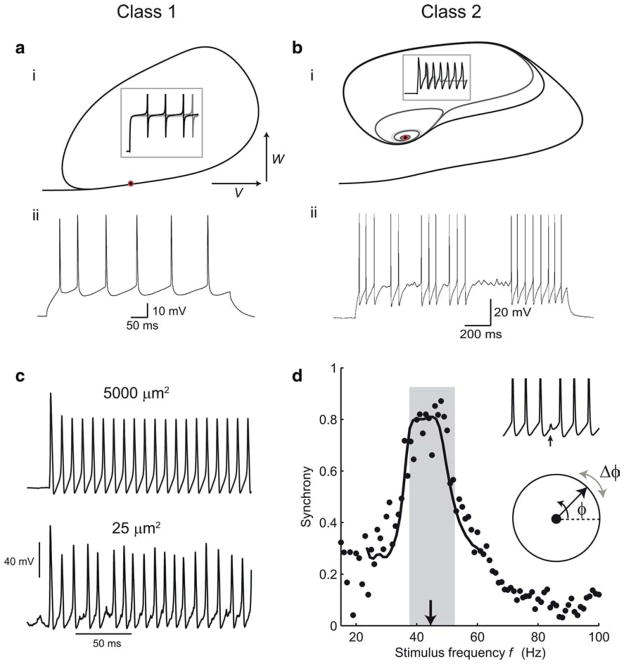
FitzHugh (1961), Morris and Lecar (1981), and others shed even more light on the nature of the dynamics at the threshold of the action potential by focusing on reduced two-dimensional models in which one variable represents activation and the other inactivation and whose trajectories can be visualized in the phase plane (Fig. 3a,b). The threshold of periodic spiking is a bifurcation from an equilibrium or fixed-point to a limit cycle of the dynamics in the phase space, as the level of the stimulus is increased. This can happen in two fundamentally different ways. Hodgkin (1948) described the existence of two different classes of regularly spiking nerve fiber in crab nerve. Class 1 nerve fibers have a continuous relationship between firing frequency and the level of the stimulus current at threshold, while class 2 fibers have a discontinuity—a nonzero minimum firing frequency. Figure 3, a and b, illustrates these two types of threshold in the Morris-Lecar model, whose parameters can be adjusted to show either type of behavior. Class 1 and 2 (also referred to as Type 1 and 2) thresholds correspond to different kinds of bifurcation: a saddle-node bifurcation and a subcritical Hopf bifurcation (Rinzel and Ermentrout, 1989; Izhikevich, 2007). In the saddle-node (strictly saddle-node on a limit cycle) bifurcation, a pair of fixed points, one stable and one unstable, lying along the limit cycle, coalesce and disappear at threshold. The dynamics are arbitrarily slow near the ghost of the fixed points, just above threshold, and therefore stable low-frequency firing is supported. Figure 3ai shows this kind of threshold behavior in the Morris-Lecar model with Class 1 parameters. In the (subcritical) Hopf bifurcation, in contrast, a limit cycle with a nonzero frequency already exists at threshold. A stable resting-state fixed point becomes unstable, and the state becomes attracted instead to the limit cycle (Fig. 3bi). The complex eigenvalues of the linearized dynamics around this fixed point mean that subthreshold oscillations, at a similar frequency to the threshold firing frequency, can occur around it.

Figure 3.

Applications of Hodgkin-Huxley theory to spike generation and timing in cortical neurons. Class 1 (a) and Class 2 (b) threshold dynamics. ai, The phase plane of the Morris-Lecar model with Class 1 dynamics shows an invariant cycle for responses to current steps just below and above threshold (in this case, all the phase plots lie on top of each other). V, Membrane potential; W, potassium activation or recovery variable. Inset, Voltage versus time responses (spikes are curtailed). Red circle indicates the coalesced fixed points at threshold. aii, Stable low-frequency firing in a nonpyramidal regular-spiking interneuron, which has a Class 1 threshold. bi, Morris-Lecar model with Class 2 parameters. Subthreshold responses spiral in to an attracting fixed point at which the Jacobian matrix of the dynamics has complex eigenvalues. Above threshold, this point becomes repelling. bii, A near-threshold response of a fast-spiking inhibitory interneuron switches between spiking at the threshold frequency and subthreshold oscillations, showing Class 2 behavior. c, Spiking in a stochastic Hodgkin-Huxley model simulated according to the method of Chow and White (1996). Reducing the membrane area and channel numbers results in a much more irregular and variable amplitude response. d, Synchronization can be predicted by phase-resetting functions. Periodic spiking is modeled as a phase variable φ with constant angular velocity (bottom inset). It is perturbed (Δφ) by synaptic inputs that change the interval to the next spike (top inset). The synaptic phase resetting function Δφ (φ) can be used to predict how well the cell synchronizes to inputs of different frequencies (main graph, synchrony is the order parameter—magnitude of the average phase vector—at the times of inputs). Black points are measured data, curve shows theoretical prediction. From Gouwens et al. (2010).

These two dynamical behaviors, which are seen even in reduced Hodgkin-Huxley models, have far-reaching implications. Class 1 neurons are effective at encoding different levels of input into a continuous range of firing rates. Class 2 neurons, however, have a built-in clock—the periods of the subthreshold oscillation and of the just-suprathreshold spike firing—and preferentially respond to periodic input of that frequency and can help to maintain a rhythm of that frequency in the network. These differences seem to explain the distinction between integrator neurons, in which the extremely slow dynamics near threshold allow the effect of a transient input current to be long-lasting, and resonator neurons (Hutcheon and Yarom, 2000; Izhikevich, 2001). Class 2 neurons also respond more reliably in their spike timing to fluctuations in input (Robinson and Harsch, 2002; Marella and Ermentrout, 2008)—in essence, they are less easily led astray into long pauses by small fluctuations, and are better-suited to spike time encoding than Class 1 neurons.

It is interesting that these two types of dynamics are found in different classes of neurons in the mammalian cortex. Regular-spiking excitatory cells—the layer 2/3 pyramidal cells and some layer 5 pyramidal cells—and nonpyramidal regular-spiking inhibitory interneurons both behave in a Class 1 manner (Fig. 3a,ii), while fast-spiking inhibitory cells (corresponding mostly to basket-morphology, parvalbumin-expressing interneurons) have a hard Class 2 threshold, and also show strong subthreshold oscillations (Fig. 3b,ii) just below threshold (Tateno et al., 2004; Tateno and Robinson, 2009). Since the threshold spike frequency is just at the lower limit of the gamma frequency range, these dynamics clearly enhance the action of fast-spiking neurons in creating gamma oscillations via rhythmic inhibition of pyramidal neurons (Mann and Paulsen, 2005; Morita et al., 2008; Sohal et al., 2009).

The standard Hodgkin-Huxley model is deterministic. Nevertheless, as Hodgkin and Huxley themselves clearly recognized, and single-channel recording confirmed in great detail (Sigworth and Neher, 1980; Sakmann and Neher, 1995), it is only a macroscopic approximation, describing the probability of large populations of independent sodium and potassium ion channels being in their open, conducting states. The stochastic openings of individual channels cause fluctuations in the membrane potential. Together with the high sensitivity of channel state transition rates to the membrane potential, this leads to complex and unpredictable behavior, which becomes more salient in small cells and cellular processes such as dendrites and axons (Faisal et al., 2005). In Figure 3c, we show spiking responses in a fully stochastic Hodgkin-Huxley model, in which all of the individual channel state transitions of channels are simulated explicitly. Understanding this kind of interplay of noise and nonlinearity, and the irregular and complex firing it can produce in neurons such as irregular-spiking cortical interneurons (Galarreta et al., 2004) is an important challenge for the future.

The spike-generating dynamics described by the Hodgkin-Huxley model are also central to understanding how neurons synchronize with each other. Flow of current through gap-junctions and at chemical synapses between two neurons allows the timing of their spikes to adjust until they are coincident, or at a stable relative delay. A powerful approach to understanding this has been the idea of phase resetting or phase response curves (Schultheiss et al., 2012), which in essence reduce the Hodgkin-Huxley model further, to just a single dimension—the phase of the neuron within the period of its spiking oscillation, as it goes around its limit cycle. This can be studied straightforwardly in experiments, even in the case of strong synaptic connections. Figure 3d shows an example (Gouwens et al., 2010) where a fast-spiking cortical cell is driven with a conductance stimulus that mimics the combined current flow through gap-junctional and GABAergic synapses generated by spikes in a neighboring fast-spiking cell. Each presynaptic spike advances or retards the phase of oscillation by a measured amount. This synaptic phase resetting function allows an accurate prediction of the degree of synchrony of presynaptic and postsynaptic spikes, as the frequency of presynaptic spikes is varied. This function encapsulates the biophysics of spike generation and the properties and timing of the synaptic connections in one relationship, describing how the Hodgkin-Huxley dynamical state is shifted along its cycle by an input. Thus, there is a direct relationship between the phase-sensitivity of the effect of an input and the dynamics of spike generation. For this reason, the spike-generating dynamics of different cell types are directly related to how they synchronize (Ermentrout, 1996). Fast-spiking interneurons in particular synchronize extremely well and rapidly, because their synaptic phase-resetting functions are sharp and have strong early phase delay and late phase advance regions (Gouwens et al., 2010). This helps to explain the widespread coordination of their inhibitory outputs on pyramidal cells during gamma oscillations in the cortex. In general, a phase-resetting relationship with prominent phase-delay and phase-advance regions (referred to as a type II phase-resetting curve) enhances the ability for stochastic synchrony in a network of coupled oscillators (Abouzeid and Ermentrout, 2009).

Hodgkin-Huxley models in computational neuroscience

The Hodgkin-Huxley model (Hodgkin and Huxley, 1952d) of the action potential in the squid giant axon has served as a foundation for models of neural dynamics on a range of spatial scales. At a fine grain, the probabilistic opening and closing of single ion channels can be described by Markov models, which make the assumption that the probability of transitioning between states depends only on the current state (Fink and Noble, 2009). At the next level, which is where Hodgkin-Huxley models apply, the numbers of ion channels are assumed to be sufficiently large that only the average conductances are represented in the equations. This approximation can become inaccurate when the structures are sufficiently small or the numbers of channels small, such as in thin axons and synaptic spines (Qian and Sejnowski, 1990; Faisal et al., 2005), as discussed in the previous section (Fig. 3c). Current digital computers can simulate thousands of Hodgkin-Huxley model neurons with realistic morphologies interacting in realistic circuits (Brette et al., 2007). For these models to accurately represent neural activity, the properties of the ion channels and their locations inside neurons must be known. For yet larger neural networks, the Hodgkin-Huxley equations can be simplified to yield models with many fewer parameters, while retaining some of the complex dynamics of real neurons (Morris and Lecar, 1981; Izhikevich, 2007). Hodgkin-Huxley neuron models, however, remain the gold standard against which these simplified models are compared.

The original Hodgkin-Huxley model included a fast sodium current, a delayed rectifier potassium current, and a leak current. Although it is not voltage-dependent, the leak current is an essential ion channel that determines the input resistance of neurons and indirectly the strengths of synaptic potentials (Coggan et al., 2010). Since then many more ion channels have been discovered that can be modeled with similar biophysical voltage-dependent activation and inactivation variables. Nature has evolved an astonishing diversity of neurons, each expressing only one set of ion channels out of billions of potential channel combinations. Each combination forms a complex dynamical system, capable of a wide range of behaviors, from fast spiking to slow spiking, from bursts of spikes to adapting spike trains, and even more complexity emerges when the spatial heterogeneity of ion channels in dendrites and axons is taken into account. Are there organizing principles that can help us make sense of this combinatorial explosion of possibilities and wealth of related data? One constraint may be to minimize energy cost needed to accomplish a desired goal.

The human brain uses more than twice as much glucose per day as the heart. Action potentials, dendritic integration, and synaptic transmission account for more than half of this energy use (Shulman et al., 2004). How can this energy be most efficiently used to generate activity or carry out computation (Laughlin et al., 1998; Levy and Baxter, 1996)? The combination of ion channels that most efficiently generates action potentials depends on the function of the neuron, such as the average firing rate and the detailed kinetics of the channels.

Some neurons fire tonically at high rates, such as fast-spiking interneurons in the cortex (20–80 Hz), and have thin spikes, but others fire at lower rates and less often, such as pyramidal neurons in the cortex (1–20 Hz), and have much thicker spikes. Are the different properties of the spikes in these neurons consistent with minimizing the cost of spiking? Also, the energy required to produce a train of spikes cannot be easily derived from the energy for producing a single spike. These questions were the focus of a recent study of the cost of spiking (Hasenstaub et al., 2010).

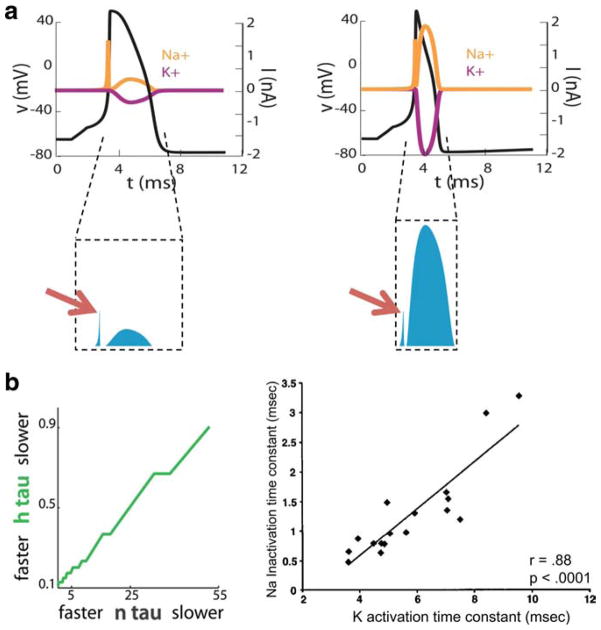
During depolarization, the sodium conductance far exceeds potassium conductance. Sodium entry during depolarization is thus limited to what is required to charge the cell’s capacitance. But, in many cells, during repolarization, both sodium and potassium channels are open and sodium enters the cell at the same time that potassium exits the cell (but see Alle et al., 2009; Carter and Bean, 2009). These fluxes mostly cancel each other, so that only a small part of the charge exchanged goes into changing the cell’s membrane potential (Fig. 4a, left). The duration of this repolarization, and thus the duration of the action potential itself, limits the rate at which the neuron can spike. Narrowing the action potential by tripling the rate of potassium channel activation increases the rate at which the model neuron is able to spike. However, because sodium channel inactivation occurs slowly, sodium channels are less inactivated earlier in the action potential. If potassium channels activate earlier, sodium and potassium conductances will overlap more extensively (Fig. 4a, right). Earlier hyperpolarization will therefore be opposed by a greater sodium current flow, increasing the total Na ⁺ influx during repolarization, and thus increasing the metabolic cost of the action potential. There is trade-off between the energy cost of action potential generation and the ability to spike rapidly.

Figure 4.

Single thin spikes are more energetically expensive than single thick spikes and the cost of a fast-spike train is minimized with fast sodium inactivation. a, Hodgkin-Huxley model of an action potential with a slow potassium activation superimposed on the resulting sodium (orange) and potassium currents (red), and the total number of transferred ions (blue). Right, Hodgkin-Huxley model of an action potential with a fast potassium activation has a thinner width and larger number of transferred ions (blue). b, The energy cost of a Hodgkin-Huxley model with fast spiking is minimized when the sodium inactivation speed is matched to the potassium activation speed. Adapted from Hasenstaub et al. (2010).

The increased cost of faster potassium channels can be minimized by speeding sodium channel inactivation, which reduces the overlap between sodium and potassium conductance opening. But this speeding is only beneficial up to the potassium conductance activation speed. This predicts that, all else being equal, cells with faster potassium channel activation kinetics should display faster sodium channel inactivation kinetics. An example of an entire family of cells with similar resting membrane potential, action potential height, and spike threshold, but with variable firing rate requirements, is found in the electric organ of weakly electric fish. The electrically active electrocytes in these fish generate the electric organ discharge at a characteristic frequency, but different fish generate this discharge at different frequencies, spanning a wide range from 50 to 200 Hz, and the same fish may change its frequency with hormonal shifts. The model predicted that at faster frequencies, electrocytes should contain potassium channels with faster activation kinetics (Fig. 4b, left), as observed experimentally (Fig. 4b, right) (McAnelly and Zakon, 2000). This relationship between sodium inactivation and potassium inactivation in electrocytes cannot be predicted from functional constraints alone, because fast sodium inactivation is not required for thin spikes or fast action potential generation.

One caveat with these predictions is that in real neurons there are many other ion channels that are distributed broadly within the neuron. The results of the model were tested by using a fast dynamic voltage clamp to inject sodium conductances with a variety of kinetics into fast-spiking interneurons that had been treated with tetrodotoxin to block the endogenous sodium current (Hasenstaub et al., 2010). The hybrid system displayed qualitatively similar relationships between sodium channel properties, bandwidth, and metabolic cost over a wide range of kinetic parameters for the injected sodium conductance. This suggests that cellular ion channel expression in neurons is optimized not merely to achieve function, but to achieve function while minimizing metabolic cost.

The mammalian genome contains genes encoding hundreds of types of ion channels, most of which can be produced in multiple splice variants and regulated at multiple phosphorylation sites by numerous intrinsic and extrinsic factors. Which combination of these ion channels will be expressed by any particular neuron, for which computational or behavioral role? Any given electrical phenotype can be produced by many combinations of ion channels (Prinz et al., 2004; Achard and De Schutter, 2006), so on functional grounds alone, this question is underconstrained.

The process of regulating which channels to express in a given neuron, how many channels to insert into membranes, and where to insert them is an active area of research in membrane protein trafficking. Many properties of ion channels, including maximum conductances and activation time constants, are dynamically regulated on a wide range of time scales, both through genetic control and in response to chemical and electrical signals that the neuron experiences. This leads to the concept of neuronal homeostasis, how the activity of a neuron can be kept in equilibrium at a targeted set point, and raises many more questions such as the nature of the set point in neurons and the mechanisms that are used to achieve it (Bell, 1992; Abbott, 2003; Marder and Goaillard, 2006).

Spiking neurons are essential for long-distance communication in the brain. Spike timing is used in the auditory system for sound localization and in the rat hippocampus for place coding. The Hodgkin-Huxley model of the action potential continues to generate new insights into the properties of neurons and neural circuits, which endow brains with powerful computational capacities that we are just beginning to understand.