Tuning the Attempt Frequency of Protein Folding Dynamics via Transition-State Rigidification: Application to Trp-cage

Abstract

The attempt frequency or prefactor (k₀) of the transition state rate equation of protein folding kinetics has been estimated to be on the order of 10⁶ s⁻¹, which is many orders of magnitude smaller than that of chemical reactions. Herein, we use the mini-protein Trp-cage to show that it is possible to significantly increase the value of k₀ for a protein folding reaction by rigidifying the transition state. This is achieved by reducing the conformational flexibility of a key structural element (i.e., an α-helix) formed in the transition state via photoisomerization of an azobenzene cross-linker. We find that this strategy not only decreases the folding time of the Trp-cage peptide by more than an order of magnitude (to ~100 ns at 25 °C) but also exposes parallel folding pathways, allowing us to provide, to the best of our knowledge, the first quantitative assessment of the curvature of the transition state free energy surface of a protein.

Conformational diffusion on an energy landscape that is biased towards the native state ensures that protein folding is a thermodynamically robust and productive event.^1–4 However, during folding, the free energy of the system does not always show a monotonic decrease; instead, it can increase over a relatively small region of the landscape, leading to the formation of folding free energy barriers. Since these barriers contain key information for achieving a comprehensive understanding of the mechanisms of protein folding, significant efforts have been made to investigate how and why such kinetic bottlenecks are generated, as well as the structural characteristics of the associated transition states.⁵ More recently, several studies have focused on elucidating the dynamic aspects of the folding free energy barrier, such as the roughness of the underlying free energy surface⁶ and the transition path time.^7–8 According to Kramers’ theory,⁹

$$k=\frac{{\omega }_{\mathrm{R}}{\omega }_{\mathrm{B}}}{2\pi \gamma }exp\left(-\frac{\mathrm{\Delta }{G}^{\ne }}{RT}\right),$$ (1)

where R is the gas constant and T is the absolute temperature, the rate of a barrier-crossing process is determined not only by the height of the barrier (ΔG^≠) but also the curvatures of the reactant ( ${\omega }_{\mathrm{R}}^2$) and transition state ( ${\omega }_{\mathrm{B}}^2$) potential wells, as well as the friction coefficient (γ). The latter manifests as the roughness of the potential energy surface. While direct experimental assessments of ω_R and ω_B are currently not possible, many previous studies^10–11 have been performed to determine the pre-exponential factor, often referred to as the attempt frequency (k₀). Interestingly, the value of k₀ for protein folding is estimated to be in the range of 10³ – 10⁶ s⁻¹,¹² which is several orders of magnitude smaller than that observed for chemical reactions and, thus, suggests that the curvature of the protein folding transition state potential well (i.e., ${\omega }_{\mathrm{B}}^2$) is intrinsically small. This is consistent with the well-recognized notion that the folding transition state consists of an ensemble of structures that contain only a fraction of the native contacts and hence is inherently flexible. On the other hand, gas phase chemical reactions between small molecules often encounter a transition state that contains a single, distinct species in a highly-constrained geometric configuration. In this regard, we hypothesize that by rigidifying the folding transition state one could significantly increase ω_B and hence k₀ (Equation 1). In this proof-of-concept study, we chose a mini-protein, Trp-cage,^13–14 as our model system and employed an azobenzene cross-linker to modify the curvature of its free energy barrier.

Trp-cage is one of the most extensively studied model peptide systems in protein folding,^15–54 which has led to a fairly detailed understanding of its folding mechanism. For example, both experimental^{22,40–41,48–50} and computational^{16–18,23–24,27,30–39,42,44,46–47} studies have shown that the α-helix is either partially or completely formed in the major folding transition state, often without the presence of many native tertiary stabilizing interactions. Thus, this feature provides a unique opportunity to modify the characteristics of the folding transition state of Trp-cage via a photoactivatable cross-linker. As shown (Figure 1), our working hypothesis is that upon imposing a geometric constraint on the Trp-cage α-helix via photo-induced isomerization of an azobenzene cross-linker, we will be able to not only initiate folding but also force the conformational search to pass through a more rigidified transition state, thus making the attempt frequency (i.e., k₀) of this folding ‘reaction’ larger.

Figure 1.

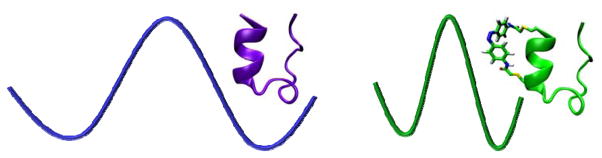
A schematic representation of how the azobenzene cross-linker alters the curvature of the folding free energy surface of Trp-cage.

We chose an amidoazobenzene derivative as the photoactivatable cross-linker based on the fact that (1) its cis isomeric form supports or stabilizes α-helical conformations when attached between the i and i+7 positions of a peptide,⁵⁵ whereas its trans form does not, (2) its trans form is thermodynamically more favorable (>95%) in the dark at room temperature,⁵⁶ (3) upon irradiation with 355 nm light, the trans to cis isomerization occurs on the picosecond timescale,⁵⁷ which is significantly faster than the folding time of Trp-cage, and (4) the spontaneous back-reaction, i.e. the cis to trans isomerization, takes place on the timescale of minutes at room temperature.⁵⁸ Specifically, we introduced the azobenzene moiety into a mutant of the Trp-cage 10b variant containing cysteine substitutions at residues 1 and 8 (sequence: CAYAQWLCDGGPSSGRPPPS), using standard cysteine alkylation methods.⁵⁵ As indicated above, the resultant Trp-cage peptide (hereafter referred to as 10b-azob) should fold only when the azobenzene cross-linker is in its cis isomeric form (Figure 1).

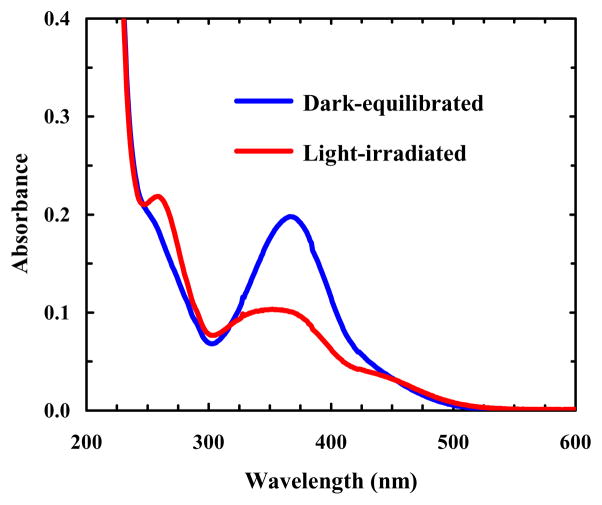
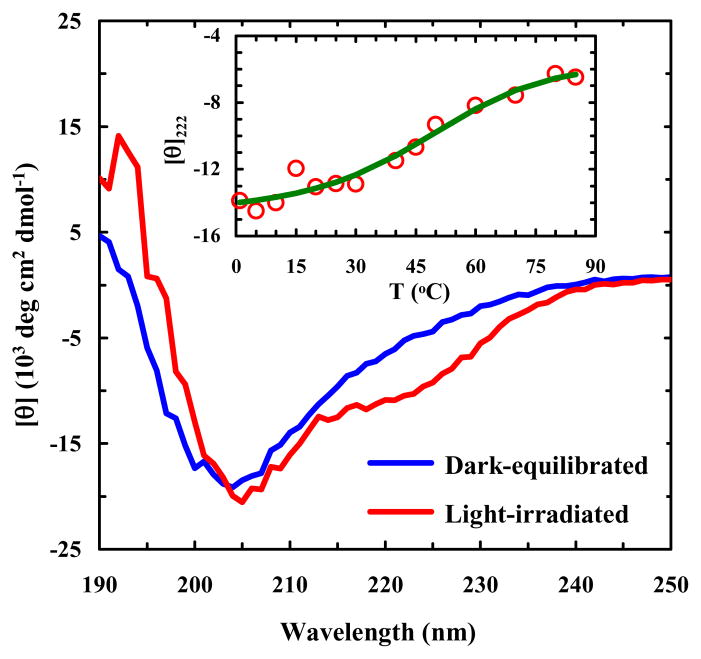
As shown (Figure 2), the π-π* transition of trans amidoazobenzene at ~367 nm has a significant decrease in intensity upon irradiation of 10b-azob with 355 nm light, whereas there is a gain in absorbance at ~258 nm, which corresponds to the π-π* transition of cis amidoazobenzene.⁵⁵ Furthermore, as expected (Figure 3), the circular dichroism (CD) spectrum of the dark-equilibrated 10b-azob sample (in a 20/80 trifluoroethanol/water mixture) indicates that the peptide adopts mostly disordered conformations, whereas the CD spectrum of the light-irradiated sample indicates that light absorption indeed prompts α-helix formation. The reason that we added trifluoroethanol (TFE), which is known to promote α-helix formation,⁵⁹ is that in pure water the light-irradiated peptide exhibits relatively low helicity. This is most likely due to the fact that addition of the azobenzene cross-linker eliminates the favorable N-terminal helical cap, which has been shown to be detrimental to the stability of Trp-cage.^60–61 More importantly, in the presence of 20% TFE the CD signal of the light-irradiated 10-azob sample at 222 nm shows a similar sigmoidal dependence on temperature as that of the wild type peptide (Figure 3, inset), suggesting that the peptide’s cage structure is formed when the azobenzene moiety is in its cis form and that the addition of TFE compensates for the loss of helix stability upon cross-linking. The latter is supported by the fact that addition of 20% TFE only leads to a small increase (~7 °C) in the thermal melting temperature of Trp-cage 10b (Supporting Information).

Figure 2.

Absorption spectra of dark-equilibrated and light-irradiated 10b-azob peptides (~10 μM), as indicated. The light-irradiated sample was prepared by irradiating the dark-equilibrated sample with 355 nm light (~8.8 mW cm⁻²) for 5 minutes.

Figure 3.

CD spectra of dark-equilibrated and light-irradiated 10b-azob samples (~33 μM in a 20/80 trifluoroethanol/water solution), as indicated. The light-irradiated sample was prepared as described in the caption of Figure 2. Inset: CD T-melt of the light-irradiated 10b-azob sample, monitored at 222 nm. The solid line is a fit of the data to a two-state model using the same thermodynamic parameters determined for the wild-type Trp-cage 10b.⁴⁰

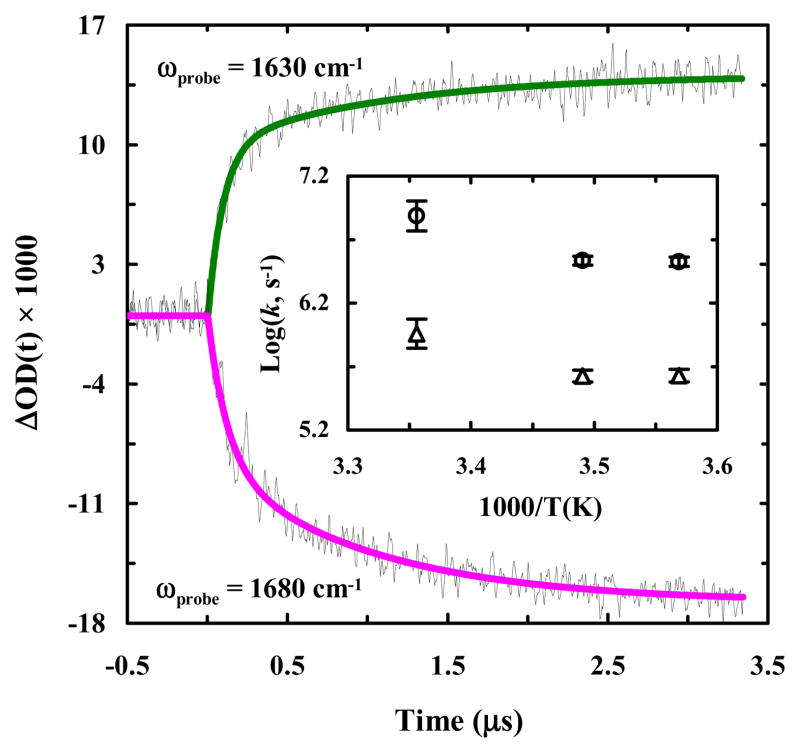
The light-induced folding kinetics of 10b-azob were probed using a time-resolved infrared (IR) apparatus.⁶² Briefly, the 355 nm pump pulse (3–5 ns) was derived from a Minilite II Nd:YAG laser (Continuum, CA), and a tunable 1001-TLC quantum cascade (QC) laser (Daylight Solutions, CA) was used as the continuous-wave (CW) IR probe. As indicated (Figure 4), the light-induced conformational dynamics of 10b-azob at 25 °C, probed at 1630 cm⁻¹ where helical content is known to absorb,⁶³ show an increase in absorbance as a function of time, consistent with the CD results (Figure 3). What is more interesting, however, is that this kinetic trace is best fit to a double-exponential with time constants that differ by an order of magnitude (i.e., 90 ns versus 1.1 μs). Further measurements at 1680 cm⁻¹, where disordered conformations have a larger absorbance, show identical results (Figure 4). Previously, we have shown that the folding time of Trp-cage 10b is approximately 1.6 μs at 25 °C.⁴⁰ Thus, the slower kinetic phase in the current case is similar to the folding kinetics of the wild type peptide, whereas the faster kinetic phase represents a previously unobserved folding event. Taken together, these results indicate that by photo-initiating isomerization of an azobenzene cross-linker added to the α-helical segment of the Trp-cage sequence, we are creating either two parallel pathways that have distinctly different folding rates or a sequential pathway that involves a folding intermediate.

Figure 4.

Conformational kinetics of 10b-azob (in a 20/80 trifluoroethanol/water solution) induced by a nanosecond 355 nm laser pulse and probed at different frequencies, as indicated. These kinetic traces were collected at 25 °C and in each case a linear and instrument-limited signal arising from the solvent due to the pump induced temperature jump (approximately 1 °C) has been subtracted for clarity. The smooth lines are fits of these traces to a double-exponential function with the following time constants (relative percentages): 90 ± 20 ns (74 %) and 1100 ± 100 ns (26 %) for 1630 cm⁻¹, and 120 ± 20 ns (54 %) and 1000 ± 90 ns (46 %) for 1680 cm⁻¹. Inset: Temperature dependence of the fast and slow rate constants of 10b-azob obtained at 1630 cm⁻¹.

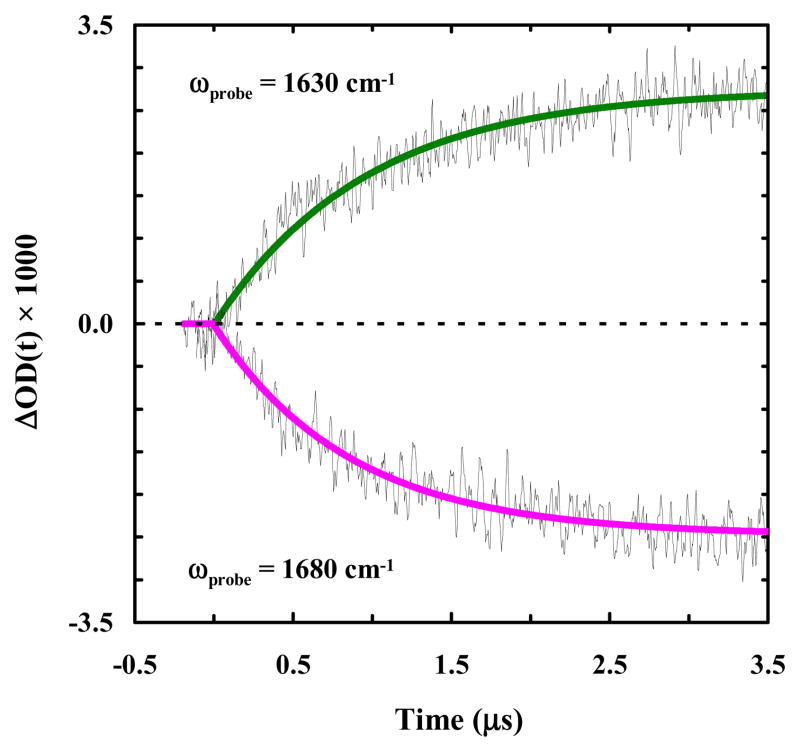
It has recently been shown that the 3₁₀-helix of Trp-cage 10b folds on the order of hundreds of nanoseconds and formation of this structure is considered to be the last step in the folding process.⁴⁰ However, it is unlikely that the fast component seen in these experiments comes from 3₁₀-helix formation for two reasons. First, 3₁₀-helices typically absorb in the 1660 cm⁻¹ region,⁶⁴ yet the ~100 ns component observed for 10b-azob is detected at both 1630 cm⁻¹ and 1680 cm⁻¹. Also, the 3₁₀-helix of Trp-cage 10b is relatively unstable and, as a result, the previous study⁴⁰ was only able to detect its folding-unfolding kinetics at temperatures below ~20 °C. Another possibility is that the fast phase reports on formation of an intermediate state that contains a native or native-like α-helix, which goes on to form the folded Trp-cage structure with a slower folding rate. To test this possibility, we studied the photo-induced conformational dynamics of another azobenzene cross-linked peptide that corresponds to the Trp-cage 10b α-helix (sequence: CAYAQWLCD, hereafter referred to as 10b-h-azob). As indicated (Figure 5), the light-induced kinetics of 10b-h-azob in the presence of 20% TFE, probed at 1630 and 1680 cm⁻¹, can be described by a single-exponential function, with a time constant of approximately 1.0 μs for both cases. This result is consistent with the study of Serrano et al., ⁶⁵ which showed that the folding time of a helical peptide with a sidechain-sidechain cross-linker is on the order of 1 μs. Perhaps most importantly, our 10b-h-azob results are in line with those of Hamm and coworkers,⁶⁶ who observed that the presence of an azobenzene cross-linker in a short α-helical peptide acts as a thermodynamic constraint rather than a dynamic one. In this regard, they observed that rather than initiating a fast downhill folding process, the azobenzene photoswitch allowed for the stabilization of metastable, non-native free-energy traps. Therefore, these results prompt us to conclude that the fast (i.e., ~100 ns) component seen in the case of 10b-azob does not arise from an early, partially-folded, on-pathway Trp-cage intermediate wherein only the α-helix is formed; instead, it corresponds to an alternative but much faster folding pathway. Similarly, a sequential scenario in which the α-helix is formed in ~1 μs followed by a 100 ns folding event can also be ruled out, as the current experimental strategy is unable to detect a fast kinetic event following a slower one. Moreover, these kinetic results also argue against the idea that the faster folding component of 10b-azob results from a decrease in the folding free energy barrier, as we would expect similar double-exponential behavior for 10b-h-azob in this case. This is because, as discussed above, the rate-limiting step in Trp-cage folding corresponds to helix formation. Thus, tertiary interactions with the rest of the 10b-azob peptide seem to play an influential role in creating this alternate protein folding pathway. Indeed, kinetic measurements carried out on 10b-azob at different temperatures reveal that both rates have very similar dependences on temperature (Figure 4, inset), further supporting the idea that the azobenzene cross-linker is not affecting the free energy barrier height but rather altering the frequency with which the system leaves the transition state region.

Figure 5.

Conformational kinetics of 10b-h-azob (in a 20/80 trifluoroethanol/water solution) induced by a nanosecond 355 nm laser pulse and probed at different frequencies, as indicated. These kinetic traces were collected at 24.4 °C and in each case a linear background signal arising from the solvent has been subtracted for clarity. The smooth lines are fits of these traces to a single-exponential function with the following time constants: 960 ± 60 ns for 1630 cm⁻¹, and 860 ± 40 ns for 1680 cm⁻¹.

In summary, because an additional parallel pathway originating from the same reactant can only lead to an increase in the overall reaction rate, our interpretation implies, as shown in the following kinetic scheme, that upon photoisomerization of the azobenzene cross-linker two distinguishable conformational ensembles (U_1,cis and U_2,cis) in the unfolded potential well of 10b-azob are rapidly formed,

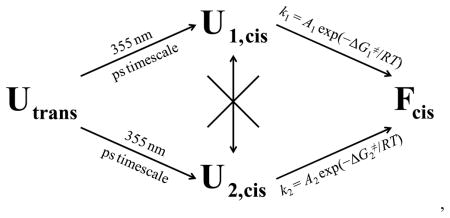
where A₁ ≈ 10A₂, $\mathrm{\Delta }{G}_1^{\ne }\approx \mathrm{\Delta }{G}_2^{\ne }$, and the exchange rate between U_1,cis and U_2,cis is significantly slower than their folding rates to form F_cis. Also of note, both k₁ and k₂ are significantly faster than the single-exponential folding rate (τ_F is in the range of 5–7 μs) of another cross-linked Trp-cage peptide.⁶¹ It was shown previously that when a helix cross-linker, m-xylene, was placed between positions 4 and 8 of the Trp-cage 10b sequence, both the folding and unfolding rates of the resultant peptide were significantly decreased in comparison to those of the wild-type Trp-cage 10b.^61,67 This was attributed to a frictional effect of m-xylene, as it was located at the most sterically congested region of the peptide. Since the azobenzene cross-linker is not only longer but also more flexible than m-xylene, it is expected to cause a much smaller perturbation due to internal friction. In addition, in keeping with the present hypothesis, the findings obtained with the m-xylene cross-linker suggest that crossing-linking a single α-helical turn is insufficient to significantly increase the rigidity of the folding transition state.

The notion that the two kinetic phases of 10b-azob arise from parallel folding pathways that have identical or comparable free energy barriers suggests that we could further estimate the value of ω_B, which, to the best of our knowledge, has never been done before. Based on Eq. 1, it is easy to show that

$$\frac{k_{\mathrm{S}}}{k_{\mathrm{F}}}=\frac{{\omega }_{\text{BS}}}{{\omega }_{\text{BF}}},$$ (2)

assuming that ω_R for both the fast and slow pathways is the same, where k_S and k_F are the rate constants of the slow and fast components, respectively, while ω_BS and ω_BF are the frequencies of the respective transition-state harmonic potential wells. In turn, these frequencies determine the free energy (G_B) of motion along the folding coordinate (q) near the transition state:

$$G_{\mathrm{B}}=\mathrm{\Delta }{G}^{\ne }-\frac{1}{2}m{\omega }_{\mathrm{B}}^2{q}^2$$ (3)

where m is the effective mass of the particle. Following Eq. 3, one can easily show that for the same displacement along the folding coordinate, i.e. Δq, the free energy difference between the two aforementioned harmonic wells would be:

$$\mathrm{\Delta }{G}_{\mathrm{B}}=\frac{1}{2}m\left({\omega }_{\text{BF}}^2-{\omega }_{\text{BS}}^2\right){(\mathrm{\Delta }q)}^2$$ (4)

Thus, by combining Eqs. 2 and 4 and using the experimentally determined values of k_S and k_F, one could solve for ω_BS and ω_BF if ΔG_B and Δq are known. While both are difficult, if not impossible, to be determined, we can make reasonable estimates in the current case. As concluded above, the fast folding phase arises from a more rigid transition state. In other words, it is the entropic effect of the azobenzene cross-linker that makes ω_BF larger. Using the values for change in conformational entropy upon helix formation determined by Hofrichter et al., ⁶⁸ we estimated the maximum entropic stabilization of helical structure arising from the azobenenze cross-linker to be approximately 6 kcal/mol. By further assuming that the peptide, which has a molecular weight of 2049.2 g/mol, needs to move a distance that is one-fourth of the radius of gyration of Trp-cage in order to cross the transition state, or Δq = 3 Å,²³ we found that ω_BS = 5.24 × 10¹⁰ rad/s. This estimate provides what, to the best of our knowledge, is the first experimental assessment of the frequency of the protein folding transition state. By further assuming that ω_R is on the same order of magnitude as ω_B, an assumption commonly used in the literature,^10,12 and D = 10⁻⁶ cm²/s as an upper limit,⁶⁹ we estimated k₀ to be 6.9 × 10⁶ s⁻¹ for the folding kinetics of the unconstrained Trp-cage peptide.

Despite its approximate nature, the above calculation yields a k₀ value that is in good agreement with previously estimated values based on measurements of the folding rate of ultrafast folders¹¹ and the rate of contact formation in unfolded protein ensembles,⁷⁰ as well as those based on simulations¹⁰ and theoretical predictions.⁷¹ In particular, this value compares well with that (10^7±1 s⁻¹) determined by Yu et al., ⁸ who used single-molecule force spectroscopy to characterize the folding free energy landscape and rate of a prion protein. Therefore, these agreements provide further support, albeit indirectly, of our interpretation and analysis of the kinetics results obtained with 10b-azob.

Although all of the evidence supports the aforementioned folding mechanism of 10b-azob, it is worth mentioning that an alternative interpretation for the observed nonexponential behavior is due to projection of the protein onto an incipient downhill folding landscape upon azobenzene isomerization. Gruebele and coworkers^72–73 have found that under certain conditions, proteins can be engineered to fold in a complex manner in which there is both a slow phase due to some molecules diffusing on a landscape containing a barrier (activated folding) and a fast phase resulting from other molecules navigating a barrier-less landscape (downhill folding). We have tentatively ruled out this possibility based on the kinetic results of 10b-h-azob (Figure 5) and the similar temperature dependence of the fast and slow rate constants of 10b-azob (Figure 4).

While extensive effort has gone into identifying the structures of folding transition states of peptides and proteins, aside from the ability to further stabilize these proteins and to obtain generic protein design strategies there have not been many examples of using this knowledge to actively change the nature of a protein’s folding, e.g. altering the shape of the protein folding free energy barrier. Here, we show, using Trp-cage as a testbed, that it is possible to tune the attempt frequency of protein folding dynamics via rigidification of the transition state. Specifically, we exploit the trans to cis isomerization of an azobenzene cross-linker via phototriggering to not only initiate folding but also provide a certain degree of constraint on the conformational flexibility of the α-helix of Trp-cage, which has previously been shown to be formed in the transition state. Transient IR measurements reveal that this strategy produces biphasic kinetics of folding, with time constants that differ by an order of magnitude (i.e., 100 ns versus 1 μs). Further control experiments on a truncate of Trp-cage containing just the α-helix segment provide strong evidence indicating that the fast kinetic phase does not arise from an intermediate; instead, it is confirmation of a parallel folding pathway whose transition-state potential well has a larger curvature in comparison to that of the wild-type Trp-cage. Moreover, from these experimental results, we are able to estimate the frequency of the transition state of Trp-cage to be on the order of 10¹⁰ rad/s.