Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Dec 1;88(3):1676–1683. doi: 10.1529/biophysj.104.051805

Nano-to-Micro Scale Dynamics of P-Selectin Detachment from Leukocyte Interfaces. III. Numerical Simulation of Tethering under Flow

Michael R King *, Volkmar Heinrich †, Evan Evans †,‡, Daniel A Hammer §
PMCID: PMC1305224  PMID: 15574709

Abstract

Transient capture of cells or model microspheres from flow over substrates sparsely coated with adhesive ligands has provided significant insight into the unbinding kinetics of leukocyte:endothelium adhesion complexes under external force. Whenever a cell is stopped by a point attachment, the full hydrodynamic load is applied to the adhesion site within an exceptionally short time—less than the reciprocal of the hydrodynamic shear rate (e.g., typically <0.01 s). The decay in numbers of cells or beads that remain attached to a surface has been used as a measure of the kinetics of molecular bond dissociation under constant force, revealing a modest increase in detachment rate at growing applied shear stresses. On the other hand, when detached under steady ramps of force with mechanical probes (e.g., the atomic force microscope and biomembrane force probe), P-selectin:PSGL-1 adhesion bonds break at rates that increase enormously under rising force, yielding 100-fold faster off rates at force levels comparable to high shear. The comparatively weak effect of force on tether survival in flow chamber experiments could be explained by a possible partition of the load amongst several bonds. However, a comprehensive understanding of the difference in kinetic behavior requires us to also inspect other factors affecting the dynamics of attachment-force buildup, such as the interfacial compliance of all linkages supporting the adhesion complex. Here, combining the mechanical properties of the leukocyte interface measured in probe tests with single-bond kinetics and the kinetics of cytoskeletal dissociation, we show that for the leukocyte adhesion complex P-selectin:PSGL-1, a detailed adhesive dynamics simulation accurately reproduces the tethering behavior of cells observed in flow chambers. Surprisingly, a mixture of 10% single bonds and 90% dimeric bonds is sufficient to fully match the data of the P-selectin:PSGL-1 experiments, with the calculated decay in fraction of attached cells still appearing exponential.

INTRODUCTION

The transient adhesive interaction between neutrophils and P-selectin on inflamed endothelium is of great physiological importance in the recruitment of flowing cells to the surrounding tissues (Muller, 2002). Rapid association and dissociation of load-bearing chemical bonds between endothelial P-selectin and neutrophil P-selectin glycoprotein ligand-1 (PSGL-1) is responsible for a slow rolling motion of neutrophils across the luminal vessel surface that has been well studied. Due to this important biological role for selectin-carbohydrate bond kinetics, several efforts have been made to experimentally characterize the lifetime of an individual selectin bond (Kaplanski et al., 1993; Alon et al., 1995; Mehta et al., 1998; Smith et al., 1999; Marshall et al., 2003; Hanley et al., 2003). The most common approach is to covalently attach or chemisorb purified selectin molecule onto a glass substrate at low density, and then introduce leukocytes in the well-defined flow of a parallel-plate flow chamber. The surface concentration of molecules is reduced to a low value that supports transient pauses as the cells flow across the reactive surface, suggesting that the observed interactions are mediated by a small number of bonds. For a single selectin bond, the duration of the cell pause is then equivalent to the bond lifetime. The force exerted by the fluid on the cell is known from fluid mechanics; however, determining the precise mechanical force experienced by the molecule requires complex analysis. The physiological ligands to P- and E-selectin are known to be concentrated at the tips of stretchy microvillus extensions from the leukocyte surface (Moore et al., 1995), and in a simple static analysis the necessary assumption of steady state and estimation of tether length (and resulting lever arm) present major uncertainties in trying to relate shear stress to the force experienced by the bond.

Recently, Ramachandran et al. (2004) experimentally studied the role that membrane tethers have in stabilizing leukocyte rolling on P-selectin. Although they focused on a higher range of shear stresses of 2–8 dyn/cm2 than examined here, they did show that at the lowest shear stress of 2 dyn/cm2 single tethers formed, whereas at the highest shear stresses of 8 dyn/cm2 multiple, wider tethers were commonly observed. Schmidtke and Diamond (2000) showed that they could form extremely long membrane tethers (>8 μm) when flowing neutrophils over a surface of platelets expressing P-selectin, and imaged using differential interference contrast microscopy.

In two companion articles (Parts I and II), we experimentally characterized the dissociation kinetics of the P-selectin:PSGL-1 bond and of a cytoskeletal anchor of PSGL-1, as well as the tether-extension and cell-compression mechanics of human neutrophils, using micropipette aspiration techniques. The complex kinetics recently observed for the P-selectin:PSGL-1 bond suggest that it may in fact dissociate via two distinct pathways, a novel fast pathway that is selected under low force and is relatively independent of the force loading, and a slower pathway whose dissociation rate exhibits the more familiar exponential dependence on the magnitude of the applied force (Evans et al., 2004). Furthermore, a distinct, stochastic unbinding event could be identified that defined the transition from a regime of linear elastic extension of the cell interface, to a viscous membrane-pulling regime. This event was attributed to dissociation of PSGL-1 from its cytoskeletal attachment, and the force dependence of this bond dissociation event was characterized. The viscous extension of long membranous tethers is responsible for partially relieving the load experienced by the P-selectin:PSGL-1 bond and results in long-lived cell tethers (∼1 s) that have been observed experimentally. Several aspects of these observations are at odds with previously proposed models for the interaction between neutrophils and P-selectin surfaces under flow. Perhaps most importantly, Bell model kinetic parameters deduced from P-selectin:PSGL-1 cell tethering experiments in the literature (Alon et al., 1995; Smith et al., 1999; Schmidtke and Diamond, 2000; Ramachandran et al., 2001, 2004; Park et al., 2002) are quite different from the values obtained from dynamic force spectroscopy (DFS) measurements in Part II of this series. The DFS measurements themselves are in closer agreement with independent measurements of P-selectin:PSGL-1 dissociation using atomic force microscopy (Hanley et al., 2003). It should be noted that these different measurement techniques have produced consistent Bell model parameters for cadherin bonds, albeit at shear rates lower than that representative of most venules (Baumgartner et al., 2000; Perret et al., 2002). Thus, the purpose of this article, Part III of a three-part series, is to assemble all of these recently observed behaviors associated with the force-induced dissociation of P-selectin bonds to neutrophil PSGL-1, into a detailed numerical model of neutrophil tethering to P-selectin under flow. It is shown here that incorporating the DFS-derived dissociation kinetics of P-selectin:PSGL-1, the cytoskeletal dissociation kinetics of neutrophil PSGL-1, and the mechanics of tether extrusion and cell interface compression, all as presented in Parts I and II, fully reproduce the tethering behavior of neutrophils on P-selectin under flow as demonstrated in previous experiments (Park et al., 2002).

METHODS

Adhesive dynamics

The simulation methods were very similar to the adhesive dynamics algorithm that has been described in several publications (Hammer and Apte, 1992; Chang et al., 2000; King and Hammer, 2001). Briefly, adhesive dynamics is a computational technique for calculating the motion of a single rigid spherical particle in the vicinity of a planar wall, subject to an external linear shear flow and various surface interaction terms such as specific chemical adhesion, electrostatic repulsion, and gravity. Analytical solutions for the creeping flow motions of a sphere near a plane are available (Goldman et al., 1967a,b; Jeffery, 1915) to determine the six independent motions of the sphere (three translational velocities and three rotational velocities) subject to the sum of external forces and torques and the strength of the imposed shear flow. Generally, random number tests are performed at each time step to determine whether any new bonds are formed and whether any existing bonds fail; however, in the current study bond reformation was disabled to focus on simulating transient attachment experiments at low surface density. Specific modifications to the original adhesive dynamics formation, described below, were made to incorporate the new kinetic and mechanical characterizations of neutrophil adhesion to P-selectin as presented in Parts I and II.

Linear elastic extension of the cell interface under a tensile point load

As demonstrated in Part I, before the dissociation of PSGL-1 from the cytoskeleton, the initial elongation of the P-selectin:PSGL-1 attachment behaves like a linearly elastic spring:

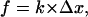graphic file with name M1.gif

where f is tensile force supported by the attachment, k = 0.25 pN/nm as measured in Part I, and Δx is the deviation attachment length. In simulations the initial attachment length was taken to be the equilibrium length of the P-selectin:PSGL-1 complex, ∼80 nm.

Cytoskeletal dissociation of PSGL-1

In Part I, it was shown that the termination of the linear elastic regime is caused by a stochastic dissociation event of PSGL-1 from the neutrophil cytoskeleton. The average dissociation kinetics of this event were characterized by the first-order rate constant:

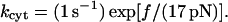graphic file with name M2.gif

Thus, over each fixed time step of the simulation, the probability for the first-order process of cytoskeletal unbinding was calculated as:

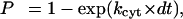graphic file with name M3.gif

and tested against a randomly generated number uniformly distributed over the interval [0,1]. A time step of dt = 10−7 s was used in all simulations.

Viscous tether extrusion

After cytoskeletal dissociation, formation and further extension of a tether between the neutrophil and a P-selectin surface is found to exhibit a primarily viscous behavior (see Part II). Specifically, the resistive force generated by the tether was shown to depend on the linear velocity of tether extension (“pulling speed,” vpull) and to plateau at a value of:

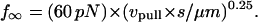graphic file with name M4.gif

The rate at which this plateau force is approached is well described by the relation:

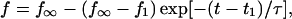graphic file with name M5.gif

where f1 and t1 are taken to be the tether force and time at the instance of cytoskeletal dissociation, respectively, and τ is a response time that is also a function of pulling speed:

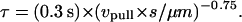graphic file with name M6.gif

Compressive cell-interfacial deformation

In an Appendix to Part I, it was shown that in response to compressive normal force, the neutrophil body will deform as a linear spring element at small deformation. Thus, we approximate the force resisting deformation of the cell as it impinges on the solid substrate as:

graphic file with name M7.gif

Where R is the radius of the cell (taken to be 4 μm), P0 was determined to equal 17 N/m2, and Δxn is the interfacial displacement normal to the wall. This compressive force dependence is predicted from the solution of an elastic sphere impinging on a solid substrate (Kosevich et al., 1986).

P-Selectin:PSGL-1 dissociation

Recently, we demonstrated that the dissociation of P-selectin:PSGL-1 bonds under force occurs via two structure-dependent pathways (Evans et al., 2004; see also Part II). The combined dissociation along these two pathways can be treated as a quasi-first-order process, as indicated by the following differential equation for the number of surviving bonds SB:

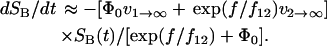graphic file with name M8.gif

Here, Φ0 is the occupancy ratio S1/S2 of the two bound states at zero force, and is a function of the difference in energy level ΔE21:

graphic file with name M9.gif

with ΔE21 determined to equal ∼4.5 kBT for this receptor-ligand pair (Evans et al., 2004). The dissociation rate of the first pathway was shown to be relatively independent of force, and equal to 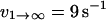Inline graphic. The second pathway was shown to follow the commonly observed exponential dependence on force (so-called “Bell model” kinetics), with an unstressed off rate of 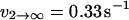Inline graphic and a characteristic force scale of f12 = 5 pN.

Specific simulations of individual attachments

Simulations of neutrophil tethering to a P-selectin surface were performed by positioning the cell one equilibrium bond length (∼80 nm) from the surface and initiating the program with either one, two, or three P-selectin:PSGL-1 bonds. The system was integrated in time until final P-selectin:PSGL-1 bond rupture occurred, at which point the cell was repositioned to the initial coordinates and the bond(s) reestablished to produce another observation of transient cellular binding. In this manner multiple tethering events were simulated at each wall shear stress ranging from 0.4–1.0 dyn/cm2, for a total time interval of 100 s to produce between 350 and 3500 individual tethering events at each set of conditions. During each simulation, values of the cell position, state of cytoskeletal and P-selectin adhesion, and the force on the bond attachment were recorded at time intervals of 0.001 s for later analysis. In the case of multiple bonds, the total force on the bond attachment was assumed to be shared between all existing bonds, due to their close proximity of attachment at the end of the same microvillus. For instance, Bruehl et al. (1996) reported an average microvillus diameter of 0.1 μm for several types of leukocytes. Additionally, because PSGL-1 is found in a dimeric form on leukocyte microvilli, double bonds may in fact be separated by far less distance. The effect of this assumption of equal force loading on the observed bond kinetics is evaluated in the Results and Discussion section.

Data analysis

To analyze the simulation data for apparent dissociation rates, every effort was taken to mimic the conditions of the experiments of Park et al. (2002). Simulation data were discretized into time intervals of 0.004 s, close to the high-speed video frame per second (fps) rate of 240 fps used by Park et al. Pause times were calculated as the time interval during which cell velocities remained below a threshold of 10 μm/s. This is well below the free-stream cell velocity of 120–300 μm/s, and corresponds to a per-frame cell displacement of only 40 nm at a frame rate of 240 fps. As done by Park et al. (2002), the natural log of the number of tethering events was plotted versus the pause time duration of each event. The negative of the regressed slope was then taken as an apparent off rate for comparison with previous experimental results. Furthermore, Park et al. (2002) binned their pause time data into temporal intervals of 1/30 s (see their Fig. 5), and this was also done in this analysis to match the analysis of Park et al.

FIGURE 5.

FIGURE 5

Open in a new tab

Dependence of the apparent off rate of the P-selectin:PSGL-1 bond on wall shear stress, as determined from the interpretation of real or simulated tethering experiments. Squares denote the experimental data of Park et al. (2002), and are compared with simulation results for either single or double bonds. Note that a mixture of single and double bonds, with a double-bond fraction of 90% agrees well with the experiments of Park et al. (2002). Also plotted for comparison is a relative weighting of 60% single bonds, 30% double bonds, and 10% triple bonds, corresponding to a Poisson distribution in bond number.

RESULTS AND DISCUSSION

Fig. 1 shows the neutrophil and tether bond outlines at t = 0 and t = 1 s during a simulation of tethering to P-selectin at a wall shear stress of 1.0 dyn/cm2. Flow is directed from left to right. In the lower graph of Fig. 1, it can be seen that the bond was initiated with a vertical orientation and a length of 80 nm. As the cell is convected forward and starts to roll over the surface, the tether elongates considerably. This increases the rotation lever arm, thus relieving some of the force on the bond as pointed out previously by others (Alon et al., 1995). The extent of interfacial cell deformation is evident from the upper graph of Fig. 1, as indicated by the apparent overlap of the cell “outline” with the planar wall located at z = 0.

FIGURE 1.

FIGURE 1

Open in a new tab

(A) Side-view outline of a tethered cell at a wall shear stress of 1.0 dyn/cm2, initially and after 1 s. The length and orientation of the tether linking the cell to the wall is plotted at intervals of 1/30 s. (B) Closeup of the bond region.

More information on the cell behavior is given in Fig. 2, where the bond force, tether length, interfacial deformation, and dissociation histograms are plotted as a function of time. The results of Fig. 2 correspond to a simulation of single P-selectin:PSGL-1 bonds at a wall shear stress of 0.7 dyn/cm2. The transition from the linear elastic regime to the viscous extrusion regime, initiated by the singular cytoskeletal dissociation event, is seen to occur at around 0.02 s for these conditions. During the initial 0.02 s, the force experienced by the bond increases sharply, while the cell-surface attachment experiences its fastest rate of growth. During this time the cell decelerates from the free-stream velocity and is pulled down toward the surface by the normal component of the tether force, as can be seen from the increased cell deformation. Cytoskeletal dissociation occurs rapidly at this shear stress, at around t = 0.02 s as evidenced by the histogram of events at the bottom of Fig. 2. Cytoskeletal dissociation marks the transition to viscous flow of a membranous tether, during which the tether length continues to increase at a slower but approximately constant rate. Due to the stochastic nature of cytoskeletal unbinding, the plots of attachment length no longer superimpose after the first 0.01 s, but rather represent the distribution of force magnitudes at the start of viscous extrusion, f1. Total tether force and cell deformation slightly decrease during the viscous tether extension phase, because the orientation of the tether becomes more aligned with the flow direction (see Fig. 1) and produces a larger component of force available to resist shear forces and less force component available to pull the cell toward the wall. We point out that in Fig. 2 for single P-selectin:PSGL-1 bonds there is significant overlap between the histograms of cytoskeletal and P-selectin bond failure, indicating that a substantial fraction of attachments fail before dissociation from the cytoskeleton and thus never exhibit the viscous tether extension behavior. Finally, it should be noted that Alon et al. (1997) in their approximate analysis of the static forces acting on tethered neutrophils, obtained an estimate of 124 pN of bond force at 1 dyn/cm2, equivalent to 87 pN of force at our shear stress of 0.7 dyn/cm2. This is quite similar to the “plateau” value shown in Fig. 2, which is perhaps not surprising because Alon et al. (1997) used reversed flow to experimentally determine the tether length to be 1.00 ± 0.32 μm, quite close to the mean and standard deviation of the simulations shown in Fig. 2. However, as discussed below, various elements missing from the analysis of Alon et al. (1997) are responsible for the differences between the bond dissociation rates that they report and those obtained from the biomembrane force probe and AFM.

FIGURE 2.

FIGURE 2

Open in a new tab

Time course of the bond force (A), tether length (B), and cell deformation (C) during individual cell tethering events at a wall shear stress of 0.7 dyn/cm2. In this case, tethers are mediated by single P-selectin:PSGL-1 bonds. Histograms of cytoskeletal and P-selectin:PSGL-1 dissociation events are given in panel D. Nine-hundred individual adhesion events are overlaid in panels A–C.

The tethering dynamics for double P-selectin:PSGL-1 bonds at a wall shear stress of 0.7 dyn/cm2 look qualitatively similar to the case for single bonds (Fig. 3). The bond force, tether length, and cell deformation all follow an identical temporal evolution as the single bond case of Fig. 2, however, the tethers are, in general, longer lived. In particular, with bond dimers there is a significant fraction of tethers with lifetime >0.2 s. In the bond lifetime histogram in Fig. 3 D, it can be seen that there is only a small amount of overlap between the cytoskeletal and P-selectin bond lifetimes, indicating that most attachments survive until the viscous extrusion phase.

FIGURE 3.

FIGURE 3

Open in a new tab

Time course of the bond force (A), tether length (B), and cell deformation (C) during individual cell tethering events at a wall shear stress of 0.7 dyn/cm2. In this case, tethers are mediated by dimeric P-selectin:PSGL-1 bonds that share force equally. Histograms of cytoskeletal and P-selectin:PSGL-1 dissociation events are given in panel D. Four-hundred individual adhesion events are overlaid in panels A–C.

The cell tethering simulations were analyzed using the methods of Alon et al. (1995), Park et al. (2002), and others, to determine the apparent dissociation rate of the P-selectin:PSGL-1 bond. Fig. 4 shows representative plots of the natural log of the number of attachment events versus the attachment duration, for either single bonds (A) or double bonds (B). Note that despite considerable scatter in the numerical data, the curves are approximately linear to the same extent as observed in flow-chamber experiments (e.g., Park et al., 2002). In fact, these data are very similar in appearance to that presented by Park et al. (2002). Thus, based on tethering data alone there are no obvious indications of nonlinearities such as tether viscoelasticity or multiple bonding that would confound the assumption of a simple, linear dissociation process.

FIGURE 4.

FIGURE 4

Open in a new tab

Pause-time distributions used to calculate the “apparent” bond dissociation constants of neutrophils interacting with a P-selectin substrate. Simulated data for either single-bond tethers (A) or double-bond tethers (B) at different wall shear stresses are presented in the same form as in the experimental study of Park et al. (2002).

Fig. 5 shows the apparent off rates obtained from adhesive dynamics simulations as a function of wall shear stress, compared with the experimental measurements of Park et al. (2002). It is evident from Fig. 5 that bond dimers increase the lifetime of the tether, or equivalently, decrease the characteristic dissociation rate, by about a factor of two. At shear stresses higher than 0.6 dyn/cm2, the apparent off rate rises dramatically for single bonds, as there are no long-lived tethers formed due to viscous extrusion, i.e., virtually all P-selectin bond failure occurs during the linear elastic phase. The experimental P-selectin:PSGL-1 tethering data of Park et al. lies between the single- and double-bond simulations of this study. As shown by the bottom dashed line in Fig. 5, the experimental data are consistent with a mixture of single and double bonds in a ratio of 10:90 single/double bonds. Such a mixture is not unreasonable, because both P-selectin and PSGL-1 are known to exist in dimeric form on the neutrophil and endothelial cell surfaces (Ramachandran et al., 2001). Also plotted for comparison is a Poisson distribution of single/double/triple bonds of 60:30:10, which corresponds to 63.2% of contact events resulting in adhesion. Such a distribution has been previously considered by Tees et al. (2001) and others in studies of selectin-mediated adhesion. It should be noted that Tees et al. concluded that 35% multiple bonds could account for only a 10% reduction in the rate of dissociation in their microcantilever study of P-selectin adhesion featuring a linear ramp in force. However, neutrophils tethering to P-selectin under flow exist in a “metastable” state, where a subtle increase in the strength of the P-selectin:PSGL-1 attachment can enable more frequent cytoskeletal detachment events and a transition to viscous tether extrusion that significantly relieves the force loading rate. Thus, because of the complex mechanics associated with the neutrophil, as characterized in the two companion articles (Parts I and II), these simulations are not directly comparable to previous microcantilever and AFM measurements.

Chen and Springer (1999) proposed that more bonds are formed at higher shear stresses, and that this provides a mechanism for neutrophils rolling via selectins to exhibit a weak dependence of rolling velocity on wall shear stress. Such a mechanism is consistent with these simulations if one considers that greater cell compression will occur at higher shear stresses, providing a larger contact area available for additional bond formation. However, the extent to which shear-induced bond formation affects overall dissociation rates was not directly addressed in this study because the present focus is on simulating transient tethering rather than stable rolling.

Additional simulations were performed to assess how changing individual model parameters affects the apparent off rate during cell tethering under flow. The results of these simulations, corresponding to a shear stress of 0.7 dyn/cm2 and either one or two initial bonds, are presented in Table 1. All off rates are presented with their standard error. All single-bond simulations reported in Table 1 were compared using a two-sample Z-test to the “base state” simulation performed using the parameter values reported in the Methods section. Additionally, a double-bond simulation sequence was performed for either force-sharing dimers as described in the Methods section, or by assuming that one bond bears all of the force initially until one of the two bond fails, at which point all of the force is transferred to the remaining bond. Results of the two double-bond scenarios were compared using a two-sample Z-test. In each of the simulations presented in Table 1, the parameter was varied to partially disable the particular mechanism of interest: for instance increasing the spring constant or characteristic viscous force to produce less deformation, or decreasing the cytoskeletal dissociation rate to hinder cytoskeletal unbinding. In all cases considered, the apparent off rate was altered to a measurable degree, with all changes except for two (k, λ) reaching p < 0.05 statistical significance. The biggest change was achieved by doubling the characteristic viscous force during tether extrusion, which has the net result of producing a shorter tether before final bond rupture. This, together with the simulation using an altered cytoskeletal dissociation rate, highlight the importance of long tether formation in producing long-lived P-selectin:PSGL-1 bonds under flow conditions.

TABLE 1.

1 Effect of various model parameters on apparent off rate at 0.7 dyn/cm2

Parameter Change Off rate ± SE (s−1) P-value
Single-bond base state 9.36 ± 1.68
Linear elasticity, k 0.25 → 0.5 pN/nm 14.34 ± 3.11 p = 0.162
Cytoskeletal unbinding, 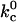Inline graphic 1 → 0.5 s−1 15.46 ± 1.95 p < 0.05
Viscous tether stretch, Inline graphic 60 → 120 pN 33.74 ± 3.07 p < 0.001
Cell compression, P0 17 → 34 N/m2 16.04 ± 2.18 p < 0.05
Initial bond length, λ 80 → 160 nm 12.83 ± 1.45 p = 0.119
Double-bond base state (force shared equally) 4.32 ± 0.32
Double bonds, sequential force loading 12.05 ± 1.32 p < 0.001
Open in a new tab

Differences were tested using two-sample Z-test.

CONCLUSIONS

In two companion articles (Parts I and II), we demonstrated the complex mechanics and dissociation kinetics observed when P-selectin:PSGL-1 bonds are retracted from a neutrophil surface in a dual micropipette geometry. Specifically, the initial extension of the cell interface was shown to exhibit linear elastic behavior, until catastrophic failure of the mechanical connection between neutrophil PSGL-1 and the cell cytoskeleton. After the stochastic cytoskeletal detachment event, the tether was found to extend according to a viscous shear-thinning rheological power-law model. Finally, the attachment terminates with dissociation of the P-selectin:PSGL-1 bond through either a fast or slow pathway. The kinetics of this P-selectin:neutrophil linkage, measured via the biomembrane force probe spanning two orders of magnitude in force loading rate, are quite different from that determined from cell tethering flow-chamber experiments reported by previous investigators. Clearly, the microscale mechanics of cells tethering under flow is complex, yet previous analyses of flow chamber experiments have assumed that a constant force is instantaneously applied via a lever arm of assumed (inferred) length. This assumption is necessary because the actual geometry of the connection between the cell and surface cannot be resolved with standard microscopy methods. In this Part III we assembled the recently uncovered mechanical and kinetic information on neutrophil adhesion to P-selectin into a comprehensive numerical simulation of neutrophil tethering to P-selectin under flow, in an attempt to reconcile our description of tether dynamics with existing flow chamber studies. We showed that this detailed model of neutrophil adhesion is entirely consistent with existing tethering studies, as exemplified by the recent study of Park et al. (2002). A mixture of single and double P-selectin:PSGL-1 bonds was sufficient to fully reproduce the behavior of tethering experiments. Thus, based on these independent experiments together with the integrative computer simulation of tethering in the shear flow geometry, we conclude that omission of the cell-interfacial elasticity, viscous tether extrusion, dissociation of PSGL-1 from the cytoskeleton, multiple bonding, and cell compression have all contributed to the inaccurate P-selectin:PSGL-1 dissociation kinetic rate constants deduced from overly simplified analyses of tethering under flow. An implication of this study is that other important adhesion molecules responsible for leukocyte adhesion under flow such as E-selectin must also be reexamined in well-controlled geometries (e.g., biomembrane force probe), to improve the estimates of the dissociation kinetics of these molecules.

Acknowledgments

This study was supported by the National Institutes of Health (grant No. HL018208 to M.R.K. and D.A.H.).

References

  1. Alon, R., S. Chen, K. D. Puri, E. B. Finger, and T. A. Springer. 1997. The kinetics of L-selectin tethers and the mechanics of selectin-mediated rolling. J. Cell Biol. 138:1169–1180. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Alon, R., D. A. Hammer, and T. A. Springer. 1995. Lifetime of the P-selectin-carbohydrate bond and its response to tensile force in hydrodynamic flow. Nature. 374:539–542. [DOI] [PubMed] [Google Scholar]
  3. Baumgartner, W., P. Hinterdorfer, W. Ness, A. Raab, D. Vestweber, H. Schindler, and D. Drenckhahn. 2000. Cadherin interaction probed by atomic force microscopy. Proc. Natl. Acad. Sci. USA. 97:4005–4010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bruehl, R. E., T. A. Springer, and D. F. Bainton. 1996. Quantitation of L-selectin distribution on human leukocyte microvilli by immunogold labeling and electron microscopy. J. Histochem. Cytochem. 44:835–844. [DOI] [PubMed] [Google Scholar]
  5. Chang, K.-C., D. F. J. Tees, and D. A. Hammer. 2000. The state diagram for cell adhesion under flow: leukocyte rolling and firm adhesion. Proc. Natl. Acad. Sci. USA. 97:11262–11267. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Chen, S., and T. A. Springer. 1999. An automatic braking system that stabilizes leukocyte rolling by an increase in selectin bond number with shear. J. Cell Biol. 144:185–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Evans, E., A. Leung, V. Heinrich, and C. Zhu. 2004. Mechanical switching and coupling between two pathways for dissociation in a P-selectin adhesion bond. Proc. Natl. Acad. Sci. USA. 101:11282–11286. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Goldman, A. J., R. G. Cox, and H. Brenner. 1967a. Slow viscous motion of a sphere parallel to a plane wall. I Motion through a quiescent fluid. Chem. Eng. Sci. 22:637–652. [Google Scholar]
  9. Goldman, A. J., R. G. Cox, and H. Brenner. 1967b. Slow viscous motion of a sphere parallel to a plane wall. II. Couette flow. Chem. Eng. Sci. 22:653–660. [Google Scholar]
  10. Hammer, D. A., and S. M. Apte. 1992. Simulation of cell rolling and adhesion on surfaces in shear flow: general results and analysis of selectin-mediated neutrophil adhesion. Biophys. J. 62:35–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hanley, W., O. McCarty, S. Jadhav, Y. Tseng, D. Wirtz, and K. Konstantopoulos. 2003. Single molecule characterization of P-selectin/ligand binding. J. Biol. Chem. 278:10556–10561. [DOI] [PubMed] [Google Scholar]
  12. Jeffery, G. B. 1915. On the steady rotation of a solid of revolution in a viscous fluid. Proc. Lond. Math. Soc. 14:327–338. [Google Scholar]
  13. Kaplanski, G., C. Farnarier, O. Tissot, A. Pierres, A. M. Benoliel, M. C. Alessi, S. Kaplanski, and P. Bongrand. 1993. Granulocyte-endothelium initial adhesion. Analysis of transient binding events mediated by E-selectin in a laminar shear flow. Biophys. J. 64:1922–1933. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. King, M. R., and D. A. Hammer. 2001. Multiparticle adhesive dynamics. Interactions between stably rolling cells. Biophys. J. 81:799–813. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kosevich, A. M., E. M. Lifshitz, L. D. Landau, and L. P. Pitaevskii. 1986. Theory of Elasticity, Vol. 7, 3rd Ed. Butterworth-Heinemann, Burlington, MA.
  16. Marshall, B. T., M. Long, J. W. Piper, T. Yago, R. P. McEver, and C. Zhu. 2003. Direct observation of catch bonds involving cell-adhesion molecules. Nature. 423:190–193. [DOI] [PubMed] [Google Scholar]
  17. Mehta, P., R. D. Cummings, and R. P. McEver. 1998. Affinity and kinetic analysis of P-selectin binding to P-selectin glycoprotein ligand-1. J. Biol. Chem. 273:32506–32513. [DOI] [PubMed] [Google Scholar]
  18. Moore, K. L., K. D. Patel, R. E. Bruehl, F. G. Li, D. A. Johnson, H. S. Lichenstein, R. D. Cummings, D. F. Bainton, and R. P. McEver. 1995. P-selectin glycoprotein ligand-1 mediates rolling of human neutrophils on P-selectin. J. Cell Biol. 128:661–671. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Muller, W. A. 2002. Leukocyte-endothelial cell interactions in the inflammatory response. Lab. Invest. 82:521–533. [DOI] [PubMed] [Google Scholar]
  20. Park, E. Y. H., M. J. Smith, E. S. Stropp, K. R. Snapp, J. A. DiVietro, W. F. Walker, D. W. Schmidtke, S. L. Diamond, and M. B. Lawrence. 2002. Comparison of PSGL-1 microbead and neutrophil rolling: microvillus elongation stabilizes P-selectin bond clusters. Biophys. J. 82:1835–1847. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Perret, E., A.-M. Benoliel, P. Nassoy, A. Pierres, V. Delmas, J.-P. Thiery, P. Bongrand, and H. Feracci. 2002. Fast dissociation kinetics between individual E-cadherin fragments revealed by flow chamber analysis. EMBO J. 21:2537–2546. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Ramachandran, V., M. Williams, T. Yago, D. W. Schmidtke, and R. P. McEver. 2004. Dynamic alterations of membrane tethers stabilize leukocyte rolling on P-selectin. Proc. Natl. Acad. Sci. USA. 101:13519–13524. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Ramachandran, V., T. Yago, T. K. Epperson, M. M. Kobzdej, M. U. Nollert, R. D. Cummings, C. Zhu, and R. P. McEver. 2001. Dimerization of a selectin and its ligand stabilizes cell rolling and enhances tether strength in shear flow. Proc. Natl. Acad. Sci. USA. 98:10166–10171. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Schmidtke, D. W., and S. L. Diamond. 2000. Direct observation of membrane tethers formed during neutrophil attachment to platelets or P-selectin under physiological flow. J. Cell Biol. 149:719–729. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Smith, M. J., E. L. Berg, and M. B. Lawrence. 1999. A direct comparison of selectin-mediated transient, adhesive events using high temporal resolution. Biophys. J. 77:3371–3383. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Tees, D. F. J., R. E. Waugh, and D. A. Hammer. 2001. A microcantilever device to assess the effect of force on the lifetime of selectin-carbohydrate bonds. Biophys. J. 80:668–682. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES