Abstract
Mechanical unfolding trajectories, generated by applying constant force in optical-tweezer experiments, show that RNA hairpins and the P5abc subdomain of the group I intron unfold reversibly. We use coarse-grained Go-like models for RNA hairpins to explore forced unfolding over a broad range of temperatures. A number of predictions that are amenable to experimental tests are made. At the critical force, the hairpin jumps between folded and unfolded conformations without populating any discernible intermediates. The phase diagram in the force–temperature (f, T) plane shows that the hairpin unfolds by an all-or-none process. The cooperativity of the unfolding transition increases dramatically at low temperatures. Free energy of stability, obtained from time averages of mechanical unfolding trajectories, coincides with ensemble averages, which establishes ergodicity. The hopping time between the native basin of attraction (NBA) and the unfolded basin increases dramatically along the phase boundary. Thermal unfolding is stochastic, whereas mechanical unfolding occurs in “quantized steps” with great variations in the step lengths. Refolding times, upon force quench, from stretched states to the NBA are at least an order of magnitude greater than folding times by temperature quench. Upon force quench from stretched states, the NBA is reached in at least three stages. In the initial stages, the mean end-to-end distance decreases nearly continuously, and there is a sudden transition to the NBA only in the last stage. Because of the generality of the results, we propose that similar behavior should be observed in force quench refolding of proteins.
Unraveling the complexity of the energy landscape of RNA molecules requires exploration of their assembly and unfolding over a wide range of external conditions. In the last decade, a combination of experiments, theoretical arguments, and simulations have been used to decipher the folding mechanisms of RNA molecules (1–3). These studies have shown that RNA folding depends critically on a number of factors, including valence and shape of counterions (4) as well as temperature. Somewhat more surprising, recent experiments have shown that the folding mechanisms depend sensitively on the initial folding conditions (5). In conventional experiments, the difficult-to-characterize unfolded conformations are typically generated by elevated temperature or by lowering the counterion concentration. In contrast, well defined and vastly different initial conditions can be realized by applying force. Indeed, in remarkable experiments, Bustamante and coworkers (6, 7) have generated mechanical unfolding trajectories for RNA hairpins and Tetrahymena thermophila ribozyme. These experiments, which used constant external force to denature folded RNA, show that unfolding involves multiple routes in which a number of kinetic intermediates are sampled in the transition from the folded state to a stretched conformation (6, 7). The lifetimes of the intermediates vary considerably, which is indicative of the large dispersion in the unfolding pathways. Thus, force unfolding is a powerful method to probe, at the single-molecule level, regions of the energy landscape that are inaccessible in conventional folding experiments. In addition to the importance of these experiments to map the RNA folding landscape response of RNA to locally applied force, they may also be relevant in understanding cellular processes such as mRNA translocation through ribosomes, viral replication, and enzymatic activity of RNA-dependent RNA polymerases.
In the force-induced unfolding experiments, mechanical force, f, was applied by using optical tweezers to either a part or the whole Tetrahymena ribozyme assembly in differing ionic conditions. In their first article, Liphardt et al. (6) showed that a simple hairpin, three-helix junction, and the P5abc subdomain of the Tetrahymena ribozyme can fold reversibly when subject to a constant force. At the transition force, the systems hop between folded and unfolded states. Assuming that the system is ergodic, the dynamics of the reversible folding was used to calculate force-dependent equilibrium properties of the RNA constructs. These experiments established that f (a new variable to initiate unfolding) is a viable way to measure free-energy difference between folded and unfolded states and to locate transition states with the mean extension of the molecule as a reaction coordinate.
Mechanical unfolding experiments on RNA have already led to a number of theoretical studies (8–11) that have addressed different aspects of forced unfolding. Inspired by these experiments and building on previous theoretical works, we report here the results for forced unfolding of a small RNA hairpin by using coarse-grained off-lattice simulations under varying forces and temperatures. We choose small hairpins for the preliminary study because they undergo reversible folding under force and represent a basic subunit of large RNA assemblies.
We address the following questions. (i) What are the forced-unfolding pathways and how they differ from thermal denaturation? (ii) How do the diagram of states change as T and f are varied? (iii) What are the differences in the time scales and pathways in force-quench refolding and thermal refolding? We find that, just as in proteins (12), forced unfolding occurs in quantized steps, whereas the thermal unfolding is stochastic. Even for the simple hairpin, we find a well defined equilibrium phase diagram in the (f, T) plane in which hairpin states are separated by a phase boundary from the unfolded states. Surprisingly, when refolding is initiated by quenching to zero force from high forces, folding occurs in multiple stages with the initial compaction being nearly continuous. Remarkably, the refolding time under force quench is nearly an order of magnitude greater than the thermal refolding time.
Methods
Hairpin Sequence. We have studied the thermal and forced unfolding of a 22-nt hairpin, P5GA, that is similar to P5ab in the P5abc domain of group I intron. Both of these structures have GA mismatches and are characterized by the presence of GAAA tetraloop. The sequence of P5GA is GGCGAAGUCGAAAGAUGGCGCC, and its NMR structure has been determined (13) (PDB ID code 1EOR).
Model. Building on our previous studies on proteins (14), we introduce a coarse-grained off-lattice model of RNA by representing each nucleotide by three beads with interaction sites corresponding to phosphate group (P), ribose group (S), and the base (B) (Fig. 1A). In this model, the RNA backbone is reduced to the polymeric structure [(P – S)n], and the base is covalently linked to the ribose center. Thus, a RNA molecule with N nucleotides corresponds to 3N interaction centers. The potential energy of a conformation is written as VTOT = VBL + VBA + VDIH + VSTACK + VNON + VELEC, where VBL (the stretching potential between covalently connected moieties) accounts for chain connectivity. The angular degrees of freedom are described by the bond angle potential, VBA, and the dihedral angle term VDIH (15). In this article, we use a Go model in which interactions in the native structure are attractive, whereas all other interactions are repulsive.
Fig. 1.
Coarse-grained representation of RNA. (A) Coarse-grained representation of a nucleotide by using three sites; namely, phosphate (P), sugar (S), and base (B) are given. (B) The secondary structure of the 22-nt P5GA hairpin in which the bonds formed between base pairs are labeled 1–9. The PDB structure (13) and the corresponding structure using the coarse grained model are shown on the right.
Simple RNA secondary structures are stabilized largely by stacking interactions whose context-dependent values are known (16, 17). In the native state, the P5GA hairpin has nine hydrogen bonds between the base pairs including two GA mismatch pairs (13). The stacking interactions that stabilize a hairpin is 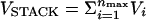 , where nmax = 8 in P5GA. The orientationally dependent term Vi is taken to be
, where nmax = 8 in P5GA. The orientationally dependent term Vi is taken to be
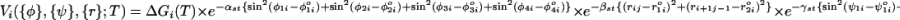 |
[1] |
where ΔG(T) =ΔH – TΔS. The bond angles {φ} are φ1i ≡ ∠SiBiBj, φ2i ≡ ∠BiBjSj, φ3i ≡ ∠Si+1Bi+1Bj–1, and φ4i ≡ ∠Bi+1Bj–1Sj–1. The distance between two paired bases rij = |Bi – Bj|; ri+1j–1 = |Bi+1 – Bj–1|; and ψ1i and ψ2i are the dihedral angles formed by the four beads BiSiSi+1Bi+1 and Bj–1Sj–1SjBj, respectively. The superscript o refers to angles and distances in the PDB structure. The values of αst, βst, and γst are 1.0, 0.3 Å–2, and 1.0, respectively. We take ΔH and ΔS from Turner's thermodynamic data set (16, 17). There are no estimates for GA-related stacking interactions, which typically do not form a stable bond and, hence, are considered a mismatch. Because of the absence of stacking parameters for the GA pair, we use the energy associated with GU in place of GA.
To mimic the hydrophobicity of purine/pyrimidine group, we use the Lennard–Jones interactions between nonbonded interaction centers. The total nonbonded potential is
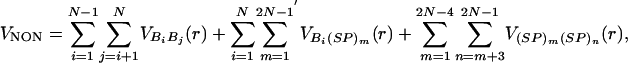 |
[2] |
where 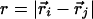 ; the prime in the second term on the Eq. 2 denotes the condition i ≠ 2m – 1; and (SP)m = Sm or Pm, depending on index m. A native contact exists between two noncovalently bound beads provided they are within a cut-off distance rc (=7.0 Å). Two beads beyond rc are considered to be nonnative. For a native contact,
; the prime in the second term on the Eq. 2 denotes the condition i ≠ 2m – 1; and (SP)m = Sm or Pm, depending on index m. A native contact exists between two noncovalently bound beads provided they are within a cut-off distance rc (=7.0 Å). Two beads beyond rc are considered to be nonnative. For a native contact,
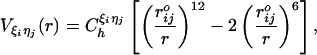 |
[3] |
where 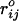 is the distance between beads in the PDB structure, and
is the distance between beads in the PDB structure, and 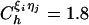 kcal/mol (1 cal = 4.18 J) for all native contact pairs except for the B10B13 base pair associated with the formation of the hairpin loop, for which
kcal/mol (1 cal = 4.18 J) for all native contact pairs except for the B10B13 base pair associated with the formation of the hairpin loop, for which 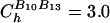 kcal/mol. The additional stability for the base pair associated with loop formation is similar to the Turner's thermodynamic rule for the free-energy gain in the tetraloop region. For beads beyond rc, the interaction is
kcal/mol. The additional stability for the base pair associated with loop formation is similar to the Turner's thermodynamic rule for the free-energy gain in the tetraloop region. For beads beyond rc, the interaction is
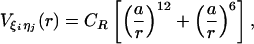 |
[4] |
with a = 3.4 Å and CR = 1 kcal/mol. The value of Ch has been chosen so that the hairpin undergoes a first-order transition from unfolded states. Our results are not sensitive to minor variations in Ch.
The electrostatic potential between the phosphate groups is assumed to be pairwise additive 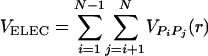 . For VPiPj(r), we assume Debye–Hückel interaction, which accounts for screening by condensed counterions and hydration effects, and is given by
. For VPiPj(r), we assume Debye–Hückel interaction, which accounts for screening by condensed counterions and hydration effects, and is given by
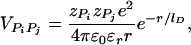 |
[5] |
where zPi = –1 is the charge on the phosphate ion, εr = ε/ε0, and the Debye length 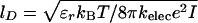 with kelec = 1/4π ε0 = 8.99 × 109 JmC–2. To calculate the ionic strength I = 1/2 Σi z2ici, we use the value ci = 200 mM NaCl from the header of PDB file (13). We use εr = 10 in the simulation (18). Because the Debye screening length
with kelec = 1/4π ε0 = 8.99 × 109 JmC–2. To calculate the ionic strength I = 1/2 Σi z2ici, we use the value ci = 200 mM NaCl from the header of PDB file (13). We use εr = 10 in the simulation (18). Because the Debye screening length 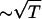 , the strength of the electrostatic interaction between the phosphate groups is temperature-dependent, even when we ignore the variations of ε with T. At room temperature (T ∼ 300 K), the electrostatic repulsion between the phosphate groups at r ∼ 5.8 Å, which is the closest distance between them, is VPiPi+1 ∼ 0.5 kcal/mol. It follows that VELEC between phosphate groups across the base pairing (r = 16 ∼ 18 Å) is almost negligible.
, the strength of the electrostatic interaction between the phosphate groups is temperature-dependent, even when we ignore the variations of ε with T. At room temperature (T ∼ 300 K), the electrostatic repulsion between the phosphate groups at r ∼ 5.8 Å, which is the closest distance between them, is VPiPi+1 ∼ 0.5 kcal/mol. It follows that VELEC between phosphate groups across the base pairing (r = 16 ∼ 18 Å) is almost negligible.
Simulations. The dynamics of stretching is obtained by integrating the Langevin equation. Forced-unfolding simulations are performed by applying a constant force to the S bead at one end of the molecule. By using a typical value for the mass of a bead in a nucleotide (Bi, Si, or Pi), m, 100 g/mol ∼ 160 g/mol, the average distance between the adjacent beads a = 4.6 Å, the energy scale εh = 1 ∼ 2 kcal/mol, and the natural time is τL = (ma2/εh)1/2 = 1.6 ∼ 2.8 ps. We use τL = 2.0 ps to convert simulation times into real times. To estimate the time scale for thermal and mechanical unfolding dynamics, we used a Brownian dynamics algorithm (15, 19) for which the natural time for the overdamped motion is τH = (ζεh/T)τL. We used 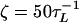 in the overdamped limit, which approximately corresponds to friction constant in water. At T = 290 K, 106 time steps correspond to 3.5 μs. To probe the thermodynamics and kinetics of folding, we used a number of physical quantities [end-to-end distance (R), fraction of native contacts (Q), structural overlap function (χ), number of hydrogen bonds nbond, etc.] to monitor the structural change in the hairpin. The free-energy profiles and the phase diagram were obtained by using an adaptation of the multiple-histogram method (20) for force unfolding of biomolecules (C.H. and D.T., unpublished data).
in the overdamped limit, which approximately corresponds to friction constant in water. At T = 290 K, 106 time steps correspond to 3.5 μs. To probe the thermodynamics and kinetics of folding, we used a number of physical quantities [end-to-end distance (R), fraction of native contacts (Q), structural overlap function (χ), number of hydrogen bonds nbond, etc.] to monitor the structural change in the hairpin. The free-energy profiles and the phase diagram were obtained by using an adaptation of the multiple-histogram method (20) for force unfolding of biomolecules (C.H. and D.T., unpublished data).
Results and Discussion
Determination of the Native State. By using a combination of multiple slow cooling, simulated annealing, and steepest-descent quenches, we determined the native structure of the hairpin. To ensure that there is no other structure with lower energy, the structure obtained from steepest descent method is reheated to T = 100 K and cooled down again. By repeating this process, we obtained the computed native conformation, which has an rms deviation of 0.1 Å with respect to the PDB structure. The bulk of the contribution to the total energy, VTOT = –154 kcal/mol, of the native conformation arises from VSTACK = –95.5 kcal/mol, VNON = –59.2 kcal/mol.
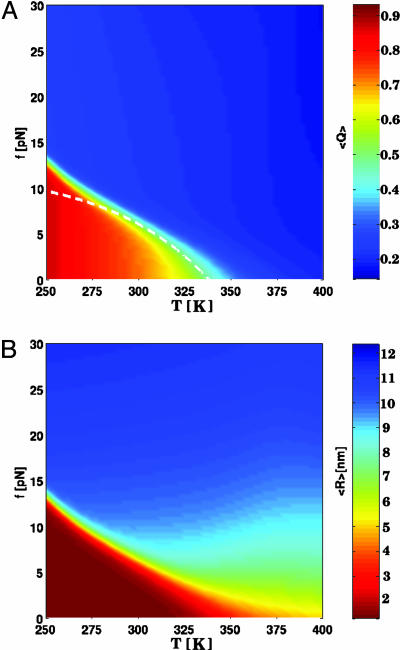
Force–Temperature (f, T) Phase Diagram. The diagram of states in the (f, T) plane shows that P5GA hairpin behaves as a “two-state” folder (Fig. 2). In the absence of force (f = 0 pN), the folding/unfolding transition midpoint is at Tm = 341 K by using 〈Q〉 as an order parameter. At T = 290 K the equilibrium force, required to unfold the P5GA is ≈7 pN (Fig. 2), which is one-half of the value for unfolding P5ab. The difference is, in all likelihood, due to the smaller length of P5GA. As force increases, TF decreases monotonically, so that the transition midpoints (Tm, fm) form a phase boundary separating the folded (〈Q〉 > 0.5 and 〈R〉 < 3 nm) and unfolded states. The phase boundary is sharp at low Tm and large fm, but it is fuzzy when the force is weak. The locus of points separating the unfolded and folded states can be fit by using
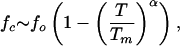 |
[6] |
where fo is the critical force at the low temperature and α (= 6.4) is a sequence-dependent exponent. The large value of α is indicative of a weak first-order transition separating the hairpin and unfolded states (12).
Fig. 2.
Phase diagram for the P5GA hairpin. (A) Diagram of states obtained by using the fraction of native contacts as the order parameter. The values of the thermal average of the fraction of native contacts, 〈Q〉, are color-coded as indicated on the scale shown on the right. The dashed line is a fit by using Eq. 6 to the locus of points in the (f, T) plane that separates the folded hairpin from the unfolded states. (B) Plot of the phase diagram in the (f, T) plane by using the mean end-to-end distance 〈R〉 as the order parameter. Although the diagram of states is qualitatively similar to A, there are quantitative differences in estimates of Tm at f = 0. However, estimates of threshold force values at T < Tm are similar in A and B.
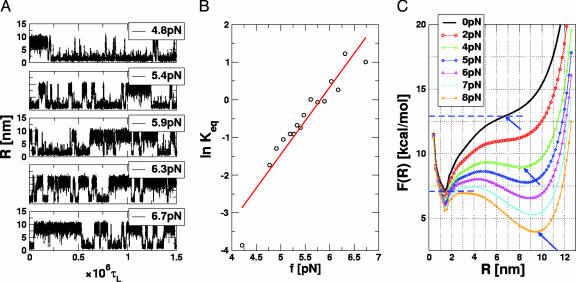
Two-State Dynamics and Equilibrium. We used the thermodynamic relation log Keq(f) = –ΔFUF/kBT + f·ΔxUF/kBT and the dependence of log Keq (Keq is computed as time averages of the traces in Fig. 3A) on f to estimate ΔFUF and ΔxUF, which is the equilibrium distance separating the native basin of attraction (NBA) and the basin corresponding to the ensemble of unfolded states (UBA). The transition midpoint K(fm) = 1 gives fm ≈ 6 pN in excellent agreement with the value obtained from the equilibrium phase diagram (Fig. 2 A), which establishes ergodicity. From the slope, ∂ log Keq(f)/∂f = 1.79 pN–1, ΔxUF ≈ 7.5 nm, we found, by extrapolation to f = 0, that ΔFUF ≈ 6.2 kcal/mol under the assumption that ΔxUF is constant and independent of f.
Fig. 3.
Hopping transitions at constant f.(A) Time traces of R at various values of constant force at T = 305 K. At f = 4.8 pN < fm ≈ 6 pN, 〈R〉 fluctuates around at low values, which shows that the NBA is preferentially populated (top time trace). As f ∼ fm (third time trace) the hairpin hops between the folded state (low R value) and unfolded states (R ≈ 10 nm). The transitions occur over a short time interval. These time traces are similar to figure 2C in ref. 6. (B) Logarithm of the equilibrium constant Keq (computed by using the time traces in A) as a function of f. The red line is a fit with log Keq = 10.4 + 1.79 f.(C) Equilibrium free energy profiles F(R) as a function of R at T = 305 K. The colors represent different f values that are shown in Inset. The arrows give the location of the unfolded basin of attraction.
The independence of ΔxUF on f was used also by Liphardt et al. (6) to estimate ΔFUF. To check the validity of this assumption, we computed free-energy profiles by using the multiple-histogram method with R as the progress variable. At T = 305 K, we find, from the free-energy profile F(R), that ΔFUF ≈ 5.8 kcal/mol and ΔxUF ≈ 5.2 nm. Although the change in ΔFUF computed from estimate of Keq(f) based on hopping dynamics and the “exact” result is small (≈7%), there is a substantial difference in ΔxUF. The exact free-energy profile (Fig. 3C) shows that ΔxUF varies with f because of large variations in the unfolded states. In general, the assumption that ΔxUF is a constant leads to an overestimate of both ΔFUF and ΔxUF.
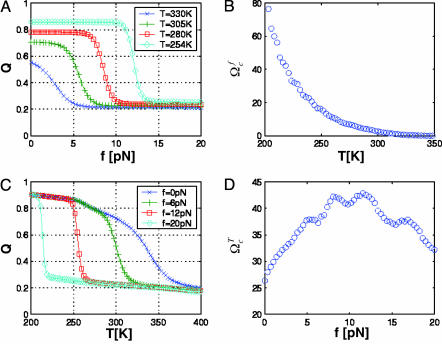
Cooperativity of Unfolding Depends on Force. Slice of the phase diagram at either constant f or constant T shows the typical sigmoidal curves for 〈Q〉 as a function of either f or T (Fig. 4). The cooperativity of the transition depends on whether T or f is held constant. We use the dimensionless cooperativity index (ΩTc)f with respect to T (21),
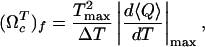 |
[7] |
where ΔT is the full width at half maximum of |(d〈Q〉/dT)max|, and Tmax is the temperature at which d〈Q〉/dT has a maximum. Similarly, the dimensionless cooperativity index with respect to f can be defined. The force-dependent cooperativity index (ΩTc)f has a maximum around f ∼ 10pN, whereas (Ωfc)T decreases monotonically to zero as T increases (Fig. 4 B and D). The difference between (ΩTc)f and (Ωfc)T arises because thermal denaturation at all forces is more stochastic, whereas forced unfolding disrupts RNA structures in steps.
Fig. 4.
Folding cooperativity. (A) Dependence of 〈Q(T, f)〉 as a function of f at various temperatures. (B) Values of (Ωfc)T as a function of temperature. (C) Variation of 〈Q(T, f)〉 as a function of T at various values of f.(D) Dimensionless cooperativity measure (ΩTc)f for 0 ≤ f ≤ 20.
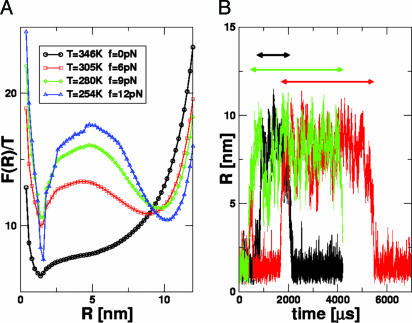
Time Scales of Hopping Transition. In the RNA pulling experiments (6), the time interval between the hopping transitions from folded to unfolded states at midpoint of force was measured at a single temperature. We calculated the dynamics along the phase boundary (Tm, fm) (Fig. 5) to evaluate the variations in the free-energy profiles and the dynamics of transition from the NBA to UBA. Along the boundary (Tm, fm), there are substantial changes in the free-energy landscape (Fig. 5A). The free-energy barrier ΔF‡ increases dramatically at low T and high f.We predict that the weakly first-order phase transition at T ≈ Tm and low f becomes increasingly stronger as we move along the (Tm, fm) boundary to low T and high f.
Fig. 5.
Hopping transitions along the phase boundary. (A) Free-energy profiles F(R) along the phase boundary (Tm, fm) (see Fig. 2). The barrier separating NBA and UBA increases at low Tm and high fm values. (B) Time traces of R obtained by using Brownian dynamics simulations. The values of T and f are 305 K and 6 pN, respectively. The arrows (black, red, and green) indicate the residence times in the NBA for three trajectories.
The two basins of attraction (NBA and UBA) are separated by a free-energy barrier whose height increases as force increases (or temperature decreases) along (Tm, fm) (Fig. 5A). The hopping time τh along (Tm, fm) is
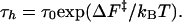 |
[8] |
To estimate the variations in τh along the (Tm, fm) boundary, we performed three very long overdamped Langevin simulations at Tm = 305 K and fm = 6 pN. The unfolding/refolding time is observed to be 1–4 ms (Fig. 5B). From the free-energy profile (Fig. 5A), we find ΔF‡/T ∼ 3, so that τ0 = 0.05 to 0.2 ms. Consequently, τh at T = 254 K and f = 12 pN is estimated to be 1–4 s, which is three orders of magnitude greater than at the higher Tm and lower fm.
Thermal Refolding and Unfolding. To induce thermal refolding, we performed a temperature quench starting from a thermally equilibrated ensemble at T = 510 K to T = 290 K < Tm. The approach to the folded RNA hairpin is monitored by using the time dependence of Q, χ, and nbond. A molecule is in the native state if Q > 0.97 and nbond = 9.0. To confirm that the conformations with these values of Q and nbond are in the NBA, we performed steepest-descent simulations from states with Q > 0.97. Most of these conformations reach the native state with χ = 0.00.
To calculate the folding time, we performed temperature-quench simulations for 100 different initially denatured conformations to obtain the distribution of the first passage times; i.e., the first time molecules reach the NBA. The initial population of unfolded molecules decays exponentially with the folding time 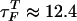 μs. Of the initially denatured molecules, ≈ 90% form folded structures in an all-or-none manner in which hairpin formation is initiated near the loop region with zipping of stabilizing contents progressing towards the end until the 5′ and 3′ contacts are established. In rare instances, the 5′ and 3′ ends meet first and zipping proceeds from the ends to the loop region (10%). Because of high entropy costs, this process is less probable.
μs. Of the initially denatured molecules, ≈ 90% form folded structures in an all-or-none manner in which hairpin formation is initiated near the loop region with zipping of stabilizing contents progressing towards the end until the 5′ and 3′ contacts are established. In rare instances, the 5′ and 3′ ends meet first and zipping proceeds from the ends to the loop region (10%). Because of high entropy costs, this process is less probable.
For comparison with mechanical unfolding, we also performed simulations to monitor thermal unfolding. Equilibrated conformations at T = 100 K are heated to T = 346 K to initiate unfolding. Unlike in the thermal refolding, in which hairpin is formed by a zipping process, there is no characteristic disruption pathway. All of the nine bonds fluctuate independently until denaturation occurs. Thus, thermal unfolding is stochastic.
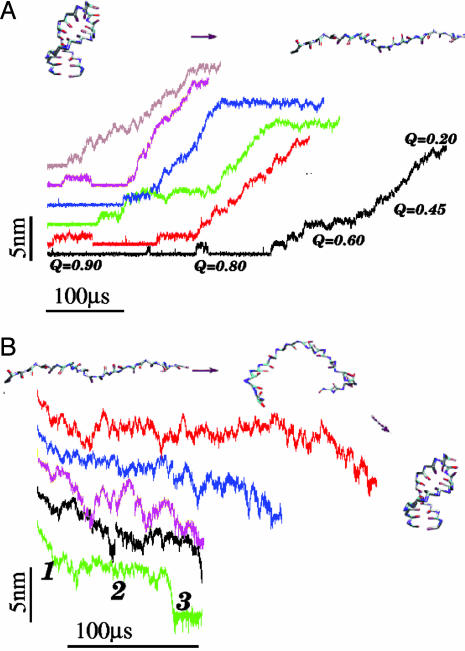
Unfolding Dynamics at Constant Force. To probe the structural transitions in the hairpin, we performed steered Langevin dynamics simulations at a constant force with T = 254 K. From the phase diagram, the equilibrium unfolding force at this temperature is 12 pN (Fig. 2 A). To monitor the complete unfolding of P5GA, in the time course of the simulations, we applied f = 42 pN to one end of the hairpin with the other end fixed. In contrast to thermal unfolding (or refolding), the initially closed hairpin unzips from the end to the loop region. The unzipping dynamics, monitored by the time dependence of R, shows “quantized staircase-like jumps” with great variations in step length, that depend on the initial conditions. The lifetimes associated with the “intermediates” vary greatly (Fig. 6A). The large dispersion reflects the heterogeneity of mechanical unfolding pathways. Approach to the stretched state that occurs in a stepwise “quantized” manner (12), which was first shown in lattice models of proteins, has recently been experimentally observed in the unzipping dynamics of DNA under constant force (22). The presence of initial condition-dependent unfolding suggests that, even in the small P5GA hairpin, several distinct “metastable intermediates” are explored upon stretching.
Fig. 6.
Force-induced unfolding and refolding. (A) Time traces of unfolding of P5GA at a constant force f = 42 pN at T = 254 K monitored by the increase in R. The values of Q at different unfolding stages are given for the trajectory in black. (B) Refolding is initiated by a force quench from the initial value f = 90 pN to f = 0. The five time traces show great variations in the relaxation to the hairpin conformation. However, in all trajectories, R decreases in at least three stages that are explicitly labeled for the trajectory in green. The trajectories in A and B are offset, for clarity.
Refolding Under Force Quench. To monitor the dynamics of approach to the NBA, we initiated refolding from extended conformations with R = 13.5 nm, prepared by stretching at T = 290 K and f = 90 pN. Subsequently, we set f = 0, and the approach to the native state was monitored. From the distribution of first passage times, the refolding kinetics follows exponential kinetics with the mean folding time of ≈191 μs, compared with 12.4 μs in the temperature quench. It is remarkable that, even though the final conditions (T = 290 K and f = 0) are the same as in thermal refolding, the time scale for hairpin formation 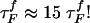 .
.
The large difference in 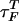 and
and 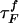 arises because the molecules under the distinct initial conditions navigate entirely different regions of the energy landscape. The distribution of R in the thermally denatured conformations is P(R)thermal ∝e–βVtot(R)/kBTH (TH is the initial temperature), whereas in the ensemble of the stretched conformation,
arises because the molecules under the distinct initial conditions navigate entirely different regions of the energy landscape. The distribution of R in the thermally denatured conformations is P(R)thermal ∝e–βVtot(R)/kBTH (TH is the initial temperature), whereas in the ensemble of the stretched conformation, 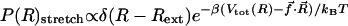 . The stretched conformations (Rext = 13.5 nm) do not overlap with the accessible regions of the canonical ensemble of thermally denatured conformations (data not shown). As a consequence, the regions of the free-energy landscape from which folding commences in force-jump folding are vastly different from those corresponding to the initial population of thermally equilibrated ensemble.
. The stretched conformations (Rext = 13.5 nm) do not overlap with the accessible regions of the canonical ensemble of thermally denatured conformations (data not shown). As a consequence, the regions of the free-energy landscape from which folding commences in force-jump folding are vastly different from those corresponding to the initial population of thermally equilibrated ensemble.
Force Quench Refolding Occurs in Multiple Stages. The pathways explored by the hairpins en route to the NBA are heterogeneous (Fig. 6B). Different molecules reach the hairpin conformation by vastly different routes. Nevertheless, the time dependence of R shows that the approach to the native conformation occurs in stages (Fig. 6B). Upon release of force, there is a rapid initial decrease in R that results in the collapse of the hairpin. Surprisingly, this process takes an average of several microseconds, which is much longer than expectations based on theories of collapse kinetics of polymer coils (23, 24). In the second stage, the hairpin fluctuates in relatively compact state with R in the broad range (25–75 Å) for prolonged time periods. On these time scales, which vary considerably depending on the molecules, conformational search occurs among compact structures. The final stage is characterized by a further decrease in R that takes the molecules to the NBA. The last stage is the most cooperative and sudden, whereas the first two stages appear to be much more continuous (Fig. 6B). Interestingly, similar relaxation patterns characterized by heterogeneous pathways and continuous collapse in the early stages have been observed in force-quench refolding of ubiquitin (25). The multistage approach to the native stage is reminiscent of the Camacho–Thirumalai proposal for protein refolding (26).
Conclusion
Use of constant force to unfold or initiate refolding (by force quench) provides glimpses of regions of the energy landscape of biomolecules that cannot be probed by conventional methods. In the mechanical unfolding experiments, the molecules go from an initial low-entropy state (folded) to another low-entropy state (stretched). Unfolding in conventional experiments results in a transition from a low-entropy folded state to a high-entropy unfolded state. This difference gives rise to vastly different mechanisms and time scales of folding and unfolding. By using coarse-grained models of RNA, we have highlighted some of the major differences by considering temperature and force effects on unfolding RNA hairpins.
Our studies have led to the following predictions, all of which are amenable to experimental tests. (i) The hairpin undergoes a first-order transition from the folded to unfolded states at a critical value of f. The transition becomes strongly first order at low temperatures and high forces. Force unfolding, at a fixed f, is more cooperative than unfolding with a fixed T, and a varied f. (ii) Unfolding of RNA occurs in steps with long pauses in a number of discrete intermediates that have a large dispersion in R values. (iii) There are great variations in the hopping times between the NBA and the UBA along the locus of points in the (f, T) plane separating the two basins of attraction. At low Tm and high fm, the hopping times are orders of magnitude greater than at T ≈ Tm and low fm. (iv) Remarkably, refolding times by force quench are much greater than folding initiated by temperature quench. The approach to the native state from stretched conformations occurs in several stages. The earliest events involve continuous changes in the progress variable that monitors folding, rather being an all-or-none process.
Acknowledgments
This work was supported in part by National Science Foundation Grant CHE02-09340.
Author contributions: D.T. designed research; C.H. performed research and analyzed data; and C.H. and D.T. wrote the paper.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: NBA, native basin of attraction; UBA, unfolded basin of attraction.
References
- 1.Onoa, B. & Tinoco, I., Jr. (2004) Curr. Opin. Struct. Biol. 14, 374–379. [DOI] [PubMed] [Google Scholar]
- 2.Treiber, D. K. & Williamson, J. R. (2001) Curr. Opin. Struct. Biol. 11, 309–314. [DOI] [PubMed] [Google Scholar]
- 3.Thirumalai, D., Lee, N., Woodson, S. A. & Klimov, D. K. (2001) Annu. Rev. Phys. Chem. 52, 751–762. [DOI] [PubMed] [Google Scholar]
- 4.Koculi, E., Lee, N., Thirumalai, D. & Woodson, S. A. (2004) J. Mol. Biol. 341, 27–36. [DOI] [PubMed] [Google Scholar]
- 5.Russell, R., Zhuang, X., Babcock, H. P., Millett, I. S., Doniach, S., Chu, S. & Herschlag, D. (2002) Proc. Natl. Acad. Sci. USA 99, 155–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Liphardt, J., Onoa, B., Smith, S. B., Tinoco, I. & Bustamante, C. (2001) Science 292, 733–737. [DOI] [PubMed] [Google Scholar]
- 7.Liphardt, J., Dumont, S., Smith, S. B., Tinoco, I. & Bustamante, C. (2002) Science 296, 1832–1835. [DOI] [PubMed] [Google Scholar]
- 8.Mueller, M., Mezard, M. & Krzakala, F. (2002) Eur. Phys. J. E 9, 67–77. [DOI] [PubMed] [Google Scholar]
- 9.Cocco, S., Marko, J. F. & Monasson, R. (2003) Eur. Phys. J. E 10, 153–161. [DOI] [PubMed] [Google Scholar]
- 10.Gerland, U., Bundschuh, R. & Hwa, T. (2001) Biophys. J. 81, 1324–1332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gerland, U., Bundschuh, R. & Hwa, T. (2003) Biophys. J. 84, 2831–2840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Klimov, D. K. & Thirumalai, D. (1999) Proc. Natl. Acad. Sci. USA 96, 6166–6170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Rudisser, S. & Tinoco, I., Jr., (2000) J. Mol. Biol. 295, 1211–1223. [DOI] [PubMed] [Google Scholar]
- 14.Klimov, D. K. & Thirumalai, D. (2000) Proc. Natl. Acad. Sci. USA 97, 7254–7259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Klimov, D. K., Betancourt, M. R. & Thirumalai, D. (1998) Folding Des. 3, 481–498. [DOI] [PubMed] [Google Scholar]
- 16.Walter, A. E., Turner, D. H., Kim, J., Lyttle, M. H., Muller, P., Mathews, D. H. & Zuker, M. (1994) Proc. Natl. Acad. Sci. USA 91, 9218–9222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mathews, D. H., Sabina, J., Zuker, M. & Turner, D. H. (1999) J. Mol. Biol. 288, 911–940. [DOI] [PubMed] [Google Scholar]
- 18.Misra, V. K. & Draper, D. E. (2001) Proc. Natl. Acad. Sci. USA 98, 12456–12461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ermack, D. L. & McCammon, J. A. (1978) J. Chem. Phys. 69, 1352–1369. [Google Scholar]
- 20.Kumar, S., Bouzida, D., Swendsen, R. H., Kollman, P. A. & Rosenberg, J. M. (1992) J. Comp. Chem. 13, 1011–1021. [Google Scholar]
- 21.Klimov, D. K. & Thirumalai, D. (1998) Folding Des. 3, 127–139. [DOI] [PubMed] [Google Scholar]
- 22.Danilowicz, C., Coljee, V. W., Bouzigues, C., Lubensky, D. K., Nelson, D. R. & Prentiss, M. (2003) Proc. Natl. Acad. Sci. USA 100, 1694–1699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Thirumalai, D. (1995) J. Phys. I. 5, 1457–1467. [Google Scholar]
- 24.Pitard, E. & Orland, H. (1998) Europhys. Lett. 41, 467–472. [Google Scholar]
- 25.Fernandez, J. M. & Li, H. (2004) Science 303, 1674–1678. [DOI] [PubMed] [Google Scholar]
- 26.Camacho, C. J. & Thirumalai, D. (1993) Proc. Natl. Acad. Sci. USA 90, 6369–6372. [DOI] [PMC free article] [PubMed] [Google Scholar]