Gel mobilities of linking-number topoisomers and their dependence on DNA helical repeat and elasticity

Abstract

Agarose-gel electrophoresis has been used for more than thirty years to characterize the linking-number (Lk) distribution of closed-circular DNA molecules. Although the physical basis of this technique remains poorly understood, the gel-electrophoretic behavior of covalently closed DNAs has been used to determine the local unwinding of DNA by proteins and small-molecule ligands, characterize supercoiling-dependent conformational transitions in duplex DNA, and to measure helical-repeat changes due to shifts in temperature and ionic strength. Those results have been analyzed by assuming that the absolute mobility of a particular topoisomer is mainly a function of the integral number of superhelical turns, and thus a slowly varying function of plasmid molecular weight. In examining the mobilities of Lk topoisomers for a series of plasmids that differ incrementally in size over more than one helical turn, we found that the size-dependent agarose-gel mobility of individual topoisomers with identical values of Lk (but different values of the excess linking number, ΔLk) vary dramatically over a duplex turn. Our results suggest that a simple semi-empirical relationship holds between the electrophoretic mobility of linking-number topoisomers and their average writhe in solution.

1. Introduction

Topological techniques have been powerful methods for characterizing the interactions of proteins [1–4] and small-molecule ligands [2, 5–8] with DNA. These techniques rely on changes in DNA topology observed after cleavage and rejoining of DNA strands. Differences in supercoiling, knotting, catenation, or combinations of these properties in a circular molecule report on perturbations of local or global DNA structure that accompany ligand binding or enzymatic activity.

Virtually all DNA molecules in all cells are supercoiled [9–14] and dramatic changes in supercoiling invariably accompany essential biological processes such as chromatin reorganization [15, 16], replication [17], transcription [9, 18, 19], recombination [20–22], and DNA repair [23]. Characterizing changes in supercoiling is therefore essential for understanding these processes in detail. Moreover, modulation of supercoiling accompanies conformational changes in duplex DNA such as cruciform extrusion [12, 24–28] and the formation of Z-DNA [12, 13, 27–30], and is thus an important topological method for analyzing alternative DNA conformations.

DNA supercoiling is parameterized in terms of a topological quantity, the linking number, Lk, which takes on integer values for any closed-circular DNA molecule [31]. Thermal fluctuations in the geometric quantities twist, Tw, and writhe, Wr, lead to a distribution of Lk values with the linking number of any particular molecule given by the well-known relation Lk =Tw+Wr [32]. The equilibrium Lk distribution can be sampled by cyclization, ligation at a nick, or topoisomerase activity and depends, through the Tw and Wr distributions, on the detailed structure of the double helix. Twist and writhe quantitatively describe the local winding of DNA strands about the molecule's central axis and winding of this axis about itself, respectively [33]. For plasmid-sized DNAs, covalent closure in vitro generates a Gaussian population containing several Lk isomers (topoisomers), which can be analyzed by agarose-gel electrophoresis [32, 34–36]. The physical basis for the electrophoretic separation of topoisomers is not well understood; however, it has been proposed that gel mobility is largely a function of the average DNA writhe, <Wr> [32, 34–39].

The actual value of Lk is rarely of interest; instead, changes in this parameter are measured by comparing Lk distributions obtained under different conditions, for example, in the presence and absence of a perturbing ligand [40]. Quantitative comparison of changes in the Lk distribution forms the basis for determining the helical repeat of DNA by the Gaussian-center [37, 39] and band-shift methods [29, 30, 37]. The underlying principle of these approaches is that an incremental change in DNA length shifts the center of the Lk distribution by a fractional amount that depends on the excess linking difference between the relaxed state of the DNA circle and the most-probable topoisomer. The relaxed state is defined in terms of a reference value of the linking number, Lk ₀ = N/h ₀, where N is the size of the molecule in base pairs and h ₀ is the DNA helical repeat in base pairs per turn. Unlike Lk values, Lk ₀ is not necessarily an integer. Therefore, the apparent magnitude of the linking difference, ΔLk = Lk – Lk ₀, measured for the most-probable topoisomer, is generally some fraction of a helical turn. According to the Gaussian-center method, Lk ₀ is found by fitting the distribution of topoisomer intensities to a Gaussian envelope that, by definition, is centered on the value Lk ₀. Note that the value of the helical repeat obtained in these measurements pertains to an Lk increment associated with the gain (or loss) of a specific DNA-sequence element and is therefore sequence dependent.

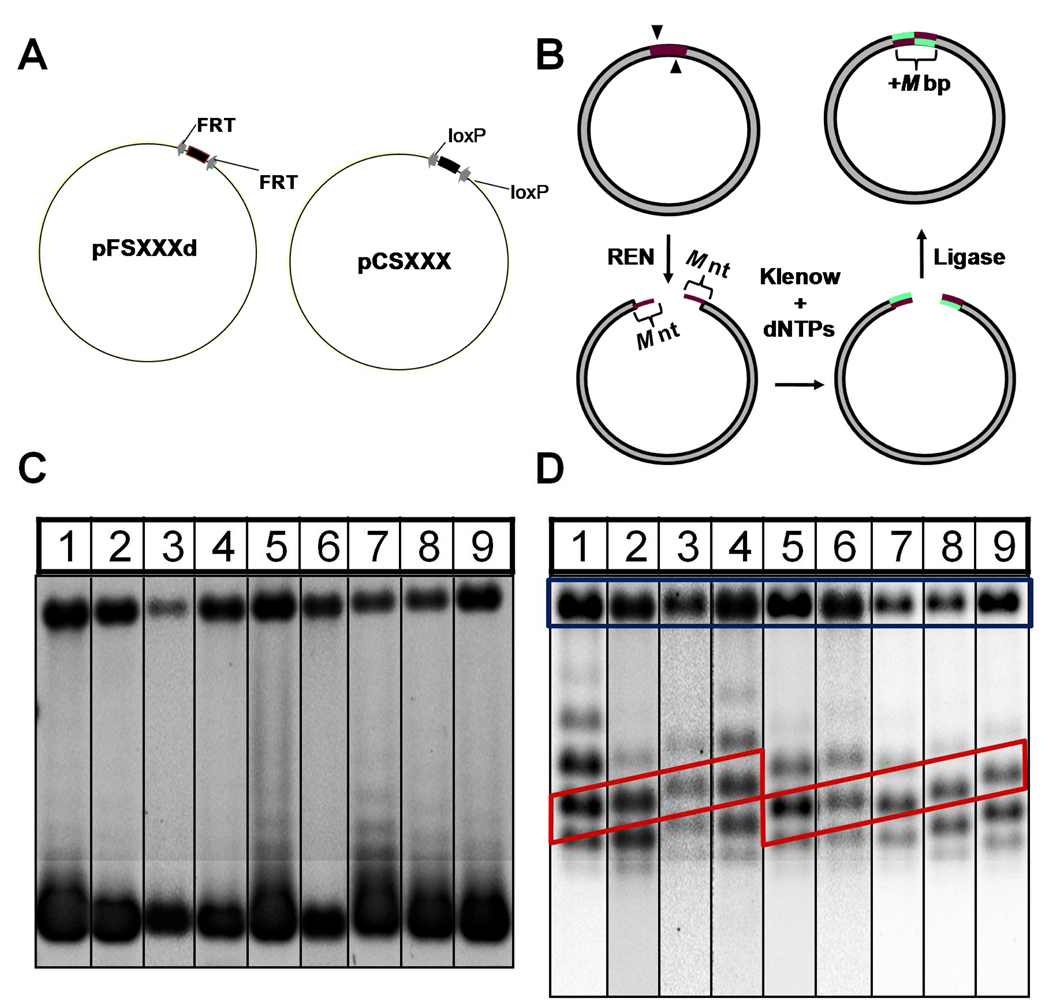
In the course of experiments undertaken to measure the helical repeat of two distinct sets of plasmids, one set having sizes near 2500 bp and another near 3400 bp (Fig. 1A), we observed that gel-electrophoretic mobilities of topoisomers having identical values of Lk do depend markedly on DNA size (Figs. 1C, 1D). DNA-length increments up to 32 bp (about 1% of average plasmid size) resulted in near-negligible changes in the gel mobilities of the nicked plasmids whereas the mobilities of specific topoisomers changed by up to two-fold. The effect is especially evident for topoisomers having low levels of supercoiling (Fig. 1D) and is manifested as a sawtooth pattern of band intensities resulting from shifts in topoisomer probabilties with changes in plasmid size. The periodicity of the DNA-size-dependent topoisomer pattern is near 10 bp, suggesting a dependence on the DNA helical repeat. We examined the topoisomer mobilities for these plasmid series as a function of ΔLk under two standard electrophoresis conditions.

Fig 1.

(A) Plasmid constructs used in the present study. Variable-length regions are indicated by the thicker arc segment between recombination target sites (gray arrows). (B) Example of the “cleavage-end repair-ligation” procedure used to construct several plasmids. Action of a restriction endonuclease at its cleavage sites (arrowheads) generates a pair of M-nt 5′ overhangs (red) that are filled by the Klenow fragment of E. coli DNA polymerase I in the presence of dNTPs (green). The plasmid is then cyclized by blunt-end ligation using T4 ligase, thereby extending the DNA duplex by M bp. (C) Gel-electrophoretic characterization of native (superhelix density ≈ −0.055) pFS2.Xd plasmids in a 0.8% agarose gel run in TBE buffer containing 0.5 µg mL⁻¹ chloroquine. Lanes 1–9 correspond to the pFS2.Xd plasmids given in Table 1 in order of increasing plasmid size. (D) Gel-electrophoretic separation of pFS2.Xd plasmids under conditions identical to those in (C) after relaxation to equilibrium with topoisomerase I as described in Materials and Methods. Gel lanes are labeled as in (C). Note the linear dependence of topoisomer mobility on construct size, highlighted by the red diagonal boxes in the figure. Bands corresponding to nicked forms are located within the blue rectangle.

Finally, detailed analysis of the gel-electrophoresis data using models for the conformational properties of superhelical DNA shows that topoisomer mobilities are fitted quite well by a straightforward empirical dependence on ΔLk that is linear in the absolute value of the average writhe, |<Wr>|. The proportion of superhelical winding present as <Wr>depends in turn on the bending and twisting rigidity of the double helix. By considering the apparent proportionality between mobility and |<Wr>|, we show that the electrophoretic behavior of superhelical molecules is well accounted for using canonical values of these elastic parameters for DNA duplexes free in solution.

2. Materials and Methods

2.1. Plasmid-DNA construction and isolation

We investigated two homologous series of plasmid DNAs (Fig. 1A, Table 1 and Table 2). The pFS2.Xd series of plasmids (Table 1) contain two directly repeated copies of the minimal FRT target sequence recognized by the Flp recombinase [41], in which the helical phasing of the FRT sites varies systematically over more than one helical turn. These plasmids were derived by subcloning FRT-bearing DNA fragments of varying length into SmaI/XmaIII and EcoRI/AatII restriction sites of pGEM-7Zf(+). Additional members of this set were generated by steps consisting of restriction-endonuclease cleavage, end repair using the Klenow fragment of DNA polymerase I, and religation as shown in Fig. 1B. The pFS2.Xd series consists of 9 constructs that cover almost two turns of double helix with an average size increment of 2.25 bp (the variable X in the plasmid designation gives the distance between the centers of FRT sites).

TABLE 1.

Listing of pFS2.Xd constructs (see “Materials and Methods”). For constructs created by the “cleavage-end repair-ligation” procedure, both the parent construct and restriction sites modified are given.

Construct	Parent plasmid	Restriction sites filled	Length, bp
pFS169d	-	NA	3412
pFS171d	-	NA	3414
pFS173d	-	NA	3416
pFS175d	-	NA	3418
pFS177d	pFS173d	Asp718	3420
pFS179d	-	NA	3422
pFS181d	pFS177d	XhoI	3424
pFS183d	pFS179d	Asp718	3426
pFS187d	pFS183d	XhoI	3430

TABLE 2.

Listing of pCS2.Xd constructs (see “Materials and Methods”). For constructs created by the “cleavage-end repair-ligation” procedure both the parental construct and restriction sites modified are specified.

Construct	Designation according to ref. [42]	Parent plasmid	Restriction site filled	Length, bp
pCS114	pRH42–616	-	NA	2484
pCS116	pRH42–686	-	NA	2486
pCS118		pCS114	BamHI	2488
pCS120	pRH42–615	-	NA	2490
pCS124		pCS120	BamHI	2494
pCS128	pRH42–614	-	NA	2498
pCS132		pCS128	BamHI	2502
pCS133	pRH42–61	-	NA	2503
pCS137	pRH42–404	-	NA	2507
pCS138	pRH42–68	-	NA	2508
pCS141		pCS137	BamHI	2511
pCS142	pRH42–407	-	NA	2512
pCS146		pCS142	BamHI	2516

A second set of plasmids bearing loxP target sites of the Cre recombination system, the pCS2.Xd series (Table 2), was generated exclusively from the family of pRH42 derivatives described in [42] using the “cleavage-end repair-ligation” procedure described above. There are 13 constructs in this set covering about three duplex turns with an average size increment of 2.67 bp. As with the pFS2.Xd constructs, "X" designates the distance between centers of the loxP sites.

All plasmids were propagated in E. coli strain DH5α. Cloning operations were confirmed by restriction analysis and dideoxynucleotide sequencing (MWG Biotech Inc, High Point NC). Plasmid DNAs were isolated by alkaline lysis and purified using two rounds of polyethylene-glycol precipitation [43]. In some cases, an additional round of purification was carried out by CsCl-ethidium bromide density-gradient centrifugation.

2.2. Preparation of topoisomers

Natively supercoiled plasmid DNA was typically relaxed to equilibrium with wheat-germ DNA topoisomerase I (Promega) at 37° C under the following reaction conditions: 50 mM Tris-Cl pH 7.5, 1 mM Na₂EDTA, 50 mM NaCl, 1 mM dithiothreitol, and 0.1 mg mL⁻¹ bovine serum albumin. We also prepared relaxed plasmids with E. coli topoisomerase I (New England Biolabs), which requires magnesium ions for activity. These reactions were carried out in NEBuffer 4 (20 mM Tris-acetate pH 7.9, 50 mM potassium acetate, 10 mM magnesium acetate, and 1 mM dithiothreitol) at 37° C. Reactions contained 4.5 ± 0.5 units of Topo I and 0.5 µg DNA in a reaction volume of 20 µL. After overnight incubation, the reactions were stopped by addition of sodium dodecyl sulfate (SDS) to a final concentration of 0.1%, further incubation at 80 °C for 20 min, and multiple rounds of extraction with phenol and phenol:chloroform:isoamyl alcohol [43].

2.3. Agarose-gel electrophoresis

Electrophoresis was carried out in 20-cm long 0.8% agarose gels (SeaKem LE, Cambrex Bioscience, Inc., Rockland MA) at 3 V cm⁻¹ in TBE (50 mM Trisborate pH 8.4, 1 mM Na₂EDTA) or TAE (45 mM Tris-acetate pH 7.9, 1 mM Na₂EDTA) buffers, as specified. In many experiments both the gel and buffer were supplemented with low concentrations of chloroquine phosphate ([Chl] ≤ 0.7 µg mL⁻¹). We found that the optimum concentration of chloroquine was about 0.5 µg mL⁻¹, which avoids overlap of positive and negative topoisomers having similar values of |ΔLk| near the position of nicked (oc) DNA. All electrophoresis runs took place for 17 h at room temperature (22° C) with continuous buffer circulation. Prior to staining, chloroquine-containing gels were soaked twice for 1-h periods in 0.5 M NaCl to remove residual intercalator followed by two 1-h washes in double-deionized H₂O. Gels were stained with 0.5 µg mL⁻¹ ethidium bromide for 30 min followed by overnight destaining in electrophoresis buffer at 4°C.

2.4. Image acquisition and data analysis

Ethidium-stained gels were imaged using a 16-bit (1:65,536 dynamic range) cooled CCD camera (Alta U32, Apogee Instruments) having 2146×1472-pixel spatial resolution. Bands were detected using a FirstLight UV transilluminator (UVP), which achieves less than 5% coefficient-of-variation illumination across the entire filter area. Digital densitometry was carried out using ImageQuant software (GE HealthCare); the intensity distributions within each lane were subsequently analyzed using Grams/AI software (Thermo Scientific) and gave center-of-mass topoisomer-band positions, X̄ _cm , as functions of ΔLk for all of the topoisomers belonging to a particular construct. In cases where adjacent topoisomer bands were well separated (ΔX̄ _cm ≫ full width at half maximum of the intensity distribution), band intensities were determined by volume integration of pixels within a mask fitted to the band profile. Not infrequently, tails of band profiles overlapped, in which case a line scan of the relevant area within a gel lane was digitized and subjected to Gaussian deconvolution using Grams/AI. The individual Gaussian peaks were then integrated to obtain topoisomer intensity values.

For the range of ΔLk values investigated here no correction was needed for topoisomer-dependent differences in ethidium affinity. Such corrections amount to less than 2% as determined from buoyant-density centrifugation data [44] or gel-electrophoresis results [45] and fall within our experimental uncertainty.

2.5. Fitting of experimental mobilities using a theoretical writhe distribution

Fig. 1D shows that the mobilities of topoisomers having identical values of Lk, but derived from plasmids of different size vary essentially linearly with the number of base pairs in the construct (Fig. 2). We conjecture, as proposed by others [32, 34–39], that the size effect on mobility is primarily due to excess writhe in molecules having the same Lk value (but different values of ΔLk). This linear dependence suggests an empirical expression for topoisomer mobility as a function of ΔLk

$$\mu (\mathrm{\Delta }Lk)=\frac{{\overline{x}}_{cm}}{E\mathrm{\Delta }t}=\alpha |<Wr>|+{\mu }_{oc}$$ (1)

where μ is the mobility, E is the electric-field strength expressed in V cm⁻¹, Δt is the duration of electrophoresis, µ_oc is the mobility of the nicked circle of the same size, and α is a constant for a particular plasmid data set and electrophoresis buffer conditions.

Fig 2.

Analysis of topoisomer mobilities. (A) Line scan of intensity along a gel lane obtained by horizontal averaging of pixel intensities across the image of a gel lane. Positions of the centers of each topoisomer band are indicated by vertical arrows. Bands correspond to topoisomers with increasing values of Lk from left to right; $L{k\prime }_0$ denotes the (integer) Lk value closest to Lk₀. The peak corresponding to the nicked form is indicated by oc. (B) Gel mobilities of topoisomers with identical values of Lk for plasmids of different size. Bands corresponding to the same topoisomer are indicated by the diagonal boxed regions. (C) Set of line scans corresponding to the left-hand portion of (B).

Eq. (1) yields a linear relationship with DNA size to the extent that excess |<Wr>| is proportional to ΔLk. The dependence of <Wr>on ΔLk is examined in greater detail below using Monte Carlo simulation. The form of Eq. (1) can be justified in terms of accounting for the observations that nicked circles (oc forms), as well as relaxed molecules (ΔLk = 0), have lower mobilities than those of any positive or negative topoisomer (|ΔLk| > 0). Moreover, the mobilities of (+) and (−) topoisomers with the same |ΔLk| resolved by two-dimensional agarose-gel electrophoresis are identical [35, 46, 47]. Although a Taylor-series expansion of µ about µ₀ would be expected to be a suitable approximation to the mobility for small values of ΔLk, the linear term in such an expansion should vanish by symmetry, leaving a leading term that is quadratic in ΔLk. The unusual form of Eq. (1) should thus be regarded as an empirical relationship.

The value of |<Wr>| appearing in Eq. (1) is implicitly determined by the helicoelastic properties of a wormlike-chain model for superhelical plasmid DNAs, namely bending and twisting flexibilities and the DNA helical repeat. We note that our analysis considers plasmid-DNA molecules in this size range as structurally and elastically homogeneous and therefore does not incorporate sequence-dependent properties such as intrinsic bending. Both experimental gel-mobility data as well as simulation results from our group indicate that intrinsic bends located within a limited region of the plasmid contour have negligible effects on the overall writhe of DNAs in this size range (unpublished results).

Numerical analysis of the mobility data is facilitated by an approximate expression for <Wr>as a function of ΔLk

$$\langle Wr(\mathrm{\Delta }Lk)\rangle =\left(\frac{{\sigma }_{Wr}^2}{{\sigma }_{Wr}^2+{\sigma }_{Tw}^2}\right)\mathrm{\Delta }Lk$$ (2)

where ${\sigma }_{Wr}^2$ and ${\sigma }_{Tw}^2$ are the respective variances of Wr and Tw in topologically unconstrained (i.e., nicked) DNA circles. This formula derives from the assumptions that the distributions of Tw and Wr for unconstrained DNA circles are independent and Gaussian [48, 49]. We use an estimate for ${\sigma }_{Wr}^2$ in Eq. (2) determined from Monte Carlo simulations of randomly cyclized DNA chains [48]

$$\frac{{\sigma }_{Wr}^2}{L}=\frac{24.8x^{7.59}+1}{2.13\cdot {10}^{-3}(x^{7.59}+1)}$$ (3)

with L the plasmid contour length in cm (equal to 3.4.10⁻⁸ N) and x = log(L / P), P denoting the wormlike-chain persistence length. A simple formula gives the Tw variance as a function of L, namely, ${\sigma }_{Tw}^2=L{k}_{\mathrm{B}}T/(4{\pi }^2\mathrm{C})$ where C is the twisting rigidity and k_B T is the thermal energy [50].

Global fitting of each data set was carried out using a computer program written in Matlab. Topoisomer mobilities, µ, were fitted simultaneously using standard non-linear least-squares optimization with Eq. (1) as the objective function and α, h₀, P, C, and an additional fitting parameter, h_r, as adjustable parameters. The last quantity, ${\mathrm{h}}_{\mathrm{r}}={\mathrm{h}}_0^{\text{rel}}/{\mathrm{h}}_0^{\text{el}}$ , enters a correction to ΔLk of the form ΔLk = Lk $\mathrm{\Delta }Lk=Lk-(N/{\mathrm{h}}_0^{\text{rel}}){\mathrm{h}}_{\mathrm{r}}$ and accounts for differences in the DNA helical repeat between topoisomerase relaxation $({\mathrm{h}}_0^{\text{rel}})$ and electrophoresis $({\mathrm{h}}_0^{\text{el}})$ solution conditions. This environmental effect on helical winding is on the order of two percent and is taken to affect all topoisomers uniformly. The fitting program is based on the Matlab routine lsqcurvefit and available on request.

2.6 Comparison to Metropolis Monte Carlo simulations

In order to validate the application of Eq. (2) to topologically constrained molecules, we compared the Wr distributions estimated in [48] with those determined for superhelical DNAs by the Metropolis Monte Carlo method [51] The Metropolis algorithm models a DNA circle of defined ΔLk as a discrete wormlike chain composed of rigid cylinders of diameter d. The value of d accounts for excluded-volume effects and depends on ionic conditions [51, 52]. Trial superhelix conformations are sampled by 2-pivot and reptation moves and are accepted or rejected according to the Metropolis criterion [53]. The Wr distribution computed from the resulting population of accepted conformations therefore models that for an ensemble of superhelical molecules at thermal equilibrium. Simulations were carried out for ensembles of 3000-bp DNA chains with P = 50 nm, C = 3.1·10⁻¹⁹ erg cm, d = 5 nm and ΔLk ranging from −20 to +2. Simulations corresponding to the different ΔLk values were run in parallel on a 20-cpu cluster of Intel Xeon processors.

3. Results and Discussion

3.1 Agarose-gel mobilities of topoisomers and their dependence on gel conditions

Agarose-gel separations of natively supercoiled and relaxed pFS plasmids are shown in Figs. 1C and 1D, respectively. In the case of the relaxed plasmids there is a pronounced dependence of topoisomer mobility on the size of the construct. Note that topoisomers belonging to different plasmids within the series, but having identical values of Lk, have markedly different mobilities (Fig. 2). We interpret this effect as being due to the excess linking-number difference, manifested mainly as excess <Wr>in plasmid-sized DNA molecules [48, 50, 51].

The linking difference, ΔLk, is affected by the ionic environment as well as binding of intercalating ligands [52, 54–57] and potentially, DNA sequence [58–61]. We therefore investigated gel mobilities of our constructs under two different electrophoresis conditions. Apart from helical twist, dependencies of other conformational or elastic parameters that affect <Wr> (e.g., bending and twisting flexibility constants) on the ionic environment remain somewhat controversial. DNA-cyclization studies suggest that bending and twisting flexibilities are relatively insensitive to ionic conditions above low (< 20 mM M⁺) ionic strength [62]. However, electrooptical measurements indicate that there is as much as a 30% decrease in DNA persistence length between 12 and 110 mM [Na⁺] [63]. We therefore left values of the persistence length, P, and twisting rigidity, C, as adjustable parameters in our analysis.

3.2. Theoretical dependence of mobility on writhe

In order to determine helical and elastic parameters for plasmids from the mobility data, we need to know the quantitative relationship between <Wr>and ΔLk given DNA size, helical repeat, and bending and twisting rigidities. Based on the assumption that the distributions of Tw and Wr for unconstrained DNA circles are independent and Gaussian, Levene and Crothers [48] derived a formula for the probability density of Wr with ΔLk specified, which we rewrite as

$$P(Wr|\mathrm{\Delta }Lk)=\frac{1}{\sqrt{2\pi {\delta }_{Wr}^2}}\text{exp}\left[-{(Wr-\langle Wr\rangle )}^2/(2{\delta }_{Wr}^2)\right]$$ (4)

where ${\delta }_{Wr}^2$ is the Wr variance in the topologically constrained system. It can easily be shown that <Wr>, corresponding to the maximum of Eq. (4), is given by Eq. (2) and that ${\delta }_{Wr}^2={\sigma }_{Tw}^2{\sigma }_{Wr}^2/\left({\sigma }_{Tw}^2+{\sigma }_{Wr}^2\right)={\sigma }_{Tw}^2\langle Wr\rangle /\mathrm{\Delta }Lk$

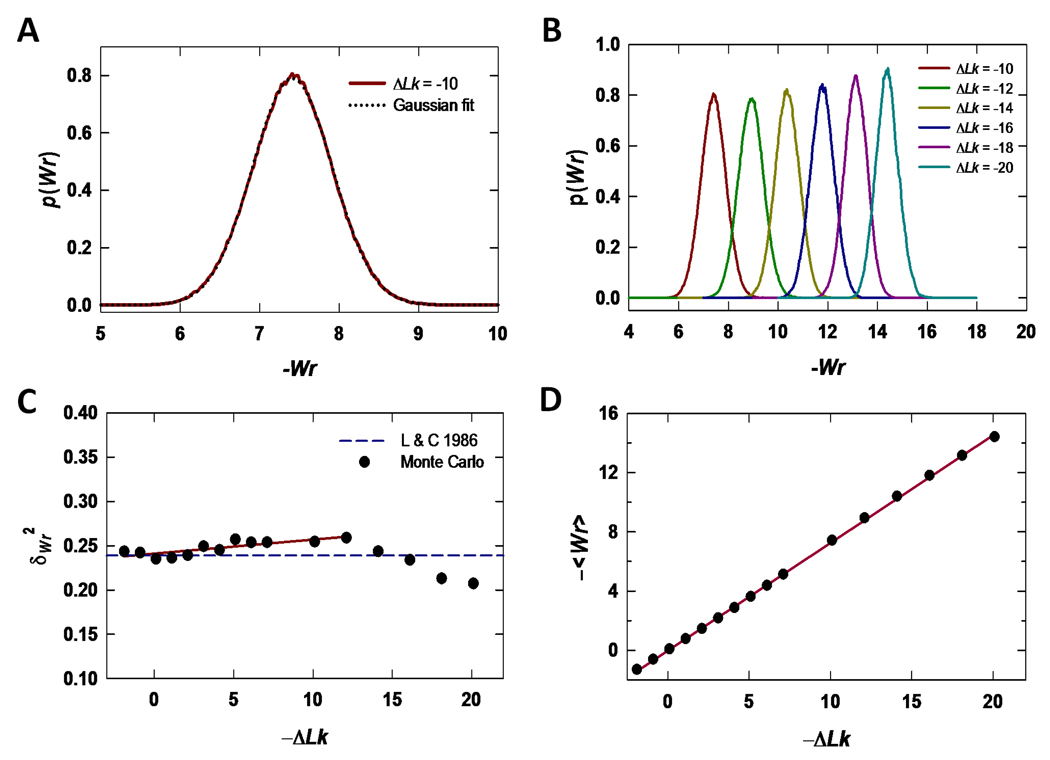
The assumption that the Wr distribution for topologically constrained molecules can be derived from the convolution of Tw and Wr distributions in the unconstrained system, or so-called factorization approximation [64], may be particularly questionable for large |ΔLk|. This could lead to significant deviations from Gaussian behavior in the Wr distribution for molecules having significant supercoiling. In addition, the Tw and Wr variances used in Eqs. (2) and Eqs. (3) are based on chains that lack excluded volume and the magnitude of an excluded-volume correction remains unknown. We examined the validity of our approximate treatment by comparing the Wr distribution obtained using Eqs. (2) – (4) with that for supercoiled DNA computed by the Metropolis Monte Carlo method (Fig. 3). These simulations modeled a 3000-bp covalently closed DNA circle with ΔLk ranging from approximately −20 to +2. Figs. 3A, B show that the Wr distribution is well described by a Gaussian probability density up to −ΔLk = 20. However, unlike Eq. (3), which is based on a model that omits dependence of the Wr variance on Lk, the Monte Carlo results show a slight increase in ${\delta }_{Wr}^2$ for −ΔLk between 0 and 12, followed by a pronounced decrease at larger Lk differences (Fig. 3C). The modest initial increase in variance may accompany the transition from the relaxed circle to a more ordered plectonemic structure, whereas the pronounced decrease seen in the limit of higher |ΔLk| may be due to the increasingly constrained final plectoneme attained with greater winding.

Fig 3.

Theoretical estimates of Wr distributions, Wr variance, and <Wr>as functions of Lk based on Metropolis Monte Carlo simulations of a 3000-bp plasmid. (A) The Wr probability density for ΔLk = −10 computed over 1·10⁷ trial moves is shown along with a Gaussian fit to this distribution. (B) Normalized Monte Carlo Wr distributions for topoisomers having ΔLk values between −20 and −10. Note the progressive narrowing of the distribution with increasing values of −ΔLk (C) Metropolis Monte Carlo Wr variance for supercoiled DNAs as a function of −ΔLk and comparison with the analysis of Levene and Crothers [48]. The solid line is a least-squares fit to the variance over the range −12 ≤ ΔLk ≤ 2. (D) Average Wr, <Wr>, as a function of −ΔLk determined by Metropolis Monte Carlo simulations. The solid curve is a linear fit to the data with slope 0.73.

Although the Wr variance deviates somewhat from that expected for a model in which Tw and Wr distributions are derived from those of topologically unconstrained molecules, the approximate model’s prediction for <Wr>agrees extremely well with that determined by Metropolis Monte Carlo simulations. As shown in Fig. 3D, Monte Carlo values of <Wr>are fitted well by a linear function of ΔLk with slope equal to 0.73, in close agreement with the value 0.75 estimated using Eq. (2). We therefore fitted topoisomer-mobility data as described in section 2.5 using values of <Wr>computed according to Eqs. (2) and Eqs. (3) without modification.

The applicability of the factorization approximation has recently been investigated in detail by Medalion et al. [64], who find that twist-writhe coupling leads to non-Gaussian behavior of the Wr distribution for chains near 900 bp. Their results also show that chains in the size range examined here do not show such deviations, further supporting the use of Eqs. (2) and Eqs. (4) in the case of 2.5-to 3.5-kb DNA molecules having significant levels of supercoiling.

We note that there is an additional related assumption about the Wr distribution in the Metropolis Monte Carlo simulation that is not addressed here. The model takes the global value of ΔTw for any configuration from the difference ΔTw = ΔLk–Wr, with Wr computed from the geometry of the DNA axis using a discrete approximation to the Gauss integral [51, 65]. Excess twist is assumed to equilibrate along the entire length of the chain, yielding a uniform twist density for the supercoiled duplex. This occurs only in the case where the chain is conformationally and elastically homogeneous; in cases where a chain contains intrinsic bends or other inhomogeneous properties, the local twist density depends on the preferred axial geometry of the chain and is not generally constant along the superhelical molecule's contour.

3.3. Helical and elasticity parameters deduced from gel-electrophoretic mobilities of topoisomers

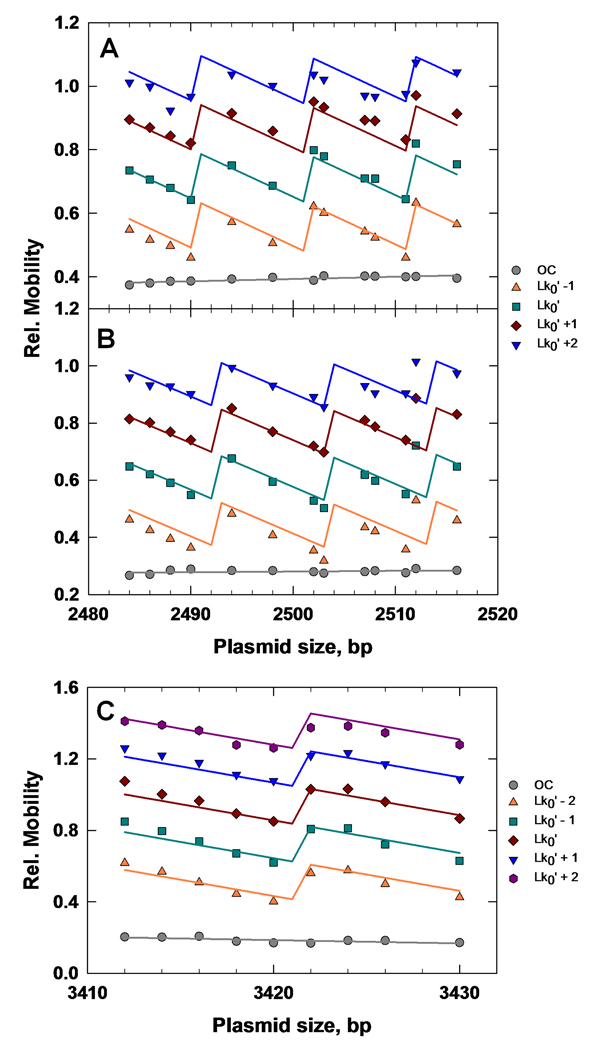
Results of optimized fitting of Eq. (1) to topoisomer mobilities are shown in Fig. 4 and gave values for α, h₀, P, C, and h_r listed in Table 3; these data sets contained either 52 or 45 data points. The mobility is a piece-wise linear function with discontinuities at transition points in the topoisomer distribution. These transition points correspond to values of the DNA length at which the center of the Lk distribution shifts by ΔLk = ±1, which is equal to h₀, by definition. Fitted values of the parameters are closely similar to those measured in solution [66] and remarkably independent of plasmid sequence and buffer system over the range explored here. We note that our mobility-fitting procedure does not depend on identifying the most-probable topoisomer in the data set because a topoisomer's mobility relative to oc DNA is an explicit function of ΔLk. One important test of the approach is therefore whether the most-probable topoisomer is correctly identified in all of the topoisomer ladders. This was confirmed by band-by-band comparisons of the observed topoisomer intensities with the rank-ordering of topoisomer probabilities generated by the fit.

Fig 4.

Fitting of topoisomer gel-mobility data according to Eq. (1). (A) pCS2.Xd mobilities in TAE buffer. (B) pCS2.Xd mobilities in TBE buffer. (C) pFS2.Xd in TBE buffer. Individual topoisomers are identified by their Lk values in legends located to the right of each figure. The value $L{k\prime }_0$ corresponds to the most-probable topoisomer for each distribution and is the nearest integral Lk value to Lk₀. Best-fit values of adjustable parameters are given in Table 3.

TABLE 3.

Best-fit helico-elastic parameters under different electrophoresis conditions. All experiments were carried out in 0.8% agarose gels containing 0.5 µg mL⁻¹ chloroquine phosphate. The quantity n_DP designates the number of data points associated with the fit. All other quantities are as defined in the text.

Plasmid Series	nDP	Buffer*	P, bp	C, 10−19 erg·cm	h0, bp· turn−1	hr	α
pCS2.Xd (2484 – 2516 bp)	52	TAE	155.2	3.007	10.44	0.9744	0.2117
″	″	TBE	144.8	2.564	10.49	0.9813	0.2315
pFS2.Xd (3412 – 3430 bp)	45	TBE	158.3	2.243	10.38	0.99	0.3053

^*TBE buffer: 50 mM Tris-borate, 1 mM Na2EDTA; pH 8.4

TAE buffer: 40 mM Tris-acetate, 1 mM Na2EDTA; pH 7.9

4. Conclusions

We have quantitatively investigated the gel-electrophoretic mobilities of homologous series of covalently closed plasmid DNAs in which DNA size varied systematically over more than one helical turn. Gel mobilities of plasmids having identical Lk values, but different levels of excess Wr, are surprisingly distinct and can be quantitatively accounted for by using the average Wr predicted for such molecules in solution. The range of DNA sizes covered in this study is typical of that used to topologically characterize interactions of DNA with proteins and other ligands. The capacity to predict Lk-dependent gel-electrophoretic properties of covalently closed DNAs from their behavior in solution stands apart from theories for the gel mobility as a function of other parameters such as DNA length [36, 67]. The functional dependence on these parameters is typically more complex and usually depends on additional variables such as the electric field and gel concentration.

Our results underscore the exquisite sensitivity of gel electrophoresis to conformational properties of superhelical DNA. Bands corresponding to the same topoisomer in molecules that are respectively 3412 and 3416 bp in size (a 1.2% length difference) differ in mobility by 15 to 20 percent. In contrast, the observed mobility difference for the corresponding nicked plasmids is zero within experimental uncertainty. Theoretically, the centers of the Wr distributions for this pair of molecules are separated by 0.28 turns under our gel-electrophoresis conditions and these Wr distributions would thus be expected to share substantial overlap. The fact that the mobility is dependent on |<Wr>| rather than the Wr distribution implies that conformational fluctuations are rapid compared with the characteristic time scale of molecular motions during electrophoresis.

We note that our model does not explain the saturation of mobility and loss of plasmid length dependence with increasing |ΔLk| (see Fig. 1C). This is because in Eq. (1) µ is directly proportional to |<Wr>|, which appears to increase without limit over the range of ΔLk studied here (Fig. 3D). The experimentally observed asymptotic trend in the mobility is evident for topoisomer numbers well within this range. An absence of saturation behavior may be due to failure of the Monte Carlo simulation to reproduce some important properties of superhelical DNA at high values of |ΔLk|. This seems unlikely since the Metropolis Monte Carlo method has successfully accounted for an extremely wide range of structural and thermodynamic parameters that have been experimentally determined for superhelical DNA [51, 52, 68]. A more likely explanation is that µ depends on additional terms in <Wr>, which become significant at higher levels of supercoiling. Relative to unknotted/unlinked superhelical DNAs, there is a much more gradual saturation of gel mobility with increasing numbers of irreducible crossings in nicked knotted or catenated DNA circles [47]. It is therefore plausible that the asymptotic mobility of supercoiled topoisomers is dominated by additional terms having a weak dependence on <Wr>and potentially stronger dependence on other conformational properties of highly plectonemically wound DNA. Despite this limitation, our findings are a basis for extending classical techniques such as the Gaussian-center method [37, 39] to sequence-dependent measurements of helical repeat and other properties of specific DNA sequences.